Evaluation and optimization of a novel cascade refrigeration system driven by waste heat

Direct discharge of waste heat from internal combustion engines (ICEs) is unfavorable for the efficient and clean fuel utilization. Here, a novel combined absorption-compression cascade refrigeration cycle is proposed to efficiently capture low-grade waste heat and supply cooling capacity for food freezing in vessels or refrigerated trucks. The intention of this work lies in: i) Comprehensively evaluating the performances of the proposed system; ii) Gaining the optimal operating conditions of the system. Aimed that, analysis models of energy, exergy, economy, and environment are set up to evaluate the sweeping performances. Further, multi-objective optimization is introduced to obtain the optimal operating parameters including evaporation and condensation temperature of the low-temperature stage, generation temperature and condensation temperature of the high-temperature stage, and cascade temperature differences. By applying multi-objective optimization, the coefficient of performance and exergy efficiency of the system are elevated from 1.283 to 1.547, and 0.222 to 0.246, respectively, the discharge amount of carbon dioxide are reduced from 71.40 to 59.57 tons year⁻¹, and annual total cost are decreased from 16,028 to 15,055 $ year⁻¹ compared to initial operating conditions.

1 Introduction

Waste heat exhausted from internal combustion engines occupy about 55%–65% of the released heat of fuel combustion, mainly taken away by engine coolant and exhaust gases and finally discharged to the atmosphere. Utilizing the waste heat to drive absorption refrigerator is an attractive research. The cascade refrigeration can widen temperature zone while ensuring its performance and is usually used on freezing occasions (Messineo, 2012). Among, absorption compression cascade refrigeration performs well due to its waste heat utilization. Many researchers have implemented amounts of studies on its performance evaluation, economy, and optimization of different cascade cycles.

Lee et al. (Lee et al., 2006) conducted a thermodynamic analysis on a cascade refrigeration cycle using CO₂ and NH₃ as refrigerants and determined the appropriate condensation temperature for optimizing the maximum COP and the minimum exergy destruction. Dopazo et al. (Alberto Dopazo et al., 2009) studied a NH₃/CO₂ cascade refrigeration system for low-temperature cooling and obtained the optimal low-temperature condensation temperature by exergy analysis and energy optimization. Bouaziz et al. (Bouaziz and Lounissi, 2015) analyzed the performance, efficiency, and exergy destruction of a novel two-stage absorption refrigeration system, and found that its performance was better than the conventional two-stage absorption refrigeration. Loonissi et al. (Lounissi and Bouaziz, 2017) analyzed an absorption/compression refrigeration cycle with the working fluids of R124-DMAC and found the refrigerator had the excellent operating conditions in the generating temperature range of 65°C–85°C. Gholamian et al. (Gholamian et al., 2018) proposed an advanced exergy analysis method to evaluate a cascade refrigeration cycle and provided references for system design, analysis, and evaluation of energy systems. Cimsit et al. (Cimsit, 2018) made a thermodynamic analysis on a double-effect absorption compression cascade refrigeration and suggested that the components with high exergy destruction rates should be paid more attentions. Agarwal et al. (Agarwal et al., 2020) investigated the influences of critical operating parameters of a triple-effect absorption cascade refrigeration on COP, exergy efficiency, exergy destruction rate, and exergy destruction ratio, and found that the system’s refrigeration coefficient and exergy efficiency were higher than the single effect and double effect absorption-compression cascade refrigeration system. Faruque et al. (Faruque et al., 2022) detailed a thermodynamic analysis of a triple effect cascade refrigeration system in ultra-low temperature application, and found that the highest COP and exergy efficiency was 0.5931% and 54.5% respectively when evaporating temperature was −100°C. Chi et al. (Chi et al., 2022) proposed a NH₃/CO₂ cascade refrigeration system with an ejector. They found that the COP and exergy efficiency of the system was about 5.4% and 4.8% higher than the conventional cascade refrigeration system.

How to evaluate a refrigeration system thoroughly? If only the thermodynamics criterion is considered, the system may be ideal but not friendly economically. If only the economic criterion is considered, the economic performance may be deficient. It may consume abundant energy or discharges amounts of pollutants to the environment. Therefore, a comprehensive evaluation criterion should be considered simultaneously, including thermodynamics, economic cost, and environmental influences. Aminyavari et al. (Aminyavari et al., 2014) modeled and analyzed an NH₃/CO₂ cascade refrigeration system from the perspectives of recycling, economy, and environment and obtained optimal design parameters of the system by applying a multi-objective genetic algorithm. Mosaffa et al. (Mosaffa et al., 2016) implemented economic and environmental analysis on an NH₃/CO₂ cascade refrigeration system with different flash tank intercoolers and obtained optimal operating conditions. Cui et al. (Cui et al., 2019) carried out energy, exergy, and economic analysis on a cascade absorption refrigeration for low-grade waste heat recovery and investigated the influence of various operating parameters on the thermodynamic properties and financial cost. Golbaten et al. (Golbaten Mofrad et al., 2020) compared and optimized the performance of a cascade refrigeration cycle based on the analytical methods of energy, exergy, economy, and environment and found that the system performance could be significantly improved by applying waste heat recovery. Kumar et al. (Kumar Singh et al., 2020) compared and analyzed the energy, exergy efficiency, and economy in a cascade refrigeration system and obtained the optimal working pairs. Mofrad et al. (Golbaten Mofrad et al., 2020) investigated a cascade refrigeration cycle with the heat recovery system. The optimization results revealed that applying the heat recovery cascade refrigeration cycle could increase 7.6% of COP and 12.5% of exergy efficiency. Yu et al. (Yu et al., 2020) analyzed a novel cascade absorption system driven by low-grade waste heat and optimized the system performance by implementing a multi-objective optimization method. Zhu et al. (Zhu et al., 2021) put forward a novel multi-target-temperature cascade system, and evaluated its optimum performances from the viewpoints of economics and thermodynamics and compared with other multi-temperature cascade systems. Mahmoudan et al. (Mahmoudan et al., 2021) evaluated a multi-level cascade system and conducted four different multi-objective optimization results. Hu et al. (Hu et al., 2022) analyzed a nested cascade refrigeration cycle with a heat recovery system and found it performed well in terms of energy, economy, and carbon emission. Gado et al. (Gado et al., 2022) assessed a cascade adsorption-compression refrigeration system by adopting renewable energy for cold storage applications based on power, exergy, exert economic, and environmental perspectives.

An absorption-compression combined refrigeration cycle activated by waste heat exhausted from an ICE to supply air-conditioning cooling capacity was proposed in our previous study (Jianbo et al., 2020). In another work, a novel cascade refrigeration with a compression refrigeration cycle cascaded in the process is proposed to provide low-temperature cooling capacity for food freezing in ships or refrigerated trucks (Han et al., 2021). Results showed that both cycles had excellent performance coefficients. However, the previous analysis is just based on thermodynamics and not comprehensive to assess its performances only from the view of thermodynamics. Here, a complete evaluation method is introduced to evaluate the performance of the proposed cascade system. Firstly, assessing models including energy, exergy, economy, and environment (4E) are developed, and the evaluation results are analyzed under different operating conditions. Secondly, the multi-objective optimization is introduced to simultaneously gain the maximum efficiency and the minimum annual total cost. The work can guide the optimal design of the cascade system.

2 Modeling

2.1 Descriptions of the cascade refrigeration

As shown in Figure 1, the cascade refrigeration system (ACR) is composed of a high-temperature stage combined absorption-compression refrigeration cycle (AR) and a low-temperature stage CO₂ subcritical compression refrigeration cycle (CR). The working fluids of R124 and DMAC are used as refrigerant and absorbent in the AR, and R744 is used as the refrigerant of CR. The work principle is described as follows.

FIGURE 1

FIGURE 1. The combined absorption-compression cascade refrigeration system.

In the high-temperature stage cycle, the high concentration solution is heated by exhaust gases from an engine in the high-pressure generator (HPG). In the HPG, the heat of exhaust is transferred to the high concentration solution. Meanwhile, the vapor is generated and the solution becomes intermediate concentration solution. Then the solution is further heated by the engine’s coolant in the low-pressure generator (LPG), and the solution becomes weak solution. The function of LPG is to effectively recover heat from the coolant of the internal combustion engine and produce some refrigerant vapor for low pressure compressor (LC). Refrigerant vapor from the LPG is cooled by the cooler to eliminate overheating and then is sucked and compressed by the low-pressure compressor (LC). The function of LC is to raise the pressure of the refrigerant vapor to the condensing pressure. The solution from the HPG participates in heat exchange in the high-temperature solution heat exchanger (HSHX), and the solution from the LPG participates in heat exchange in the low-temperature solution heat exchanger (LSHX). The functions of HSHX and LSHX are to enhance the heat utilization efficiency. Both the refrigerants generated in HPG and LHP enter the condenser, in which it is cooled to saturated or super-cooled liquid. After throttling, it enters the condensing evaporator, in which it is evaporated and supplies a low-temperature heat source for the CR cycle. Meanwhile, the low-temperature refrigerant is cooled to liquid in the condensing evaporator. Then, it enters the evaporator to produce a low-temperature cooling capacity. Finally, the vapor is sucked and compressed by the high-pressure compressor (HC).

2.2 Evaluation models

2.2.1 Energy model

Equilibrium equations of mass flow and the mass fraction are expressed as

${\dot{m}}_{\mathrm{S}}\left(1-X_{\mathrm{S}}\right)={\dot{m}}_{\mathrm{S}\mathrm{W}}\left(1-X_{\mathrm{S}\mathrm{W}}\right)(1)$

${\dot{m}}_{\mathrm{W}}\left(1-X_{\mathrm{W}}\right)={\dot{m}}_{\mathrm{S}\mathrm{W}}\left(X_{\mathrm{S}\mathrm{W}}\right)(2)$

The isentropic efficiency of the compressor is calculated by the following formula [3]

${\eta }_{\mathrm{s}}=1-\left(0.04\times r_{\mathrm{P}}\right)(3)$

The energy balance equation is

$\sum Q=\sum W+\sum {\dot{m}}_{\mathrm{o}\mathrm{u}\mathrm{t}}{h}_{\mathrm{o}\mathrm{u}\mathrm{t}}-\sum {\dot{m}}_{\mathrm{i}\mathrm{n}}{h}_{\mathrm{i}\mathrm{n}}(4)$

Equations (1–4) are extended in Table 1 for all the system components.

TABLE 1

TABLE 1. Energy equations of the cascade refrigeration system.

Coefficient of performance

$\mathrm{C}\mathrm{O}\mathrm{P}=Q_{\mathrm{E}\mathrm{C}}/\left(W_{\mathrm{H}\mathrm{C}}+W_{\mathrm{L}\mathrm{C}}+W_{\mathrm{P}\mathrm{u}\mathrm{m}\mathrm{p}}\right)(5)$

2.2.2 Exergy model

By applying the first and second laws of thermodynamics, the steady-state form of the equilibrium equation of the control volume can be expressed.

$\frac{d{\dot{E}}_{\mathrm{C}\mathrm{V}}}{dt}={\displaystyle \sum }_j{\dot{E}}_{\mathrm{j}}^{\mathrm{Q}}-{\dot{E}}^{\mathrm{W}}+{\displaystyle \sum }_i{\dot{E}}_{\mathrm{i}\mathrm{n}}-{\displaystyle \sum }_e{\dot{E}}_{\mathrm{o}\mathrm{u}\mathrm{t}}-{\dot{E}}_{\mathrm{D}}=0(6)$

Exergy consists of four elements: physical, chemical, potential, and dynamic terms. In the absence of electromagnetic, electric, nuclear, and surface tension effects, it is assumed that variation of potential energy and kinetic energy can be neglected (Bejan et al., 1995)

$\dot{E}={\dot{E}}^{\mathrm{P}\mathrm{H}}+{\dot{E}}^{\mathrm{C}\mathrm{H}}(7)$

Chemical exergy consists of reaction exergy, diffusion exergy, and mixing exergy. There is no chemical reaction in the system, so the reaction exergy is discharged. No mass and momentum exchange between the working mediums in the system and the outside exist, so diffusion and mixing exergy are discharged. So the chemical exergy is ignored in the system. Therefore, only physics exergy is considered in this work. The following formula determines it.

${\dot{E}}^{\mathrm{P}\mathrm{H}}=\dot{m}\left[\left(h-h_0\right)-T_0\left(s-s_0\right)\right](8)$

If a working fluid is liquid, it can be defined as a function of temperature and heat capacity (Cengel and Boles, 2005)

$s_{\mathrm{A}}-s_{\mathrm{B}}=C_{\mathrm{p}}\ln \frac{T_{\mathrm{A}}}{T_{\mathrm{B}}}(9)$

According to the exergy balance Equations (6–9), the exergy destruction formulas for all components are listed in Table 2.

$q_{\mathrm{v}}=\frac{Q}{{\rho }_{\mathrm{a}}{C}_{\mathrm{p}\mathrm{a}}\left(t_{\mathrm{a}2}-t_{\mathrm{a}1}\right)}(10)$

TABLE 2

TABLE 2. Exergy destruction equations.

Where the expression of ' $t_{a2}-t_{a1}$' is the temperature difference of outside air.

The input power of the fan motor is expressed as

$W_{\mathrm{f}\mathrm{a}\mathrm{n}}=\frac{q_{\mathrm{v}}\left(\Delta P^{\prime }+\Delta P^{″}\right)}{{\eta }_{\mathrm{f}\mathrm{a}\mathrm{n}}}(11)$

The dynamic pressure and static pressure can be expressed as (Hesselgreaves, 2001)

$\Delta P^{\prime }=\frac{{\rho }_{\mathrm{a}}{w_{\mathrm{y}}}^2}{2}(12)$

$\Delta P^{″}=0.108\frac{b}{d_{\mathrm{e}}}{\left({\rho }_{\mathrm{a}}{w}_{\mathrm{y}}\right)}^{1.7}(13)$

Entrance exergy into the system can be expressed as

${\dot{E}}_{\mathrm{i}\mathrm{n}}=W_{\mathrm{H}\mathrm{C}}+W_{\mathrm{L}\mathrm{C}}+W_{\mathrm{P}\mathrm{u}\mathrm{m}\mathrm{p}}+W_{\mathrm{f}\mathrm{a}\mathrm{n},\mathrm{C}\mathrm{A}}+W_{\mathrm{f}\mathrm{a}\mathrm{n},\mathrm{E}\mathrm{C}}+W_{\mathrm{f}\mathrm{a}\mathrm{n},\mathrm{A}\mathrm{b}\mathrm{s}}+{\dot{E}}_{\mathrm{E}\mathrm{x}\mathrm{h}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{t},\mathrm{H}\mathrm{P}\mathrm{G}}+{\dot{E}}_{\mathrm{C}\mathrm{o}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t},\mathrm{H}\mathrm{P}\mathrm{G}}(14)$

Exit exergy of the system can be expressed as

${\dot{E}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=Q_{\mathrm{E}\mathrm{C}}\left(1-\frac{t_0}{t_{\mathrm{C}\mathrm{L}}}\right)(15)$

Therefore, the total exergy destruction can be expressed as (TJJTEMoTPA, 1985)

${\dot{E}}_{\mathrm{D},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\dot{E}}_{\mathrm{i}\mathrm{n}}-{\dot{E}}_{\mathrm{o}\mathrm{u}\mathrm{t}}={\displaystyle \sum }_k{\dot{E}}_{\mathrm{D},\mathrm{k}}(16)$

The energy efficiency of the system can be determined as (TJJTEMoTPA, 1985)

${\eta }_{\mathrm{E}\mathrm{x}}=\frac{{\dot{E}}_{\mathrm{o}\mathrm{u}\mathrm{t}}}{{\dot{E}}_{\mathrm{i}\mathrm{n}}}=1-\frac{{\dot{E}}_{\mathrm{D},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{{\dot{E}}_{\mathrm{i}\mathrm{n}}}(17)$

2.2.3 Economy model

Aimed at exploring the influences of operation parameters on the economic performance of the cascade system, it is necessary to implement the economic analysis. The capital cost and operating cost are considered in the total cost. Besides, the environmental cost of carbon dioxide emissions is also included in the total cost. Therefore, the total cost of the cascade system (Ċ_total) includes the capital cost $({\displaystyle \sum }_k{\dot{Z}}_{\mathrm{k}})$, operating cost (Ċ_op), and environmental cost of carbon dioxide emission (Ċ_env), which can be expressed as

${\dot{C}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\displaystyle \sum }_k{\dot{Z}}_{\mathrm{k}}+{\dot{C}}_{\mathrm{o}\mathrm{p}}+{\dot{C}}_{\mathrm{e}\mathrm{n}\mathrm{v}}(18)$

2.2.3.1 Capital cost

The heat exchangers occupy the principal cost of the system. The heat transfer area (A) of all heat exchangers involved in the system can be calculated as follow.

$A=\frac{Q}{U\times \Delta t}(19)$

Among them, Δt are the temperature differences of working fluids. U is the overall heat transfer coefficient, which is mainly decided by heat transfer coefficients inside the tube (${\dot{\alpha }}_{\mathrm{i}}$) and heat transfer coefficient outside the tube (${\dot{\alpha }}_{\mathrm{o}}$).

${\alpha }_{\mathrm{i}}=\frac{{\lambda }_{\mathrm{i}}}{d_{\mathrm{i}}}Nu=0.023\frac{{\lambda }_{\mathrm{i}}}{d_{\mathrm{i}}}R{e}^{0.8}P{r}^{0.3}(20)$

${\alpha }_{\mathrm{o}}=0.52\frac{{\lambda }_0}{d_0}R{e_{\mathrm{f}}}^{0.5}P{r_{\mathrm{f}}}^{0.36}{\left(P{r}_{\mathrm{f}}/P{r}_{\mathrm{w}}\right)}^{0.25}(21)$

The overall heat transfer coefficient of all heat exchangers is listed in Table 3 (Cooper and JDJhet, 1983; Shah and Sekulic, 2002; Bejan and Kraus, 2003).

TABLE 3

TABLE 3. Overall heat transfer coefficient of the cascade refrigeration system.

Compared with other main components of the system, the investment cost of valves, refrigerants, and connecting pipes can be ignored. The capital costs of heat exchangers are listed in Table 4.

TABLE 4

TABLE 4. Capital costs of the cascade refrigeration system.

The corresponding cost is obtained by using the capital recovery factor (CRF) [34]

$CRF=\frac{i{\left(1+i\right)}^N}{{\left(1+i\right)}^N-1}(22)$

Where, CRF is a function of the annual interest rate (i) and N is the reference years (i.e., Service life).

Conversion of capital cost can be expressed as

${\dot{Z}}_{\mathrm{k}}=CRF\times Z_{\mathrm{k}}\times \varphi (23)$

$\forall \mathrm{k}\in EQS\cap \left\{\mathrm{C}\mathrm{A},\mathrm{E}\mathrm{C},\mathrm{c}\mathrm{a}\mathrm{s},\mathrm{H}\mathrm{P}\mathrm{G},\mathrm{H}\mathrm{S}\mathrm{H}\mathrm{X},\mathrm{L}\mathrm{P}\mathrm{G},\mathrm{L}\mathrm{S}\mathrm{H}\mathrm{X},\mathrm{A}\mathrm{b}\mathrm{s},\mathrm{C}\mathrm{o}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{r},\mathrm{H}\mathrm{C},\mathrm{L}\mathrm{C},\mathrm{P}\mathrm{u}\mathrm{m}\mathrm{p}\right\}$

2.2.3.2 Operating cost

The operating cost includes the cost of the fuel and the electrical energy input of the compressor and solution pump, which can be expressed as

${\dot{C}}_{\mathrm{o}\mathrm{p}}=top\left({\dot{C}}_{\mathrm{i}}^{\mathrm{f}}{\dot{B}}_{\mathrm{i}}+{\dot{C}}_{\mathrm{i}}^{\mathrm{e}\mathrm{l}}{\dot{W}}_{\mathrm{i}}\right)(24)$

2.2.3.3 Environmental cost

Carbon dioxide emissions are considered to be an essential factor in the work, and the corresponding environmental cost can be expressed as

${\dot{C}}_{\mathrm{e}\mathrm{n}\mathrm{v}}=\frac{m_{{\mathrm{C}\mathrm{O}}_2}}{1000}\times {\dot{C}}_{{\mathrm{C}\mathrm{O}}_2}(25)$

Where, $m_{{\mathrm{C}\mathrm{O}}_2}$ is obtained by the following formula

$m_{{\mathrm{C}\mathrm{O}}_2}={\mu }_{{\mathrm{C}\mathrm{O}}_2}{W}_{\mathrm{t}}top(26)$

2.3 Simulation algorithm

Figure 2 shows the algorithm simulation model of the cascade refrigeration system. As shown in the figure, models of energy, exergy, and economy are all involved. The evaluation indexes, including COP, exergy efficiency (ƞ_Ex), and annual total cost (Ċ_total) of the cascade refrigeration system, are taken into consideration in the model.

FIGURE 2

FIGURE 2. The simulation algorithm of combined absorption-compression cascade refrigeration system.

3 Results and discussions

3.1 Model verification

To validate the constructed models of the cascade refrigeration system, the basic performance parameters of the system, including the exergy destruction rate of all components, COP, the exergy efficiency, and annual total cost, are compared with the results by Deymi (Deymi-Dashtebayaz et al., 2021). The refrigerating capacity, ambient temperature, condensation temperature of the high-temperature stage, evaporation temperature of low-temperature phase and cascade temperature difference are 10 kW, 25°C, 40°C, −50°C, and 5°C, respectively.

As shown in Figure 3A, the variation trend of COP is similar, and the COP in this work is lower than that of Deymi under the same operating conditions. As shown in Figure 3B, the variation trend of exergy efficiency is similar, and the exergy efficiency of the cascade system is higher than that of Deymi. This is due to the fact that the waste heat of an internal combustion engine is rationally utilized in this work. As shown in Figure 3C, the annual total cost first declines and then increases with the rise of condensation temperature of the low-temperature stage. The total annual cost in this study is higher than that of Deymi due to more components in the proposed cycle. As shown, good agreements within an acceptable error between modeling results obtained for COP, the exergy efficiency, and annual total cost in this study and those presented by Deymi (Deymi-Dashtebayaz et al., 2021).

FIGURE 3

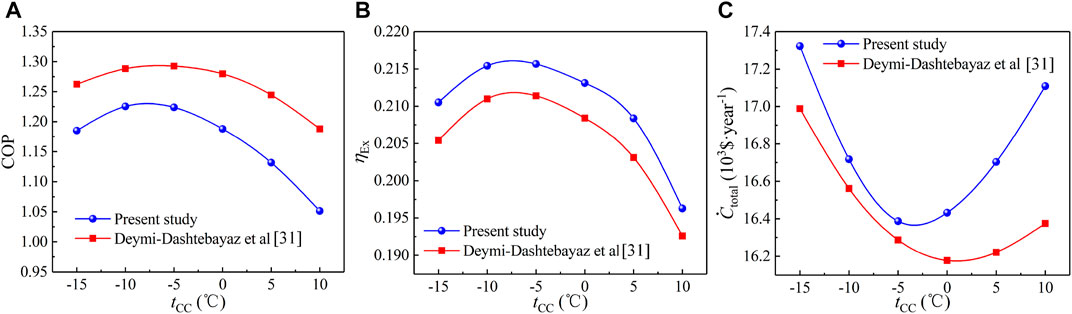
FIGURE 3. Comparison between modeling results in present study and computational results of Deymi [36]

3.2 Comprehensive analysis and discussion

Based on the above models, the overall performances of the cascade cycle are analyzed and discussed by taking a combined absorption-compression cascade refrigeration system as a case using FORTRAN software. Essential parameters of the cascade system are listed in Table 5.

TABLE 5

TABLE 5. Input values of the constant modeling parameters.

Grassmann diagram of exergy balance for the cascade refrigeration system is shown in Figure 4. As shown, the entrance exergy, the exit exergy, and the total exergy destruction are 21.353 kW, 4.605 kW, and 16.748 kW, respectively, when the refrigerating capacity, the ambient temperature, the condensation temperature of the high-temperature stage, the evaporation temperature of the low-temperature phase, cold refrigerated space temperature and cascade temperature difference are 15 kW, 25°C, 40°C, −50°C, −45°C, and 5°C, respectively.

FIGURE 4

FIGURE 4. Grassmann diagram for exergy balance of the cascade refrigeration.

The system’s performance can be well observed by investigating the total exergy destruction of the proposed cycle. Under operating conditions of 15 kW refrigerating capacity and 45°Cof t_Abs, Variations of exergy destruction with operating temperatures are depicted in Figure 5.

FIGURE 5

FIGURE 5. Variations of exergy destruction.

Figure 5A shows that the exergy destruction of the cascade system declines with t_EC increasing from −55°C to −45°C. The power consumption of the fan and compressor decreases with the rise of t_EC, which means a reduction in input exergy. Therefore, a higher t_EC is beneficial for the reduction of total exergy destruction. As shown in Figure 5B, with the increase of t_CC, the total exergy destruction first decreases and then elevates, with a minimum value of 16.697 kW when t_CC is about −7.4°C. It can be concluded that an existing preferable t_CC is to minimize the total exergy destruction. It can be found in Figures 5C,D that the varying tendency of total exergy destruction elevates with the increase of t_CA and Δt_cas. The reason is that the rise of both t_CA and Δt_cas can cause a surge in power consumption, which implies an increase of input exergy. Therefore, the lower t_CA and Δt_cas can promote the reduction of total exergy destruction.

Exergy efficiency (η_Ex) and coefficient of performance (COP) are crucial indexes in evaluating the cascade system. Usually, a high COP implies an excellent performance for a refrigeration system. However, the energy balance and conversion efficiency could not reflect the utilization degree of energy. So, it is necessary to analyze COP and η_Ex simultaneously. Figure 6 illustrates variations of COP and η_Ex with operating parameters.

FIGURE 6

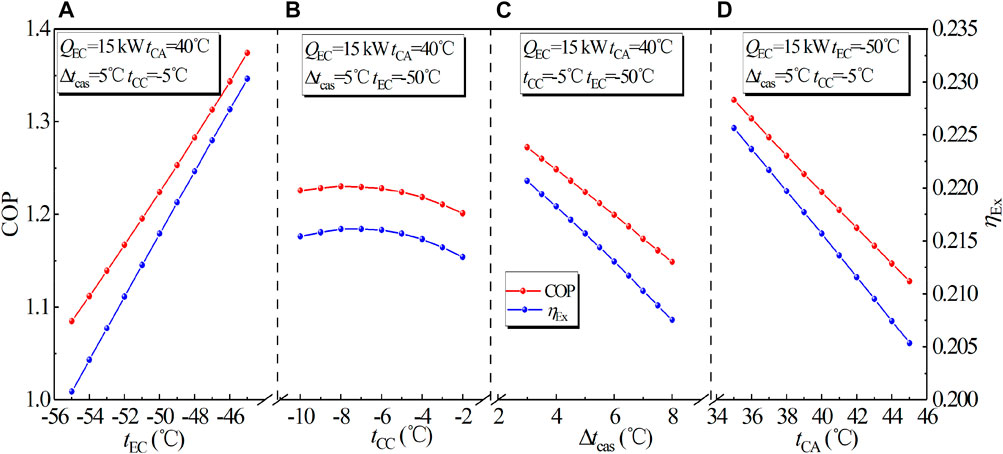
FIGURE 6. Variation of COP and exergy efficiency with CO₂ evaporation temperature and CO₂ condensation temperature, cascade temperature difference and R124 condensation temperature.

As shown in Figure 6A, both COP and ƞ_Ex increase with the rises of t_EC under the same working conditions. COP elevates from 1.085 to 1.374, with an increment of 0.289, and ƞ_Ex also elevates from 0.20 to 0.23. The total power consumption declines with t_EC increasing, the input exergy decreases, and the output exergy remains unchanged. Both factors cause the increment of COP and ƞ_Ex. Hence, a high t_EC is recommended from viewpoints of energy and exergy. As shown in Figure 6B, both COP and ƞ_Ex first rises and then decline with the increase of t_CC. When t_CC is −7.4°C, COP reaches a maximum value of 1.231. When t_CC is −6.7°C, ƞ_Ex has a maximum value of 0.216, which indicates that there is a preferable ƞ_Ex to maximize the efficiency of the cascade system. As depicted in Figures 6C,D that both COP and ƞ_Ex show downward tendencies with the rise of the t_CA and Δt_cas. The total power consumption of the system increases with the rise of the both temperatures, which causes the increase of input exergy and the decline of ƞ_Ex. Therefore, the low t_CA and Δt_cas can enhance the performance of the system.

Based on the above analysis, the crucial parameters affecting the system are acquired based on the first and second laws of thermodynamics. Moreover, these parameters also affect the total cost. Therefore, the total cost of the cascade system, including capital cost, maintenance cost, and environmental cost of carbon dioxide emission also need investigation. Figure 7 shows the variation of annual total cost with the crucial parameters.

FIGURE 7

FIGURE 7. Variations of annual total cost under different thermal parameters.

As shown in Figure 7A, annual total cost gradually declines with t_EC increasing from −50°C to −40°C. However the operating and environmental emission costs decline with the increase of t_EC. The decline of both is more obvious than the increase of capital cost. Therefore the annual total cost tends to gradual decline. As shown in Figure 7B, with t_CC increasing from −10°C to −2°C, annual total cost first decreases and then increases, and there is a minimum value of 16,511.7 $ year⁻¹ when t_CC is −6.0°C. As shown in Figure 7C, with the increase of t_CA from 35°C to 45°C, the annual total cost first reduces and then increases with the rise of both temperatures, and there is a minimum value of 16,413.9 $ year⁻¹ when t_CA is 37.7°C. Under the same working conditions, Figure 7D shows the annual total cost elevates from 16,198.6 $ year⁻¹ to 17,290.6 $ year⁻¹, with an increment of 1,092.0 $ year⁻¹, when Δt_cas increases from 3°C to 8°C. It can be concluded that an appropriate reduction of Δt_cas is conducive to reduce the cost of the system.

The refrigeration system in this work is a combined absorption-compression cascade refrigeration system. High-pressure generator and low-pressure generator can ensure the most efficient use of the waste heat exhaust gases and jacket water from internal combustion engine of vehicles or ships and reduce energy consumption. Therefore, generating temperature plays a vital role on the performances in the cascade system.

Figure 8 shows the impact of the temperature of the high-pressure generator and low-pressure generator on the system thermo-economic performance under the same evaporator temperature, condenser temperature, cascade condenser temperature, absorber temperature and cascade condenser temperature differences. As shown in Figure 8A, the exergy destruction of the system rises, and exergy efficiency and performance coefficient are reduced with the temperature rise of high pressure generator (t₁). As t₁ increases from 120°C to 140°C, the annual total cost decreases rapidly at first, and then shows a trend of slow increase. The effect of the temperature of the low-pressure generator (t₄) on the cascade system thermo-economic performance is not quite the same as that of t₁. With t₄ rising from 76°C to 86°C (Figure 8B), the exergy destruction of the cascade system is elevated, while exergy efficiency and performance coefficient show the opposite trend. With the rise of t₄, the annual total cost declines first and then rises. There is a minimum annual total cost. When t₄ is 84°C, the annual total cost reaches a minimum value of 15,207.9 $ year⁻¹.

FIGURE 8

FIGURE 8. Variations of thermo-economic performances with generator temperatures.

3.3 Multi-objective optimization

The optimal operating condition of the cascade system is worth studying to achieve the simultaneous optimization of performance index and economic index. Therefore the multi-objective optimization on the performance and economy for the cascade system is implemented in this section.

3.3.1 Optimization method and procedures

Three indexes including COP, η_Ex, and Ċ_total are the primary evaluation indices for the system. COP and η_Ex are only related to operating temperatures, and Ċ_total is related to working conditions and device scale. The high COP is the basis of a high-efficiency system when designing a refrigeration system. Under this case, the developed system may produce low exergy destruction. However, low exergy destruction usually implies a high investment cost. Therefore, the multi-objective optimization method is used to achieve good thermodynamics and economic performance simultaneously (Nasruddin et al., 2016). When η_Ex reaches the maximum, Ċ_total should get the minimum. To express the optimization model more distinctly, the optimization method is implemented using the expression of (1-η_Ex) replacing η_Ex. The optimization model is transformed into minimization (1-η_Ex) and Ċ_total. The multi-objective optimization model can be expressed as follows

$\min F\left(x\right)=\left[f_1\left(x\right),f_2\left(x\right)\right](27)$

$g\left(x\right)\le 0;y\left(x\right)=0;x_{\mathrm{l}}<x_{\mathrm{u}}(28)$

Where f₁(x) and f₂(x) are the objective functions to be optimized (In this work, they represent (1-η_Ex) and Ċ_total respectively), x is the decision variable to be iterated to find the optimal objective function, and g(x) and y(x) are the inequality and equality constraints of the optimization model, where x_l and x_u are the iterative limits of minimizing the input values (decision variables) of the objective function.

Four design variables affecting the performances of the system are considered, which is evaporation temperature (t_EC) and condensation temperature of the low-temperature stage (t_CC), condensation temperature of the high-temperature phase (t_CA), and heat transfer temperature difference (Δt_cas). According to the working conditions of the cycle, the range of each variable is restricted as follows

$-{56}^{\circ }\mathrm{C}\le t_{\mathrm{E}\mathrm{C}}\le -{45}^{\circ }\mathrm{C}(29)$

$-{10}^{\circ }\mathrm{C}\le t_{\mathrm{C}\mathrm{C}}\le -2^{\circ }\mathrm{C}(30)$

${35}^{\circ }\mathrm{C}\le t_{\mathrm{C}\mathrm{A}}\le {45}^{\circ }\mathrm{C}(31)$

$3^{\circ }\mathrm{C}\le \Delta t_{\mathrm{c}\mathrm{a}\mathrm{s}}\le {10}^{\circ }\mathrm{C}(32)$

The objective function is calculated based on the genetic algorithm simulation model of multi-objective optimization. The specific calculation process is shown in Figure 9.

FIGURE 9

FIGURE 9. Schematic diagram of the multi-objective optimization.

3.3.2 Optimization analysis

In this work, MATLAB software is used to solve the multi-objective optimization analysis model. Figure 10 shows correlations between the annual total cost (Ċ_total) and exergy efficiency (η_Ex) under the conditions of 15 kW refrigeration capacity and 45°C of t_CA. It can be found that (1-η_Ex) becomes smaller and the annual total cost declines with the rise of Ċ_total. It is difficult to meet the optimal thermodynamics performance and economy simultaneously. It also can be found that a higher η_Ex implies a higher Ċ_total. In this research, the vertical line of the Pareto optimal Frontier is chosen, and the intersection of the two is the best point of multi-objective optimization.

FIGURE 10

FIGURE 10. Pareto optimal Frontier from multi-objective optimization.

The linear weighted sum method is a Multi Criteria Decision Making (MCDM) technique, which assigns weight coefficients to each object according to its importance and then optimizes its linear combination to solve multi-objective programming problems. Linear weighted sum method has been employed for choosing the best optimum operating condition and parameter among the Pareto Front in this paper.

Here are the steps of that MCDM.

For the Pareto Front data, the best optimum operating condition and parameter are selected and transformed into the optimal solution of the following functions.

${\min }_{\mathrm{x}}\in {\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{m}}}{\omega }_{\mathrm{k}}{f}_{\mathrm{k}}\left(x\right)(33)$

Where k = 2, m = 2, f₁(x) is (1-η_Ex) and f₂(x) is the annual total cost (Ċ_total), ω_k(x) is the weight coefficient.

${\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{m}}}{\omega }_{\mathrm{k}}=1(34)$

ω₁(x) is the weight coefficient of (1-η_Ex), and its value is 0.5, ω₂(x) is the weight coefficient of Ċ_total, 0.5.

The values of decision variables under different optimization mode are listed in Table 6. The power consumption, emission of CO₂, and three annual costs are shown in Figure 11 under the conditions of these decision variables in Table 6.

TABLE 6

TABLE 6. Decision variables.

FIGURE 11

FIGURE 11. Comparison of power, CO₂ emissions and three kinds of annual costs.

As shown in Figure 11A, the power of the pump and compressor are different for different optimization. HC has a minimum capacity of 4.91 kW when thermodynamic optimization is performed for the cascade system. Compared with the base case, the power of HC is reduced by 1.586 kW. When multi-objective optimization is performed, the power of LC and pump reach a minimum of 2.820 kW and 1.461 kW respectively, with respective decrements of 0.589 kW and 0.329 kW compared with the base case.

Figure 11B shows the power consumption of fans under different optimizations. These fans are used for heat dissipations of the condenser, the evaporator, and the absorber. The power consumption of evaporator fan for all the optimization methods is 0.109 kW. The minimum power consumption of the absorber fan is 0.250 kW in the multi-objective optimization, which is reduced by 0.022 kW compared with the base case. The emission of CO₂ strongly influences the environmental cost. As shown in Figure 11C, it can be found that the minimum emission of CO₂ under thermodynamic optimization is 58,462.7 kg, and it is 61,377.5 kg when the economics optimization is implemented. As shown in Figure 11D, the equipment cost reaches a minimum value of 4,534 $ year⁻¹ when economic optimization is implemented, and the operating cost reaches a minimum value of 4,708 $ year⁻¹ when thermodynamic optimization is implemented. Compared with the base case, the environmental cost is reduced from 6,426 $ year⁻¹ to 5,361 $ year⁻¹, with a maximum reduction of 1,164 $ year⁻¹ when thermodynamic optimization is carried out.

It can be found in Figure 12A that the exergy destruction reaches a minimum of 13.954 kW under the condition of thermodynamic optimization and is reduced by 2.227 kW compared with the base case. It means that the performance improvement of system is also significant. The maximum exergy destruction under economic optimization conditions is 14.456 kW, decreasing to 14.144 kW under multi-objective optimization conditions. It can be found in Figures 12B,C that COP and exergy efficiency of the system can reach 1.580 and 0.248 respectively, based on thermodynamic optimization, the thermodynamic performance is the best at this time. Compared with the base case, COP and exergy efficiency are raised by 0.297 and 0.026 respectively, and the thermodynamic performance of the system was significantly improved. It can be found in Figure 12D that the lowest annual total cost is reduced from 16,027.5 to 14,946.7 $ year⁻¹ when the economy is optimized. As shown in Figures 12B,D, under the multi-objective optimization, the COP of the system can reach 1.547, the exergy efficiency can reach 0.246, and the annual total cost can drop to 15,055.2 $ year⁻¹, balancing the thermodynamic and economic objectives. The combined cascade refrigeration system has the best operating conditions in this optimization case.

FIGURE 12

FIGURE 12. Comparison of Exergy destruction, COP, exergy efficiency and annual total cost.

4 Conclusion

The overall performances of absorption-compression cascade refrigeration activated by the waste heat from ICE are evaluated from the viewpoints of energy, exergy, economy, and environment in this work. Firstly, the models of COP and exergy efficiency are obtained and validated by the previous study. Secondly, the exergy and economy analysis are implemented. Finally, the multi-objective optimization is introduced to acquire optimal operating parameters. Some conclusions can be drawn as follows.

1) Energy and exergy analysis indicate that the exergy destruction of the cascade refrigeration system has a minimum value of 16.697 kW when t_CC is about −7.4°C. Preferable COP of 1.231 and ƞ_Ex of 0.216 can contribute to the high efficiency of the cascade system.

2) Economy and environmental analysis indicate that the annual total cost of the cascade system first declines and then rises with the increase of t_CC and t_CA. There is a minimum value of 16,511.7 $ year⁻¹ when t_CC is −6.0°C, and there is a minimum value of 16,413.9 $ year⁻¹ when t_CA is 37.7°C. By employing the multi-objective optimization, the COP, exergy efficiency and the annual total cost of the system can reach 1.547, 0.246, and 15,055.2 $ year⁻¹ respectively.

3) The thermodynamic and economic indexes under the multi-objective optimization are more excellent than that of the single-objective optimization.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WZ: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; HZ: Data Curation, Writing—Original Draft; ZX: Visualization, Investigation; DS: Resources, Supervision; CS: Software, Validation XZ: Writing—Review and Editing JL (Corresponding Author):Funding Acquisition, Resources, Supervision, Writing—Review and Editing.

Funding

This research work is financially supported by the Natural Science Foundation of Shandong Province (No.ZR2020QE208), and National Natural Science Foundation of China (No. 52276205).

Conflict of interest

Authors WZ, HZ, ZX, DS, CS, and XZ were employed by the company Shengli Oilfield Branch of Sinopec.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agarwal, S., Arora, A., and Arora, B. B. (2020). Energy and exergy analysis of vapor compression–triple effect absorption cascade refrigeration system. Eng. Sci. Technol. Int. J. 23 (3), 625–641. doi:10.1016/j.jestch.2019.08.001

CrossRef Full Text | Google Scholar

Alberto Dopazo, J., Fernández-Seara, J., Sieres, J., and Uhia, F. J. (2009). Theoretical analysis of a CO₂–NH₃ cascade refrigeration system for cooling applications at low temperatures. Appl. Therm. Eng. 29 (8-9), 1577–1583. doi:10.1016/j.applthermaleng.2008.07.006

CrossRef Full Text | Google Scholar

Aminyavari, M., Najafi, B., Shirazi, A., and Rinaldi, F. (2014). Exergetic, economic and environmental (3E) analyses, and multi-objective optimization of a CO₂/NH₃ cascade refrigeration system. Appl. Therm. Eng. 65 (1-2), 42–50. doi:10.1016/j.applthermaleng.2013.12.075

CrossRef Full Text | Google Scholar

Baghernejad, A., (2013). Thermoeconomic methodology for analysis and optimization of a hybrid solar thermal power plant. Int. J. Green Energy 10 (6), 588–609. doi:10.1080/15435075.2012.706672

CrossRef Full Text | Google Scholar

Bejan, A., and Kraus, A. D. J. W. (2003). Heat transfer handbook. New Jersey, United States: John Wiley and Sons.

Google Scholar

Bejan, A., Tsatsaronis, G., and Moran, M. J. (1995). Thermal design and optimization. New Jersey, United States: John Wiley and Sons.

Google Scholar

Bouaziz, N., and Lounissi, D. (2015). Energy and exergy investigation of a novel double effect hybrid absorption refrigeration system for solar cooling. Int. J. Hydrogen Energy 40 (39), 13849–13856. doi:10.1016/j.ijhydene.2015.05.066

CrossRef Full Text | Google Scholar

Cengel, Y. A., and Boles, M. A. (2005). Thermodynamics: An engineering approach. Europe: McGraw-Hill2009.

Google Scholar

Chi, W., Yang, Q., Chen, X., Liu, G., Zhao, Y., and Li, L. (2022). Performance evaluation of NH₃/CO₂ cascade refrigeration system with ejector subcooling for low-temperature cycle. Int. J. Refrig. 136, 162–171. doi:10.1016/j.ijrefrig.2022.01.005

CrossRef Full Text | Google Scholar

Cimsit, C. (2018). Thermodynamic performance analysis of the double effect absorption-vapour compression cascade refrigeration cycle. J. Therm. Sci. Technol. 13 (1), JTST0007–13. doi:10.1299/jtst.2018jtst0007

CrossRef Full Text | Google Scholar

Cooper, A., and Jdjhet, U. (1983). Heat exchanger design handbook. Boca Raton: CRC Press.

Google Scholar

Cui, P., Yu, M., Liu, Z., Zhu, Z., and Yang, S. (2019). Energy, exergy, and economic (3E) analyses and multi-objective optimization of a cascade absorption refrigeration system for low-grade waste heat recovery. Energy Convers. Manag. 184 (15), 249–261. doi:10.1016/j.enconman.2019.01.047

CrossRef Full Text | Google Scholar

Deymi-Dashtebayaz, M., Sulin, A., Ryabova, T., Sankina, I., Farahnak, M., and Nazeri, R. (2021). Energy, exergoeconomic and environmental optimization of a cascade refrigeration system using different low GWP refrigerants. J. Environ. Chem. Eng. 9 (6), 106473. doi:10.1016/j.jece.2021.106473

CrossRef Full Text | Google Scholar

Faruque, M. W., Nabil, M. H., Uddin, M. R., Monjurul Ehsan, M., and Salehin, S. (2022). Thermodynamic assessment of a triple cascade refrigeration system utilizing hydrocarbon refrigerants for ultra-low temperature applications. Energy Convers. Manag. 14, 100207. doi:10.1016/j.ecmx.2022.100207

CrossRef Full Text | Google Scholar

Gado, M. G., Ookawara, S., Nada, S., and Hassan, H. (2022). Renewable energy-based cascade adsorption-compression refrigeration system: Energy, exergy, exergoeconomic and enviroeconomic perspectives. Energy 253, 124127. doi:10.1016/j.energy.2022.124127

CrossRef Full Text | Google Scholar

Gebreslassie, B. H., Groll, E., and Garimella, S. V. (2012). Multi-objective optimization of sustainable single-effect water/Lithium Bromide absorption cycle. Renew. Energy 46, 100–110. doi:10.1016/j.renene.2012.03.023

CrossRef Full Text | Google Scholar

Gebreslassie, B. H., Guillén-Gosálbez, G., Jiménez, L., and Boer, D. (2009). Design of environmentally conscious absorption cooling systems via multi-objective optimization and life cycle assessment. Appl. Energy 86 (9), 1712–1722. doi:10.1016/j.apenergy.2008.11.019

CrossRef Full Text | Google Scholar

Gholamian, E., Hanafizadeh, P., and Ahmadi, P. (2018). Advanced exergy analysis of a carbon dioxide ammonia cascade refrigeration system. Appl. Therm. Eng. 137 (5), 689–699. doi:10.1016/j.applthermaleng.2018.03.055

CrossRef Full Text | Google Scholar

Golbaten Mofrad, K., Zandi, S., Salehi, G., and Khoshgoftar Manesh, M. H. (2020). 4E analyses and multi-objective optimization of cascade refrigeration cycles with heat recovery system. Therm. Sci. Eng. Prog. 19, 100613–100627. doi:10.1016/j.tsep.2020.100613

CrossRef Full Text | Google Scholar

Han, X., Li, J., Kong, X., Sun, T., Zhang, C., and Yin, L. (2021). Thermodynamic performance study on a novel absorption-compression cascade refrigeration activated by an internal combustion engine. Int. J. Energy Res. 45 (6), 9595–9612. doi:10.1002/er.6484

CrossRef Full Text | Google Scholar

Hesselgreaves, J. E. J. M-H. B. C., Inc. Compact heat exchangers 2001.

Google Scholar

Hu, R., Liu, X., Zhang, X., and Yang, L. (2022). Analysis of energy, economy, and carbon emission of nested cascade refrigeration cycle with heat recovery system. Int. J. Refrig. 136, 94–102. doi:10.1016/j.ijrefrig.2022.01.016

CrossRef Full Text | Google Scholar

Jianbo, L., Kai, L., Xiaolong, H., Chen, Z., Fulin, C., and Xiangqiang, K. (2020). A novel absorption–compression combined refrigeration cycle activated by engine waste heat. Energy Convers. Manag. 205 (1), 112420. doi:10.1016/j.enconman.2019.112420

CrossRef Full Text | Google Scholar

Kotas, T. J. (1985). The exergy method of thermal plant analysis. Amsterdam, Netherlands: Elsevier, 288–292.

Google Scholar

Kumar Singh, K., Kumar, R., and Gupta, A. (2020). Comparative energy, exergy and economic analysis of a cascade refrigeration system incorporated with flash tank (HTC) and a flash intercooler with indirect subcooler (LTC) using natural refrigerant couples. Sustain. Energy Technol. Assessments 39, 100716–100733. doi:10.1016/j.seta.2020.100716

CrossRef Full Text | Google Scholar

Lee, T-S., Liu, C-H., and Chen, T-W. (2006). Thermodynamic analysis of optimal condensing temperature of cascade-condenser in CO₂/NH₃ cascade refrigeration systems. Int. J. Refrig. 29 (7), 1100–1108. doi:10.1016/j.ijrefrig.2006.03.003

CrossRef Full Text | Google Scholar

Lounissi, D., and Bouaziz, N. (2017). Exergetic analysis of an absorption/compression refrigeration unit based on R124/DMAC mixture for solar cooling. Int. J. Hydrogen Energy 42 (13), 8940–8947. doi:10.1016/j.ijhydene.2016.11.082

CrossRef Full Text | Google Scholar

Mahmoudan, A., Samadof, P., Hosseinzadeh, S., and Garcia, D. A. (2021). A multigeneration cascade system using ground-source energy with cold recovery: 3E analyses and multi-objective optimization. Energy 223 (15), 121185–121202. doi:10.1016/j.energy.2021.121185

CrossRef Full Text | Google Scholar

Messineo, A. (2012). R744-R717 cascade refrigeration system: Performance evaluation compared with a HFC two-stage system. Energy Procedia 14 (18), 56–65. doi:10.1016/j.egypro.2011.12.896

CrossRef Full Text | Google Scholar

Mosaffa, A. H., Farshi, L. G., Infante Ferreira, C. A., and Rosen, M. (2016). Exergoeconomic and environmental analyses of CO₂/NH₃ cascade refrigeration systems equipped with different types of flash tank intercoolers. Energy Convers. Manag. 117 (1), 442–453. doi:10.1016/j.enconman.2016.03.053

CrossRef Full Text | Google Scholar

Nasruddin, S. S., Giannetti, N., and Arnas, L. (2016). Optimization of a cascade refrigeration system using refrigerant C₃H₈ in high temperature circuits (HTC) and a mixture of C₂H₆/CO₂ in low temperature circuits (LTC). Appl. Therm. Eng. 104 (5), 96–103. doi:10.1016/j.applthermaleng.2016.05.059

CrossRef Full Text | Google Scholar

Önder, K., Şencan, A., and Kalogirou, S. A. (2007). Thermoeconomic optimization of a LiBr absorption refrigeration system. Chem. Engineering&Processing Process Intensif. 46 (12), 1376–1384. doi:10.1016/j.cep.2006.11.007

CrossRef Full Text | Google Scholar

Rezayan O, A. B., and Behbahaninia, A. (2011). Thermoeconomic optimization and exergy analysis of CO₂/NH₃ cascade refrigeration systems. Energy Oxf. 36 (2), 888–895. doi:10.1016/j.energy.2010.12.022

CrossRef Full Text | Google Scholar

Rubio-Maya, C., Pacheco-Ibarra, J. J., Belman-Flores, J. M., Galvan-Gonzalez, S. R., and Mendoza-Covarrubias, C. (2012). NLP model of a LiBr–H₂O absorption refrigeration system for the minimization of the annual operating cost. Appl. Therm. Eng. 37 (5), 10–18. doi:10.1016/j.applthermaleng.2011.12.035

CrossRef Full Text | Google Scholar

Sayyaadi, H., and Nejatolahi, M. (2011). Multi-objective optimization of a cooling tower assisted vapor compression refrigeration system. Int. J. Refrig. 34 (1), 243–256. doi:10.1016/j.ijrefrig.2010.07.026

CrossRef Full Text | Google Scholar

Shah, R. K., and Sekulic, D. P. (2002). Fundamentals of heat exchanger design: Fundamentals of heat exchanger design.

Google Scholar

Tatchell, D. G. J. I. JoH., and Transfer, M. (1987). in Handbook of single-phase convective heat transferSadik Kaka. Editors R. K. Shah, and W. Aung (New York: Wiley).

Google Scholar

TjjtemoTPA, K. (1985). The exergy method of thermal plant analysis, 288–292.

Google Scholar

Wang, J., Zhai, Z., Jing, Y., and Zhang, C. (2010). Particle swarm optimization for redundant building cooling heating and power system. Appl. Energy 87 (12), 3668–3679. doi:10.1016/j.apenergy.2010.06.021

CrossRef Full Text | Google Scholar

Yu, M., Chen, Z., Yao, D., Zhao, F., Pan, X., Liu, X., et al. (2020). Energy, exergy, economy analysis and multi-objective optimization of a novel cascade absorption heat transformer driven by low-level waste heat. Energy Convers. Manag. 221 (1), 113162. doi:10.1016/j.enconman.2020.113162

CrossRef Full Text | Google Scholar

Zhu, Y., Peng, Z., Wang, G., and Zhang, X. R. (2021). Thermodynamic analysis of a novel multi-target-temperature cascade cycle for refrigeration. Energy Convers. Manag. 243, 114380. doi:10.1016/j.enconman.2021.114380

CrossRef Full Text | Google Scholar

Glossary

Nomenclature

b Fin width (m)

$\mathit{B}$ Fuel exergy (kW)

${\dot{\mathit{C}}}_{{\mathbf{C}\mathbf{O}}_{\mathbf{2}}}$ Carbon dioxide emission cost ($·ton⁻¹)

${\dot{\mathit{C}}}_{\mathbf{e}\mathbf{l}}$ Unit cost of electricity ($·kWh^-1)

${\dot{\mathit{C}}}_{\mathbf{e}\mathbf{n}\mathbf{v}}$ Annual cost of environment ($·year^-1)

${\dot{\mathit{C}}}^{\mathit{f}}$ Unit cost of fuel ($·kWh^-1)

${\dot{\mathit{C}}}_{\mathbf{o}\mathbf{p}}$ Annual cost of plant operation ($·year^-1)

C_p Specific Heat (kJ·(kg·K)⁻¹)

${\dot{\mathit{C}}}_{\mathbf{t}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l}}$ Air constant pressure specific volume (kJ·(kg·K)⁻¹)

C_total Annual total cost ($·year^-1)

d₀ Inner diameter of heat exchange tube (m)

d_i Outer diameter of heat exchange tube (m)

$\dot{\mathit{E}}$ Exergy (kW)

F_of Surface area (m²)

F_i Internal surface area (m²)

F_r Surface area of copper pipe (m²)

F_f Rib surface area (m²)

$\mathit{h}$ Specific enthalpy (J·kg^-1)

$\mathit{U}$ heat transfer coefficient (W·(°C⋅m²)⁻¹)

i Interest rate (%)

m Mass (ton)

$\dot{\mathit{m}}$ Mass flow rate (kg·s^-1)

N Equipment service life (year)

P Pressure (Bar)

Q Heat load (kW)

X Mass fraction (%)

${\mathit{r}}_{\mathbf{i}}$ Dirt thermal resistance in tube (m²·°C⋅W⁻¹)

${\mathit{r}}_{\mathbf{o}}$ Fouling thermal resistance outside the tube (m²·°C⋅W⁻¹)

r_P Compression ratio

$\mathit{s}$ Entropy (kJ·(kg·K)⁻¹)

t Temperature (°C)

t₀ Ambient temperature (°C)

t_CL Cold refrigerated space temperature (°C)

top Annual operation time (hour)

${\mathit{w}}_{\mathbf{y}}$ Face velocity (m·s^-1)

$\mathit{W}$ Power (kW)

Z Cost ($)

$\dot{\mathit{Z}}$ Annual cost ($·year^-1)

Greek symbols

${\mathit{\alpha }}_{\mathbf{i}}$ Heat transfer coefficient inside the tube (W·(°C⋅m²)⁻¹)

${\mathit{\alpha }}_{\mathbf{o}}$ Heat transfer coefficient outside the tube (W·(°C⋅m²)⁻¹)

${\mathit{\rho }}_{\mathbf{a}}$ Air density (kg·m^-3)

∆ Delta

$\mathit{\lambda }$ Thermal conductivity of tube wall (W·(m·°C)⁻¹)

${\mathit{\lambda }}_{\mathbf{i}}$ Thermal conductivity in tube (W·(m·°C)⁻¹)

${\mathit{\lambda }}_{\mathbf{u}}$ Thermal conductivity of frost or water (W·(m·°C)⁻¹)

δ Wall thickness (m)

δ_u Thickness of frost or water film (m)

ξ Coefficient of moisture

ξ_u Frost or water film increases the coefficient of air resistance

η_f Rib efficiency

η_fan Fan efficiency

η_Ex Exergy efficiency

η_s Isentropic efficiency of the compressor

$\mathit{\varphi }$ _{Maintenance cost factor}

${\mathit{\mu }}_{{\mathbf{C}\mathbf{O}}_{\mathbf{2}}}$ _{Emission conversion factor of electricity from grid}

Superscripts

CH Chemical

PH Physical

Subscripts

a Air

Abs Absorber

C Condenser

cas cascade

CE Condensing-evaporator

CA Condenser of high-temperature stage

CC Condenser of low-temperature stage

CL Cold space

CRF Capital recovery factor

D Destruction

E Evaporator

EA Evaporator of high-temperature stage

EC Evaporator of low-temperature stage

Ex Exergy

G Generator

M Middle

R Condensing vapor of high temperature stage

R1 High-pressure vapor of high temperature stage

R2 Low-pressure vapor of high temperature stage

R3 Vapor of low temperature stage

S Strong solution

SW Median solution

W Weak solution

1–23 Status points