Md Zahidul Islam
Yuzhang Lin
Vinod M. Vokkarane1
Venkatesh Venkataramanan- 1Department of Electrical and Computer Engineering, University of Massachusetts, Lowell, MA, United States
- 2National Renewable Energy Laboratory, Golden, CO, United States
Smart grid technologies are based on the integration of the cyber network and the power grid into a cyber-physical power system (CPPS). The increasing cyber-physical interdependencies bring about tremendous opportunities for the modeling, monitoring, control, and protection of power grids, but also create new types of vulnerabilities and failure mechanisms threatening the reliability and resiliency of system operation. A major concern regarding the interdependent networks is the cascading failure (CF), where a small initial disturbance/failure in the network results in a seemingly unexpected large-scale failure. Although there has been a significant volume of recent work in the CF research of CPPS, a comprehensive review remains unavailable. This article aims to fill the gap by providing a systematic literature survey regarding the modeling, analysis, and mitigation of CF in CPPS. The open research questions for further research are also discussed. This article allows researchers to easily understand the state of the art of CF research in CPPS and fosters future work required towards full resolutions to the remaining questions and challenges.
1 Introduction
Smart grid technologies have been transforming power grid operation and control paradigms in the recent decades. Beyond the physical power delivery infrastructure, a smart grid is equipped with smart sensing devices, advanced communication network, and powerful computing resources for monitoring operating conditions, transferring data, and optimizing resource allocation for the grid, respectively. With the integration of the cyber network, the power grid evolves into the so-called cyber-physical power system (CPPS).
Although the cyber-physical nature of modern power grids is advantageous in many ways, it poses major challenges on the reliability and resiliency of system operation as well. In CPPS, the cyber and the physical networks are highly interdependent. As a result, the grid becomes more vulnerable and prone to natural disasters and man-made attacks. In the CPPS, a small malfunction/failure in one network can affect the functionality of the other network, which may in turn affect the former one; this vicious cycle may continue until a cascade of failures occur with catastrophic consequences. For example, in September 2003, a severe blackout occurred in Italy due to the initial disconnection of one power station from the grid, which then led to the failure of several nodes in the cyber network. As a result, the grid could not be effectively monitored by the cyber network, leading to the failure of additional power stations and transmission lines (Buldyrev et al., 2010). Similarly, a cyber-attack on the Ukrainian power grid caused outages in 2015. The CF effects in the interdependent CPPS accelerated failure propagation in the grid, resulting in a large-scale blackout. A detailed survey on the CF in the power grid can be found in (Haes Alhelou et al., 2019).
Over the past decades, extensive research has been conducted in the field of cascading failure (CF) of the physical power grid (Guo et al., 2017) (Nakarmi et al., 2020). However, those studies are not enough to characterize the CF in CPPS because of the interdependency between the cyber and physical networks. In recent years, several failure propagation models have been proposed for analyzing the CF in interdependent networks. Some of the models incorporate the individual network properties whereas others mainly focus on unifying the mechanisms of failures in different networks (Buldyrev et al., 2010) (Ji et al., 2016). As a typical example of CF in interdependent networks, the study of CF in CPPS has emerged as an important research topic, and many interesting works have been published in the recent years. Despite a few related attempts, a comprehensive review on the state-of-the-art techniques of CF modeling, analysis, and mitigation in CPPS remains unavailable to summarize and guide research in this field. Jufri et al. (2019) reviews the existing research works on enhancing the resiliency of CPPS for preventing and mitigating CF, but it does not discuss the modeling of failure propagation in CPPS. The interdependencies and CF in general cyber-physical systems (CPS) are reviewed in (Li et al., 2019), but it is does not provide an in-depth coverage on the CPPS, especially with unique physical properties of power grids compared with other networks. Liu et al. (2021) provides a concise review of CF modeling and analysis in future power grids from two major perspectives: cyber network integration into the grid and high penetration of power electronics, but it lacks a detailed CF modeling and mitigation strategy. Guo et al. (2017) presents a comprehensive survey on techniques for CF modeling and analysis in physical power grids. Although it discussed the impact of the cyber network, a systematic review from the cyber-physical perspective remains missing.
To fill the aforementioned gap, a thorough review of CF modeling, analysis, and mitigation in CPPS will be provided in this article. First, background research regarding CF in power grid, communication network, and general interdependent networks will be reviewed. Next, the models of various CPPS components adopted by existing CF analysis will be categorized. They include the models of power flow in the power grid, the models of data flow (routing) in the communication network, the models of cyber-physical interdependencies, and the models of intra-network and inter-network failure propagation. This will be followed by a categorization of the CF analysis methods, including simulation-based methods, percolation-theory-based methods, and Markov-chain-based methods. Subsequently, mitigation strategies for CF in CPPS is summarized, and the linkage between CF mitigation and the concept of resilience is introduced. The paper concludes by extensive discussions on the remaining challenges to be addressed and potential future research directions. The overall structure of the paper is given in Figure 1. Overall, the article will answer many of the common questions regarding CF in CPPS and allow researchers to grasp a holistic picture of the landscape of this increasingly popular research field.
FIGURE 1. Overall structure of the review paper.
The rest of the paper is organized as follows. Section 2 will present a brief overview of background research on CF analysis in siloed power grid and communication network, and introduce general concepts and theories of CF in interdependent networks; essential concepts and definitions of CF in CPPS will be given in Sections 3, 4 describes in detail the modeling techniques for various components in CPPS for CF analysis; several categories of methodologies for CF analysis will be described in Sections 5, 6 presents CF mitigation strategies as well as their linkage to the concept of resilience; future research questions are summarized and discussed in Section 7. Finally, Section 8 concludes the paper.
2 Background research: Cascading failure in power grids, communication networks, and general interdependent networks
CF is a prominent phenomenon in many complex infrastructures such as power grid (Schäfer et al., 2018), water system (Sitzenfrei et al., 2011), gas system (Bao et al., 2021), IoT network (Zhao and Xing, 2020), etc. The main reason of CF is that the components in a complex network rely on and coordinate with each other for fulfilling the functionalities of the network. As a result, a malfunction/fault in one component may affect the functionalities of other components and make them fail. This process may start with an insignificant failure in the network, but continue to fail many more components progressively, and therefore is referred to as a cascading failure process. At the end of a CF, a large portion of the network may collapse, and the remaining portion may be unable to meet the demand of the operators and the users. The main challenge of CF research is to understand the mechanisms of CF, identify possible failure paths, recognize early failures, and take precautions to avoid a cascading effect. In recent years, the difficulty of modeling and analyzing CF has been exacerbated by the interdependency between multiple complex networks. In view of the challenges, many approaches have been developed for modeling, analysis, and mitigation of the CF of both individual and interdependent networks. While this review primarily focuses on CF in CPPS, this section will first provide a brief description of the CF process in siloed power grid and communication network; the general concepts of CF in interdependent networks will also be introduced.
2.1 Cascading failure in power grid
In a power grid, CF can be viewed as a series of outages followed by an initial outage of a component. It can be analyzed with power flow models based on physical laws (e.g., Kirchhoff’s Law and Ohm’s Law) and the capacity constraint of the grid components. In a power grid, electric power is transferred from generators to loads via transmission/distribution lines, i.e., branches. In this process, the power is distributed among different branches according to the power flow model. However, when disturbances occur and cause a branch failure, the power flow will be redistributed among the remaining active branches to create a new equilibrium. In this process, the redistributed power may overload (i.e., exceed the flow capacity of) some active branches and/or cause under- or overvoltage at some buses, resulting in further failures in sequence due to the triggering of overcurrent or under- or overvoltage relays (Simpson-Porco et al., 2016). Additionally, due to the increased penetration of renewable energy resources (RES), power grids experience low-inertia conditions prone to frequency instability and CF in the system (Jalali et al., 2019). A number of CF events in power grids have been reported over the past few decades. They were initially triggered by a wide variety of mechanisms such as line overloading, device malfunction, and lack of coordination between operation and planning (Haes Alhelou et al., 2019). As the causes and propagations of CF are complex and diverse, many models and methodologies are present to study the CF in power grids. Among them, two main categories will be briefly reviewed here: simplified statistical models, and detailed physics-based models.
The simplified statistical models render a fast and approximate overview of probable CF paths neglecting the detailed physical properties of a grid. As a result, these statistical models can simulate CF in a large-scale grid with tractable complexity. For example, the CASCADE model studies the loading effect of grid components on CF with several simplified assumptions of power grid properties (Dobson et al., 2004). CASCADE simulates CF with several iterative failure stages. The model initializes a disturbance and checks the loading conditions of all the grid components. A failure is triggered if an overloaded component exists, and the loads of the failed components are equally distributed among all other components. Then the next stage of failures starts by checking and loading conditions of all the remaining components again. This model shows that the distribution of the failed components follows a quasi-multinomial joint distribution and presents an analytical solution to calculation of the probability distribution of the number of failed components due to an initial failure. Similar to the CASCADE model, the Branching Process (BP) model provides an analytical solution to the calculation of the probability distribution of the number of line outages and amount of load shedding due to CF by estimating the influence of a failed component on the following stage of failures using stochastic processes (Qi et al., 2013). The CF simulation using the BP model is shown to yield fair approximate results with respect to those achieved using more complex models, but with significantly lower computational complexity.
Obviously, the main limitation of the simplified statistical models is inaccuracy. In contrast, the detailed physics-based models study the CF incorporating the physical properties of power grids. Within this category there are two subcategories of models: static and dynamic. In static models, the power grid dynamics are neglected, and the steady-state operational condition is typically analyzed using DC power flow models. For example, the ORNL-PSERC-Alaska (OPA) model considers the standard DC power flow and solves an integer linear programming (ILP) problem for generation and load redispatch after line outages due to overloading (Carreras et al., 2003). This model runs iteratively to find failed lines based on a probabilistic model with respect to overloading conditions. The static models with DC power flows are adopted in many CF analyses (Soltan et al., 2017) (Yan et al., 2015) and mitigation strategies (Das et al., 2022). In dynamic models, the dynamic behavior of the grid is captured throughout the CF process. For achieving compatible accuracy levels, AC power flow models are often adopted (Noebels et al., 2022). For example, the Cascading Outage Simulator with Multiprocess Integration Capabilities (COSMIC) model uses differential equations to represent the dynamics of generators and loads (Song et al., 2016). This model helps understand the CF caused by dynamic grid events such as switching and high volumes of load or generator disconnection or reconnection. Both static and dynamic models have benefits and drawbacks. The static models are relatively faster than the dynamic models. However, in practice, the power grid responds to an initial outage with real-time control and protection mechanisms, which may result in a different steady state than the predicted one by static models. Therefore, dynamic models can capture more failure mechanisms and predict the propagation of CF more precisely.
Other than the above-described methods, there are several models to study the CF in power grids, which can be categorized based on their properties, such as topological models, modified topological models, stochastic simulation models, etc. Some of the specific examples from all the above models are the multi-timescale quasi-dynamic model (Yao et al., 2016), the improved OPA model (Mei et al., 2009), and the Markov transition model (Wang et al., 2012) (Rahnamay-Naeini et al., 2014). Recently, machine learning-based data-driven models have also been used to predict the CF propagation path in the power grid (Shuvro et al., 2019) (Pi et al., 2018). Detailed information about these methods can be found in the existing review papers (Guo et al., 2017) (Abedi et al., 2019) (VaimanBellChenChowdhuryDobsonHines et al., 2012) and will not be elaborated here.
2.2 Cascading failure in communication network
Communication network has become an inseparable part of modern societies. Each individual infrastructure, e.g., power grid, water system, etc., is equipped with a communication network to allow for situational awareness and control. However, the communication network itself can suffer from a CF, deteriorating the performance of the infrastructures dependent on it. Communication networks transfer data among different devices (data sources and sinks) via links and routers. Routers find paths and forward data via links between sources and destinations. Links and routers have limited data transfer capacities, and they may malfunction when the volume of data flow surpasses their capacities. Because of the initial failure of a few components (links, routers), data flows could be redistributed to the other active components, leading to further failures. This process is repeated until a significant portion of the network fails. In this subsection, the methodologies for CF analysis in communication networks will be introduced first, followed by various network examples such as wireless sensor networks (WSN) and the internet of things (IoT).
The CF models for communication networks can be categorized into deterministic models and stochastic models (Lehmann and Bernasconi, 2010). In deterministic models, the data load of the failed components is distributed to other active components with some deterministic rules. For instance, (Wang and Chen, 2008) provides a load redistribution model in which the data load of a failed edge is redistributed to its neighboring edges based on their weights (i.e., flow capacities). Based on this model, the authors investigate the robustness of weighted networks against cascading failure and identify the appropriate weights that provide the best robustness in typical communication network models, including small-world and scale-free networks. Wang et al. (2020a), on the other hand, employs a global load redistribution model in which the load in the network is set to the node’s betweenness centrality after an initial failure. The authors use this model to identify the network’s critical nodes, the failure of which accelerates CF events in the network. However, since the deterministic load redistribution only approximates the load in the network for triggering the next stage of failure due to overload, it may not fully reflect the complete or most probable set of failures that may occur. Unlike deterministic models, stochastic models adopt a more comprehensive analytical approach. For example, (Ren et al., 2018) proposes a conditional Markov state transition model to describe the failure propagation in a network due to node overloading and also shows how the failures are temporally dependent.
Although the general deterministic and stochastic models largely reflect the CF behavior of communication networks, a few adjustments are required to describe the CF in WSN and IoT networks since they have some distinct features and utilize low-capacity components. As the use of WSN and IoT networks have increased significantly in recent years, the study of CF in these networks receives special attention in the literature (Fu et al., 2020) (Xing, 2021). To study the CF in WSN, (Hu et al., 2015) sets the node traffic to its betweenness centrality and considers traffic overload and invalid connectivity of the nodes as the causes of failures. With these assumptions, (Hu et al., 2015) describes a CF model for WSN considering the dynamic load change in the network. Fu et al. (2021) considers both node and link capacities in CF analysis and assumes that a node can self-recover after a certain time as may occur in WSN. With the rising concept of internet of thing (IoT) many devices are being connected, and it becomes necessary to study the CF of IoT infrastructures. A detailed review on CF analysis and reliability for IoT infrastructures is provided for a wide range of IoT applications in (Xing, 2021). Fu and Yang (2021) considers the layered architecture and realistic characteristics of IoT, and presents a CF model driven by overload in relay nodes, base stations, and communication links.
2.3 Cascading failure in general interdependent networks
From the discussion of CF in siloed power grids and communication networks in the previous two subsections, it is seen that the network components may fail due to the redistribution of loads of the failed component within the same network. In the case of interdependent networks, the process of CF could be even more complicated. In addition to intra-network failure propagation, inter-network failure propagation may also occur. Unlike intra-network failure propagation, load redistribution does not take place across networks; rather, inter-network failure propagations are caused by the dependence of components in one network on the functionalities of the failed components in the other network. Due to the mutual dependency between the two networks, failures may propagate back and forth between networks and lead to a multi-network CF. There are several general methodologies for characterizing CF propagation in interdependent networks. In this subsection, we will review some of those methods and mention a few specific examples of CF in interdependent networks.
For the general modeling and analysis of CF in interdependent networks, it is challenging to incorporate the detailed physical properties of each network into the study. Rather, generic probabilistic analysis is usually adopted. Some of the methods for interdependent CF analysis are described below. i) Percolation-theory-based methods. Any complex network can be represented as a graph, where the nodes represent the components of the network and the edges represent the connectivity among the components. Two complex networks can be coupled to create interdependent networks by considering dependency among the nodes of the two networks. As the percolation theory provide a probabilistic framework for capturing the interaction among nodes and links in graphs, it is used for the CF analysis in many interdependent networks (Buldyrev et al., 2010). ii) Markov-chain-based methods. The CF is a sequence of failure events occurring one after another, which can be analyzed using Markov chain models with the assumption that the current failure events only depends on the failure events that immediately preceed them (Rahnamay-Naeini and Hayat, 2016); iii) Branching-process-based methods. The branching process can be used for CF analysis assuming that each failure component in the current stage will affect the next-stage failures with a probability (Qi et al., 2017). iv) Machine-learning-based methods. With the advancement of artificial intelligence, there are increasing attempts of using data-driven methods to analyze CF in interdependent networks (Maghsoodi and Khansari, 2021). It has the prerequisite of a large training dataset for learning the cascading failure paths within and cross the networks.
CF can occur in many real-world cases of interdependent networks where two or multiple networks depend on each other for proper operation. For electric power grid, the counter dependent network can vary from water supply systems to natural gas networks and others. In interdependent electric power-water infrastructures, pump stations, control units, and storage tanks in water network are dependent on power supply from nearby electric substations (Zhang et al., 2016) (Wang et al., 2022). Meanwhile, several types of power plants, such as coal-fired power plants and nuclear power plants, depend on water supply for proper operation. Similarly, in electric power-gas infrastructures, the two networks are coupled through electricity-driven gas compressors and gas-fired electricity generators (Bao et al., 2020). As a result, a malfunction in one network may affects the production process of the counter one. A catastrophic CF in power-gas infrastructures occurred in Texas, United States in February 2021, affecting millions of people and causing hundreds of billions of capital losses (Extreme winter weather causes u.S. Blackouts, 2022) (Busby et al., 2021). Aside from the electric power grid, there are many other interconnected networks of significance. For instance, a syncretic railway network (SRN) comprising regional railway network and urban rail transit network is studied in (Liu et al., 2022a). A CF analysis is performed for interdependent road-channel network to assess urban flood propagation on the road network due to channel failure (overflow), where the channel is responsible for dumping the road’s rainfall runoff (Dong et al., 2020).
3 Cascading failure in CPPS
The previous section reviews the background research of CF in power grids and communication networks, and introduces the general concept of CF in interdependent networks. This section will now concentrate on discussing the CF in CPPS. The CPPS model will be defined using graph theory and the CF propagation paths will be discussed in detail.
3.1 CPPS model
An abstract diagram of an interdependent CPPS is presented in Figure 2A. The power grid and the cyber network are represented by two separate graphs each having nodes and edges. Note that the communication network comprises networking devices (e.g., routers) and communication media, whereas the cyber network comprises communication networks, sensors, and controllers. The nodes in the power grid represent the buses at substations and the edges represent branches such as transmission/distribution lines and transformers. The nodes in the power grid are heterogeneous and include generation buses, transmission/distribution buses, and load buses. Similarly, the nodes in the cyber network represent control centers, controllers, sensors, and routers, and the edges represent the data transfer media, i.e., communication links. The terminal devices (sensors/controllers) are installed at different buses in the power grid, which monitor and control the power grid and communicate with the control center via intermediate routers in the cyber network. In Figure 2A, terminal devices are shown in the cyber network and are coupled with routers to enable communication. The interdependence between the two networks is shown in dashed lines. Both unidirectional and bidirectional dependencies are shown, where the terminal devices of the cyber network and the nodes of the power grid have bidirectional dependencies, and routers have unidirectional dependencies on the power grid (Abdelmalak et al., 2022). The reason for this consideration is that the power grid supplies power to both terminal devices and routers, whereas only the terminal devices monitor and control the power nodes.
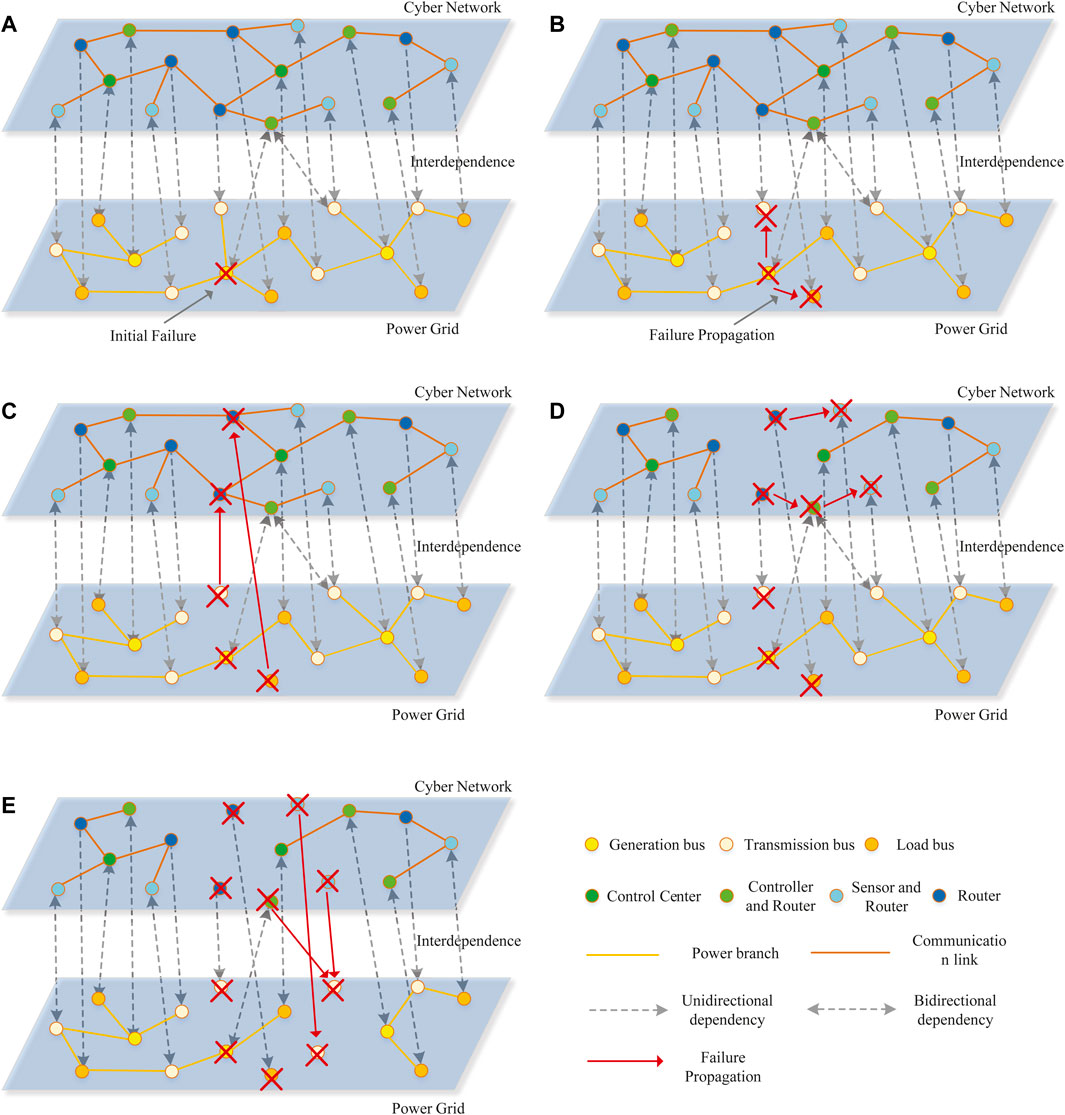
FIGURE 2. Failure propagation in interdependent CPPS. (A) Example CPPS model with interdependency. (B) Failure propagation in the power grid due to an initial failure in the power grid, i.e., intra-domain failure in the power grid. (C) Power-dependent cyber network failure, i.e., inter-domain failure in the cyber network. (D) Failure propagation in the cyber network due to its own failure, i.e., intra-domain failure in the cyber network. (E) Cyber-dependent power grid failure, i.e., inter-domain failure in the power grid.
3.2 Failure propagation in interdependent CPPS
The power grid depends on the cyber network for proper operation and control, whereas the cyber network depends on the power grid for energy supply. Sensors monitor the operating conditions of the power grid and report measurements to the control centers using available routes in the cyber network. After analyzing the received data, the control centers send control commands to controllers via available routes. When power grid nodes cannot be monitored and controlled due to the failures of cyber nodes, it is referred to as inter-domain failure in the power grid (Zhang and Yağan, 2020). Similarly, when a cyber node shuts down because it does not receive energy supply from the power grid, it is referred to as inter-domain failure in the cyber network (Zhang and Yağan, 2020). Additionally, after a failure in the power grid, the load of the failed power transfer path is redistributed to the other active paths leading to further overloading and power outages, which is referred to as intra-domain failure in the power grid. Similarly, a failure in the cyber network may result in additional failures in the network, which is referred to as intra-domain failure in the cyber network. Although the scale of the initial failures may be small, the process progressively triggers a cascade of failures with catastrophic consequences due to both intra-domain and inter-domain failure propagations. The mechanisms of failure propagations are explained with an example shown in Figures 2B–E. For demonstration, it is considered that a fault occurs to a generator node in the power grid. Due to this fault, the generator cannot supply power to two of its neighboring nodes which leads to load shedding (Figure 2B). As the loads at two power nodes fail due to the failure in the power grid, it is an intra-domain failure in the power grid. Subsequently, the counter dependent nodes in the cyber network fail as they loss their power supply, which is referred to as the inter-domain failure in the cyber network (Figure 2C). Then, the failure propagates within the cyber network because some of the cyber nodes become disconnected from the network, which is an intra-domain failure in the cyber network (Figure 2D). This triggers the failure of generators at power nodes due to the lack of monitoring and control from the failed cyber nodes, which is the inter-domain failure in the power grid (Figure 2E). This process continues until the system stabilizes again, i.e., when no new failure is triggered, and the system ends up operating in a significantly degraded state.
4 Cascading failure modeling in CPPS
With the advent of the CPPS, the study of dynamic interactions between the power grid and the cyber network has drawn the attention of research communities. With proper modeling, the characteristics of the interdependent systems can be captured, and further analysis can be performed to identify the vulnerabilities and reduce the catastrophic consequences of CFs. There are several important components to be considered in the CF modeling in CPPS. In this section, we will study the CPPS modeling techniques adopted by recent literature on CF analysis. These techniques are summarized in Table 1.
TABLE 1. Summary of CPPS modeling.
4.1 Modeling of the power flow in power grid
When a power branch/bus fails, the topology of the power grid changes, and the load of the failed branch/bus redistributes to the active branches/buses following the power flow model based on physical laws (e.g., Kirchhoff’s Law and Ohm’s Law in AC circuits) and control laws (e.g., automatic generation control and economic dispatch). After the occurrence of the faults, the updated operating condition associated with the new topology can be obtained by power flow analysis. For analyzing CF, power flow models with varying accuracy and computational efficiency are considered. They can be broadly categorized as DC power flow models and AC power flow models (Cetinay et al., 2018). The DC models can approximate the power flow in the system with lower computational complexity when the voltage magnitude differences or phase angle differences along the branches are small. However, it leads to approximation errors in power flow solutions especially when there are large differences of voltage magnitudes or phase angles between two terminal buses of a branch, which typically happens under heavy loading conditions (Li et al., 2018a). Some methods have considered DC optimal power flow (DCOPF) to obtain the maximum benefits from the DC power flow analysis, as optimal power flow problems are inherently computational intensive (Chen et al., 2019a) (Pan et al., 2020). To obtain the accurate operating conditions of the system, AC power flow models are more effective but at the expense of higher computational complexity (Li et al., 2018a) (Gao et al., 2021). Instead of using the DC or AC models, it is assumed in (Zhang and Yağan, 2020) that the load of the failed branch is redistributed globally and equally among the active lines arguing that it is a reasonable assumption under the DC power flow model and also follows the long-range nature of the Kirchhoff’s Laws. With the assumptions, (Zhang and Yağan, 2020) shows that the obtained simulation results match the analytical ones derived in the article. (Prusty and Jena, 2017) thoroughly reviews the probabilistic load flow models, uncertainty characterizations, and uncertainty handling methods and proposes an analytical model for estimating the probabilistic load flow results while accounting for the photovoltaic generation and load demand uncertainties.
4.2 Modeling of intra-domain failure propagation in power grid
When the current of a branch exceeds its power flow capacity, the branch will fail if no control action is taken within a certain time limit because of the activation of relay protection (Kiliçkiran et al., 2018). After the initial failure, the load of the failed branch will be redistributed to the other active branches, which may overload the active branches, resulting in additional failures. The modeling of failure propagation within a power grid can be classified into two categories namely deterministic and stochastic models. In deterministic models, a branch fails instantly when there is an overcurrent flowing along the branch (Li et al., 2021), and a bus fails when the voltage of the bus exceeds the allowable thresholds (Gao et al., 2021). However, (Gao et al., 2020) argues that as the power grid is equipped with an increasing number of renewable resources and controllable loads, the power flow will become more uncertain, and the deterministic model cannot generate the accurate behaviors of failures. With this argument, the authors propose a stochastic failure model for estimating the failed components in the grid. In this model, it is assumed that every electrical component can fail with a certain probability at any minuscule time and a model is developed for determining the number of failed components at any given time. Besides failures due to overcurrents along branches and over/undervoltages at buses, there are other types of failures as such as over-heating failure and hidden failure (e.g., malfunction of protective devices) (Li et al., 2021). According to (Cordova-Garcia et al., 2019), the use of automatic active control strategies may lead to more frequent reconfiguration of the grid in order to maximize grid operating conditions, which may induce overheating in the grid and increase intra-domain failure propagation.
4.3 Modeling of data flow (routing) in communication network
The proper modeling of routing is one of the important requirements for modeling, analysis, and mitigation of CF in CPPS. In CPPS, as fast and secure communication is required between the terminal devices (sensors/controllers) installed at power grid nodes and the control center, different routing algorithms are presented in the literature to fulfill the requirements (Sabbah et al., 2014). The routing algorithms find the minimum-cost paths between sources and destinations. The algorithms can use either global information or decentralized information about the network to generate data transfer paths. In the case of global information-oriented algorithms, the routers or a central controller of software-defined network (SDN) gathers and stores the global topology information for determining the optimal paths of data flows; whereas in decentralized information-oriented algorithms, each router/node finds paths based on the information obtained from its neighboring nodes. Han et al. (2018) determines the routing paths centrally by applying the Flued-Marshal algorithm for finding the overall weighted shortest path between a terminal device and the control center, where the weights are the queue length of packets along the path. Li et al. (2021) uses the publish–subscribe network (PSN) strategy to create a multicast tree between the control center and the terminal devices fulfilling the delay and the bandwidth requirements. The global information is also used in (Cordova-Garcia et al., 2019) to minimize the packet transmission delay, propagation delay, and the expectation of service delay along the path. Gao et al. (2021) considers decentralized information to construct the least-score paths from the source to the destination, where the scores are the weighted sum of the queue length of packets at the neighboring nodes of the source and the shortest hop count from the neighboring nodes to the destination. Instead of using the direct score, (Cai et al., 2016) uses probabilistic score values for selecting the routes.
4.4 Modeling of intra-domain failure propagation in communication network
When a fault occurs in the communication network, it may propagate within the network and affect its overall performance. The initial failure can occur due to internal faults of the devices, external disasters, or cyber-attacks. With the initial fault in the network, the data flows of the faulty nodes reroute to the other active nodes, which may increase congestion in the active nodes and cause overloading. As a result, the active nodes may malfunction and drop data packets (Gao et al., 2020). This process may continue and propagate to the entire network until additional measures are taken. Han et al. (2018) consider the concept of the round-trip time (RTT) in the data transfer and assume that the network malfunctions when the data cannot be transferred within the RTT threshold. The intra-domain failure in the network is simplified in (Zhang and Yağan, 2020) with the assumption that a node remains functioning as long as it belongs to the largest connected components (giants) in the network.
4.5 Modeling of interdependencies
In CPPS, the power grid and the cyber network are coupled together; where the power grid depends on the cyber network for its monitoring and control and the cyber network depends on the power grid for the energy supply. In literature, different types of dependency are considered between the two networks namely unidirectional and bidirectional interdependency. Gao et al. (2021) consider the unidirectional interdependency between the power grid and the cyber network, where only the power grid depends on the cyber network for its operation and control, but the cyber network is independent of the grid, arguing that the network has backup power sources installed. In the case of bidirectional interdependency, the following interdependencies are considered for analyzing the robustness of CPPS. I) One-to-one interdependency: each grid node is related to each cyber node (Zhang and Yağan, 2020); ii) one-to-multiple interdependency: each grid node is related to multiple cyber nodes or vice versa (e.g., redundant control) (Chen et al., 2018); iii) multiple-to-multiple interdependency: multiple nodes of one network are related to multiple nodes of another network (Shao et al., 2011). There are some other interdependencies within the above three categories such as topological-characteristic-based interdependency and random interdependency. In topological-characteristic-based interdependent models, an assortativity coefficient is defined to find the nodes with similar topological characteristics (e.g., degree, betweenness) to couple them together (Liu et al., 2022b). To compare the performance of different types of interdependencies, (Yagan et al., 2012) defines a random interdependency, where the interdependent networks are partitioned into multiple subgroups with an equal number of nodes for each subgroup. Then, each node of an interdependent subgroup is correlated with j (j is within the range of 0 to the number of nodes in the subgroup) other nodes with a probability. Abdelmalak et al. (2022) describes the modeling techniques for CPPS interdependence in detail considering the power grid as a distributed and autonomous system. It provides evaluation criteria for interdependence modeling, and describes potential applications of CPPS interdependence modeling techniques. Clearly, cascading failure analysis is one of the domains for application.
4.6 Modeling of inter-domain failure in power grid and communication network
The inter-domain failure occurs when the failure/malfunction of one network affects the other network due to the interdependent nature of CPPS. A common practice regarding inter-domain failure research is that the cyber node fails instantly when the corresponding grid node fails and vice versa. However, a few studies assume that the power or cyber node does not necessarily fail instantly due to the failure of a node in the counter system but imposes a probability of failure (Qu et al., 2019). Gao et al. (2021) define a threshold of average transmission time in the cyber network and assumes that when the data cannot be transferred within the threshold, the control center would lose the control of the grid nodes with a certain probability. Cordova-Garcia et al. (2019) argue that the control-command transfer from the control center to the grid nodes is asynchronous, i.e., time-varying, which can escalate further failures in the power grid. To reduce the effect of asynchronous control, the authors propose a load-shedding scheme to shed large loads at those nodes, where the control action can be performed with low delay. Cai et al. (2016) use the overcurrent relay operating time as the threshold and assume that the overloaded grid branch will trip when the data-exchanging model requires more time steps for the data transfer than the threshold. They also assume that due to the failure of a grid node, the dependent node in the cyber network will fail with a low probability. Li et al. (2021) and Han et al. (2018) use the RTT as a threshold to identify the failed grid nodes when the data transfer delay exceeds the threshold. Although most of the above models consider cyber failure propagation to the power grid, there is modeling of failure propagation in the opposite direction as well. Das et al. (2017) proposes an influence model based on a networked Markov chain framework to incorporate the power-dependent failure into the cyber network. In this model, the functionality state of a cyber node is modeled by combining its internal state with that of the related grid node. Qu et al. (2019) considers both power and cyber nodes to fail due to capacity overload, thereby failing the counter system’s dependent node. Based on the assumption, the paper presents an optimal load allocation strategy in both the power grid and the cyber network to limit the effects of the CF.
5 Cascading failure analysis in CPPS
The modeling of different components in the CPPS is described in the previous section. Based on the models of different components, several categories of methods have been proposed in the literature to analyze the CF in CPPS. The objective of CF analysis is to examine the behavior of CPPS, especially the propagation of failures and their consequences, in the event of initial failures due to internal or external disturbances. These studies allow us to understand how the CPPS will respond during any failure events and what measures should be taken to mitigate the impacts based on the identified vulnerabilities. In this section, we will categorize the existing methods for CF analysis and describe the concepts and features of each category in detail. The summary of the methods is provided in Table 2.
TABLE 2. Comparison of cascading failure analyses in CPPS.
5.1 CF analysis based on deterministic or probabilistic simulation
The most widely used category of analyses in practice is numerical simulations. They find out the paths of CF propagation based on computations of system operation conditions using pre-determined CPPS models with detailed physical and the operational properties, e.g., power flow analysis in the power grid and routing analysis in the cyber network. The simulation of the CF process begins with a selected initial failure of the devices in either the power grid or the cyber network, and the sequence of failures to occur is determined using both intra-domain and inter-domain failure propagation models. After the propagation of the failures, the final states of the systems are obtained and the consequences are quantified. This process can be repeated many times to find out a representative or critical set of failure propagation paths under various operating conditions, initial failure scenarios, or random sampling results. The existing simulation-based methods can be described in several categories. i) Asynchronous-model-based analysis. In this category, failures propagate in either the power grid or the cyber network at each stage. Once the failure propagation in one network is completed, the next stage of the failure in another network starts with the incorporation of both intra-domain and the inter-domain effects. Zhang and Yağan (2020) uses the asynchronous model to evaluate the robustness of CPPS against CF initiated by random attacks. It covers intra-domain failures in both networks, but only power-dependent failure in a cyber network is included for interdependency. However, this model simplifies the power flow model and ignores the data flow model in cyber network. On the contrary, considering AC power flow, Boyaci et al. (2022) uses the asynchronous model to estimate the blackout probability triggered by attacks on both grid buses and branches. ii) Deterministic-model-based analysis. In this category, the assumption for CF analysis is that the occurrence of a failure can be deterministically calculated with physical laws. Li et al. (2021) considers deterministic failures in the power grid when the power flow exceeds the branch capacity and studies the probability of load loss ratio in the grid. iii) Stochastic-model-based analysis. Unlike deterministic models, the CF analysis is performed to incorporate the stochastic nature of the failures. Gao et al. (2020) considers the stochasticity in power flow due to increased renewable penetration and develops a model for analyzing the CF under uncertain power flow patterns. Simulation-based analysis is the most practical and accurate method for understanding the behaviors of CF in CPPS once the operating conditions, initial failure conditions, and failure propagation models are determined. However, the astronomical number of possible conditions, scenarios, and random samples make it very challenging to scale the methods to large systems. Therefore, efficient screening of critical cases is a significant challenge to address for scalability of simulation-based methods.
5.2 CF analysis based on percolation theory
The application of the percolation theory in complex networks is a well-established research direction. With the help of statistical physics principles and game theory, the percolation theory analyzes the phase transition of a network to determine the giant clusters that appear within the network (Li et al., 2021). In the context of cascading failure, percolation theory is also extensively used to determine the transition threshold above which there will be a catastrophe and cascading failure will happen. For a given graph G (v, e), if we consider the failure probability of edges e as ϕ, then there presents a threshold of ϕ between 0 and 1 when a giant failed/sustained component appears and the threshold can be determined using the percolation theory. When the failure probability is considered only for the edges, it is called bond percolation, whereas, the consideration of failure in nodes is called site percolation (Li et al., 2021). With the defined control threshold of interdependency, (Chen et al., 2018) measures the critical point (the initial failure fraction of the entire network) for CF in CPPS using percolation theory and found that both increasing the interdependency and decreasing the control threshold enhance the robustness of the system. In (Huang et al., 2013), the size of the functioning components after CF is calculated in a k-to-n interdependency model (each grid node is controlled by k cyber nodes, each cyber nodes control n grid nodes) and a relationship between robustness and cost is deduced to help determine a tradeoff between the two parameters for building a reliable smart grid infrastructure. The percolation-theory-based methods provide a unique perspective and in-depth insight into the occurrence of CF in CPPS without extensive repeated simulations. However, these methods usually overlook the detailed physical and operational properties of both the power grid and the cyber network during the CF, and it requires careful examination whether the generic simplified probabilistic model can truly represent the failure propagation patterns in a real-world CPPS (Parandehgheibi et al., 2014).
5.3 CF analysis based on Markov chain
The Markov chain (MC) model is a stochastic model used to describe a sequence of linked events, where each event depends only on the immediately preceding event. Rahnamay-Naeini and Hayat (2016) describes an Inter-Dependent Markov Chain (IDMC) model for CF analysis, where two separate MC models are coupled to describe the inter-domain and intra-domain failures in CPPS. It considers two separate probabilities to relate power-dependent communication failure and communication-dependent power failure, respectively, which can be used to control the level of interdependency between the two networks. It also provides an analytical solution to describe the steady state of the cyber-physical IDMC model. Simulation results show that two reliable networks may be combined into an unreliable one because of the interdependency. The MC model is also used to analyze the CF in cyber networks considering both the intra-domain and inter-domain failures (Das et al., 2017). The article also considers the repairability of both cyber and power nodes, where a failed node can recover from failure with a probability. Based on the simulations, it shows the impact of intra-domain and inter-domain failures on cyber networks and the positive impacts of adding node repairability. Similarly, (Shuvro et al., 2017) studies the impact of cyber failures on power grid reliability based on the MC model. It defines a power-cyber interdependence function to capture the influence of cyber failures on the grid based on the hop distance to the control center and the degree centrality of cyber nodes. Based on the simulation results, the key insight of the article is that the cyber dependency of the grid has a significant impact on the probability of blackout. Similar to the percolation theory, the Markov chain model provides elegant results for the entire profile of CF propagation paths with guided simulations. However, the simplified assumptions about the characteristics of the power grid and the cyber network may lead to inaccurate results and miss severe individual failure cases. Furthermore, the assumptions about failure probabilities play a critical role in Markov chain models and must be carefully derived and verified.
6 Cascading failure mitigation in CPPS
The ultimate goal of modeling and analyzing CF is to prevent its occurrence or mitigate its impact. In order to discuss the mitigation strategies against CF, the concept of resilience will be introduced first. According to the US National Infrastructure Advisory Council (NIAC), the resilience of infrastructure systems is defined as “their ability to predict, absorb, adapt, and/or quickly recover from a disruptive event such as natural disasters” (Wu and Li, 2021). In case of CPPS, the resiliency can be explained by its functionality curve F (t) as shown in Figure 3, which can be divided into three stages: preparedness, response, and recovery stages. In the preparedness stage, the system maintains its normal functionality, F (t0). In the response stage, the system initially manages to sustain its full functionality at F (t0) under certain failures by utilizing redundant components in the system. However, if the failure propagation continues and a CF is triggered, the functionality of the system starts to degrade sharply. As the system stabilizes upon the completion of failure propagation, the functionality degrades from A to B at time t2, as shown in Figure 3. Points A and B can be used to quantify the vulnerability of CPPS during the response stage. Finally, in the recovery stage, adequate measures are taken to quickly restore the system’s functionality to its initial operation at time t3. In this subsection, CF mitigation strategies will be described in accordance with different stages of the resilience curve in Figure 3. The methods are summarized in Table 3.
FIGURE 3. Resilience curve of CPPS.
TABLE 3. Summary of mitigation cascading failure strategies in CPPS.
6.1 System hardening
Hardening refers to preplanning measures during the design of CPPS to handle a certain level of failure in the system without initializing the CF, which takes place in the preparedness stage of the resilience curve in Figure 3 (Ghanbari et al., 2018) (Chen et al., 2019b). In the power grid, branches and generators should have headroom capacities over their normal loads so that when any failure occurs, the active components can handle the redistributed loads (Zhang and Yağan, 2016). Similarly, the cyber network should be designed such that it can tackle additional data flow through the nodes/edges after an initial failure. However, as the extension of capacity requires extensive capital cost, an optimal search for the critical nodes/edges is necessary for the capacity enhancement to mitigate CF (Ghanbari et al., 2018) (Wu et al., 2021a). The topology of the cyber and physical systems also has a great impact on the robustness of the system. For instance, it is found that the scale-free cyber network is more robust than the small-world network against random failures (Li et al., 2021). In (Chen et al., 2019b), the authors study the impact of different topologies on CF and suggest modifications of the topologies of both cyber and physical networks considering their interdependence to limit the scale and impact of the CF under different cyber-attack strategies.
6.2 Varying the interdependency
As the cyber-physical interdependence heavily affects the paths and properties of failure propagation, the robustness of coupled networks against cascading failures is studied under different levels of interdependencies (Banerjee et al., 2017) (Gao et al., 2012). There are several approaches considered in the literature to increase the robustness of CPPS by varying the interdependency between the power grid and the cyber network (Yagan et al., 2012) (Liu et al., 2022b) (Kong, 2019). One of the approaches is to increase the number of autonomous nodes by decoupling the interdependency between the two networks. In power grid, FACTS devices such as shunt, series, and unified controllers can be installed to control the voltage of power node and the active and reactive power flow of power branches within a certain range without reliance on a cyber network (Han et al., 2018). Similarly, the interdependency of cyber nodes on the power nodes can be decreased by installing backup power sources, e.g., uninterrupted power sources (UPS), on site. Here, effective placement of the FACTS and backup power sources is necessary, as discussed in (Kong, 2022). In contrast to the above approach, proper enhancement of cyber-physical interdependency can also make the CPPS robust against CF (Korkali et al., 2017). For instance, both one-to-multiple and multiple-to-multiple interdependencies are more robust against CF than one-to-one interdependency (Yagan et al., 2012). In these models, a cyber node can have energy supply from multiple power nodes, and a power node can be equipped with redundant sensors and controllers at multiple cyber nodes. The interdependence based on intra-domain characteristics also impacts the robustness, as shown in (Liu et al., 2022b), where an assortative coefficient metric is defined based on the intra-domain characteristics to generate different levels of interdependency between the two networks and used to evaluate the robustness of the system against CF. In (Kong, 2019), an optimal configuration of interdependence is obtained by employing sufficient power-disjoint communication routes for the data transfer. Lastly, it should be pointed out that this category of CF mitigation strategies take place both in the preparedness stage and the response stage of the resilience curve of Figure 3. On the one hand, the system needs to be sufficiently prepared before a failure occurs, such as by installing FACTS devices and backup power sources, which lies in the preparedness stage. On the other hand, the installed devices must be properly operated to limit the propagation of failures, which lies in the response stage. For example, in (Han et al., 2018), the power input from the installed FACTS devices is regarded as a constraint in order to achieve an optimal cascade mitigation strategy.
6.3 Optimal response and recovery
Following an initial failure in CPPS, response strategies can be adopted to halt the propagation of the failure in the networks, which lies in the response stage of the resilience curve in Figure 3. The most difficult task in this process is determining the precise location of the initial fault in the networks. Tootaghaj et al. (2019) proposes an optimal response strategy that can stop CF even if the fault location is unknown or only partially known. Here, the authors formulate cost flow assignment as a linear programming optimization problem to minimize the total cost of redispatching generation and shedding loads in the power grid. Neglecting the intrinsic properties of the individual network, (Chen et al., 2021) proposes a strategy for increasing the robustness of interdependent networks by intentionally removing a few nodes and links after an initial failure. The authors argue that intentional node and link removal strategies can effectively interdict the propagation path of cascading failure, which is economical and efficient.
Although the response stage improves the robustness of the networks and minimizes the effects of CF, the system performance may still be partially degraded during a cascading failure. A fast recovery plan is necessary to bring the system back to its normal condition, as shown in the recovery stage of the resilience curve in Figure 3. As the recovery resources are often limited, several optimization models are proposed for the best allocation of the resources to maximize the functionality of the network. Almoghathawi et al. (2019) propose multi-objective restoration models for K interdependent networks using the mixed-integer programming (MIP) to maximize the resilience and minimize the cost subject to the network flow constraint, interdependence, available resources, and other related constraints. Zhao et al. (2016) propose a multi-stage recovery model using integer linear programming (ILP) and design two algorithms based on relaxation and bounding of the ILP and dynamic programming for solving the problem in large-scale interconnected systems. Wu et al. (2021b) proposes an optimization model that incorporates recovery resources, recovery activity execution modes, the precedence of damaged components, and the availability, cost, and timing of recovery resources to achieve optimal recovery in terms of system resiliency. The authors solve the optimization model with a modified simulated annealing algorithm and quantify the model’s real-time performance with a CF model. Li et al. (2022) assumes cyber-physical dependency and uses Q-learning to find the best sequence combination for recovering failed loads with limited resources. The model incorporates the recovery process within the framework of the cascading failure model. However, the method ignores critical power system operational constraints, such as bus voltage, and necessitates a large amount of memory with high computational complexity. Overall, although physical power grid restoration has been extensively studied, research on recovery plans that account for the impact of cyber networks, especially the interactions between the two networks in a CF, remain relatively unmature.
7 Future research directions
Although abundant research work has been conducted on the CF of siloed power grids, the CF of CPPS is a historically less explored topic and have received rapidly growing attention in the recent years. As observed from the literature review, many recent attempts have been made to understand and tackle various challenges regarding CF in CPPS. However, as an emerging research topic, there are still many factors to be carefully addressed towards more accurate, efficient, and comprehensive solutions. Based on the literature review, possible future research directions are suggested as follows.
(1) Incorporation of heterogenous components and failure propagation mechanisms. In a CPPS, the power grid and the cyber network are driven by heterogeneous laws: the power flows are driven by circuit laws, and the data flows are driven by router forwarding policies. Furthermore, the components in each network itself, and the interaction mechanisms between components in different networks, are highly heterogenous. Although the models and analyses of individual networks and components are relatively mature, the question remains how to develop a general theory or methodology that covers all heterogeneous components and mechanisms without unacceptable simplifications that significantly degrades accuracy. In fact, this is a major challenge encountered by the modeling and analysis of CF in any interdependent networks (Wang et al., 2020b).
(2) Creditable modeling of failure probabilities under scarce data. As renewable energy generation and demand-side participation become more prevalent, power grid operating points and dynamics become more uncertain and unpredictable. Therefore, stochastic models and methods are required to accurately portray the profile of possible or probable failure propagation paths. However, it is could be difficult to build trustworthy stochastic models as historical data of failures, especially large-scale CF, is often scarce (Tomsovic et al., 2005). Furthermore, the historical data of one system cannot be safely reused to characterize other systems, as the stochastic properties of the failures are high dependent on system-specific parameters such as geographical locations, network topologies, resource distribution, and operating paradigms. Therefore, future studies should consider how to model and validate the stochastic properties of failures in CPPS with high trustworthiness especially when historical data is scarce (Wu et al., 2021c) (Dobson, 2012).
(3) Situational awareness during cyber-physical CF. The situational awareness of the physical power grid is ensured by successful sensing, communication, and computing via the cyber network. When failures propagate to the cyber network, the situational awareness of the power grid may be degraded, which disables proper and timely decision making and accelerates the cascade of failures (Panteli et al., 2013). The cascading failure of the power grid in the Northeast region in North America in August 2003 was known to be partially attributed to the failure of cyber systems and the lack of situational awareness (Muir and Lopatto, 2004). Furthermore, situational awareness is required not only for the physical power grid but also for the cyber network itself. Hardware failures or cyber attacks must be quickly detected, identified, localized, and isolated to allow effective decision making and prevent wide spreading of failures. Therefore, it is essential to incorporate the factor of situational awareness into CF models and investigate effective measures to prevent the spread of failures under limited situational awareness or to agilely restore situational awareness (Edib et al., 2021) (Edib et al., 2020). Furthermore, the impact of the simultaneous failure of multiple networks, such as the SCADA and PMU networks, is worth further investigation.
(4) Dynamic response to prevent failure propagation. As shown in the resilience curve in Figure 3, there are three stages to enhance the resilience of CPPS: preparedness, response, and recovery stages. The CF mitigation strategies reviewed in Section 6 work mostly in the preparedness and recovery stages. However, targeting the preparedness and recovery stages only is not enough. In the preparedness stage, it is impossible to predict and prepare for all possible scenarios of failures/disturbances due to their astronomical numbers. Meanwhile, although a successful recovery stage is important for shorten the period of outages, it cannot really stop the failure propagation and limit the scale and degree of the performance degradation. Therefore, agile response actions during the CF are the key to preventing failure propagation and limit the consequences of CF. For instance, dynamic reconfiguration of the network, as one of the efficient response actions, has been widely studied for the siloed power grids and can also be explored for the CPPS (Ding et al., 2017) (Pournaras et al., 2013). It takes place during the response stage of the resilience curve, where the system is reconfigured after any failures such that the existing components can take over the responsibility of the failed ones without being overloaded. Additionally, a remedial action scheme (RAS) coordinating actions such as generation tripping, load shedding, or system reconfiguration is used to limit the impact of cascading in the response to contingencies that cannot be constrained with normal protection and control devices (Mahmoudi et al., 2017). Although RAS has been extensively researched for siloed power grids, it is critical to extend RAS methodologies to CPPS.
(5) Scalability of CF analysis to large-scale systems. The existing simulation-based CF analysis methods, as discussed in Section 5, achieves higher accuracy at the expense of higher complexity since they consider the physical properties of CPPS during the analysis. When the scale of the system becomes large, the possible scenarios become astronomical and it is impossible to enumerate all possible scenarios via simulation. On the other hand, the percolation theory-based CF analysis methods, as discussed in Section 5, does not consider detailed physical properties of the components and can provide scalable analytical solutions for understanding the consequences of CF without enumerate all possible scenarios. However, due to the lack of consideration of detailed physical properties, the later methods may yield inaccurate results. Therefore, scalable yet accurate methods for CF analysis in CPPS remains a significant gap (Liu et al., 2022c). Note that efficient screening of critical initial contingency (failure) scenarios that may lead to severe CF is a possible solution that has been extensively studied for siloed power grids (Narimani et al., 2022). However, more investigation is required to extend the methodologies to CPPS.
(6) Cyber-physical CF due to malicious cyber attacks. The integration of a cyber network creates a large surface for cyber attacks against the power grid. There is growing research on the modeling of and defense against cyber attacks in power grids (Che et al., 2019). However, most of the existing literature only focus on hardening strategies implemented in the preparedness stage, or detection strategies implemented in the response stage (Clark and Zonouz, 2019). There is still a lack of strategies to suppress the impact of attacks in the response stage (e.g., attack isolation and data rerouting) and to recover system performance in the recovery stage (e.g., security upgrade, malware cleaning, and data recovery) (Sahu et al., 2021). These aspects require further investigation in order to establish a holistic framework for handling CF due to malicious cyber attacks.
(7) Use of distributed energy resources and edge computing resources to mitigate CF impacts. The CF phenomenon of CPPS is largely due to the centralized operation paradigm, the interdependency between different components, and long-distance transfer of energy and data. Local and distributed operation paradigms can effectively reduce the complexity and interdependency of the networks and thus reduce the risks of CF. The decentralization of CPPS operation can be realized by distributed energy resources (DERs) in the power grid and edge computing resources in the cyber network, which can achieve self-sufficiency in local areas without long-distance transfer of energy and data (Maharjan et al., 2015) (Li et al., 2018b). For example, in the event of bulk power grid failures, self-healing cyber-physical microgrids can be formed with DERs to maintain the power supply to critical loads (Vu et al., 2020). Similarly, edge computing resources can fulfill many real-time monitoring, optimization, control, and protection requirements without the need of a remote centralized controller (Liu et al., 2019) (Gai et al., 2019).
(8) Incorporation of human factors in cyber-physical CF. Although most control and decision-making processes are automated in CPPS, human is kept in the loop for many applications at the high level. During a large-scale CF where pre-computed plans or intelligent real-time decision-making tools are not available or sufficient, human intervention plays a critical role in determining the course of the event. In power grids, CF events attributed to or magnified by human errors have been reported in the past (Anderson, 2004). Human errors can arise from a variety of factors, including the external environment, a lack of experience and expertise, and the complexity of the tasks (Bao et al., 2018). Note that failures occurring concurrently in and propagating across cyber and physical networks significantly increase the complexity of operational tasks and hinders human understanding of the situation and possible measures to be taken. Although numerous studies have been conducted to explore human aspects on CF in physical power grids, there is lack of study on the impact of human behaviors in interdependent power grids and cyber networks.
8 Conclusion
The increasing interdependency between power grids and cyber networks leads to the so-called CPPS with higher heterogeneity and complexity. In recent years, several large-scale CF events have been observed in CPPS, motivating research on the modeling, analysis, and mitigation of CF considering the cyber-physical nature of smart grids. This paper systematically summarizes the state-of-the-art research on cyber-physical CF in CPPS. It starts with the motivation of the review, followed by background research conducted on siloed power grid and communication network, as well as on interdependent networks in general. Then, existing techniques for the modeling, analysis, and mitigation of CF in CPPS are categorized, and their linkage with the concept of resilience is discussed. The literature survey portrays the vibrant research efforts on this topic, while also revealing many outstanding questions and challenges to be further addressed. This paper concludes by discussing possible future research directions and recommendations.
Author contributions
MZI performed the literature search, summarize the literature, and drafted the manuscript. YL participated in the literature search, developed manuscript structure, and revised the manuscript. VVo and VVe provided insight into cyber-physical interdepence and revised the manuscript.
Funding
This work relates to Department of Navy award N00014-22-1-2001 issued by the Office of Naval Research.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelmalak, M., Venkataramanan, V., and Macwan, R. (2022). A survey of cyber-physical power system modeling methods for future energy systems. IEEE Access 10, 99875–99896. doi:10.1109/access.2022.3206830
Abedi, A., Gaudard, L., and Romerio, F. (2019). Review of major approaches to analyze vulnerability in power system. Reliab. Eng. Syst. Saf. 183, 153–172. doi:10.1016/j.ress.2018.11.019
Almoghathawi, Y., Barker, K., and Albert, L. (2019). Resilience-driven restoration model for interdependent infrastructure networks. Reliab. Eng. Syst. Saf. 185, 12–23. doi:10.1016/j.ress.2018.12.006
Anderson, G., Donalek, P., Farmer, R., Hatziargyriou, N., Kamwa, I., and Kundur, P. (2004). Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 20 (4), 1922–1928. doi:10.1109/TPWRS.2005.857942
Banerjee, J., Das, A., and Sen, A. (2017). “A survey of interdependency models for critical infrastructure networks,”. arXiv preprint arXiv:1702.05407.
Bao, M., Ding, Y., Yin, X., Shao, C., and Ye, C. (2021). Definitions and reliability evaluation of multi-state systems considering state transition process and its application for gas systems. Reliab. Eng. Syst. Saf. 207, 107387. doi:10.1016/j.ress.2020.107387
Bao, Y., Guo, C., Zhang, J., Wu, J., Pang, S., and Zhang, Z. (2018). Impact analysis of human factors on power system operation reliability. J. Mod. Power Syst. Clean Energy 6 (1), 27–39. doi:10.1007/s40565-016-0231-6
Bao, Z., Jiang, Z., and Wu, L. (2020). Evaluation of bi-directional cascading failure propagation in integrated electricity-natural gas system. Int. J. Electr. Power & Energy Syst. 121, 106045. doi:10.1016/j.ijepes.2020.106045
Boyaci, O., Narimani, M. R., Davis, K., and Serpedin, E. (2022). “Spatio-temporal failure propagation in cyber-physical power systems,” in 2022 International Conference on Smart Grid and Renewable Energy (SGRE), Doha, 20-22 March 2022.
Buldyrev, S., Parshani, R., Paul, G., Stanley, H., and Havlin, S. (2010). Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028. doi:10.1038/nature08932
Busby, J. W., Baker, K., Bazilian, M. D., Gilbert, A. Q., Grubert, E., Rai, V., et al. (2021). Cascading risks: Understanding the 2021 winter blackout in Texas. Energy Res. Soc. Sci. 77, 102106. doi:10.1016/j.erss.2021.102106
Cai, Y., Cao, Y., Li, Y., Huang, T., and Zhou, B. (2016). Cascading failure analysis considering interaction between power grids and communication networks. IEEE Trans. Smart Grid 7 (1), 530–538. doi:10.1109/tsg.2015.2478888
Carreras, B., Lynch, V., Dobson, I., and Newman, D. E. (2003). Critical points and transitions in an electric power transmission model for cascading failure blackouts. Chaos (Woodbury, N.Y.) 12, 985–994. doi:10.1063/1.1505810
Cetinay, H., Soltan, S., Kuipers, F. A., Zussman, G., and Mieghem, P. V. (2018). Comparing the effects of failures in power grids under the ac and dc power flow models. IEEE Trans. Netw. Sci. Eng. 5 (4), 301–312. doi:10.1109/tnse.2017.2763746
Che, L., Liu, X., Ding, T., and Li, Z. (2019). Revealing impacts of cyber attacks on power grids vulnerability to cascading failures. IEEE Trans. Circuits Syst. II Express Briefs 66 (6), 1058–1062. doi:10.1109/tcsii.2018.2869941
Chen, C., Ju, W., Sun, K., and Ma, S. (2019). Mitigation of cascading outages using a dynamic interaction graph-based optimal power flow model. IEEE Access 7, 168637–168648. doi:10.1109/access.2019.2953774
Chen, L., Gorbachev, S., Yue, D., Dou, C., Li, S., Ge, H., et al. (2021). Protection strategies of active defense in cyber-physical power systems. Europhys. Lett. 136 (3), 38002. doi:10.1209/0295-5075/ac4eca
Chen, L., Yue, D., and Dou, C. (2019). Optimization on vulnerability analysis and redundancy protection in interdependent networks. Phys. A Stat. Mech. its Appl. 523, 1216–1226. doi:10.1016/j.physa.2019.04.235
Chen, Y., Li, Y., Li, W., Wu, X., Cai, Y., Cao, Y., et al. (2018). Cascading failure analysis of cyber physical power system with multiple interdependency and control threshold. IEEE Access 6, 39353–39362. doi:10.1109/access.2018.2855441
Clark, A., and Zonouz, S. (2019). Cyber-physical resilience: Definition and assessment metric. IEEE Trans. Smart Grid 10 (2), 1671–1684. doi:10.1109/tsg.2017.2776279
Cordova-Garcia, J., Wang, X., Xie, D., Zhao, Y., and Zuo, L. (2019). Control of communications-dependent cascading failures in power grids. IEEE Trans. Smart Grid 10 (5), 5021–5031. doi:10.1109/tsg.2018.2873217
Das, P., Shuvro, R. A., Povinelli, K., Sorrentino, F., and Hayat, M. M. (2022). Mitigating cascading failures in power grids via markov decision-based load-shedding with dc power flow model. IEEE Syst. J. 16 (3), 4048–4059. doi:10.1109/jsyst.2022.3175359
Das, P., Shuvro, R. A., Wang, Z., Naeini, M. R., Ghani, N., and Hayat, M. M. (2017). “Stochastic failure dynamics in communication network under the influence of power failure,” in 2017 IEEE 13th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Rome, 09-11 October 2017.
Ding, T., Lin, Y., Bie, Z., and Chen, C. (2017). A resilient microgrid formation strategy for load restoration considering master-slave distributed generators and topology reconfiguration. Appl. Energy 199, 205–216. doi:10.1016/j.apenergy.2017.05.012
Dobson, I., Carreras, B., and Newman, D. E. (2004). A loading-dependent model of probabilistic cascading failure. Probab. Eng. Inf. Sci. 19, 15–32. doi:10.1017/s0269964805050023
Dobson, I. (2012). Estimating the propagation and extent of cascading line outages from utility data with a branching process. IEEE Trans. Power Syst. 27 (4), 2146–2155. doi:10.1109/tpwrs.2012.2190112
Dong, S., Yu, T., Farahmand, H., and Mostafavi, A. (2020). Probabilistic modeling of cascading failure risk in interdependent channel and road networks in urban flooding. Sustain. Cities Soc. 62, 102398. doi:10.1016/j.scs.2020.102398
Edib, S. N., Lin, Y., Vokkarane, V. M., Qiu, F., Yao, R., and Zhao, D. (2021). Optimal pmu restoration for power system observability recovery after massive attacks. IEEE Trans. Smart Grid 12 (2), 1565–1576. doi:10.1109/tsg.2020.3028761
Edib, S. N., Lin, Y., Vokkarane, V., Qiu, F., Yao, R., and Zhao, D. (2020). “Pmu and communication infrastructure restoration for post-attack observability recovery of power grids,” in 2020 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), USA, 11-13 November 2020.
Extreme winter weather causes u.S. Blackouts (2022). Extreme winter weather causes u.S. Blackouts. earthobservatory.nasa.Gov. (Accessed Oct 1, 2022).
Fu, X., Li, W., Yang, Y., and Postolache, O. (2021). Cascading failures analysis of wireless sensor networks with varying routing schemes. IEEE Sensors J. 21 (8), 10193–10203. doi:10.1109/jsen.2021.3059731
Fu, X., Pace, P., Aloi, G., Yang, L., and Fortino, G. (2020). Topology optimization against cascading failures on wireless sensor networks using a memetic algorithm. Comput. Netw. 177, 107327. doi:10.1016/j.comnet.2020.107327
Fu, X., and Yang, Y. (2021). Modeling and analyzing cascading failures for internet of things. Inf. Sci. 545, 753–770. doi:10.1016/j.ins.2020.09.054
Gai, K., Wu, Y., Zhu, L., Xu, L., and Zhang, Y. (2019). Permissioned blockchain and edge computing empowered privacy-preserving smart grid networks. IEEE Internet Things J. 6 (5), 7992–8004. doi:10.1109/jiot.2019.2904303
Gao, J., Buldyrev, S., Stanley, H., and Havlin, S. (2012). Networks formed from interdependent networks. Nat. Phys. 8, 40–48. doi:10.1038/nphys2180
Gao, X., Peng, M., and Tse, C. K. (2021). Cascading failure analysis of cyber physical power systems considering routing strategy. IEEE Trans. Circuits Syst. II: Express Briefs, 08 April 2021.
Gao, X., Peng, M., Tse, C. K., and Zhang, H. (2020). A stochastic model of cascading failure dynamics in cyber-physical power systems. IEEE Syst. J. 14 (3), 4626–4637. doi:10.1109/jsyst.2020.2964624
Ghanbari, R., Jalili, M., and Yu, X. (2018). Correlation of cascade failures and centrality measures in complex networks. Future Gener. Comput. Syst. 83, 390–400. doi:10.1016/j.future.2017.09.007
Guo, H., Zheng, C., Iu, H., and Fernando, T. (2017). A critical review of cascading failure analysis and modeling of power system. Renew. Sustain. Energy Rev. 80, 9–22. doi:10.1016/j.rser.2017.05.206
Haes Alhelou, H., Hamedani-Golshan, M. E., Njenda, T. C., and Siano, P. (2019). A survey on power system blackout and cascading events: Research motivations and challenges. Energies 12, 682–684. doi:10.3390/en12040682
Han, Y., Guo, C., Ma, S., and Song, D. (2018). Modeling cascading failures and mitigation strategies in pmu based cyber-physical power systems. J. Mod. Power Syst. Clean Energy 6 (5), 944–957. doi:10.1007/s40565-018-0407-3
Hu, X., Li, W., and Fu, X. (2015). “Analysis of cascading failure based on wireless sensor networks,” in 2015 IEEE International Conference on Systems, Man, and Cybernetics, China, 09-12 October 2015.
Huang, Z., Wang, C., Stojmenovic, M., and Nayak, A. (2013). Balancing system survivability and cost of smart grid via modeling cascading failures. IEEE Trans. Emerg. Top. Comput. 1 (1), 45–56. doi:10.1109/tetc.2013.2273079
Jalali, A., Dozein, M. G., and Mancarella, P. (2019). “Frequency stability provision from battery energy storage system considering cascading failure s with applications to separation events in Australia,” in 2019 IEEE Milan PowerTech, Milan, Italy, 23-27 June 2019.
Ji, X., Wang, B., Liu, D., Dong, Z., Chen, G., Zhu, Z., et al. (2016). Will electrical cyber–physical interdependent networks undergo first-order transition under random attacks? Phys. A Stat. Mech. its Appl. 460, 235–245. doi:10.1016/j.physa.2016.05.017
Jufri, F. H., Widiputra, V., and Jung, J. (2019). State-of-the-art review on power grid resilience to extreme weather events: Definitions, frameworks, quantitative assessment methodologies, and enhancement strategies. Appl. Energy 239, 1049–1065. doi:10.1016/j.apenergy.2019.02.017
Kiliçkiran, H. C., Şengör, İ., Akdemir, H., Kekezoğlu, B., Erdinç, O., and Paterakis, N. G. (2018). Power system protection with digital overcurrent relays: A review of non-standard characteristics. Electr. Power Syst. Res. 164, 89–102. doi:10.1016/j.epsr.2018.07.008
Kong, P. (2019). Optimal configuration of interdependence between communication network and power grid. IEEE Trans. Industrial Inf. 15 (7), 4054–4065. doi:10.1109/tii.2019.2893132
Kong, P. Y. (2022). Optimal backup power deployment for communication network with interdependent power network. IEEE Access 10, 17287–17299. doi:10.1109/access.2022.3150318
Korkali, M., Veneman, J., Tivnan, B., Bagrow, J., and Hines, P. (2017). Reducing cascading failure risk by increasing infrastructure network interdependence. Sci. Rep. 7, 44499. doi:10.1038/srep44499
Lehmann, J., and Bernasconi, J. (2010). Stochastic load-redistribution model for cascading failure propagation. Phys. Rev. E 81 (3), 031129. doi:10.1103/physreve.81.031129
Li, J., Li, Y., and Su, Q. (2022). Sequential recovery of cyber-physical power systems based on improved q-learning. J. Frankl. Inst. doi:10.1016/j.jfranklin.2022.05.043
Li, J., Shi, C., Chen, C., and Dueñas-Osorio, L. (2018). A cascading failure model based on ac optimal power flow: Case study. Phys. A Stat. Mech. its Appl. 508, 313–323. doi:10.1016/j.physa.2018.05.081
Li, J., Wang, Y., Huang, S., Xie, J., Shekhtman, L., Hu, Y., et al. (2019). Recent progress on cascading failures and recovery in interdependent networks. Int. J. Disaster Risk Reduct. 40, 101266. doi:10.1016/j.ijdrr.2019.101266
Li, W., Yang, T., Delicato, F. C., Pires, P. F., Tari, Z., Khan, S. U., et al. (2018). On enabling sustainable edge computing with renewable energy resources. IEEE Commun. Mag. 56 (5), 94–101. doi:10.1109/mcom.2018.1700888
Li, X., Jiang, C., Du, R., Wang, R., Fei, M., Li, X., et al. (2021). Optimization and control of cyber–physical power systems under dual-network interactive cascading failure. Control Eng. Pract. 111, 104789. doi:10.1016/j.conengprac.2021.104789
Li, M., Liu, R. R., Lu, L., Hu, M. B., Xu, S., and Zhang, Y. C. (2021). Percolation on complex networks: Theory and application. Phys. Rep. 907, 1–68. doi:10.1016/j.physrep.2020.12.003
Liu, D., Zhang, X., and Tse, C. K. (2021). A tutorial on modeling and analysis of cascading failure in future power grids. IEEE Trans. Circuits Syst. II Express Briefs 68 (1), 49–55. doi:10.1109/tcsii.2020.3040860
Liu, H., Chen, X., Huo, L., Zhang, Y., and Niu, C. (2022). Impact of inter-network assortativity on robustness against cascading failures in cyber–physical power systems. Reliab. Eng. Syst. Saf. 217, 108068. doi:10.1016/j.ress.2021.108068
Liu, S., Yin, C., Chen, D., Lv, H., and Zhang, Q. (2022). Cascading failure in multiple critical infrastructure interdependent networks of syncretic railway system. IEEE Trans. Intelligent Transp. Syst. 23 (6), 5740–5753. doi:10.1109/tits.2021.3057404
Liu, Y., Yang, C., Jiang, L., Xie, S., and Zhang, Y. (2019). Intelligent edge computing for iot-based energy management in smart cities. IEEE Netw. 33 (2), 111–117. doi:10.1109/mnet.2019.1800254
Liu, Y., Zhang, A., Dehghanian, P., Jung, J. K., Habiba, U., and Overbye, T. J. (2022). “Modeling and analysis of cascading failures in large-scale power grids,” in 2022 IEEE Kansas Power and Energy Conference (KPEC), USA, 25-26 April 2022.
Maghsoodi, M. H., and Khansari, M. (2021). “Predicting cascading failure with machine learning methods in the interdependent networks,” in 2021 11th International Conference on Computer Engineering and Knowledge (ICCKE), Mashhad, 28-29 October 2021.
Maharjan, S., Zhang, Y., Gjessing, S., Ulleberg, O., and Eliassen, F. (2015). “Providing microgrid resilience during emergencies using distributed energy resources,” in 2015 IEEE Globecom Workshops (GC Wkshps), USA, 06-10 December 2015.
Mahmoudi, M. M., Kincic, S., Zhang, H., and Tomsovic, K. (2017). “Implementation and testing of remedial action schemes for real-time transient stability studies,” in 2017 IEEE Power & Energy Society General Meeting, USA, 16-20 July 2017.
Mei, S., He, F., Zhang, X., Wu, S., and Wang, G. (2009). An improved opa model and blackout risk assessment. IEEE Trans. Power Syst. 24 (2), 814–823. doi:10.1109/tpwrs.2009.2016521
Muir, A., and Lopatto, J. (2004). Final report on the august 14, 2003 blackout in the United States and Canada: Causes and recommendations. Washington, DC and Ottawa, Canada: US-Canada power system outage task force
Nakarmi, U., Rahnamay Naeini, M., Hossain, M. J., and Hasnat, M. A. (2020). Interaction graphs for cascading failure analysis in power grids: A survey. Energies 13, 2219–9. doi:10.3390/en13092219
Narimani, M. R., Huang, H., Umunnakwe, A., Mao, Z., Sahu, A., Zonouz, S., et al. (2022). Generalized contingency analysis based on graph theory and line outage distribution factor. IEEE Syst. J. 16 (1), 626–636. doi:10.1109/jsyst.2021.3089548
Noebels, M., Preece, R., and Panteli, M. (2022). Ac cascading failure model for resilience analysis in power networks. IEEE Syst. J. 16 (1), 374–385. doi:10.1109/jsyst.2020.3037400
Pan, H., Lian, H., Na, C., and Li, X. (2020). Modeling and vulnerability analysis of cyber-physical power systems based on community theory. IEEE Syst. J. 14 (3), 3938–3948. doi:10.1109/jsyst.2020.2969023
Panteli, M., Crossley, P. A., Kirschen, D. S., and Sobajic, D. J. (2013). Assessing the impact of insufficient situation awareness on power system operation. IEEE Trans. Power Syst. 28 (3), 2967–2977. doi:10.1109/tpwrs.2013.2240705
Parandehgheibi, M., Modiano, E., and Hay, D. (2014). “Mitigating cascading failures in interdependent power grids and communication networks,” in 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, 03-06 November 2014.
Pi, R., Cai, Y., Li, Y., and Cao, Y. (2018). Machine learning based on bayes networks to predict the cascading failure propagation. IEEE Access 6, 44815–44823. doi:10.1109/access.2018.2858838
Pournaras, E., Yao, M., Ambrosio, R., and Warnier, M. (2013). “Organizational control reconfigurations for a robust smart power grid,” in Internet of things and inter-cooperative computational technologies for collective intelligence (Germany: Springer).
Prusty, B. R., and Jena, D. (2017). A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach. Renew. Sustain. Energy Rev. 69, 1286–1302. doi:10.1016/j.rser.2016.12.044
Qi, J., Dobson, I., and Mei, S. (2013). Towards estimating the statistics of simulated cascades of outages with branching processes. IEEE Trans. Power Syst. 28 (3), 3410–3419. doi:10.1109/tpwrs.2013.2243479
Qi, J., Ju, W., and Sun, K. (2017). Estimating the propagation of interdependent cascading outages with multi-type branching processes. IEEE Trans. Power Syst. 32 (2), 1–1223. doi:10.1109/tpwrs.2016.2577633
Qu, Z., Dong, Y., Qu, N., Wang, L., Li, Y., Zhang, Y., et al. (2019). Survivability evaluation method for cascading failure of electric cyber physical system considering load optimal allocation. Math. Problems Eng. 2019, 1–15. doi:10.1155/2019/2817586
Rahnamay-Naeini, M., and Hayat, M. M. (2016). Cascading failures in interdependent infrastructures: An interdependent markov-chain approach. IEEE Trans. Smart Grid 7 (4), 1997–2006. doi:10.1109/tsg.2016.2539823
Rahnamay-Naeini, M., Wang, Z., Ghani, N., Mammoli, A., and Hayat, M. M. (2014). Stochastic analysis of cascading-failure dynamics in power grids. IEEE Trans. Power Syst. 29 (4), 1767–1779. doi:10.1109/tpwrs.2013.2297276
Ren, W., Wu, J., Zhang, X., Lai, R., and Chen, L. (2018). A stochastic model of cascading failure dynamics in communication networks. IEEE Trans. Circuits Syst. II Express Briefs 65, 632–636. doi:10.1109/tcsii.2018.2822049
Sabbah, A. I., El-Mougy, A., and Ibnkahla, M. (2014). A survey of networking challenges and routing protocols in smart grids. IEEE Trans. Industrial Inf. 10 (1), 210–221. doi:10.1109/tii.2013.2258930
Sahu, A., Mao, Z., Wlazlo, P., Huang, H., Davis, K., Goulart, A., et al. (2021). Multi-source multi-domain data fusion for cyberattack detection in power systems. IEEE Access 9, 119118–119138. doi:10.1109/access.2021.3106873
Schäfer, B., Witthaut, D., Timme, M., and Latora, V. (2018). Dynamically induced cascading failures in power grids. Nat. Commun. 9, 1975. doi:10.1038/s41467-018-04287-5
Shao, J., Buldyrev, S., Havlin, S., and Stanley, H. (2011). Cascade of failures in coupled network systems with multiple support-dependence relations. Phys. Rev. E 83 (3), 036116. doi:10.1103/physreve.83.036116
Shuvro, R. A., Das, P., Hayat, M. M., and Talukder, M. (2019). “Predicting cascading failures in power grids using machine learning algorithms,” in 2019 North American Power Symposium (NAPS), USA, 13-15 October 2019.
Shuvro, R. A., Wang, Z., Das, P., Naeini, M. R., and Hayat, M. M. (2017). “Modeling impact of communication network failures on power grid reliability,” in 2017 North American Power Symposium (NAPS), USA, 17-19 September 2017.
Simpson-Porco, J. W., Dörfler, F., and Bullo, F. (2016). Voltage collapse in complex power grids. Nat. Commun. 7 (1), 10790–10798. doi:10.1038/ncomms10790
Sitzenfrei, R., Mair, M., Möderl, M., and Rauch, W. (2011). Cascade vulnerability for risk analysis of water infrastructure. Water Sci. Technol. a J. Int. Assoc. Water Pollut. Res. 64, 1885–1891. doi:10.2166/wst.2011.813
Soltan, S., Mazauric, D., and Zussman, G. (2017). Analysis of failures in power grids. IEEE Trans. Control Netw. Syst. 4 (2), 288–300. doi:10.1109/tcns.2015.2498464
Song, J., Cotilla-Sanchez, E., Ghanavati, G., and Hines, P. D. H. (2016). Dynamic modeling of cascading failure in power systems. IEEE Trans. Power Syst. 31 (3), 2085–2095. doi:10.1109/tpwrs.2015.2439237
Tomsovic, K., Bakken, D. E., Venkatasubramanian, V., and Bose, A. (2005). Designing the next generation of real-time control, communication, and computations for large power systems. Proc. IEEE 93 (5), 965–979. doi:10.1109/jproc.2005.847249
Tootaghaj, D. Z., Bartolini, N., Khamfroush, H., He, T., Chaudhuri, N. R., and Porta, T. L. (2019). Mitigation and recovery from cascading failures in interdependent networks under uncertainty. IEEE Trans. Control Netw. Syst. 6 (2), 501–514. doi:10.1109/tcns.2018.2843168
Vaiman, M., Bell, K., Chen, Y., Chowdhury, B., Dobson, I., Hines, P., et al. (2012). Risk assessment of cascading outages: Methodologies and challenges. IEEE Trans. Power Syst. 27 (2), 631–641. doi:10.1109/tpwrs.2011.2177868
Vu, T. V., Nguyen, B. L. H., Cheng, Z., Chow, M. Y., and Zhang, B. (2020). Cyber-physical microgrids: Toward future resilient communities. IEEE Ind. Electron. Mag. 14 (3), 4–17. doi:10.1109/mie.2019.2958039
Wang, B., Zhang, Z., Qi, X., and Liu, L. (2020). Identify critical nodes in network cascading failure based on data analysis. J. Netw. Syst. Manag. 28 (1), 21–34. doi:10.1007/s10922-019-09499-8
Wang, F., Magoua, J. J., Li, N., and Fang, D. (2020). Assessing the impact of systemic heterogeneity on failure propagation across interdependent critical infrastructure systems. Int. J. Disaster Risk Reduct. 50, 101818. doi:10.1016/j.ijdrr.2020.101818
Wang, F., Magoua, J. J., and Li, N. (2022). Modeling cascading failure of interdependent critical infrastructure systems using hla-based co-simulation. Automation Constr. 133, 104008. doi:10.1016/j.autcon.2021.104008
Wang, W.-X., and Chen, G. (2008). Universal robustness characteristic of weighted networks against cascading failure. Phys. Rev. E 77 (2), 026101. doi:10.1103/physreve.77.026101
Wang, Z., Scaglione, A., and Thomas, R. J. (2012). “A markov-transition model for cascading failures in power grids,” in 2012 45th Hawaii International Conference on System Sciences, USA, 04-07 January 2012.
Wu, G., Li, M., and Li, Z. (2021). A gene importance based evolutionary algorithm (giea) for identifying critical nodes in cyber–physical power systems. Reliab. Eng. Syst. Saf. 214, 107760. doi:10.1016/j.ress.2021.107760
Wu, G., Li, M., and Li, Z. S. (2021). Resilience-based optimal recovery strategy for cyber–physical power systems considering component multistate failures. IEEE Trans. Reliab. 70 (4), 1510–1524. doi:10.1109/tr.2020.3025179
Wu, G., and Li, Z. (2021). Cyber—physical power system (cpps): A review on measures and optimization methods of system resilience. Front. Eng. Manag. 8 (4), 503–518. doi:10.1007/s42524-021-0163-3
Wu, X., Wu, D., and Modiano, E. (2021). Predicting failure cascades in large scale power systems via the influence model framework. IEEE Trans. Power Syst. 36 (5), 4778–4790. doi:10.1109/tpwrs.2021.3068409
Xing, L. (2021). Cascading failures in internet of things: Review and perspectives on reliability and resilience. IEEE Internet Things J. 8 (1), 44–64. doi:10.1109/jiot.2020.3018687
Yagan, O., Qian, D., Zhang, J., and Cochran, D. (2012). Optimal allocation of interconnecting links in cyber-physical systems: Interdependence, cascading failures, and robustness. IEEE Trans. Parallel Distributed Syst. 23 (9), 1708–1720. doi:10.1109/tpds.2012.62
Yan, J., Tang, Y., He, H., and Sun, Y. (2015). Cascading failure analysis with dc power flow model and transient stability analysis. IEEE Trans. Power Syst. 30 (1), 285–297. doi:10.1109/tpwrs.2014.2322082
Yao, R., Huang, S., Sun, K., Liu, F., Zhang, X., and Mei, S. (2016). A multi-timescale quasi-dynamic model for simulation of cascading outages. IEEE Trans. Power Syst. 31 (4), 3189–3201. doi:10.1109/tpwrs.2015.2466116
Zhang, Y., and Yağan, O. (2016). Optimizing the robustness of electrical power systems against cascading failures. Sci. Rep. 6, 27625. doi:10.1038/srep27625
Zhang, Y., and Yağan, O. (2020). Robustness of interdependent cyber-physical systems against cascading failures. IEEE Trans. Automatic Control 65 (2), 711–726. doi:10.1109/tac.2019.2918120
Zhang, Y., Yang, N., and Lall, U. (2016). Modeling and simulation of the vulnerability of interdependent power-water infrastructure networks to cascading failures. J. Syst. Sci. Syst. Eng. 25 (1), 102–118. doi:10.1007/s11518-016-5295-3
Zhao, G., and Xing, L. (2020). Reliability analysis of iot systems with competitions from cascading probabilistic function dependence. Reliab. Eng. Syst. Saf. 198, 106812. doi:10.1016/j.ress.2020.106812
Keywords: cyber-physical system, power grid, communication network, cascading failure, resilience, interdependency, critical infrastructure
Citation: Islam MZ, Lin Y, Vokkarane VM and Venkataramanan V (2023) Cyber-physical cascading failure and resilience of power grid: A comprehensive review. Front. Energy Res. 11:1095303. doi: 10.3389/fenrg.2023.1095303
Received: 11 November 2022; Accepted: 25 January 2023;
Published: 09 February 2023.
Edited by:
Zhengmao Li, Nanyang Technological University, SingaporeReviewed by:
Chen Chen, Xi’an Jiaotong University, ChinaGuangxiao Zhang, Nanyang Technological University, Singapore
Yesen Yan, in collaboration with reviewer GZ
Heling Yuan, Nanyang Technological University, Singapore
Zhao Shi, in collaboration with reviewer HY
Nan Zhou, Nanyang Technological University, Singapore
Dunjian Xie, in collaboration with reviewer NZ
Copyright © 2023 Islam, Lin, Vokkarane and Venkataramanan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuzhang Lin, yuzhang_lin@uml.edu