Joint game-theoretical optimization for load aggregators in demand response market considering the breach of residential consumers

Demand response (DR) with the participation of load aggregator (LA) has received extensive attention in recent years due to the increasing energy demand. However, LA has to face the risk that consumers may refuse to be controlled by LA due to the uncertainty of energy consumption on demand side. Therefore, this paper proposes a joint game-theoretical optimization for LAs in DR day-ahead market and intraday market considering the breach of residential consumers. In day-ahead market, LA will compete with other LAs and obtain the optimal bidding amount through a non-cooperative game process, to obtain the maximal self-profit. In intraday market, in order to make up for the breach amount of consumers, DR resource-deficit LAs can purchase resource from DR resource-surplus LAs via Nash bargaining process. Basically, Nash bargaining model is formulated and solved by translating the optimization problem into two sub-problems. Finally, a case study is performed to show the effectiveness of the proposed DR framework. Simulation results show that the whole profit of all LAs increases 25.9% compared with the scenario where LAs only participate in day-ahead market and will be punished by DR market due to the bidding breach.

1 Introduction

Energy consumption is the main source of carbon emissions, in which power industry accounts for about 41%. Therefore, solving the carbon emissions in power industry will contribute to achieving the zero-carbon goal. In recent years, the development of renewable energy generation is an effective means to reduce the emissions from generation side (Jin et al., 2022). Meanwhile, it is also a negligible way to develop energy efficiency management technology from demand side. Under the background, demand response is extensively employed to improve energy consumption efficiency and reduce carbon emissions (Schneider et al., 2022)(Ghasemi and Enayatzare, 2018). However, considering energy consumption level of individual is too low to participate in DR market, load aggregator (LA) is generally introduced to aggregate DR resource of consumers to be in DR (Lu et al., 2020)(Bao and Zeng, 2021). LA can exploit DR potential of demand side deeply and improve the performance of DR in load shaping (Ovalle P Vuelvas et al., 2021)- (Mohseni et al., 2021a).

Current DR framework with LA is roughly categorized into two types from the level of decision-maker’s number, i.e., individual-based and multiple individuals-based decision. Authors in (Li et al., 2022) propose an optimal incentive model based on the principal-agent theory for LA, in order to attract shiftable loads to DR. Simulation result shows that LA needs to adjust the intensity of incentive contracts based on resource scarcity. While in (Di Somma et al., 2019), a stochastic mixed-integer linear programming model is formulated to solve LA’s optimal bidding strategy considering the presence of demand flexibility. As for multiple individuals-based decision, game theory, which is good at solving the optimization problem of multiple decision-making subjects, has been widely employed to describe the competition behavior among LAs (Yang et al., 2013)(Maharjanc et al., 2013). For example, authors in (Mohseni et al., 2021b) reveal the strategic behavior of energy utilities, LAs, and consumers by describing Stackelberg game relationship, and meanwhile, the proposed game-based mechanism can reduce lifetime cost of the system. While in (Liu et al., 2017), a non-cooperative game model is constructed for multiple LAs to solve the optimal bidding strategy of each LA in day-ahead DR market.

The above research mainly focuses on the formulation of DR mechanism from the aspect of LAs. However, the characteristic of DR resource on demand side is generally neglected, such as, the uncertainty of energy consumption. Accordingly, some researchers concentrate on DR resource modeling in proposing DR framework. Authors in (Song et al., 2020) (Wang et al., 2020a) establish a new model to quantify the uncertainty of energy consumption on residential side and then the bidding optimization model for LA is constructed considering the uncertainty. A robust optimal bidding model in (Wang et al., 2020b) is proposed considering the uncertainty of distributed generation and price-based responsive load. In (Zhang et al., 2015), an energy storage capacity optimization model is developed based on grading compensation rules, in order to compensate for energy shortage resulting from the uncertainty factors. By reviewing the referred research, the uncertainty of energy consumption is usually solved from optimization technology and auxiliary equipment. Actually, except for the above ways, the influence of demand side’s uncertainty on DR can also be solved via DR market mechanism. Accordingly, in this paper, a DR market consisting of day-ahead market and intraday market is proposed to solve the breach of residential consumers caused by the uncertainty of energy consumption. In order to solve the trading problem in two DR markets, a joint game-theoretical optimization approach is proposed, which consists of non-cooperative game and Nash bargaining game. In day-ahead market, all LAs participate in the bidding competition for market share with other LAs under non-cooperative game mode considering profit-oriented character of individual. In real-time scheduling, each LA controls the operation of DR resource according to the bidding amount. However, it is difficult for some LAs to complete the bidding amount due to the breach of consumers. Therefore, in intraday market, LAs will take part in DR resource matching trading. In the trading, resource-deficit LA can purchase emergent DR resource from resource-surplus LA. In order to maximize their own interest, the seller and the buyer will start negotiations about trading price and amount. Consequently, such negotiation process can be described as Nash bargaining game. The Nash bargaining trading in intraday market can reduce the influence of the uncertainty on DR and contribute to the performance of DR. In brief, the contributions of this paper are as follows.

(1) A DR framework is proposed to solve the breach problem of DR resource by proposing a joint game-theoretical optimization approach in DR day-ahead market and intraday market.

(2) A non-cooperative game approach is formulated to describe the competition behavior of LAs in day-ahead market and optimize the bidding strategy for peak load shifting.

(3) A Nash bargaining game is designed to match the trading between the resource-deficit LAs and resource-surplus LAs to make up for the breach amount of LAs.

The proposed DR framework is introduced in Section 2. In Section 3, 4, the joint game-theoretical approach is formulated. Then, case study is presented in Section 5. Finally, this paper is concluded in Section 6.

2 The proposed DR framework

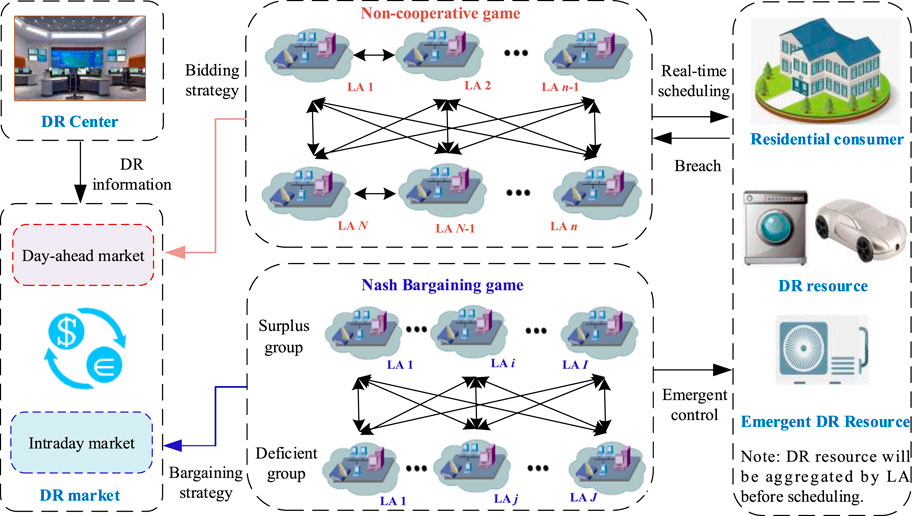
The proposed framework for residential DR program consists of day-ahead market and intraday market, which is shown in Figure 1. In day-ahead market, each LA competes with other LAs for the bidding amount of load reduction to maximize the self-profit. And then during real-time scheduling period, LA controls the operation state of DR resource of residential consumers according to the bidding amount. Note that, before performing DR program, LA will sign the contract with consumers and can control DR resource of consumers. However, due to the randomness of energy consumption on residential side, some consumers may fail to respond to the scheduling scheme of LA, resulting in missed bidding amount. Therefore, such LAs can purchase emergent DR resource (e.g., air conditioner) via intraday market to make up for the deficit.

FIGURE 1

FIGURE 1. DR framework considering day-ahead market and intraday market.

Basically, this paper formulates the following scenario. DR center broadcasts DR price information to day-ahead market. There are N LAs who will participate in the bidding competition in the market. According to the broadcasted information, LAs will make the optimal bidding strategy to maximize the self-profit with non-cooperative game manner. While in DR intraday market, LAs are divided into two groups: one has the surplus DR resource, the other has the deficit. The surplus LA can sell DR resource to the deficit LA. In order to improve the success rate of the trading, Nash bargaining game is introduced into the trading between seller and buyer. Additionally, the proposed DR framework needs to be supported by grid’s physical platform. Therefore, it is assumed that: (a) LAs can communicate with DR center via bi-directional information network. (b) Advanced metering infrastructure is equipped on residential side, including smart meter, bidirectional information network, and measuring-data management system.

3 Non-cooperative game in day-ahead market

In day-ahead market, the information about DR period and price will be broadcasted to all LAs. Based on the broadcasted information, LAs will submit their own bidding amount to the market. Assume that DR is conducted during and N LAs participating in the market constitutes the set $\mathcal{H}=\left\{\mathrm{1,2},\cdots ,H\right\}$. The bidding amount of LA n is $L_n^h$ in period h, then the total bidding amount in the market can be expressed as:

$L_h={\displaystyle \sum }_{n=1}^N{L}_n^h.(1)$

Considering DR has an effluence on the consumption satisfaction of consumers, LA will make an economic compensation to consumers. Assume that compensation price is γ dollars/MWh, and then the total profit of LA n is:

$U_n={\displaystyle \sum }_{h=1}^H\left(p_h{L}_n^h-\gamma L_n^h\right),(2)$

where p_h is DR price with dollars/MWh. Since DR price is determined by DR market, assume that DR price is in linear correlation with the bidding amount in the market. That is

$p_h=b_h-a_h{L}_h,(3)$

where $a_h>0,b_h>0$ are price parameters whose values are correlated with period h. Accordingly, LA’s target is to maximize the profit, which can be expressed as

$\left\{\begin{array}{l}\max U_n\left(L_n^h\right)\\ \mathrm{s}.\mathrm{t}.0\le L_n^h\le L_n^{h,\max }\end{array}\right.,(4)$

where $L_n^{h,\max }$ is the maximal DR resource of consumers in period h for LA n. Since the market price p_h is determined by the whole bidding amount, the decision-making process of LA will be affected by the decision-making behavior of other LAs. That is, day-ahead bidding process of LA is a typical non-cooperative game. The formulated non-cooperative game is presented as follows (Guo et al., 2021):

$•$  Players: all LAs in day-ahead market;

 $•$ Strategy: LA $n\in \mathcal{N}$ optimizes its bidding strategy $L_n^h$;

$•$  Payoffs: the total profit of LA n during the whole periods is

$U_n({\mathit{L}}_n,{\mathit{L}}_{-n})={\displaystyle \sum }_{h=1}^H\left(p_h{L}_n^h-\gamma \right.L_n^h),(5)$

where ${\mathit{L}}_n=\left[L_n^1,L_n^2,\cdots ,L_n^H\right]$ is the bidding strategy set of LA n during H time periods, ${\mathit{L}}_{-n}=\left[{\mathit{L}}_1,\cdots ,{\mathit{L}}_{n-1},{\mathit{L}}_{n+1},\cdots ,{\mathit{L}}_N\right]$ is the bidding strategy set of other LAs except LA n. Each LA will optimize the bidding amount of DR resource to maximize its own payoff according to the strategies of other LAs until no LA wants to change. Such equilibrium state is called Nash equilibrium, which can be expressed as follows:

$U_n\left({\mathit{L}}_n^{\ast },{\mathit{L}}_{-n}^{\ast }\right)\ge U_n\left({\mathit{L}}_n,{\mathit{L}}_{-n}^{\ast }\right)\forall n\in \mathcal{N},(6)$

where $\left({\mathit{L}}_n^{\ast },{\mathit{L}}_{-n}^{\ast }\right)$ is the Nash equilibrium for the formulated non-cooperative game.

4 Nash bargaining game in intraday market

Due to the randomness of energy consumption, consumers cannot completely obey the control of LA. It is unavoidable for consumers to break the contract during real-time scheduling. Consequently, it is difficult to achieve the target for LAs who have obtained the high bidding amount in day-ahead market. Therefore, such LAs have to purchase emergent DR resource from intraday market, otherwise they will be punished by the market. The trading process in the intraday market is described with Nash bargaining game.

4.1 Breach model of DR resource

Assume that the breach amount of consumers is $B_n^h$ in the control region of LA n. It is obvious that the value of $B_n^h$ is in [0, $L_n^h$]. In order to describe the probabilistic property of the breach amount, the truncated normal distribution is adopted to simulate stochastic distribution of $B_n^h$. That is, $B_n^h\sim N\left({\mu }_n,{\sigma }_n^2,{\delta }_n^{\mathrm{l}},{\delta }_n^{\mathrm{u}}\right)$ and the probability density function is (Pearn et al., 2007)

$\begin{array}{l}F\left(B_n^h,{\mu }_n,{\sigma }_n^2,{\delta }_n^{\mathrm{l}},{\delta }_n^{\mathrm{u}}\right)=\left\{\begin{array}{cc}\frac{\phi \left(\frac{B_n^h-{\mu }_n}{{\sigma }_n}\right)}{\sigma \left[\mathrm{\Phi }\left(\frac{{\delta }_n^{\mathrm{u}}-{\mu }_n}{{\sigma }_n}\right)-\mathrm{\Phi }\left(\frac{{\delta }_n^{\mathrm{l}}-{\mu }_n}{{\sigma }_n}\right)\right]}& {\delta }_n^{\mathrm{l}}\le B_n^h\le {\delta }_n^{\mathrm{u}}\\ 0& B_n^h>{\delta }_n^{\mathrm{u}},B_n^h<{\delta }_n^{\mathrm{l},}\end{array}\right.\end{array}(7)$

where ${\mu }_n$ and ${\sigma }_n^2$ are the expectation and variance of the normal distribution, ${\delta }_n^{\mathrm{l}}$ and ${\delta }_n^{\mathrm{u}}$ are the upper and lower limits of $B_n^h$, $\phi \left(•\right)$ and $\mathrm{\Phi }\left(•\right)$ are the probability density function and cumulative distribution function of standard normal distribution.

Considering the worst case is that all consumers break the contract while the best case is that all consumers obey the control of LA. Therefore, the upper and lower limits of $B_n^h$ can be set as ${\delta }_n^{\mathrm{l}}=0$ and ${\delta }_n^{\mathrm{u}}=L_n^h$. Accordingly, the expected breach amount in the control region of LA n can be expressed as

$E{B}_n^h={\mu }_n+{\sigma }_n\frac{\phi \left(-{\mu }_n/{\sigma }_n\right)-\phi \left(L_n^h-{\mu }_n/{\sigma }_n\right)}{\mathrm{\Phi }\left(L_n^h-{\mu }_n/{\sigma }_n\right)-\mathrm{Ф}\left(-{\mu }_n/{\sigma }_n\right)}.(8)$

Note that, the expected breach amount $E{B}_n^h$ is mainly suitable for the case that the bidding amount $L_n^h$ is greater than 0. It is obvious that $E{B}_n^h=0$ when the bidding amount is equal to 0. For breach amount $E{B}_n^h$, LA will be punished by DR market. Assume that the penalty price increases with the increase of the breach amount, which is designed as

$f\left(E{B}_n^h\right)=k_1+k_{2}E{B}_n^h,(9)$

where k₁ and k₂ are price parameters determined by DR market.

4.2 Emergent DR resource model

LA needs emergent DR resource to make up the breach amount caused by consumers. Considering the interruptible characteristic of air conditioner, LA can take air conditioner as the emergent DR resource. In order to reduce the influence of DR on consumers, the control of air conditioner must satisfy consumer’s comfortable demand. That is, the indoor temperature with air conditioner must be in a certain range after conducting DR program. The relationship between the indoor temperature and the operation state of air conditioner is shown as (Lu, 2012) (Bashash and Fathy, 2012)

$T_{\mathrm{i}\mathrm{n}}\left(h+1\right)={\mathrm{e}}^{-∆h/\mathrm{R}\mathrm{C}}{T}_{\mathrm{i}\mathrm{n}}\left(h\right)+\left(1-{\mathrm{e}}^{-∆h/\mathrm{R}\mathrm{C}}\right)T_{\mathrm{o}\mathrm{u}\mathrm{t}}\left(h\right)-\eta R\left(1-{\mathrm{e}}^{-∆h/RC}\right)P_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}S\left(h\right),(10)$

where T_in is the indoor temperature, T_out is the environmental temperature, $P_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}$ is the energy demand of air conditioner during period h, η is the energy efficiency ratio of air-conditioner, R is the equivalent thermal resistance, C is equivalent heat capacity, e is the natural constant, S(h) is the operation state of air conditioner (i.e., S(h) = 0 represents the off state and S(h) = 1 represents the on state). LA will decide whether to control air conditioner according to the indoor temperature $T_{\mathrm{i}\mathrm{n}}\left(h+1\right)$ and the setting temperature of consumer $T_{\max }$. Air conditioner cannot be controlled if $T_{\mathrm{i}\mathrm{n}}\left(h+1\right)>T_{\max }$, otherwise it will take part in the emergent control. Accordingly, the aggregated emergent DR resource can be expressed as

$L_{n,\mathrm{a}\mathrm{c}}^h={\displaystyle \sum }_{n_{\mathrm{a}\mathrm{c}}=1}^{N_{\mathrm{a}\mathrm{c}}}{P}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}^{n_{\mathrm{a}\mathrm{c}}}{J}_{n_{\mathrm{a}\mathrm{c}}}^h,(11)$

where $J_{n_{\mathrm{a}\mathrm{c}}}^h=1$ represents consumer m’s air conditioner is in DR, otherwise $J_{n_{\mathrm{a}\mathrm{c}}}^h=0$; $N_{\mathrm{a}\mathrm{c}}$ represents the number of consumers who are controlled by LA n.

4.3 Nash bargaining model in intraday market

According to the aggregated emergent DR resource $L_{n,\mathrm{a}\mathrm{c}}^h$ and the breach amount $E{B}_n^h$, LA can determine if it can make up for the shortage of bidding amount. However, it is impossible that all LAs can solve the problem of breach amount with its own emergent DR resource. More possibly, some LAs may have surplus DR resource after making up for the shortage, while other LAs still have the deficit. The resource-surplus LA expects to sell DR resource for the higher profit, while the resource-deficit LA expects to purchase the resource to reduce the penalty cost. In order to realize the maximization of resource utilization and social benefit, these LAs can make an energy trading via intraday market. The deficit or surplus amount of LA n in period h is

$L_{n,\mathrm{e}\mathrm{r}}^h=L_{n,\mathrm{a}\mathrm{c}}^h-E{B}_n^h,(12)$

where $L_{n,\mathrm{e}\mathrm{r}}^h>0$ represents LA n has the surplus DR resource in period h, otherwise $L_{n,\mathrm{e}\mathrm{r}}^h\le 0$. Assume that N₁ LAs have surplus DR resource with the set ${\mathcal{N}}_1=\left\{\mathrm{1,2},\cdots ,N_1\right\}$ and N₂ LAs have deficit in DR resource with the set ${\mathcal{N}}_2=\left\{\mathrm{1,2},\cdots ,N_2\right\}$. In order to describe the trading among resource-surplus LAs and resource-deficit LAs, Nash bargaining game theory (Fan et al., 2018) (Li et al., 2021) is employed. Nash bargaining model can be formulated as

$\max {\displaystyle \prod }_{n_1=1}^{N_1}{\left(A_{n_1}^0-A_{n_1}+{\pi }_{n_1}\right)}^{{\lambda }_{n_1}}{\displaystyle \prod }_{n_2=1}^{N_2}{\left(A_{n_2}^0-A_{n_2}-{\pi }_{n_2}\right)}^{{\lambda }_{n_2}},(13)$

where variable $A_{n_1}^0$ and $A_{n_2}^0$ are the breaking points of negotiation between the resource-surplus LA n₁ (i.e., the seller) and the resource-deficit LA n₂ (i.e., the buyer). Note that, Nash bargaining process is conducted during each time period. The trading in intraday market is independent during different time periods. Each LA can determine its role, i.e., seller or buyer, according to the resource-surplus/deficit. Furthermore, the breaking point of negotiation usually refers to the sellers and the buyers cannot reach the negotiation. In the proposed scenario, the breaking point of negotiation is the case where both parties do not participate in the trading in intraday market. That is, the cost of the seller is 0 and the cost of the buyer is the penalty cost due to the breach of consumers. Accordingly, the expression of $A_{n_1}^0$ and $A_{n_2}^0$ are

$\left\{\begin{array}{l}{A}_{n_1}^0=0\\ A_{n_2}^0=\left|L_{n_2,\mathrm{e}\mathrm{r}}^h\right|f\left(\left|L_{n_2,\mathrm{e}\mathrm{r}}^h\right|\right),\end{array}\right.(14)$

Variable $A_{n_1}$ and $A_{n_2}$ are the cost of LA n₁ and n₂ in the trading. The resource-surplus LAs have to pay the compensation to consumers. The resource-deficit LAs have to pay the trading cost to the sellers and the penalty of the deficit to DR market. Accordingly, $A_{n_1}$ and $A_{n_2}$ can be expressed as following forms

$\left\{\begin{array}{l}{A}_{n_1}=c_{n_1}{\displaystyle \sum }_{n_2=1}^{N_2}{Q}_{n_1{n}_2}^h\\ A_{n_2}=f\left({\displaystyle \sum }_{n_1=1}^{N_1}{Q}_{n_1{n}_2}^h-\left|L_{n_2,\mathrm{e}\mathrm{r}}^h\right|\right)\cdot \left({\displaystyle \sum }_{n_1=1}^{N_1}{Q}_{n_1{n}_2}^h-\left|L_{n_2,\mathrm{e}\mathrm{r}}^h\right|\right),\end{array}\right.(15)$

Where $Q_{n_1{n}_2}^h$ is the trading volume between LA n₁ and n₂, $c_{n_1}$ is the compensation price to consumers.

Variable ${\pi }_{n_1}$ and ${\pi }_{n_2}$ are the payments of the seller and the buyer. Accordingly, the expression of ${\pi }_{n_1}$ and ${\pi }_{n_2}$ are

$\left\{\begin{array}{l}{\pi }_{n_1}={\displaystyle \sum }_{n_2=1}^{N_2}{Q}_{n_1{n}_2}^h{P}_{n_1{n}_2}^h\\ {\pi }_{n_2}={\displaystyle \sum }_{n_1=1}^{N_1}{Q}_{n_1{n}_2}^h{P}_{n_1{n}_2,}^h\end{array}\right.(16)$

where $P_{n_1{n}_2}^h$ is the trading price between LA n₁ and LA n₂.

Variable ${\lambda }_{n_1}$ and ${\lambda }_{n_2}$ are the bargaining power of LA n₁ and n₂, which are used to measure the contribution of each LA in the trading. The bargaining power is generally determined according to the supply-demand relationship between the buyer and the seller and their marginal contributions. In order to calculate the bargaining power, the negotiation weight has to be introduced. In the proposed scenario, if the total emergent DR resource is larger than the total breach amount, the negotiation weight of the buyer will be higher. Otherwise, the negotiation weight of the seller will be higher. Assume that the negotiation weights of the buyer and the seller are $w_{\mathrm{s}\mathrm{e}\mathrm{l}},w_{\mathrm{b}\mathrm{u}\mathrm{y}}\in \left[\mathrm{0,1}\right]$, which are satisfied

$\left\{\begin{array}{l}{w}_{\mathrm{s}\mathrm{e}\mathrm{l}}\ge w_{\mathrm{b}\mathrm{u}\mathrm{y}}\mathrm{i}\mathrm{f}{\displaystyle \sum }_{n_1=1}^{N_1}{L}_{n_1,\mathrm{e}\mathrm{r}}^h\le {\displaystyle \sum }_{n_2=1}^{N_2}-L_{n_2,\mathrm{e}\mathrm{r}}^h\\ w_{\mathrm{s}\mathrm{e}\mathrm{l}}\le w_{\mathrm{b}\mathrm{u}\mathrm{y}}\mathrm{i}\mathrm{f}{\displaystyle \sum }_{n_1=1}^{N_1}{L}_{n_1,\mathrm{e}\mathrm{r}}^h\ge {\displaystyle \sum }_{n_2=1}^{N_2}-L_{n_2,\mathrm{e}\mathrm{r}}^h\\ w_{\mathrm{s}\mathrm{e}\mathrm{l}}+w_{\mathrm{b}\mathrm{u}\mathrm{y}}=1,\end{array}\right.(17)$

Basically, the bargaining power of LA can be defined according to its own contribution in its own set. That is

$\left\{\begin{array}{l}{\lambda }_{n_1}=w_{\mathrm{s}\mathrm{e}\mathrm{l}}\frac{L_{n_1,\mathrm{e}\mathrm{r}}^h}{{\displaystyle \sum }_{n_1}{L}_{n_1,\mathrm{e}\mathrm{r}}^h},\forall n_1\in {\mathcal{N}}_1\\ {\lambda }_{n_2}=w_{\mathrm{b}\mathrm{u}\mathrm{y}}\frac{L_{n_2,\mathrm{e}\mathrm{r}}^h}{{\displaystyle \sum }_{n_2}{L}_{n_2,\mathrm{e}\mathrm{r}}^h},\forall n_2\in {\mathcal{N}}_2,\end{array}\right.(18)$

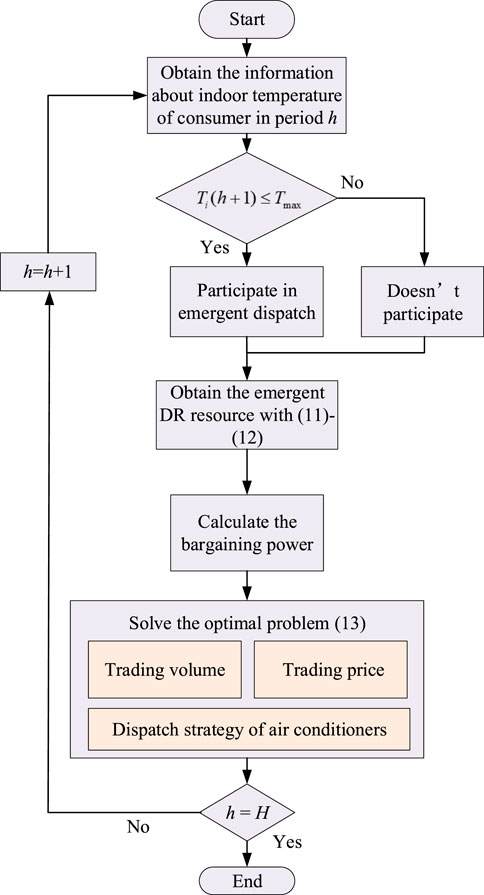
According to the above analysis, Nash bargaining process among LAs in intraday market is shown in Figure 2. Nash bargaining process during each period h are.

FIGURE 2

FIGURE 2. Nash bargaining process of LA in intraday market.

Step 1. Ascertain the breach amount of DR resource and the aggregated emergent DR resource based on (11).

Step 2. Calculate the resource redundancy or deficit of LA based on (12).

Step 3. Calculate the bargaining power of LA based on (17)∼(18).

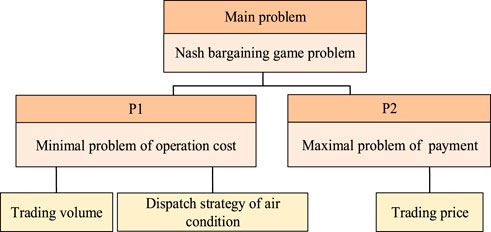
Step 4. Optimize the trading volume and price according to Nash bargaining model (13).The formulated Nash bargaining model is a non-convex optimization problem due to the binary variable in constraints (Robu et al., 2016)- (Kim et al., 2019). In order to solve the problem, optimization problem (13) can be translated into two sub-problems P1 and P2. The decomposition is shown in Figure 3.P1: Minimize the operation cost

$\min {\displaystyle \sum }_{n_1=1}^{N_1}{A}_{n_1}+{\displaystyle \sum }_{n_2=1}^{N_2}{A}_{n_2}.(19)$

P2: Maximize the payment

$\max \left[{\lambda }_{n_1}{\displaystyle \sum }_{n_1=1}^{N_1}\ln \left(A_{n_1}^0-{\overline{A}}_{n_1}+{\pi }_{n_1}\right)+{\lambda }_{n_2}{\displaystyle \sum }_{n_2=1}^{N_2}\ln \left(A_{n_2}^0-{\overline{A}}_{n_2}-{\pi }_{n_2}\right)\right].(20)$

where ${\overline{A}}_{n_1}$ and ${\overline{A}}_{n_2}$ are the optimal solution of problem P1.

FIGURE 3

FIGURE 3. The decomposition of Nash bargaining problem.

Theorem 1. .Nash bargaining solution of problem (13) is equivalent to the solution of problem (19).

Proof. .Assume that the optimal solution of (13) is $\left\{A_{n_1}^{*},{\pi }_{n_1}^{*},A_{n_2}^{*},{\pi }_{n_2}^{*}\right\}$ for LA $n_1\in {\mathcal{N}}_1,n_2\in {\mathcal{N}}_2$, but ${\displaystyle \sum }_{n_1=1}^{N_1}{A}_{n_1}^{*}+{\displaystyle \sum }_{n_2=1}^{N_2}{A}_{n_2}^{*}$ is not the minimal value of problem (19). There exists $A_{n_2}^{\prime }\ne A_{n_2}^{*}$ that satisfies

${\displaystyle \sum }_{n_1=1}^{N_1}{A}_{n_1}^{*}+{\displaystyle \sum }_{n_2=1}^{N_2}{A}_{n_2}^{\prime }<{\displaystyle \sum }_{n_1=1}^{N_1}{A}_{n_1}^{*}+{\displaystyle \sum }_{n_2=1}^{N_2}{A}_{n_2}^{*}$

Let $∆A_{n_2}=A_{n_2}^{\prime }-A_{n_2}^{*}$, then

${\displaystyle \sum }_{n_2=1}^{N_2}∆A_{n_2}<0(21)$

When

$\left\{\begin{array}{l}{A}_{n_1}=A_{n_1}^{*},{\pi }_{n_1}={\pi }_{n_1}^{*}{n}_1=1,...,N_1\\ A_{n_2}=A_{n_2}^{*}+∆A_{n_2}{n}_2=1,...,N_2\\ {\pi }_{n_2}={\pi }_{n_2}^{*}-∆A_{n_2}{n}_2=1,...,N_2-1\\ {\pi }_{N_2}={\pi }_{N_2}^{*}-∆A_{N_2}+\omega \end{array}\right.$

model (13) can be written as

$\begin{array}{l}{\displaystyle \prod }_{n_1=1}^{N_1}{\left(A_{n_1}^0-A_{n_1}+{\pi }_{n_1}\right)}^{{\lambda }_{n_1}}{\displaystyle \prod }_{n_2=1}^{N_2}{\left(A_{n_2}^0-A_{n_2}-{\pi }_{n_2}\right)}^{{\lambda }_{n_2}}\\ ={\displaystyle \prod }_{n_1=1}^{N_1}{\left(A_{n_1}^0-A_{n_1}^{*}+{\pi }_{n_1}^{*}\right)}^{{\lambda }_{n_1}}{\displaystyle \prod }_{n_2=1}^{N_2-1}\left(A_{n_2}^0-(A_{n_2}^{*}+\Delta A_{n_2}^{*})-({\pi }_{n_2}^{*}-\Delta A_{n_2}^{*}){)}^{{\lambda }_{n_2}}\right.\\ \times (A_{N_2}^0-(A_{N_2}^{*}+\Delta A_{N_2}^{*})-({\pi }_{N_2}^{*}-\Delta A_{N_2}^{*}+\omega ){)}^{{\lambda }_{n_2}}\\ ={\displaystyle \prod }_{n_1=1}^{N_1}{\left(A_{n_1}^0-A_{n_1}^{*}+{\pi }_{n_1}^{*}\right)}^{{\lambda }_{n_1}}{\displaystyle \prod }_{n_2=1}^{N_2-1}{\left(A_{n_2}^0-A_{n_2}^{*}-{\pi }_{n_2}^{*}\right)}^{{\lambda }_{n_2}}\\ \times (A_{N_2}^0-A_{N_2}^{*}-({\pi }_{N_2}^{*}+\omega ){)}^{{\lambda }_{N_2}}\end{array}(22)$

Since ${\displaystyle \sum }_{n_1=1}^{N_1}{\pi }_{n_1}={\displaystyle \sum }_{n_2=1}^{N_2}{\pi }_{n_2}$, $\omega ={\displaystyle \sum }_{n_2=1}^{N_2}∆A_{n_2}<0$. That is

$\begin{array}{l}{\displaystyle \prod }_{n_1=1}^{N_1}{\left(A_{n_1}^0-A_{n_1}+{\pi }_{n_1}\right)}^{{\lambda }_{n_1}}{\displaystyle \prod }_{n_2=1}^{N_2}{\left(A_{n_2}^0-A_{n_2}-{\pi }_{n_2}\right)}^{{\lambda }_{n_2}}\\ >{\displaystyle \prod }_{n_1=1}^{N_1}{\left(A_{n_1}^0-A_{n_1}^{*}+{\pi }_{n_1}^{*}\right)}^{{\lambda }_{n_1}}{\displaystyle \prod }_{n_2=1}^{N_2}{\left(A_{n_2}^0-A_{n_2}^{*}-{\pi }_{n_2}^{*}\right)}^{{\lambda }_{n_2}}\end{array}(23)$

Inequality (23) is inconsistent with the condition that $\left\{A_{n_1}^{*},{\pi }_{n_1}^{*},A_{n_2}^{*},{\pi }_{n_2}^{*}\right\}$ is the optimal solution of (13). Proof is completed.After solving problem P1, $A_{n_1}$ and $A_{n_2}$ in model (13) can be considered as the constants. In order to improve the efficiency, the optimal solution of problem P2 can be obtained with Lagrange multiplier theory. The total profit $\overline{W}$ for all LAs under the optimal solution $\left\{A_{n_1}^{*},A_{n_2}^{*}\right\}$ can be expressed as

$\left\{\begin{array}{l}\overline{W}={\displaystyle \sum }_{n_1=1}^{N_1}{\overline{W}}_{n_1}+{\displaystyle \sum }_{n_2=1}^{N_2}{\overline{W}}_{n_2}\\ {\overline{W}}_{n_1}=A_{n_1}^0-{\overline{A}}_{n_1}\\ {\overline{W}}_{n_2}=A_{n_2}^0-{\overline{A}}_{n_2}\end{array}\right.(24)$

Where ${\overline{W}}_{n_1}$ and ${\overline{W}}_{n_2}$ are the cost savings of LA n₁ and n₂ via energy trading in intraday market.

Theorem 2. The payment ${\pi }_{n_1}$ and ${\pi }_{n_2}$ can be obtained with following distribution rule

$\left\{\begin{array}{l}{\pi }_{n_1}={\lambda }_{n_1}\cdot \overline{W}-{\overline{W}}_{n_1}\\ {\pi }_{n_2}={\overline{W}}_{n_2}-{\lambda }_{n_2}\cdot \overline{W}\end{array}\right.(25)$

Proof. Problem P2 can be translated into

$\max {\displaystyle \sum }_{n_1=1}^{N_1}{\lambda }_{n_1}\ln \left({\overline{W}}_{n_1}+{\pi }_{n_1}\right)+{\displaystyle \sum }_{n_2=1}^{N_2}{\lambda }_{n_2}\ln \left({\overline{W}}_{n_2}+{\pi }_{n_2}\right)(26)$

Since the buyer and the seller are equal in payment, there exists

${\displaystyle \sum }_{n_1=1}^{N_1}{\pi }_{n_1}={\displaystyle \sum }_{n_2=1}^{N_2}{\pi }_{n_2}(27)$

By introducing Lagrange multiplier $\theta$, Lagrange function is:

$L={\displaystyle \sum }_{n_1=1}^{N_1}{\lambda }_{n_1}\ln \left({\overline{W}}_{n_1}+{\pi }_{n_1}\right)+{\displaystyle \sum }_{n_2=1}^{N_2}{\lambda }_{n_2}\ln \left({\overline{W}}_{n_2}+{\pi }_{n_2}\right)+\theta \left({\displaystyle \sum }_{n_1=1}^{N_1}{\pi }_{n_1}-{\displaystyle \sum }_{n_2=1}^{N_2}{\pi }_{n_2}\right)(28)$

Accordingly

$\left\{\begin{array}{l}\frac{\partial L}{\partial {\pi }_{n_1}}=\frac{{\lambda }_{n_1}}{{\overline{W}}_{n_1}+{\pi }_{n_1}}+\theta =0\\ \frac{\partial L}{\partial {\pi }_{n_2}}=\frac{-{\lambda }_{n_2}}{{\overline{W}}_{n_2}+{\pi }_{n_2}}-\theta =0\end{array}\right.(29)$

Therefore,

$\left\{\begin{array}{l}{\pi }_{n_1}=-\frac{{\lambda }_{n_1}}{\theta }-{\overline{W}}_{n_1}\\ {\pi }_{n_2}=\frac{{\lambda }_{n_2}}{\theta }+{\overline{W}}_{n_2}\end{array}\right.(30)$

Since ${\displaystyle \sum }_{n_1=1}^{N_1}{\lambda }_{n_1}+{\displaystyle \sum }_{n_2=1}^{N_2}{\lambda }_{n_2}=1$, hence

$\theta =-\frac{1}{{\displaystyle \sum }_{n_1=1}^{N_1}{\overline{W}}_{n_1}+{\displaystyle \sum }_{n_2=1}^{N_2}{\overline{W}}_{n_2}}=-\frac{1}{\overline{W}}(31)$

Therefore,

$\left\{\begin{array}{l}{\overline{W}}_{n_1}+{\pi }_{n_1}={\lambda }_{n_1}\cdot \overline{W}\\ {\overline{W}}_{n_2}-{\pi }_{n_2}={\lambda }_{n_2}\cdot \overline{W}\end{array}\right.(32)$

According to model (32), each LA can obtain its own payment through its bargaining power and the total profit. Proof is completed.

5 Case study

In this section, a case study is presented to show the performance of the proposed DR framework. Assume that there are 5 LAs who will participate in DR market. DR center determines that DR program is performed during 18:00–20:00 and each time period is 15 min. That is, DR framework will be conducted during $\mathcal{H}=\left\{\mathrm{1,2},\cdots ,8\right\}$ periods.

5.1 Game result in day-ahead market

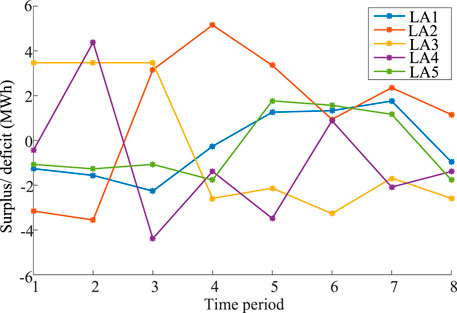
Figure 4 shows the optimal bidding result of 5 LAs in day-ahead market. During time period 1–8, the bidding amount of LAs follows the similar trend of DR price. For example, the bidding amount of LA 1 increases from 1.85 MWh in period 1 to 1.97 MWh in period 5 and then decreases to 1.88 MWh in period 8. However, LA 2 and LA 4 have the same bidding amount during all periods. The main reason is that LA 2 and LA 4 cannot bid higher amount even if DR price is high due to the limitation of the aggregated DR resource. On the other hand, since LA 5 has more DR resource, comparing with other LAs, the bidding amount reaches the highest level in period 5 with the highest DR price. From the above analysis, it depicts that dynamic adjustment of DR price can guide LAs to participate in the competition in day-ahead market. When load on demand side is in a high level, DR center can raise DR price by regulating parameters $a_h,b_h$. The high DR price can absorb LAs bidding more DR resource. When load on demand side is in a low level, DR center can cut down DR price to reduce DR cost.

FIGURE 4

FIGURE 4. Bidding result of 5 LAs in day-ahead market.

5.2 Bargaining result in intraday market

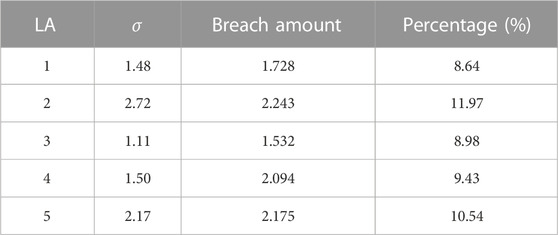
Since residential consumers have various energy consumption characteristics, consumers’ breach amount in each LA’s region will be different. Therefore, assume that the parameters of normal distribution of breach amount for 5 LAs are μ = 0, σ = [1.48, 2.72, 1.11, 1.50, 2.17]. According to model (8), the breach amount of all LAs can be calculated. Table 1 shows 5 LAs’ expected value of breach amount during time period 1. In the table, the breach amount of LA 2 has account for a high percentage 11.97% since the variance of the normal distribution of LA 2 is set as the highest value 2.72. The breach amount may lead to the failure in completing load-peak shaving scheme of DR center. It demonstrates that the breach amount of LAs has a negative influence on DR program. Therefore, it is necessary to introduce the intraday market to make up for the disadvantage of day-ahead market.

TABLE 1

TABLE 1. The expected value of breach amount of 5 LAs in period 1.

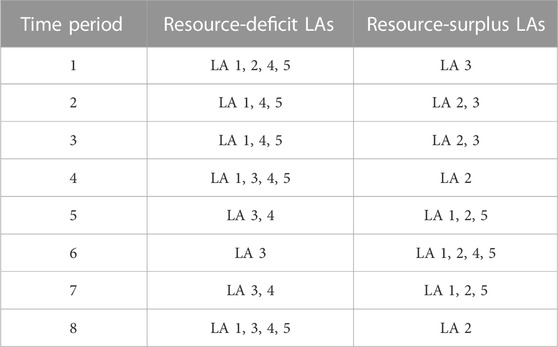
According to the breach amount and emergent DR resource, resource-surplus LAs and resource-deficit LAs during each time period can be determined, which are presented in Figure 5 and Table 2. It shows that the surplus/deficit has a strong randomness in each period due to the randomness of energy consumption on residential side. For example, the deficit of DR resource of LA 2 has reached to about 5 MWh during time period 4. From Table 2, it depicts that the division of LAs are dynamic and different during each time period. For example, during period 1, LA 1, 2, 4, 5 belongs to resource-deficit group and LA 3 is in resource-surplus group. However, each LA plays a complete opposite role during period 6. But overall, the resource-deficit exceeds the resource-surplus in the intraday market. Due to the shortage of emergent DR resource, breach amount of LAs cannot be fully compensated even if all the emergent DR resource is traded.

FIGURE 5

FIGURE 5. The resource-surplus/deficit amount of LAs in each time period.

TABLE 2

TABLE 2. The resource-surplus/deficit state of LAs in each time period.

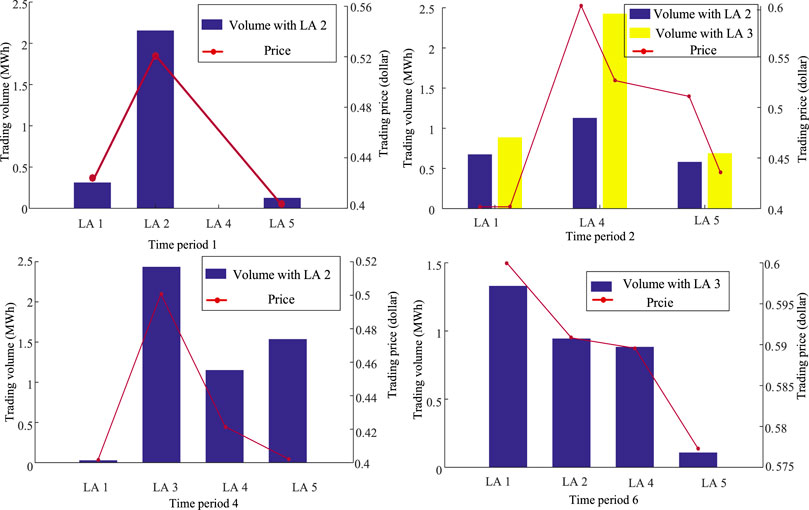
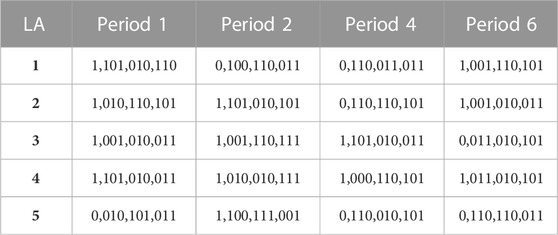
According to Figure 5 and Table 2, the trading can be matched among the resource-surplus LAs and the resource-deficit LAs. Under Nash bargaining game framework, the trading results during time period 1, 2, 4, 6 are shown in Figure 6. Here, the trading during period 1 is taken as an example. According to Table 2, it is known that the demand exceeds the supply during period 1. The resource-surplus side is only LA 3 and the resource-deficit side contains LA 1, LA 2, LA 4, LA 5. Basically, the trading volumes of LA 3 with the resource-deficit LAs are 0.32 MWh, 2.21 MWh, 0 MWh, and 1.06 MWh, respectively. The trading prices are 0.43 dollars/kWh, 0.53 dollars/kWh, 0 dollars/kWh and 0.4 dollars/kWh, respectively. After the trading, the resource-surplus LAs will schedule its emergent DR resource to make up for the breach. It is apparent that the breach amount of DR resource can be reduced to a great extent. Therefore, by introducing the intraday market, DR resource on residential side can realize the efficient utilization and load-peak shaving scheme of DR center can be completed to the greatest extent. In addition, the control strategy of air conditioners during time period 1, 2, 4, 6 is presented in Table 3. In the table, symbol 0 represents air conditioner is in close state and symbol 1 is in open state. Since controlling each air conditioner may lead to the computational burden, 100 air conditioners is aggregated into one group as a dispatching unit. Therefore, Table 3 shows the control strategies of 10 groups and the operation state of air conditioner is the same in each group.

FIGURE 6

FIGURE 6. Nash bargaining result during time period 1, 2, 4, 6.

TABLE 3

TABLE 3. Control strategy of air conditioners during time period 1, 2, 4, 6.

5.3 Payment analysis of LA

The proposed DR scheme cannot only make full use of DR resource, but also contribute to the profit of LAs. Concretely, the profits of 5 LAs in intraday market are 888.9 dollars, 1887.5 dollars, 1696.6 dollars, 2254.7 dollars, 529.8 dollars. Figure 7 shows the profit of each LA in each time period. It demonstrates that all LAs can realize the increase of profit and the total profit of 5 LAs reaches 7257.5 dollars. Therefore, it is profitable for LAs to participate in Nash bargaining game to maximize the benefit of DR resource on residential side.

FIGURE 7

FIGURE 7. Profits of 5 LAs in intraday market.

Furthermore, in order to analyze the profit of LAs comprehensively, 3 cases are introduced to show the profit of LAs in DR market. Case 1 is the scenario where LAs only participate in day-ahead market and will be punished by DR market due to the bidding breach. Case 2 is the scenario where LAs will participate in DR intraday market but the trading mode is based on the non-cooperative bidding game. Case 3 is our proposed joint game-theoretical approach. The profits of LAs in different scenarios are shown in Table 4. From the table, one can see that LAs in case 3 will obtain the highest profits comparing with other Cases. The whole profit of all LAs increases 25.9%, 19.5% compared with the profit in case 1 and 2, respectively. It demonstrates that Nash bargaining game is more suitable to the intraday market comparing with non-cooperative bidding game.

TABLE 4

TABLE 4. Profits of LAs in different cases.

6 Conclusion

In this paper, a joint game-theoretical optimization for LAs in DR market is proposed considering the breach of residential consumers due to the uncertainty of energy consumption. Basically, DR market is divided into day-ahead market and intraday market. In day-ahead market, each LA participates in the competition of bidding amount with other LAs and the decision-making tool is non-cooperative game. In intraday market, Nash bargaining game is proposed to match the trading of emergent DR resource between the resource-deficit LAs and resource-surplus LAs, to reduce the influence of consumer’s breach. Simulation results show that the proposed game-based approach can reduce the influence of the uncertainty on DR and improve the performance of DR program. From the perspective of LAs, the whole profit of all LAs increases 25.9% compared with the single day-ahead market. From the perspective of DR center, load-peak shaving scheme can be completed to the greatest extent.

In this paper, we assume that air conditioner is taken as the emergent DR resource to make up for the resource deficit caused by the breach of residential consumers. However, emergent control of air conditioner may have a negative influence of consumers on energy consumption satisfaction. Therefore, it is worthwhile to study the emergent control problem considering the satisfaction of consumers. Additionally, we assume that DR price is in linear correlation with the bidding amount in day-ahead market, hence energy demand level of grid cannot affect DR market. Therefore, it is also worthwhile to design a comprehensive DR pricing mechanism.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, CY; Methodology, WM and XL; Software, WM; Validation, XD and QW; Formal analysis, WM; Investigation, CY; Resources, XD; Data curation, QW; Writing—original draft preparation, CY; Writing—review and editing, XL; Supervision, XL All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Jiangsu Province (Grant No. BK20221165).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bashash, S., and Fathy, H. (2012). Modeling and control of aggregate air conditioning loads for robust renewable power management. IEEE Trans. Control Syst. Technol 21 (4), 1318–1327. doi:10.1109/tcst.2012.2204261

CrossRef Full Text | Google Scholar

Di Somma, M., Graditi, G., and Siano, P. (2019). Optimal bidding strategy for a DER aggregator in the day-ahead market in the presence of demand flexibility. IEEE Trans. Industrial Electron 66 (2), 1509–1519. doi:10.1109/tie.2018.2829677

CrossRef Full Text | Google Scholar

Fan, S., Ai, Q., and Piao, L. (2018). Bargaining-based cooperative energy trading for distribution company and demand response. Appl. energy 226, 469–482. doi:10.1016/j.apenergy.2018.05.095

CrossRef Full Text | Google Scholar

Ghasemi, A., and Enayatzare, M. (2018). Optimal energy management of a renewable-based isolated microgrid with pumped-storage unit and demand response. Renew. Energy 123, 460–474. doi:10.1016/j.renene.2018.02.072

CrossRef Full Text | Google Scholar

Guo, N., Wang, Y., and Yan, G. (2021). A double-sided non-cooperative game in electricity market with demand response and parameterization of supply functions. Int. J. Electr. Power & Energy Syst 126, 106565. doi:10.1016/j.ijepes.2020.106565

CrossRef Full Text | Google Scholar

Hao, W., and Huang, J. (2017). Cooperative planning of renewable generations for interconnected microgrids. IEEE Trans. Smart Grid 7 (5), 2486–2496.

Google Scholar

Jin, J., Wen, Q., Cheng, S., Qiu, Y., Zhang, X., and Guo, X. (2022). Optimization of carbon emission reduction paths in the low-carbon power dispatching process. Renew. Energy 188, 425–436. doi:10.1016/j.renene.2022.02.054

CrossRef Full Text | Google Scholar

Kim, H., Lee, J., Bahrami, S., and Wong, V. W. S. (2019). Direct energy trading of microgrids in distribution energy market. IEEE Trans. Power Syst 35 (1), 639–651. doi:10.1109/tpwrs.2019.2926305

CrossRef Full Text | Google Scholar

Krueger, H., and Cruden, A. (2018). Modular strategy for aggregator control and data exchange in large scale Vehicle-to-Grid (V2G) applications. Energy Procedia 151, 7–11. doi:10.1016/j.egypro.2018.09.019

CrossRef Full Text | Google Scholar

Bao, M., and Zeng, D. (2021). A Bi-level model for the bidding strategy of an inter-regional electricity trading aggregator considering reliability requirements and transmission losses. IEEE Access 9, 13476–13487. doi:10.1109/access.2021.3051654

CrossRef Full Text | Google Scholar

Li, G., Li, Q., Song, W., and Wang, L. (2021). Incentivizing distributed energy trading among prosumers: A general Nash bargaining approach. Int. J. Electr. Power & Energy Syst 131, 107100. doi:10.1016/j.ijepes.2021.107100

CrossRef Full Text | Google Scholar

Li, W., Han, R., Zhang, J., Sun, C., and Fu, P. (2022). An incentive strategy of shiftable load participation in demand response based on user electricity preference. Front. Energy Res. 9, 678828. doi:10.3389/fenrg.2021.678828

CrossRef Full Text | Google Scholar

Liu, X., Gao, B., and Luo, J. (2017). Non-cooperative game based hierarchical dispatch model of residential loads. Automation Electr. Power Syst 41 (14), 54–60.

Google Scholar

Lu, N. (2012). An evaluation of the HVAC load potential for providing load balancing service. IEEE Trans. Smart Grid 3 (3), 1263–1270. doi:10.1109/tsg.2012.2183649

CrossRef Full Text | Google Scholar

Lu, X., Li, K., Wang, F., Mi, Z., Sun, R., and Wang, X., (2020). Optimal bidding strategy of DER aggregator considering dual uncertainty via information gap decision theory. IEEE Trans. Industry Appl 57 (1), 158–169. doi:10.1109/tia.2020.3035553

CrossRef Full Text | Google Scholar

Maharjanc, S., Zhu, Q., Zhang, Y., Gjessing, S., and Basar, T. (2013). Dependable demand response management in the smart grid: A Stackelberg game approach. IEEE Trans. Smart Grid 4 (1), 120–132. doi:10.1109/tsg.2012.2223766

CrossRef Full Text | Google Scholar

Mohseni, S., Brent, A., Kelly, S., Browne, W. N., and Burmester, D. (2021). Strategic design optimisation of multi-energy-storage-technology micro-grids considering a two-stage game-theoretic market for demand response aggregation. Appl. Energy 287, 116563. doi:10.1016/j.apenergy.2021.116563

CrossRef Full Text | Google Scholar

Mohseni, S., Brent, A., Scott, K., Browne, W. N., and Burmester, D. (2021). Strategic design optimisation of multi-energy-storage-technology micro-grids considering a two-stage game-theoretic market for demand response aggregation. Appl. Energy 287, 116563. doi:10.1016/j.apenergy.2021.116563

CrossRef Full Text | Google Scholar

Ovalle P Vuelvas, J., Fajardo, A., Correa-Florez, C. A., and Ruiz, F. (2021). Optimal portfolio selection methodology for a demand response aggregator. Energies 14 (23), 7923. doi:10.3390/en14237923

CrossRef Full Text | Google Scholar

Pearn, W., Hung, H., Peng, N., and Huang, C. (2007). Testing process precision for truncated normal distributions. Microelectron. Reliab 47, 2275–2281. doi:10.1016/j.microrel.2006.12.001

CrossRef Full Text | Google Scholar

Robu, V., Chalkiadakis, G., Kota, R., Rogers, A., and Jennings, N. R. (2016). Rewarding cooperative virtual power plant formation using scoring rules. Energy 117, 19–28. doi:10.1016/j.energy.2016.10.077

CrossRef Full Text | Google Scholar

Schneider, I., Roozbehani, M., and Dahleh, M. (2022). An online learning framework for targeting demand response customers. IEEE Trans. Smart Grid 13 (1), 293–301. doi:10.1109/tsg.2021.3121686

CrossRef Full Text | Google Scholar

Song, Z., Shi, J., Li, S., Chen, Z., Yang, W., and Zhang, Z. (2020). Day ahead bidding of a load aggregator considering residential consumers demand response uncertainty modeling. Appl. Sci 10 (20), 7310. doi:10.3390/app10207310

CrossRef Full Text | Google Scholar

Wang, F., Ge, X., Yang, P., Li, K., Mi, Z., and Siano, P., (2020). Day-ahead optimal bidding and scheduling strategies for DER aggregator considering responsive uncertainty under real-time pricing. Energy 213, 118765. doi:10.1016/j.energy.2020.118765

CrossRef Full Text | Google Scholar

Wang, F., Xiang, B., Li, K., Ge, X., Lu, H., and Lai, J., (2020). Smart households’ aggregated capacity forecasting for load aggregators under incentive-based demand response programs. IEEE Trans. Industry Appl 56 (2), 1086–1097. doi:10.1109/tia.2020.2966426

CrossRef Full Text | Google Scholar

Yang, P., Tang, G., and Nehorai, A. (2013). A game-theoretic approach for optimal time-of-use electricity pricing. IEEE Trans. Power Syst 28 (2), 884–892. doi:10.1109/tpwrs.2012.2207134

CrossRef Full Text | Google Scholar

Zhang, K., Song, Y., and Yan, Z. (2015). Energy storage capacity optimization for load aggregators considering probability of demand response resources’ breach. Automation Electr. Power Syst 39, 127–133.

Google Scholar