Note on the performance of parametrization strategies to determine the decay heat of PWR fuel

The behavior of fuel assembly safety properties such as decay heat is often parametrized by a set of proxy variables such as burnup and by categorical variables like UOX or MOX. The standards ANS5.1 and DIN-25463 are examples of this strategy. They face the challenge to accurately approximate a wide range of possible fuel assembly states which occur in practice because they traditionally do not follow the nuclide vector evolution with a detailed microscopic model. While burnup is widely regarded as an important fuel parameter it is only an approximation or proxy for the physical relevant quantity which is the fuel nuclide vector. The performance of one of the latest and most advanced decay heat standards, DIN-25463-2014, is compared with Studsvik’s best-estimate code SSP SNF which uses a state-of-the-art microscopic model. Both the differences in initial nuclide vector after irradiation and the differences in decay heat between 1 s and 60 years are analyzed. Comparisons with realistic PWR core fuel inventories show that the margin between SSP SNF and DIN-25463-2014 varies in a range ±5% which is a manifestation of the challenge to accurately approximate the fuel state without detailed microscopic model. Given today’s small compute footprint of best-estimate codes for decay heat determination we conclude that parametrization strategies have little advantage except for applications like system codes used in transient analyses.

1 Introduction

The decay heat is an important safety parameter in many nuclear applications: it determines the fraction of energy not generated by fission but through delayed radioactive decay following a fission event, it determines the necessary capacity of emergency core cooling systems and of the active and passive heat removal systems for storage and transportation of nuclear fuel. With limited compute resources in the 1970s and 1980s decay heat and other safety parameters have often been parametrized by a set of proxy variables like burnup and by categorical variables like UOX or MOX fuel. We call these variables “proxy” because they do not represent the underlying physical quantity which is relevant for decay heat calculation: the nuclide vector of the fuel. For example, at constant burnup an infinite number of different nuclide vectors are possible because an infinite number of different irradiation histories can lead to the same integral energy release. In place of using an exact microscopic description of the evolution of the nuclide vector the parametrization strategies rely on fitting functions of 2nd tier parameters like burnup and fuel type to high-quality results from codes based on microscopic models or to empirically determined isotopic decay heat data.

Decay heat standards like ANS-5.1 (American Nuclear Society and ANSI/ANS-5.1-1979, 1979; American Nuclear Society and ANSI/ANS-5.1-2014, 2019) and DIN-25463 (Deutsches Institut für Normung, 2014b) are classical examples for this approach. The early versions of these standards in 1979 and 1982 used comparatively simple parametrizations. This had the advantage that calculations did only require a minimum amount of evaluated nuclear data like energy release per fission event and were limited to a handful of contributions of some important nuclides. No resource intensive summation of the many potential individual nuclide contributions was necessary.

In parallel more sophisticated codes like ORIGEN2 (Hesse, 1988), OREST (Croff, 1983), ORIGEN-S (Gauld, 2005) or SSP SNF (Becker et al., 2009; Simeonov and Wemple, 2017; Simeonov and Wemple, 2019) (from Studsvik SSP) were developed and offered best-estimate determination of nuclide vectors and decay heat. This spurred further development of the aforementioned standards and the newest version of DIN-25463 (Deutsches Institut für Normung, 2014b) uses a very detailed parametrization schema. For example, the standard (Deutsches Institut für Normung, 2014b) which is valid for UOX LWR fuel and decay times up to 60 years uses more than 1933 constants. They are used to approximate cross sections of selected actinides and fission products as a function of burnup, to describe 7 selected fission product decay and mutation chains, to couple 21 actinides through decay and breeding and to account for the yields of 51 fission products. By comparison the very early standard (American Nuclear Society and ANSI/ANS-5.1-1979, 1979) needs little more than 138 constants to determine decay heat (by fitting exponential functions to pulse thermal and fast fission data).

The challenge for these parameterization strategies is the requirement to approximate a wide range of possible fuel assembly states which can occur in practice. For example, while most PWR cycles are between 12 and 18 months long, there can also be very short cycles of a few months if a plant faces final shutdown. If UOX and MOX fuel or low and high burnup fuel is collocated in a reactor core the neutron spectrum changes compared to the field in an infinite lattice of identical fuel types. Lattice homogeneity is an implicit assumption in most standards. Also, UOX is often used in combination with strong neutron absorbers like UO2 plus Gadolinium or UO2 plus a boron coating—a combination of factors which are not accounted for in the above-mentioned standards, too. Sometimes ERU fuel from enriched reprocessed uranium is used. Modern parametrization strategies used in machine learning (Fernandez et al., 2017; Ebiwonjumi et al., 2021) would possibly be able to describe all these variations with reasonable accuracy, but would depend on a representative, large-scale training data set.

The popularity of the decay heat standards can partly be explained by their small computational footprint. However, compute power today is no longer a limitation for these kinds of calculations and using codes like ORIGEN-S has become equally effective in most practical situations. Sometimes the inventory codes are already part of the nuclear design systems and the parameter transfer between the individual codes such as the reactor burnup code and the inventory code are tuned and optimized for the staged application. This is the case, for example, with the Studsvik core design system CMS, where the required input data between the reactor burnup code SIMULATE and its inventory code SNF are coordinated. SNF extracts the nuclide vector after irradiation or at any other time for each fuel assembly and subsequently determines decay heat with microscopic decay channel data from the latest ENDF/B file. More than 568 relevant nuclides are followed. The method is very similar to the route followed by the other above-mentioned sophisticated codes and has been validated with experimental data from the Swedish CLAB facility, too [for example, (Børresen et al., 2004)].

In the following sections we compare results from the latest DIN-25463-2014 and SSP SNF for a range of different irradiation histories and fuel conditions in order to assess the level of conservativeness of the parametrization approach. It is shown that this margin has considerable range of variation. Given today’s small computational costs of using codes like ORIGEN-2 or SSP SNF we see no longer any advantage of using classical parametrizations.

In section 2 the initial nuclide vector as determined by DIN-25463-2014 and by SSP SNF (Version 1.6) is compared for generic power histories of PWR fuel for different burnups. In section 3 the decay heat is compared for fuel (Table 1) in a PWR core with realistic irradiation history and fuel conditions. Section 4 summarizes the considerations. While state-of-the-art codes like SSP SNF or ORIGEN-S have in the past been benchmarked against decay heat measurements and post irradiation nuclide vector measurements this to our knowledge has not been done for DIN-25435-2014, for example,. Therefore, in the following SSP SNF is used as reference solution.

TABLE 1

TABLE 1. 16 × 16 PWR fuel general parameters.

2 Nuclide vector at end of irradiation for decay heat determination

Decay heat determination is usually a two-phase process: determining the nuclide vector evolution during irradiation (CASMO/SIMULATE) and solving the Bateman equation (Bateman, 1910) to follow the decay chains (SSP SNF). Since decay heat contributes up to 10% of thermal energy generation its determination is already naturally part of core design and burnup calculations. If the nuclide vector of two fuels at the end of irradiation is identical, then differences between different decay heat codes are either the result of differences in integration techniques or due to different subsets of nuclides being followed during decay (assuming identical, initial microscopic data).

The purpose of the following comparison is to demonstrate that the quality of approximation of nuclide vector evolution as determined with DIN-25463-2014 is a function of burnup (or equivalently irradiation time) and to quantify the differences using SSP SNF as reference. While SSP SNF uses a state-of-the-art microscopic model to determine the nuclide vector during irradiation (by using the information provided from the lattice physics code CASMO) DIN-25463-2014 reconstructs it for selected 72 nuclides by means of using tabularized cross sections for fission and absorption as a function of burnup in 1-group energy approximation and various other proximations for the neutron flux and breeding and decay chains.

We compared the nuclides vectors (i.e., concentrations in grams per ton heavy metal) for Uranium and Uranium-Gadolinium fuel after irradiation for 20, 40, 80, 160 and 320 days and a flat power history (corresponding to burnup between 8 and 14 MW d/kgU). DIN-25463-2014 is generally applicable between 0 and 80 MW d/kgU burnup and in these calculations we deliberately focused on low burnup fuel assemblies which are often relevant if a power plant nears end-of-life operation. Fuel assemblies are treated as a point model or equivalently as an infinite lattice of homogenous nodes in all 3 spatial directions. Power was adjusted between both fuel types to yield identical burnup, i.e., Uranium fuel with 320 days of irradiation has the same burnup as Uranium-Gadolinium fuel after 320 days of irradiation. Uranium fuel has 4.0 w/o U235 enrichment, Gd₂O₃ concentration is 7% in 8 pins. Fuel assemblies are 16 × 16 PWR type with 20 guide tubes used in German Vor-Konvoi reactors (more fuel specific data can be obtained from (Strasser and Rudling, 2007; Bläsius et al., 2020) and Figure 1). In Figure 2 the relative differences of the set of heavy nuclides tracked in DIN-25463-2014 is compared to results from SSP SNF. For important heavy nuclides like U235, U238, Pu239 the differences are small and no more than 5%. For higher actinides the differences are noticeably larger and reach up to 80%. With increasing burnup, the differences get smaller. There is a small trend of higher differences for Uranium-Gadolinium fuel compared to Uranium fuel.

FIGURE 1

FIGURE 1. PWR 16 × 16-20 Uranium/Uranium-Gadolinium fuel for German Vor-Konvoi reactors.

FIGURE 2

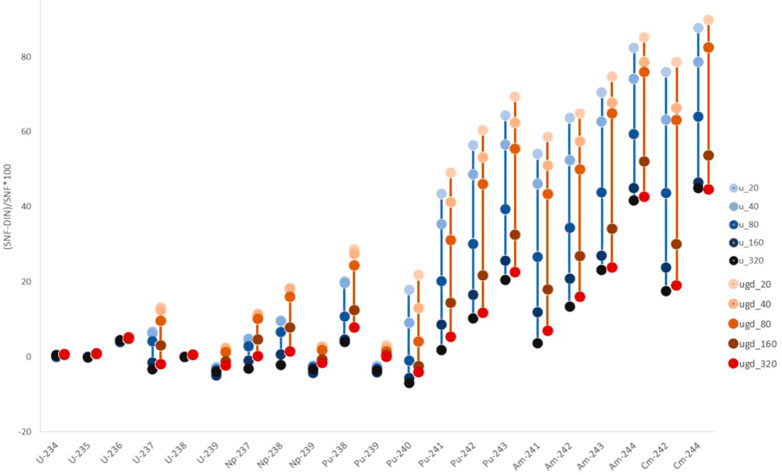
FIGURE 2. Relative differences (DIN-25463-2014 versus SSP SNF) between nuclide concentrations after irradiation of 20, 40, 80, 160 and 320 days (corresponding to burnup range from 8 to 14 MW d/kgU) of Uranium (blue) and Uranium-Gadolinium (orange) PWR fuel for selected heavy nuclides.

Secondly, the same set of comparisons were made for fission products tracked in DIN-25463-2014, see Figure 3. Very little difference in trend between Uranium and Uranium-Gadolinium fuel is observed (because at equal burnup differences in fission product yield between these two fuel types can only come from spectral differences which is a second order effect). Most differences are below 20%. For some nuclides like Rh104, Cs133, Cs136 and Eu156 the impact of burnup on differences is very visible and decreases for larger irradiation times. This strong dependency is partly due to the decay constants of these nuclides or their predecessors being in the range of the irradiation time of the examples considered. Overall, the differences between DIN-25463-2014 and SSP SNF are smaller for fission products and less dependent on burnup. These results confirm the expectation that the quality of approximation of nuclide vector evolution in DIN-25463-2014 depends on burnup, other irradiation factors and affects different nuclides differently (using SSP SNF as reference) and show quantitatively how large these differences are.

FIGURE 3

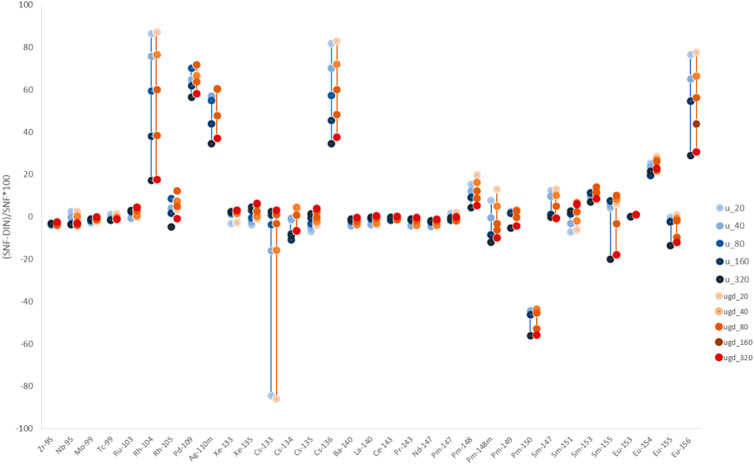
FIGURE 3. Relative differences (DIN-25463-2014 versus SSP SNF) between nuclide concentrations after irradiation of 20, 40, 80, 160 and 320 days (corresponding to burnup range from 8 to 14 MW d/kgU) of Uranium (blue) and Uranium-Gadolinium (orange) PWR fuel for selected fission products.

3 Decay heat comparisons of a typical set of PWR spent fuel

While in section 2 nuclide vector data at end of irradiation for flat power histories and infinite lattice conditions can be directly extracted from CASMO this section focusses on nuclide vectors obtained from core management calculations with CASMO/SIMULATE. In the following the differences in decay heat between SSP SNF and DIN-25463-2014 for Uranium, Uranium-Gadolinium and MOX fuel are considered. The fuel inventory is taken from the core of a German Vor-Konvoi PWR (Kernkraftwerk Grohnde, 2012) with a 16 × 16 fuel matrix and an average linear power of 215 W/cm. Enrichment is between 4.0 and 4.4 w/o U235 and maximum Gd₂O₃ concentration is 7%. The core is operated with 193 fuel assemblies which have been irradiated between 12 and 60 months. The power histories and nuclide vectors were taken from realistic core depletion calculations with CASMO5/SIMULATE5 (Bahadir and Lindahl, 2009). Decay times range from 1 s to 60 years after shutdown (the upper range of DIN-25463-2014 applicability). Figure 4 shows the end-of-cycle burnup distribution of all fuel assemblies. In these calculations the decay heat has been determined node-wide for each of a fuel assembly’s 32 nodes in both the DIN-25463-2014 and SSP SNF case. In the latter case the nuclide vector evolution for each node depends on the node specific cross sections and irradiation conditions. In case of DIN-25463-2014 each node is treated stand-alone and its power history is used ex post to reconstruct the nuclide vector.

FIGURE 4

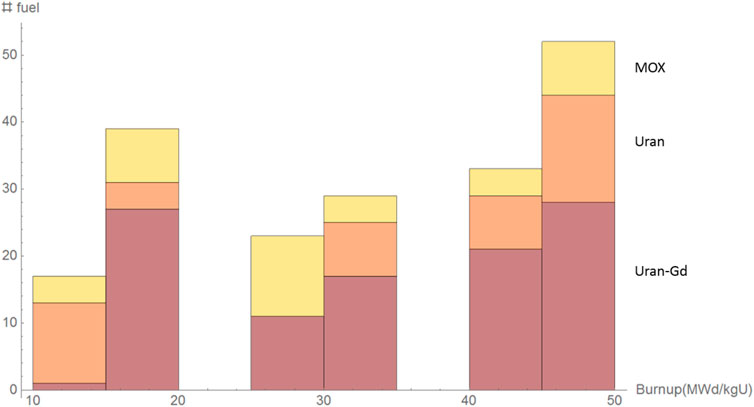
FIGURE 4. Burnup distribution of the plant’s 193 fuel assemblies after end of cycle group by fuel type.

3.1 Uranium fuel

There are 48 Uranium fuel assemblies in the core. Figure 5 shows four distinct clusters for the differences of decay heat between SSP SNF and DIN-25463-2014. The different clusters correspond to the number of cycles fuel assemblies were in the core. All 48 assemblies are plotted per decay time, but for similar burnup almost all lie on top of each other, giving rise to the mentioned four groups. Generally speaking, the margin between DIN-25463-2014 and SSP SNF is decreasing slightly for very short time scales and again increasing for intermediary ones. At the end of the range of DIN-25463-2014 applicability the margins quickly decline and, in some cases, best-estimate code SSP SNF calculates slightly larger values of the decay heat. However, these values are within the expected uncertainty band also recommended in DIN-25463 (1-sigma of about 5% at small cooling times down to about 3% for large cooling times).

FIGURE 5

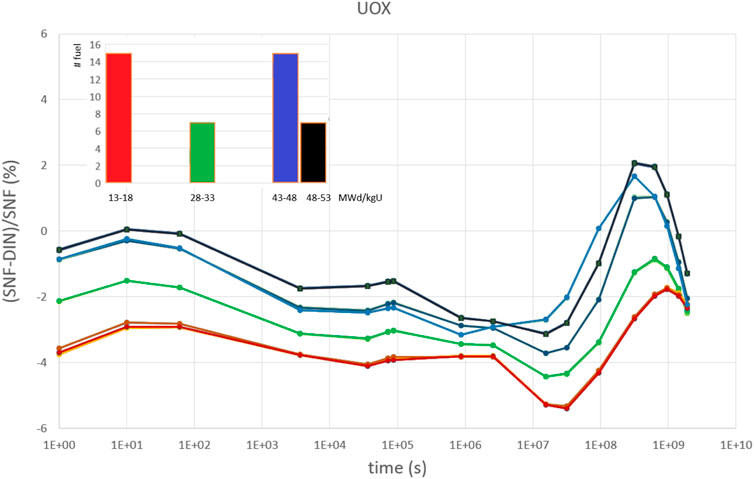
FIGURE 5. Relative differences of decay heat between SSP SNF and DIN-25463-2014 for 48 Uranium fuel assemblies (red: 1st cycle fuel assemblies, blue: 3rd and 4th cycle fuel assemblies) between 1 s and 60 years.

3.2 Uranium-Gadolinium fuel

Overall, 105 Uranium-Gadolinium fuel assemblies were irradiated. Clustering is weaker, but the correlation seen for Uranium fuel is still present: the higher the fuel’s cycle number, the smaller the margin between SSP SNF and DIN-25463-2014 results (Figure 6). Again, for very large time scales, there are some cases in which SSP SNF calculates larger values. The strong variation in code differences at the upper end of the range indicates that contribution of some nuclides relevant in this regime are missing in the nuclide vector tracking of DIN-25463-2014. For example, in (Ebert, 2001) among the top ranged ten nuclides are Y90 and Sr90 which are not considered in DIN-25463-2014.

FIGURE 6

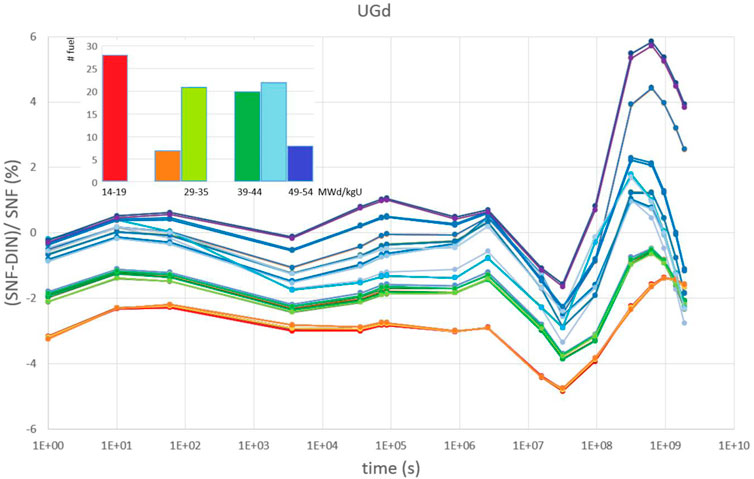
FIGURE 6. Relative differences of decay heat between SSP SNF and DIN-25463-2014 for 105 Uranium-Gadolinium fuel assemblies (red: 1st cycle fuel assemblies, blue: 3rd and 4th cycle fuel assemblies) between 1 s and 60 years.

3.3 MOX fuel

The plant’s cycle had 40 MOX fuel assemblies and results are shown in Figure 7. The code differences have the same overall trends as in the previous cases. The spread of differences appears smaller. Due to the limited number of fuel assemblies for MOX and UOX it cannot be concluded if code agreement for MOX fuel is systematically better.

FIGURE 7

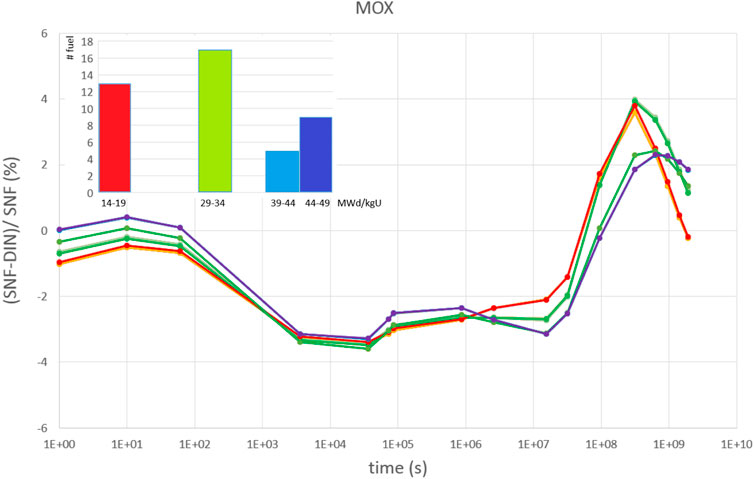
FIGURE 7. Relative differences of decay heat between SSP SNF and DIN-25463-2014 for 40 MOX fuel assemblies (red: 1st cycle fuel assemblies, blue: 3rd and 4th cycle fuel assemblies) between 1 s and 60 years.

The process of creation and destruction of nuclides through fission, neutron absorption and decay is highly non-linear and therefore it can be expected that the power history of the fuel has an important influence on the quality of the nuclide vector and on the decay heat.

3.4 Dependence on power history

Even though the aforementioned standards are conservative—given a known power history—the determination of a specific fuel assembly’s power history requires detailed reactor physics simulations and is more resource intensive than the standards’ calculation themselves. In the following we briefly analyze why knowledge of power history is important. In Figure 8 the variability of the nuclide vector for some selected actinides and fission products is shown for a UOX fuel with 50 MW d/kgU burnup generated from 2000 potential power histories. They are generated randomly with the boundary condition that the fuel is irradiated in four 12-month cycles with relative power level between 0.5 and 2.0 of nominal power and shutdown time is ranging between 20 days and 4 years after each cycle. The nuclide vector is determined immediately after the last cycle without shutdown cooling. The results show that while burnup monitors like Nd-148 are expectedly a reliable indicator for total energy release other nuclides’ concentrations can vary considerably. Not all nuclides are equally relevant for all cooling time periods, see the ranking in (Ebert, 2001), for example,. Also, measurement theory comparisons in (Gauld et al., 2010) showed good agreements for a narrow time window of cooling time. However, in the 100-year cooling period Am241, for example, becomes one of the leading decay heat contributors and it has a stronger dependence on power history compared to other actinides, as seen in Figure 8. Using power histories from core tracking calculations therefore appears prudent.

FIGURE 8

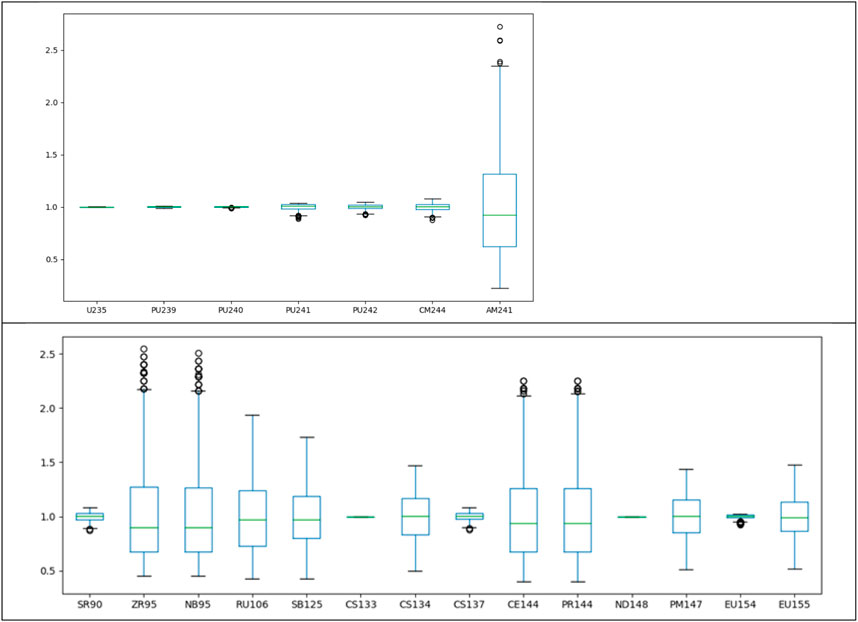
FIGURE 8. Nuclide vector sensitivity (relative difference to reference nuclide vector from flat power history) of selected nuclides immediately after irradiation for a 50 MW d/kgU UOX fuel determined for 2000 potential power histories from SSP SNF. Shown are the relative differences between reference concentration and concentrations from perturbed power history per nuclide with a box plot: the line in the center of the box is the median, the box upper and lower boundary is the upper and lower quartile, the whiskers limit all data points up to 1.5 times the inter quartile range and the remaining points outside of this range are shown individually with black circles.

4 Conclusion

The performance of two strategies for determining the decay heat has been compared: on the one hand a parametrization strategy as pursued by DIN-25463-2014. On the other hand, a strategy to use a best-estimate approach based on microscopic data like the one used by SSP SNF. Differences in decay heat outcomes are primarily driven by differences in the nuclide vectors at the end of irradiation and by the choice of the subgroup of nuclides followed during subsequent decay. In particular we found indications that for cooling times near the end of applicability of DIN-25463-2014 between 10⁸ and 10⁹s SNF SSP gives slightly higher results. Our analysis compared results both for generic power histories and for power histories from realistic core depletion calculations. The exact determination of the nuclide vector at end of irradiation is a challenge for parametrization strategies due to the many possible fuel assembly states: the variation in power history for different fuel types and for different core positions, the change in neutron spectrum depending on the state of fuel assembly neighbors, and the type and presence of additional neutron absorbers or position of control rods, to mention a few of the relevant factors.

Given today’s small compute footprint of best-estimate codes for decay heat determination we conclude that parametrization strategies have little advantage except for applications like system codes used in transient analyses. For situations which require source term determination for spent fuel loading, interim storage and disposal the integration of the Bateman equations is today no longer a time limiting factor and there is no advantage in our opinion to use a parametrization strategy. We have also shown that the power history is a very important input for the determination of the nuclide vector at the end of irradiation and therefore high-quality results for decay heat and other source terms require detailed core physics calculations and input from core power tracking. Hence using the decay heat standards with simplified power histories in our opinion is no longer state-of-the-art in these scenarios. We conclude that parametrization strategies should be abandoned in favor of integrated core physics calculations which determine both power history and nuclide vector as part of a single calculation chain.

In other scenarios like transient and accident analyses many national rules and regulations still require the use of the mentioned decay heat standards. In Germany, for example, the rules KTA 3301, 3303 and 3413 all explicitly mention DIN-25463 as a requirement. Considering today’s computational capabilities and the complex parameterization of standards like DIN-25463-2014, we conclude that using best estimate inventory codes to calculate decay heat plus uncertainty provides the most reliable results and requires little work compared to using the standard. Even though DIN-25463-2014 is more complicated to apply than an inventory code and the advantages of a standard in this regard are no longer available, it can be useful for conservative estimates. However in above mentioned national rules and regulations state-of-the-art calculations should be treated on par with the mentioned standards.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Proprietary. Requests to access these datasets should be directed to MS, bWFyY3VzLnNlaWRsQGVvbi5jb20=.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

MS was employed by PreussenElektra GmbH, JB was employed by Studsvik Scandpower GmbH, MK, HG, and K-MH were employed by TÜV NORD EnSys GmbH &. Co. KG.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

American Nuclear Society, ANSI/ANS-5.1-1979 (1979). American nuclear society, ANSI/ANS-5.1-1979, Grange Park: Decay Heat Power in Light Water Reactors.

Google Scholar

American Nuclear Society, ANSI/ANS-5.1-2014 (2019). American nuclear society, ANSI/ANS-5.1-2014, Grange Park: Decay Heat Power in Light Water Reactors.

Google Scholar

Bahadir, T., and Lindahl, S.-Ö. (2009). “Studsvik’s next generation nodal code SIMULATE-5.” in Advances in nuclear fuel management IV. USA: Hilton Head Island, SC.

Google Scholar

Bateman, H. (1910). The solution of a system of differential equations occurring in the theory of radioactive transformations. Math. Proc. Camb. Philosophical Soc. 15, 423–427.

Google Scholar

Becker, A., Anton, G., and Børresen, S. (2009). “SNF: Spent fuel analyses based on CASMO/SIMULATE in-core fuel management,” in Advances in nuclear fuel management IV. SC, USA: Hilton Head Island.

Google Scholar

Bläsius, C., Arndt, J., and Schimpfke, T. (2020). Strukturmechanische Forschungen zur Entstehung von Brennelementverformungen in DWR und deren Einfluss auf die Auslegungsreserven im Normalbetrieb und bei Störfällen. Cologne, Germany: GRS report.

Google Scholar

Børresen, S., Bahadir, T., and Kruners, M. (2004). Validation of CMS/SNF calculations against preliminary CLAB decay heat measurements, ANS transactions. Washington, D. C.: Winter Meeting.

Google Scholar

Croff, A. G. (1983). ORIGEN2: A versatile computer code for calculating the nuclide compositions and characteristics of nuclear materials. Nucl. Technol. 62, 335–352. doi:10.13182/nt83-1

CrossRef Full Text | Google Scholar

Deutsches Institut für Normung (2014b). Berechnung der Zerfallsleistung der Kernbrennstoffe von Leichtwasserreaktoren - teil 2: Uran-Plutonium-Mischoxid (MOX)-Kernbrennstoff für Druckwasserreaktoren. Berlin: Beuth Verlag GmbH. DIN 25463-2:2014-02.

Google Scholar

Ebert, D. D. (2001). Nuclide importance to criticality safety, decay heating and source terms related to transport and interim storage if high-burnup LWR fuel. Oak Ridge, TN, United States: NUREG/CR-6700.

Google Scholar

Ebiwonjumi, B., Cherezov, A., Dzianisau, S., and Lee, D. (2021). Machine learning of LWR spent nuclear fuel assembly decay heat measurements. Nucl. Eng. Technol. 53 (11), 3563–3579. doi:10.1016/j.net.2021.05.037

CrossRef Full Text | Google Scholar

Fernandez, M. G., Tokuhiro, A., Welter, K., and Wu, Q. (2017). Nuclear energy system's behavior and decision making using machine learning. Nucl. Eng. Des. 324, 27–34. doi:10.1016/j.nucengdes.2017.08.020

CrossRef Full Text | Google Scholar

Gauld, I. C., Illas, G., Murphy, B. D., et al. (2010). Validation of SCALE5 decay heat predictions for LWR spent nuclear fuel. Oak Ridge, TN, United States: NUREG/CR-6972.

Google Scholar

Gauld, I. C. (2005). ORIGEN-S: Depletion module to calculate neutron activation, actinide transmutation, fission product generation, and radiation source term”. ORNL/TM-2005/39Version 6.1.

Google Scholar

Hesse, U. (1988). OREST—the HAMMER-ORIGEN burnup program system: Method and results. Nucl. Technol. 82 (2), 173–186. doi:10.13182/nt88-a34106

CrossRef Full Text | Google Scholar

Kernkraftwerk Grohnde (2012). Atw international journal for nuclear power, Berlin: INFORUM VERLAGS-VERWALTUNGSGESELLSCHAFT MBH, 18–20.

Simeonov, T., and Wemple, C. (2019). A procedure for verification of Studsvik's spent nuclear fuel code SNF. Kerntechnik 84 (4), 246–251. doi:10.3139/124.190005

CrossRef Full Text | Google Scholar

Simeonov, T., and Wemple, C. (2017). Development in Studsvik's system for spent fuel analyses. Munich, Germany: 27 AER symposium.

Google Scholar

Strasser, A., and Rudling, P. (2007). Fuel fabrication process handbook, ANT international. Sweden: Surahammer.

Google Scholar