Abstract
This paper considers a dual objective distributed coordination problem for a flywheel energy storage matrix system. On one hand, the power output of the entire flywheel energy storage matrix system should track its reference command, which is generated by a linear command generator. On the other hand, the state-of-energy of all the flywheels should be balanced. In contrast to the existing result which employed a common state-of-energy generator as the external model by making use of global system information. By taking advantage of average consensus algorithms, a novel asymptotic internal model based control method is proposed in this paper which eliminates the need of the external model. It is proven that the steady-state of the asymptotic internal model turns out to be a common state-of-energy generator for all the flywheels under the composite average consensus algorithms, which lends itself to the solution to the dual objective distributed coordination problem. Comprehensive case studies in different scenarios are conducted to examine the performance of the proposed control method.
1 Introduction
Flywheels have many merits in comparison with other types of energy storage units, such as high energy density, fast response, low maintenance, long life-time and environmental friendliness. For example, the traditional applications of flywheel energy storage include power quality improvement Akram et al. (2020); Jia et al. (2022) and uninterruptible power supply Gengji and Ping (2016); Li et al. (2018). While, for these scenarios, in contrast to flywheels, batteries or super-capacitors can barely last for over a decade since the cycles for these applications are too frequent. By storing energy as the kinetic energy in the rotational mass, flywheel energy storage systems can be implemented in many practical situations Amiryar and Pullen (2017); Arani et al. (2017); Mousavi et al. (2017); Faisal et al. (2018); Olabi et al. (2021); Choudhury (2021); Li and Palazzolo (2022). There have been thus far various design and control methods developed for flywheel energy storage systems, such as the neutral-point potential control Li Z. et al. (2022), active disturbance rejection Chang et al. (2015); Ghanaatian and Lotfifard (2019), wide speed range operation Zhang and Yang (2017), DC-link voltage control Zhang and Yang (2018); Gong et al. (2020), robust control Zhang et al. (2021); Liang et al. (2022), and learning based intelligent control He et al. (2022); Yin and Li (2022), just to name a few. On the other hand, flywheels have recently found applications in many new areas, such as energy management for railways Canova et al. (2022); Li J. et al. (2022), offshore wind farm power transmission Daoud et al. (2016); Tomczewski et al. (2019), vehicle energy harvesting Ahamad et al. (2019); Thormann et al. (2021), and so on.
Though flywheels are competitive in energy density, they have relatively low power density. To solve this issue, a possible way is to connect multiple flywheels together into a flywheel energy storage matrix system (FESMS). An important application scenario for FESMS is to support wind turbine generator system Cao et al. (2016); Lai et al. (2018); Wei et al. (2018); Sun et al. (2020). Some pioneering works have been established on the design and control of FESMS. In Cao et al. (2016), a fully distributed dispatching algorithm for FESMS was proposed, which does not rely on central controller and requires no prior knowledge of the communication network topology. Lai et al. (2018) developed a coordination control scheme consisting of a charge–discharge control strategy and a safeguard mechanism for a FESMS with an aggregated connection topology. A simple but effective neuroadaptive PID control algorithm for adjusting the flywheel speed to achieve timely charge or discharge of the unit was derived. To solve the problems of over-charging, over-discharging, and overcurrent caused by traditional charging–discharging control strategies, Shi et al. (2019) proposed a charging–discharging coordination control strategy based on the equal incremental principle, which aims to minimize the total loss and establish a mathematical model of optimal coordination control with the constraints of total charging–discharging power, rated power limit, over-charging, over-discharging, and overcurrent. Two novel control strategies based on event triggering and self-triggering were studied in Sun et al. (2020) for the cooperative operation of a FESMS. Different from the traditional sampling mechanism, a periodic sampling-based event-triggered condition based on the disagreement vector and the measurement error was proposed for solving the FESMS dispatch problem.
Regarding the upper level coordination of a large scale integrated energy storage system, there are mainly two fundamental control objectives. On one hand, the total power output of the integrated energy storage system should meet its reference command so as to provide timely qualified service to the grid, such as frequency or voltage regulation. On the other hand, the state-of-charge (SOC) or state-of-energy (SOE) of all the energy storage units should be balanced so that the maximum power capacity of the integrated energy storage system can be maintained for all the time. Seminal works on the dual objective coordination of battery energy storage systems can be found in Lu et al. (2014, 2015); Cai and Hu (2016); Morstyn et al. (2016, 2018). While, there have been less efforts devoted to the dual objective coordination of FESMS. In Zhang et al. (2022), allocation of the total charging and discharging power of wind farms to individual flywheel unit was considered, where SOE consensus algorithms under both undirected and unbalanced directed graphs were developed. Nevertheless, Zhang et al. (2022) does not consider the specific dynamics of the flywheel systems. In contrast, Liu et al. (2021) studied the dual objective coordination of FESMS taking into consideration the detailed flywheel dynamics, where it is revealed that the dual control objective can be achieved if and only if the SOE of each flywheel converges to a common SOE generator, which was shown to be a nonautonomous dynamic system with the reference command for the entire FESMS as the external input. By explicitly implementing this nonautonomous dynamic system as an external model, the coordination problem for the FESMS was solved in Liu et al. (2021) by a distributed control approach. However, a drawback of this control approach lies in that the implementation of the external model depends on the system parameters of all the flywheel systems, which are global system information. Therefore, this control approach might not be realistic in some practical cases.
To further solve this issue, in this paper, a novel control method is proposed to solve the dual objective coordination problem for a FESMS. By taking advantage of average consensus algorithms, a novel asymptotic internal model based control method is proposed in this paper which eliminates the need of the external model as in Liu et al. (2021). It is proven that the steady-state of the asymptotic internal model turns out to be a common state-of-energy generator for all the flywheels under the composite average consensus algorithms. Then, by driving the SOE of the flywheel to this asymptotic internal model, the dual objective coordination problem for FESMS can be solved in a fully distributed way. Moreover, it is shown by numerical simulations that the proposed control method shows potential robustness against unreliable communication links, power output saturation, and inter-system time-delay issues.
The rest of this paper is organized as follows. The notation used in this paper are summarized in Section 3. Section 4 introduces the problem formulation. The design and analysis of the asymptotic internal model based coordination are detailed in Section 5. Comprehensive case studies are given in Section 6. Finally, this paper is concluded by Section 7.
2 Notation
denotes the real number field. For , i = 1, … , m, . . A graph consists of a node set and an edge set . For i, j = 1, 2, … , N, i ≠ j, an edge of from node i to node j is denoted by (i, j), and node i is called a neighbor of node j. Let denote the set consisting of all the neighbors of node i. If if and only if , then the edge (i, j) is called undirected. If all the edges of a graph are undirected, then the graph is called undirected. If contains a sequence of edges of the form (i1, i2), (i2, i3), …, (ik, ik+1), then the set {(i1, i2), (i2, i3), …, (ik, ik+1)} is called a path of from node i1 to node ik+1 and node ik+1 is said to be reachable from node i1. For an undirected graph, if there exists a path between any two different nodes, then it is called connected. A graph is said to contain a spanning tree if there exists a node in such that all the other nodes are reachable from it, and this node is called the root of the spanning tree. A matrix is said to be a weighted adjacency matrix of a graph if aii = 0; ; and . Moreover, for an undirected graph, aij = aji. Let be such that and lij = −aij if i ≠ j. is called the Laplacian of associated with the weighted adjacency matrix .
3 Problem formulation
Consider a FESMS with N heterogenous flywheel systems. For i = 1 … , N, as in Liu et al. (2021), the SOE dynamics of the ith flywheel are given by:where ϕi(t), Ii, Bvi denote the SOE, flywheel inertia, and friction coefficient, respectively. with ωimax denoting the maximum admissible angular velocity of the ith flywheel. Pi(t) is the net power output of the ith flywheel, where Pi(t) > 0 means power flow from flywheel to the grid, and Pi(t) < 0 vice versa. Here, Pi(t) is taken as the control input.
Letdenote the power output of the entire FESMS, and PREF(t) denote the reference command for PFESMS(t), which is assumed to be generated by the following command generatorwhere is the internal state of the command generator, and are constant matrices.
The communication network for the FESMS together with the command generator is modeled as a graph , where and . Here, the node 0 is associated with the command generator, and the node i is associated with the ith flywheel of the FESMS. For i = 0, 1, … , N, j = 1, … , N, if and only if the jth flywheel can receive the information from the command generator or the ith flywheel. Let be a subgraph of with and . Let be the weighted adjacency matrix of and be the Laplacian of . The following assumption is imposed on the communication network.
Assumption 1. The graphcontains a spanning tree with node 0 as the root. Moreover, the graphis undirected and connected.Assumption 1 means that the information of the command generator can be transmitted to each flywheel system through a communication path.Now, the dual objective coordination problem for the FESMS is described as follows.
Problem 1. Given systems (1), (2) and the communication network, design a distributed control inputPi, such thatand fori, j = 1, … , N,i ≠ j,The control objective 3) means that the power output of the entire FESMS should meet its reference command, while the control objective 4) means that the SOE of all the flywheels should be balanced. To simultaneously achieve these two control objectives, the following lemma is established in Liu et al. (2021).
Lemma 1. (Lemma 1 ofLiu et al. (2021)) The following two equations simultaneously holdif and only if, fori = 1, … , N,ϕi(t) = ψ0(t), whereψ0(t) is governed bywithLemma 1 reveals that the power tracking and SOE balancing control objectives together limit the SOE trajectories of all the flywheels to the solution of some common nonautonomous dynamic system (6), which is depicted by the system parameters of all the flywheels and takes the power reference command for the FESMS as the external input. Note that the system parameters Bvi, Ii and γi of all the flywheels are global system information. By directly taking system 6) as an external model, a distributed control approach was proposed in Liu et al. (2021) to solve Problem 1. However, the implementation of system 6) would not be possible without the acquirement of global system information and thus might not be feasible in practice. In this paper, an asymptotic internal model based method is further proposed to solve Problem 1, where, as will be proven later, system 6) turns out to be the common steady-state of all the asymptotic internal models of the flywheels. In this way, global system information is no longer required to solve Problem 1. The details of the asymptotic internal model based coordination will be given in the next section.
4 Asymptotic internal model based coordination
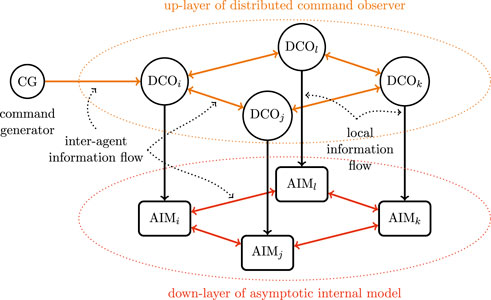
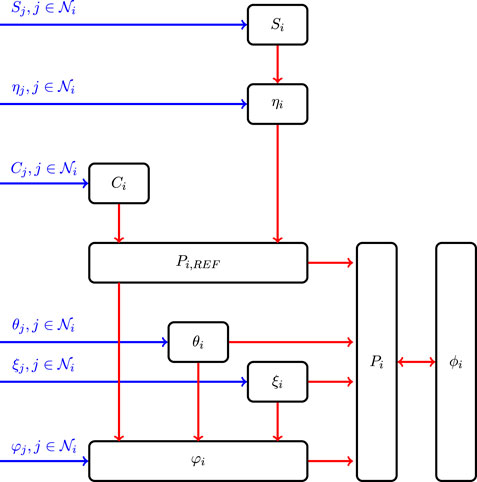
For
i= 1,
…,
N, the control law for the
ith flywheel system consists of the following three parts:
1. Up-layer of distributed command observer
2. Down-layer of asymptotic internal model
3. Local SOE tracking controller
where , , , are the estimates of S0, C0, η0(t), and PREF(t), respectively. are consensus parameters. is the state of the asymptotic internal model. μS, μC, μη, μθ, μξ, μφ, κ are positive control gains. The inter-agent and local information flow regarding the two-layer control 8) and 9) is illustrated by Figure 1, where “DCO” and “AIM” refer to distributed command observer and asymptotic internal model, respectively.
FIGURE 1
The inter-agent and local information flow regarding the two-layer control (8) and (9).
Now, we are ready to present the following main result.
Theorem 1. Given systems (1), (2), under Assumption 1, if none of the eigenvalues ofS0has positive real part, then the control law (8)-(10) solves Problem 1 for anyμS, μC, μη, μθ, μξ, μφ, κ > 0.Proof: For i = 1, … , N, let , , , . Then, by Theorem 4.6 of Cai et al. (2022), it follows that all , , and will all decay to zero exponentially.Let . Since the graph is undirected, aij = aji for i, j = 1, … , N, i ≠ j. Therefore,which means for all t ≥ 0,Moreover, by Corollary 2.9 of Ren and Beard (2008), under Assumption 1, all θi(t)’s will reach consensus exponentially, i.e.,Therefore, for i = 1, … , N,exponentially. Following the same procedure, for i = 1, … , N, it follows thatexponentially. Since for all i = 1, … , N, , , it follows that for all t ≥ 0, θi(t), ξi(t) > 0. As a result, control law (9c) and (10) are well imposed. DefineThen, by (7), 14 and 15, it follows thatexponentially.Letting φ(t) = col (φ1(t), …, φN(t)), Δα(t) = diag{2θ1(t)/ξ1(t), …, 2θN(t)/ξN(t)}, and givesNote that PREF(t) must be bounded in practice, and thus will also be bounded. Since is positive definite for all t ≥ 0, φ(t) will be bounded for all t ≥ 0.Rewrite (9c) as followswhereSince all tend to zero exponentially and φi(t) is bounded, δi(t) also tends to zero exponentially. Let δ(t) = col (δ1(t), …, δN(t)). Then we haveDefine U = (U1, Ur) where and is arbitrariliy chosen such that U is orthogonal. Then,Since U−1U = IN, . Therefore, . Let . Since , we have . Then, under Assumption 1, J is symmetric and all the eigenvalues of J are positive. Let . Then we havewhere . Let , with and . Then system (22) can be split into the following two subsystemsSince tends to zero exponentially and α0IN−1 + μφJ is positive definite, it follows that tends to zero exponetially. As a result, by noting thatit concludes thati.e.,Furthermore, by 9c and 16, it follows that there implicitly exists a nonautonomous dynamic system (6) such that limt→∞(φi(t) − ψ0(t)) = 0 for all i = 1, … , N. Then, by Lemma 1, it suffices to show limt→∞(ϕi(t) − φi(t)) = 0.Submitting (10) into 1) givesDefine . Then we haveSince κ > 0, by (26), it follows that and the proof is thus complete.The working principle for the asymptotic internal model 9) is as follows. First, the consensus algorithms (9a) and (9b) are adopted to estimate the global system information α0 and β0. Based on the esitmated α0 and β0, i.e., 2θi(t)/ξi(t) and 2/Nξi(t), a local certainty equivalent internal model is ready. Then, more importantly, the states of the internal models of all the flywheels should reach a common trajectory. To this end, the consensus term is resorted to and added to the dynamics of the internal mode, which makes it an asymptotic internal mode in the sense that the states of all the internal models will eventually reach a common trajectory.The information flow among the three parts of the control law (8)–(10) is shown in Figure 2.
FIGURE 2
Information flow among the three parts of the control law (8)–(10).
5 Case studies
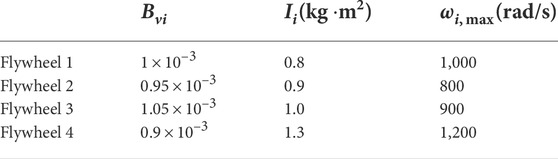
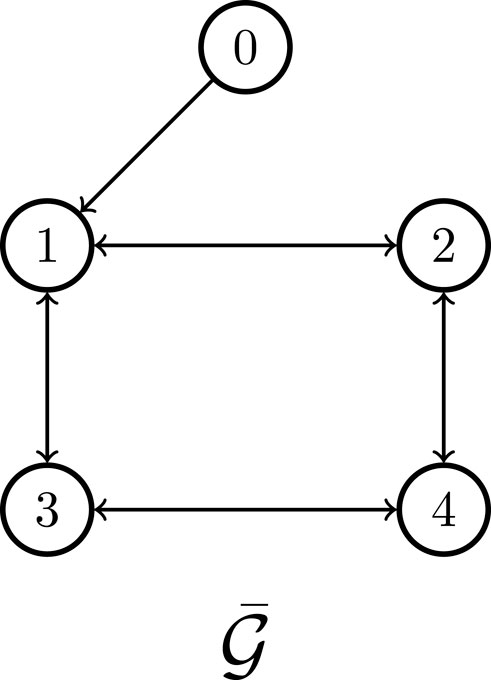
In this section, we consider a FESMS consisting of four flywheels as in Liu et al. (2021). The system parameters are given in Table 1, which come from the works in Ghanaatian and Lotfifard (2019); Liu et al. (2021). Moreover, the communication graph is shown in Figure 3, where node 0 represents the command generator, and node i represents the ith flywheel, i = 1, … , 4. The command generator is designed as
TABLE 1
| Bvi | Ii(kg ⋅m2) | ωi, max(rad/s) | |
|---|---|---|---|
| Flywheel 1 | 1 × 10–3 | 0.8 | 1,000 |
| Flywheel 2 | 0.95 × 10–3 | 0.9 | 800 |
| Flywheel 3 | 1.05 × 10–3 | 1.0 | 900 |
| Flywheel 4 | 0.9 × 10–3 | 1.3 | 1,200 |
System friction, inertia and energy capacity parameters.
FIGURE 3
Communication network .
Thus, PREF(t) = 25 sin (0.05t) kw. In what follows, we will conduct case studies in different scenarios to examine the performance of the proposed control method.
Case 1: standard case.
The control gains are selected to be
and κ = 1. The system initial values are given by
and for i = 1, 2, 3, 4,
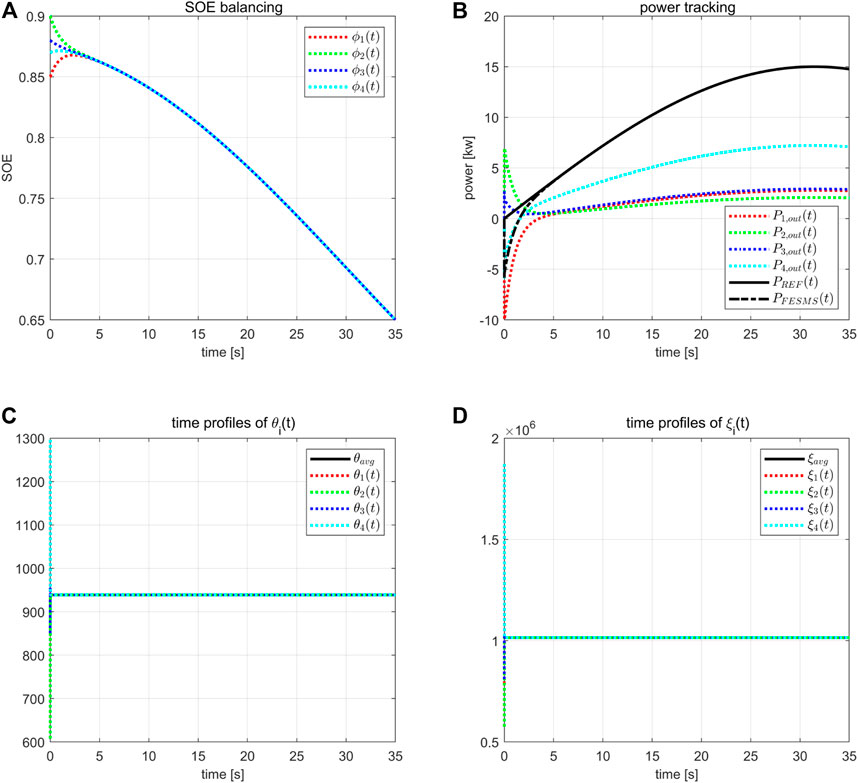
The system performance is shown by Figure 4. It can be seen from subfigures (a) and (b) that both SOE balancing and power tracking have been successfully achieved. Moreover, letThen by subfigures (c) and (d), it can be observed that θi(t) and ξi(t) converge to θavg and ξavg, respectively. Thus, the external model as in Liu et al. (2021) is no longer required, which depends on the global system information of θavg and ξavg.
FIGURE 4
Control performance for the standard case.
Case 2: effect of unreliable communication links.
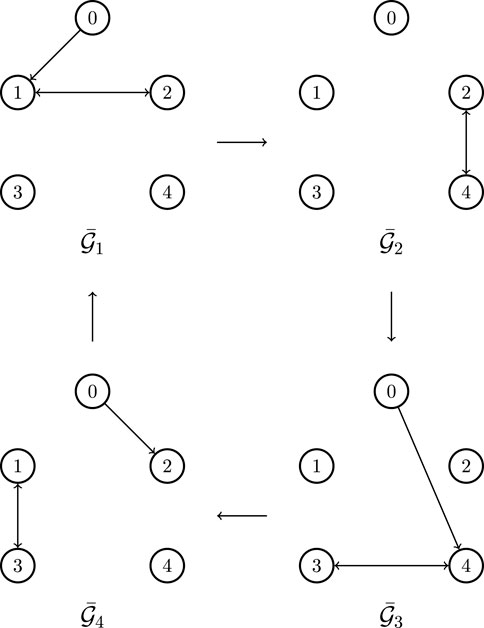
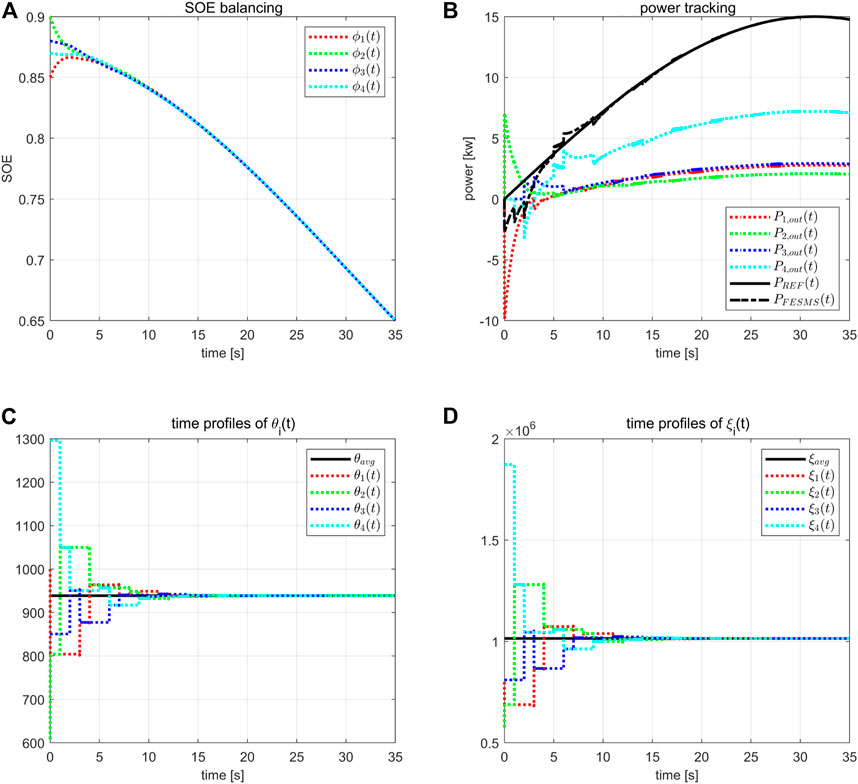
In the standard case, we assume the communication network to be static and reliable. While, in practice, due to malicious attack or equipment failure, the communication links might not always be reliable. In this case, we will check the control performance of the proposed control method subject to unreliable communication links. In particular, the communication network is assumed to switch among four subgraphs , , , periodically every 1s, as shown in Figure 5. The same control gains and system initial values as in Case 1 are employed. The system performance is shown by Figure 6. By subfigures (a) and (b), it can be seen the proposed control method shows certain robustness against unreliable communication links in the sense that the control objectives of SOE balancing and power tracking can still be achieved, though requiring longer time to reach steady state. Moreover, once the steady state is reached, the effect of the unreliable communication links would be minor. Similarly, it also takes longer time for θi(t) and ξi(t) to reach consensus. Note that for all the four subgraphs , , , , the communication links between flywheels are undirected. If these links become directed, then the average consensus on θi(t) and ξi(t) might be violated.
FIGURE 5
Unreliable switched communication network .
FIGURE 6
Control performance subject to unreliable communication links.
Case 3: effect of power output saturation.
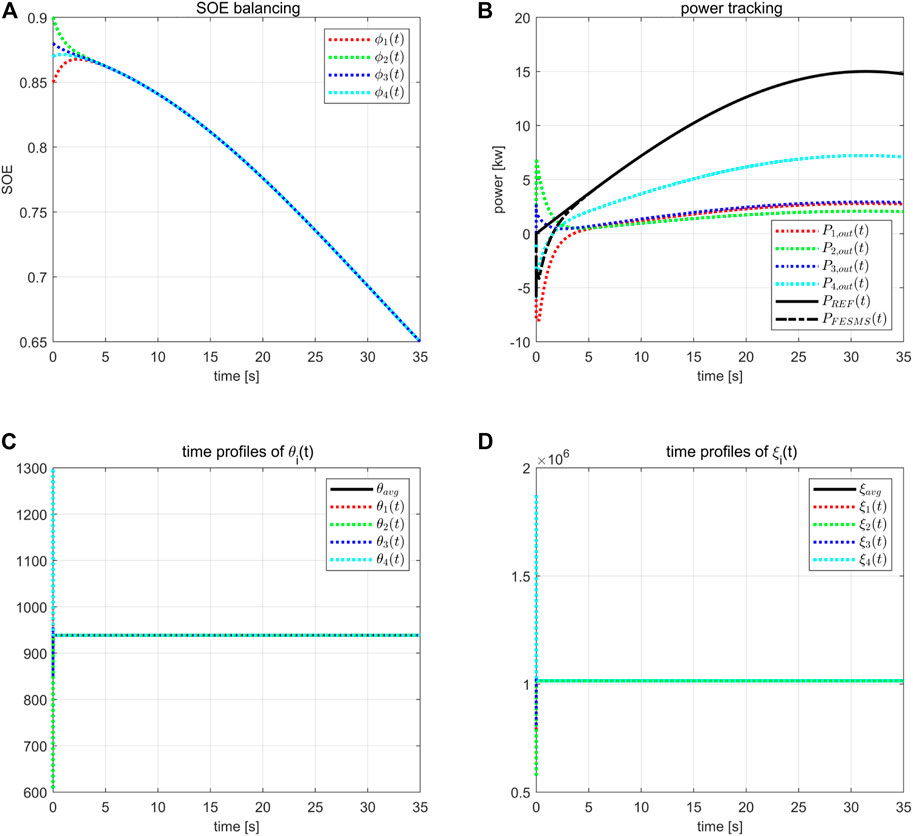
In practice, the power output of the flywheel is always subject to saturation. In this case, we will consider the effect of power output saturation. Supposewhere Pα > 0 and Pβ < 0 are the limits. In the simulation, we let Pα = −Pβ = 8kw. The same control gains and system initial values as in Case 1 are employed. The system performance is shown by Figure 7. It can be seen that as long as the saturation does not conflict with the steady-state power output, both the control objectives of SOE balancing and power tracking can still be achieved, which means that the saturation function can be directly applied to the proposed power control input.
FIGURE 7
Control performance subject to power output saturation.
Case 4: effect of time-delay.
In this case, we check the effect of time-delay of the communication network on the control performance. Consider a constant inter-system time-delay, where the time-delay between flywheel 1 and flywheel two is 1 × 10−4sec; between flywheel two and flywheel four is 2 × 10−4sec; between flywheel three and flywheel four is 3 × 10−4sec; between flywheel 1 and flywheel three is 4 × 10−4sec. The same control gains and system initial values as in Case 1 are employed. The system performance is shown by Figure 8. It can be seen that though the SOE balancing control objective can be achieved, the power tracking cannot be exactly realized. In this sense, the proposed control method shows certain sensitivity to time-delay. In general, the longer the time-delay is, the worse the control performance is. It would be an interesting topic to consider how to compensate the communication time-delay in the future. Nevertheless, in practice, the time-delay over normal transmission lines is usually on the order of 5 × 10−7sec/100m. Therefore, the proposed control method will be definitely feasible for cable communication network.
FIGURE 8
Control performance subject to time-delay.
6 Conclusion
This paper considers the dual objective distributed coordination problem for a FESMS. To eliminate the need of an external model which depends on global system information as in Liu et al. (2021), a novel asymptotic internal model based control method is proposed in this paper by taking advantage of the average consensus algorithms. It is proven that the steady-state of the asymptotic internal model turns out to be a common state-of-energy generator for all the flywheels, which lends itself to the solution to the dual objective distributed coordination problem.
Comprehensive numerical case studies show that the proposed control method has certain robustness against unreliable communication links and time-delay in information transmission. While, the unreliable communication would result in undesired oscillations in system transient response, and the information transmission delay would lead to steady-state tracking errors regarding power dispatch. Moreover, we also consider the constraint on power output saturation for the flywheels, and the obtained results indicate that the proposed control method can be directly integrated with the power limits without destabilizing the closed-loop system.
It is worth mentioning that in this paper, only homogeneous flywheel energy storage units are considered which are governed by the dynamic Eq. 1. Nevertheless, the proposed control approach can also handle the dual objective control problem for an energy storage system made up of heterogeneous energy storage units whose dynamic equations are in the same form of Eq. 1. While, it would be interesting to consider the dual objective control problem for an energy storage system with heterogeneous energy storage units of different dynamic equations in the future.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
HC contributed to all the contents of this paper.
Funding
This work was supported in part by the National Nature Science Foundation of China under Grant 61803160, and in part by the Guangdong Nature Science Foundation under Grant 2020A1515010810.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
AIM, asymptotic internal model; CG, command generator; DCO, distributed command observer; FESMS , flywheel energy storage matrix system; SOC, state-of-charge; SOE, state-of-energy.
Nomenclature
- ϕi(t)
The SOE of the ith flywheel
- Pi(t)
the net power output of the ith flywheel
- Bvi
the friction coefficient of the ith flywheel
- Ii
the inertia of the ith flywheel
- ωimax
the maximum admissible angular velocity of the ith flywheel
- γi
1/ωimax^2
- PFESMS(t)
the power output of the entire FESMS
- PREF(t)
the reference command for PFESMS(t)
- S0
the system matrix of the command generator
- C0
the output matrix of the command generator
- η0(t)
the internal state of the command generator
the communication graph
- ϕ0(t)
the common trajectory for all the flywheels
- α0, β0
the system parameters governing the common trajectory
- Si(t)
the estimation of matrix S0 by the ith flywheel
- Ci(t)
the estimation of matrix C0 by the ith flywheel
- ηi(t)
the estimation of η0 by the ith flywheel
- Pi,REF(t)
the estimation of PREF(t) by the ith flywheel
- θi(t)
the consensus parameter for Bvi/γi of the ith flywheel
- ξi(t)
the consensus parameter for Ii/γi of the ith flywheel
- φi(t)
the state of the asymptotic internal model of the ith flywheel
- αi(t), βi(t)
the estimation of α0 and β0 by the ith flywheel, respectively
References
1
AhamadN. B. b.SuC.-L.ZhaoxiaX.VasquezJ. C.GuerreroJ. M.LiaoC.-H. (2019). Energy harvesting from harbor cranes with flywheel energy storage systems. IEEE Trans. Ind. Appl.55, 3354–3364. 10.1109/TIA.2019.2910495
2
AkramU.NadarajahM.ShahR.MilanoF. (2020). A review on rapid responsive energy storage technologies for frequency regulation in modern power systems. Renew. Sustain. Energy Rev.120, 109626. 10.1016/j.rser.2019.109626
3
AmiryarM. E.PullenK. R. (2017). A review of flywheel energy storage system technologies and their applications. Appl. Sci.7, 286. 10.3390/app7030286
4
AraniA. K.KaramiH.GharehpetianG.HejaziM. (2017). Review of flywheel energy storage systems structures and applications in power systems and microgrids. Renew. Sustain. Energy Rev.69, 9–18. 10.1016/j.rser.2016.11.166
5
CaiH.HuG. (2016). Distributed control scheme for package-level state-of-charge balancing of grid-connected battery energy storage system. IEEE Trans. Ind. Inf.12, 1919–1929. 10.1109/TII.2016.2601904
6
CaiH.SuY.HuangJ. (2022). Cooperative control of multi-agent systems: Distributed-observer and distributed-internal-model approaches. Switzerland: Springer Cham.
7
CanovaA.CampanelliF.QuercioM. (2022). Flywheel energy storage system in Italian regional transport railways: A case study. Energies15, 1096. 10.3390/en15031096
8
CaoQ.SongY.-D.GuerreroJ. M.TianS. (2016). Coordinated control for flywheel energy storage matrix systems for wind farm based on charging/discharging ratio consensus algorithms. IEEE Trans. Smart Grid7, 1259–1267. 10.1109/TSG.2015.2470543
9
ChangX.LiY.ZhangW.WangN.XueW. (2015). Active disturbance rejection control for a flywheel energy storage system. IEEE Trans. Ind. Electron.62, 991–1001. 10.1109/TIE.2014.2336607
10
ChoudhuryS. (2021). Flywheel energy storage systems: A critical review on technologies, applications, and future prospects. Int. Trans. Electr. Energy Syst.31, e13024. 10.1002/2050-7038.13024
11
DaoudM. I.MassoudA. M.Abdel-KhalikA. S.ElserougiA.AhmedS. (2016). A flywheel energy storage system for fault ride through support of grid-connected vsc hvdc-based offshore wind farms. IEEE Trans. Power Syst.31, 1671–1680. 10.1109/TPWRS.2015.2465163
12
FaisalM.HannanM. A.KerP. J.HussainA.MansorM. B.BlaabjergF. (2018). Review of energy storage system technologies in microgrid applications: Issues and challenges. IEEE Access6, 35143–35164. 10.1109/ACCESS.2018.2841407
13
GengjiW.PingW. (2016). Rotor loss analysis of pmsm in flywheel energy storage system as uninterruptable power supply. IEEE Trans. Appl. Supercond.26, 1–5. 10.1109/TASC.2016.2594826
14
GhanaatianM.LotfifardS. (2019). Control of flywheel energy storage systems in the presence of uncertainties. IEEE Trans. Sustain. Energy10, 36–45. 10.1109/TSTE.2018.2822281
15
GongL.WangM.ZhuC. (2020). Immersion and invariance manifold adaptive control of the dc-link voltage in flywheel energy storage system discharge. IEEE Access8, 144489–144502. 10.1109/ACCESS.2020.3013137
16
HeH.LiuY.BaL. (2022). A nonlinear dynamic model of flywheel energy storage systems based on alternative concept of back propagation neural networks. J. Comput. Nonlinear Dyn.17. 10.1115/1.4054681
17
JiaY.WuZ.ZhangJ.YangP.ZhangZ. (2022). Control strategy of flywheel energy storage system based on primary frequency modulation of wind power. Energies15, 1850. 10.3390/en15051850
18
LaiJ.SongY.DuX. (2018). Hierarchical coordinated control of flywheel energy storage matrix systems for wind farms. Ieee. ASME. Trans. Mechatron.23, 48–56. 10.1109/TMECH.2017.2654067
19
LiJ.XinD.WangH.LiuC. (2022a). “Application of energy storage system in rail transit: A review,” in In 2022 International Conference on Power Energy Systems and Applications, Singapore, Singapore, 25-27 February 2022 (Singapore: ICoPESA), 539–552. 10.1109/ICoPESA54515.2022.9754481
20
LiX.AnvariB.PalazzoloA.WangZ.ToliyatH. (2018). A utility-scale flywheel energy storage system with a shaftless, hubless, high-strength steel rotor. IEEE Trans. Ind. Electron.65, 6667–6675. 10.1109/TIE.2017.2772205
21
LiX.PalazzoloA. (2022). A review of flywheel energy storage systems: State of the art and opportunities. J. Energy Storage46, 103576. 10.1016/j.est.2021.103576
22
LiZ.NieZ.XuJ.LiH.AiS. (2022b). Harmonic analysis and neutral-point potential control of interleaved parallel three-level inverters for flywheel energy storage system. Front. Energy Res.9, 811845. 10.3389/fenrg.2021.811845
23
LiangY.LiangD.KouP.JiaS.ChuS.WangH.et al (2022). Linear robust discharge control for flywheel energy storage system with rlc filter. IEEE Trans. Industry Appl.1, 15. 10.1109/TIA.2022.3189967
24
LiuH.GaoH.GuoS.CaiH. (2021). Coordination of a flywheel energy storage matrix system: An external model approach. IEEE Access9, 34475–34486. 10.1109/ACCESS.2021.3061743
25
LuX.SunK.GuerreroJ. M.VasquezJ. C.HuangL. (2015). Double-quadrant state-of-charge-based droop control method for distributed energy storage systems in autonomous dc microgrids. IEEE Trans. Smart Grid6, 147–157. 10.1109/TSG.2014.2352342
26
LuX.SunK.GuerreroJ. M.VasquezJ. C.HuangL. (2014). State-of-charge balance using adaptive droop control for distributed energy storage systems in dc microgrid applications. IEEE Trans. Ind. Electron.61, 2804–2815. 10.1109/TIE.2013.2279374
27
MorstynT.HredzakB.AgelidisV. G. (2016). Cooperative multi-agent control of heterogeneous storage devices distributed in a dc microgrid. IEEE Trans. Power Syst.31, 2974–2986. 10.1109/TPWRS.2015.2469725
28
MorstynT.SavkinA. V.HredzakB.AgelidisV. G. (2018). Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a dc microgrid. IEEE Trans. Smart Grid9, 4735–4743. 10.1109/TSG.2017.2668767
29
MousaviG. S.FarajiF.MajaziA.Al-HaddadK. (2017). A comprehensive review of flywheel energy storage system technology. Renew. Sustain. Energy Rev.67, 477–490. 10.1016/j.rser.2016.09.060
30
OlabiA. G.WilberforceT.AbdelkareemM. A.RamadanM. (2021). Critical review of flywheel energy storage system. Energies14, 2159. 10.3390/en14082159
31
RenW.BeardR. W. (2008). Distributed consensus in multi-vehicle cooperative control:theory and applications. London: Springer.
32
ShiC.WeiT.TangX.ZhouL.ZhangT. (2019). Charging–discharging control strategy for a flywheel array energy storage system based on the equal incremental principle. Energies12, 2844. 10.3390/en12152844
33
SunY.HuJ.LiuJ. (2020). Periodic event-triggered control of flywheel energy storage matrix systems for wind farms. IET Control Theory &. Appl.14, 1467–1477. 10.1049/iet-cta.2018.5731
34
ThormannB.PuchbauerP.KienbergerT. (2021). Analyzing the suitability of flywheel energy storage systems for supplying high-power charging e-mobility use cases. J. Energy Storage39, 102615. 10.1016/j.est.2021.102615
35
TomczewskiA.KasprzykL.NadolnyZ. (2019). Reduction of power production costs in a wind power plant–flywheel energy storage system arrangement. Energies12, 1942. 10.3390/en12101942
36
WeiG.JianchengZ.ChongL.HaoS. (2018). Control method of flywheel energy storage array for grid-connected wind-storage microgrid. Energy Storage Sci. Technol.7, 810. 10.12028/j.issn.2095-4239.2018.0013
37
YinL.LiY. (2022). Fuzzy vector reinforcement learning algorithm for generation control of power systems considering flywheel energy storage. Appl. Soft Comput.125, 109149. 10.1016/j.asoc.2022.109149
38
ZhangW.LiY.WuG.RaoZ.GaoJ.LuoD. (2021). Robust predictive power control of n*3-phase pmsm for flywheel energy storage systems application. Energies14, 3684. 10.3390/en14123684
39
ZhangX.YangJ. (2018). A dc-link voltage fast control strategy for high-speed pmsm/g in flywheel energy storage system. IEEE Trans. Ind. Appl.54, 1671–1679. 10.1109/TIA.2017.2783330
40
ZhangX.YangJ. (2017). A robust flywheel energy storage system discharge strategy for wide speed range operation. IEEE Trans. Ind. Electron.64, 7862–7873. 10.1109/TIE.2017.2694348
41
ZhangZ.MengK.LiuQ.WuH. (2022). Hierarchical energy coordination of flywheel energy storage array system for wind farms based on consensus algorithm. AIP Adv.12, 035005. 10.1063/5.0083391
Summary
Keywords
flywheel energy storage system, average consensus, internal model, multiagent system, state of energy
Citation
Cai H (2022) Asymptotic internal model based coordination of a flywheel energy storage matrix system. Front. Energy Res. 10:998921. doi: 10.3389/fenrg.2022.998921
Received
20 July 2022
Accepted
17 August 2022
Published
16 September 2022
Volume
10 - 2022
Edited by
Lin Qiu, University of Science and Technology Beijing, China
Reviewed by
Hossam A. Gabbar, Ontario Tech University, Canada
Gevork B. Gharehpetian, Amirkabir University of Technology, Iran
Updates
Copyright
© 2022 Cai.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: He Cai, caihe@scut.edu.cn
This article was submitted to Energy Storage, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.