A combined day-ahead and intraday optimal scheduling strategy considering a joint frequency regulation reserve scheme among wind, photovoltaic, and thermal power

Under the premise of establishing a certain reserve power for frequency regulation, a new energy power plant (NEPP) transformed by frequency regulation control can participate in system frequency regulation. Considering the problem of cooperation between multiple NEPPs for reserve power for frequency regulation, this article presents a joint frequency regulation reserve scheme spanning wind, photovoltaic, and thermal power. A group of NEPPs composed of all NEPPs in the system works in the state of dynamic stepped output derating and participates in system frequency regulation together with thermal power units. Based on the joint frequency regulation reserve scheme and considering that the accuracy of new energy forecast directly affects the frequency regulation effect of NEPPs, we propose a combined day-ahead and intraday scheduling strategy considering the joint frequency regulation reserve scheme and derive the relevant scheduling model. The improved IEEE RTS 24-bus system is used as the test system for calculation. The results of the calculations show that the proposed strategy can optimize the participation scheme of frequency regulation of new energy, reduce the power and economic losses of new energy caused by participation in frequency regulation, and improve the ability of the power system to accommodate the output power of new energy under the premise of ensuring that the steady-state frequency deviation does not exceed the allowable frequency limits.

1 Introduction

Improving the accommodation ability of new energy power generation is an efficient method for the traditional power system to realize the transition to low carbon. However, new energy power generation, represented by wind turbines and photovoltaics (PVs), has a fluctuating and uncertain power output that brings more power disturbance to the power system. This increasing power disturbance increases the demand for frequency regulation of reserve power. In the traditional power system, the frequency response capability of thermal power units is limited by their installed capacity and regulation speeds. Moreover, the new energy power generation connected to the power grid by power electronic converters operates in a state of maximum power point tracking without frequency regulation of reserve power, so that new energy power generation cannot participate in frequency regulation. With the increased scale of new energy connecting to the grid, the demand for frequency regulation reserve power may not be satisfied by the frequency response capability of the system. Thus, the power system needs more frequency response capability to meet the increasing demand for reserve power frequency regulation, and the system may not have enough ability to accommodate all the output power of new energy, which complicates the scheduling and operation of the power system with large-scale grid-connected new energy.

Owing to the development of new energy power generation control strategies, many theoretical studies about the new energy participating in frequency regulation have been conducted, showing that new energy power generation can theoretically participate in frequency. Sun and Jia (2018) used single-stage PV generation as the research target and proposed a novel system frequency support strategy based on the active power reserve. Rajan and Fernandez (2019) proposed a PV power control strategy for frequency regulation without any energy storage system. Zhang et al. (2019) analyzed how PV generation can affect the frequency stability of the power grid and introduced the current technical route of PV frequency regulation. An et al. (2020) proposed an enhanced frequency regulation strategy for wind turbines based on the conventional over-speed de-loading control. Li et al. (2021) compared different control strategies for wind turbines, such as virtual inertia control, droop control, virtual synchronizer technology, rotation speed control, pitch angle control, and additional energy storage systems; moreover, they clarified the principles, advantages, disadvantages, and application scope of each control strategy. Fan and Tang (2022) proposed a two-layer control strategy for wind farms participating in grid frequency regulation for problems caused by the direct switching of frequency power distribution and wind turbine control strategy.

Trials of new energy participation in frequency regulation have been carried out in many places in China, verifying that such regulation is feasible in the actual power system. The northwestern Chinese power grid has organized new energy sources to participate in rapid-frequency regulation research and has carried out pilot tests at the sending end of the large power grid (Chu et al., 2019; Ma et al., 2019). The southern Chinese power grid has stipulated that grid-connected new energy stations should have frequency regulation capability; therefore, the modification and detection of the frequency regulation capacity of the new energy station have been carried out simultaneously and step-by-step (Mu et al., 2021). The northeastern Chinese power grid has launched a pilot project enabling renewable power plants to actively support the power system, including by improving the primary frequency regulation capability (Liu et al., 2020).

Based on the studies mentioned previously, some researchers have presented scheduling strategies for considering new energy participation in frequency regulation. Ye et al. (2016) considered that PV power plants (PPPs) work in an output power derating state to participate in frequency regulation, and they proposed a unit commitment model according to the frequency response capability of PPPs and the dynamic frequency limit. Hao et al. (2020) considered wind turbines to participate in primary frequency regulation in deloaded operating mode, together with conventional units, and proposed an intra-day dispatch model considering the coordination optimization of the steady and transient states. Li et al. (2020) tried to incorporate the capability of wind plants in frequency regulation into daily scheduling and then proposed a frequency-constrained unit commitment model with wind plants, combining different response strategies of wind plants and incorporating them into the unit commitment model. Lu et al. (2021) proposed a frequency safety constraint construction method considering the frequency nadir and deduced a unit commitment model considering the frequency dynamic safety constraint with wind power and PV-integrated inertial control. Ge et al. (2021) deduced a distributed robust unit commitment model that considers the synchronous inertia of the synchronous generator unit and the virtual inertia and droop control of the wind power unit in the system. Ouyang et al. (2021) proposed power system frequency regulation based on dynamic variable-speed wind turbine power reserve and deduced a new grid scheduling mode based on dynamic wind power reserve. Zhang et al. (2022) proposed a frequency security-constrained scheduling approach considering wind farms and providing frequency support and reserve. A comparative table of the references mentioned in this paragraph is shown in Table 1.

TABLE 1

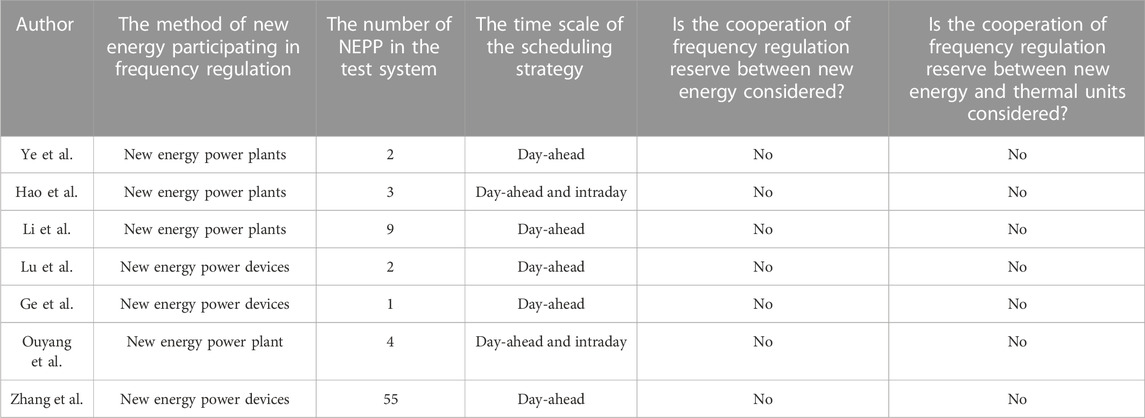
TABLE 1. Comparison of existing power system dispatching strategies, considering new energy participating frequency regulation.

The aforementioned studies can improve the frequency response capability of the power system, reduce to a certain extent the power loss of new energy caused by an insufficient frequency response capability of the system, and improve the new energy accommodation ability of the system. However, some points in the aforementioned studies still need further research. As the scale of grid-connected new energy power generation gradually increases, the number of NEPPs and new energy power units in the system will gradually rise. Moreover, new energy is gradually being regarded as a frequency regulation resource, and because there are often many types of frequency regulation resources in the system, it is necessary to consider the cooperation between these different types in the system; however, few studies have paid attention to this important subject.

To solve the problem mentioned in the previous paragraph, we propose an optimal combined day-ahead and intraday scheduling strategy that considers a joint frequency regulation reserve scheme among wind, photovoltaic, and thermal power:

1) A joint frequency regulation scheme among wind, photovoltaic, and thermal power is designed. In this scheme, the group of NEPPs works in the state of dynamic-stepped output derating.

2) An optimal combined day-ahead and intraday scheduling strategy considering the joint frequency regulation reserve scheme is proposed, and the corresponding scheduling model is derived.

According to the calculation results of the test system, the strategy proposed in this paper can reduce the reserve power provided by the new energy working in the state of output derating, reduce the new energy power loss and economic loss caused by participating in system frequency regulation, and improve the new energy accommodation capability of the system under the premise of ensuring that the steady-state frequency deviation of the system does not exceed the limit, which can provide a certain reference for the operation of the actual power system.

The rest of this paper is organized as follows. The second section describes the method by which NEPPs participate in frequency regulation. The third section introduces the joint frequency regulation scheme and deduces its objective function and constraints. The fourth section gives calculation and analysis results to discuss and prove the role of the proposed scheduling strategy. The last section concludes this paper.

2 New energy participation in frequency regulation

At present, the method by which new energy generation participates in frequency regulation can be divided in two ways: the new energy power device participate in frequency regulation or the NEPP participate in frequency regulation.

Grid-connected new energy power devices in China generally do not have frequency response capabilities. To realize their participation in frequency regulation, every new energy power device that does not have frequency response capability must be transformed. In contrast, wind power plants (WPPs) and PPPs have been equipped with basic automatic generation control (AGC) systems. Under the premise of setting up reserve power, the NEPP can participate in secondary frequency regulation. Hence, the NEPP can participate in primary frequency regulation by adding a special new energy fast power control device based on AGC. In this case, the workload and economic cost are less than the transformation of each new energy device. Therefore, this is a feasible way for new energy to participate in frequency regulation.

2.1 Frequency regulation characteristics of thermal units

The thermal power unit has a droop characteristic between the active power and the frequency. When the system frequency is between the frequency regulation dead band and the maximum allowed steady-state frequency limits, the droop characteristic can be determined by Eq. 1:

$\begin{array}{c}{\mathit{p}}_{\mathit{g}}={\mathit{p}}_{\mathit{g},\mathbf{0}}-{\mathit{p}}_{\mathit{g},\mathit{n}}\frac{\mathit{f}-{\mathit{f}}_{\mathit{g},\mathit{d}\mathit{b}}}{{\mathit{f}}_{\mathit{n}}},\end{array}(1)$

where $p_{g,0}$ is the initial power of the thermal power unit; $p_g$ is the output power of thermal power unit after primary frequency regulation; $p_{g,n}$ is the installed capacity of the thermal power unit; $f$ is the frequency measured in the connecting point to the grid; $f_n$ is the rated frequency of the system, with value of $f_n$ being 50 Hz in China; and $f_{ne,db}$ is the frequency dead band of the thermal power units, which is set at 0.033 Hz.

The power–frequency droop characteristic curve of the thermal power units is shown in Figure 1, where $∆p$ is the responded power limit for primary frequency regulation of the thermal power unit and ${∆f}_{\mathit{max}}$ is the maximum allowed frequency deviation when the system is in steady state, with the value of ${∆f}_{\mathit{max}}$ set at 0.2 Hz.

FIGURE 1

FIGURE 1. Power frequency droop characteristic curve.

In this paper, the responded power limit for primary frequency regulation of the thermal power unit $∆p$ is jointly determined by maximum allowed frequency deviation, the installed capacity, the difference coefficient, and the dead band of frequency regulation of the thermal power unit, as shown in Eq. 2:

$\begin{array}{c}∆{\mathit{p}}_{\mathit{g},\mathit{f}\mathit{r}}=\frac{{\mathit{p}}_{\mathit{g},\mathit{n},\mathit{i}}}{{\mathit{f}}_{\mathit{n}}{\mathit{\delta }}_{\mathit{g},\mathit{i}}\%}\left(∆{\mathit{f}}_{\mathit{max}}-∆{\mathit{f}}_{\mathit{d}\mathit{b},\mathit{g},\mathit{i}}\right),\end{array}(2)$

where $∆p_{g,fr}$ is the maximum responded power for primary frequency regulation of the thermal power unit; and $p_{g,n,i}$, ${\delta }_{g,i}\%$, and $∆f_{db,g,i}$ are the installed capacity, the difference coefficient, and the dead band of frequency regulation of the thermal power unit, respectively.

2.2 Characteristics of new energy power plant participation in frequency regulation

The transformed NEPP can participate in primary and secondary frequency regulation. The control structure of NEPP is shown in Figure 2.

FIGURE 2

FIGURE 2. Frequency regulation control structure diagram for NEPPs.

During operation, the NEPP participating in frequency regulation operates in a state of output power derating. The whole plant is taken as the control object, which can calculate the power caused by the frequency change measured in the grid connection point and accept the power adjustment instruction sent by the system scheduling center. Based on the operation of each unit in the power plant, the power that must be adjusted is distributed to each unit through the link of active power distribution in the power plant (Mu et al., 2021).

The transformed NEPP, as shown in Figure 2, has a droop characteristic between the active power and the frequency, which is similar to the thermal power unit. The power–frequency droop characteristic of the NEPP can also be expressed by Eq. 1. The power–frequency droop characteristic curve of the NEPP is shown in Figure 1.

As can be seen in Figure 1, the NEPP participating in frequency regulation needs to be set for upward and downward reserve power for frequency regulation. The values of upward and reserve power are both more than $∆p$. Therefore, $2∆p$ is defined as the threshold of frequency regulation of NEPP in this article. If the output power of the NEPP is more than $2∆p$, the NEPP is considered as being able to participate in frequency regulation, which is termed its “frequency regulation ability” in this paper.

2.3 Output model of new energy power plants

NEPPs participating in frequency regulation should set reserve power by operating in a state of output power derating, which includes reserve power for both primary and secondary frequency regulation.

To reduce the economic loss of the NEPPs caused by too much reserve power, the reserve power for the secondary frequency regulation is not set independently. Thus, the remaining reserve power after primary frequency regulation is regarded as the reserve power for secondary frequency regulation.

If the NEPP needs to participate in frequency regulation, then the reserve power for its frequency regulation must be set. Similar to the thermal power unit, the reserve power for NEPP frequency regulation $∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r}}$ is jointly determined by the NEPP’s installed capacity, the difference coefficient, and the dead band of frequency regulation. The relationship between the aforementioned quantities can also be expressed as Eq. 2.

As only NEPPs with frequency regulation ability can participate in frequency regulation, a state variable $K_{nes,fr,i,t}$ is introduced to represent the frequency response capability of the $i$th NEPP during time $t$. The value 1 means that the plant is able to participate in frequency regulation, and the value 0 means that the plant is incapable of participating in frequency regulation. The actual value of $K_{nes,fr,i,t}$ is derived from the $p_{ne,forecast,i,t}$ described in Section 2.2.

Based on the aforementioned analysis, the output model of the NEPP participating in frequency regulation can be shown in Eqs 3–6:

$\begin{array}{c}{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}+{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}\le {\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{i},\mathit{t},}\end{array}(3)$

$\begin{array}{c}{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}-{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}\ge \mathbf{0},\end{array}(4)$

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}={\mathit{K}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{a},\mathit{i},\mathit{t}}∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r},\mathit{i}},\end{array}(5)$

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}={\mathit{K}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{a},\mathit{i},\mathit{t}}∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r},\mathit{i}},\end{array}(6)$

where $p_{ne,i,t}$ and $p_{ne,forecast,i,t}$ are the planned output power and the forecast output power of the $i$^th NEPP during time $t$; and $r_{ne,up,i,t}$ and $r_{ne,dn,i,t}$ are the upward and downward reserve power of the $i$^th NEPP during time $t$.

In this mode of operation, $K_{nes,fa,i,t}$ determines whether the NEPP needs to set reserve power for frequency regulation.

3 Optimal scheduling strategy and model

This section formulates in turn the joint frequency regulation reserve scheme, the scheduling strategy, and the scheduling model.

3.1 Joint frequency regulation reserve scheme

Too little frequency regulation reserve power provided by new energy may cause an insufficient frequency response capability in the system, which will probably have difficulty satisfying the frequency regulation demand. In contrast, too much frequency regulation reserve power provided by the new energy may cause the NEPP to have large power and economic losses. Hence, it is particularly important for NEPPs to reasonably determine the time to participate in frequency regulation and the value of reserve power for frequency regulation. It is necessary to design a joint scheme to consider the cooperation of frequency regulation reserve power among wind, photovoltaic, and thermal power.

3.1.1 Cooperation between new energy and thermal power

Generally, with the increasing scale of new energy, more and more NEPPs are being connected to the system, which may make cooperation between new energy and thermal power more difficult in terms of frequency regulation. All NEPPs in the system can be regarded as a group, which can reduce the difficulty of frequency regulation cooperation. For the group of NEPPs, the output is equal to the sum of the output of all NEPPs, and the reserve power is equal to the sum of the reserve power of all NEPPs. The actual output power derating state of each NEPP depends on the output power derating state of the NEPP group.

The group of NEPPs should undertake only the auxiliary task of frequency regulation. This means that when the frequency response capability of thermal power units cannot satisfy the demand of reserve power for frequency regulation, the group of NEPPs should participate in frequency regulation. In addition, when the frequency response capability of thermal power units can satisfy the demand of reserve power for frequency regulation, the plant group should not participate in frequency regulation. Therefore, the group of NEPPs and the NEPP work in a state of dynamic output power derating, and the participation state of frequency regulation (PSFR) of NEPPs is determined by the operating state of the thermal power units and the demand of reserve power for frequency regulation.

Based on the aforementioned analysis, the state variable $U_{neg,fr}$ is introduced. A value of 1 means that the group of NEPPs participates in frequency regulation and that some NEPPs in the group need to participate in frequency regulation, and a value of 0 means that the group of NEPPs does not participate in frequency regulation or that any NEPP in the group need not participate in frequency regulation.

$U_{neg,fr}$ should satisfy the constraint shown in Eq. 7:

$\begin{array}{c}\begin{array}{c}{\mathit{U}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{f}\mathit{r},\mathit{t}}\le {\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t},}\\ \forall \mathit{i},\mathit{i}=\mathbf{1,2},\dots ,{\mathit{N}}_{\mathit{g},}\end{array}\end{array}(7)$

where $U_{g,i}$ is a state variable that represents the state of the $i$^th thermal power unit during time $t$, where 1 means that the thermal power unit operates in the startup state and 0 means that the thermal power unit operates in the shutdown state, and $N_g$ is the number of thermal power units.

3.1.2 Cooperation between all new energy power plants

When the group of NEPPs needs to participate in frequency regulation, unnecessary reserve power may be caused if all NEPPs in the group work in the output power derating state according to a unified state. Therefore, a method called “stepped reserve power for frequency regulation” for the group of NEPPs is proposed. Only some NEPPs in the group are selected to participate in frequency regulation, according to the demand of reserve power for frequency regulation when the group of NEPPs needs to participate in frequency regulation.

The method of stepped reserve power for frequency regulation is shown in Figure 3. The frequency regulation reserve power of the NEPP group increases with an increased equivalent frequency regulation demand undertaken by the NEPP group. The number of new energy stations that need to participate in frequency regulation is determined by the equivalent frequency regulation demand undertaken by the NEPP group.

FIGURE 3

FIGURE 3. The method of stepped reserve power for frequency regulation.

Based on the aforementioned analysis, the PSFR may be different between different NEPPs, and the cooperation of frequency regulation between each NEPP in the group should also be considered. Therefore, the state variable $U_{nes,fa,i,t}$ is introduced, representing the participating state of the $i$^th single NEPP in the group during time $t$. A value of 1 means that the NEPP participates in frequency regulation, and a value of 0 means that the NEPP does not.

In this paper, only two types of NEPPs are considered: PPPs and WPPs.

Considering the differences in operational characteristics between different types of NEPPs, participation in frequency regulation will cause wear and tear to wind power units. Therefore, the PPP is of higher priority than WPP in frequency regulation (Liu et al., 2020).

For a system containing $N_w$ WPPs and $N_p$ PPPs, the $U_{nes,fr,i,t}$ of the $i$^th WPP in any scheduling period should satisfy the constraint shown in Eq. 8:

$\begin{array}{c}\begin{array}{c}{\mathit{U}}_{\mathit{w}\mathit{p}\mathit{p},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}\le {\mathit{U}}_{\mathit{p}\mathit{p}\mathit{p},\mathit{f}\mathit{r},\mathit{j},\mathit{t},}\\ \forall \mathit{i},\mathit{i}=\mathbf{1,2},\dots ,{\mathit{N}}_{\mathit{w}},\\ \forall \mathit{j},\mathit{j}=\mathbf{1,2},\dots ,{\mathit{N}}_{\mathit{p}}.\end{array}\end{array}(8)$

Among the same types of NEPPs, a NEPP with better output power state has a larger margin of output power adjustment. Thus, it takes the initiative to derate its output power as reserve power for frequency regulation, which has little impact on its economic benefits. Therefore, a NEPP with a better output power is of higher priority than a NEPP with a worse output power in frequency regulation.

The output power rate $r_{ne,output,i,t}$ is introduced to characterize the output power state of the $i$^th NEPP during the time $t$:

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{o}\mathit{u}\mathit{t}\mathit{p}\mathit{u}\mathit{t},\mathit{i},\mathit{t}}=\frac{{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{o}\mathit{u}\mathit{t}\mathit{p}\mathit{u}\mathit{t},\mathit{i},\mathit{t}}}{{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{n},\mathit{i}}}\end{array}.(9)$

A NEPP with a larger value of $r_{ne,output}$ has a better output power state. The output power states of the same type of NEPPs can be ranked from good to bad, as shown in Eq. 10:

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{o}\mathit{u}\mathit{t}\mathit{p}\mathit{u}\mathit{t},\mathit{i}\mathbf{1},\mathit{t}},{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{o}\mathit{u}\mathit{t}\mathit{p}\mathit{u}\mathit{t},\mathit{i}\mathbf{2},\mathit{t}},\dots ,{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{o}\mathit{u}\mathit{t}\mathit{p}\mathit{u}\mathit{t},\mathit{i}{\mathit{N}}_{\mathit{s}\mathit{a}\mathit{m}\mathit{e}},\mathit{t}}\end{array},(10)$

where $N_{same}$ is the number of the same type of NEPP, $i1$ is the number of the NEPP with the highest output rate, $i2$ is the number of the NEPP with the second highest output rate, and $\mathit{i}{\mathit{N}}_{\mathit{s}\mathit{a}\mathit{m}\mathit{e}}$ is the number of the NEPP with the lowest output rate.

The variable $o_{ne,same,i,t}$ represents the frequency regulation sequence of the same type of NEPP. The relation between $r_{ne,output,i,t}$ and $o_{ne,same,i,t}$ can be described by Eq. 11:

$\begin{array}{c}{\mathit{o}}_{\mathit{n}\mathit{e},\mathit{s}\mathit{a}\mathit{m}\mathit{e},\mathit{j},\mathit{t}}=\mathit{i}\mathit{j}\end{array},(11)$

where $ij$ is the number of the NEPP with the $j$th highest output rate.

NEPPs of the same type should participate in frequency regulation based on $o_{ne,same,i,t}$. Therefore, the $U_{nes,fr,i,t}$ of the same type of NEPP should satisfy the constraint shown in Eq. 12:

$\begin{array}{c}{\mathit{U}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{t}}\left({\mathit{o}}_{\mathit{n}\mathit{e},\mathit{s}\mathit{a}\mathit{m}\mathit{e},\mathit{i},\mathit{t}}\right)\ge {\mathit{U}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{t}}\left({\mathit{o}}_{\mathit{n}\mathit{e},\mathit{s}\mathit{a}\mathit{m}\mathit{e},\mathit{i}+\mathbf{1},\mathit{t}}\right).\end{array}(12)$

Considering the joint frequency regulation reserve scheme, the group of NEPPs should work in a state of stepped output power derating, and the NEPP should work in a state of dynamic output power derating. Whether the NEPP must set the reserve power for frequency regulation is jointly determined by $U_{neg,fr,t}$, $U_{nes,fr,i,t}$, and $K_{nes,fr,i,t}$.

3.2 The scheduling strategy

Unlike thermal power units, the output power of new energy is volatile and uncertain. On one hand, this volatility makes the output power of new energy fluctuate rapidly within an hour. Thus, the traditional scheduling strategy for the hourly time scale may not be suitable for power systems with a high proportion of new energy. On the other hand, the uncertainty gives the output power of new energy the characteristic of forecast accuracy as related to time, which means more recent forecasts will have higher accuracy (Cui et al., 2021). Moreover, the traditional day-ahead scheduling strategy cannot fully utilize this characteristic. Therefore, a combined day-ahead and intraday scheduling strategy that considers the joint frequency regulation reserve scheme is proposed in this paper. The schematic diagram of this scheduling strategy is shown in Figure 4.

FIGURE 4

FIGURE 4. Schematic diagram of the scheduling strategy proposed in this paper.

As shown in Figure 4, the proposed scheduling strategy is divided into two parts according to different scheduling times: day-ahead scheduling and intraday rolling scheduling.

The day-ahead scheduling is implemented every 24 h, with a cycle of 24 h and a time resolution of 15 min. The startup and shutdown states of thermal power units can be determined in day-ahead scheduling.

The intraday rolling scheduling is implemented every 15 min, with a cycle of 4 h and a time resolution of 15 min. Intraday rolling scheduling can determine the output power state of thermal power units and the PSFR of NEPPs.

Compared with the traditional scheduling strategy, the scheduling strategy proposed in this paper is improved in two main areas. First, it adds new energy pre-processing links based on the traditional scheduling strategy. Because the joint frequency regulation reserve scheme is considered in this scheduling strategy, the frequency regulation ability and the sequence of output power derating should be determined according to the new energy forecast and the cooperation principle of frequency regulation reserve described in detail in Section 3.1 in the new energy pre-processing link. Second, it adds a NEPP output model that considers the joint frequency regulation reserve scheme and the constraint of steady frequency deviation considering new energy frequency regulation to the traditional scheduling model, which is described in detail in Section 3.3 and Section 3.4.

In this strategy, the actual PSFR for NEPPs is an optimized, calculated variable in the scheduling strategy, which is jointly determined by the demand of reserve power for frequency regulation and the operation state of thermal power units. When the demand for reserve power for frequency regulation of the system is small, the frequency response capability of thermal power units in the system can satisfy it, and no single NEPP in the group needs to participate in frequency regulation. When the demand for reserve power for frequency regulation increases further, the frequency response capability of thermal power units in the system cannot satisfy the demand, and some NEPPs in the group must therefore participate in frequency regulation. When the demand for reserve power for frequency regulation of the system increases further, even if all NEPPs in the group participate in frequency regulation, the frequency response capability of the system still cannot satisfy the demand, and some NEPPs in the group will be forced to reduce their output power to reduce the demand of reserve power for frequency regulation, so as to satisfy the demand.

This scheduling strategy can flexibly formulate the participation scheme of NEPP frequency regulation based on the demand for reserve power and the frequency response capability of conventional thermal power units. Furthermore, it fully uses the time-dependent characteristics of the forecast accuracy and improves the economy of NEPP frequency regulation.

3.3 Day-ahead scheduling model

3.3.1 Objective function

Searching for the minimum operation cost of all thermal power units is often used as the objective function of the traditional power system scheduling model. The operation cost of all thermal power units includes the coal consumption, startup, and reserve power costs. The scheduling strategy proposed in this paper accounts for the frequency regulation capability of NEPP and pursues more new energy accommodation under the premise of ensuring that the system steady-state frequency deviation does not exceed the limit. Therefore, based on the operating cost of thermal power, this paper adds the operation cost of new energy, which is composed of frequency regulation reserve cost and new energy load reduction and curtailment penalty, to form the operation cost of the system. The objective function in day-ahead scheduling can be shown as follows:

$\begin{array}{c}\mathbf{min}{\mathit{F}}^{\mathit{d}\mathit{a}}={\mathit{f}}_{\mathit{g}}^{\mathit{d}\mathit{a}}+{\mathit{f}}_{\mathit{n}\mathit{e},}^{\mathit{d}\mathit{a}}\end{array}(13)$

$\begin{array}{c}{\mathit{f}}_{\mathit{g}}^{\mathit{d}\mathit{a}}={\mathit{f}}_{\mathit{g},\mathit{c}\mathit{c}}^{\mathit{d}\mathit{a}}+{\mathit{f}}_{\mathit{g},\mathit{s}\mathit{u}}^{\mathit{d}\mathit{a}}+{\mathit{f}}_{\mathit{g},\mathit{r}}^{\mathit{d}\mathit{a}}\end{array},(14)$

$\begin{array}{c}{\mathit{f}}_{\mathit{n}\mathit{e}}^{\mathit{d}\mathit{a}}={\mathit{f}}_{\mathit{n}\mathit{e},\mathit{w}\mathit{a}\mathit{s}\mathit{t}\mathit{e}}^{\mathit{d}\mathit{a}}+{\mathit{f}}_{\mathit{n}\mathit{e},\mathit{r}}^{\mathit{d}\mathit{a}},\end{array}(15)$

$\begin{array}{c}{\mathit{f}}_{\mathit{g},\mathit{c}\mathit{c}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{{\mathit{T}}^{\mathit{d}\mathit{a}}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{g}}}\left({\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\left({\mathit{a}}_{\mathit{g},\mathit{c}\mathit{c},\mathit{i}}{\left.{\left(\mathit{p}\right.}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right)}^{\mathbf{2}}+{\mathit{b}}_{\mathit{g},\mathit{c}\mathit{c},\mathit{i}}{\mathit{p}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{c}}_{\mathit{g},\mathit{c}\mathit{c},\mathit{i}}\right)\right),\end{array}(16)$

$\begin{array}{c}{\mathit{f}}_{\mathit{g},\mathit{s}\mathit{u}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{{\mathit{T}}^{\mathit{d}\mathit{a}}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{g}}}\left({\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\left(\mathbf{1}-{\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t}-\mathbf{1}}^{\mathit{d}\mathit{a}}\right){\mathit{C}}_{\mathit{g},\mathit{s}\mathit{u},\mathit{i}}\right),\end{array}(17)$

$\begin{array}{c}{\mathit{f}}_{\mathit{g},\mathit{r}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{{\mathit{T}}^{\mathit{d}\mathit{a}}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{a}\mathit{g}\mathit{c}}}\left({\mathit{C}}_{\mathit{g},\mathit{r},\mathit{u}\mathit{p},\mathit{i}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{a},\mathit{g},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{C}}_{\mathit{g},\mathit{r},\mathit{d}\mathit{n},\mathit{i}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{a},\mathit{g},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right),\end{array}(18)$

$\begin{array}{c}{\mathit{f}}_{\mathit{n}\mathit{e},\mathit{w}\mathit{a}\mathit{s}\mathit{t}\mathit{e}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{{\mathit{T}}^{\mathit{d}\mathit{a}}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}\left({\mathit{C}}_{\mathit{n}\mathit{e},\mathit{w}\mathit{a}\mathit{s}\mathit{t}\mathit{e},\mathit{i}}\left({\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}-{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}-{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right)\right),\end{array}(19)$

$\begin{array}{c}{\mathit{f}}_{\mathit{n}\mathit{e},\mathit{r}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{{\mathit{T}}^{\mathit{d}\mathit{a}}}{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}\left({\mathit{C}}_{\mathit{n}\mathit{e},\mathit{r},\mathit{i}}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{C}}_{\mathit{n}\mathit{e},\mathit{r},\mathit{i}}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right),\end{array}(20)$

where $X^{da}$ represents that $X$ is a variable in day-ahead scheduling; $F^{da}$ is the operation cost of the system; $f_g^{da}$ and $f_{ne}^{da}$ are the operation costs of all thermal units and the operation cost of the NEPP group; $f_{g,cc}^{da}$, $f_{g,su}^{da}$, and $f_{g,r}^{da}$ are the costs of coal consumption for total thermal power units, the startup cost for total thermal power units, and the cost of reserve power for all thermal power units, respectively; $f_{ne,waste}^{da}$ and $f_{ne,r}^{da}$ are the punish cost of the forced output power derating of the NEPP group and the reserve power cost of the NEPP group; $T^{da}$ is the scheduling period number; $p_{g,i,t}^{da}$ is the output power of the $i$^th thermal power unit during the time $t$; $a_{g,cc,i}$, $b_{g,cc,i}$, and $c_{g,cc,i}$ are cost coefficients of coal consumption of the $i$^th thermal power unit; $r_{\mathit{s}\mathit{f}\mathit{a},g,up,i,t}^{da}$ and $r_{\mathit{s}\mathit{f}\mathit{a},g,dn,i,t}^{da}$ are the upward and downward reserve power for secondary frequency regulation of the $i$^th AGC unit during time $t$; $C_{g,su,i}$ is the startup cost coefficient of the $i$^th thermal power unit; $C_{g,r,up,i}$ and $C_{g,r,dn,i}$ are the cost coefficients of upward and downward reserve power for secondary frequency regulation of the $i$^th AGC unit; $C_{ne,waste,i}$ and $C_{ne,r,i}$ are the cost coefficients of forced derating punish and reserve power of the $i$th NEPP; and $N_g$, $N_{agc}$, and $N_{ne}$ are the numbers of thermal power units, AGC units, and new energy power units, respectively.

3.3.2 Constraints

The constraints of the optimal scheduling model of the power system primarily include the output power constraint of thermal power units, the ramping constraints of thermal power units, the minimum startup and shutdown time constraints of thermal power units, and the power balance constraints. These constraints are not repeated in this paper for lack of space but are described in detail in the references. In addition to the aforementioned constraints, the constraints of NEPPs and of the steady-state frequency deviation in the context of the joint frequency regulation scheme are also considered in this paper.

Based on the analysis presented in Section 2.1, $r_{ne,up,i,t}^{da}$ and $r_{ne,dn,i,t}^{da}$ are jointly determined by $U_{neg,fr,t}^{da}$, $U_{nes,fr,i,t}^{da}$, and $K_{nes,fr,i,t}^{da}$ in the scheme of joint frequency regulation reserve. Therefore, the reserve power for frequency regulation of the NEPP can be shown as Eqs 21–22:

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}={\mathit{U}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{f}\mathit{r},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{U}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{K}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r},\mathit{i}}\end{array},(21)$

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}={\mathit{U}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{f}\mathit{r},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{U}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{K}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r},\mathit{i}.}\end{array}(22)$

Eqs 3–4, Eqs 7–12, and Eqs 21–22 constitute the constraints of NEPPs.

The constraints of steady-state frequency deviation can be transformed into the constraints of reserve power for frequency regulation, meaning that the capacity of reserve power for frequency regulation of the total system should exceed the demand of reserve power for frequency regulation of the system, as shown in Eqs. 23–24:

$\begin{array}{c}{\mathit{R}}_{\mathit{f}\mathit{a},\mathit{c}\mathit{a}\mathit{p},\mathit{u}\mathit{p},\mathit{t}}^{\mathit{d}\mathit{a}}\ge {\mathit{R}}_{\mathit{f}\mathit{a},\mathit{d}\mathit{e}\mathit{m},\mathit{t}}^{\mathit{d}\mathit{a}}\end{array},(23)$

$\begin{array}{c}{\mathit{R}}_{\mathit{f}\mathit{a},\mathit{c}\mathit{a}\mathit{p},\mathit{d}\mathit{n},\mathit{t}}^{\mathit{d}\mathit{a}}\ge {\mathit{R}}_{\mathit{f}\mathit{a},\mathit{d}\mathit{e}\mathit{m},\mathit{t}}^{\mathit{d}\mathit{a}},\end{array}(24)$

where $R_{fa,cap,up,t}^{da}$ and $R_{fa,cap,dn,t}^{da}$ are the capacity of upward and downward reserve power for frequency regulation of the total system during time $t$; and $R_{fa,dem,t}^{da}$ is the demand of reserve power for frequency regulation of the total system during the time $t$.

Only the demand for system frequency regulation caused by the forecasted error of new energy output power and load is considered in this paper. Like the output power uncertainty of new energy and power load, the forecasted error and the demand of reserve power for frequency regulation are both uncertain, which makes the demand for reserve power for frequency regulation impossible to describe accurately and likely makes the available reserve power provided by new energy for frequency regulation lower than the scheduled reserve power provided by new energy. To address the aforementioned problem, this study regards the forecast error rate of the forecasted quantity in the system as a fuzzy variable, using a method of fuzzy chance-constrained programming based on credibility measurement to solve the model.

Thus, the demand for reserve power for frequency regulation of the system can be expressed as Eqs 25–26:

$\begin{array}{c}{\mathit{R}}_{\mathit{f}\mathit{a},\mathit{d}\mathit{e}\mathit{m},\mathit{t}}^{\mathit{d}\mathit{a}}={\mathit{\epsilon }}_{\mathit{l}\mathit{d},\mathit{t}}^{\mathit{d}\mathit{a}}-{\mathit{\epsilon }}_{\mathit{n}\mathit{e}\mathit{g},\mathit{t}}^{\mathit{d}\mathit{a}}={\mathit{\epsilon }}_{\mathit{l}\mathit{d},\mathit{t}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}{\mathit{\epsilon }}_{\mathit{n}\mathit{e}\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}},\end{array}(25)$

$\begin{array}{c}{\mathit{\epsilon }}_{\mathit{X},\mathit{t}}^{\mathit{d}\mathit{a}}={\mathit{X}}_{\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{t}}^{\mathit{d}\mathit{a}}{\stackrel{\sim }{\mathit{e}}}_{\mathit{X}}^{\mathit{d}\mathit{a}},\end{array}(26)$

where ${\epsilon }_{ld,t}^{da}$, ${\epsilon }_{neg,t}^{da}$, and ${\epsilon }_{nes,i,t}^{da}$ are forecast errors of the load, the output power of the group of NEPPs, and the output power of $i$^th NEPPs during time $t$, respectively; $X_{forecast,t}^{da}$ is the forecast value of required forecasted quantity in the system during time $t$; ${\stackrel{\sim }{e}}_X^{da}$ represents that $e_{X,t}^{da}$ is a fuzzy variable; and $e_{X,t}^{da}$ is the error rate of $X$ during time $t$.

The total reserve power for frequency regulation of the system consists of the reserve power for primary frequency regulation of thermal power units, the reserve power for secondary frequency regulation of AGC units, and the reserve power for frequency regulation of the NEPP group.

The maximum upward and downward reserve power for primary frequency regulation provided by the $i$^th thermal power unit during time $t$ can be shown in Eqs 27–29:

$\begin{array}{c}{\mathit{r}}_{\mathit{p}\mathit{f}\mathit{r},\mathit{g},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}=\mathbf{min}\left({\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{p}}_{\mathit{g},\mathit{max},\mathit{i}}-{\mathit{p}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}},{\mathit{R}}_{\mathit{g},\mathit{u}\mathit{p},\mathit{i}},∆{\mathit{p}}_{\mathit{g},\mathit{f}\mathit{a},\mathit{i}}\right),\end{array}(27)$

$\begin{array}{c}{\mathit{r}}_{\mathit{p}\mathit{f}\mathit{r},\mathit{g},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}=\mathbf{min}\left({\mathit{p}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}-{\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{p}}_{\mathit{g},\mathit{min},\mathit{i}},{\mathit{R}}_{\mathit{g},\mathit{d}\mathit{n},\mathit{i}},∆{\mathit{p}}_{\mathit{g},\mathit{f}\mathit{a},\mathit{i}}\right),\end{array}(28)$

$\begin{array}{c}∆{\mathit{p}}_{\mathit{g},\mathit{f}\mathit{a},\mathit{i}}=\frac{{\mathit{p}}_{\mathit{g},\mathit{n},\mathit{i}}}{{\mathit{f}}_{\mathit{n}}{\mathit{\delta }}_{\mathit{g},\mathit{i}}\%}\left(∆{\mathit{f}}_{\mathit{max}}-∆{\mathit{f}}_{\mathit{g},\mathit{d}\mathit{z},\mathit{i}}\right)\end{array},(29)$

where $p_{g,\mathit{max},i}$ and $p_{g,\mathit{min},i}$ are the maximum and minimum output power of the $i$^th thermal power unit, respectively; $R_{g,up,i}$ and $R_{g,dn,i}$ are the upper and lower climbing limits of the $i$^th thermal power unit, respectively; $∆p_{g,fr,i}$ is the responded power limit of primary frequency regulation of the $i$^th thermal power unit; and $p_{g,n,i}$, ${\delta }_{g,i}\%$, and $∆f_{g,ne,i}$ are the installed capacity, the difference coefficient, and the frequency dead band of the $i$^th thermal power unit, respectively.

The maximum upward and downward reserve power for secondary frequency regulation provided by the $i$^th AGC unit during the time $t$ can be shown in Eqs 30–31:

$\begin{array}{c}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}=\mathit{min}\left({\mathit{U}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{p}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{max},\mathit{i}}-{\mathit{p}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}},{\mathit{R}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{u}\mathit{p},\mathit{i}}\right),\end{array}(30)$

$\begin{array}{c}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}=\mathit{min}\left({\mathit{p}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}-{\mathit{U}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{p}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{min},\mathit{i}},{\mathit{R}}_{\mathit{a}\mathit{g}\mathit{c},\mathit{d}\mathit{n},\mathit{i}}\right).\end{array}(31)$

Under the influence of forecast error, the upward and downward reserve power for frequency regulation provided by the group of NEPPs during time $t$ can be shown in Eqs 32–33:

$\begin{array}{c}\left.{\mathit{r}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{u}\mathit{p},\mathit{t}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}(\mathbf{1}+{\stackrel{\sim }{\mathit{e}}}_{\mathit{n}\mathit{e}}^{\mathit{d}\mathit{a}})\right)\end{array},(32)$

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{d}\mathit{n},\mathit{t}}^{\mathit{d}\mathit{a}}={\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}(\mathbf{1}+{\stackrel{\sim }{\mathit{e}}}_{\mathit{n}\mathit{e}}^{\mathit{d}\mathit{a}})).\end{array}(33)$

To sum up, the constraints of steady-state frequency deviation can be shown in Eqs 34–35, which utilize fuzzy chance constraints:

$\begin{array}{c}\mathit{C}\mathit{r}\left\{{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{g}}}{\mathit{r}}_{\mathit{p}\mathit{f}\mathit{r},\mathit{g},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{a}\mathit{g}\mathit{c}}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{r}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{u}\mathit{p},\mathit{t}}^{\mathit{d}\mathit{a}}\ge {\mathit{R}}_{\mathit{f}\mathit{a},\mathit{d}\mathit{e}\mathit{m},\mathit{t}}^{\mathit{d}\mathit{a}}\right\}>{\mathit{\alpha }}^{\mathit{d}\mathit{a}},\end{array}(34)$

$\begin{array}{c}\mathit{C}\mathit{r}\left\{{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{g}}}{\mathit{r}}_{\mathit{p}\mathit{f}\mathit{r},\mathit{g},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{a}\mathit{g}\mathit{c}}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{r}}_{\mathit{n}\mathit{e}\mathit{g},\mathit{d}\mathit{n},\mathit{t}}^{\mathit{d}\mathit{a}}\ge {\mathit{R}}_{\mathit{f}\mathit{a},\mathit{d}\mathit{e}\mathit{m},\mathit{t}}^{\mathit{d}\mathit{a}}\right\}>{\mathit{\alpha }}^{\mathit{d}\mathit{a}},\end{array}(35)$

where ${\alpha }^{da}$ is the confidence level of the fuzzy chance constraint in day-ahead scheduling.

3.4 Intraday rolling scheduling model

3.4.1 Objective function

The startup and shutdown scheme of thermal power units determined in the day-ahead scheduling does not change in intraday rolling scheduling, and the startup cost of thermal power units in the intraday scheduling model is the same as $f_{g,su}^{da}$. The rest of the objective function is consistent with day-ahead scheduling:

$\begin{array}{c}\mathit{min}{\mathit{F}}^{\mathit{d}\mathit{i}}={\mathit{f}}_{\mathit{g}}^{\mathit{d}\mathit{i}}+{\mathit{f}}_{\mathit{n}\mathit{e}}^{\mathit{d}\mathit{i}}\end{array},(36)$

$\begin{array}{c}{\mathit{f}}_{\mathit{g}}^{\mathit{d}\mathit{i}}={\mathit{f}}_{\mathit{g},\mathit{c}\mathit{c}}^{\mathit{d}\mathit{a}}\left({\mathit{U}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}},{\mathit{p}}_{\mathit{g},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}\right)+{\mathit{f}}_{\mathit{g},\mathit{s}\mathit{u}}^{\mathit{d}\mathit{a}}+{\mathit{f}}_{\mathit{g},\mathit{r}}^{\mathit{d}\mathit{a}}\left({\mathit{r}}_{\mathit{s}\mathit{f}\mathit{a},\mathit{g},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}},{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{a},\mathit{g},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}\right),\end{array}(37)$

$\begin{array}{c}{\mathit{f}}_{\mathit{n}\mathit{e}}^{\mathit{d}\mathit{a}}={\mathit{f}}_{\mathit{n}\mathit{e},\mathit{w}\mathit{a}\mathit{s}\mathit{t}\mathit{e}}^{\mathit{d}\mathit{a}}\left({\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}},{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}},{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}\right)+{\mathit{f}}_{\mathit{n}\mathit{e},\mathit{r}}^{\mathit{d}\mathit{a}}\left({\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}},{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}\right),\end{array}(38)$

where $X^{di}$ represents that the variable $X$ is a variable in intraday scheduling.

3.4.2 Constraints

Constraints for intraday rolling scheduling are similar to constraints for day-ahead scheduling.

The minimum startup and shutdown time constraints of thermal power units need not be considered in intraday scheduling because the startup and shutdown scheme of thermal power units is not changed in intraday scheduling.

The constraints of NEPPs in intraday scheduling are minimally different from the day-ahead scheduling. Since the startup and shutdown schemes of thermal power units are not changed, $r_{ne,up,i,t}^{di}$ and $r_{ne,dn,i,t}^{di}$ are jointly determined by $U_{nes,fr,i,t}^{di}$ and $K_{nes,fr,i,t}^{di}$, the reserve power for frequency regulation of the NEPP, which can be shown as Eqs 39–40:

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}={\mathit{U}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}{\mathit{K}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r},\mathit{i},}\end{array}(39)$

$\begin{array}{c}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}={\mathit{U}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}{\mathit{K}}_{\mathit{n}\mathit{e}\mathit{s},\mathit{f}\mathit{r},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}}∆{\mathit{p}}_{\mathit{n}\mathit{e},\mathit{f}\mathit{r},\mathit{i}}.\end{array}(40)$

The remaining constraints are the same as in day-ahead scheduling, only changing $X^{da}$ to $X^{di}$.

3.5 Transformation and solution of the model

Both the day-ahead and the intraday rolling scheduling models are nonlinear mixed-integer programming problems with fuzzy variables. As the model is difficult to solve directly, it must be transformed.

3.5.1 Transformation of the model

The membership function of fuzzy variables can be represented by trapezoidal membership function (Liu, B. and Peng, J., 2005), as shown in Eq. 41:

$\begin{array}{c}\mathit{\mu }\left({\stackrel{\sim }{\mathit{e}}}_{\mathit{X}}\right)=\left\{\begin{array}{cc}\frac{{\mathit{e}}_{\mathit{X},\mathbf{4}}-{\mathit{e}}_{\mathit{X}}}{{\mathit{e}}_{\mathit{X},\mathbf{4}}-{\mathit{e}}_{\mathit{X},\mathbf{3}}}& {\mathit{e}}_{\mathit{X},\mathbf{3}}\le {\mathit{e}}_{\mathit{X}}\le {\mathit{e}}_{\mathit{X},\mathbf{4}},\\ \mathbf{1}& {\mathit{e}}_{\mathit{X},\mathbf{2}}\le {\mathit{e}}_{\mathit{X}}\le {\mathit{e}}_{\mathit{X},\mathbf{3},}\\ \frac{{\mathit{e}}_{\mathit{X}}-{\mathit{e}}_{\mathit{X},\mathbf{1}}}{{\mathit{e}}_{\mathit{X},\mathbf{2}}-{\mathit{e}}_{\mathit{X},\mathbf{1}}}& {\mathit{e}}_{\mathit{X},\mathbf{1}}\le {\mathit{e}}_{\mathit{X}}\le {\mathit{e}}_{\mathit{X},\mathbf{2},}\\ \mathbf{0}& \mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r},\end{array}\right.\end{array}(41)$

where $\mu \left({\stackrel{\sim }{e}}_X\right)$ is the trapezoidal membership function of ${\stackrel{\sim }{e}}_X$; and $e_{X,1}$, $e_{X,2}$, $e_{X,3}$, and $e_{X,4}$ are membership function parameters of ${\stackrel{\sim }{e}}_X$.

The fuzzy chance constraint can be turned into its crisp equivalent form by the method proposed by Liu, B. and Peng, J. (2005). Thus, the corresponding crisp equivalent forms of Eqs 34–35 can be shown in Eqs 42–43:

$\begin{array}{c}\begin{array}{c}\left(\mathbf{2}-\mathbf{2}{\mathit{\alpha }}^{\mathit{d}\mathit{a}}\right)\left({\mathit{p}}_{\mathit{l}\mathit{d},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{e}}_{\mathit{l}\mathit{d},\mathbf{3}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}\left(({\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right){\mathit{e}}_{\mathit{n}\mathit{e},\mathbf{2}}^{\mathit{d}\mathit{a}}\right))+(\mathbf{2}{\mathit{\alpha }}^{\mathit{d}\mathit{a}}\\ -\mathbf{1}\left)\right({\mathit{p}}_{\mathit{l}\mathit{d},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{e}}_{\mathit{l}\mathit{d},\mathbf{4}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}\left(({\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right){\mathit{e}}_{\mathit{n}\mathit{e},\mathbf{1}}^{\mathit{d}\mathit{a}}\left)\right)-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{g}}}{\mathit{r}}_{\mathit{p}\mathit{f}\mathit{r},\mathit{g},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\\ -{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{a}\mathit{g}\mathit{c}}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{u}\mathit{p},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\le \mathbf{0},\end{array}\end{array}(42)$

$\begin{array}{c}\begin{array}{c}\left(\mathbf{2}-\mathbf{2}{\mathit{\alpha }}^{\mathit{d}\mathit{a}}\right)\left({\mathit{p}}_{\mathit{l}\mathit{d},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{e}}_{\mathit{l}\mathit{d},\mathbf{3}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}\left(({\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right){\mathit{e}}_{\mathit{n}\mathit{e},\mathbf{2}}^{\mathit{d}\mathit{a}}\right))+(\mathbf{2}{\mathit{\alpha }}^{\mathit{d}\mathit{a}}\\ -\mathbf{1}\left)\right({\mathit{p}}_{\mathit{l}\mathit{d},\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{c}\mathit{a}\mathit{s}\mathit{t},\mathit{t}}^{\mathit{d}\mathit{a}}{\mathit{e}}_{\mathit{l}\mathit{d},\mathbf{4}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}\left(({\mathit{p}}_{\mathit{n}\mathit{e},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}+{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\right){\mathit{e}}_{\mathit{n}\mathit{e},\mathbf{1}}^{\mathit{d}\mathit{a}}\left)\right)-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{g}}}{\mathit{r}}_{\mathit{p}\mathit{f}\mathit{r},\mathit{g},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\\ -{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{a}\mathit{g}\mathit{c}}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{n}\mathit{e}}}{\mathit{r}}_{\mathit{n}\mathit{e},\mathit{d}\mathit{n},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{a}}\le \mathbf{0},\end{array}\end{array}(43)$

where $p_{ld,forecast,t}^{da}$ is the forecast power load during time $t$ in day-ahead scheduling; $e_{ld,1}^{da}$, $e_{ld,2}^{da}$, $e_{ld,3}^{da}$, and $e_{ld,4}^{da}$ are membership function parameters of the fuzzy variable ${\stackrel{\sim }{e}}_{ld}^{da}$; and $e_{ne,1}^{da}$, $e_{ne,2}^{da}$, $e_{ne,3}^{da}$, and $e_{ne,4}^{da}$ are membership function parameters of the fuzzy variable ${\stackrel{\sim }{e}}_{ne}^{da}$.

3.5.2 Solution of the model

The model can be transformed into mixed-integer quadratic programming problems, which can be well solved by the commercial solver Gurobi. Therefore, the transformed model was solved using MATLAB R2018b with the Gurobi solver in this paper, and the computing environment was an Intel Core i5-8300h CPU with 8GB RAM.

4 Case study

4.1 The test system

The improved IEEE RTS 24-bus system, which can be obtained by adding a group of NEPPs to the original IEEE RTS-24 bus system (Grigg et al., 1996), was selected as the test system for this paper. The improved system has 26 thermal power units and a group of NEPPs that include three WPPs with an installed capacity of 300 MW and three PPPs with an installed capacity of 200 MW. The structure of the improved IEEE RTS 24-bus system is shown in Figure 5. The 25th and 26th thermal power units are set as the AGC unit because of high ramping rate, and all power units except for AGC units participate in primary frequency regulation. The parameters of thermal power units can be obtained from Wang et al. (1995). The frequency regulation parameters of thermal power units and NEPPs are shown in Table 2, and the membership function parameters of fuzzy variables are shown in Table 3. The confidence level of chance constraints was set to 0.8 in day-ahead scheduling and 0.9 in intraday rolling scheduling, and the cost coefficient of forced derating punish was set to 50 $·(MW·15 min)⁻¹.

FIGURE 5

FIGURE 5. Structure of the improved IEEE RTS 24-bus system.

TABLE 2

TABLE 2. parameters of frequency regulation.

TABLE 3

TABLE 3. Membership function parameters of fuzzy variables.

The forecast curve of the required forecasted quantity in the system was obtained by adding white noise to the actual curve (Bao et al., 2016). The actual curve is shown in Figure 6, and the day-ahead forecast curve and the intraday forecast curve are shown in Figure 7.

FIGURE 6

FIGURE 6. Actual curve of the quantity in a system that needs to be forecasted.

FIGURE 7

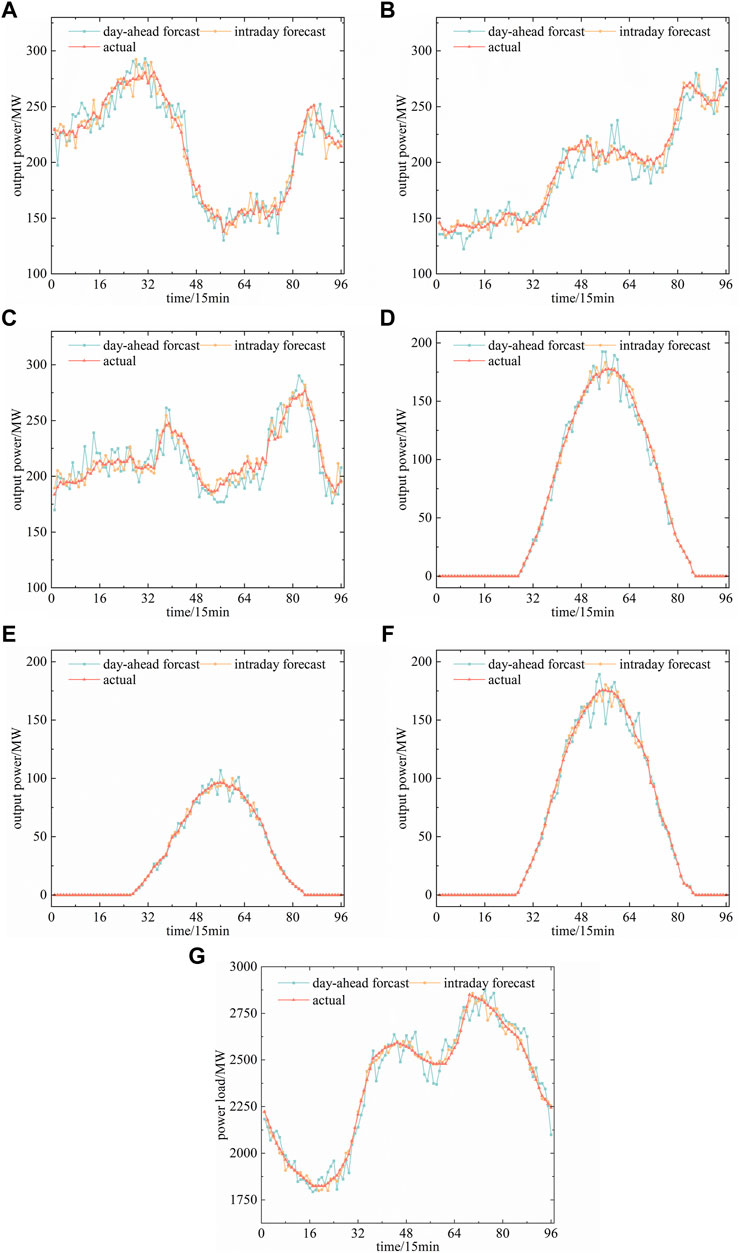
FIGURE 7. Forecast curves of the quantity in a system that needs to be forecasted: (A) WPP1, (B) WPP2, (C) WPP3, (D) PPP1, (E)PPP2, (F)PPP3, and (G) power load.

4.2 Calculation results

The system scheduled result is shown in Figure 8. The frequency response capability of thermal power units cannot satisfy the demand of reserve power for frequency regulation in the 14th, 31st, or 36th to 87th scheduling periods; some NEPPs in the group must set reserve power and participate in frequency regulation. In addition, the forced output power derating of the new energy with an extremely small value only exists in the 37th, 44th, and 66th scheduling periods.

FIGURE 8

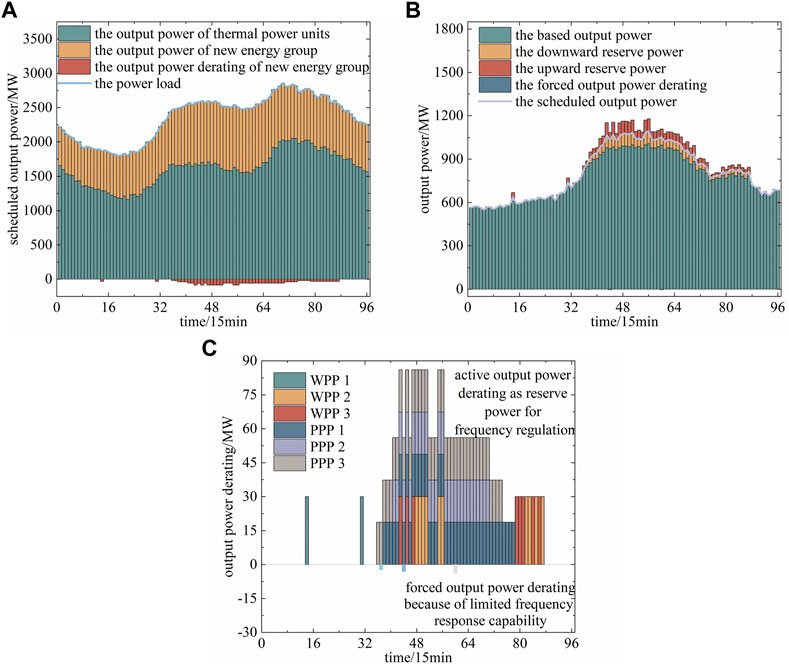
FIGURE 8. System scheduling results: (A) scheduled result of the system, (B) scheduled result of the new energy, and (C) output power derating of new energy.

To verify the effectiveness of the joint frequency regulation scheme, the system’s PSFR from the 65th to 80th scheduling periods in day-ahead scheduling and intraday scheduling were analyzed separately, as shown in Figure 9.

FIGURE 9

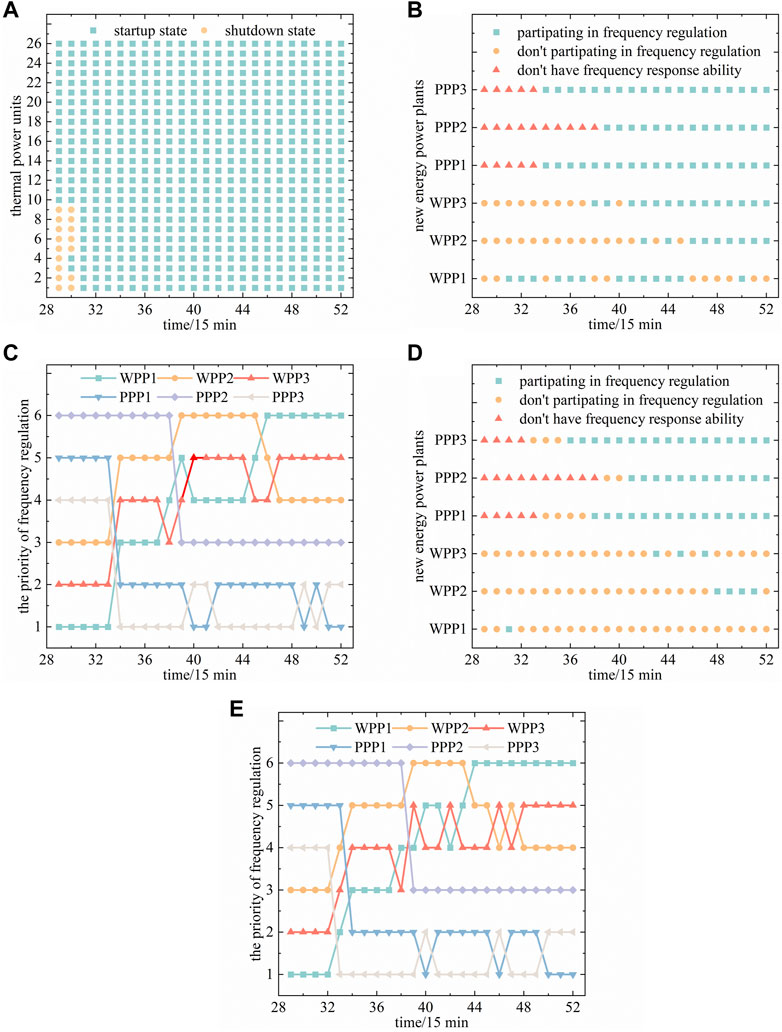
FIGURE 9. PSFR of the system in selected periods: (A) startup and shutdown states of thermal power units, (B) PSFR of NEPPs in day-ahead scheduling, (C) participation sequence of frequency regulation of NEPPs in day-ahead scheduling, (D) PSFR of NEPPs in intraday scheduling, and (E) participation sequence of frequency regulation of NEPPs in intraday scheduling.

As shown in Figures 9A, B, some new energy stations participate in frequency regulation from the 31st period through the 52nd period. At this time, all thermal power units are online, which conforms to the cooperation principle of frequency regulation between new energy and thermal power described in Section 3.1.1.

Figures 9B–E show that NEPPs with a higher priority level give priority to setting reserve power for frequency regulation, which conforms to the cooperation principle of frequency regulation between each NEPP in the group of NEPPs described in Section 3.1.2.

4.3 Comparison and analysis

Four comparative scheduling strategies are added to further verify the effectiveness of the scheduling strategy proposed in this paper as follows:

S1: A traditional day-ahead scheduling strategy considering the traditional system reserve power and the traditional AGC reserve power constraint (Lin et al., 2014).

S2: A scheduling strategy based on S1 that considers the constraint of reserve power for regulation, with the frequency response capability provided only by thermal power units.

S3: A scheduling strategy based on S2 that considers the frequency response capability of new energy but does not consider the joint frequency regulation reserve scheme for wind, photovoltaic, and thermal power.

S4: A scheduling strategy based on S3 that considers the joint frequency regulation reserve scheme for wind, photovoltaic, and thermal power.

S5: A combined day-ahead and intraday scheduling strategy based on S4, which is the proposed strategy in this paper.

To better control the differences between the aforementioned scheduling strategies, the time resolution was set to 15 min. Moreover, the fuzzy chance-constrained programming method based on credibility measures was used to solve the models in S2, S3, S4, and S5, and the confidence level of chance constraints was set to 0.8 in day-ahead scheduling and 0.9 in intraday rolling scheduling.

4.3.1 The analysis of frequency regulation effect

A series of analyses were conducted on the frequency regulation effect of the system, and the calculation result is shown in Figure 10.

FIGURE 10

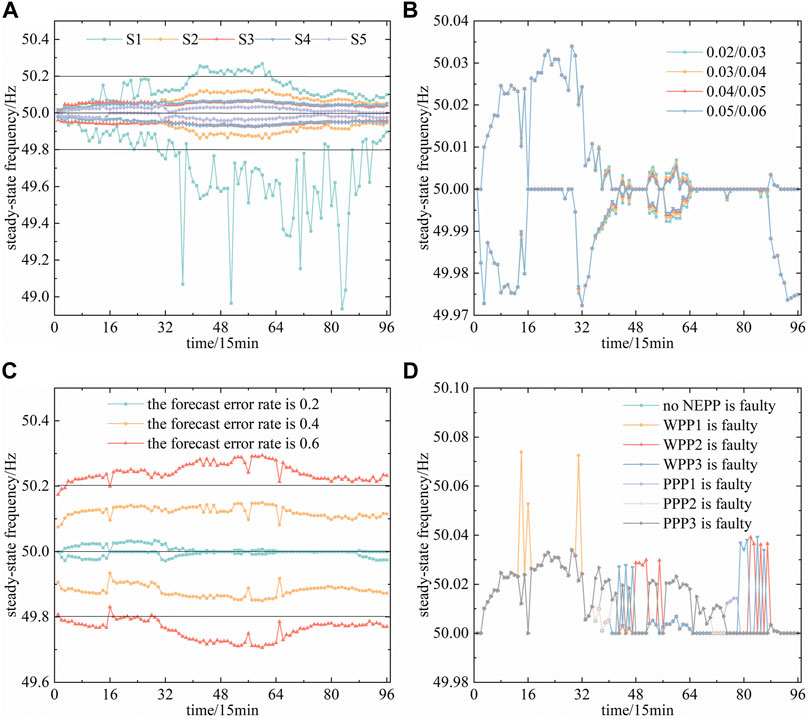
FIGURE 10. Steady-state frequency deviation of the system: (A) steady-state frequency deviation of the power system in the five scheduling strategies, (B) steady-state frequency deviation in S5 when changing difference coefficients of NEPPs, (C) steady-state frequency deviation in S5 when the error of new energy forecast is large, and (D) steady-state frequency deviation in S5 when the NEPP is faulty.

The power disturbance of the system $∆p_t$ was set to $\pm 30\%{\displaystyle \sum }_{i=1}^{N_{ne}}\left(p_{ne,forecast,i,t}^{da}\right)$ in day-ahead scheduling and $\pm 20\%{\displaystyle \sum }_{i=1}^{N_{ne}}\left(p_{ne,forecast,i,t}^{da}\right)$ in intraday scheduling during the scheduling time t, and the steady-state frequency deviation was calculated by Eq. 44,

$\begin{array}{c}∆{\mathit{f}}_{\mathit{t}}=\left(∆{\mathit{p}}_{\mathit{t}}-{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{a}\mathit{g}\mathit{c}}}{\mathit{r}}_{\mathit{s}\mathit{f}\mathit{r},\mathit{a}\mathit{g}\mathit{c},\mathit{i},\mathit{t}}\right)/{\mathit{k}}_{\mathit{S}},\end{array}(44)$

where $∆f_t$ is the steady-state frequency deviation and $k_S$ is the unity regulation power of the total system.

The calculation result is given in Figure 10A, which shows that the steady-state frequency deviation in S1 exceeds the allowable frequency limits. This is because the constraints of steady-state frequency deviation are not considered in S1, while they are considered in S2, S3, S4, and S5 so that they can ensure that the steady-state frequency deviation is always within the allowable frequency limits in S2, S3, S4, and S5.

On the basis of the S5 proposed in this paper, the difference coefficient of the NEPP is changed and the scheduling model is calculated. The difference coefficients of the WPP/PPP were set to 0.02/0.03, 0.03/0.04, 0.04/0.05, and 0.05/0.06, with the remaining parameters of the NEPP unchanged. The calculation result is shown in Figure 10B.

According to Eq. 2, as the difference coefficient becomes bigger, the primary frequency regulation power reserve of the NEPP gradually decreases; if the output derating is still conducted according to the scheduling plan, there will have more reserve power for secondary frequency regulation, which will make the steady-state frequency deviation of the system smaller, as shown in Figure 10B.

When the new energy forecast error is large, the power disturbance faced by the system is relatively large, which affects the frequency regulation effect of the system. For S5, the new energy forecast error rates of 0.2, 0.4, and 0.6 were calculated, with the calculation results shown in Figure 10C.

As shown in Figure 10C, with the increase of new energy forecast error, the steady-state frequency deviation of the system gradually increases. When the error rate of the new energy forecast increases to a certain level (as shown in Figure 10C at 0.6), the steady-state frequency deviation of the system may exceed the allowable limit. In order to avoid this situation, the NEPPs may be forced to derate the output.

When the frequency regulation control of NEPPs is faulty, the output power of NEPPs cannot be derated according to the scheduling plan, which is equivalent to reducing the reserve power of the system for frequency regulation while facing the positive power disturbance generated by the faulty NEPP.

When the overall forecast error of new energy is negative, the positive power disturbances generated by the faulty NEPP cancel each other out and the total power disturbance of the system becomes smaller, which does not adversely affect the frequency regulation effect of the system. Therefore, this paper focuses on the situation in which the overall forecast error of new energy is positive and the frequency regulation control for new energy is faulty.

When the overall forecast error of new energy is positive, the positive power disturbance generated by the faulty NEPP makes the total power disturbance of the system bigger, which adversely affects the frequency regulation effect of the system.

For S5, the error rate of new energy prediction was taken to be +20%, and it was assumed that WPP1, WPP2, WPP3, PPP1, and PPP2 were faulty and that PPP3 failed. The calculation results are shown in Figure 10D.

Figure 10D shows that when any NEPP in the system is faulty, although the steady-state frequency deviation of the system becomes larger, it does not exceed the allowable limit.

4.3.2 The analysis of scheduling strategy effect

Under the premise of ensuring that steady-state frequency deviation does not exceed the allowable frequency limits, the following analysis was carried out for S2, S3, S4, and S5.

The costs of S2, S3, S4, and S5 are shown in Table 4.

TABLE 4

TABLE 4. Costs of the four scheduling strategies.

As shown in Table 1, S5 has the lowest total cost, compared with S2, S5 considers the frequency response capability of new energy power generation, which can improve the frequency response capability of the total system and avoid the high value of $f_{ne,waste}$ in S2. Compared with S3, S5 considers the joint frequency regulation scheme between new energy and thermal power, which can avoid the problem of NEPPs with frequency regulation capability always derating output as reserve power and reduce the high-valued $f_{ne,r}$ in S3. Compared with S4, S5 uses a more accurate forecast for rolling calculation based on the calculation result of S4, which can further reduce $f_{ne,r}$ in S4.

Further analysis of the new energy accommodation ability of the system is shown in Figure 11.

FIGURE 11

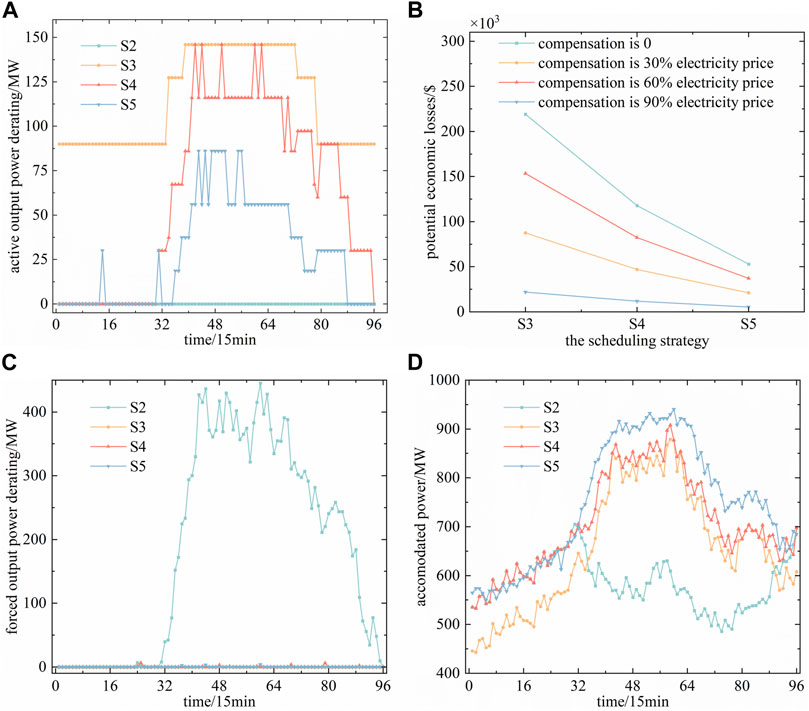
FIGURE 11. Scheduled result of new energy in the four scheduling strategies: (A) active output power derating, (B) potential economic loss, (C) forced output power derating, and (D) accommodated electricity.

The new energy generation participating in frequency regulation needed to derate its output power as reserve power for frequency regulation is shown in Figure 11A.

As shown in Figure 11A, the reserve power for frequency regulation of new energy does not exist in S2 because the frequency response capability of new energy is not considered in S2. Moreover, the reserve power for frequency regulation of new energy exists in S3, S4, and S5, but the values of reserve power are different in S3, S4, and S5. Since the joint frequency regulation scheme is not considered in S3, NEPPs with frequency response capability must derate their output power for reserve power of frequency regulation, and the value of reserve power provided by new energy in S3 is higher than in S4 or S5. S4 and S5 consider joint frequency regulation, with S5 as an intraday rolling scheduling based on the day-ahead scheduling S4, and S5 is implemented based on a recent forecast of new energy output power and power load. As the recent forecast has higher accuracy, the demand for reserve power of frequency regulation in S5 is lower than in S4, and the value of reserve power provided by new energy in S5 is lower than in S4.

The frequency regulation capability of new energy is considered in S3, S4, and S5. The output power of NEPPs needs to be derated as frequency regulation reserve, which causes certain power loss and economic loss to the NEPP. In S3, the output power of NEPPs with frequency regulation capabilities must always be derated as frequency regulation reserve. The cumulative power of output derating for frequency regulation in the entire scheduling cycle is 2738.667 Mwh, accounting for 14.808% of the total forecast of new energy power. In S4, the group of NEPPs works in a state of dynamic stepped output derating, and the output power of NEPPs is only derated as frequency regulation reserve during the high-frequency regulation demand period. The cumulative power of output derating for frequency regulation in the entire scheduling cycle is 1471.167 Mwh, accounting for 7.955% of the total forecast of new energy power. In S5, the demand for frequency regulation reserve is reduced because of the use of more accurate new energy intraday forecast data, and the frequency regulation provided by the group of NEPPs working in the state of dynamic stepped output derating is further reduced. The cumulative power of output derating for frequency regulation in the entire scheduling cycle is 663.333 Mwh, accounting for 3.588% of the total forecast of new energy power.

It is analyzed from the perspective of potential economic losses of new energy groups, which are shown in Figure 11B.

The fluctuation of electricity price and frequency regulation reserve compensation were not considered, and the fixed electricity price was set as 80$/MWh. The potential economic losses of the group of NEPPs caused by output derating in S3, S4, and S5 are 219093.332, 117693.333, and 53066.667, respectively. Furthermore, considering the compensation for frequency reserve, the compensation ratio of frequency regulation was set as 30%, 60%, and 90% of the electricity price. In S3, the potential economic losses of the group of NEPPs are 87637.333, 153365.333, and 21909.333, respectively. In S4, the potential economic losses of the group of NEPPs are 47077.333, 82385.333, and 11769.333, respectively. In S5, the potential economic losses of the group of NEPPs are 21226.667, 37146.667, and 5306.667, respectively.

As Figure 11B shows, in the three types of power system strategy scheduling that consider new energy to participate in system frequency regulation, S5, the scheduling strategy proposed in this paper, has the smallest output derating and smallest potential economic losses.

The frequency response capability may not satisfy the demand of reserve power for frequency regulation in some scheduling periods, so that the new energy generation is probably forced to derate its output power, as shown in Figure 11C.

Figure 11C shows that the forced output power derating of new energy in S2 is much higher than in S3, S4, or S5 because the frequency response capability of new energy is not considered in S2. The output power of new energy in S2 is forced to derate to satisfy the system frequency regulation reserve power demand from the 31st period to the 96th period, with a high demand for frequency regulation because of the insufficient frequency response capability of thermal power units. The frequency response capability of new energy is considered in S3, S4, and S5, and the frequency response capability of the system can satisfy the demand of reserve power for frequency regulation, so the forced output power derating of new energy is almost 0.

In this paper, the accommodated power of new energy was considered to be equal to the forecast power of the new energy minus the forced power derating caused by the insufficient frequency regulation capability of the system and the active power derating of the new energy. The accommodated power of new energy is shown in Figure 11D.

Figure 11D shows that S5 has the most accommodated power of new energy in most scheduling periods. The total accommodated electricity of new energy in S2, S3, S4 and S5 is calculated as 8517.444 MWh, 10950.203 MWh, 11440.652 MWh, and 12363.027 MWh, respectively, and the total accommodation rates of new energy in S2, S3, S4, and S5 are 0.789, 0.852, 0.930, and 0.970, respectively. Thus, the accommodation ability of new energy in S5 is higher than in S2, S3, and S4.

As shown by the aforementioned comparison of the five scheduling strategies, the combined day-ahead and intraday scheduling strategy proposed in this study—which considers a joint frequency regulation reserve scheme for wind, photovoltaic, and thermal power—has the lowest cost and highest new energy accommodation ability under the premise of ensuring that the steady-state frequency deviation does not exceed the allowable frequency limits.

5 Conclusion

Based on the differences in operating characteristics between various frequency regulation resources in the system, a joint frequency regulation reserve scheme was designed between the group of NEPPs and thermal power units. A multi-time-scale scheduling strategy was proposed based on the joint frequency regulation scheme, and its model was deduced and was solved by the Gurobi solver in MATLAB. The superiority and limitations to the scheduling strategy proposed in this paper can be drawn from the aforementioned analysis as discussed as follows:

5.1 The effectiveness of the scheduling strategy

1) The frequency regulation capability of new energy and the constraint of steady-state frequency deviation are both considered in this strategy, which can improve the frequency regulation capability of the system and ensure that the steady-state frequency is within the allowable range.

2) A joint frequency regulation reserve scheme including wind, photovoltaic, and thermal power was designed in this paper. In the scheme, the group of NEPPs works in a state of dynamic stepped output power derating, and the frequency regulation cooperation is considered. The comparison and analysis show that this scheme has the smallest new energy frequency regulation reserve power, which can effectively reduce the power and economic losses caused by the new energy participating in system frequency regulation.

3) This article proposes a combined day-ahead and intraday power system scheduling strategy considering the joint frequency regulation reserve scheme. On one hand, when the intraday rolling scheduling is carried out, the high-precision new energy forecast may reduce the frequency regulation demand of the system, in turn reducing the frequency regulation reserve power provided by the new energy. On the other hand, considering the frequency regulation capability of the new energy, the frequency regulation ability of the system is improved, which can avoid the large quantity of forced output derating of new energy caused by insufficient frequency regulation capability of the system.

4) In general, in the combined day-ahead and intraday power system scheduling strategy considering the joint frequency regulation reserve scheme across wind, photovoltaic, and thermal power proposed in this paper, although the output power derating of NEPPs must be carried out, it improves the frequency regulation capability of the system so as to avoid a large amount of forced output derating of new energy. The new energy accommodation and new energy accommodation rate of the system are both improved.

5.2 The limitations to the scheduling strategy

1) The frequency regulation capability of the NEPPs is affected by the prediction error value of the new energy output power. If the prediction error is large, the available reserve capacity for frequency regulation of new energy power plants in actual operation will be quite different than in the scheduling plan, which is described in detail in Section 4.3.1.

2) The dynamic frequency response model of the system has not been researched in this paper. When the system has a large active power disturbance for a short time, it may have a very high instantaneous frequency drop rate due to insufficient system inertia.

3) The strategy proposed in this article is rather simple in terms of frequency regulation cooperation between NEPPs. Photovoltaic power plants always have a higher priority for participating in frequency regulation than wind power plants, and they must always set the frequency regulation reserve, which may affect the enthusiasm of frequency regulation for photovoltaic power plants. Between different wind power plants, those with higher output rates are prioritized for power derating, and the operating status of wind turbines inside the wind power plants is not considered, which may lead to an increased mechanical loss of the internal wind turbine during some periods.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

SZ: idea, methodology, and writing—original draft preparation. HW: writing—review and editing. WW: academic regulation supervision. XC: engineering—practical guidance.

Funding

This work was supported by the National Key R&D Program of China (2021YFB1507005) and the Key Research and Development Program of Xinjiang Uygur Autonomous Region (2022B01020-3).

Conflict of interest

XC was employed by the company State Grid Xinjiang Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

AGC, automatic generation control; NEPP, new energy power plant; PV, photovoltaics; PSFR, participation state of frequency regulation; PPP, PV power plant; WPP, wind power plant.

References

An, Y., Li, Y., Zhang, J., Wang, T., and Liu, C. (2020). “Enhanced frequency regulation strategy for wind turbines based on over-speed de-loading control,” in 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 04-07 June 2020, 442–446. doi:10.1109/ACPEE48638.2020.9136254

CrossRef Full Text | Google Scholar

Bao, Y., Wang, B., Li, Y., and Yang, S. (2016). Rolling dispatch model considering wind penetration and multi-scale demand response resources. Proc. CSEE 31 (17), 4589–4600. doi:10.13334/j.0258-8013.pcsee.151343

CrossRef Full Text | Google Scholar

Chu, Y., Xu, H., Cheng, S., Liu, X., Guo, X., Li, Z., et al. (2019). “Actual measurement and analysis of fast response capability of photovoltaic plants participating in the frequency regulation of northwest power grid,” in 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi'an, China, 21-24 October 2019, 825–829. doi:10.1109/APAP47170.2019.9224642

CrossRef Full Text | Google Scholar

Cui, Y., Zhang, J., Zhong, W., Wang, Z., and Zhao, Y. (2021). Scheduling strategy of wind penetration multi-source system considering multi-time scale source-load coordination. Power Syst. Technol. 45 (05), 1828–1837. doi:10.13335/j.1000-3673.pst.2019.2577

CrossRef Full Text | Google Scholar

Fan, H., and Tang, M. (2022). A two-layer control strategy of the wind farm participating in grid frequency regulation. Alex. Eng. J. 61 (8), 6371–6381. doi:10.1016/j.aej.2021.11.064

CrossRef Full Text | Google Scholar

Ge, X., Liu, Y., Fu, Y., and Jia, F. (2021). Distributed robust unit commitment considering the whole process of inertia support and frequency regulations. Proc. CSEE 41 (12), 4043–4058. doi:10.13334/j.0258-8013.pcsee.200974

CrossRef Full Text | Google Scholar

Grigg, C., Wong, P., Albrecht, P., Allan, R., Bhavaraju, M., Billinton, R., et al. (1996). The IEEE reliability test system-1996. A report prepared by the reliability test system task force of the application of probability methods subcommittee. IEEE Trans. Power Syst. 14 (3), 1010–1020. doi:10.1109/59.780914

CrossRef Full Text | Google Scholar

Hao, L., Ji, J., Jiang, R., Chen, H., Fang, B., and Li, Y. (2020). “Intra-day rolling dispatch considering large-scale wind power participation in primary frequency regulation and unit fast start-up capability,” in 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October 2020 - 01 November 2020, 1923–1928. doi:10.1109/EI250167.2020.9347042

CrossRef Full Text | Google Scholar

Li, H., Lu, Z., Qiao, Y., and Zhang, B. (2020). “Frequency dynamics constrained unit commitment with wind plants,” in 2020 IEEE Power & Energy Society General Meeting (PESGM), QC, Canada, 02-06 August 2020, Montreal, 1–5. doi:10.1109/PESGM41954.2020.9281617

CrossRef Full Text | Google Scholar

Liu, B., and Peng, J. (2005). A course in uncertainty theory. Beijing: Tsinghua University Press.

Google Scholar

Li, W., Zhu, X., Zhou, H., Yao, W., and Wen, J. (2021). “Overview of frequency regulation technology of power system with high wind power penetration,” in 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 08-09 December 2021, 1176–1182. doi:10.1109/POWERCON53785.2021.9697583

CrossRef Full Text | Google Scholar

Lin, T., Ye, J., Chen, R., Xu, X., and Qin, X. (2014). Study on unit commitment with steady-state frequency constraints of power system including large-scale wind turbine. J. Electr. Power Sci. Technol. 29 (04), 18–24.

Google Scholar

Liu, Y., Shao, G., Zang, H., and Wang, C. (2020). Analysis of renewable energy participation in primary frequency regulation and parameter setting scheme of power grid. Power Syst. Technol. 44 (02), 683–689. doi:10.13335/j.1000-3673.pst.2019.0822

CrossRef Full Text | Google Scholar

Lu, J., Mao, Y., Liu, L., Cheng, H., Zhang, J., and Zhang, X. (2021). “Unit commitment of power system with wind power and photovoltaic considering frequency safety constraint,” in 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23-25 December 2021, 1486–1493. doi:10.1109/iSPEC53008.2021.9735461

CrossRef Full Text | Google Scholar

Ma, X., Sun, X., Cheng, L., Guo, X., Liu, X., and Wang, Z. (2019). “Parameter setting of new energy sources generator rapid frequency response in northwest power grid based on multi-frequency regulation resources coordinated controlling,” in 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi'an, China, 21-24 October 2019, 218–222. doi:10.1109/APAP47170.2019.9224749

CrossRef Full Text | Google Scholar

Mu, R., Wu, S., Chen, J., and He, T. (2021). Study on the detection technology of frequency regulation capability of grid connected new energy station. Yunnan Electr. Power 49 (06), 80–86.

Google Scholar

Ouyang, J., Yuan, Y., Li, M., Pang, M., Jiang, H., and Zhong, L. (2021). Optimal dispatching method of high-proportion wind power systems considering wind power reserve for frequency adjustment. Power Syst. Technol. 45 (06), 2192–2201. doi:10.13335/j.1000-3673.pst.2020.1049

CrossRef Full Text | Google Scholar

Rajan, R., and Fernandez, F. M. (2019). Power control strategy of photovoltaic plants for frequency regulation in a hybrid power system. Int. J. Elect. Power Energy Syst. 110, 171–183. doi:10.1016/j.ijepes.2019.03.009

CrossRef Full Text | Google Scholar

Sun, M., and Jia, Q. (2018). “A novel frequency regulation strategy for single-stage grid-connected PV generation,” in 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20-22 October 2018, 1–6. doi:10.1109/EI2.2018.8582246

CrossRef Full Text | Google Scholar

Wang, S. J., Shahidehpour, S. M., Kirschen, D. S., Mokhtari, S., and Irisarri, G. D. (1995). Short-term generation scheduling with transmission and environmental constraints using an augmented Lagrangian relaxation. IEEE Trans. Power Syst. 10 (3), 1294–1301. doi:10.1109/59.466524

CrossRef Full Text | Google Scholar

Ye, J., Lin, T., Bi, R., Chen, R., and Xu, X. (2016). “Unit commitment in isolated grid considering dynamic frequency constraint,” in 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, 17-21 July 2016, 1–5. doi:10.1109/PESGM.2016.7741654

CrossRef Full Text | Google Scholar

Zhang, J., Wang, N., Huang, R., Ma, M., and He, S. (2019). Survey on frequency regulation technology of power grid by high-penetration PV. Power Syst. Prot. Control 47 (15), 179–186. doi:10.19783/j.cnki.pspc.181042

CrossRef Full Text | Google Scholar

Zhang, Z., Zhou, M., Wu, Z., Liu, S., Guo, Z., and Li, G. (2022). A frequency security constrained scheduling approach considering wind farm providing frequency support and reserve. IEEE Trans. Sust. Energy 13 (2), 1086–1100. doi:10.1109/TSTE.2022.3150965

CrossRef Full Text | Google Scholar