Abstract
The MMC-HVDC transmission system of wind farms has a very broad application prospect, but there is gradually growing major concern that the system is prone to broadband oscillation. And the mechanism of oscillation also remains to be clarified. In this article, based on the basic principle of eigenvalue analysis, the theoretical calculation equation of the quantitative evaluation index of the participation factor is deduced. The small-signal model of the MMC-HVDC transmission system for a wind farm is established. Combining with the case of 200 wind turbines connected to the grid, the eigenvalue analysis method is used to obtain the dominant oscillation mode of the system. The participation factors of 11 oscillation modes of the system are calculated to further analyze the relationship between the oscillation modes and the state variables in the MMC-HVDC transmission system of the wind farms. And the correlation between the participation factors of each oscillation mode, wind farm, and the MMC system is investigated, which laid a foundation for the formulation of broadband oscillation suppression strategies.
1 Introduction
The MMC-HVDC transmission system of wind farms has a very broad application prospect, but with the continuous construction of related engineering projects, the broadband oscillation problem of the system has gradually become prominent. According to relevant reports, there have been numerous wind farms connected to the actual project of MMC-HVDC in China and abroad, and the phenomenon of broadband oscillation instability appears in the system debugging or production operation stage. For instance, the grid-connected project of the VSC-HVDC system of the doubly fed wind farm in Nan’ao, Guangdong Province, China, experienced oscillation during the system commissioning, which eventually led to the outage of the system (Lu et al., 2015). In addition, the Shanghai Nanhui demonstration project also encountered similar problems in the initial commissioning stage (Wang et al., 2017).
The oscillation problem of traditional power systems is mainly caused by the single oscillation mode of the synchronous generator, which only oscillates in the local regional power grid. The broadband oscillation problem of wind farms through the MMC-HVDC transmission system is caused by the interaction and coupling of power electronic equipment, various control links, and transmission network electrical equipment. The manifestation is the continuous oscillation of divergence in a wide frequency range, which has multimodal characteristics and shows indigenous time-varying characteristics. If the broadband oscillation problem of the MMC-HVDC transmission system of wind farms is not effectively solved, it will cause damage to the power supply side power generation equipment, which will result in the tripping of new energy stations and active power shortage of the power grid. Moreover, the generated oscillation components will be transmitted to the user side through the transmission network, which will eventually cause a large area of power outages and pose a great threat to the safe and stable operation of the power grid (Cai et al., 2021). However, the mechanism and characteristics of the oscillation are not clear (Sun et al., 2021). Therefore, analyzing the broadband oscillation mode, dynamic characteristics, and correlation with the participation factor of the MMC-HVDC transmission system of wind farms in-depth will lay the foundation for the formulation of broadband oscillation suppression strategy, which has very important theoretical and engineering significance for the safe and stable operation of the grid connecting system.
At present, there are many analysis methods of broadband oscillation mechanisms in China and abroad, which include the impedance analysis method (Rygg et al., 2016; Shah and Parsa, 2017; Wen et al., 2017), frequency scanning method (Yang et al., 2020), complex torque coefficient method, time domain simulation method, and eigenvalue analysis method.
In Liu et al. (2016), the RLC impedance circuit model is used to retain the dynamic characteristics of each part of the DFIG, and circuit parameters are used to qualitatively and quantitatively analyze the stability of the DFIG series compensated transmission system. In regard to the stability problem caused by the interaction between the DFIG and flexible transmission system, the impedance analysis method has been adopted by Sun et al. (2018), and it has been found that under certain operating conditions, the DFIG and flexible system constitute an equivalent negative resistance resonant circuit, which leads to subsynchronous oscillations of the system. However, the disadvantage of the impedance analysis method is that it cannot give the coupling relationship of various physical quantities in the system nor can it reflect the internal dynamic characteristics of the system.
Research of Tang et al. (2022) and Suriyaarachchi et al. (2013) have been based on the frequency scanning method. The stability characteristics of the doubly fed wind farm connected to the grid through series compensation have been analyzed by Tang et al. (2022), and the system oscillation characteristics and influencing factors have also been investigated. The results have shown that the increase of series compensation degree and decrease of wind speed would lead to system oscillation. In Suriyaarachchi et al. (2013), the existence of unstable points in the doubly fed wind power grid-connected system was first studied by the frequency scanning method, and the oscillation mechanism of the system was then further analyzed by other methods. It was found that the subsynchronous oscillation was caused by the state variables of the wind turbine and the grid side, and the participation of the control system was not high. However, the frequency scanning method could not reveal the mechanism of system oscillation, and the accuracy of the analysis results was greatly related to the scanning step length.
In order to make the complex torque coefficient method suitable for analyzing the interaction mechanism between the controllers of the wind power grid-connected system, there are two main development directions currently (Tang et al., 2019). One is to ignore the mechanical part of the system and only consider the electrical part of the system. The complex torque coefficient of the electrical system is used to assess whether the system has the risk of oscillation. Research by Tang et al. (2021) is an example in this direction, in which the equivalent model of the DFIG converter is constructed by ignoring the mechanical part of the system. And then based on the compound torque coefficient method, the influence of system structure parameters and control parameters on electrical damping is studied. The other is to divide the system into parts to be studied and the rest, and then represent them by two electrical subsystems respectively, so as to identify the part to be studied. This method has been adopted by Hu et al. (2017), through which the phase-locked loop control part of a doubly fed induction generator is formed into a subsystem, and the influence of the phase-locked loop control parameters on the small signal stability of the wind farm is analyzed. However, this method is only suitable for analyzing the stability of the single-input single-output system and is difficult to be applied in large-scale wind power grid-connected systems.
The time-domain simulation method can not only directly observe whether there is an oscillation phenomenon in the system but also exhibit the ability to simulate the stability change of the system under disturbance or fault conditions. However, it is difficult to analyze the generation mechanism and influencing factors of oscillation (Xie et al., 2017; Chen et al., 2022).
In Wang et al. (2015) and Huang et al. (2019), the eigenvalue analysis method is used to study the stability of wind power grid-connected systems. And the influence of wind speed, number of wind turbines, and control system parameters on system stability and oscillation frequency are analyzed. In Kunjumuhammed et al. (2017), Chen et al. (2018), Shao et al. (2019), and Guo et al. (2020), the small-signal model of the wind farm sending out through a flexible transmission system is established, the dominant participation factors of each oscillation mode of the system are investigated, and the corresponding oscillation suppression strategy is proposed. The eigenvalue analysis based on the small-signal model can not only obtain the system oscillation mode and its participation factor but also be combined with the classical or modern control theory to guide the design of the oscillation suppression controller, which is an important method for system stability analysis.
In this article, based on the basic principle of eigenvalue analysis, the theoretical calculation method of the quantitative evaluation index of participation factors is investigated. Based on the small-signal model of the wind farm sending out through the MMC-HVDC transmission system, the eigenvalue analysis method is used to obtain the dominant oscillation mode of the system. And the correlation in-between the participation factors of each oscillation mode and the wind farm and the MMC system is analyzed, which provides the basis for the oscillation suppression method.
2 Mathematical model of system of wind farm sending out through direct current transmission
2.1 Equivalent circuit of system of wind farm sending out through direct current transmission
The system of wind farm sending out through DC transmission consists of the wind farm, boost transformer, AC cable, and the MMC-HVDC system, in which the MMC-HVDC system includes matching transformer, sending-end converter (SEC), DC submarine cable, and receiving-end converter (REC).
Assuming that the AC power grid on the coast is a robust power grid, that is, when the MMC-HVDC system runs steadily, the receiving-end converter can almost completely track the reference value of the DC voltage. The influence of the REC side on the SEC side is so small that it can be ignored. Therefore, in order to simplify the analysis, the DC side of the SEC can be replaced by a constant DC voltage source to simulate the DC voltage control effect of the REC. In addition, in order to improve the simulation efficiency, the stand-alone equivalent method is adopted in this article to model the wind farm equivalently (An et al., 2018). And the equivalent circuit of the DC transmission system of the wind farm is presented in Figure 1.
FIGURE 1
Structure diagram of a simplified system.
In Figure 1, the wind farm is simplified as a single typhoon. and are the port voltage and current of the permanent magnet synchronous generator, respectively. and are the output voltage and current of the grid-side converter in the wind farm, respectively. , , and are the resistance and inductance of simplified lines. is the equivalent boost transformer, is the matching transformer, and and are the leakage inductance of and , respectively. is the capacitance of the collector line, and is the filter capacitance of the SEC in the MMC-HVDC system.
2.2 Small-signal model of system of wind farm sending out through direct current transmission
Combined with the dynamic model of the wind turbine (Gao, 2021) and MMC system (Bergna-Diaz et al., 2018), and based on the interface model of the wind farm and MMC system (Liu et al., et al.), a complete system dynamic model of the wind farm sending out through MMC-HVDC can be obtained. After linearization of the overall dynamic model at the steady-state equilibrium point, the small-signal model of the system of the wind farm sending out through MMC-HVDC can be described as follows:where matrix A is the state matrix of the small-signal model of the system, and the small signal stability of the system is related to the eigenvalue of A; matrix B is the input matrix of the system. is the state variable of the linearized system of the wind farm sending out through MMC-HVDC, , in which is the state variable of the wind turbine after stand-alone equivalence and is the state variable of the MMC system. is the input variable of the linearized system of the wind farm sending out through MMC-HVDC, , in which represents the input variable of the wind turbine after stand-alone equivalent and represents the input variable of the MMC system.
The state variables of the wind turbines can be written as and the input variable of the wind turbines can be written as . The state variables of the MMC system is and the input variables of the MMC system is .
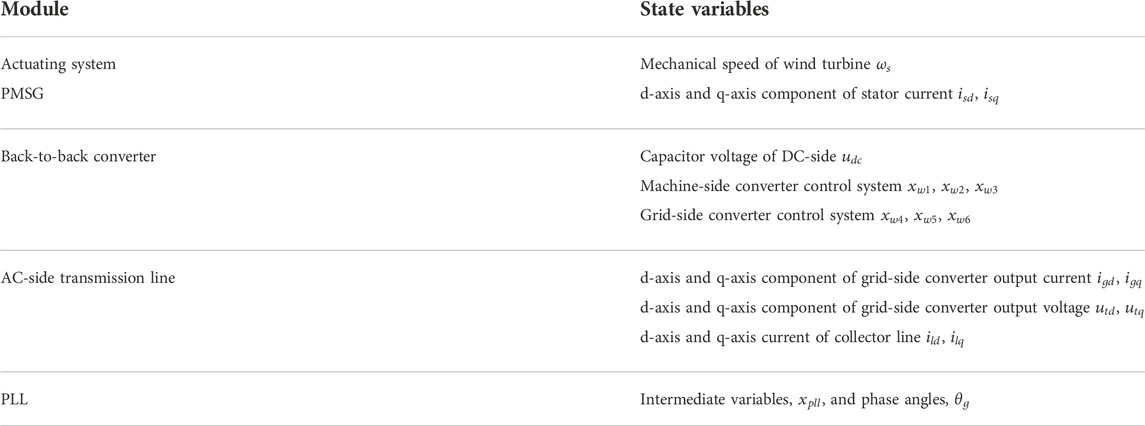
In order to distinguish the meaning of each state variable, the state variables are clarified according to each module of the wind turbine in this article, and the classification results are shown in Table 1. At the same time, the state variables are classified according to each module of the MMC system, and the classification results are shown in Table 2.
TABLE 1
| Module | State variables |
|---|---|
| Actuating system | Mechanical speed of wind turbine |
| PMSG | d-axis and q-axis component of stator current , |
| Back-to-back converter | Capacitor voltage of DC-side |
| Machine-side converter control system , , | |
| Grid-side converter control system , , | |
| AC-side transmission line | d-axis and q-axis component of grid-side converter output current , |
| d-axis and q-axis component of grid-side converter output voltage , | |
| d-axis and q-axis current of collector line , | |
| PLL | Intermediate variables, , and phase angles, |
Classification and meaning of wind turbine state variables.
TABLE 2
| Module | State variables |
|---|---|
| Main circuit | d-axis and q-axis voltage , |
| d-axis and q-axis current at AC-side , | |
| Internal circulation of MMC , , | |
| Differential mode equivalent capacitance voltage , , , | |
| Common-mode equivalent capacitor voltage , , | |
| Control system | Intermediate variable of voltage control system , , , |
| Intermediate variables of circulation suppression controller , |
Classification and meaning of state variables of the MMC system.
3 Participation factor of broadband oscillation quantitative evaluation index
The eigenvalue analysis method can find out the main oscillation mode of the system, and it can also obtain the participation factor of the oscillation mode and the eigenvalue sensitivity of the system parameters. The calculation method of the quantitative evaluation index of the participation factor is investigated below.
For any eigenvalue of state matrix A, if the non-zero vector , the following relationship should be satisfied:
Then the vector is called the right eigenvector corresponding to the eigenvalues . In the same way, if the non-zero vector , the following relationship would be satisfied:
The vector is called the left eigenvector corresponding to the eigenvalues . With the aim of quantitatively analyzing the impact of each state variable in different oscillation modes, the following participation matrix p is defined:where the participation factor can quantitatively reflect the correlation between the oscillation mode and the system state variables, which means the influence of the system state variables on the oscillation mode . The calculation expression is as follows: and mentioned above are the elements of column i and row k in the eigenvector matrices V and U, respectively.
The greater the value of the participation factor , indicating that the higher the correlation between the oscillation mode and the state variables , the greater the impact of .
4 Analysis of oscillation characteristics
4.1 System oscillation mode
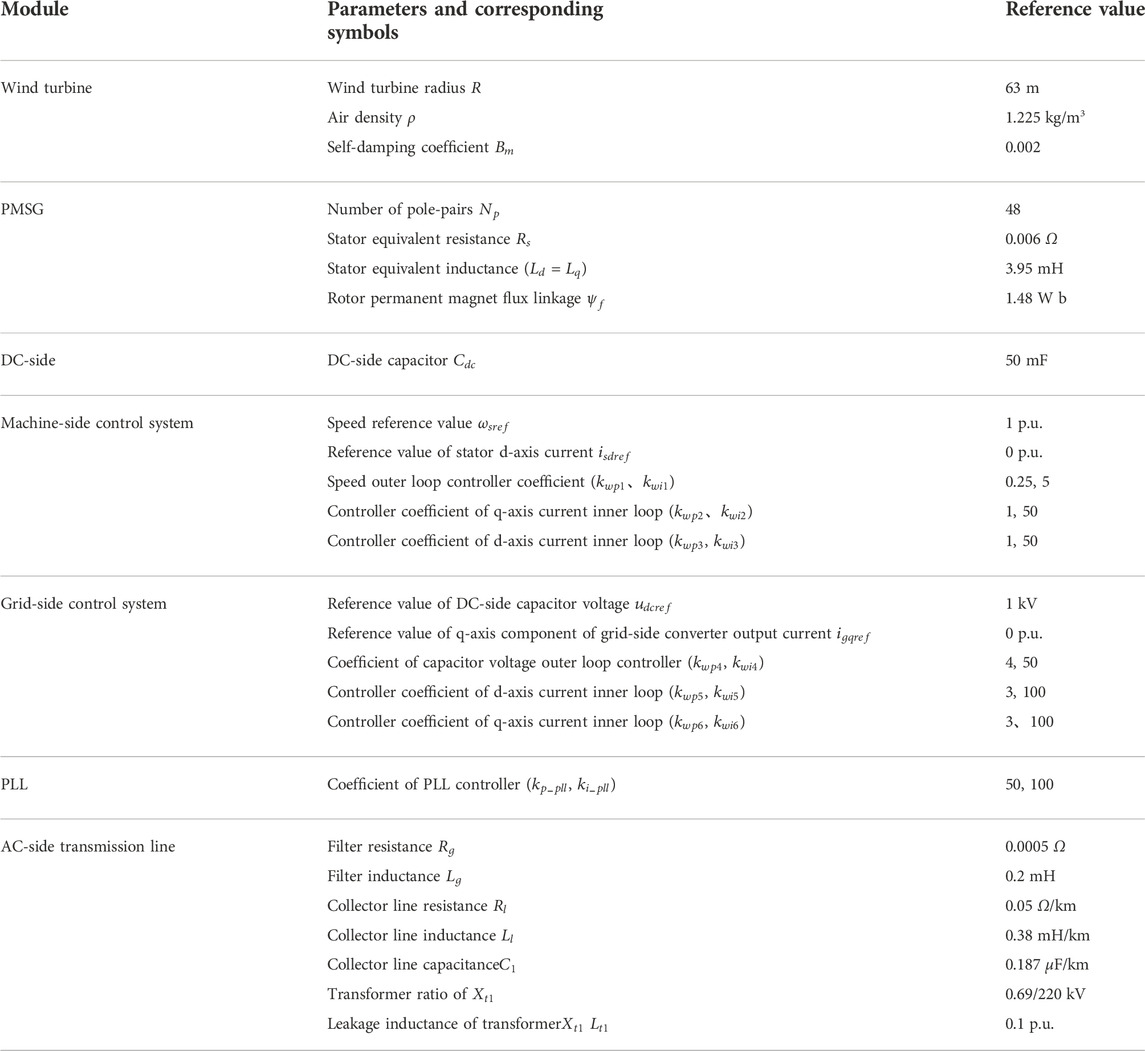
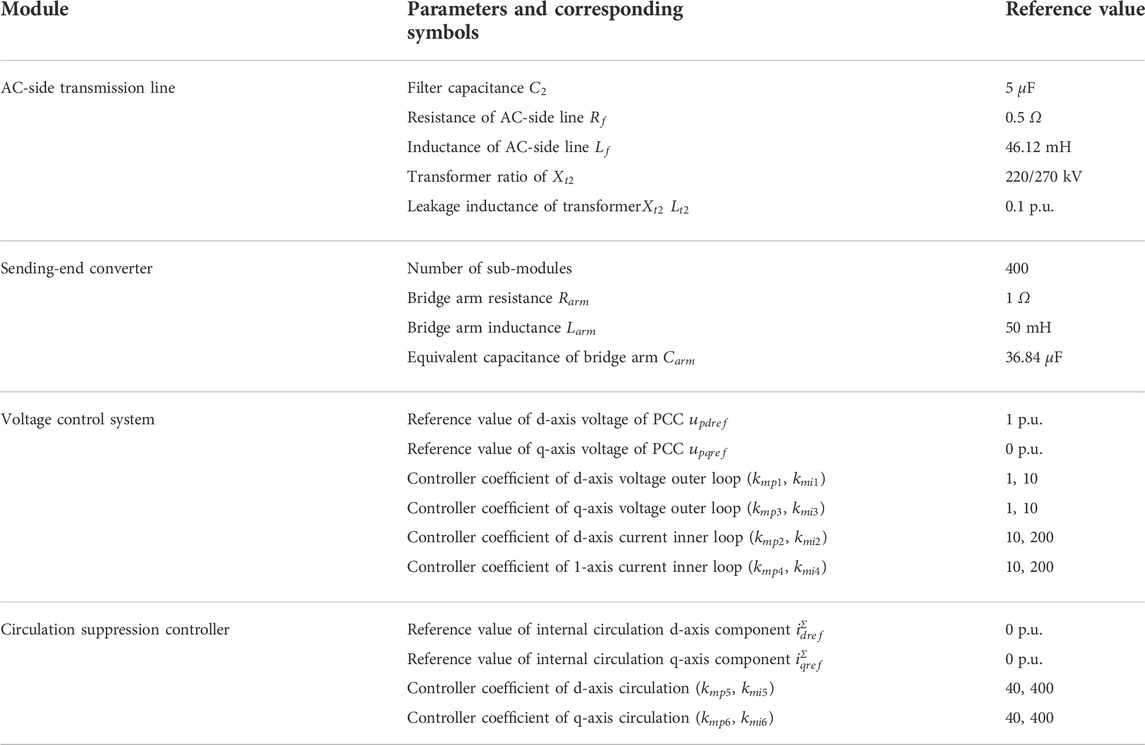
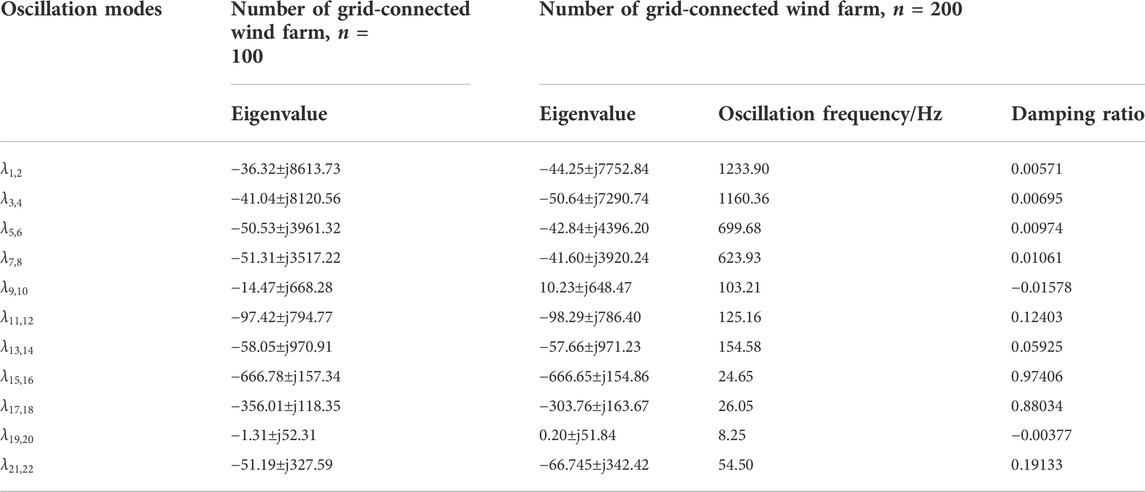
The research results of Xie et al. (2016) show that with the increase in the number of grid-connected direct-drive fans, the damping level of the system shows a downward trend, which increases the risk of oscillation of the system. In this article, the number of grid-connected direct-drive fans is set to 100, and then the number is increased to 200. The specific parameters of direct-drive fans are shown in Table 3, and the parameters of the MMC system are shown in Table 4.
TABLE 3
| Module | Parameters and corresponding symbols | Reference value |
|---|---|---|
| Wind turbine | Wind turbine radius | 63 m |
| Air density | 1.225 kg/m3 | |
| Self-damping coefficient | 0.002 | |
| PMSG | Number of pole-pairs | 48 |
| Stator equivalent resistance | 0.006 | |
| Stator equivalent inductance () | 3.95 mH | |
| Rotor permanent magnet flux linkage | 1.48 W b | |
| DC-side | DC-side capacitor | 50 mF |
| Machine-side control system | Speed reference value | 1 p.u. |
| Reference value of stator d-axis current | 0 p.u. | |
| Speed outer loop controller coefficient (、) | 0.25, 5 | |
| Controller coefficient of q-axis current inner loop (、) | 1, 50 | |
| Controller coefficient of d-axis current inner loop (, ) | 1, 50 | |
| Grid-side control system | Reference value of DC-side capacitor voltage | 1 kV |
| Reference value of q-axis component of grid-side converter output current | 0 p.u. | |
| Coefficient of capacitor voltage outer loop controller (, ) | 4, 50 | |
| Controller coefficient of d-axis current inner loop (, ) | 3, 100 | |
| Controller coefficient of q-axis current inner loop (, ) | 3、100 | |
| PLL | Coefficient of PLL controller (, ) | 50, 100 |
| AC-side transmission line | Filter resistance | 0.0005 |
| Filter inductance | 0.2 mH | |
| Collector line resistance | 0.05 /km | |
| Collector line inductance | 0.38 mH/km | |
| Collector line capacitance | 0.187 /km | |
| Transformer ratio of | 0.69/220 kV | |
| Leakage inductance of transformer | 0.1 p.u. |
Parameters of PMSG wind power system.
TABLE 4
| Module | Parameters and corresponding symbols | Reference value |
|---|---|---|
| AC-side transmission line | Filter capacitance | 5 |
| Resistance of AC-side line | 0.5 | |
| Inductance of AC-side line | 46.12 mH | |
| Transformer ratio of | 220/270 kV | |
| Leakage inductance of transformer | 0.1 p.u. | |
| Sending-end converter | Number of sub-modules | 400 |
| Bridge arm resistance | 1 | |
| Bridge arm inductance | 50 mH | |
| Equivalent capacitance of bridge arm | 36.84 | |
| Voltage control system | Reference value of d-axis voltage of PCC | 1 p.u. |
| Reference value of q-axis voltage of PCC | 0 p.u. | |
| Controller coefficient of d-axis voltage outer loop (, ) | 1, 10 | |
| Controller coefficient of q-axis voltage outer loop (, ) | 1, 10 | |
| Controller coefficient of d-axis current inner loop (, ) | 10, 200 | |
| Controller coefficient of 1-axis current inner loop (, ) | 10, 200 | |
| Circulation suppression controller | Reference value of internal circulation d-axis component | 0 p.u. |
| Reference value of internal circulation q-axis component | 0 p.u. | |
| Controller coefficient of d-axis circulation (, ) | 40, 400 | |
| Controller coefficient of q-axis circulation (, ) | 40, 400 |
MMC system parameters.
Based on the small-signal model of the system of the wind farm sending out through MMC-HVDC established above, the initial values of each state variable in the small-signal model are obtained by power flow calculation, and then the main oscillation modes of the system are calculated by the eigenvalue analysis method. The final results are shown in Table 5.
TABLE 5
| Oscillation modes | Number of grid-connected wind farm, n = 100 | Number of grid-connected wind farm, n = 200 | ||
|---|---|---|---|---|
| Eigenvalue | Eigenvalue | Oscillation frequency/Hz | Damping ratio | |
| −36.32j8613.73 | −44.25j7752.84 | 1233.90 | 0.00571 | |
| −41.04j8120.56 | −50.64j7290.74 | 1160.36 | 0.00695 | |
| −50.53j3961.32 | −42.84j4396.20 | 699.68 | 0.00974 | |
| −51.31j3517.22 | −41.60j3920.24 | 623.93 | 0.01061 | |
| −14.47j668.28 | 10.23j648.47 | 103.21 | −0.01578 | |
| −97.42j794.77 | −98.29j786.40 | 125.16 | 0.12403 | |
| −58.05j970.91 | −57.66j971.23 | 154.58 | 0.05925 | |
| −666.78j157.34 | −666.65j154.86 | 24.65 | 0.97406 | |
| −356.01j118.35 | −303.76j163.67 | 26.05 | 0.88034 | |
| −1.31j52.31 | 0.20j51.84 | 8.25 | −0.00377 | |
| −51.19j327.59 | −66.745j342.42 | 54.50 | 0.19133 | |
Main oscillation modes of the system of the wind farm sending out via MMC-HVDC.
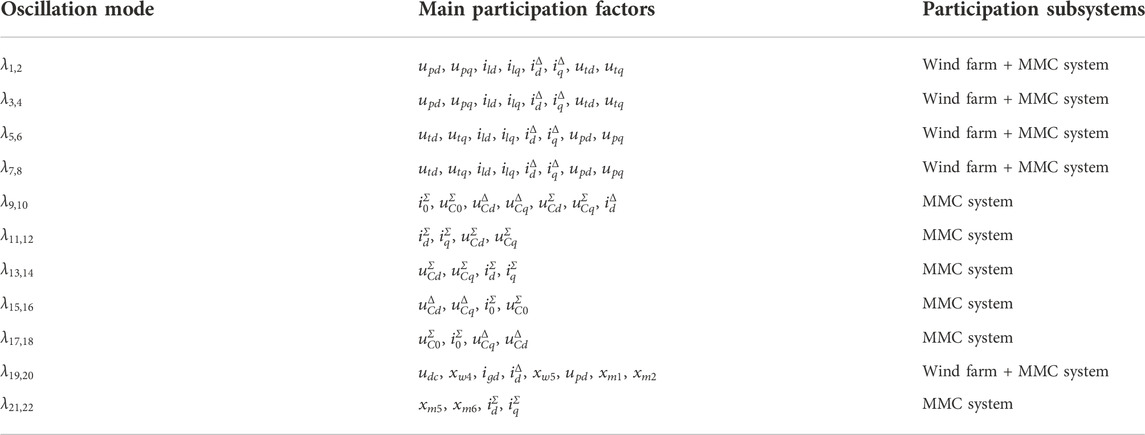
It can be concluded from Table 1 that there are 11 main oscillation modes in the system of the wind farm sending out via MMC-HVDC, which includes 4 sub/super synchronous oscillation modes, , , , and ; 5 intermediate frequency oscillation modes, namely, , , , , and ; and 2 high-frequency oscillation modes and . In addition, it can be seen from the table above that when the number of direct drive fans connected to the grid is 200, the damping ratio of oscillation modes and in the system is negative, and the damping ratio of other oscillation modes is still positive. In addition, it can be seen from Table 1 that when the number of direct drive fans connected to the grid is 200. According to the former analysis, these two oscillation modes with a negative damping state will lead to the oscillation operation of the system of wind farm sending out via MMC-HVDC, which has the greatest impact on the stability of the system. The damping ratio of other oscillation modes in the system is positive, and the damping ratio of these oscillation modes is large, which is not easy to cause a negative damping state.
4.2 Analysis of the correlation between participation factors and state variables under different oscillation modes
In order to further analyze the relationship between the oscillation modes and the state variables in the system of the wind farm sending out via MMC-HVDC, the participation factors of 11 oscillation modes of the system are calculated and normalized. The results are shown in Figure 2.
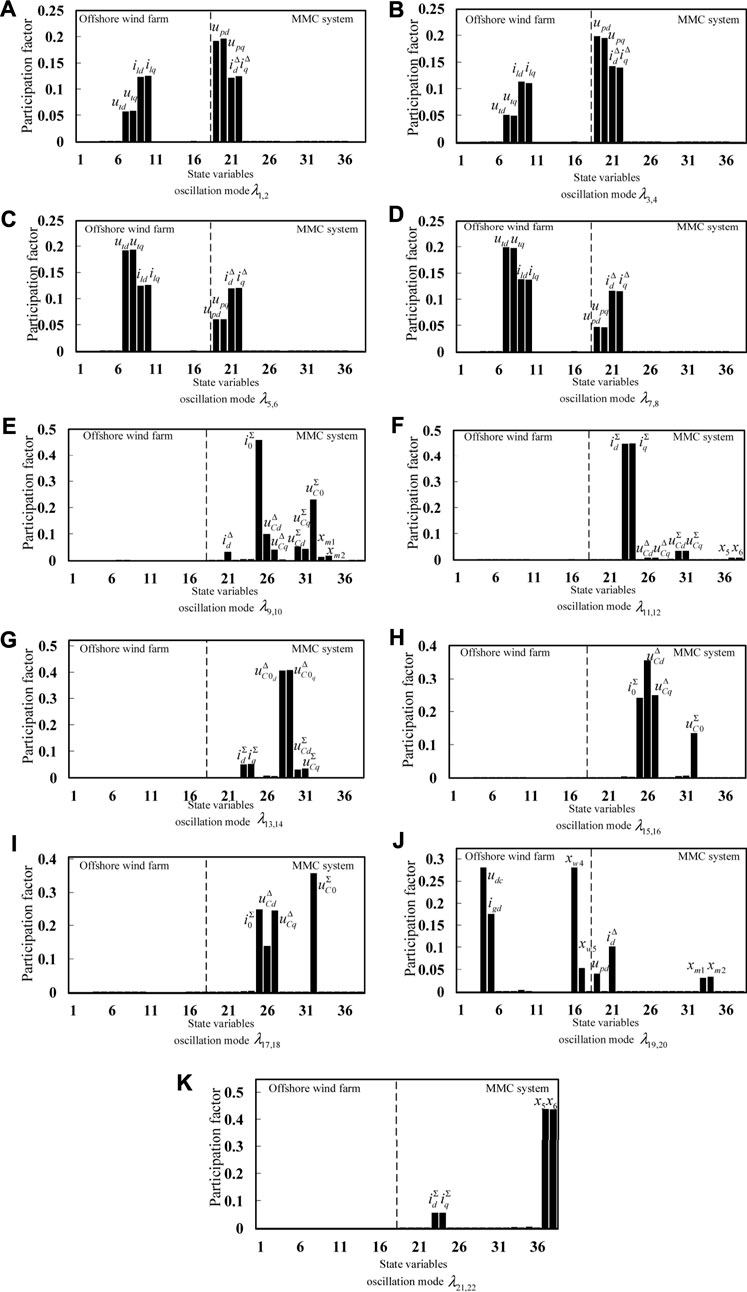
FIGURE 2
Participation factors of 11 oscillation modes of the system. The part label (A–K) is used for the distinction between results of 11 oscillation modes, there is no additional description needed.
It can be seen from Figure 2 that the participation variables of the oscillation modes , , , and are the same, and they are all dominated by state variables , , , , , , , and . It is related to the state variables of AC cable connecting the wind farm system, but the dominant participation factors of each oscillation mode are not the same. Oscillation modes and are dominated by state variables and of the MMC system, while oscillation modes and are dominated by state variables and of the wind farm system.
State variables related to oscillation modes are mainly variables and of the MMC system, and their participation factors are 0.4627 and 0.2312, respectively. It can be seen that this oscillation mode is generated within the MMC system and is not much related to the wind farm. In addition, because the damping ratio of the oscillation mode is negative, the stability of the system is greatly affected.
The oscillation mode is mainly related to , , , and . They are state variables of the MMC system. The dominant participation factors are and . The oscillation mode is mainly related to , , , , , and . They are state variables of the MMC system. The dominant participation factors are and .
The participation variables of the oscillation modes and are all the same. They are all related to the state variables of the MMC system, which includes , , , and . The participation factors of oscillation mode can be ranked in the descending order as follows: , , , and . The participation factors of the oscillation mode can be ranked in the descending order as follows: , , , and , which is the opposite to that of the oscillation modes .
The state variables related to the oscillation mode mainly include , , , and of the wind farm system and , , , and of the MMC system. It can be seen that the oscillation mode is not only related to the constant DC voltage control link of the grid-side converter control system of the wind farm but also related to the constant d-axis AC voltage control link of the SEC. In addition, since the damping ratio of the oscillation mode is also negative, it has a great impact on the stability of the system.
The main participation variables of the oscillation mode are , , , and . And their participation factors are 0.05585, 0.05584, 0.43757, and 0.43651, respectively.
Therefore, the oscillation modes can be classified according to the correlation between the participation factors of each oscillation mode and the wind farm and MMC system, as is shown in Table 6.
TABLE 6
| Oscillation mode | Main participation factors | Participation subsystems |
|---|---|---|
| , , , , , , , | Wind farm + MMC system | |
| , , , , , , , | Wind farm + MMC system | |
| , , , , , , , | Wind farm + MMC system | |
| , , , , , , , | Wind farm + MMC system | |
| , , , , , , | MMC system | |
| , , , | MMC system | |
| , , , | MMC system | |
| , , , | MMC system | |
| , , , | MMC system | |
| , , , , , , , | Wind farm + MMC system | |
| , , , | MMC system |
The main participation factors and subsystems of each oscillation mode.
It can be seen from Table 6 that the oscillation modes , , , , and are related to the wind farm and MMC system. While the oscillation modes , , , , , and are generated within the MMC system, and there is no obvious correlation with the wind farm. In addition, the oscillation modes and are in a negative damping state, in which the oscillation mode is mainly related to the state variables and , and the oscillation mode is generated by the coupling between the wind farm control system and the SEC voltage control system.
5 Conclusion
In this article, the theoretical calculation equations of the quantitative evaluation index of the participation factor are derived, and the small-signal model of the system of the wind farm sending out through MMC-HVDC is constructed. Taking the equivalent circuit of the simplified DC transmission system of the wind farm with 200 direct-drive wind turbines connected to the grid as an example, the oscillation mode of the system was analyzed by using the eigenvalue analysis method based on the quantification of the participation factor. The contribution is summarized below:
1) When the number of wind turbines connected to the grid increases, the oscillation modes and with a negative damping state appear in the system. It is verified that with the increase in the number of grid-connected direct-drive fans, the damping level of the system will decrease and the risk of oscillation of the system will increase.
2) The oscillation modes and will lead to the oscillation operation of the system of the wind farm sending out via MMC-HVDC, which has the greatest impact on the stability of the system. The damping ratio of the other oscillation modes in the system is positive, and the damping ratio of these oscillation modes is large, which has a small effect on the stability of the system.
3) By calculating the participation factors of the two oscillation instability modes, it was found that the oscillation mode is caused by the zero-sequence current inside the MMC system, which is not much related to the wind farm. While the oscillation mode is caused by the interaction and coupling between the wind farm and the MMC system.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
QP, SJ, and CQ contributed to conception and design of the study. QP organized the database. SJ and CQ performed the statistical analysis. QP wrote the first draft of the manuscript. SJ, CQ, TA, XB, and WZ wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
The Science and Technology Project of State Grid Zhejiang Electric Power Co., Ltd. (B311DS22100A).
Conflict of interest
QP, SJ, and CQ, were employed by State Grid Zhejiang Electric Power Co., Ltd.
The authors declare that this study received funding from State Grid Zhejiang Electric Power Co., Ltd. The funder had the following involvement in the study: study design, data collection and analysis, decision to publish, preparation of the manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
An Z. Shen C. Zheng Z. Wang Z. Wei W. (2018). Assessment method for equivalent models of wind farms based on direct-driven wind generators considering randomness. Proc. CSEE38 (22), 6511–6520. 10.13334/j.0258-8013.pcsee.180617
2
Bergna-Diaz G. Freytes J. Guillaud X. D’ Arco S. Suul J. A. (2018). Generalized voltage-based state-space modelling of modular multilevel converters with constant equilibrium in steady-state. IEEE J. Emerg. Sel. Top. Power Electron.6 (2), 707–725. 10.1109/JESTPE.2018.2793159
3
Cai X. Yang R. Zhou J. Fang Z. Yang M. Shi X. et al (2021). Review on offshore wind power integration via DC transmission. Automation Electr. Power Syst.45 (21), 2–22.
4
Chen B. Lin T. Chen R. Guo Z. Sheng Y. Xu X. (2018). Characteristics of multi-band oscillation for direct drive wind farm interfaced with VSC-hvdc system. Trans. China Electrotech. Soc.33 (S1), 176–184. 10.19595/j.cnki.1000-6753.tces.180954
5
Chen S. Cao Q. Jia M. (2022). Concepts, characteristics and prospects of application of digital twin in power system. Proc. CSEE42 (02), 487–499. 10.13334/j.0258-8013.pcsee.211594
6
Gao M. (2021). Study on parameter identification of doubly-fed wind turbine and dynamic equivalent method of wind farm. Beijing: North China Electric Power University.
7
Guo X. Li Y. Xie X. Hou Y. Zhang D. (2020). Sub-synchronous oscillation characteristics caused by PMSG-based wind plant farm integrated via flexible HVDC system. Proc. CSEE40 (04), 1149–1160+1407. 10.13334/j.0258-8013.pcsee.182540
8
Hu J. Wang B. Wang W. Tang H. Chi Y. Hu Q. (2017). Small signal dynamics of DFIG-based wind turbines during riding through symmetrical faults in weak AC grid. IEEE Trans. Energy Convers.32 (2), 720–730. 10.1109/tec.2017.2655540
9
Huang B. Sun H. Liu Y. Wang L. Chen Y. (2019). Study on subsynchronous oscillation in D‐PMSGs‐based wind farm integrated to power system. IET Renew. Power Gener.13 (1), 16–26. 10.1049/iet-rpg.2018.5051
10
Kunjumuhammed L. P. Bikash C. P. Gupta R. Dyke K. J. (2017). Stability analysis of a PMSG-based large offshore wind farm connected to a VSC-hvdc. IEEE Trans. Energy Convers.32 (3), 1166–1176. 10.1109/tec.2017.2705801
11
Liu H. Xie X. Zhang C. Li Y. Hu Y. (2016). Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model. IEEE Trans. Power Syst.32 (1), 474–483. 10.1109/tpwrs.2016.2558840
12
Liu Y. Wang J. Wang Z. Chen W. Ye Y. Fu C. et al Research on AC admittance matrix modeling and frequency coupling effect of MMCHVDC under power control. Proc. CSEE, 1–14.
13
Lu J. Dong P. Shi G. Cai X. Li X. (2015). Subsynchronous oscillation and its mitigation of MMC-based HVDC with large doubly-fed induction generator-based wind farm integration. Proc. CSEE35 (19), 4852–4860. 10.13334/j.0258-8013.pcsee.2015.19.002
14
Rygg A. Molinas M. Zhang C. Cai X. (2016). A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems. IEEE J. Emerg. Sel. Top. Power Electron.4 (4), 1383–1396. 10.1109/jestpe.2016.2588733
15
Shah S. Parsa L. (2017). Impedance modeling of three-phase voltage source converters in DQ, sequence, and phasor domains. IEEE Trans. Energy Convers.32 (3), 1139–1150. 10.1109/tec.2017.2698202
16
Shao B. Zhao S. Pei J. Li R. Song S. (2019). Subsynchronous oscillation characteristic analysis of grid-connected DDWFs via VSC-HVDC system. Power Syst. Technol.43 (09), 3344–3355. 10.13335/j.1000-3673.pst.2018.2567
17
Sun K. Yao W. Cai Y. Wen J. (2021). Impedance modeling and analysis of medium-frequency oscillation caused by VSC-hvdc connected to local weak grid and DFIG-based wind farms. Front. Energy Res.9. 10.3389/fenrg.2021.693903
18
Sun K. Yao W. Wen J. (2018). Mechanism and characteristics analysis of subsynchronous oscillation caused by DFIG-based wind farm integrated into grid through VSC-hvdc system. Proc. CSEE38 (22), 6520–6533. 10.13334/j.0258-8013.pcsee.172415
19
Suriyaarachchi D. Annakkage U. D. Karawita C. Jacobson D. A. (2013). A procedure to study sub-synchronous interactions in wind integrated power systems. IEEE Trans. Power Syst.28 (1), 377–384. 10.1109/tpwrs.2012.2204283
20
Tang A. Lu Z. Yang H. Zou X. Huang Y. Zheng X. (2021). Digital/analog hybrid simulation platform of distributed power flow controller based on ADPSS and dspace. CSEE J. Power Energy Syst.7 (1), 181–189. 10.17775/CSEEJPES.2020.02210
21
Tang A. Shao Y. Xu Q. Zheng X. Zhao H. Xu D. (2019). Multi-objective coordination control of distributed power flow controller. CSEE J. Power Energy Syst.5 (03), 348–354. 10.17775/CSEEJPES.2018.01450
22
Tang A. Zhou W. Song J. Qiu P. Chen Q. Zhai X. et al (2022). Optimal output power coordinated control strategy of distributed power flow controller. Int. J. Electr. Power & Energy Syst.140, 108075. 10.1016/j.ijepes.2022.108075
23
Wang L. Xie X. Jiang Q. Liu H. Li Y. Liu H. (2015). Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system. IEEE Trans. Power Syst.30 (5), 2772–2779. 10.1109/tpwrs.2014.2365197
24
Wang L. Xie X. Liu H. Zhan Y. He J. Wang C. (2017). Review of emerging SSR/SSO issues and their classifications. J. Eng.2017 (13), 1666–1670. 10.1049/joe.2017.0615
25
Wen B. Burgos R. Boroyevich D. Mattavelli P. Shen Z. (2017). AC stability analysis and dq frame impedance specifications in power-electronics-based distributed power systems. IEEE J. Emerg. Sel. Top. Power Electron.5 (4), 1455–1465. 10.1109/jestpe.2017.2728640
26
Xie X. Liu H. He J. Zhang C. Qiao Y. (2016). Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems. Proc. CSEE36 (09), 2366–2372. 10.13334/j.0258-8013.pcsee.2016.09.007
27
Xie X. Zhang X. Liu H. Li Y. Zhang C. (2017). Characteristic analysis of subsynchronous resonance in practical wind farms connected to series-compensated transmissions. IEEE Trans. Energy Convers.32 (3), 1117–1126. 10.1109/tec.2017.2676024
28
Yang L. Xu Z. Wang X. Xing F. Xu Z. Yang L. (2020). Analysis on harmonic resonance of offshore wind farm transmitted by VSC - HVDC system. Guangdong Electr. Power33 (07), 1–10.
Summary
Keywords
wind farm sending system, oscillation characteristics, participation factor, oscillation mod, correlations
Citation
Peng Q, Jingen S, Qian C, Wei Z, Bingyu X and Aihong T (2022) Research on oscillation characteristics of wind farm sending system based on participation factor. Front. Energy Res. 10:997782. doi: 10.3389/fenrg.2022.997782
Received
19 July 2022
Accepted
16 August 2022
Published
08 September 2022
Volume
10 - 2022
Edited by
Xiao Wang, Wuhan University, China
Reviewed by
Wang Xiang, Huazhong University of Science and Technology, China
Hengrui Ma, Qinghai University, China
Yuan Chen, Anhui University, China
Fei Tang, Wuhan University, China
Updates
Copyright
© 2022 Peng, Jingen, Qian, Wei, Bingyu and Aihong.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tang Aihong, tah@whut.edu.cn
This article was submitted to Smart Grids, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.