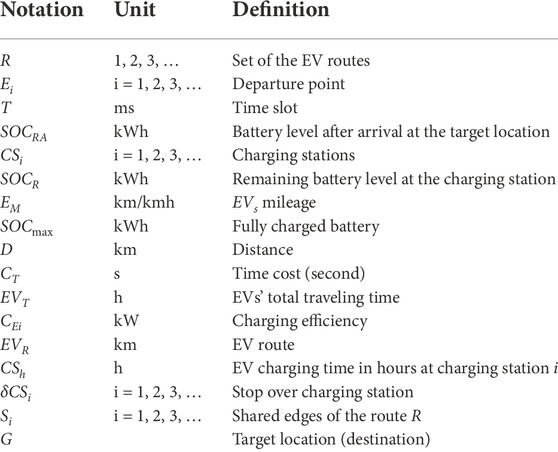
- Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences (CAS), Shenzhen Guangdong, China
The optimal path planning for EVs (electric vehicles) has gained great attention during the last decade due to the zero pollution emission characteristics and limited power capacity of EV batteries. In this paper, an optimal route search is proposed considering multiple charging stations in a dynamic urban environment, while it is still applicable when the initial available amount of the battery fails to cover a certain travel range. The TRDP (transit route design problem) and TNDP (transit node design problem) are used to search for the most feasible routes based on time and driving range via the improved route-assisted rapid random tree (RA-RRT*) algorithm. Considering the status of charge of an EV’s battery during optimal routes search, three states are investigated between the destination and the aggregators: (1) bypassing the aggregators, (2) stopping over a single aggregator, and (3) stopping over multiple aggregators. During the states (2) and (3), it is required that the EVs be charged at the charging stations obtained by the RA-RRT* algorithm while approaching the destination. The proposed algorithm is tested on a random dataset under certain conditions, that is, traffic flow with congestion and assigned target locations from a given map data, with comparison experiments for efficacy verification.
1 Introduction
Electric vehicles (EVs) have paved the way for green and intelligent transportation systems over the last few decades. EVs are gradually taking the place of fuel-powered vehicles due to their minimum mileage cost and environment-friendly characteristics of no carbon emissions. The main obstacle to EV’s promotion is the limited battery capacity through which EVs cannot cover long distances (Zhou et al., 2020).
In recent years, EV-related energy-harvesting schemes have received a lot of attention to increase the driving range with smart route search algorithms. The related factors, that is, battery capacity, charging duration, and charging station placement, should be explicitly considered during the route planning of the EVs (El-Taweel and Farag, 2019). A reinforcement learning (RL) model is developed for EV energy management by optimal route planning (Zhang et al., 2020a), where the RL model is used to evaluate each route and approximate the energy consumption. A transit route network-based path planning model, TRDP (transit route design problem), has been introduced to reduce the time consumption with the shortest optimal route (Yang and Jiang, 2020).
To reduce the complexity of the TRDP model, an optimization model, TNDP (transit node design problem), has been developed considering time and the xy-dimension to obtain the optimal path location (Sun et al., 2020). A significant gap is discussed between the theory and practice of the TNDP model by addressing multiple routes, nodes, and the selection of the route and node (Durán-Micco and Vansteenwegen, 2021). A multi-level network system based on different modes of transportation, that is, subway, trolleybus, and common bus, and the user constraints such as bus routes and city size has been proposed to design the transit route network in urban areas (Chavhan et al., 2021), which is applied to the Mandle dataset to reduce the travel time cost. In a study by Hellsten et al. (2021), a heuristic route network is discussed based on multi-commodity network scenarios, that is, exponentially increasing route formulation, polynomial-based path indices, and time indices. An ant colony algorithm is introduced to further reduce the complexities involved in the optimal route search task (Ghaffari et al., 2022), while a genetic algorithm (GA) can also be implied for the optimization of large-scale routes via the network data obtained from multiple cities (Bourbonnais et al., 2021). In (Miandoabchi et al., 2012), a synchronous city road network with vehicle routes has been studied via a hybrid GA and clonal selection scheme. A cloud-enabled real-time routing scheme for MoD (mobility on demand) requiring on-route charging has been developed, aiming to improve the comfort of EV users (Ammous et al., 2018). The MoD suggests that with charging delays, the total trip time for all clients will be increased in comparison to the corresponding travel lengths.
A significant amount of research has been carried out to improve the efficacy of the route search algorithms by using the traffic information from ITS (intelligent transportation systems) in terms of minimal distance and travel time cost (Tisa, 2022). The navigation systems of EVs can be updated with new technologies when the charging infrastructure is considered during route planning (Morlock et al., 2019).
An optimal route selection for EVs toward charging stations considering the traffic congestion is obtained by using Yen’s algorithm with the information of transportation and distribution systems (Zhang et al., 2019). The A* algorithm is used to obtain the K-short path in order to get the K-shortest-path-joint-routing-scheduling (KSP-JRS), which can minimize the power consumption by shortest route selection while increasing the revenue via the discharge battery to the grid (Liu et al., 2020). A polynomial-time variant-based algorithm has been derived to obtain the optimal path between two target locations (Baum et al., 2020). In order to plan a simultaneous search for both velocity and path while avoiding obstacles, the A* algorithm has been implemented in multiple dimensions, including position, velocity, and heading angle (Morsali et al., 2020). A modified and efficient random with star tree network (RRT*) model for online informative path planning (Schmid et al., 2020) has been developed to use the single search tree expansion with a continuous pattern to obtain a refined path. In a study by Qi et al. (2020), a multi-objective dynamic rapidly exploring random tree (MOD-RRT*) algorithm has been developed that can navigate the path in an unknown dynamic environment to choose an optimal node while considering the length and smoothness of the path over a short period of time. By merging the urban electrified transportation network with the power grid, an intelligent path planning method has been developed for each EV to participate in the traffic network. It can ensure the timeliness of path planning by updating the connection weights in real-time while using the Floyd algorithm to search for the shortest path in a directed weight graph (Zhou et al., 2022). An optimal route can be achieved for public buses via the Greedy and Dijkstra algorithms by labeling the available passenger pick-up and drop-off station data with unique identities (Wei et al., 2020). To achieve an optimal and free route, an extended framework of the RRT has been introduced by utilizing the way-points of a straight line while producing a collision-free path (Hu et al., 2020). Considering the EVs’ charging demand and distribution network penetration, a spatial and temporal distribution prediction model has been developed with reliability assessment (Zhang et al., 2020b).
Although rapid RRT* can be used to overcome the time and space complexity of the RRT, the RRT* is not capable of achieving optimality in a finite amount of time. Thus, an RA-RRT* (route-assisted rapid random tree) model is proposed in the paper to obtain the minimized power consumption in EVs via the shortest path toward the destination, where the initial route is obtained by the RRT* algorithm as the estimation to configure the exploration. To achieve the optimal route in a short time, the RA-RRT* can achieve fast convergence blue by sampling. The main contributions of the paper are summarized as follows:
• A new cost function is defined in TRDP, considering both the time and EV optimal demand of the route search with a given route set. The cost function is written as a linearized mathematical modeling scheme in order to calculate the optimal route calculation with minimized time and distance.
• An RA-RRT* algorithm is proposed to generate a route set based on the demand instructions in response to the departure and destination.
• The obtained model is deployed in an undirected environment and compared with the A* and Dijkstra algorithms to verify the efficiency of fast target location detection in a wide domain area.
The remainder of the paper is organized as follows: Section 2 describes the system model and problem formulation. The RA-RRT* algorithm design and implementation in a dynamic environment are discussed in Section 3. Experiments and results are analyzed in Section 4. The conclusion is provided in Section 5.
2 Problem formulation
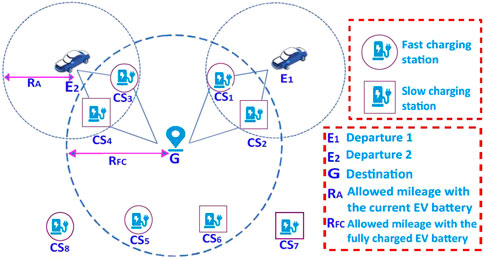
Here, multiple routes can be selected for large-scale vehicles with different types of aggregators and battery replacement centers, as depicted in Figure 1. The aggregators are divided into two categories: fast charging (FC) and slow charging (SC). The route is named EV assist route (EV-AR), which allows the users to charge or replace the battery before reaching the low limit SOCmin (minimum state of charge) so as to complete the current travel demand.
In Figure 1, the road network is directed by graph point (destination)
The real-time data are collected from the Shenzhen Transportation Bureau. The TRDP model indicates its applicability for EV-AR with discrete and non-linear characteristics. The TNDP (Transit Node Design Problem) is further considered for the optimal selection of the aggregators (Weng et al., 2020) (Nikolić and Teodorović, 2014). In order to obtain an efficient assistant route network model from the TRDP and TNDP models, the following assumptions are made:
1) The EVs’ road network is considered to be indirectly connected;
2) The distance between the charging stations is within the range of EVs’ battery limit;
3) The aggregators are enough on the EVs’ route to fulfill the EVs’ charging demand;
4) When the EV user needs to travel long distances, a battery exchange scheme could be introduced to avoid more charging time;
5) The power supply from the G2A (Grid to Aggregator) can provide enough power to the EV users.
The efficiency of the EV-AR design has to be evaluated, and certain assumptions are made to evaluate the solution of TRDP. In order to minimize the travel distance cost, the aggregators are placed at the maximum traffic flow positions. The availability of more electric piles is considered at each charging station to avoid congestion at one charging station.
3 The RA-RRT* model for path planning
In this paper, an optimal path is designed where the EVs can easily reach the charging station, battery replacement center, and destination with minimal route selection and maximum mileage.
Let a space X be configured, where the traffic congestion is defined as Xobs, the free region is Xfree = X/Xobs and the goal G is the destination. A feasible route x(t)ϵXfree can be found via the RRT* in the T interval, starting from r [0, T]ϵR, which begins from X (0) = Estart to X(T) = EEnd, consistent with the given constraints of the system. During the search for the feasible routes, RRT* conserves a tree network τ = (Ei, G) of the vertices (starting points) Ei from the space Xfree, while G represents the destination. The RRT* algorithm can be performed as follows:
Sampling: It is a random process where a route rrand = Xfree is taken from the traffic congestion-free space.
Distance: It provides the route cost between target points without traffic congestion. The cost can be calculated in the form of Euclidean distance.
Nearest neighbor: Function Nearest (τ, rrand) is used to obtain the maximum nearby nodes between τ = (Ei, G) to rrand with respect to the distance cost.
Collision check: The collision check is obtained by Obstaclefree(x) while examining the route x [0, T] if it is lies in range of the free space Xfree during the [0, T] interval.
Nearby vertices: Function Near(τ, rrand, n) provides the adjacent nodes in the space α(logn/n) around rrand where α is a constant dependent on the route plan, while n is the iteration number.
ExtractNode: In order to obtain a new node, the state function ExtractNode (rinitial, rnew, τ) adds a route rnew to the tree τ = (Ei, G) and connects it to the previously existing node rinitial.
Reroute: The state function Reroute (Rnear, rmin, rnew) examines the routes to check whether the rnew is less than the older route cost. If the state rnew > rpreviouse, the new route is replaced by the old one due to the minimum distance cost.
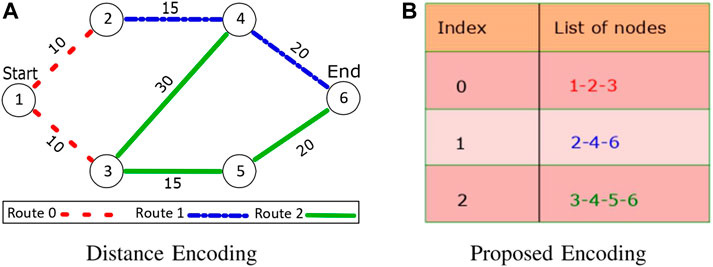
The steps involved in the RA-RRT* are defined in Algorithm 1. Steps 1 to 4 and 7 to 13 are the same as those in RRT* algorithm, while the RA-RRT* algorithm is modified by the incursion of Steps 5 to 6 and 14 to 19. In the proposed RA-RRT* algorithm, the initial found route (e.g., in Step 14) returns the iteration number n which is further used for biased sampling so as to insert the time interval b (Step 4), to repeat the tree search growth during that period. The optimized route is obtained via the function (τ, routecost) ← RouteOptimization (τ, rinit, rgoal) by connecting the feasible nodes from the initial route rinit to the destination rgoal and returns the cost in Step 16. A connected topology network is depicted in Figure 2 with random route costs among different nodes. The route topology network in Figure 2A describes the distance in km between different charging stations, while the possible routes are extracted in Figure 2B. In Step 18,
As shown in Figure 1, multiple routes toward G are taken, named EV-AR. The assist routes point the EVs toward G and different charging stations (CSi), which play a vital role in EV energy management. While approaching G, the first task is to select the potential CSi with the help of EV-AR along with optimal route selection.
In order to obtain the EV-AR, it is required to search for the most cost-effective routes in terms of less power consumption, less distance, and maximum mileage considering traffic congestion and road infrastructure. The range RA of the EVs can be calculated using the current battery level (SOCR) and EVs’ mileage (EM) as follows,
The full range RFC can be obtained with the fully charged battery level SOCmax and EM,
As described earlier, the selection of the charging stations for EVs is based on their locations and types of charging. With FC aggregator, the charging time duration is only 30 min to be fully charged (Duan et al., 2020), but it requires an isolated infrastructure of power supply, which is not economically feasible.
In the proposed scheme, the charging aggregator selection is defined as the charging efficiency CEi, which is equal to the output of the electric power. The selection of the route in terms of a charging aggregator can be defined in the following scenarios:
1. Bypassing the aggregators;
2. Stopping over single aggregator;
3. Stopping over multiple aggregators
Bypassing the aggregators: If the EVs have enough power to reach the destination, the conventional route calculation, that is, Dijkstra (Algorithm 2), is considered to be efficient. Hence, the EVs’ remaining battery level at the arrival point (SOCRA) is obtained with the SOCR at departure Ei, route distance D (Start, End), and EM,
During the bypassing, the status SOCRA > 0 is always satisfied.
Stopping over single aggregator: When the EVs cannot reach their destinations with the SOCR, the users have to charge the battery on their routes. In Figure 1, the EVs’ RA level is denoted by the two small circles with two departure points E1 and E2, while the RFC is represented by a large circle with the center of the destination G.
The overlapped areas show that the EVs have to be recharged if RFC > RA. Therefore, it is necessary to search for the optimal route toward the CSi while covering the distance D to G. The overlapped area around the EVs is distributed irregularly; hence, Euclidean distance is used to calculate D to the nearest aggregator.
The charging time cost CT from the initial point to the target while reaching a single aggregator can be calculated as,
By setting E1 as the charging point CSh(1, 2, 3, … ), Eq. 4 can be rewritten as,
where h is the charging time. Similarly, the total travel time cost from the starting point to the endpoint while stopping by a single aggregator can be obtained as,
EVT (Ei, G) and EVs battery SOCRA are used as the EV-AR, and then the EVs’ total routes EVR can be calculated as follows,
where δSC1 is the charging station, while R is the route between two adjacent nodes presented in Figure 2A. Similarly, EVs’ total travel distance EVD is calculated as,
It can further be modified with N number of search targets,
and SOCRA of EVs at the destination is calculated as,
Stopping over multiple aggregators: The EVs have to be charged at more than one aggregator when traveling a long distance. The charging time cost with multiple aggregators is calculated as,
Then, the route can be obtained as,
whereas the optimal route equation can be modified as the successive product of routes set from the departure point to the destination,
and the overall distance from the starting point to the destination is calculated as,
To sum up, the total time taken by the EVs from the starting point to the destination is expressed as,
Similarly, the remaining battery level at the destination can be obtained from the statistics of SOCmax and overall covered distance,
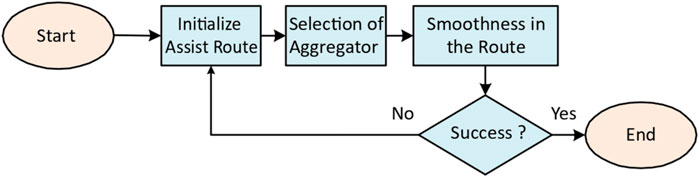
Assistive route analysis: The developed RA-RRT* model is implied on a given set of data collected from the Public Transport Bureau of Shenzhen, Guandong Province, China, including the longitudinal angles, latitudinal angles, and the public transport terminal locations. The retrieved routes by RA-RRT* can be reduced in length with the dynamic constraints on its trajectory. The entire framework is depicted in Figure 3, which is implemented as follows:
A suitable aggregator is selected considering the route and battery status details, that is, RA, RFC. In order to obtain the smooth route, an efficient route formulation strategy is jointly used with the obtained route details (Eqs 1-16). The routes are plotted based on the provided details of the route transfer mechanism among different traffic terminals using python gmplot function. Furthermore, the latitudinal and longitudinal angular data are converted into distance by using the Haversine Formula in Algorithm 3 as follows,
where dlat is the error between the two consecutive latitudinal angles lati, while dlon is the error between the two consecutive longitudinal angles loni and np is the python numpy library which is a source for multiple functions, that is, N-dimensional array. c and d are constant variables, while r is the radius of the Earth, equal to 6,371 km.
4 Experiment and result analysis
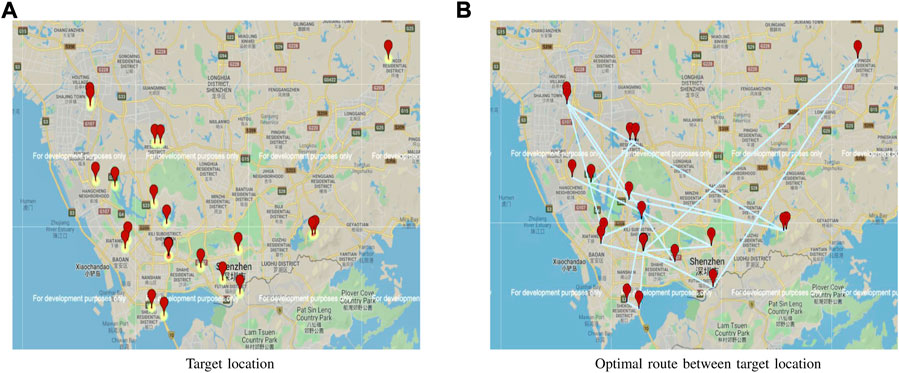
In this section, experiments are performed to verify the efficacy of the proposed RA-RRT* model for EV optimal path planning. The experiments are conducted on a Windows operating system with an Intel Core i7 with a RAM of 16 GHz and 8 GHz processor. Simulation experiments are carried out by using the software tool Python (Jupyter notebook and PyCharm environment). GMPLOT, a Google map plot function built into the Python library, is used to obtain the locations on the map with latitudinal and longitudinal angles retrieved from different target locations. In Figure 4A, the target locations are identified using a heat map function, while the routes between the target locations are plotted in Figure 4B. The route distances between different public transport terminals can be calculated via the heuristic (Dijkstra) algorithm.
Two scenarios have been considered to validate the RA-RRT* model. During the 1st scenario, the RA-RRT* model is used for the optimal route selection between the target locations, that is, start point, endpoint, and charging station CSi, while the algorithm is implemented for traffic congestion avoidance in the 2nd scenario.
4.1 Optimal route selection
The developed RA-RRT* algorithm is used on the target locations obtained by the Haversine formula (Mahariba et al., 2022) in Figure 4, from a given set of data. The average mileage per kilowatt-hour (kWh) is taken as 6 km, while the full battery capacity is taken as 24 kWh.
The known initial SoCini of the EV is used to calculate RA and RFC. The target locations are presented with the start points (highlighted in Figure 5) and final point in an undirected and non-convex environment in Figure 5. Based on the given target locations, the distance, point of aggregators, and route search time are calculated and listed in Table 2.
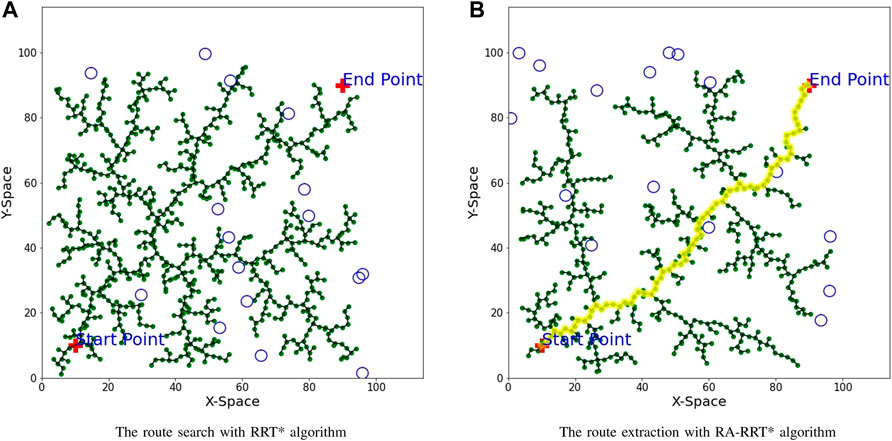
FIGURE 5. Optimal path achievement with the nearest charging stations with RRT* and RA-RRT* algorithms.
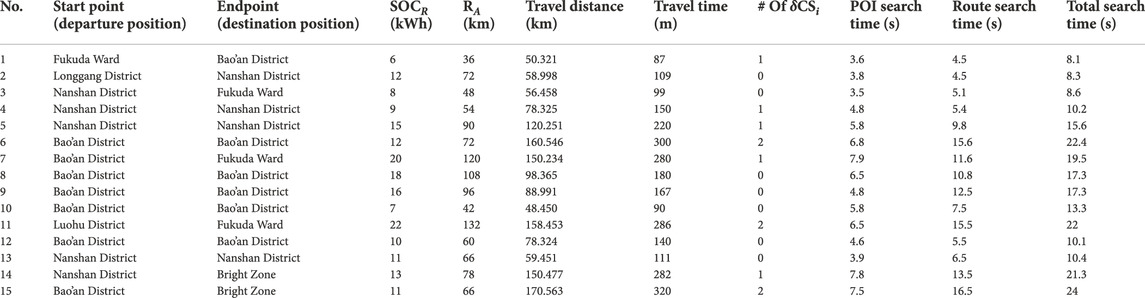
TABLE 2. Search time results for routes’ and aggregators’ selections with the proposed RA-RRT* algorithm.
In Figure 5A, the starting point and the end point are taken at axis (10,10) and (90,90), respectively. The charging stations are denoted as circles in the free search area. Figure 5B shows the results of the optimal routes between two points via the proposed RA-RRT* algorithm. While approaching the target location with the shortest route, it has considered passing across the route if it has enough aggregators. The obtained route is highlighted with a yellow color, which is smooth between the start point, charging station allocation, and destination. In order to avoid the charging shortage, an early warning model about insufficient battery levels can be developed by using the appropriate energy consumption factor (Wang et al., 2021).
4.2 Bypassing the traffic congestion
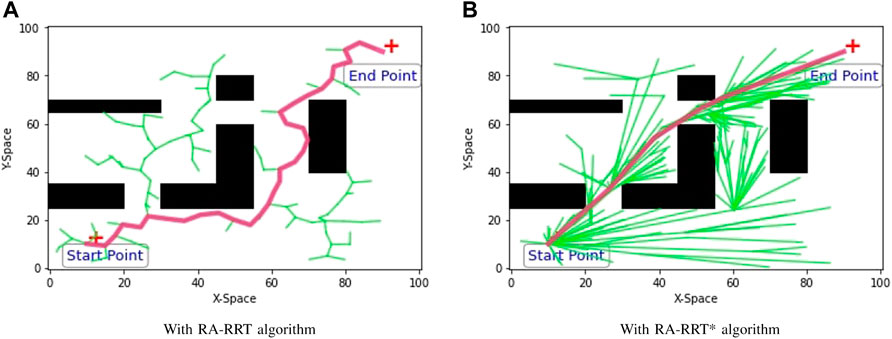
The proposed RA-RRT* algorithm is further elucidated in a 2D environment considering the traffic congestion to be formed as blocks Xobs with the indirect connection between the starting point and the destination, shown in Figure 6A.
In Figure 6A, the departure point is taken at (10,10) with map location at north-south, while the destination point is taken at (90,90), the east-west positions, respectively. It is a non-smooth path search in the free space Xfree = X/Xobs; hence, the RA-RRT* model is further compared with the RRT* by increasing the number of search samplings in the free space to find an initial route immediately. The RA-RRT*-based graph is achieved in Figure 6B, illustrating the improved results in terms of route smoothness and length.
4.3 The comparison among path planning algorithms
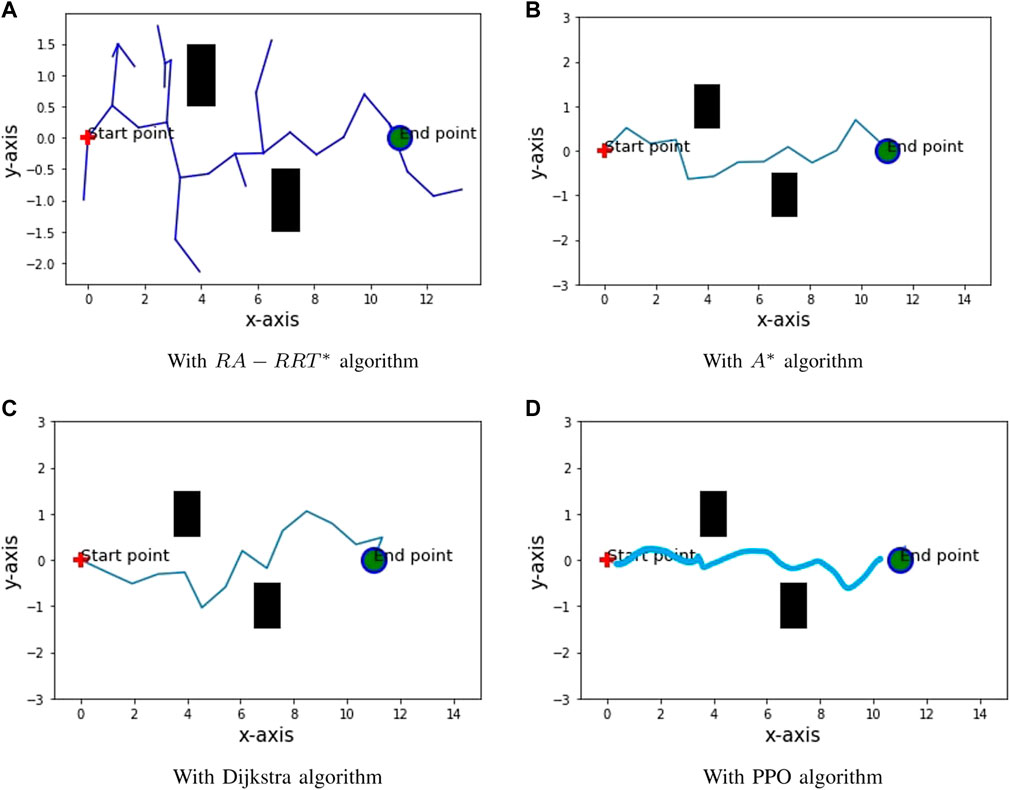
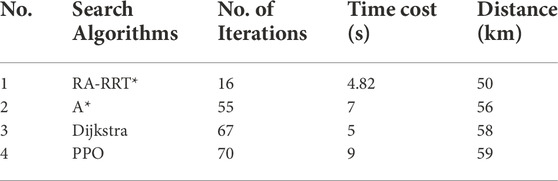
The performance of the proposed RA-RRT* is compared with both A* and Dijkstra algorithm in Figure 7. The obtained results in Table 3 can demonstrate that the RA-RRT* is faster compared to both A* and Dijkstra algorithms in the search for the target location. In order to retrieve the optimal route toward the target location, RA-RRT* compiled 16 iterations, while A* and Dijkstra took 55 and 67 compilation iterations, respectively. The algorithms are evaluated in Table 3 based on their iteration time costs. During charging station searching and following the optimal path towards the destination, the wide-spreading search property of the RA-RRT* algorithm makes it more suitable for multiple targets searching simultaneously.
Furthermore, a deep reinforcement learning algorithm, the Proximal Policy Optimization algorithm (PPO), is used for path planning comparison with the RA-RRT* model in an obstacle environment. The PPO algorithm (Sadhukhan and Rastko, 2022) performs on an iteration basis to search for the target location with more time consumption for the target location, while RA-RRT* can explore in all directions due to its tree search property with less time consumption. The PPO algorithm is carried out in a Jupyter notebook on a Windows operating system with an Intel Core i7 with a RAM of 16 GHz and 8 GHz processor.
In Table 4, a metric evaluation of the RA-RRT* algorithm with the A*, RRT*, and Dijkstra algorithms regarding speed and accuracy is shown. It is found that the A* algorithm is more efficient in a directional and known environment, whereas the Dijkstra and RRT* algorithms are more feasible in an undirected environment (Erokhin et al., 2018). Based on the experimental results, the proposed RA-RRT* is proven to be more efficient due to the requirement to simultaneously search for the charging stations and the minimum optimal path in an undirected environment because of the tree structure.
5 Conclusion
In this paper, a route search-based problem has been carried out with the proposed RA-RRT* algorithm via an assistive route heuristic model, achieving fast route search capability for multiple targets in a wide range area. Different scenarios are considered with stops at a single aggregator, multiple aggregators, or for battery replacement. A comparative analysis of the proposed model is taken with the A*, Dijkstra, and PPO algorithms, where the proposed RA-RRT* model is more feasible for multi-target fast route search results in an undirected environment. Further research will apply the proposed RA-RRT* algorithm for real-time path planning in autonomous urban driving scenarios.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SM: investigation, methodology, simulation analysis, and writing—original draft. YZ: supervision, resources, project administration, and writing—review and editing.
Funding
This work was supported in part by the National Natural Science Foundation of China Ref. U1913201, and Ref. 61973296, in part by the Shenzhen Science and Technology Innovation Commission Project Grant Ref. JCYJ20170818153635759, Ref. JCYJ20200109114839874 and Ref. JCYJ20210324101215039.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ammous, M., Belakaria, S., Sorour, S., and Abdel-Rahim, A. (2018). Optimal cloud-based routing with in-route charging of mobility-on-demand electric vehicles. IEEE Trans. Intell. Transp. Syst. 20 (7), 2510–2522. doi:10.1109/tits.2018.2867519
Baum, M., Dibbelt, J., Pajor, T., Sauer, J., Wagner, D., and Zundorf, T. (2020). Energy-optimal routes for battery electric vehicles. Algorithmica 82 (5), 1490–1546. doi:10.1007/s00453-019-00655-9
Bourbonnais, P. L., Morency, C., Trépanier, M., and Martel-Poliquin, E. (2021). Transit network design using a genetic algorithm with integrated road network and disaggregated O–D demand data. Transportation 48 (1), 95–130. doi:10.1007/s11116-019-10047-1
Chavhan, S., Gupta, D., Nagaraju, C., Khanna, A., and Rodrigues, J. J. P. C. (2021). An efficient context-Aware vehicle incidents route service management for intelligent transport system. IEEE Syst. J. 16 (1), 487–498. doi:10.1109/jsyst.2021.3066776
Duan, X., Hu, Z., and Song, Y. (2020). Bidding strategies in energy and reserve markets for an aggregator of multiple EV fast-charging stations with battery storage. IEEE Trans. Intell. Transp. Syst. 22 (1), 471–482. doi:10.1109/tits.2020.3019608
Durán-Micco, J., and Vansteenwegen, P. (2021). A survey on the transit network design and frequency setting problem. Public Transp. 14 (1), 155–190. doi:10.1007/s12469-021-00284-y
El-Taweel, N. A., and Farag, H. (2019). Integrated utility-transit model for optimal configuration of battery electric bus systems. IEEE Syst. J. 14 (1), 738–748. doi:10.1109/jsyst.2019.2926460
Erokhin, A., Erokhin, V., and Sotnikov, S. (2018). Optimal multi-robot path finding algorithm based on A*. Proc. Comput. Methods Syst. Softw. 860 (1), 172–182. doi:10.1007/978-3-030-00184-1_16
Ghaffari, A., Mesbah, M., Khodaii, A., and MirHassani, S. A. (2022). Risk-based formulation of the transit priority network design. IEEE Trans. Intell. Transp. Syst. 23 (7), 8895–8905. doi:10.1109/tits.2021.3087525
Hellsten, E., Koza, D. F., Contreras, I., Cordeau, J. F., and Pisinger, D. (2021). The transit time constrained fixed charge multi-commodity network design problem. Comput. Oper. Res. 136 (1), 105511–105536. doi:10.1016/j.cor.2021.105511
Hu, B., Cao, Z., and Zhou, M. (2020). An efficient RRT-based framework for planning short and smooth wheeled robot motion under kinodynamic constraints. IEEE Trans. Ind. Electron. 68 (4), 3292–3302. doi:10.1109/tie.2020.2978701
Liu, P., Wang, C., Hu, J., Fu, T., Cheng, N., Zhang, N., et al. (2020). Joint route selection and charging discharging scheduling of EVs in V2G energy network. IEEE Trans. Veh. Technol. 69 (10), 10630–10641. doi:10.1109/tvt.2020.3018114
Mahariba, A. J., Uthra, R. A., and Brunet, R. G. (2022). Estimation of shortest route with minimum travel time using GIS and MSSTT algorithm. Adv. Constr. Manag. 191 (1), 565–579. doi:10.1007/978-981-16-5839-6_48
Miandoabchi, E., Farahani, R. Z., Dullaert, W., and Szeto, W. Y. (2012). Hybrid evolutionary metaheuristics for concurrent multi-objective design of urban road and public transit networks. Netw. Spat. Econ. 12 (3), 441–480. doi:10.1007/s11067-011-9163-x
Morlock, F., Rolle, B., Bauer, M., and Sawodny, O. (2019). Time optimal routing of electric vehicles under consideration of available charging infrastructure and a detailed consumption model. IEEE Trans. Intell. Transp. Syst. 21 (12), 5123–5135. doi:10.1109/tits.2019.2949053
Morsali, M., Frisk, E., and Åslund, J. (2020). Spatio-temporal planning in multi-vehicle scenarios for autonomous vehicle using support vector machines. IEEE Trans. Intell. Veh. 6 (4), 611–621. doi:10.1109/tiv.2020.3042087
Nikolić, M., and Teodorović, D. (2014). A simultaneous transit network design and frequency setting: Computing with bees. Expert Syst. Appl. 41 (16), 7200–7209. doi:10.1016/j.eswa.2014.05.034
Qi, J., Yang, H., and Sun, H. (2020). MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment. IEEE Trans. Ind. Electron. 68 (8), 7244–7251. doi:10.1109/tie.2020.2998740
Sadhukhan, P., and Rastko, R. (2022). Selmic. “Proximal policy optimization for formation navigation and obstacle avoidance. Int. J. Intelligent Robotics Appl. 65 (1), 1–14. doi:10.1007/s41315-022-00245-z
Schmid, L., Pantic, M., Khanna, R., Ott, L., Siegwart, R., and Nieto, J. (2020). An efficient sampling-based method for online informative path planning in unknown environments. IEEE Robot. Autom. Lett. 5 (2), 1500–1507. doi:10.1109/lra.2020.2969191
Sun, G., Tian, Z., Liu, R., Jing, Y., and Ma, Y. (2020). Research on coordination and optimization of order allocation and delivery route planning in take-out system. Math. Problems Eng. 20 (20), 1–16. doi:10.1155/2020/7248492
Tisa (2022). Tpeg. Available at: “https://tisa.org/”.
Wang, Z., Song, C., Zhang, L., Zhao, Y., Liu, P., and Dorrell, D. G. (2021). A data-driven method for battery charging capacity abnormality diagnosis in electric vehicle applications. IEEE Trans. Transp. Electrific. 8 (1), 990–999. doi:10.1109/tte.2021.3117841
Wei, M., Liu, T., Sun, B., and Jing, B. (2020). Optimal integrated model for feeder transit route design and frequency-setting problem with stop selection. J. Adv. Transp. 20 (20), 1–12. doi:10.1155/2020/6517248
Weng, D., Zheng, C., Deng, Z., Ma, M., Bao, J., Zheng, Y., et al. (2020). Towards better bus networks: A visual analytics approach. IEEE Trans. Vis. Comput. Graph. 27 (2), 817–827. doi:10.1109/tvcg.2020.3030458
Yang, J., and Jiang, Y. (2020). Application of modified NSGA-II to the transit network design problem. J. Adv. Transp. 20 (20), 1–24. doi:10.1155/2020/3753601
Zhang, C., Liu, Y., Wu, F., Tang, B., and Fan, W. (2020). Effective charging planning based on deep reinforcement learning for electric vehicles. IEEE Trans. Intell. Transp. Syst. 22 (1), 542–554. doi:10.1109/tits.2020.3002271
Zhang, Q., Wu, K., and Shi, Y. (2020). Route planning and power management for PHEVs with reinforcement learning. IEEE Trans. Veh. Technol. 69 (5), 4751–4762. doi:10.1109/tvt.2020.2979623
Zhang, X., Li, P., Hu, J., Liu, M., Wang, G., Qiu, J., et al. (2019). Yen’s algorithm-based charging facility planning considering congestion in coupled transportation and power systems. IEEE Trans. Transp. Electrific. 5 (4), 1134–1144. doi:10.1109/tte.2019.2959716
Zhou, X., Zou, S., Wang, P., and Ma, Z. (2020). ADMM-based coordination of electric vehicles in constrained distribution networks considering fast charging and degradation. IEEE Trans. Intell. Transp. Syst. 22 (1), 565–578. doi:10.1109/tits.2020.3015122
Keywords: path planning, heuristic model, aggregators, electric vehicles, TRDP
Citation: Muhammad S and Zhou Y (2023) Path planning for EVs based on RA-RRT* model. Front. Energy Res. 10:996726. doi: 10.3389/fenrg.2022.996726
Received: 18 July 2022; Accepted: 31 October 2022;
Published: 13 January 2023.
Edited by:
Shabana Urooj, Princess Nourah bint Abdulrahman University, Saudi ArabiaReviewed by:
Linfei Yin, Guangxi University, ChinaAbdul Quadir Md, Vellore Institute of Technology (VIT), India
Emmanouil Rigas, Aristotle University of Thessaloniki, Greece
Navaid Z. Rizvi, Gautam Buddha University, India
Copyright © 2023 Muhammad and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yimin Zhou, eW0uemhvdUBzaWF0LmFjLmNu
 Said Muhammad
Said Muhammad Yimin Zhou
Yimin Zhou