Quadratic regression estimation of hybridized nanoliquid flow using Galerkin finite element technique considering shape of nano solid particles

Because of its multivariate particle suspension approach, the developing class of fluid has a better level of stability as well as increased heat transfer. In this regard, hybrid nanofluid outperforms ordinary fluid and even well-known nanofluid. In a slick environment, we investigate its fluidity and heat transfer qualities. Nano-leveled particle morphologies, porousness materials, variable thermal conductivity, slippage velocity, and thermal radiative effects are all being studied. The Galerkin finite element method is a numerical methodology for numerically solving the governing equations (G-FEM). For this analysis, a Powell-Eyring hybrid nanofluid (PEHNF) flowing via a permeable stretchable surface is used, which comprises two types of nanoparticles (NP), copper (Cu), and titanium alloy (Ti₆Al₄V) dispersed in sodium alginate (C₆H₉NaO₇). The heat transfer ratio of PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) remained much greater than that of conventional nanofluids (Cu-C₆H₉NaO₇), with a range of 43%–54%. When lamina particles are present, the thermal conductivity of the boundary layer increases dramatically, while spherical nanoparticles have the lowest thermal conductivity. As nanoparticles are added under their fractional sizes, radiative heat conductance, and flexible heat conductance, the system’s entropy increases. The flow system’s ability to transport mass decreases when molecule diffusivity decreases dramatically. This is theoretically related to a rise in Schmidt number against molecular diffusivity.

Introduction

Different simulations, including the regulator rule scheme, Carreau’s scheme, Cross’ scheme, and Ellis’s scheme, are offered to shed light on the behavior of HNFs, however, few researchers have investigated the Williamson liquid scheme (WLS). Williamson (1929) thought about the flow of hybrid nanofluids (HNFs) such as (pseudo-plastic liquids), proposed an equation system to represent the flow of HNFs, and then empirically verified the results. In an advanced gravitational investigation, researchers proposed that an echoing level of a WLS should movement concluded an inspired superficial. A real fluid has both the lowest and highest operational viscosities that relate to its molecular structure. The WLS measures together the lowest and highest thicknesses. During the attendance of revolution, Said et al. (Said et al., 2021) planned a 3D-class of HNF to additional upsurge the heat transfer (HT) rate completed by widening slip. Mandal et al. (Mandal et al., 2022) exploited an artificial neural network to form investigational statistics. Saha et al. (Saha et al., 2022) described an investigation of HT and rheological possessions of HNFs for refrigeration presentations. Survey studies by Al‐Chlaihawi et al. (Al‐Chlaihawi et al., 2022), Kursus et al. (Kursus et al., 2022), Xiong et al. (Xiong et al., 2021), and Muneeshwaran et al. (Muneeshwaran et al., 2021) respectively, can be located in this direction, while Dubey et al. (Dubey and Sharma, 2022) offered a short survey in HNF on mechanics revisions. Syed and Jamshed (Hussain and Jamshed, 2021) considered the movement of MHD tangent HNF via a strained slip’s boundary layer. In accumulation, the demonstration of the extended HT of tangent hyperbolic fluids crossways a nonlinearly fluctuating slide containing HNFs was tested by Qureshi (Qureshi, 2022), Jamshed et al. (Jamshed et al., 2021a), and Parvin et al. (Parvin et al., 2021).

Puneeth et al. (Shankaralingappa et al., 2021) measured 3D-assorted convection movement of HNFs of a non-linear widening surface using a modified Buongiorno’s nanofluids model (MBNM). Rana et al. (Rana et al., 2021) presented a study of HNF movement past a perpendicular platter with nanoparticle aggregation kinematics, the current slide, and important buoyancy force possessions utilizing MBNM. Mahanthesh et al. (Mahanthesh et al., 2021) estimated the HT optimization of HNFs with the help of MBNM. Owhaib and Al-Kouz (Owhaib and Al-Kouz, 2022) and Owhaib et al. (Owhaib et al., 2021) employed the concept of MBNM in 3D systems of movement and HT of bi-directional overextended HNF film showing an exponential heat generation. Hussain et al. (Hussain et al., 2022a) characterized a biochemical response and current of HNFs flow-through solar gatherer as potential solar energy applying the idea of MBNM. Roşca et al. (Roşca et al., 2021) engaged the movement and HT of a stretching/shrinking slip by the virtue of MBNM. Akram et al. (Akram et al., 2022) analyzed the electroosmotic movement of silver-water HNF controlled by using two altered methods for NF including the MBNM. Areekara et al. (Areekara et al., 2022) suggested a study on NF movement with asymmetrical heat foundation and representative boundary conditions with the application by MBNM.

Nanofluids own the characteristics of the non-Newtonian fluid, together with the viscoelastic properties. Extended experimental work research is required to develop nanofluid viscosity models for use in simulation studies (Wang and Mujumdar, 2008; Bilgili et al., 2021). Therefore, the Powell-Eyring fluid is considered in the current model, together with the significance of non-Newtonian fluid properties. This type of fluid is proposed by Powell and Eyring (Hayat and Nadeem, 2018) in 1944. Moreover, Powell-Eyring fluid is one type of visco-elastic fluid. Eyring–Powell fluid model implements a higher-level complicated mathematical framework, but it is found to be the greater model over previous viscoelastic fluid models. This model is founded on the kinetic theories of liquids, not on empirical expressions. In addition, Eyring–Powell fluid model has Newtonian properties at low and great shear stress. Examples of Powell-Eyring fluids are polymer melts and solids suspended in non-Newtonian liquids. The significant implementations of Powell-Eyring fluid have been observed in engineering, manufacturing, and industrial areas such as polymers, pulp, plasma, and other biological technology. However, several researchers have investigated the properties of non-Newtonian Powell-Eyring nanofluid (Hayat et al., 2015; Malik et al., 2015; Hayat et al., 2017). Aziz and Afy (El-Aziz and Afify, 2019) chose the shooting technique, together with the Buongiorno nanofluid model to obtain the Casson nanofluid’s numerical solution over a stretching sheet. At the initial stages of flow (primary and secondary flow), they concluded that the Hall parameter upsurges in the convective rate of heat and mass transfer, together with the drag coefficient. Moreover, the nanoparticle volume concentration parameter increases for increasing velocity slip values. Consequently, the Sherwood number is reduced. Subsequently, the influences on the magnet field and Soret-Dufour have been reportedly on non-rotational Newton’s Oldroyd-B nanofluid stream bounded by the stretched sheet (Ali et al., 2021). This model is also being restricted under the modification of Fourier’s law. For the step of numerical findings, the Galerkin-Finite element system was developed.

Porous media models (PMMs), frequently referred to as porous materials, have pores (vacuums). The thin part of the material is referred to as the “matrix” or “frame.” Typically, a fluid is injected into the pores (fluid or fume). Though the material that makes up the frame is regularly hard, structures like foams might profit from the idea of PMM. To apply solar heat, Jamshed et al. (Jamshed et al., 2021b) employed PMM in solar aircraft combining tangent HNFs. Using the PMM in HNFs, Shahzad et al. (Shahzad et al., 2021) developed a comparative mathematical study of HT. Numerical conduct of a 2D-Magneto double-diffusive convection flow of HNF over PMM was provided by Parvin et al. (Parvin et al., 2021). Faisal et al. (Shahzad et al., 2022a) reported that using HNFs rather than PMM increased the thermal efficacy of solar water pumps. Banerjee and Paul (Banerjee and Paul, 2021) examined the most recent research and advancements concerning PMM combustion applications. For pebble-bed devices, Zou et al. (Zou et al., 2022) designed an explicit system of stone heat in the PMM. PMM substantiation using stress drip dimensions was suggested by Lee et al. (Lee et al., 2022). On a constructed soaking soil pile model, Cui et al. (Cui et al., 2021) investigated a numerical analysis of the solution for longitudinal quivering of a fluctuating pile based on PMM. A machine learning approach was taken by Alizadeh et al. (Alizadeh et al., 2021) to calculate transference and thermodynamic processes in metaphysical systems HT in HNFs movement in PMM. A non-homogenous HNF was proposed by Rashed et al. (Rashed et al., 2021) for 3D convective movement in enclosures with assorted PMM (AdnanKhan et al., 2021; Adnan and Ashraf, 2022a; Khan et al., 2022a; Alharbi et al., 2022; Ashraf et al., 2022a; Ashraf et al., 2022b; Adnan and Ashraf, 2022b; Khan et al., 2022b; Khan et al., 2022c; Murtaza et al., 2022). presented the latest updating that involves the traditional nanofluids with the features of heat and mass transmission in a different physical situation.

The rate of HT through a component thickness of a material per unit area per temperature variation is known as the variable thermal conductivity (VTC) of that material. Alternatively said, the VTC is inversely proportional to the temperature capacity. Gbadeyan et al. (Olabode et al., 2021) studied the effect of VTC and thickness on Casson NF movement with convective warming and velocity slide. Mabood et al. (Mabood et al., 2021) impacted the Stefan blowing and mass convention on the movement of HNF of VTC in a revolving disk. Abouelregal et al. (Abouelregal et al., 2021) checked the thermo-viscoelastic fractional model of revolving HNFs with VTC owing to mechanical and current loads. Swain et al. (Swain et al., 2021) utilized the HT and stagnation‐point movement of influenced HNFs with VTC. Also, Ahmed et al. (Ahmed et al., 2021) considered the HT of MHD movement of HNFs via an exponential penetrable widening arched surface with VTC. Mahdy et al. (Mahdy et al., 2021) employed the VTC and hyperbolic two-temperature philosophy throughout the magneto-photothermal model of semiconductors induced by laser pulses. Hobiny and Ibrahim (Hobiny and Abbas, 2022) analyzed the impacts of VTC in a semiconducting medium utilizing the finite element technique. Ahmad et al. (Ahmad et al., 2022a) studied the unsteady 3D-bio convective movement of HNFs by an exponentially widening sheet with VTC and chemical reaction. Din et al. (Din et al., 2022) assumed the entropy generation from convective released moving exponential porous fins with VTC and interior temperature compeers. For more details see Refs (Akgül et al., 2022; Attia et al., 2022; Ahmad et al., 2022b; Bilal et al., 2022; Qureshi et al., 2022; Safdar et al., 2022).

A statistical technique called quadratic regression estimation (QRE) is considered to identify the parabola equation that finest fits a given collection of data. Finding the equation of the conventional line that most closely fits a collection of information is the goal of this sort of regression, which is an extension of modest linear regression. Jamei et al. (Jamei et al., 2022) estimated the thickness of HNFs for current energy using the QRE. Nandi et al. (Nandi et al., 2022a; Nandi et al., 2022b) suggested different investigations on HNFs based on QRE. Bhattacharyya et al. (Bhattacharyya et al., 2022) introduced a numerical and statistical method to capture the movement characteristics of HNFs containing copper and grapheme HNs utilizing QRE. Kumbhakar and Nandi (Kumbhakar and Nandi, 2022) presented an unsteady MHD radiative-dissipative movement of HNFs of a widening sheet with slide and convective conditions employing QRE. Said et al. (Said et al., 2022) considered the application of the original outline by collaborative boosted QRE of HNFs. Chen et al. (Chen et al., 2022a; Chen et al., 2022b) gave a long approximation of the physical properties of HNFs.

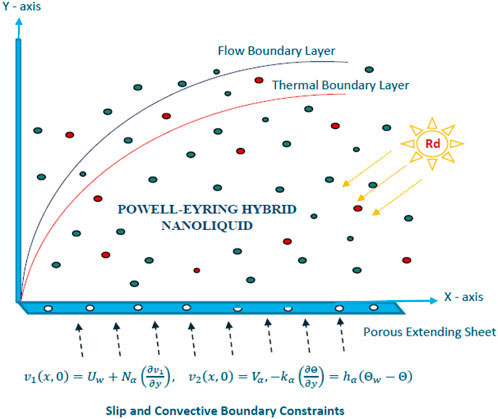
By focusing on the flowing rapidity of a Powell-Eyring HNFs as well as thermal transmission with changing heat and current conductance flowing through a stretched permeable material, this work intends to bridge a gap in the previous survey and fill a knowledge gap. The flow of nanoliquid was geometrically modeled using a single-phase nanoliquid. The foundation liquid in the investigation of copper (Cu) and titanium alloy (Ti₆Al₄V) hybrid nanoparticles is sodium alginate (C₆H₉NaO₇). The regulatory equations of the Powell-Eyring hybridization nanoliquid are transformed into ordinary differential equations (ODEs). The influences of porous parameters, thermal radiative fluxing, and variable thermal conductance are considered in the examination. Then, the effects of the slippage velocity and nanoparticle shape factors are probed in flowing and entropy aspects. The obtained ODEs are solved numerically using the Galerkin finite element technique and the necessary prevailing parametric parameters. Numerical results are shown graphically, and comments are built upon. In-depth research has been done on the possessions of particle morphologies, the convective slide boundary condition, the thermal energy movement, and the slippery velocity.

Flow examination

Analysis of movement shows how a superficial moves horizontally at an accelerating rate.

$U_w\left(x,t\right)=\frac{ex}{1-\Omega t},(1)$

where $e$ is the preliminary increasing amount. Solitary slip heat is ${\Theta }_w\left(x,t\right)={\Theta }_{\infty }+\frac{e^{*}x}{1-\Omega t}$ and based on the suitability, pretend to be stable at $x=0$, $e^{*},$ ${\Theta }_w$ and ${\Theta }_{\infty }$ let the current difference ratio, surface heat, and free-streaming heat, consistently.

Under the following hypotheses and constraints, the theoretical framework is selected:

1) Unsteady two-dimensional laminar flowing.

2) Boundary-layer guesstimate.

3) Modified Buongiorno's structure.

4) Non-Newtonian PEHNFs.

5) Different effects i.e., porous medium, variable thermal conductivity, radiative flowing, and nanomolecules shaped influence.

6) Penetrable expanding surface.

7) Slip and convective boundary constraints.

The exact formulary of the stress tensor of fluid follows the Powell-Eyring relationship is provided as (Aziz et al., 2021):

${\tau }_{ij}={\mu }_{hnf}\left(\frac{\partial u_i}{\partial x_j}\right)+\frac{1}{\stackrel{\sim }{\zeta }}{\mathit{sinh}}^{-1}\left(\frac{1}{{\varrho }^{*}}\frac{\partial u_i}{\partial x_j}\right).(2)$

Here, ${\mu }_{hnf}$ is the mechanical viscosity of PEHNF, and $\stackrel{\sim }{\zeta }$ and ${\varrho }^{*}$ are matter constants. The movement geometric is illuminated in Figure 1.

FIGURE 1

FIGURE 1. Flow model illustration.

Framed model

Classic formulas (Aziz et al., 2021) of a viscidness P-EHNF beside with entropy assembly befittingly adapted underneath normal boundary-layer approximations via a penetrable substantial, porous medium, variable thermal conductivity, and radiative flowing are

$\frac{\partial v_1}{\partial x}+\frac{\partial v_2}{\partial y}=0,(3)$

$\frac{\partial v_1}{\partial t}+v_1\frac{\partial v_1}{\partial x}+v_2\frac{\partial v_1}{\partial y}=\left({\nu }_{hnf}+\frac{1}{{\rho }_{hnf}\stackrel{\sim }{\zeta }{\varrho }^{*}}\right)\frac{{\partial }^2{v}_1}{\partial y^2}-\frac{1}{2\stackrel{\sim }{\beta }{\varrho }^{{*}^3}{\rho }_{hnf}}{\left(\frac{\partial v_1}{\partial y}\right)}^2\frac{{\partial }^2{v}_1}{\partial y^2}-\frac{{\mu }_{hnf}}{{\rho }_{hnf}k}{v}_1,(4)$

$\frac{\partial \Theta }{\partial t}+v_1\frac{\partial \Theta }{\partial x}+v_2\frac{\partial \Theta }{\partial y}=\frac{1}{\left(\rho C_p\right){\kappa }_{hnf}}\left[\frac{\partial }{\partial y}\left({\kappa }_{hnf}^{*}\left(\Theta \right)\frac{\partial \Theta }{\partial y}\right)\right]-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\left[\frac{\partial q_r}{\partial y}\right],(5)$

$v_1\frac{\partial C^{*}}{\partial x}+v_2\frac{\partial C^{*}}{\partial y}=D_B\frac{{\partial }^2{C}^{*}}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^2\Theta }{\partial y^2}-k_1\left(C^{*}-C_{\infty }^{*}\right).(6)$

the suitable boundary conditions are (Aziz et al., 2021):

$v_1\left(x,0\right)=U_w+N_{\alpha }\left(\frac{\partial v_1}{\partial y}\right),v_2\left(x,0\right)=V_{\alpha },-k_{\alpha }\left(\frac{\partial \Theta }{\partial y}\right)=h_{\alpha }\left({\Theta }_w-\Theta \right)C^{*}=C_w^{*},(7)$

$v_1\to 0,\Theta \to {\Theta }_{\infty },C^{*}\to C_{\infty }^{*}asy\to \infty .(8)$

Where a flow speed is of the structure $v⃖=\left[v_1\left(x,y,t\right),v_2\left(x,y,t\right),0\right]$. Time is denoted by $t$, $\Theta$ signifies a fluid temperature. The penetrability of an expanding plate is symbolized by $V_{\alpha }$. $N_{\alpha }$ is the slip length. The porousness of NF is characterized by $k$. The additional parameters like thermal conductivity of nanosolid and heat transmission factor are represented by $k_0$ and $h_f$, respectively.

The mongrelized nanoliquid is combined principally with Cu nano molecules in machine grease standard liquid at a constant fractional size (${\varphi }_{Cu}$) and it is put at 0.09 all about the study. Ti₆Al₄V NP were put together into HNFs consuming attentiveness scope (${\varphi }_{TA}$).

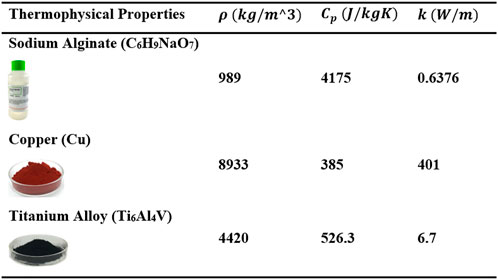
The combination of nanomolecules in the basefluid runs to a difference in the characteristics thermophysically. Table 1 summarises the relevant parameters for PENF (Reddy et al., 2014; Din et al., 2022).

TABLE 1

TABLE 1. Thermo-physical properties of PENF.

$\varphi$ is the nanomolecules fractional volume factor. ${\mu }_f$, ${\rho }_f$, ${\left(C_p\right)}_f$, ${\sigma }_f$ and $k_f$ are dynamical viscidness, density, efficient heat capacitance, and the electrical and thermal conductance of the base fluid, correspondingly. The further attributes ${\rho }_s$, ${\left(C_p\right)}_s$, ${\sigma }_f$ and $k_s$ are the density, active heat capacitance, and the electrical and thermal conductance of nanomolecules, correspondingly. The physical properties of PEHNF are defined in Table 2 (Devi and Devi, 2016).

TABLE 2

TABLE 2. Thermophysical properties of PEHNF.

Herein, ${\mu }_{hnf}$, ${\rho }_{hnf}$, $\rho {\left(C_p\right)}_{hnf}$ and ${\kappa }_{hnf}$ indicates the dynamic viscous, density, specific temperature capacitor, and current conductivity of HNF. $\varphi$ is a fractional size factor and ${\varphi }_{hnf}={\varphi }_{Cu}+{\varphi }_{TA}$ is the size parameter of solid-nanoparticle combination. ${\mu }_f$, ${\rho }_f$, ${\left(C_p\right)}_f$ and ${\kappa }_f$ are dynamic viscosity, density, specific heat capacity, and the thermal conducting of the ordinary fluid. ${\rho }_{p_1}$, ${\rho }_{p_2}$, ${\left(C_p\right)}_{p_1}$, ${\left(C_p\right)}_{p_2}$, ${\kappa }_{p_1}$ and ${\kappa }_{p_2}$ are the density constancy, precise heat competence, and current conducting of the solid-nanoparticle.

Heat conditional of heat conducting for hybrid nanoliquid blend is followed as (Jamshed et al., 2021c):

${\kappa }_{hnf}^{*}\left(\mathit{\Theta }\right)=k_{hnf}\left[1+\gamma \left(\Theta -{\Theta }_{\infty }\right){\left({\Theta }_w-{\Theta }_{\infty }\right)}^{-1}\right](9)$

The significance of several nanomolecules shaped is identified as the nanomolecules shaped influence. Figure 2 gives the values of the practical shaped component for different element shapes are obtained as (Akgül et al., 2022): Figure 3 demonstrates the themophysical values of the used materials of HNF.

FIGURE 2

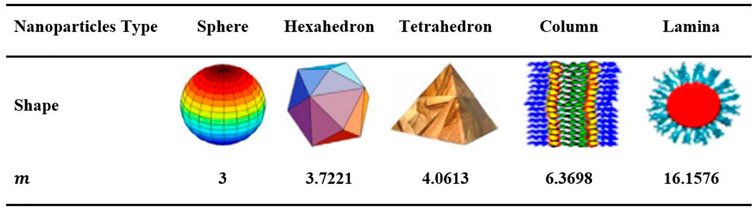
FIGURE 2. Standards of the practical shaped element for diverse particle shaped. The material possessions of the crucial sodium alginate (C₆H₉NaO₇) and the various NP exploited in this research are indicated in Figure 3 (Xu and Chen, 2017; Makinde et al., 2018; Jamshed et al., 2021d).

FIGURE 3

FIGURE 3. Substance effects of C₆H₉NaO₇ and NPs at 293 K.

PEHNF radiative flow only travels a little space resulting in the thickener of NF. Because this is happening, Rosseland’s guesstimate for radiative fluxing (Shahzad et al., 2022b), is used in Eq. 5 and it is given

$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial {\Theta }^4}{\partial y},(10)$

Where ${\sigma }^{*}$ is Stefan-Boltzmann amount and $k^{*}$ is the absorbing factor.

Model solution

Boundary-value problem (BVP) formulas (3–6) are converted in the definition of the similarity procedure that converts the regulating PDEs to ODEs. Advancing streaming function $\psi$ as the next

$v_1=\frac{\partial \psi }{\partial y},v_2=-\frac{\partial \psi }{\partial x}.(\mathrm{10a})$

and similarity transformations are

$\delta \left(x,y\right)=\sqrt{\frac{e}{{\nu }_f\left(1-\Omega t\right)}}y,\psi \left(x,y\right)=\sqrt{\frac{{\nu }_{f}e}{\left(1-\Omega t\right)}}xf\left(\delta \right),\theta \left(\delta \right)=\left(\Theta -{\Theta }_{\infty }\right){\left({\Theta }_w-{\Theta }_{\infty }\right)}^{-1}{h}_{\delta }\left(\Theta -{\Theta }_{\infty }\right)\left({\Theta }_w-{\Theta }_{\infty }\right).(11)$

into Eqs. 3–6. We get

$\left(\frac{1}{{\varphi }_{x_1}{\varphi }_{x_2}}+\frac{{\beta }_1}{{\varphi }_{x_1}}\right)f^{‴}+f{f}^{″}-{f^{\prime }}^2-\xi \left(f^{\prime }+\frac{\delta }{2}{f}^{″}\right)-\frac{{\beta }_1{\beta }_2}{{\varphi }_{x_2}}{f^{″}}^2{f}^{‴}-\Gamma f^{\prime }=0,(12)$

${\theta }^{″}\left(1+\gamma \theta +\frac{1}{{\varphi }_{x_4}}{P}_r{N}_r\right)+\gamma {{\theta }^{\prime }}^2+P_r\frac{{\varphi }_{x_3}}{{\varphi }_{x_4}}\left[f{\theta }^{\prime }-f^{\prime }\theta -\xi \left(\theta +\frac{\delta }{2}{\theta }^{\prime }\right)\right]=0.(13)$

$h^{″}+P_{r}Scf{h}^{\prime }+\frac{Nt}{Nb}{\theta }^{″}-Sc\varkappa h=0.(14)$

with

$f\left(0\right)=S,f^{\prime }\left(0\right)=1+\epsilon f^{″}\left(0\right),{\theta }^{\prime }\left(0\right)=-B_{\alpha }\left(1-\theta \left(0\right)\right)f^{\prime }\left(\delta \right)\to 0,f^{″}\left(\delta \right)\to 0,\theta \left(\delta \right)\to 0,h\left(\delta \right)\to 0as\delta \to \infty .\}(15)$

where ${\varphi }_{x_i}^{\prime }s$; $1\le i\le 4$ in Eqs. 12, 13 establishes the thermophysical characteristics of the Powell-Eyring nanofluid.

${\varphi }_{x1}=(1-{\varphi }_{Cu}{)}^{2.5}(1-{\varphi }_{TA}{)}^{2.5},{\mathrm{\varphi }}_{\mathrm{x}2}=(1-{\varphi }_{TA})\left\{\left(1-{\varphi }_{Cu}\right)+{\varphi }_1{\rho }_{p1}/{\rho }_f\right\}+{\varphi }_{TA\frac{{\rho }_{p2}}{{\rho }_f}},(16)$

${\varphi }_{x_3}=\left(1-{\varphi }_{TA}\right)\left\{\left(1-{\varphi }_{Cu}\right)+{\varphi }_{Cu}\frac{{\left(\rho C_p\right)}_{p_1}}{{\left(\rho C_p\right)}_f}\right\}+{\varphi }_{TA}\frac{{\left(\rho C_p\right)}_{p_2}}{{\left(\rho C_p\right)}_f},(17)$

${\varphi }_{x_4}=\left[\frac{\left({\kappa }_{p_2}+\left(m-1\right){\kappa }_{nf}\right)-\left(m-1\right){\varphi }_{Ti{O}_2}\left({\kappa }_{nf}-{\kappa }_{p_2}\right)}{\left({\kappa }_{p_2}+\left(m-1\right){\kappa }_{nf}\right)+{\varphi }_{Ti{O}_2}\left({\kappa }_{nf}-{\kappa }_{p_2}\right)}\right]\left[\frac{\left({\kappa }_{p_1}+\left(m-1\right){\kappa }_f\right)+{\varphi }_{Cu}\left({\kappa }_f-{\kappa }_{p_1}\right)}{\left({\kappa }_{p_1}+\left(m-1\right){\kappa }_f\right)-\left(m-1\right){\varphi }_{Cu}\left({\kappa }_f-{\kappa }_{p_1}\right)}\right].(18)$

Meticulous authentication is done on Eq. 3. Notation $\prime$ is used for the demonstration of derivatives concerning $\delta$. The parametric values were defined in Table 3.

TABLE 3

TABLE 3. Explanation of the entrenched control constraints.

It is noticed a variety of factors depend on the similarity variable $″\Omega ″$ and unsteadiness. Consequently, to acquire non-similar solutions for the suggested problematic computational results are processed for local similar considerations.

Drag force and nusselt quantity

The drag force $C_f$ together with a Nusselt amount $N{u}_x$ are the physical amounts of importance that dominate the light and can be confirmed as (Aziz et al., 2021)

$C_f=\frac{{\tau }_w}{{\rho }_f{U}_w^2},N{u}_x=\frac{x{q}_w}{k_f\left({\mathit{\Theta }}_w-{\mathit{\Theta }}_{\infty }\right)}(19)$

where ${\tau }_w$ and $q_w$ correspond to the heating flux revealed by

${\tau }_w={\left(\left({\mu }_{hnf}+\frac{1}{\stackrel{\sim }{\zeta }{\varrho }^{*}}\right)\frac{\partial v_1}{\partial y}-\frac{1}{6\stackrel{\sim }{\zeta }{\varrho }^{{*}^3}}{\left(\frac{\partial v_1}{\partial y}\right)}^3\right)}_{y=0},q_w=-k_{hnf}\left(1+\frac{16}{3}\frac{{\sigma }^{*}{T}_{\infty }^3}{{\kappa }^{*}{\nu }_f{\left(\rho C_p\right)}_f}\right){\left(\frac{\partial \Theta }{\partial y}\right)}_{y=0}.(20)$

Employing the dimensionless makeovers (11), one acquires

$C_{f}R{e}_x^{\frac{1}{2}}=\left[\left(\frac{1}{{\varphi }_{x_1}{\varphi }_{x_2}}+{\beta }_1\right)f^{″}\left(0\right)-\frac{{\beta }_1{\beta }_2}{3}{\left(f^{″}\left(0\right)\right)}^3\right],N{u}_{x}R{e}_x^{-\frac{1}{2}}=-\frac{k_{hnf}}{k_f}\left(1+N_r\right){\theta }^{\prime }\left(0\right).(21)$

Where $N{u}_x$ signifies Nusselt quantity and $C_f$ specify the skin resistance. $R{e}_x=\frac{u_{w}x}{{\nu }_f}$ signifies $R{e}_x=\frac{u_{w}x}{{\nu }_f}$ signifies local Reynolds amount based on $u_w\left(x\right)$.

Numerical implementation: Galerkin finite element method

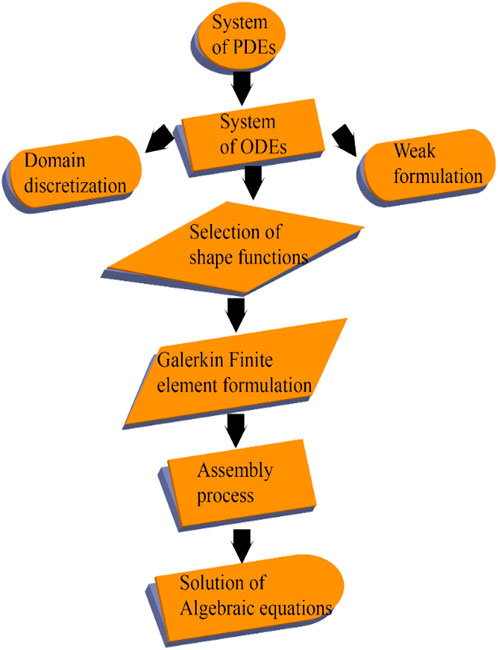
The relevant constraints of the present system were studied numerically using the finite element technique. The finite element approach is based on the partitioning of the desired domain into elements (finite). The FES (finite element scheme) is covered in this section. Figure 4 depicts the flow chart of the finite element method. This method has been employed in numerous computational fluid dynamics (CFD) problems; the assistances of employing this methodology are discussed further below. II- A Galerkin finite element manner (G-FEM) is utilized to determine the solutions of highly elliptic equations (Brewster, 1992) (non-linear). Using a finite element technique, the domain of the current exemplary is broken into small parts. G-FEM is used in a variety of applications, including electrical systems, solid mechanics, chemical processes, and fluid-related challenges. The phases of the G-FEM strategy are as next:

FIGURE 4

FIGURE 4. G-FEM flow diagram.

Phase-I. Weak form is derived from strong form (mentioned ODEs), and residuals are computed.

Phase -II. Shape functions are linearly taken, and G-FEM is used to generate a weak form.

Phase -III. The assembly method is used to build stiffness elements, and a global stiffness matrix is created.

Phase -IV. Using the Picard linearizing technique, an algebraic structure (non-linear equalities) is produced.

Phase -V. Employing the next halting conditions, algebraic equations are simulated using 10−5 (computational tolerance).

$\left|\frac{{\delta }_{i+1}-{\delta }_i}{{\delta }^i}\right|<{10}^{-5}.(23)$

Additionally, the Galerkin restricted constituent technique’s watercourse summary is represented in Figure 4.

Code authentication

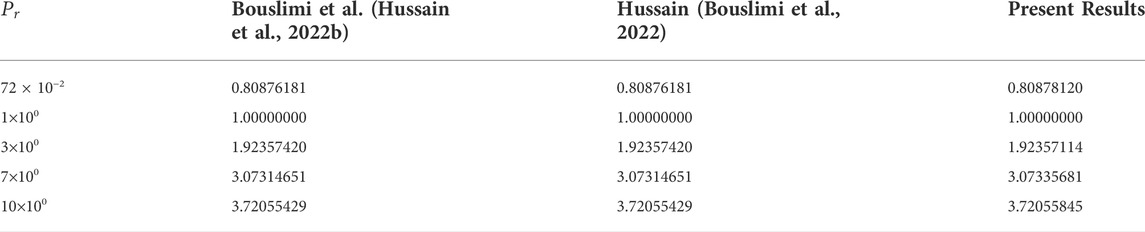
On the one hand, the validity of the computational technique was tested by comparing the current method’s performance to the available data on heat transfer rate in Refs. (Hussain et al., 2022b; Bouslimi et al., 2022). Table 3 demonstrates the consistent comparison found across the investigations. The current study’s provided results, on the other hand, are quite accurate.

Irreversibility analysis (second law of thermodynamics)

A crucial aspect that interests scientists and researchers is the reduction of energy resource waste. Therefore, these necessary outcomes for researchers are gained by enhancing the functionality of earlier systems. Systems’ entropy creation is examined in order to achieve energy irreversibility and reduce waste. Design is prearranged about entropy generation in NFs (Hussain, 2022)

$E_G=\frac{k_{hnf}}{{\Theta }_{\infty }^2}\left\{{\left(\frac{\partial \Theta }{\partial y}\right)}^2+\frac{16}{3}\frac{{\sigma }^{*}{\Theta }_{\infty }^3}{{\kappa }^{*}{\nu }_f{\left(\rho C_p\right)}_f}{\left(\frac{\partial \Theta }{\partial y}\right)}^2\right\}+\frac{{\mu }_{hnf}}{{\Theta }_{\infty }}{\left(\frac{\partial v_1}{\partial y}\right)}^2+\frac{{\mu }_{hnf}{v}_1^2}{k{\Theta }_{\infty }}(21)$

The irreversibility of thermal transport is represented by the leading term in the preceding equation, while the frictional and porous media effects are represented by the following terms. The nondimensional entropy establishment is prearranged by $N_G$ [(Jamshed and Nisar, 2021; Jamshed et al., 2022a)].

$N_G=\frac{{\Theta }_{\infty }^2{e}^2{E}_G}{k_f{\left({\Theta }_w-{\Theta }_{\infty }\right)}^2}.(22)$

Eq. 11 is utilized to obtain a dimensionless equation regarding entropy formation as follows,

$N_G=R_e\left[{\varphi }_4\left(1+N_r\right){{\theta }^{\prime }}^2+\frac{1}{{\varphi }_{x_1}}\frac{B_r}{\Lambda }\left({f^{″}}^2+\Gamma {f^{\prime }}^2\right)\right],(23)$

Here, $R_e$and $B_r$indicate Reynolds and Brinkmann quantities. $\Lambda$ signs nondimensional current gradient.

Quadratic regression assessment of frictional force and thermal gradients of the surface

Quadratic regression analysis (QRA) is the statistical procedure that was used to test the elements that influence the flow in the system one at a time. Technically, this process works with the single key aspect and tends to explore its significance over the flow by keeping the other constraints as constants. In this section, the features of frictional force and Nusselt quantity are examined under Quadratic regression analysis (QRA).

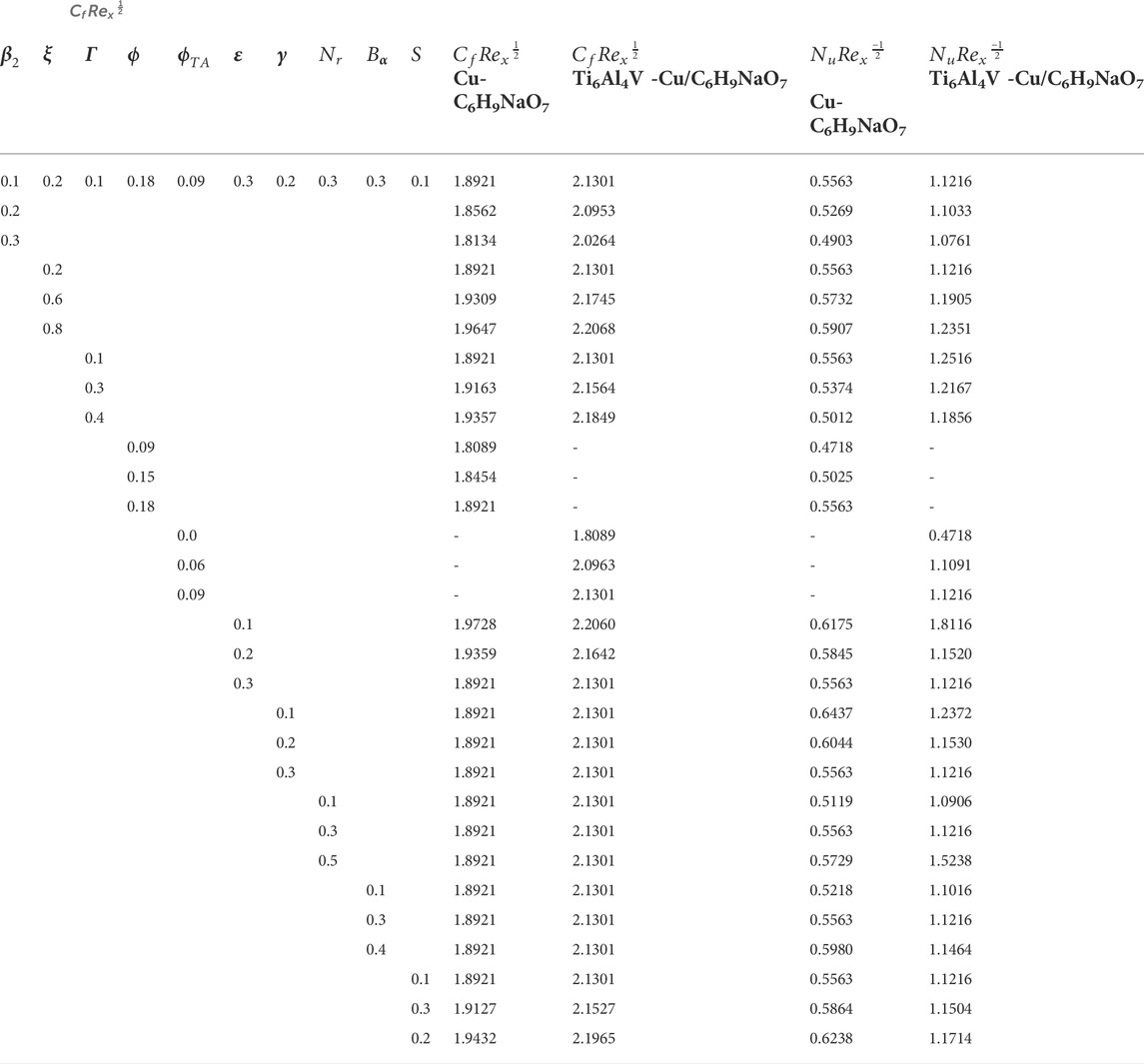
Regarding the frictional factor $f_x$ , after testing with 100 combinations of suction (S) and speed slippage constrain ($\epsilon$) between 0.2 and 1.1, it was noted that those constraints tend to resist frictional factors.

QRA for the predicted $C{f}_x$ owed to pressure influence $S$ and speed slippage $\epsilon$ variation is delivered by

${Cf}_{x\left(est\right)}={Cf}_x+h_{1}S+h_1\epsilon +h_3{S}^2+h_4{\epsilon }^2+h_{5}S\epsilon ,(24)$

Likewise, towards the Quadratic regression assessment of Nusselt quantity $N{u}_x$, time-dependent variant $\xi$ and radiative variable $N_r$ were tested under 100 consistent values were presented as

${Nu}_{x\left(est\right)}={Nu}_x+p_1\xi +p_1{N}_r+p_3{\xi }^2+p_4{\left(N_r\right)}^2+p_5\xi N_r,(25)$

with $h_1,h_2,h_3,h_4,h_5$ and are the factors of QRA to guide for the reduced $C{f}_x$ and $N{u}_x$, congruently.

Tables 4, 5 illustrate correspondences between the frictional factor $\left(C{f}_x\right)$ and the Nusselt quantity $\left(N{u}_x\right)$ under significant constraints for ${\beta }_1$ = $0.1$, ${\beta }_2$, = $0.3,$ , $\xi =0.2,\Gamma$ = $0.1$, $\varphi$ = $0.18$, ${\varphi }_{Cu}$ = $0.09$, $\epsilon$ = $0.3$, $\gamma$ = 0.2, $N_r$ = $0.3$, $B_{\alpha }$ = $0.3$, $S$ = $0.1$, $m=3$, $P_r$ = $6.5$, $R_e$ = $5$ and $B_r$ = $5$. The ideal relative error limits ${\sigma }_1$ was deduced by the relation ${\sigma }_1=\left|{Cf}_{x\left(est\right)}-{Cf}_x\right|/C{f}_x$, similarly, ${\sigma }_2=\left|{Nu}_{x\left(est\right)}-{Nu}_x\right|/N{u}_x$ is employed for the relative error limits ${\sigma }_2$. It can be evident that for the factors $S$ or $N_r$, both the frictional factor $\left(C{f}_x\right)$ and the Nusselt quantity $\left(N{u}_x\right)$ tends to reduce the higher values of influencing factors. Variations in the velocity slip clarify the dominance of speed slippage ε over the suction factor S in the shear stress manipulations.

TABLE 4

TABLE 4. Comparing of $-{\theta }^{\prime }\left(0\right)$ with $\mathit{Pr}$ when $\xi =0$, $\varphi =0$, ${\varphi }_{hnf}=0$, $\gamma =0$, $\epsilon =0$, $N_r=0$, $S=0$ and $B_{\alpha }\to \infty$.

TABLE 5

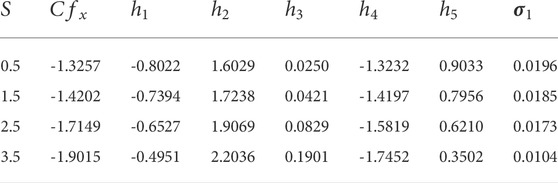
TABLE 5. Frictional factor $\left(C{f}_x\right)$ and ideal relative error bound $\left({\sigma }_1\right)$ for various values of suction ($S$) and speed slippage constraint ($\epsilon$).

Because of the thermal outcome, the thermal slippage constrain plays a vital role in the heat transference rate. The reduced frictionless force mechanisms hold an upper hand over the QRA technique with fast and better convergence when the optimal regression estimate was introduced to the process and the percentage difference tends to be nearly zero.

Outcomes and review

Results of the numerical procedure adapted for the parametrical studies were showcased and discussed in this section. Influence constraints like ${\beta }_1$, ${\beta }_2$, $\xi ,$ $\Gamma$, $\varphi$, $\epsilon$, $N_r$, $B_{\alpha }$, $S$, $\gamma$, $R_e$ and $B_r$ were worked over the crucial aspects of flow, thermal, entropy, and concentration dispersion in the system. Plots from 6(a)-11(b) for C₆H₉NaO₇ traditional PENF and Ti₆Al₄V-Cu/C₆H₉NaO₇ PEHNF tend to visually illustrate the outcomes and significant impact of such parameters.

Impact of powell-eyring parameter $\left({\mathit{\beta }}_{\mathbf{2}}\right)$

The illustration of the non-Newtonian Powell-Eyring fluid term (${\beta }_2$) on the model profiles (flow velocity, temperature, and entropy) against a rising stream term (${\beta }_2$) were depicted in Figures 5A,B,C. The velocity profile (Figure 5A) is decreased as the material term increases due to the material term shear being induced by infinite fluid viscosity. As a result, yield stress restricts the flow, resulting in a velocity decrement towards the infinite fluid stream. The heat propagation in the Powell-Eyring fluid heat propagation was boosted, as shown in Figure 5B. This effect is caused by the support of the stretching surface in overcoming the material yield stress dominance. In addition, temperature-dependent control fluid viscosity causes the temperature distribution to rise at various levels. As the Powell-Eyring effect is augmented, the molecular bond is disrupted, and the particles are allowed to move freely. As a result, Powell-Eyring ‘s term has a minimal rising effect Figure 5B. In Figure 5C, the entropy variation is plotted versus the Powell-Eyring term. Under the increment of ${\beta }_2$, the curves show different patterns. It illustrates an augmentation near the stretching wall, while a modest reduction is detected at a distance from it. The reason for this illustration is that when a large temperature gradient occurs at the surface, more entropy is produced, causing higher oscillations in nanoparticle mobility.

FIGURE 5

FIGURE 5. (A) $f^{\prime }\left(\delta \right)$, (B) $\theta \left(\delta \right)$, and (C) $N_G$ with diverse ${\beta }_2$ values.

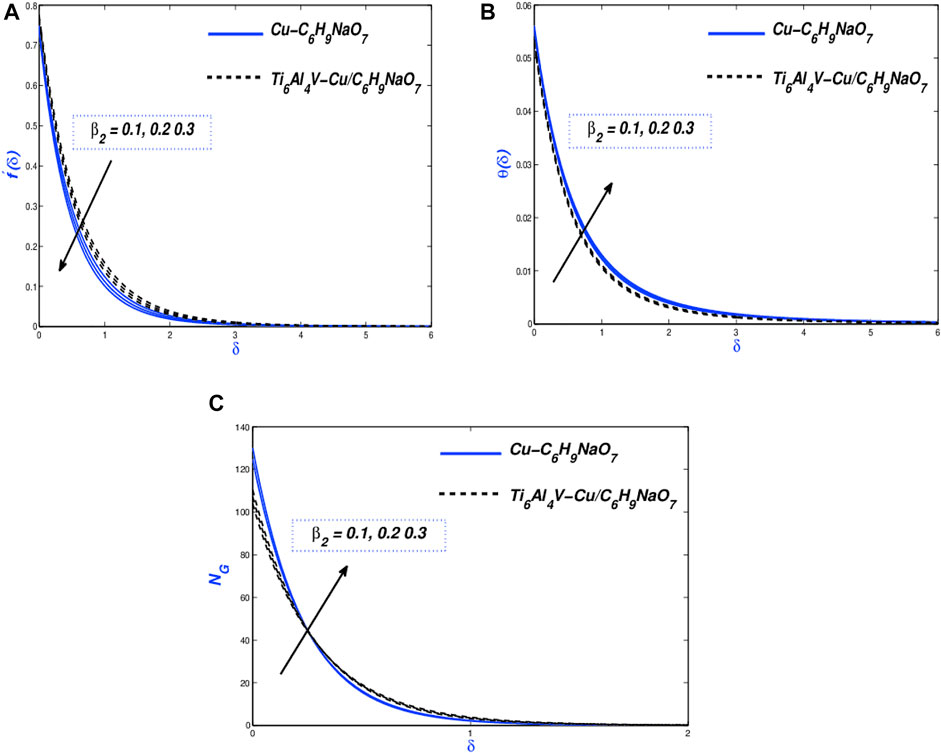
Impact of penetrable material factor ($\mathit{\Gamma }$)

The graphical results of permeability parameter $\left(\Gamma \right)$ against the flow, thermal, and entropy distribution of PENF (Cu-C₆H₉NaO₇) and PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) are presented in Figure 6A–C. Figure 6A shows the descending behavior of Powell-Eyring ‘s non-liquid flow curve through the porous medium, resulting in a plate surface while velocity is dragged. In fact, as the porosity effect enhances, the flow pores increase significantly, resulting in fewer nanoparticle collisions and lower heat generation. Viscous force controls buoyancy, thereby slowing the flow rate. The opposite effect is portrayed in Figure 6B. As shown in Figure 6B, increasing the porosity effect enhances the flow temperature. Figure 6C portrayed the entropy generated $N_G$ against $\left(\Gamma \right)$. This shows an increment near the surface, whereas a slight reduction is observed away from the surface. This result is caused by the large temperature difference near the surface, which causes more entropy to be produced. In industrial applications, the contribution of the porous medium permeability is to control the spin coating flow properties. Greater permeability, which can be depicted as bigger pore spaces provide better nanoparticle percolation. Besides, this effect (higher mobility) relates to reduced friction at the sheet surface.

FIGURE 6

FIGURE 6. (A) $f^{\prime }\left(\delta \right)$, (B) $\theta \left(\delta \right)$, and (C) $N_G$ with diverse $\Gamma$ values.

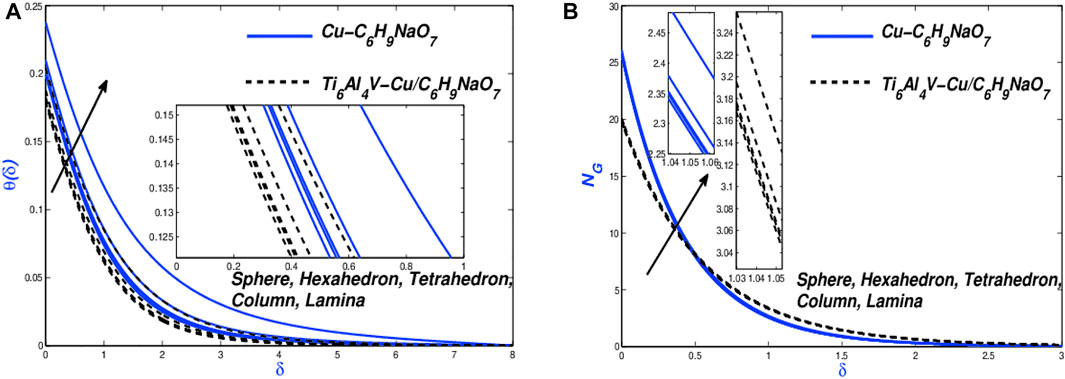
Diverse nanoparticles shaped parameter $\mathit{m}$ trace

Finally, the achieved outcome of the impact of the changes in various parameters and 5 shape nanoparticles by the names of a sphere, hexahedron, tetrahedron, column, and lamina on the profile of temperature and entropy have been analyzed and investigated in Figure 7A,B. In Figure 7A, the influence of the increment in nanoparticle shape parameter $\left(m\right)$ on the profile of temperature has been depicted, observations show that the temperature increment because of the ascent in shape factors. Physically the increment in thermal conductivity and thermal boundary-layer thickener are the main causes of such an outcome. Additionally compared to a sphere, hexahedron, tetrahedron, and column shape nanoparticles, lamina has engendered more enhancement in the temperature (Pasha et al., 2022). Besides, the function of temperature for lamina shape nanoparticles has been continuously more than that of a sphere, hexahedron, tetrahedron, column shape nanoparticles, the temperature range in PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) case is higher than that of PENF (Cu-C₆H₉NaO₇) case. The impact of increasing the nanoparticle shape parameter $\left(m\right)$ on the profile of entropy has been presented in Figure 7B, and measurements demonstrate that entropy increases as shape factors increase. It is worth noting that the PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) nanofluid phase had a higher initial entropy than the PENF (Cu-C₆H₉NaO₇) nanofluid phase. Later, when the shape factor is separated from the stream by a sufficient distance, it fiercely behaves in the other direction and influences the entropy rate in the stretching porous device, as observed.

FIGURE 7

FIGURE 7. (A) $\theta \left(\delta \right)$ and (B) $N_G$ with diverse $m$ values.

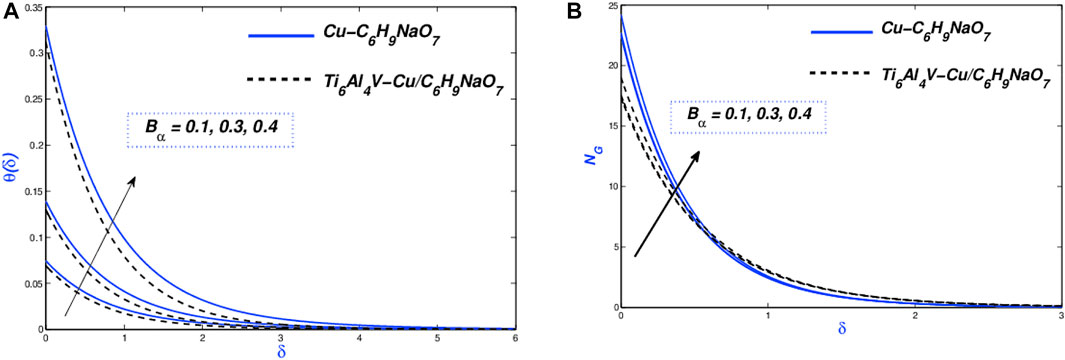
Impact of the biot number (${\mathit{B}}_{\mathit{\alpha }}$)

The visualization of the temperature profile against Biot numbers $\left(B_{\alpha }\right)$ for PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) and PENF (Cu-C₆H₉NaO₇) nanoparticles is displayed in Figure 8A. Overall, the enhancing $\left(B_{\alpha }\right)$ rises a temperature. The thermal thin state is regarding the low Biot number: The condition of uniform temperature region within the body (nano-polymer surface). Higher values of $B_{\alpha }$ indicate the thermal thick state in which non-uniform of temperature domains occur. The plot of $N_G$ against $\left(B_{\alpha }\right)$as displayed in Figure 8B discovers that the entropy profile is insensitive (only slight changes) with the increasing $\left(B_{\alpha }\right)$ at the stretching surface, compared to the position away from it. It is found that less enhancement in entropy profile is observed near the stretching walls. However, a decline in entropy generation is observed with the growth of $\left(B_{\alpha }\right).$

FIGURE 8

FIGURE 8. (A) $\theta \left(\Gamma \right)$ and (B) $N_G$ with diverse $B_{\alpha }$ values.

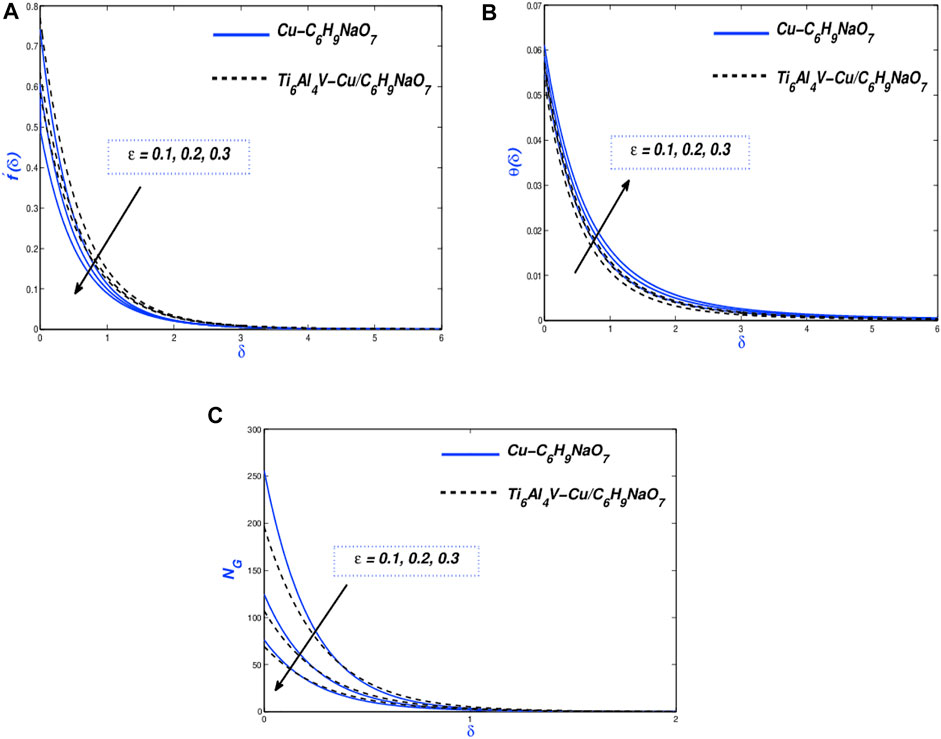
Impact of velocity slip variable ($\mathit{\epsilon }$)

The impacts of velocity slip parameters (ε) on the velocity field, temperature field, and entropy generation are plotted in Figure 9A–C, by choosing C₆H₉NaO₇ as the base fluid. The effect of the strain parameter is reported from the PENF (Cu-C₆H₉NaO₇) and PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) momentum distribution (Figure 9A). This parameter is obtained from the boundary conditions of the current model. The gradual increment of the velocity slip enhances the fluid viscosity, thus decreasing the fluid velocity. The higher concentration of slip velocity (ε) values lowers the thermal boundary layer thickness (Figure 9B), which the diminution of the profile is associated with the Williamson nanofluids. At the same time, the slip velocity parameter slows the collisions with molecular diffusion. When the concentration of nanoparticles is higher in a system, the system is associated with the instantaneous possessions of thermal convection, transmission, and kinematic viscosity. Figure 9C shows the plot of entropy generated ($N_G$) versus (ε). The plot of $N_G$ shows an effective reduction in this profile because the location is far from the plate. Due to the act of the velocity slip, entropy gradually decreases.

FIGURE 9

FIGURE 9. (A) $f^{\prime }\left(\delta \right)$, (B) $\theta \left(\delta \right),$ and (C) $N_G$ with diverse $\epsilon$ values.

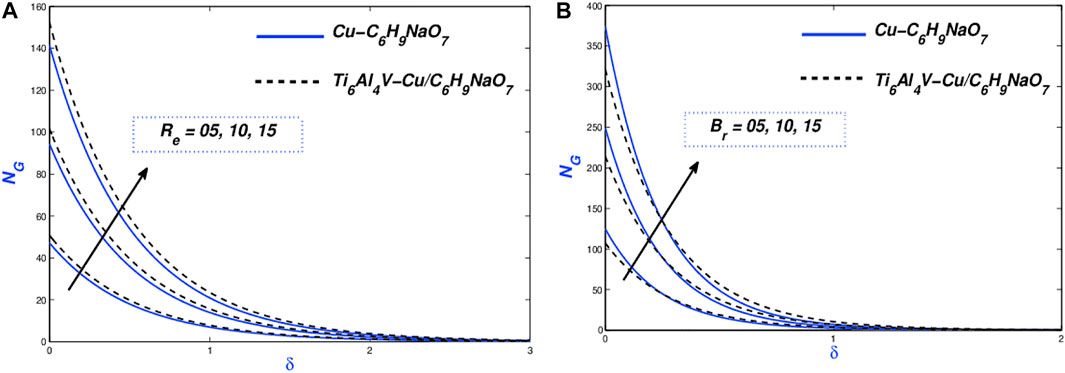
Entropy changes regarding Reynolds (${\mathit{R}}_{\mathit{e}}$) and brinkman numbers (${\mathit{B}}_{\mathit{r}}$)

The effect of the Reynolds number ($R_e$) on the entropy profile is shown in Figure 10A when both types of nanofluids are bounded by the stretching sheet. It is noted that the higher $R_e$ boosts the level of entropy that can be generated in the fluid system. Figure 10B shows the relationship between the entropy generation $N_G$ and the values of the Brinkman number ($B_r$), showing that increasing Brinkman number ($B_r$) enhances entropy generation. Brinkman number ($B_r$) defines the viscous influence of fluid behavior. As a consequence, high Brinkman numbers ($B_r$) denotes that fluid friction is the utmost factor of entropy generation. In both the Reynolds number and Brinkman number relationship, Cu-C₆H₉NaO₇ nanoparticles are found to have higher entropy level, compared to Ti₆Al₄V-Cu/C₆H₉NaO₇ nanoparticles.

FIGURE 10

FIGURE 10. $N_G$ with diverse (A) $R_e$ and (B) $B_r$ values.

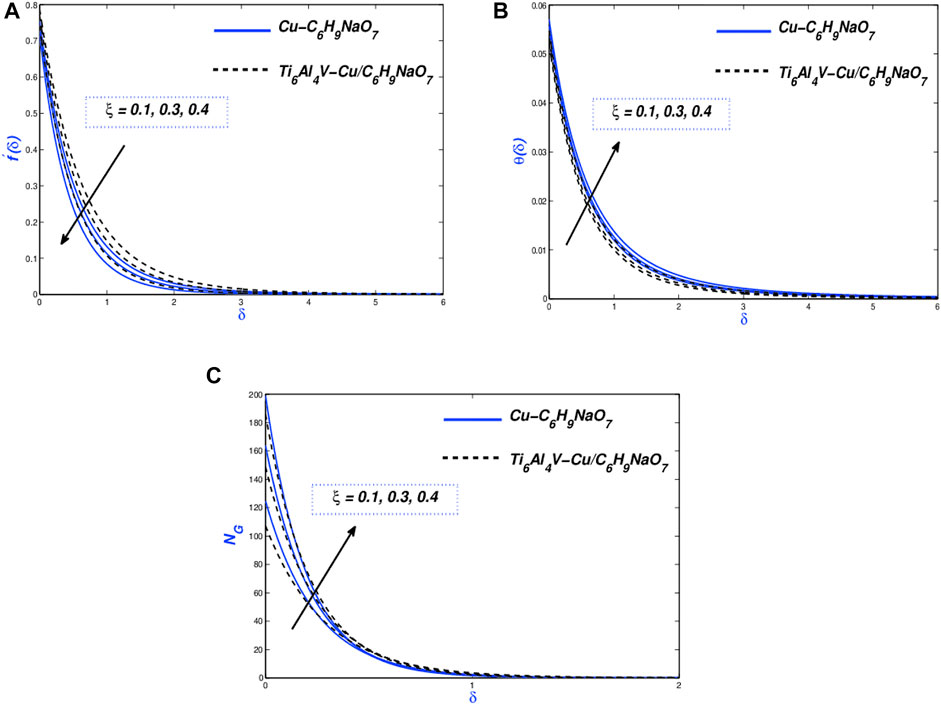
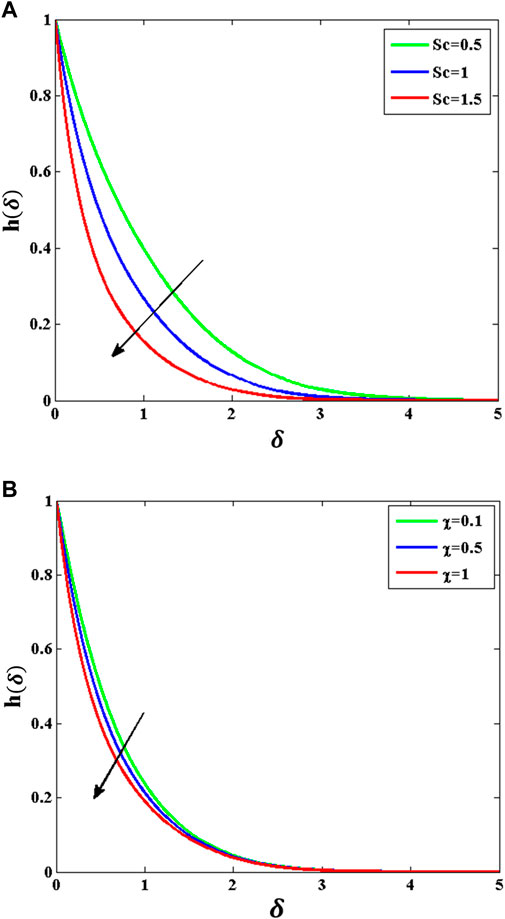
Concentration changes regarding schmidt number $(\mathit{S}\mathit{c}$) and chemical reaction parameter ($\mathit{\varkappa }$)

Figure 11A exhibits dispersal of concentration $h\left(\delta \right)$ towards the significant Schmidt number $(Sc$) which has a vital impact on it. Technically for the higher Schmidt number $(Sc$), the progress in the molecular diffusion tends to get reduced which restricts the mass transference in the system which can be visualized from Figure 11A. On other hand, Figure 11B discloses the influence of chemical reaction constraints on mass diffusion. The effective chemical reaction process exerts more mass in the system which makes the mass transference process harder and this may lead to the deceleration noted in Figure 11B for the higher values of chemical reaction constraint.

FIGURE 11

FIGURE 11. (A). Concentration $h\left(\delta \right)$ via $Sc$ (B). Concentration $h\left(\delta \right)$ via $\varkappa$.

Parametrical study on drag force $\left({\mathit{C}}_{\mathit{f}}\right)$ and nusselt number $\left({\mathit{N}}_{\mathit{u}}\right)$

The coefficients in the components of the flow and heat transmission are namely dragged force $\left(C_f\right)$ and Nusselt numbers $\left(N{u}_x\right)$, respectively. These parameters are tabulated in Tables 5, 6 showing their numerical values. Table 7 shows that a frictional force factor has non-uniform changes for both of the nanoparticles with an increasing $\epsilon$ and $\xi .$ Also, it is observed that the drag force coefficient upsurges with an increment of $\Gamma$ and $\varphi$. Besides, the reduction is remarked with rising $\epsilon$ for both the case of nanoparticles. Furthermore, the increasing values of $B_{\alpha }$ and $N_r$ have no impact on drag force coefficient for both PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) and PENF (Cu-C₆H₉NaO₇) nanoparticles. The Nusselt number enhances with an augmentation $\xi$, whereas an opposite function is remarked with the addition of ${\beta }_2,\gamma$ and $N_r$ for both PEHNF (Ti₆Al₄V-Cu/C₆H₉NaO₇) and PENF (Cu-C₆H₉NaO₇) nanoparticles (Figure 7).

TABLE 6

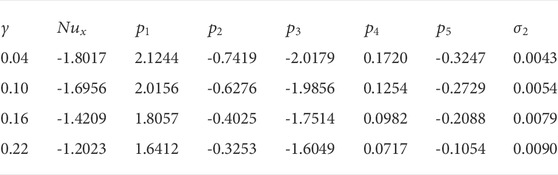
TABLE 6. Nusselt quantity $\left(N{u}_x\right)$ and ideal relative error bound $\left({\sigma }_2\right)$ for various values of time-dependent variant $\left(\xi \right)$ and radiative variable $(N_r$).

TABLE 7

TABLE 7. $C_{f}R{e}_x^{\frac{1}{2}}$ and $N_{u}R{e}_x^{\frac{-1}{2}}$ values at $P_r=6.5$, ${\beta }_1=0.01$ and $m=3$.

Concluding consequences and forthcoming course

In this mathematical investigation, the heat transmission in a Powell-Eyring hybrid nanofluid (PEHNF) model bounded by an expanding surface is investigated. This model is implemented in a thermal system, which is inspired by the modified Buongiorno’s NF prototype. The presence of nanoparticles such as Cu-C₆H₉NaO₇ and Ti₆Al₄V-Cu/C₆H₉NaO₇ nanoparticles are implemented in this model. The influences of porous media, thermal radiative flow, and variable thermal conductivity are taken into account in the mathematical model. Furthermore, the effect of the nanoparticles’ shape factors is determined, and their impacts can be observed in thermal and entropy aspects. The numerical solutions for the current mathematical model can be achieved by following these steps: 1) Apply similarity solution to convert PDEs to ODEs, and 2) solve the ODEs with Galerkin finite element plan. The primary outcomes from this investigation are listed for the profiles such as velocity, temperature, and concentration, together with the coefficients of drag force and Nusselt number. These outcomes are listed below:

1) Along the far stream, the velocity field is reduced for the upsurging Powell-Eyring fluid (${\beta }_2$), porosity $\left(\Gamma \right)$, volume fraction $\left(\varphi \right),$ and velocity slip $\left(\epsilon \right)$.

2) The temperature profile of Powell-Eyring fluid for both cases of Cu-C₆H₉NaO₇ (conventional nanofluid) and Ti₆Al₄V-Cu/C₆H₉NaO₇ (hybrid nanofluid) intensifies under the increment of $\gamma ,\Gamma ,\varphi$and $B_{\alpha }$.

3) The temperature distribution is affected by most of the physical quantities, which denotes that nanofluids have a high heat exchange rate. This property helps control the temperature during spin coating processes.

4) The entropy profile against Powell-Eyring fluid (${\beta }_2$), Porosity term $\left(\Gamma \right)$, volume fraction $\left(\varphi ,{\varphi }_{hnf}\right)$ and Biot number $\left(B_{\alpha }\right)$ and shape factor $\left(m\right)$ explore dual behavior.

5) The shape of nanoparticles is namely sphere, hexahedron, tetrahedron, lamina, and column. Among them, lamina has the greatest impact on the function of temperature and entropy.

6) The ability of the flow system toward the mass transference gets reduced as the molecular diffusivity drops significantly. This can be technically connected with the increase in Schmidt number versus the molecular diffusivity.

7) The remarkable change in frictional force factor for Ti₆Al₄V-Cu/C₆H₉NaO₇ and Cu-C₆H₉NaO₇ nanofluids can be seen, compared to the Nusselt number coefficient for the porosity and volume fraction.

Future track

These outcomes can be a guideline for the industry and technology, to choose the appropriate working fluid for improved productivity in the associated device or prototype Subsequently, this research work can be extended by applying the model of rotating disk flow considering ferromagnetic nanoparticles (Jamshed et al., 2021e; Pasha et al., 2022). The FEM could be applied to a variety of physical and technical challenges in the future (Jamshed et al., 2022b; Hussain et al., 2022b; Hussain et al., 2022a).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

WJ, MR and SS formulated the problem. WJ and RI solved the problem. WJ, MR, SS, RI, BS, RS, AP, ME, SH and ED computed and scrutinized the results. All the authors equally contributed in writing and proof reading of the paper. All authors reviewed the manuscript.

Acknowledgments

Authors are grateful to the Deanship of Scientific Research, Islamic University of Madinah, Ministry of Education, KSA for supporting this research work through research project grant under Research Group Program/1/804.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abouelregal, A. E., Ahmad, H., Nofal, T. A., and Abu-Zinadah, H. (2021). Thermo-viscoelastic fractional model of rotating nanobeams with variable thermal conductivity due to mechanical and thermal loads. Mod. Phys. Lett. B 35 (18), 2150297. doi:10.1142/s0217984921502973

CrossRef Full Text | Google Scholar

Adnan, , and Ashraf, W. (2022a). Numerical thermal featuring in γAl₂O₃-C₂H₆O₂ nanofluid under the influence of thermal radiation and convective heat condition by inducing novel effects of effective Prandtl number model (EPNM). Adv. Mech. Eng., 14(6), p.168781322211065, doi:10.1177/16878132221106577

CrossRef Full Text | Google Scholar

Adnan, , and Ashraf, W., (2022b). Thermal efficiency in hybrid (Al₂O₃-CuO/H₂O) and ternary hybrid nanofluids (Al₂O₃-CuO-Cu/H₂O) by considering the novel effects of imposed magnetic field and convective heat condition. Waves in Random and Complex Media, pp.1–16.

CrossRef Full Text | Google Scholar

Adnan, , Khan, U., Ahmed, N., Manzoor, R., and Mohyud-Din, S. T. (2021). Impacts of various shaped Cu-nanomaterial on the heat transfer over a bilateral stretchable surface: Numerical investigation. Adv. Mech. Eng. 13 (12), 168781402110674. doi:10.1177/16878140211067420

CrossRef Full Text | Google Scholar

Ahmad, S., Naveed Khan, M., and Nadeem, S. (2022). Unsteady three dimensional bioconvective flow of Maxwell nanofluid over an exponentially stretching sheet with variable thermal conductivity and chemical reaction. Int. J. Ambient Energy in press, 1–11. doi:10.1080/01430750.2022.2029765

CrossRef Full Text | Google Scholar

Ahmad, N., Mehmood, N., and Akgül, A. (2022). Applications of some new Krasnoselskii-type fixed-point results for generalized expansive and equiexpansive mappings. Adv. Contin. Discret. Model. 2022 (1), 30–19. doi:10.1186/s13662-022-03704-w

CrossRef Full Text | Google Scholar

Ahmed, K., Akbar, T., Muhammad, T., and Alghamdi, M. (2021). Heat transfer characteristics of MHD flow of Williamson nanofluid over an exponential permeable stretching curved surface with variable thermal conductivity. Case Stud. Therm. Eng. 28, 101544. doi:10.1016/j.csite.2021.101544

CrossRef Full Text | Google Scholar

Akgül, E. K., Akgül, A., Jamshed, W., Rehman, Z., Nisar, K. S., Alqahtani, M. S., et al. (2022). Analysis of respiratory mechanics models with different kernels. Open Phys. 20 (1), 609–615. doi:10.1515/phys-2022-0027

CrossRef Full Text | Google Scholar

Akram, J., Akbar, N. S., and Tripathi, D. (2022). Analysis of electroosmotic flow of silver-water nanofluid regulated by peristalsis using two different approaches for nanofluid. J. Comput. Sci. 62, 101696. doi:10.1016/j.jocs.2022.101696

CrossRef Full Text | Google Scholar

Al‐Chlaihawi, K. K., Alaydamee, H. H., Faisal, A. E., Al‐Farhany, K., and Alomari, M. A. (2022). Newtonian and non‐Newtonian nanofluids with entropy generation in conjugate natural convection of hybrid nanofluid‐porous enclosures: A review. Heat. Trans. 51 (2), 1725–1745. doi:10.1002/htj.22372

CrossRef Full Text | Google Scholar

Alharbi, K. A. M., Khan, U., Ahammad, N. A., Ullah, B., Wahab, H. A., Zaib, M., et al. (2022). Heat transport mechanism in Cu/water and (Cu–Al2O3)/water under the influence of thermophysical characteristics and non-linear thermal radiation for Blasius/Sakiadis models: Numerical investigation. J. Indian Chem. Soc. 99 (8), 100578. doi:10.1016/j.jics.2022.100578

CrossRef Full Text | Google Scholar

Ali, B., Hussain, S., Nie, Y., Hussein, A. K., and Habib, D. (2021). Finite element investigation of Dufour and Soret impacts on MHD rotating flow of Oldroyd-B nanofluid over a stretching sheet with double diffusion Cattaneo Christov heat flux model. Powder Technol. 377, 439–452. doi:10.1016/j.powtec.2020.09.008

CrossRef Full Text | Google Scholar

Alizadeh, R., Abad, J. M. N., Ameri, A., Mohebbi, M. R., Mehdizadeh, A., Zhao, D., et al. (2021). A machine learning approach to the prediction of transport and thermodynamic processes in multiphysics systems-heat transfer in a hybrid nanofluid flow in porous media. J. Taiwan Inst. Chem. Eng. 124, 290–306. doi:10.1016/j.jtice.2021.03.043

CrossRef Full Text | Google Scholar

Areekara, S., Mackolil, J., Mahanthesh, B., Mathew, A., and Rana, P. (2022). A study on nanoliquid flow with irregular heat source and realistic boundary conditions: A modified buongiorno model for biomedical applications. Z. Angew. Math. Mech. 102 (3), e202100167. doi:10.1002/zamm.202100167

CrossRef Full Text | Google Scholar

Ashraf, W., Junaid Anjum, H., and Khan, I. (2022a). Energy transformation and entropy investigation in the nanofluid composed by γ-nanomaterial over a permeable convective surface with solar thermal radiation: Numerical analysis. Front. Energy Res. 10, 507.

Google Scholar

Ashraf, W., Khan, I., Shemseldin, M. A., and Mousa, A. A. A. (2022b). Numerical energy storage efficiency of MWCNTs-propylene glycol by inducing thermal radiations and combined convection effects in the constitutive model. Front. Chem. 10, 879276. doi:10.3389/fchem.2022.879276

CrossRef Full Text | Google Scholar

Attia, N., Akgül, A., Seba, D., Nour, A., and Asad, J. (2022). A novel method for fractal-fractional differential equations. Alexandria Eng. J. 61 (12), 9733–9748. doi:10.1016/j.aej.2022.02.004

CrossRef Full Text | Google Scholar

Aziz, A., Jamshed, W., Aziz, T., Bahaidarah, H., and Ur Rehman, K. (2021). Entropy analysis of Powell–Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation. J. Therm. Anal. Calorim. 143 (2), 1331–1343. doi:10.1007/s10973-020-10210-2

CrossRef Full Text | Google Scholar

Banerjee, A., and Paul, D. (2021). Developments and applications of porous medium combustion: A recent review. Energy 221, 119868. doi:10.1016/j.energy.2021.119868

CrossRef Full Text | Google Scholar

Bhattacharyya, A., Sharma, R., Hussain, S. M., Chamkha, A. J., and Mamatha, E. (2022). A numerical and statistical approach to capture the flow characteristics of Maxwell hybrid nanofluid containing copper and graphene nanoparticles. Chin. J. Phys. 77, 1278–1290. doi:10.1016/j.cjph.2021.09.015

CrossRef Full Text | Google Scholar

Bilal, S., Shah, I. A., Akgül, A., Tekin, M. T., Botmart, T., Yahia, I. S., et al. (2022). A comprehensive mathematical structuring of magnetically effected Sutterby fluid flow immersed in dually stratified medium under boundary layer approximations over a linearly stretched surface. Alexandria Eng. J. 61 (12), 11889–11898. doi:10.1016/j.aej.2022.05.044

CrossRef Full Text | Google Scholar

Bilgili, F., Nathaniel, S. P., Kuşkaya, S., and Kassouri, Y. (2021). Environmental pollution and energy research and development: An environmental kuznets curve model through quantile simulation approach. Environ. Sci. Pollut. Res. 28 (38), 53712–53727. doi:10.1007/s11356-021-14506-0

CrossRef Full Text | Google Scholar

Bouslimi, J., Alkathiri, A. A., Alharbi, A. N., Jamshed, W., Eid, M. R., and Bouazizi, M. L. (2022). Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation. Nanotechnol. Rev. 11 (1), 1219–1236. doi:10.1515/ntrev-2022-0070

CrossRef Full Text | Google Scholar

Brewster, M. Q. (1992). Thermal radiative transfer and properties. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Chen, T. C., Hammid, A. T., Akbarov, A. N., Shariati, K., Dinari, M., and Ali, M. S. (2022). Estimating the physical properties of nanofluids using a connectionist intelligent model known as gaussian process regression approach. Int. J. Chem. Eng. 2022, 1–14. doi:10.1155/2022/1017341

CrossRef Full Text | Google Scholar

Chen, T. C., Majdi, H. S., Ismael, A. M., Pouresmi, J., Ahangari, D., and Noori, S. M. (2022). Insights into the estimation of the enhanced thermal conductivity of phase change material-containing oxide nanoparticles using gaussian process regression method. Int. J. Chem. Eng. 2022, 1–10. doi:10.1155/2022/7119336

CrossRef Full Text | Google Scholar

Cui, C., Meng, K., Xu, C., Liang, Z., Li, H., and Pei, H. (2021). Analytical solution for longitudinal vibration of a floating pile in saturated porous media based on a fictitious saturated soil pile model. Comput. Geotechnics 131, 103942. doi:10.1016/j.compgeo.2020.103942

CrossRef Full Text | Google Scholar

Devi, S. S. U., and Devi, S. A. (2016). Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 94 (5), 490–496. doi:10.1139/cjp-2015-0799

CrossRef Full Text | Google Scholar

Din, Z. U., Ali, A., De la Sen, M., and Zaman, G. (2022). Entropy generation from convective–radiative moving exponential porous fins with variable thermal conductivity and internal heat generations. Sci. Rep. 12 (1), 1791–1811. doi:10.1038/s41598-022-05507-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubey, V., and Sharma, A. K. (2022). A short review on hybrid nanofluids in machining processes. Adv. Mater. Process. Technol., 1–14. doi:10.1080/2374068x.2022.2087315

CrossRef Full Text | Google Scholar

El-Aziz, M. A., and Afify, A. A. (2019). Effect of Hall current on MHD slip flow of Casson nanofluid over a stretching sheet with zero nanoparticle mass flux. Thermophys. Aeromech. 26 (3), 429–443. doi:10.1134/s0869864319030119

CrossRef Full Text | Google Scholar

Hayat, T., and Nadeem, S. (2018). Flow of 3D Eyring-Powell fluid by utilizing Cattaneo-Christov heat flux model and chemical processes over an exponentially stretching surface. Results Phys. 8, 397–403. doi:10.1016/j.rinp.2017.12.038

CrossRef Full Text | Google Scholar

Hayat, T., Ashraf, B., Shehzad, S. A., and Abouelmagd, E. (2015). Three-dimensional flow of Eyring Powell nanofluid over an exponentially stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 25, 593–616. doi:10.1108/hff-05-2014-0118

CrossRef Full Text | Google Scholar

Hayat, T., Ullah, I., Alsaedi, A., and Farooq, M. (2017). MHD flow of Powell-Eyring nanofluid over a non-linear stretching sheet with variable thickness. Results Phys. 7, 189–196. doi:10.1016/j.rinp.2016.12.008

CrossRef Full Text | Google Scholar

Hobiny, A. D., and Abbas, I. (2022). The impacts of variable thermal conductivity in a semiconducting medium using finite element method. Case Stud. Therm. Eng. 31, 101773. doi:10.1016/j.csite.2022.101773

CrossRef Full Text | Google Scholar

Hussain, S. M., and Jamshed, W. (2021). A comparative entropy based analysis of tangent hyperbolic hybrid nanofluid flow: Implementing finite difference method. Int. Commun. Heat Mass Transf. 129, 105671. doi:10.1016/j.icheatmasstransfer.2021.105671

CrossRef Full Text | Google Scholar

Hussain, S. M., Jamshed, W., Safdar, R., Shahzad, F., Mohd Nasir, N. A. A., and Ullah, I. (2022). Chemical reaction and thermal characteristiecs of maxwell nanofluid flow-through solar collector as a potential solar energy cooling application: A modified Buongiorno's model. Energy & Environment, 0958305X221088113. doi:10.1177/0958305X221088113

CrossRef Full Text | Google Scholar

Hussain, S. M., Jamshed, W., Pasha, A. A., Adil, M., and Akram, M. (2022b). Galerkin finite element solution for electromagnetic radiative impact on viscid Williamson two-phase nanofluid flow via extendable surface. Int. Commun. Heat Mass Transf. 137, 106243. doi:10.1016/j.icheatmasstransfer.2022.106243

CrossRef Full Text | Google Scholar

Hussain, S. M. (2022). Irreversibility analysis of time-dependent magnetically driven flow of sutterby hybrid nanofluid: A thermal mathematical model. Waves in Random and Complex Media, 1. doi:10.1080/17455030.2022.2089369

CrossRef Full Text | Google Scholar

Jamei, M., Karbasi, M., Mosharaf-Dehkordi, M., Olumegbon, I. A., Abualigah, L., Said, Z., et al. (2022). Estimating the density of hybrid nanofluids for thermal energy application: Application of non-parametric and evolutionary polynomial regression data-intelligent techniques. Measurement 189, 110524. doi:10.1016/j.measurement.2021.110524

CrossRef Full Text | Google Scholar

Jamshed, W., and Nisar, K. S. (2021). Computational single‐phase comparative study of a Williamson nanofluid in a parabolic trough solar collector via the Keller box method. Int. J. Energy Res. 45 (7), 10696–10718. doi:10.1002/er.6554

CrossRef Full Text | Google Scholar

Jamshed, W., Prakash, M., Devi, S., Ibrahim, R. W., Shahzad, F., Nisar, K. S., et al. (2021). A brief comparative examination of tangent hyperbolic hybrid nanofluid through a extending surface: Numerical keller–box scheme. Sci. Rep. 11 (1), 24032–32. doi:10.1038/s41598-021-03392-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamshed, W., Nisar, K. S., Ibrahim, R. W., Shahzad, F., and Eid, M. R. (2021). Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. J. Mater. Res. Technol. 14, 985–1006. doi:10.1016/j.jmrt.2021.06.031

CrossRef Full Text | Google Scholar

Jamshed, W., Devi, S. U., and Nisar, K. S. (2021). Single phase based study of Ag-Cu/EO Williamson hybrid nanofluid flow over a stretching surface with shape factor. Phys. Screen. 96 (6), 065202. doi:10.1088/1402-4896/abecc0

CrossRef Full Text | Google Scholar

Jamshed, W., Şirin, C., Selimefendigil, F., Shamshuddin, M. D., Altowairqi, Y., and Eid, M. R. (2021). Thermal characterization of coolant Maxwell type nanofluid flowing in parabolic trough solar collector (PTSC) used inside solar powered ship application. Coatings 11 (12), 1552. doi:10.3390/coatings11121552

CrossRef Full Text | Google Scholar

Jamshed, W., Nasir, N. A. A. M., Isa, S. S. P. M., Safdar, R., Shahzad, F., Nisar, K. S., et al. (2021). Thermal growth in solar water pump using Prandtl–eyring hybrid nanofluid: A solar energy application. Sci. Rep. 11 (1), 18704–18721. doi:10.1038/s41598-021-98103-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamshed, W., Safdar, R., Rehman, Z., Lashin, M. M., Ehab, M., Moussa, M., et al. (2022). Computational technique of thermal comparative examination of Cu and Au nanoparticles suspended in sodium alginate as Sutterby nanofluid via extending PTSC surface. J. Appl. Biomaterials Funct. Mater. 20, 228080002211040. doi:10.1177/22808000221104004

CrossRef Full Text | Google Scholar

Jamshed, W., Eid, M. R., Safdar, R., Pasha, A. A., Isa, S. S. P. M., Adil, M., et al. (2022). Solar energy optimization in solar-HVAC using sutterby hybrid nanofluid with smoluchowski temperature conditions: A solar thermal application. Sci. Rep. 12, 11484. doi:10.1038/s41598-022-15685-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, U., Abdul Wahab, H., Syed, H., Ullah, B., and Adnan, (2022). Numerical study of heat transport mechanism in hybrid nanofluid [(Cu-Al2O3)/water] over a stretching/shrinking porous wedge. Proc. Institution Mech. Eng. Part E J. Process Mech. Eng., 095440892211079. doi:10.1177/09544089221107981

CrossRef Full Text | Google Scholar

Khan, U., Ahmed, N., and Khan, I. (2022). Heat transfer evaluation in MgZn₆Zr/C₈H₁₈ [(Magnesium-Zinc-Zirconium)/Engine oil] with non-linear solar thermal radiations and modified slip boundaries over 3-dimensional convectively heated surface. Front. Energy Res., 351.

Google Scholar

Khan, U., Adnan, Ullah, B., Abdul Wahab, H., Ullah, I., Almuqrin, M. A., and Khan, I. (2022). Comparative thermal transport mechanism in Cu-H₂O and Cu-Al2O₃/H₂O nanofluids: Numerical investigation. Waves in Random and Complex Media, 1–16. doi:10.1080/17455030.2021.2023783

CrossRef Full Text | Google Scholar

Kumbhakar, B., and Nandi, S. (2022). Unsteady MHD radiative-dissipative flow of Cu-Al₂O₃/H₂O hybrid nanofluid past a stretching sheet with slip and convective conditions: A regression analysis. Math. Comput. Simul. 194, 563–587. doi:10.1016/j.matcom.2021.12.018

CrossRef Full Text | Google Scholar

Kursus, M., Liew, P. J., Che Sidik, N. A., and Wang, J. (2022). Recent progress on the application of nanofluids and hybrid nanofluids in machining: A comprehensive review. Int. J. Adv. Manuf. Technol. 121, 1455–1481. doi:10.1007/s00170-022-09409-4

CrossRef Full Text | Google Scholar

Lee, J., King, S., Hassan, Y. A., Nguyen, T., Balestra, P., Schunert, S., et al. (2022). “Pronghorn porous media model validation with pressure drop measurements,” in Paper in the 19th international topical meeting on nuclear reactor thermal hydraulics (NURETH-19), Brussels, Belgium, March 6 - 11.

Google Scholar

Mabood, F., Rauf, A., Prasannakumara, B. C., Izadi, M., and Shehzad, S. A. (2021). Impacts of Stefan blowing and mass convention on flow of Maxwell nanofluid of variable thermal conductivity about a rotating disk. Chin. J. Phys. 71, 260–272. doi:10.1016/j.cjph.2021.03.003

CrossRef Full Text | Google Scholar

Mahanthesh, B., Shehzad, S. A., Mackolil, J., and Shashikumar, N. S. (2021). Heat transfer optimization of hybrid nanomaterial using modified buongiorno model: A sensitivity analysis. Int. J. Heat Mass Transf. 171, 121081. doi:10.1016/j.ijheatmasstransfer.2021.121081

CrossRef Full Text | Google Scholar

Mahdy, A. M. S., Lotfy, K., El-Bary, A., and Tayel, I. M. (2021). Variable thermal conductivity and hyperbolic two-temperature theory during magneto-photothermal theory of semiconductor induced by laser pulses. Eur. Phys. J. Plus 136 (6). doi:10.1140/epjp/s13360-021-01633-3

CrossRef Full Text | Google Scholar

Makinde, O. D., Mahanthesh, B., Gireesha, B. J., Shashikumar, N. S., Monaledi, R. L., and Tshehla, M. S. (2018). MHD nanofluid flow past a rotating disk with thermal radiation in the presence of aluminum and titanium alloy nanoparticles. Defect Diffusion Forum 384, 69. doi:10.4028/www.scientific.net/DDF.384.69

CrossRef Full Text | Google Scholar

Malik, M. Y., Khan, I., Hussain, A., and Salahuddin, T. (2015). Mixed convection flow of MHD eyring-powell nanofluid over a stretching sheet: A numerical study. AIP Adv. 5 (11), 117118. doi:10.1063/1.4935639

CrossRef Full Text | Google Scholar

Mandal, D. K., Biswas, N., Manna, N. K., Gayen, D. K., Gorla, R. S. R., and Chamkha, A. J. (2022). Thermo-fluidic transport process in a novel M-shaped cavity packed with non-Darcian porous medium and hybrid nanofluid: Application of artificial neural network (ANN). Phys. Fluids 34 (3), 033608. doi:10.1063/5.0082942

CrossRef Full Text | Google Scholar

Muneeshwaran, M., Srinivasan, G., Muthukumar, P., and Wang, C. C. (2021). Role of hybrid-nanofluid in heat transfer enhancement–A review. Int. Commun. Heat Mass Transf. 125, 105341. doi:10.1016/j.icheatmasstransfer.2021.105341

CrossRef Full Text | Google Scholar

Murtaza, R., Hussain, I., Rehman, Z., Khan, I., and Andualem, M. (2022). Thermal enhancement in Falkner–Skan flow of the nanofluid by considering molecular diameter and freezing temperature. Sci. Rep. 12 (1), 9415–9514. doi:10.1038/s41598-022-13423-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Nandi, S., Kumbhakar, B., and Seth, G. S. (2022). Quadratic regression analysis of unsteady MHD free convective and radiative–dissipative stagnation flow of hybrid nanofluid over an exponentially stretching surface under porous medium. Chin. J. Phys. 77, 2090–2105. doi:10.1016/j.cjph.2021.12.011

CrossRef Full Text | Google Scholar

Nandi, S., Kumbhakar, B., and Sarkar, S. (2022). MHD stagnation point flow of Fe₃O₄/Cu/Ag-CH₃OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. Int. Commun. Heat Mass Transf. 130, 105791. doi:10.1016/j.icheatmasstransfer.2021.105791

CrossRef Full Text | Google Scholar

Olabode, J. O., Idowu, A. S., Akolade, M. T., and Titiloye, E. O. (2021). Unsteady flow analysis of Maxwell fluid with temperature dependent variable properties and quadratic thermo-solutal convection influence. Partial Differ. Equations Appl. Math. 4, 100078. doi:10.1016/j.padiff.2021.100078

CrossRef Full Text | Google Scholar

Owhaib, W., and Al-Kouz, W. (2022). Three-dimensional numerical analysis of flow and heat transfer of bi-directional stretched nanofluid film exposed to an exponential heat generation using modified Buongiorno model. Sci. Rep. 12 (1). doi:10.1038/s41598-022-13351-6

CrossRef Full Text | Google Scholar

Owhaib, W., Basavarajappa, M., and Al-Kouz, W. (2021). Radiation effects on 3D rotating flow of Cu-water nanoliquid with viscous heating and prescribed heat flux using modified Buongiorno model. Sci. Rep. 11 (1). doi:10.1038/s41598-021-00107-x

CrossRef Full Text | Google Scholar

Parvin, S., Isa, S. S. P. M., Jamshed, W., Ibrahim, R. W., and Nisar, K. S. (2021). Numerical treatment of 2D-Magneto double-diffusive convection flow of a Maxwell nanofluid: Heat transport case study. Case Stud. Therm. Eng. 28, 101383. doi:10.1016/j.csite.2021.101383

CrossRef Full Text | Google Scholar

Pasha, A. A., Islam, N., Jamshed, W., Alam, M. I., Jameel, A. G. A., Juhany, K. A., et al. (2022). Statistical analysis of viscous hybridized nanofluid flowing via Galerkin finite element technique. Int. Commun. Heat Mass Transf. 137, 106244. doi:10.1016/j.icheatmasstransfer.2022.106244

CrossRef Full Text | Google Scholar

Qureshi, Z. A., Bilal, S., Khan, U., Akgül, A., Sultana, M., Botmart, T., et al. (2022). Mathematical analysis about influence of Lorentz force and interfacial nano layers on nanofluids flow through orthogonal porous surfaces with injection of SWCNTs. Alexandria Eng. J. 61 (12), 12925–12941. doi:10.1016/j.aej.2022.07.010

CrossRef Full Text | Google Scholar

Qureshi, M. A. (2022). Thermal capability and entropy optimization for Prandtl-Eyring hybrid nanofluid flow in solar aircraft implementation. Alexandria Eng. J. 61 (7), 5295–5307. doi:10.1016/j.aej.2021.10.051

CrossRef Full Text | Google Scholar

Rana, P., Mahanthesh, B., Mackolil, J., and Al-Kouz, W. (2021). Nanofluid flow past a vertical plate with nanoparticle aggregation kinematics, thermal slip and significant buoyancy force effects using modified Buongiorno model. Waves in Random and Complex Media, 1. doi:10.1080/17455030.2021.1977416

CrossRef Full Text | Google Scholar

Rashed, Z. Z., Alhazmi, M., and Ahmed, S. E. (2021). Non-homogenous nanofluid model for 3D convective flow in enclosures filled with hydrodynamically and thermally heterogeneous porous media. Alexandria Eng. J. 60 (3), 3119–3132. doi:10.1016/j.aej.2021.01.049

CrossRef Full Text | Google Scholar

Reddy, N. B., Poornima, T., and Sreenivasulu, P. (2014). Influence of variable thermal conductivity on MHD boundary layer slip flow of ethylene-glycol based Cu nanofluids over a stretching sheet with convective boundary condition. Int. J. Eng. Math. 2014, 905158. doi:10.1155/2014/905158

CrossRef Full Text | Google Scholar

Roşca, N. C., Roşca, A. V., Aly, E. H., and Pop, I. (2021). Flow and heat transfer past a stretching/shrinking sheet using modified buongiorno nanoliquid model. Mathematics 9 (23), 3047. doi:10.3390/math9233047

CrossRef Full Text | Google Scholar

Safdar, R., Jawad, M., Hussain, S., Imran, M., Akgül, A., and Jamshed, W. (2022). Thermal radiative mixed convection flow of MHD Maxwell nanofluid: Implementation of buongiorno's model. Chin. J. Phys. 77, 1465–1478. doi:10.1016/j.cjph.2021.11.022

CrossRef Full Text | Google Scholar

Saha, A., Manna, N. K., Ghosh, K., and Biswas, N. (2022). Analysis of geometrical shape impact on thermal management of practical fluids using square and circular cavities. Eur. Phys. J. Spec. Top. 231, 2509–2537. doi:10.1140/epjs/s11734-022-00593-8

CrossRef Full Text | Google Scholar

Said, Z., Sundar, L. S., Tiwari, A. K., Ali, H. M., Sheikholeslami, M., Bellos, E., et al. (2021). Recent advances on the fundamental physical phenomena behind stability, dynamic motion, thermophysical properties, heat transport, applications, and challenges of nanofluids.Phys. Rep. 946, 1–94. doi:10.1016/j.physrep.2021.07.002

CrossRef Full Text | Google Scholar

Said, Z., Sharma, P., Tiwari, A. K., Huang, Z., Bui, V. G., Hoang, A. T., et al. (2022). Application of novel framework based on ensemble boosted regression trees and Gaussian process regression in modelling thermal perfopHASErmance of small-scale Organic Rankine Cycle (ORC) using hybrid nanofluid. J. Clean. Prod. 360, 132194. doi:10.1016/j.jclepro.2022.132194

CrossRef Full Text | Google Scholar

Shahzad, F., Jamshed, W., Ibrahim, R. W., Sooppy Nisar, K., Qureshi, M. A., Hussain, S. M., et al. (2021). Comparative numerical study of thermal features analysis between Oldroyd-B copper and molybdenum disulfide nanoparticles in engine-oil-based nanofluids flow. Coatings 11 (10), 1196. doi:10.3390/coatings11101196

CrossRef Full Text | Google Scholar

Shahzad, F., Jamshed, W., DeviS, S. U., Safdar, R., Prakash, M., Ibrahim, R. W., et al. (2022). Raising thermal efficiency of solar water‐pump using Oldroyd‐B nanofluids' flow: An optimal thermal application. Energy Science & Engineering. doi:10.1002/ese3.1173

CrossRef Full Text | Google Scholar

Shahzad, F., Jamshed, W., Nisar, K. S., Nasir, N. A. A. M., Safdar, R., Abdel-Aty, A. H., et al. (2022). Thermal analysis for Al₂O₃–sodium alginate magnetized Jeffrey’s nanofluid flow past a stretching sheet embedded in a porous medium. Sci. Rep. 12 (1), 1. doi:10.1038/s41598-022-06983-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Shankaralingappa, B. M., Madhukesh, J. K., Sarris, I. E., Gireesha, B. J., and Prasannakumara, B. C. (2021). Influence of thermophoretic particle deposition on the 3D flow of sodium alginate-based Casson nanofluid over a stretching sheet. Micromachines 12 (12), 1474. doi:10.3390/mi12121474

PubMed Abstract | CrossRef Full Text | Google Scholar

Swain, K., Mahanthesh, B., and Mebarek‐Oudina, F. (2021). Heat transport and stagnation‐point flow of magnetized nanoliquid with variable thermal conductivity, Brownian moment, and thermophoresis aspects. Heat. Transf. 50 (1), 754–767. doi:10.1002/htj.21902

CrossRef Full Text | Google Scholar

Wang, X. Q., and Mujumdar, A. S. (2008). A review on nanofluids-part II: Experiments and applications. Braz. J. Chem. Eng. 25, 631–648. doi:10.1590/s0104-66322008000400002

CrossRef Full Text | Google Scholar

Xiong, Q., Altnji, S., Tayebi, T., Izadi, M., Hajjar, A., Sundén, B., et al. (2021). A comprehensive review on the application of hybrid nanofluids in solar energy collectors. Sustain. Energy Technol. Assessments 47, 101341. doi:10.1016/j.seta.2021.101341

CrossRef Full Text | Google Scholar

Xu, X., and Chen, S. (2017). Cattaneo–Christov heat flux model for heat transfer of Marangoni boundary layer flow in a copper–water nanofluid. Heat. Trans. Asian. Res. 46 (8), 1281–1293. doi:10.1002/htj.21273

CrossRef Full Text | Google Scholar

Zou, L., Hu, G., O'Grady, D., and Hu, R. (2022). Explicit modeling of pebble temperature in the porous-media model for pebble-bed reactors. Prog. Nucl. Energy 146, 104175. doi:10.1016/j.pnucene.2022.104175

CrossRef Full Text | Google Scholar