- 1Laboratory of Industrial and Information Technology (LTII), Faculty of Technology, University of Bejaia, Bejaia, Algeria
- 2Centre for Ocean Energy Research, Maynooth University, Maynooth, Kildare, Ireland
- 3Department of Electrical and Electronics Engineering, National Institute of Technology, Delhi, India
- 4Department of Electrical Engineering, Graphic Era (Deemed to be University), Dehradun, India
- 5Department of Electrical Engineering, College of Engineering, Taif University, Taif, Saudi Arabia
- 6Electrical Engineering Department, Faculty of Engineering, Aswan University, Aswan, Egypt
Many studies have been made on the double-fed induction generator wind turbine system (DFIG-WTS) in recent decades due to its power management capability, speed control operation, low converter cost, and minimized energy losses. In contrast, induction machine control is a more complex task because of its multivariable and nonlinear nature. In this work, a new robust nonlinear generalized predictive control (RNGPC) is developed to maximize the extracted energy from the wind without the use of aerodynamic torque measurements or an observer. The aim of the predictive control is to produce an anticipated impact by employing explicit knowledge of the present condition. By revisiting the cost function of the conventional nonlinear generalized predictive control (NGPC), which is based on Taylor series expansion, in that way, the resilience of the system is improved. An integral action is included in the nonlinear predictive controller. As a result, if the closed loop system is stable, the suggested controller totally eliminates the steady state error, even if unknown perturbations and mismatched parameters are present. The output locating error’s convergence to the source is utilized to show the locked system’s stability. Simulation results demonstrate and verify the efficiency, the good performance, and robustness of this proposed control technique.
Introduction
Due to its multiple advantages over other types of wind turbines, the doubly fed induction generator (DFIG) is becoming more common in wind generation. In general, the system is designed to operate in a 33% slip range. In this situation, the power requirement of the rotor converter is 25% of the maximum power of the wind turbine (Malik et al., 2021). The supply of the rotor by a converter, with variable frequency, makes it possible to separate the mechanical speed of the rotor from the frequency of the electrical grid. The control system for an induction machine is more complicated because it is a multivariable, nonlinear, and highly linked system. Techniques like voltage-field-oriented control and power-torque direct control, which use a linear conventional controller like the proportional-integral-predictive (PID) controller, have not always achieved flawless results (Tamalouzt et al., 2021).
An important number of nonlinear controls have appeared in the literature to ensure better performances control of a DFIG-based wind turbine. In Gupta and Shukla, 2022, an algorithm is proposed for the improvement of the DFIG by sharing between the converters (machine-side and grid-side) an optimal reactive power. An active disturbance rejection control with important robustness properties to design the current control law is developed in Beltran-Pulido et al., 2018 to enhance the ride-through low voltage. A coordinated super-twisting sliding mode control is investigated in Xiong et al., 2019 for grid synchronization and power optimization of the conversion system. A new exponential reaching law-based sliding mode control is proposed in Liu et al., 2018 for hastening the approaching process and lowering the system chattering phenomena. A multi-objective particle swarm optimization algorithm in studied in Aguilar et al., 2020, improving dynamic stability under electrical disturbances and thereby assisting the ride-through low voltage.
However, to ensure higher performances of the DFIG-based wind energy converter, it requires the utilization of advanced nonlinear controllers. Indeed, model predictive control (MPC) emerged in the late 70s (Mahmoud and Oyedeji, 2019), and since then, it has evolved into a variety of forms such as model algorithmic control, predictive functional control (Nosratabadi et al., 2019), generalized predictive control (Wang and Li, 2022), extended horizon adaptive control (Younesi et al., 2022), and robust model predictive control (Pradhan et al., 2022).
The MPC is a plant model-based feedback control approach that forecasts future plant outputs over a specific time horizon. These predictions are then utilized to choose the optimum control by solving an optimization problem while adhering to a set of constraints (Schwenzer et al., 2021). To deal with the features and control needs of specific types of variable-speed wind turbines, a revisiting variant of a recent adaptive second-order sliding algorithm is presented in Evangelista et al., 2016. Robust adaptive MPC constructed through linear matrix inequality and obtained estimation with a nonlinear observer is designed in Zhang et al., 2019a for the optimal, effective, and robust operation of the conversion system. Based on an analysis of the effectiveness of nonlinear MPC with a fixed weight coefficient under various wind conditions, a fuzzy regulator is created to update the weight coefficient of the cost function, and an improved multi-objective marine predator algorithm is proposed in Song et al., 2022b for optimization on energy capture and generator torque fluctuation. A DFIG wind system based on balanced and unbalanced network conditions is proposed using a universal and low-complexity model predictive direct power control (Zhang et al., 2019b). To handle high-voltage ride through, a P-Q coordination-based MPC is developed in Zhou et al., 2021. On the basis of intelligent scenario generation (ISG), a stochastic model predictive yaw control (SMPYC) technique is suggested in Song et al., 2022a. Here, the ISG approach is suggested to develop scenarios that define the uncertainty of wind direction prediction. Then, the yaw action is improved using the suggested scenario-based SMPYC to increase the energy capture effectiveness of WTs.
For mechanical sensorless control technology of induction machines, several solutions have been developed. A direct torque control associated with an artificial neural network was applied to a dual power induction motor (Tamalouzt et al., 2022). This strategy is carried out without a mechanical sensor using the extended Kalman filter as an observer. In order to ensure the estimation of the five-phase induction motor rotor speed, the authors, in Tamalouzt et al., 2022, performed two approaches: the first is based on the adaptive flux and speed observer, the second, on the other hand, is based on a model reference adaptive system estimator. A disturbance observer is constructed to estimate the aerodynamic torque in Ouari et al., 2014a, and a nonlinear generalized predictive control for wind energy conversion systems is proposed to achieve the controller’s robustness. For induction motor drives, a load torque observer based on a second-order sliding mode technique is suggested (El Daoudi et al., 2021).
The present study is aimed to design a robust controller in order to maximize the amount of energy taken from the wind without the use of an observer or aerodynamic torque measurements. The system’s robustness is increased by revising the cost function of the traditional nonlinear generalized predictive control (NGPC), which is based on Taylor series expansion. The nonlinear predictive controller includes an integral action. As a result, assuming that the closed loop system is stable, the proposed controller completely eliminates the steady state error, even in the presence of unknown disturbances and mismatched parameters. The convergence of the output locating error to the source is used to demonstrate the stability of the locked system. The validation of the trajectory following and perturbation rejection of the applied control using simulation results of the dynamic behavior of the researched system was performed under Matlab/Simulink.
The paper is organized as follows: in the Introduction section, the DFIG wind turbine system is described, and in the DFIG wind turbine system description and energy conversion section, the DFIG modeling is examined. The Proposed robust nonlinear generalized predictive control section develops the proposed structure controller. Finally, in the Simulation results Section, the simulation results are presented.
DFIG wind turbine system description and energy conversion
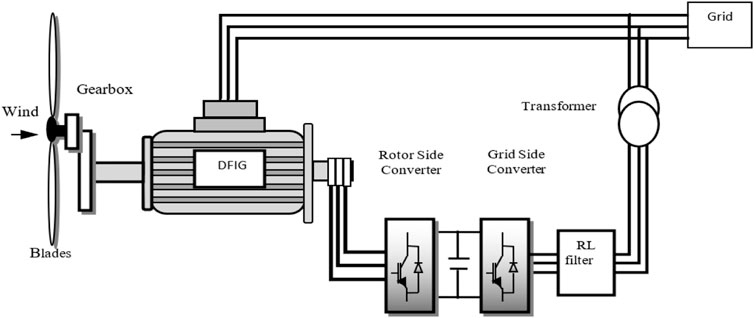
The DFIG wind turbine system is depicted schematically in Figure 1. The stator is directly linked to the three-phase power grid, while the rotor is fed at a variable frequency through the AC-DC-AC converter (Tamalouzt et al., 2021).
Modeling of the wind turbine
Only a small portion of the acquired wind energy can be converted by a wind turbine; thus, the wind’s mechanical power is calculated as follows (Soliman et al., 2021; Belkhier et al., 2022):
where
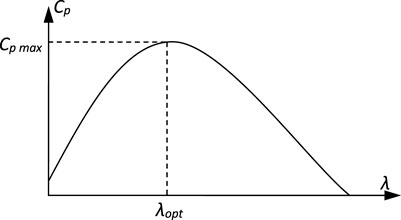
The blade’s tip-speed ratio
It is preferable for the generator to have a power characteristic that follows the maximum
The control block’s rotor speed and active power references were provided by maximum power point tracking (MPPT), while the reactive power was set to zero to obtain a unity power factor (Belkhier et al., 2022).
where Pgrid−refis the electrical grid's active power reference, Ωr−ref is the rotor speed reference, λopt is the optimal speed ratio, and Cp−max is the maximal power coefficient.
Model of the DFIG
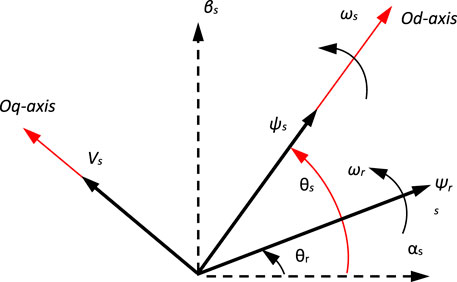
The DFIG model is commonly characterized by the following state equations in the synchronous orientation frame when the d-axis is aligned with the stator flow vector (Figure 3) and by disregarding the stator resistance (Pradhan et al., 2022):
where
In the Park transformation of the rotor quantities, the relative angle between the rotor and the Park reference (dq-axis) is used, which is determined as
The generator torque can then be expressed by
The following formulas give active and reactive stator powers:
The mechanical equation is
where
Proposed robust nonlinear generalized predictive control
The predictive control idea is to create an anticipatory effect using the explicit knowledge of the current state (Ouari et al., 2014b; Tamalouzt et al., 2022). The classical cost function is given as
In this study, a robust nonlinear generalized predictive control (RNGPC) is suggested to solve the robust control problem by revising the classical cost function (9). Consider the nonlinear multivariable system:
where x and
with
To solve the nonlinear optimization problem (11), the predicted term
Replacing (12) in (13)
Since
The Lie derivation of function h(x) along a vector field f(x) is indicated by
Invoking (15) and (16) with (14) yields
with
It is possible to write (17) in the following format:
where
If all output systems have the same relative degree r,
where
Replacing (19) in (11), the expression of the novel cost function will be
where
The condition that must be met in order to achieve optimal control is given by
According to (20) and (21), the optimal control is calculated as follows:
If n = m, then the optimal control can be indicated as follows:
where
An integral action is included in the nonlinear predictive controller (23). As a result, the suggested controller completely eliminates the steady state error even in the presence of unknown perturbations.
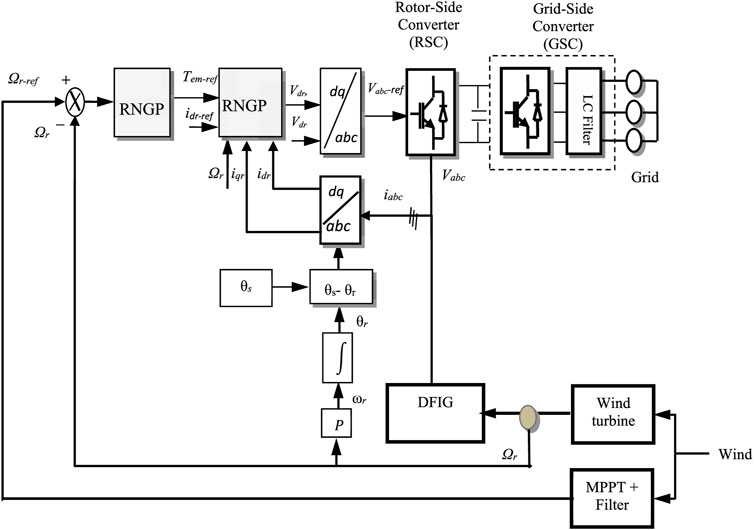
The control system’s proposed topology consists of two loops: an inner loop that controls torque and direct current and an outside loop that controls DFIG speed (Figure 4). The rotor speed reference is specified in (4). To reduce the control effort, the reference speed signal is passed via a second-order linear filter, which is provided by
where wn = 5 and
Predictive control of electromagnetic torque and current (inner loop)
The electromagnetic torque reference is calculated from the speed controller (outer loop), and to keep the DFIG reactive power at zero, the d-axis rotor current reference is determined. From (5), the electrical equations are written in the matrix form as follows:
with
The following are the outputs that will be regulated in the inner loop:
The relative degrees
with
Thus, as follows, the predicted term is expanded into a second-order Taylor series expansion:
where
where
where
Predictive control of the speed (outer loop)
The DFIG’s mechanical dynamics are given by the equation below:
where
We do not consider the aerodynamic torque in the mechanical Equation 8. The relative degree of the outputs
where
A second-order Taylor series expansion is used to expand the expected term
where
Replacing (32) in (23), the optimal control is calculated as
where
Closed-loop system stability
The convergence of the output tracking error to the origin can be used to demonstrate the closed-loop system’s stability. Substituting control law (33) into Equation 31 yields
where Kp is the proportional gain, Ki is the integral gain, and Kd is the derivative gain.
As a result of (34), the closed loop system’s characteristic polynomial equation is given as
Computing the solutions of Equation 35 may be used to determine the stability condition that is given as follows:
The true parts of the roots (36) are positive because the predicted time T is positive can be proven to be negative.
Simulation results
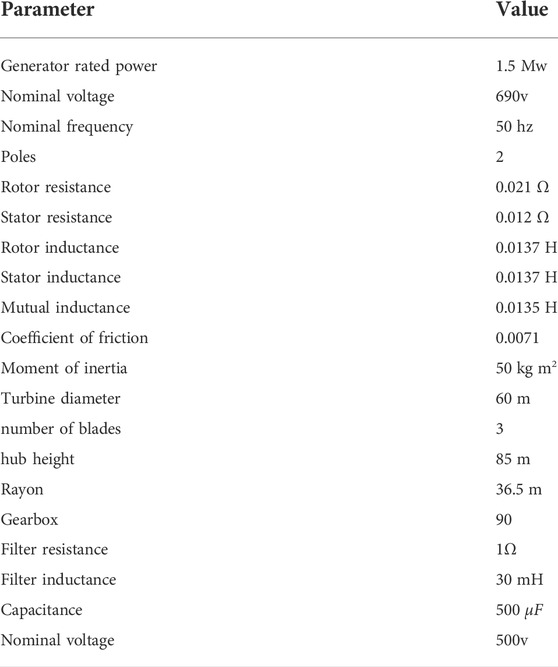
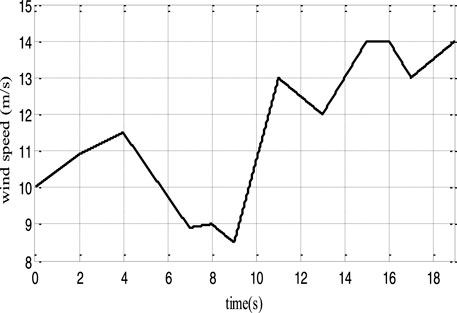
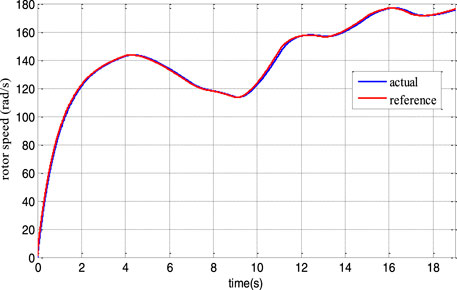
The operation performance of the DFIG wind system and control scheme has been investigated using Matlab/Simulink software. Table 1 lists the system’s parameters. The prediction horizon is set to Tp1 = 0.5 ms (inner loop) and Tp2 = 5 ms (outer loop). Figure 5 depicts the wind speed profile utilized in the simulation.
Reference tracking test performance
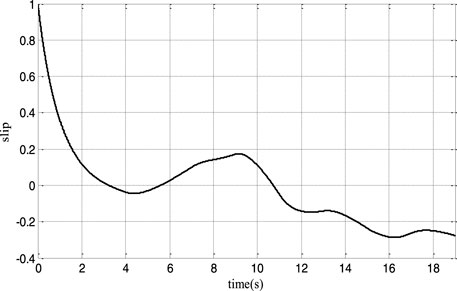
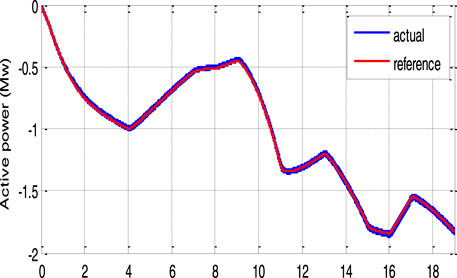
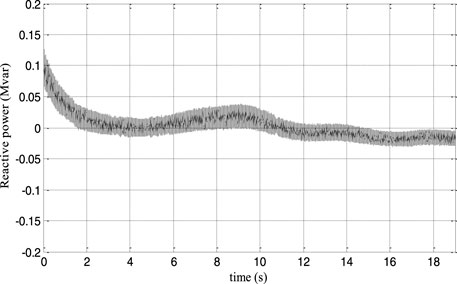
Figures 6, 7 show that the rotor speed and electromagnetic torque follow their references correctly and with good performance. Figure 8 depicts the DFIG slip’s'. As a consequence, in Figure 9, the DFIG active power flawlessly tracks its reference to enhance the conversion efficiency. From Figure 10, it can be noticed that the DFIG reactive power is kept at zero, which helps to adjust for the grid power factor. The rotor voltage-current at sub-synchronous (s > 0), synchronous (s = 0), and hyper-synchronous modes (s < 0) is plotted in Figure 11. These results clearly show that the proposed RNGPC algorithm provides great performance in both steady state and dynamic modes.
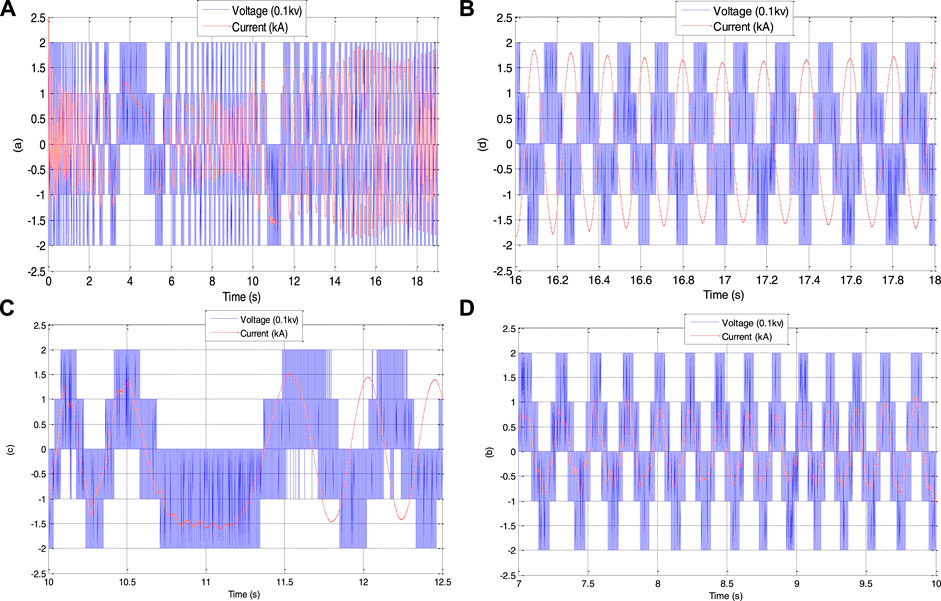
FIGURE 11. (A) Rotor voltage and current, (B) sub-synchronous mode, (C) synchronous mode, and (D) super-synchronous mode.
Robustness under DFIG’s parameter and prediction horizon variations
The values for the parameter variations included in the DFIG model are as follows: 10% in the coefficient of friction at t = 7s and 25% in the rotor resistance at t = 10s. This test is also used to assess the controller’s performance when the prediction horizon is changed. Only the outer loop Tp2 prediction horizon is lowered from 15 ms to 1.5 ms. These variations are not taken into account in the controller.
Figures 12, 13 show that despite the DFIG’s parameter fluctuation, the system response converges to the reference values. Indeed, the speed and the electromagnetic torque track perfectly their references. From Figures 14, 15, the control effort is limited by the speed filter; thus, a smaller prediction horizon results in faster disturbance rejection.
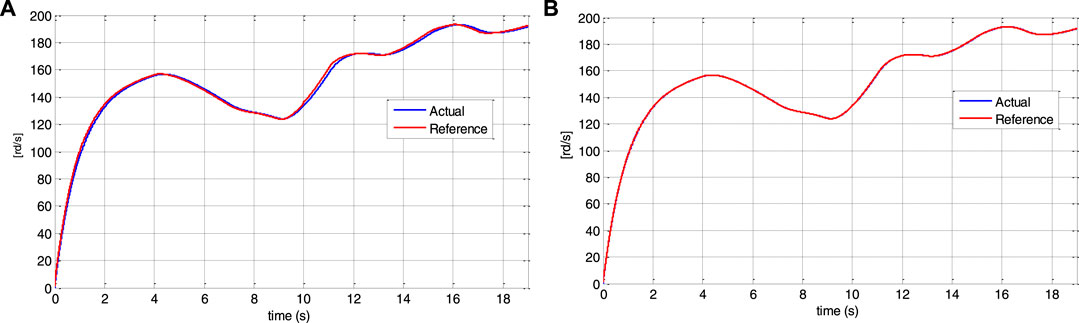
FIGURE 12. Speed tracking underprediction horizon change: (A) for Tp2 = 15 ms and (B) for Tp2 = 1.5 ms.
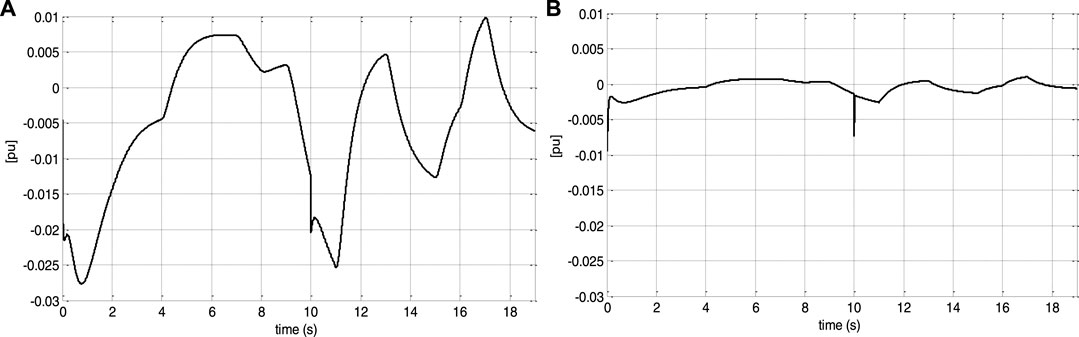
FIGURE 13. Speed tracking error under prediction horizon change: (A) for Tp2 = 15 ms and (B) for Tp2 = 1 ms.
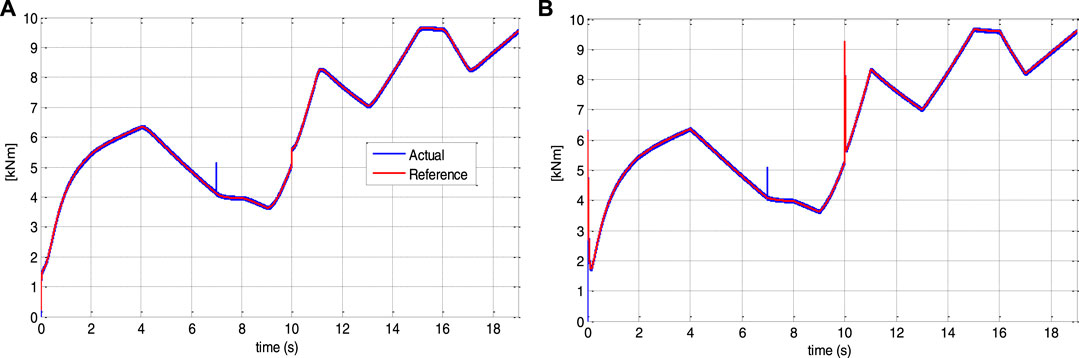
FIGURE 14. Electromagnetic torque tracking underprediction horizon change: (A) for Tp2 = 15 ms and (B) for Tp2 = 1.5 ms.
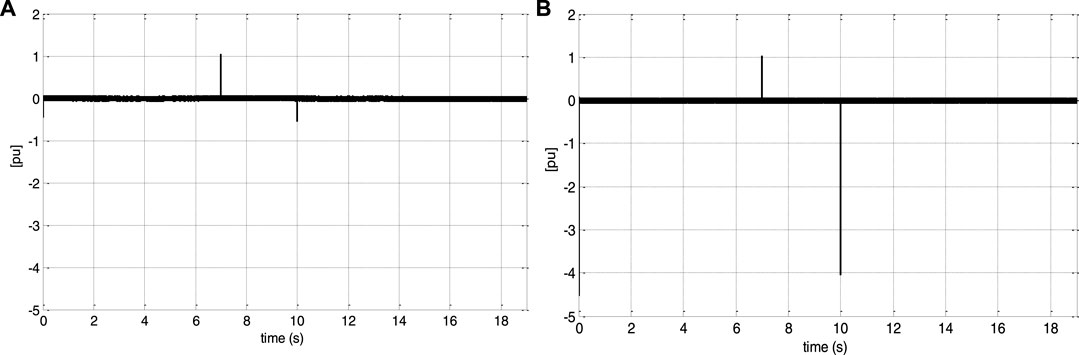
FIGURE 15. Electromagnetic torque tracking error underprediction horizon change: (A) for Tp2 = 15 ms and (B) for Tp2 = 1.5 ms.
Conclusion
A robust nonlinear generalized predictive controller for a DFIG wind turbine system has been devised in this study. A novel finite horizon cost function is introduced into the control law to ensure robustness against aerodynamic torque and parameter fluctuations without the necessity for an aerodynamic torque observer. The active power delivered to the grid varies with wind speed and follows the optimal wind power precisely. The simulation results show that the control architecture is resistant to unknown aerodynamic torques. This supports the suggested control’s efficiency and dependability in tracking the projected references. The RNGPC’s efficacy and resilience are confirmed by simulation results under a variety of operating conditions and DFIG parameter variations.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
References
Aguilar, M. E. B., Coury, D. V., Reginatto, R., and Monaro, R. M. (2020). Multi-objective PSO applied to PI control of DFIG wind turbine under electrical fault conditions. Electr. Power Syst. Res. 180, 106081. doi:10.1016/j.epsr.2019.106081
Belkhier, Y., Achour, A., Ullah, N., and Shaw, R. N. (2022). Modified passivity-based current controller design of permanent magnet synchronous generator for wind conversion system. Int. J. Model. Simul. 42 (2), 192–202. doi:10.1080/02286203.2020.1858226
Beltran-Pulido, A., Cortes-Romero, J., and Coral-Enriquez, H. (2018). Robust active disturbance rejection control for LVRT capability enhancement of DFIG-based wind turbines. Control Eng. Pract. 77, 174–189. doi:10.1016/j.conengprac.2018.06.001
El Daoudi, S., Lazrak, L., El Ouanjli, N., and Ait Lafkih, M. (2021). Applying sliding mode technique for the nonlinear DTC-SPWM control strategy of sensorless squirrel cage asynchronous motor. Int. J. Dyn. Control 9 (4), 1633–1644. doi:10.1007/s40435-021-00758-8
Evangelista, C. A., Pisano, A., Puleston, P., and Usai, E. (2016). Receding horizon adaptive second-order sliding mode control for doubly-fed induction generator based wind turbine. IEEE Trans. Control Syst. Technol. 25 (1), 73–84. doi:10.1109/tcst.2016.2540539
Gupta, S., and Shukla, A. (2022). Improved dynamic modelling of DFIG driven wind turbine with algorithm for optimal sharing of reactive power between converters. Sustain. Energy Technol. Assessments 51, 101961. doi:10.1016/j.seta.2022.101961
Liu, Y., Wang, Z., Xiong, L., Wang, J., Jiang, X., Bai, G., et al. (2018). DFIG wind turbine sliding mode control with exponential reaching law under variable wind speed. Int. J. Electr. Power & Energy Syst. 96, 253–260. doi:10.1016/j.ijepes.2017.10.018
Mahmoud, M. S., and Oyedeji, M. O. (2019). Adaptive and predictive control strategies for wind turbine systems: A survey. IEEE/CAA J. Autom. Sin. 6 (2), 364–378. doi:10.1109/jas.2019.1911375
Malik, M. Z., Baloch, M. H., Gul, M., Kaloi, G. S., Chauhdary, S. T., and Memon, A. A. (2021). A research on conventional and modern algorithms for maximum power extraction from wind energy conversion system: A review. Environ. Sci. Pollut. Res. 28 (5), 5020–5035. doi:10.1007/s11356-020-11558-6
Nosratabadi, S. M., Bornapour, M., and Gharaei, M. A. (2019). Grasshopper optimization algorithm for optimal load frequency control considering predictive functional modified PID controller in restructured multi-resource multi-area power system with redox flow battery units. Control Eng. Pract. 89, 204–227. doi:10.1016/j.conengprac.2019.06.002
Ouari, K., Ouhrouche, M., Rekioua, T., and Nabil, T. (2014). Nonlinear predictive control of wind energy conversion system using DFIG with aerodynamic torque observer. J. Electr. Eng. 65 (6), 333–341. doi:10.2478/jee-2014-0055
Ouari, K., Rekioua, T., and Ouhrouche, M. (2014). Real time simulation of nonlinear generalized predictive control for wind energy conversion system with nonlinear observer. ISA Trans. 53 (1), 76–84. doi:10.1016/j.isatra.2013.08.004
Pradhan, P. P., Subudhi, B., and Ghosh, A. (2022). A new optimal model predictive control scheme for a wind energy conversion system. Int. J. Numer. Model. 35 (3), e2976. doi:10.1002/jnm.2976
Schwenzer, M., Ay, M., Bergs, T., and Abel, D. (2021). Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 117 (5), 1327–1349. doi:10.1007/s00170-021-07682-3
Soliman, M. S., Belkhier, Y., Ullah, N., Achour, A., Alharbi, Y. M., Al Alahmadi, A. A., et al. (2021). Supervisory energy management of a hybrid battery/PV/tidal/wind sources integrated in DC-microgrid energy storage system. Energy Rep. 7, 7728–7740. doi:10.1016/j.egyr.2021.11.056
Song, D., Li, Z., Wang, L., Jin, F., Huang, C., Xia, E., et al. (2022a). Energy capture efficiency enhancement of wind turbines via stochastic model predictive yaw control based on intelligent scenarios generation. Appl. Energy 312 (2022), 118773. doi:10.1016/j.apenergy.2022.118773
Song, D., Tu, Y., Wang, L., Jin, F., Li, Z., Huang, C., et al. (2022b). Coordinated optimization on energy capture and torque fluctuation of wind turbines via variable weight NMPC with fuzzy regulator. Appl. Energy 312 (2022), 118821. doi:10.1016/j.apenergy.2022.118821
Tamalouzt, S., Belkhier, Y., Sahri, Y., Bajaj, M., Ullah, N., Chowdhury, M., et al. (2021). Enhanced direct reactive power control-based multi-level inverter for DFIG wind system under variable speeds. Sustainability 13 (16), 9060. doi:10.3390/su13169060
Tamalouzt, S., Belkhier, Y., Sahri, Y., Ullah, N., Shaw, R.N., and Bajaj, N. (2022). New direct reactive power control based fuzzy and modulated hysteresis method for micro-grid applications under real wind speed, Energy Sources, Part A: Recovery, Utilization, and Environmental Effects. 44:2, 4862–4887. doi:10.1080/15567036.2022.2081741
Wang, H., and Li, Z. S. (2022). Multi-Area load frequency control in power system integrated with wind farms using fuzzy generalized predictive control method. IEEE Trans. Reliab., 1–11. doi:10.1109/tr.2022.3177045
Xiong, L., Li, P., Wu, F., Ma, M., Khan, M. W., and Wang, J. (2019). A coordinated high-order sliding mode control of DFIG wind turbine for power optimization and grid synchronization. Int. J. Electr. Power & Energy Syst. 105, 679–689. doi:10.1016/j.ijepes.2018.09.008
Younesi, A., Tohidi, S., and Feyzi, M. R. (2022). An improved long‐horizon model predictive control for DFIG in WECS with variable sampling‐time. IET Renew. Power Gen. 16 (3), 517–531. doi:10.1049/rpg2.12357
Zhang, H., Hao, J., Wu, C., Li, Y., and Sahab, A. (2019). A novel LMI-based robust adaptive model predictive control for DFIG-based wind energy conversion system. Syst. Sci. Control Eng. 7 (1), 311–320. doi:10.1080/21642583.2019.1663291
Zhang, Y., Jiao, J., Xu, D., Jiang, D., Wang, Z., and Tong, C. (2019). Model predictive direct power control of doubly fed induction generators under balanced and unbalanced network conditions. IEEE Trans. Ind. Appl. 56 (1), 771–786. doi:10.1109/tia.2019.2947396
Zhou, C., Wang, Z., Xin, H., and Ju, P. (2021). A PQ coordination based model predictive control for dfig high-voltage ride through. IEEE Trans. Energy Convers. 37, 254–263. doi:10.1109/tec.2021.3088464
Nomenclature
ΩtΩr Turbine, generator speed (rd/s)
Tt,Tr Aerodynamic and generator torque(N.m)
Ωr-ref Reference generator speed
G Gear ratio
Pgrid -ref Reference grid active power (W)
η System (wind turbine + DFIG) efficiency
Pr, Qr Active and reactive rotor power (W,Var)
Vs Stator voltages (v)
Rr, Lr Per-phase rotor resistance and self-inductance
M, P Mutual inductance, number of pole pairs
J, fr Moment of inertia, coefficient of friction
s,σ Generator slip and dispersion ratio
Tp Predictive time
Keywords: DFIG wind turbine systems, robust generalized predictive control, doubly fed induction generator, wind, controller
Citation: Ouari K, Belkhier Y, Djouadi H, Kasri A, Bajaj M, Alsharef M, Elattar EE and Kamel S (2022) Improved nonlinear generalized model predictive control for robustness and power enhancement of a DFIG-based wind energy converter. Front. Energy Res. 10:996206. doi: 10.3389/fenrg.2022.996206
Received: 17 July 2022; Accepted: 01 August 2022;
Published: 23 September 2022.
Edited by:
Dongran Song, Central South University, ChinaReviewed by:
Feihhang Zhou, Xi’an University of Posts and Telecommunications, ChinaJian Yang, Central South University, China
Copyright © 2022 Ouari, Belkhier, Djouadi, Kasri, Bajaj, Alsharef, Elattar and Kamel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kamel Ouari, a2FtZWwub3VhcmlAdW5pdi1iZWphaWEuZHo=; Salah Kamel, c2thbWVsQGFzd3UuZWR1LmVn
†These authors have contributed equally to this work
 Kamel Ouari
Kamel Ouari Youcef Belkhier
Youcef Belkhier Hafidh Djouadi
Hafidh Djouadi Amel Kasri
Amel Kasri Mohit Bajaj
Mohit Bajaj Mohammad Alsharef5†
Mohammad Alsharef5† Salah Kamel
Salah Kamel