A control strategy for improving power system resilience in N-k contingency

With the global climate change, the frequency of extreme weather is getting higher and higher, and the threat to the safe operation of the power system is gradually increasing, which is likely to cause large-scale power outages and then result in N-k contingencies. Meanwhile, the Modular Multi-level Converter (MMC) based Multi-Terminal High Voltage Direct Current (MTDC) power system has been confirmed that can provide the possibility for the network interconnection between regional power systems and various renewable energy resources to boost supply reliability and economy. To enhance the resilience of the power grid, a generation rescheduling scheme by optimal emergency control that considers the risk-based dynamic security constraint and reactive power constraints is proposed. Based on the transient stability criterion of the rotor angle speed of the center of inertia (COI), the active power is adjusted to improve the transient stability of the system. The usefulness of the proposed control strategy is highlighted on a 10-machine-39-bus hybrid power system built on MATMTDC, a MATLAB-based open-source software. The obtained results demonstrate that the state optimization control strategy is capable of enhancing the resilience of hybrid power systems and improving the transient stability when suffering N-k contingencies.

1 Introduction

Power system is an essential part of modern society. With the development of human society and the exploitation and utilization of fossil energy, the global average temperature is gradually rising Michael (2016). Excessive emission of greenhouse gases such as carbon dioxide increase the frequency of extreme natural disasters such as typhoons and floods, which in turn destroys the stability of security of the power system Perera, et al. (2020). In response to energy shortages and climate change, most countries are trying to upgrade and transform traditional power systems into green and low-carbon new-generation integrated energy power systems. Rural energy internet (REI) is a practice of energy transition. It contributes to a high proportion of renewable energy for rural energy through the energy transition change, and effectively reduces carbon emissions. Long, et al. (2022). Besides, offshore wind power is all over the world. Therefore, it has an important strategic position in the transformation of the global energy structure. Multi-terminal high voltage direct current with modular multi-level converter (MMC-MTDC) has the advantages of conventional DC transmission system, such as long-distance transmission, the polarity of voltage in the dc bus remaining unchanged when power flow is reversed, and can realize multi-power supply and multi-landing point power supply, making it becomes the best choice for the offshore wind power and large interconnection of power systems.

By surveying the origins of blackouts, it can be concluded that most of them are caused by extreme weather, such as typhoons Panteli, et al. (2017). The coastal area frequently faces severe typhoon weather, which may lead to cascading failures occurring in the power system, and significantly threaten the secure and reliable operation. For example, in 2019, the super typhoon Lekima caused 6 million users to experience a power outage in coastal China, with cumulative economic losses as high as $7.4 billion. In the same year, severe typhoon Faxai caused serious damage to transmission lines and towers in Japan, resulting in power outages for nearly 1 million customers. In 2020, typhoon Hagupit made 584 lines of Zhejiang Power Grid out of use and affected 1.986 million households. Flood disaster caused by heavy rainfall in 2020, a total of 25400 areas of Jiangxi power grid were threatened by floods, and 1.493435 million customers were affected. Icy weather in 2021 led to large-scale power outages in Texas, USA, and finally accumulated load shedding 20000 MW. Not only does extreme weather cause direct damage to components of the power system, but N-k contingencies may also occur, causing instability to the power grid. Therefore, in order to reduce the damage to the power system caused by the typhoon, how to enhance the resilience of the MMC-MTDC system under N-k contingencies is a problem worth exploring.

Some research papers mainly focus on definitions and metrics of the resilience of power systems. Lin et al. (2018); Jufri, et al. (2019) reviews engineering resilience definitions, differences between resilience and reliability, and adverse weather events and their impacts on power systems. A review for resilience-related definitions, taxonomy on known, unknown, and unknowable extreme events, impact of resilience on power systems, and resilience enhancement methods is provided in Gholami, et al. (2018). The paper also discusses a resilience assessment framework and identifies and classifies effective strategies for resilience improvement according to four main criteria: preventive, corrective, restorative, and multifaceted. Several researches focus on specific system types, such as microgrids and hybrid grids. Hussain, et al. (2019) review the role of a microgrid in power system resilience enhancement. In Farzin, et al. (2016), a hierarchical outage management algorithm has been proposed for multiple microgrids. It was implemented after extreme weather events and in emergency conditions. Ti, et al. (2022) propose a cyber-physical power system (CPPS) resilience assessment method considering space-time characteristics of disasters and cyber-physical multi-coupling features. In Wang, et al. (2019), Benders decomposition is applied, an iterative relaxation procedure is developed, and a tri-level robust line hardening method is presented, coupled with multiple provisional microgrids to improve the distribution system resilience. Statistical machine learning theories are proposed to help to solve the multi-scenario new energy integration problem Fu, et al. (2020); Fu (2022). Based on these theories, there are many technologies are used to solve the optimal planning and probabilistic power flow calculations. By greatly improving the computational speed of these problems, the resilience of the system is improved. Li, et al. (2020) propose a minimax-regret robust resilience-constrained unit commitment (RCUC) for NGUs, which can enhance the resilience of the integrated power distribution and natural gas system (IDGS). The proposed DRL-based methods in Vlachogiannis and Hatziargyriou (2004); Xu, et al. (2012); Xu, et al. (2020); Yang, et al. (2020); Duan, et al. (2020); Wang, et al. (2020a) are adequate to provide control actions without accurate system knowledge to maintain voltage constraints under N-1 contingency.

Bie, et al. (2017); Li, et al. (2019) have proved that enhancing power system resilience is an important way to alleviate the impact of typhoon extreme weather events on the power grid. However, the studies are less concerned about the control strategy of MMC-MTDC resilience enhancement under typhoon weather. Typhoon extreme weather is a high-risk emergency and may cause cascading failure in the power system, resulting in N-k (k ≥ 2) contingencies. Schneider, et al. (2016) presents a connection/disconnection strategy for multi-microgrids during or after N-k contingencies occur to reduce the load curtailment cost. Wang et al. (2020b) presented a new converter station structure that employed ESS technology to improve ac and dc fault ride-through performance in an MTDC grid. Esfahani et al. (2020) present a new bi-level robust ROUC model for the optimal operation of an active distribution network to enhance its operational resilience against extreme windstorms. The above researches are either for traditional power systems or transient strategies under the N-1 condition. It is needed to propose a control strategy to improve the resilience of the MMC-MTDC system when N-k contingencies occur.

In this brief, the resilience of the power system is defined as the change of the output power of generators and MMC. The high resilience means the power system can avoid a large degree of machine cutting and load shedding when violent typhoon weather causes N-k contingency of the power grid. In this paper, a resilient enhancement control strategy is proposed. When the transmission system with MTDC encounters N-k contingency caused by typhoon weather, the power grid will adjust its operation status by the control strategy, which is based smooth scheduling optimization model. The model considers system safety operation constraints and power supply reliability constraints. When N-k contingency occurs, emergency load shedding is the first step to keep power system stability at an acceptable level. And the objective function of the optimization model is to enhance the resilience of the power system and minimize the generation rescheduling cost and the incremental change of the power system state variables before and after N-k contingency.

The remaining part of the article proceeds as follows: In Section 2, the modeling of the generator and MMC-MTDC transmission are described. The optimal model of the resilient control strategy is discussed in Section 3. The effect of the proposed control strategy is analyzed in Section 4. At last, the conclusion is presented in the last section.

2 The power grid with modular multi-level converter-multi-terminal high voltage direct current modeling

2.1 Generator modeling

A fourth-order synchronous generator model with a first-order excitation controller taken into consideration is employed here. In this model, damp windings are ignored, but the effect of damping can be accounted for by increasing the damping constant D. A n machine power system, in which the nth machine is chosen as the reference machine, can be denoted as follows.

$\frac{d{\delta }_i}{dt}={\omega }_i(1)$

$2M_i\frac{d{\omega }_i}{dt}=-D_i{\omega }_i+P_{mi}-P_{ei}(2)$

$\frac{d{E}_{qi}}{dt}=\frac{\left(E_{fi}-E_{qi}^{\prime }+\left(x_{di}-x_{di}^{\prime }\right)I_{di}\right)}{T_{d0i}^{\prime }}(3)$

$\frac{d{E}_{di}}{dt}=\frac{\left(-E_{di}^{\prime }+\left(x_{qi}-x_{qi}^{\prime }\right)I_{qi}\right)}{T_{q0i}^{\prime }}(4)$

The algebraic equations can be described as:

$I_{di}=\frac{\left(v_{qi}-E_{qi}^{\prime }\right)}{x_{di}^{\prime }}(5)$

$I_{qi}=-\frac{\left(v_{di}-E_{di}^{\prime }\right)}{x_{qi}^{\prime }}(6)$

$P_{ei}=E_{qi}^{\prime }{I}_{qi}+E_{di}^{\prime }{I}_{di}+\left(x_{di}^{\prime }-x_{qi}^{\prime }\right)I_{di}{I}_{qi}(7)$

$v_{di}=-V_i\sin \left({\delta }_i-{\theta }_i\right)(8)$

$v_{qi}=-V_i\cos \left({\delta }_i-{\theta }_i\right)(9)$

where i = 1,2, … ,n. And ω, δ, M, D denotes the synchronous angular speed, the rotor angle, inertia, and the damping coefficient of the generator i; x_di, x_qi, x′_di, x′_qi, E_fdi, E′_di, E′_qi, T′_d0i, T′_q0i is the d,q-axis reactance, d,q-axis transient reactance, excitation voltage, d,q-axis transient Electromotive Force, field circuit time constant in seconds; V_i, θ_i, P_mi, P_ei represents the voltage magnitude, the angle of bus node connected to the generator i, the initial active power output, and the active electromagnetic power of ith generator; v_d, v_q is d,q-axis of stator voltage.

2.2 AC grid modeling

The AC grid, which is always modeled in the synchronously rotational xy coordinate, is between the synchronous generators and the grid-side MMCs. It can be modeled as:

$I=YU(10)$

where I is the injected current vector, U is the voltage vector, and Y represents the nodal admittance matrix.

2.3 Modular multi-level converter modeling

A per-phase schematic of the MMC is shown in Figure 1. Each phase leg of the MMC comprises two arms: the upper and the lower. Each arm is equipped with N series-connected submodules shown in Figure 2. For the purpose of dynamic modeling, the dc bus can generally be considered to have pure capacitive characteristics, with a capacitance 2C_d, from the neutral to the positive poles, and negative poles respectively, i.e. a pole-to-pole capacitance. These capacitances represent a lumped model of the pole-to-neutral capacitances of the positive and negative-pole dc cables interconnecting two MMC’s in a high-voltage direct current (HVDC) transmission.

FIGURE 1

FIGURE 1. A per-phase schematic of an MMC.

FIGURE 2

FIGURE 2. A submodule of an MMC.

The effective DC bus dynamics of an MMC including submodule capacitors can be written as.

$\frac{d{V}_{di}}{dt}=\frac{1}{C_{di}^{\prime }}\left(I_{di}-\frac{P_{di}}{V_{di}}\right)(11)$

where $C_{di}^{\prime }=C_{di}+\frac{2M{C}_i}{N_i}$ is the effective DC bus capacitance in Fraud. V_di, I_di and P_di are the pole-to-pole DC bus voltage, the dc current flowing into MMC and the active power output of the MMC, respectively; C_di is the installed DC bus capacitance of an MMC; C_i denotes the capacitance of a submodule in an MMC; M and N_i represent the number of phases and the number of submodules per arm of an MMC, respectively.

The averaged dynamic model of the MMC is modeled for both inverter-side and rectifier-side MMCs of the MMC-MTDC system. The dynamic of the MMC converter connected to node i can be expressed in dq reference frame by

$\frac{d{i}_{sdi}}{dt}=\frac{2}{L_i}\left(e_{sdi}-v_{di}-\frac{1}{2}{R}_i{i}_{sdi}+\frac{1}{2}{\omega }_s{L}_i{i}_{sqi}\right)(12)$

$\frac{d{i}_{sqi}}{dt}=\frac{2}{L_i}\left(e_{sqi}-v_{qi}-\frac{1}{2}{R}_i{i}_{sqi}-\frac{1}{2}{\omega }_s{L}_i{i}_{sdi}\right)(13)$

where e_sdi, e_sqi is the d,q-axis component of MMC output voltage respectively; v_di, v_qi denotes the d,q-axis component of the bus voltage at the point of common coupling (PCC) with the MMC; i_sdi and i_sqi are the d,q-axis component of the output current of MMC in p.u.

Assume that the d-axis of the dq reference frame is aligned with the voltage vector ${\overrightarrow{V}}_i$ of the PCC bus of a MMC, we have $v_{di}=\left|{\overrightarrow{V}}_i\right|$ and $v_{qi}=0$. Therefore, the active and reactive power outputs of an MMC can be described as

$\{\begin{array}{l}{P}_{di}=v_{di}{i}_{sdi}\\ Q_{di}=-v_{di}{i}_{sqi}\end{array}(14)$

The outer-loop controller of MMC plays an important role in the stability of the power system. For the rectifier-side MMC, control objectives are to maintain DC bus voltage and regulate the reactive power output of the MMC. Assume that the rectifier-side MMC is connected on node j, and state equations of the outer-loop controllers are

$\{\begin{array}{l}{i}_{sdj}^{ref}=x_{dcj}+\frac{1}{2}{\alpha }_d{C}_{dj}^{\prime }\frac{V_{dj}^2-V_{dj}^{ref2}}{P_{base}}\\ i_{sqj}^{ref}=x_{qj}+K_{Po}^q\left(Q_{dj}^{ref}-Q_{dj}\right)\end{array}(15)$

where x_dcj, x_qj are the state variable of the DC voltage controller of an MMC and reactive power output controller, which are obtained by

$\{\begin{array}{l}\frac{d{x}_{dcj}}{dt}=\frac{1}{2}{\alpha }_{id}{C}_{dj}\frac{V_{dj}^2-V_{dj}^{ref2}}{P_{base}}\\ \frac{d{x}_{qj}}{dt}=K_{Io}^q\left(Q_{dj}^{ref}-Q_{dj}\right)\end{array}(16)$

where α_d, α_id, P_base and $V_{dcj}^{ref}$represents the proportional, integral coefficient of the DC voltage controller, the base power in MVA and the DC voltage reference of rectifier-side MMCj, respectively. The parameters K^q_Po, K^q_Io, x_qj and Q^ref_di represent the proportional, integral coefficient, state variable of reactive power output controller and reactive power reference, respectively.

For the inverter-side MMC, control targets normally are to regulate the active and reactive power output of MMC. The reactive power controller of inverter-side MMC is the same as that adopted on the rectifier-side. Assume that the inverter-side MMC is connected to node i, and the dq reference frame is aligned with the voltage vector, i.e., $v_{di}=\left|{\overrightarrow{V}}_i\right|$and $v_{qi}=0$. The current reference iref sdi is generated by

$i_{sdi}^{ref}=x_{pi}+K_{Po}^p\left(P_{di}^{ref}-P_{di}\right)(17)$

where x_pi is the state variable of the active power controller, whose dynamics can be written as

$\frac{d{x}_{pi}}{dt}=K_{Io}^p\left(P_{di}^{ref}-P_{di}\right)(18)$

where K^p_Po, K^p_Io P^ref_di is the proportional, integral coefficient of the active power controller and the active power output reference of rectifier MMCi, respectively.

In the MMC-MTDC system, the converter stations use a DC voltage-active power droop control method. When the active power of the system is out of balance, the DC voltage of the system changes, and under the droop control characteristics of MMC, the transmitted active power is converted into the control signal with the output voltage as the command to adjust the active power output. The droop controller reacts to the output signal based on the adjusted power, which achieves self-regulation and automatic power distribution. The controller is shown in Figure 3 and the active power delivered to converter i can be expressed by

$V_{di}=V_{di}^{ref}+K_i^{droop}\left(P_i^{ref}-P_i\right)(19)$

where K^droop_i is the droop factor of the converter station.

FIGURE 3

FIGURE 3. The DC voltage-active power droop control of MMC-MTDC system.

3 Resilience enhancement control strategy for N-k contingencies

When the power system encounters extreme typhoon weather, N-k contingency may occur, resulting in instability of the power system. In this case, generators in the power grid may exceed the synchronous speed and rotate at different rates, causing the generators in the power system to become unsynchronized and unstable. In this paper, a resilience enhancement control strategy is proposed. The objective of this control strategy is to reduce the amount of change of the output power of generators and MMCs and minimize the increment change of the angular speed of the center of inertia (COI). The control strategy is used to improve the resilience of the power system by increasing the recovery speed of the MMC-MTDC system after N-k contingencies occur.

3.1 Dynamic PI Control Strategy

In this paper, the resilience is defined as the ability to remain stable when N-k contingencies occur and recover from N-k contingencies. Improving the response speed of the power system to restore transient stability can effectively improve the resilience of the power system. The outer-loop controller of MMC, which uses the PI controller, has an important influence on the stability of the power system. The traditional PI control only considers the control effect when the power system is stable, and ignores the control effect after the power system encounters extreme typhoon weather, affecting the power system’s response time to restore transient stability. Based on the above considerations, a dynamic PI control strategy is proposed.

After N-k contingency occurs, the focus of consideration is to reduce the overshoot, the number of oscillations, and how to improve the ability to stabilize quickly. According to the classical control theory, when the k_p is larger, the system response speed is faster. At the same time, it should be noted that the rise of k_i is prone to overshoot, so the k_p must be properly controlled. Therefore, the dynamic control strategy is to adjust the dynamic adjustment factor η by judging the relationship between e and the threshold value m₀,

$k_{pi}=\eta {\alpha }_d(20)$

The dynamic adjustment factor is mainly to solve the adjustment ability of the system when N-k contingency occurs, which is described as

$\eta =\{\begin{array}{l}0.5,\left|e\right|>m_0\\ 1,\left|e\right|<m_0\end{array}(21)$

where $e=V_{di}-V_{di}^{ref}$, V_d is the DC bus voltage.

3.2 State Transition Optimization Model

During the operation of the power system, load shedding is usually not adopted to maintain the transient stability of the system due to its disadvantages, such as economic loss and power supply reliability reduction. However, N-k faults (k ≥ 2) may also be encountered in the actual operation of the power system. Some of these faults will lead to serious consequences, even reaching the accident level. The supply-demand of the load bus in the area affected by the N-k contingencies will be unbalanced, which will significantly affect the transmission efficiency of the line, and the probability of transmission line outage will also increase. Therefore, it is necessary to carry out emergency load shedding and reschedule the output power of generators to make the power system operate within safe conditions.

The buses to be reduced in load are generally those whose transmission power exceeds the limit or whose transmission power loss increases. And the amount of active power load-shedding depends on the limit value of grid operation. In the actual power grid operation, the final realization of the action export is the safety and stability control device. In the event of a preset fault, the stabilization control device can realize functions such as shedding loads or units to ensure system stability. It has the advantages of solid pertinence and high reliability. The smaller the load shedding, the stronger the system’s resilience. However, under N-k contingencies, the load shedding action is far from maintaining the power grid’s transient stability, so it is necessary to take more effective measures to enhance the system’s resilience after the load shedding action.

In Section 2, the dynamic mathematical model of the MMC-MTDC system has been presented. It can be seen that the dynamic of power system can be described by a set of differential-algebraic equations. Based on the modified Euler method, the equations can be converted into a series of algebraic equations. Then, the model of state smooth optimization can be modeled as a nonlinear programming problem, which can be mathematically described by (22)-(36):

$Objective\mathit{min}C={\displaystyle \sum }_{m=1}^{N_{\mathrm{G}}}{c}_m\left|\Delta P_{\mathrm{G}m}^{c_k}\right|+{\displaystyle \sum }_{m=1}^{N_{\mathrm{G}}}{\left({\omega }_m^{c_k}-{\omega }_{\mathrm{C}\mathrm{O}\mathrm{I}}^{c_k}\right)}^2+{\Vert z_t-h\left(x^{c_k}\right)\Vert }_1(22)$

${\mathrm{s.t}.:P}_{Gi}^{{\mathrm{c}}_k}-P_{\mathrm{D}i}^{{\mathrm{c}}_k}={\displaystyle \sum }_{j\in {\mathrm{\Omega }}_B}{V}_i^{{\mathrm{c}}_k}{V}_j^{{\mathrm{c}}_k}\left(G_{ij}^{{\mathrm{c}}_k}\cos {\theta }_{ij}^{{\mathrm{c}}_k}+B_{ij}^{{\mathrm{c}}_k}\sin {\theta }_{ij}^{{\mathrm{c}}_k}\right)(23)$

$Q_{Gi}^{c_k}-Q_{Di}^{c_k}={\displaystyle \sum }_{j\in {\mathrm{\Omega }}_B}{V}_i^{c_k}{V}_j^{c_k}\left(G_{ij}^{c_k}\sin {\theta }_{ij}^{c_k}-B_{ij}^{c_k}\cos {\theta }_{ij}^{c_k}\right)(24)$

$P_{ij}^{c_k}=-{\left(V_i^{c_k}\right)}^2{G}_{ij}^{c_k}+V_i^{c_k}{V}_j^{c_k}\left(G_{ij}^{c_k}\cos {\theta }_{ij}^{c_k}+B_{ij}^{c_k}\sin {\theta }_{ij}^{c_k}\right)(25)$

$Q_{ij}^{c_k}={\left(V_i^{c_k}\right)}^2{B}_{ij}^{c_k}+V_i^{c_k}{V}_j^{c_k}\left(G_{ij}^{c_k}\sin {\theta }_{ij}^{c_k}-B_{ij}^{c_k}\cos {\theta }_{ij}^{c_k}\right)(26)$

${\omega }_{\mathrm{C}\mathrm{O}\mathrm{I}}^{c_k}=\frac{{\displaystyle \sum }_{m=1}^{N_G}{M}_i{\omega }_m^{c_k}}{M_{total}},m=\mathit{1},...,N_{\mathrm{G}}(27)$

$\left|{\omega }_m^{c_k}-{\omega }_{\mathrm{C}\mathrm{O}\mathrm{I}}^{c_k}\right|\le {\omega }^{\max }(28)$

$V_i^{\min }\le V_i^{{\mathrm{c}}_k}\le V_i^{\max }(29)$

$P_{Gm}^{\min }\le P_{Gm}^{c_k}\le P_{Gm}^{\max },m=1,\dots ,N_G(30)$

$Q_{Gm}^{\min }\le Q_{Gm}^{c_k}\le Q_{Gm}^{\max },m=1,\dots ,N_G(31)$

$\left|\Delta P_{Dn}^{c_k}\right|\le {\gamma }_p\cdot P_{Dn},n\notin {\mathbf{\Omega }}_S(32)$

$\left|\Delta Q_{Dn}^{c_k}\right|\le {\gamma }_q\cdot Q_{Dn},n\notin {\mathbf{\Omega }}_S(33)$

$\left|\Delta P_{D{n}^{*}}^{c_k}\right|\le {\gamma }_p\cdot P_{D{n}^{*}}^{c_k},n^{\ast }\in {\mathbf{\Omega }}_S(34)$

$\left|Q_{D{n}^{*}}^{c_k}\right|\le {\gamma }_q\cdot Q_{D{n}^{*}}^{c_k},n^{\ast }\in {\mathbf{\Omega }}_S(35)$

$P_{MMCn}^{c_k}\le P_{MMC}^{Cap},n=1,...,N_{\mathrm{M}\mathrm{M}\mathrm{C}}(36)$

where ΔP^ck_Gm is the active power adjustment of the mth SG, and c_m is its cost coefficient; ω^ck_COI represents the rotor angle speed of the center of inertia (COI); z_t represents a measurement vector that includes bus voltage magnitudes, that are V^ck_i and V^ck_i, phase angle deviation θ_ij, bus power injections and MMC output active power before N-k contingencies occur; h(x^ck) is the contingency state vector functions, which indicates a state measurement vector, including the voltage magnitude, phase angle deviation, bus power injection and MMC output active power after N-k contingencies. Meanwhile, h(x^ck) has the same dimension as z_t. x^ck is the state variable of selected buses that generate measured value, it includes bus voltage magnitudes, that are V^ck_i and V^ck_j, and phase angle deviation θ_ij after N-k contingency. P^ck_Di and Q^ck_Di are the active and reactive power load demand of the ith bus after N-k contingency (k = 1,2, … ), i∈Ω_B, Ω_B is the set of system buses. Eqs. 23–26 are the node power balance equation. P^ck_ij and Q^ck_ij are active and reactive power flow from the ith bus to the jth bus after N-k contingency. ω^max is the threshold value of the transient stability criterion in this paper. Furthermore, V^max_i and V^min_i are the lower and upper limits for V_i. P^min_Gm, Q^min_Gm, P^max_Gm, and Q^max_Gm are the mth generator’s active and reactive power capacity limits. The inequality (32)-(35) indicates the power demand constraints also apply on the changed load bus. γ_p, γ_q is the fluctuation limit coefficient of load bus power injections. ΔP^ck_Dn, ΔQ^ck_Dn denotes the power change of the nth load bus power demand after contingencies. P^ck_Dn^* is the active power demand of the n^*th load bus that belongs to set Ω_S, and Q^ck_Dn^* is the reactive power demand. P^ck_MMCi, P^Cap_MMCi represents the active power output of MMC i after kth contingency and the rated capacity of the MMC-MTDC, respectively.

The proposed control strategy can be explained as follows. Firstly, the power system topology is determined, and the system measurements also can be obtained. When a severe external shock acts on the power grid and then causes some system components to fall, the system structure will drastically change to another structure, causing the state variable x^ck to change drastically. Then the power system is in an unstable state. To minimize the generation costs and enhance the resilience of the power system, a new generator scheduling scheme is given. Considering generator capacity limit, MMC capacity limit, voltage operation limits, power balance constraints, active and reactive power demand constraints, an optimal model is proposed in this paper. By sequentially solving the state transition optimization model (22)-(36), the amounts of generation rescheduling can be obtained successively. After implementing the rescheduling scheme, the security of the system can return to an acceptable level. Then, the transient stability criterion takes effect. When ω^ck_m > ω^ck_COI, the rotor speed of the generator will increase. According to the transient stability criterion, the rotor speed of the generator should be reduced by adjusting the generator output power. Conversely, when ω^ck_m < ω^ck_COI, the rotor speed of the generator should be increased. In summary, the purpose of the optimal emergency control strategy is to minimize the change of the operation value of the power grid which is related to the system resilience after N-k contingency occurs, while maintaining the system state is also in a safe interval and the grid in transient stability. Figure 4 illustrates the overall framework of the method.

FIGURE 4

FIGURE 4. Flowchart of the control strategy.

4 Case study

In this section, a modified 10-machine 39-bus system is adopted to study the proposed method. The topology of the test system is shown in Figure 5. In this system, MMC is installed at nodes 11, 12, and 13, and the original AC transmission line is replaced by the MMC-MTDC transmission system. The proposed strategy is simulated on MATLAB, and the simulation time length is 15 s. The tolerance of stop criteria is ζ = 1e-6. The parameters of the power grid and the MMC are shown in the following Table 1.

FIGURE 5

FIGURE 5. The framework of the MMC-MTDC test model.

TABLE 1

TABLE 1. The Parameters of grid and MMC.

In this case, when t = 1s, the AC transmission line 16–18 is damaged by a typhoon, and the N-1 contingency occurs on the test system. Suppose that the typhoon continues to expand its influence, causing line 19–9 to be damaged at t = 2 s, and N-2 contingency occurs in the system. The value of generation rescheduling and MMC output before and after the optimal state transition control strategy for N-2 contingency is given in Table 2. The simulation results of the system with the proposed control strategy and no control strategy are shown in Figure 6. From the result of generator rescheduling, it can learn that the generators far away from the fault area do not cut off more active power output to ensure the smoothness of the system state and the minimum of the system operating cost.

TABLE 2

TABLE 2. Value of generator.

FIGURE 6

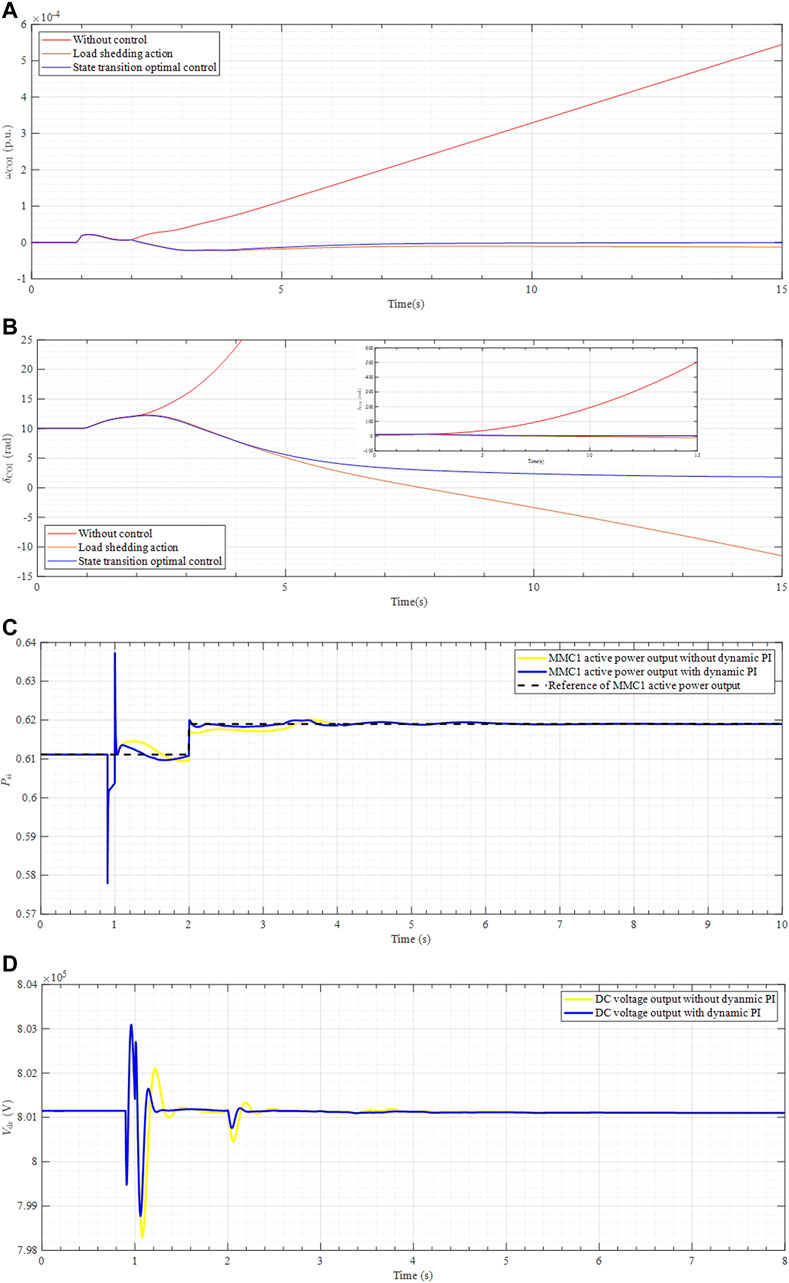
FIGURE 6. Dynamic of the 10-machine 39-bus system in the case when N-2 contingency occurs. (A) Angle speed of the center of inertia. (B) Rotor angle of the center of inertia. (C) Active power output of the inverter-side MMC. (D) DC voltage output of the rectifier-side MMC.

From Figure 6A, we can observe that after the occurrence of N-2 contingency, the proposed control strategy can stabilize the value of rotor angle speed of the COI at the initial value nearly. Without using the resilience enhancement control strategy, the generator speed will exceed the safety limit after a certain period. And Figure 6B shows the rotor angle of the COI of the generator under different conditions. The active power output of inverter-side MMC is shown in Figure 6C. We can clearly see that the output value of MMC1 is extremely close to the reference value after a period of time. The advantage of dynamic PI control is that it reduces the overshoot of the inverter-side MMC active power output after the power system encounters a fault shock, and tracks the reference value of its active power well, thus improving the toughness of the power system. Figure 6D means that when the power system encounters emergencies at t = 1 s and t = 2 s, the DC voltage of the rectifier-side MMC will suffer a certain degree of decline and can be restored to near the expected value after the control strategy takes effect. The dynamic PI control strategy has a better dynamic performance than the tradition PI control. The rotor angle speed of the COI is decreased to 1e-6 at t = 8 s, which means the power system is operating in a new stable condition.

Moreover, assumed that the typhoon continues to destroy the power system, causing the line 20–21 to fall off at t = 4 s, N-3 contingency occurs. From Table 3, which is the new operating condition after solving the optimization model, we can clearly see that the new operating condition of generators is close to the old one, and the amount of change of generator active power output is less. Therefore, the main control effect of the state transition optimization model is the COI adjustment method. Figures 7A,B shows that after implementing the generator rescheduling plan, the angular speed of the rotor will increase, and the power system will be unstable. To solve this problem, the adjustment strategy acting on the generator should be taken into effect. It can see that the state transition control strategy has a positive effect on recovering the transient stability after the power system encounters N-k contingency. As is shown in Figure 7C, MMC1 adjusts its active power output to meet the load demand changes caused by the fault. DC voltage output has a small fluctuation when the line 20–21 falls off, then will quickly return to a stable level due to the resilience of the power system.

TABLE 3

TABLE 3. Value of generator.

FIGURE 7

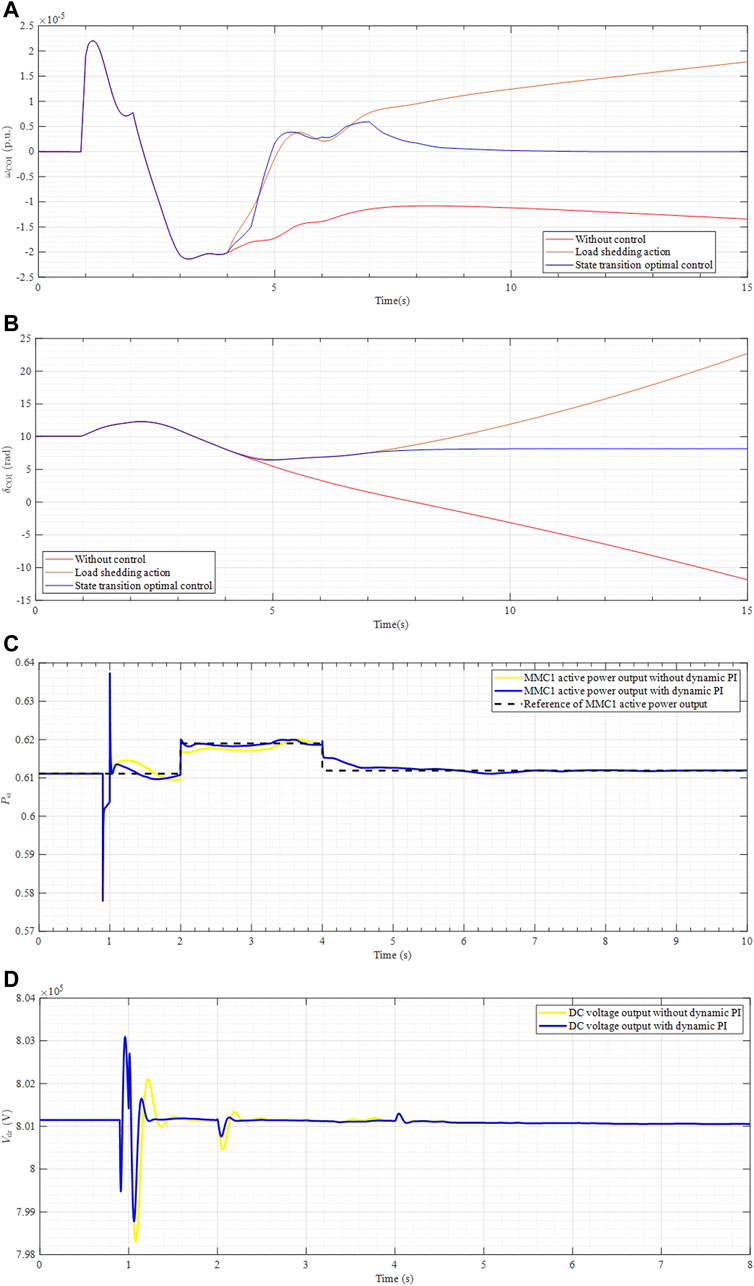
FIGURE 7. Dynamic of the 10-machine 39-bus system in the case when N-3 contingency occurs. (A) Angle speed of the center of inertia. (B) Rotor angle of the center of inertia. (C) Active power output of the inverter-side MMC. (D) DC voltage output of the rectifier-side MMC.

5 Conclusion

This paper proposes a state transient optimization model for generation rescheduling and an adjustment basis for generator mechanical torque to solve the problem of power system resilience enhancement caused by N-k contingency of multi-terminal HVDC grids under extreme weather such as typhoons. Firstly, solving the optimization model can get the parameter of the power system for adjustment. The optimization model can minimize the change amount of the power output of the system, which can enhance the resilience of the power system. Then, based on the role of the center of inertia in the power system, the output power of the MMC and generator mechanical torque is adjusted to ensure transient angle stability. And the dynamic PI control used in the outer-loop controller of MMC has a positive impact on the dynamic performance optimization of the system and improves the resilience of the system to a certain extent. The advantages of this strategy are it considers the cost of generator rescheduling, the dynamic security constraint of the power system, the smoothing operation of the MMC station, and the balance of load demand after N-k contingency occurs. The proposed control strategy can reduce the change of the system state, which increases the resilience of the system, and ensure the power grid has a sufficient transient stability margin so that the system can maintain transient stability after encountering N-k contingency. The simulation results show that the proposed control strategy can enhance the transient stability in cascading contingency with a long interval, such as typhoons extreme weather.

However, the limitation of this control strategy is that it can only be applied to the transient stability control of power systems under cascading failures caused by typhoon weather. For N-k contingency caused by ice disasters, the control strategy proposed in this paper cannot completely improve the transient stability of the system due to the relatively complicated establishment of the ice-covering model. Besides, the solution process of the optimization model is relatively cumbersome. Therefore, future works should expand the application scope of this method, establish a more general fault analysis model to solve the transient stability problem of the power system under N-k contingency and enhance the resilience of the MMC-MTDC system. At the same time, the model solution process should be optimized.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

ZS contributed to all aspects of this work and conducted data analysis. HW, TW, and XW gave useful comments, suggestions to this work, and affect the process of the research. All authors reviewed the manuscript.

Funding

This paper has been jointly supported by the National Natural Science Foundation of China (Grant No. 52177102), the Natural Science Foundation of Guangdong Province (Grant No. 2021A1515011685), and the Foundations of Shenzhen Science and Technology Committee (Grant No. JCYJ20190808143619749, GJHZ20200731095610032).

Conflict of interest

Author HL was employed the CYG SUNRI CO., LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bie, Z., Lin, Y., Li, G., and Li, F. (2017). Battling the extreme: A study on the power system resilience. Proc. IEEE 105, 1253–1266. doi:10.1109/JPROC.2017.2679040

CrossRef Full Text | Google Scholar

Duan, J., Shi, D., Diao, R., Li, H., Wang, Z., Zhang, B., et al. (2020). Deep-reinforcement-learning-based autonomous voltage control for power grid operations. IEEE Trans. Power Syst. 35, 814–817. doi:10.1109/TPWRS.2019.2941134

CrossRef Full Text | Google Scholar

Esfahani, M., Amjady, N., Bagheri, B., and Hatziargyriou, N. (2020). Robust resiliency-oriented operation of active distribution networks considering windstorms. IEEE Trans. Power Syst. 35, 3481–3493. doi:10.1109/TPWRS.2020.2977405

CrossRef Full Text | Google Scholar

Farzin, H., Fotuhi-Firuzabad, M., and Moeini-Aghtaie, M. (2016). Enhancing power system resilience through hierarchical outage management in multi-microgrids. IEEE Trans. Smart Grid 7, 2869–2879. doi:10.1109/TSG.2016.2558628

CrossRef Full Text | Google Scholar

Fu, X., Guo, Q., and Sun, H. (2020). Statistical machine learning model for stochastic optimal planning of distribution networks considering a dynamic correlation and dimension reduction. IEEE Trans. Smart Grid 11, 2904–2917. doi:10.1109/TSG.2020.2974021

CrossRef Full Text | Google Scholar

Fu, X. (2022). Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control Mod. Power Syst. 1, 5–63. doi:10.1186/s41601-022-00228-z

CrossRef Full Text | Google Scholar

Gholami, A., Shekari, T., Amirioun, M., Aminifar, F., Amini, M., and Sargolzaei, A. (2018). Toward a consensus on the definition and taxonomy of power system resilience. IEEE Access 6, 32035–32053. doi:10.1109/ACCESS.2018.2845378

CrossRef Full Text | Google Scholar

Hussain, A., Bui, V., and Kim, H. (2019). Microgrids as a resilience resource and strategies used by microgrids for enhancing resilience. Appl. Energy 240, 56–72. doi:10.1016/j.apenergy.2019.02.055

CrossRef Full Text | Google Scholar

Jufri, F., Widiputra, V., and Jung, J. (2019). State-of-the-art review on power grid resilience to extreme weather events: Definitions, frameworks, quantitative assessment methodologies, and enhancement strategies. Appl. energy 239, 1049–1065. doi:10.1016/j.apenergy.2019.02.017

CrossRef Full Text | Google Scholar

Li, G., Qiu, A., Huang, G., Gui, H., and Bie, Z. (2019). New challenges and future research prospects in power system against to extreme events (in Chinese). Smart Power Secur. 47, 1–11. doi:10.3969/j.issn.1673-7598.2019.08.001

CrossRef Full Text | Google Scholar

Li, Y., Li, Z., Wen, F., and Shahidehpour, M. (2020). Minimax-regret robust co-optimization for enhancing the resilience of integrated power distribution and natural gas systems. IEEE Trans. Sustain. Energy 11, 61–71. doi:10.1109/TSTE.2018.2883718

CrossRef Full Text | Google Scholar

Lin, Y., Bie, Z., and Qiu, A. (2018). A review of key strategies in realizing power system resilience. Glob. Energy Interconnect. 1, 70–78. doi:10.14171/j.2096-5117.gei.2018.01.009

CrossRef Full Text | Google Scholar

Long, H., Fu, X., Kong, W., Chen, H., Zhou, Y., and Yang, F. (2022). Key technologies and applications of rural energy internet in China. Inf. Process. Agric. doi:10.1016/j.inpa.2022.03.001

CrossRef Full Text | Google Scholar

Michael, B. M. (2016). Energy and climate: Vision for the future. Oxford and New York: Oxford University Press, 1–15. doi:10.1093/oso/9780190490331.001.0001

CrossRef Full Text | Google Scholar

Panteli, M., Pickering, C., Wilkinson, S., Dawson, R., and Mancarella, P. (2017). Power system resilience to extreme weather: Fragility modeling, probabilistic impact assessment, and adaptation measures. IEEE Trans. Power Syst. 32, 3747–3757. doi:10.1109/TPWRS.2016.2641463

CrossRef Full Text | Google Scholar

Perera, A. T. D., Nik, V. M., Chen, D., Scartezzini, J., and Hong, T. (2020). Quantifying the impacts of climate change and extreme climate events on energy systems. Nat. Energy 5, 150–159. doi:10.1038/s41560-020-0558-0

CrossRef Full Text | Google Scholar

Schneider, K., Tuffner, F., Elizondo, M., Liu, C., Xu, Y., and Ton, D. (2016). “Evaluating the feasibility to use microgrids as a resiliency resource,” in IEEE power and energy society general meeting (PESGM), 1. doi:10.1109/PESGM.2016.7741723

CrossRef Full Text | Google Scholar

Ti, B., Li, G., Zhou, M., and Wang, J. (2022). Resilience assessment and improvement for cyber-physical power systems under typhoon disasters. IEEE Trans. Smart Grid 13, 783–794. doi:10.1109/TSG.2021.3114512

CrossRef Full Text | Google Scholar

Vlachogiannis, J., and Hatziargyriou, N. (2004). Reinforcement learning for reactive power control. IEEE Trans. Power Syst. 19, 1317–1325. doi:10.1109/TPWRS.2004.831259

CrossRef Full Text | Google Scholar

Wang, S., Ahmed, K., Adam, G., Massoud, A., and Williams, B. (2020b). A novel converter station structure for improving multiterminal HVDC system resiliency against AC and DC faults. IEEE Trans. Ind. Electron. 67, 4270–4280. doi:10.1109/TIE.2019.2926036

CrossRef Full Text | Google Scholar

Wang, S., Duan, J., Shi, D., Xu, C., Li, H., Diao, R., et al. (2020a). A data-driven multi-agent autonomous voltage control framework using deep reinforcement learning. IEEE Trans. Power Syst. 35, 4644–4654. doi:10.1109/TPWRS.2020.2990179

CrossRef Full Text | Google Scholar

Wang, X., Li, Z., Shahidehpour, M., and Jiang, C. (2019). Robust line hardening strategies for improving the resilience of distribution systems with variable renewable resources. IEEE Trans. Sustain. Energy 10, 386–395. doi:10.1109/TSTE.2017.2788041

CrossRef Full Text | Google Scholar

Xu, H., Domínguez-García, A., and Sauer, P. (2020). Optimal tap setting of voltage regulation transformers using batch reinforcement learning. IEEE Trans. Power Syst. 35, 1990–2001. doi:10.1109/TPWRS.2019.2948132

CrossRef Full Text | Google Scholar

Xu, Y., Zhang, W., Liu, W., and Ferrese, F. (2012). Multiagent-based reinforcement learning for optimal reactive power dispatch. IEEE Trans. Syst. Man. Cybern. C 42, 1742–1751. doi:10.1109/TSMCC.2012.2218596

CrossRef Full Text | Google Scholar

Yang, Q., Wang, G., Sadeghi, A., Giannakis, G., and Sun, J. (2020). Two-timescale voltage control in distribution grids using deep reinforcement learning. IEEE Trans. Smart Grid 11, 2313–2323. doi:10.1109/TSG.2019.2951769

CrossRef Full Text | Google Scholar