- 1College of Computer Science and Technology, Qingdao University, Qingdao, China
- 2School of Electronic Information and Electrical Engineering, Shanghai Jiaotong University, Shanghai, China
- 3Department of Computer Science, Morgan State University, Baltimore, MD, United States
- 4School of Software, Shandong University, Jinan, China
- 5Beijing Jingyi City Science and Industry Co., Ltd, Beijing, China
Deep learning models trained from smart meter data have proven to be effective in predicting socio-demographic characteristics of electricity consumers, which can help retailers provide personalized service to electricity customers. Traditionally, deep learning models are trained in a centralized manner to gather large amounts of data to ensure effectiveness and efficiency. However, gathering smart meter data in plaintext may raise privacy concerns since the data is privately owned by different retailers. This indicates an imminent need for privacy-preserving deep learning. This paper proposes several secure multi-party computation (MPC) protocols that enable deep learning training and inference for electricity consumer characteristics identification while keeping the retailer’s raw data confidential. In our protocols, the retailers secret-share their raw data to three computational servers, which implement deep learning training and inference through lightweight replicated secret sharing techniques. We implement and benchmark multiple neural network models and optimization strategies. Comprehensive experiments are conducted on the Irish Commission for Energy Regulation (CER) dataset to verify that our MPC-based protocols have comparable performance.
1 Introduction
Nowadays, smart meters are widely applied in residential households, which allow both customers and retailers to learn a large amount of accurate electricity consumption data (Wang et al., 2015; Mallapuram et al., 2017). In general, these fine-grained data are closely bound up with electricity consumption behavior of customers (Liang et al., 2019). Data analytics can extract the deeper insights from smart meter data, which can be used to enhance efficiency, save energy and improve smart grid systems. A vast amount of studies in machine learning algorithms have been applied to smart meter data, including classification, regression, clustering, and sparse coding (Chicco, 2016). Applications include non-technical loss detection (Jokar et al., 2015; Júnior et al., 2016), price strategy (Chen et al., 2016; Li et al., 2016), demand response program enrollment (Wang et al., 2016a; Chen and Liu, 2017), load forecasting (Taieb et al., 2016) and the electricity consumer characteristics identification (Beckel et al., 2014).
Understanding the relationship between electricity consumer characteristics and smart meter data benefits most participants in the electricity market. Through the estimated electricity consumer characteristics, retailers can infer consumer consumption patterns and thus improve demand response programs, provide more personalized services and promote energy efficiency. There is no doubt that this will significantly enhance the competitiveness of retailers who are proficient in this capability. On the other hand, customers will enjoy better services and save energy due to the technological advances.
In the literature, several data analysis methods are applied to extract mathematical models that enable the identification of electricity consumer characteristics from smart meter data. Generally, these methods consist of three phases: feature extraction, feature selection and classification or regression. In order to infer the socio-demographic characteristics of electricity consumers from smart meter data, Beckel et al. (2013) propose a automatic classification system called CLASS, and the characteristic prediction accuracies of this system are higher than 70%. Viegas et al. (2016) estimate the characteristics of consumers by transparent fuzzy models. Wang et al. (2016b) utilize non-negative sparse coding to extract hidden consumption patterns and implement classification using support vector machine (SVM). Zhong and Tam (2014) achieve the classification of customers by discrete Fourier transform. The majority of these works rely on manually extracting features, while the manually extracted features may not effectively model the high variability and nonlinearity of individual load profiles. To solve this problem, the emerging deep learning techniques (LeCun et al., 2015) are applied to electricity consumer characteristics identification. Wang et al. (2018) leverage convolutional neural networks (CNN) to extract the highly nonlinear features from massive load profiles, and demonstrate the effectiveness by experiments on the Irish CER dataset. Lin et al. (2021) combine CNN and long short-term memory (LSTM) to predict the household characteristics.
Training an accurate deep learning model requires a large amount of available data. However, smart meter data is privately held by different retailers. In order to solve this problem, the previous works assume that there is a server having access to the raw data of retailers so that it can provide machine learning services in a centralized manner. Note that smart meter data and socio-demographic characteristics are sensitive information for consumers. Information leakage may lead to dissatisfaction from customers and public opinion attacks from competitors. As a result, retailers may not reveal raw data to the server due to privacy concerns and potential business risks. In addition, governments are also pushing for strict regulation of data privacy. For instance, the General Data Protection Regulation (GDPR) is already in effect in the European Union.
Secure multi-party computation (MPC) (Yao, 1986; Goldreich et al., 2019) provide a solution to these privacy-preserving issues, which is an important cryptographic technique that is commonly employed in previous studies for privacy-preserving machine learning, such as SecureML (Mohassel and Zhang, 2017), ABY3 (Mohassel and Rindal, 2018), SecureNN (Wagh et al., 2019) and Falcon (Wagh et al., 2021). Secure multi-party computation enables multiple parties P1, … , Pn to collectively compute a function f with their private input x1, … , xn and without revealing any information except the output. In this paper, we leverage replicated secret sharing techniques to construct MPC protocols for deep learning. The secret sharing based protocols require that all computing parties stay online during the execution process and have sufficient computing power. Consider that some retailers may not be able to meet both requirements, we assume that retailers distribute smart meter data in the form of secret shares to three servers, which provide the deep learning training and inference services. Such an outsourced computation pattern has proven to be very practical (Zhang et al., 2020; Zhang et al., 2021; Lu et al., 2022).
1.1 Our contributions
We summarize our contributions as follows.
• We design several MPC protocols that enable privacy-preserving deep learning training and inference for electricity consumer characteristics identification while keeping the retailer’s raw data confidential. In our protocols, we implement two deep neural network models and multiple optimization strategies.
• To relieve the burden on retailers, we propose a system architecture that allows retailers to not have to engage in online computation. Retailers only need to upload secret shares of their smart meter data.
• To demonstrate the practicality, we implement our protocols based on the MP-SPDZ framework (Keller, 2020) and conduct a series of experiments on the Irish Commission for Energy Regulation (CER) dataset (Commission for Energy Regulation, 2012).
1.2 MPC frameworks
In recent years, MPC has evolved from theoretical research to provide practical privacy-preserving protocols for many machine learning tasks, such as training and evaluation of linear regression, logistic regression and neural networks (Mohassel and Zhang, 2017; Mohassel and Rindal, 2018; Wagh et al., 2019, 2021). Here, we give a brief overview on works related to our protocols. ABY3(Mohassel and Rindal, 2018) follow the same blueprint as ABY(Demmler et al., 2015) by mixing replicated secret sharing with garbled circuits. Eerikson et al. (2019) introduce an optimization that can leverage pseudo-random generator (PRG) to reduce the communication costs of input sharing in replicated secret sharing. Keller and Sun, (2021) implement purely training of neural network in MPC with 99% accuracy. Furthermore, Keller and Sun, (2021) discuss in detail how to implement various building block of secure computation with replicated secret sharing.
1.3 Road map
The rest of the paper is organized as follows: we present the problem statement in Section 2. In Section 3, we introduce basic three-party protocol. We introduce in detail how to construct the required secure computation building blocks in Section 4. In Section 5, we discuss the building blocks for deep learning. We report the experimental results in Section 6. Finally, we conclude this paper in Section 7.
2 Problem statement
2.1 Notation
We summarize the notations used in this paper in Table 1.
2.2 Privacy-preserving deep learning
Deep learning is broadly applied in many domains, such as language translation and image classification, often leading to breakthroughs in each domain. The model used for deep learning is a deep neural network, which consists of linear layers and nonlinear layers. Linear layers, including fully connected layers and convolutional layers, can be reduced to arithmetic operations as multiplications and vector dot products. While the activation functions required for the nonlinear layers, such as ReLU functions and max-pooling functions, can be efficiently implemented on binary circuits. Privacy-preserving deep learning is very challenging due to it involves the “mixed” evaluation of arithmetic and binary circuits. The previous works have proposed two main cryptographic approaches that can implement privacy-preserving deep learning: homomorphic encryption (Paillier, 1999; Gentry, 2009) and MPC. The (fully) homomorphic encryption is mainly used for computing linear layers in two-party (client-server model) secure neural network inference. The nonlinear layers in two-party secure neural network inference are usually implemented via oblivious transfer (OT) (Asharov et al., 2013) or garbled circuit (GC) (Yao, 1986), which are important cryptographic primitives of MPC. The studies on secure neural network training mainly focus on two types of three-party MPC protocols (Mohassel and Rindal, 2018; Wagh et al., 2019, 2021) for efficiency. The first have the two computing parties performing the secure neural network training by two-party additive secret sharing and the remaining party generating the materials required by the two computing parties The second utilize the three-party replicated secret sharing to accomplish the secure neural network training. In both scenarios, the participants who own the data are not directly involved in the computation, but instead distribute the raw data to the three computing parties in the form of secret shares. In this paper, we investigate how to use the three-party replicated secret sharing technique to construct privacy-preserving deep learning protocols.
2.3 System architecture
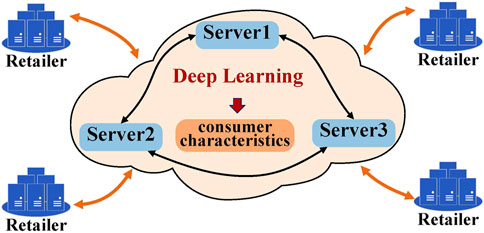
This paper targets to privacy-preserving deep learning (PPDL) for electricity consumer characteristics identification. Our system architecture is shown in Figure 1. At the core, there are two types of entities: the retailer and the server. Retailers are the owner of smart meter data and wish to accomplish the training of the deep neural network models. Since deep learning is a data-driven analytics approach, different retailers wish to work together to ensure the effectiveness of the models. Let N be the number of retailers. The smart meter dataset of the nth retailer is denoted by Dn (n ∈ {1, 2, … , N}) and the dataset consisting of all Dn is denoted by D. Traditionally, this can be achieved through the Machine-Learning-as-a-Service (MLaaS) architecture, which leverages the power of the computational servers. Many major companies such as Amazon, Google, or Microsoft all provide computational services. Since smart meter data is privacy sensitive, retailers want to ensure confidentiality while enjoying the benefits of the computational servers. As a result, retailers are reluctant to supply the smart meter data in plain text, but the ciphertexts of the smart meter data are supplied instead. In addition, it may be impractical to keep all retailers online at the same time to perform the active data interactions required by the MPC protocols. Hence, our system should allow retailers to stay offline after uploading the shares of smart meter data.
In our system, three servers S0, S1, S2 play the role of computing parties to ease the burden on retailers. We assume that government or other social deterrents are sufficient to make the servers strictly execute the protocol and not collude with each other. Similar to the popular security designs in recent years (Mohassel and Rindal, 2018; Wagh et al., 2021), servers use the lightweight replicated secret sharing techniques to collaboratively accomplish the secure deep neural network training. The workflow of our system is as follows. Before deep neural network training, retailers encrypt their smart meter data by splitting it into three secret shares, which can form three unique pairs. Retailers distribute each pair to a server. With shared smart meter data, servers perform the training of deep learning models by invoking various secure computation building blocks, such as dot product, secure comparison and oblivious selection. The trained model parameters are stored on the server in the form of secret shares. Retailers or other users can query the system or download the model parameters directly.
2.4 Security model
Security definition. Our protocol works under a three-party honest-majority setting in which an adversary
We use the simulation-based security definition (Canetti, 2001; Goldreich, 2009; Araki et al., 2016) for three-party computation (3PC). A 3PC protocol Π computes a functionality
Definition 1. A protocol Π securely computes a deterministic functionality f in the presence of static semi-honest adversaries if there exist a probabilistic polynomial time simulator
by only taking Pi’s input xi, output
Three-party decision tree evaluation. Our PPDL protocols are special cases of three-party secure computation. In our protocols, there are three servers S0, S1 and S2 hold the secret shares of D. The three servers perform privacy-preserving deep learning (training and inference) using secret-sharing. Our protocols allow the servers to learn some public information during PPDL protocols. In particular, we allow Si to learn some public information about each D (e.g, the number of retailers, the size of each Dn), for which we denote as
Security in hybrid model. In this paper, we rely on necessary secure computation protocols (e.g., random bit generation, domain conversion, secure comparison and dot product) to design our PPDL protocols. Since security of these secure components has already been proven secure, we will directly use their corresponding ideal functionalities in our design. This approach is known as the hybrid model (Canetti, 2001; Hazay and Lindell, 2010) and is commonly used in existing works.
3 Three-party MPC protocol
In this paper, we use replicated secret sharing techniques (Mohassel and Rindal, 2018; Eerikson et al., 2019; Keller and Sun, 2021) to construct MPC protocols for deep learning, which can be traced back to Benaloh and Leichter, (1988). We begin by introducing the basic secret sharing framework and then move on to high-level building blocks.
3.1 Secret sharing scheme
Replicated secret sharing is a variant of additive secret sharing by appending redundant shares. As we mentioned, three servers S0, S1 and S2 play the role of computing parties to perform three-party MPC protocols. We denote the next and previous servers of Si as Si−1, Si+1, i.e., the indices are computed modulo three. The secret value x is represented as the sum of the three secret shares: x = x0 + x1 + x2 (mod M), where xi−1 and xi+1 are sent to Si. Such a 2-out-of-3 replicated secret sharing is denoted as [x]M. In this paper, we set M = 2l to utilize the properties of the ring. In general, the computation with M = 2 is known as binary circuits, while computing with larger moduli is called arithmetic circuits. In addition, if M is clear from context, we will omit this from the sharing notation.
3.2 Generating randomness
Throughout this paper, we require to generate randomness using pseudo-random generators (PRG). In the initialization phase, Si and Si+1 share a key of PRG so that they can generate the same random number ri,i+1. That is, each server will hold two PRG keys during the protocol. To generate a 3-out-of-3 additive secret sharing of zero, each server Si compute ri−1,i and ri,i+1 and set ri,i+1 − ri−1,i as its share. To generate a 2-out-of-3 replicated secret sharing of a random number, each server Si compute ri−1,i and ri,i+1 and set (ri−1,i, ri,i+1) as its share.
3.3 Input and open secret values
There are two types of inputting parties in our protocols. The first type of inputting parties sample and distribute secret shares from external to the servers, e, g, retailers. The second are computing parties, i.e. Servers, who need to share secret values for some building blocks. In our protocols, servers sample and distribute secret shares based on the method of Eerikson et al. (2019). If Si wish to share a secret value x, then xi is set to zero and xi−1 is generated by Si and Si+1 using PRG. With xi and xi−1, Si can compute xi+1 and send it to Si−1.
Open secrets also have two types of situations. In order to open a secret value x to retailers or other entities, each server sends one share to the receiver, who can reconstruct x by computing x = x0 + x1 + x2 (mod M). To open a secret value x to all servers, Si send xi+1 to Si+1. We emphasize that the values revealed to the servers are independent of the dataset or model parameters. Hence, it does not leak sensitive information.
3.3.1 Linear operations
The additive property of the secret sharing scheme implies that linear operations can be computed locally. Let c be a public constant and [x] [y] be shared values. The addition of [x] and [y] can be computed as [x] + [y] = [x + y]≔(x1 + y1, x2 + y2, x3 + y3). The same applies to subtraction. In addition, we define [x ± c] as (x1 ± c, x2, x3) to add or subtract a shared value with a public constant. As for the scalar multiplication c [x], we define as c [x] = [cx]≔(cx0, cx1, cx2).
3.3.2 Multiplication
The multiplication of two secret values [x] and [y] is shown below:
We can obsever that each server can compute one summand using its own share. Let z = xy = z0 + z1 + z2 and z0 = x1y1 + x1y2 + x2y1, z1 = x2y2 + x2y0 + x0y2, z2 = x0y0 + x0y1 + x1y0, where zi can be locally computed by Si. Then, servers perform the operation called re-sharing to hold two shares as defined. To this end, each server Si need to sends zi to another server. However, since z0, z1 and z2 are not entirely randomized, servers need to generate a 3-out-of-3 sharing of zero to mask them. Let (α0, α1, α2) be a 3-out-of-3 sharing of zero and Si hold αi. Si computes
4 Building blocks for secure computation
In this section, we will describe the building blocks for secure computation in the RSS setting. To the best of our knowledge, we are the first to apply these techniques to privacy-preserving deep learning for electricity consumer characteristics identification.
4.1 Multiplication of fixed-point values
Since computing with floating-point number is extremely expensive (Aliasgari et al., 2013), decimals are usually represented as fixed-point numbers in the MPC protocols, e.g. Catrina and Saxena, (2010). A decimal x is represented as x = ⌊x ⋅ 2p⌉, where p is a positive integer used to specify the precision. For the case of addition or subtraction, the precision of the results will not change. However, the multiplication of two fixed-point numbers doubles the precision (x ⋅ 2p) ⋅ (y ⋅ 2p) = xy ⋅ 22p, which causes the precision to accumulate until it overflows M. To address this problem, the previous works have proposed a method known as truncation. There are three ways to implement truncation.
• The easiest way is to multiply the result of each multiplication by 2−p. However, this method can lead to errors with a certain probability and the absolute value of the errors is 1. For more details, we refer the readers to Mohassel and Zhang, (2017).
• The most effective way to reduce the negative impact of errors is the nearest truncation, which requires to shift the result by p bits after adding 2p−1 to the integer representation The nearest truncation can be instantiated by mixed-circuit computation (Dalskov et al., 2021).
• Catrina and Saxena, (2010) present a solution called probabilistic truncation that can effectively balance cost and accuracy. This method utilizes the uniformly selected random numbers. Let x be the truncated secret value and r be a random number. Servers first compute [x + r] = [x] + [r] and then perform truncation. Finally, servers remove the mask r to obtain [x]. For instance, if x = 0.6, then x will round to 1 with 60% probability. In this work, we mainly use probabilistic truncation.
4.2 Dot product
The dot product is the core building block of the linear layer. Let x and y be two m-dimensional vectors. The dot product of. x and y is shown below:
Intuitively, the dot product of x and y should be reduced to m parallel multiplications and one summation, which requires m re-sharing operations and m truncations. However, it is feasible to reduce the usage of truncation and resharing by delaying them to after the summation. Each server can first compute one of the three sums in the last term locally. Then, all servers perform re-sharing and truncation on the sums. In this way, the communication cost of one dot product is the same as a single multiplication.
4.3 Domain conversion
Recall that we use two different versions of replicated secret sharing techniques. The first is the arithmetic sharing with M = 2l, which is more suitable for arithmetic operations such as addition, multiplication and dot product. The second is the binary sharing with M = 2, which is more suitable for binary operations and non-linear operations that need to access the individual bits directly, such as comparison. For situations that require both versions, the ideal solution is to construct efficient building blocks that allow the secret sharing of two versions to convert to each other. Especially in deep learning, domain conversion is the bridge between linear layers and nonlinear layers. For brevity, we use Bit2A and A2B to represent the conversions in two directions, respectively.
4.3.1 Random bit generation
An efficient solution of Bit2A is to leverage XOR operation, which can be defined as the function f (x, y) = x + y − 2 ⋅ x ⋅ y for
4.3.2 Bit2A
With the arithmetic sharing of random bits, Bit2A can be implemented by the idea of “daBits” (Rotaru and Wood, 2019). A daBit is a random bit that is shared in both arithmetic and Boolean circuits. Let r be a random bit and [r] [r]2 be available. Servers can mask a secret bit b with r and open b ⊕ r without leaking any information. Then, servers can remove the mask r in arithmetic circuits to obtain [b].
To construct a daBit, servers need to invoke one random bit generation to obtain [r]. On the other hand, as introduced by Escudero et al. (2020) [r]2 can be locally generated for powers of two are compatible. Observe that
Hence, servers can locally generate [r]2 by extracting the least significant bit of [r].
4.3.3 A2B
A2B can be considered as a special case of bit decomposition. In this paper, we adopt the method proposed by Araki et al. (2016); Mohassel and Rindal, (2018) to perform A2B. Recall that the arithmetic sharing of x is [x]≔(x0, x1, x2). We use [x]B to denote a vector of l binary secret sharing which encodes
4.4 Secure comparison
The comparison is essential for the implementation of a lot of activation functions, such as ReLU functions, max-pooling functions and approximate sigmoid functions. The comparison is defined as
4.5 Oblivious selection
Oblivious Selection is an essential building block for segmentation functions. It can avoid participants learning which branch is selected. Oblivious selection can be reduced to a polynomial. Taking the 1-out-of-2 oblivious selection as an example, let x and y represent the branches and b ∈ {0, 1} represent the condition. The oblivious selection can be done by x + b ⋅ (y − x). And so on, the oblivious selection with more branches can be implemented by polynomials with higher orders.
4.6 Division
Since arithmetic operations are performed on the ring
4.7 Logarithm and exponentiation
Similar to division, logarithm and exponentiation are implemented by numerical methods (Aly and Smart, 2019). We use logax and xy to represent the instances of logarithm and exponentiation, respectively, where x and y are two secret values and a is an arbitrary public base.
Logax can be reduced to loga2 ⋅ log2x. Then, x is represent as x = b ⋅ 2c such that log2x can be computed by log2x = log2b + c, where
Xy can be reduced to
The above three operations are approximated by numerical methods, the accuracies of which depend on the number of iterations or the truncation method used for multiplication.
5 Building blocks for deep learning
In this section, we will introduce how to construct the building blocks for deep learning.
5.1 Fully connected layers
A fully connected layer is also called a dense layer, which is a linear transformation parameterized by the weight W and the bias b. Let x be the input to a fully connected layer. The output u can be computed by u = W ⋅ x + b. The matrix multiplications are implemented by dot products. To save communication rounds, all dot products of a matrix multiplication are computed in parallel.
5.2 Convolution layers
Convolutional layers are the main layers for feature extraction. Each convolutional layer has a certain number of kernels (also known as filters). These kernels are represented as vectors so that the convolution can be performed using only dot products. Furthermore, these dot products are also computed in parallel to reduce communication rounds.
5.3 ReLU
ReLU functions (Nair and Hinton, 2010) enhance the nonlinear relationship between the layers of the neural network, which can be mathematically defined as follows
ReLU functions can be reduced to one comparison and one oblivious selection. The comparison results of forward propagation are reused in backward propagation to reduce the invocations of comparison.
5.4 Softmax
The objective of softmax functions is to present the results of multi-classification in the form of probabilities. The probability of the ith class can be computed as follows, and the classification result is the class corresponding to the maximum probability.
5.5 Sigmoid
Sigmoid is one of the most widely used activation functions. However, since sigmoid requires costly exponential operations, previous works usually use segmentation functions to approximate it. There are two method to approximately compute sigmoid: 3-piece approximation (Mohassel and Zhang, 2017) and 5-piece approximation (Hong et al., 2020). The two piecewise functions are shown below:
In this way, sigmoid functions can be implemented by comparison and oblivious selection In the experiments for binary classifications, we use the 5-piece sigmoid function.
5.6 Max-pooling
Pooling layers can effectively reduce the size of the parameter matrix and thus reducing parameters in the final connection layer. Therefore, adding pooling layers can speed up the computation and prevent overfitting. In this paper, we mainly use max-pooling, the functionality of which is to return the maximum value of a small window. To reduce communication rounds, the input secret shared values are grouped in the form of a balanced tree to allow multiple comparisons to be computed in parallel.
5.7 Stochastic gradient descent (SGD)
SGD is an efficient approximation algorithm for gradually searching for a local optimum of a problem. As a widely used optimization function, SGD has proven to converge to a global minimum and is usually very fast in practice. In addition, how to securely compute SGD with MPC has been explored by a series of studies, which only involves basic arithmetic operations. As a result, we mainly focus on SGD in this paper. The workflow of SGD algorithm is as follows: the coefficients are initialized to random values or all zeros. In each iteration, a coefficient wj is updated as
where α is the learning rate, B is the mini-batch size and li is the loss regarding the ith sample in the mini-batch.
6 Case studies
In this section, we conduct a series of experiments based on the Irish CER dataset to demonstrate that our protocols not only efficiently maintain the confidentiality of the raw data, but also ensure the accuracy of the models.
6.1 Dataset description
We conduct experiments on a public dataset provided by Commission for Energy Regulation. (2012), which is the regulator for the electricity and natural gas sectors in Ireland. The CER dataset contains raw smart meter data of 4,232 residential consumers. The smart meter data is recorded at an interval of 30 min over a total of 75 weeks. In the data cleansing process, if the measurements for one of the weeks have missing data, we will delete the load profiles of this week. Besides, we limit each week starting on Friday. We select a total of 20,000 weeks of smart meter data, where the measurements of 17,000 weeks are used to train the models, and the rest are used to test the model performance.
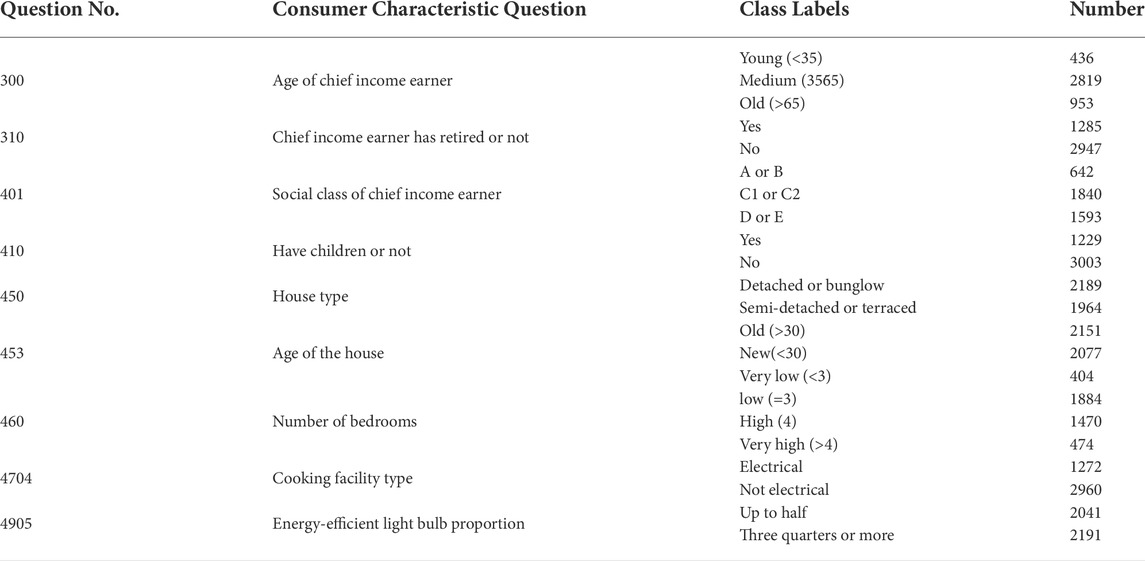
In addition to smart meter data, the CER dataset also contains the characteristics information of the participants, which is privately collected through the questionnaire. The surveyed issues are mainly in three categories: the occupant socio-demographic information (e.g., employment, social class), consumption habits (e.g., the number of energy-efficient light bulbs), home appliances (e.g., cooking facility type). We select nine survey questions for benchmarking, which are listed in Table 2.
6.2 Setup
We implement privacy-preserving deep learning for electricity consumer characteristics identification using the MP-SPDZ framework (Keller, 2020). The framework enables benchmarking the secure program with a series of generic MPC protocols. All experiments are run on a commodity desktop equipped with Intel (R) Core i7-11700K CPU at 3.60 GHz × 16 running Ubuntu 20.04 on VMware Workstation allocated with 32 GB memory, ignoring network latework. We set the batch size to B = 128 and the bit length to l = 64. The learning rate α is settled for 0.01. The fixed-point values are set to 16-bit precision with probabilistic truncation. We mainly use the two neural networks shown in Table 3, 4. Network A is used to train the binary-class classifiers for #310, #410, #450, #4704, #4905, while Network B is used to train the multi-class classifiers for #300, #401, #453, #460. The computation costs and accuracies reported are averaged over ten runs. The accuracies are recorded at 10 epochs.
6.3 Performance evaluation
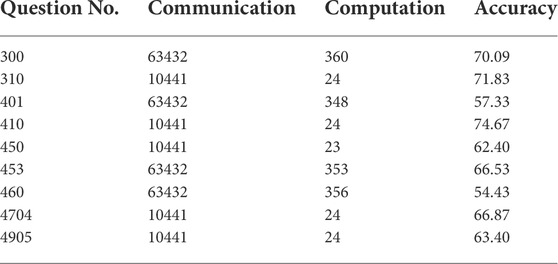
Table 5 details the performance of the two deep neural network models we tested. Network A consists of three fully connected layers, where the first and second fully connected layers use the ReLU activation function. For the output layer of Network A, we set the sigmoid function as activation function. The computation cost required for Network A is desirable, only 24 s for each epoch. While the communication cost is 10,441 MB for each epoch. Network B contains two convolutional layers and one fully connected layer, all of which use the ReLU activation function. After the second convolution layer, we set a max-pooling layer with a window size of 2 × 2. For the output layer of Network B, we set the softmax function as activation function. Compared with Network A, Network B needs to invoke more secure comparisons and multiple costly building blocks, including division, logarithm and exponentiation. So, it requires more communication and computation costs. The computation cost required for Network B is around 354 s for each epoch, while the communication cost is 63,432 MB for each epoch. The communication and computation costs required are practically affordable for the resource-rich servers. In addition, the random bit generation can be performed in the preprocessing phase when servers are idle, so as to reduce the burden on servers to provide privacy-preserving deep learning services.
Now, we report the average accuracy of the survey questions. One third of the survey questions have accuracies higher than 70%, which are #300, #310 and #410. The classifiers for these three survey questions are all trained using network A. The survey question #410 has the highest accuracy of 74.67%. Only two survey questions have accuracies less than 60%, which are #401 and #460. The accuracy of the remaining survey questions is 60% ∼ 70%. In summary, the accuracy of Network A is comparable, while Network B needs to be adjusted to improve the accuracy.
7 Conclusion
We implement privacy-preserving deep learning for electricity consumer characteristics identification by lightweight replicated secret sharing techniques, which not only enable to protect the retailer’s sensitive raw data but also achieve favorable performance. Our system allows retailers to stay offline after uploading the shares of smart meter data, and the burden of computation is transferred to three powerfully equipped servers. After the training of the models, retailers can enjoy the inference service provided by servers or download the model parameters directly. Future work might consider improving the accuracy of the deep neural network models.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
ZZ: Conceptualization, Methodology, Resources, Validation, Visualization, Writing—Original Draft, Writing—Review and Editing. QL: Funding Acquisition, Writing—Review and Editing, Project Administration. HX: Resources, Validation. GX: Validation, Visualization. FK: Software, Supervision. YY: Software, Validation, Language Modification.
Funding
This work is supported by Project funded by China Postdoctoral Science Foundation under Grant 2022T150416 and sponsored by Shanghai Pujiang program under Grant 21PJ1407000.
Conflict of interest
Author YY was employed by the company Beijing Jingyi city science and Industry Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aliasgari, M., Blanton, M., Zhang, Y., and Steele, A. (2013). Secure computation on floating point numbers. (San Diego, CA, United States: computer arithmetic).
Aly, A., and Smart, N. P. (2019). “Benchmarking privacy preserving scientific operations,” in International Conference on Applied Cryptography and Network Security (Springer), 509–529.
Araki, T., Furukawa, J., Lindell, Y., Nof, A., and Ohara, K. (2016). “High-throughput semi-honest secure three-party computation with an honest majority,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 805–817.
Asharov, G., Lindell, Y., Schneider, T., and Zohner, M. (2013). “More efficient oblivious transfer and extensions for faster secure computation,” in Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security,535–548.
Beckel, C., Sadamori, L., and Santini, S. (2013). “Automatic socio-economic classification of households using electricity consumption data,” in Proceedings of the fourth international conference on Future energy systems, 75–86.
Beckel, C., Sadamori, L., Staake, T., and Santini, S. (2014). Revealing household characteristics from smart meter data. Energy 78, 397–410. doi:10.1016/j.energy.2014.10.025
Benaloh, J., and Leichter, J. (1988). “Generalized secret sharing and monotone functions,” in Conference on the Theory and Application of Cryptography (Springer), 27–35.
Canetti, R. (2001). “Universally composable security: A new paradigm for cryptographic protocols,” in Proceedings 42nd IEEE Symposium on Foundations of Computer Science (IEEE), 136–145.
Catrina, O., and Saxena, A. (2010). “Secure computation with fixed-point numbers,” in Financial Cryptography and Data Security, 14th International Conference, FC 2010, Tenerife, Canary Islands, January 25-28, 2010, Revised Selected Papers.
Chen, S., and Liu, C.-C. (2017). From demand response to transactive energy: State of the art. J. Mod. Power Syst. Clean. Energy 5, 10–19. doi:10.1007/s40565-016-0256-x
Chen, S., Love, H. A., and Liu, C.-C. (2016). Optimal opt-in residential time-of-use contract based on principal-agent theory. IEEE Trans. Power Syst. 31, 4415–4426. doi:10.1109/tpwrs.2016.2518020
Chicco, G. (2016). “Customer behaviour and data analytics,” in 2016 International Conference and Exposition on Electrical and Power Engineering (EPE) (IEEE), 771.
Commission for Energy Regulation (CER) (2012). CER smart metering Project - electricity customer behaviour trial, 2009-2010. [Online]. Available at: https://www.ucd.ie/issda/data/commissionforenergyregulationcer/.
Dalskov, A. P. K., Escudero, D., and Keller, M. (2021). “Fantastic four: Honest-majority four-party secure computation with malicious security,” in USENIX Security Symposium.
Demmler, D., Schneider, T., and Zohner, M. (2015). “Aby-a framework for efficient mixed-protocol secure two-party computation,” in NDSS.
Eerikson, H., Keller, M., Orlandi, C., Pullonen, P., Puura, J., and Simkin, M. (2019). Use your brain! arithmetic 3pc for any modulus with active security In 5:1–5:24. ePrint Arch. doi:10.4230/LIPIcs.ITC.2020.5
Escudero, D., Ghosh, S., Keller, M., Rachuri, R., and Scholl, P. (2020). “Improved primitives for mpc over mixed arithmetic-binary circuits,” in Annual International Cryptology Conference.
Gentry, C. (2009). “Fully homomorphic encryption using ideal lattices,” in Proceedings of the forty-first annual ACM symposium on Theory of computing, 169–178.
Goldreich, O. (2009). Foundations of cryptography: Volume 2, basic applications. (Cambridge, United Kingdom: Cambridge University Press).
Goldreich, O., Micali, S., and Wigderson, A. (2019). “How to play any mental game, or a completeness theorem for protocols with honest majority,” in Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali, 307–328.
Goldschmidt, R. E. (1964). Applications of division by conPrivacy-preserving household characteristic identification with federatedvergence. Ph.D. thesis. (Cambridge, MA, United States: Massachusetts Institute of Technology).
Hart, J. F. (1978). Computer approximations. (Malabar, FL, United States: Krieger Publishing Co., Inc).
Hazay, C., and Lindell, Y. (2010). Efficient secure two-party protocols: Techniques and constructions. (Berlin, Germany: Springer Science and Business Media).
Hong, C., Huang, Z., Lu, W.-j., Qu, H., Ma, L., Dahl, M., et al. (2020). “Privacy-preserving collaborative machine learning on genomic data using tensorflow,” in Proceedings of the ACM Turing Celebration Conference-China, 39–44.
Jokar, P., Arianpoo, N., and Leung, V. C. (2015). Electricity theft detection in ami using customers’ consumption patterns. IEEE Trans. Smart Grid 7, 216–226. doi:10.1109/tsg.2015.2425222
Júnior, L. A. P., Ramos, C. C. O., Rodrigues, D., Pereira, D. R., de Souza, A. N., da Costa, K. A. P., et al. (2016). Unsupervised non-technical losses identification through optimum-path forest. Electr. Power Syst. Res. 140, 413–423. doi:10.1016/j.epsr.2016.05.036
Keller, M. (2020). “Mp-spdz: A versatile framework for multi-party computation,” in CCS ’20: 2020 ACM SIGSAC Conference on Computer and Communications Security.
Keller, M., and Sun, K. (2021). Secure quantized training for deep learning. arXiv preprint arXiv:2107.00501
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi:10.1038/nature14539
Li, R., Wang, Z., Gu, C., Li, F., and Wu, H. (2016). A novel time-of-use tariff design based on Gaussian mixture model. Appl. energy 162, 1530–1536. doi:10.1016/j.apenergy.2015.02.063
Liang, H., Ma, J., Sun, R., and Du, Y. (2019). A data-driven approach for targeting residential customers for energy efficiency programs. IEEE Trans. Smart Grid 11, 1229–1238. doi:10.1109/tsg.2019.2933704
Lin, J., Ma, J., and Zhu, J. (2021). Privacy-preserving household characteristic identification with federated learning method. IEEE Trans. Smart Grid 13, 1088–1099. doi:10.1109/tsg.2021.3125677
Lu, Q., Li, S., Zhang, J., and Jiang, R. (2022). Pedr: Exploiting phase error drift range to detect full-model rogue access point attacks. Comput. Secur. 114, 102581. doi:10.1016/j.cose.2021.102581
Mallapuram, S., Ngwum, N., Yuan, F., Lu, C., and Yu, W. (2017). “Smart city: The state of the art, datasets, and evaluation platforms,” in 2017 IEEE/ACIS 16th International Conference on Computer and Information Science (ICIS) (IEEE), 447–452.
Mohassel, P., and Rindal, P. (2018). “Aby3: A mixed protocol framework for machine learning,” in Proceedings of the 2018 ACM SIGSAC conference on computer and communications security, 35–52.
Mohassel, P., and Zhang, Y. (2017). “Secureml: A system for scalable privacy-preserving machine learning,” in 2017 IEEE symposium on security and privacy (SP) (IEEE), 19.
Nair, V., and Hinton, G. E. (2010). “Rectified linear units improve restricted Boltzmann machines vinod nair,” in Proceedings of the 27th International Conference on Machine Learning (ICML-10).
Paillier, P. (1999). “Public-key cryptosystems based on composite degree residuosity classes,” in International conference on the theory and applications of cryptographic techniques (Springer), 223–238.
Rotaru, D., and Wood, T. (2019). “Marbled circuits: Mixing arithmetic and boolean circuits with active security,” in International Conference on Cryptology in India (Springer), 227–249.
Taieb, S. B., Huser, R., Hyndman, R. J., and Genton, M. G. (2016). Forecasting uncertainty in electricity smart meter data by boosting additive quantile regression. IEEE Trans. Smart Grid 7, 2448–2455. doi:10.1109/tsg.2016.2527820
Viegas, J. L., Vieira, S. M., and Sousa, J. (2016). “Mining consumer characteristics from smart metering data through fuzzy modelling,” in International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems (Springer), 562–573.
Wagh, S., Gupta, D., and Chandran, N. (2019). Securenn: 3-party secure computation for neural network training. Proc. Priv. Enhancing Technol., 26–49. doi:10.2478/popets-2019-0035
Wagh, S., Tople, S., Benhamouda, F., Kushilevitz, E., Mittal, P., and Rabin, T. (2021). Falcon: Honest-majority maliciously secure framework for private deep learning. Proc. Priv. Enhancing Technol. 1, 188–208. doi:10.2478/popets-2021-0011
Wang, Y., Chen, Q., Gan, D., Yang, J., Kirschen, D. S., and Kang, C. (2018). Deep learning-based socio-demographic information identification from smart meter data. IEEE Trans. Smart Grid 10, 2593–2602. doi:10.1109/tsg.2018.2805723
Wang, Y., Chen, Q., Kang, C., and Xia, Q. (2016a). Clustering of electricity consumption behavior dynamics toward big data applications. IEEE Trans. Smart Grid 7, 2437–2447. doi:10.1109/tsg.2016.2548565
Wang, Y., Chen, Q., Kang, C., Xia, Q., and Luo, M. (2016b). Sparse and redundant representation-based smart meter data compression and pattern extraction. IEEE Trans. Power Syst. 32, 2142–2151. doi:10.1109/tpwrs.2016.2604389
Wang, Y., Chen, Q., Kang, C., Zhang, M., Wang, K., and Zhao, Y. (2015). Load profiling and its application to demand response: A review. Tinshhua. Sci. Technol. 20, 117–129. doi:10.1109/tst.2015.7085625
Yao, A. C.-C. (1986). “How to generate and exchange secrets,” in 27th Annual Symposium on Foundations of Computer Science (sfcs 1986) (IEEE), 162–167.
Zhang, H., Gao, P., Yu, J., Lin, J., and Xiong, N. N. (2021). Machine learning on cloud with blockchain: A secure, verifiable and fair approach to outsource the linear regression. arXiv preprint arXiv:2101.02334
Zhang, H., Yu, J., Tian, C., Xu, G., Gao, P., and Lin, J. (2020). Practical and secure outsourcing algorithms for solving quadratic congruences in internet of things. IEEE Internet Things J. 7, 2968–2981. doi:10.1109/jiot.2020.2964015
Keywords: machine learning, secure multi-party computation, replicated secret sharing, smart meter, characteristics identification
Citation: Zhang Z, Lu Q, Xu H, Xu G, Kong F and Yu Y (2022) Privacy-preserving deep learning for electricity consumer characteristics identification. Front. Energy Res. 10:992117. doi: 10.3389/fenrg.2022.992117
Received: 12 July 2022; Accepted: 25 July 2022;
Published: 26 September 2022.
Edited by:
Dou An, MOE Key Laboratory for Intelligent Networks and Network Security, ChinaReviewed by:
Kuangyu Zheng, Beihang University, ChinaMingjian Jiang, Qingdao University of Technology, China
Copyright © 2022 Zhang, Lu, Xu, Xu, Kong and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qian Lu, bHVxaWFuQHFkdS5lZHUuY24=
 Zhixiang Zhang
Zhixiang Zhang Qian Lu
Qian Lu Hansong Xu
Hansong Xu Guobin Xu3
Guobin Xu3