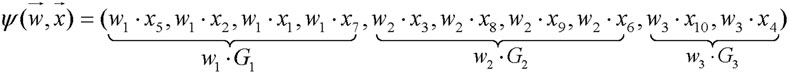Coarse-to-fine evolutionary search for large-scale multi-objective optimization: An application to ratio error estimation of voltage transformers

Multi-objective optimization problems (MOPs) are commonly confronted in various fields, such as condition monitoring for renewable energy systems, and ratio error estimation of voltage transformers. With the increase in decision variables of MOPs, their exponentially growing search spaces are challenging for existing evolutionary algorithms. To handle this challenge, this paper suggests a coarse-to-fine large-scale evolutionary multi-objective search, called CF-LEMO. In the coarse search phase, CF-LEMO performs evolutionary search on both the original and transformed large-scale MOPs alternately, accelerating the population to approach the Pareto-optimal fronts. In addition, to alleviate the issue of diversity loss, we design a diversity preservation mechanism to preserve a well-distributed archive to support subsequent fine search. In the fine search stage, CF-LEMO conducts local search on the current population to mine high-quality solutions, which are used to update the population and archive. Then, based on the archive, the multi-objective optimization based on decomposition is employed to evolve all decision variables, so as to obtain a population with good convergence and diversity near the Pareto-optimal fronts. To assess the effectiveness of the proposed CF-LEMO, we compare its performance against four representative baseline algorithms on a benchmarks suite LSMOP1-LSMOP9 with 2 and 3 objectives. The empirical results confirm its super performance by significanlty outperforming all the four competitors on 12 out of 18 benchmarks. Moreover, the experiments demonstrate the superior performance of CF-LEMO in sovling multi-objective ratio error estimation problems with up to 6,000 decision variables.

1 Introduction

Multi-objective optimization problems (MOPs) are common in diverse fields (Abdel-Basset et al., 2021; Li T. et al., 2021; Jiang et al., 2021; Wang et al., 2021; Liao and Li, 2022; Zong et al., 2022). For instance, ratio error (RE) estimation of voltage transformers involves three conflicting objectives, e.g., the total time-varying REs, the sum of the RE variation, and the variance of the phase angle RE variations (Fadaee and Radzi, 2012; He et al., 2020). Scheduling workflows for cloud platforms need to balance makespan and monetary cost (Chen et al., 2021; Belgacem and Beghdad-Bey, 2022). They are mathematically constructed as:

$P1:\left\{\begin{array}{cc}\hfill \text{Minimize}\hfill & \hfill \vec{f}\left(\vec{x}\right)=\left[f_1\left(\vec{x}\right),f_2\left(\vec{x}\right),\dots ,f_m\left(\vec{x}\right)\right]\text{,}\hfill \\ \hfill \text{S.t.}\hfill & \hfill \vec{x}\in \mathrm{\Omega },\hfill \end{array}\right.(1)$

where $\vec{x}=(x_1,x_2,\dots ,x_n)$ denotes a decision vector, m and n respectively indicate the count of objectives and decision variables, $\mathrm{\Omega }\subseteq {\mathbb{R}}^n$ represents MOP’s feasible area. The objective function $\vec{f}(\vec{x})$ is to map each n-dimensional feasiable decision vector to an m-dimensional objective vector.

Real-world MOPs often involve hundreds or thoudsands of decision variables, which are generally termed large-scale MOPs (LSMOPs). With the increase in decision variables of an LSMOP, its search space grows exponentially and fitness landscape becomes more complex. During the past 3 decades, the studies on large-scale multi-objective optimization have attracted increasing enthusiasms, and evolutionary algorithms have been extensively accepted as one practical technique to resolve LSMOPs (Yi et al., 2020; Hong et al., 2021; Omidvar et al., 2021; Tian et al., 2021). So far, scholars have suggested a large number of evolutionary optimization approaches to solve LSMOPs, and these existing approaches can be roughly partitioned into three categories (Tian et al., 2021): powerful search mechanism, decision variable decomposition, and problem transformation.

The first category is to develop powerful search mechanisms to reproduce superior quality offspring populations by evolving all the decision variables. For instance, to tackle thousands of decision variables, Hong et al. used a probabilistic prediction model to enhance population convergence while employing importance sampling to maintain the population diversity (Hong et al., 2022). Ghorbanpour et al. proposed an integer programming-based initialization, crossover, and mutation operators to resolve multi-objective energy disaggregation problems (Ghorbanpour et al., 2021). Yang et al. suggested a fuzzy evolution strategy to blur LSMOPs’ decision vectors to compress the search space, such accelerating the convergence of populations (Yang et al., 2021). Huang et al. suggested an ensemble of multiple offspring reproduction and environmental selection operators to handle the massive volume of search space in the voltage transformer ratio error estimation problems (Huang et al., 2021). Rizk et al. suggested a multi-orthogonal opposition scehme to diversify offspring solutions (Rizk-Allah et al., 2020). Li et al. formulated the power flow optimization with uncertain wind and solar energy into multi-objective problems, and introduced constraint handle technique to resolve it (Li et al., 2022). Kropp et al. proposed a sparse population sampling approach to initialized population for large-scale sparse multi-objective algorithms (Kropp et al., 2022). Liu et al. employed a feedforward neural network to learn a gradient-descent-like direction to reproduce offspring solutions for efficiently tackling LSMOPs (Liu et al., 2022).

The second category is based on decision variable decomposition. The approaches belonging to this category often divide the decision variables into multiple groups, and then evolve the decision variables in different groups alternately. For instance, Antonio et al. suggested to randomly divide decision variables into multiple groups, and employed the cooperative coevolutionary framework to evolve each group of decision variables (Antonio and Coello, 2013). Sander et al. employed differential grouping techniques Omidvar et al. (2017) to detect the interactions among decision variables, and assigned the ones interating with each other into the same group (Sander et al., 2018). There also exist some works (Ma et al., 2016; Zhang et al., 2018; Chen et al., 2020) performing variable analysis to decompose decision variables. Yang et al. suggested a coarse-to-fine decomposition to divide the reservoir flood control problem into a sequence of sub-problems being solved simultaneously (Yang et al., 2022). Although random grouping approaches are simple and easy, they ignore the interactions among decision variables, which likely push the populations to local optimal regions. Besides, the differential grouping technique and variable analysis consume considerable function evaluations to group decision variables, which is inefficient to solve real-world LSMOPs.

The third category is to reformulate the original LSMOPs into simplified ones, and perform evolutionary search on both the original and transformed problems. For instance, Zille et al. suggested a weighted optimization framework (WOF) to transform orginal LSMOPs into small-scale multi-objective weight optimization problems by assigning a weight to the decision variables in the same group (Zille et al., 2018). Liu et al. improved WOF using a random dynamic grouping approach to adjust group size and a multiple search strategies assisted particle swarm optimization (Liu et al., 2020). Li et al. integrated the problem reformulation technique with decomposition-based MOEAs to handle the growing complex relationships among decision variables (Li L. et al., 2021). He et al. used the decision vectors of obtained solutions to reformulate the original LSMOPs into small-scale single-objective problem (He et al., 2019). Qin et al. suggested to perform directed sampling on solutions nearer to ideal point for assisting reproducing an offspring population (Qin et al., 2021).

Compared with the other two categories of approaches, problem reformulatation-based approaches are more prevalent in solving real-world LSMOPs (Feng et al., 2021). On the one hand, the search spaces of LSMOPs can be drastically compressed by suitable reformulatation functions to improve algorithms’ search efficiency. On the other hand, problem reformulatation approaches are handy for inseparable LSMOPs without deliberate handling interactions among decision variables. However, these approaches accelerate the population to only a tiny fraction of the Pareto-optimal front. Besides, local search shows competitive capability in solving large-scale single-objective optimization problems and small-scale MOPs (Tseng and Chen, 2009; Chen et al., 2015), but is rarely used to solve large-scale MOPs. Furthermore, recent study (Pang et al., 2022) pointed out a counterintuitive observation that traditional EMO algorithms performs better than state-of-the-art LEMO algorithms on some LSMOPs.

Inspired by the above existing works, we develop a coarse-to-fine evolutionary search to handle exponentially growing search spaces of LSMOPs. The proposed CF-LEMO first carries out coarse search in the simplified search spaces to quickly approximate a tiny fraction of the Pareto-optimal front. Meanwhile, to alleviate the issue of diversity loss during coarse search process, a diversity preservation mechanism is designed to maintain the archive based on fitness between solutions and subproblems, such preserving a well-distributed archive for the subsequent fine search. Then, CF-LEMO leverages traditional MOEAs, such as local search and decomposition based MOEAs, to perform fine search on the results of coarse search, so as to obtain a population with well diversity and convergence.

We organize this paper as follows. Section 2 elaborates the proposed CF-LEMO, including problem transformation, pseudo-codes, and descriptions. Then, Section 3 provides comparison experiments on benchmark functions and ratio error estimation of voltage transformers to verify CF-LEMO’s effectiveness. At last, this paper is concluded in Section 4.

2 Algorithm design

This section introduces the transformation method to reformulate the LSMOPs, and details the proposed CF-LEMO.

2.1 Problem transformation

We divide the large-scale decision variabels into g groups, denoted as (G₁, G₂, …, G_g), and assign a weight w_k to the decision variables in the kth group G_k. Referring to works (Yang et al., 2008; Zille et al., 2018), given a fixed decision vector $\vec{x}$, we employ a transformation function $\psi (\vec{w},\vec{x})$ to reformulate the original LSMOP in (1) as a small-scale multi-objective weight optimization problem as follows.

$P2:\left\{\begin{array}{cc}\hfill \text{Minimize}\hfill & {\vec{f}}_{\vec{x}}\left(\vec{w}\right)=\left[f_{1,\vec{x}}\left(\vec{w}\right),f_{2,\vec{x}}\left.\left(\vec{w}\right)\right),\dots ,f_{m,\vec{x}}\left(\vec{w}\right)\right]\text{,}\hfill \\ \hfill \text{S.t.}\hfill & \vec{w}\in \mathrm{\Phi }\subseteq {\mathbb{R}}^n,\hfill \\ \hfill \hfill & f_{j,\vec{x}}\left(\vec{w}\right)=f_j\left(\psi \left(\vec{w},\vec{x}\right)\right),j\in \left\{\mathrm{1,2},\dots ,m\right\},\hfill \\ \hfill \hfill & \psi \left(\vec{w},\vec{x}\right)≔\left(w_1\cdot G_1,w_2\cdot G_2,\cdots ,w_g\cdot G_g\right),\hfill \end{array}\right.(2)$

Figure 1 provides an intuitive example to the illustrate the transformation function. Suppose an MOP has ten decision variables $\vec{x}=\{x_1,x_2,\dots ,x_{10}\}$, which are divided into three groups, denoted as G₁ = {x₅, x₂, x₁, x₇}, G₂ = {x₃, x₈, x₉, x₆}, and G₃ = {x₁₀, x₄}. For a given decision vector $\vec{x}$, after assigning a weight to all the variables in one group, the 10-dimensional problem is transformed into a 3-dimensional problem.

FIGURE 1

FIGURE 1. An example of the transformation function.

Using the above transformation method, an n-dimensional LSMOP is reduced into one with g decision variables. If it satisfies g ≪ n, the dimensionality of the original LSMOP is reduced substantially.

2.2 Description of CF-LEMO

The main process of the proposed CF-LEMO are summarized in Algorithm 1. CF-LEMO’s main inputs include the original problem, transformed problem, population size, and termination condition. After CF-LEMO finishes the optimization process, it output a population for decision makers.

ALGORITHM 1

Algorithm 1. The main process of CF-LEMO.

As illustrated in Algorithm 1, CF-LEMO starts with initializing a set of weight vectors, a random population, and an empty archive. Notice that the ith element A_i of the archive stores the solution reserved by the ith weight vector.

In the coarse search phase (Lines 5–21), CF-LEMO consumes α (0 < α < 1) of the total function evaluations to search original space and transformed space in turn. When searching the original space, CF-LEMO performs variantion operator on all decision variables to obtain an offspring population and environmental selection operator to update the population (Lines 6–8). It also updates the archive using the current population (Line 9), and selects m + 1 well-diversified solutions (Line 10) to support the search of transformed space. The selected m + 1 solutions include m extreme solutions and one solution with the maximum acute angle to these extreme solutions. Then, CF-LEMO searches the transformed space as follows. For each selected solution, it evolves the weight vector of the transformed LSMOPs to reproduce a weight population (Line 14), and applies each weight vector to the selected solution to obtain the corresponding solution in the original space (Line 18). Also, the new generated solutions by evolving the weight vector will update the archive (Line 21).

In the fine search phase (Lines 22–32), CF-LEMO consumes β − α (α < β < 1) of the total function evaluations to perform local search (Lines 23–25). During this sub-phase, CF-LEMO reproduces an offspring population by perturbing the decision variables one by one (Line 23), and update the population and archive (Lines 24–25). After the local search, the algorithm merges the population P and the archive A. If the ith solution A_i in the archive is better than the ith solution P_i in the population, A_i will replace the P_i. After that, CF-LEMO employs the decomposition based MOEA to further search well-diversified and well-distributed solutions using the remaining function evaluations.

The pseudo-code of the function UpdateArchive() is briefly shown in Algorithm 2. Its main inputs are the current population, the archive, and the set of weight vectors. After this function runs, a new archive will be returned.

ALGORITHM 2

Algorithm 2. Function UpdateArchive().

As illustrated in Algorithm 2, function UpdateArchive() first assigns each solution in the population P to the weight vector with the best fitness (Line 2). Note that A_j stores all the solutions assigned to the jth weight vector. Then, this function traverses the solution set assigned to each weight vector, and retains a solution with the best fitness value for each weight vector (Lines 4–6).

3 Experiment studies

In this section, we verify the performance of CF-LEMO by comparing it with four baselines in the context of a complicated benchmark functions and 5 test cases on ratio error estimation of voltage transformers.

3.1 Experimental setup

Comparison algorithms: We choose four relevant baseline MOEAs for performance comparison: WOF (Zille et al., 2018), NSLS (Chen et al., 2015), CCGDE3 (Antonio and Coello, 2013), and NSGA-III (Deb and Jain, 2014). WOF suggests a weighted optimization framework to transform large-scale decision variables into small-scale weight variables, and employs existing MOEAs to successively optimize the original and transformed problems during each iteration. NSLS employs a local search mechanism to reproduce offspring population, and is a representative MOEAs based on local search. CCGDE3 embeds a cooperative coevolution mechanism into existing MOEAs to handle large-scale decision variables. NSGA-III is the recent version of the popular multi-objective optimization algorithm NSGA-II, and NSGA-III employs a reference-vector-based selection mechanism to balance the convergence and diversity for the solutions in the last accepted front.

Significance test: Similar to existing works (Chen et al., 2019; Wang et al., 2019; Ishibuchi et al., 2022; Lin et al., 2022), we adopt the Wilcoxon’s ranksum test with a confidence level of 0.05 to distinguish the statistical significance between the CF-LEMO and the corresponding competitors. The signs + , − , and ≈ respectively represent that the corresponding MOEA performs significantly better, worse, and similar to the CF-LEMO on a test case.

Benchmark functions: LSMOP1-LSMOP9 (Cheng et al., 2017) are tailored for meansure the performance of MOEAs in solving large-scale MOPs. They reflect challenges in real-world applications, such as complex relationships among decision variables and inhomogeneous correlations from decision variables to objectives.

Population size: The population sizes of 2- and 3-objective benchmark functions are set to 100 and 190, respectively.

Stop Condition: Similar to works (Deb and Jain, 2014; Chen et al., 2015; Zille et al., 2018), the maximum number of fitness evaluations is set to n × 10⁴, where n is the number of decision variables.

Metrics: The inverted generational distance (IGD) (Zitzler et al., 2003) and hypervolume (HV) (While et al., 2006) are employed for performance measurement. Both the IGD and HV metrics are capable of simultaneously measuring the convergence and diversity of the populations obtained by MOEAs. When caculating the IGD metric, about 10,000 uniformly distributed Pareto optimal points on the PF are sampled for each benchmark function. Besides, the HV metric refers to the volume of objective space construted by a reference vector and the objective vectors of the obtained solutions. The reference vector is set as 1.5 times the upper bounds of each benchmark function’s PF.

All the experiments are run on a workstation with 64-bit operating system, 256 GB memory, two Intel(R) Xeon(R) Gold 6226R CPU @ 2.90GHz.

3.2 Comparison on benchmarks

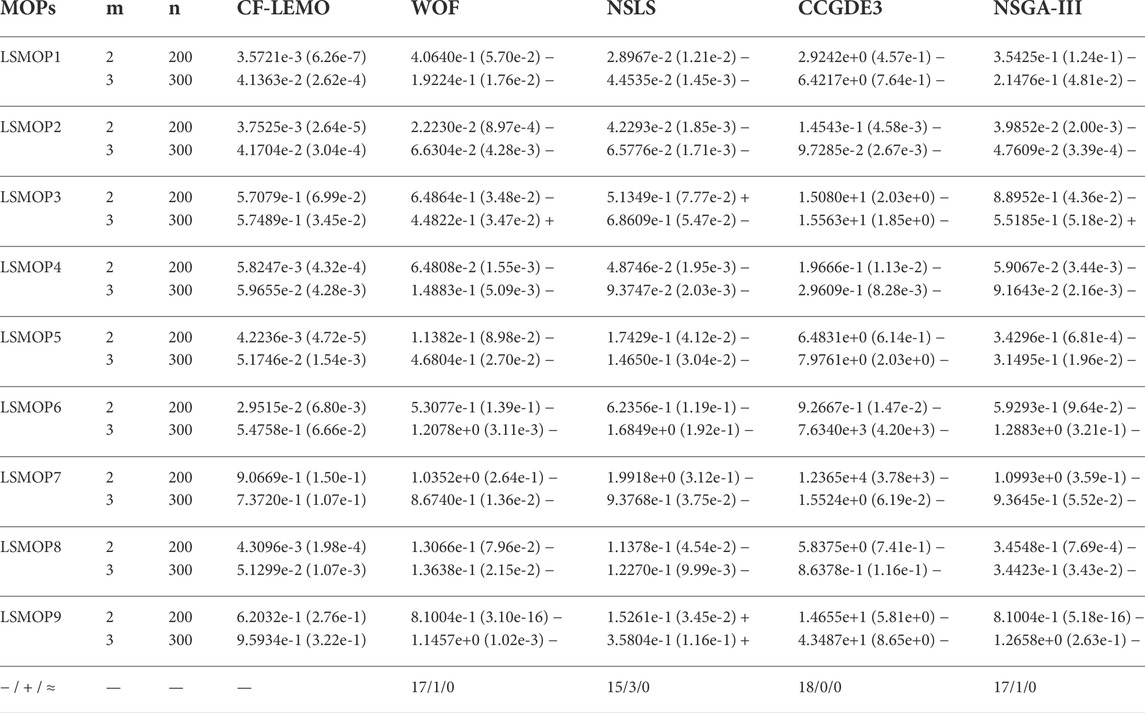
In terms of IGD metrics, the average values and standard deviations (in brackets) of the algorithms CF-LEMO, WOF, NSLS, CCGDE3, and NSGA-III are summarized in Table 1.

TABLE 1

TABLE 1. IGD values of the five algorithms on benchmarks LSMOP1-LSMOP9 with 2- and 3-objectives.

As illustrated in Table 1, the proposed CF-LEMO poses better overall performance than all the four comparison MOEAs. Specifically, CF-LEMO obtains 14 out of 18 lowest IGD values, while comparison algorithms WOF, NSLS, CCGDE3, and NSGA-III respectively only obtain 1, 3, 0, and 0 best results. These numerical results demonstrate the competitive performance of the CF-LEMO in solving complex LSMOPs.

The main difference between CF-LEMO and WOF is that the proposed CF-LEMO employs an archive to store a set of well-diversified solutions to support fine search, and a multi-objective local search to improve the results of coarse search. The comparison results in Table 1 show that CF-LEMO significantly outperforms WOF except for the tri-objective LSMOP3. The comparison results demonstrate that the proposed components in CF-LEMO, i.e., diversity maintaince and local search mechanism, is effective.

NSLS is a multi-objective optimization algorithm based on local search. In each generation, it perturbs the decision variables one by one to obtain an offspring population. It poses the best performance among the four comparison algorithms, but it is far inferior to CF-LEMO proposed in this paper. This can be explained as that even if local search has strong exploitative ability, simple local search based MOEA is difficult to cope with the exponential growth of search space.

For baseline CCGDE3 employing cooperative coevolutionary framework to deal with the large-scale decision variables, it performs the worst among the five algorithms. This can be explained as that the relationships among decision variables of LSMOPs and the landscapes are complex. The random grouping mechanism in CCGDE3 divides the interacting decision variables into the same group with very low probability, which seriously weakens the performance of the cooperative coevolutionary framework. The comparison between CF-LEMO and CCGDE3 shows that the problem transformation-based mechanism is more effective than the cooperative coevolutionary framework in dealing with complex LSMOPs to a certain extent.

NSGA-III is a representative multi-objective optimization algorithm, which has been widely used for experimental comparison. Recent study (Pang et al., 2022) shows that in the benchmark suite LSMOP1-LSMOP9 (Cheng et al., 2017), the NSGA-III performs better than many recent large-scale multi-objective optimization algorithms. As shown in Table 1, CF-LEMO is much better by significantly outperming NSGA-III on 17 out of the 18 benchmark functions. These comparison results demonstrate the superior performance of CF-LEMO over the traditional multi-objective optimization algorithms.

Figure 2 depicts the populations with the lowest IGD values obtained by the five algorithms on LSMOP1, LSMOP2, LSMOP6, and LSMOP8 with 200 decision variables.

FIGURE 2

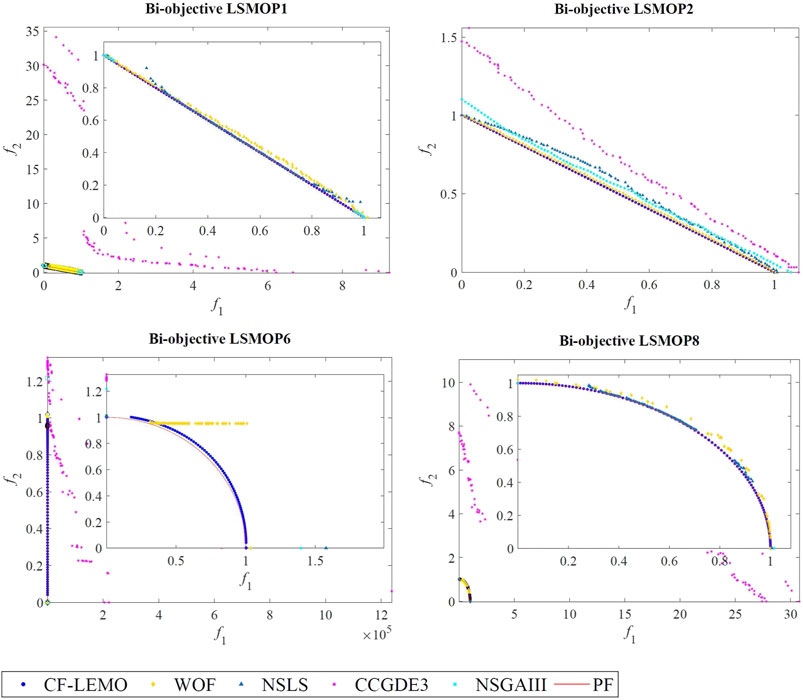
FIGURE 2. Output populations of CF-LEMO, WOF, NSLS, CCGDE3, and NSGA-III on bi-objective LSMOP1, LSMOP2, LSMOP6, and LSMOP8.

As can be seen in Figure 2, on the four benchmark functions, the populations obtained by CCGDE3 are far away from their PFs, indicating poor convergence of the CCGDE3. These are consistent with the extremely high IGD values of CCGDE3 in the Table 2. Compared with the CCGDE3, the other four MOEAs, i.e., CF-LEMO, WOF, NSLS, and NSGA-III, can converge to near PFs.

TABLE 2

TABLE 2. HV values of the five algorithms on solving TREE1-TREE6.

More specifically, the proposed CF-LEMO performs better than all the comparison MOEAs in terms of both convergence and diversity. For example, on bi-objective LSMOP1 with a linear PF, the diversity of CF-LEMO is similar to that of WOF, while CF-LEMO obviously has better convergence. For NSGA-III, its output population only converges to two extreme points. For NSLS, it poses poor convergence and diversity near the two extreme points. On benchmark function bi-objective LSMOP6, the advantage of CF-LEMO is more obvious. The population obtained by CF-LEMO can approximate PF as a whole, while comparison algorithms WOF, NSLS, and NSGA-III only converge to a tiny part of the PF. On LSMOP8 with a concave PF, the CF-LEMO outputs a set of superior-quality of solutions, followed by NSLS and WOF, with CCGDE3 worest.

3.3 Comparison on ratio error estimation of voltage transformers

To further study the performance of the proposal and four comaprison MOEAs on a real-world application of time-varying ratio error estimation (TREE) in voltage transformers (He et al., 2020). We choose five LSMOPs with large-scale decision variables and multiple conflicting objectives, termed TREE1 to TREE6. To be specific, TREE1 and TREE2 have two objectives and 3,000 decision variables, TREE3-TREE5 have two objectives and 6,000 decision variables. We set the maximum number of fitness evaluations as 3 × 10⁶ and 6 × 10⁶ for TREE1-TREE2 and TREE3-TREE5, respectively.

Table 2 illustrates the statistics of HV results produced by the five algorithms. The reason for the NaN results is that no feasiable solutions are obtained by the corresponding MOEAs. It is clear that the proposed CF-LEMO significantly outperforms all the four competitors by obtaining the highest HV values in 4 out of the 5 application cases. Based on the experimental results on TREE1-TREE6, it exhibits that the proposed CF-LEMO is superior over baselines for resolving LSMOPs on ratio error estimation of voltage transformers.

4 Conclusion

In this paper, we design a coarse-to-fine evolutionary search to handle large-scale multi-objective optimization problems, which are common in various fileds, such as condition monitoring for renewable energy systems, and cloud workflow scheduling. In the coarse search phase, the proposal leverages the problem transformation technique to simplify the complex original LSMOPs into small-scale multi-objective weight optimization problems, resulting in the rapid convergence of the population towards the Pareto-optimal fronts. Meanwhile, an archive equipped with a diversity maintenance mechanism is employed to perserve a set of well-diversified solutions. In the fine search phase, the proposal employs traditional MOEAs, such as local search and decomposition based MOEAs, to further push the solutions in the population and archive to well approximate the Pareto-optimal fronts. Finally, we conduct numerical experiments on a challenging benchmark test suite and multi-objective ratio error estimation problems for voltage transformers to verify the superior performance of the proposed CF-LEMO in resolving multi-objective problems with large-scale decision variables.

The problem transformation approaches are fundamental for the population to quickly approach the Pareto-optimal fronts of LSMOPs. But, the coarse search stage of the proposed CF-LEMO directly employs an existing problem transformation approach. Then, designing more powerful transformation approaches is our future research direction. Besides, many real-world multi-objective optimization problems often involve complex constraints and dynamic environments, which are tough tasks for evolutionary optimization. Thus, designing problem-specific strategies to handle these tasks deserves further research.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/BIMK/PlatEMO.

Author contributions

JL: investigation, methodology, writing-original draft preparation. KZ: experiments, review, and editing. LX: conceptualization, review, and supervision.

Funding

This research work is supported by the National Social Science Fund of China (Grand No. 18BTQ055), and the Special Project in Major Fields of Guangdong Universities (Grand No. 2021ZDZX1019).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Basset, M., Mohamed, R., and Mirjalili, S. (2021). A novel whale optimization algorithm integrated with Nelder–Mead simplex for multi-objective optimization problems. Knowledge-Based Syst. 212, 106619. doi:10.1016/j.knosys.2020.106619

CrossRef Full Text | Google Scholar

Antonio, L. M., and Coello, C. A. C. (2013). “Use of cooperative coevolution for solving large scale multiobjective optimization problems,” in IEEE Congress on Evolutionary Computation (Cancun, Mexico: IEEE), 2758–2765.

CrossRef Full Text | Google Scholar

Belgacem, A., and Beghdad-Bey, K. (2022). Multi-objective workflow scheduling in cloud computing: Trade-off between makespan and cost. Clust. Comput. 25, 579–595. doi:10.1007/s10586-021-03432-y

CrossRef Full Text | Google Scholar

Chen, B., Zeng, W., Lin, Y., and Zhang, D. (2015). A new local search-based multiobjective optimization algorithm. IEEE Trans. Evol. Comput. 19, 50–73. doi:10.1109/tevc.2014.2301794

CrossRef Full Text | Google Scholar

Chen, H., Cheng, R., Wen, J., Li, H., and Weng, J. (2020). Solving large-scale many-objective optimization problems by covariance matrix adaptation evolution strategy with scalable small subpopulations. Inf. Sci. 509, 457–469. doi:10.1016/j.ins.2018.10.007

CrossRef Full Text | Google Scholar

Chen, H., Tian, Y., Pedrycz, W., Wu, G., Wang, R., and Wang, L. (2019). Hyperplane assisted evolutionary algorithm for many-objective optimization problems. IEEE Trans. Cybern. 50, 3367–3380. doi:10.1109/tcyb.2019.2899225

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Zhu, X., Liu, G., and Pedrycz, W. (2021). Uncertainty-aware online scheduling for real-time workflows in cloud service environment. IEEE Trans. Serv. Comput. 14, 1167–1178. doi:10.1109/tsc.2018.2866421

CrossRef Full Text | Google Scholar

Cheng, R., Jin, Y., Olhofer, M., and sendhoff, B. (2017). Test problems for large-scale multiobjective and many-objective optimization. IEEE Trans. Cybern. 47, 4108–4121. doi:10.1109/tcyb.2016.2600577

PubMed Abstract | CrossRef Full Text | Google Scholar

Deb, K., and Jain, H. (2014). An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 18, 577–601. doi:10.1109/tevc.2013.2281535

CrossRef Full Text | Google Scholar

Fadaee, M., and Radzi, M. (2012). Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: A review. Renew. Sustain. Energy Rev. 16, 3364–3369. doi:10.1016/j.rser.2012.02.071

CrossRef Full Text | Google Scholar

Feng, Y., Feng, L., Kwong, S., and Tan, K. C. (2021). A multi-variation multifactorial evolutionary algorithm for large-scale multi-objective optimization. IEEE Trans. Evol. Comput. 26, 248–262. doi:10.1109/tevc.2021.3119933

CrossRef Full Text | Google Scholar

Ghorbanpour, S., Pamulapati, T., Mallipeddi, R., and Lee, M. (2021). Energy disaggregation considering least square error and temporal sparsity: A multi-objective evolutionary approach. Swarm Evol. Comput. 64, 100909. doi:10.1016/j.swevo.2021.100909

CrossRef Full Text | Google Scholar

He, C., Cheng, R., Zhang, C., Tian, Y., Chen, Q., and Yao, X. (2020). Evolutionary large-scale multiobjective optimization for ratio error estimation of voltage transformers. IEEE Trans. Evol. Comput. 24, 868–881. doi:10.1109/tevc.2020.2967501

CrossRef Full Text | Google Scholar

He, C., Li, L., Tian, Y., Zhang, X., Cheng, R., Jin, Y., et al. (2019). Accelerating large-scale multiobjective optimization via problem reformulation. IEEE Trans. Evol. Comput. 23, 949–961. doi:10.1109/tevc.2019.2896002

CrossRef Full Text | Google Scholar

Hong, H., Ye, K., Jiang, M., Cao, D., and Tan, K. C. (2022). Solving large-scale multiobjective optimization via the probabilistic prediction model. Memet. Comput. 14, 165–177. doi:10.1007/s12293-022-00358-9

CrossRef Full Text | Google Scholar

Hong, W.-J., Yang, P., and Tang, K. (2021). Evolutionary computation for large-scale multi-objective optimization: A decade of progresses. Int. J. Autom. Comput. 18, 155–169. doi:10.1007/s11633-020-1253-0

CrossRef Full Text | Google Scholar

Huang, C., Li, L., He, C., Cheng, R., and Yao, X. (2021). “Operator-adapted evolutionary large-scale multiobjective optimization for voltage transformer ratio error estimation,” in International Conference on Evolutionary Multi-Criterion Optimization (Berlin, Germany: Springer), 672–683.

CrossRef Full Text | Google Scholar

Ishibuchi, H., Pang, L. M., and Shang, K. (2022). Difficulties in fair performance comparison of multi-objective evolutionary algorithms [research frontier]. IEEE Comput. Intell. Mag. 17, 86–101. doi:10.1109/mci.2021.3129961

CrossRef Full Text | Google Scholar

Jiang, Z.-Z., Feng, G., Yi, Z., and Guo, X. (2021). Service-oriented manufacturing: A literature review and future research directions. Front. Eng. Manag. 9, 71–88. doi:10.1007/s42524-021-0171-3

CrossRef Full Text | Google Scholar

Kropp, I., Nejadhashemi, A. P., and Deb, K. (2022). Benefits of sparse population sampling in multi-objective evolutionary computing for large-scale sparse optimization problems. Swarm Evol. Comput. 69, 101025. doi:10.1016/j.swevo.2021.101025

CrossRef Full Text | Google Scholar

Li, L., He, C., Cheng, R., and Pan, L. (2021a). “Large-scale multiobjective optimization via problem decomposition and reformulation,” in IEEE Congress on Evolutionary Computation (Kraków, Poland: IEEE), 2149–2155.

CrossRef Full Text | Google Scholar

Li, S., Gong, W., Wang, L., and Gu, Q. (2022). Multi-objective optimal power flow with stochastic wind and solar power. Appl. Soft Comput. 114, 108045. doi:10.1016/j.asoc.2021.108045

CrossRef Full Text | Google Scholar

Li, T., Tao, S., He, K., Lu, M., Xie, B., Yang, B., et al. (2021b). V2G multi-objective dispatching optimization strategy based on user behavior model. Front. Energy Res. 494. doi:10.3389/fenrg.2021.739527

CrossRef Full Text | Google Scholar

Liao, Z., and Li, S. (2022). Solving nonlinear equations systems with an enhanced reinforcement learning based differential evolution. Complex Syst. Model. Simul. 2, 78–95. doi:10.23919/csms.2022.0003

CrossRef Full Text | Google Scholar

Lin, A., Yu, P., Cheng, S., and Xing, L. (2022). One-to-one ensemble mechanism for decomposition-based multi-objective optimization. Swarm Evol. Comput. 68, 101007. doi:10.1016/j.swevo.2021.101007

CrossRef Full Text | Google Scholar

Liu, R., Liu, J., Li, Y., and Liu, J. (2020). A random dynamic grouping based weight optimization framework for large-scale multi-objective optimization problems. Swarm Evol. Comput. 55, 100684. doi:10.1016/j.swevo.2020.100684

CrossRef Full Text | Google Scholar

Liu, S., Li, J., Lin, Q., Tian, Y., and Tan, K. C. (2022). Learning to accelerate evolutionary search for large-scale multiobjective optimization. IEEE Trans. Evol. Comput. 2022, 1. doi:10.1109/tevc.2022.3155593

CrossRef Full Text | Google Scholar

Ma, X., Liu, F., Qi, Y., Wang, X., Li, L., Jiao, L., et al. (2016). A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables. IEEE Trans. Evol. Comput. 20, 275–298. doi:10.1109/tevc.2015.2455812

CrossRef Full Text | Google Scholar

Omidvar, M. N., Li, X., and Yao, X. (2021). “A review of population-based metaheuristics for large-scale black-box global optimization: Part A,” in IEEE Transactions on Evolutionary Computation. doi:10.1109/TEVC.2021.3130838

CrossRef Full Text | Google Scholar

Omidvar, M. N., Yang, M., Mei, Y., Li, X., and Yao, X. (2017). DG2: A faster and more accurate differential grouping for large-scale black-box optimization. IEEE Trans. Evol. Comput. 21, 929–942. doi:10.1109/tevc.2017.2694221

CrossRef Full Text | Google Scholar

Pang, L. M., Ishibuchi, H., and Shang, K. (2022). Counterintuitive experimental results in evolutionary large-scale multi-objective optimization. IEEE Trans. Evol. Comput. 2022, 1. doi:10.1109/tevc.2022.3161363

CrossRef Full Text | Google Scholar

Qin, S., Sun, C., Jin, Y., Tan, Y., and Fieldsend, J. (2021). Large-scale evolutionary multiobjective optimization assisted by directed sampling. IEEE Trans. Evol. Comput. 25, 724–738. doi:10.1109/tevc.2021.3063606

CrossRef Full Text | Google Scholar

Rizk-Allah, R. M., Hassanien, A. E., and Slowik, A. (2020). Multi-objective orthogonal opposition-based crow search algorithm for large-scale multi-objective optimization. Neural comput. Appl. 32, 13715–13746. doi:10.1007/s00521-020-04779-w

CrossRef Full Text | Google Scholar

Sander, F., Zille, H., and Mostaghim, S. (2018). “Transfer strategies from single-to multi-objective grouping mechanisms,” in Proceedings of the Genetic and Evolutionary Computation (New York, NY, USA: ACM), 729–736.

CrossRef Full Text | Google Scholar

Tian, Y., Si, L., Zhang, X., Cheng, R., He, C., Tan, K. C., et al. (2021). Evolutionary large-scale multi-objective optimization: A survey. ACM Comput. Surv. 54, 1–34. doi:10.1145/3470971

CrossRef Full Text | Google Scholar

Tseng, L.-Y., and Chen, C. (2009). “Multiple trajectory search for unconstrained/constrained multi-objective optimization,” in IEEE Congress on Evolutionary Computation (Trondheim, Norway: IEEE), 1951–1958.

CrossRef Full Text | Google Scholar

Wang, L., Pan, Z., and Wang, J. (2021). A review of reinforcement learning based intelligent optimization for manufacturing scheduling. Complex Syst. Model. Simul. 1, 257–270. doi:10.23919/csms.2021.0027

CrossRef Full Text | Google Scholar

Wang, Z., Ong, Y.-S., Sun, J., Gupta, A., and Zhang, Q. (2019). A generator for multiobjective test problems with difficult-to-approximate pareto front boundaries. IEEE Trans. Evol. Comput. 23, 556–571. doi:10.1109/tevc.2018.2872453

CrossRef Full Text | Google Scholar

While, L., Hingston, P., Barone, L., and Huband, S. (2006). A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 10, 29–38. doi:10.1109/tevc.2005.851275

CrossRef Full Text | Google Scholar

Yang, R., Qi, Y., Lei, J., Ma, X., and Zhang, H. (2022). A parallel multi-objective optimization algorithm based on coarse-to-fine decomposition for real-time large-scale reservoir flood control operation. Water Resour. manage. 36, 3207–3219. doi:10.1007/s11269-022-03196-z

CrossRef Full Text | Google Scholar

Yang, X., Zou, J., Yang, S., Zheng, J., and Liu, Y. (2021). A fuzzy decision variables framework for large-scale multiobjective optimization. IEEE Trans. Evol. Comput. 2021, 1. doi:10.1109/tevc.2021.3118593

CrossRef Full Text | Google Scholar

Yang, Z., Tang, K., and Yao, X. (2008). Large scale evolutionary optimization using cooperative coevolution. Inf. Sci. 178, 2985–2999. doi:10.1016/j.ins.2008.02.017

CrossRef Full Text | Google Scholar

Yi, J.-H., Xing, L.-N., Wang, G.-G., Dong, J., Vasilakos, A. V., Alavi, A. H., et al. (2020). Behavior of crossover operators in NSGA-III for large-scale optimization problems. Inf. Sci. 509, 470–487. doi:10.1016/j.ins.2018.10.005

CrossRef Full Text | Google Scholar

Zhang, X., Tian, Y., Cheng, R., and Jin, Y. (2018). A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization. IEEE Trans. Evol. Comput. 22, 97–112. doi:10.1109/tevc.2016.2600642

CrossRef Full Text | Google Scholar

Zille, H., Ishibuchi, H., Mostaghim, S., and Nojima, Y. (2018). A framework for large-scale multiobjective optimization based on problem transformation. IEEE Trans. Evol. Comput. 22, 260–275. doi:10.1109/tevc.2017.2704782

CrossRef Full Text | Google Scholar

Zitzler, E., Thiele, L., Laumanns, M., Fonseca, C. M., and Da Fonseca, V. G. (2003). Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 7, 117–132. doi:10.1109/tevc.2003.810758

CrossRef Full Text | Google Scholar

Zong, X., Yuan, Y., and Wu, H. (2022). Multi-objective optimization of multi-energy flow coupling system with carbon emission target oriented. Front. Energy Res. 10, 451. doi:10.3389/fenrg.2022.877700

CrossRef Full Text | Google Scholar