Multi-objective optimal dispatching of virtual power plants considering source-load uncertainty in V2G mode

To solve the risks brought by the uncertainty of renewable energy output and load demand to the virtual power plant dispatch, a multi-objective information gap decision theory (IGDT) dispatching model for virtual power plants considering source-load uncertainty under vehicle-to-grid (V2G) is proposed. With the lowest system operating cost and carbon emission as the optimization objectives, the multi-objective robust optimization model for virtual power plants is constructed based on the uncertainties of wind output, photovoltaic output and load demand guided by the time of use price. The weights of uncertainties quantify the effects of uncertainty factors. The adaptive reference vector based constrained multi-objective evolutionary algorithm is used to solve it. The weight coefficients, evasion coefficients of uncertainties and the penetration rate of electric vehicles are analyzed for the optimal dispatching of the virtual power plant. The algorithm results show that the method can effectively achieve load-side peak shaving and valley filling and has superiority in terms of economy, environmental benefits, robustness and stability.

1 Introduction

Distributed energy is widely used in building new power systems with its multiple advantages such as green, low-carbon, flexible and renewable (China International Economic Exchange Center and State Power Investment Group Co. Ltd, 2021). And distributed energy has intense volatility and intermittent drawbacks; in the future, large-scale and high-ratio access will bring no small challenge to power system stability and energy security. Therefore, building a new power system with more flexible and resilient operation becomes urgent. The virtual power plant (VPP) participates in the power market operation as a particular power plant by aggregating and controlling wind turbines, photovoltaic, energy storage, electric vehicles and other controllable loads through advanced communication technologies. Through the complementary advantages and optimal allocation within the VPP, the randomness and volatility of renewable energy are smoothed out, and the multi-energy complementarity on the power side and flexible interaction on the load side is realized. Therefore, it is of great practical value to study the optimal dispatching and operation method of VPPs to realize the optimal utilization of distributed energy (Taheri et al., 2020; Yi et al., 2020).

For the problems brought by renewable energy, domestic and foreign research mainly regulates from generation and user sides (Liu et al., 2020). In practice, the limited capacity of the power generation equipment configuration leads to many abandoned wind and photovoltaic (PV) problems. Therefore, starting from the user side and tapping the user potential is an effective way to operate the VPP economically and achieve renewable energy consumption. Wang et al. (2022a) proposed a peak-shaving cooperative dispatching strategy to guide EVs to participate in auxiliary services through price signals and verified the economics of the proposed EV peak-shaving collaborative dispatching strategy for electricity costs. Wang et al. (2022b) proposed a hierarchical optimal dispatching model for EVs in V2G, analyzed the benefits of both EV owners and distribution network participants in the V2G process, and verified the economics and feasibility of the proposed model. However, the objective functions of the studies above mainly focus on the economic benefits, and the effects of multiple factors such as the economy and environmental protection are not considered comprehensively. In the reference (Zhang et al., 2022), to evaluate the feasibility of V2G as flexible storage, an optimization-based system planning framework was proposed to simulate the stochastic characteristics of EV fleets, and the economic and environmental benefits of the model were verified using an improved NSGA-II algorithm. Sc and Zl (2019) proposed a multi-objective approach for network reconfiguration, which considered renewable energy sources and EV access to the distribution system. The Analytic hierarchy process determined the weights of individual objectives, and the model was solved using an improved genetic algorithm. However, although these studies take into account the economic and environmental aspects, they do not consider the uncertainty of renewable energy output faced by the system.

Meanwhile, the uncertainty of a high percentage of renewable energy output is one of the hot spots of current research. Reference (FALSAFI et al., 2014; ALABDULWAHAB et al., 2015; BAI et al., 2016; Lu et al., 2020; Qian et al., 2021) studies the scenario-based stochastic planning method to consider the uncertainty of wind power output or electricity price forecast for wind farms. Stochastic programming requires a large number of data samples of random variables and an accurate probability distribution function to obtain the optimal operation. Fang et al. (Fang et al., 2022) uses stochastic optimization and robust optimization to deal with the uncertainty of the load side and generation side respectively. Wang et al. (Wang et al., 2020) constructed a two-stage distributed robust optimization model of wind and solar power output prediction error fuzzy set. The robust optimization method needs to consider the worst case, and its extremely low occurrence probability makes the scheduling plan of the virtual power plant more conservative, and the economy is poor. Reference (MORALES et al., 2010; CATALÃO et al., 2011; Zhong et al., 2020) studies the system scheduling considering the uncertainty of wind power output based on fuzzy theory. Pan et al. (2018) studied the scheduling problem of an electric thermal multi-energy coupling system connected with a large number of electric vehicles, and analyzed the uncertainty of load demand and wind power output based on fuzzy theory. The optimal solution of fuzzy programming should be obtained based on empirical probability and reasonable fuzzy membership function. Reference (Zhang et al., 2019; Niu et al., 2021; Zeng et al., 2021; Jiang et al., 2022) adopts the interval optimization method to consider the uncertainty of renewable energy and load demand. Interval optimization does not need to assume the probability distribution of uncertain variables, but needs to choose a reasonable confidence interval. Information gap decision theory (IGDT) is a non-probabilistic risk assessment method, which can link the prediction deviation with the optimal objective function to maximize the uncertainty variable disturbance while ensuring the lowest objective value. Reference (CAO et al., 2018; Ye et al., 2021) realized multi-source joint dispatching of power systems based on information gap theory, and carried out microgrid operation planning; Reference (Peng et al., 2020; Niu et al., 2021) studies the impact of renewable energy output based on classification probability opportunity constraint information gap decision theory on distribution network energy storage configuration effect; Reference (Li et al., 2019; Li et al., 20222022), based on information gap theory, studied the stochastic optimal scheduling strategy of integrated energy system considering carbon trading mechanism and carbon capture.

Based on the above references, a multi-objective IGDT dispatching model for VPPs in V2G mode considering source-load uncertainty is constructed with the optimization objectives of minimum operating cost and minimum carbon emission. To fully reflect the scenery-load uncertainty, a risk-averse strategy is introduced to build a robust IGDT model, which is solved using an adaptive reference vector based constrained multi-objective evolutionary algorithm (MOEA). Finally, the effectiveness and superiority of the proposed method in coping with the source load uncertainty are verified by case calculations, and the comprehensive goal of minimizing the system operation cost and carbon emission is achieved.

2 VPP containing orderly charging and discharging of electric vehicles

2.1 Virtual power plant framework

The VPP model studied in this paper integrates Wind Turbine (WT), Photovoltaic (PV), Gas Turbine (GT), Energy Storage System (ESS), Charging Pile and Electric Vehicle (EV) and other common electrical load. User-side load and distributed power are coordinated to establish a VPP with EVs. The overall framework is shown in Figure 1. The power grid and the gas company are the primary sources of energy supply for the VPP. The new energy generation units are wind turbines and photovoltaic power plants, and the gas turbines consume gas to supply power to the user-side load. The gas turbine and the energy storage system have the fast regulation capability, which is complementary to the non-regulation of renewable energy and can effectively suppress the volatility of scenery power and improve the consumption of new energy generation. The V2G technology dispatches EVs to smooth out the fluctuation of new energy generation and reduce the impact of the randomness of renewable energy on the power system so that the system can operate efficiently, stably and safely. However, the traditional economic dispatch to balance the uncertainty of scenic power output can cause excessive calls of gas turbines, significantly reducing environmental benefits. Therefore, to limit the total carbon emission of VPPs, carbon emission cost is introduced into the operation cost to optimize the ratio of each distributed energy output and make the dispatching result of VPP balance economic and environmental benefits.

FIGURE 1

FIGURE 1. Framework of virtual power plant with electric vehicles.

2.2 Operation process

2.1.1 Renewable energy power generation units

Wind and photovoltaic energy are renewable energy prioritized to be connected to the grid. The output of other controllable power sources in the VPP will be coordinated to complete the planned output to prioritize the utilization of renewable energy.

2.1.2 Gas turbine and energy storage system

There is a specific error between the predicted and actual output of wind power and PV. The deviation of the VPP output is adjusted by the optimal control of the gas turbine and the charging and discharging of the energy storage system so that the actual output of the VPP tracks the planned output. When the output deviation exceeds 0, the ESS is charged; if the output deviation still exists after setting the ESS, the GT output is reduced to meet the VPP output plan. When the output deviation is less than 0, the ESS is discharged first, and if the deviation still exists, the GT is compensated for the output on a priority basis; if the output deviation still exists, the power will be purchased from the superior grid to meet the planned output of VPP.

2.1.3 Electric vehicle

2.1.3.1 Electric vehicle charging behaviour

Electric vehicle currently has a bi-directional flow, and the user travel demand must be met before the energy storage capacity of EVs can be fully utilized (Zhu et al., 2021; Shi et al., 2022).

Average mileage per trip indicates the average driving mileage of a single trip, and according to the “China New Energy Vehicle Big Data Research Report (2020)" released by the New Energy Vehicle National Big Data Alliance, the data source of real-time monitoring operation data of new energy electric vehicles in 2019 was used for statistical analysis and fitting. It is found that its average mileage per trip approximately obeyed a normal distribution with the following probability density function:

$f_s\left(x\right)=\frac{A_s}{{\sigma }_s\sqrt{2\pi }}\exp \left[-\frac{{\left(x-{\mu }_s\right)}^2}{2{\sigma }_s^2}\right](1)$

where $A_s$ is 89.99, ${\sigma }_s$ takes 1.05, ${\mu }_s$ and takes 2.99.

The statistics in Figure 2 show that the average driving range of electric vehicles is mainly 2–15 km.

FIGURE 2

FIGURE 2. Probability density of electric vehicle average mileage.

The electric vehicle’s on-grid and off-grid moments approximately obey log-normal distribution. For travel moments, the following normal distribution:

$f_t=\{\begin{array}{l}\frac{1}{\sqrt{2\pi {\sigma }_t^2}}\exp \left[-\frac{{\left(\ln x-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right],0<x⩽{\mu }_t+12\\ \frac{1}{\sqrt{2\pi {\sigma }_t^2}}\exp \left[-\frac{{\left(x-24-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right],{\mu }_t+12<x⩽24\end{array}(2)$

For the return moment:

$f_r=\{\begin{array}{l}\frac{1}{\sqrt{2\pi {\sigma }_r^2}}\exp \left[-\frac{{\left(\ln x-{\mu }_r\right)}^2}{2{\sigma }_r^2}\right],0<x⩽{\mu }_r+12\\ \frac{1}{\sqrt{2\pi {\sigma }_r^2}}\exp \left[-\frac{{\left(x-24-{\mu }_r\right)}^2}{2{\sigma }_r^2}\right],{\mu }_r+12<x⩽24\end{array}(3)$

The EV charging data in this paper is selected from the typical daily charging data of a charging station in Shanghai in summer, as shown in Figure 3. The figure shows small charging peaks around 10:00 and 19:00, and 13:00–15:00 is the prominent charging peak.

FIGURE 3

FIGURE 3. Electric vehicle charging station charging volume on a typical summer day.

2.1.3.2 Electric vehicle V2G model

In the actual calculation process, it is necessary to make the following assumptions for the lithium-ion battery of EVs: the discharge power of the power battery of the electric vehicle is approximately a straight line; The response of EV users to the time of use price follows specific probability characteristics. Based on the above two assumptions, the discharge behaviour of electric vehicles follows a binomial distribution:

$P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c}}:B\left(Q,P\right)(4)$

$P=\frac{R_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV}^t}{R_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV,\max }}(5)$

Where $P$ is the probability of EV discharge. $R_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV}^t$ is the EV discharge price provided by the grid at time t. $R_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV}^t$ is the highest discharge price customized by the superior grid. It is easy to see that the probability of EV users responding to the grid incentive is positively correlated with the real-time electricity price. The higher the discharge price provided by the grid in real-time, the greater the probability of EV users responding to the grid incentive. Incentive mechanisms are set up to allow more EV users to participate more deeply in V2G. The VPP sets the compensation price for V2G services based on the quality of EV participation in auxiliary services, and EV users profit more if they participate in peak shaving when the grid load fluctuates.

In this article, electricity price changes guide users to adjust the energy consumption period through the electricity price change. The time-of-use price is divided according to the energy consumption periods and combined with customer demand response. The price changes are used to motivate customers to shift their loads. During the peak period, the EV users are guided to change the load by raising the price to reduce the peak-valley difference. Meanwhile, specific incentives are provided to users to motivate them to participate in the discharge behaviour when the price is high to compensate for the volatility and randomness of renewable energy.

3 Deterministic dispatching model of VPP with electric vehicles

3.1 Objective function

Objective function 1 is to minimize the operating cost of the VPP system, which is expressed as:

$\min C_1={\displaystyle \sum }_{t=1}^T\left(C_W^t+C_{PV}^t+C_{GT}^t+C_{grid}^t+C_{ES}^t+C_{EV}^t\right)(6)$

Where $C_1$ is the economic cost of VPP in one dispatching cycle, $T$ is 24h. $C_W^t$, $C_{PV}^t$, $C_{GT}^t$, $C_{grid}^t$, $C_{ES}^t$, $C_{EV}^t$ are the operation and management cost of WT, the operation and management cost of PV plant, the cost of GT power generation, the cost of purchased electricity, the loss cost of ESS, and the battery degradation cost respectively.

(1) The operation and management cost of WT

$C_W^t=c_W{P}_W^t(7)$

Where $c_W$ is the operation and management factor of WT; $P_W^t$ is the WT output at time t.

(2) The operation and management cost of PV

$C_{PV}^t=c_{PV}{P}_{PV}^t(8)$

Where $c_{PV}$ is the PV plant operation and management factor; $P_{PV}^t$ is the PV power output at time t.

(3) The cost of GT power generation

$C_{GT}^t=c_{GT}{P}_{GT}^t+C_{fp}{P}_{GT}^t(9)$

$C_{fp}=\frac{C_{NG}}{{\eta }_e{L}_{NG}}(10)$

Where $c_{GT}$ is the GT operation management factor, $P_{GT}^t$ is the actual GT output, $C_{fp}$ is the GT unit fuel cost factor. $C_{NG}$ is the natural gas price, ${\eta }_e$ is the gas turbine power generation efficiency, $L_{NG}$ is the natural gas low-level calorific value.

(4) The cost of purchased electricity

$C_{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}^t=R_e^t{P}_{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}^t(11)$

where $R_e^t$ is the purchased price for at time t, and $P_{grid}^t$ is the power purchased at time t.

(5) The loss cost of energy storage system

The loss cost of the energy storage system, including the operation and maintenance cost of the energy storage system $C_{OM}^t$, and the energy loss cost of the energy storage system $C_{el}^t$, is as follows.

$C_{ES}^t=C_{OM}^t+C_{el}^t(12)$

$C_{OM}^t=\beta \times \left(P_{c,ES}^t+P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},ES}^t\right)+\alpha \times P_r(13)$

$C_{el}^t=\phi \times \left[\left(1-{\eta }_c\right)\times P_{c,ES}^t+\left(1-{\eta }_{\mathit{d}\mathit{i}\mathit{s}\mathit{c}}\right)\times P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},ES}^t\right](14)$

Where: $\beta$ is the cost factor of energy storage battery operation; $P_{c,ES}^t$ is the charging power of energy storage battery at time i; $P_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c},ES}^t$ is the discharging power of energy storage battery at time i; $\alpha$ is the maintenance cost factor of energy storage per unit power; $P_r$ is the rated power of energy storage battery; $\phi$ is the cost factor of energy loss of energy storage battery; ${\eta }_c$ and ${\eta }_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}}$ are the charging and discharging efficiency of energy storage.

(6) The battery degradation cost

$C_{EV}^t=a_{EV}{\left(P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV}^t\right)}^2+b_{EV}{P}_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV}^t+c_{EV}(15)$

Where: $P_{disc,EV}^t$ is the EV discharge power at time I; $a_{EV}$, $b_{EV}$, and $c_{EV}$ are the battery depreciation cost coefficients of EV, which are 0.003 ¥/kWh, 0.11¥/kWh, -0.02¥/kWh, respectively.

Objective function 2 is to minimize the carbon dioxide emissions of VPP. WT, PV and ESS produce almost no carbon emissions. The carbon emissions of the VPP constructed in this paper consist of two primary sources, electricity purchased from the superior grid and electricity generated by GT, and its expression is

$C_2={\mu }_{c,grid}{P}_{grid}^t+{\mu }_{c,GT}{P}_{GT}^t(16)$

Where, ${\mu }_{c,grid}$ and ${\mu }_{c,GT}$ are the carbon emission factors of grid and gas turbine respectively, and the values are 0.75 and 0.226 kg/kWh respectively.

3.2 Constraints

(1) Power balance constraint

VPP purchases electricity and natural gas resources from the higher energy network and supplies energy to the multi-energy users through various energy conversion equipment with the following power balance constraints.

$P_L^t=P_{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}^t+P_W^t+P_{PV}^t+P_{GT}^t(17)$

Where $P_L^t$ is the electricity load of VPP at time t. $P_{GT}^t$ is the electrical power generated by the GT.

(2) Wind and photovoltaic output constraints

$\{\begin{array}{l}0\le P_W^t\le P_{W,\max }^t\\ 0\le P_{PV}^t\le P_{PV,\max }^t\end{array}(18)$

Where $P_{W,\max }^t$ is the maximum value of wind power generation in period t, and is the maximum value of photovoltaic power generation in period t.

(3) Output constraint and climbing constraint of GT units

$P_{\text{GT},\min }⩽P_{\text{GT}}^t⩽P_{\text{GT},\max }(19)$

$-P_{\text{RD}}⩽P_{\text{GT}}^t-P_{\text{GT}}^{t-1}⩽P_{\text{RU}}(20)$

Where $P_{\text{RD}}$ and $P_{\text{RU}}$ are the minimum and maximum ramp rates of GT, respectively. $P_{\text{GT},\min }$ and $P_{\text{GT},\max }$ are the upper and lower limits of the output of the gas unit, respectively.

(4) ESS constraints

$\{\begin{array}{l}{K}_c^t=K_{\mathit{d}\mathit{i}\mathit{s}\mathit{c}}^t\\ S_{\min }⩽S^t⩽S_{\max }\\ S^t=S^{t-1}\left(1-\delta \right)+\frac{\left(P_{c,ES}^t{\eta }_c-P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},ES}^t{\eta }_{\mathit{d}\mathit{i}\mathit{s}\mathit{c}}\right)\Delta t}{E}\end{array}(21)$

Where $K_c^t$, $K_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}}^t$ are the charge and discharge coefficients of ESS, respectively. $S_{\min }$, $S_{\max }$ are the ESS’s minimum and maximum capacity states, respectively. $S^t$, $S^{t-1}$ are the remaining capacity states of ESS at time t and time t-1, respectively; $\mathit{\delta }$ is the self-discharge rate of ESS; $\mathit{E}$ is the capacity of ESS.

(5) EV charging and discharging constraints and capacity constraints

$P_{c,EV}^t⩽P_{c,1}{N}_{EV}^t(22)$

$P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},EV}^t⩽P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},1}{N}_{EV}^t(23)$

$SO{C}_{\min }<SO{C}_{EV}^t<SO{C}_{\max }(24)$

$S_{EVi\_\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}}=N\left(D_{EVi}\ast S_{EVi\max },{{\sigma }_1}^2\right)(25)$

$S_{EVi\_\mathit{e}\mathit{n}\mathit{d}}=SO{C}_{i,\max }(26)$

Where, $P_{c,1}$ and $P_{\mathit{d}\mathit{i}\mathit{s}\mathit{c},1}$ are the charging and discharging power of a single EV, respectively. $N_{EV}^t$ is the number of EVs in the off-road state at time t. $\mathit{S}O{C}_{EV}^t$ is the average charge state of controllable EVs at time t; $\mathit{S}O{C}_{\min }$ is the minimum SOC value allowed for EVs; $\mathit{S}O{C}_{\max }$ is the maximum SOC value allowed for EVs. i is the ith dispatchable EV. $S_{EVi\_\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}}$ is the initial charge, $\mathit{N}\left(\right)$ is the normal distribution function, $D_{EVi}$ is the depth of discharge, ${{\sigma }_1}^2$ and is the variance of the initial charge distribution. $S_{EVi\_\mathit{e}\mathit{n}\mathit{d}}$ is the power level at the moment of pickup.

4 IGDT-based VPP dispatching model

4.1 IGDT-based VPP dispatching model

In the deterministic dispatching model established in Chapter 3, the wind turbine output, PV output and base load are deterministic quantities. At the same time, in the existing system, all three parameters are volatile and uncertain. The IGDT model can construct the most considerable extensive uncertainty fluctuation intervals under the condition that the optimization result is not worse than the preset value, to avoid the influence of uncertainty on the solution result. For this paper, the uncertainty sets of wind turbine output, PV output, and base load are modelled as shown in (27).

$\{\begin{array}{l}U\left({\alpha }_W,{\stackrel{\sim }{P}}_W^t\right)=\left\{P_W^t:\left|P_W^t-{\stackrel{\sim }{P}}_W^t\right|⩽{\alpha }_W{\stackrel{\sim }{P}}_W^t\right\}\\ U\left({\alpha }_{PV},{\stackrel{\sim }{P}}_{PV}^t\right)=\left\{P_{PV}^t:\left|P_{PV}^t-{\stackrel{\sim }{P}}_{PV}^t\right|⩽{\alpha }_{PV}{\stackrel{\sim }{P}}_{PV}^t\right\}\\ U\left({\alpha }_{\mathrm{L}},{\stackrel{\sim }{P}}_L^t\right)=\left\{P_L^t:\left|P_L^t-{\stackrel{\sim }{P}}_L^t\right|⩽{\alpha }_{\mathrm{L}}{\stackrel{\sim }{P}}_L^t\right\}\\ {\alpha }_W⩾0,{\alpha }_{PV}⩾0,{\alpha }_{\mathrm{L}}⩾0\end{array}(27)$

Where: ${\stackrel{\sim }{P}}_W^t$, ${\stackrel{\sim }{P}}_{PV}^t$, ${\stackrel{\sim }{P}}_L^t$ are the predicted values of WT output, PV output and load at time t; $P_W^t$, $P_{PV}^t$, $P_L^t$ are the actual values of WT output, PV output and load at time t; ${\alpha }_W$, ${\alpha }_{PV}$, ${\alpha }_{\mathrm{L}}$ are the uncertainty radius of WT output, PV output and load, respectively.

The comprehensive uncertainty radius of the system $\psi$ is obtained by the weighted sum form:

$\psi ={\lambda }_W{\alpha }_W+{\lambda }_{PV}{\alpha }_{PV}+{\lambda }_L{\alpha }_L(28)$

Where, ${\lambda }_W$, ${\lambda }_{PV}$, ${\lambda }_L$ are the weight coefficients of WT output, PV output, and load demand uncertainty radius respectively, which can reflect the different demand levels for wind-PV-load uncertainty by decision-makers.

The IGDT theory consists of risk aversion strategy (RAS) and risk seeker strategy (RSS). RAS maximizes the impact of uncertainty on the solution outcome by constructing a robust model (RM), and RSS maximizes the return from uncertainty risk by constructing an opportunity model (OM). The optimization objective of this paper is to avoid the impact of wind-PV-load uncertainty on VPP optimal scheduling results. Therefore, the RAS strategy is chosen to build IGDT robust model.

According to the objective functions $C_1$ and $C_2$ in Chapter 3, the robust optimization model of IGDT for VPP is:

$\{\begin{array}{l}\max \psi \\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}0\le \psi \le 1\\ C_1\left(\mathbf{X},{\mathbf{P}}_{W,t},{\mathbf{P}}_{PVt},{\mathbf{P}}_{L,t}\right)\le f_{c1}\\ C_2\left(\mathbf{X},{\mathbf{P}}_{W,t},{\mathbf{P}}_{PV,t},{\mathbf{P}}_{L,t}\right)\le f_{c2}\\ f_{c1}=\left(1+\sigma \right)f_{c10}\\ \begin{array}{l}{f}_{c2}=\left(1+\sigma \right)f_{c20}\\ \mathit{e}\mathit{q}\mathit{u}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(6\right)-\mathit{e}\mathit{q}\mathit{u}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(28\right)\end{array}\end{array}\end{array}(29)$

where $f_{c10}$ and $f_{c20}$ are the minimum system operating costs and minimum CO₂ emissions, respectively, under the deterministic model. $f_{c1}$ and $f_{c2}$ are respectively the optimal solution of system operating cost and the optimal solution of carbon dioxide emissions acceptable to decision-makers under the uncertainty model. $\psi$ is the deviation coefficient of the uncertainty, $\psi >0$. $\sigma$ is the evasion coefficient of uncertainty, which indicates the range of change that the decision-maker can accept. The larger, the greater the degree of risk evasion and the stronger the robustness.

The cost of renewable energy is far less than that of purchased electricity, and its carbon dioxide emissions are approximately zero. When the WT and PV output is smaller and the load is larger, the system operation cost is higher, and the carbon emission is larger. Therefore, (29) is simplified to an optimization model to improve the solution efficiency, as shown in (30).

$\{\begin{array}{l}\max \psi \\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}0\le \psi \le 1\\ C_1\left(\mathbf{X},{\mathbf{P}}_{W,t},{\mathbf{P}}_{PVt},{\mathbf{P}}_{L,t}\right)\le f_{c1}\\ C_2\left(\mathbf{X},{\mathbf{P}}_{W,t},{\mathbf{P}}_{PV,t},{\mathbf{P}}_{L,t}\right)\le f_{c2}\\ f_{c1}=\left(1+\sigma \right)f_{c01}\\ \begin{array}{l}{f}_{c2}=\left(1+\sigma \right)f_{c02}\\ P_W^t=\left(1-{\alpha }_W\right){\stackrel{\sim }{P}}_W^t\\ P_{PV}^t=\left(1-{\alpha }_{PV}\right){\stackrel{\sim }{P}}_{PV}^t\\ P_L^t=\left(1+{\alpha }_L\right){\stackrel{\sim }{P}}_L^t\\ \mathit{e}\mathit{q}\mathit{u}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(4\right)-\mathit{e}\mathit{q}\mathit{u}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(13\right),\mathit{e}\mathit{q}\mathit{u}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(14\right)-\mathit{e}\mathit{q}\mathit{u}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(26\right)\end{array}\end{array}\end{array}(30)$

4.2 Solving algorithm

This paper uses an adaptive reference vector based constrained-MOEA (ARVC-MOEA) algorithm to solve the IGDT multi-objective dispatching model. ARVC-MOEA is evolved from multi-objective evolutionary algorithm (MOEA). MOEA is very successful in solving unconstrained multi-objective optimization problems. When dealing with constrained multi-objective optimization problems, suitable constraint processing techniques are needed to handle equation and inequality constraints.

To address the difficulties in dealing with constrained problems in MOEA, an adaptive reference vector based constrained-MOEA is used in this paper. The algorithm classifies the populations in the initial stage: one class does not consider the constraints so that the populations can cross intervals with an extensive range of constraints; the other class considers the constraints so that the populations remain well distributed. In the last stage, the algorithm constructs a local distribution enhanced region through local search. At the early stage of the algorithm, some unconstrained populations can guide the population to cross infeasible intervals and improve convergence speed. In the later stage, the algorithm uses a weakly distributive aggregation function to enhance the search capability by expanding the search range of reference vectors that are not helpful to population evolution.

ARVC-MOEA divides the reference vector into the main and auxiliary reference vectors. The auxiliary reference vector is adaptively adjusted to assist the algorithm in solving different constraints, while the main reference vector is globally unchanged to ensure the rationality and stability of the algorithm. Compared with MOEA, ARVC-MOEA can obtain better search performance and faster convergence speed by hybrid computation of split categories and improve the solution efficiency (Shi and Shi, 2022).

The solution flow of the VPP optimal dispatching model based on the adaptive reference vector based constrained-MOEA is shown in Figure 4.

FIGURE 4

FIGURE 4. Flow of adaptive reference vector based constrained-MOEA for solving.

5 Example analysis

5.1 System parameter setting

This paper uses the VPP system shown in Figure 1 for verification analysis. The VPP consists of a 900 kW wind farm, a 500 kW PV plant, two 440 kW gas turbines and a 400 kW energy storage system. The load includes residential, general commercial and industrial loads. The natural gas price is 2.5 ¥/m^3, and the low calorific value of natural gas is 9.7 kWh/m³. The detailed parameters of the WT, PV, GT and ESS are shown in Table 1. The electricity price is based on the Shanghai two-part summer time-of-use price, with peak hours from 08:00 to 11:00, 13:00 to 15:00, and 18:00 to 21:00; valley hours from 22:00 to 06:00 the next day, and the other hours are the normal periods. The time-of-use price is shown in Table 2. ARVC-MOEA algorithm parameters are set: the population size is 50, the generation interval of the update mark is 50, and the number of terminating iterations is 1,000 generations.

TABLE 1

TABLE 1. Relevant parameters.

TABLE 2

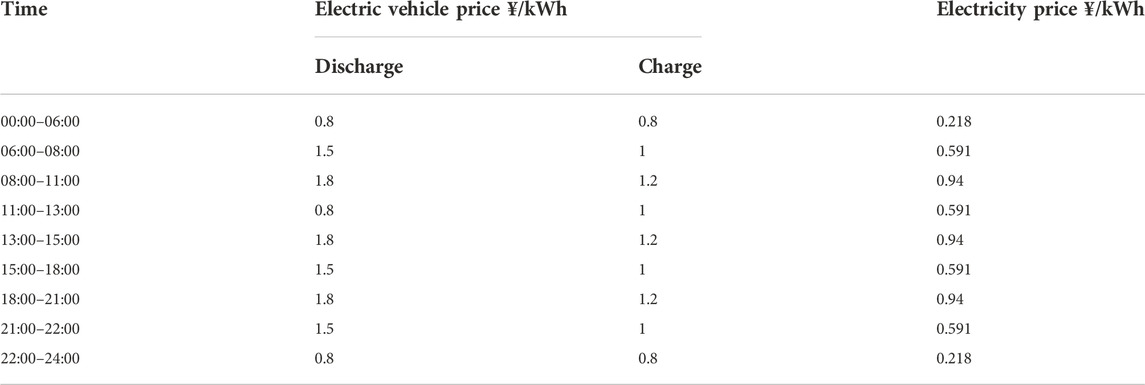
TABLE 2. Electricity for base load and electric vehicle charging and discharging time-of-use prices.

The forecast values of WT and PV output and load are shown in Figure 5.

FIGURE 5

FIGURE 5. Wind and photovoltaic output curves on a typical day.

5.2 Analysis of dispatching results based on IGDT model

The system parameters and the predicted values of wind-PV-load are substituted into the deterministic dispatching model and solved to obtain the overall optimal solutions $f_{c10}$ = ¥10,636.4 and $f_{c20}$ = 13942.55 kg. Figure 6 shows the optimal dispatching results corresponding to the optimal compromise solutions obtained based on the IGDT model. A positive power value indicates energy supply, and a negative power value indicates energy consumption. From Figure 6, it can be seen that from 00:00 to 06:00 a.m., the electricity price is at the valley period. V2G guides the EV users to charge during this period while the ESS enters the charging state. The GT output increases significantly from 06:00 to 08:00, while the EVs and ESSs continue to charge during the normal period. In the peak period, VPP reduces the purchased electricity through optimal dispatching and turns to natural gas and ESS to compensate for the economic burden caused by the peak price. The GT output increases significantly, and the ESS performs discharge to meet the load demand. Meanwhile, guided by the time-of-use price strategy and V2G, EVs serve as a power supply for the power system, reducing the peak load and the VPP operation cost during peak hours.

FIGURE 6

FIGURE 6. Dispatching results based on the IGDT model.

5.1.1 The effect of the evasion coefficient on the dispatching results of the IGDT model

The uncertainty radius, system operation cost and carbon emissions trends of the uncertainty model are shown in Figure 7 by setting the evasion coefficient to vary in 0–0.1. The operating cost and carbon emissions are expressed in per unit value (p.u.). The figure shows that the uncertainty radius keeps increasing with the increase of the evasion coefficient, and the system operation cost and carbon dioxide emission increase. This is because the robust model under the RAS believes that uncertainty makes the target expectation develop in an unfavourable direction. The uncertainty factor is not conducive to the reduction of the objective function. The larger the uncertainty radius, the smaller the risk caused by the uncertainty of WT output, PV output and the load; therefore, the higher the system operation cost and carbon emission. The increase in uncertainty radius represents improving the system’s ability to withstand wind-PV-load uncertainty. The dispatching scheme in this case, can better cope with the long-term uncertainty of wind-PV-load, and VPP can select an appropriate evasion coefficient according to the cost it can bear.

FIGURE 7

FIGURE 7. Trends in operating cost, carbon emissions and uncertainty radius.

5.1.2 The effect of weight coefficients on the dispatching results of the IGDT model

Set the evasion coefficient $\sigma$ as 0.02, and select different weight coefficients to optimize the IGDT dispatching model, and the results are shown in Table 3. From the table, it can be seen that different weight coefficients affect the results of single uncertainty radius ${\alpha }_W$ , ${\alpha }_{PV}$ , ${\alpha }_{\mathrm{L}}$ solutions. The smaller the uncertainty radius is, the more sensitive the system will be to the fluctuation of this uncertainty factor. The decision-maker can set each weighting factor based on the principle that the higher the sensitivity, the higher the weighting factor. Take the weight coefficients ${\lambda }_W=5$, ${\lambda }_{PV}=1$, ${\lambda }_L=5$ as an example, at this time ${\alpha }_W=0.0278$, ${\alpha }_{PV}=0.616$, ${\alpha }_{\mathrm{L}}\approx 0$. The system’s operating cost under this weight coefficient is ¥12,157.1and the carbon emission is 14,280.5 kg. It shows that when the actual value of WT output fluctuates within 61.6%, the actual value of PV output fluctuates within 2.78%, and the load demand forecast is accurate, the total dispatch cost of the system will not exceed ¥12,157.1. Under the IGDT robust model with RAS, the conventional unit output increases to cope with the uncertainty of wind-PV-load, increasing the operating cost and carbon emission. Compared with the deterministic model, the IGDT robust model with RAS is more conservative.

TABLE 3

TABLE 3. Uncertainty radius with different types of weight coefficient.

Compared with the deterministic model, the IGDT robust model under RAS is more conservative. Although different weighting coefficients have a large impact on the single uncertainty radius, they have a small impact on but not on the integrated uncertainty radius of the system. Take ${\lambda }_W=5$, ${\lambda }_{PV}=1$, ${\lambda }_L=5$, and ${\lambda }_W=5$, ${\lambda }_{PV}=1$, ${\lambda }_L=10$ for example, where $\psi$ is 0.7521. This is because although the load has uncertainty, the daily fluctuation range of the load is limited, while the load fluctuation has a certain regularity. Compared with PV and WT output, the uncertainty of load is smaller, so the radius of comprehensive uncertainty of the system does not change much. The scheduling decision maker can set each weighting factor according to the actual system situation and historical experience, based on the principle that the higher the sensitivity, the higher the weighting factor.

5.3 Effect of V2G on the load curve

GT output and purchased electricity have made major contributions to the operation cost and carbon emissions, and the discussion of GT and purchased electricity before and after dispatching is more important. Figure 8 shows the comparison of GT output and purchased electricity before and after the system considers V2G. The solid line part considers V2G. Before and after EVs dispatching, the output of GT and purchased electricity have changed, and the change of purchased electricity is more obvious. After the EVs participates in the dispatching, the peak load is significantly reduced. Under the comprehensive goal of considering economic and environmental benefits, the system reduces the purchased electricity from the superior power grid. The reduced purchased electricity in the peak time has made a great contribution to reducing the operating cost of the system. Meanwhile, the carbon emission coefficient of power grid is higher than that of GT, the decrease of purchased electricity reduces carbon emissions significantly. Some EVs in peak hours are dispatched to charge at valley time, which increases the load during this period. Because of the cheap electricity price at valley time, the system chooses to purchase more electricity from the superior power grid to reduce the operation cost.

FIGURE 8

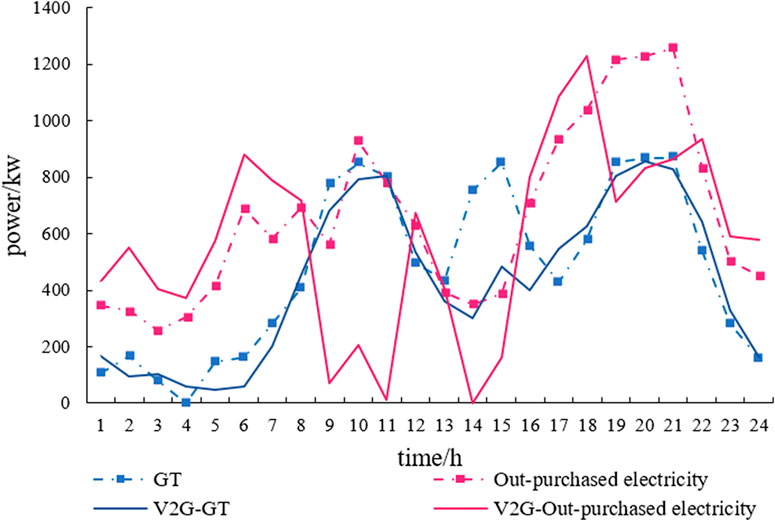
FIGURE 8. Comparison of GT output and purchased electricity before and after the system considers V2G.

Figure 9 shows the comparison of EV charging and discharging as well as load before and after optimization. The bar chart comparison shows that V2G increases the EV significantly in both the normal and valley periods. EV has played a full role in filling the valley, reducing the charging cost of EC owners, and has played a positive role on both the supply and user sides. EV discharges during peak hours of 08:00–11:00, 13:00–15:00 and 18:00–21:00, which play a peak-shaving role on the load curve and at the same time reduce the amount of electricity purchased by VPP from the superior grid during the peak hours. On the premise of meeting the needs of EV owners, V2G gently transfers the load during peak hours to normal and valley hours. The peak EV charging load from 13:00 to 15:00 is assigned to the normal period at noon and afternoon, and that from 18:00 to 22:00 is transferred to 22:00 to the early morning of the next day to achieve the purpose of peak shaving and valley filling. Overall, by comparing the load curves, we can see that the curve after dispatching tends to be smoother. V2G can smooth the load curve and narrow the load peak-valley difference, which effectively increases the operating economy and safety of the system.

FIGURE 9

FIGURE 9. Comparison of load curve before and after dispatching.

Before and after optimization, the electricity consumption changed by the load curve follows the “equal area principle” in principle. The increased electricity consumption after optimization (the part of the optimized curve is higher than the pre-optimized curve, S₂ in Figure 9) and the cut electricity consumption (the part of the pre-optimized curve is higher than the optimized curve, S₁ in Figure 9) should be equal. Since EV owners rarely release excess electricity to the upper grid when charging freely. In V2G mode, VPP will dispatch EVs with discharge potential to discharge according to the owner’s electricity demand and current electricity. Therefore, the actual optimized increased electricity consumption is smaller than the cut electricity consumption.

For EV orderly charging under different responsiveness, the GT power generation cost, purchased electricity cost, system operation cost and the battery degradation cost are shown in Figure 10, and the carbon emissions and peak valley difference ratio are shown in Figure 11. All data are per unit values based on the Res = 50%. Combining the two figures, it can be seen that as the percentage of EV users participating in dispatching increases, the operating cost decreases from ¥13,123.36 to ¥10,652.7, and the carbon emission decreases from 14,447.51kg to 13,423.74 kg. Although the battery degradation cost increases with the increase of responsiveness, the operating cost still decreases due to the reduction of GT output and out-purchased electricity, as well as the dual impact of EVs participating in V2G on the power side and load side. At the same time, a high proportion of EVs with orderly charging participate in economic dispatch can effectively reduce the load peak-to-valley difference. Therefore, adopting time-of-use prices or other incentives to increase the responsiveness of EV orderly charging is conducive to smoothing the load curve, reducing system operating costs, and improving the environmental benefits of VPP.

FIGURE 10

FIGURE 10. Comparison of operating costs for EVs with different responsiveness.

FIGURE 11

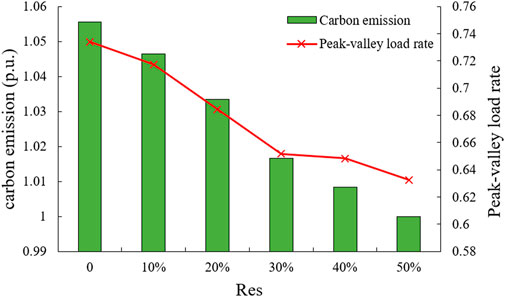
FIGURE 11. Comparison of carbon emissions, peak-to-valley difference rate under different responsiveness of EV.

5.4 ARVC-MOEA algorithm superiority analysis

To verify the superiority of ARVC-MOEA applied in this paper to handle the multi-objective model considering source load uncertainty, NSGA-II and MOCD/E algorithms are used to solve the IGDT-based VPP multi-objective model in V2G mode, respectively. All algorithms with a population size of 50 and a termination iteration number of 1,000 generations are used. The best Pareto Frontier obtained after six runs are shown in Figure 12. The Pareto Frontier for the three algorithms shows that the operating costs and carbon emissions are generally in a mutually constraining relationship. This is because to achieve smaller carbon emissions, more EVs need to be mobilized to participate in V2G regulation, and the corresponding GT output and out-purchased electricity will be smaller during peak hours, and vice versa. Therefore, the applied ARVC-MOEA processing of the multi-objective model considering the source-load uncertainty has a smaller operating cost for a certain carbon emission. From the figure, it can be seen that the Pareto front obtained by ARVC-MOEA is located at the bottom and has the largest span, and is more complete than the other two algorithms in the global non-inferior target domain. ARVC-MOEA introduces primary and secondary reference vectors, and solves different kinds of constraints by adaptively adjusting the secondary reference vectors. ARVC-MOEA effectively improves the ability of solving constraints and the search ability of solutions while ensuring the rationality and stability of the algorithm.

FIGURE 12

FIGURE 12. Comparison of the best Pareto Frontier for different algorithms.

6 Conclusion

Based on the operational characteristics of multi-source VPPs and the V2G characteristics of electric vehicles, this paper establishes a multi-objective IGDT optimal dispatching model for VPP in V2G mode, considering source-load uncertainties with the system operating costs and carbon emissions as the optimization objectives. The superior ARVC-MOEA algorithm is used for an efficient solution, and the following conclusions are drawn (Ma et al., 2016):

(1) The multi-objective IGDT optimal dispatching model of VPP, considering source-load uncertainty in V2G mode, can fully ensure the economic and environmental benefits of the system. It can obtain the optimal dispatching scheme of VPP with the integrated optimal system operation cost and carbon emission.

(2) The IGDT-based uncertainty optimization dispatching model quantifies uncertainty from a risk-averse perspective and provides a robust dispatching model for decision-makers. By setting weight coefficients, the influence of wind-PV-load uncertainty on dispatching operation can be quantified, which can provide a reference for the optimal dispatching of multi-source VPPs.

(3) Based on time-of-use price, V2G is used to transfer EVs’ charging and discharging periods. Incorporating the demand side adjustable resources into the power balance can realize the “peak cutting and valley filling” of the load curve, alleviate the energy supply pressure and improve the power supply reliability.

(4) The Pareto optimal Frontier obtained by ARVC-MOEA is better than the NSGA-II algorithm and the MOCDE algorithm in terms of accuracy and completeness.

In this paper, the model used for EV dispatching is relatively simple. The future research will consider the two-stage optimization strategy of orderly charging and discharging of EVs.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LR, DP, and DW contributed to conception and design of the study. LR organized the database. LR performed the statistical analysis. LR wrote the first draft of the manuscript. LR, JL, HZ, and DW wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (NSFC) under Project No. 92067105 and Project No.71871160, the Shanghai Science and Technology Commission Program under Project No.20020500500, and the Shanghai Sailing Program under Project No.20YF1414900.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alabdulwahab, A., Abusorrah, A., Zhang, X., and Mohammad, S. (2015). Coordination of interdependent natural gas and electricity infrastructures for firming the variability of wind energy in stochastic day-ahead scheduling. IEEE Trans. Sustain. Energy 6 (2), 606–615. doi:10.1109/TSTE.2015.2399855

CrossRef Full Text | Google Scholar

Bai, L., Li, F., Cui, H., Jiang, T., Hong, B., and Jin, X. (2016). Interval optimization based operating strategy for gas-electricity integrated energy systems considering demand response and wind uncertainty. Appl. Energy 167, 270–279. doi:10.1016/j.apenergy.2015.10.119

CrossRef Full Text | Google Scholar

Cao, X., Wang, J., and Zeng, B. (2018). A chance constrained information-gap decision model for multi-period microgrid planning. IEEE Trans. Power Syst. 33 (3), 2684–2695. doi:10.1109/TPWRS.2017.2747625

CrossRef Full Text | Google Scholar

Catalão, J., Pousinho, H., and Mendes, V. (2011). Optimal offering strategies for wind power producers considering uncertainty and risk. IEEE Syst. J. 6 (2), 270–277. doi:10.1109/JSYST.2011.2163009

CrossRef Full Text | Google Scholar

Falsafi, H., Zakariazadeh, A., and Jadid, S. (2014). The role of demand response in single and multi-objective wind-thermal generation scheduling: A stochastic programming. Energy 64, 853–867. doi:10.1016/j.energy.2013.10.034

CrossRef Full Text | Google Scholar

Fang, F., Yu, S., and Xin, X. (2022). Data-Driven-based stochastic robust optimization for a virtual power plant with multiple uncertainties. IEEE Trans. Power Syst. 37 (1), 456–466. doi:10.1109/TPWRS.2021.3091879

CrossRef Full Text | Google Scholar

Wei, H., Zhang, Y., Wang, Y., Hua, W., Jing, R., and Zhou, Y. (2022). Planning integrated energy systems coupling V2G as a flexible storage. Energy 239, 122215. doi:10.1016/j.energy.2021.122215

CrossRef Full Text | Google Scholar

Jiang, T., Li, X., Kou, X., Zhang, R., Tian, G., and Li, F. (2022). Available transfer capability evaluation in electricity-dominated integrated hybrid energy systems with uncertain wind power: An interval optimization solution. Appl. Energy 314, 119001–122619. doi:10.1016/j.apenergy.2022.119001

CrossRef Full Text | Google Scholar

Li, J., Wang, J., Cao, X., Zhou, X., and Lu, S. (2019). A chance-constrained IGDT model for joint planning of wind farm, energy storage and transmission. Power Syst. Technol. 43 (10), 3715–3724. doi:10.13335/j.1000-3673.pst.2018.1929

CrossRef Full Text | Google Scholar

Li, P., Yu, X., Zhang, Y., Zhou, Q., Tian, C., and Qiao, H. (2022). Multi-objective stochastic scheduling optimization model for rural virtual power plant considering carbon capture and power-to-gas. Electr. Power Constr. 43 (07), 24–36. doi:10.16182/j.issn1004731x.joss.22-0189

CrossRef Full Text | Google Scholar

Liu, C., Zhuo, J., Zhao, D., Li, S., Chen, J., Wang, J., et al. (2020). A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids. Proc. CSEE 40 (01), 1–18+369. doi:10.13334/j.0258-8013.pcsee.190212

CrossRef Full Text | Google Scholar

China International Economic Exchange Center & State Power Investment Group Co.Ltd. (2021). Report on the peak carbon emission and carbon neutrality. Beijing: Social Sciences Academic Press.

Google Scholar

Lu, Z., Xu, X., Yan, Z., Wu, J., Sang, D., and Wang, S. (2020). Overview on data-driven optimal scheduling methods of power system in uncertain environment. Automation Electr. Power Syst. 44 (21), 172–183. doi:10.7500/AEPS20200202004

CrossRef Full Text | Google Scholar

Ma, Z., Zou, S., Ran, L., Shi, X., and Hiskens, A. L. (2016). Efficient decentralized coordination of large-scale plug-in electric vehicle charging. Automatica 69 (C), 35–47. doi:10.1016/j.automatica.2016.01.035

CrossRef Full Text | Google Scholar

Morales, J., Conejo, A., and Pérez-Ruiz, J. (2010). Short-term trading for a wind power producer. IEEE Trans. Power Syst. 25 (1), 554–564. doi:10.1109/TPWRS.2009.2036810

CrossRef Full Text | Google Scholar

Niu, D., Ji, Z., Li, W., Xu, X., and Liu, D. (2021). Research and application of a hybrid model for mid-term power demand forecasting based on secondary decomposition and interval optimization. Energy 234, 121145–125442. doi:10.1016/j.energy.2021.121145

CrossRef Full Text | Google Scholar

Pan, Z., Wang, K., Qu, Kaiping., Yu, T., Wang, D., and Zhang, X. (2018). Coordinated optimal dispatch of electricity-gas-heat multi-energy system considering high penetration of electric vehicles. Automation Electr. Power Syst. 42 (4), 104–112. doi:10.7500/AEPS20170527007

CrossRef Full Text | Google Scholar

Peng, C., Chen, L., Zhang, J., and Sun, H. (2020). Multi-objective optimal allocation of energy storage in distribution network based onClassified probability chance constraint information gap decision theory. Proc. CSEE 40 (09), 2809–2819. doi:10.13334/j.0258-8013.pcsee.190551

CrossRef Full Text | Google Scholar

Qian, W., Zhao, C., Wan, C., Huang, Y., Zhu, B., and Chen, W. (2021). Probabilistic forecasting based stochastic optimal dispatch and control method of hybrid energy storage for smoothing wind power fluctuations. Automation Electr. Power Syst. 45 (18), 18–27. doi:10.7500/AEPS20200616007

CrossRef Full Text | Google Scholar

Sc, A., and Zl, B. (2019). Multi-objective network reconfiguration considering V2G of electric vehicles in distribution system with renewable energy. Energy Procedia 158, 278–283. doi:10.1016/j.egypro.2019.01.089

CrossRef Full Text | Google Scholar

Shi, F., and Shi, X. (2022). Adaptive reference vector based constrained multi-objective evolutionary algorithm. J. Comput. Appl. 42 (02), 543–549. doi:10.11772/j.issn.1001-9081.2021020337

CrossRef Full Text | Google Scholar

Shi, W., Qin, W., Wang, L., Yao, H., Jing, X., Zhu, Y., et al. (2022). Regional power grid LSTM dispatching strategy considering electric vehicle demand and time of use price difference. Proc. CSEE 42 (10), 3573–3587. doi:10.13334/j.0258-8013.pcsee.202473

CrossRef Full Text | Google Scholar

Taheri, S., Salles, M., and Costa, E. (2020). Optimal cost management of distributed generation units and microgrids for virtual power plant scheduling. IEEE Access 8, 208449–208461. doi:10.1109/ACCESS.2020.3039169

CrossRef Full Text | Google Scholar

Wang, L., Zhu, Z., Jiang, C., and Li, Z. (2020). Bi-level robust optimization for distribution system with multiple microgrids considering uncertainty distribution locational marginal price. IEEE Trans. Smart Grid 12 (2), 1104–1117. doi:10.1109/TSG.2020.3037556

CrossRef Full Text | Google Scholar

Wang, M., Lu, L., and Xiang, Y. (2022). Coordinated scheduling strategy of electric vehicles for peak shaving considering V2G price incentive. Electr. Power Autom. Equip. 42 (04), 27–33+85. doi:10.16081/j.epae.202201009

CrossRef Full Text | Google Scholar

Wang, Z., Liu, Y., and Su, Q. (2022). Load frequency control of multi area V2G system based on sliding mode control. Control Eng. China, 1–8. doi:10.14107/j.cnki.kzgc.20210092

CrossRef Full Text | Google Scholar

Ye, H., Liu, S., Hu, J., Xiong, X., and Tan, Y. (2021). Multi-source joint dispatching strategy for a power system with concentrating solar power plants based on. IGDT 49 (23), 35–43. doi:10.19783/j.cnki.pspc.202114

CrossRef Full Text | Google Scholar

Yi, Z., Xu, Y., Gu, W., and Wu, W. (2020). A multi-time-scale economic scheduling strategy for virtual power plant based on deferrable loads aggregation and disaggregation. IEEE Trans. Sustain. Energy 11 (3), 1332–1346. doi:10.1109/TSTE.2019.2924936

CrossRef Full Text | Google Scholar

Zeng, L., Xu, J., Wu, M., Tang, J., Wu, Q., Wang, Q., et al. (2021). Day-ahead interval optimization for CCHP system considering uncertainty of wind power and PV. Int. J. Electr. Power & Energy Syst. 138, 107895–110615. doi:10.1016/j.ijepes.2021.107895

CrossRef Full Text | Google Scholar

Zhang, C., Chen, H., Shi, K., Liang, Z., Mo, W., and Hua, D. (2019). A multi-time reactive power optimization under interval uncertainty of renewable power generation by an interval sequential quadratic programming method. IEEE Trans. Sustain. Energy 10 (3), 1086–1097. doi:10.1109/TSTE.2018.2860901

CrossRef Full Text | Google Scholar

Zhong, W., Huang, S., Cui, Y., Xu, J., and Zhao, Y. (2020). Coordinated optimal dispatch of wind power solar thermal carbon capture virtual power plant considering source load uncertainty. Power Syst. Technol. 44 (09), 3424–3432. doi:10.13335/j.1000-3673.pst.2019.1986

CrossRef Full Text | Google Scholar

Zhu, L., Huang, H., Gao, S., He, Y., and Bian, Y. (2021). Research on optimal load allocation of electric vehicle considering wind power consumption. Proc. CSEE 41 (S1), 194–203. doi:10.13334/j.0258-8013.pcsee.202473

CrossRef Full Text | Google Scholar