- 1College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen, China
- 2School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen, China
- 3College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen, China
In recent years, with the continued development and popularity of sustainable energy sources and the increasing utilization of solar energy, accurate solar radiation prediction has become important. In this paper, we propose a new model based on deep learning, Feature-enhanced Gated Recurrent Unit, hereafter referred to as FEGRU, for solar radiation prediction. This model takes the source data with one-dimensional convolution and self-attention to feature attention and processes the data features, and then GRU performs feature extraction on solar irradiance data. Finally, the data dimensionality is transformed by a fully connected layer. The main advantage of FEGRU is that it does not require auxiliary data, but only time series data of solar irradiance can be used for good solar irradiance prediction. Our experiments with solar irradiance samples in Lyon, France, show that our model has better prediction results than the baseline model.
1 Introduction
Energy Li et al. (2021); Ahmad S. et al. (2018) has been a part of everyone’s concern since mankind entered modern civilization. Solar energy is a renewable energy source. Generally speaking, solar energy refers to the sun’s thermal radiation energy, which is mainly expressed as what we often call the sun’s rays. In modern society, solar energy is generally used to generate electricity or to provide energy for water heaters. It is worth mentioning that solar energy has certain advantages over other renewable energy sources because it is clean, substantial, reduces environmental pollution, and has a wide application potential Liu (2014). If we can make more accurate short-term predictions of solar radiation, we can plan ahead for better energy management. This plays an important role in many aspects of the industry, like thermal power plants, hydroelectric plants, and other power plants, to keep the voltage and frequency of the grid stable. If we can plan and schedule energy more rationally Ahmad et al. (2020b); Ahmad H. et al. (2018), we can make it fully effective in the economic sphere. We can make plans according to consumers’ needs for energy. For example, intelligent energy consumption managementsystems that take into account consumer consumption goals Yaqub et al. (2016), wind energy Ma et al. (2020) supplier bidding strategies Zhang et al. (2021), and joint energy management and energy trading Ahmad et al. (2020a). In recent years, global energy issues have received more and more attention, among which the prediction of solar irradiance has gradually attracted a lot of attention from academia and industry.
2 Related work
For energy prediction, there are roughly four categories of methods. These are physical models, statistical models, hybrid models, and artificial intelligence models. Among the first type of physical models there is a classical Salman et al. (2018) model designed with a microcontroller based battery charge controller and using a controller with a maximum power point tracker MPPT operating at a given insolation and temperature condition. The second class of statistical models is more classical and includes those of AR, MA, ARMA, ARIMA, etc. Yamak et al. (2019) Colak et al. (2015) Shadab et al. (2019) Shadab et al. (2020). Although these models are able to capture the data characteristics to some extent. But on the other hand, the results derived from these models are often the basis of fitted curves obtained from sample time series, which are then carried on inertially along with the existing patterns. In other words, the mean and variance of the data do not change much in theory. Next, these models are quite limited in their ability to handle high-dimensional time series data. In the third category of hybrid models, Caldas and Alonso-Suárez (2019) Caldas et al. proposed a hybrid prediction method. This method collects all-day images and irradiance data in real time and uses it as data for prediction. The model converts the obtained all-sky images and geographic information into corresponding solar irradiance estimates and uses these values for prediction in real time. Experiments show that the model is capable of making some short-term predictions of solar resources under different solar irradiance conditions. The fourth type of approach is artificial intelligence. Thanks to the development of technology in recent years, computers are advancing rapidly and their computing power is growing exponentially. More and more researchers Wang et al. (2020) are experimenting with machine learning as well as deep learning methods to serve energy prediction directly or indirectly. Typical artificial intelligence methods include support vector machines (SVMs) Hou et al. (2018), extreme learning machines Bouzgou and Gueymard (2017), wavelet transforms Zhang et al. (2020), deep learning Wang et al. (2019), and integration learning AlKandari and Ahmad (2020). For example, the support vector machine (SVM) method is one of the machine learning methods, which belongs to the binary classification algorithm. Support vector machine (SVM) is a relatively simple supervised learning algorithm for classification or regression. It is more suitable for classification, but sometimes very useful for regression as well. Basically, a support vector machine finds a hyperplane that creates a boundary between data types. Machine learning methods Wu et al. (2022); Li et al. (2022); Fu (2022) have also indirectly played a significant role in energy problems. Researchers Fu (2022) used statistical machine learning models of linear regression, probability distributions, Markov chains, isoperimetric transformations, maximum likelihood estimators, stochastic response surfaces, and centroid methods to model erratic weather, photovoltaic generation, thermal loads, power flow, and uncertainty programming. Researchers Fu et al. (2020) also employed statistical machine learning theory to solve the optimal planning of capacitors, specifically by formulating methods such as Markov chains and conjugate functions to capture weather deformability and correlation and introducing probabilistic inequality theory to directly estimate the objective and constraint functions of stochastic programming models. These methods effectively address the optimal planning of capacitors. In the solar irradiance prediction task, Dong et al. (2020) optimizes the hyperparameters in this framework by building a special convolutional neural network prediction framework based internally on regional site meteorological data and the corresponding time, in addition to the chaotic GA/PSO1 hybrid algorithm. The optimization of hyperparameters can further improve the performance of the model, and thanks to the superiority of the hybrid algorithm, this reduces the human and financial resources required to tune the model to some extent. Liu et al. (2019) liu et al. proposed a new spatio-temporal prediction model by combining spatio-temporal information with the task of predicting solar irradiance information. The model embeds data from multiple stations into the convolution operator of the model to extract spatial features. At the same time, a gated loop unit is used to extract temporal features enabling the model to extract spatio-temporal features simultaneously to obtain more accurate prediction results.
In this paper, a new FEGRU model for solar irradiance prediction is proposed to improve the prediction performance of solar irradiance by using the convolution of self-attention blocks on solar irradiance data. Compared with other methods, the contribution of this paper is mainly in two aspects. 1. We propose to combine one-dimensional convolution and self-attention and apply it to a recursive cell to improve the accuracy of solar irradiance prediction; 2. we verify the feasibility, effectiveness and superiority of our proposed FEGRU model using actual solar irradiance information collected from Lyon, France. the main advantage of FEGRU is that no auxiliary data are required and good solar irradiance prediction can be performed by time series data of solar irradiance only.
The rest of the paper is organized as follows: Section 3 presents the principles of FEGRU, including its specific model structure as well as the data preprocessing part. Section 4 presents the details of the model we used and the comparison model employed. Section 5 and Section 6 present the case study and the final summary, respectively.
3 Proposed FEGRU for solar irradiance prediction
Our proposed FEGRU model is composed of a one-dimensional convolutional and self-attention module and a variant GRU and finally a fully connected layer. The model obtains special data features by one-dimensional convolutional self-attention of the input solar irradiance data, then embeds the data features into a recursive unit GRU to capture the solar irradiance data features, and finally maps them through a fully connected layer. The FEGRU model is described in detail below. In this section, we detail the training process part by providing a detailed description of the FEGRU model structure and a detailed mathematical formulation.
Definition: As an example, we take the actual solar irradiance information dataset collected in Lyon, France, which has categories of geographic parameters, meteorological parameters, and time series data. We choose solar irradiance information to be used as prediction information for our current model. In this paper, our T denotes the number of information collected by this node of a sensor with longitude latitude of 4.9225 E, 45.7786 N in Lyon, France, at 1-min intervals (e.g., this node with longitude latitude of 4.9225 E, 45.7786 N in Lyon, France, is used to sample every 1 min, so we can understand that the sensor is sampled a total of T times, each time at 1 min interval). XtϵRi is used to represent the solar irradiance information on this node at moment i. In this article Xt = Input [t].
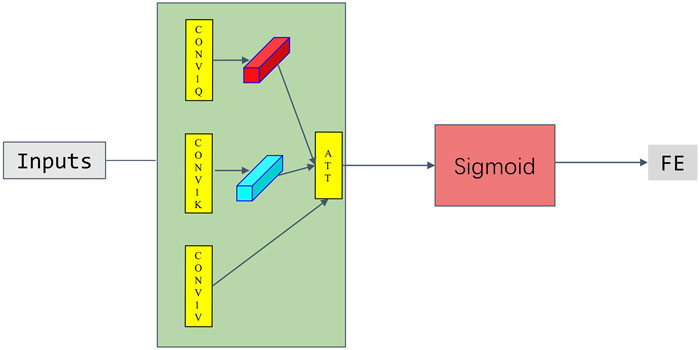
3.1 Feature-enhanced module
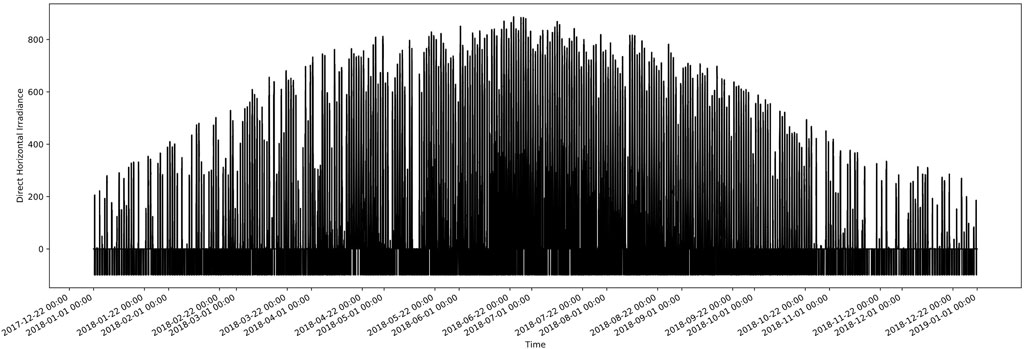
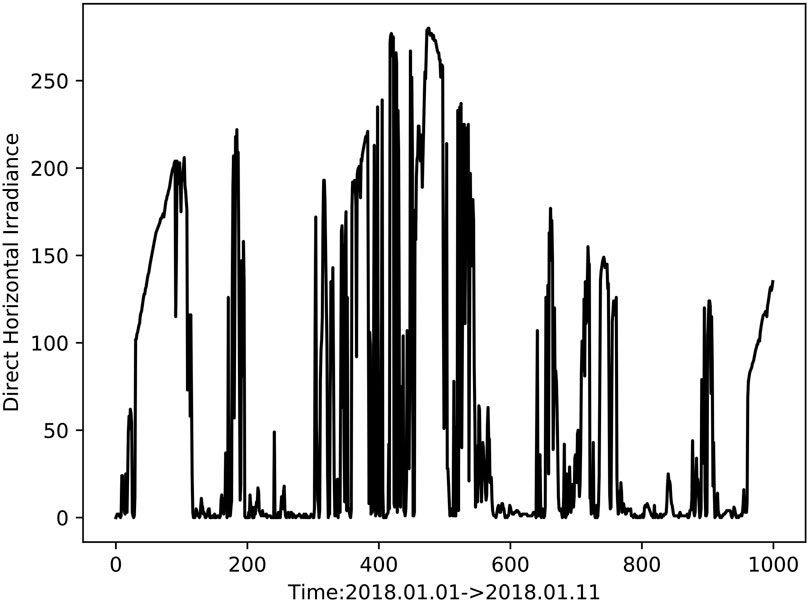
For our solar irradiance data information, we visualize the source data of the solar irradiance information in the Lyon, France sample, and it is obvious from Figure 1 that the direct horizontal irradiance data has large fluctuations and more negative values, so we preprocess it in order to allow the model to focus on the hidden features behind the data. That is, most of the zero and negative values in the direct horizontal irradiance are removed. We introduce the data from January 1, 2018 to January 11, 2018 for visualization, and we can see that the source data becomes similar to Figure 2. It is worth mentioning that our preprocessing session leads to the fact that the solar irradiance data here are not sampled in the same amount on each day. For example, after preprocessing as shown in Figure 2, only 136 solar irradiance sampling points existed on January 1, 2018, and only 15 solar irradiance sampling points existed on January 2, 2018. We can clearly see from the visualizations in Figures 1, 2 that the data fluctuations are very large, in order for our model to capture the hidden information behind the data. We designed the Feature-enhanced module for this purpose to make the model perform better. By performing a one-dimensional convolution of the input three channels of solar irradiance data and using a self-attention mechanism, we enable the model to attention the hidden features in the solar irradiance data, thus enabling the model to obtain better prediction performance.
Here is the mathematical expression for the Feature-enhanced module:
where WQ, WK, and WV are each learnable weight matrices, Tr represents the transpose of the matrix, * represents the matrix multiplicator, and σ represents the Sigmoid function.
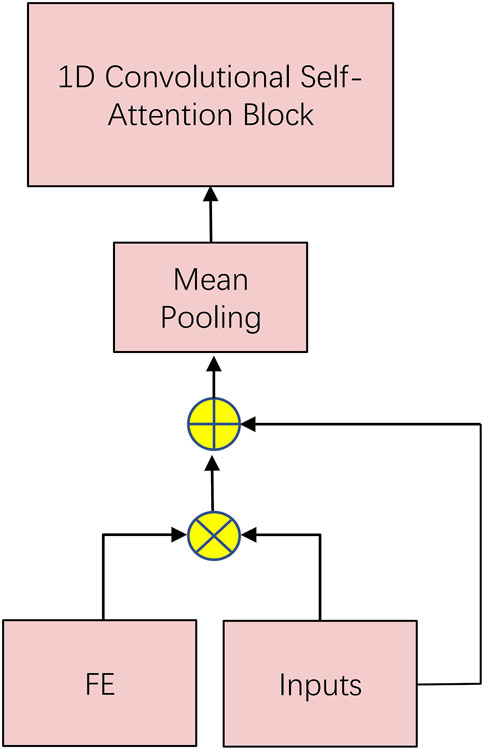
3.2 Feature fusion module
In our experiments, to mitigate the effects of gradient disappearance and gradient explosion on the model, we added a feature fusion module to make the model perform better, as shown in Figures 3, 4. To be precise, we add a residual module and averaging pooling operation to the feature fusion. This is done by multiplying the solar irradiance input data with the Feature-enhanced module and then adding it to itself and averaging the pooling operation.
The mathematical expression is shown below:
@Represents dot product.
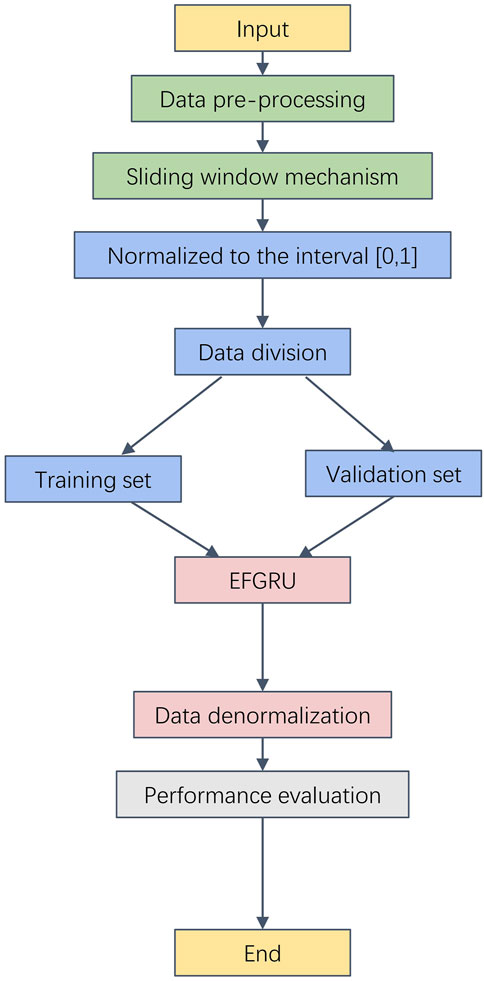
The following summarizes the training process of the FEGRU model. The process can be divided into the following main parts. 1. Using the collected solar irradiance data information from Lyon, France, the data preprocessing in Section 3 was first performed. The preprocessed solar irradiance data information is then used as the overall dataset information for the model. 2. normalize the values of the overall solar irradiance data set to the interval [0,1]. 3. Divide the normalized overall data into training and test sets in the ratio of 8 to 2. 4. The training set data are put into the EFGRU model for training. 5. The optimizer for the parameters of the FEGRU model is the Adam optimizer. The MSE loss function plus the L2 regularization term is used for the loss function. 6. loss calculation is performed at each epoch and back propagation is performed to update the parameters.
The main steps of the FEGRU model training process are shown in Figure 5.
Finally, the internal equation of the FEGRU model is as follows:
4 Experiments
In this section, we present information related to the FEGRU model experiments separately, including the description of the Lyon, France dataset, model evaluation metrics, model parameter settings, comparative model.
4.1 Dataset details
The experiments of our FEGRU model were performed on data collected by sensors with longitude, latitude and altitude of 4.9225E, 45.7786N and 170 m, respectively, in Lyon, France, from March 25, 2018 to October 27, 2018. The dataset includes altitude of the sun, azimuth of the sun (from North to East), global horizontal illuminance, diffuse horizontal illuminance, global vertical north illuminance, global vertical east illuminance, global vertical south illuminance, global vertical west illuminance, global horizontal irradiance, diffuse horizontal irradiance, zenith luminance (11° aperture), relative humidity, wind direction (from North to North), and the temperature of the air. wind direction (from North to East), wind speed, dry bulb temperature irradiance, illuminance shadow band correction factor, irradiance shadow band correction factor, direct horizontal irradiance, global horizontal UVA irradiance, global horizontal UVB irradiance. We choose direct horizontal irradiance as the information task that we want to predict. In our experiments, we normalize the information of the input solar irradiance data to the interval [0,1]. It is also worth mentioning that we used 80% of the data as the training set and the remaining 20% as the test set and trained the FEGRU model using the Adam optimizer. We predicted the solar irradiance data information for this sensor for the next 60 and 90 min.
4.2 Evaluation metrics
To evaluate our proposed FEGRU model, we used three metrics widely used in time-series prediction, namely the mean absolute error (MAE) Chai and Draxler (2014), root mean square error (RMSE) Chai and Draxler (2014), and coefficient of determination (R2) Barrett (2000). RMSE is more commonly used in deep learning and is often used to measure the deviation between the predicted and true values, and it is considered to be an excellent error measure for numerical prediction. MAE is often associated with regression models and is the more classical regression model evaluation metric. In this case, the mean absolute error of the model for the test dataset is the average of the absolute values of the individual prediction errors for all instances in the test dataset. Each prediction error refers to the difference between the true value and the predicted value. The R2 is the square of the correlation between the predicted and true values and can be used to measure whether the model’s prediction is valid.
In brief, the lower the RMSE and MAE the better, and the higher the R2 the better.
1)Root Mean Squared Error (RMSE):
2)Mean Absolute Error (MAE):
3)Coefficient of Determination (R2):
where yi and
Specifically, RMSE, MAE and MAPE are used to measure the prediction error: the smaller the value, the better the prediction.
4.3 Model parameter settings
In our model, we manually set some hyperparameters to ensure that our proposed model achieves the best prediction. Specifically, the parameters that are relatively important for the FEGRU model include: training ephemeris, batch size, and learning rate. In our experiments on the Lyon, France dataset, we set the learning rate to 0.001, the batch size to 32, and the training epoch to 100. Our proposed model algorithm takes about 2 h to run, which is within the range we can accept. In deep learning algorithms, some complex algorithms may have to be run for several days to complete the final convergence. The complexity of our proposed model algorithm is also not too high in terms of running time analysis.
4.4 Contrast models
In our experiments, we compare our proposed FEGRU model with SVR, ARIMA, and GRU models to evaluate the effectiveness of our model. Bae et al. (2016) Support vector machines (SVMs) are widely used not only for classification problems in machine learning, but also for the analysis of regression problems. Gilbert (2005) ARIMA model is a popular and widely used statistical method for time series prediction.Sharif Atique Atique et al. (2019) and others then used ARIMA to predict the total daily solar power generation. GRU Dey and Salem (2017) is a classical variant of recurrent neural network RNN and, like LSTM, was also proposed to solve the long-term memory and back propagation in GRU and LSTM networks have a simpler model structure and better results compared to the network, and are often applied in most of the time-series prediction problems.
5 Experimental results analysis
By preprocessing the data on the source data information set in Lyon, France, the data information is made to appear to have a slightly smaller sample size compared to the source data information slightly less, but we did this in order to allow the model to receive more efficient data and thus improve the final prediction results of the model. By analyzing the experimental results, firstly, we can clearly see from the prediction span that the prediction effect of GRU and FEGRU is getting worse as the prediction span increases. This is shown by the increase of RMSE and MAE and the decrease of R2. However, SVR has a brief decrease in RMSE and MAE as the prediction span increases. This may be because the stability of SVR to outliers gradually manifests itself as the prediction span increases. The prediction performance of the ARIMA model does not change with the increase of the prediction span. Secondly, we see that EFGRU achieves excellent prediction performance for the prediction span of solar irradiance in the next 60 min and the next 90 min. We can clearly see from the figure that the RMSE and MAE of FEGRU are both the lowest values, and R2 is both the highest value, and we have bolded the optimal values of RMSE, MAE, and R2 in Tables 1 and 2.
6 Conclusion and future work
In this paper, a new model is proposed for application to the solar irradiance prediction problem. In order to enhance the prediction performance of the model, the source data are preprocessed to remove most of the consecutive zero and negative values from the solar irradiance. The model is able to extract the key data features from the source data by one-dimensional convolution of the input preprocessed data information and self-attention, which enables our model to achieve better results in the solar irradiance prediction problem. Our experiments show that our model performs better than SVR, ARIMA, and GRU models for prediction spans of the next 60 min and the next 90 min. It is worth mentioning that the model uses only direct horizontal irradiance alone during training and prediction, which is the solar irradiance data mentioned in this paper. On the other hand, if we want to improve the prediction performance of our proposed model in the future, our future work should focus on the full and effective use of the auxiliary data in the Lyon, France dataset to improve the prediction performance of the model.
Data availability statement
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding authors.
Author contributions
TK: Conceptualization, Methodology, validation, Writing—original draft. HW: Methodology, Data curation, Visualization, Software. TW: Writing—Resources, Software, Formal analysis, writing—original draft. JP: Writing—review and editing, Funding acquisition. HJ: Conceptualization, Writing—Supervision.
Funding
This paper has been jointly supported by the National Natural Science Foundation of China (Grant No. 52177102), the Natural Science Foundation of Guangdong Province (Grant No. 2021A1515011685), and the Foundations of Shenzhen Science and Technology Committee (Grant No. JCYJ20190808143619749, GJHZ20200731095610032).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
I would first like to thank my paper advisor Professor Wang Huaizhi of the College of Mechatronics and Control Engineering, Shenzhen University The door to Prof. Wang office was always open whenever I ran into a trouble spot or had a question about my research or writing. He consistently allowed this paper to be my own work, but steered me in the right the direction whenever he thought I needed it. I would also like to thank the experts who were involved in the validation survey for this research project: Dazhong Ma, Northeastern University, China and Xuguang Hu, Northeastern University, China. Without their passionate participation and input, the validation survey could not have been successfully conducted. Finally, I must express my very profound gratitude to my parents and to my partner for providing me with unfailing support and continuous encouragement. This accomplishment would not have been possible without them.
References
Ahmad, H., Ahmad, A., and Ahmad, S. (2018a). “Efficient energy management in a microgrid,” in 2018 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET) (Islamabad, Pakistan: IEEE), 1–5. doi:10.1109/PGSRET.2018.8685946
Ahmad, S., Ahmad, A., Naeem, M., Ejaz, W., and Kim, H. S. (2018b). A compendium of performance metrics, pricing schemes, optimization objectives, and solution methodologies of demand side management for the smart grid. Energies 11, 2801. doi:10.3390/en11102801
Ahmad, S., Alhaisoni, M. M., Naeem, M., Ahmad, A., and Altaf, M. (2020a). Joint energy management and energy trading in residential microgrid system. IEEE Access 8, 123334–123346. doi:10.1109/access.2020.3007154
Ahmad, S., Naeem, M., and Ahmad, A. (2020b). Unified optimization model for energy management in sustainable smart power systems. Int. Trans. Electr. Energy Syst. 30, e12144. doi:10.1002/2050-7038.12144
AlKandari, M., and Ahmad, I. (2020). Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Inf.. doi:10.1016/j.aci.2019.11.002
Atique, S., Noureen, S., Roy, V., Subburaj, V., Bayne, S., and Macfie, J. (2019). “Forecasting of total daily solar energy generation using arima: A case study,” in 2019 IEEE 9th annual computing and communication workshop and conference (CCWC) (Las Vegas, NV, USA: IEEE), 0114–0119. doi:10.1109/CCWC.2019.8666481
Bae, K. Y., Jang, H. S., and Sung, D. K. (2016). Hourly solar irradiance prediction based on support vector machine and its error analysis. IEEE Trans. Power Syst. 32, 1–945. doi:10.1109/tpwrs.2016.2569608
Barrett, G. B. (2000). The coefficient of determination: Understanding r squared and r squared. Math. Teach. 93, 230–234. doi:10.5951/mt.93.3.0230
Bouzgou, H., and Gueymard, C. A. (2017). Minimum redundancy–maximum relevance with extreme learning machines for global solar radiation forecasting: Toward an optimized dimensionality reduction for solar time series. Sol. Energy 158, 595–609. doi:10.1016/j.solener.2017.10.035
Caldas, M., and Alonso-Suárez, R. (2019). Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renew. energy 143, 1643–1658. doi:10.1016/j.renene.2019.05.069
Chai, T., and Draxler, R. R. (2014). Root mean square error (rmse) or mean absolute error (mae). Geosci. Model. Dev. Discuss. 7, 1525–1534.
Colak, I., Yesilbudak, M., Genc, N., and Bayindir, R. (2015). “Multi-period prediction of solar radiation using arma and arima models,” in 2015 IEEE 14th international conference on machine learning and applications (ICMLA) (Miami, FL, USA: IEEE), 1045–1049. doi:10.1109/ICMLA.2015.33
Dey, R., and Salem, F. M. (2017). “Gate-variants of gated recurrent unit (gru) neural networks,” in 2017 IEEE 60th international midwest symposium on circuits and systems (MWSCAS) (Boston, MA, USA: IEEE), 1597–1600. doi:10.1109/MWSCAS.2017.8053243
Dong, N., Chang, J.-F., Wu, A.-G., and Gao, Z.-K. (2020). A novel convolutional neural network framework based solar irradiance prediction method. Int. J. Electr. Power & Energy Syst. 114, 105411. doi:10.1016/j.ijepes.2019.105411
Fu, X., Guo, Q., and Sun, H. (2020). Statistical machine learning model for stochastic optimal planning of distribution networks considering a dynamic correlation and dimension reduction. IEEE Trans. Smart Grid 11, 2904–2917. doi:10.1109/tsg.2020.2974021
Fu, X. (2022). Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control Mod. Power Syst. 7, 5–13. doi:10.1186/s41601-022-00228-z
Gilbert, K. (2005). An arima supply chain model. Manag. Sci. 51, 305–310. doi:10.1287/mnsc.1040.0308
Hou, K., Shao, G., Wang, H., Zheng, L., Zhang, Q., Wu, S., et al. (2018). Research on practical power system stability analysis algorithm based on modified svm. Prot. Control Mod. Power Syst. 3, 11–17. doi:10.1186/s41601-018-0086-0
Li, D., Zhao, Y., and Zhao, Y. (2022). A dynamic-model-based fault diagnosis method for a wind turbine planetary gearbox using a deep learning network. Prot. Control Mod. Power Syst. 7, 22–14. doi:10.1186/s41601-022-00244-z
Li, Y., Xue, W., Wu, T., Wang, H., Zhou, B., Aziz, S., et al. (2021). Intrusion detection of cyber physical energy system based on multivariate ensemble classification. Energy 218, 119505. doi:10.1016/j.energy.2020.119505
Liu, G. (2014). Sustainable feasibility of solar photovoltaic powered street lighting systems. Int. J. Electr. Power & Energy Syst. 56, 168–174. doi:10.1016/j.ijepes.2013.11.004
Liu, Y., Qin, H., Zhang, Z., Pei, S., Wang, C., Yu, X., et al. (2019). Ensemble spatiotemporal forecasting of solar irradiation using variational bayesian convolutional gate recurrent unit network. Appl. Energy 253, 113596. doi:10.1016/j.apenergy.2019.113596
Ma, Z., Guo, S., Xu, G., and Aziz, S. (2020). Meta learning-based hybrid ensemble approach for short-term wind speed forecasting. IEEE Access 8, 172859–172868. doi:10.1109/access.2020.3025811
Salman, S., Xin, A., and Zhouyang, W. (2018). Design of a p-&-o algorithm based mppt charge controller for a stand-alone 200w pv system. Prot. Control Mod. Power Syst. 3, 25–28. doi:10.1186/s41601-018-0099-8
Shadab, A., Ahmad, S., and Said, S. (2020). Spatial forecasting of solar radiation using arima model. Remote Sens. Appl. Soc. Environ. 20, 100427. doi:10.1016/j.rsase.2020.100427
Shadab, A., Said, S., and Ahmad, S. (2019). Box–jenkins multiplicative arima modeling for prediction of solar radiation: A case study. Int. J. Energy Water Res. 3, 305–318. doi:10.1007/s42108-019-00037-5
Wang, F., Zhang, Z., Liu, C., Yu, Y., Pang, S., Duić, N., et al. (2019). Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting. Energy Convers. Manag. 181, 443–462. doi:10.1016/j.enconman.2018.11.074
Wang, H., Cai, R., Zhou, B., Aziz, S., Qin, B., Voropai, N., et al. (2020). Solar irradiance forecasting based on direct explainable neural network. Energy Convers. Manag. 226, 113487. doi:10.1016/j.enconman.2020.113487
Wu, K., Gu, J., Meng, L., Wen, H., and Ma, J. (2022). An explainable framework for load forecasting of a regional integrated energy system based on coupled features and multi-task learning. Prot. Control Mod. Power Syst. 7, 24–14. doi:10.1186/s41601-022-00245-y
Yamak, P. T., Yujian, L., and Gadosey, P. K. (2019). “A comparison between arima, lstm, and gru for time series forecasting,” in Proceedings of the 2019 2nd International Conference on Algorithms, Computing and Artificial Intelligence, 49–55.
Yaqub, R., Ahmad, S., Ahmad, A., and Amin, M. (2016). Smart energy-consumption management system considering consumers’ spending goals (sems-ccsg). Int. Trans. Electr. Energy Syst. 26, 1570–1584. doi:10.1002/etep.2167
Zhang, R., Aziz, S., Farooq, M. U., Hasan, K. N., Mohammed, N., Ahmad, S., et al. (2021). A wind energy supplier bidding strategy using combined ega-inspired hpsoifa optimizer and deep learning predictor. Energies 14, 3059. doi:10.3390/en14113059
Keywords: solar irradiance prediction, deep learning, feature-enhanced gate recurrent unit, self-attention, solar energy
Citation: Kang T, Wang H, Wu T, Peng J and Jiang H (2022) Solar irradiance prediction based on self-attention recursive model network. Front. Energy Res. 10:977979. doi: 10.3389/fenrg.2022.977979
Received: 25 June 2022; Accepted: 25 July 2022;
Published: 05 September 2022.
Edited by:
Xueqian Fu, China Agricultural University, ChinaReviewed by:
Muhammad Aamir, Huanggang Normal University, ChinaSadiq Ahmad, ECE Department COMSATS University Islambad, Pakistan
Copyright © 2022 Kang, Wang, Wu, Peng and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huaizhi Wang, d2FuZ2h6QHN6dS5lZHUuY24=; Ting Wu, dHd1OTIwQGhvdG1haWwuY29t
 Ting Kang
Ting Kang Huaizhi Wang
Huaizhi Wang Ting Wu
Ting Wu Jianchun Peng1
Jianchun Peng1 Hui Jiang
Hui Jiang