A novel method for life estimation of power transformers using fuzzy logic systems: An intelligent predictive maintenance approach

Power transformers are a fundamental component of the modern power distribution network. The fault-free operation of step-up and step-down transformers is of prime importance to the continuous supply of electrical energy to the consumers. To ensure such efficient operation, power distribution companies carry out routine maintenance of distribution transformers through preplanned schedules. The efficacy of such maintenance depends on a proper understanding of the transformer and its components and efficient prediction of faults in these components. There are several components whose condition can be studied to predict transformer failures and therefore the overall health of a transformer. These include transformer windings, insulations, transformer oil, core insulations, and ferromagnetic cores. This work develops a new, simplified fuzzy logic–based method to predict the health of a transformer by taking into account the state of several individual components. Case studies are used to demonstrate the efficacy of the developed method.

1 Introduction

In the power system, the cost of electricity produced and supplied to consumer significantly depends on the level of reliability that is attained and the effective maintenance of power system equipment. This also impacts the stability of the power system and the life span of associated equipment (Nurcahyanto et al., 2019). Industrial, commercial, and domestic consumer power supply failures result in technical and financial loss to power utilities. The most expensive equipment for substation/grid stations is transformers, which comprise 60% of the total investment (Idrees et al., 2019). The faults usually experienced in transformers may be categorized into two types on the basis of location, i.e., internal and external faults. External faults are usually line to line (L-L), line to line to line (L-L-L), and line to line to ground (L-L-L-G), which are rare faults, whereas line to line to ground (L-L-G) and line to ground (L-G) are frequently occurring faults. Internal faults are as follows: winding insulation degradation that results in inter-turn faults, winding defects, and earth faults. Overload conditions for long durations, excessive overvoltages, inrush current, and failure of cooling equipment are among several reasons for insulation failure (Bhide et al., 2010). Electrical insulation has a shared function in providing mechanical support, heat dissipation, electrical isolation, and personal safety. There are three major types of insulation in a transformer: solid, liquid, and gas. The most widely used insulation type is solids. This can be found inside transformers, and on transmission lines, capacitors, motors, cables, etc. The damage to solid insulation is usually non-reversible and destructive (Cygan and Laghari, 1990). In addition to frequent faults, transformer insulation undergoes different kinds of stresses (mechanical, electrical, environmental, and thermal) throughout its life period. This results in insulation degradation, lower withstanding capability during short circuit and overvoltage conditions, and reduced life span of the transformer. Therefore, in order to have a reliable and efficient operation, the health assessment of transformers is considered an important parameter among power utilities (Arshad et al., 2004).

The major focus of this research is to analyze the deformation/displacement of active parts of transformers along with the solid and liquid insulation, which may be degraded with time, and to establish an accurate way to estimate the remnant life of the transformer. This evaluation also includes the identification of faulty equipment/assets having high failure risk or are at end of the life span so that asset managers can expedite the replacement or repairing of such assets (Contin et al., 2011).

The health assessment of transformers has been discussed in the literature, and various algorithms have been proposed that include the following: formulating detailed mathematical models/algorithms that encompass a tier method; scoring/ranking method; multi-feature factor assessment model; and matrices/entropy weight health index (EWHI) method (Azmi et al., 2017). However, health index evaluation by mathematical modeling is considered to be a complex process because at the same time, different stresses act that may cause inconsistencies. Another approach is the use of the weighting average (Assessment, 2020). Despite the simplicity of weighting methods, the determination of the weight factors is based on the rules of thumb and experienced guesses, which differ from one expert to another. In addition, setting a sharp threshold of diagnostic measurements for scoring is very difficult. Another research proposes a Bayesian multinomial logistic regression model for estimating the HI of transformers (Sarajcev et al., 2018). However, it omits effects associated with the inherent ordering of categories, which can also be the case with applications of ANNs and some other ML models used for classification tasks. In addition, online learning/monitoring can be implemented in the present model, which can be used for health management. Regression models are used to evaluate health index (%HI) in terms of percentage for condition assessment, which is discussed in Leauprasert (2020), but they lack comprehensible interpretation of their parameters and explanatory power. Also, the HI values may lie outside the intended range. For AI methods, a large number of data with known conditions are saved in the database and then used as training and testing data, but they are still subjective (Jian et al., 2020). Online condition monitoring is employed for HI based on DGA interpretation using the C4.5 algorithm with a decision tree of a machine-learning model for transformers. The algorithm uses the ML software (WEKA and Orange) to give the best learning outcome, and the results are compared with those of the support vector machine, neural network, naïve Bayes, and nearest neighbor models in Basuki (2018). Based on SPSS statistical tools, a HI model is established but more research can be extended to other fields such as transmission, distribution systems, and other substation equipment. A devoted online condition monitoring approach only for 33 kV steel mill transformers is established using fuzzy models as discussed in Patil et al. (2020) for health index (HI) computation and estimation of remnant life in a fuzzy mode, but research can be continued for higher voltage transformers, so a generalized fuzzy model that is applicable to all other transformers such as generation and transmission may be formed. Seven models based on adaptive neuro-fuzzy inference system (ANFIS), multiple linear regression (MLR), and other simpler approaches are investigated in Prasojo et al. (2019) to deal with missing furan data in power transformers. The offered multiple computation methods can still be enhanced by mentioning historical factors in the calculation, instead of only forecasting single instances. A distribution transformer health index is analyzed online for condition monitoring (Davies and Roose) and utilizes different parameters of the transformer through an energy monitoring system such as current and voltage. In order to verify the proposed algorithm, a study on a 50-kVA distribution transformer is also performed, but the same can be extended to other bigger transformers, which, instead of approximation from data, apply practical sensors to measure the parameter to validate their sensitivity.

Based on the results of DGA performed on oil and fuzzy logic system, the health index of the transformer is proposed in Arshad et al. (2010), but DGA results can be found from different techniques, and instead of standard mathematical modeling of these techniques, these are knowledge- and experience-based. Sometimes, the results do not follow offered codes of present methods, and then, it becomes difficult to analyze them. In this regard, the modification in current DGA techniques is applied with help of the gene expression programming (GEP) algorithm in Islam (2012) for DGA standardizing and identifying transformer criticality. Another author developed a fuzzy logic model for the transformer to assist the asset management in developing a decision-making strategy by integrating criticality based on diagnostic testing techniques in Arshad et al. (2014), but the remnant life of the transformer is not discussed. Another research focused on data acquired from liquid insulation parameters such as DGA, water content, furan, and interfacial tension (IFT) for analyzing health conditions and operating temperature for assessing the remnant life of the transformer (Bakar and Abu-Siada, 2016). Another paper established a mathematical model of health index, and then, these values are applied to fuzzy models to evaluate failure, risk, and maintenance model, and the same is verified with the help of simulation, but the model lacks the feedback system for addressing maintenance problems (Rosero-z, 2018). Enhanced health assessment based on the fuzzy logic system of DGA only is proposed in Aburaghiega (2018), but the model does not focus on all the problems linked with asset management.

The transition of the utility grid toward a pervasive and smart grid has brought new opportunities for automatic fault detection and prevention (Ben Dhaou et al., 2017). The predictive maintenance of the power transformer using industrial internet of things (IIoT) and machine-learning techniques has received ample attention in both academic and industrial work (De Faria et al., 2015; Mahmoud et al., 2021).

Most of the research so far has focused on the degradation of oil alone using DGA for transformer health index assessment, whereas no specific attention is given to the integrated model for fault identification using Duval triangle 1 and other diagnostic parameters (Dukarm et al., 2020). High and low energy arcing, partial discharge, and hot spots of various temperature ranges are major types of faults that can be identified using Duval triangle 1 (Assessment, 2020), but there is no region for a normal aging condition that may result in a diagnosis of either one of the mentioned faults if careless implementation is adopted. To avoid this problem, dissolved gases should be assessed along with an assessment of insulation paper (Mawelela et al., 2020). The above-mentioned problem can be analyzed by considering other diagnostic parameters such as hottest spot temperature of winding, insulation resistance/polarization index, dissipation factor of system insulation, and remnant life of the transformer based on the relative aging rate of insulation material. This point encourages the formation of new algorithm and models. In this regard, this research focuses on fuzzy logic systems (FLS) to deal with the uncertainty involved in identifying the different faults, which are related to aging of insulation paper along with mineral oil. Using this analysis, defuzzification will be applied to each predicate, which is related to a precise fault/defect condition with a membership function that specifies the degree of confidence associated with output. Another reason for implementing the fuzzy logic system is that it is easy to design, can handle a large number of inputs, and is insensitive to parametric variation. Moreover, analytical models developed so far exhibit complexity when dealing with a large number of inputs and system becomes difficult to design and analyze (Azmi et al., 2017).

Therefore, this research utilizes an integrated fuzzy logic system based on Duval triangle 1, which will focus on fault identification and failures related to insulation oil and remnant life of the transformer based on the hottest spot temperature of winding/relative aging rate in addition to dissolved gas analysis (DGA), dielectric strength of oil, hottest spot temperature of winding, insulation resistance and polarization index, and dissipation factor to calculate health assessment and remnant life of the transformer to ensure that proper decision-making strategy, i.e., replacing, repairing, or refurbishment, can be implemented for effective health monitoring system of the transformer (Arshad et al., 2004).

The research will be useful to avoid cascaded failure of the power system, inconvenience, and economic loss due to power outages. Major insulation used in transformers is Kraft paper and insulation mineral oil, and its mechanical strength of transformers depends on it. With time, due to various stresses (thermal, mechanical, and environmental) the paper ages, which results in the deteriorating performance of a transformer. For example, during short circuit events, the paper insulation may fail to withstand stresses due to reduction in mechanical strength, ferroresonance, and vibrations resulting from the excessive switching operation. This may eventually, after accumulation, lead to a transformer catastrophic disaster if no corrective action (replacing, repairing, or refurbishment) is taken (Azis et al., 2014). It will also avoid removing substation transformer from service before completing their actual life span because in the past, older equipment was renewed before reaching the end of the lifetime of the equipment and the main reasons for the change were the growth of the load and their operational limits (Velásquez and Lara, 2017). The contributions of this study are listed below:

• To identify the incipient faults and identification of faulty accessories, which cannot be taken out of service immediately.

• To estimate remnant life of the transformer.

• To provide accurate estimates of the transformer aging and insulation aging so that timely repair, replacement, or refurbishment can be performed.

• To prevent sudden failures in transformers prior to the completion of expected life, which will cause more significant losses due to accelerated aging effect.

• To reduce costs of periodic diagnostic testing and by workers.

2 Methodology

The fuzzy-based model for health and life estimation of the transformer works using the data obtained from diagnostic testing performed either during factory testing or as a result of in-service tripping or during maintenance. The parameters used are dielectric strength (DES, i.e., water content of oil, breakdown voltage, and dielectric dissipation factor (DDF@100°C) of oil), dissolved gas analysis (DGA), insulation resistance and polarization index, hot spot temperature of winding, and dissipation factor of insulation system. Moreover, in addition to life and health estimation, fault-type identification is performed using Duval triangle 1 (DT1) based on the results of DGA. Transformer health index evaluation is assessed by integrating the aforesaid parameters. The analysis of the transformer insulation degradation and mechanical condition will be evaluated by the use of fuzzy logic systems. These models overcome the complexity and consistency limitation of mathematical modeling by integrating its criticality. Gasses developed as a result of the dissolved gas analysis test provided the information about the thermal condition of oil. There are other methods such as the key gas, the Doernenburg ratio, and the IEC ratio method. However, there are certain limitations to these methods: The key gas method gives faulty identification (50%) when applied through software and 30% wrong identification when applied manually. Similarly, the Doernenburg ratio is a historic method used less frequently, and it only identifies a limited number of faults. Similarly, the IEC ratio is valid only when a sufficient amount of gas is generated. In view of the above, Duval triangle 1 is used that can identify six types of faults and does not have above-mentioned limitations (Abu-Siada and Hmood, 2015). Results of breakdown voltage, dissipation factor, and water content are used to verify the dielectric condition of oil (Chantola et al., 2018). The most significant factor in contributing to the health of the transformer is the top oil temperature rise because it served as a basis for the hottest spot temperature rise of winding (Davies and Roose,). Fuzzy logic is considered as one of many soft computing techniques similar to the human thinking process. It is often utilized in our daily lives and uses simple linguistic variables as decision-making segments, which are easily comprehendible as compared to analytical models. The three steps are involved in the fuzzy logic system, which comprise fuzzification, fuzzy inference process, and defuzzification.

Fuzzification derives the membership functions (MF), which means converting crisp input (classical set theory) to fuzzy set to varying degrees (Bai and Wang, 2006). Each input of the fuzzy system is represented independently by either trapezoidal or triangular shape of membership functions (MF). Individual membership functions (MF) are marked over their complete range by linguistic variables such as “low,” “medium,” “high,” and “very high” to indicate criticality/health index for transformer health. A fuzzy rule base contains “IF-THEN” statements, which are applied to the inference system. A large number of fuzzy rules are implemented for a complex system to represent diagnostic representation (Idrees et al., 2019). The final output of the fuzzy inference engine is still not in the form to be used, so the fuzzy output (linguistic variable) is converted to crisp output by means of the defuzzification process.

For this purpose, three methods: the center of gravity method (COG), the height method (HM), and the mean of maximum method (MOM), are commonly implemented based on their advantages. The most popular is the center of gravity method because the entire shape of the output membership function is not reflected in the MOM, but it only considers highest degrees in that function. It is difficult to distinguish between different shapes of output membership functions having highest degrees, because it generates the same result. The HM technique is only applicable when the output membership function is an accumulated union result of symmetrical functions (Bai and Wang, 2006).

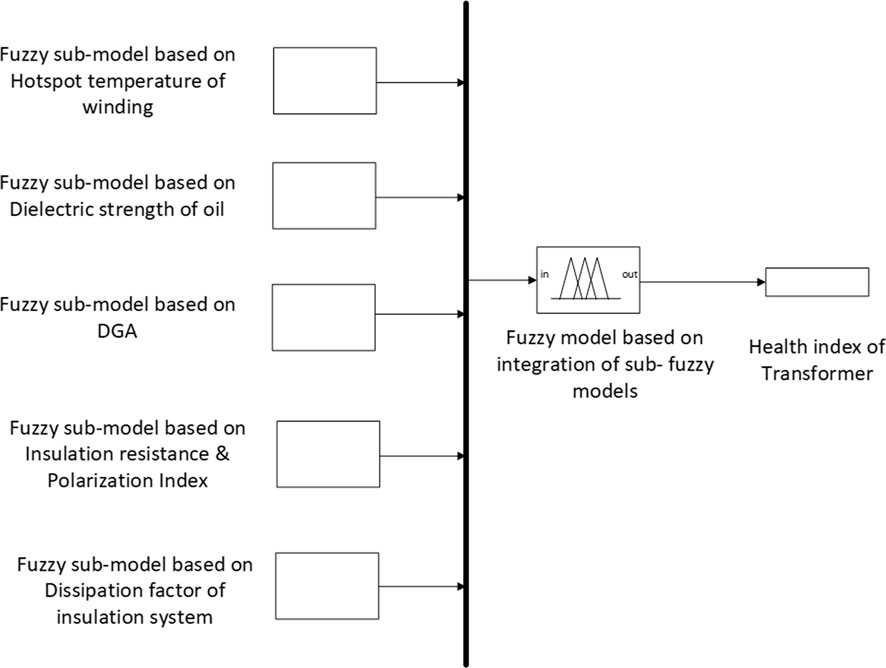
MATLAB is used to implement fuzzy logic controllers. To achieve accuracy, the problem is divided into subfuzzy models and their integration provides a complete health assessment of a transformer.

3 Results

The aforesaid model is developed and verified from power transformers being used in Pakistan. The data obtained after detailed factory testing of the transformers are used as input for the established model.

3.1 Fuzzy sublogic based on dielectric strength of oil

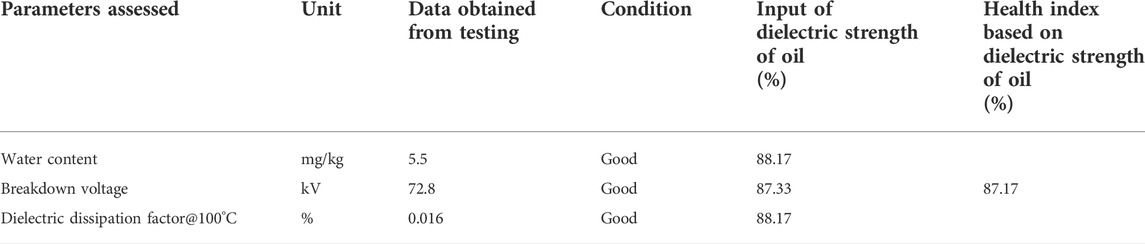
In order to evaluate the dielectric strength (DES) of oil, three parameters (water content of oil, breakdown voltage, and dielectric dissipation factor (DDF@100°C) of oil) are utilized. The condition of oil depends on all of these parameters, and if anyone is outside its specified range, the overall dielectric strength will be lower.

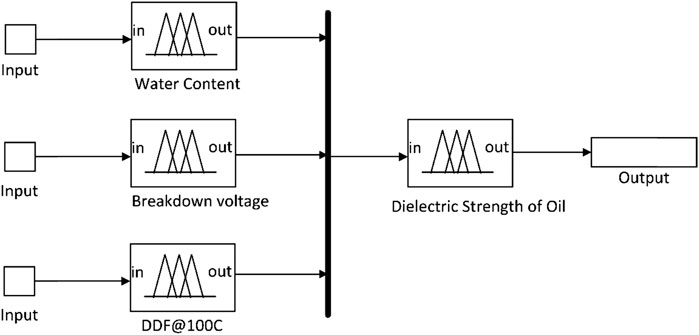
To achieve adequate breakdown voltage and minimal dissipation losses, mineral insulating oil must have a low water content when delivered to avoid free water separation. Mineral insulating oil’s breakdown voltage reflects how well it can withstand electrical stress in electrical equipment. The dielectric dissipation factor (DDF@100°C) is an indicator for evaluating dielectric losses in oil. Higher DDF values than those required by standards can indicate polar pollutants in the oil or poor refining quality (IEC 60296, 2020). Individual fuzzy models of water content, breakdown voltage, and dielectric dissipation factor of oil are derived to monitor the condition of oil, and then, these are integrated to calculate the overall dielectric strength of oil, which can be seen in Figure 1. The model is implemented using the data obtained from testing performed on a newly bought uninhibited oil, i.e., mineral insulating oil that contains no oxidation inhibitor or other antioxidant additives. The effectiveness of the model can be verified from Table 1 which indicates that the condition of oil is good, which results in the higher health index of the transformer because the oil is new. Each individual input parameter is designated as “critical,” “normal,” and “good.” The percentage between 0 and 100% is assigned to the output of fuzzy logics of water content, breakdown voltage, (DDF@100°C), and overall DES of oil. Figure 2A represents that a total of 9 fuzzy rules are used to calculate the dielectric strength of oil. The output (DES) will give a value close to 100% if all the individual input parameters are in good condition, and similarly, the output will give a value close to 0% if any of the individual input parameters are in critical condition. The surface representation of input parameters and corresponding output (DES) is shown in Figure 2B. It can be seen that if percentages of breakdown voltage or water content are lower, then output (DES) as shown in the surface is also lower. Similarly, for different percentages, the output (DES) varies accordingly.

FIGURE 1

FIGURE 1. Fuzzy sublogic based on dielectric strength of oil.

TABLE 1

TABLE 1. Health index based on dielectric strength of oil.

FIGURE 2

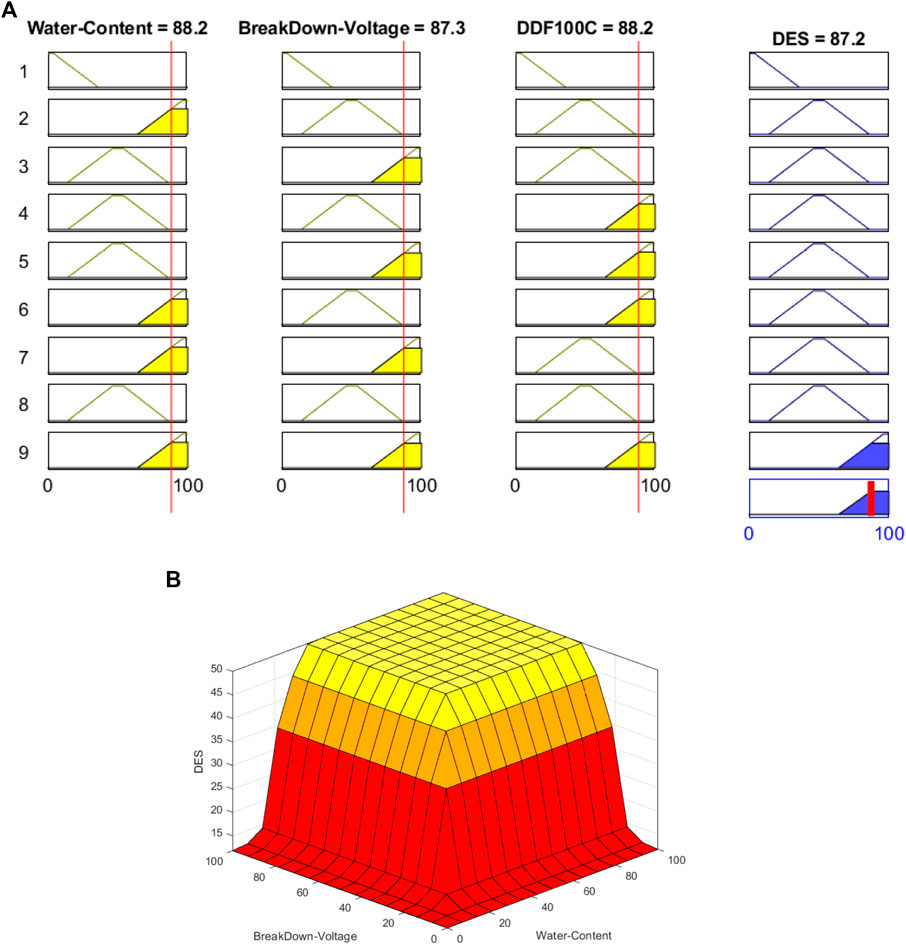
FIGURE 2. (A) Rules used in fuzzy sublogic for dielectric strength of oil. (B) Surface formed for dielectric strength of oil.

3.2 Fuzzy sublogic based on dissolved gas analysis

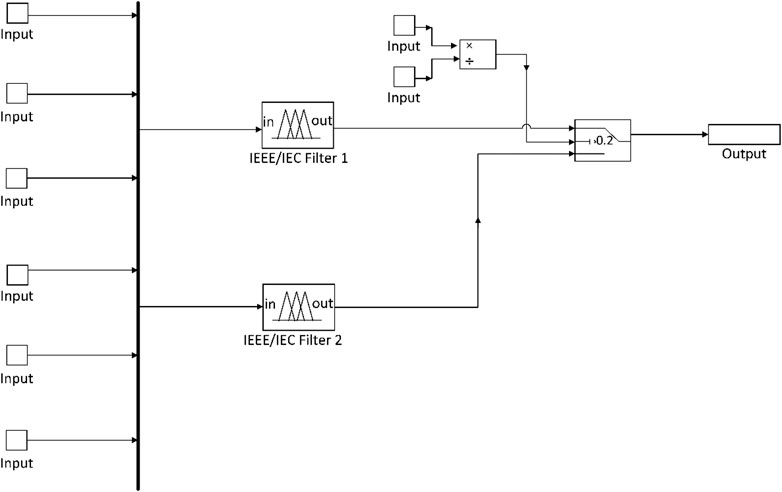
The submodel as shown in Figure 3 is based on nine gasses (H₂, CH₄, C₂H₂, C₂H₄, C₂H₆, CO, CO₂, O₂, and N₂), which are formed in case of faults. Firstly, IEEE/IEC (IEC 60599, 2015) (C57.104, 2019) fuzzy logic–based filter is applied to determine whether any of the aforesaid gases are within their specified limits or not. For this purpose, 90th and 95th percentile gas concentrations as a function of O₂/N₂ ratio and age of health of the transformer are utilized.

FIGURE 3

FIGURE 3. Fuzzy sublogic based on dissolved gas analysis.

Corona partial discharge and stray gassing of oil is a reason for the emission of hydrogen (H₂). It is also produced by sparking discharges and arcs, but C₂H₂ is considerably a better indicator in such cases. It could also be caused by a chemical reaction with galvanized steel.

The heating of oil or paper produces methane (CH₄), ethane (C₂H₆), and ethylene (C₂H₄). Arcing in oil or paper at temperatures exceeding 1,000°C generates acetylene (C₂H₂). Under normal operating conditions, transformers with no internal fuses, switches, or other arcing mechanisms should not produce any C₂H₂. When C2H2 is found, it is common to observe elevated levels of H₂ or C₂H₄. The combustion of cellulose produces carbon monoxide (CO) and carbon dioxide (CO₂) (Azis et al., 2014).

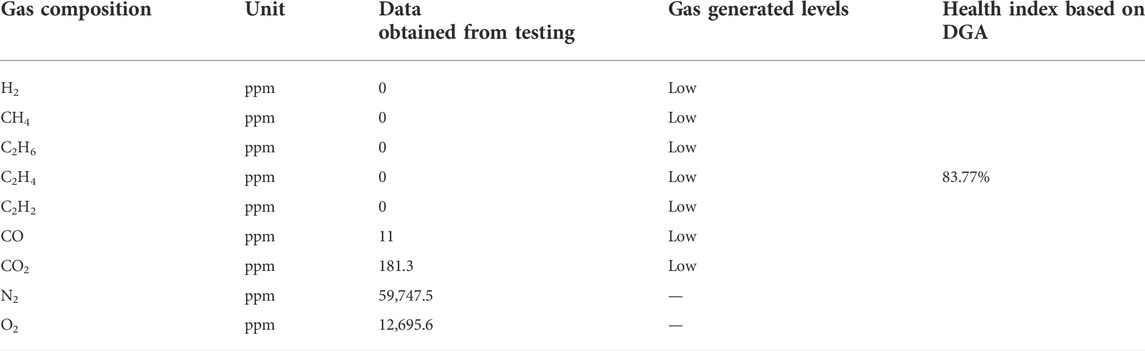
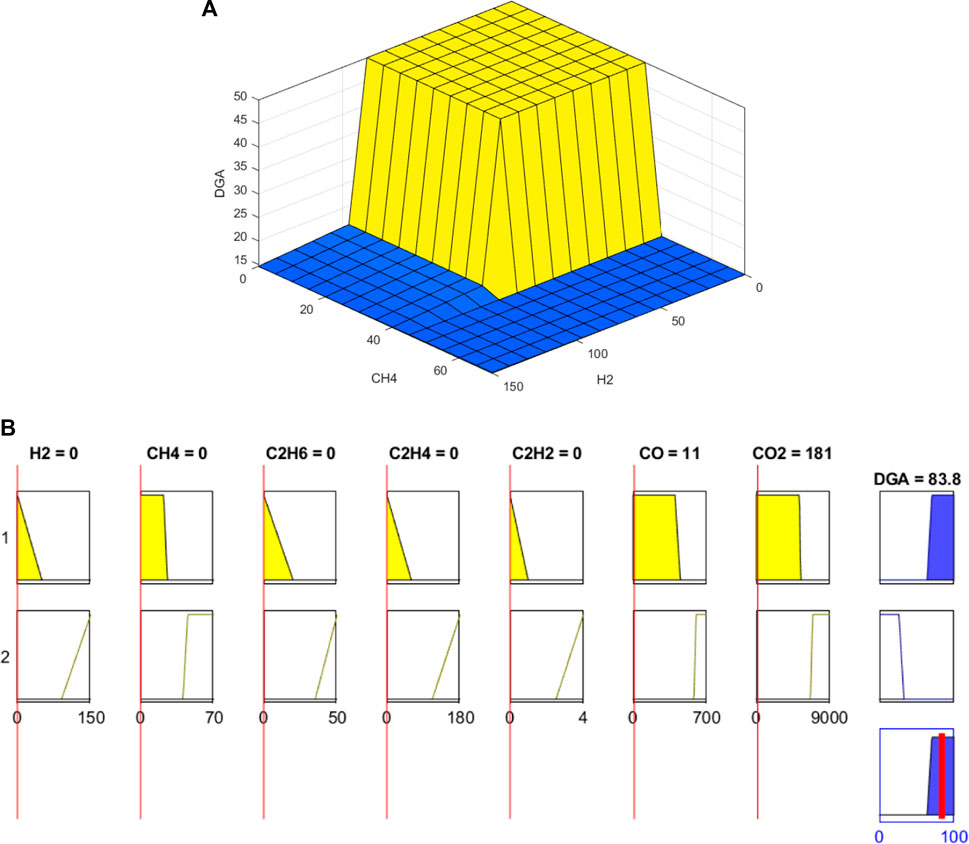
The quantity of gas generated as shown in Table 2 is low after the DGA is performed on the mineral oil, and consequently, the health index based on dissolved gas analysis has higher values of 83.77%. Each individual quantity of gas generated is designated as “high,” “medium,” and “low.” The percentage between 0 and 100% is assigned to the output of DGA. Figure 4B shows values of H_2, CH₄, C₂H₂, C₂H₄, and C₂H₆ are zero, which means that any of the aforesaid gas is not generated. The output (DGA) will give a value close to 100% if all the gases are within a specified range, and similarly, the output will give a value close to 0% if any gas exceeds the range as shown in Figure 4A.

TABLE 2

TABLE 2. Health index based on dissolved gas analysis.

FIGURE 4

FIGURE 4. (A) Surface formed for DGA. (B) Rules used in fuzzy sublogic for DGA.

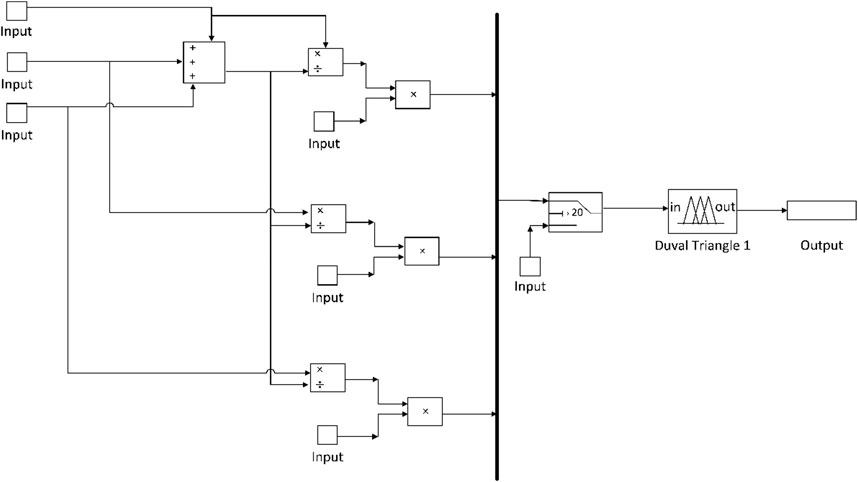
3.2.1 Fault identification based on Duval triangle 1

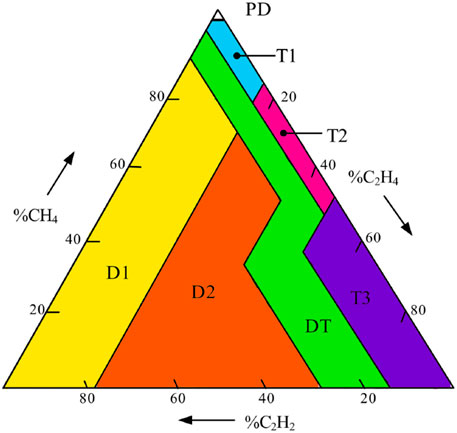
Duval triangle 1 (DT1) is a fault identification method based on the gasses obtained from dissolved gas analysis (DGA). This method utilizes percentages of three gasses (%CH4, %C2H4, and %C2H2) to identify six types of faults mentioned in Table 3. The percentages are calculated using Eqs 1–3. The percentages are plotted on Duval triangle 1 as shown in Figure 5. %C₂H₂ is marked along the x-axis, %CH₄ on the left side, and %C₂H₄ on the right side of Duval triangle. The advantage of this method always identifies fault visually and evolution with respect to time in the transformer (Poonnoy et al., 2021). The identification of an unusual situation is the first step in interpreting DGA data. When identified, it should be followed by a severity assessment and fault diagnosis. DGA’s problem identification and severity assessment component compare gas levels generated by specific faults and rates of change with their respective limit and assign a status condition based on whether limits (if any) were exceeded. When a problem is suspected, a reliable methodology, such as the Duval triangle 1 method as shown in Figure 6, can be used to identify or diagnose the problem.

$\%C{H}_4=\frac{C{H}_4}{\left(C{H}_4+C_2{H}_2+C_2{H}_4\right)}100(1)$

$\%C_2{H}_2=\frac{C_2{H}_2}{\left(C{H}_4+C_2{H}_2+C_2{H}_4\right)}100(2)$

$\%C_2{H}_4=\frac{C_2{H}_4}{\left(C{H}_4+C_2{H}_2+C_2{H}_4\right)}100(3)$

TABLE 3

TABLE 3. Fault identification based on Duval triangle 1.

FIGURE 5

FIGURE 5. Conventional Duval triangle 1.

FIGURE 6

FIGURE 6. Fuzzy sublogic based on Duval triangle 1.

The Duval triangle 1 method employs three fault gases that depends on temperature rise in case of fault. Duval triangle 1 analyzes major gases such as methane (CH₄) for low-energy or low-temperature faults; ethylene (C₂H₄) for high-temperature faults; and acetylene (C₂H₂) for extremely high-temperature or high-energy/arcing faults. This method allows the identification of the six basic types of faults shown in Table 3 plus mixtures of electrical/thermal faults (Azis et al., 2014).

Table 3 identifies the type of fault based on the output of Duval triangle 1. Each fault type is designated by a specific fault symbol. For example, if the output of Duval triangle is between 28.58 and 42.86, then the fault type is thermal fault T1, 300°C < t < 700°C. Figure 7B shows that a total of 11 rules are used to develop a fuzzy submodel for Duval triangle 1. The results of DGA showed that no gases of CH₄, C₂H₂, and C₂H₄ are generated, so their percentage is also zero, and the result from the output of Duval triangle 1 is zero, which means that no fault is detected. Figure 7A shows the surface formed for DGA, which represents, e.g., that when the value of CH₄ is greater than 98%, no matter what is the value of C₂H₄, the output will be between 1.00 and 14.29, which means the fault type is PD (partial discharge of corona type) as also shown in Table 3.

FIGURE 7

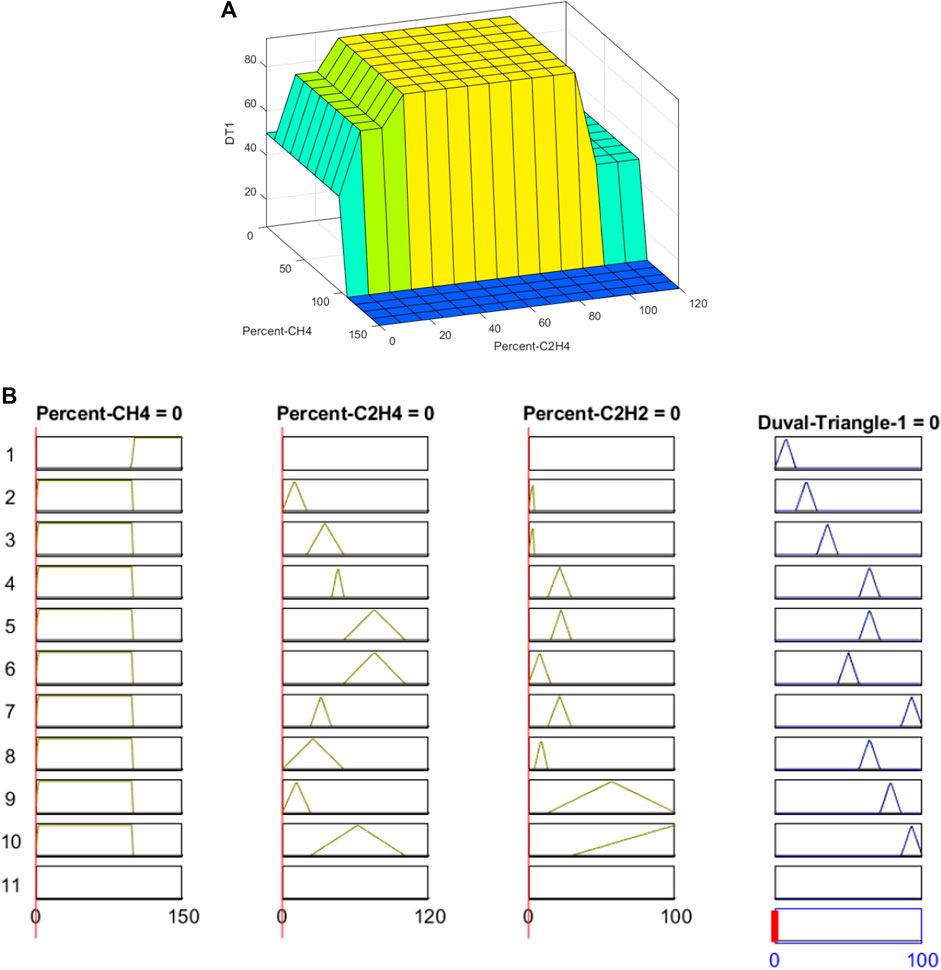
FIGURE 7. (A) Surface formed for Duval triangle 1. (B) Rules used in fuzzy sublogic for Duval triangle 1.

3.3 Fuzzy sublogic based on the hot spot temperature of winding

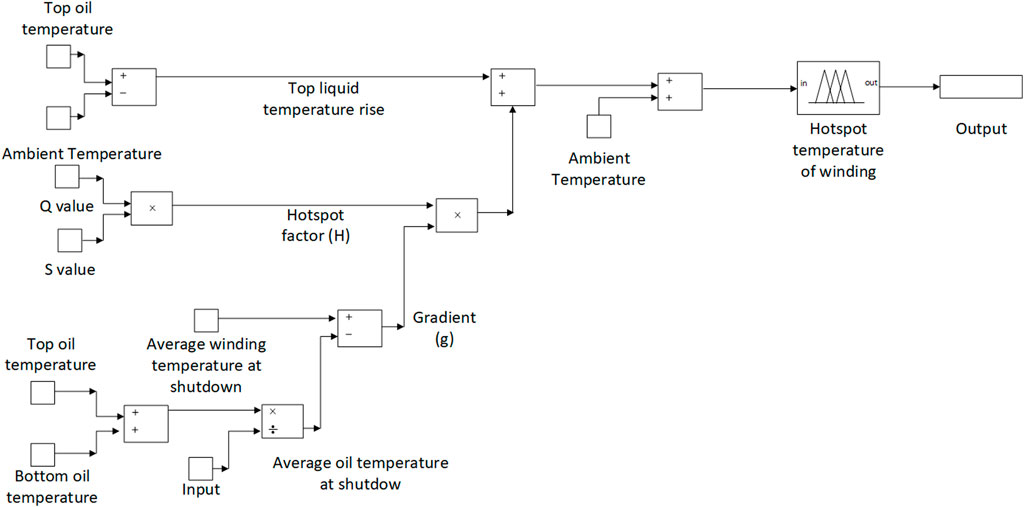
Fuzzy sublogic based on the hot spot temperature of winding is shown in Figure 8. The hot spot is the maximum temperature occurring in any part of a winding insulation system, and it is assumed to represent the thermal limitation of transformers. If the hot spot winding temperature rise is not directly measured, an estimate of its value can be made starting from the results of the temperature rise test or using either design data or results of tests performed on similar transformers.

FIGURE 8

FIGURE 8. Fuzzy sublogic based on the hot spot temperature of winding.

The following equation can be used to determine the hot spot winding temperature:

$△{\theta }_h=△{\theta }_o+Hg(4)$

$H=QS(5)$

${\theta }_h=△{\theta }_h+{\theta }_{am}(6)$

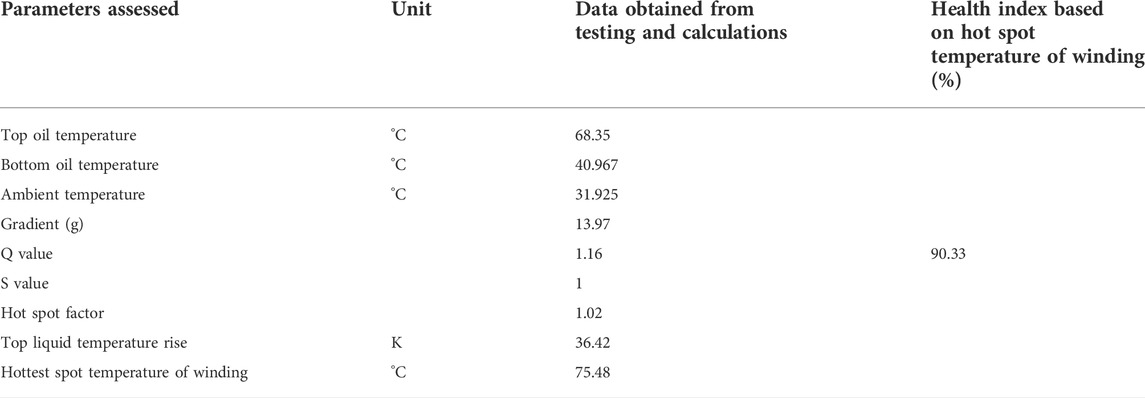
where ∆θ_o is the top liquid temperature rise in the tank, H is the hot spot factor, g is the average winding-to-average liquid gradient, θ_h is the top liquid temperature, and θ_am is ambient temperature. The difference between the average winding temperature rise and the average liquid temperature rise is utilized to calculate the average thermal gradient between each winding and liquid along the limb (g). For each winding, the corresponding hot spot factor (H = QS) that depends on Factor Q is the additional loss and is determined by the ratio of the specific loss in the region of the leakage flux concentration (top winding) to the winding’s average specific loss. Factor S is the efficiency of liquid cooling circuits within the coil (Velásquez and Lara, 2017). Parameters such as top oil temperature, bottom oil temperature, and ambient temperature obtained from diagnostic testing as shown in Table 4 are used for the calculation of the hot spot temperature of winding. Figure 9A shows that a total of 3 rules are used to develop the fuzzy submodel. The hot spot temperature of winding is lower, i.e., 75.5°C, that’s why the health index is better. As the hot spot temperature of winding increases, the health index decreases; i.e., for the hot spot temperature of winding greater than 140°C, the health index decreases to less than 20% as shown in Figure 9B.

TABLE 4

TABLE 4. Health index based on the hot spot temperature of winding.

FIGURE 9

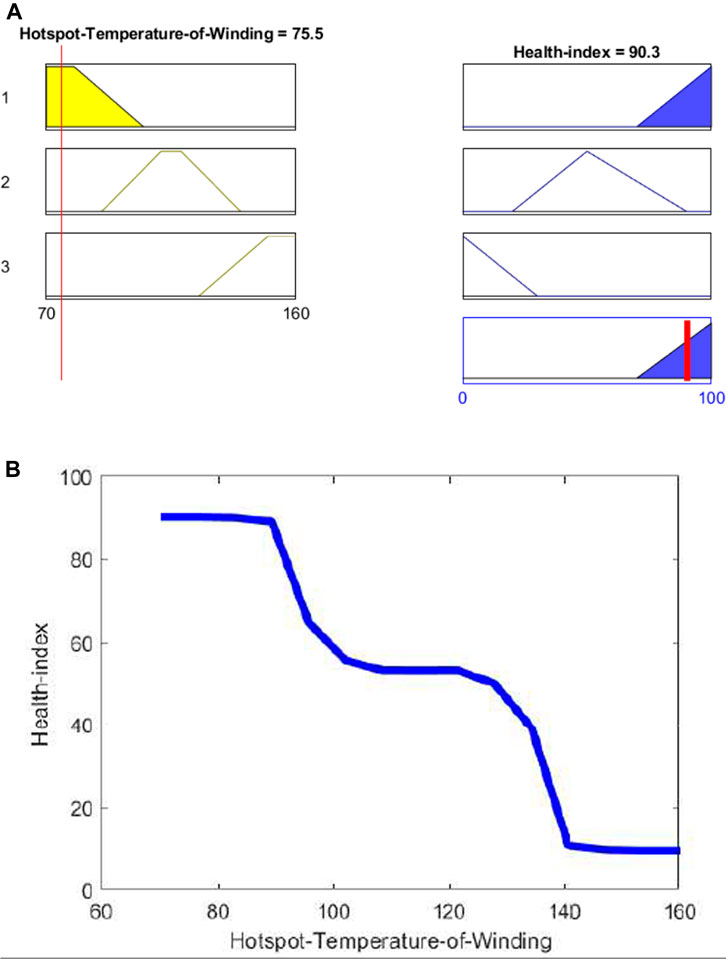
FIGURE 9. (A) Rules used in fuzzy sublogic for the hot spot temperature of winding. (B) Plot formed for the hot spot temperature of winding.

3.3.1 Remnant life of the transformer based on the relative aging rate

In recent years, extensive work has been carried out on paper degradation, indicating that cellulose aging may be described by the combination of three processes, i.e., oxidation, hydrolysis, and pyrolysis. In a real transformer, all these processes act simultaneously. This hampers the application of one model describing the full complexity of degradation processes. Which process will dominate depends on the temperature and the conditions (oxygen, water, and acid content). To characterize the aging of the cellulose breakdown process, various parameters may be used. In reality, mechanical strength is critical for the winding paper to withstand shear forces during short circuits. However, due to the folded geometry of paper in a transformer, the tensile strength of paper samples from used transformers cannot be determined. As a result, determining the degree of polymerization (DP) in order to define the state of an insulation paper is more convenient. When DP is decreased to 200 percent or 35 percent, the tensile strength is retained, but the paper quality (i.e., mechanical strength) is typically considered so bad that this marks the “end of life” for such an insulating substance, although the dielectric strength may be still at an acceptable level (Biçen et al., 2011). The submodel is shown in Figure 10.

FIGURE 10

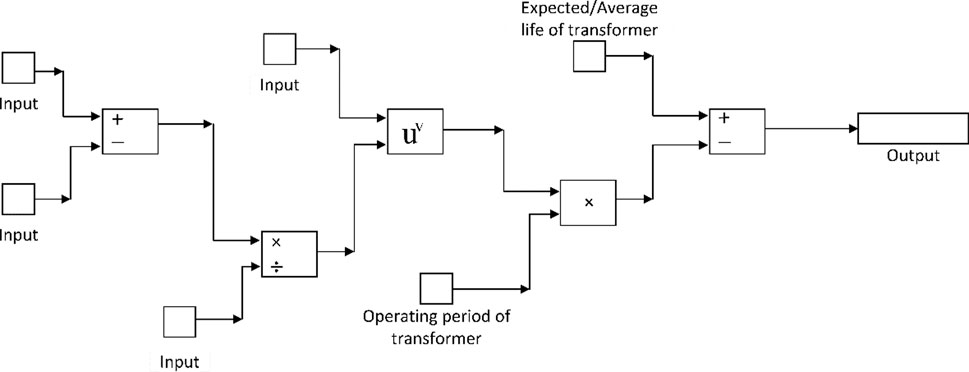
FIGURE 10. Fuzzy sublogic model of the remnant life of the transformer based on the relative aging rate.

Although insulation deterioration is a time-dependent function of temperature, moisture content, oxygen content, and acid content, the model utilized in this article is only based on the insulation temperature as the governing parameter. Because temperature distribution is not uniform, the area operating at the highest temperature usually suffers the most degradation. As a result, the winding hot spot temperature can be used to describe the rate of aging (Mann, 2013). In this case, the relative aging rate V is defined as follows:

${\text{V}=2}^{\frac{\left({\text{θ}}_{\text{h}}-98\right)}{6}}(7)$

The loss-of-life L of the insulation paper over a certain period of time is given by the following formula:

$L={\displaystyle \sum _{n=1}^N{V}_n{t}_n}(8)$

Here, V_n represents the relative aging rate for nth interval; t_n represents the nth time interval. n represents the number of each interval; N represents the total number of intervals considered in a certain period.

The remnant life R of the transformer based on the loss of life of the insulation paper and relative aging rate is given by the following formula:

$\text{R}=\left(\text{Expected}/\text{Average}\text{life}\text{of}\text{transformer}\right)-\text{Loss}\text{of}\text{life}(9)$

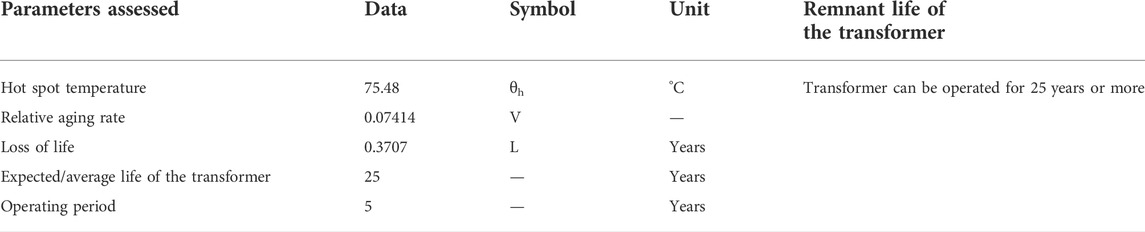
The remnant life of the power transformer operating for 5 years comes out to be 25 more years as shown in Table 5 because the hot spot temperature of winding is low and relative aging of paper insulation is slow. The life of the power transformer will be reduced to half if the hot spot temperature exceeds 98°C because the relative aging will be twice.

TABLE 5

TABLE 5. Estimating the remnant life of the transformer based on the relative aging rate.

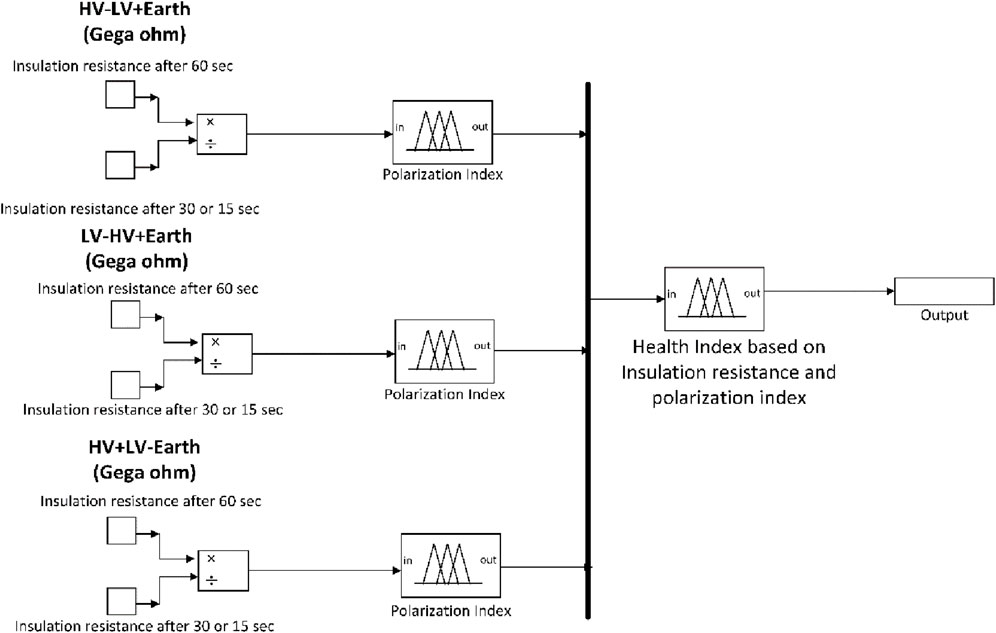
3.4 Fuzzy sublogic based on Insulation resistance and polarization index

The fuzzy submodel of insulation resistance and polarization index is depicted in Figure 11. The insulation resistance of a transformer winding depends on insulation type, condition, and applying techniques. Insulation resistance varies according to insulation thickness and is inversely proportional to conductor surface area. Insulation resistance testing is a DC voltage test, and this voltage must be within a specified limit suitable for the designed winding’s rating and the fundamental insulation condition. This is especially important when considering small and low-voltage machines, often known as wet windings. The applied test voltage may overstress the insulation, resulting in insulation failure if the test voltage is too high. Insulation resistance tests are typically performed using steady direct voltages with negative polarity. The negative polarity is favored to compensate for the phenomenon of electroendosmosis (Wen et al., 2020).

FIGURE 11

FIGURE 11. Fuzzy sublogic based on insulation resistance and polarization index.

Normally, the polarization index is defined as the ratio of the DC resistance value (IR10) measured after 10 min to the DC resistance value (IR1) measured after 1 min. The polarization index represents the slope of the characteristic curve and can be used to evaluate the insulation quality. It is also a normal practice to take readings at different intervals other than 60 min or 1 min to offer more accuracy and to allow the data to be graphed on a logarithmic scale.

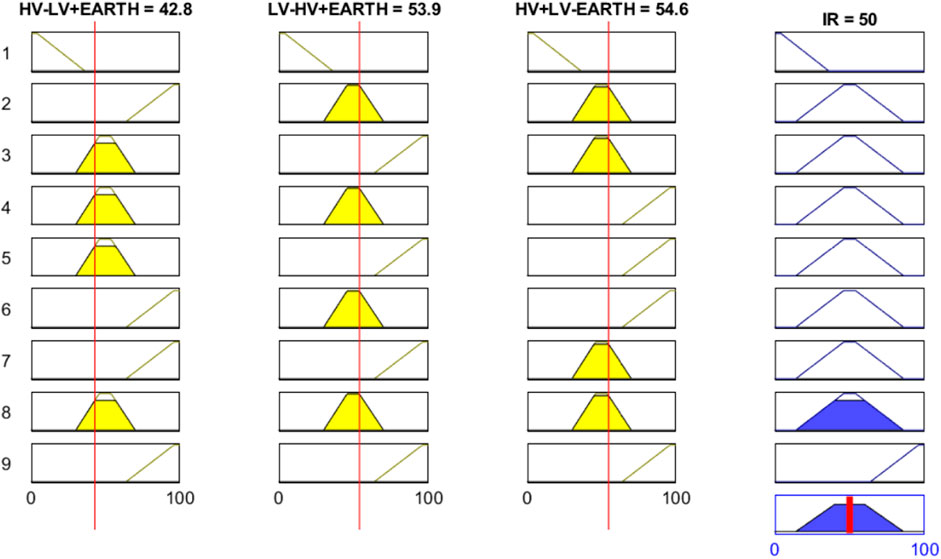
Absorption currents in insulation materials, such as asphaltic mica, sometimes take 10 min or more to decay to near zero. Nowadays, the absorption current may decay to near zero in little time in insulation material, and as a result, it is becoming a practice to calculate a version of the traditional P.I. for modern insulation. This defining characteristic results in direct voltage applied for shorter duration, and consequently, the winding must be grounded for shorter time. Since the absorption current in modern windings is nearly zero after a few minutes, the test time can be significantly reduced without any loss of information regarding the degree of contamination or moisture absorption present (Fa, 1988). Figure 12 shows that a total of 9 rules are used to develop the fuzzy submodel. The insulation resistance for all the condition lies in an average range that’s why the overall result is 50% which is shown in Table 6.

TABLE 6

TABLE 6. Health index based on insulation resistance and polarization index.

FIGURE 12

FIGURE 12. Rules used in fuzzy sublogic for insulation resistance and polarization index.

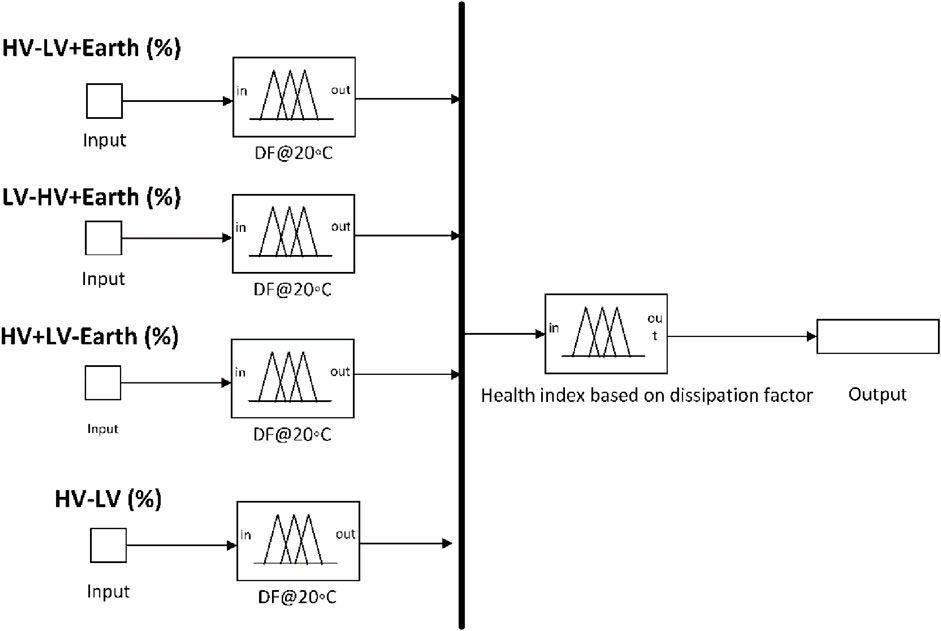
3.5 Fuzzy sublogic based on Dissipation factor of the insulation system

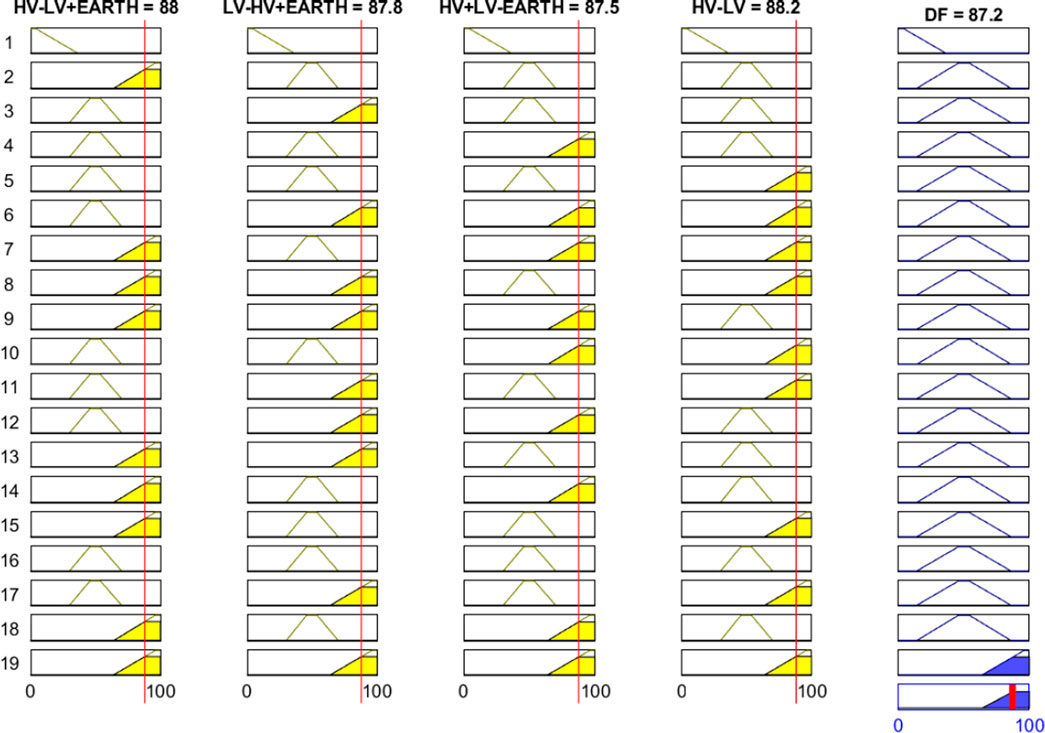
For the sake of this discussion, both PF and DF are regarded as functionally similar; nonetheless, the calculations differ. Remember that tan-delta is another common term for these functionally identical tests. The DF as shown in Figure 13 has long been recognized as one of the most effective means of measuring a transformer’s overall status, and it is important to a transformer condition-based maintenance program. Because the capacitance value and related charging current are necessary to calculate the DF, the AC capacitance test is a subset of the DF test. Because of their close relationship, both values are usually examined jointly. Transformer DF testing can assist in establishing whether the level of contamination is above acceptable risk criteria or whether mechanical damage due to bulk coil movement is a possibility. The DF is one of the most effective ways for identifying moisture and pollution within a transformer, although it is also affected by bushing conditions and testing conditions. The capacitance measurement (as part of the DF test) can assist in determining whether the coil has moved in bulk or whether a layer of insulation has been shorted (Faria et al., 2018). Figure 14 shows that a total of 19 rules are used to develop the fuzzy submodel for the determination of dissipation factor of the insulation system. Fuzzy submodel showed health index of 87.2% in Table 7 which reflects lower value of dissipation factor of insulation system which will result in lower power loss/absorbed by dielectric material or internal resistance resulting in high quality capacitance of overall system.

TABLE 7

TABLE 7. Health index based on dissipation factor of the insulation system.

FIGURE 13

FIGURE 13. Fuzzy sublogic based on dissipation factor of the insulation system.

FIGURE 14

FIGURE 14. Rules used in fuzzy sublogic for dissipation factor of the insulation system.

4 Integration of fuzzy submodels

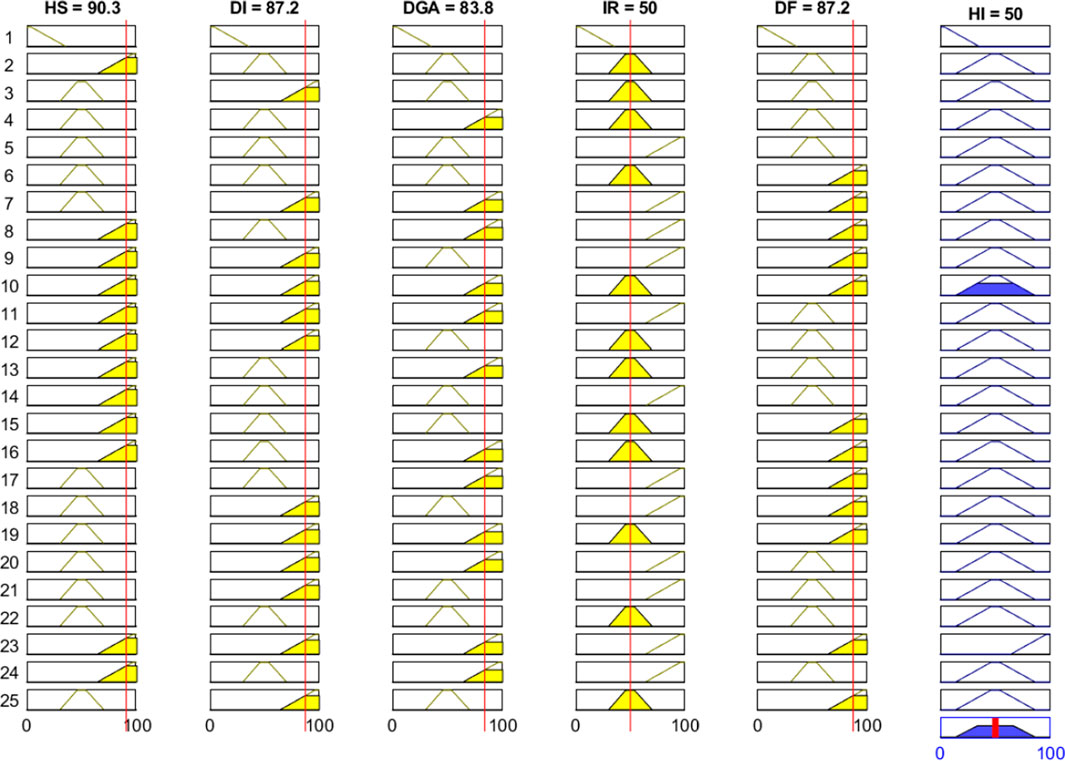
The submodels obtained previously are integrated as shown in Figure 15 to calculate the overall health of the transformer. Figure 16 represents that a total of 25 fuzzy rules are used to develop the overall model. The output (HI) will give a value close to 100% if all the individual input parameters are in good condition, and similarly, the output will give a value close to 0% if any of the individual input parameters are in critical condition. Table 8 shows the results of all fuzzy submodels. The health index of transformer results in 50% due to lower value of insulation resistance and polarization index.

TABLE 8

TABLE 8. Health index based on fuzzy submodels.

FIGURE 15

FIGURE 15. Fuzzy sublogic based on submodels.

FIGURE 16

FIGURE 16. Rules used in fuzzy sublogic for submodels.

5 Discussion

This work outlines a comprehensive, component-wise health estimation method for power transformers. The methodology accurately estimates the health of transformer components and predicts the remnant life of the transformer. This method has been tested on new and old transformers at various stages of service life, and has yielded satisfactory results as can be seen in the various results and discussion sections. For example, the results obtained from this work show that the transformers operating for 5 years have a health index of around 50%. For such transformers, all the parameters show good health indices except insulation resistance/polarization index, which results in an overall average health of the transformer. The lower health index based on insulation resistance/polarization index is an indication of degradation of the transformer insulation due to aging as no fault is detected based on results obtained from fault identification through Duval triangle 1. Therefore, after the extensive presentation of results and discussions, it can be concluded that the method is effective and predicts the health and remnant life of power transformers effectively.

6 Conclusion

This work develops a new, integrated fuzzy logic–based method to predict the health of power transformers by taking into account the state of several individual transformer components such as dielectric strength of oil, dissolved gas analysis (DGA), hottest spot temperature of winding, insulation resistance and polarization index, and dissipation factor of system insulation. A case study is used to demonstrate the efficacy of the developed method. The results obtained from remnant life based on the relative aging rate show slow aging. For transformers with faulty insulation resistance/polarization index of the transformer at the time of manufacturing, there are variations in insulation resistance/polarization index when compared to results of factory testing. Based on the results obtained from the testing of various distribution transformers, it is concluded that the proposed method accurately predicts the health status and remnant life of power transformers.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization: MF, KH, and SR; data curation: MA, FA, KA, and IB; formal analysis: MF, MA, FA, KA, and IB; funding acquisition: MA, FA, KA, and IB; investigation: MF; methodology: MF; project administration: KH and FA; resources: MF, KH, MK, MA, KA, and IB; software: MF and MK; supervision: KH, SR and MK; validation: MK, MA, and KA; visualization: MF; writing—original draft: MF and KH; writing—review and editing: KH, MA, FA, KA, and IB.

Funding

The authors acknowledge the support provided by the Deanship of Scientific Research at Jouf University under grant No. (DSR-2021-02-0302).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abu-Siada, A., and Hmood, S. (2015). A new fuzzy logic approach to identify power transformer criticality using dissolved gas-in-oil analysis. Int. J. Electr. Power & Energy Syst. 67, 401–408. doi:10.1016/j.ijepes.2014.12.017

CrossRef Full Text | Google Scholar

Aburaghiega, E. (2018). “Enhancement of power transformer state of health diagnostics based on fuzzy logic system of DGA,” in 2018 twent. Int. Middle east power syst. Conf., 400–405.

CrossRef Full Text | Google Scholar

Arshad, M., Islam, S., and Khaliq, A. (2014). Fuzzy logic approach in power transformers management and decision making. IEEE Trans. Dielectr. Electr. Insul. 21 (5), 2343–2354. doi:10.1109/TDEI.2014.003859

CrossRef Full Text | Google Scholar

Arshad, M., Islam, S., and Member, S. (2010). Fuzzy logic approach to identify transformer criticality using dissolved gas analysis. 1–5.

Google Scholar

Arshad, M., Islam, S. M., and Khaliq, A. (2004). Power transformer asset management, 21–24.

Google Scholar

Assessment, C. (2020). An intelligent system for condition assessment of power transformers, 14–22.

Google Scholar

Azis, N., Liu, Q., and Wang, Z. D. (2014). Ageing assessment of transformer paper insulation through post mortem analysis. IEEE Trans. Dielectr. Electr. Insul. 21 (2), 845–853. doi:10.1109/TDEI.2013.004118

CrossRef Full Text | Google Scholar

Azmi, A., Jasni, J., Azis, N., and Kadir, M. Z. A. A. (2017). Evolution of transformer health index in the form of mathematical equation. Renew. Sustain. Energy Rev. 76, 687–700. doi:10.1016/j.rser.2017.03.094

CrossRef Full Text | Google Scholar

Bai, Y., and Wang, D. (2006). Fundamentals of fuzzy logic control — fuzzy sets, fuzzy rules and defuzzifications. Advanced Fuzzy Logic Technologies in Industrial Applications In Editor Y. Bai, H. Zhuang, and D. Wang (Springer, London: Advances in Industrial Control), 17–36. doi:10.1007/978-1-84628-469-4_2

CrossRef Full Text | Google Scholar

Bakar, N. A., and Abu-Siada, A. (2016). Fuzzy logic approach for transformer remnant life prediction and asset management decision. IEEE Trans. Dielectr. Electr. Insul. 23 (5), 3199–3208. doi:10.1109/tdei.2016.7736886

CrossRef Full Text | Google Scholar

Basuki, A. (2018). “Online dissolved gas analysis of power transformers based on decision tree model,” in 2018 conf. Power eng. Renew. Energy, 1–6.

CrossRef Full Text | Google Scholar

Ben Dhaou, I., Kondoro, A., Kelati, A., Rwegasira, D. S., Naiman, S., Mvungi, N. H., et al. (2017). Communication and security technologies for smart grid. Int. J. Embed. Real-Time Commun. Syst. 8 (2), 305–331. doi:10.4018/978-1-5225-5649-7.ch016

CrossRef Full Text | Google Scholar

Bhide, R. S., Srinivas, M. S. S., and Banerjee, A. (2010). Analysis of winding inter-turn fault in transformer : A review and transformer models.

Google Scholar

Biçen, Y., Çilliyüz, Y., Aras, F., and Aydugan, G. (2011). “An assessment on aging model of IEEE/IEC standards for natural and mineral oil-immersed transformer,” in Proc. - IEEE int. Conf. Dielectr. Liq.. doi:10.1109/ICDL.2011.6015442

CrossRef Full Text | Google Scholar

C57.104 (2019). “IEEE guide for the interpretation of gases generated in mineral oil-immersed transformers,” in Ieee std C57.104.

Google Scholar

Chantola, A., Sharma, M., and Saini, A. (2018). “Integrated fuzzy logic approach for calculation of health index of power transformer,” in Proc. Int. Conf. Inven. Commun. Comput. Technol. ICICCT 2018, 1045–1050. Icicct. doi:10.1109/ICICCT.2018.8473316

CrossRef Full Text | Google Scholar

Contin, A., Rabach, G., Borghetto, J., and De Nigris, M. (2011). Frequency-response analysis of power transformers by means of fuzzy tools, 900–909.

CrossRef Full Text | Google Scholar

Cygan, P., and Laghari, J. R. (1990). Models for insulation aging under electrical and thermal multistress. IEEE Trans. Elect. Insul. 25 (5), 923–934. doi:10.1109/14.59867

CrossRef Full Text | Google Scholar

Davies, K., and Roose, L. Online distribution service transformer health assessment using real-time grid energy monitor, 2–7.

De Faria, H., Costa, J. G. S., and Olivas, J. L. M. (2015). A review of monitoring methods for predictive maintenance of electric power transformers based on dissolved gas analysis. Renew. Sustain. Energy Rev. 46, 201–209. doi:10.1016/j.rser.2015.02.052

CrossRef Full Text | Google Scholar

Dukarm, J., Draper, Z., and Piotrowski, T. (2020). Diagnostic simplexes for dissolved-gas analysis. Energies 13, 6459. doi:10.3390/en13236459

CrossRef Full Text | Google Scholar

Fa, C. (1988). Tile characteristics of insulation resistance of transfofmers w a n g 1sgiqing, 463–466.

Google Scholar

Faria, G., Pereira, M., Lopes, G., Villibor, J., Tavares, P., and Faria, I. (2018). “Evaluation of capacitance and dielectric dissipation factor of distribution transformers-experimental results,” in 2018 IEEE electr. Insul. Conf. EIC, 336–339. doi:10.1109/EIC.2018.8481052

CrossRef Full Text | Google Scholar

Idrees, M., Riaz, M. T., Aashir, W., Zahir, J. P., Raza, H. A., Khan, M. A., et al. (2019). Fuzzy logic based calculation and analysis of health index for power transformer installed in grid stations. RAEE 2019 - Int. Symp. Recent Adv. Electr. Eng. 4, 1–6. doi:10.1109/RAEE.2019.8887016

CrossRef Full Text | Google Scholar

IEC 60296 (2020). Fluids for electrotechnical applications – mineral insulating oils for electrical equipment.” IEC 60296.

Google Scholar

IEC 60599 (2015). Mineral oil-filled electrical equipment in service-Guidance on the interpretation of dissolved and free gases analysis. IEC 60599.

Google Scholar

Islam, S. (2012). A new approach to identify power transformer criticality and asset management decision based on. Dissolved Gas-in-Oil Anal. 19 (3), 1007–1012.

Google Scholar

Jian, W., Wenbing, Z., Demeng, B., and Kuihua, W. (2020). The new developed health index for power transformer condition assessment, 1880–1884.

Google Scholar

Leauprasert, K. (2020). Intelligent machine learning techniques for condition assessment of power transformers, 65–68. Icpei.

Google Scholar

Mahmoud, M. A., Md Nasir, N. R., Gurunathan, M., Raj, P., and Mostafa, S. A. (2021). The current state of the art in research on predictive maintenance in smart grid distribution network: Fault’s types, causes, and prediction methods—a systematic review. Energies 14, 5078. doi:10.3390/en14165078

CrossRef Full Text | Google Scholar

Mann, P. (2013). Determination of transformer life expectancy. Electr. Eng. 82 (8), 512–514. doi:10.1109/ee.1963.6540988

CrossRef Full Text | Google Scholar

Mawelela, T. U., Nnachi, A. F., Akumu, A. O., and Abe, B. T. (2020). “Fault Diagnosis of power transformers using duval triangle,” in 2020 IEEE PES/IAS PowerAfrica, PowerAfrica, 1–5. doi:10.1109/PowerAfrica49420.2020.9219802

CrossRef Full Text | Google Scholar

Nurcahyanto, H., Nainggolan, J. M., Ardita, I. M., and Hudaya, C. (2019). Analysis of power transformer’s lifetime using health index transformer method based on artificial neural network modeling. Proc. Int. Conf. Electr. Eng. Inf. 2019, 574–579. doi:10.1109/ICEEI47359.2019.8988870

CrossRef Full Text | Google Scholar

Patil, A. J., Singh, A., and Jarial, R. K. (2020). An integrated fuzzy based online monitoring system for health index and remnant life computation of 33 kV steel mill transformer. 2020 int. Conf. Ind. 4.0 technol. I4Tech, 176–181. doi:10.1109/I4Tech48345.2020.9102698

CrossRef Full Text | Google Scholar

Poonnoy, N., Suwanasri, C., and Suwanasri, T. (2021). Fuzzy logic approach to dissolved gas analysis for power transformer failure index and fault identification. Energies 14 (1), 36–17. doi:10.3390/en14010036

CrossRef Full Text | Google Scholar

Prasojo, R. A., Maulidevi, N. U., Soedjarno, B. A., and Suwarno, S. (2019). “Health index analysis of power transformer with incomplete paper condition data,” in 4th int. Conf. Cond. Assess. Tech. Electr. Syst. CATCON 2019, 3–6. doi:10.1109/CATCON47128.2019.CN0073

CrossRef Full Text | Google Scholar

Rosero-z, L. (2018). Analysis of maintenance in transformers based on a fuzzy logic method. 3.

CrossRef Full Text | Google Scholar

Sarajcev, P., Jakus, D., Vasilj, J., and Nikolic, M. (2018). Analysis of transformer health index using bayesian statistical models.

Google Scholar

Velásquez, R. M. A., and Lara, J. V. M. (2017). Principal components analysis and adaptive decision system based on fuzzy logic for power transformer. Fuzzy Inf. Eng. 9 (4), 493–514. doi:10.1016/j.fiae.2017.12.005

CrossRef Full Text | Google Scholar

Wen, L., Xiao-Mei, Z., Shan-Shan, Z., Liang-Xian, Z., Zhao, Z., and Xiaong-Yu, K. (2020). “Research on lead insulation structure of 750kV auto-transformer,” in 7th IEEE int. Conf. High volt. Eng. Appl. ICHVE 2020 - proc., 17–20. doi:10.1109/ICHVE49031.2020.9279682

CrossRef Full Text | Google Scholar