Multi-time scale trading profit model of pumped storage power plant for electricity market

Pumped storage power plant (PSPP) has the upper hand on economy and cleanness. It also has the functions of frequency regulation, phase regulation, and spare, which have been instrumental in maintaining the stability of power system operation. But now the mechanism for PSPP to become involved in electricity market transactions in China is imperfect. How to properly establish a multi-time scale trading profit model and reasonably allocate the capacity of PSPP has been instrumental in realizing the economic operation of the power system. So, this article analyzes the mechanism for PSPP to become involved in electricity market trading by providing combined electricity supply services and ancillary services, and establishes an optimization model with respect to economic optimization. At the same time, considering the volatility of electricity prices in the spot market, the risk of PSPP becoming involved in electricity market trading is measured by conditional Value at Risk (CVaR) to achieve economic optimization while minimizing the risk. The case studies demonstrate that the proposed profit model can enhance the revenue and decrease the risk of PPSP.

1 Introduction

Since the transitional burning of fossil fuels has led to global warming, reducing greenhouse gas emissions has become an urgent problem (Luka et al., 2017). However, at present, power generation in China’s power industry is still dominated by thermal power, it is particularly important to replace traditional thermal power with clean energy power generation. And accelerating the construction of a new type of power system based on clean energy, so as to achieve the objective of carbon peaking and carbon neutrality (Yang et al., 2021). However, on the one hand, the prediction of the amount of clean energy generation is difficult, such as wind power is severely affected by wind and is highly random; on the other hand, when transmission lines are congested or underloaded, excessive clean energy generation will be cut, leading to energy waste and low utilization (Guo et al., 2021). Therefore, energy storage is particularly important for power systems containing clean energy, energy storage not only can enhance the utilization of clean energy but also increase the dependability of electricity supply (Pang et al., 2021).

PSPP is considered to be a good solution for energy storage units. Firstly, Pumped storage does not emit carbon dioxide when generating electricity as a clean energy source. Secondly, the high flexibility of PSPP dispatch has a significant effect on the constant operation of the power system. Thus, with the further advancement of green energy generation, the role of the PSPP will become more important in the power system (Jahns et al., 2020).

However, because China’s electricity market is not mature enough, it is tough for PSPP to recover its costs by making profits only based on the difference between peak and valley electricity prices. Therefore, various scholars have studied the cost recovery and benefits situation of PSPP. Masoumzadeh et al. (2018) pointed out that the current cost of PSPP is comparatively high, but government support and decreasing technology costs could create conditions for full-scale adoption of PSPP in the electricity market. Julian et al. (2020) proposed a combination of long-term and short-term cycles for pumped storage power plants, which greatly reduces the cost of pumped storage power plants, but this combination requires strict requirements for the construction location of pumped storage power plants and the surrounding theoretical environment. Zhao et al., 2021 used the cooperative game approach to share the cost of auxiliary services of pumped storage power plants and develop a compensation mechanism for auxiliary services, but in their study, they mainly focused on peak-shaving auxiliary services only, and the remaining several auxiliary services were not fully considered. Sospiro et al. (2021) mainly consider the environmental and social aspects of pumped storage plants and focus on the environmental aspects of the auxiliary services of pumped storage plants, but do not consider the cost recovery of pumped storage itself. However, the cost reclaim mechanism and revenue mechanism of PSPP studied by most scholars nowadays are not perfect, and most of them only share the cost for a single ancillary service, which cannot give full play to the profitability of each ancillary service of PSPP, making it difficult for PSPP to obtain considerable revenue.

Moreover, the current electricity price mechanism is not sufficient and the fluctuation of electricity price is random, which has a certain impact on the economic, stable and efficient operation of PSPP. Li et al. (2022) proposed a two-part tariff for pumped storage plants to promote wind power consumption, but the pricing mechanism is not very different from the traditional two-part tariff, and the role of the ancillary services market is not considered in the trading process. Lazar et al. (2020) analyze the role of peaking services of pumped storage power plants on the power system and analyze the uncertain relationship between tariff difference and revenue, but only the time-of-use tariff of pumped storage power plants is considered, so the tariff mechanism is single. He et al. (2022) designed a two-part tariff mechanism for different stages of pumped storage power plants to enable pumped storage plants to earn significant revenues, but did not consider pumped storage as an independent trading entity and considered only peaking auxiliary services. AK et al. (2019) propose a situational method to work out the return of PSPP by considering the volatility of electricity prices and using historical electricity prices. And Koko et al. (2018) improved the current time-of-use Pricing (TOU) by dividing the TOU into a weekday TOU and a weekend TOU. By treating weekday TOU and weekend TOU as variables, the consumption cost of residential customers at different times is effectively reduced. However, most of the current studies on pumped storage electricity tariff mechanisms only involve a single unit price, like TOU and double-stage tariff, without combining different tariff mechanisms.

PSPP not only faces the challenge of imperfect tariff mechanisms but also the challenge of the imperfect electricity market. Most studies have been conducted mainly for a single electricity market. Zejneba et al. (2022) compared the benefits between pumped storage plants and battery storage and demonstrated that pumped storage is the most efficient energy storage technology available. However, only energy arbitrage returns were considered when comparing the two, without diversifying to consider returns in other markets. Rodica and Corentin, (2021)analyze the energy and capacity benefits of pumped storage plants and propose the type of contract that mixes capacity and energy, but it can only be applied to competitive electricity markets and does not adequately consider the ancillary service benefits of pumped storage plants. Huang et al. (2022) introduced pumped storage into the Midcontinent Independent System Operator (MISO) day-ahead market in combination with other units to improve the flexibility of MISO day-ahead market dispatch and to improve the system economics through pumped storage. Luo et al. (2020) considered the impact of the pollutant trading market on system economics while considering the optimal economics of multi-energy systems. The pollutant emissions are reduced while achieving the optimal system economy. In addition to studies considering only a single electricity market, some scholars have also studied multiple electricity markets. Mosquera-Lopez and Nursimulu (2019) contrasted the price drivers of the spot and medium- and long-term market (MLTM), concluding that the determinants of the spot market were renewable energy and electricity demand, while the determinants of MLTM are the prices of natural gas as well as coal. Zhu et al. (2021) researched the mixed electricity market, extended the definition of the mixed electricity market, and compared and analyzed two different contract decision models of shared contract and wholesale price contract to study the pricing strategy of clean energy grid connection. Parinaz et al. (2022) transformed the terraced hydro plants into pumped storage plants to achieve enhanced returns but did not consider the transformation costs and medium- and long-term market transactions in the process. Mou (2019) proposed to use the spot market to make up for the defect of the two-sided market as well as combine different ancillary service trading models to obtain more profitability for PSPP. However, it did not consider the potential revenue of ancillary services, which led to the underestimation of the revenue of PSPP. In a summary, the current research on multiple electricity markets is not sufficient, and most of them only consider the research on the single spot market, and the research on competitive bidding in the multi-time scale electricity market is less. At the same time, there is less research on the ancillary service market of PSPP, which does not effectively leverage the ancillary services of PSPP to increase revenue. Thus, there is a need to further improve the electricity market mechanism to achieve a reasonable allocation of resources for PSPP, to obtain higher revenue.

At the same time, with the gradual opening and improvement of the electricity market, different bidding strategies will bring different levels of risk, and the relationship between the balance of risk and its economic benefits should also be addressed. Li et al. (2021) proposed a p-robust algorithm to calculate the risk caused by the uncertainty of electricity price on the revenue of pumped storage power plants, but it needs to sacrifice part of the profit while reducing the risk of pumped storage revenue. Luo et al. (2021) considered the uncertainty of distributed energy sources and the role of energy storage devices on multiple time scales to optimize the operation of the electric grid. Yang et al. (2020) proposed a demand response model of energy storage operators to take part in the MLTM to reduce the uncertainty risk while lowering the power purchase cost for operators through flexible energy storage systems. Liu et al. (2021) considered the randomness and volatility of wind power in multiple microgrids and established a random planning model, which provided a strategy for the balance of benefits and risks. Tian et al. (2020) put forward a bidding method to avoid risks for PSPP, which reduces the risk of participating in the market through downside risk constraints. Gao et al. (2019) used the conditional value at risk (CVaR) theory to study the uncertainty of virtual power plant (VPP) market prices and proposed a bi-level model to optimize the operating strategies in the day-ahead and real-time markets. Canakoglu and Adiyeke, (2020) proposed a variety of pricing models for power products based on price uncertainty. The portfolio problem of mean-square optimization and conditional Value at Risk was solved by combining price forecasting and risk management. From above discussion, it can be concluded that there are few studies on the balance between return and risk for PSPP, and most of the studies on PSPP only consider the maximization of power plant return and ignore the risk caused by the volatility of electricity prices. Therefore, how to balance the relationship between return and risk is crucial for PSPP.

Considering the above problems, this article improves from the following aspects:

1) In the study of spot market trading of PSPP, the actual called rotating reserve capacity is considered to complement the power revenue and increase the total revenue of PSPP participating in the spot market, and the impact of different called price factors on the revenue of PSPP is analyzed.

2) Combining the electricity supply services and ancillary services, the trading mechanism of PSPP participating in the MLTM and the spot market is proposed, and an optimization model with respect to economic optimality is established, and compared it with the current double-stage tariff mechanism in my country to prove that ancillary services are of great significance to the cost recovery of PSPP.

3) Considering the volatility of electrovalence in the spot market, the risk of PSPP taking part in the electricity market is measured by CVaR to achieve economic optimization while minimizing the risk, and the validity of the model is proved through comparative analysis.

The rest of the article is shown below. Section 2 discusses the tariff mechanism of PSPP. Afterward, Section 3 proposes a profit model for PSPP. Next, Section 4 verifies the validity of the model through example analysis. Finally, Section 5 summarises this article.

2 Electricity price mechanism of pumped storage power plant

At present, the electricity price mechanism of PSPP in China is mainly TOU and double-stage tariff.

2.1 Time-of-use

The TOU refers to the cost of charging electricity for each period according to the average marginal cost of system operation. The periods are from the division of a 24-h day according to the system operation condition (Zhao et al., 2022). Further improving the TOU, especially reasonably widening the price difference between peak and valley tariffs, is conducive to PSPP to obtain higher electric energy returns, and to create more space for the development of PSPP, thus further helping new energy accommodation.

2.2 Double-stage tariff

The double-stage tariff is a method that combines the basic tariff corresponding to the capacity and the electricity tariff corresponding to the electricity consumption to determine the tariff (Tan et al., 2021). When the double-stage tariff is applied, it can reflect the benefits of PSPP in all aspects. On the one hand, the electricity tariff reflects the basic operation mode of PSPP using the peak-to-valley price difference, and on the other hand, the capacity tariff reflects the multiple values of the ancillary services of PSPP such as peak-shaving and backup, which has an important impact on improving the benefits of PSPP.

3 Profit model of pumped storage power plant

In the electricity market environment, PSPP can provide multiple types of products in MLTM and spot market due to their superior performance. For example, electric energy products and ancillary service products include spinning reserve, black start, and so on. PSPP can reveal the value of its own power and capacity by taking part in the electricity market bidding and gain considerable profits.

3.1 Profit of pumped storage power plant taking part in the spot market

In this article, the profit of PSPP included electric energy spot market profit and spot profit from ancillary services. In the electric energy spot market, PSPP can earn revenue by purchasing and selling electricity at different times using the peak-to-valley difference. In the spot market for ancillary services, PSPP can generate profits through rapid start-up or rapid change in operating conditions and playing a standby role.

The profit model of PSPP taking part in the spot market is as (1).

$\begin{array}{c}{F}_1={\displaystyle \sum _{i=1}^{24}{\displaystyle \sum _{\omega =1}^{N_{\omega }}{\pi }_{\omega }\cdot \left({\delta }_i{p}_i^{e,s}{q}_i^{e,s}-\left(1-{\delta }_i\right)p_i^{buy}{q}_i^{buy}+{\delta }_i\left(p_i^{c,s}{q}_i^{c,s}+p_i^{c,s^{\prime }}{q}_i^{c,s^{\prime }}\right)\right)}}\end{array}(1)$

where, ${\pi }_{\omega }$ is the probability of various typical electricity price scenarios; ${\delta }_i$ is the working state of the PSPP, including pumping and power generation, the pumping state is represented by 0, and the power generation state is represented by 1; $p_i^{e,s}$ is the feed-in price of PSPP in the ith time period; $q_i^{e,s}$ is the on-grid energy of PSPP in the ith time period; $p_i^{buy}$ is the purchased price of PSPP in the ith time period, because PSPP purchases electricity from the power grid as a large user, considering the usage fee of the power grid, the purchased price of PSPP in the same period should be higher than the on-grid electricity price, so the purchased price of PSPP is 1.1 times the on-grid electricity price.; $q_i^{buy}$ is the amount of electricity purchased of PSPP in the ith time period; $q_i^{c,s}$ is the spinning reserve capacity; $p_i^{c,s}$ is the electricity price of spinning reserve capacity in the ith time period; $q_i^{c,s\prime }$ is the actual called spinning reserve capacity in the ith time period; $p_i^{c,s\prime }$ is the electricity price of the actual called spinning reserve capacity in the ith time period.

3.2 Price uncertainty in pumped storage power plant market based on conditional value at risk

Since the uncertainty of electricity prices in the spot market effect on the bidding strategy of PSPP, this paper measures the risk because of the uncertainty of electrovalence in the spot market by applying the conditional value at risk (CVaR) (do Prado and Chikezie, 2021). The specific expressions are as (2).

$\begin{array}{c}{X}_{CVaR}=X_{VaR}-\frac{1}{1-\alpha }{\displaystyle \sum _{\omega =1}^{N_{\omega }}{\pi }_{\omega }{\left[F_1-X_{VaR}\right]}^{+}}\end{array}(2)$

where, $X_{VaR}$ denotes the VaR; ${\left[F_1-X_{VaR}\right]}^{+}$ is the difference between the spot market return and the VaR; $\alpha$ is the confidence level.

3.3 Profit of pumped storage participation in medium- and long-term market

The profits of PSPP participating in MLTM are divided into profits of electric energy and profits of ancillary services. PSPP obtain profits of electric energy from signing MLTM contracts for the provision of electricity, and obtain profits of ancillary services from the black-start ancillary service provided.

Since the time scale of MLTM and the spot market are different, it is necessary to decompose MLTM electric energy. In this paper, the daily power decomposition curve is selected from the peak and flat curve model: the day is divided into peak, flat and valley sections, which can be negotiated by the historical load characteristics of PSPP or other ways to determine the peak, flat and valley load power.

The profit model of PSPP taking part in MLTM is as (3).

$\begin{array}{c}{F}_2={\displaystyle \sum _{i=1}^{24}{p}_i^{e,f}{q}_i^{e,f}+p_h{t}_h/365}\end{array}(3)$

where, $p_i^{e,f}$ is electricity prices of MLTM contracts, $q_i^{e,f}$ is the daily decomposition electricity of PSPP in the ith time period; $p_h$ is the black start service fee provided by PSPP; $t_h$ is the annual black start service time of PSPP.

3.4 Cost model of pumped storage power plant

In addition to considering the power purchase cost of PSPP in the spot market, this paper also considers the start-up and stop-up cost of PSPP and the deviation cost of decomposing electricity in MLTM.

The cost model of the PSPP is as (4).

$\begin{array}{c}C=C_s+C_o\end{array}(4)$

where, $C_s$ is the start-up and shutdown cost; $C_o$ is the deviation cost of decomposing electricity in MLTM.

The start-up and shutdown cost $C_s$ represents the total start-up and shutdown cost of PSPP in 1 day.

$C_s\begin{array}{c}={\displaystyle \sum _{i=1}^{24}{C}_{qt}{n}_i^{qt}}\end{array}(5)$

where, $C_{qt}$ refers to the start-up and shutdown cost of a single unit; $n_i^{qt}$ is the number of units started/stopped in the ith time period.

The deviation cost $C_o$ refers to the cost caused by the difference between the actual decomposed electricity and the planned decomposed electricity of PSPP.

$C_o\begin{array}{c}=M{\displaystyle \sum _{i=1}^{24}\mathrm{\Delta }{\omega }_i}\end{array}(6)$

where, $\mathrm{\Delta }{\omega }_i$ is the electricity deviation of MLTM electricity decomposition in the ith time period; M is the electricity deviation penalty factor.

3.5 Profit model of pumped storage power plant

The objective function consists of four terms.

$F\begin{array}{c}=max\left(F_1+F_2-C+\beta \cdot X_{CVaR}\right)\end{array}(7)$

where, the first term is the profit of PSPP in the spot market; the second term is the profit of PSPP in MLTM; the third term is the cost model of PSPP; the last term is the product of the conditional VaR ${\text{X}}_{\text{CVaR}}$ and the risk preference coefficient $\text{β}$. The risk appetite coefficient $\text{β}$ indicates the degree of the risk.

3.6 Constraints

3.6.1 Output constraints

$q_{min}\le q_i^{e,s}\le q_{max}(8)$

$q_{min}\le q_i^{c,s}\le q_{max}(9)$

$q_{min}\le q_i^{buy}\le q_{max}(10)$

$q_{min}\le q_i^{e,f}\le q_{max}(11)$

$q_{min}\le q_i^{e,s}+q_i^{c,s}+q_i^{buy}+q_i^{e,f}\le q_{max}(12)$

$q_i^{c,s^{\prime }}\le q_i^{c,s}(13)$

where, $q_{min}$ is the minimum allowable generation/pumping power for each time period; $q_{max}$ is the maximum allowable generation/pumping power for each time period.

3.6.2 Maximum continuous pumping and power generation time constraints

$T_1\le T_p(14)$

$T_2\le T_g(15)$

where, $T_1$ is the continuous pumping time variable and $T_2$ is the continuous power generation time variable; $T_p$ is the maximum allowable continuous pumping time; and $T_g$ is the maximum allowable continuous power generation time.

3.6.3 Reservoir capacity constraints

$x_{min}\le x_i\le x_{max}(16)$

$x_i=x_{i-1}+\lambda \begin{array}{c}\left(1-{\delta }_i\right)q_i^{buy}-{\delta }_i\left(q_i^{e,s}+q_i^{c,s}\right)\end{array}(17)$

where, $x_i$ is the reservoir capacity converted to power generation in the ith time period; $x_{max}$ is the equivalent power generation of maximum reservoir capacity; $x_{min}$ is the equivalent generating capacity of minimum reservoir capacity; $\lambda$ is the total efficiency of PSPP power generation, taken as 75%.

3.6.4 Outbound flow constraints

$Q_{i,min}\le Q_i\le Q_{i,max}(18)$

where, $Q_{i,min}$ is the minimum discharge flow allowed in the ith time period of PSPP; $Q_i$ is the average discharge flow in the ith time period of PSPP; $Q_{i,max}$ is the maximum discharge flow allowed in the ith time period of PSPP.

3.6.5 Spinning reserve market constraints

$q_i^{c,s^{\prime }}=k_{c,s}{q}_i^{c,s}(19)$

$p_i^{c,s^{\prime }}=k_i{p}_i^{e,s}(20)$

The actual called spinning reserve capacity is only part of the bidded spinning reserve capacity, and because the actually called spinning reserve capacity cannot be accurately predicted. Thus, a factor $k_{c,s}$ is set to indicate the proportion of the actual called capacity to the bidded capacity. $k_i$ is the price factor of the called capacity in the spinning reserve market, indicating that the price of the called capacity in the ith time period is $k_i$ times of the on-grid electricity price in the same period.

3.6.6 The conditional value at risk correlation constraints

CVaR represents the profit of PSPP in changes of the electricity market under certain time and confidence conditions. And the higher the value of CVaR, the lower the risk.

$\begin{array}{c}{X}_{VaR}-{{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{\omega =1}^{N_{\omega }}{\pi }_{\omega }\cdot F_1\le \left[F_1-X_{VaR}\right]}}}^{+}\end{array}(21)$

${\left[F_1-X_{VaR}\right]}^{+}\ge 0(22)$

where, $X_{VaR}$ denotes the VaR; ${\left[F_1-X_{VaR}\right]}^{+}$ is the difference between the spot market return and the VaR.

3.6.7 Daily decomposition electricity constraints

$q_{i,min}^{e,f}\le q_i^{e,f}\le q_{i,max}^{e,f}(23)$

$q_i=q_i^{e,f}+q_i^{e,s}+q_i^{c,s}(24)$

$C_i={\displaystyle \sum _{x\in X}{c}_{x,i},X=\{p,f,v\}}(25)$

$c_{x,i}={\gamma }_x{C}_i={\displaystyle \sum _{t\in T_x}{q}_i^c\mathrm{\Delta }T}(26)$

where, $q_{i,max}^{e,f}$ and $q_{i,min}^{e,f}$ are the upper and lower limits of daily decomposition electricity of the unit, which are determined according to the technical parameters of the unit, contract completion and maintenance plan; $q_i$ is the total output in the ith time period of PSPP; $C_i$ is the daily contracted electricity of PSPP; p,f and v represent peak, flat, and valley hours, respectively; $c_{x,i}$ is the contracted electricity in the ith time period of PSPP; $T_x$ is the set of time period indicators included in the ith time period; ${\gamma }_x$ is the proportion of the decomposition electricity in the ith time period of PSPP to the contracted electricity. $\mathrm{\Delta }T$ refers to a certain time period in $T_x$; $q_i^c$ refers to the decomposition electricity of $\mathrm{\Delta }T$.

4 Case studies

This paper uses the CPLEX solver on the MATLAB software platform to solve the established multi-time scale profit model and derive the optimization results.

4.1 Pumped storage power plant taking part in the spot electricity energy market only

When PSPP only participates in the spot market bidding, only the spot market part of the profit model is considered, MLTM and ancillary service market parts are not considered, and the offset cost of MLTM power decomposition is not considered. The parameters of a typical PSPP are shown in Table 1.

TABLE 1

TABLE 1. Actual parameters of PSPP.

Two sets of electricity price scenarios are determined to research the profits of PSPP under different electricity tariff scenarios. The different electricity tariff scenarios are shown in Figure 1.

Scenario 1: The market demand for electricity is large, the electricity supply is insufficient, and the price difference between peak and valley is large.

Scenario 2: A small market demand for electricity, with sufficient power supply and a low peak-to-valley price difference.

FIGURE 1

FIGURE 1. Two scenarios of electricity tariff.

The profits of PSPP under the two scenarios are shown in Table 2. The operation of PSPP under scenario 1 is shown in Figure 2.

TABLE 2

TABLE 2. Comparison of profit of PSPP under different scenarios.

FIGURE 2

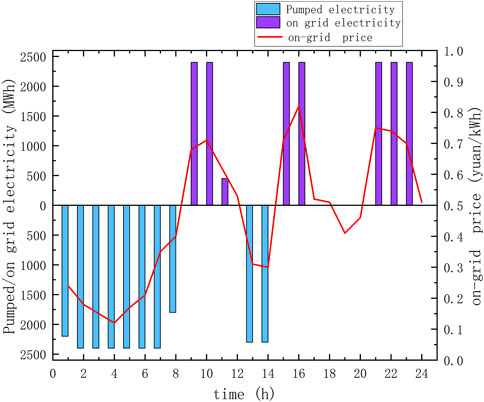
FIGURE 2. Optimal operation of PSPP that only participate in the electric energy spot market in scenario 1.

As can be seen in Figure 2, PSPP pump during the low tariff hours of 0:00–8:00 and 13:00–14:00, and sell electricity online during the peak tariff hours of 9:00–11:00, 15:00–16:00, and 21:00–23:00, using the difference between peak and valley tariffs to obtain the power revenue.

From Table 2 it can be obtained that there is a positive correlation between the profit of PSPP and the peak-to-valley electricity price difference. When the peak-to-valley electricity price difference is high, the profit of PSPP is high, and vice versa. This is because PSPP relies on the peak-to-valley electricity price difference to earn the profit, purchasing electricity for pumping at low prices and selling it at high prices.

According to the static investment of PSPP of 4,500 CNY/kW per unit kilowatt and the capital internal rate of return of 8%, the capacity tariff is 685 CNY/kW, which translates into a daily capacity profit of 4,505,100 CNY. Therefore, PSPP cannot rely on the spot market alone to recover costs and gain more profit, but also need to participate in the ancillary service market bidding and MLTM bidding.

4.2 Pumped storage power plant taking part in both the electric energy and ancillary services spot market

The profit obtained when a PSPP taking part in the ancillary services market is related to two aspects. On the one hand, the capacity tariff in the ancillary services market and, on the other hand, the tariff coefficient in the ancillary services market. This section still takes the example of a domestic PSPP in Section 4.1, and the specific parameters remain the same. Take $k_{c,s}=0.1$, $k_i=2$, $c_i$ = 0.15 CNY/kWh.

Considering the uncertainty of electricity prices, ten typical electricity price scenarios are generated as shown in Figure 3. The corresponding probabilities of each electricity price scenario are shown in Table 3. Scenario 1 and Scenario 2 are typical scenarios in Section 4.1. In this section, three typical electricity price scenarios with the highest probability are selected for comparative analysis. The selected scenarios are scenario 1, scenario 2 and scenario 7, the corresponding optimal daily operation mode is shown in Figures 4, 5, 6.

FIGURE 3

FIGURE 3. Ten typical electricity price scenarios.

TABLE 3

TABLE 3. Probability of ten electricity price scenarios.

FIGURE 4

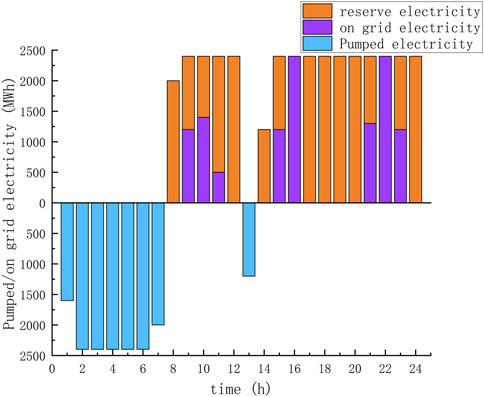
FIGURE 4. Optimal operation of PSPP that both participate in electric energy and ancillary services spot market in scenario 1.

FIGURE 5

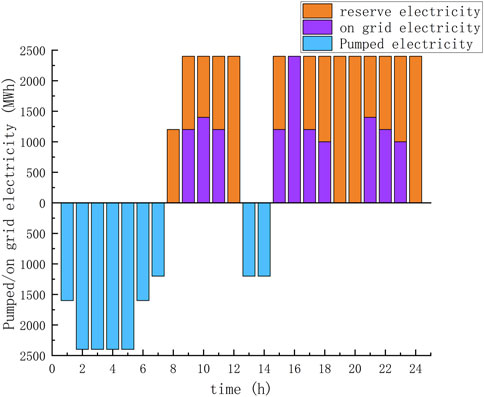
FIGURE 5. Optimal operation of PSPP that both participate in electric energy and ancillary services spot market in scenario 2.

FIGURE 6

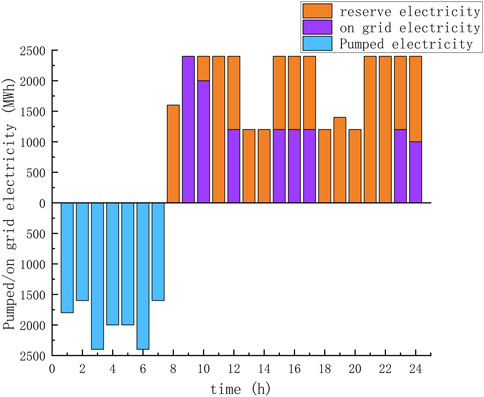
FIGURE 6. Optimal operation of PSPP that both participate in electric energy and ancillary services spot market in scenario 7.

It can be seen from Figures 4, 5, 6 that PSPP mainly purchases electricity during the early morning valley hours of 1:00–7:00 and sell electricity during the peak hours of 9:00–11:00, 15:00–17:00 and 21:00–23:00 to recover costs through the peak-to-valley tariff difference. Meanwhile, PSPP mainly provide rotating backup services at 8:00–12:00 and 15:00–24:00 to achieve PSPP cost recovery. The total returns of the three typical scenarios were respectively 8,954,200 CNY, 7,635,100CNY and 8,126,410CNY. It can be seen that taking part in both the ancillary service spot market bidding and the electric energy spot market bidding can recover the cost of PSPP and obtain more profits. And through comparison, it can be found that the more PSPP participating in the auxiliary service market, the higher the income will be.

4.3 Comparison with a single double-stage tariff

Combined with the electricity consumption characteristics of the provincial grid where PSPP is located, the peak and valley hours on the power generation side are divided as follows: peak hours: 9:00–16:00, flat hours: 17:00–24:00, valley hours: 0:00–8:00; the tariff for flat hours is 0.44 CNY/kWh, the tariff for valley hours is 0.24 CNY/kWh, and the tariff for peak hours is 0.59 CNY/kWh. The actual capacity profit of PSPP is about 931 million CNY per year, which translates into a capacity tariff of 388.73 CNY/kWh, while the theoretical capacity tariff should reach 685 CNY/kWh based on the capital internal rate of return of 8%. Therefore, the current profit of PSPP is low, and the specific double-stage tariff scheme is shown in Table 4.

TABLE 4

TABLE 4. Scheme of double-stage tariff.

The profit of pumped storage under the double-stage tariff is compared with the profit of pumped storage under the multi-electricity market environment in Section 4.2. To ensure the accuracy of the comparison results, the tariff under the electricity market conditions is set according to the TOU in the double-stage tariff case, and the results are shown in Table 5.

TABLE 5

TABLE 5. Profit of PSPP under different electricity tariff schemes.

As can be seen from Table 5, the market return on electricity energy under the electricity market bidding is lower than the return on electricity under the single double-stage tariff. In contrast, the ancillary service profit under the electricity market tariff is more than twice as high as the capacity profit under the single double-stage tariff, making the total profit higher than the total profit under the single double-stage tariff. The comparison shows that the capacity cost recovery of PSPP in the electricity market environment is not enough to rely on the power profit alone, and the level of profit in the ancillary services market has an important impact on the cost recovery of PSPP.

4.4 Pumped storage power plant taking part in medium- and long-term market bidding and spot market bidding

When PSPP takes part in both MLTM and the spot market, they need to break down MLTM power into the spot market and reasonably allocate it with the spot market capacity to obtain considerable profit. Firstly, the monthly contract of PSPP is decomposed to each day, and then the 24-h decomposition is adopted day ahead, and the contracted power corresponding to the output in the whole optimization cycle can be provided to the trading center as the result of contract decomposition. Conventional medium- and long-term decomposition curves include the following: Daily average decomposition, Peak-period decomposition, Normal-period decomposition, Valley-period decomposition, and Peak-valley-normal period decomposition (Wu et al., 2022). The pumped storage plant in the example of this paper adopts Peak-valley-normal period decomposition The daily power decomposition is carried out by determining the ratio of peak, flat and valley load segments according to the historical load, and its typical daily decomposition curve is shown in Figure 7.

FIGURE 7

FIGURE 7. Time share power curve for daily contracts.

From Figure 7, PSPP suppresses the volatility of spot electricity prices by decomposing medium- and long-term contracted electricity on a time-by-time basis and replacing part of the spot electricity. Meanwhile, the profit of PSPP included three components. The first component is the profit from PSPP taking part in the spot market. The additional profit of MLTM contracts to damp fluctuations in spot electricity prices is expressed through MLTM contracted electricity prices minus the product of the electricity prices for each period in the spot market and MLTM decomposition to spot. The third component is the benefit of PSPP providing black-start services in MLTM. MLTM contract tariff for PSPP is 0.55CNY/kWh, the annual black-start service of PSPP is shown in Table 6, and MLTM decomposition of the power output is shown in Figure 8.

TABLE 6

TABLE 6. Black-start service for PSPP.

FIGURE 8

FIGURE 8. MLTM decomposition of PSPP output.

At this point, the total profit of PSPP is 13.625 million CNY, which is significantly improved compared with the profit of participation in the spot market alone, while also smoothing out the risk caused by the randomness of the spot electricity price. The joint bidding strategy of the MLTM and spot market is obtained through the daily contract decomposition curve, which verifies the rationality and effectiveness of the model.

4.5 Impact of risk preference coefficients on returns

Because the risk in this paper only considers the risk caused by the volatility of electricity prices in the spot market, in order to compare the impact of different risk preference coefficient settings on the profit of PSPP, this section only uses the example in Section 4.2 as a reference and does not consider the impact of MLTM on PSPP, and calculates the expected profit and CVaR values of PSPP under different risk preference coefficients. The results are shown in Figure 9.

FIGURE 9

FIGURE 9. Expected profits of PSPP under different risk preferences.

It can be seen that as the risk preference coefficient increases, the expected total profit gradually decreases and the CVaR gradually increases, at which time a higher capacity price and price coefficient of the called electricity is required to complete the cost-benefit recovery. When the risk preference coefficient is small, the expected total profit decreases slowly with the increase of CVaR. However, when the risk preference coefficient is large, the expected total profit decreases significantly even if the CVaR increases by a small value.

4.5.1 β = 10

When $\beta =10$ , PSPP is extremely risk-averse and will adopt a very conservative strategy at this time, and its most profitable daily operation mode is shown in Figure 10.

FIGURE 10

FIGURE 10. Operation of PSPP ($\text{β}=10$).

Compared with the operation mode at $\beta =1$, it can be seen that at this time, for the purpose of reducing the risk and increasing the profit expectation of the tail, PSPP tends to take part more in the spinning reserve market to earn capacity profit for the power extracted during the low period, so as to reduce the risk brought by the uncertainty of electrovalence. At this time, the total profit is 8,315,000 CNY, which is slightly lower than that at $\beta =1$ in Section 4.2. However, the risk is also relatively low. At the same time, reducing the amount and frequency of pumping during the low period reduces the losses of PSPP, which is beneficial to prolong the life of the unit.

4.5.2 β = 0

When $\text{β}=0$, PSPP only aims at the maximum expected profit and will adopt a more aggressive strategy, which will have a greater impact on the stable profit of PSPP. At this time, PSPP can participate in the bidding of the day-ahead electricity market and the spinning reserve market, respectively, with a fixed percentage all the time, which can buffer the risk to a certain extent.

Assume that the percentage of pumped storage participating in the day-ahead electricity market is in the range of 10%–90%, and at the same time, assume that the price of the transferred power in the spinning reserve capacity is fixed in the electricity market environment, i.e., k is taken as 1.1. The profit of PSPP at this time is shown in Figure 11.

FIGURE 11

FIGURE 11. The profit of PSPP when the price coefficient of the transferred power is 1.1.

From Figure 11, it can be seen that when PSPP participates in the ancillary service market with a proportion of 80%, PSPP can obtain a maximum profit. Because the electric energy income obtained by PSPP only through a single peak-to-valley electricity price difference is limited, and the provision of ancillary services is the main way for PSPP to improve its own income. b. In the actual electricity market environment, the price of the transferred power in the spinning reserve capacity will also change with the change of supply and demand. However, it will be greater than the feed-in tariff in the day-ahead electricity market. Thus, the price coefficient of the transferred power in the spinning reserve market is chosen to range from 1 to 3, and the percentage of PSPP participating in the spot market is tentatively set at 80%. The change of PSPP profit with the change of price coefficient is shown in Figure 12.

FIGURE 12

FIGURE 12. PSPP revenue when participating in 80% of the ancillary services market.

It can be seen from Figure 12 that theoretically, the greater the price coefficient of the transferred electricity, the more profit of the PSPP. However, in practice, it is necessary to consider the real market situation, when the price of the ancillary services provided by PSPP is higher, the capacity of the ancillary services sold will be lower, and the profit of PSPP will also be lower. Thus, it is necessary to set the price coefficient of the called electricity reasonably.

5 Conclusion

In this paper, the trading mechanism of PSPP in the MLTM and spot market are analyzed. The participation of PSPP in the multi-time scale electricity market is considered, by combining energy and ancillary services. A profit model with respect to optimal economy and lowest risk is established to achieve a reasonable capacity allocation of PSPP in the multi-time scale electricity market.

(1) When PSPP participates in the spot market, it gains energy through the peak-to-valley price difference. The total profit is 3,995,000 CNY when the peak-to-valley price is 0.7 CNY/kWh and 1,501,300 CNY when the peak-to-valley price is 0.45 CNY/kWh. For every 1% decrease in peak-to-valley tariff difference, the total profit from PSPP decreases by 2.5%. When PSPP takes part in both the spot market and the ancillary service market, the total profit is 8,954,200 CNY, which is more profitable than the single participation in the spot market, and the recovery of the cost of PSPP can be achieved through reasonable participation in the ancillary service market.

(2) Since the volatility of real-time electricity prices can have an impact on the profit of pumped storage, different PSPPs have different risk preferences, and the expected total profit of PSPP gradually decreases while the CVaR gradually increases, when the risk preference coefficient increases. The profit of PSPPs under different risk preference coefficients is analyzed to provide a power allocation scheme for PSPPs with different risk preferences.

(3) This paper decomposes MLTM contract power into day-ahead 24-h power, and conducts market trading together with the spot market, so that the volatility of real-time power prices in the spot market can be smoothed out through the stable prices in MLTM. Thus, greater profits can be obtained while reducing the profit risks.

In this paper, the quotas in the ancillary services market decomposition of MLTM contracts to the spot market are not considered, which will be included in future studies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YaL: conceptualization, data curation, writing-original draft, writing—review and editing. SZ: conceptualization, data curation, writing-original draft, writing—review and editing. BZ: conceptualization, data curation, writing-original draft, writing—review and editing. GL: conceptualization, data curation, funding acquisition, writing—review and editing. BH: funding acquisition, methodology, project administration. YuL: conceptualization, data curation, writing—review and editing. ZX: formal analysis, validation, visualization, writing—review and editing.

Funding

This work was partially supported by the National Natural Science Foundation of China (62173082), the Fundamental Research Funds for the Central Universities (N2104014), the Guangdong Basic and Applied Basic Research Foundation (2021A1515110778), the State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (LAPS21007), and the Liaoning Revitalization Talents Program (XLYC1902090).

Conflict of interest

Authors BH and YuL were employed by State Grid Liaoning Electric Power Co., Ltd., and Information and Telecommunication Branch, State Grid Liaoning Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ak, M., Kentel, E., and Savasaneril, S. (2019). Quantifying the revenue gain of operating a cascade hydropower plant system as a pumped-storage hydropower system. Renew. Energy 139, 739–752. doi:10.1016/j.renene.2019.02.118

CrossRef Full Text | Google Scholar

Canakoglu, E., and Adiyeke, E. (2020). Comparison of electricity spot price modelling and risk management applications. Energies 13 (18), 4698. doi:10.3390/en13184698

CrossRef Full Text | Google Scholar

do Prado, J. C., and Chikezie, U. (2021). A decision model for an electricity retailer with energy storage and virtual bidding under daily and hourly CVaR assessment. IEEE Access 9, 106181–106191. doi:10.1109/ACCESS.2021.3100815

CrossRef Full Text | Google Scholar

Gao, R., Guo, H., Zhang, R., Mao, T., Xu, Q., Zhou, B., et al. (2019). A two-stage dispatch mechanism for virtual power plant utilizing the CVaR theory in the electricity spot market. Energies 12 (17), 3402. doi:10.3390/en12173402

CrossRef Full Text | Google Scholar

Guo, Z., Wei, W., Chen, L., Dong, Z., and Mei, S. (2021). Impact of energy storage on renewable energy utilization: A geometric description. IEEE Trans. Sustain. Energy 12 (2), 874–885. doi:10.1109/TSTE.2020.3023498

CrossRef Full Text | Google Scholar

He, Y., Liu, Y., Li, M., and Zhang, Y. (2022). Benefit evaluation and mechanism design of pumped storage plants under the background of power market reform - a case study of China. Renew. Energy 191, 796–806. doi:10.1016/j.renene.2022.03.070

CrossRef Full Text | Google Scholar

Huang, B., Chen, Y., and Baldick, R. (2022). A configuration based pumped storage hydro model in the MISO day-ahead market. IEEE Trans. Power Syst. 37 (1), 132–141. doi:10.1109/TPWRS.2021.3097270

CrossRef Full Text | Google Scholar

Jahns, C., Podewski, C., and Weber, C. (2020). Supply curves for hydro reservoirs – estimation and usage in large-scale electricity market models. Energy Econ. 87, 104696. doi:10.1016/j.eneco.2020.104696

CrossRef Full Text | Google Scholar

Julian, D., Behnam, Z., Rafael, L., Paulo, S., Andreas, N., Nivalde, J., et al. (2020). Existing and new arrangements of pumped-hydro storage plants. Renew. Sustain. Energy Rev. 129, 109914–110321. doi:10.1016/j.rser.2020.109914

CrossRef Full Text | Google Scholar

Koko, S. P., Kusakana, K., and Vermaak, H. J. (2018). Optimal power dispatch of a grid-interactive micro-hydrokinetic-pumped hydro storage system. J. Energy Storage 17, 63–72. doi:10.1016/j.est.2018.02.013

CrossRef Full Text | Google Scholar

Lazar, Š., Saša, M., and Vladan, R. (2020). Pumped hydroelectric energy storage as a facilitator of renewable energy in liberalized electricity market. Energies 13, 6076. doi:10.3390/en13226076

CrossRef Full Text | Google Scholar

Li, H., Zheng, H., Zhou, B., Li, G., Yang, B., Hu, Bo., et al. (2022). Two-Part Tariff of pumped storage power plants for wind power accommodation. Sustainability 14 (9), 5603. doi:10.3390/su14095603

CrossRef Full Text | Google Scholar

Li, Z., Zhang, Q., Guo, Q., and Sayyad, N. (2021). Pumped hydro energy storage arbitrage in the day-ahead market in smart grid using stochastic p-robust optimization method. Sustain. Cities Soc. 75, 103274. doi:10.1016/j.scs.2021.103274

CrossRef Full Text | Google Scholar

Liu, Y., Liu, T., and He, S. (2021). Coordination and optimization of CCHP microgrid group game based on the interaction of electric and thermal energy considering conditional value at risk. IEEE Access 9, 88664–88673. doi:10.1109/ACCESS.2021.3089591

CrossRef Full Text | Google Scholar

Luka, P., Hrvoje, M., Luka, P., Xuebin, W., Milan, V., Houzhang, T., et al. (2017). Coupling of cleaner production with a day-ahead electricity market: A hypothetical case study. J. Clean. Prod. 143, 1011–1020. doi:10.1016/j.jclepro.2016.12.019

CrossRef Full Text | Google Scholar

Luo, Y., Nie, Q., Yang, D., and Zhou, B. (2021). Robust optimal operation of active distribution network based on minimum confidence interval of distributed energy beta distribution. J. Mod. Power Syst. Clean. Energy 9 (2), 423–430. doi:10.35833/MPCE.2020.000198

CrossRef Full Text | Google Scholar

Luo, Y., Zhang, X., Yang, D., and Sun, Q. (2020). Emission trading based optimal scheduling strategy of energy hub with energy storage and integrated electric vehicles. J. Mod. Power Syst. Clean. Energy 8 (2), 267–275. doi:10.35833/MPCE.2019.000144

CrossRef Full Text | Google Scholar

Masoumzadeh, A., Nekouei, E., Alpcan, T., and Chattopadhyay, D. (2018). Impact of optimal storage allocation on price volatility in energy-only electricity markets. IEEE Trans. Power Syst. 33, 1903–1914. doi:10.1109/TPWRS.2017.2727075

CrossRef Full Text | Google Scholar

Mosquera-Lopez, S., and Nursimulu, A. (2019). Drivers of electricity price dynamics: Comparative analysis of spot and futures markets. Energy Policy 126, 76–87. doi:10.1016/j.enpol.2018.11.020

CrossRef Full Text | Google Scholar

Mou, D. G. (2019). Pumped storage hydro power’s function in the electricity market under the electricity deregulation background in China-A case study of Fujian province. Energy & Environ. 30 (6), 951–968. doi:10.1177/0958305X18813727

CrossRef Full Text | Google Scholar

Pang, N., Meng, Q., and Nan, M. (2021). Multi-criteria evaluation and selection of renewable energy battery energy storage system-A case study of tibet, China. IEEE Access 9, 119857–119870. doi:10.1109/ACCESS.2021.3107192

CrossRef Full Text | Google Scholar

Parinaz, T., Emre, N., and Ayse, S. (2022). Operational benefit of transforming cascade hydropower stations into pumped hydro energy storage systems. J. Energy Storage 51, 104444–152X. doi:10.1016/j.est.2022.104444

CrossRef Full Text | Google Scholar

Rodica, L., and Corentin, S. (2021). Market strategies for large-scale energy storage: Vertical integration versus stand-alone player. Energy Policy 151, 112169–114215. doi:10.1016/j.enpol.2021.112169

CrossRef Full Text | Google Scholar

Sospiro, P., Nibbi, L., Liscio, M. C., and De Lucia, M. (2021). Cost–benefit analysis of pumped hydroelectricity storage investment in China. Energies 14 (24), 8322. doi:10.3390/en14248322

CrossRef Full Text | Google Scholar

Tan, Y., Xiong, Y., Gao, H., Li, X., and Zhao, H. (2021). Less is more? The strategic role of retailer's capacity. Prod. Oper. Manag. 30 (10), 3354–3368. doi:10.1111/poms.13438

CrossRef Full Text | Google Scholar

Tian, M., Yan, S., Tian, X., Nojavan, S., and Jermsittiparsert, K. (2020). Risk and profit-based bidding and offering strategies for pumped hydro storage in the energy market. J. Clean. Prod. 256, 120715. doi:10.1016/j.jclepro.2020.120715

CrossRef Full Text | Google Scholar

Wu, Y., Wu, J., and De, G. (2022). Research on trading optimization model of virtual power plant in medium- and long-term market. Energies 15 (3), 759. doi:10.3390/en15030759

CrossRef Full Text | Google Scholar

Yang, M., Zhang, L., Zhao, Z., and Wang, L. (2021). Comprehensive benefits analysis of electric vehicle charging station integrated photovoltaic and energy storage. J. Clean. Prod. 302, 126967. doi:10.1016/j.jclepro.2021.126967

CrossRef Full Text | Google Scholar

Yang, S., Tan, Z., Liu, Z., Lin, H., Ju, L., Zhou, F., et al. (2020). A multi-objective stochastic optimization model for electricity retailers with energy storage system considering uncertainty and demand response. J. Clean. Prod. 277, 124017. doi:10.1016/j.jclepro.2020.124017

CrossRef Full Text | Google Scholar

Zejneba, T., Reinhard, H., Amela, A., and Albert, H. (2022). Economics of electric energy storage. The case of Western Balkans. Energy 238, 121669–125442. doi:10.1016/j.energy.2021.121669

CrossRef Full Text | Google Scholar

Zhao, D., Wang, H., Huang, J., and Lin, X. (2022). Time-of-Use pricing for energy storage investment. IEEE Trans. Smart Grid 13 (2), 1165–1177. doi:10.1109/TSG.2021.3136650

CrossRef Full Text | Google Scholar

Zhao, J., He, Y., Fang, Y., Weng, Y., Ma, W., Xiao, S., et al. (2021). Multi-source optimal dispatch considering ancillary service cost of pumped storage power station based on cooperative game. Energy Rep. 7, 173–186. doi:10.1016/j.egyr.2021.10.040

CrossRef Full Text | Google Scholar

Zhu, Z., Kong, L., Aisaiti, G., Song, M., and Mi, Z. (2021). Pricing contract design of a multi-supplier-multi-retailer supply chain in hybrid electricity market. Ind. Manag. Data Syst. 121 (7), 1522–1551. doi:10.1108/IMDS-09-2020-0543

CrossRef Full Text | Google Scholar