- 1K.A. CARE Energy Research and Innovation Center, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
- 2Department of Electrical Engineering, Indian Institute of Technology Delhi, New Delhi, India
- 3Electrical Engineering Department and Center for Renewable Energy and Power Systems, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
- 4SDAIA-KFUPM Joint Research Center for Artificial Intelligence, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
This work investigates the application of sliding mode control (SMC) on a doubly fed induction generator (DFIG). In conventional control schemes like PI controllers, the responses are relatively slow, and the transient state is often subjected to sustained oscillation. Further, the PI control achieves lesser invariance behavior against system uncertainties, and the selection of its gain parameters is a skillful task. In contrast, the SMC is well-known for its faster convergence, robustness, and better transient and steady-state behavior. In this study, the nonsingular fast terminal sliding mode control (NSFTSMC) is applied in the speed loop of the rotor side vector control of DFIG. The proposed NSFTSMC scheme results in less speed fluctuation with a change in wind speed, which is maintained by controlling the torque component of the current (
1 Introduction
Deregulation of energy has led to less investment in larger conventional power plants and more investment into alternative non-conventional electrical power sources. Moreover, increase in the environmental pollution is of great concern (Necoechea-Porras et al., 2021). To solve these problems, two major technologies are playing pivotal role. One is to switch the electricity production from conventional fossil fuel-based sources to renewable energy-based sources. And the other is the use of efficient power electronic conversion in generation, distribution, and end-user applications (Abu-Rub et al., 2014). These distributed energy resources are finding place in microgrids which is the future of the power systems (Ahmad et al., 2019). presents a comprehensive market model to incorporate the renewable energy sources-based microgrids into Indian electricity market. A review is presented (Asaad et al., 2021), where the details of the wind energy generation in Indian perspective is discussed.
Out of all renewable energy resources, wind energy extraction is the fastest growing technology, and it is most viable option to complement other types of pollution-free generating systems (Bou-Rabee et al., 2020). Regular progress in wind-energy conversion systems was seen since 1970s, and the rapid development started in 1990s. The wind turbine-generator concepts and control strategies were developed, and various kinds of wind generators were built since then. Powerful control structures were developed to overcome the wind and grid side intermittencies (Slootweg et al., 2003; Li and Chen, 2008; Boukhezzar and Siguerdidjane, 2011). The control schemes have changed from conventional PI to nonlinear control, as it is much nearer in accuracy with the actual system (Elkington and Ghandhari, 2009; Hu et al., 2010). Implementation of these modern control schemes has become viable due to the developments in the microprocessor and semiconductor technology (Abu-Rub et al., 2014). Out of the wind turbine generator system configurations doubly fed induction generator (DFIG) comprises of approximately 55% of the total systems (Li and Chen, 2008; Abu-Rub et al., 2014). The main reasons being the variable speed range of ±30% of synchronous speed and that the converter ratings are of slip power rating. This leads to high energy yield and lower component stress (Boukhezzar and Siguerdidjane, 2011).
Field oriented control (FOC) and other (Ayedin et al., 2016) vector control techniques are employed to control the DFIG power electronics. FOC is commonly used in DFIGs due to its ability to control the machine speed more efficiently (Krishnan, 2001). Stator flux-oriented-FOC was first employed in (Pena et al., 1996). It was later used extensively (Tapia et al., 2003; Qiao et al., 2008), where the current component (q-axis) controls the active power, and the d-axis is employed to control the reactive power. While, in the stator voltage oriented-FOC, a contrary structure is used (Subudhi and Ogeti, 2018). Proportional-Integral (PI) controllers are commonly used in these schemes.
On the other hand, the sliding mode control (SMC) is a variable structure control technique in which an unstable system varies between the two structures using SMC to make the overall performance of the system stable (Utkin, et al., 2017). In addition, the switching between the two structures equips the controller with invariance property against model uncertainties and disturbances. Besides, the SMC method is easy to construct, achieves faster convergence, smooth response, better steady-state behavior, and easy to guarantee the finite-time stability of the system in theory (Chojaa, et al., 2021;
Amrr, et al., 2022). However, in practical scenario, achieving a finite time result with absolute zero error convergence is unrealistic. Therefore, recently, new results of practical finite time stability are proposed (Zhu, et al., 2011; Amrr, et al., 2020; Fu et al., 2021). Here, the closed loop signals converge to a small residual bound in the neighborhood of zero within finite time. In view of this result, the proposed work presents a nonsingular fast terminal sliding mode control (NSFTSMC) approach (Yang and Yang, 2011) for tracking the angular speed in the speed loop of the rotor side vector control of DFIG. The system is also subjected to the external load disturbances, which may cause fluctuations in the performance. In this work, the nonsingular fast terminal sliding mode control (NSFTSMC) is applied in the speed loop of the rotor side vector control of DFIG. The proposed NSFTSMC scheme results in less speed fluctuation with a change in wind speed, which is maintained by controlling the torque component of the current (
The rest of the paper is organized as follows. In Section 2, a brief discussion on the machine model, aerodynamic model and the drive-train model is done. Section 3 presents vector control of grid side converter control with the basic PI concept taken. Then, FOC is implemented to the machine side converter control scheme with conventional PI controllers. The speed loop is dealt with simple PI controller in this case. In Section 4, the proposed NSFTSMC is designed for the speed loop and the stability analysis of the closed loop system is presented. Section 5 illustrates the comparative results and Section 6 concludes the paper.
2 Aerodynamics and machine model
The overall arrangement of a DFIG-based wind turbine generator (DFIG-WTGS) is shown in Figure 1A. The generator is connected to the wind turbine through a drive train system consisting of low-speed shaft, high speed shaft and the gear box system. A wound rotor induction generator is employed whose rotor either feeds the grid or takes the power into the machine thereby making the super-synchronous as well as the sub synchronous generation possible as shown in Figures 1B,C, respectively. The power entering the machine is the slip power and as a result the power capacity of the converters is of slip power rating. A back-to-back converter is employed to control the power entering the machine or leaving it. Moreover, active and reactive power flow from the stator of the machine can be controlled through the rotor side converter and the power flow in the rotor side is controlled by grid-side converter. This is achieved by keeping the DC-link voltage constant. In this manner DFIG-WTGS is isolated from the grid and making them both fluctuation-recumbent to each other.

FIGURE 1. (A) DFIG-WTGS Configuration Connected to Grid; power flow diagram of a DFIG in (B) Super-Synchronous and (C) Sub-Synchronous modes; and (D)
In all, three controls are needed to be developed to control the power being fed to the grid. The RSC and GSC employ electrical control schemes where PWM signals are provided to both the converters and the switching angles of the IGBTs may be changed with the fluctuation in the DC-link voltage. The third control scheme is required to control the pitch of the rotor blades which operates when the speed of the wind exceeds the rated speed.
2.1 Aerodynamic model
The aerodynamics of the wind-turbine can be shown by well-known curves known a power coefficient curves or,
where,
where, R is the radius of the wind turbine in meters,
where,
2.2 Drive train model
A three-bladed horizontal axis wind turbine consists of six masses which can be lumped together to form a two-mass equivalent system, as shown in Figure 1E. It can be employed with reasonable accuracy for transient analysis (Boukhezzar and Siguerdidjane, 2011).
The equations for the two-mass model is given as (Muyeen et al., 2007):
where,
where,
2.3 Induction generator model
The DFIG voltage equations can be written in abc domain as:
The above equations are transformed into synchronously rotating reference frame to achieve dc values (Anaya-Lara et al., 2009; Krause et al., 2013):
where,
where,
The electromagnetic torque developed can be given as:
and the power expression of the stator and rotor side are given as:
The capital letters subscript are used for the stator side and the lower letter subscript for the rotor side. Also, the ‘
2.4 Voltage source converter model
The basic configuration of voltage source converter is shown as in Figure 2A. In the abc domain the equations are written as:
where,
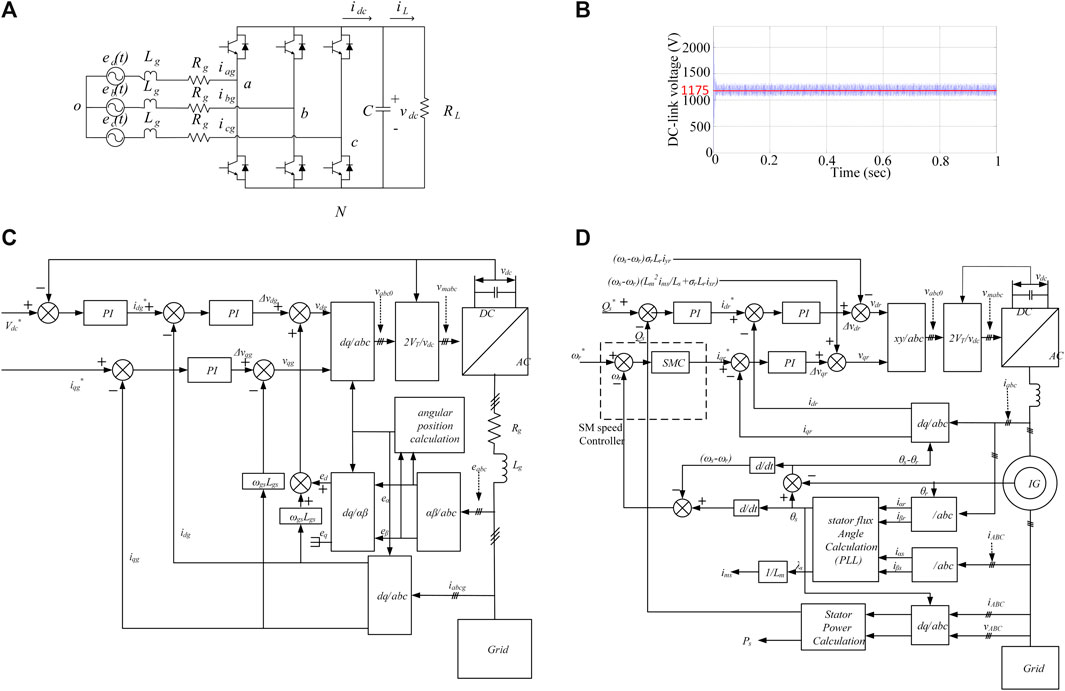
FIGURE 2. (A) voltage source converter configuration; (B) DC-link voltage behavior; (C) the grid side control scheme; (D) the rotor side control scheme with SMC implementation in the speed control loop.
and if a balanced three phase system is considered, then
and.
By applying PWM switching conditions and converting the equations onto the reference frame of the source voltage vector we can have following equations:
where,
3 Conventional control scheme
On the machine side, the DFIG requires two control schemes under consideration, the grid side control (GSC) and the rotor side control (RSC). The objective of the GSC is to maintain the zero DC-link voltage irrespective of the direction and magnitude of the rotor power. Reactive power regulation is done through GSC; while the main objective of the RSC is to regulate both the active power and the reactive power on the stator side independently. Another controller that is used is the pitch angle controller which is employed to control the mechanical power available at the shaft of the wind turbine when the speed of the wind is above the rated value.
3.1 GSC controller design
Two control loops work simultaneously.
Eq. 28 can be rearranged as:
Transforming the above equation into synchronously rotating reference frame, and aligning the d-axis along the grid voltage vector
Now aligning along the grid voltage vector
Now let
and
Eqs. 39–40 can be rearranged as
This indicates that
Substituting these values in Eqs 37, 38 we achieve following equations:
The power-balance equation across the DC-link is written as:
Above Equation can also be written as:
where,
Since
Therefore, the relation between
Since,
Eq. 49 becomes
Therefore, the feedback loop and the PI controller generates a reference value of
The reactive power exchanged through the GSC can be determined as follows
So, the reactive power may be regulated by regulating
The overall control scheme can be seen in Figure 2C.
3.2 RSC controller design
Like GSC, RSC consists of cascaded control loops. The inner current control loop regulates the
In the stator-flux oriented reference frame theory, the
Following results are achieved when applied to Eqs. 14–22
where,
The stator power equations may be represented as
Eqs. 63–64 indicate that the stator active and reactive powers can be regulated independently by controlling
Firstly, the inner control loops; after proceeding as in the GSC control design, Eqs. 60, 61 may be written as:
Where,
4 Proposed nonsingular fast terminal sliding mode control
This section presents the rotor side vector control of DFIG using nonsingular fast terminal sliding mode control (NSFTSMC). Before going into the control design part, the dynamic model of vector drive of DFIG is given (Bose, 2002). Therefore, let us consider
Further, the second order mechanical dynamic equation of DFIG can be written in Laplace domain as (Zadehbagheri, et al., 2013)
where
where
Eqs. 69 and 72 are the state space equations that can be rewritten in a simplified form as
where
Assumption 1. The load disturbance is bound such that
Lemma 1. (Fu et al., 2021) considers a continuous system
then, the solution of system
where.
4.1 Controller design and stability analysis
The proposed control scheme is based on nonsingular fast terminal sliding surface (NSFTSS). The structure of the surface is inspired from (Tiwari, et al., 2012; Amrr and Nabi, 2020) and defined as
where
In view of the derivative of
where
and
where
Theorem 1. Considering the sliding dynamics (80) and the proposed NSFTSMC law (75) under Assumption 1. The action of the proposed methodology will achieve the practical finite time stability and the sliding surface
The time derivative of
Substituting the proposed control law
where
where
5 Results
The DFIG with the above-discussed NSFTSMC scheme is implemented on the RSC of the DFIG as shown in Figure 2D. The system is connected to the grid and validated in MATLAB/Simulink environment as shown in Figure 3A. The DFIG ratings are taken from the technical report by (Miller et.al., 2003). The wind is emulated in the Simulink environment by using a signal builder block as a sampled Gaussian noise, as discussed by in (Patel and Beik, 2021). Figure 3B shows random behavior of wind. The rated wind speed is 15 m/s.
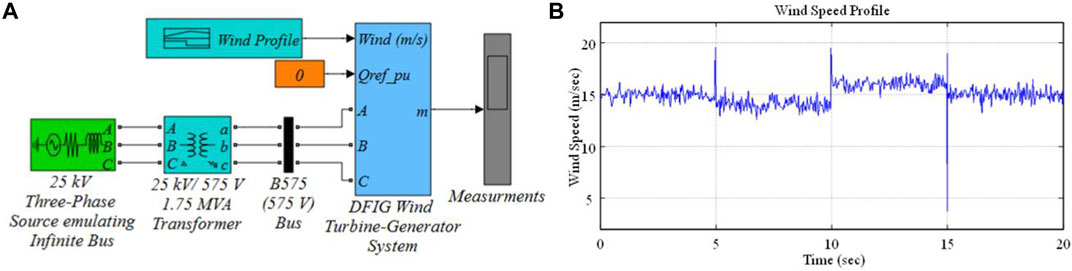
FIGURE 3. (A) The system configuration under study; (B) wind speed variation subjected to the wind turbine blades.
Conventional PI speed controller and NSFTSMC schemes were implemented, and the performance was compared. The analysis is as follows. The rotor shaft’s base speed is 1.2 times the synchronous speed of the machine. The actual rotor shaft speed behavior with both PI and NSFTSMC is shown in Figure 4A. It can be observed that the speed of the rotor is more stable with the NSFTSMC as compared with conventional PI Control, when the turbine is subjected to a wind speed change. It is also observed that the rotor speed settles much faster with NSFTSMC than the PI controller. The DC-link voltage remains unaltered with both the control schemes as seen in Figure 4B. The pitch angle variation (Figure 4C), however, is more stable in the case of conventional PI than the NSFTSMC. The grid side voltage performance is shown in Figure 4D and exhibits similar behavior with both control schemes. Figure 4E exhibits the output current of phase A, and it is seen that there are disturbances with the NSFTSMC, and this disturbance is also observed in active power (Figure 4F) and electromagnetic torque (Figure 4H). The reactive power behavior of the machine is similar for both machines as exhibited Figure 4G.
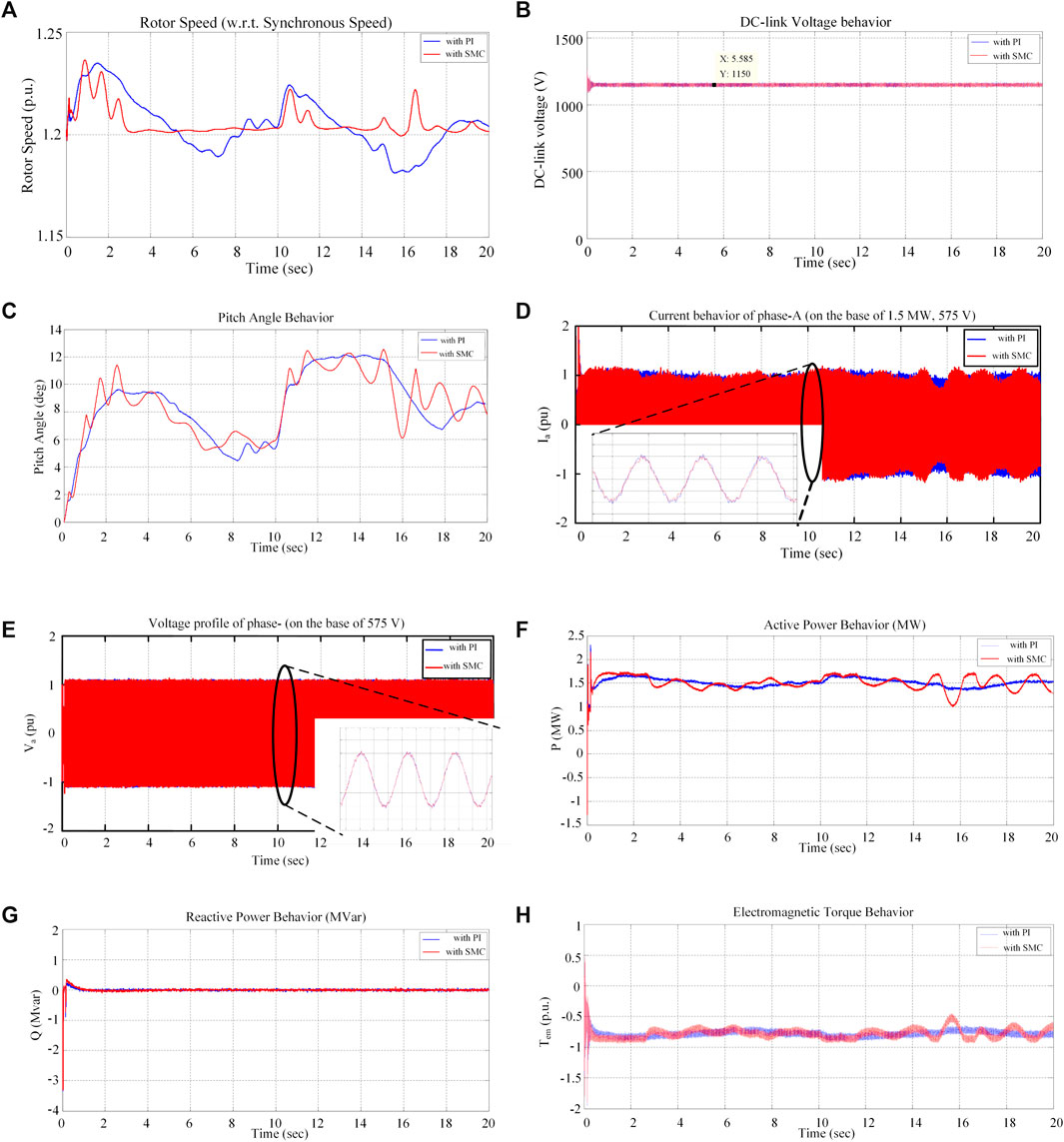
FIGURE 4. Results showing the comparative behavior of the SMC based speed control with respect to the conventional PI control in terms of (A) machine rotor speed; (B) DC-link voltage; (C) Pitch angle; (D) voltage profile of phase-A; (E) current profile of phase-A; (F) active power behavior; (G) reactive power; and (H) electromagnetic torque.
6 Conclusion
In this work, the sliding mode control (SMC) is investigated for speed control of a doubly fed induction generator (DFIG). The nonsingular fast terminal sliding mode control (NSFTSMC) was applied in the speed loop of the rotor side vector control of DFIG. The proposed NSFTSMC scheme results in less speed fluctuation with a change in wind speed, which is maintained by controlling the torque component of the current (
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MA contributed to conception, methodology, and design of the study. MA and SA carried out the formal analysis. MA organized the database and software coding. SA and MA performed the mathematical analysis and theoretical investigation. MA realized the numerical results. MA wrote the first draft of the manuscript. MA, SA, and MK wrote sections of the manuscript. MK supervised this work. MK provide the laboratory resources. MK arranged the funding acquisition. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
The research is funded in part by the Interdisciplinary Research Center for Renewable Energy and Power Systems (IRC-REPS) at KFUPM under Project No. INRE2106.
Acknowledgments
The authors would like to acknowledge the support provided by the K. A. CARE Energy Research and Innovation Center and SDAIA-KFUPM Joint Research Center for Artificial Intelligence (JRC-AI) at the King Fahd University of Petroleum and Minerals (KFUPM), Dhahran 31261, Kingdom of Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abu-Rub, H., Malinowski, M., and Al-Haddad, K. (2014). Power electronics for renewable energy systems, transportation and industrial applications. 1st ed. Wiley. doi:10.1002/9781118755525
Ahmad, F., Alam, M. S., and Shahidehpour, M. (2019). Profit maximization of microgrid aggregator under power market environment. IEEE Syst. J. 13, 3388–3399. doi:10.1109/jsyst.2018.2829343
Amrr, S. M., Ahmad, J., Waheed, S. A., Sarwar, A., Saidi, A. S., and Nabi, M. (2022). Finite-time adaptive sliding mode control of a power converter under multiple uncertainties. Front. Energy Res. 580. doi:10.3389/fenrg.2022.901606
Amrr, S. M., and Alturki, A. (2021). Robust control design for an active magnetic bearing system using advanced adaptive smc technique. IEEE Access, 9, 155662–155672. doi:10.1109/ACCESS.2021.3129140
Amrr, S. M., and Nabi, M. (2019). Attitude stabilization of flexible spacecraft under limited communication with reinforced robustness. Trans. Inst. Meas. Control 41 (16), 4475–4487. doi:10.1177/0142331219860651
Amrr, S. M., and Nabi, M. (2020). Finite-time fault tolerant attitude tracking control of spacecraft using robust nonlinear disturbance observer with anti-unwinding approach. Adv. Space Res. 66 (7), 1659–1671. doi:10.1016/j.asr.2020.06.019
Amrr, S. M., Srivastava, J. P., and Nabi, M. (2020). Robust attitude stabilization of spacecraft under constrained network with hysteresis quantizer. IEEE J. Miniat. Air Space Syst. 2 (3), 129–139. doi:10.1109/jmass.2020.3039977
Anaya-Lara, O., Jenkins, N., Ekanayake, J., Cartwright, P., and Hughes, M. (2009). Wind energy generation: modeling and control. UK: John Wiley & Sons.
Asaad, M., Ahmad, F., Alam, M. S., and Sarfaraz, M. (2021). Smart grid and indian experience: a review. Resour. Policy 74, 101499. doi:10.1016/j.resourpol.2019.101499
Ayedin, E., Polat, A., and Ergene, L. T. (2016). “Vector control of dfig in wind power applications,” in ICRERA-2016, 478–483. doi:10.1109/ICRERA.2016.7884383
Bose, B. K. (2002). Modern power electronics and ac drives. Upper Saddle River, New Jersey, USA: Prentice Hall PTR.
Bou-Rabee, M., Lodi, K. A., Ali, M., Ansari, M. F., Tariq, M., and Sulaiman, S. A. (2020). One-month-ahead wind speed forecasting using hybrid ai model for coastal locations. IEEE Access 8, 198482–198493. doi:10.1109/ACCESS.2020.3028259
Boukhezzar, B., and Siguerdidjane, H. (2011). Nonlinear control of a variable-speed wind turbine using a two-mass model. IEEE Trans. Energy Convers. 26 (1), 149–162. doi:10.1109/tec.2010.2090155
Chojaa, H., Derouich, A., Chehaidia, S. E., Zamzoum, O., Taoussi, M., and Elouatouat, H. (2021). Integral sliding mode control for dfig based wecs with mppt based on artificial neural network under a real wind profile. Energy Rep. 7, 4809–4824. doi:10.1016/j.egyr.2021.07.066
Elkington, K., and Ghandhari, M. (2009). “Comparison of reduced order doubly fed induction generator models for nonlinear analysis,” in IEEE Electrical Power & Energy Conference, 1–6. doi:10.1109/EPEC.2009.5420984
Fu, C., Wang, Q. G., Yu, J., and Lin, C. (2021). Neural network-based finite-time command filtering control for switched nonlinear systems with backlash-like hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 32 (7), 3268–3273. doi:10.1109/tnnls.2020.3009871
Hu, J., Nian, H., Hu, B., He, Y., and Zhu, Z. Q. (2010). Direct active and reactive power regulation of dfig using sliding-mode control approach. IEEE Trans. Energy Convers. 25 (4), 1028–1039. doi:10.1109/tec.2010.2048754
Krause, P. C., Wasynczuk, O., Sudhoff, S. D., and Pekarek, S. D. (2013). Analysis of electric machinery and drive systems. 3rd ed. Wiley.
Li, H., and Chen, Z. (2008). Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2 (2), 123–138. doi:10.1049/iet-rpg:20070044, No
Miller, N., Price, W., and Sanchez-Gasca, J. (2003). Dynamic modeling of ge 1.5 and 3.6 wind turbine-generators for stability simulations. Ontario: IEEE Power Engineering Society General Meeting. doi:10.1109/PES.2003.1267470
Muyeen, S. M., Ali, M. H., Takahashi, R., Murata, T., Tamura, J., Tomaki, Y., et al. (2007). Comparative study on transient stability analysis of wind turbine generator system using different drive train models. IET Renew. Power Gener. 1 (2), 131–141. doi:10.1049/iet-rpg:20060030
Necoechea-Porras, P. D., López, A., and Salazar-Elena, J. C. (2021). Deregulation in the energy sector and its economic effects on the power sector: a literature review. Sustainability 13 (6), 3429. available. doi:10.3390/su13063429
Neto, A. S., Ferreira, S. L. A., Arruda, J. P., Neves, F. A. S., Rosas, P. A. C., and Cavalcanti, M. C. (2007). Reduced order model for grid connected wind turbines with doubly fed induction generators. IEEE Int. Symposium Industrial Electron., 2655–2660. doi:10.1109/ISIE.2007.4375027
Ontiveros, L. J., Mercado, P. E., and Suvire, G. O. (2010). “A new model of the double-feed induction generator wind turbine,” in 2010 IEEE transmission and distribution conference and exposition, Sao Paulo. doi:10.1109/TDC-LA.2010.5762892
Patel, M. R., and Beik, O. (2021). Wind and solar power systems: design, analysis, and operation. 3rd ed. Florida, USA: CRC Press.
Pena, R., Clare, J. C., and Asher, G. M. (1996). A Doubly fed induction generator using back-to-back pwm converters supplying an isolated load from a variable speed wind turbine. IEE Proc. Electr. Power Appl. 143 (5), 380–387. doi:10.1049/ip-epa:19960454
Qiao, W., Zhou, W., Aller, J. M., and Harley, R. G. (2008). Wind speed estimation based sensorless output maximization control for a wind turbine driving a dfig. IEEE Trans. Power Electron. 23 (3), 1156–1169. doi:10.1109/tpel.2008.921185
Slootweg, J. G., de Hann, S. W. H., Polinder, H., and Kling, W. L. (2003). General model for representing variable speed wind turbines in power system dynamics simulations. IEEE Trans. Power Syst. 18 (1), 144–151. doi:10.1109/tpwrs.2002.807113
Subudhi, B., and Ogeti, P. S. (2018). Optimal preview stator voltage-oriented control of dfig wecs. IET Gener. Transm. &. Distrib. 12 (4), 1004–1013. doi:10.1049/iet-gtd.2016.2027
Tapia, A., Tapia, G., Ostolaza, J. X., and Sáenz, J. R. (2003). Modeling and control of a wind turbine driven doubly fed induction generator. IEEE Trans. Energy Convers. 18 (2), 194–204. doi:10.1109/tec.2003.811727
Tiwari, P. M., Janardhanan, S., and Masuq-un-Nabi., (2012). Spacecraft attitude control using non-singular finite time convergence fast terminal sliding mode. Int. J. Instrum. Technol. 1 (2), 124–142. doi:10.1504/ijit.2012.053289
Utkin, V., Guldner, J., and Shi, J. (2017). Sliding mode control in electro-mechanical systems. 2nd ed. Boca Raton: CRC Press. doi:10.1201/9781420065619
Yang, L., and Yang, J. (2011). Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 21 (16), 1865–1879. doi:10.1002/rnc.1666
Zadehbagheri, M., Ildarabadi, R., and Nejad, M. B. (2013). Sliding mode control of a doubly-fed induction generator (dfig) for wind energy conversion system. Int. J. Sci. Eng. Res. 4 (11), 1573–1581.
Zhu, Z., Xia, Y., and Fu, M. (2011). Attitude stabilization of rigid spacecraft with finite‐time convergence. Int. J. Robust Nonlinear Control 21 (6), 686–702. doi:10.1002/rnc.1624
Nomenclature
Symbol
description
Te, TL Electromagnetic and load torque
Keywords: DFIG (double fed induction generator), sliding mode control, wind energy system, field oreinted control, MPPT, pitch angle control
Citation: Ali M, Amrr SM and Khalid M (2022) Speed control of a wind turbine–driven doubly fed induction generator using sliding mode technique with practical finite‐time stability. Front. Energy Res. 10:970755. doi: 10.3389/fenrg.2022.970755
Received: 16 June 2022; Accepted: 01 August 2022;
Published: 13 September 2022.
Edited by:
Saad Mekhilef, Swinburne University of Technology, AustraliaReviewed by:
Salman Ahmad, Islamic University of Science and Technology, IndiaAsaad Mohammad, Auckland University of Technology, New Zealand
Furkan Ahmad, Hamad bin Khalifa University, Qatar
Md Reyaz Hussan, Qatar University, Qatar
Copyright © 2022 Ali, Amrr and Khalid. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Khalid, bWtoYWxpZEBrZnVwbS5lZHUuc2E=
 Mohammad Ali
Mohammad Ali Syed Muhammad Amrr
Syed Muhammad Amrr Muhammad Khalid
Muhammad Khalid