Optimal operation of park-level integrated energy system based on multi-agent cooperative game

As the effects of climate change and environmental pollution become more serious, the requirements of low carbon emission are put forward to the operation of integrated energy systems. Under this trend, a cooperative-game-based operation optimization model for integrated energy systems is proposed in this paper. This model can achieve the multi-agent allocation and coordinate the operating costs and carbon emissions. The Anderson-accelerated-based alternating direction multiplication (AA-ADMM) method is used to improve the efficiency of solving the proposed model. Thereafter, the benefit of each agent is allocated by the Shapley value. Results indicate that the proposed model can provide a reasonable trade-off between operating costs and carbon emissions, and the proposed benefit allocation strategy is effective.

1 Introduction

Recently, humanity is facing the energy shortage and global warming. This trend has led to the formation of the Climate Ambition Coalition by 66 countries to achieve carbon neutrality targets. (UNFCCC, 2019). Under energy and policy pressure, traditional independent energy systems are facing the challenges of energy underutilization and substandard usage. To deal with this, the Park-level integrated energy systems (PIES) have been constructed to achieve the efficient integration of combined heat and power (CHP), storage, and energy conversion components. However, the conflict of interests between these agents restricts the efficiency of PIES. As a result, it is important to optimize and coordinate the operation of multiple agents in the PIES to reduce operating costs and carbon emissions.

Many scholars have conducted a lot of research on the operation of park-level integrated energy systems. A NSGA-III-based solving approach (Deng Y et al., 2021) is developed to find the non-dominated solutions of the model. A synergistic strategy is proposed to achieve efficient energy utilization by recovering waste heat (Wu et al., 2019). This reference (Ha et al., 2022) proposes an optimized model. The proposed model provides a more efficient network to scale down the environmental and economic impacts of electricity storage. A multi-objective optimization model achieves a win-win situation in terms of operation, economy, environmental friendliness, and safety (Zhang et al., 2019). The reference (Wang et al., 2020) presents an integrated energy system to improve the efficiency of wastewater reuse. The CHP is used to improve the energy supply flexibility and conversion efficiency of integrated energy systems (Ma et al., 2021). An integrated energy system optimal dispatch model is established from the perspective of flexibility and economy considering the conversion of multiple energy forms and multiple time scales (Tang et al., 2021). An integrated energy system optimal dispatch model is used to operate the coupled demand response characteristics of multiple energy streams (Tang et al., 2021). However, few studies focus on the coordination of multiple agents in integrated energy systems.

The game theory is widely applied to balance the contradiction between agents in the PIES. Nash is one of the main research directions. The reference (Jing et al., 2020) proposes a Nash-type noncooperative game model between agents that can well ensure fairness and reduce trading costs. The reference (Geng et al., 2020) establishes an operation optimization model to distribute the coalition benefits by Nash negotiation. The reference (Jing et al., 2021) applied the Nash approach in the energy interaction between multiple device subjects to improve utilization efficiency and reduce costs. In addition, the game theory has been widely used to improve the benefits of multiple subjects while resolving conflicts. The reference (Yuan, 2021) uses a typical robust optimization to deal with the uncertainty of energy control. An evolutionary game approach (Gao et al., 2021) that considers individual finite rationality is proposed. This method can effectively improve energy efficiency. A game stochastic optimization allocation method is used to assign the weights of renewable energy consumption responsibilities of market players (Jiao et al., 2022). The reference (Jing et al., 2018) constructs the cost and emission constraints to achieve benefit sharing among multiple agents based on cooperative game theory, and a mixed integer linear programming (MILP) model is developed to analyze the impact of benefit allocation. However, the allocation of interests of multiple agents with multiple objectives is not considered in the above methods.

Based on this, a cooperative-game-based operation optimization model considering multi agents of the PIES is proposed in this paper. The main contributions of this study are as follows.

1) A cooperative-game-based optimization model of PIES is proposed to balance the interests of multiple agents. Moreover, the Anderson-accelerated-based ADMM algorithm is employed to efficiently obtain the optimal scheduling strategy.

2) The Shapley method is used to allocate the benefits of each agent after cooperation, and more users can be motivated to build an integrated energy system through cooperation.

3) A game method is used to determine the weight of operational objectives including the operation cost and carbon emission.

2 The structure of PIES

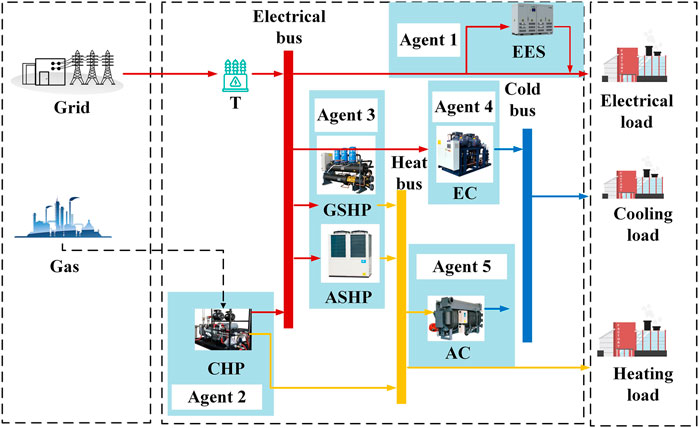
Generally, most of the current operation modes are independent devices. The users cannot realize multi-energy coupling, and this operation mode has a high economic cost and low energy utilization rate. PIES is a representative multi-energy coupled systems today. Therefore, the PIES is considered as a research issue in this paper. Its characteristics can significantly improve energy utilization efficiency, and reduce system operating costs and CO₂ emissions. The structure of the PIES in Figure 1. Multiple energy sources work together to break down the blockade of independent operation.

FIGURE 1

FIGURE 1. Structure of park-level integrated energy system.

3 A cooperative-game-based operation optimization model of PIES

The idea of cooperative game includes two aspects. First, the AA-ADMM is used to obtain the pareto frontier, which can ensure the optimality of the overall benefit. Then, the Shapley value method is employed to distribute the obtained benefits according to the contributions of each coalition.

3.1 The multi-agent cooperative game optimization model

In this paper, the economy and environmental friendliness are used as the operational objectives in the proposed multi-agent cooperative game optimization model. It can help to get an objective allocation result of the overall optimal benefit. This multi-objective problem can be a good solution to the problem of overall benefit loss in the practical operation process. The specific objectives and system constraints are shown below.

3.1.1 Objective function

1) Economic Objectives

The operation optimization of PIES aims to achieve the lowest total operating cost,

$\begin{array}{c}\min f_C=C_{gas}+C_{grid}+C_{EM}+C_{EI}\\ C_{grid}={\displaystyle \sum }_d{\displaystyle \sum }_{t\in T}{k}_{grid}{P}_{grid}\\ C_{gas}={\displaystyle \sum }_d{\displaystyle \sum }_{t\in T}{k}_{gas}{P}_{gas}\\ C_{EM}={\displaystyle \sum }_d{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k=1}^m{\omega }_k{P}_t^k\\ C_{EI}={\displaystyle \sum }_{k=1}^m{k}_I{P}^c\end{array}(1)$

where f_C is the annual operation cost of the overall system; d is the typical seasonal day; the simulation step is 1 h, T = 24; P_grid and P_gas are the purchasing power of electricity and gas; k_grid and k_gas are the prices of electricity and gas, respectively; m is the total number of devices; ω_k is the maintenance cost of equipment k, P^k_t is the output power at moment t, k_I is the initial investment factor of each equipment, P^c represents the equipment capacity.

2) Environmental Objectives

The environmental friendly objective of PIES operation is to minimize CO₂ emissions,

$\min f_E={\displaystyle \sum }_d{D}_d{\displaystyle \sum }_{t\in T}\left({\alpha }_{grid}{P}_{grid}+{\alpha }_{gas}{P}_{gas}\right)(2)$

where f_E is the CO₂ emission of the overall system; α_grid and α_gas are the CO₂ emission factors for natural gas combustion and grid purchased electricity, respectively.

3.1.2 System main constraints

1) Component Constraints

As shown in Figure 1, the main component in operation includes CHP, transformer (T), ground source heat pump (GSHP), air source heat pump (ASHP), electric chiller (EC), absorption chiller (AC) and electric energy storage (EES).

Operation equality constraints.

$P_{CHP}={\eta }_{CHP}{G}_{CHP}={\eta }_{CHP}{F}_{CHP}\left(t\right)q_g(3)$

$H_{CHP}={\mu }_{CHP}{\eta }_{CHP}{G}_{CHP}(4)$

$H_{Ashp}={\eta }_{Ashp}{P}_{Ashp}{H}_{\mathrm{G}shp}={\eta }_{Gshp}{P}_{Ghsp}(5)$

$O_{EC}={\eta }_{EC}{P}_{EC}{O}_{AC}={\eta }_{AC}{P}_{AC}(6)$

$\begin{array}{c}{\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathit{Exp}}=\mathrm{S}\mathrm{O}\mathrm{C}\left(T\right)\\ {\mathrm{S}\mathrm{O}\mathrm{C}}_{1}Cap={\mathrm{S}\mathrm{O}\mathrm{C}}_{Ini}Cap+P_1^{\mathit{s}}{\eta }_{\mathit{s}}-P_1^d/{\eta }_d\\ {\mathrm{S}\mathrm{O}\mathrm{C}}_{t}Cap={\mathrm{S}\mathrm{O}\mathrm{C}}_{t-1}Cap+P_t^{\mathit{s}}{\eta }_{\mathit{s}}-P_t^d/{\eta }_d\end{array}(7)$

where the subscripts denote the components, P, G, H, and O denote the electricity power, gas input, heating power, and cooling output, respectively; η denotes the efficiency of components; F_CHP(t) denotes natural gas flow; q_g is the calorific value of natural gas; μ_CHP is the thermal conversion coefficient of CHP; η_s and η_d are the battery charging and discharging efficiency respectively; Cap is the energy storage capacity; SOC_t is the state of EES charge at time t; P^s_t and $P_t^d$ are the EES charging and discharging power at time t, respectively; SOC_Exp denotes the final value (desired value) of the energy storage system; SOC_Ini denotes the initial value of the energy storage system.

Operation inequality constraints.

$P_{CHP}^{\min }\le P_{CHP}\le C_{CHP}(8)$

$\left|P_t^{CHP}-P_{t-1}^{CHP}\right|\le \Delta P_{\max }^{CHP}(9)$

${\mathrm{S}\mathrm{O}\mathrm{C}}_{\min }⩽{\mathrm{S}\mathrm{O}\mathrm{C}}_t⩽{\mathrm{S}\mathrm{O}\mathrm{C}}_{\max }(10)$

$\begin{array}{c}{P}_{\min }^{\mathit{s}}\le P_t^{\mathit{s}}\le P_{\max }^{\mathit{s}}\\ P_{\min }^d\le P_t^d\le P_{\max }^d\end{array}(11)$

$0\le P_{EC}\le C_{EC}0\le H_{AC}\le C_{AC}(12)$

$P_{Ashp}^{\min }\le P_{Ashp}\le C_{Ashp}0\le P_{Gshp}\le C_{Gshp}(13)$

where C denotes the capacity of components; P^min is the lower limit of equipment output; ΔP^CHP_max is the upper climbing rate of CHP unit; SOC_min and SOC_max are the minimum and maximum constraints of charge state; P^s_max and P^d_max are the maximum constraints of charge and discharge power; P^s_min and P^d_min are the maximum constraints of charge and discharge power, respectively.

2) Energy Balance Constraints

$P_{grid}+P_{CHP}+P_t^s=L_E\left(t\right)+P_{EB}+P_{Ashp}+P_{Gshp}+P_{EC}+P_t^d(14)$

$L_H\left(t\right)+H_{AC}=H_{EB}+H_{Gshp}+H_{Ashp}+H_{CHP}(15)$

$O_{EC}+O_{AC}=L_C\left(t\right)(16)$

$P_{gas}=G_{CHP}(17)$

$\begin{array}{l}0\le P_{grid}\le P_{grid,\max }\\ 0\le P_{gas}\le P_{gas,\max }\end{array}(18)$

where L_E(t), L_H(t), and L_C(t) are loads of electricity, heat, and cooling; P_grid,max and P_gas,max are the purchasing power bounds of electricity and gas.

3.2 The solution approach for multiple objectives

A reasonable operation optimization strategy is an important means to ensure the economic stability and efficient energy supply of the system. PIES can cause optimization conflicts due to its multi-objective properties. Therefore, it is necessary to resolve the conflicting benefits of multiple optimization objectives. The optimization model can be considered as:

$\{\begin{array}{c}\min \left(f_C,f_E\right)\\ s.t.\begin{array}{cc}& \left(3\right)-\left(18\right).\end{array}\end{array}(20)$

The solution process is played by two virtual participants to achieve the desired economic and environmental optimality. The problem has been proved in the reference (Lan et al., 2021). To facilitate the solution, the minimum problem Eq. 20 is converted to a maximum optimization problem,

$\begin{array}{c}\underset{\mathit{x}\in \mathit{S}}{\max }\left(l_1^m-f_C\left(x\right)\right)\left(l_2^m-f_E\left(x\right)\right)\\ s.t.\begin{array}{cc}& \left(3\right)-\left(18\right)\end{array}\end{array}(21)$

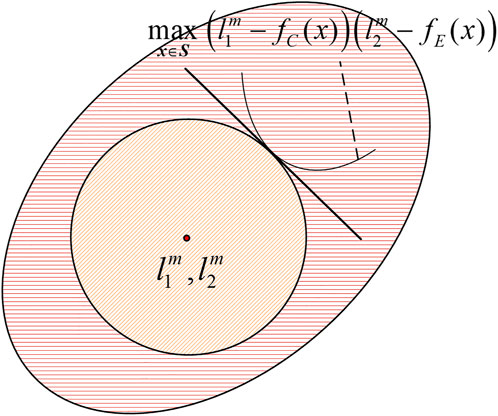
The preconditions of the multi-objective game include reaching the optimal benefit, i.e., the Pareto solution. Thus, the set S in Eq. 21 is the Pareto frontier of the problem Eq. 20, and $l_1^m$ and $l_2^m$ are the highest unilateral costs (Tan et al., 2021). The geometric representation of (21) is shown in Figure 2.

FIGURE 2

FIGURE 2. The geometric representation of the multi-objective game model.

The large ellipse in Figure 2 shows the feasible domain, $l_1^m$ and $l_2^m$ are the worst target values. The curve is the game function, and the line is the Pareto front. The boundary of the circle represents the same distance point from the worst objective value. The physical meaning of the optimization is to ensure that the solution under the feasible domain can achieve the maximum value of both sides.

To solve the above multi-objective game optimization problem, this paper uses the ADMM algorithm. The method has a good application in the game model (Luo et al., 2022). The core idea is to equivalently decompose the objective function of the original problem into several solvable subproblems, then solve each subproblem in parallel. Finally, it can coordinate the solutions of the subproblems to obtain the global solution to the original problem.

The standard form of the conventional ADMM algorithm is as follows (Wu et al., 2019).

$\begin{array}{c}\min f\left(x\right)+g\left(z\right)\\ s.t.Ax+Bz=c\end{array}(22)$

In Eq.22, f(x), g(z) are two convex functions, Ax + Bz = c is the equation constraint. The ADMM algorithm has a faster convergence rate and finds higher quality solutions in the optimization of solutions under multiple objective functions (Cao., 2020; Huang et al., 2021). The ADMM solution for Eq. 21 is essentially a nonconvex problem, so it is difficult to solve this problem directly. The model Eq. 21 can be transformed as follows (Ma et al., 2021),

$\begin{array}{c}\min -\left[\ln \left(l_1^m-f_C\left(x\right)\right)+\ln \left(l_2^m-f_E\left(x\right)\right)\right]\\ s.t.\left(3\right)-\left(18\right)\end{array}(23)$

The ADMM algorithm is a decomposition of both the variables and the objective function. The two parts satisfy a linear relationship, which can be represented by the following Lagrangian function.

$L_p\left(x,z,\lambda \right)=f\left(x\right)+g\left(z\right)+{\lambda }^T\left(Ax+Bz-c\right)+\rho /2\Vert Ax+Bz-c|{|}_2^2(24)$

where L_p(x,z,λ) is the augmented Lagrangian function; λ is the dual variable; ρ > 0 is the penalty function. Then the format of update iterations can be,

$\{\begin{array}{c}{x}^{k+1}=\underset{x}{argmin}{L}_{\rho }\left(x,z^k,{\lambda }^k\right)\\ z^{k+1}=\underset{z}{argmin}{L}_{\rho }\left(x^{k+1},z,{\lambda }^k\right)\\ {\lambda }^{k+1}={\lambda }^k+\rho \left(A{k}^{k+1}+B{x}^{k+1}-c\right)\end{array}(25)$

Moreover, this paper uses AA-ADMM to further accelerate the ADMM algorithm. The AA-ADMM can speed up the calculation and improve the convergence accuracy. The Anderson’s acceleration method should satisfy that the sum of weighting coefficients is one and it is convergent. In this paper, the total of multiple objectives weights is 1. Moreover, the game formula is obtained by the deformation of the quadratic function. The quadratic function has the iterative convergence property. Therefore, the Anderson’s acceleration method can be applied in the proposed model. The main idea of Anderson acceleration is to use the current iteration x_k and the previous m iterations to make the residuals of new iterations as small as possible. Based on Eq. 24, the iterative form of fixed-point iteration is,

$\left(z^{k+1},{\lambda }^{k+1}\right)=G\left(z^k,{\lambda }^k\right)(26)$

Using u= λ / ρ, the iteration of the multi-objective system is obtained as,

$\{\begin{array}{c}{X}_i^{k+1}=\underset{P_i}{argmin}\left(f_i\left(X_i\right)+\frac{\rho }{2}{\left(X_i-{\overline{X}}^k+u_i^k\right)}^2\right)\\ u_i^{k+1}=u_i^k+e^{k+1}\end{array}(27)$

where $X_i^{k+1}$ is the cost value after k+1 iterations, the optimal solution is obtained by,

$\begin{array}{cc}{X}_i^{k+1}=\frac{\rho \left({\overline{X}}^k-e^k\right)-\rho u_i^k-c_{2i}}{\rho +2c_1}& i=\mathrm{1,2},\cdots ,n\end{array}(28)$

In the ADMM algorithm, the iteration is ended when both the original residuals and the pairwise residuals are less than the convergence accuracy,

$\{\begin{array}{c}{u}_i^{k+1}-u_i^k={\displaystyle \sum }_{i=1}^n{X}_i^{k+1}-X_n⩽{\epsilon }_A\\ \rho \left({\overline{X}}^{k+1}-{\overline{X}}^k\right)⩽{\epsilon }_B\end{array}(29)$

where ${\epsilon }_A$ and ${\epsilon }_B$ is the convergence accuracy of the original residuals and dual residuals.

The optimal scheduling solution process of the cooperative game model under multiple objectives is shown in Figure 3.

FIGURE 3

FIGURE 3. Optimized scheduling solution process.

3.3 Shapley value benefit allocation method

Allocation is an important concept in cooperative games. The distribution of benefits ensures that the benefits gained by cooperation are greater than the benefits of operating alone. In this paper, the Shapley value method is used to solve the benefit distribution problem in the cooperative game. The contribution of each alliance is used to determine the benefit distribution. In addition, the classification of alliances is based on the energy coupling relationship, e.g., GSHP and ASHP use electricity to generate heat, CHP burns gas to produce electricity and heat.

It is considered that the benefits received by multiple agents in operation are allocated as φ_i(v). V represents the cooperative surplus, and i represents the coalition agent. In this paper, v is the difference between the independent mode and cooperation mode. The benefits of the coalitions are allocated according to the following equation (Duan et al., 2022).

$\begin{array}{c}{\varphi }_i\left(v\right)={\displaystyle \sum }_{S\subseteq N}W\left(\left|S\right|\right)\left[v\left(S\right)-v\left(S-\left\{i\right\}\right)\right]\\ i=\mathrm{1,2},\cdots ,n\end{array}(30)$

$W\left(\left|S\right|\right)=\frac{\left(\left|S\right|-1\right)!\left(n-\left|S\right|\right)!}{n!}(31)$

where S denotes the number of participants in the set N of coalition members; v(s) is the overall operating cost of PIES; v(s-{i}) is the operating cost of the cooperative coalition without i; v(s)-v(s-{i}) means the marginal contribution of the agent to the coalition S; W|S| is the probability of the occurrence of the coalition S.

4 Case studies

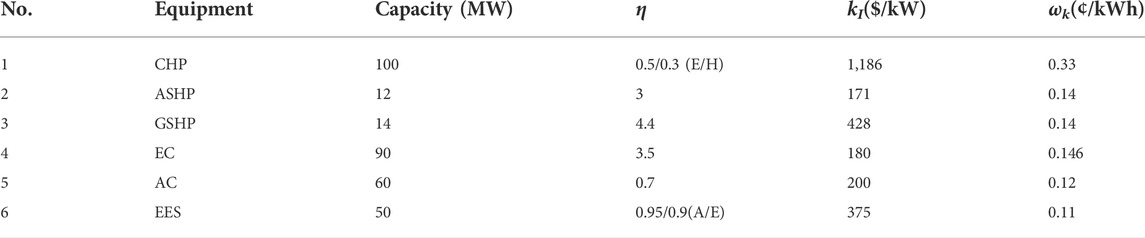
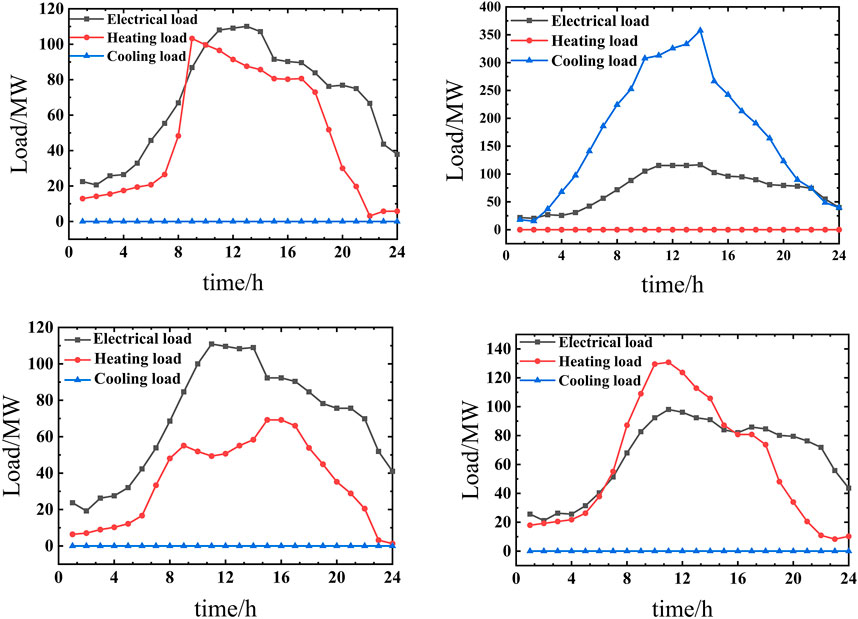
The optimal operation solution of PIES is obtained by solving the proposed cooperative game model through AA-ADMM. The benefits generated after the cooperation are distributed by the Shapley value method. The convergence accuracy of the AA-ADMM algorithm is set to 10^–4. There are five agents in PIES, that is, EES, EC, GSHP&ASHP, CHP, and AC. The parameters are shown in Table 1. The electrical, thermal and cooling load curves are shown in Figure 4.

TABLE 1

TABLE 1. Component parameters.

FIGURE 4

FIGURE 4. Load curves of four typical days.

The prices of electricity are 1.14 CNY/kWh during peak hours (12–14, 19–22), 0.46 CNY/kWh during valley hours (1–7, 23, 24), and 0.84 CNY/kWh during normal hours (8–11, 15–18). The price of natural gas is 0.25 CNY/kWh. The purchase limit of electricity and natural gas is 200 MW. The carbon emission factors of natural gas and electricity are 0.22 kg/kWh and 0.968 kg/kWh, respectively.

4.1 Results of multi-agent game optimization

The multi-agent cooperative game optimization is performed to find the optimal operation strategy. The AA-ADMM algorithm can find the weight parameters of two objectives, operations costs, and carbon emissions.

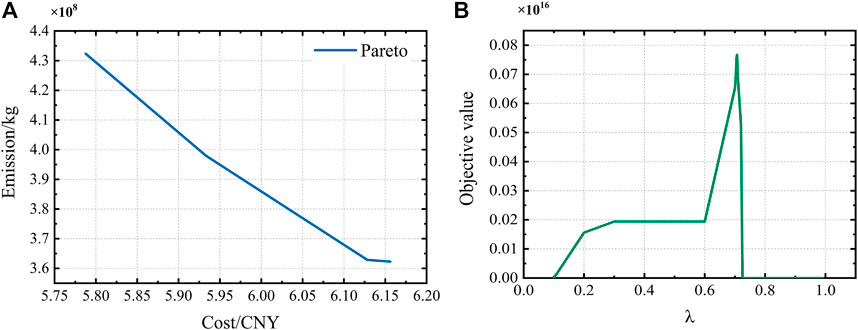
The (Figure 5A) show that cost and CO₂ emissions are mutually exclusive objectives, and a decrease in one is necessarily accompanied by an increase in the other one. The optimal operating cost f_C is 5.9332×10⁸ CNY and carbon emission f_E is 3.9796 × 10⁸ kg. As shown in (Figure 5B), the optimal target value corresponds to a specific weight λ of 0.7071.

FIGURE 5

FIGURE 5. (A) Optimal solution on the Pareto. (B) Optimization objective value.

After getting the target weights, the game operation considering multi-agent is performed. There are two modes of PIES operation, mode A is the separate operation mode and mode B is the optimized cooperative operation model. The optimization results of the operation cost and carbon emission of the two modes are shown in Table 2.

TABLE 2

TABLE 2. Results of operation mode.

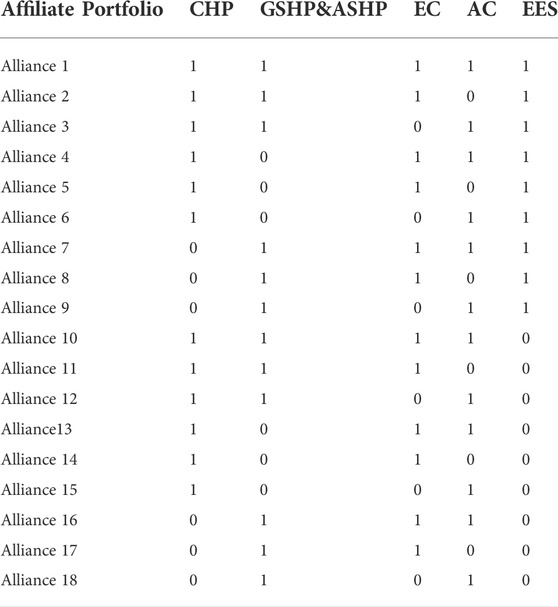
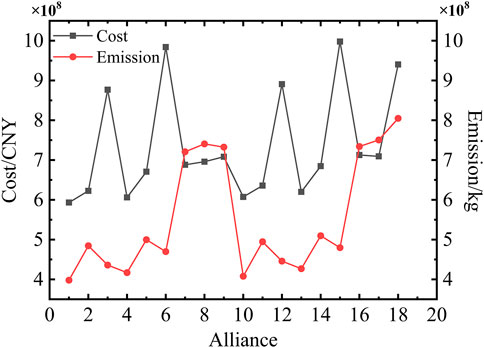
Considering the contribution of all the sub-alliances, the Shapley value method is used to allocate benefits to the alliances. All feasible sub-alliances are shown in Table 3. The optimization results of the sub-alliance operation are shown in Figure 6.

TABLE 3

TABLE 3. Achievable gaming alliance combinations.

FIGURE 6

FIGURE 6. Optimization results for all sub-affiliate operations.

As shown in Table 2 and Figure 6, the total cost and carbon emission are positively correlated expect the cases without EC. This is because the efficiency of EC is lower than that of AC. For alliances 8, 16, 17, 18, and 19, the supply of heat load mainly comes from electric components, which causes the increase in carbon emissions.

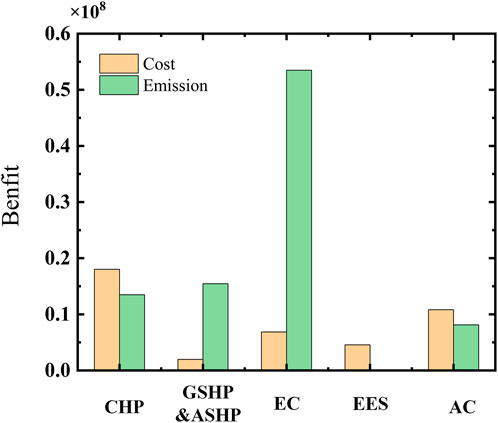
The total economic benefit and carbon emission benefit using the cooperative operation are 0.4222×10⁸ CNY and 0.9056 × 10⁸ kg, respectively. As shown in Figure 7, since CHP can meet most of the electric and heat load, it obtains the economic benefit 0.1802 × 10⁸ CNY. The large capacity of CHP leads to the high carbon emission, its carbon emission allocation changes from 0.1529 × 10⁸ kg to 0.1349 × 10⁸ kg. Because of the high efficiency, EC has the economic benefit of 0.0686 × 10⁸ CNY, and the carbon emission allocation benefit is 0.5349 × 10⁸kg. The economic and carbon emission benefits of GSHP and ASHP are 0.0196× 10⁸ CNY and 0.1546 × 10⁸kg, respectively. This is because their electricity can be supplied by not only grid but also CHP, and the efficiency of electro-thermal coupling components is high. As the impact of energy storage on carbon emission is extremely low, its carbon emission benefit is zero.

FIGURE 7

FIGURE 7. Benefit distribution results.

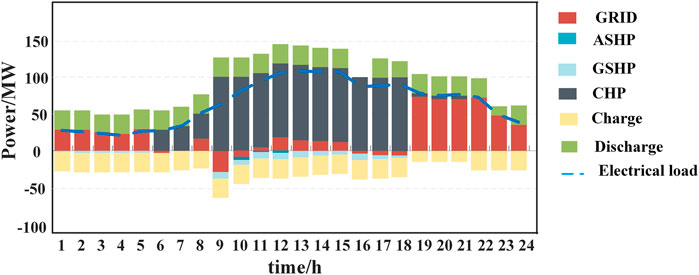
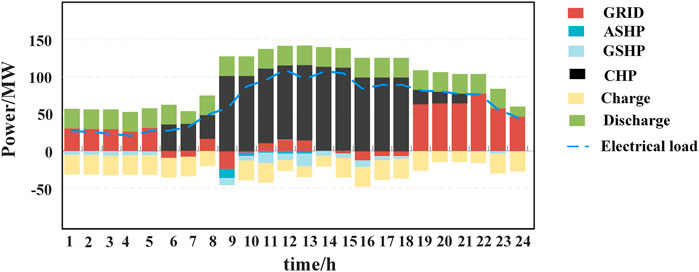
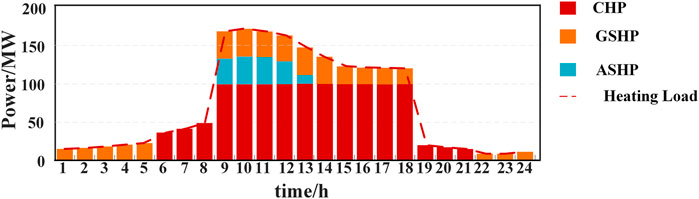
The optimal operation strategies of PIES components in spring and winter are shown in Figures 8–11.

FIGURE 8

FIGURE 8. The optimal electricity operation strategies in spring.

FIGURE 9

FIGURE 9. The optimal heat operation strategies in spring.

FIGURE 10

FIGURE 10. The optimal electricity operation strategies in winter.

FIGURE 11

FIGURE 11. The optimal heat operation strategies in winter.

As shown in Figures 8–11, the proposed optimization operation strategy can realize the balance of multiple energy. Compared with electricity, due to the cheaper price and the lower carbon emission of gas, the peak hour load is supplied by CHP. Compared to ASHP, GSHP has better efficiency performance. Therefore, GSHP also is the main component to supply the heat load, and ASHP is always used to meet the peak load in winter.

4.2 Analysis of algorithm performance

1) Weight analysis

When the specific weight λ is 0, the operating cost f_C is 6.1561 × 10⁸ CNY and f_E is 3.6229 × 10⁸ kg. In his cases, the operation strategy is the worst operation cost. When the λ is 1, the operating cost f_C is 5.7876 × 10⁸ CNY and the carbon emission f_E is 4.3235 × 10⁸ kg. In this case, the solution approaches its worst carbon emission.

It can be intuitively seen that the weight of 0.7071 is a compromise value and can reach the solution balancing two objectives, thus verifying the feasibility of the multi-objective solution method in this paper.

2) Algorithm Comparison

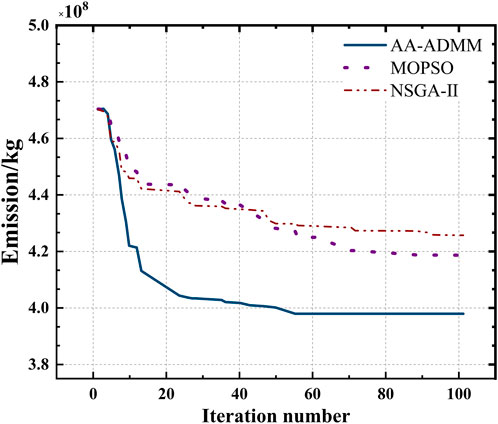
To verify the effectiveness and advancement of the AA-ADMM algorithm, it is compared with Non-dominated Sorting Genetic Algorithms (NSGA-II) and Multiple Objective Particle Swarm Optimization (MOPSO) algorithms. AA-ADMM possesses a faster solving speed and obtains better objective values. The solution iteration processes of three algorithms are shown in Figure 12.

FIGURE 12

FIGURE 12. Iterative process of the three optimization algorithms.

5 Conclusion

In this paper, a cooperative-game-based multi-agent optimization model is proposed to explore a new mode of park operation under the current development of decentralized and park-based energy systems. The proposed model is solved by the AA-ADMM algorithm to find a high-quality solution satisfying the system constraints, and the benefits of the saved costs are allocated using the Shapley value method. Through verification, the method in this paper has the following significant advantages.

1) The PIES cooperative game model can make excellent use of equipment supply properties to couple multiple energy sources for coordinated operation. It alleviates the problem of energy inefficiency and maximizes operational efficiency. This method provides ideas for decentralization and park development. The method can extend the application scenario to achieve a larger range of peer-to-peer transactions.

2) The AA-ADMM can effectively solve the multi-objective optimization problem of the energy system. It can realize the rational allocation of resources and find a reasonable trade-off between operating costs and carbon emissions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KX: Conceptualization, Methodology, Validation, Formal analysis, Writing-review, and editing. KH: Conceptualization, Methodology, Software, Formal analysis, Writing-review, and editing. ZL: Conceptualization, Writing-review, and editing, Data curation. WS: methodology, writing reviewing and editing.

Funding

This work was supported by the National Natural Science Foundation of China Smart Grid Joint Foundation (Grant No. U2066211).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, S. (2020). Distributed optimal scheduling of electrically interconnected integrated energy systems. Guangzhou: South China University of Technology.

Google Scholar

Deng, Y., Zhang, Y., Luo, F., and Mu, Y. (2021). Hierarchical energy management for community microgrids with integration of second-life battery energy storage systems and photovoltaic solar energy. IET Energy Syst. Integr. 4 (2), 206–219. doi:10.1049/esi2.12055

CrossRef Full Text | Google Scholar

Duan, J., Xie, J., Feng, L., and Chen, F. (2022). Gain allocation strategy of wind-light-water-hydrogen multi-body energy system based on cooperative game theory. Power Grid Technol. 46 (05), 1703–1712. doi:10.13335/j.1000-3673.pst.2021.2084

CrossRef Full Text | Google Scholar

Gao, B., Chen, C., Qin, Y., Liu, X., and Zhu, Z. (2021). Evolutionary game-theoretic analysis for residential users considering integrated demand response. J. Mod. Power Syst. Clean Energy 9 (6), 1500–1509. doi:10.35833/MPCE.2019.000030

CrossRef Full Text | Google Scholar

Geng, Q., Hu, Y., He, J., Zhou, Y., and Zhao, W. (2020). Optimal operation of integrated community energy system based on Nash bargaining. Electr. Power Constr. 41 (1), 114–125. doi:10.3969/j.issn.1000-7229.2020.01.014

CrossRef Full Text | Google Scholar

Ha, T., Xue, Y., Lin, K., Zhang, Y., Thang, V., and Nguyen, T. (2022). Optimal operation of energy hub based micro-energy network with integration of renewables and energy storages. J. Mod. Power Syst. Clean Energy 10 (1), 100–108. doi:10.35833/MPCE.2020.000186

CrossRef Full Text | Google Scholar

He, C., Cheng, S., Xu, J., and Fang, Z. (2020). Coordinated optimal scheduling of integrated energy system considering multi-time scale and hybrid energy storage system. Proc. CSU-EPSA 32 (2), 7797–7884. doi:10.19635/j.cnki.csu-epsa.000363

CrossRef Full Text | Google Scholar

Huang, T., Singhania, P., Sanjabi, M., Mitra, P., and Razaviyayn, M. (2021). “Alternating direction method of multipliers for quantization,” in International Conference on Artificial Intelligence and Statistics, Valencia, Spain, Mar 28, 2022 to Mar 30, 2022, 208–216. PMLR.

Google Scholar

Jiao, Y., Xie, M., and Liu, M. (2022). Research on the weight Allocation method of renewable energy consumption responsibility of market players based on stochastic optimization of evolutionary game. South. Energy Constr. 9 (1), 122–129. doi:10.16516/j.gedi.issn2095-8676.2022.01.018

CrossRef Full Text | Google Scholar

Jing, R., Wang, J., Shah, N., and Guo, M. (2021). Emerging supply chain of utilising electrical vehicle retired batteries in distributed energy systems. Adv. Appl. Energy 1, 100002. doi:10.1016/j.adapen.2020.100002

CrossRef Full Text | Google Scholar

Jing, R., Wang, M., Liang, H., Wang, X., Li, N., Shah, N., et al. (2018). Multi-objective optimization of a neighborhood-level urban energy network : Considering Game-theory inspired multi-benefit allocation constraints. Appl. energy 231, 534–548. doi:10.1016/j.apenergy.2018.09.151

CrossRef Full Text | Google Scholar

Jing, R., Xie, M., Wang, F., and Chen, L. (2020). Fair P2P energy trading between residential and commercial multi-energy systems enabling integrated demand-side management. Appl. Energy 262262, 114551. doi:10.1016/j.apenergy.2020.114551

CrossRef Full Text | Google Scholar

Lan, P., Shen, X., Wu, G., Liu, J., Zhao, H., and Wang, H. (2021). Distributed optimal scheduling of transmission-distribution-gas system based on alternating directional multiplier method. Automation Electr. Power Syst. 45 (23), 21–30. doi:10.7500/AEPS20210519010

CrossRef Full Text | Google Scholar

Luo, P., Zhou, H., and Xu, L. (2022). Optimal scheduling of multi-microgrid day-ahead based on interval optimization for combined cooling, heating and power supply. Automation Electr. Power Syst. 46 (09), 137–146. doi:10.7500/AEPS20210121001

CrossRef Full Text | Google Scholar

Ma, H., Chen, Q., Hu, B., Sun, Q., Li, T., and Wang, S. (2021). A compact model to coordinate flexibility and efficiency for decomposed scheduling of integrated energy system. Appl. energy 285, 116474. doi:10.1016/j.apenergy.2021.116474

CrossRef Full Text | Google Scholar

Ma, T., Pei, W., Xiao, H., Li, D., Lv, X., and Hou, K. (2021). A cooperative operation method of wind-light-hydrogen multi-body energy system based on Nash negotiation theory. Chin. J. Electr. Eng. 41 (01), 25–39+395. doi:10.13334/j.0258-8013.pcsee.200956

CrossRef Full Text | Google Scholar

Tan, C., Geng, S., Tan, Z., Wang, G., Pu, L., and Guo, X. (2021). Integrated energy system–hydrogen natural gas hybrid energy storage system optimization mode-L based on cooperative game under carbon neutrality. J. Energy Storage 38, 102539. doi:10.1016/j.est.2021.102539

CrossRef Full Text | Google Scholar

Tang, X., Hu, Y., Geng, Q., and Xu, X. (2021). Multi-time-scale optimal scheduling of integrated energy system considering multi- energy flexibility. Automation Electr. Power Syst. 45 (4), 81–90. doi:10.7500/AEPS20200602010

CrossRef Full Text | Google Scholar

UNFCCC. (2019). Climate ambition alliance: Nations renew their push toupscale action by 2020 and achieve net zero CO2 emissions by 2050, Available at: https://unfccc.int/news/climate-ambition-alliance-nations-renew-their-push-to-upscale-action-by-2020-and-achieve-net-zero.

Google Scholar

Wang, Y., Li, J., Wang, S., Yang, J., Qi, C., Guo, H., et al. (2020). Operational optimization of wastewater reuse integrated energy system. Energy 200, 117309. doi:10.1016/j.energy.2020.117309

CrossRef Full Text | Google Scholar

Wang, Y., Wang, X., Sun, Q., Zhang, Y., Liu, Z., and He, J. (2022). Real-time collaborative optimization strategy of multiple subjects in integrated energy system cluster based on energy sharing. Automation Electr. Power Syst. 46 (04), 56–65. doi:10.7500/AEPS20210511007

CrossRef Full Text | Google Scholar

Wu, D., Han, Z., Liu, Z., Li, P., Ma, F., Zhang, H., et al. (2019). Comparative study of optimization method and optimal operation strategy for multi-scenario integrated energy system. Energy 217, 119311. doi:10.1016/j.energy.2020.119311

CrossRef Full Text | Google Scholar

Wu, M., Kou, L., and Zhang, J. (2019). A Nash bargaining method for economic optimal dispatching of multi-operator microgrid day-ahead. China Electr. Power 52 (11), 19–27. doi:10.11930/j.issn.1004-9649.201905076

CrossRef Full Text | Google Scholar

Yuan, H. (2021). Community energy trading model and optimal operation strategy based on Nash bargaining cooperative game. Nanning: Guangxi University. doi:10.27034/d.cnki.ggxiu.2021.001159

CrossRef Full Text | Google Scholar

Zhang, Y., Ai, X., Wen, J., Fang, J., and He, H. (2019). Data-adaptive robust optimization method for the economic dispatch of active distribution networks. IEEE Trans. Smart Grid 10 (4), 3791–3800. doi:10.1109/TSG.2018.2834952

CrossRef Full Text | Google Scholar