
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 04 October 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.970293
This article is part of the Research Topic Modern World Heat Transfer Problems: Role of Nanofluids and Fractional Order Approaches View all 18 articles
Due to their accelerated rate of heat transfer, nanofluids are of immense interest. This work analyzes an innovative concept of hybrid nanoemulsion with an optimized design under the chemical radiative flow and its thermophysical properties. We are able to achieve great aspects of the flow with the assistance of the sheet’s permeable texture and inclined surface. Furthermore, the effects of thermal conductivity mix convection, chemical reaction, and thermal radiations on velocity, temperature, and concentration fields are also investigated. After converting the fundamental equations to ordinary differential equations with the use of similarity transportation, the problem is then solved analytically with the HAM technique. To investigate key attributes and parameters, a hybrid nanofluid with Ag and Al2O3 nanoparticles as well as Al2O3 for conventional nanofluids with the base solvent water is taken. To illustrate the effects of chemical radiative and mix convection on the thin-film flow, numerous graphs, charts, and tables are shown. Calculations and reviews are performed for reduced friction coefficient, heat, and mass transportation. According to this study, hybrid nanofluids have a higher heat-transfer rate than nanofluids when exposed to thermal radiation and at the appropriate surface angle of inclination. Due to
Table 1 shows the thermophysical properties of the materials. It is common practice to utilize the power-law model when modeling the flow of fluids that have a viscosity that varies with shear. On the other hand, it is not possible to forecast the results of elasticity. Fluids of the second or third grade have the potential to produce the desired outcomes in terms of elasticity. However, in these models, the viscosity is not shear-dependent. Furthermore, they are impotent to assess the effects of reducing stress. A subcategory of fluids known as the Maxwell model, which has become more popular, can identify stress relaxation. A perfectly viscous obstruction and a strictly elastic spring can be represented, much like in the Maxwell model. Maxwell nanofluid flow simulations have drawn the attention of numerous researchers. Abro et al. (2020), Sharama et al. (2020), and Ramesh et al. (2020) have used various mathematical models for the Maxwell fluid flow. The influence of radiative heat flux on the flow of Maxwell nanofluids across a chemically reacting spiraling disc was analyzed by Ahmed et al. (2020). Hussain et al. (2020) took into consideration the mathematical analysis of a Maxwell nanofluid with hydromagnetic dissipative and radiation. Jawad et al. (2021) have analyzed the entropy impact on the flow of Maxwell fluids using stretched surfaces.
The most appealing and affordable method of thermal transportation was proposed by the revolutionary advancement in science using the concept of nanoparticles. Researchers are constantly examining the thermal characteristics of nanoparticles related to engineering and manufacturing usages because they have the highest proficiency of thermal transportation and stable forceful features. The formation of nanofluids is caused by the dispersion of nanoparticles in the base solvent. Plications for nanofluids are anticipated in a variety of fields, including nuclear engineering, mechanical and cooling devices, extrusion systems, and many others. In recent years, the role of nanofluids in energy production has moved into more essential applications. When nanoparticles are adequately dissolved in the base fluid, it is expected that mass and heat transmission will improve. Nanofluids are widely used in biotechnology, medicine delivery, renewable energy, and several technical fields. Choi (1995) coordinated the basic analysis and experimental investigation of the nanofluid characteristics. The thermal measurements of a nanofluid containing micropolar material were described by Khan et al. (2020) using modified diffusion concepts. Khan et al. (2019) have depicted the Oldroyd-B nanofluid flow using the optimal Prandtl number technique. Turkyilmazoglu (2020) used the single-phase model to declare the stability of nanofluids. The impact of porous space over moving surfaces susceptible to the Jeffrey nanofluid was determined by Khan and Shehzad (2020). The dual solution prediction for the nanofluid flow subject to asymmetrical slip was observed by Nadeem et al. (2020). Some other researchers have proposed different forms of nanofluids to study the many uses of nanofluids in various aspects (Sabir et al., 2019; Umar et al., 2020; Ayub et al., 2021a; Ayub et al., 2021b; Sabir et al., 2021).
As an alternative to conventional fluids, nanofluids are renowned for their exceptional capacity to transport energy. In order to make it significantly better, the hybrid nanoliquid is being produced. When two or more types of metals are combined in such a way as to produce different chemical bonds, the resulting substances are referred to be hybrid metals. A “hybrid nanofluid” can also be created by the uniform dispersion of two very small particles into the liquid that is acting as the mother liquid. Comparing this highly developed type of solution to unitary nanofluids or any other common functional fluids, it shows promising heat transmission. The innovative uses for hybrid nanosolutions include the fabrication of aviation devices, power systems, welding, lubricants, spacecraft, and electronic cooling devices. The influence of the magnetic field in the transverse direction to the flow field is discussed by Devi and Devi (2016). Babar and Ali (2019) discussed the specific thermophysical environment, applications, setup, and inherent issues of hybrid composites. Recently, more studies about hybrid nanofluid flow through various configurations can be decoded in Acharya et al. (2020), Yaseen et al. (2022), and Joshi et al. (2022).
The transportation of liquids in thin layers is frequently seen in daily life; one illustration of this is the way raindrops move across rooftops, road surfaces, and window glass. Understanding the process of thin films is crucial since they frequently occur in nature and have numerous useful applications. Whether there are inertial forces present or absent, thin films of liquids are driven by surface or body forces. Depending on the flow pattern under consideration, the strength of these forces acting on the fluid may be increased or decreased. In situations like dropping films or spray coating, inertia is crucial, but it is sometimes disregarded when the flow Reynolds number is low, as in the flow motion over an inclined plane in a sluggish motion. Thin-film flows have drawn a great deal of interest in recent years. Photovoltaic panels, lamination, biofluid flows, hydrophilicity, and other commercial and technical applications all involve film flowing over stirring flat, vertical, and inclined planes (Liu et al., 2017). The first person to look at the case of the dropping liquid films was Nusselt (1916). Jeffrey (1925) also explored the film flow in the scenario of an inclined plane. There are a lot of research studies on film flow on diverse models, which may be found in the Refs. Wang, 1990; Qasim et al., 2016; Zhang et al., 2021; Shah et al., 2022.
The radiation impact plays an important role in almost all the design approaches. Thermal radiation plays a significant role in a variety of mechanical processes, such as missiles, nuclear power plants, spacecraft and other communications satellites, steam turbines, and the many driving mechanisms for aviation. In addition to radiation, Ghadikolaei et al. (2018) and Ali et al. (2020) focused on the thermal radioactive effects in addition to the transfer of nanofluids when studying peristaltic pressing. CuO-Ag/water micropolar hybrid nanofluid flow across a vertically positioned plate was studied by Gumber et al. (2022) with the help of heat radiation and the suction/injection mechanism.
The possibilities for higher thermal transport illustrate the knowledge of the existing literature. Recent investigations of unsteady thin-film flow impacted by advanced ablation/accretion (Wang, 1990; Qasim et al., 2016; Zhang et al., 2021; Shah et al., 2022) address conventional heat transmission modes. We focused on expanding such work to include the chemical radiative effect and the mix convectional characteristics of Maxwell hybrid nanofluid flow. The cited works mentioned aforesaid highlight that less attention is paid to the study of nanofluid flow impressions over an inclined stretched plane keeping insight of Maxwell fluid flow. Nevertheless, the flow of the hybrid nanofluid in the same context is rare. We in this exploration discussed the hybrid nanofluid flow comprising silver with aluminum oxide, nanocomposites, and thin-film flow over an inclined plane. The thermal effects of the nanocomposites are also taken into account in the presence of radiation. The composite factor of the particles plays a significant role in thermal conduction. The film width along with the applied magnetic field has been studied additionally in the graphical form by using the HAM method. The impression of varied parameters versus involved profiles is studied logically.
The following are some of the innovative aspects of this work:
• Due to the intensive use of both laboratory and computational studies, the novel heat-transfer fluid is focused on the appropriate Maxwell fluid-based Al2O3-Ag-hybrid nanofluid.
• To explore the heat-transfer phenomenon, a thin film of Maxwell hybrid nanofluid flow on an inclined extended surface using thermal conductivity models has been used.
• To find an analytical solution for heat-transfer effects in hybrid nanofluid flow with thermal radiation, chemical reaction, porosity, and mix convection present.
• The governing equations for heat, mass transport, and fluid motion are transformed into self-similar differential equations using the standard factors, and the HAM method is then used to evaluate them analytically.
• The results are represented in diagrams that correspond to various numeric values of the relevant parameters.
Chemical radiative and convectional heat exchange between the surface and the surrounding fluid is essential in many real-world applications involving the cooling or heating of surfaces. The problem is more realistic and produces better results because of its cumulative proportion.
Let us examine the improvement of energy and mass transformation in time-dependent thin-film flow of Maxwell fluids with hybrid and mononanoparticles. Over an extended inclined plane making an angle
1 The surface over which the thin film exists is moving with velocity
2 The surface temperature of the extending sheet is signified as “
3
4 h(t) represents the thickness of the film.
5 We consider pressure to be constant.
6 The nanoparticles Al2O3 and Ag are used.
7 The magnetic field in a perpendicular direction is defined as
8.8 The flow configuration for the problem is shown in Figure 1.
The fundamental equations for boundary layers that govern flow, heat, and mass transfer have the following forms (Jawad et al., 2021; Acharya et al., 2020; Zhang et al., 2021; Shah et al., 2022; Gumber et al., 2022):
The components of velocity are represented by
Therefore, we assumed the composition of Ag into Al2O3/H2O; in the proposed investigation, a hybrid nanofluid was developed. Al2O3 nanoparticles (
The physical conditions for the thin-film flow are defined as
The non-dimensional variables and coordinates that we present are as follows (Zhang et al., 2021; Shah et al., 2022):
where
Eq. 1 is satisfied, while Eqs 2–4 are transformed as
where
The transform forms of the physical conditions are taken as
The skin friction and the local Nusselt and Sherwood numbers are defined as
where
The transformed terms are stated as
In this section, we display and discuss the results that were computed using the aforementioned technique, HAM. Additionally, as illustrated in Figures 2–17 and Tables 2,Tables 3, the performance of hybrid nanofluid and nanofluid flow
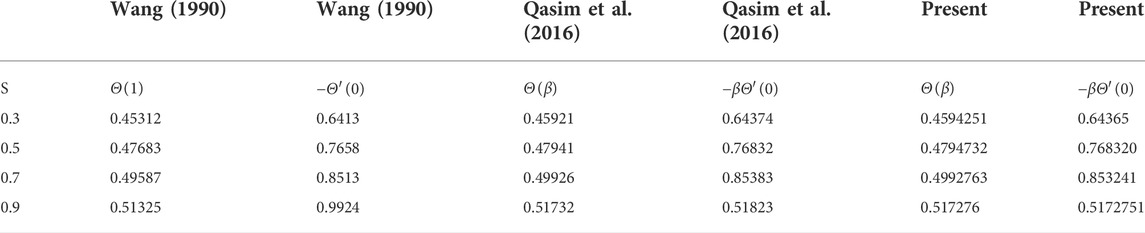
TABLE 2. Comparison between the published work and present work for the surface and wall temperature gradients considering common factors using the regular fluid having

TABLE 3. Comparison between the published work and present work for the Sherwood number considering the common factor using the regular fluid having
The characteristics of
The changes in the
Figure 13 illustrates how the presence of
We focused on describing the chemical radiative and convectional effects on the hydrothermal characteristics of two different types of Maxwell nanoliquids, the Ag hybrid nanofluid and Al2O3 regular nanofluid, during the entire study. Over a permeable stretched inclined surface, the desired thin-film flow has been passed. Through tables and figures, exhaustive properties of porosity, volume fraction, unsteadiness, radiation, chemical reaction, and thermal and mass buoyancy components are explained. Through a comprehensive examination, some guiding points help focus our attention on the following findings:
• Maxwell hybrid nanofluids’ thin-film flow is slowed down by increased
•
• For the thermal profile,
• For the concentration profile, the thin film of the hybrid fluid is more influenced than the nanofluid by
• The skin friction coefficient, Nusselt number, and Sherwood number reduce when uplifting the parameter
These results of thin-film flows can also be used for other models like discs and cylinders, different flow factors, and trihybrid nanofluids with the execution of numerical and analytical techniques.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
TG, modeling and solution; SM, writing draft WA, editing. ETE, Validated, MFY and KG, participated in revision and provide funding source.
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4331317DSR78).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Abro, K. A., Soomro, M., Atangana, A., and Gómez-Aguilar, J. F. (2020). Thermophysical properties of Maxwell nanofluids via fractional derivatives with regular kernel. J. Therm. Analysis Calorim. 147, 1–11. doi:10.1007/s10973-020-10287-9
Acharya, N., Maity, S., and Kundu, P. K. (2020). Influence of inclined magnetic field on the flow of condensed nanomaterial over a slippery surface: The hybrid visualization. Appl. Nanosci. 10 (2), 633–647. doi:10.1007/s13204-019-01123-0
Ahmed, J., Khan, M., and Ahmad, L. (2020). Radiative heat flux effect in flow of Maxwell nanofluid over a spiraling disk with chemically reaction. Phys. A Stat. Mech. its Appl. 551, 123948. doi:10.1016/j.physa.2019.123948
Ali, L., Liu, X., and Ali, B. (2020). Finite element analysis of variable viscosity impact on MHD flow and heat transfer of nanofluid using the cattaneo-christov model. Coatings 10 (4), 395. doi:10.3390/coatings10040395
Ayub, A., Sabir, Z., Altamirano, G. C., Sadat, R., and Ali, M. R. (2021). Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller–Box and BVP4C method. Eng. Comput. 1, 1–15.
Ayub, A., Wahab, H. A., Shah, S. Z., Shah, S. L., Darvesh, A., Haider, A., et al. (2021). Interpretation of infinite shear rate viscosity and a nonuniform heat sink/source on a 3D radiative cross nanofluid with buoyancy assisting/opposing flow. Heat. Transf. 50 (5), 4192–4232. doi:10.1002/htj.22071
Babar, H., and Ali, H. M. (2019). Towards hybrid nanofluids: Preparation, thermophysical properties, applications, and challenges. J. Mol. Liq. 281, 598–633. doi:10.1016/j.molliq.2019.02.102
Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publications-Fed 231, 99–106.
Devi, S. A., and Devi, S. S. U. (2016). Numerical investigation of hydromagnetic hybrid Cu - Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 17 (5), 249–257. doi:10.1515/ijnsns-2016-0037
Ghadikolaei, S. S., Hosseinzadeh, K., Ganji, D. D., and Jafari, B. (2018). Nonlinear thermal radiation effect on magneto Casson nanofluid flow with Joule heating effect over an inclined porous stretching sheet. Case Stud. Therm. Eng. 12, 176–187. doi:10.1016/j.csite.2018.04.009
Gumber, P., Yaseen, M., Rawat, S. K., and Kumar, M. (2022). Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differ. Equations Appl. Math. 5, 100240. doi:10.1016/j.padiff.2021.100240
Hussain, S. M., Sharma, R., Mishra, M. R., and Alrashidy, S. S. (2020). Hydromagnetic dissipative and radiative graphene Maxwell nanofluid flow past a stretched sheet-numerical and statistical analysis. Mathematics 8 (11), 1929. doi:10.3390/math8111929
Jawad, M., Saeed, A., and Gul, T. (2021). Entropy generation for MHD Maxwell nanofluid flow past a porous and stretching surface with Dufour and Soret effects. Braz J. Phys. 51 (3), 469–480. doi:10.1007/s13538-020-00835-x
Jeffreys, H. (1925). LIV. The flow of water in an inclined channel of rectangular section. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 49 (293), 793–807. doi:10.1080/14786442508634662
Joshi, N., Upreti, H., and Pandey, A. K. (2022). MHD Darcy-Forchheimer Cu-Ag/H2O-C2H6O2 hybrid nanofluid flow via a porous stretching sheet with suction/blowing and viscous dissipation. Int. J. Comput. Methods Eng. Sci. Mech. 1, 1–9.
Khan, S. U., Rauf, A., Shehzad, S. A., Abbas, Z., and Javed, T. (2019). Study of bioconvection flow in Oldroyd-B nanofluid with motile organisms and effective Prandtl approach. Phys. A Stat. Mech. its Appl. 527, 121179. doi:10.1016/j.physa.2019.121179
Khan, S. U., and Shehzad, S. A. (2020). Flow of Jeffrey nanofluids over convectively heated oscillatory moving sheet with magnetic field and porosity effects. J. Por Media 23 (9), 907–922. doi:10.1615/jpormedia.2020025508
Khan, S. U., Shehzad, S. A., Rauf, A., and Abbas, Z. (2020). Thermally developed unsteady viscoelastic micropolar nanofluid with modified heat/mass fluxes: A generalized model. Phys. A Stat. Mech. its Appl. 550, 123986. doi:10.1016/j.physa.2019.123986
Liu, Y., Itoh, M., and Kyotoh, H. (2017). Flow of a falling liquid curtain onto a moving substrate. Fluid Dyn. Res. 49 (5), 055501. doi:10.1088/1873-7005/aa7ee8
Nadeem, S., Israr-ur-Rehman, M., Saleem, S., and Bonyah, E. (2020). Dual solutions in MHD stagnation point flow of nanofluid induced by porous stretching/shrinking sheet with anisotropic slip. AIP Adv. 10 (6), 065207. doi:10.1063/5.0008756
Qasim, M., Khan, Z. H., Lopez, R. J., and Khan, W. A. (2016). Heat and mass transfer in nanofluid thin film over an unsteady stretching sheet using Buongiorno’s model. Eur. Phys. J. Plus 131 (1), 1–11. doi:10.1140/epjp/i2016-16016-8
Ramesh, K., Khan, S. U., Jameel, M., Khan, M. I., Chu, Y. M., and Kadry, S. (2020). Bioconvection assessment in Maxwell nanofluid configured by a Riga surface with nonlinear thermal radiation and activation energy. Surfaces Interfaces 21, 100749. doi:10.1016/j.surfin.2020.100749
Sabir, Z., Akhtar, R., Zhiyu, Z., Umar, M., Imran, A., Wahab, H. A., et al. (2019). A computational analysis of two-phase casson nanofluid passing a stretching sheet using chemical reactions and gyrotactic microorganisms. Math. Problems Eng. 2019, 1–12. doi:10.1155/2019/1490571
Sabir, Z., Imran, A., Umar, M., Zeb, M., Shoaib, M., and Raja, M. A. Z. (2021). A numerical approach for 2-D Sutterby fluid-flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm. Sci. 25 (3), 1975–1987.
Shah, S. A., Mouldi, A., and Sene, N. (2022). Nonlinear convective SiO2 and TiO2 hybrid nanofluid flow over an inclined stretched surface. J. Nanomater. 2022, 1–15.
Sharma, R., Hussain, S. M., Raju, C. S. K., Seth, G. S., and Chamkha, A. J. (2020). Study of graphene Maxwell nanofluid flow past a linearly stretched sheet: A numerical and statistical approach. Chin. J. Phys. 68, 671–683. doi:10.1016/j.cjph.2020.10.013
Turkyilmazoglu, M. (2020). Single phase nanofluids in fluid mechanics and their hydrodynamic linear stability analysis. Comput. Methods Programs Biomed. 187, 105171. doi:10.1016/j.cmpb.2019.105171
Umar, M., Sabir, Z., Imran, A., Wahab, A. H., Shoaib, M., and Raja, M. A. Z. (2020). The 3-D flow of Casson nanofluid over a stretched sheet with chemical reactions, velocity slip, thermal radiation and Brownian motion. Therm. Sci. 24 (5), 2929–2939. doi:10.2298/tsci190625339u
Wang, C. Y. (1990). Liquid film on an unsteady stretching surface. Quart. Appl. Math. 48 (4), 601–610. doi:10.1090/qam/1079908
Yaseen, M., Rawat, S. K., and Kumar, M. (2022). Hybrid nanofluid (MoS 2 -SiO 2/water) flow with viscous dissipation and Ohmic heating on an irregular variably thick convex/concave‐shaped sheet in a porous medium. Heat. Trans. 51 (1), 789–817. doi:10.1002/htj.22330
Zhang, Y., Shahmir, N., Ramzan, M., Ghazwani, H. A. S., and Malik, M. Y. (2021). Comparative analysis of Maxwell and Xue models for a hybrid nanofluid film flow on an inclined moving substrate. Case Stud. Therm. Eng. 28, 101598. doi:10.1016/j.csite.2021.101598
Keywords: Maxwell hybrid nanofluid, thin film, heat and mass transfer, inclined stretching sheet, MgO and TiO2
Citation: Gul T, Mukhtar S, Alghamdi W, Tag Eldin E, Yassen MF and Guedri K (2022) The radiative flow of the thin-film Maxwell hybrid nanofluids on an inclined plane in a porous space. Front. Energy Res. 10:970293. doi: 10.3389/fenrg.2022.970293
Received: 15 June 2022; Accepted: 01 August 2022;
Published: 04 October 2022.
Edited by:
Umar Khan, Hazara University, PakistanReviewed by:
Basharat Ullah, Mohi-Ud-Din Islamic University, PakistanCopyright © 2022 Gul, Mukhtar, Alghamdi, Tag Eldin, Yassen and Guedri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elsayed Tag Eldin, RWxzYXllZC50YWdlbGRpbkBmdWUuZWR1LmVn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.