Remaining useful life prediction of lithium-ion batteries based on wavelet denoising and transformer neural network

It is imperative to accurately predict the remaining useful life (RUL) of lithium-ion batteries to ensure the reliability and safety of related industries and facilities. In view of the noise sequence embedded in the measured aging data of lithium-ion batteries and the strong nonlinear characteristics of the aging process, this study proposes a method for predicting lithium-ion batteries’ RUL based on the wavelet threshold denoising and transformer model. To specify, firstly, the wavelet threshold denoising method is adopted to preprocess the measured discharging capacity data of lithium-ion batteries to eliminate some noise signals. Second, based on the denoised data, the transformer model output’s full connection layer is applied to replace the decoder layer for establishing the RUL prediction model of lithium-ion batteries. Finally, the discharging capacity of each charging–discharging cycle is predicted iteratively, and then the RUL of lithium-ion batteries can be calculated eventually. Two groups of lithium-ion batteries’ aging data from the Center for Advanced Life Cycle Engineering (CALCE) at the University of Maryland and the laboratory at Anqing Normal University (AQNU) are employed to verify the proposed method, individually. The experimental results demonstrate that this method can overcome the impacts of data measurement noise, effectively predict the RUL of lithium-ion batteries, and present a sound generalization ability and high accuracy.

1 Introduction

Thanks to the advantages of high energy density, long storage life, high safety, and no pollution, lithium-ion batteries are widely applied in the field of electric vehicles (Yuan et al., 2015; Wang et al., 2021). However, with the use of electric vehicles starting, irreversible electrochemical reactions occur in the onboard lithium-ion batteries, which will increase their internal resistance and decrease their maximum available capacity, leading to the attenuation of their remaining useful life (RUL) and a serious reduction of the driving distances of electric vehicles (Guha and Patra., 2018; Ansari et al., 2022). Besides, it is well known that the discharging capacity of lithium-ion batteries is poor in a low-temperature environment. Consequently, the accurate RUL is difficult to be predicted (Zhang D. et al., 2022). If the lithium-ion battery continues to work even after reaching its failure threshold, it will attenuate drastically, which may result in serious safety accidents (Liu et al., 2020). Therefore, accurate prediction of the battery RUL is of great significance to guarantee the safe and reliable operation of electric vehicles (Murugan et al., 2022).

RUL refers to the quantity of charging–discharging cycles required for the maximum available capacity of the power battery attenuating to the specified failure threshold (Zhao et al., 2022). The RUL prediction is a process of forecasting and calculating the residual power battery’s life based on its historical data through certain mathematical approaches (Dong et al., 2020). The existing RUL prediction methods for lithium-ion batteries can mainly divide into model-driven and data-driven (Cadini et al., 2019; Song et al., 2022).

The model-driven method establishes a mathematically physical model by analyzing the battery performance degradation and failure mechanism for better predicting lithium-ion batteries RUL. The commonly-used lithium-ion battery models mainly include the electrochemical model, equivalent circuit model, and empirical degradation model. The electrochemical model primarily follows the internal chemical reaction mechanism of the lithium-ion battery to establish the corresponding algebraic or differential equations for forecasting the RUL. Its accuracy is high, but the model parameters are easily affected by temperature and other factors. Consequently, it is difficult to identify the parameters and the modeling procedure is really complex (Xiong et al., 2018). The equivalent circuit model adopts the traditional circuit elements like resistance, capacitance, and a constant voltage source to constitute a circuit network for describing the externality of the power battery (Guha and Patra, 2018). This model considers the battery degradation mechanism, but its establishment depends on impedance and other data difficult to obtain in practice. Furthermore, the empirical degradation model is mainly based on the exponential model of battery capacity and filtering algorithm to predict RUL (Zhang et al., 2018). Kalman filter (Xiong et al., 2012), sliding mode observer (Liu and Zhang., 2021), and particle filter (Morstyn et al., 2017; Pugalenthi et al., 2018) have all been commonly-applied model methods, which have achieved good research results. However, it has also been quite difficult to establish an accurate and universal mathematically physical model to characterize the attenuation process of lithium-ion battery capacity due to the severe onboard working conditions and the variability of the application environment.

The data-driven approach makes it possible to prognosticate the RUL of lithium-ion batteries by analyzing past data, mining intrinsic principles governing capacity decline, and utilizing mathematical algorithms to analyze, expand, and promote data. This method is simple and does not need to consider the complex mechanism of the power battery. It is suitable for the real vehicle operating environment. Common data-driven methods include the artificial neural network (ANN), (Ansari et al., 2021), support vector regression (SVR) (Xue et al., 2020), relevance vector regression (RVR) (Chen et al., 2021), and gaussian process regression (GPR) (Li et al., 2019). The transformer model, a deep learning neural network, has succeeded in the field of natural language processing and has steadily moved to the field of time-series prediction owing to its unique structure, long-distance modeling capability, and outstanding parallel computing capacity (Tian et al., 2022; Vallés-Pérez et al., 2022).

Considering the capacity regeneration phenomenon in the degradation process of lithium-ion batteries and the noise signal generated by load random interference in the measurement, data preprocessing technology is also widely used to improve the accuracy of RUL prediction, including empirical mode decomposition (EMD) (Zhang et al., 2017), variational modal decomposition (VMD) (Zhang et al., 2021), variational filtering (VF) (Jiao et al., 2020), and particle filter (PF) (Ahwiadi and Wang, 2019), etc. The method employed in this study, based on wavelet threshold denoising (WTD) (Zhang et al., 2015), cannot only effectively filter the noise but also maximize the noise and guarantee that the effective signal is not lost. The combination of a data-driven method and data preprocessing technology can further realize RUL’s accurate prediction (Huang et al., 2022).

Based on the above analyses, the key factors affecting the accuracy of RUL prediction are data preprocessing and its modeling methods. In this study, the discharging capacity is selected as the health indicator and a prediction method is proposed. The main contributions are summarized as follows:

The wavelet threshold denoising data preprocessing technology is utilized to eliminate the capacity data noise signals, which not only smooths the capacity data but also retains the original characteristics of the capacity data and avoids the influence of noise components.

With the long-distance modeling ability and the feature representation technique of the series data of the transformer model, the decoder part of the original model is replaced by the output’s full connection layer, and the RUL prediction framework of the improved transformer model is established to output the predicted values. The experimental results show that the wavelet denoising and transformer model can be effectively applied to the RUL prediction of the lithium-ion battery.

Two groups of battery capacity data from the Center for Advanced Life Cycle Engineering (CALCE) at the University of Maryland and the laboratory at the Anqing Normal University (AQNU) are applied to separately verify the RUL prediction method proposed in this study. The results exhibit that the performance of this method is superior to the existing prediction methods.

The rest is summarized below. Section 2 introduces the basic principles of wavelet threshold denoising and the transformer model. Section 3 specifies the proposed RUL prediction experiment scheme for lithium-ion batteries, including data preprocessing technique, experimental procedures, and evaluation criteria. Section 4 elaborates on the experimental results and compared experiment analyses. Section 5 describes the concluding observations.

2 Theoretical basis for remaining useful life prediction

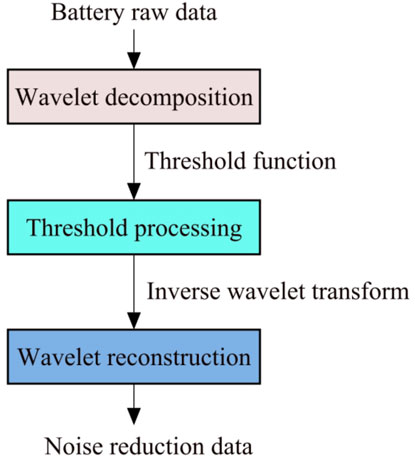
2.1 Wavelet threshold denoising

Wavelet analysis is based on the characteristic that the original signal is generally concentrated in the low-frequency region. First, a wavelet transform is performed on the high-frequency noisy signal $x\left(t\right)$ to obtain a group of wavelet decomposition coefficients $W_{j,k}$ and then a threshold value λ is set for the wavelet coefficients according to the characteristics of the transformed signal. This threshold is the dividing line to process high-frequency wavelet coefficients. For those with amplitudes lower than this threshold, they will be removed directly; for those with amplitudes greater than the threshold, they will be retained. After the wavelet decomposition coefficients are processed by the threshold, the wavelet estimation coefficient $\overline{W_{j,k}}$ is obtained to limit $\Vert \overline{W_{j,k}}-W_{j,k}\Vert$ to the minimum. Finally, the estimated wavelet coefficient $\overline{W_{j,k}}$ is used for wavelet reconstruction to acquire the estimation signal $\overline{W_{j,k}}$ as the denoised signal. The principle of this wavelet threshold denoising is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of wavelet threshold denoising.

In the process of wavelet threshold denoising, the commonly-used threshold functions mainly include the hard threshold function, soft threshold function, and semi-soft threshold function. Their formulas are as follows:

The expression of the hard threshold function is:

$\overline{W_{j,k}}=\{\begin{array}{l}{W}_{j,k},\left|W_{j,k}\right|\ge \lambda \\ 0,\left|W_{j,k}\right|\mathrm{<}\lambda \end{array}(1)$

The expression of the soft threshold function is:

$\overline{W_{j,k}}=\{\begin{array}{l}\mathrm{sgn}\left(W_{j,k}\right)(\left|W_{j,k}\right|-\lambda ),\left|W_{j,k}\right|\ge \lambda \\ 0,\left|W_{j,k}\right|\mathrm{<}\lambda \end{array}(2)$

The expression of the semi-soft threshold function is:

$\overline{W_{j,k}}=\{\begin{array}{l}\mathrm{sgn}\left(W_{j,k}\right)\left|W_{j,k}\right|-\lambda +\frac{2\lambda }{1+e^{2W_{j,k}/\lambda }},\left|W_{j,k}\right|\ge \lambda \\ 0,\left|W_{j,k}\right|\mathrm{<}\lambda \end{array}(3)$

where $W_{j,k}$ represents the wavelet estimation coefficient; $\overline{W_{j,k}}$ is the wavelet decomposition coefficient; $\mathrm{sgn}\left(\right)$ indicates the symbol function, and $\lambda$ refers to the threshold value.

Wavelet threshold estimation is the optimal threshold obtained under the limitation of minimum and maximum estimation for the joint distribution of multidimensional independent normal variables. The selection formula of this threshold value is:

${\lambda }_j=\sigma \sqrt{2\log \left(N\right)}(4)$

where ${\lambda }_j$ is the threshold under the scale $j$; $\sigma$ refers to the noise’s standard variance, and $N$ represents the signal length. The wavelet denoising method can effectively eliminate or weaken the noise signal in the lithium-ion battery capacity’s measured data and restore the raw data.

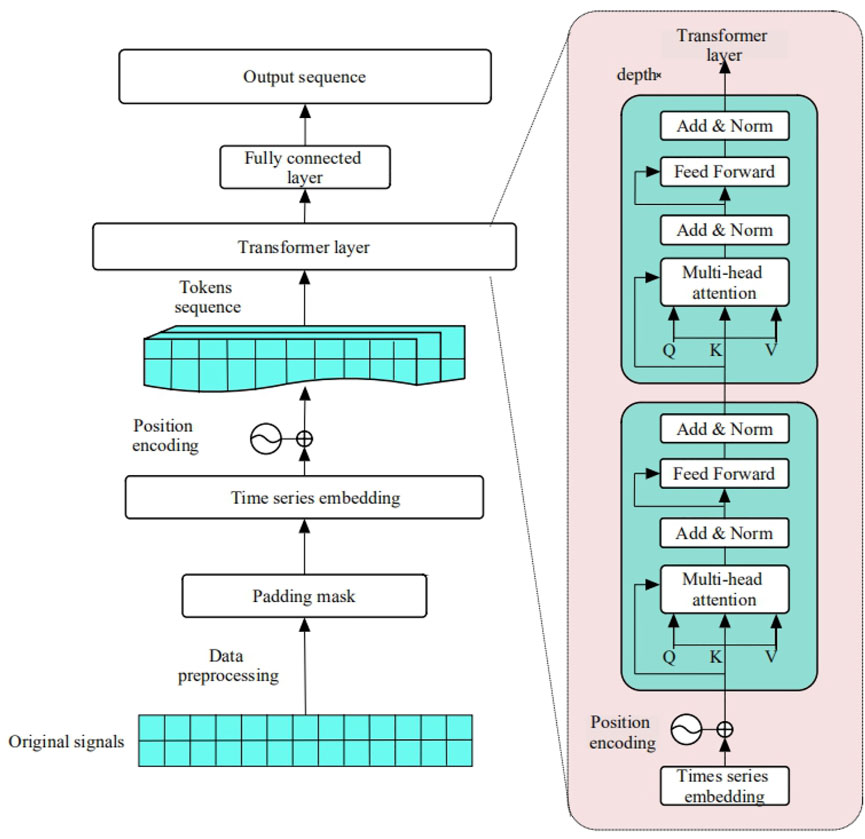
2.2 Time-series transformer

The transformer model relies on the attention mechanism to draw the global dependency between input and output. Like most neural series transformation models, it has an encoder-decoder structure. The encoder maps the input time-series $X=(X_1,X_2,\cdots \text{ , }{X}_n)$ represented by the capacity data to the continuous representation series $Z=(Z_1,Z_2,\cdots \text{ , }{Z}_n)$. Under the condition of fixed $Z$, the decoder generates output time-series $Y=(Y_1,Y_2,\cdots \text{ , }{Y}_n)$ from one element at a time. In each step of time-series prediction, the model is automatically regressed, and when generating the output series at the $n+1$ time, the output series generated at the last $n$ time will be used as an additional input. The transformer time-series model’s architecture is shown in Figure 2.

FIGURE 2

FIGURE 2. Transformer time-series model’s architecture.

The encoder part selects the original capacity data as the input, while the decoder part replaces the decoder with the full connection layer to predict the unknown capacity data value by the auto-regressive method (Jin et al., 2022). The decoder uses the attention mechanism to connect with the encoder, and “pays attention” to the most useful part of the input capacity data value before prediction, in which the padding mask part will be input for the mask to avoid gaining future values during training.

In the time-series prediction task, the transformer actually adopts the calculation method of scaled dot product attention, which is also an attention mechanism that links the different positions of a single series to calculate the representation of the series. Its general calculation process is shown in Figure 3.

FIGURE 3

FIGURE 3. General calculation process of attention mechanism.

According to the three variables of query, key, and value gained from the linear mapping of the input series, the attention function is employed to calculate the Q matrix and K matrix for achieving the attention weight matrix. Based on this, the similarity between Q and K is also calculated to obtain the output matrix A. The calculation process is as follows:

$A=\text{softmax}(Q{K}^T/\sqrt{d_h}),A\in R^{d\times 3d_h}(5)$

In the time-series, query, key, value, and output are all vectors. Furthermore, calculate the Value according to A and obtain the weighted sum. The calculation process is as follows:

$SA\left(z\right)=AV(6)$

In order to improve the diversity of features, a multi-head attention layer is employed to calculate multiple self-attention heads in parallel. Eventually, the final results are obtained by splicing the outputs of all attention heads (Zhang Q. et al., 2022).

Positional encoding is adopted to prevent the loss of position information in the series of input batch capacity data. Its principle is to add sine and cosine data of different frequencies to the input series as position codes so that the model can capture the relative position relationship of input variables. The calculation process is expressed in Eqs 7 and 8.

$P{E}_{(pos,2i)}=\sin \left(pos/{10000}^{2i/d}\right)(7)$

$P{E}_{(pos,2i+1)}=\cos \left(pos/{10000}^{2i/d}\right)(8)$

where pos is the position of each capacity value in the whole series; $i\in [0,\cdots \text{ , }d/2]$ is used to calculate the index of the channel dimension. For the same $i$, the coding of the $2i+1$ and the $2i+1$ positions on the channel is the sine and cosine values with the same angular velocity to ensure that the position-coding can be added to the input embedding.

3 Remaining useful life prediction's experiment scheme

3.1 Experimental data

Two kinds of lithium-ion battery datasets with different electrode materials and discharge environments are used to verify the performance of the proposed algorithm.

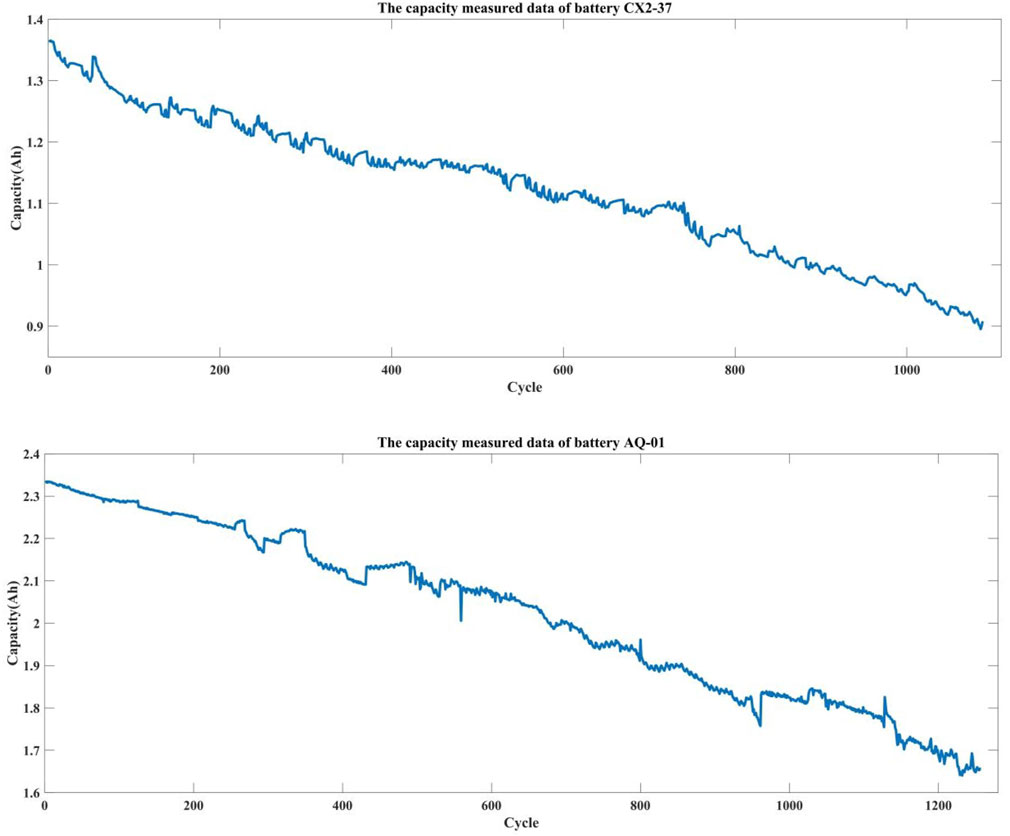
The first group of the battery degradation data is obtained from the University of Maryland’s CALCE company. The battery aging test was realized by using the ArbinBT2000 battery test system. In the test, the LiCoO₂ battery named CX2-37 accepted the standard constant current/voltage protocol, charged at 0.5C constant current (C is the measurement of the charging–discharging current to the nominal capacity) until the terminal voltage reached 4.2 V, then charged at the constant voltage of 4.2 V until the charging current dropped below 0.05 A. Discharging was operated at a 1C constant current until the battery terminal voltage of CX2-37 dropped to 2.7 V.

The second set of lithium-ion battery aging data was measured in the laboratory of AQNU university based on the high-performance battery test system (Zhang et al., 2021). Experimental equipment is shown in Figure 4. For simplicity, this lithium-ion battery capacity data is named AQ-01 in this study. Table 1 presents the summary of its specifications.

FIGURE 4

FIGURE 4. Experimental equipment.

TABLE 1

TABLE 1. Specifications of AQ-01 battery.

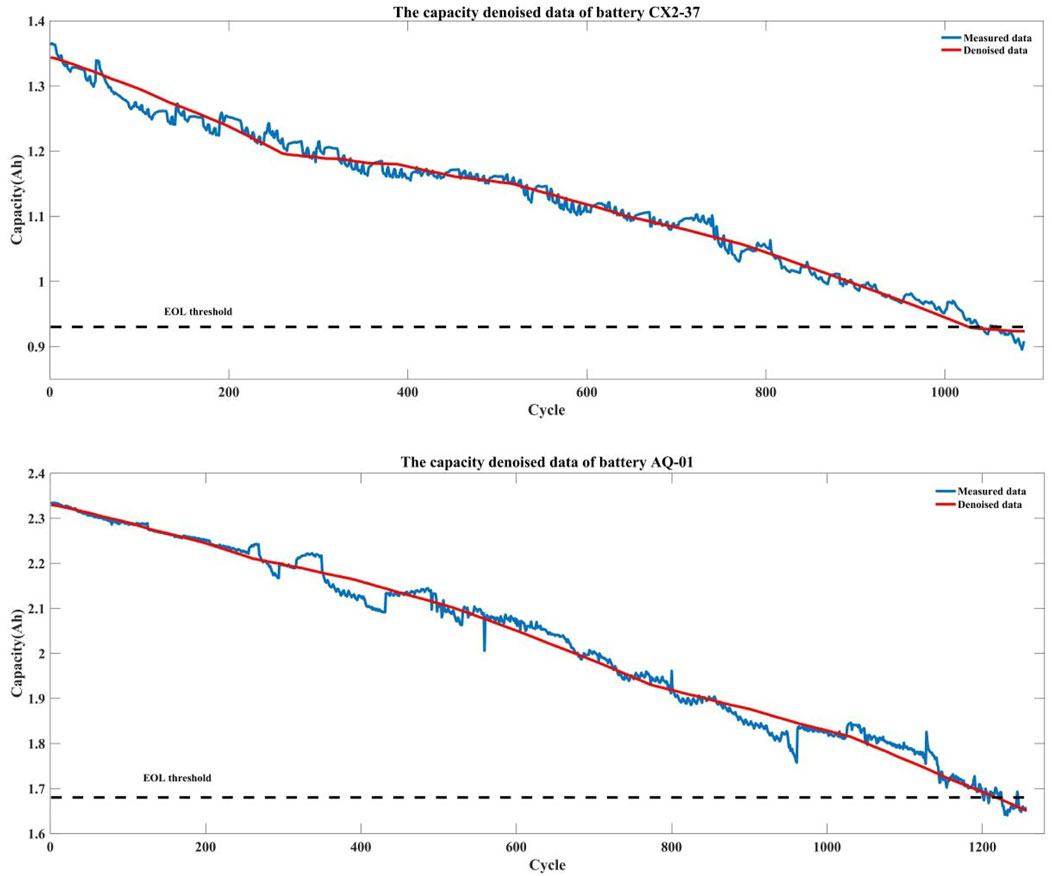
The validity of the proposed prediction method is verified by using two groups of battery degradation data of CX2-37 and AQ-01. According to the international standard, the lithium-ion battery performance test stipulates that it shall be kept in a normal working state at a normal temperature (25 ± 2) °C. When the actual capacity of the battery drops below 70–80% of the rated capacity, the lithium-ion battery is considered to be invalid. In order to ensure the safety and reliability of the system operation, the EOL threshold of all the used batteries is both set to about 70% of the rated capacity when the experiments will be terminated. Therefore, the rated capacity of battery CX2-37 is 1.33 Ah, and the EOL threshold configuration is 0.93 Ah. The rated capacity of AQ-01 battery is 2.4 Ah, and the EOL threshold is set to 1.68 Ah. The measured capacity data of CX2-37 and AQ-01 batteries are listed in Figure 5.

FIGURE 5

FIGURE 5. Measured capacity data of CX2-37 and AQ-01.

3.2 Experimental procedure

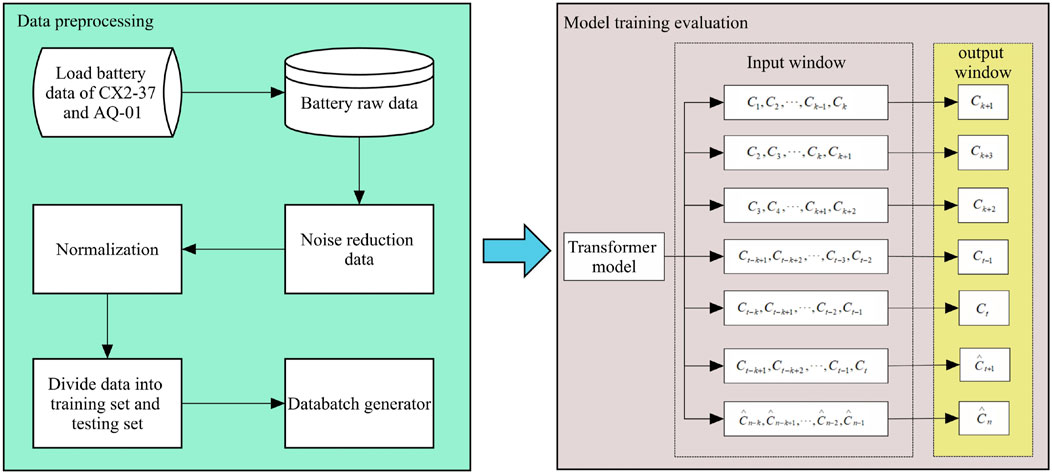
In order to better reflect the generalization of the proposed method. Experimental verification of transformer method is made with the selected two groups of the lithium-ion battery capacity data from CALCE and AQNU laboratory. The framework of the RUL prediction method proposed in this study is shown in Figure 6.

FIGURE 6

FIGURE 6. RUL prediction method’s framework.

More specifically, there are five steps to realize the goal prediction.

Step 1: Select the discharging capacity as the health indicator reflecting the degradation trend of RUL, remove the noise signal of the raw data by wavelet threshold denoising method, and obtain the capacity series with a relatively stable degradation trend.

Step 2: Standardize the capacity data after denoising and smoothing.

Step 3: Divide the first 50% of the battery capacity data equally as the training set and the last 50% as the testing set. Build the transformer model in Pytorch and train the capacity series data to obtain the RUL prediction model.

Step 4: Use the transformer model to establish the mapping relationship between the early and late stages of the capacity, iteratively predicts the unknown discharging capacity of each charging–discharging cycle, then calculate the RUL of the lithium-ion battery.

Step 5: Apply different evaluation indexes to evaluate the prediction results.

3.3 Model evaluation indexes

The lithium-ion battery RUL is defined as the number of remaining useful cycles from the beginning of prediction to the end of battery life. When the actual capacity of the battery degrades to the failure threshold, the battery life is considered to be over. The RUL calculation formula of the battery is as follows:

$T_{rul}=T_{eol}-T_{cur}(9)$

The calculation formula of the battery’s RUL prediction value can be expressed in Eq. 10.

${\stackrel{⌢}{T}}_{rul}={\stackrel{⌢}{T}}_{eol}-{\stackrel{⌢}{T}}_{cur}(10)$

Absolute error (AE), mean absolute error (MAE), and root mean square error (RMSE) are adopted as the evaluation criteria of the prediction model. Their calculation formulas are as follows:

$AE=\left|T_{rul}-{\stackrel{⌢}{T}}_{rul}\right|(11)$

$MAE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|x\left(i\right)-\stackrel{⌢}{x}\left(i\right)\right|}(12)$

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left[x\left(i\right)-\stackrel{⌢}{x}\left(i\right)\right]}^2}}(13)$

where $T_{rul}$ is the number of remaining useful cycles at the end of the actual battery life; $T_{cur}$ represents the cycle’s starting position, while $T_{eol}$ is the number of cycles at the end of the battery life in the actual state; ${\stackrel{⌢}{T}}_{rul}$ indicates the number of remaining useful cycles at the end of the battery life in the predicted case; ${\stackrel{⌢}{T}}_{eol}$ refers to the number of cycles at the end of the battery life in the predicted case; $x\left(i\right)$ is the real value of capacity, and $\stackrel{⌢}{x}\left(i\right)$ stands for the predicted capacity.

It should be noticed that RMSE is the most comprehensive evaluation index, which can measure the fitness between the prediction curve and the actual degradation trend. The closer RMSE is to 0, the better the prediction effect.

4 Experimental results and discussions

4.1 Denoising results

Due to an irreversible chemical reaction, the discharging capacity of the lithium-ion battery will show a detailed downward trend owing to the repeated charging and discharging. The capacity data measurement process is affected by electromagnetic interference, instrument error, and changes in the external environment. The nonlinear capacity data is mixed with noise signals, and the capacity regeneration phenomenon makes the degradation track rise rapidly, briefly, and irregularly in an uncertain period, which adds difficulty to the training process of the model.

In order to remove the irregular fluctuations in the capacity curve and retain the original characteristics of the data, it helps the model achieve better learning results in the training stage. The raw data of battery capacity of CX2-37 and AQ-01 are smoothed by the wavelet threshold denoising method, and the large and small noise signals are eliminated. The effect of processed battery capacity data is shown in Figure 7.

FIGURE 7

FIGURE 7. Capacity data of CX2-37 and AQ-01 batteries processed by wavelet threshold denoising.

4.2 Prediction results

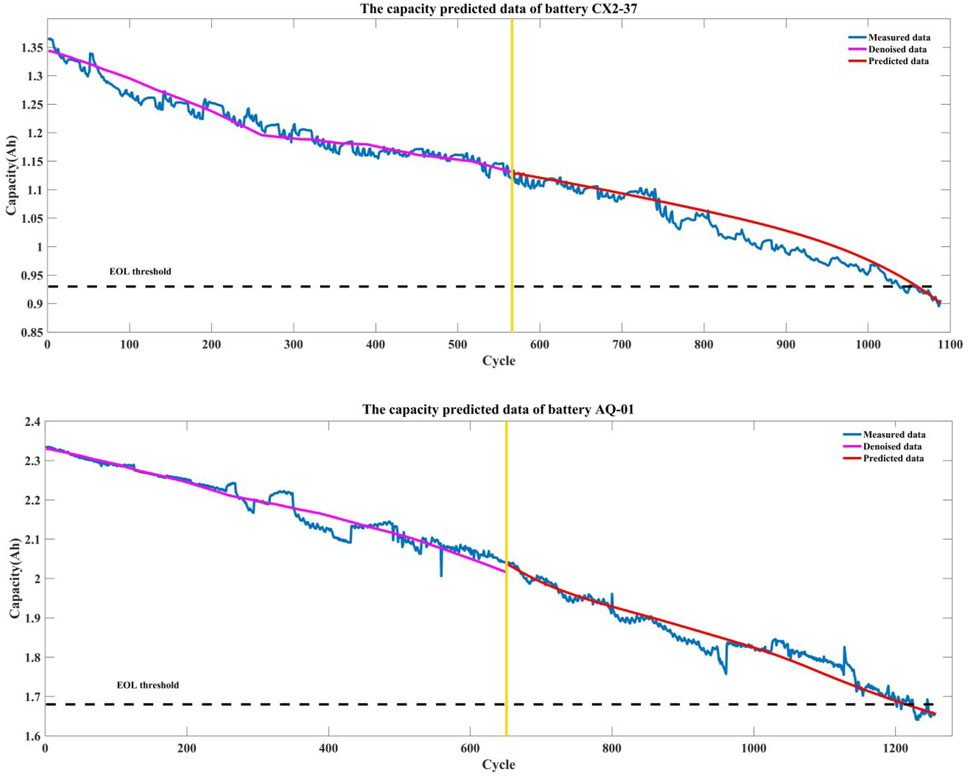
AE, MAE, and RMSE methods are individually adopted to evaluate the accuracy of the capacity data predicted by the RUL of lithium-ion batteries. Experiments are carried out through two groups of battery degradation data of CX2-37 and AQ-01. Both groups of capacity data set 50% of the series length as the prediction starting point, and the established transformer neural network model is employed to conduct the capacity prediction experiment. The prediction results are shown in Figure 8 and Table 2 gives the statistical errors of the above experimental results.

FIGURE 8

FIGURE 8. Transformer model’s capacity prediction results.

TABLE 2

TABLE 2. Statistical errors of the transformer algorithm.

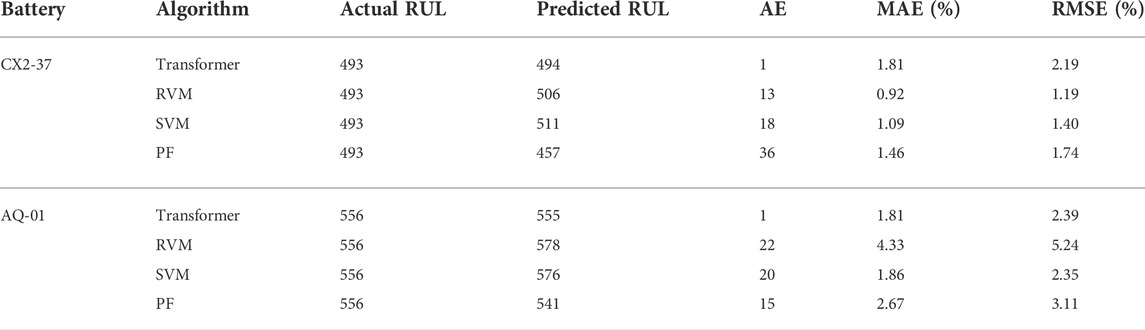
The prediction results of both CX2-37 and AQ-01 batteries both illustrate that the degradation trend can be accurately captured according to the mapping relationship between cycle and actual capacity, but the prediction results gradually deviate from the actual degradation curve with the increase of cycle times. From the capacity degradation trend line shown in Figure 8 and the data analysis in Table 2, the RUL prediction accuracy of CX2-37 battery based on the transformer model is 494, and 1 cycle later than the true RUL, which MAE is 1.81% and RMSE is 2.19%. The RUL prediction accuracy of AQ-01 battery is 556, and 1 cycle earlier than the true RUL, in which MAE is 1.81% and RMSE is 2.39%. It demonstrates that this method has an accurate RUL prediction effect. It also shows the degradation trend prediction curve of AQ-01 battery is closer to the original curve than that of CX2-37 battery. A possible reason is transformer model mines the correlation from the global relationship and the accuracy highly depends on data, which needs a lot of training to build a better RUL prediction model. It reflects that AQ-01 battery has the best prediction results due to its long sequence length of data and better training effect.

4.3 Compared experiment

To further verify the reliability of the wavelet threshold denoising and transformer model RUL prediction methods proposed in this study, the relevance vector machine (RVM), support vector regression (SVR), and particle filter (PF) methods are separately adopted to compare and analyze with the transformer model prediction method, for proving the transformer model’s accuracy and superiority in predicting the RUL. The capacity prediction results of CX2-37 and AQ-01 batteries based on the transformer, RVM, SVR, and PF methods are shown in Figure 9, while Table 3 gives the statistical errors of the above experimental results.

FIGURE 9

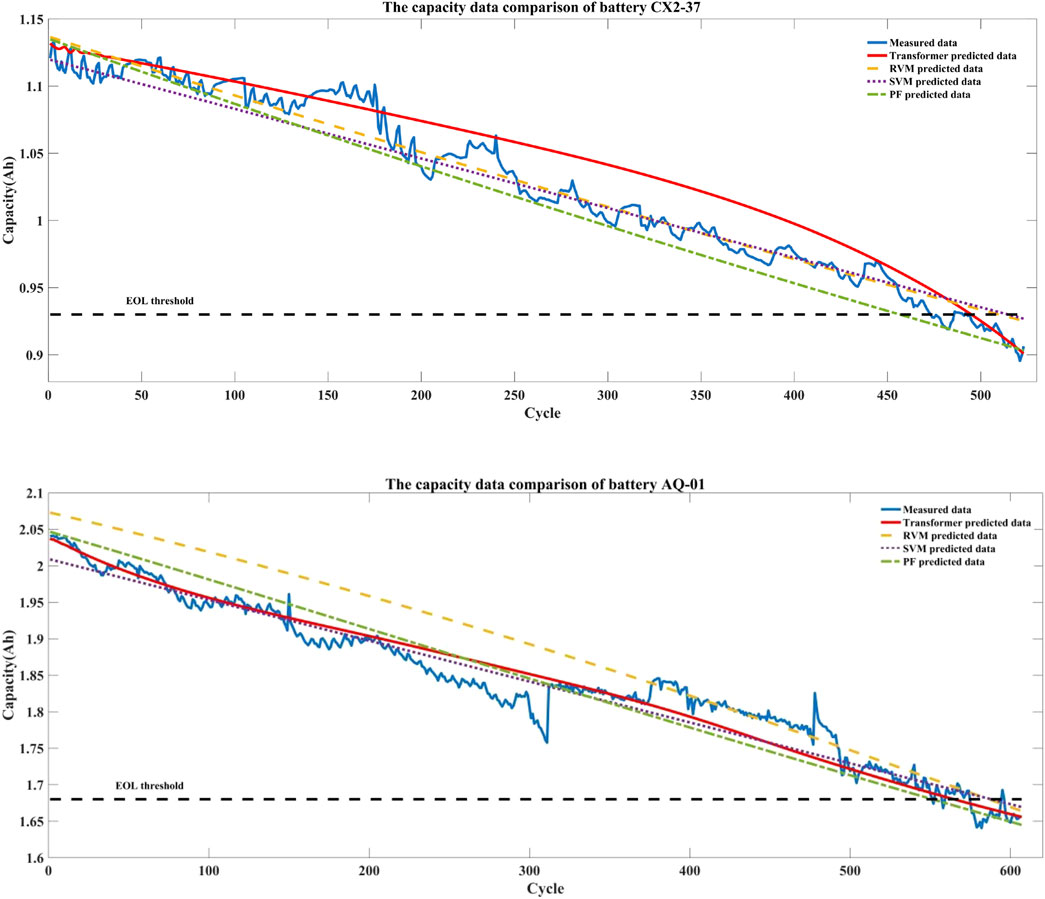
FIGURE 9. Compared experiment results between different prediction methods for CX2-37 and AQ-01 batteries.

TABLE 3

TABLE 3. Statistical errors of the comparison experiment.

According to the capacity degradation trend line in Figure 9 and the errors in Table 3, this prediction method is proven to offer a better prediction accuracy. The prediction errors of CX2-37 battery based on the transformer, RVM, SVR, and PF methods are 1, 13, 18, and 36, respectively. The prediction errors of AQ-01 battery based on the transformer, RVM, SVR, and PF are 1, 22, 20, and 15, respectively. Among them, the prediction results of CX2-37 battery seriously deviate from the cycle range of the real threshold based on the PF method, but the prediction effect on AQ-01 battery is significantly better than those of the compared methods, as the effects of both MAE and RMSE are less than 2.4%.

By comparing with traditional RVM, SVR, and PF algorithms, it is found that the transformer neural network achieves the best prediction effect owing to the superior long-series data processing ability. According to Figure 9, it can also be seen that the degradation trend prediction curve of AQ-01 battery based on the PF method is close to the original curve, but the CX2-37 battery comparison prediction curve obviously deviates from the original aging curve under the same condition. This is the reason for the low accuracy of feature recognition. The transformer model has the advantage of constructing a global information interaction mechanism, which helps to establish a more sufficient feature display. At the same time, the modal data can be fused efficiently. Therefore, a better fitting trend is reflected in the two groups of experimental data and reflects that the transformer prediction method has a better generalization ability. However, the global attention mechanism also brings a large amount of computation, especially in intensive prediction tasks with facing long series of inputs. In addition, the training process of the transformer model is unstable and sensitive to parameters. Therefore, the wavelet threshold denoising method is used to smooth the original data, so as to better predict the future capacity of lithium-ion batteries and improve the prediction accuracy.

5 Conclusion

In this study, an RUL prediction method for lithium-ion batteries based on wavelet threshold denoising and transformer model has been proposed. First, the discharging capacity has been selected as the health indicator, and the wavelet threshold denoising method has been adopted to eliminate the noise signal caused by the actual measurement and instrument errors in the raw data. Second, the pre-processed data have been equally divided into the training set and testing set. Based on the training set, the transformer neural network has been used to establish the RUL prediction model of the lithium-ion battery. Moreover, two groups of experimental data from CALCE and AQNU laboratories have been chosen to verify the reliability of the proposed method. The conclusions are summarized as follows:

The onboard battery is affected by various uncertain factors during the working process, which causes the gathered data to contain noises and fluctuations. Directly using the raw data to predict the signal affects the prediction accuracy of this model. Consequently, the necessary data preprocessing method has been utilized to improve the prediction accuracy of this prediction model in this study.

Owing to the long-distance modeling ability and the feature representation ability of the series data in the transformer model, an RUL prediction framework based on the transformer neural network has been established, while a new RUL prediction method for lithium-ion batteries has been proposed and good prediction results have been achieved.

Two groups of battery capacity data from CALCE and AQNU laboratories have been employed to verify the RUL prediction method. The experimental results have shown that the prediction effect of the proposed method is superior to those of some existing calculation ones, among which the effects of MAE and RMSE are kept within 1.81 and 2.39%, respectively.

To conclude, the RUL prediction method for lithium-ion batteries consists of the data preprocessing by wavelet threshold denoising and the transformer model with a high prediction accuracy, reducing the prediction error and providing a new idea for the existing RUL prediction research of lithium-ion batteries. This method could also be applied to the prediction of other similar issues.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

WH: methodology, software, validation, investigation, writing—original draft preparation, visualization. SZ: methodology, data curation, validation, writing—reviewing, and editing.

Funding

This study was supported by The Natural Science Research Key Project of Education Department of Anhui Province Grant No. KJ2020A0509, Anhui Provincial Natural Science Foundation Grant No. 2008085MF197, Graduate Academic Innovation Project of Anqing Normal University Grant No. 2021yjsXSCX009.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahwiadi, M., and Wang, W. (2019). An enhanced mutated particle filter technique for system state estimation and battery life prediction. IEEE Trans. Instrum. Meas. 68 (3), 923–935. doi:10.1109/TIM.2018.2853900

CrossRef Full Text | Google Scholar

Ansari, S., Ayob, A., Hossain, L., Hussain, A., and Saad, M. H. M. (2021). Multi-channel profile based artificial neural network approach for remaining useful life prediction of electric vehicle lithium-ion batteries. Energies 14 (22), 7521. doi:10.3390/EN14227521

CrossRef Full Text | Google Scholar

Ansari, S., Ayob, A., Hossain, L., Hussain, A., and Saad, M. H. M. (2022). Multi-channel profile based artificial neural network approach for remaining useful life prediction of electric vehicle lithium-ion batteries. Energies 14 (22), 7521. doi:10.3390/EN14227521

CrossRef Full Text | Google Scholar

Cadini, F., Sbarufatti, C., Cancelliere, F., and Giglio, M. (2019). State-of-life prognosis and diagnosis of lithium-ion batteries by data-driven particle filters. Appl. Energy 235, 661–672. doi:10.1016/j.apenergy.2018.10.095

CrossRef Full Text | Google Scholar

Chen, Z., Shi, N., Ji, Y., Niu, M., and Wang, Y. (2021). Lithium-ion batteries remaining useful life prediction based on BLS-RVM. Energy 234, 121269. doi:10.1016/J.ENERGY.2021.121269

CrossRef Full Text | Google Scholar

Dong, G., Yang, F., Wei, Z., Wei, J., and Tsui, K.-L. (2020). Data-driven battery health prognosis using adaptive brownian motion model. IEEE Trans. Ind. Inf. 16 (7), 4736–4746. doi:10.1109/TII.2019.2948018

CrossRef Full Text | Google Scholar

Guha, A., and Patra, A. (2018). Online estimation of the electrochemical impedance spectrum and remaining useful life of lithium-ion batteries. IEEE Trans. Instrum. Meas. 67 (8), 1836–1849. doi:10.1109/TIM.2018.2809138

CrossRef Full Text | Google Scholar

Guha, A., and Patra, A. (2018). State of health estimation of lithium-ion batteries using capacity fade and internal resistance growth models. IEEE Trans. Transp. Electrific. 4 (1), 135–146. doi:10.1109/TTE.2017.2776558

CrossRef Full Text | Google Scholar

Huang, K., Ding, H., and Guo, Y. (2022). Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory networkr. Trans. China Electrotech. Soc. 37 (7), 57–70. doi:10.19595/j.cnki.1000-6753.tces.210860

CrossRef Full Text | Google Scholar

Jiao, R., Peng, K., and Dong, J. (2020). Remaining useful life prediction of lithium-ion batteries based on conditional variational autoencoders-particle filter. IEEE Trans. Instrum. Meas. 99, 8831–8843. doi:10.1109/tim.2020.2996004

CrossRef Full Text | Google Scholar

Jin, Y., Hou, L., and Chen, Y. (2022). A time series transformer based method for the rotating machinery fault diagnosis. Neurocomputing 494, 379–395. doi:10.1016/J.NEUCOM.2022.04.111

CrossRef Full Text | Google Scholar

Li, X., Wang, Z., and Yan, J. (2019). Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 421, 56–67. doi:10.1016/j.jpowsour.2019.03.008

CrossRef Full Text | Google Scholar

Liu, H., Chen, F., Tong, Y., Wang, Z., Yu, X., Huang, R., et al. (2020). Impacts of driving conditions on EV battery pack life cycle. World Electr. Veh. J. 11, 17. doi:10.3390/wevj11010017

CrossRef Full Text | Google Scholar

Liu, R., and Zhang, C. (2021). An active balancing method based on SOC and capacitance for lithium-ion batteries in electric vehicles. Front. Energy Res. 9, 773838. doi:10.3389/fenrg.2021.773838

CrossRef Full Text | Google Scholar

Morstyn, T., Savkin, A. V., Hredzak, B., and Agelidis, V. G. (2017). Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a DC microgrid. IEEE Trans. Smart Grid 9 (5), 4735–4743. doi:10.1109/TSG.2017.2668767

CrossRef Full Text | Google Scholar

Murugan, M., Saravanan, A., Elumalai, P. V., Murali, G., Dhineshbabu, N., Kumar, P., et al. (2022). Thermal management system of lithium-ion battery packs for electric vehicles: An insight based on bibliometric study. J. Energy Storage 52, 104723. doi:10.1016/j.est.2022.104723

CrossRef Full Text | Google Scholar

Pugalenthi, K., and Raghavan, N. (2018). A holistic comparison of the different resampling algorithms for particle filter based prognosis using lithium-ion batteries as a case study. Microelectron. Reliab. 91, 160–169. doi:10.1016/j.microrel.2018.08.007

CrossRef Full Text | Google Scholar

Song, T., Liu, C., Wu, R., Jin, Y., and Jiang, D. (2022). A hierarchical scheme for remaining useful life prediction with long short-term memory networks. Neurocomputing 487, 22–33. doi:10.1016/j.neucom.2022.02.032

CrossRef Full Text | Google Scholar

Tian, Y., Wang, Y., Wang, J., Wang, X., and Wang, F. (2022). Key problems and progress of vision transformers: The state of the art and prospects. Acta Autom. Sin. 48 (4), 957–979. doi:10.16383/j.aas.c220027

CrossRef Full Text | Google Scholar

Vallés-Pérez, I., Soria-Olivas, E., Martínez-Sober, M., Serrano-Lopez, A. J., Gomez-Sanchis, J., and Mateo, F. (2022). Approaching sales forecasting using recurrent neural networks and transformers. Expert Syst. Appl. 201, 116993. doi:10.1016/J.ESWA.2022.116993

CrossRef Full Text | Google Scholar

Wang, S., Jin, S., Deng, D., and Fernandez, C. (2021). A critical review of online battery remaining useful lifetime prediction methods. Front. Mech. Eng. 7 (1), 1–19. doi:10.3389/fmech.2021.719718

CrossRef Full Text | Google Scholar

Xiong, R., He, H., Sun, F., and Zhao, K. (2012). Evaluation on state of charge estimation of batteries with adaptive extended kalman filter by experiment approach. IEEE Trans. Veh. Technol. 62 (1), 108–117. doi:10.1109/TVT.2012.2222684

CrossRef Full Text | Google Scholar

Xiong, R., Li, L., Li, Z., Yu, Q., and Mu, H. (2018). An electrochemical model based degradation state identification method of lithium-ion battery for all-climate electric vehicles application. Appl. Energy 219, 264–275. doi:10.1016/j.apenergy.2018.03.053

CrossRef Full Text | Google Scholar

Xue, Z., Zhang, Y., Cheng, C., and Ma, G. (2020). Remaining useful life prediction of lithium-ion batteries with adaptive unscented kalman filter and optimized support vector regression. Neurocomputing 376, 95–102. doi:10.1016/j.neucom.2019.09.074

CrossRef Full Text | Google Scholar

Yuan, X., Liu, X., and Zuo, J. (2015). The development of new energy vehicles for a sustainable future: A review. Renew. Sustain. Energy Rev. 42, 298–305. doi:10.1016/j.rser.2014.10.016

CrossRef Full Text | Google Scholar

Zhang, C., He, Y., Yuan, L., and Xiang, S. (2017). Capacity prognostics of lithium-ion batteries using EMD denoising and multiple kernel RVM. IEEE Access 5, 12061–12070. doi:10.1109/access.2017.2716353

CrossRef Full Text | Google Scholar

Zhang, C., He, Y., Yuan, L., Xiang, S., and Wang, J. (2015). Prognostics of lithium-ion batteries based on wavelet denoising and DE-RVM. Comput. Intell. Neurosci. 14, 1–8. doi:10.1155/2015/918305

CrossRef Full Text | Google Scholar

Zhang, C., Zhao, S., and He, Y. (2021). An integrated method of the future capacity and RUL prediction for lithium-ion battery pack. IEEE Trans. Veh. Technol. 71 (3), 2601–2613. doi:10.1109/TVT.2021.3138959

CrossRef Full Text | Google Scholar

Zhang, D., Tan, C., Ou, T., Zhang, S., Li, L., and Ji, X. (2022a). Constructing advanced electrode materials for low-temperature lithium-ion batteries: A review. Energy Rep. 8, 4525–4534. doi:10.1016/J.EGYR.2022.03.130

CrossRef Full Text | Google Scholar

Zhang, L., Mu, Z., and Sun, C. (2018). Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter. IEEE Access 6, 17729–17740. doi:10.1109/ACCESS.2018.2816684

CrossRef Full Text | Google Scholar

Zhang, Q., Qin, C., Zhang, Y., Bao, F., and Liu, P. (2022b). Transformer-based attention network for stock movement prediction. Expert Syst. Appl. 202, 117239. doi:10.1016/J.ESWA.2022.117239

CrossRef Full Text | Google Scholar

Zhao, S., Zhang, C., and Wang, Y. (2022). Lithium-ion battery capacity and remaining useful life prediction using board learning system and long short-term memory neural network. J. Energy Storage 52, 104901. doi:10.1016/j.est.2022.104901

CrossRef Full Text | Google Scholar