
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 08 August 2022
Sec. Smart Grids
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.968873
This article is part of the Research Topic Key Technologies, Markets, and Policies towards A Smart Renewables-Dominated Power System View all 13 articles
The proportion of renewable energy is increasing rapidly to develop low-carbon power systems and the intermittence nature of renewable energy harms the security operation of power systems. The participation of interruptible loads is an effective means to handle the intermittence of renewable energy. However, the capacity value of interruptible loads has not been fully recognized, which results in limited involvement of interruptible loads in power system operations. Hence, it is urgent to analyze the capacity value of interruptible loads. In this paper, a capacity value calculation method of interruptible loads is proposed. A joint optimal operation model of interruptible loads and multiple power sources including thermal power units, hydropower units, and wind turbines is established to realize the application paradigm of power system operations with interruptible loads. Case analysis based on the operation data of the power system in a particular area verifies that the proposed method can effectively recognize the capacity value of interruptible loads and reduce the installed capacity of thermal power units. It thereby lays the theoretical foundation for analyzing the role of interruptible loads in the low-carbon transition of the electric energy industry.
The electric energy industry accelerates the transformation to low-carbon nowadays. In the future, power systems will use a high proportion of renewable energy as the main body of the power system. However, due to the uncertainty, volatility, and intermittence of renewable energy, the power system operations in the future will face severe challenges (Mashhour et al., 2010; Sarkhani. et al., 2011). In power systems, if conventional generators are the only type of means used to handle the intermittence of renewable energy, these generators are started and stopped frequently or their outputs are changed dramatically. This increases the difficulty of dispatching and reduces the economy of power systems (Sampang et al., 2018). Demand response has developed rapidly in recent years. It has gradually become a vital force that can support power systems to peak load shifting, and absorb renewable energy (Bessler and Jung, 2016), and its status is becoming more and more critical (Sivaneasan et al., 2016). Hence, measures to maintain the security operation of power systems with high proportion of intermittent renewable energy should not only be implemented on the power resource side but also the demand side.
Demand response is generally divided into incentive-based demand response and price-based demand response according to the response mode of the demand side (Devatgaran et al., 2013). Interruptible loads are an incentive-based demand response (Li et al., 2013). According to the contracts signed by users in advance, the loads will be cut off according to the agreement when the peak load is very high, or the security operation of power systems is threatened. Users will be given specific compensations after the loads are cut off (Sharma et al., 2018; Wang et al., 2020). The interruptible loads are developing rapidly and have enormous potential. In recent years, plenty of regions have successively introduced relevant policies on interruptible loads (Argiento et al., 2012). With the advancement of the electricity market, it has become inevitable for interruptible loads to participate in the electricity market in the future (Sampang et al., 2018). At this stage, the interruptible loads pricing mechanism is still dominated by the government, which cannot fully reflect the value of interruptible loads to power systems. Therefore, the value of the interruptible loads deserves careful analysis to develop effective price mechanisms in the future electricity market. Interruptible loads mainly play the role of peak load shifting in power systems (Mashhour et al., 2010). The effect of interruptible loads in power system operations is similar to energy storage systems. Therefore, interruptible loads have a particular capacity value. In the crucial period when interruptible loads need to be developed urgently, research on capacity value analysis has essential theoretical and practical value.
Some papers have had some exploratory analysis on the value of interruptible loads. Wang et al. (2004) analyzed the value of interruptible loads under different conditions such as advance time of interrupting notification and the duration of interrupting. Li (2017) analyzed the value brought by demand-side users of different scales as the interruptible loads; however, few types of users were analyzed, which ultimately failed to reflect the capacity value of interruptible loads. Shao et al. (2012) studied the value of interruptible loads to different bodies such as users, electricity companies, and society; however, the analysis process lacked quantitative calculations and could not expressly reflect capacity value. Li et al. (2013) analyzed the benefit of interruptible loads under different subsidy schemes from load aggregators; however, the load aggregators’ scale was small. Zhang et al. (2016) uses the stochastic operation simulation method to analyze the value of interruptible loads participating in the electricity market; however, the analyzed capacity value is not comprehensive enough.
Based on the above analysis, the research gap in the existing literature is that there is no unified method and standard for analyzing the capacity value of interruptible loads, which results in limited involvement of interruptible loads in power system operations and hinders the improvement of power system security while incorporating a high proportion of renewable energy. Hence, this paper proposes a capacity value calculation method of interruptible loads and establishes a mathematical model for the optimal joint operation of interruptible loads, thermal power units, hydropower units, and wind turbines. The proposed method can effectively recognize the capacity value of interruptible loads and reduce the installed capacity of thermal power units. The content is arranged as follows. Section 2 introduces the methodology, framework, and vital technologies of the capacity value analysis of interruptible loads; Section 3 presents the operation simulation model of interruptible loads and the calculation process of the capacity value; Section 4 shows the case analysis on a power system in a particular region; Section 5 is the conclusion of this paper.
The coordinated operation of interruptible loads and power systems can enhance the security and sustainability of power systems. In this paper, the capacity value of the interruptible loads is a value brought to the security operation of power systems. However, the capacity value is difficult to be reflected in power systems directly. Theoretically, the installed capacity of thermal power units can reflect the capacity value of interruptible loads on the premise of ensuring the balance of power consumption.
To address the above issue, we proposed a calculation method of the capacity value of interruptible loads and established a mathematical model of the coordinated operation of thermal power units, hydropower units, wind turbines, and interruptible loads in a regional power system that ensures the balance of power consumption with external electricity. The regional power system is considered infinite, ignoring the internal operation constraints and the grid structure. The frame of the value analysis of interruptible loads capacity is shown in Figure 1.
Interruptible load controlling is a load regulation method that considers both the system security and the users’ wishes. The users sign agreements with the relevant departments of power systems in advance. During the peak period of power consumption, the interruptible loads can be activated to maintain the power balance of the systems. When the interruptible load needs to be activated to maintain the security operation of power systems, the dispatching department will interrupt them according to the former agreements (Sivaneasan et al., 2016). The realization process of interruptible loads is shown in Figure 2.
Early interruptible loads only existed among large industrial users for various reasons: single management means, low management efficiency, and insufficient power grid intelligence. Due to the lack of experience managing interruptible loads and imperfect value analysis, large industrial users did not attend early interruptible loads practices for a large amount. With the continuous improvement of the intelligence level of power systems in recent years, the types of users that can participate in the implementation of interruptible loads have been expanded from single large industrial users to medium and small industrial users and even commercial users. Medium and small users will participate in interruptible loads mainly through load aggregators.
In the foreseeable future, the proportion of renewable energy units such as wind turbines in power systems will increase, and the power balance of power systems will face new challenges. Interruptible loads will play a more important role in peak shaving and maintaining the balance of power consumption with intermittent renewable energy in the future, as shown in Figure 3.
The aggregation modeling method of thermal power units mainly superimposes the output constraints and ramping constraints, installs the capacity of all thermal power units in the regional power system, and obtains the new output constraints, ramping constraints, and installed capacity of the aggregation thermal power unit
Where
The aggregation modeling method of the hydropower unit is similar to the aggregation modeling method of the above-mentioned thermal power unit. Superimpose the upper and lower limits of all hydropower units in the regional power system within a dispatch period to obtain the upper and lower limits of the aggregation hydropower unit; superimpose the installed capacity of all hydropower units to get the installed capacity of the aggregation hydropower unit:
Where
The wind power output curve is generated using Conditional Generative Adversarial Networks (CGAN) (Kim, 2021). The generator maps the noise vector z in the low-dimensional space to the high-dimensional space to generate new samples close to the actual data (Xu et al., 2020). The discriminator’s function is judging whether the input data is actual data. Usually, the generator and the discriminator are two convolutional neural networks with symmetrical structures. The robust feature extraction capability of the convolutional network can improve the quality of the generated data (Mohseni et al., 2020). Through the adversarial training of the two networks, the generator finally learns the distribution characteristics of the original data and can generate data that conforms to the real laws. The wind turbine output curve prediction process is shown in Figure 4.
First, the noise vector z is sampled from a Gaussian distribution with a mean of 0 and a standard deviation of 1. It is horizontally spliced with the wind power output historical data (conditional label c) and input to the generator to generate the generated samples. The generated and actual samples are combined with the corresponding condition labels and then input to the discriminator. In the game training process, the generator tries to generate new samples close to the actual data under condition c. The discriminator tries to distinguish between actual data or generated data under condition c, and the two progress together in this process. Finally, the output of the aggregation wind turbine Pw,t is obtained through training.
The loss functions of the discriminator and generator are:
Where E is the expectation;
The objective function of the CGAN prediction process is:
The principle of constructing the objective function is that while training the generator, the generator tries to generate data that meets the mapping of condition c and the distribution of actual data to deceive the discriminator. At this time, the training objective of CGAN is to minimize the above objective function. While training, the discriminator tries to distinguish between actual data and generated data under condition c, so the objective function needs to be maximized while training the discriminator. The CGAN training process is essentially a game of minimum and maximum values. After the training is over, the generator can learn the mapping relationship between the actual data and condition c to generate data that obey the real law under condition c.
To minimize the total cost of regional power system operation, the power generation cost of aggregation thermal power units and the power abandonment penalty of renewable energy are considered to meet regional power system power consumption balance constraints, thermal power unit output constraints, and ramping constraints. The objective function is as follows:
Where T is the total number of periods;
Where a, b, and d are the coefficients between the thermal power unit’s power and the generator’s cost.
The abandoned wind power and hydropower in the system are calculated as follows:
Where
In the operation simulation model of interruptible loads, the regional power system is regarded as an infinite power system. The constraints within the system and the power consumption of the lines in the system are ignored.
Where
Where
Where
Where
where
The constraints of interruptible loads include interruption quantity constraint, maximum interruption time constraint, minimum interruption time constraint, maximum interruption number of times constraint, and minimum interruption interval constraint (Sousa et al., 2017). Because the interruptible loads in the model are the actual interruptible loads in the regional power system, the operation is simulated on a typical day. The constraints of the maximum interruption time, the maximum number of interruptions, and the minimum interruption interval are not considered. However, the total outage power constraint of the interruptible loads in 1 day is added.
Where
Where
Where
Due to the existence of the generator cost function of the aggregation thermal power unit in the objective function, the model of the interruptible loads and the coordinated operation of thermal power, hydropower, wind turbine, and the regional power system, which comprehensively considers the constraints in 3.2, is a mixed-integer nonlinear programming problem. When solving, the power generator cost of the aggregation thermal power unit should be linearized by the following formula:
Where
After piecewise linearization of the power generator cost of the aggregation thermal power unit, the model becomes a mixed-integer linear programming problem in each piecewise interval, which can be solved by using the mature linear programming commercial solver, Gurobi.
Figure 5 shows the flow of capacity value calculation for interruptible loads
(1) Data preprocessing: thermal units’ and hydropower units’ aggregation; use CGAN to predict the output curve of the aggregation wind turbine; linearize the power generator cost of the aggregation thermal power unit;
(2) On a typical day, simulate the operation of the regional power system when there are no interruptible loads; obtain the output of the aggregation thermal power unit;
(3) Add the interruptible loads to the system; all other parameters remain unchanged and perform the operation simulation on the same typical day again;
(4) In the case of the interruptible loads and the coordinated operation of the regional power system, calculate the output of the thermal power unit in the system;
(5) Judge whether the capacity of thermal power units in the system put into operation is higher than the rated value. If it is not higher than the rated value, perform step (7); if it is higher than the rated value, perform step (6);
(6) Reduce the installed capacity of the thermal power unit, and then perform step (4);
(7) Calculate the difference between the capacity of the thermal power unit after and before the interruptible loads are added to the system. The formula for calculating the benefit of interruptible loads capacity is:
Where
We designed the following cases to quantitatively calculate the value of interruptible loads in regional power systems with intermittent renewable energy in the future.
The data in the calculation example is based on the actual installed capacity and actual local loads of a regional power system in a particular region. The parameters of the system in 2025 and the annual load growth rate are set as 5.0. The data sampling interval is 1 h. The data of external power is the planned external power in the region in 2025. The minimum output of thermal power units is 50% of the installed capacity. Interruptible load refers to a load that can be positively activated 1 hour in advance. Its capacity forecasts in 2025, according to the growth rate of 5.0%, is about 2,000 MW, and the other scenarios, including the capacity of 4,000 and 6,000 MW, are used for comparison. The minimum interruption time is set to 1 h, and the maximum interruption energy in 1 day in the three scenarios is set to 16,000, 32,000, and 48,000 MWh, respectively. Other parameters of the system are shown in Table 1:
In this regional power system in 2025, the day with the largest daily peak-to-valley difference was selected as typical day 1, and the day with the highest load was selected as typical day 2. The change of the installed capacity of thermal power units before and after the interruptible loads participated in the operation of power systems is calculated. The local load and external power on the typical day 1 and 2 are shown in Figures 6, 7, respectively. The output forecast of wind turbines on two typical days is shown in Figure 8.
Figures 9–11 are the comparison of the thermal power unit’s output before and after the interruptible loads participate in the system operation under three different scenarios on typical day 1; Figures 12–14 are the comparison of thermal power unit’s output before and after the interruptible loads participate in the system operation under three different scenarios on typical day 2.
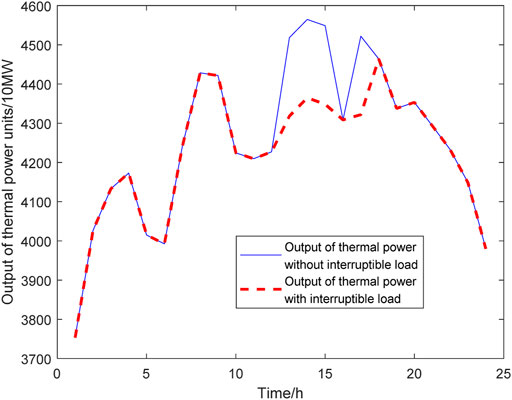
FIGURE 9. Comparison of the output of thermal power units on typical day 1 with two million kW interruptible loads.
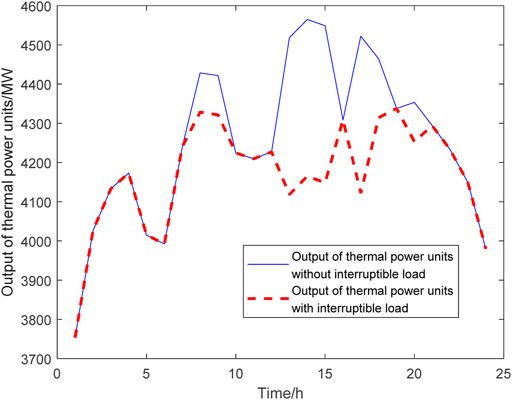
FIGURE 10. Comparison of the output of thermal power units on typical day 1 with 4 million kW interruptible loads.
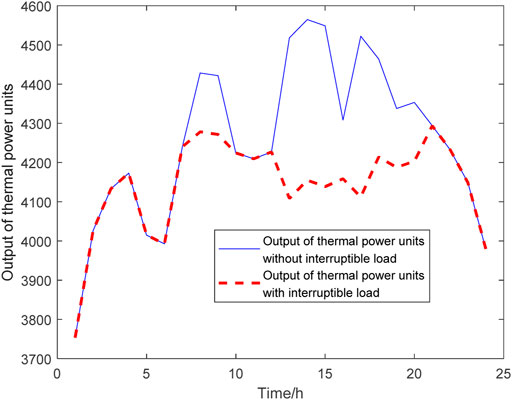
FIGURE 11. Comparison of the output of thermal power units on typical day 1 with 6 million kW interruptible loads.
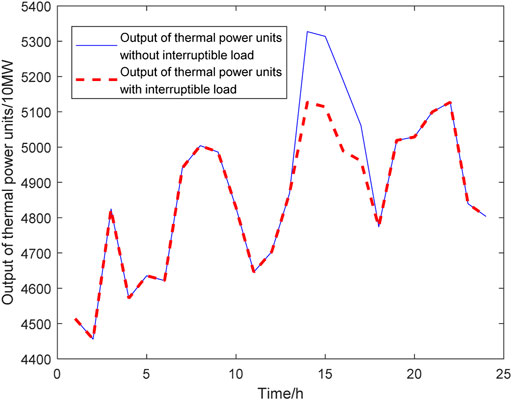
FIGURE 12. Comparison of the output of thermal power units on typical day 2 with 2 million kW interruptible loads.
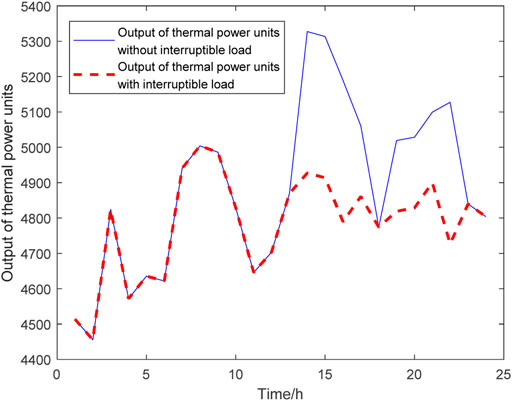
FIGURE 13. Comparison of the output of thermal power units on typical day 2 with 4 million kW interruptible loads.
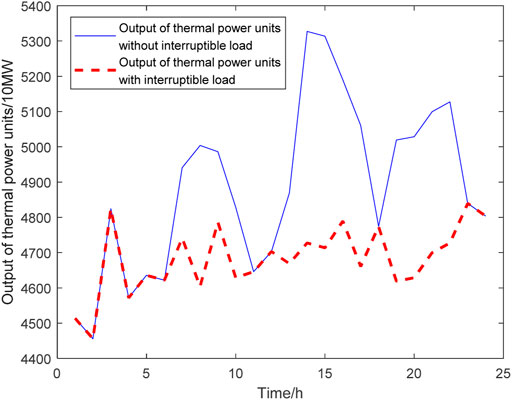
FIGURE 14. Comparison of the output of thermal power units on typical day 2 with 6 million kW interruptible loads.
On typical day 1, the operation simulation is carried out for two cases whether the interruptible loads participate in the operation of power systems. Compared with the time when the interruptible loads do not participate in the operation of power systems when the interruptible loads capacity is 2,000 MW, the addition of the interruptible loads can reduce 1,005.84 MW of thermal power units; when the interruptible loads capacity is 4,000 MW, the addition of interruptible loads can reduce the thermal power assembly by 2,270.40 MW of thermal power units; when the interruptible loads capacity is 6000MW, the addition of interruptible loads can reduce 2,712.21 MW of thermal power units. On typical day 2, the operation simulation is carried out for two cases whether the interruptible loads participate in the operation of power systems. Compared with the time when the interruptible loads do not participate in the operation of power systems when the interruptible loads capacity is 2 MW, the addition of the interruptible loads can reduce 1999.73 MW of thermal power units; when the interruptible loads capacity is 4 MW, the addition of interruptible loads can reduce 3,232.26 MW of thermal power plants; when the interruptible loads capacity is 6 MW, the addition of interruptible loads can reduce 4,876.73 MW of thermal power units.
In summary, the benefit statistics of interruptible loads capacity are shown in Table 2:
In the simulation analysis of the operation of the interruptible loads, the multiple units, and power systems, it is undeniable that interruptible loads have plenty of capacity value in the operation of power systems. However, this paper uses the data of typical days for analysis. The response time of the interruptible loads used is short, which cannot wholly reflect the capacity value of different types of interruptible loads. The interruptible loads capacity in the calculation example is predicted according to the electricity consumption growth rate according to the current interruptible loads capacity of power systems in a particular region. The proposed method effectively calculates the value of interruptible loads in regional power systems with intermittent renewable energy. In the future construction of power systems, the capacity of the interruptible loads will be higher than that in the calculation example, and the interruptible loads will be able to reflect a higher capacity value.
The participation of interruptible loads is an effective means to handle the intermittence of renewable energy, so the capacity value analysis of interruptible loads is an urgent problem. In this paper, combined with the functional characteristics of interruptible loads in power systems, a mathematical model for the optimal joint operation of interruptible loads, several units, and the operation simulation analysis are carried out based on actual operation data of power systems in a particular region. By comparing the changes in the installed capacity of thermal power units in power systems under the two conditions of whether the interruptible loads participate in the operation of power systems, the capacity value of the interruptible loads is calculated quantitatively. The installed capacity of thermal power units can be reduced obviously. The proposed method can effectively promote the participation of interruptible loads in power systems with intermittent renewable energy.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
HF: Conceptualization, Methodology, Software, and Writing—Original Draft. HW: Methodology, Software, and Validation. YX: Investigation, Data Curation. JH: Visualization, Writing—Original Draft. WZ: Software. XX: Supervision, Project administration, Writing—Review, and Editing.
Authors HW, YX, JH, and WZ were employed by Economic and Technological Research Institute of State Grid Zhejiang Electric Power Company.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Argiento, R., Faranda, R., Pievatolo, A., and Tironi, E. (2012). Distributed interruptible load shedding and micro-generator dispatching to benefit system operations. IEEE Trans. Power Syst. 27 (2), 840–848. doi:10.1109/tpwrs.2011.2173217
Bessler, S., and Jung, O. (2016). “Energy management in microgrids with flexible and Interruptible load,” in 2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), 06-09 September 2016 (Minneapolis, MN, USA: IEEE), 1–6. doi:10.1109/ISGT.2016.7781238
Davatgaran, V., Mortazavi, S. S., Saniei, M., and Khalifeh, M. (2013). “Different strategies of Interruptible load contracts implemented in reliability constrained unit commitment,” in 2013 21st Iranian Conference on Electrical Engineering (ICEE), 14-16 May 2013 (Mashhad, Iran: IEEE), 1–6. doi:10.1109/iraniancee.2013.6599884
Dey, D., and Basak, C. K. (2017). “Cost optimization of a wind power integrated thermal power plant,” in 2017 International Conference on Computer, Electrical & Communication Engineering (ICCECE), 22-23 December 2017 (Kolkata, India: IEEE), 1–5. doi:10.1109/iccece.2017.8526198
Kim, M. (2021). ML/CGAN: Network attack analysis using CGAN as meta-learning. IEEE Commun. Lett. 25 (2), 499–502. doi:10.1109/lcomm.2020.3029580
Li, H. Z., Wang, B., Su, C. B., Guo, S., and Li, C. J. (2013). Selection assessment of Interruptible load participating in market reserve during peak period and benefit measurement. Power Syst. Prot. Control 41 (10), 39–44. doi:10.7667/j.issn.1674-3415.2013.10.007
Li, J. (2017). Analysis on application and benefit of interruptible load in power demand side management. Ind. Technol. Innov. 04 (02), 153–155. doi:10.14103/j.issn.2095-8412.2017.02.042
Mashhour, M., Golkar, M. A., and Tafreshi, S. M. (2010). “Efficient aggregation of distributed generations and interruptible load: A new tool for market integration of distributed recourses,” in 2010 7th International Conference on the European Energy Market, 23-25 June 2010 (Madrid, Spain: IEEE), 1–6. doi:10.1109/EEM.2010.5558776
Mohseni, S., Brent, A. C., Burmester, D., and Browne, W. (2020). “A game-theoretic approach to model interruptible load: Application to micro-grid planning,” in 2020 IEEE Power & Energy Society General Meeting (PESGM), 02-06 August 2020 (Montreal, QC, Canada: IEEE), 1–5. doi:10.1109/PESGM41954.2020.9281836
Sampang, C., Ibarbia, P. I. S. D., Laxamana, C. T., and Nerves, A. C. (2018). “Optimal scheduling strategy for virtual power plants with interruptible load,” in 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), 07-10 October 2018 (Kota Kinabalu, Malaysia: IEEE), 616–620. doi:10.1109/APPEEC.2018.8566675
Sarkhani, S., Soleymani, S., Mozafari, B., and Afaghzadeh, H. (2011). “Impact of distributed generation and Interruptible load on energy supply strategies of distribution companies in day-ahead market,” in 16th Electrical Power Distribution Conference, 19-20 April 2011 (Bandar Abbas, Iran: IEEE), 1.
Shao, S., Pipattanasomporn, M., and Rahman, S. (2013). Development of physical-based demand response-enabled residential load models. IEEE Trans. Power Syst. 28 (2), 607–614. doi:10.1109/tpwrs.2012.2208232
Sharma, J., Prakash, V., and Bhakar, R. (2018). “Interruptible load constrained primary frequency response scheduling with photovoltaic generation,” in 2018 20th National Power Systems Conference (NPSC), 14-16 December 2018 (Tiruchirappalli, India: IEEE), 1–6. doi:10.1109/npsc.2018.8771760
Sivaneasan, B., Thachinamoorthi, K., and Goh, K. P. (2016). “Interruptible load scheme: Demand response management for buildings,” in 2016 IEEE Region 10 Conference (TENCON), 22-25 November 2016 (Singapore: IEEE), 1716–1719. doi:10.1109/tencon.2016.7848311
Sousa, J. C., Saavedra, O. R., and Lima, S. L. (2018). Decision making in emergency operation for power transformers with regard to risks and interruptible load contracts. IEEE Trans. Power Deliv. 33 (4), 1556–1564. doi:10.1109/tpwrd.2017.2764466
Wang, B., Li, Y., Ming, W., and Wang, S. (2020). Deep reinforcement learning method for demand response management of interruptible load. IEEE Trans. Smart Grid 11 (4), 3146–3155. doi:10.1109/tsg.2020.2967430
Wang, J., Wang, X., Zhang, X., and Zhang, Z. (2004). Interruptible load management in power market and interim system Part 2 Operation of Interruptible load. Electr. Power Autom. Equip. 6, 1–5. doi:10.3969/j.issn.1006-6047.2004.06.001
Xu, H., Geng, S., Qiao, Y., Xu, K., and Gu, Y. (2020). “Combining CGAN and mil for hotspot segmentation in bone scintigraphy,” in ICASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 04-08 May 2020 (Barcelona, Spain: IEEE), 1404–1408. doi:10.1109/icassp40776.2020.9052946
Yang, B., Cao, X., Cai, Z., Yang, T., Chen, D., Gao, X., et al. (2020). “Unit commitment comprehensive optimal model considering the cost of wind power curtailment and deep peak regulation of thermal unit,” in IEEE Access (IEEE), 871318–871325. doi:10.1109/ACCESS.2020.2983183
Keywords: interruptible loads, capacity value, energy transition, operation simulation, optimized operation, unit aggregation
Citation: Fan H, Wang H, Xu Y, Hu J, Zhang W and Xiao X (2022) Capacity value analysis of interruptible loads in regional power systems with intermittent renewable energy. Front. Energy Res. 10:968873. doi: 10.3389/fenrg.2022.968873
Received: 14 June 2022; Accepted: 11 July 2022;
Published: 08 August 2022.
Edited by:
Yang Li, Hohai University, ChinaReviewed by:
Mingfei Ban, Northeast Forestry University, ChinaCopyright © 2022 Fan, Wang, Xu, Hu, Zhang and Xiao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xuanyi Xiao, eGlhb3h5NkAxNjMuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.