Exergy-economic analysis and evaluation method of park-level integrated energy system

The park-level integrated energy system (PIES) has been developing rapidly in recent years due to its economic and environmental advantages. PIES is a typical user-side energy supply system with multiple energy forms such as solar energy, electrical energy, cool energy, and heat energy inside the system. The coupling between these energy sources and the differences in the quality of these energy sources make its analysis and evaluation a difficult task for PIES research. In order to solve the problems, an analysis and evaluation method of PIES based on exergy economics is proposed, which lays the foundation for the subsequent optimization of system operation. First, a unified analysis model of PIES is developed based on exergy economics theory. Second, the corresponding analysis and evaluation method for this model is proposed. In this method, the exergy efficiency and exergy loss are used as the evaluation index of system energy consumption characteristics, while the exergy loss cost and exergy economic coefficient are used as the evaluation index of system economic characteristics. Meanwhile, an evaluation procedure for using this method is also designed. Lastly, the effectiveness of the given approach is validated in a PIES case in Guangzhou. The results show that the proposed model can accurately calculate the exergy cost of each energy link. The proposed evaluation method can not only analyze the performance of subsystems within a single system but also compare the advantages and disadvantages between different systems.

1 Introduction

The promotion of integrated energy projects has escalated in the context of “carbon peak” and “carbon neutrality” (Long et al., 2022) Amongst various types of integrated energy system (IES), the park-level IES (PIES) is a typical user-side multi-energy coupling and supply mode that has garnered investment from an increasing number of integrated energy service providers (IESPs) (Mu et al., 2022). Given the coupling of multi-energy resources including new energy like photovoltaic power (Fu, 2022), a more suitable andcomprehensive index system of the PIES is imperative in comparison to traditional energy infrastructure compared (Zhao et al., 2021). However, due to the difference in the quality of different energies, the analysis and evaluation of PIES have become a crucial and intriguing issue.

Presently, the main methods for analyzing PIES are energy analysis and exergy analysis. The energy analysis exclusively dependents on thermodynamics first law which focuses only on the quantity of energy rather than its quality (Tahir et al., 2022). Thus, it cannot guide the rational use of energy. Compared with the energy analysis, the exergy analysis is based on both laws of thermodynamics which further considers the changes in system capability for work, indicating the nature of energy usage (Chen et al., 2020). These two analytical methodologies are common in the analysis of multi-energy systems (Nazerifard et al., 2021; Khani et al., 2022). However, they are compared solely on the basis of the system’s energy consumption parameters, ignoring its economic features. Therefore, researchers shifted the issue to investigate system performance from the economic point of view as well. In such a context, exergy economic analysis is proposed in this work. The proposed method integrates thermal characteristics and economic benefits of the system, and can achieve maximum energy saving while ensuring the economy (Behzadi et al., 2018; Haydargil and Abuşoğlu, 2018; Meesenburg et al., 2018; Saloux et al., 2019; Xiao et al., 2021b).

Beginning in the 1960s, many scholars conducted in-depth research on the exergy economics theory (El-Sayed and Evans, 1970; Lozano and Valero, 1993; A et al., 1986; Wang and Zhang, 1995). As the study of exergy economics continues to grow, more and more scholars are using it in different energy fields. (Qin and Hao, 2017). calculates the exergy economic cost of each component of the sewage source heat pump system and gives an assessment about its thermal economic benefits. However, the research is limited to the equipment level. (Sánchez Villafana and Vargas Machuca Bueno, 2019). performs an exergy economic analysis of an air Brayton cycle thermal power plant and analyzes the exergy economic cost of the system at different operating parameters. In addition, (Rongrong et al., 2018; Jixuan et al., 2020), conducts an exergy economic analysis of solar energy systems considering carbon capture technologies. Their models are too detailed and cumbersome which are not suitable for complex energy systems. For PIES, an exergy model for a multigeneration system of combined cooling, heating, and power (CCHP) is proposed and the average exergy cost under a life cycle assessment (LCA) is obtained (Chaiyat, 2021). (Picallo-Perez et al., 2022) makes exergy economic analysis in advanced cogeneration systems in buildings. However, the difference in the grade of different energies is not considered, and the influence of the exergy loss in the energy network transfer on the system performance is also ignored. The calculated exergy cost is different from the real value, and it does not fully reflect the principle of high quality and good price in economics. (Ameri and Mohammadzadeh, 2018). makes thermodynamic and exergy economic analyses of a novel integrated solar combined cycle (ISCC) power plant and determines the components with the most exergy destruction. (Sha and Jiong, 2022). analyzes the performance degradation process of IES using the exergy economic analysis method, evaluating the cumulative and transmission impact of irreversible loss across thermal cycles. It can be seen that the exergy economic analysis method is used for diagnosis and analysis of complex energy systems in addition to the calculation of the exergy cost. However, it has not been used as an analytical evaluation method for PIES.

A comprehensive and accurate analysis and evaluation of PIES is an important basis for subsequent system operation optimization and planning. (Fu et al., 2017). proposes an information entropy approach to quantify uncertainty in an IES but an overall assessment of system performance is lacking. Taking university IES as an example, (Lai and Yang, 2021), uses the ratio of the index of the information amount to replace human subjective ratio of the importance degree, and improves the empowerment method of the analytic hierarchy process (AHP) method so as to evaluate the IES under the background of energy Internet. (Yang et al., 2018). designs a multi-criteria integrated evaluation method that considers the aspects of technology, economy, environment, and society based on the improved grey incidence evaluation method. It is used to evaluate some community energy planning options. With the aim of minimizing technology, environment and economy (Wang et al., 2019) designs and evaluates the IES with CCHP in order to reduce carbon emissions and increase system automation. In (Zhou et al., 2019), the subjective weights of criteria are analyzed based on the intuitionistic fuzzy decision-making trial and evaluation laboratory method. The objective weight is calculated by entropy method. And the extended TODIM method is used to select different schemes. However, the above analysis methods only start from the perspective of energy analysis without considering the variation of energy quality. Thus, the evaluation of system performance is inaccurate. (Khani et al., 2021). designs a novel cooling, power and pure water trigeneration system considering thermodynamics and exergy economics. And a comprehensive parametric study is provided to evaluate the system performance by changing the key variables. In (Taheri et al., 2021), energy, exergy, exergy economics, and environmental relationships are used to assess the performance of a new biomass-based power, refrigeration, natural gas, and hydrogen production system. For a novel supercritical CO ₂ cycle-based combined cycle for solar power tower plants, (Taheri et al., 2022), conducted a comprehensive analysis of the effects of different parameters on the system and key variables through the energy, mass, and exergy balances. It can be seen that the above literature does not uniformly model PIES. More importantly, there is no unified analysis and evaluation index proposed from the perspective of exergy economics. Besides, most of the current evaluation methods only consider independent energy systems (Tahir et al., 2021). These methods are difficult to use as a basis for guiding the improvement of system performance of PIES.

To sum up, this paper proposes an analysis and evaluation method of PIES based on the exergy economic theory. To quantify the different energy qualities, a unified analysis model of PIES is established. On the basis of the above model, an analysis and evaluation method which comprehensively considers the evaluation index of system energy consumption characteristics and economic characteristics is proposed. Finally, a PIES in Guangzhou is used as an example to verify the effectiveness and feasibility of the proposed method. Moreover, the measures to improve its performance are proposed.

The main contributions are summarized as follows.

1) Based on exergy economics, a unified analysis model of PIES is established, including physical model and mathematical model. The model quantifies the difference in quality of different energy and incorporates the transfer pipeline into the modeling, taking into account the losses generated by exergy transfer in the energy network. The exergy cost can be calculated accurately.

2) Taking exergy efficiency and exergy loss as the evaluation index of system energy consumption characteristics, and exergy loss cost and exergy economic coefficient as the evaluation index of system economic characteristics, an analysis and evaluation method and process is proposed.

3) Taking a park-level integrated energy system in Guangzhou as an example, the superiority of the proposed model and analysis and evaluation method is verified.

Section 2 denotes the physical model of PIES. Section 3 denotes the mathematical model of PIES where the exergy cost calculation method is proposed. Section 4 presents the evaluation method of PIES based on exergy economics. Results are compared and analyzed in Section 5. Finally, conclusions are drawn in Section 6.

2 PIES physical model based on exergy economics

2.1 System description

The PIES with CHP system is becoming more and more popular. It can convert various energy sources such as natural gas, solar energy and electricity into heating, cooling and power energy that can meet the needs of users in the region (Zhou et al., 2019). To meet production and living needs, PIES generally consists of photovoltaic power generation, energy storage, charging pile, air conditioning, hot water, ventilation, lighting and other terminal energy subsystems. The overall structure of PIES studied in this paper is shown in Figure 1.

FIGURE 1

FIGURE 1. Framework of PIES

The system is mainly used in large commercial office parks, where energy demands are intensive and diverse, with high electrical loads and cooling demands in summer. Solar power technology, natural gas integrated energy technology and energy storage batteries are used as the main means of energy supply. Energy transmission and distribution networks and energy storage facilities are constructed and improved to meet the demand for cooling, heating and electricity loads. And then a complete park-level energy Internet is built.

2.2 Exergy flow network model description

There are energy conversion equipment, energy storage equipment, energy transfer lines/piping, and many different energy-using loads in PIES. To analyse PIES based on exergy economics, it is necessary to divide PIES into several subsystems at first. There is no unique classification standard, and the classification standard is generally determined according to the needs of one’s own research. In this paper, the exergy flow is defined as the exergy conversion route of energy from the input end to the output end, so that a specific PIES exergy flow network model diagram can be established (as shown in Figure 2). Among them, the system exergy network wiring topology can be deleted or expanded according to the characteristics of building energy consumption.

FIGURE 2

FIGURE 2. Exergy flow network model diagram of PIES.

When applying the exergy economics method to PIES, the following considerations are made for the exergy loss generated by the energy transfer process:

1) Considering from the perspective of energy types, the exergy losses in the process of natural gas and electric power transmission are ignored.

2) Considering from the perspective of distance, the exergy loss caused by the energy transfer between the equipment in the refrigeration main computer room of the central air-conditioning is ignored. At the same time, the long-distance transmission pipeline of cold, heat and gas supplying energy between different energy stations or energy stations to the load is modeled as a subsystem.

3 PIES mathematical model based on exergy economics

3.1 Exergy calculation model

Considering the existence of multiple forms of energy in PIES and the differences in the working ability of different energies, the energy-level coefficient (Chen et al., 2020) is introduced to quantify the differences in energy quality. Therefore, the equation defining the conversion relationship between energy and exergy is

$\lambda =\frac{E_x}{E}(1)$

where E represents the energy; E_x represents the exergy; energy-level coefficient λ represents the proportion of energy accounted for by exergy, 0 < λ < 1. Numerically, the exergy in the current state of the system is equal to the product of the energy corresponding to that state and the energy-level coefficient. Therefore, the exergy content of different types of energy sources (natural gas, hot steam, electricity, etc.) can be solved based on the energy-level coefficients.

The energy level coefficient is influenced by the type, form and temperature of the energy as well as the ambient temperature. Therefore, the energy is divided into different energy types for separate calculations (Ahern and E, 1980).

3.1.1 Natural gas

The energy level coefficient λ_G for natural gas is

${\lambda }_{\text{G}}=1-\frac{T_0}{T-T_0}\ln \frac{T}{T_0}(2)$

Where T₀ denotes the ambient temperature in K; T denotes the complete combustion temperature of natural gas.

3.1.2 Steam

The energy-level coefficients λ_S for steam are shown in Equation 3.

${\lambda }_S=1-\frac{T_0}{T_S}(3)$

where T_Sdenotes the saturation temperature corresponding to the steam pressure in K.

3.1.3 Electricity, heat and cold

The energy-level coefficient for electricity, heat and cold loads are shown in Equation 4, Equation 5, Equation 6.

${\lambda }_E=1(4)$

${\lambda }_{\text{H}}=1-\frac{T_0}{T_H}(5)$

${\lambda }_C=\frac{T_0}{T_C}-1(6)$

where T_H and T_C denote the transfer temperature of heat and cold load respectively, both in K.

3.2 Cost sharing model based on exergy economics

Considering that there is more than one output exergy of the subsystem, the energy grades of different output exergy are different. Therefore, cost sharing of the different output exergy is required. Only on the basis of being able to quantify the energy quality differences uniformly, the multi-energy coupled PIES can be analyzed and evaluated.

When the output contains several energy sources with different energy grades, for example, a CCHP system outputs both high-grade electricity and low-grade cold and heat energy. The traditional cost sharing method assumes that all output exergy has the same unit economic cost, which cannot reflect the difference in the value of different exergy (Gaggioli and Wepfer, 1980). For the shortcomings of the traditional cost sharing method, the energy-level coefficient method has been proposed (Lazzaretto and Tsatsaronis, 1997). In other words, the unit economic cost of the output exergy is determined by the energy-level coefficient, thus reflecting the difference in the quality of the exergy. However, the apportionment simply using the energy-level coefficient can lead to a significant undervaluation of low-grade exergy. Therefore, this paper uses the improved energy-level coefficient method, which means that the exponential function of the energy-level coefficient is used as a parameter to reflect the difference in the quality of the output exergy. 0 < λ < 1, 1 < e^λ < e, which ensures that low-grade exergy have the same base value.

For the multi-output subsystem, its cost sharing model can be obtained as follows.

$\frac{c_1}{{\text{e}}^{{\lambda }_1}}=\dots \dots =\frac{c_k}{{\text{e}}^{{\lambda }_k}}(7)$

Where c₁⋯c_k represent the unit exergy economic cost of 1 to k different output exergy of the subsystem. and λ₁⋯λ_k represent the energy-level coefficient of 1 to k different output exergy of the subsystem.

3.3 Exergy costing model based on exergy economics

According to the needs of problem analysis, PIES can be divided into m subsystems, and the subsystems are interconnected by n exergy flows. Based on known exergy parameters, the cost balance equation and supplementary equation are listed for the divided subsystem to obtain the unit exergy economic cost of cooling, heating and power products.

In view of the complex exergy distribution and many parameters of the system studied in this paper, the matrix analysis method (Tahir et al., 2021) is used to study the cost change of the system. At this point the subsystem cost balance equation is

$A\times E_x\times c+Z=0(8)$

Where A (m × n) is event matrix, representing the connection between subsystems and exergy; matrix elements A_ij are +1 or −1 or 0; +1 denotes the j − th exergy flow into the i − th system, − 1 means outflow and 0 means no connection between the two; E_x is the n × n exergy matrix; c is n × 1 unit exergy economic cost matrix; Z is m × 1 non-energy cost matrix. To obtain the non-energy cost per unit of time, the non-energy cost of the subsystem is discounted over the economic life cycle as shown in Equation 9.

$Z=\frac{\phi f}{H}{Z}_0(9)$

Where Z₀ denotes the equipment cost of the subsystem, H denotes the annual operating hours of the subsystem, φ denotes the maintenance factor of the subsystem, and f denotes the annualization factor.

In PIES, the number n of the exergy flows are generally larger than the number m of subsystems, and the number of unknowns is more than the number of equations, so n − m supplementary equations need to be established for the system.

1) Input exergy cost supplementary equation

$A_1\times E_x\times c-C=0(10)$

Where A₁ (s × n) is input exergy matrix, which represents that the exergy costs for s input systems are known; C represents the input exergy total cost matrix.

2) Output exergy cost sharing equation

$A_2\times E_x\times c=0(11)$

Where A₂ (r × n) is multi-product exergy matrix. To facilitate the solution, Equations 8 and 10 and 11 are organized into a uniform form to obtain:

$A^{\prime }\times E_x\times c+Z^{\prime }=0(12)$

Where $A^{\prime }(n\times n)=\left(\begin{array}{c}\hfill A\hfill \\ \hfill A_1\hfill \\ \hfill A_2\hfill \end{array}\right)$, $Z^{\prime }(n\times 1)=\left(\begin{array}{c}\hfill Z\hfill \\ \hfill -C\hfill \\ \hfill 0\hfill \end{array}\right)$.

4 PIES evaluation method based on exergy economics

4.1 PIES evaluation index

Energy analysis tracks the “quantitative” changes in the transfer of energy through the system but ignores the “qualitative” changes. Exergy analysis proposes the concept of exergy to make up for this deficiency. In this paper, exergy loss and exergy efficiency are used as evaluation indexes of system energy consumption characteristics. Among them, exergy loss is used to characterize the reduction of energy quality and work capacity in the transmission process, and exergy efficiency is used to characterize the utilization of exergy by equipment and links in the system.

Although the exergy analysis can analyze the system both qualitatively and quantitatively, it ignores the cost factor in production and cannot reflect the economic value of exergy. The exergy economic cost analysis applies the concept of “cost” in economics to the concept of “exergy” in thermodynamics, which can provide a more comprehensive evaluation of complex energy systems. In this paper, the exergy cost and the exergy economic coefficient are used as the evaluation indexes of the system’s economic characteristics. Among them, exergy loss cost is used to characterize the economic loss caused by the reduction of energy quality in the transmission process, and exergy economic coefficient is used to characterize the economic potential of the system energy saving.

4.1.1 Energy consumption characteristic indexes

The exergy loss represents the difference between the sum of various input exergy and the sum of various output exergy in the subsystem, as shown in Equation 13:

$E_{x_{\mathit{loss,i}}}=E_{x_{\mathit{in,i}}}-E_{x_{\mathit{out,i}}}(13)$

Where $E_{x_{\mathit{in,i}}}$ represents the input exergy of subsystem i; $E_{x_{\mathit{out,i}}}$ represents the output exergy of subsystem i.

The exergy efficiency represents the ratio of the sum of various output exergy to the sum of various input exergy in the subsystem, as shown in Equation 14:

${\eta }_i=E_{x_{\mathit{out,i}}}/E_{x_{\mathit{in,i}}}(14)$

4.1.2 Economic characteristic indexes

The exergy loss cost of the subsystem is determined by the amount of exergy loss and its unit exergy economic cost, as shown in Equation 15:

$C_{\mathit{loss,i}}=E_{x_{\mathit{loss,i}}}\times c_{\mathit{loss,i}}(15)$

Where Ex_loss,i represents the exergy loss of subsystem i; C_loss,i represents the exergy loss cost of subsystem i; c_loss,i represents the unit exergy economic cost of exergy loss of subsystem i.

The exergy economic coefficient represents the proportion of the non-energy cost of the subsystem in the total cost of the system, as shown in Equation 16:

${\omega }_i=\frac{Z_i}{E_{x_{\mathit{loss,i}}}\times c_{\mathit{loss,i}}+Z_i}(16)$

Where ω_i represents the exergy economic coefficient of subsystem i.

For the whole system, this paper proposes that the total exergy economic coefficient can be used to express the proportion of system non-energy cost in the total cost, as shown in Equation 17:

$\omega =\frac{\sum Z_i}{\sum E_{x_{\mathit{loss,i}}}\times c_{\mathit{loss,i}}+\sum Z_i}(17)$

Where ω represents the exergy economic coefficient of system.

Equations 16 and 17 not only reveal the economic benefits of PIES, but also clearly show the exergy utilization degree of the system and each subsystem. In addition, when studying the economic benefits of different systems, the total exergy economic coefficient can also be used for comparison between systems.

4.2 PIES evaluation process

To carry out the most realistic analysis and evaluation of PIES, this paper uses the energy-level coefficient to perform exergy calculation and cost sharing, and finally the real exergy economic cost is calculated. Based on this, the PIES is analyzed and evaluated using the evaluation indexes mentioned above. The specific process is shown in Figure 3.

FIGURE 3

FIGURE 3. Analysis and evaluation flowchart of PIES based on the exergy economics.

Firstly, a PIES model based on exergy economics is established and then, the model is solved to obtain the unit exergy economic cost of PIES based on different cost sharing methods. Secondly, the optimal cost sharing mode is selected to obtain the energy consumption characteristic index and economic characteristic index of PIES. Finally, performance analysis is performed based on the indexes to evaluate the subsystem which proposes suggestions for improving the system performance.

It should be noted that the above-mentioned characteristic index of energy consumption can only be used as the index of the “exergy utilization degree” of the subsystem. When making performance comparisons between subsystems within a system or between systems, due to the technical and economic inequalities of the exergy losses generated in each subsystem, the comprehensive performance of the system cannot be correctly evaluated by using the energy consumption characteristic index. This is also the main reason for exergy economics modeling and analysis. A more comprehensive analysis and evaluation of the performance of PIES can be made by considering thermodynamic and economic factors in an integrated manner.

5 Case study

5.1 Setting

Based on the above evaluation method, the PIES in Guangzhou is taken as the research object to be analyzed and evaluated. The park has a floor area of about 20,000 m² and consists of an office building and a shopping mall. The area of the office building and the shopping mall is about 10,000 m² each, and a water-cooled central air conditioning system is used. For power generation, there is a CHP system, and a 300 kWp photovoltaic power generation system is installed on the roof. The power generated by the photovoltaic system and gas turbine is considered to be self-consumed within the office and shopping mall electrical system.

To sharpen the focus of the analysis, electric energy storage device and chilled water storage device without energy conversion are ignored as well as other electricity loads other than electric air conditioners, charging piles and electric cooking appliance. The system model is shown in Figure 4.

FIGURE 4

FIGURE 4. Model diagram of PIES based on exergy economics.

The data of the system at 14:00 in mid-August was selected for analysis. The ambient temperature on that day was 35°C. The price of electricity for commercial and office is 1 CNY/kWh and the price of natural gas is 2.45 CNY/m³. The low calorific value of natural gas is 9.77 kWh/m³, and the peak value of photovoltaic power generation is 1 kWp/m³ under ideal conditions. The ideal energy efficiency ratio of the refrigeration compressor is 29.815 according to the ideal Carnot cycle efficiency formula.

For load, 30 7 kW AC charging piles are installed outdoors. The office area has 35 rooms, each with an area of 200 m² and four 9 kW fan coils. The mall area has 10 rooms, each with the same configuration as above. It also has 10 large open rooms, each with an area of 5,000 m², with a total of three 500 kW cold air cabinets installed. The exergy values of the system are shown in Table 1.

TABLE 1

TABLE 1. Exergy parameters of PIES.

To further calculate the unit exergy economic cost of each exergy, the non-energy cost of each subsystem is discounted. The summary is shown in Table 2.

TABLE 2

TABLE 2. Cost parameters and non-energy cost values for each subsystem of PIES.

5.2 Cash analysis

Comparing the improved energy-level coefficient sharing method proposed in this paper with the traditional sharing method and energy-level coefficient sharing method, a summary of each unit exergy economic cost is calculated as shown in Table 3.

TABLE 3

TABLE 3. Unit exergy economic cost based on different sharing methods.

It can be seen that the unit exergy economic cost of the two products produced by the gas turbine under the traditional apportionment method is both 0.4214 CNY/kWh, which does not conform to the law of high quality and good price. According to the energy-level coefficient method, the cost of electricity exergy and heat exergy is 0.5707 CNY/kWh and 0.2528 CNY/kWh, reflecting the value difference. However, the heat exergy cost is only 44% of the electricity exergy cost, which means the value of low-quality exergy is underestimated. According to the improved energy-level coefficient method, the cost of electricity exergy and heat exergy is 0.5271 CNY/kWh and 0.3020 CNY/kWh. The heat exergy cost accounts for 57% of the electricity exergy cost, which is 19% higher than the previous method. It not only reflects the law of high quality and good price, but also makes the value of low-grade exergy be reasonably displayed.

The studied method can make reasonable cost apportionment for cooling, heating and power products, which can get more realistic unit exergy economic cost and facilitate subsequent analysis. Also setting prices based on cost comparison results can achieve better pricing fairness for users with different needs.

Assuming that the external input energy of the PIES is sufficient, this paper prices the exergy loss at the average unit exergy economic cost of the subsystem input exergy. The parameters of each subsystem evaluation index are summarized in Table 4.

TABLE 4

TABLE 4. Evaluation index parameters of PIES.

A comprehensive analysis of the performance of each subsystem shows that the photovoltaic system produces the most exergy loss, which is caused by the current low efficiency of converting solar energy into electricity. The exergy loss cost generated by electric air conditioners is the highest, exceeding gas turbine, because the unit exergy cost of cooling is much higher than natural gas exergy. The exergy loss generated by the refrigerant piping is far lower than other subsystems, but the exergy loss cost is not low due to the high economic cost of the unit cold exergy. It can be seen that the closer to the end, the higher the exergy loss cost, which is due to the increase in the economic cost of the end unit exergy. Therefore, the measures to reduce the end of exergy can more effectively improve the economy of the system.

From the perspective of system integrity, the exergy efficiency of the central air conditioning is only 0.28, but its exergy economic coefficient is 0.44. It means that a small additional non-energy cost can still be invested at this point, but obviously it does not improve the energy consumption characteristics of the system significantly. This is because the central air conditioning converts high-grade electric energy into low-grade cold energy, and the degradation of energy brings great exergy loss, which is a defect of energy supply path. The exergy efficiency of the refrigerant piping is 0.78, but its exergy economic coefficient is only 0.02. Although it accounts for a small exergy loss of the entire system, the exergy loss cost is greatly increased because the front end is connected to central air conditioning. Therefore, while additional investment in pipes and pipe cooling materials, the proportion of central air conditioning cooling should be reduced as much as possible. It should only be used as a supplementary means of waste gas refrigeration to achieve cascade utilization of energy.

In this PIES, since solar energy is a free resource, the photovoltaic system has only a non-energy cost, and the exergy economic coefficient is 1, which is not more analysis. The exergy coefficient of the transformer is the highest, so continuing to increase its investment in the optimization of the system is not obvious. The exergy economic coefficients of gas turbine, lithium bromide absorption chiller, and electric wiring are all far below the reference value. At this time, increasing the non-energy cost input can improve the energy consumption characteristics and economic characteristics of the system. For gas turbine and lithium bromide absorption chiller, unit with higher efficiency can be replaced. For electrical wiring, the losses can be reduced by optimizing the distribution system structure and cable cross-section.

The reason why electric cooking appliance has a higher exergy loss cost and a much smaller exergy economic coefficient than gas cooking appliance is that the electric cooking appliance converts high-grade electrical energy into low-grade heat energy. This also results in a higher unit exergy economic cost of heating in the electric cooking appliance. In response to this phenomenon, the investment in electric cooking appliance should not be increased, but the proportion of heating by gas cooking appliance should be increased to save exergy and money.

In order to compare the economics between different PIES, the above model is set as model A, and the model without CHP system but with municipal cold source cooling mode is set as model B, as shown in Figure 5.

FIGURE 5

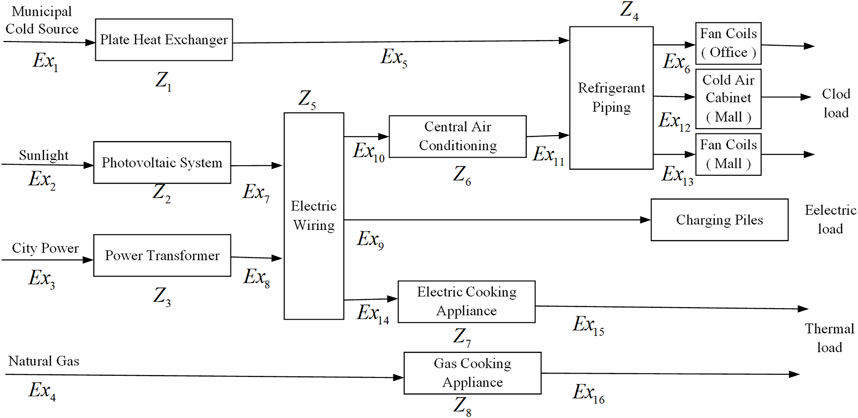
FIGURE 5. Model diagram of PIES based on exergy economics in the municipal cold source cooling mode.

The evaluation index parameters of these two models can be obtained as shown in Table 5.

TABLE 5

TABLE 5. Parameters of evaluation indexes for different models.

Since there are differences in the subsystems, it is not possible to visually compare the advantages and disadvantages of the two systems through the performance parameters of the subsystems, so this paper proposes the total economic exergy coefficient as a comparison between different systems. It can be seen that the total exergy economic coefficient of model A is larger than model B. The specific difference is reflected in the exergy loss cost. This is because PIES with CHP achieves a stepped utilization of energy and reduces municipal power purchases, which not only improves energy utilization but also improves economic efficiency.

6 Conclusion

This work provides an analysis and assessment approach for PIES based on exergy economics. An improved cost sharing model is employed to obtain the real exergy cost. Additionally, a comprehensive evaluation method and process considering energy consumption characteristics and economic characteristics are designed. Finally, a PIES in Guangzhou is used as an example for verification. The calculation example shows:

1) The exergy model of PIES established in this paper is in line with the real-life situation and fully considers the impact of the exergy loss in the network, which can accurately calculate the exergy cost of each energy link.

2) In comparison to the traditional cost-sharing technique and the energy-level coefficient method, the improved energy-level coefficient approach can more accurately depict the value of low-grade energy while also reflecting the value of diverse forms of energy exergy.

3) A more accurate and comprehensive evaluation of the system performance is made by considering energy consumption characteristics and economic characteristics, and the system performance is improved accordingly.

We limited our analysis of PIES to a specific time period. On this basis, the specific strategies for energy system operation optimization can be proposed subsequently by considering the impact of dynamic electricity price, energy storage devices, dynamic loads and power electronic devices on the PIES(Fu et al., 2020; Xiao et al., 2021a; Wei et al., 2022).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LM conceived the study and HC was responsible for overall direction and planning. XL conceptualized the study and LM designed the model and JC designed the computational framework. LM and XL wrote the manuscript with input from all authors. HC and ZZ modified the manuscript and polished content. XL and ZD contributed to writing-editing.

Funding

This work was supported by the National Natural Science Foundation of China under Grant (51937005).

Conflict of interest

LM was employed by Architectural, Design Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

A, V., A, L. M., and M, M. (1986). “Part i on the exergetic cost; part ii on the thermoeconomic cost; part iii exergy saving and thermoeconomics,” in A general theory of exergy saving. Editor G. R. A (New York: ASME), 1–21.

Google Scholar

Ahern and E, J. (1980). Exergy method of energy systems analysis. New York: John Wiley & Sons.

Google Scholar

Ameri, M., and Mohammadzadeh, M. (2018). Thermodynamic, thermoeconomic and life cycle assessment of a novel integrated solar combined cycle (iscc) power plant. Sustain. Energy Technol. Assessments 27, 192–205. doi:10.1016/j.seta.2018.04.011

CrossRef Full Text | Google Scholar

Behzadi, A., Gholamian, E., Ahmadi, P., Habibollahzade, A., and Ashjaee, M. (2018). Energy, exergy and exergoeconomic (3e) analyses and multi-objective optimization of a solar and geothermal based integrated energy system. Appl. Therm. Eng. 143, 1011–1022. doi:10.1016/j.applthermaleng.2018.08.034

CrossRef Full Text | Google Scholar

Chaiyat, N. (2021). A multigeneration system of combined cooling, heating, and power (cchp) for low-temperature geothermal system by using air cooling. Therm. Sci. Eng. Prog. 21, 100786. doi:10.1016/j.tsep.2020.100786

CrossRef Full Text | Google Scholar

Chen, H., Chen, S., Li, M., and Chen, J. (2020). Optimal operation of integrated energy system based on exergy analysis and adaptive genetic algorithm. IEEE Access 8, 158752–158764. doi:10.1109/ACCESS.2020.3018587

CrossRef Full Text | Google Scholar

El-Sayed, Y. M., and Evans, R. B. (1970). Thermoeconomics and the design of heat systems. J. Eng. Power 92, 27–35. doi:10.1115/1.3445296

CrossRef Full Text | Google Scholar

Fu, X., Guo, Q., and Sun, H. (2020). Statistical machine learning model for stochastic optimal planning of distribution networks considering a dynamic correlation and dimension reduction. IEEE Trans. Smart Grid 11, 2904–2917. doi:10.1109/TSG.2020.2974021

CrossRef Full Text | Google Scholar

Fu, X. (2022). Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control Mod. Power Syst. 7, 5. doi:10.1186/s41601-022-00228-z

CrossRef Full Text | Google Scholar

Fu, X., Sun, H., Fu, Q. G., Sun, H., Guo, Q., Pan, Z., et al. (2017). Uncertainty analysis of an integrated energy system based on information theory. Energy 122, 649–662. doi:10.1016/j.energy.2017.01.111

CrossRef Full Text | Google Scholar

Gaggioli, R. A., and Wepfer, W. J. (1980). Exergy economics: I. Cost accounting applications. Energy 5, 823–837. doi:10.1016/0360-5442(80)90099-7

CrossRef Full Text | Google Scholar

Haydargil, D., and Abuşoğlu, A. (2018). A comparative thermoeconomic cost accounting analysis and evaluation of biogas engine-powered cogeneration. Energy 159, 97–114. doi:10.1016/j.energy.2018.06.102

CrossRef Full Text | Google Scholar

Jixuan, W., Wensheng, L., Xin, M., Xiaozhen, L., Yanfeng, G., Zuodong, Y., et al. (2020). Study on the coupling effect of a solar-coal unit thermodynamic system with carbon capture. Energies 13, 4779. doi:10.3390/en13184779

CrossRef Full Text | Google Scholar

Khani, L., Jabari, F., Mohammadpourfard, M., and Mohammadi-ivatloo, B. (2021). Design, evaluation, and optimization of an efficient solar-based multi-generation system with an energy storage option for Iran’s summer peak demand. Energy Convers. Manag. 242, 114324. doi:10.1016/j.enconman.2021.114324

CrossRef Full Text | Google Scholar

Khani, L., Mohammadpour, M., Mohammadpourfard, M., Heris, S. Z., and Akkurt, G. (2022). Thermodynamic design, evaluation, and optimization of a novel quadruple generation system combined of a fuel cell, an absorption refrigeration cycle, and an electrolyzer. Int. J. Energy Res. 46, 7261–7276. doi:10.1002/er.7634

CrossRef Full Text | Google Scholar

Lai, X., and Yang, S. (2021). Integrated energy system assessment based on improved critic-ahp method under energy internet. J. Sociol. Ethnology 1, 115–122. doi:10.23977/jsoce.2021.030802

CrossRef Full Text | Google Scholar

Lazzaretto, A., and Tsatsaronis, G. (1997). On the quest for objective equations in exergy costing. Proc. ASME Adv. Energy Syst. Div. doi:10.1115/IMECE1997-0989

CrossRef Full Text | Google Scholar

Long, H., Fu, X., Kong, W., Chen, H., Zhou, Y., and Yang, F. (2022). Key technologies and applications of rural energy internet in China. doi:10.1016/j.inpa.2022.03.001

CrossRef Full Text | Google Scholar

Lozano, M., and Valero, A. (1993). Theory of the exergetic cost. Energy 18, 939–960. doi:10.1016/0360-5442(93)90006-Y

CrossRef Full Text | Google Scholar

Meesenburg, W., Ommen, T., and Elmegaard, B. (2018). Dynamic exergoeconomic analysis of a heat pump system used for ancillary services in an integrated energy system. Energy 152, 154–165. doi:10.1016/j.energy.2018.03.093

CrossRef Full Text | Google Scholar

Mu, Y., Wang, C., Cao, Y., Jia, H., Zhang, Q., and Yu, X. (2022). A cvar-based risk assessment method for park-level integrated energy system considering the uncertainties and correlation of energy prices. Energy 247, 123549. doi:10.1016/j.energy.2022.123549

CrossRef Full Text | Google Scholar

Nazerifard, R., Khani, L., Mohammadpourfard, M., Mohammadi-Ivatloo, B., and Akkurt, G. G. (2021). Design and thermodynamic analysis of a novel methanol, hydrogen, and power trigeneration system based on renewable energy and flue gas carbon dioxide. Energy Convers. Manag. 233, 113922. doi:10.1016/j.enconman.2021.113922

CrossRef Full Text | Google Scholar

Picallo-Perez, A., Sala-Lizarraga, J. M., Escudero-Revilla, C., Hidalgo-Betanzos, J. M., and Ruiz de Vergara, I. (2022). Thermoeconomic analysis in advanced cogeneration systems in buildings. Front. Energy Res. 9, 802971. doi:10.3389/fenrg.2021.802971

CrossRef Full Text | Google Scholar

Qin, N., and Hao, P. Z. (2017). The operation characteristics of sewage source heat pump system and the analysis of its thermal economic benefits. Appl. Therm. Eng. 124, 1083–1089. doi:10.1016/j.applthermaleng.2017.05.204

CrossRef Full Text | Google Scholar

Rongrong, Z., Hongtao, L., Hao, W., Hai, Y., and Yongping, Y. (2018). Analysis of integration of mea-based co2 capture and solar energy system for coal-based power plants based on thermo-economic structural theory. Energies 11, 1284. doi:10.3390/EN11051284

CrossRef Full Text | Google Scholar

Saloux, E., Sorin, M., and Teyssedou, A. (2019). Exergo-economic analyses of two building integrated energy systems using an exergy diagram. Sol. Energy 189, 333–343. doi:10.1016/j.solener.2019.07.070

CrossRef Full Text | Google Scholar

Sánchez Villafana, E. D., and Vargas Machuca Bueno, J. P. (2019). Thermoeconomic and environmental analysis and optimization of the supercritical CO2 cycle integration in a simple cycle power plant. Appl. Therm. Eng. 152, 1–12. doi:10.1016/j.applthermaleng.2019.02.052

CrossRef Full Text | Google Scholar

Sha, L., and Jiong, S. (2022). Improved thermoeconomic energy efficiency analysis for integrated energy systems. Processes 10, 137. doi:10.3390/pr10010137

CrossRef Full Text | Google Scholar

Taheri, M. H., Khani, L., Mohammadpourfard, M., Aminfar, H., and Akkurt, G. G. (2022). Multi‐objective optimization of a novel supercritical CO₂ cycle-based combined cycle for solar power tower plants integrated with SOFC and LNG cold energy and regasification. Int. J. Energy Res. 46, 12082–12107. doi:10.1002/er.7972

CrossRef Full Text | Google Scholar

Taheri, M. H., Khani, L., Mohammadpourfard, M., and Aminfar, H. (2021). Multi-objective optimization of a novel biomass-based multigeneration system consisting of liquid natural gas open cycle and proton exchange membrane electrolyzer. Int. J. Energy Res. 45, 16806–16823. doi:10.1002/er.6931

CrossRef Full Text | Google Scholar

Tahir, M. F., Haoyong, C., and Guangze, H. (2021). A comprehensive review of 4e analysis of thermal power plants, intermittent renewable energy and integrated energy systems. Energy Rep. 7, 3517–3534. doi:10.1016/j.egyr.2021.06.006

CrossRef Full Text | Google Scholar

Tahir, M. F., Haoyong, C., and Guangze, H. (2022). Evaluating individual heating alternatives in integrated energy system by employing energy and exergy analysis. Energy 249, 123753. doi:10.1016/j.energy.2022.123753

CrossRef Full Text | Google Scholar

Wang, J., and Zhang, H. (1995). Power engineering thermoeconomics. Beijing: Water Conservancy and Electric Power Press.

Google Scholar

Wang, Y., Wang, X., Yu, H., Huang, Y., Dong, H., Qi, C., et al. (2019). Optimal design of integrated energy system considering economics, autonomy and carbon emissions. J. Clean. Prod. 225, 563–578. doi:10.1016/j.jclepro.2019.03.025

CrossRef Full Text | Google Scholar

Wei, C., Zhao, Y., Zheng, Y., Xie, L., and Smedley, K. M. (2022). Analysis and design of a nonisolated high step-down converter with coupled inductor and zvs operation. IEEE Trans. Ind. Electron. 69, 9007–9018. doi:10.1109/tie.2021.3114721

CrossRef Full Text | Google Scholar

Xiao, D., Chen, H., Wei, C., and Bai, X. (2021a). Statistical measure for risk-seeking stochastic wind power offering strategies in electricity markets. J. Mod. Power Syst. Clean Energy 2021, 1–6. doi:10.1109/TIE.2021.3114721

CrossRef Full Text | Google Scholar

Xiao, D., do Prado, J. C., and Qiao, W. (2021b). Optimal joint demand and virtual bidding for a strategic retailer in the short-term electricity market. Electr. Power Syst. Res. 190, 106855. doi:10.1016/j.epsr.2020.106855

CrossRef Full Text | Google Scholar

Yang, K., Ding, Y., Zhu, N., Yang, F., and Wang, Q. (2018). Multi-criteria integrated evaluation of distributed energy system for community energy planning based on improved grey incidence approach: A case study in tianjin. Appl. Energy 229, 352–363. doi:10.1016/j.apenergy.2018.08.016

CrossRef Full Text | Google Scholar

Zhao, J., Chen, L., Wang, Y., and Liu, Q. (2021). A review of system modeling, assessment and operational optimization for integrated energy systems. Sci. China Inf. Sci. 64, 191201–191223. doi:10.1007/s11432-020-3176-x

CrossRef Full Text | Google Scholar

Zhou, J., Wu, Y., Wu, C., Deng, Z., Xu, C., and Hu, Y. (2019). A hybrid fuzzy multi-criteria decision-making approach for performance analysis and evaluation of park-level integrated energy system. Energy Convers. Manag. 201, 112134. doi:10.1016/j.enconman.2019.112134

CrossRef Full Text | Google Scholar