Numerical analysis of thermal transportation in nanodiamond and silver-based nanofluid using the Cattaneo–Christov heat flux model

Zuhra, Samina; Sikander, Waseem; Elkotb, Mohamed Abdelghany; Tag-Eldin, E. M.; Khattak, Sana Gul; Yassen, Mansour F.

doi:10.3389/fenrg.2022.967444

ORIGINAL RESEARCH article

Front. Energy Res., 29 August 2022

Sec. Process and Energy Systems Engineering

Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.967444

This article is part of the Research Topic Modern World Heat Transfer Problems: Role of Nanofluids and Fractional Order Approaches View all 18 articles

Numerical analysis of thermal transportation in nanodiamond and silver-based nanofluid using the Cattaneo–Christov heat flux model

Samina Zuhra¹

Waseem Sikander²*

Mohamed Abdelghany Elkotb^3,4

E. M. Tag-Eldin⁵

Sana Gul Khattak⁶

Mansour F. Yassen^7,8

¹Department of Computing and Technology, Abasyn University, Peshawar, Khyber Pakhtunkhwa, Pakistan
²Department of Mathematics and Statistics, University of Haripur, Haripur, Khyber Pakhtunkhwa, Pakistan
³Mechanical Engineering Department, College of Engineering, King Khalid University, Abha, Saudi Arabia
⁴Mechanical Engineering Department, College of Engineering, Kafrelsheikh University, Kafr El Sheikh, Egypt
⁵Faculty of Engineering and Technology, Future University in Egypt, New Cairo, Egypt
⁶Department of Physics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan
⁷Department of Mathematics, College of Science and Humanities, Prince Sattam Bin Abdulaziz University, Al-Kharj, Al-Aflaj, Saudi Arabia
⁸Department of Mathematics, Faculty of Science, Damietta University, Damietta, Egypt

Background and Purpose: Studying the effects of suction and injection on heat transportation in nanofluids for time-dependent boundary layer flow is a key topic in fluid dynamics. Aerodynamics and the sciences of space both make extensive use of these types of flow. In this research, nanodiamond and silver nanoparticles in water-type base-fluid nanofluids flow are analyzed under the effects of thermal radiation and non-Fourier theory.

Methodology: A mathematical system having certain physical variations of the flow model is converted to a non-dimensional ordinary differential equation system via suitable similarity transformation variables. Then the flow model is numerically solved by RK4 and a shooting technique to describe the dynamics of the nanofluids under varied flow conditions. RK4 with the shooting approach gives a rapid result with high convergence accuracy. The relevant characteristics of physical quantities evaluated by an inclusive numerical scheme are observed for flow pattern, temperature distribution, and nanofluids concentration variations in the presence of suction and injection fluxes.

Finding: According to the findings, both ND-H₂O and Ag-H₂O have outstanding thermal performance characteristics. The Ag-based nanofluid, however, has a better heat transfer capability. To validate the analysis, a graphical and tabular comparison is presented under specified assumptions. The key finding is that, with the injection effect, the heat flow rate is larger than with the suction effect. The unsteadiness parameter causes a drop in the velocity profile, whereas energy distribution rises with this parameter.

Introduction

The thermal performance of fluids is critical in the industrial and technical sectors. Many industrial and technical operations need a large quantity of heat transmission. Traditional liquids do not provide the required quantity of heat to complete the operation, which explains why there has been a need to understand how to enhance the heat transmission of ordinary liquids. Ultimately, in order to increase heat transfer in conventional liquids, researchers and scientists have devised the idea of utilizing metallic and non-metallic substances, in the form of nanoparticles, in the host liquid. These fluids’ exceptional heat transfer capabilities have improved industrialists’ and engineers’ impact on the contemporary world. Nanofluids have been employed in aerodynamics, computer chips, medical sciences, the cosmetics industry, aviation parts manufacturing, and many other industries. As a result of the aforementioned uses, heat transport research is unavoidable. In many engineering areas, the modeling of unsteady flow phenomena is becoming more relevant. In turbomachinery, for instance, this encompasses the contact between stationary and rotating components, pistons engine, fluid–structure interactions, helicopter aerodynamics, applications in the automotive industry, the DNS or LES of turbulent flows, nuclear explosions, and so on. The heat transportation rate has been investigated for time-dependent nanofluid flow incorporating magnetic field and thermal conduction effects (Lahmar et al., 2020), for unsteady bioconvection hybrid nanofluid flow over a movable rotating disk in upward and downward directions (Jayadevamurthy et al., 2020), for time-dependent Carreau nanofluid flow under the effect of variable conductivity (Irfan et al., 2020), for unsteady nanofluid flow through a movable upper plate alongside suction and magnetic effects (Shuaib et al., 2020), and so on (Sreedevi et al., 2020; Khan et al., 2021; Alsallami et al., 2022; Raja et al., 2022; Rehman et al., 2022).

Nanodiamond particle dispersion in the host fluid water has been investigated theoretically and experimentally by many researchers aiming to enhance the thermal performance. Sundar et al. (2021) experimentally investigated the entropy and exergy of heat in nanodiamond/water nanofluid flow. With increasing nanofluid particle loadings, research has found a significant rise in the heat transfer coefficient and Nusselt number. Nanodiamond/water and cobalt oxide/water nanofluids have been placed in a square cavity containing heaters and treated to investigate the heat transfer rate (Kalidasan and Kanna, 2017). Numerical analysis has been made for entropy generation in laminar convective nanodiamond/water nanofluid through a rectangular channel (Uysal et al., 2019). Entropy generation has been estimated for tangent hyperbolized hybrid nanofluid that enhances the thermal transportation capacity of regular fluid (Hussain and Jamshed, 2021). Similarly, tangent hyperbolized hybrid nanofluid in a solar wing parabolic trough solar collector, used in solar plants, has been studied by Jamshed et al. (2021a). The nanopolishing behavior of suspended nanodiamond in elasto-hydrodynamic lubrication has been studied by Shirvani et al. (2016). Similarly the silver/water nanofluid flow over a vertical Riga plate has been studied by Rawat et al. (2019). Analysis of the turbulent convective force of Ag/HEG type nanofluid flow that flows through a circular channel, silver/water nanofluid flow in mini channels, Ag/HEG water nanofluid in pipes, and Ag/water nanofluid inside a semi-circular lid-driven cavity has been conducted by Ny et al. (2016), Sinz et al. (2016), Raja Bose et al. (2017), and Hadavand et al. (2019), respectively. Bhatti et al. (2022a) studied nanofluids composed of nanoparticles such that nanodiamond and silica in the host fluid water flow through the elastic surface located exponentially, and Bhatti et al. (2022b) studied hybrid nanofluids comprising cobalt-oxide/graphene oxide nanoparticles in the base fluid water that flows across a circular elastic surface in a porous medium. This research is significant for improving the optical thermal performance in solar energy conversion systems. Dogonchi et al. (2017) analyzed the magnetohydrodynamic graphene oxide/water type nanofluid through a permeable channel under the effect of thermal radiation and found that when the Reynolds number and extension ratio increase, so does the skin friction coefficient. Alizadeh et al. (2018) studied the micropolar nanofluid flow that passes through penetrable sheets. According to their findings, the Nusselt number is a rising function of volume friction and thermal radiation. Dib et al. (2015) studied the thermal transportation phenomena in nanofluid through a squeezing medium and found that nanofluids with different types have positive effects on heat transfer. Sheikholeslami et al. (2012) examined the heat transfer rate in copper/water nanofluid flow between two rotating stretched surfaces. Their findings showed that the surface heat transfer rate increases the volume fraction of nanomaterials. Entropy generation has been measured by Jamshed (2021) in the MHD flow of Maxwell nanofluid that passes infinite horizontal sheets in terms of the imposed viscous dissipation and thermal radiation effects. Many researchers have been paying close attention to the study of nanofluid flow through porous surfaces, and Henry Darcy’s 1856 Darcy model is the most used model in this kind of study (Darcy, 1965). Khanafer and Vafai (2019) discussed in detail the usages of nanofluid in a porous medium. Shahsavar et al. (2020) investigated the effects of a permeable medium using a silver/water nanofluid with a heat sink filled with metal foam, utilizing the first and second laws of thermodynamics. Bioconvection phenomena have been used by Bhatti et al. (2022c) in magnetohydrodynamic Williamson nanofluid flow that passes a circular permeable medium when a nanofluid flows through a cylinder entirely saturated with a porous medium. Other useful literature about nanofluids in a porous medium can be found in Ahmed et al. (2019), Menni et al. (2019), Zuhra et al. (2020), and Wang et al. (2022).

Considerable focus has been placed on the flow and heat transmission of viscous fluids via surfaces that are constantly stretching in a fluid medium. Innovative and pioneering studies about stretching the surface for the fluid flow include those of Sakiadis (1961) and Crane (1970). Many researchers have since built on Crane’s and Sakiadis’s groundbreaking work to investigate various elements of flow and heat transmission in an infinite domain of fluid through a stretched sheet (Laha et al., 1989; Afzal, 1993; Wang, 2006; Ahmed et al., 2022a; Ashraf et al., 2022; Elattar et al., 2022). These investigations are based on continuous flow. A quick stretching of the flat sheet or a steep shift in the sheet’s temperature might cause the flow field and heat transmission to be unstable in some instances. Hossain et al. (1999) investigated the effect of radiation on free convection from a porous vertical plate. Prasannakumara et al. (2017) reported on the convective thermal performance of an unstable nanofluid passing through a stretchy sheet. They presented their findings for dusty nanofluid, concluding that a higher radiative surface is preferable for dusty nanofluid thermal increase. Bhattacharyya and Layek (2014) studied the heat transport of nanofluids in the presence of applied Lorentz forces. The time-dependent non-Newtonian Casson nanofluid flow through a slippery surface was assessed by Jamshed et al. (2021b) for entropy generation and thermal transportation measurement. Dutta et al. (1985) investigated the temperature behavior of a normal liquid across a stretchy sheet in the presence of a continuous heat flow condition. Many researchers have studied exponentially extending sheets (Magyari and Keller, 1999; Rehman et al., 2017; Mushtaq et al., 2019), which have the most important technological and industrial applications.

The heat conduction law developed by Fourier (Fourier and Darboux, 1822) has been used to forecast heat transfer behavior in a variety of practical circumstances. Since this model generates a parabolic energy equation, any initial perturbation would have a significant impact on the system under study. Fourier’s law has been adjusted multiple times to solve this contradiction (Dong et al., 2011; Zhang et al., 2013; Reddy and Sreedevi, 2021). Fourier’s law was updated by Cattaneo (1948) by including the relaxation time for heat flux, which is defined as the time it takes for heat conduction to stabilize once a temperature gradient has been introduced. Christov (2009) proposed a materially invariant version of Cattaneo’s model based on Oldroyd’s upper-convected derivative. To date, significant research has been undertaken on nanofluidic flow models adding non-Fourier heat conduction theory (Alhowaity et al., 2022; Imtiaz et al., 2022; Salmi et al., 2022). In the present paper, non-Fourier heat flux theory and thermal radiation effects are imposed to investigate the heat transfer rate in two different types of nanofluids composed of nanodiamond-water and silver-water over an unsteady stretching sheet. Suction and injection fluxes are also considered in the model. The thermal properties of both nanoparticles are different; hence, this study shows the best heat transfer performance rate. The non-dimensional system of equations is achieved via the adjustment of suitable similarity variables in the traditional form of the flow model with many assumptions, which are further solved through the shooting technique. The resulting data are compared to the physical characteristics, and the findings are shown graphically in the form of graphs. Using Mathematica 11.0, a graphical comparison study is used to verify the colloidal analyses. The hydrothermal efficiency of heat transfer systems improved with smaller silver/water nanoparticle size and concentrations. Silver nanoparticles, when used in small enough concentrations and with a small enough size, may reduce the pressure drop and erosion problems that arise during the suspension of nanoparticles in the host fluid. Thus, such a type of nanoparticle is more stable in nanofluid over a long time. Additionally, thermal fluids based on nanodiamond may improve thermal conductivity by as much as 70%. Therefore, both of the nanofluids possess good thermal conductivity. Nanodiamond nanofluid is mostly used in electron microscopy, Raman spectroscopy, and X-ray diffraction analyses.

The flow model and its formulation

The model considers the unsteady, incompressible nanofluids flow that passes over a stretchable surface located horizontally. The nanofluids are composed of two types of nanoparticles, namely nanodiamond and silver nanoparticles, suspended in base fluid water. The flow is assumed under the effects of suction injection and non-Fourier theory for the stability of heat transfer at the boundary layer flow. In Cartesian coordinates, the flow scenario is configured as two-dimensional and unidirectional. Let $\hat{u}$ and $\hat{v}$ be the nanofluidic velocities in the horizontal $x_$ and vertical $y_$ directions, respectively. $T$ is the temperature variation with ambient temperature $T_{\infty}$ . Figure 1 displays the flow pattern of ND-H₂O and Ag-H₂O nanofluids flow across an unstable stretching sheet.

FIGURE 1

FIGURE 1. Flow geometry of nanodiamond-water and silver-water nanofluids.

Governing equation: In light of the aforementioned restrictions, the following is the form of mass, momentum, and energy conservations (Ahmed et al., 2022b):

\frac{\partial \hat{u}}{\partial \hat{x}} + \frac{\partial \hat{v}}{\partial \hat{y}} = 0 (1)

\frac{\partial \hat{u}}{\partial \hat{t}} + \hat{u} \frac{\partial \hat{u}}{\partial \hat{x}} + \hat{v} \frac{\partial \hat{u}}{\partial \hat{y}} = \frac{μ_{n f}}{ρ_{n f}} (\frac{\partial^{2} \hat{u}}{\partial {\hat{y}}^{2}}) (2)

\frac{\partial \hat{T}}{\partial \hat{t}} + \hat{u} \frac{\partial \hat{T}}{\partial \hat{x}} + \hat{v} \frac{\partial \hat{T}}{\partial \hat{y}} = \frac{k_{n f}}{{(ρ C_{p})}_{n f}} (\frac{\partial^{2} \hat{T}}{\partial {\hat{y}}^{2}}) + λ (\begin{array}{l} (\hat{u} \frac{\partial \hat{u}}{\partial \hat{x}} + \hat{v} \frac{\partial \hat{u}}{\partial \hat{y}}) \frac{\partial \hat{T}}{\partial \hat{x}} + (\hat{u} \frac{\partial \hat{v}}{\partial \hat{x}} + \hat{v} \frac{\partial \hat{v}}{\partial \hat{y}}) \frac{\partial \hat{T}}{\partial \hat{y}} \\ + {\hat{u}}^{2} \frac{\partial^{2} \hat{T}}{\partial {\hat{x}}^{2}} + {\hat{v}}^{2} \frac{\partial^{2} \hat{T}}{\partial {\hat{y}}^{2}} + 2 \hat{u} \hat{v} \frac{\partial^{2} \hat{T}}{\partial \hat{y}} \end{array}) (3)

where $μ_{n f}$ is dynamic viscosity, $ρ_{n f}$ is density, $k_{n f}$ is thermal conductivity, and ${(ρ C_{p})}_{n f}$ is heat capacity defined as:

\begin{array}{l} ρ_{n f} = ((1 - ϕ) + ϕ ρ_{s} {(ρ_{f})}^{- 1} ρ_{f} \\ {(ρ C_{p})}_{n f} = ((1 - ϕ) + ϕ {(ρ C_{p})}_{s} {(ρ C_{p})}_{f}^{- 1}) {(ρ C_{p})}_{f} \\ μ_{n f} = μ_{f} {(1 - ϕ)}^{2.5} \\ k_{n f} = k_{s} ((k_{s} + 2 k_{f}) - 2 ϕ (k_{f} - k_{s})) {((k_{s} + 2 k_{f}) + ϕ (k_{f} - k_{s}))}^{- 1} \end{array}

According to the above assumption, the acceptable flow conditions at the surface and far from it are defined as:

\hat{u} = {\hat{u}}_{0} \frac{(\hat{x} {\hat{l}}^{- 1})}{(1 + a \hat{t})}, \hat{v} = {\hat{v}}_{w} (\hat{t}), \hat{T} = {\hat{T}}_{\infty} + \frac{{\hat{T}}_{0} ({\hat{x}}^{n} {\hat{l}}^{- n})}{{(1 + a \hat{t})}^{c}} at the surface (4)

\hat{u} \to 0, a n d \hat{T} \to T_{\infty} far from the surface (5)

where $γ, {\hat{T}}_{\infty}, {\hat{u}}_{0}, {\hat{T}}_{0}$ are positive constants with reference length l, n, and c. Moreover, if $R e = \frac{l {\hat{u}}_{0}}{{\hat{v}}_{f}} a n d P r = \frac{{\hat{v}}_{f}}{k_{f}},$ then the stream function $φ (\hat{x}, \hat{y})$ can be defined as:

φ (\hat{x}, \hat{y}) = \frac{\frac{\hat{x}}{l}}{(\sqrt{R e} \sqrt{(1 + γ \hat{t})})} f (η) (6)

From the stream function, velocity components may be expressed as:

\hat{u} = \frac{\partial φ (\hat{x}, \hat{y})}{\partial \hat{y}}, \hat{v} = - \frac{\partial φ (\hat{x}, \hat{y})}{\partial \hat{x}}

Suitable similarity variables for the above model are defined as:

η = \frac{1}{l} {(\frac{R e}{(1 + a \hat{t})})}^{1 / 2} \hat{y}, and \hat{T} = {\hat{T}}_{\infty} + {\hat{T}}_{0} \frac{({\hat{x}}^{n} l^{- n})}{{(1 + a \hat{t})}^{c}} θ (η) (7)

As a result, the velocities components in horizontal and vertical directions are defined as:

\hat{u} = \frac{{\hat{u}}_{0} \hat{x}}{(l (1 + a \hat{t}))} f^{'} (η) (8)

\hat{v} = - \frac{{\hat{u}}_{0}}{(\sqrt{R e} \sqrt{(1 + a \hat{t})})} f (η) (9)

The required partial derivatives can be formulated as follows:

\begin{array}{l} \frac{\partial \hat{u}}{\partial \hat{x}} = \frac{{\hat{u}}_{0}}{l (1 + γ \hat{t})} f^{'} (η), \frac{\partial \hat{u}}{\partial \hat{y}} = \frac{{\hat{u}}_{0} \hat{x} \sqrt{R e}}{l^{2} {(1 + a \hat{t})}^{\frac{3}{2}}} f^{″} (η), \frac{\partial^{2} \hat{u}}{\partial {\hat{y}}^{2}} = \frac{{\hat{u}}_{0} \hat{x} R e}{l^{3} {(1 + a \hat{t})}^{\frac{3}{2}}} f^{‴} (η), \frac{\partial \hat{v}}{\partial \hat{x}} = 0, \\ \frac{\partial \hat{u}}{\partial \hat{t}} = - {\hat{u}}_{0} \frac{\hat{x} a}{l {(1 + a \hat{t})}^{2}} f^{'} (η) - \frac{{\hat{u}}_{0} \hat{x} a \hat{y} \sqrt{R e}}{2 {\hat{l}}^{2} {(1 + a \hat{t})}^{\frac{5}{2}}} f^{″} (η), \frac{\partial \hat{T}}{\partial \hat{x}} = \frac{\hat{n} {\hat{T}}_{0} {(\frac{\hat{x}}{\hat{l}})}^{n - 1}}{l {(1 + a \hat{t})}^{c}} θ (η), \frac{\partial^{2} \hat{T}}{\partial {\hat{y}}^{2}} = \frac{{\hat{T}}_{0} {(\frac{\hat{x}}{\hat{l}})}^{c} \sqrt{R e}}{l^{2} {(1 + a \hat{t})}^{c + 1}} θ^{″} (η) \\ \frac{\partial \hat{T}}{\partial \hat{t}} = - {\hat{T}}_{0} \hat{c} {(\frac{\hat{x}}{l})}^{c} \frac{a}{{(1 + a \hat{t})}^{(c + 1)}} θ (η) - \frac{{\hat{T}}_{0} (\frac{\hat{x}}{l}) a \hat{y} \sqrt{R e}}{2 \hat{l} {(1 + a \hat{t})}^{c + \frac{3}{2}}} θ^{'} (η), \frac{\partial \hat{T}}{\partial \hat{y}} = \frac{{\hat{T}}_{0} {(\frac{\hat{x}}{\hat{l}})}^{c} \sqrt{R e}}{l {(1 + a \hat{t})}^{c + \frac{1}{2}}} θ^{'} (η) \end{array} (10)

Substituting Eqs 8–10 into Eqs 1–5 yields the following non-dimensional system of momentum and energy equation:

f^{‴} (η) + d_{1} (f (η) f^{″} (η) - {f^{'}}^{2} (η) + A (f^{'} (η) + 0.5 η f^{″} (η))) = 0, (11)

θ^{″} (η) + d_{2} (\begin{array}{l} \Pr A (\hat{c} θ (η) + 0.5 η θ^{'} (η)) + \Pr (η θ (η) f^{'} (η) + θ^{'} (η) f (η)) \\ + \Pr γ (f (η) f^{'} (η) θ^{'} (η) - f^{2} (η) θ^{″} (η)) \end{array}) = 0, (12)

where $A = \frac{γ l}{{\hat{u}}_{0}}$ is the unsteadiness parameter, and where $\Pr = \frac{{\hat{v}}_{f}}{k_{f}}$ , $d_{1} = {(1 - ϕ)}^{2.5} (1 - ϕ + ϕ \frac{ρ_{s}}{ρ_{f}})$ , and

d_{2} = \frac{(1 - ϕ) + ϕ \frac{{(ρ {\hat{C}}_{p})}_{s}}{{(ρ {\hat{C}}_{p})}_{f}}}{(({\hat{k}}_{s} + 2 {\hat{k}}_{f}) - 2 ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})) {(({\hat{k}}_{s} + 2 {\hat{k}}_{f}) + ϕ ({\hat{k}}_{f} - {\hat{k}}_{s}))}^{- 1}}

The corresponding boundary conditions of Eq. 11 and Eq. 12 are:

f (η) = f_{w}, f^{'} (η) = 1, θ (η) = 1, a t η = 0, (13)

f^{'} (η) \to 0, θ (η) \to 0, a t η \to \infty, (14)

Solution process of the nanofluidic system

Computational fluid dynamics (CFD) has been an increasingly significant technology in chemical and engineering since the 1990s. Transport processes including heat, momentum, and mass transfer may be studied using CFD (Thabet and Thabit, 2018). In CFD, the geometry of the process being modeled is first split into tiny volumes called computational meshes. It is then applied and solved for each mesh point using the governing equations (such as heat and mass transport, as well as boundary conditions). Graphical representations of mesh findings are the most typical way to analyze CFD results (Pandey et al., 2017). In order to solve highly nonlinear differential equations involving energy, temperature, and air velocity, CFD uses numerical shooting and RK4 methods.

Basic principles of the shooting technique

The transport equations are quite nonlinear and can be affected by boundary circumstances. The RK4 scheme and shooting approach may be used to compute this numerically. This method has a small margin of error. Converting the resultant differential equations into first-order equations is the first step in solving the framed model of a nanofluid flow problem. The essential replacements for the aforementioned step are as follows:

{(f, f^{'}, f^{″}, θ, θ^{'})}^{T} = {({\hat{x}}_{1}, {\hat{x^{'}}}_{1} = {\hat{x}}_{2}, {\hat{x^{'}}}_{2} = {\hat{x}}_{3}, {\hat{x}}_{4}, {\hat{x}}^{'}_{4} = {\hat{x}}_{5})}^{T} (15)

Some assumptions are made to solve the fluidic model:

• a relevant value for $η$ , representing the field distance, is taken as 10 for the far field;

• conditions in the far field w.r.t. $η \to \infty$ are $\hat{f^{'}} (η) \to 1, \hat{θ} (η) \to 0, \hat{G} (η) \to 0$ ;

• the scale of convergence is 10^–5; and

• for calculations, the step size is recorded as $η$ = 0.025.

Eqs 11–14 can thus be written as:

(\begin{array}{l} f^{'} \\ f^{″} \\ f^{‴} \\ θ^{'} \\ θ^{″} \end{array}) = (\begin{array}{l} {\hat{x}}_{2} \\ {\hat{x}}_{3} \\ - d_{1} ({\hat{x}}_{1} {\hat{x}}_{3} - {\hat{x}}_{2}^{2} + A ({\hat{x}}_{2} + 0.5 η {\hat{x}}_{2})) \\ {\hat{x}}_{5} \\ \frac{- d_{2}}{(1 - \Pr γ {\hat{x}}_{1}^{2})} (\Pr A (\hat{c} {\hat{x}}_{4} + 0.5 η x_{5}) + \Pr (n x_{4} x_{2} + x_{5} x_{1}) - P r γ ({\hat{x}}_{1} {\hat{x}}_{2} {\hat{x}}_{57})) \end{array}) (16)

The corresponding conditions according to the variables are as follows:

{\begin{cases} {\hat{x}}_{1} (0) = f_{w}, {\hat{x}}_{2} (0) = 1, {\hat{x}}_{4} (0) = 1, \\ {\hat{x}}_{2} (\infty) = 0, {\hat{x}}_{4} (\infty) = 0. \end{cases} (17)

which can be determined via the shooting method and the first-order system in Eqs 11–14 is integrated via the RK4 scheme.

Results and discussion

The intended domain’s flow properties are greatly modified by varying the amount of flow. As a result, this section investigates the behavior of the non-dimensional flow field $f^{'} (η)$ and energy distribution $θ (η)$ of ND-H₂O and Ag-H₂O nanofluids by adjusting the flow quantities. Using the shooting technique in Eqs 11–12 with the boundary conditions in Eqs 13–14 provides the significant results of the proposed model. Table 1 show the values of four main thermophysical properties of nanodiamond, Silver and water (Ahmed et al., 2022b). Table 2 shows the close agreement of the shooting-RK4 technique with the existing literature for the proposed flow model.

TABLE 1

TABLE 1. Thermophysical values of nanodiamond and silver nanoparticles.

TABLE 2

TABLE 2. Assessment of present study with literature.

Flow distribution $f^{'} (η)$

The velocity of a nanofluid in relation to $f_{w}$ is given by $f^{'} (η)$ . Figures 2A,B

FIGURE 2

FIGURE 2. Influence of (A) suction and (B) injection on the velocity profile.

depict the flow of ND-H₂O and Ag-H₂O nanofluids as a function of suction and injection values. As shown in Figure 2A, the velocity $f^{'} (η)$ for both nanofluids decreases because of higher suction impacts at the plates. As a result of the suction effects, more nanofluid particles adhere to the surface, lowering the velocity profile. The motion of Ag-H₂O quickly decreases as the nanofluid gets thicker for the higher density compared to the ND nanoparticles. Because of the low density of ND, the fluid velocity $f^{'} (η)$ (ND-H₂O) decreases slowly. The effects of injecting fluid from the surface on ND-H₂O and Ag-H₂O velocity $f^{'} (η)$ are shown in Figure 2B. As a result of the fluid particles being physically separated from the sheet surface because of injection, their momentum has increased, causing an upturn in the flow. ND-H₂O has a lower density; therefore, intermolecular interactions are lessened, allowing fluid particles to move freely across the required area. In comparison to Ag-H₂O nanofluid, the velocity of ND-H₂O increases more suddenly as a response of this. The velocity $f^{'} (η)$ of a nanofluid in relation to the unsteadiness parameter $A$ are presented in Figures 3A,B,C showing the impacts of the time-dependent quantity on nanofluid velocities at fixed suction and injection, respectively. Both ND-H₂O and Ag-H₂O nanofluids yielded similar results. The velocity $f^{'} (η)$ decreases rapidly as the unsteadiness parameter increases in the presence of suction/injection and when there is no suction or injection over the surface. The fluid motion decreases towards the surface and then begins to rise. The decrease in the fluid’s velocity, $f^{'} (η)$ slows down over time, eventually disappearing asymptotically beyond values greater than 5.

FIGURE 3

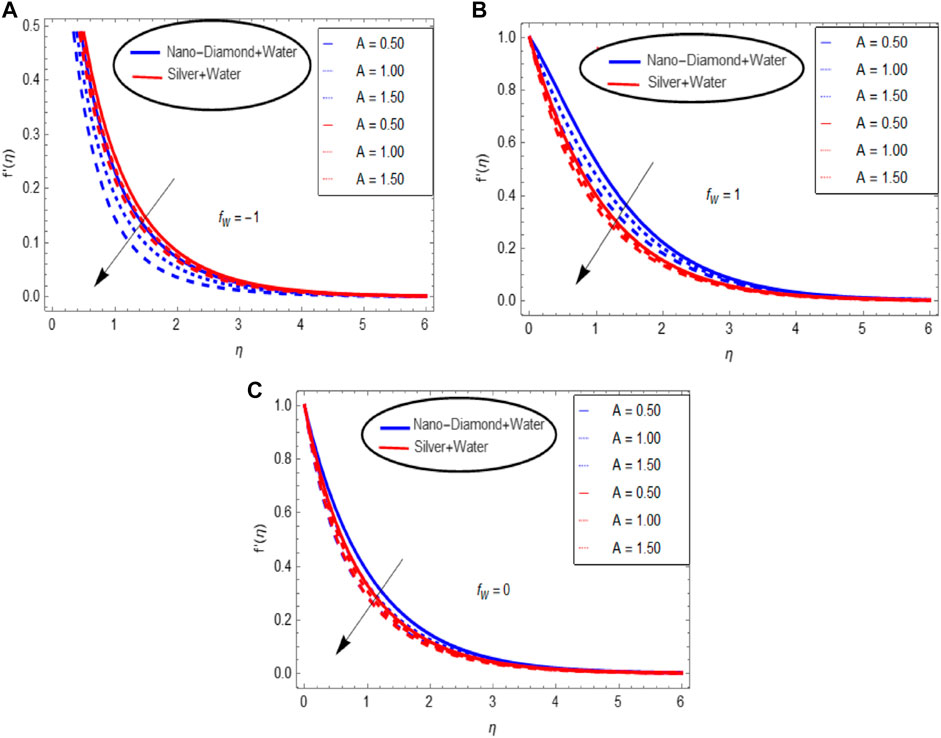
FIGURE 3. Influence of the unsteadiness parameter in the presence of (A) suction, (B) injection, and (C) without suction/injection on the velocity profile.

The temperature distribution $θ (η)$

The significant thermal physical properties of nano-materials are critical in determining the heat transport procedure of nanofluids. These values have a substantial impact on the fluid’s thermal properties. As a result, this section presents the temperature profile $θ (η)$ of ND-H₂O and Ag-H₂O as a function of several factors. These factors are estimated in the presence of suction or injection fluxes to control the boundary layer and reduce the losses of energy in the medium. Figures 4A,B,C show the time-dependent parameter in the presence of suction effect, injection, and no suction/injection impacts on energy distribution, respectively. Due to the unsteadiness parameter, the temperature of the nanofluids rises significantly. Suction causes the fluid velocity to rise quickly, resulting in an increase in the kinetic energy of the fluid particles. The collision of particles increases as the kinetic energy of the particles increases. As a result, the temperature quickly rises. Due to increased injection effects near the surface, the temperature quickly rises. In these cases, the silver/water nanofluid temperature increases more rapidly compared to the ND/water nanofluid. Figures 5A,B,C display the influence of the Prandtl number, thermal relaxation parameter, and suction/injection for temperature distributions. The boundary layer thickness of energy distribution has an inverse relationship with thermal diffusivity, which slows down the temperature profile for both nanofluids. At the initial boundary layer, the thickness rapidly decreases, but further away, the energy distribution shows a constant decrease when the values of the Prandtl parameter increase simultaneously. Thermal relaxation time occurs when time is required for thermal conductivity in the region far from the directly heated surface. Here, thermal relaxation does not affect the energy distribution at the boundary layer surface but decreases this temperature distribution far from the boundary layer. The presence of suction and injection fluxes boosts the heat distribution source, as shown in Figure 5C. Moreover, the silver/water nanofluid temperature increases more rapidly compared to the ND/water nanofluid.

FIGURE 4

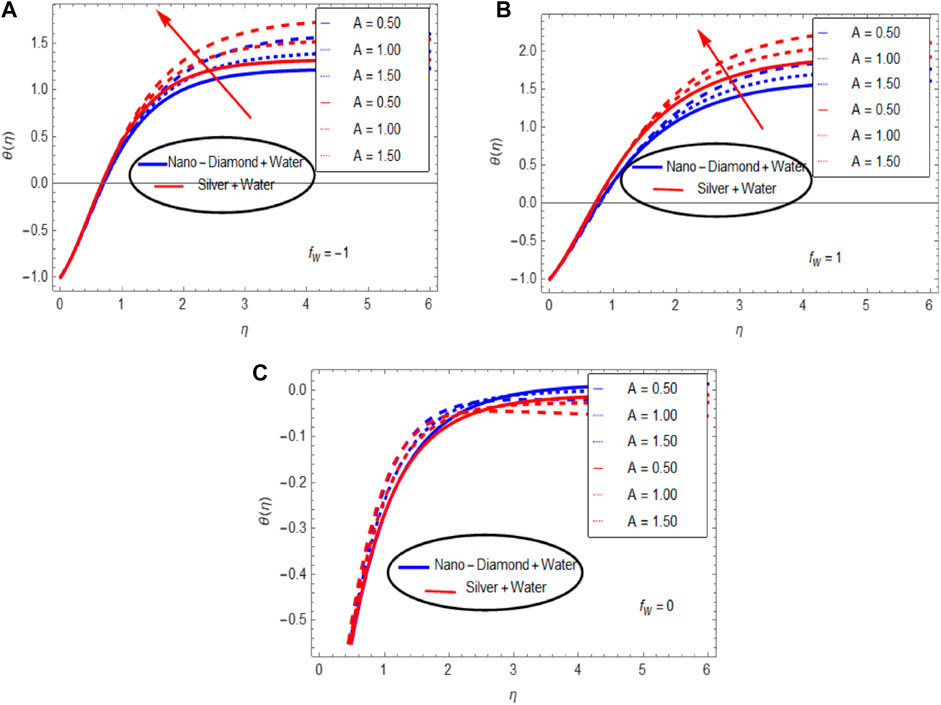
FIGURE 4. Influence of the unsteadiness parameter in the presence of (A) suction, (B) injection, and (C) without suction/injection on the temperature distribution.

FIGURE 5

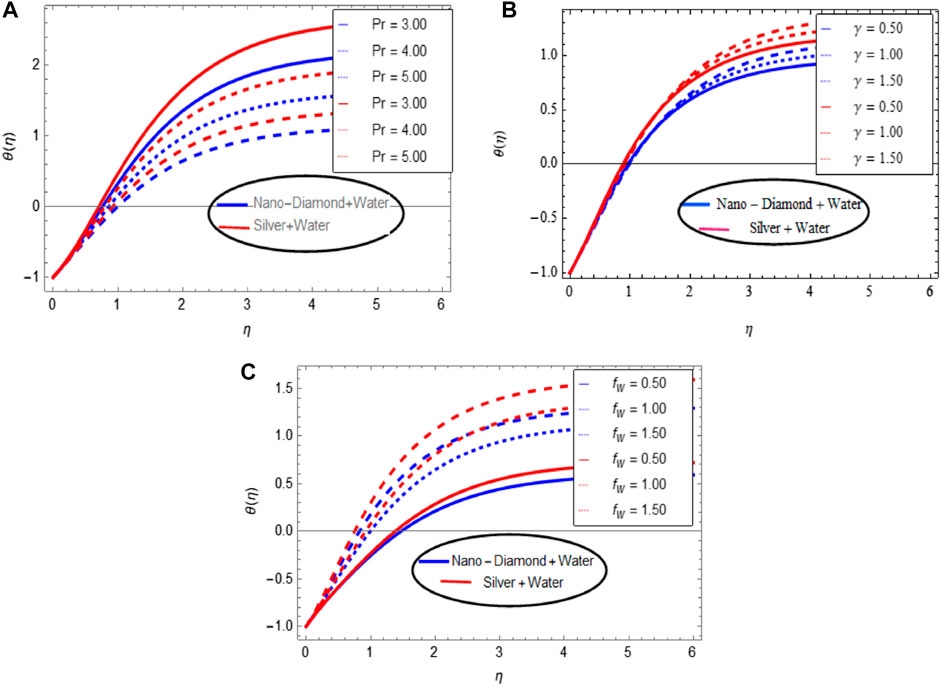
FIGURE 5. Influence of (A) Prandtl number, (B) thermal relaxation parameter, and (C) suction/injection on the temperature distribution.

The volume fraction ( $ϕ$ )

Nanomaterials effectively change the thermophysical parameters in nanofluids, which plays an important role in the heat transfer process. Figures 6A,B show the values for the effective density, thermal conductivity, and dynamic viscosity for the nanofluids under study, respectively. The thermal conductivity of Ag-H₂O is greater than that of ND-H₂O, as can be seen upon close examination. As a result, Ag-H₂O nanofluid is a better conductor and has excellent heat transmission properties. Similarly, increasing the volumetric proportion of nanomaterials improves their effective density and heat capacity.

FIGURE 6

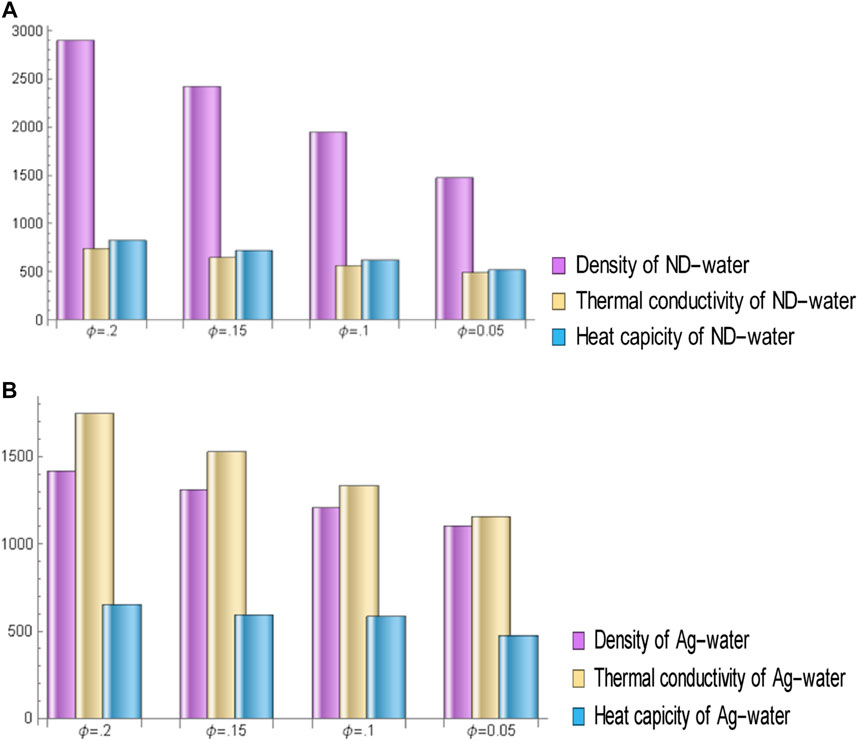
FIGURE 6. (A) Influence of volume fraction on the thermos-physical values for nanodiamond/water. (B) Influence of volume fraction on the thermos-physical values for silver/water.

Major findings

The current investigation focuses on the thermal transfer enhancement over the unsteady surface of nanofluids composed of nanodiamond-water and silver-water. The flow model is taken under the effect of heat source sink, thermal radiation, and non-Fourier heat theory. Such flows may occur on the bonnet of a vehicle, on the surface of a solar thermal aircraft, and on the surface of a bullet. An unstable surface has been used to study the effects of embedded factors on heat transport in ND-H₂O and Ag-H₂O nanofluids. According to the results of this study, nanofluids are better heat conductors than normal liquids and might be employed for industrial and technical applications.

The main findings are as follows:

• When suction increases, the flow speed drops rapidly but the flow is boosted under the effect of the injection parameter.

• The velocity profile decreases for the unsteadiness parameter in the presence of suction/injection parameters.

• The energy distribution rises rapidly with the unsteadiness parameter and is high on the far boundary.

• The effect of the Prandtl number drops the temperature of the flow but, due to the thermal relaxation parameter, energy distribution rises and is stable on the boundary.

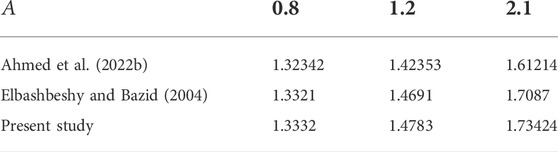
• Numerical shooting along with RK4 gives the best assessment results in comparison with the existing literature.

• The thermal conductivity of Ag-H₂O is found to be higher than that of ND- H₂O. Since it is a better conductor and has a higher heat capacity, Ag-H₂O nanofluid is a superior choice.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Program under Grant No. RGP. 2/19/43.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afzal, N. (1993). Heat transfer from a stretching surface. Int. J. Heat Mass Transf. 36 (4), 1128–1131. doi:10.1016/s0017-9310(05)80296-0

ORIGINAL RESEARCH article

Numerical analysis of thermal transportation in nanodiamond and silver-based nanofluid using the Cattaneo–Christov heat flux model

Introduction

The flow model and its formulation

Solution process of the nanofluidic system

Basic principles of the shooting technique

Results and discussion

Flow distribution f′(η)

The temperature distribution θ(η)

The volume fraction (ϕ)

Major findings

Data availability statement

Author contributions

Acknowledgments

Conflict of interest

Publisher’s note

References

Nomenclature

Greek Symbols

Flow distribution $f^{'} (η)$

The temperature distribution $θ (η)$

The volume fraction ( $ϕ$ )