An approximate dynamic programming method for unit-based small hydropower scheduling

Hydropower will become an important power source of China’s power grids oriented to carbon neutral. In order to fully exploit the potential of water resources and achieve low-carbon operation, this paper proposes an approximate dynamic programming (ADP) algorithm for the unit-based short-term small hydropower scheduling (STSHS) framework considering the hydro unit commitment, which can accurately capture the physical and operational characteristics of individual units. Both the non-convex and non-linearization characteristics of the original STSHS model are retained without any linearization to accurately describe the hydropower production function and head effect, especially the dependence between the net head and the water volume in the reservoir, thereby avoiding loss of the actual optimal solution due to the large error introduced by the linearization process. An approximate value function of the original problem is formulated via the searching table model and approximate policy value iteration process to address the “curse of dimensionally” in traditional dynamic programming, which provides an approximate optimal strategy for the STSHS by considering both algorithm accuracy and computational efficiency. The model is then tested with a real-world instance of a hydropower plant with three identical units to demonstrate the effectiveness of the proposed method.

1 Introduction

With the high proportion of renewable energy penetration in power system, hydropower is of great significance for achieving the “dual carbon” national goal as a clean energy source with almost zero carbon emissions. Different from other countries’ energy structure, China has the richest hydropower resources in the world, which can be a natural advantage to reduce the carbon dioxide emissions in daily operation of power grid. Short-term hydropower scheduling (STHS), which aims to determine the optimal hydropower generation strategy for each hydroelectric unit during a time horizon from several minutes or hours to 1 day, plays an essential role in the daily or shorter operation of power systems to maximize the utilization of the potential hydropower resources. STHS problems are generally formulated for hydropower plants, i.e., aggregating all the hydroelectric units in a plant and taking them as one equivalent unit to significantly reduce the size of the STHS problem (Zhao et al., 2021). However, these equivalent models neglect the detailed characterization of the properties of the hydroelectric units and thus are not suitable for the STSHS problem, which requires a more accurate and detailed representation of the nonlinear hydropower production function (HPF) and head effect of each unit (Guisández and Pérez-Díaz, 2021; Diniz and Maceira, 2008). Therefore, the representation of more details, such as exact unit commitment and nonconvex HPF, is needed to express the operating characteristics of small hydropower in unit-based (“unit-based” refers to “regarding each hydro-turbine generator unit in a plant as an independent entity”) STSHS more accurately.

STHS considering hydro unit commitment (HUC) is a combinatorial, non-convex and non-linear optimization problem (Catalão et al., 2010; Postolov and Iliev, 2022; Wang et al., 2022). The STHS problem has been extensively investigated by researchers in recent years (Chen et al., 2016). For an aggregated hydropower plant and a single hydropower unit, the interior-point method (IPM) can effectively address non-linear constraints in the STHS, but it cannot solve STHS problems with 0–1 binary variables (Apostolopoulou and McCulloch, 2019; Cheng et al., 2022). Mixed-integer linear programming (MILP) is one of the most widespread methods for STHS problems considering HUCs due to its modelling flexibility, simple and efficient software environment, and global search capability (Guedes et al., 2017). In (Cheng et al., 2016), a MILP model for HUC is developed, and the unit performance curves are discretized into a set of piecewise curves based on a discretized net head such that the head effect can be modelled. In (Zhao et al., 2021), a MILP-based HUC framework is proposed to solve the irregular forbidden zone-related constraints for very large hydropower plants. In (Guisández and Pérez-Díaz, 2021), five MILP formulations for piecewise linearization of the HPF equation are discussed: the traditional method based on a single concave piecewise-linear flow-power function (Conejo et al., 2002; Kong et al., 2020), the rectangle method (Borghetti et al., 2008; D’Ambrosio et al., 2010), the logarithmic independent branching 6-stencil method (Huchette and Vielma, 2017), the quadrilateral method (Keller and Karl, 2017), and the parallelogram method (PAR) (Guisández and Pérez-Díaz, 2021). The above-mentioned linearization methods can mitigate the computational burden, and the errors caused by linearization can be accepted in the economic dispatch of large hydropower stations with high head-power dependency and large installed capacity (Shi et al., 2017; Zhang et al., 2021). However, in the STHS of small hydropower plants, the operating net head of hydroelectric units is generally low, and the water volume of reservoirs and the installed capacity of hydro plants are generally small; therefore, the head effect is obvious. The effects of linearization errors in both the net head and the output can be ignored only if the breakpoints are sufficiently dense in the piecewise linearization process (Skjelbred et al., 2020). Nevertheless, with an increase in the density of breakpoints, the advantage of MILP in improving the solution efficiency is often lost with the sharp increase in the time cost.

To solve the above-mentioned large-scale, discrete non-convex and non-linear optimization problem of the unit-based STSHS (Marchand et al., 2018), dynamic programming (DP) has been applied effectively in the hydro scheduling field due to its superior performance in handling discrete variables and non-convex and non-linear constraints in STSHS problems (Morillo et al., 2020). DP decomposes a multi-stage decision problem into a number of single-stage sub-problems and can obtain the global optimal solution in most cases. However, DP is difficult to solve even for medium-sized scheduling problems because the computational burden increases exponentially with the dimensionality of the state space. To alleviate the problem of the curse of dimensionality, several variants of DP have been proposed in recent years. In (Flamm et al., 2021), a two-stage dual dynamic programming method is proposed to reconstruct the nonlinear problem; the approach is notable for its calculation accuracy and solving efficiency. In (Feng et al., 2017), an orthogonal discrete differential dynamic programming (ODDDP) method is introduced. The orthogonal experimental design can select some small but representative state combinations, thereby alleviating the curse of dimensionality. Although these improved DP methods have achieved various degrees of success in terms of alleviating the curse of dimensionality, the computational burden may still be intolerable when the problem scale reaches a certain degree. In addition, to ensure computational efficiency, the nonlinear expression of HPF in the literature is usually not sufficiently accurate, and the impacts of power generation on the water head are also not considered, so it is not suitable for STSHS. Thus, there is an urgent need to develop new efficient algorithms to improve the computational efficiency and convergence accuracy for STSHS.

Approximate dynamic programming (ADP) is an important and powerful artificial intelligence optimal method (Zeng et al., 2019) that has attracted considerable attention in the fields of power system scheduling (Lin et al., 2019; Zhu et al., 2019; Lin et al., 2020; Zhu et al., 2020). The theory of ADP was proposed by Powell W.B. (Powell, 2011), and its core idea is to avoid the traversal of all states to reduce the computational burden of value function approximation (VFA) while ensuring approximate accuracy. ADP has been successfully applied to power system optimization. In (Xue et al., 2022), an ADP algorithm proposed for the real-time schedule of an integrated heat and power system established the mapping relationship between the battery and heat storage tank to approximate the value function through a table function model, thereby achieving the approximation of the optimal value function by traversing discrete values with fewer state variables. In (Shuai et al., 2019), an ADP algorithm based on a piecewise-linear approximation strategy was employed to address the fluctuations in renewable energy generation and electricity prices in the real-time dispatching of microgrids. In (Shuai et al., 2020), a hybrid approximate dynamic programming method was proposed by combining model predictive control and ADP. The model was then applied to the real-time scheduling of gas-electricity integrated energy systems, successfully addressing the tight coupling between time periods caused by the material balance equation of natural gas systems. ADP inherits all the advantages of DP and can efficiently address discrete or continuous, linear or nonlinear, deterministic or stochastic problems (Qiu et al., 2020). However, to the best of our knowledge, few published studies have been conducted on solving the unit-based STSHS framework, especially when the HUC problem is non-convex and the HPF is a bivariate quadratic equation.

This paper formulates the unit-based STSHS optimization problem considering HUC as a mixed-integer nonlinear programming (MINLP) model, which includes the constraints that can describe the HPF and head effect of hydroelectric units accurately. We propose the ADP algorithm to solve the STSHS model without any approximation treatment of the nonlinear constraints.

The contributions of this paper are summarized as follows:

1) An ADP algorithm is proposed to solve the STSHS model. The intractable MINLP problem is reformulated into a solvable NLP problem by decomposing the multi-period optimization into multiple single-period optimizations for the sake of computational tractability. The non-linear expression of HPF and the head effect is retained to ensure the optimality of the schedule strategy.

2) A table function model is developed to establish the mapping relationship between the discrete states of the water volume of the reservoir and the value function; by such means, the high-dimensional state variables are aggregated to approximate the value function, and the optimal value function is approximated by the value iteration method. Thus, schedule strategy optimality and a computationally efficient policy are achieved.

3) A state space compression strategy, according to the operation characteristics of small hydropower plants, is proposed for the consideration of both the effectiveness and optimization ability. This compression strategy can remove the redundant states from the search space by analyzing the variation in available water in each period, which does not reduce the number of discrete states. This strategy not only ensures the optimization ability but also greatly reduces the scale of the problem and further improves the computational efficiency.

The rest of this paper is organized as follows: Section 2 describes the STSHS framework, including the start-up and shutdown of each hydro unit. Section 3 proposes the ADP algorithm for the HUC, which is the main contribution of this paper. In Section 4, we test the proposed ADP algorithm on a realistic instance of a hydropower station with three identical units to verify the effectiveness of our method. Finally, Section 5 presents conclusions.

2 Description of short-term small hydropower scheduling framework considering hydro unit commitment

2.1 Objective function

The objective of the optimal operation of the STSHS is to find the maximum power generation of all the small hydropower units in the entire scheduling horizon, which can be expressed as

$\max F_p={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^m{d}_{i,t}\cdot p_{i,t}\cdot \mathrm{\Delta }t}}(1)$

The output power $p_{i,t}$ is defined by the HPF, and it can generally be expressed as

$p_{i,t}=G\cdot {\eta }_{i,t}^{\mathrm{Gen}}\left(p_{i,t}\right)\cdot {\eta }_{i,t}^{\mathrm{Turb}}\left(h_{i,t},q_{i,t}\right)\cdot h_{i,t}\cdot q_{i,t}(2)$

The hydro turbine efficiency ${\eta }_{i,t}^{\mathrm{Turb}}$ is associated with converting the water head potential energy in the reservoir into mechanical energy in the hydro turbine; therefore, it primarily depends on the water head and turbine flow. ${\eta }_{i,t}^{\mathrm{Turb}}$ decreases as turbine flow increases after reaching the optimum efficiency point. Similarly, the hydropower generation efficiency ${\eta }_{i,t}^{\mathrm{Gen}}$ is related to the conversion of mechanical energy into electrical energy in the generator, which is usually higher than 95%, and it increases monotonically as the output power of the generator increases.

Since the mathematical expression of the hydro unit efficiency function is considerably complicated, a fixed constant is typically used to replace the efficiency function irrespective of the characteristics of the HPF, which will lead to larger errors. To describe the input–output relationship of the efficiency function implicitly in the HPF more accurately, this paper conducts a polynomial fitting of the water head and water flow in the HPF based on the Hill diagram of the hydropower unit (Zhang et al., 2021; Zhao et al., 2021), which can be expressed as

$p_{i,t}=a_i{h}_{i,t}^2+b_i{q}_{i,t}^2+c_i{h}_{i,t}{q}_{i,t}+d_i{h}_{i,t}+e_i{q}_{i,t}+f_i(3)$

where $a_i$, $b_i$, $c_i$, $d_i$, $e_i$ and $f_i$ are the quadratic fitting coefficients of the HPF, which models the relationship between the power output of hydroelectric unit $i$ and the water discharge and net head.

2.2 Constraints

The STSHS problem is subject to a variety of constraints, including water balance, water level, water head, and other operating limits.

2.2.1 Water balance constraint

The volume change of the reservoir is affected by the inflow, water discharge and spillage of the reservoir. The water balance equation is denoted as

$r_{t+1}=r_t-\left({\displaystyle \sum _{i=1}^m{q}_{i,t}}+s_t-j_t\right)\mathrm{\Delta }t(4)$

2.2.2 Water volume constraints

As the water volume of the reservoir at the end of the last period is the initial volume of the next dispatch horizon, to ensure the normal operation of the reservoir in the next dispatch horizon, the water volume of the reservoir at the beginning and the end of the dispatch horizon should be restricted as

$\{\begin{array}{l}{r}_0=r^{\mathrm{init}}\\ r_T=r^{\mathrm{final}}\end{array}(5)$

2.2.3 Limit constraints of water volume

$r^{\min }\le r_t\le r^{\max }(6)$

2.2.4 Net head balance constraint

$h_t=h_t^{\mathrm{up}}-h_t^{\mathrm{dw}}(7)$

2.2.5 Net head effect constraints

The head effect has a direct impact on the unit’s efficiency and operating limits, which is the crucial part of the formulation of the STSHS problem. For a fixed-head hydropower plant, the net head is relatively high; thus, the effect of water level changes in the forebay and tailrace caused by power generation can be ignored. However, for a low-head hydropower plant, the changes in the water levels of the forebay and tailrace have relatively obvious impacts on the net head. Therefore, the relationship between the forebay level and the water volume, as well as the tailrace level and the outflow, can be expressed as

$h_t^{\mathrm{up}}=a^{\mathrm{up}}{r}_t^2+b^{\mathrm{up}}{r}_t+c^{\mathrm{up}}(8)$

$h_t^{\mathrm{dw}}=a^{\mathrm{dw}}{\left({\displaystyle \sum _{i=1}^m{q}_{i,t}+s_t}\right)}^2+b^{\mathrm{dw}}\left({\displaystyle \sum _{i=1}^m{q}_{i,t}+s_t}\right)+c^{\mathrm{dw}}(9)$

where $a^{\mathrm{up}}$, $b^{\mathrm{up}}$ and $c^{\mathrm{up}}$ are the fitting coefficients of the relationship between the forebay level and water volume. $a^{\mathrm{dw}}$, $b^{\mathrm{dw}}$ and $c^{\mathrm{dw}}$ are the fitting coefficients of the relationship between the tailrace level and the total outflow of the hydropower plant, respectively.

2.2.6 Limits of net head

$h^{\min }\le h_t\le h^{\max }(10)$

2.2.7 Output limits

$d_{i,t}{p}_i^{\min }\le p_{i,t}\le d_{i,t}{p}_i^{\max }(11)$

2.2.8 Constraints of water discharge

$d_{i,t}{q}_i^{\min }\le q_{i,t}\le d_{i,t}{q}_i^{\max }(12)$

3 Approximate dynamic programming

3.1 Process of approximate dynamic programming

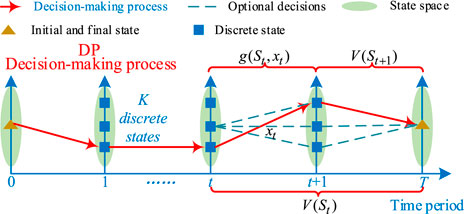
ADP is an excellent method proposed by Powell to solve the curse of dimensionality problem of dynamic programming (Xue et al., 2022). A diagram of the use of ADP to solve the STSHS problem is illustrated in Figure 1, in which the system state $S_t$ includes the reservoir volume of the water head and the on/off status of the unit. The decision variables $x_t$ include the allocation of power generation flow, water spillage, and the start-up/shutdown action of units during each period. $S_{t+1}$ is the state vector of the next period after decision $x_t$ is executed in state $S_t$. $g\left(S_t,x_t\right)$ denotes the benefit generated by reaching state $S_{t+1}$ after executing $x_t$. The value function $V\left(S_t\right)$ reflects the influence of the current state on the revenue from period $t$ to $T$, that is, the maximum power generation during $\left[t,T\right]$.

FIGURE 1

FIGURE 1. Diagram of ADP solution.

According to the optimality principle, the above $T$ stage maximum profit problem can be transformed into $T$ single-period decision-making problems with the Bellman equation so that the optimal solution can be obtained via step-by-step recursion, which can be expressed as

$V\left(S_t\right)=\max \left[g\left(S_t,x_t\right)+V\left(S_{t+1}\right)\right](13)$

The solution of the Bellman equation is based on the calculation of the value functions of all states in the state space. However, current computer technology is still insufficient to traverse the combination of the enormous state space and decision space. The key idea of ADP is to use the approximate value function ${\tilde{V}}_k\left(S_{t+1}\right)$ instead of $V_k\left(S_{t+1}\right)$ and to approximate the optimal value function in an iterative manner, thereby avoiding direct calculation of the value function.

The basic process of value function iteration is as follows:

First, set the initial value of the approximate value function of each state. Then, calculate the approximate value function from period 0 to period $T$; the optimal solution of this iteration is determined based on the rule that the function value of the last period is optimal. Next, proceed to the next iteration according to the updated approximation function. In this way, the approximate value function is gradually approximated to the optimal value function through the iterative process. In each iteration, instead of traversing the entire state space to calculate the value function, only a small number of states participate in the calculation in each period, so the computational complexity no longer increases exponentially with an increase in the number of state variables and the total number of periods, thereby overcoming the curse of dimensionality.

The value function approximation (VFA) methods commonly used in ADP include table function approximation, piecewise linear function approximation and neural network approximation, among which table function approximation is a basic but very effective method that can accurately approximate the complex non-linear value function in hydro economic dispatch. Hence, the look-up table model is applied to approximate the value function, and the value iteration method is employed to solve the Bellman equation.

3.2 Lookup table for the short-term small hydropower scheduling problem

The optimization strategy based on the look-up table establishes a mapping relationship between the discretized system state variables and the sum of the power generation of each time period. The table function is used to approximate the real value function, and by means of variable decoupling between time periods, the original MINLP problem can be decomposed into multiple NLP sub-problems containing only continuous variables to reduce the difficulty of solving.

The continuous variables in the state variables are discretized as

$\mathrm{\Delta }{S}_i=\left(S_i^{\max }-S_i^{\min }\right)/\left(K_i-1\right)(14)$

where $\mathrm{\Delta }{S}_i$ represents the discretization step size of the continuous variable. $S_i^{\max }$ and $S_i^{\min }$ are the upper and lower limits of the variable, respectively. $K_i$ is the number of discrete variables. In this paper, the water volume of the reservoir is discretized into $K_r$ states, and the on/off status of $m$ units is $2^m$, so the size of the state space is $M=2^m\times K_r$. After the process of discretization, we can initialize an empty value table to measure the value of being in a state, and the size of the table is $M\times T$.

3.3 Approximate value iteration

The value iteration of ADP forms a value function sequence by continuously updating the value table to approximate the optimal value function. In each iteration, the decision is determined by the estimated value of the current value function and the state variable, which can be expressed as

$x_t^k=\arg \max \left\{g_t\left(S_t,x_t\right)+\gamma {\tilde{V}}_t^{k-1}\left(G\left(S_t\right)\right)\right\}(15)$

where $\gamma \in \left(\mathrm{0,1}\right)$ is the decay factor. When $\gamma$ is 0, the value function focuses on only the immediate benefits after the decision is made in the current period, and the algorithm becomes a short-sighted myopic algorithm. When $\gamma$ approaches 1, the algorithm pays more attention to the benefits in the future period, which is more conducive to obtaining the optimal value table of the whole period. $G\left(S_t\right)=\left\{r_t,d_{1,t},\dots ,d_{m,t}\right\}$ is the aggregated state variable.

After completing the decision for each period, the observed value ${\widehat{v}}_t^k$ of the value function of the current state is calculated as

${\widehat{v}}_t^k=\min \left\{g_t\left(S_t,x_t\right)+{\tilde{V}}_t^{k-1}\left(G\left(S_t\right)\right)\right\}(16)$

Then, the value function of the previous period is updated as

${\tilde{V}}_{t-\mathrm{\Delta }t}^k\left(G\left(S_{t-\mathrm{\Delta }t}^k\right)\right)={\alpha }^k{\widehat{v}}_t^k+\left(1-{\alpha }^k\right){\tilde{V}}_{t-\mathrm{\Delta }t}^{k-1}\left(G\left(S_{t-\mathrm{\Delta }t}^k\right)\right)(17)$

where ${\alpha }^k\in \left(\mathrm{0,1}\right)$ is the step size in the k-th value iteration.

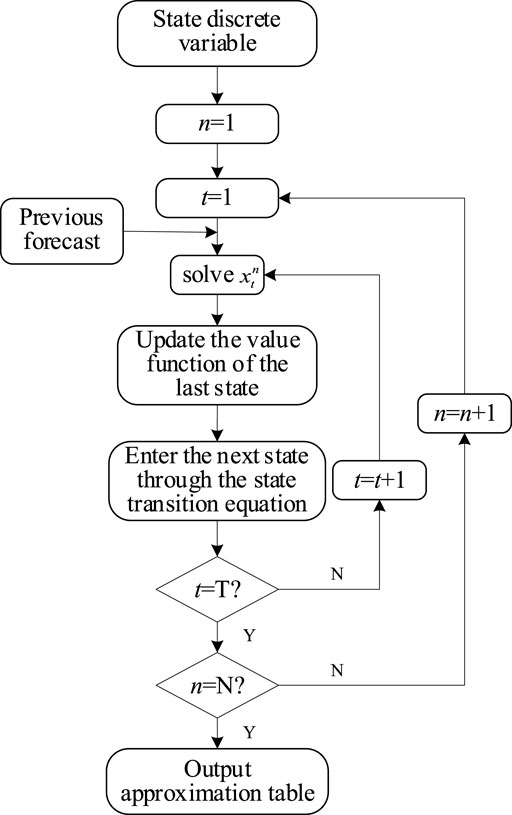
In the process of value iteration, only the value function corresponding to the state accessed in each period is updated. In other words, in the approximate value table, only the cells corresponding to the current reservoir volume and the unit on/off status are updated. In each iteration, the corresponding elements accessed in the table function are updated in a forward manner step by step until a converged approximation table is obtained. The iterative process for updating the value table is shown in Figure 2.

FIGURE 2

FIGURE 2. Iteration flow chart of the approximate value table.

3.4 Compression of state space

In the above ADP algorithm, for each time period t, all discrete states are traversed when solving 15) to select the optimal decision-making action, which makes the solution process highly time-consuming. Therefore, to reduce the computational burden caused by the increase in discrete states, considering the operation mode of determining electricity-by-water of small hydropower, we compress the existing state space to further reduce the solution time.

First, the forecasting information of water inflow is developed to compress the search space of discrete states of water volume. For period t of the k-th iteration, the total available water volume $q_{k,t}^{\text{avl}}$ can be defined as

$q_{k,t}^{\mathrm{avl}}=j_t\cdot \mathrm{\Delta }t-\left(r_{k,t+1}-r_{k,t}\right)(18)$

To ensure $q_{k,t}^{\text{avl}}>0$, the upper bound of the search space of the water volume $r_{k,t+1}$ in the next period should not exceed $j_t\mathrm{\cdot }\mathrm{\Delta }t+r_{k,t}$. In addition, to avoid unreasonable water abandonment, the total available water should not exceed the upper limit of the power generation flow of the units; that is, the lower bound of the search space of the water volume $r_{k,t+1}$ in the next period should not be lower than $j_t\cdot \mathrm{\Delta }t+r_{k,t}-{\displaystyle \sum _{i=1}^m{q}_i^{\max }}$. Therefore, the search space for discrete states of water volume can be restricted to:

$\{\begin{array}{l}{r}_{k,t+1}^{\min }=j_t\cdot \mathrm{\Delta }t+r_{k,t}-{\displaystyle \sum _{i=1}^m{q}_i^{\max }}\\ r_{k,t+1}^{\max }=j_t\cdot \mathrm{\Delta }t+r_{k,t}\end{array}(19)$

Similar strategies can be used to compress the on/off status of units in the search space. For period t in the k-th iteration, if the difference between the total available water in this period and the previous period satisfies $\mathrm{\Delta }{q}_{k,t}^{\mathrm{avl}}=q_{k,t}^{\mathrm{avl}}-q_{k,t-1}^{\mathrm{avl}}>0$, unnecessary traversal of the state that requires a shutdown action to reach should be avoided. For instance, if the current unit status is [1,100], then [0100] and [1,000] should be eliminated in the decision space during this period. In contrast, if the available water volume is reduced compared with that in the previous period, the statuses that require a start-up action to reach should be avoided. Therefore, [1,110], [1,101] and [1,111] should be excluded from the search space.

The scale of the problem is greatly reduced by adopting the above compression processing strategy of the search space. For the hydro units of the identical model, their output characteristics are exactly the same. For the objective of maximum power generation, the exchange of on/off status between units will not affect the optimization results, so the optional states can be further compressed. For example, for the same four hydro units, assuming that the state in a certain period is [1,100], regardless of the trend of available water, the five statuses [1,010], [1,001], [0110], [0101] and [0011] in the state space can be represented by the original state [1,100], so these five states can be eliminated from the search space. When the number of units of the same model increases, the proposed strategy makes the state space no longer grow exponentially but increase linearly, further reducing the decision space, thereby greatly reducing the computational burden.

3.5 Description of non-convex operational zone in approximate dynamic programming process

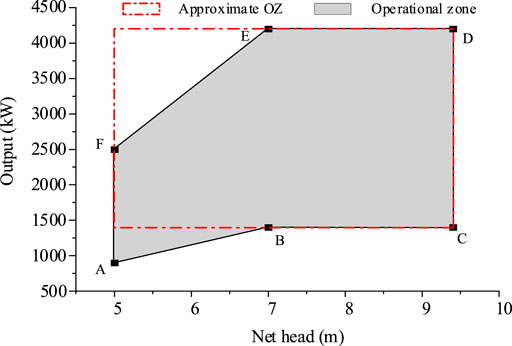
The operational zone (OZ) of small hydropower units is usually a non-convex polygon region, as shown in Figure 3.

FIGURE 3

FIGURE 3. The operational zone of small hydropower units.

The boundaries of the irregularly shaped OZ vary with the net head and have several inflection points, such as points B and E, as illustrated in Figure 3, which makes the OZ a non-convex region. The mathematical representation of the irregularly shaped OZ can be derived as follows:

$\{\begin{array}{l}{k}_i^{AB}\left(h_{i,t}-h_i^A\right)+p_i^A\le p_{i,t}\le k_i^{FE}\left(h_{i,t}-h_i^F\right)+p_i^F,h_i^A\le h_{i,t}\le h_i^B\\ p_i^B\le p_{i,t}\le p_i^E,h_i^B\le h_{i,t}\le h_i^C\end{array}(20)$

where $h_i^A$, $h_i^B$, $h_i^C$ and $h_i^F$ represent the net head of points A, B, C and F, respectively. $p_i^A$, $p_i^E$ and $p_i^F$ indicate the unit output of points A, E and F, respectively. $k_i^{AB}$ and $k_i^{FE}$ denote the slopes of $\overrightarrow{AB}$ and $\overrightarrow{FE}$, respectively. If we employ a regularly shaped rectangle to approximate OZ, such as the red dotted box shown in Figure 3, the approximate OZ would not only raise the lower limit of unit output under the lower net head but also reduce the final generation. However, it will fail to ensure the safety of unit operation when the water discharge is large. Generally, such a non-convex region cannot be perfectly represented with linear constraints in programming models unless additional 0–1 variables are introduced.

Under the ADP framework proposed in this paper, the irregularly shaped OZ can be perfectly expressed. In each single-period optimization process, the variation in water volume is a constant. As a result, the optimal result of water discharge for each unit is obtained before solving the single-period sub-problem, which means the net head has already been pre-designated. Thus, the upper and lower boundaries of the OZ can be dynamically updated as the net head changes.

4 Case studies

A small hydropower plant in southern China is adopted as a test system to verify the effectiveness of the proposed formulation and methodology. The parameters of each unit are illustrated in Table 1. All simulations are implemented with MATLAB R2021a using a PC with a 3.6 GHz AMD R7 4700G processor and 16 GB of RAM. The scheduling period is 24 h, and the time resolution is 1 h.

TABLE 1

TABLE 1. Parameters of hydro units.

4.1 Iterative process of the approximate value function

To express the dynamic approximation process of the value function, we define the change rate of the approximation function as follows:

$\eta \left({\tilde{V}}_{k,t}\right)=\left({\tilde{V}}_{k,t}-{\tilde{V}}_{opt,t}\right)/\left({\tilde{V}}_{0,t}-{\tilde{V}}_{opt,t}\right)\times 100\%(21)$

The indicator $\eta \left({\tilde{V}}_{k,t}\right)$ reflects the differences in the value function of each period compared with the optimal value function in the k-th iteration. The change in this difference represents the adjustment of the state of the ADP algorithm in the iterative process to achieve the maximum power generation. For instance, if the initial value function ${\tilde{V}}_{0,t}$ of period t is greater than the optimal value function ${\tilde{V}}_{opt,t}$, and $\eta \left({\tilde{V}}_{k,t}\right)>0$ in the k-th iteration, then there is ${\tilde{V}}_{k,t}>{\tilde{V}}_{opt,t}$, indicating that the value function of the state during the current period is better than the optimal value function. However, due to the significant impact on the state of t+1 and subsequent periods, which restricts future power generation, it is discarded in the subsequent iteration process. In contrast, if $\eta \left({\tilde{V}}_{k,t}\right)<0$, then ${\tilde{V}}_{k,t}<{\tilde{V}}_{opt,t}$, indicating that the approximation of the value function in the current period is inferior to the optimal value function. Therefore, a better strategy will be sought in the subsequent iteration process.

Figure 4A shows the change rate of the approximate value function of the three units in 24 time periods with the ADP iteration process, and the change rate convergence curve for each time period is shown in Figure 4B. Figure 4 shows that $\eta \left({\tilde{V}}_{k,t}\right)$ oscillates positively and negatively with the value iteration process and finally converges to 0, indicating that the algorithm gradually updates the strategy in the iterative process and approaches the optimal value function to achieve the goal of maximum power generation.

FIGURE 4

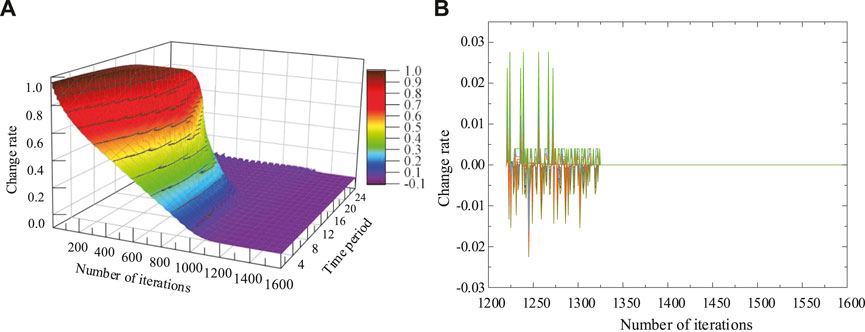
FIGURE 4. Approximate value function iteration process. (A) Full view; (B) Front view of iterations after 1200.

4.2 Optimization results of single-unit short-term small hydropower scheduling

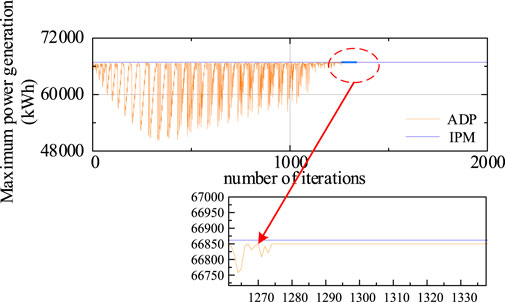
To clarify the approximation process of the power generation obtained by the proposed ADP algorithm to the optimal solution, the discrete state number Kr of the water volume is taken as 51, and the single-unit optimization convergence curve of the ADP algorithm is obtained as depicted in Figure 5. The ADP algorithm converges to the optimal generation of 66,849.81 kWh when the number of iterations reaches 1,325, which is only 0.0194% different from the optimal result of 66,862.79 kWh obtained by IPM, thereby demonstrating the optimality of the proposed ADP algorithm in solving the STSHS.

FIGURE 5

FIGURE 5. Convergence curves of ADP and IPM.

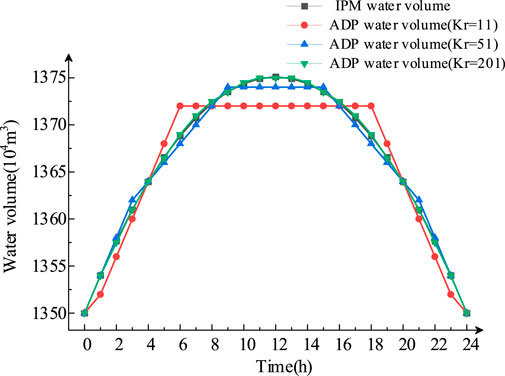
To illustrate the influence of Kr on the approximation of the optimal solution of the non-linear problem by the ADP algorithm, the number of discrete states Kr of water volume is taken as 11, 51, and 201, and the optimization results of single-unit STSHS by ADP and IPM are compared, as shown in Figure 6. As Kr increases, the water volume of ADP gradually approaches the optimal water volume of IPM. When Kr is 201, the water volume curve of ADP almost overlaps with that of IPM, which indicates that the decision made by ADP in each period will gradually approach the optimal as the number of discrete points of water volume increases.

FIGURE 6

FIGURE 6. Changes in the water volume under different numbers of discrete points.

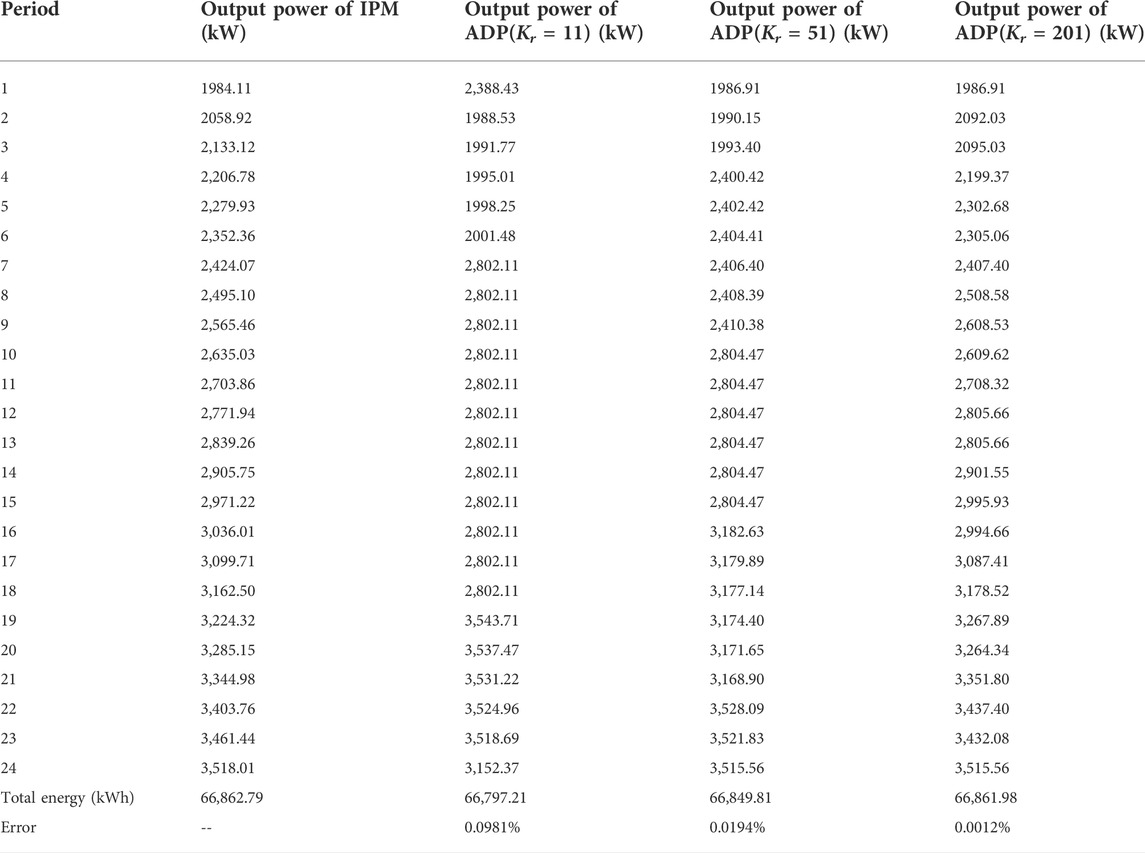
To further illustrate the performance of the ADP algorithm, Table 2 lists the unit output of the IPM and ADP algorithms in all 24 time periods. Table 2 shows that as the number of discrete states of water volume increases, the approximate solution obtained by ADP gradually approaches the optimal solution obtained by IPM. When Kr = 11, the error compared to the maximum power generation of IPM is reduced to 0.0982%, which can fully meet the needs of engineering applications. When Kr is increased to 201, the error compared to the maximum power generation of IPM is only 0.0012%. The above results show that for the STSHS problem, the error between the solution of the ADP algorithm and the optimal solution is extremely small, and the quality of the solution can be significantly improved by increasing the number of discrete states, further indicating that the proposed algorithm has superior convergence performance and practical engineering value.

TABLE 2

TABLE 2. Comparison of IPM and ADP optimization results.

4.3 Optimization results of multiple-unit short-term small hydropower scheduling

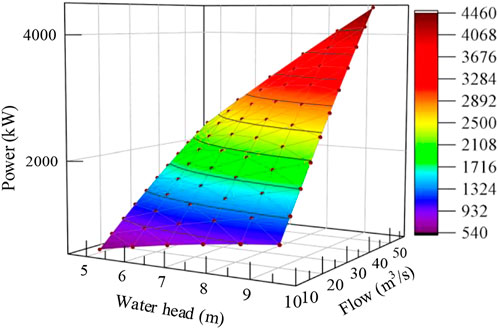
When the STSHS model includes 0–1 variables representing the on/off status of the units, it cannot be solved by IPM. With the maturity of the solving technology of the MILP problem, the MILP model of the STSHS problem can be achieved via piecewise linearization and then using a commercial solver to obtain the optimal solution. In this paper, PAR is used to perform piecewise linearization of the HPF function (3). The number of discrete points of net head M_h = 6, the number of discrete points of water discharge M_q = 11, and the obtained approximate output surface is shown in Figure 7.

FIGURE 7

FIGURE 7. Approximate output surface using the PAR method (M_h = 6, M_q = 11)

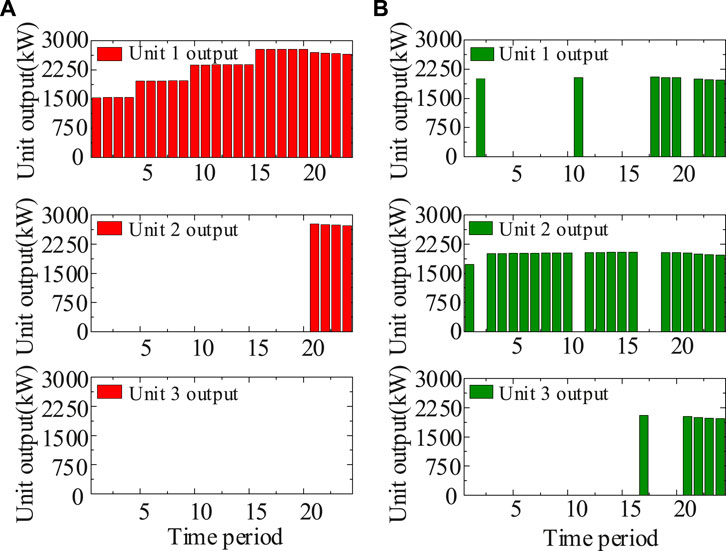
For the STSHS problem involving three units, the state discrete number K_r of the water volume is set to 51, and the unit output optimization results obtained using ADP and PAR-MILP are shown in Figure 8.

FIGURE 8

FIGURE 8. Comparison of unit output between ADP and PAR-MILP. (A) ADP; (B) MILP.

Figure 8 shows that the units start and stop frequently in the MILP results. One reason is that the output characteristics of the three hydropower units are the same. The second reason is that, ignoring the start-up and shutdown costs of small-capacity hydropower units, if the inflow is small, the reservoir tends to store water to raise the net head, and the amount of water available for power generation is limited, resulting in an unnecessary start and stop. In comparison, the optimization results of unit commitment obtained via ADP are more stable and reasonable, among which unit 3 is not even turned on during the whole scheduling period. The reason is that in the ADP algorithm, the search space for the unit commitment decision is compressed, and the redundant on/off state is eliminated from the decision space. As a result, a relatively smooth unit commitment scheme can be obtained without applying additional constraints, such as unit start/stop costs.

Next, to further verify that the ADP algorithm proposed in this paper more easily achieves a satisfactory trade-off between solving efficiency and solution optimality compared with other algorithms, we compare the optimization results of MILP, MINLP and myopic methods with ADP. The Gurobi 9.1.2 commercial solver is used for MILP, and the LINGO commercial solver is used for MINLP. The results of the power outputs of each method under different reservoir inflows are shown in Figure 9, and the time consumption and total generation results are shown in Table 3.

FIGURE 9

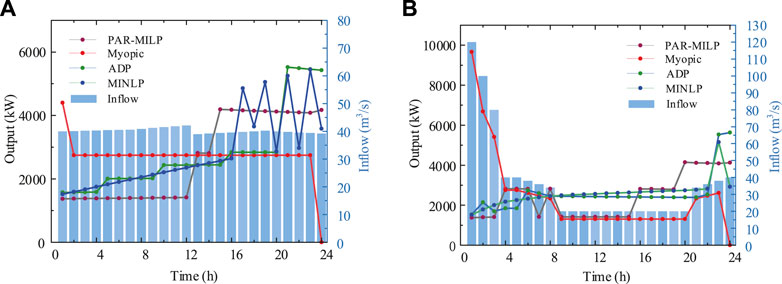
FIGURE 9. Comparison of the output of each method under different inflows. (A) Case 1: Relatively smooth inflow; (B) Case 2: Inflow with a significant drop.

TABLE 3

TABLE 3. Comparison of optimization results of each method.

As shown in Figure 9 and Table 3, regardless of the inflow changes, the generation results of ADP and MINLP are extremely close and larger than those of other methods because they completely retain the nonlinearity of HPF and the head effect. Although the myopic algorithm also completely retains the original non-linearity, due to its short-sighted characteristics, the impacts of the current strategy on the subsequent period cannot be considered in the decision-making process, and the power generation obtained is the lowest. Especially after rainfall, when the water inflow gradually decreases, the disadvantages of the myopic algorithm become more obvious. As shown in Figure 9B, myopic tends to maximize the water discharge during each time period, ignoring the reduction of net head in the next time period, which causes the total generation to be 7.5% less than that of the ADP method. Using commercial solvers directly to solve MINLP problems can also produce high-quality solutions, which are only 0.2% different from the ADP results, but the time consumption is 20 times greater than that of ADP. Although PAR-MILP approximates the nonlinear HPF surface by piecewise approximation, the energy generation optimization result is not substantially different from that of ADP, but the corresponding time cost is still much higher than that of ADP. The comparison results indicate that the solution quality of ADP is remarkable among the four algorithms on the premise of ensuring the optimization accuracy level within 0.2%. In terms of computational efficiency, ADP is superior to MILP and MINLP.

4.4 Effect of state space compression

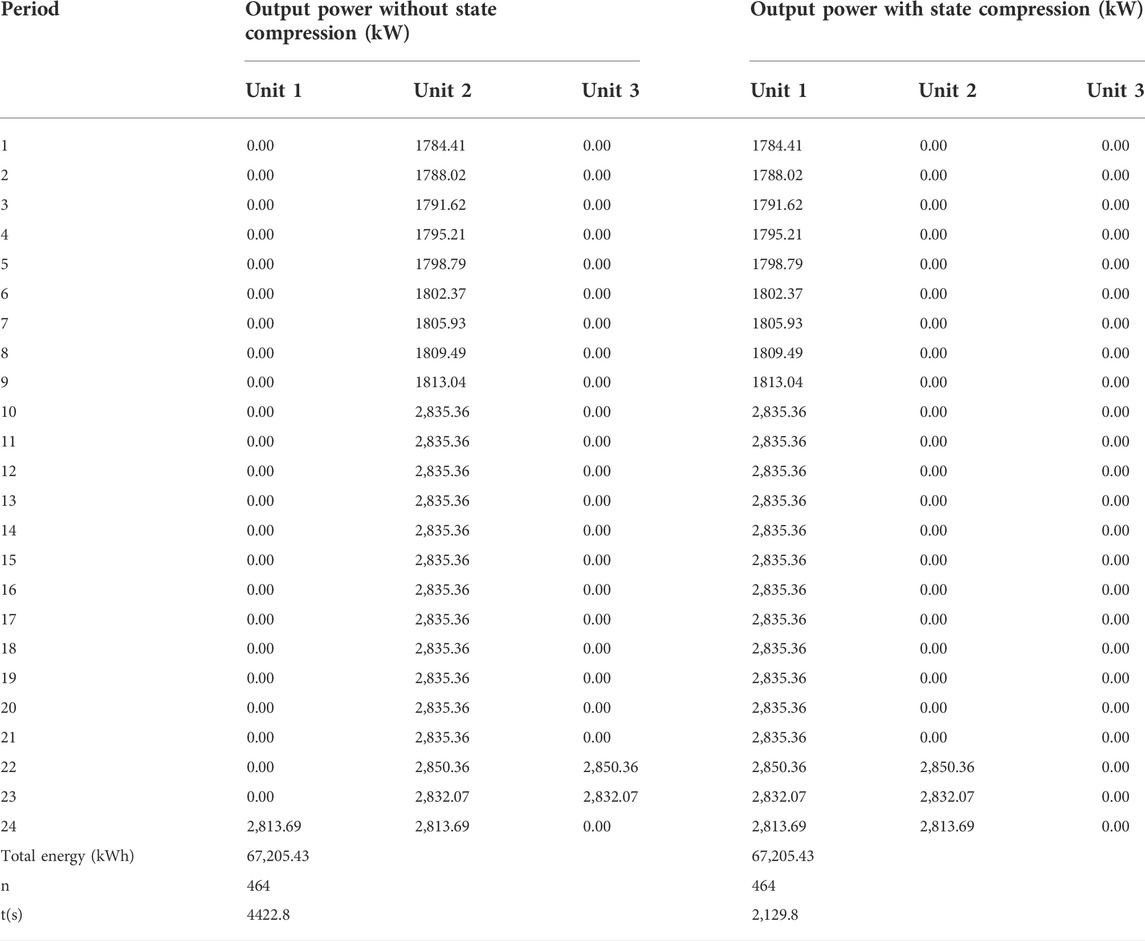
To further illustrate the effect of the proposed state space compression strategy in improving the efficiency of ADP, the number of discrete states K_r of the water volume is set to 21, and the optimization results before and after state space compression are obtained, as shown in Table 4, where n is the number of ADP iterations and t is the time consumption of ADP.

TABLE 4

TABLE 4. Comparison of optimization results before and after space compression.

Table 4 shows that the optimal power generation obtained by the ADP algorithm before and after state space compression is the same, indicating that the states eliminated by the proposed compression strategy are redundant states that do not need to be traversed and will not affect the algorithm’s optimization ability. In addition, the execution time of ADP after state compression is reduced by 51.84%, which demonstrates that the proposed compression strategy significantly improves the solution efficiency and is suitable for cases with multiple hydropower units, showing its potential practicability and validity for solving the STSHS problem.

4.5 The effect of value table size on approximate dynamic programming optimization results

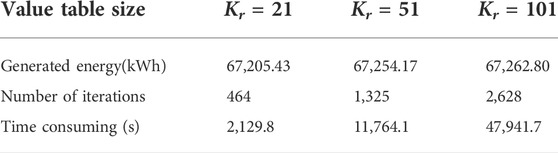
To clarify the relationship between the approximate accuracy of ADP and the size of the value table, we set the discrete number K_r of the water volume to 21, 51, and 101, which means that the adjacent state intervals of the water volume are 50,000 m³, 20,000 m³, and 10,000 m³, respectively. To ensure that the reservoir can reach the maximum water storage capacity, the initial volume of the reservoir is set to 13.4 million m³. The simulation results of ADP with different values are shown in Table 5.

TABLE 5

TABLE 5. Comparison of ADP optimization results with different value table sizes.

Table 5 shows that as the size of the value table increases, the power generation gradually increases, indicating that the quality of the solution also improves. In addition, the number of iterations and solution time increase linearly with the size of the value table. A possible explanation for this is that as the number of discrete states increases, the value table must be updated more often to better approximate the value function, so the number of iterations required to converge increases. In addition, since the state of the water volume is more discrete, in the ADP algorithm, more sub-problems must be solved in each period and in each iteration to make the optimal decision, resulting in an increase in the time consumption of each iteration. Therefore, when using ADP to solve the STSHS problem with unit commitment, a trade-off should be made between approximation accuracy and calculation time according to engineering requirements.

5 Conclusion

An ADP solution algorithm is proposed for the problem of short-term economic dispatch of small hydropower. The mapping relationship between the discrete state of the water volume and the value function is established through the table function model. Furthermore, the state space is compressed, and the MINLP problem is transformed into multiple NLP sub-problems to reduce the model complexity.

A comparison with the IPM optimization results shows that ADP and IPM tend to produce the same solution in the case of single-unit operation, which proves that the proposed ADP method can obtain high-quality solutions.

For the case of multi-unit optimal scheduling, comparison with the results of myopic, MILP and MINLP shows that ADP obtains better power generation results than myopic and MILP because it retains the nonlinearity of the original model. In addition, the solution time required to make MINLP obtain the same level of optimization results as ADP will obviously exceed that of ADP. This verifies that the proposed method can consider both the quality of the solution and the computational efficiency in solving the non-convex nonlinear SHED problem.

The results of ADP optimization with space compression show that the proposed space compression strategy can effectively reduce the number of candidate decision-making actions in the iterative process and significantly improve the solution efficiency.

Simulation results with different table sizes show that the proposed algorithm can achieve a balance between optimality and solution efficiency by setting the discrete number of water volumes.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YJ: Software; Formal analysis; Investigation; Writing-Original Draft; Data Curation; Visualization. HW: Conceptualization; Methodology; Resources; Data Curation; Writing-Review & Editing Supervision; Funding acquisition.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51967002) and in part by the Guangxi Special Fund for Innovation-Driven Development (AA19254034).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Apostolopoulou, D., and Mcculloch, M. (2019). Optimal short-term operation of a cascaded hydro-solar hybrid system: A case study in Kenya. IEEE Trans. Sustain. Energ. 10 (4), 1878–1889. doi:10.1109/TSTE.2018.2874810

CrossRef Full Text | Google Scholar

Borghetti, A., D'Ambrosio, C., Lodi, A., and Martello, S. (2008). An MILP approach for short-term hydro scheduling and unit commitment with head-dependent reservoir. IEEE Trans. Power Syst. 23 (3), 1115–1124. doi:10.1109/TPWRS.2008.926704

CrossRef Full Text | Google Scholar

Catalão, J., Pousinho, H., and Mendes, V. M. F. (2010). Mixed-integer nonlinear approach for the optimal scheduling of a head-dependent hydro chain. Electr. Power Syst. Res. 80 (8), 935–942. doi:10.1016/j.epsr.2009.12.015

CrossRef Full Text | Google Scholar

Chen, Y., Liu, F., Liu, B., Wei, W., and Mei, S. (2016). An efficient MILP approximation for the hydro-thermal unit commitment. IEEE Trans. Power Syst. 31 (4), 3318–3319. doi:10.1109/TPWRS.2015.2479397

CrossRef Full Text | Google Scholar

Cheng, C., Wang, J., and Wu, X. (2016). Hydro unit commitment with a head-sensitive reservoir and multiple vibration zones using MILP. IEEE Trans. Power Syst. 31 (6), 4842–4852. doi:10.1109/TPWRS.2016.2522469

CrossRef Full Text | Google Scholar

Cheng, X., Feng, S., Zheng, H., Wang, J., and Liu, S. (2022). A hierarchical model in short-term hydro scheduling with unit commitment and head-dependency. Energy 251, 123908. doi:10.1016/j.energy.2022.123908

CrossRef Full Text | Google Scholar

Conejo, A., Arroyo, J., Contreras, J., and Villamor, F. (2002). Self-scheduling of a hydro producer in a pool-based electricity market. IEEE Trans. Power Syst. 17 (4), 1265–1272. doi:10.1109/TPWRS.2002.804951

CrossRef Full Text | Google Scholar

D’Ambrosio, C., Lodi, A., and Martello, S. (2010). Piecewise linear approximation of functions of two variables in MILP models. Operations Res. Lett. 38 (1), 39–46. doi:10.1016/j.orl.2009.09.005

CrossRef Full Text | Google Scholar

Diniz, A., and Maceira, M. (2008). A four-dimensional model of hydro generation for the short-term hydrothermal dispatch problem considering head and spillage effects. IEEE Trans. Power Syst. 23 (3), 1298–1308. doi:10.1109/TPWRS.2008.922253

CrossRef Full Text | Google Scholar

Feng, Z., Niu, W., Cheng, C., and Liao, S. (2017). Hydropower system operation optimization by discrete differential dynamic programming based on orthogonal experiment design. Energy 126, 720–732. doi:10.1016/j.energy.2017.03.069

CrossRef Full Text | Google Scholar

Flamm, B., Eichler, A., Warrington, J., and Lygeros, J. (2021). Two-stage dual dynamic programming with application to nonlinear hydro scheduling. IEEE Trans. Control Syst. Technol. 29 (1), 96–107. doi:10.1109/TCST.2019.2961645

CrossRef Full Text | Google Scholar

Guedes, L., de Mendonca Maia, P., Lisboa, A., Vieira, D., and Saldanha, R. (2017). A unit commitment algorithm and a compact MILP model for short-term hydro-power generation scheduling. IEEE Trans. Power Syst. 32 (5), 3381–3390. doi:10.1109/TPWRS.2016.2641390

CrossRef Full Text | Google Scholar

Guisández, I., and Pérez-Díaz, J. (2021). Mixed integer linear programming formulations for the hydro production function in a unit-based short-term scheduling problem. Int. J. Electr. Power & Energy Syst. 128, 106747. doi:10.1016/j.ijepes.2020.106747

CrossRef Full Text | Google Scholar

Huchette, J., and Vielma, J. (2017). Nonconvex piecewise linear functions: Advanced formulations and simple modeling tools. Available at: https://arxiv.org/pdf/1708.00050v3.pdf (Accessed July 19, 2020).

Google Scholar

Keller, M., and Karl, H. (2017). Response-time-optimized service deployment: MILP formulations of piece-wise linear functions approximating bivariate mixed-integer functions. IEEE Trans. Netw. Serv. Manage. 14 (1), 121–135. doi:10.1109/TNSM.2016.2611590

CrossRef Full Text | Google Scholar

Kong, J., Skjelbred, H., and Fosso, O. (2020). An overview on formulations and optimization methods for the unit-based short-term hydro scheduling problem. Electr. Power Syst. Res. 178, 106027. doi:10.1016/j.epsr.2019.106027

CrossRef Full Text | Google Scholar

Lin, S., Fan, G., Jian, G., and Liu, M. (2020). Stochastic economic dispatch of power system with multiple wind farms and pumped‐storage hydro stations using approximate dynamic programming. IET Renew. Power Gener. 14 (13), 2507–2516. doi:10.1049/iet-rpg.2019.1282

CrossRef Full Text | Google Scholar

Lin, S., Wang, Y., Liu, M., Fan, G., Yang, Z., Li, Q., et al. (2019). Stochastic optimal dispatch of PV/wind/diesel/battery microgrids using state‐space approximate dynamic programming. IET Gener. Transm. &amp. Distrib. 13 (15), 3409–3420. doi:10.1049/iet-gtd.2018.5840

CrossRef Full Text | Google Scholar

Marchand, A., Gendreau, M., Blais, M., and Emiel, G. (2018). Fast near-optimal heuristic for the short-term hydro-generation planning problem. IEEE Trans. Power Syst. 33 (1), 227–235. doi:10.1109/TPWRS.2017.2696438

CrossRef Full Text | Google Scholar

Morillo, J., Zéphyr, L., Pérez, J., Lindsay Anderson, C., and Cadena, Á. (2020). Risk-averse stochastic dual dynamic programming approach for the operation of a hydro-dominated power system in the presence of wind uncertainty. Int. J. Electr. Power & Energy Syst. 115, 105469. doi:10.1016/j.ijepes.2019.105469

CrossRef Full Text | Google Scholar

Postolov, B., and Iliev, A. (2022). New metaheuristic methodology for solving security constrained hydrothermal unit commitment based on adaptive genetic algorithm. Int. J. Electr. Power & Energy Syst. 134, 107163. doi:10.1016/j.ijepes.2021.107163

CrossRef Full Text | Google Scholar

Powell, W. (2011). Approximate dynamic programming: Solving the curses of dimensionality. Hoboken, NJ: John Wiley & Sons, Inc. Press.

Google Scholar

Qiu, Y., Lin, J., Liu, F., Song, Y., Chen, G., Ding, L., et al. (2020). Stochastic online generation control of cascaded run-of-the-river hydropower for mitigating solar power volatility. IEEE Trans. Power Syst. 35 (6), 4709–4722. doi:10.1109/TPWRS.2020.2991229

CrossRef Full Text | Google Scholar

Shi, L., Wang, R., and Yao, L. Z. (2017). Modelling and solutions of coordinated economic dispatch with wind–hydro–thermal complex power source structure. IET Renew. Power Gener. 11 (3), 262–270. doi:10.1049/iet-rpg.2016.0429

CrossRef Full Text | Google Scholar

Shuai, H., Ai, X., Fang, J., Ding, T., Chen, Z., Wen, J., et al. (2020). Real-time optimization of the integrated gas and power systems using hybrid approximate dynamic programming. Int. J. Electr. Power & Energy Syst. 118, 105776. doi:10.1016/j.ijepes.2019.105776

CrossRef Full Text | Google Scholar

Shuai, H., Fang, J., Ai, X., Tang, Y., Wen, J., He, H., et al. (2019). Stochastic optimization of economic dispatch for microgrid based on approximate dynamic programming. IEEE Trans. Smart Grid 10 (3), 2440–2452. doi:10.1109/TSG.2018.2798039

CrossRef Full Text | Google Scholar

Skjelbred, H. I., Kong, J., and Fosso, O. (2020). Dynamic incorporation of nonlinearity into MILP formulation for short-term hydro scheduling. Int. J. Electr. Power & Energy Syst. 116, 105530. doi:10.1016/j.ijepes.2019.105530

CrossRef Full Text | Google Scholar

Wang, J., Zheng, H., Feng, S., Chen, C., Liu, S., Wang, Y., et al. (2022). Comparison of efficient procedures for hydropower unit commitment. Energy Rep. 8, 2472–2479. doi:10.1016/j.egyr.2022.01.184

CrossRef Full Text | Google Scholar

Xue, X., Ai, X., Fang, J., Yao, W., and Wen, J. (2022). Real-time schedule of integrated heat and power system: A multi-dimensional stochastic approximate dynamic programming approach. Int. J. Electr. Power & Energy Syst. 134, 107427. doi:10.1016/j.ijepes.2021.107427

CrossRef Full Text | Google Scholar

Zeng, P., Li, H., He, H., and Li, S. (2019). Dynamic energy management of a microgrid using approximate dynamic programming and deep recurrent neural network learning. IEEE Trans. Smart Grid 10 (4), 4435–4445. doi:10.1109/TSG.2018.2859821

CrossRef Full Text | Google Scholar

Zhang, Y., An, X., and Wang, C. (2021). Data-driven two-stage stochastic optimization model for short-term hydro-thermal-wind coordination scheduling based on the dynamic extreme scenario set. Sustain. Energy Grids Netw. 27, 100489. doi:10.1016/j.segan.2021.100489

CrossRef Full Text | Google Scholar

Zhao, Z., Cheng, C., Liao, S., Li, Y., and Lu, Q. (2021). A MILP based framework for the hydro unit commitment considering irregular forbidden zone related constraints. IEEE Trans. Power Syst. 36 (3), 1819–1832. doi:10.1109/TPWRS.2020.3028480

CrossRef Full Text | Google Scholar

Zhu, J., Mo, X., Zhu, T., Guo, Y., Luo, T., Liu, M., et al. (2019). Real-time stochastic operation strategy of a microgrid using approximate dynamic programming-based spatiotemporal decomposition approach. IET Renew. Power Gener. 13 (16), 3061–3070. doi:10.1049/iet-rpg.2019.0536

CrossRef Full Text | Google Scholar

Zhu, J., Wang, C., Guo, Y., Luo, T., Mo, X., Xia, Y., et al. (2020). Approximate dynamic programming‐based decentralised robust optimisation approach for multi-area economic dispatch considering wind power uncertainty. IET Renew. Power Gener. 14 (13), 2376–2385. doi:10.1049/iet-rpg.2019.0794

CrossRef Full Text | Google Scholar

Nomenclature

Sets and indices

i index of hydro units

M set of units

t index of periods

T set of time periods

Parameters

h_i,t net head of reservoir at period t

h^max maximum net head of the reservoir (m)

h^min minimum net head of the reservoir (m)

pmax i maximum production of unit i (kW)

pmin i minimum production of unit i (kW)

qmax i maximum water discharge of unit i (m³/s)

qmin i minimum water discharge of unit i (m³/s)

r^final water volume of the reservoir at the end of the last period (m³)

r^init water volume of the reservoir at the beginning of the initial period (m³)

r^max maximum water volume of the reservoir (m³)

r^min minimum water volume of the reservoir (m3)

Δt length of each time period (h)

Variables

d_i,t binary variable, which is equal to 1 if hydro unit i is online at period t and 0 otherwise

h_t net head of reservoir at period t

hdw t tailrace level of the reservoir at period t (m)

hup t forebay level of the reservoir in period t (m)

j_t inflow of reservoir at period t (m³/s)

p_i,t power output of hydro unit i at period t

q_i,t water discharge of unit i at period t

r_t water volume of the reservoir at period t (m³)

s_t total reservoir spillage in period t (m³/s)