Suction effect on MHD flow of Brinkman-type fluid with heat absorption and first-order chemical reaction

Suction/injection is a mechanical effect and used to control the energy losses in the boundary layer region by reducing the drag on the surface. In this study, unsteady MHD flow of Brinkman-type fluid with suction/injection, heat absorption, and chemical reaction is investigated and an analytical solution is established. The corresponding results for temperature, concentration, and velocity fields are obtained with the help of the Laplace transformation method analytically. The physical effects of thermal and mass Grashoff number, Prandtl number, Schmidt number, heat absorption parameter, first-order chemical reaction parameter, suction/injection, Brinkman parameter, and magnetic parameter have been discussed graphically. Finally, it is observed that in the presence of suction effect, fluid’s velocity decreases gradually by increasing the value of suction parameter while show an increasing trend for the increasing value of the injection parameter.

Introduction

In nature, the convectional flow of fluids is not only induced by the temperature gradient but it is also generated due to the non-homogeneous concentration field. In several industrial and biological processes, the heat and mass transfer take place in chorus as a result of pooled buoyancy forces. In the presence of magnetic fields, such natural flows induced unevenness of thermal and species balances which are of great importance and have several applications in polymer industries and biological sciences. Matin et al. (2012) discussed the mixed convectional flow of nanofluid past an extended surface under the influence of the fluctuating magnetic field. Khan et al. (2018) analyzed the MHD flow of viscous fluid enclosed in an open channel. Unsteady free convective viscous fluid under a uniform magnetic field through porous media has been examined by Patel et al. (2015). Paul (2017) discussed the MHD free convection flow and presented the physical significance of magnetic force on fluid motion. Umavathi et al. (2018) also took into account the subjectivity of Lorentz forces on the electrically conducting fluid flow through a couple of parallel porous plates. Ali et al. (2013) investigated analytically the double convectional flow with heat and mass transport in the presence of Lorentz forces. Ahmed et al. (2017) extended his work for an L-shaped porous medium and discussed the flow of fluid induced by temperature and concentration gradients. Babu et al. (2017) considered natural convected viscous fluid flow over an extended permeable flat surface in the presence of magnetic field of constant magnitude. Some studies regarding heat and mass transfer are found in Ahmad et al. (2019); Ahmed et al. (2019); Adnan et al. (2020); Ahmad et al. (2020); Khan et al. (2020); Yu-Ming Chu et al. (2020).

The suction/injection effect is significant in the boundary flow and is applied to minimize the energy losses due to the surface drag. This effect is also applied to construct the biological and mechanical suction devices. Bose et al. (2016) analyzed the suction/injection for MHD convective flow of fluid over a swinging role of the permeable plate. Modather et al. (2009) discussed MHD flow over an oscillatory surface of micropolar fluid. Jha et al. (2017) compared the numerical and analytical solutions by considering the effect of suction/injection. Ravindran (2013) examined slot suction/injection for convectional flow and established numerical results for the conic domain. Aman (2017) established the results for the flow past an extended porous flat plate by imposing suction/injection on the boundary. Jha et al. (2015), Jha et al. (2018) presented the analytical solutions of natural convected flow with and without thermal radiation effects in vertical microchannel accompanied with a magnetic force by applying the suction/injection effect in the boundary layer region. Zeeshan et al. (2018) discussed the fluid motion generated by unbalanced temperature and mass distribution and blustered the effective role of uniform suction on fluid flow in the region of the boundary layer. Also, several other results regarding suction/injection boundary flows for transport phenomenon are found in Das (2010); Rajesh et al. (2010); Baoku et al. (2013); Ghosh et al. (2014); Akinshilo et al. (2017); Faladea et al. (2017).

The research work cited earlier regarding suction/injection is performed by numerical techniques. There is no exact result for velocity subjected to suction/injection and our main aim of the present research was to fill this gap. In this study, an unsteady free convectional flow of chemically reacting Brinkman-type fluid by imposing suction/injection on the boundary is shown. The Laplace transformation technique is applied to obtain the analytical expressions for temperature, concentration, and velocity. The role of suction/injection in the flow domain is also explained with other physical parameters graphically.

Formulation of problem

Suppose Brinkman fluid is lying at rest over an infinite plate placed in the xz − plane in such a way that the y-axis is taken along the outward normal to the plane of plate. In the beginning, time fluid with plate is in static equilibrium and physical state is described by temperature T_∞ and concentration C_∞ as shown in Figure 1. After the time t > 0, plate is supposed to move with velocity U₀f(t). Where f(t) satisfied f (0) = 0. A constant temperature T_w is maintained with the concentration level near the plate. The flow is directed in the z-direction and the velocity gradient exists in the direction of the y-axis so velocity is as $\vec{V}=\vec{V}(\mathrm{0,0},w)=w(y,t)\widehat{k}$, where the unit vector $\widehat{k}$ is pointed in the direction of velocity. A suctional velocity orthogonal to the plane of plate may be written as v = −v₀. The momentum, energy, and mass balance equations which govern the flow may be taken in the following form (Modather et al., 2009; Bose et al., 2016):

$\begin{array}{ll}\hfill & \frac{\partial w\left(y,t\right)}{\partial t}-v_0\frac{\partial w\left(y,t\right)}{\partial y}+\beta w\left(y,t\right)=\nu \frac{{\partial }^{2}w\left(y,t\right)}{\partial y^2}+g{\beta }_T\left(T\left(y,t\right)-T_{\infty }\right)\hfill \\ \hfill & +g{\beta }_C\left(C\left(y,t\right)-C_{\infty }\right)-\frac{\sigma B_0^{2}w\left(y,t\right)}{\rho },\hfill \end{array}(1)$

$\frac{\partial T\left(y,t\right)}{\partial t}-v_0\frac{\partial T\left(y,t\right)}{\partial y}=\frac{k}{\rho C_P}\frac{{\partial }^{2}T\left(y,t\right)}{\partial y^2}-\frac{Q}{\rho c_p}\left(T\left(y,t\right)-T_{\infty }\right),(2)$

$\frac{\partial C\left(y,t\right)}{\partial t}-v_0\frac{\partial C\left(y,t\right)}{\partial y}=D\frac{{\partial }^{2}C\left(y,t\right)}{\partial y^2}-K_r\left(C\left(y,t\right)-C_{\infty }\right),(3)$

where ρ is the density, v₀ is the constant suction velocity, β is the Brinkman parameter, w is the velocity of fluid, t is time, T is the fluid temperature, T_w is thermal state at wall, T_∞ is temperature at infinity, k denotes thermal conduction, β_T and β_C denote the constant of volumetric expansion, Cp is specific heat at perseverance, force (pressure), Q ≥ 0 is heat absorption, K_r is the chemical reaction parameter, B₀ is the constant magnetic field, and D is mass diffusion.

FIGURE 1

FIGURE 1. Flow geometry.

The adequate conditions at boundary for field variables are:

$\begin{array}{ll}\hfill & w\left(y,0\right)=0,T\left(y,0\right)=T_{\infty },C\left(y,0\right)=C_{\infty },\hfill \\ \hfill & w\left(0,t\right)=U_{0}f\left(t\right),T\left(0,t\right)=T_w,C\left(0,t\right)=C_w,\hfill \\ \hfill & w\left(\infty ,t\right)=0,T\left(\infty ,t\right)=T_{\infty },C\left(\infty ,t\right)=C_{\infty }.\hfill \end{array}(4)$

By inserting the following relations in Eqs 1–4:

$\begin{array}{ll}\hfill y^{\ast }& =\frac{\left(U_0\right)y}{\nu },t^{\ast }=\frac{U_0^{2}t}{\nu },w^{\ast }=\frac{w}{U_0},T^{\ast }=\frac{T-T_{\infty }}{T_w-T_{\infty }},\hfill \\ \hfill & C^{\ast }=\frac{C-C_{\infty }}{C_w-C_{\infty }},\mathrm{G}\mathrm{r}=\frac{g{\beta }_T\left(T_w-T_{\infty }\right)\nu }{U_0^3},\hfill \\ \hfill & \mathrm{G}\mathrm{m}=\frac{g{\beta }_C\left(C_w-C_{\infty }\right)\nu }{U_0^3},\mathrm{P}\mathrm{r}=\frac{\mu C_P}{k},\mathrm{S}\mathrm{c}=\frac{\nu }{D},\hfill \\ \hfill & M=\frac{\sigma B_0\nu }{U_0^2},Q_0=\frac{Q\nu }{\rho C_P{U}_0^2},\lambda =\frac{K_r\nu }{U_0^2},s=\frac{v_0}{U_0},\hfill \\ \hfill & {\beta }_0=\frac{\nu \beta }{U_0^0},\hfill \end{array}(5)$

we obtained the following equations:

$\begin{array}{cc}\hfill & \frac{\partial w\left(y,t\right)}{\partial t}-s\frac{\partial w\left(y,t\right)}{\partial y}+\frac{\nu \beta w\left(y,t\right)}{w_0^2}=\frac{{\partial }^{2}w\left(y,t\right)}{\partial y^2}+\mathrm{G}\mathrm{r}T\left(y,t\right)\hfill \\ \hfill & +\mathrm{G}\mathrm{m}C\left(y,t\right)-Mw\left(y,t\right),\hfill \end{array}(6)$

$\frac{\partial T\left(y,t\right)}{\partial t}-s\frac{\partial T\left(y,t\right)}{\partial y}=\frac{1}{\mathrm{Pr}}\frac{{\partial }^{2}T}{\partial y^2}-Q_{0}T\left(y,t\right),(7)$

$\frac{\partial C\left(y,t\right)}{\partial t}-s\frac{\partial C\left(y,t\right)}{\partial y}=\frac{1}{\mathrm{S}\mathrm{c}}\frac{{\partial }^{2}C}{\partial y^2}-\lambda C\left(y,t\right),(8)$

$\begin{array}{ll}\hfill & w\left(y,0\right)=0,T\left(y,0\right)=0,C\left(y,0\right)=0,\hfill \\ \hfill & w\left(0,t\right)=h\left(t\right),T\left(0,t\right)=1,C\left(0,t\right)=1,\hfill \\ \hfill & w\left(\infty ,t\right)=0,T\left(\infty ,t\right)=0,C\left(\infty ,t\right)=0.\hfill \end{array}(9)$

Solution of problem

Calculation of temperature

Eq. 7 with Laplace transform and condition (9)₁, is transformed to ordinary differential equations in $\bar{T}$

$\frac{{\partial }^2\bar{T}\left(y,q\right)}{\partial y^2}+\mathrm{Pr}s\frac{\partial \bar{T}}{\partial y}-\mathrm{Pr}\left(q+Q_0\right)\bar{T}\left(y,q\right)=0.(10)$

Eq. 10 satisfies

$\bar{T}\left(0,q\right)=\frac{1}{q},\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{0.17em}\bar{T}\left(\infty ,q\right)=0.(11)$

The solution of Eq. 10 subjected to condition (11) is as follows:

$\bar{T}\left(y,q\right)=\frac{1}{q}\exp \left(-y\left(\frac{\mathrm{Pr}s}{2}+\sqrt{{\left(\frac{\mathrm{Pr}s}{2}\right)}^2+\mathrm{Pr}\left(q+Q_0\right)}\right)\right).(12)$

In a suitable form:

$\bar{T}\left(y,q\right)=e^{-y{c}_1}\frac{1}{q}\exp \left(-y\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right).(13)$

where $c_1=\left(\frac{\mathrm{Pr}s}{2}\right)$ and $d_1=\frac{\mathrm{Pr}{s}^2}{4}+Q_0$.

Eq. 13 is re-transformed in the t-domain by inversion of Laplace transform with composite formula as:

$\begin{array}{ll}\hfill T\left(y,t\right)=& \frac{{\mathrm{e}}^{-y{c}_1}}{2}\left[\exp \left(-y\mathrm{Pr}\sqrt{d_1}\right)\times \mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\mathrm{Pr}}{2\sqrt{t}}-\sqrt{d_{1}t}\right)+\right.\hfill \\ \hfill & \left.\exp \left(-y\mathrm{Pr}\sqrt{d_1}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\mathrm{Pr}}{2\sqrt{t}}+\sqrt{d_{1}t}\right)\right].\hfill \end{array}(14)$

Calculation of concentration

In a similar manner as adopted in the case of the temperature field, Eq. 8 with respective boundary conditions from Eq. 9 can be solved for the concentration field as follows:

$\bar{C}\left(y,q\right)=\frac{1}{q}\exp \left(-y\left(\frac{\mathrm{S}\mathrm{c}s}{2}+\sqrt{{\left(\frac{\mathrm{S}\mathrm{c}s}{2}\right)}^2+\mathrm{S}\mathrm{c}\left(q+\lambda \right)}\right)\right).(15)$

In a suitable form:

$\bar{C}\left(y,q\right)={\mathrm{e}}^{-y{c}_2}\frac{1}{q}\exp \left(-y\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right),(16)$

where $c_2=\left(\frac{\mathrm{S}\mathrm{c}s}{2}\right)$, $d_2=\frac{\mathrm{S}\mathrm{c}{s}^2}{4}+\lambda$.

Eq. 16 is re-transformed as:

$\begin{array}{ll}\hfill C\left(y,t\right)& =\frac{{\mathrm{e}}^{-y{c}_2}}{2}\left[\exp \left(-y\mathrm{S}\mathrm{c}\sqrt{d_2}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\mathrm{S}\mathrm{c}}{2\sqrt{t}}-\sqrt{d_{2}t}\right)\right.\hfill \\ \hfill & \left.+\exp \left(-y\mathrm{S}\mathrm{c}\sqrt{d_2}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\mathrm{S}\mathrm{c}}{2\sqrt{t}}+\sqrt{d_{2}t}\right)\right].\hfill \end{array}(17)$

Velocity

   Imposing Laplace transform to Eq. 6, we obtain the following transformed ordinary differential equation:

$\frac{{\partial }^2\bar{w}\left(y,q\right)}{\partial y^2}+s\frac{\partial \bar{w}\left(y,q\right)}{\partial y}-\left(q+M+{\beta }_0\right)\bar{w}\left(y,q\right)=-\mathrm{G}\mathrm{r}\bar{T}\left(y,q\right)-\mathrm{G}\mathrm{m}\bar{C}\left(y,q\right).(18)$

Eq. 18 is in hold for following specification:

$\bar{w}\left(0,q\right)=\bar{f}\left(q\right)\bar{w}\left(\infty ,q\right)=0.(19)$

Eq. 18 with condition (19) can be solved and after performing lengthy calculation, its solution takes the following form:

$\begin{array}{ll}\hfill \bar{w}\left(y,q\right)& =\bar{f}\left(q\right)\exp \left(-y\left(a+\sqrt{q+b}\right)\right)\hfill \\ \hfill & +\frac{\mathrm{G}\mathrm{r}\left[\exp \left(-y\left(a+\sqrt{q+b}\right)\right)-\exp \left(-y\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)\right)\right]}{\left[{\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)}^2-s\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)-\left(q+M+{\beta }_0\right)\right]q}\hfill \\ \hfill & +\frac{\mathrm{G}\mathrm{m}\left[\exp \left(-y\left(a+\sqrt{q+b}\right)\right)-\exp \left(-y\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)\right)\right]}{\left[{\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)}^2-s\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)-\left(q+M+{\beta }_0\right)\right]q},\hfill \end{array}(20)$

where $a=\frac{s}{2}$ and b = a² + M + β₀.

In a suitable form:

$\begin{array}{ll}\hfill & \bar{w}\left(y,q\right)={\mathrm{e}}^{-ya}\bar{f}\left(q\right)\exp \left(-y\sqrt{q+b}\right)\hfill \\ \hfill & +\frac{\mathrm{G}\mathrm{r}}{\left[{\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)}^2-s\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)-\left(q+M+{\beta }_0\right)\right]}\hfill \\ \hfill & \times \left[{\mathrm{e}}^{-ya}\frac{1}{q}\exp \left(-y\sqrt{q+b}\right)-{\mathrm{e}}^{-y{c}_1}\frac{1}{q}\exp \left(-y\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)\right]\hfill \\ \hfill & +\frac{\mathrm{G}\mathrm{m}}{\left[{\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)}^2-s\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)-\left(q+M+{\beta }_0\right)\right]}\hfill \\ \hfill & \times \left[{\mathrm{e}}^{-ya}\frac{1}{q}\exp \left(-y\sqrt{q+b}\right)-{\mathrm{e}}^{-y{c}_2}\frac{1}{q}\exp \left(-y\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)\right].\hfill \end{array}(21)$

Consider the following equations:

$F_1\left(y,q\right)=\exp \left(-y\sqrt{q+b}\right),(22)$

$F_2\left(y,q\right)=\frac{1}{q}\exp \left(-y\sqrt{q+b}\right),(23)$

$F_3\left(y,q\right)=\frac{1}{q}\exp \left(-y\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right),(24)$

$F_4\left(y,q\right)=\frac{1}{q}\exp \left(-y\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right),(25)$

and

$A_1\left(q\right)=\frac{1}{\left[{\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)}^2-s\left(c_1+\sqrt{\mathrm{Pr}}\sqrt{q+d_1}\right)-\left(q+M+{\beta }_0\right)\right]},(26)$

$A_2\left(q\right)=\frac{1}{\left[{\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)}^2-s\left(c_2+\sqrt{\mathrm{S}\mathrm{c}}\sqrt{q+d_2}\right)-\left(q+M+{\beta }_0\right)\right]},(27)$

Eqs 26, 27 can be written in a suitable form as follows:

$\begin{array}{ll}\hfill A_1\left(q\right)& =\frac{1}{\left(m_1-m_2\right)\left(\mathrm{Pr}-1\right)}\left[\frac{\left(r_1+m_1\right)}{\left(q-m_1\right)}-\frac{\left(r_1+m_2\right)}{\left(q-m_2\right)}-\frac{r_2\left(d_1+m_1\right)}{\sqrt{q+d_1}\left(q-m_1\right)}\right.\hfill \\ \hfill & \left.+\frac{r_2\left(d_1+m_2\right)}{\sqrt{q+d_1}\left(q-m_2\right)}\right],\hfill \end{array}(28)$

$\begin{array}{ll}\hfill A_2\left(q\right)& =\frac{1}{\left(m_3-m_4\right)\left(\mathrm{S}\mathrm{c}-1\right)}\left[\frac{\left(r_3+m_3\right)}{\left(q-m_3\right)}-\frac{\left(r_3+m_4\right)}{\left(q-m_4\right)}-\frac{r_4\left(d_2+m_3\right)}{\sqrt{q+d_2}\left(q-m_3\right)}\right.\hfill \\ \hfill & +\left.\frac{r_4\left(d_2+m_4\right)}{\sqrt{q+d_2}\left(q-m_4\right)}\right],\hfill \end{array}(29)$

where

$r_1=\frac{c_1^2+\mathrm{Pr}{d}_1+s{c}_1-M-{\beta }_0}{\mathrm{Pr}-1}$, $r_2=\frac{\sqrt{\mathrm{Pr}}(2c_1+s)}{\mathrm{Pr}-1}$, $r_3=\frac{c_2^2+\mathrm{S}\mathrm{c}{d}_2+s{c}_2-M-{\beta }_0}{\mathrm{S}\mathrm{c}-1}$, $r_4=\frac{\sqrt{\mathrm{S}\mathrm{c}}(2c_2+s)}{\mathrm{S}\mathrm{c}-1}$,

$\left(m_1,m_2\right)=\frac{-\left(2r_1-r_2^2\right)\pm \sqrt{{\left(2r_1-r_2^2\right)}^2-4\left(r_1^2-r_2^2{d}_1\right)}}{2},$

and

$\left(m_3,m_4\right)=\frac{-\left(2r_3-r_4^2\right)\pm \sqrt{{\left(2r_3-r_4^2\right)}^2-4\left(r_3^2-r_4^2{d}_2\right)}}{2}.$

Inverting the Laplace transform in Eqs 22–25 and Eqs 28, 29.

$\begin{array}{ll}\hfill F_1\left(y,t\right)& =\frac{1}{2}\left[\exp \left(-y\sqrt{b}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y-2\sqrt{b}t}{2\sqrt{t}}\right)\right.\hfill \\ \hfill & \left.+\exp \left(y\sqrt{b}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y+2\sqrt{b}t}{2\sqrt{t}}\right)\right],\hfill \end{array}(30)$

$\begin{array}{ll}\hfill F_2\left(y,t\right)& =\frac{1}{2}\left[\exp \left(-y\sqrt{b}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y}{2\sqrt{t}}-\sqrt{bt}\right)\right.\hfill \\ \hfill & +\left.\exp \left(-y\sqrt{b}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y}{2\sqrt{t}}-\sqrt{bt}\right)\right],\hfill \end{array}(31)$

$\begin{array}{ll}\hfill F_3\left(y,t\right)& =\frac{1}{2}\left[\exp \left(-y\sqrt{\mathrm{P}\mathrm{r}{d}_1}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\sqrt{\mathrm{Pr}}}{2\sqrt{t}}-\sqrt{d_{1}t}\right)\right.\hfill \\ \hfill & \left.+\exp \left(-y\sqrt{\mathrm{P}\mathrm{r}{d}_1}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\sqrt{\mathrm{Pr}}}{2\sqrt{t}}+\sqrt{d_{1}t}\right)\right],\hfill \end{array}(32)$

$\begin{array}{ll}\hfill F_4\left(y,t\right)& =\frac{1}{2}\left[\exp \left(-y\sqrt{\mathrm{S}\mathrm{c}{d}_2}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\sqrt{\mathrm{S}\mathrm{c}}}{2\sqrt{t}}-\sqrt{d_{2}t}\right)\right.\hfill \\ \hfill & \left.+\exp \left(-y\sqrt{\mathrm{S}\mathrm{c}{d}_2}\right)\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{y\sqrt{\mathrm{S}\mathrm{c}}}{2\sqrt{t}}+\sqrt{d_{2}t}\right)\right],\hfill \end{array}(33)$

and

$\begin{array}{ll}\hfill A_1\left(t\right)& =\frac{1}{\left(\mathrm{Pr}-1\right)\left(m_1-m_2\right)}\left[\left(r_1+m_1\right){\mathrm{e}}^{m_{1}t}-\left(r_1+m_2\right){\mathrm{e}}^{m_{2}t}\right.\hfill \\ \hfill & \left.-r_2\left(d_1+m_1\right)r_2\left(d_1+m_2\right)\frac{{\mathrm{e}}^{m_{1}t}}{\sqrt{d_1+m_1}}\mathrm{e}\mathrm{r}\mathrm{f}\left(\sqrt{\left(d_1+m_1\right)t}\right)\right],\hfill \end{array}(34)$

$\begin{array}{ll}\hfill A_2\left(t\right)& =\frac{1}{\left(\mathrm{S}\mathrm{c}-1\right)\left(m_3-m_4\right)}\left[\left(r_3+m_3\right){\mathrm{e}}^{m_{3}t}-\left(r_3+m_4\right)e^{m_{4}t}\right.\hfill \\ \hfill & \left.-r_4\left(d_2+m_3\right)r_4\left(d_2+m_4\right)\frac{{\mathrm{e}}^{m_{3}t}}{\sqrt{d_2+m_3}}\mathrm{e}\mathrm{r}\mathrm{f}\left(\sqrt{\left(d_2+m_3\right)t}\right)\right].\hfill \end{array}(35)$

After inverting Laplace transform in Eq. 21 and using Eqs 30–35, finally we obtained the velocity in the t-domain.

$\begin{array}{ll}\hfill w\left(y,t\right)& =\exp \left(-ya\right){\int }_0^{t}f\left(t-\tau \right)F_1\left(\tau \right)d\tau \hfill \\ \hfill & +\mathrm{G}\mathrm{r}{\int }_0^t{A}_1\left(t-\tau \right)\left[\exp \left(-ya\right)F_2\left(\tau \right)-\exp \left(-y{c}_1\right)F_3\left(\tau \right)\right]d\tau \hfill \\ \hfill & +\mathrm{G}\mathrm{m}{\int }_0^t{A}_2\left(t-\tau \right)\left[\exp \left(-ya\right)F_2\left(\tau \right)-\exp \left(-y{c}_2\right)F_4\left(\tau \right)\right]d\tau .\hfill \end{array}(36)$

Some specifications on arbitrary function f (t)

The velocity w (y, t), given by Eq. 36, mainly contains two terms: the first term is the mechanical contribution due to the motion of plate with an arbitrary velocity while the other part of the solution is the result of heat and mass transfer. Therefore, the mechanical part is given as follows:

$w_m\left(y,t\right)=\exp \left(-ya\right){\int }_0^{t}f\left(t-\tau \right)F_1\left(\tau \right)d\tau .(37)$

Case-I [f(t) = t^α].

By introducing the f(t) = t^α in Eq. 37 when plate is moving with a variable velocity.

$w_m\left(y,t\right)=\exp \left(-ya\right){\int }_0^t{\left(t-\tau \right)}^{\alpha }{F}_1\left(\tau \right)d\tau .(38)$

Case-II [f(t) = sin (wt)].

$w_m\left(y,t\right)=\exp \left(-ya\right){\int }_0^t\sin \left(w\left(t-\tau \right)\right)F_1\left(\tau \right)d\tau .(39)$

Numerical discussion and results

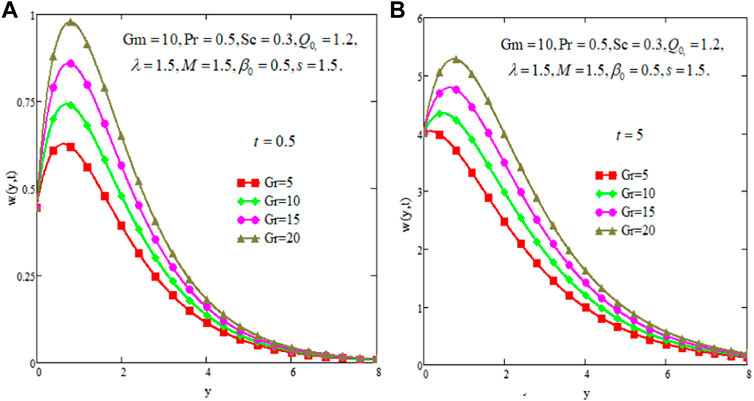
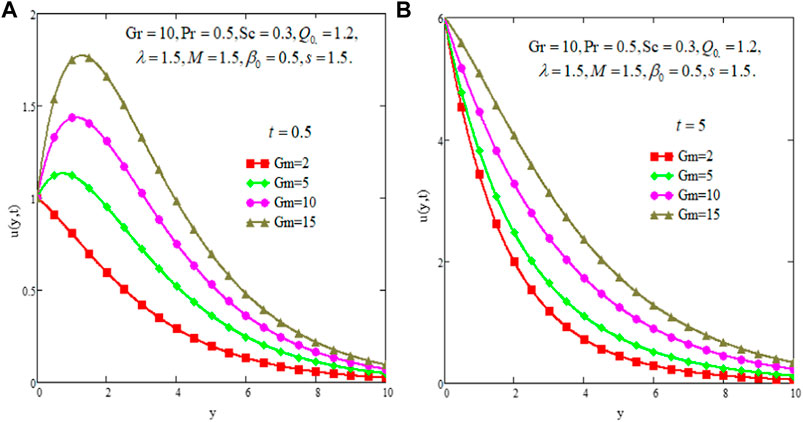
In this section, the impact of suction/injection and the other physical parameters in the flow domain are explained graphically. The effect of Gr for small and large times is elaborated in Figures 2A,B. Increasing values of Gr refer to stronger buoyancy forces which generate more convectional effects, therefore; velocity profiles exhibit an increasing trend due to an increasing Gr in both figures drawn for small and large times and fluid velocity is higher for large time than that for the small time. Figures 3A,B depicts the influence of mass Grashoff number Gm on velocity profiles. Figures outlined revealed that fluid velocity speeds up under the successive increment in the values of Gm. The greater values of Gm mean that there are large bouncy forces due to the concentration gradient which generate more fluid motion.

FIGURE 2

FIGURE 2. Velocity due to Gr for small time (A) and for large time (B).

FIGURE 3

FIGURE 3. Velocity due to Gm for Small time (A) and for large time (B).

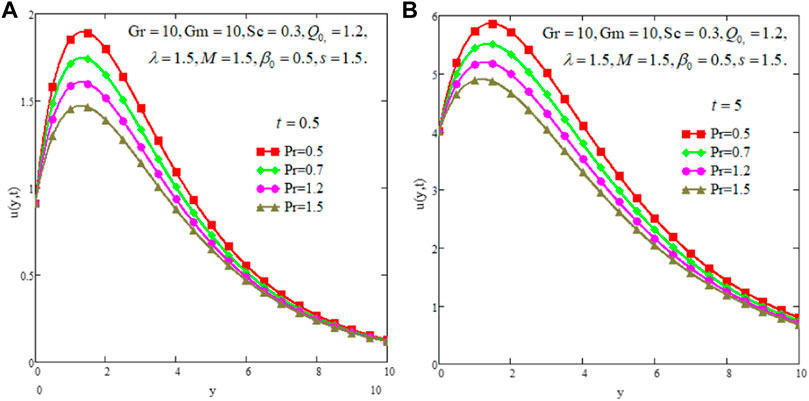
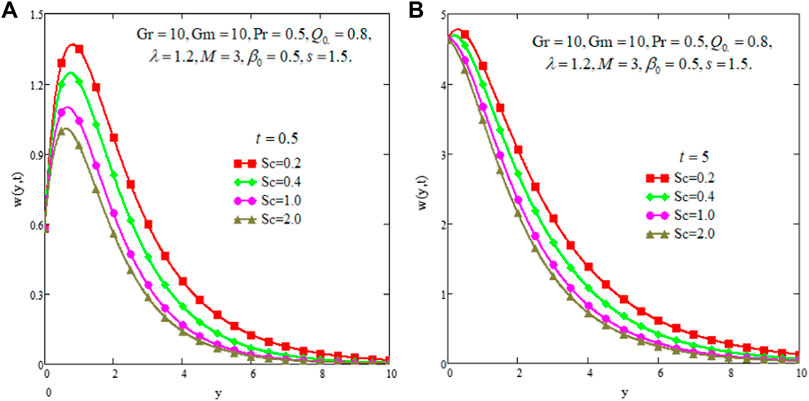
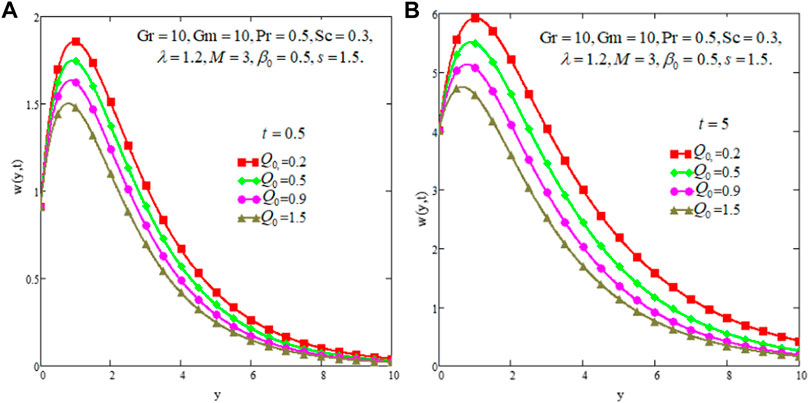
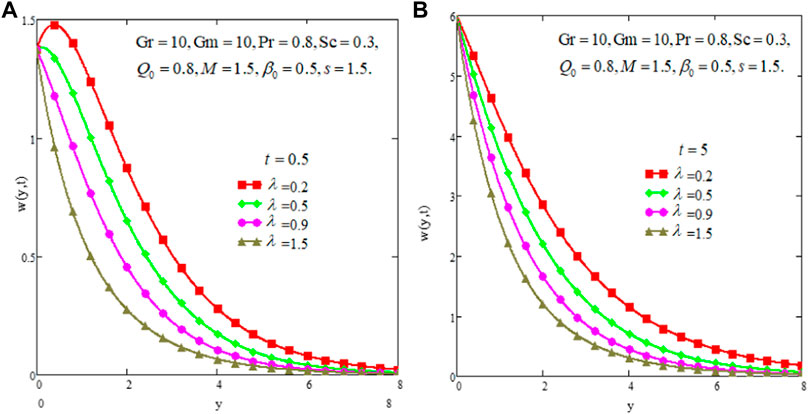
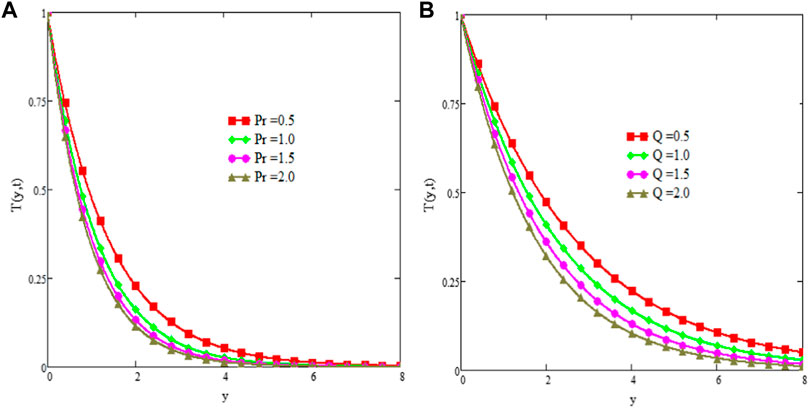
The effect of Pr is discussed in Figures 4A,B. From the figures it is shown that there is a decreasing trend in velocity profiles for Pr. For larger values of Pr, the viscous forces dominate the inertial forces and create more internal friction in the fluid flow and consequently fluid slows down. Figures 5A,B present the effect of Sc on fluid velocity. As shown in both figures, velocity slows down for enhancing values of Sc but fluid velocity is higher for large time than that for the small time. In Figures 6A,B, the effect of heat absorption parameter Q₀ on fluid velocity is depicted. The figure graphic shows that the increase in Q₀ slows down the fluid motion. Whenever large numeric values are given to Q₀, the fluid temperature is lowered down and consequently the fluid velocity decreases. However, for the large time; the fluid velocity remains higher than that for the small time. The effects of chemical reaction parameter λ are shown in Figures 7A,B. The fluid velocity behaves against λ in similar a manner as due to Q₀.

FIGURE 4

FIGURE 4. Velocity due to Pr for small time (A) and for large time (B).

FIGURE 5

FIGURE 5. Velocity due to Sc for small time (A) and for large time (B).

FIGURE 6

FIGURE 6. Velocity due to Q₀ for small time (A) and for large time (B).

FIGURE 7

FIGURE 7. Velocity due to λ for small time (A) and for large time (B).

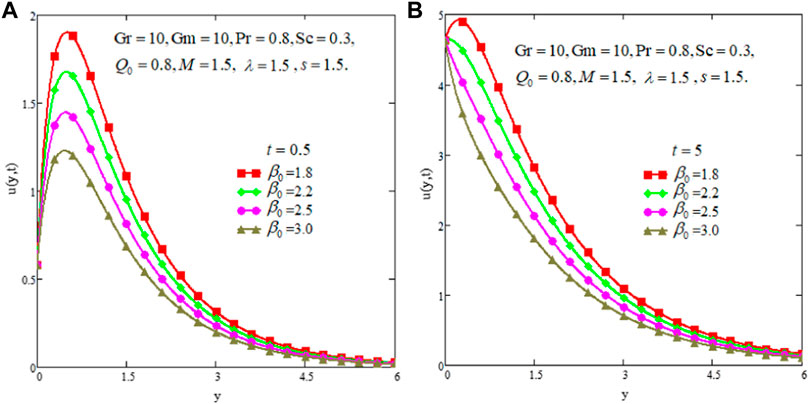
The subjectivity of fluid velocity under magnetic force is outlined in Figures 8A,B and fluid is retarded with the magnetic parameter. The physical significance of this effect is that the stronger magnetic field opposes the force to fluid velocity, therefore; the fluid motion slows down. The influence of the Brinkman parameter is shown in Figures 9A,B. It is clear that velocity profiles lower down with an enhancing β₀ for small and large times. β₀ is the material constant and its higher value refers to more thick fluid. Therefore, the higher value of β₀ means that there is more dragging force to fluid flow, so consequently fluid velocity slows down.

FIGURE 8

FIGURE 8. Velocity due to M for small time (A) and for large time (B).

FIGURE 9

FIGURE 9. Velocity profile due to β₀ variation for small time (A) and for large time (B).

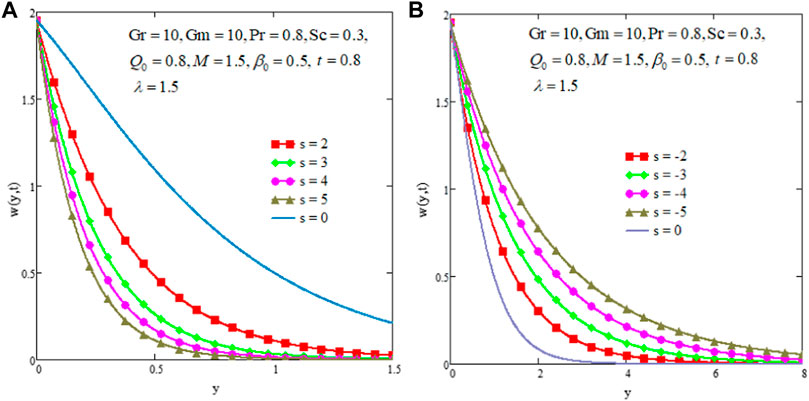
The suction/injection effects on fluid velocity are presented in Figures 10A,B. The s > 0 refers to suction while s < 0 indicates the injection and s = 0 means no suction/injection in the flow domain. Figure 10A shows the effect of parameter s and it is observed that the fluid velocity decreases with the increasing values of suction parameter (s > 0). Figure 10B shows the variation in velocity of fluid with respect to injection and from this figure, it is clear that the fluid speeds up with injection (s < 0). In Figures 11A,B, the temperature profile is plotted for the variation of Pr and Q, respectively. From the figures it is observed that temperature profiles lower down for the increasing value of Pr and Q.

FIGURE 10

FIGURE 10. Velocity profile due to suction (s > 0) (A) and injection (s < 0) (B).

FIGURE 11

FIGURE 11. Temperature profiles for Pr (A) and Q (B) variations.

Conclusion

The mathematical model of unsteady natural flow of MHD Brinkman-type fluid with suction/injection, heat absorption, and chemical reaction of first-order is considered. The corresponding solutions of temperature, concentration, and velocity fields are established. The physical effects of parameters are seen graphically. Moreover, it is clear that in the presence of suction at the boundary the flow slows down while for the injection effect flow speeds up. The key outcomes of the study are listed as follows:

• The s > 0 refers to the suction and hence an increasing value of s slowdowns the fluid flow.

• The s < 0 refers to the injection and by increasing the numeric value of (−s), it speedups the fluid flow.

• The fluid velocity increases for Gr, Gm, time, t, and injection parameter (-s).

• The fluid velocity decreases for M, β₀, t, Q₀, λ, and suction parameter (s).

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found here. No link.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The study was supported by the National Natural Science Foundation of China (No. 71601072), the Fundamental Research Funds for the Universities of Henan Province (No. NSFRF210314), and the Innovative Research Team of Henan Polytechnic University (No. T2022-7).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adnan, , Ali Zaidi, S. Z., Khan, U., Abdeljawad, T., Ahmed, N., Mohyud-Din, S. T., et al. (2020). Investigation of thermal transport in multi-shaped Cu nanomaterial-based nanofluids. Materials 13, 2737. doi:10.3390/ma13122737

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad, M., Imran, M. A., and Nazar, M. (2020). Mathematical modeling of (Cu−Al2O3) water based Maxwell hybrid nanofluids with Caputo-Fabrizio fractional derivative. Adv. Mech. Eng. 12 (9), 168781402095884–11. doi:10.1177/1687814020958841

CrossRef Full Text | Google Scholar

Ahmad, M., Imran, M. A., Aleem, M., and Khan, I. (2019). A comparative study and analysis of natural convection flow of MHD non-Newtonian fluid in the presence of heat source and first-order chemical reaction. J. Therm. Anal. Calorim. 137 (5), 1783–1796. doi:10.1007/s10973-019-08065-3

CrossRef Full Text | Google Scholar

Ahmed, N., Adnan, , Khan, U., Zaidi, S. Z. A., Faisal, I., and Mohyud-Din, S. T. (2019). Heat transfer intensification in hydromagnetic and radiative 3D unsteady flow regimes: A comparative theoretical investigation for aluminum and γ-aluminum oxides nanoparticles. J. Cent. South Univ. 26, 1233–1249. doi:10.1007/s11771-019-4083-x

CrossRef Full Text | Google Scholar

Ahmed, S., Azeem, N. J., and Yunus Khan, T. M. (2017). Heat and mass transfer in an L shaped porous medium. IOP Conf. Ser. Mat. Sci. Eng. 225, 012011–17. doi:10.1088/1757-899x/225/1/012011

CrossRef Full Text | Google Scholar

Akinshilo, A. T., Olofinkua, J. O., and Olaye, O. (2017). Flow and heat transfer analysis of the sodium alginate conveying copper nanoparticles between two parallel plates. J. Appl. Comput. Mech. 3 (4), 258–266.

Google Scholar

Ali, F., Khan, I., Shafie, S., and Musthapa, N. (2013). Heat and mass transfer with free convection mhd flow past a vertical plate embedded in a porous medium. Math. Problems Eng. 2013, 1–13. doi:10.1155/2013/346281

CrossRef Full Text | Google Scholar

Aman, S., Salleh, M. Z., Ismail, Z., and Khan, I. (2017). Exact solution for heat transfer free convection flow of Maxwell nanofluids with graphene nanoparticles. J. Phys. 2017, 1–14.

CrossRef Full Text | Google Scholar

Babu, D. D., Venkateswarlu, S., and Reddy, E. K. (2017). Heat and mass transfer on mhd free convective flow of second grade fluid through porous medium over an infinite vertical plate. IOP Conf. Ser. Mat. Sci. Eng. 225, 012267–555. doi:10.1088/1757-899x/225/1/012267

CrossRef Full Text | Google Scholar

Baoku, I. G., Olajuwon, B. I., and Mustapha, A. O. (2013). Heat and mass transfer on a MHD third grade fluid with partial slip flow past an infinite vertical insulated porous plate in a porous medium. Int. J. Heat Fluid Flow 40, 81–88. doi:10.1016/j.ijheatfluidflow.2013.01.016

CrossRef Full Text | Google Scholar

Bose, D., and Basu, U. (2016). MHD convective flow of non-Newtonian fluid through porous medium over an oscillating porous plate with suction. Int. J. Comput. Appl. 134 (10), 15–19. doi:10.5120/ijca2016908066

CrossRef Full Text | Google Scholar

Das, K. (2010). Exact solution of MHD free convection flow and mass transfer near a moving vertical plate in presence of thermal radiation. Afr. J. Math. Phys. 8, 29–41.

Google Scholar

Faladea, J. A., Ukaegbu, C., EgerebSamue, A. C., and Adesanya, O. (2017). MHD oscillatory flow through a porous channel saturated with porous medium. Alexandria Eng. J. 56 (1), 147–152. doi:10.1016/j.aej.2016.09.016

CrossRef Full Text | Google Scholar

Ghosh, A. K., Datta, S. K., and Sen, P. (2014). A note on hydromagnetic flow of an Oldroyd-B fluid near an infinite plate induced by half rectified sine pulses. Open J. Fluid Dyn. 4, 226–240. doi:10.4236/ojfd.2014.42017

CrossRef Full Text | Google Scholar

Jha, B. K., Aina, B., and Ajiya, A. T. (2015). Role of suction/injection on mhd natural convection flow in a vertical microchannel. Int. J. Energy Technol. 7 (2), 30–39.

Google Scholar

Jha, B. K., Iro, C., and Joseph, S. B. (2017). Effects of suction-injection-combination (SIC) on transient free-convective-radiative flow in a vertical porous channel. Proc. Institution Mech. Eng. Part E J. Process Mech. Eng. 231 (2), 73–82. doi:10.1177/0954408915576300

CrossRef Full Text | Google Scholar

Jha, B. K., Isah, B. Y., and Uwanta, I. J. (2018). Combined effect of suction/injection on mhd free-convection flow in a vertical channel with thermal radiation. Ain Shams Eng. J. 9, 1069–1088. doi:10.1016/j.asej.2016.06.001

CrossRef Full Text | Google Scholar

Khan, U., Adnan, , Ahmed, N., Mohyud-Din, S. T., Chu, Y.-M., Khan, I., et al. (2020). γ-Nanofluid thermal transport between parallel plates suspended by micro-cantilever sensor by incorporating the effective Prandtl model: Applications to biological and medical sciences. Molecules 25, 1777. doi:10.3390/molecules25081777

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, Z. A., Haq, S., Khan, T. S., Khan, I., and Tlilid, I. (2018). Unsteady MHD flow of a Brinkman type fluid between two side walls perpendicular to an infinite plate. Results Phys. 9, 1602–1608. doi:10.1016/j.rinp.2018.04.034

CrossRef Full Text | Google Scholar

Matin, M. H., Nobar, M. R., and Jahangiri, P. (2012). Entropy analysis in mixed convection MHD flow of nanofluid over a non-linear stretching sheet. J. Therm. Sci. Technol. 7 (1), 104–119. doi:10.1299/jtst.7.104

CrossRef Full Text | Google Scholar

Modather, M., Rashad, A. M., and Chamkha, A. J. (2009). An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turkish J. Eng. Environ. Sci. 33, 245–257.

Google Scholar

Patel, H. K., Singh, R. K., and Singh, T. R. (2015). Transient free convective mhd flow through porous medium in slip flow regime. IOSR J. Math. 11 (5), 52–58.

Google Scholar

Paul, A., and Dek, R. K. (2017). Unsteady natural convection flow past an infinite cylinder with thermal and mass stratification. Int. J. Eng. Math. 2017, 1–13. doi:10.1155/2017/8410691

CrossRef Full Text | Google Scholar

Rajesh, V., and Varma, S. V. K. (2010). Heat source effects on mhd flow past an exponentially accelerated vertical plate with variable temperature through a porous medium. Int. J. Appl. Math. Mech. 6 (12), 68–78.

Google Scholar

Ravindran, R., and Ganspathirao, M. (2013). Non-uniform slot suction/injection into mixed convection boundary layer flow over vertical cone. Appl. Math. Mech. 34, 1327–38. doi:10.1007/s10483-013-1748-7

CrossRef Full Text | Google Scholar

Umavathi, J. C., Chamkh, A. J., and Shekar, M. (2018). Free convection flow of an electrically-conducting micropolar fluid between parallel porous vertical plates using differential transform. J. Appl. Comput. Mech. 4 (4), 286–298.

Google Scholar

Yu-Ming Chu, A., Khan, U., Ahmed, N., Din, S. T. M., and Khan, I. (2020). Heat and mass transport investigation in radiative and chemically reacting fluid over a differentially heated surface and internal heating. Open Phys. 18 (1), 842–852. doi:10.1515/phys-2020-0182

CrossRef Full Text | Google Scholar

Zeeshan, K., Ilyas, K., Murad, U., and Tlili, I., (2018). Effect of thermal radiation and chemical reaction on non-Newtonian fluid through vertical stretching porous plate with uniform suction. Results Phys. 9, 1086–1095.

Google Scholar