- 1Department of Mathematics, University of Management and Technology, Lahore, Pakistan
- 2Department of Computer Engineering, Biruni University, Zeytinburnu, Istanbul, Turkey
- 3Department of Medical Research, China Medical University, Taichung, Taiwan
- 4King Fahd University of Petroleum and Minerals, Department of Mathematics and Statistics, Dhahran, Saudi Arabia
- 5Department of Physics, College of Khurma University College, Taif University, Taif, Saudi Arabia
The aim of the article is two-fold. We first analyze and investigate free convective, unsteady, MHD blood flow with single- and multiwalled carbon nanotubes (S&MWCNTs) as nanoparticles. The blood flow has been taken across an upright vertical plate, oscillating in its own plane, and engrafted in a porous medium with slip, radiation, and porosity effects. Nanofluids consist of human blood as the base fluid and SWCNTs and MWCNTs as nanoparticles. The second aim is to discuss the three different definitions of fractional derivatives, namely, Caputo (C), Caputo–Fabrizio (CF), and Atangana–Baleanu (ABC), to obtain the solutions of such proposed models by the Adomian decomposition method. The impact of fractional and physical parameters on the concentration, velocity, and temperature of human blood in the presence of the slip effect is studied and projected diagrammatically. The article ends by providing numerical results such as the reliableness, efficiency, and significant features that are simple in computation with eminent accuracy of the process for non-Newtonian Casson nanofluid fractional order models. It is observed that the velocity of the fluid decreases with SWCNTs’ and MWCNTs’ volume fraction, and an increase in the CNTs’ volume fraction increases blood temperature, which ultimately enhances heat transfer rates. The results acquired are in excellent correspondence with the reported results.
Introduction
Recently, the contemplation of fractional calculus has been broadened with eminent implication because of its diverse applications in physical sciences, hydraulics, mathematical physics, electric electronic network, wave theory, nuclear and chemical industries, etc. (Podlubny, 1999; Tarasov, 2010; Uchaikin, 2013; Herrmann, 2014; Li and Zeng, 2015; Povstenko, 2015; Li and Cai, 2019). It is notable that the classical derivative (integer-order operator) is local while the noninteger operators specified as Riemann–Liouville, Caputo, Caputo–Fabrizio, and Atangana–Baleanu are nonlocal operators. The nonlocality enables us to foresee the advanced stage of the system and reckons the present and its continuing phases. It is always a challenging task for researchers to accomplish analytical or exact solutions of nonlinear models by fractional operators due to their complexity. In the past couple of years, several investigators have worked to inquire about the fractional differential operators in varied aspects. Caputo and Fabrizio (Caputo, 1967) modified the existing Caputo operator in a new conformation, and Atangana and Baleanu evoked a new fractional manipulator labeled Atangana–Baleanu derivative by combining Riemann–Liouville and Caputo differential operators.
In this article, we have concentrated on convective heat conveyance, which plays a critical role in the working of non-Newtonian fluid streams. The mechanics of non-Newtonian flux exhibits an exceptional challenge for mathematicians, physicists, and engineers. This is due to the fact that non-Newtonian fluids (NNFs) because of their complex behavior cannot be described mathematically using a single constitutive equation catering to all parameters. For this, a dedicated constitutive model is needed to describe such flows, for instance, in the case of Brinkman fluid (Ali et al., 20201094), viscoplastic fluids (Hassan et al., 2013), second-grade fluid (Ali et al., 2016; Imran et al., 2017b), Walter’s-B fluid (Ali et al., 2014; Imran et al., 2018), Bingham plastic (Kleppe and Marner, 1970), and Maxwell fluids (Tahir et al., 2017). Among the non-Newtonian fluid models, the Casson model is highly recommended by numerous researchers. Let us consider that such nonlinearity is expressed in numerous domains such as food processing, oil suspensions of pigments to predict flow behavior, mud drilling processors, blood flow in the circulatory system, and other fields of bioengineering.
It should be pointed out that Casson initiated these models for the nonlinear flow of pigment–oil suspensions. The Casson fluid is a pseudoplastic, also termed shear thinning. It possesses infinite viscosity and acts like solids at zero shear rate, termed as yield stress, below which no flow occurs. If yield stress is more than shear stress, i.e., viscosity (η = 0), the fluid behaves as a solid. In other situations, when shear stress is higher than yield stress, the fluid starts to accelerate.
Many researchers have considered the Casson fluid model and investigated its behavior in different situations; Bhattacharyya investigated the boundary layer stagnation point flow of a Casson-type fluid with heat transfer along a stretching or shrinking sheet of infinite length (Bhattacharyya, 2013). In another research article, he figured out the exact results for boundary layer flux of a Casson liquid flowing across a porous stretching/shrinking sheet (Bhattacharyya et al., 2014). Hayat et al. (Hayat et al., 2012) studied the boundary layer flux of MHD Casson liquid across an elongated sheet. Nadeem et al. (Nadeem et al., 2012) investigated the influence of electricity on the boundary layer flux of a Casson liquid flowing across an exponentially contracting canvas.
Raju et al. (Raju et al., 2016) reckoned the Casson liquid to analyze the significance of magnetic flux by an elongated canvass and comprehended the fact that an induced magnetized field possesses the tendency to increase the heat transferal rate. Kumar et al. investigated the combined effect of magnetic flux and heat source and worked out the numerical results for a Casson liquid flowing through two parallel plates (Kumar et al., 2018a). In another study, Kumar et al. investigated the conjugate impact of mass and heat transferal rate of MHD Casson fluid under Brownian motion, and thermophoresis demonstrated that the fluid’s temperature is manipulated by the Casson parameter (Kumar et al., 2018b).
Kataria and Patel established the effluence, thermic, and mass transmit characteristics of Casson MHD liquid and ascertained that modified magnetic flux decays its speed and boundary layer heaviness (Kataria and Patel, 2018). Casson fluid’s stagnancy point has been illustrated by Shaw et al. (Shaw et al., 2019) to determine encroachment of radiation, thermic dissemination, and diffusion thermal effectuates due to chemical reactions. Hussanan et al. (Hussanan et al., 2016) demonstrated unsteady invariant warmth transferal flux of Casson-type fluid bearing the checks of Newtonian heating and thermal radiation across an oscillating upright erect plate of infinite dimensions. They concluded that the velocity of Casson fluid decreases due to the Casson parameter and it shows an oscillating turnover for dissimilar phase angles. More research in this area has been conducted by various researchers (Kameswaran et al., 2014; Animasaun et al., 2015; Ramesh and Devakar, 2015; Ahmed et al., 2016; Imran et al., 2016; Ahmad et al., 2019; Rehman et al., 2019; Sheikh et al., 2020; Aleem et al., 2021).
In this article, our major objective is to demonstrate free convective, MHD unsteady blood flow with single (SWCNTs) and multiwalled carbon nanotubes (MWCNTs) as nanospecks. The blood flow is considered over an oscillating vertically upright plate engrafted in a porous medium with slip, radiation, and porosity effects. Nanofluids consist of human blood as the base fluid and SWCNTs and MWCNTs as nanoparticles. Three fractional approaches Caputo (C), Caputo–Fabrizio (CF), and Atangana–Baleanu (ABC) are used to develop the fractional blood flow model, which is solved using the Adomian decomposition method (ADM). Equations of dimensionless temperature, velocity, and concentration fields have been solved analytically, and the results are compared. The graphical analysis is performed to envision the effect of fractional and tangible flow parameters on velocity u, concentration C, and temperature θ using MathCad and Mathematica software packages. This article is structured as follows. In section 1, latest research related to Casson fluid and its application in the industry are presented, and in Section 2, problem formulation and assumptions are illustrated. In section 3, we have developed a fractional model for Casson nanofluid and its solution with the Adomian decomposition method with Caputo, Caputo Fabrizio, and Atangana–Baleanu fractional operators that are given in Sections 4 and 5. The obtained results are analyzed and discussed in Section 6. Solutions obtained via ADM are compared with existing literature results and are presented in Section 6.
Problem formulation
We investigate an unsteady viscoelastic incompressible Casson nanofluid containing human blood as the base liquid and CNTs as nanoparticles. It flows across an infinite vertical upright plate located in the xy-plane implanted in a porous medium and is fixed in the x-direction, whereas y-axis is normal to the plate. Consequently, the rate of flow is enclosed only in the half plane where y > 0. At t = 0, the nanofluid and plate are at rest with the set temperature T∞ and concentration C∞. The base fluid, which is human blood, and nanoparticles (SWCNTs and MWCNTs) are considered to be in thermal equilibrium. As time increases t = 0+, the plate starts its sinusoidal oscillation with slip effect at the boundary, and its velocity at the boundary wall is
1) The plate is assumed to be electrically conducting and bearing uniform magnetic flux Bo, which is applied in the direction perpendicular to the plate.
2) The slip boundary condition at the wall is considered, and the relative velocity between the wall and fluid is directly proportional to the shear rate or the rate of deformation at the wall.
3) Since the flow is unidirectional, all tangible variables are functions of time t and space coordinate y.
4) The impression of enforced magnetic flux is negligible, referring to a really small magnetized Reynolds’ number Re.
5) The Casson nanofluid consists of SWCNTs and MWCNTs of invariant kinematic viscosity νnf occupying a semifinite space y > 0.
Under these assumptions and using Boussinesq’s approximation, the governing equations for energy, diffusion, and momentum are (Imran et al., 2017a; Khalid et al., 2018).
Under Rossenold approximation for radiative heat flux, by assuming that the temperature difference between fluid T and ambient T∞ is very small, Eq. 2 becomes (Imran et al., 2017a)
where u, C, T, qr, σ∗, κ∗, g, γ, D, μnf, κnf, Cpnf, βCnf, βTnf are velocity, concentration, temperature, radiative heat flux, Stefan–Boltzman constant, mean absorption coefficient, gravity, Casson parameter, molecular diffusion constant, dynamic viscosity of Casson nanofluid, thermal conductivity, heat capacitance, and diffusion and thermal expansion coefficients of nanoparticles, respectively.
The appropriate initial and boundary conditions are as follows:
A theoretical model for nanofluids was introduced by Xue (Xue, 2005) based on Maxwell theory for elliptic-shaped rotational CNTs with a large axial ratio, and compensating space distribution impact is used and given as follows:
where κnf, κf, and κCNT are the thermal conduction coefficients of the nanofluid, base liquid, and carbon nanotubes (S&MWCNTs), respectively. The theoretical density values are described by Yu et al. (Yu et al., 2008) as follows:
where ρf is blood density, ϕ is the volume fraction of nanoparticles, and ρCNT is the density of carbon nanotubes (S&MWCNTs). The effective dynamic viscosity μnf for cylindrical nanotubes can be defined in two ways as proposed by Loganathan et al. (Loganathan et al., 2015) and Rajesh et al. (Rajesh et al., 2016).
where μf and μnf are densities of blood as the base fluid and the nanofluid with CNTs. Heat capacitance for nanofluid is as follows:
The thermal and diffusion expansion are defined by Bourantas and Loukopoulos (Bourantas and Loukopoulos, 2014) as follows:
where ρ is the density; ϕ is the nanoparticle volume fraction; and

TABLE 1. Thermophysical traits of SWCNTs, MWCNTs, and human blood (Casson, 1959; Pramanik, 2014; Imran et al., 2017a).
Introducing dimensionless variables
Using dimensionless parameters from Eq. 8 in Eqs. (1) and (3)––(7), we get
and dimensionless initial and boundary conditions are as follows:
where
where Sc is the dimensionless Schmidt number, Gr and Gm are thermal and mass Grashof numbers, respectively, Preff is the effective Prandtl number depend on radiation-conduction parametric quantity Nr and Prandtl number Pr, M is the magnetic field parameter, η is slip, and K is the porosity parameter. Solving Eqs. (9)–(11) under conditions (12)–(14) is generalized by adapting Caputo (Caputo, 1967), Caputo–Fabrizio (Caputo and Fabrizio, 2015), and Atangana–Baleanu (Atangana and Baleanu, 2016) fractional operators. The obtained fractional model is solved using ADM (Stehfest, 1970; Tzou, 1997; Sarwar, 2020).
Proposed fractional-order nanofluid model
Equations 10 and 11 are homogenous and Eq. 9 is a nonhomogeneous second-order PDE. We construct the fractional-order Casson nanofluid models by changing time derivative with Caputo (C), Caputo–Fabrizio (CF), and Atangana–Baleanu (ABC) fractional derivatives. We get
where 0 < α, β, δ ≤ 1, q ∈ {α, β, δ}, and
• the fractional Caputo differential operator of order q ∈ (0, 1) and a function f(t) ∈ H1 [a, b] is defined (Caputo, 1967) as follows:
• the Caputo–Fabrizio fractional derivative of order q ∈ (0, 1) and a function f(t) ∈ H1 [a, b] is defined (Caputo and Fabrizio, 2015) as follows:
• the new fractional derivative Atangana–Baleanu operator of order q ∈ (0, 1) (Atangana and Baleanu, 2016) is as follows:
where
Formulation of Adomian decomposition method
As mentioned, ADM is used for approximation. The algorithm of fractional ADM is as follows:
1) Consider the fractional PDE as follows:
where
We write Eq. 21 in the form
2) Using the fractional integral Iq on both sides of Eq. 22, we get
This methods gives the solution Ψ in convergent series form as
and the decomposition of
In the work by Adomian (Adomian, 1988; Adomian, 1994), he provided the algorithm to find any kind of nonlinearity. To calculate the Adomian polynomials An−1 in Eq. 25, we consider the following general formula:
3) Substitute Eq. 24 and Eq. 25 into both sides of Eq. 23, we get
4) Using Ψ0 as an initial condition with Eq. 27, we can obtain Ψ1, Ψ2, ⋯.
5) Substituting these Ψ0, Ψ1, Ψ2, ⋯ in Eq. 24, Ψ(t, s) is obtained in a convergent series solution.
Numerical study
In order to solve the model (15)–(17) with Eqs 12–14, the given initial estimates are recommended to begin the simulations u0 = t2e−y, θ0 = e−y, and C0 = e−y. We assume that α = β = δ.
Application of ADM with the caputo derivative
In problems (15)–(17), we consider
Result of the fractional temperature field:
Result of the fractional velocity field:
Application of ADM with the Caputo–Fabrizio derivative
In problems (15)–(17), we consider
Fractional temperature field’s result is as follows:
Fractional velocity field’s result is as follows:
Application of ADM with the Atangana–Baleanu derivative
In problems (15)–(17), we consider
Fractional temperature field’s result is as follows:
Fractional velocity field’s result is as follows:
Nusselt number, Sherwood number, and skin friction
Heat and mass transfer rates and skin friction for ADMC, ADMCF, and ADMAB are obtained using results from Section 5.1, Section 5.2, and Section 5.3.
The numerical analyses for Nusselt number, Sherwood number, and skin friction under the influence of fractional parameters are given in Tables 2–4 for all three models.
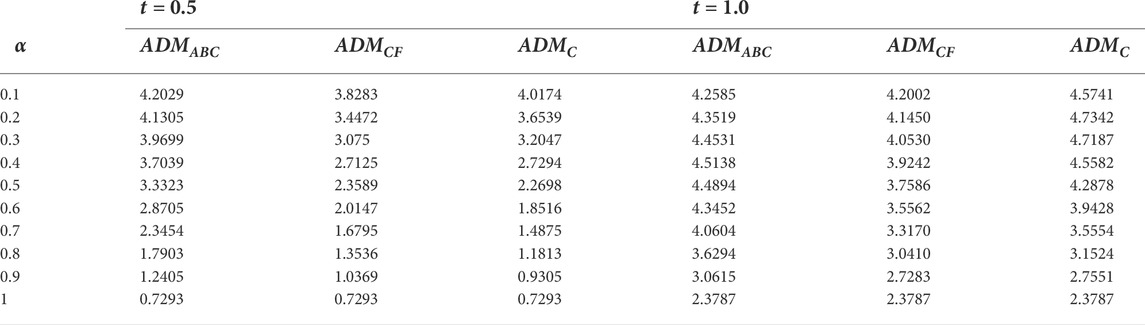
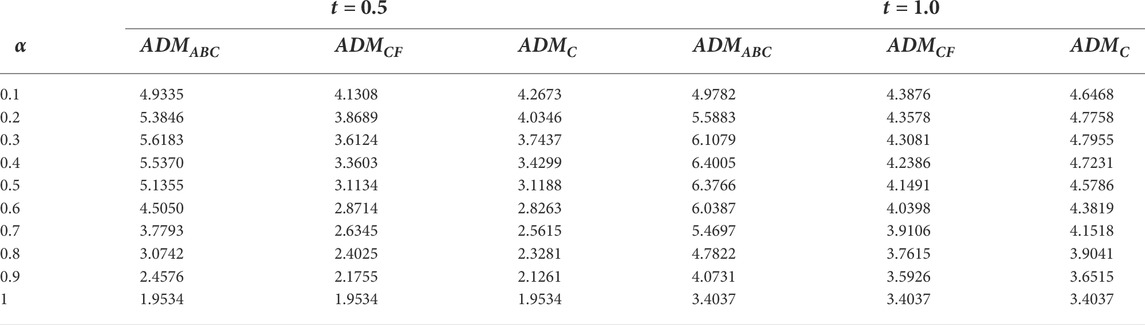
TABLE 2. Effect of fractional parameter on skin friction Cf for K = 3, M = 0.5, η = 0.1, Gr = 0.3, Gm = 0.01 γ = 0.2, Pr = 25, Nr = 18, and Sc = 0.22.
Results and discussions
In the present study, a fractional model is articulated utilizing three different differential approaches, i.e., Caputo (C), Caputo– Fabrizio (CF), and Atangana–Baleanu (ABC). ADM is used to obtain semianalytical solutions for compactness, velocity, and temperature domains. The received upshots are projected graphically to present the influence of fractional and flow parameters.
General approximative numerical solutions for unfirm incompressible, viscoelastic Casson nanofluid carrying human blood as the base fluid and CNTs (SWCNTs/ MWCNTs) as nanoparticles were obtained by ADM. It was reckoned that the upright plate was translating in its plane having velocity U0f(t), where U0 is the characteristic velocity and f(t) is a piecewise continuous function specified on [0, ∞) satisfying the condition f (0) = 0. In the present study, f(t) = t2 was presumed, which makes us speculate that the plate is rendered with unvarying apparent motion and hence also the fluid. The physical characteristics of blood and CNTs (SWCNTs/ MWCNTs) are acquired from Table 1 for numeric calculation.
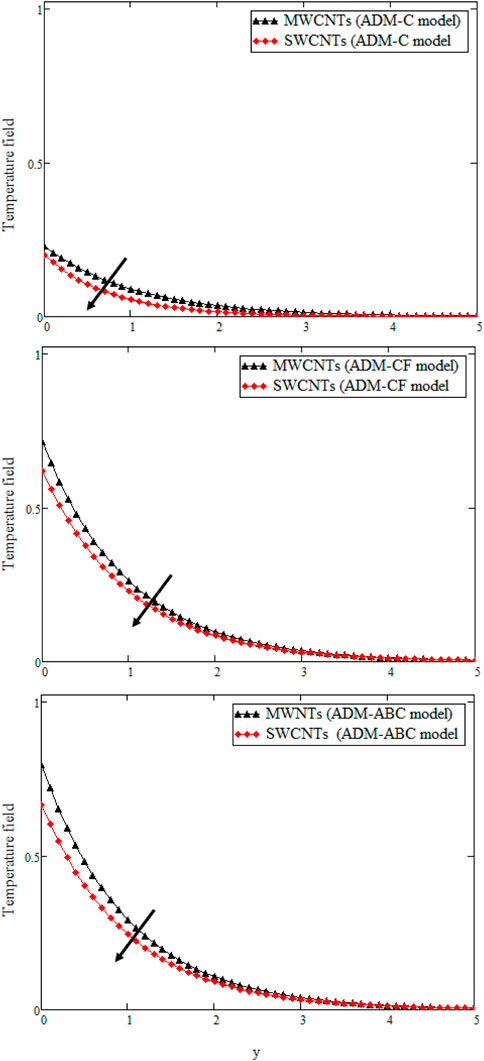
The temperature for SWCNT and MWCNT human blood-based nanofluid is compared in Figure 2. It is evident that the MWCNT Casson fluid depicts more heat conduction as compared to SWCNT nanoparticles. This is due to the differences between the thermal conductivities of both types of nanoparticles. the thermal conductivity for MWCNTs is 3000Wm−1K−1 while for SWCNTs it is 6600Wm−1K−1, which clearly shows that the temperature of MWCNTs has higher values as compared to SWCNTs. A similar behavior can be seen for all three models, which was described by Imran et al. (2020).
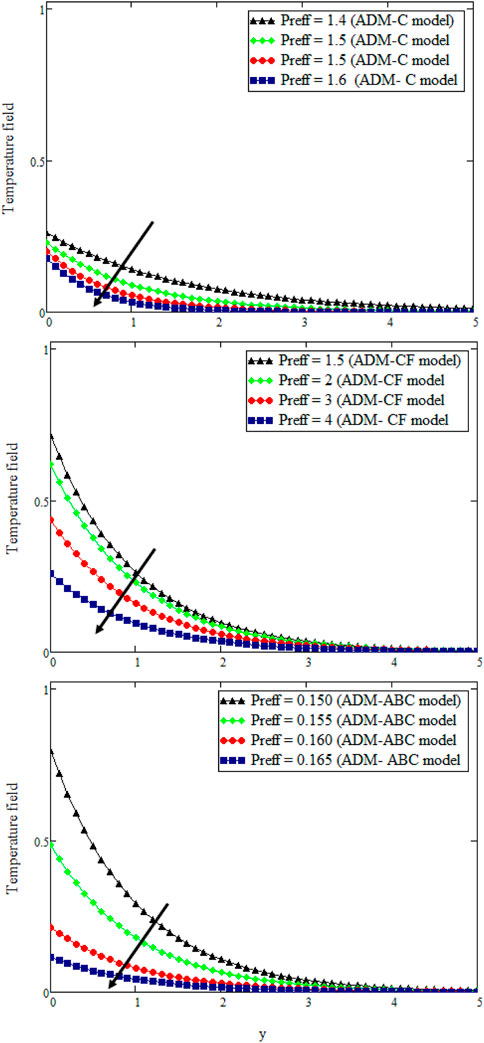
Figure 3 Plots revealing the impact of Preff on temperature fields obtained by the three fractional approaches. It can be clearly seen from the graph that temperature and boundary layer thickness are reduced by maximizing Preff. The value of Preff depends on the radiation–conduction parametric quantity Nr and Prandtl number Pr. Graphically, as the Preff value intensifies, the fluid temperature is minimized. When the Preff value is increased, it reduces thermal conductivity and enhances liquid viscosity leading to an abbreviation of the thickness of the thermic boundary layer. Nonetheless, the ADMAB model delineates this deportment better due to the presence of Mittag–Leffler kernel when equated with ADMCF and ADMC models. All models demonstrate a similar pattern.
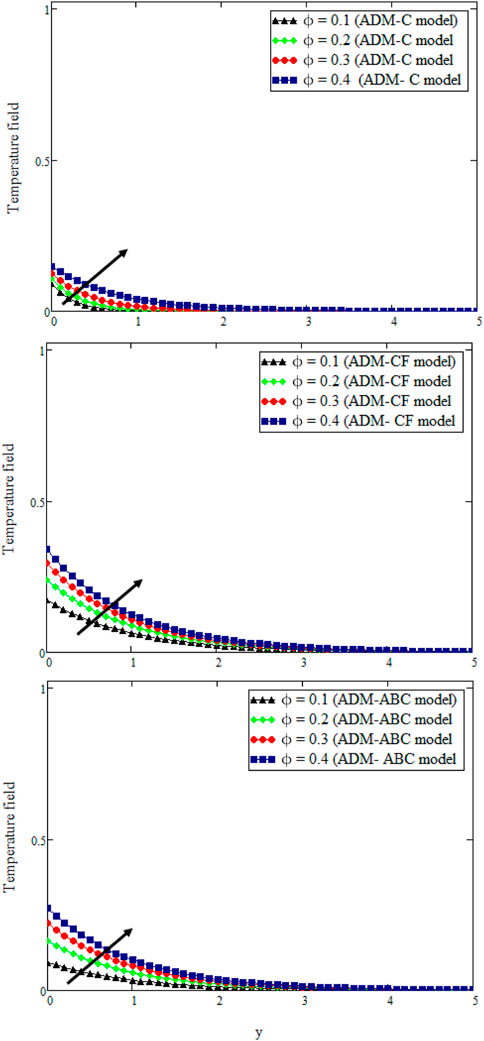
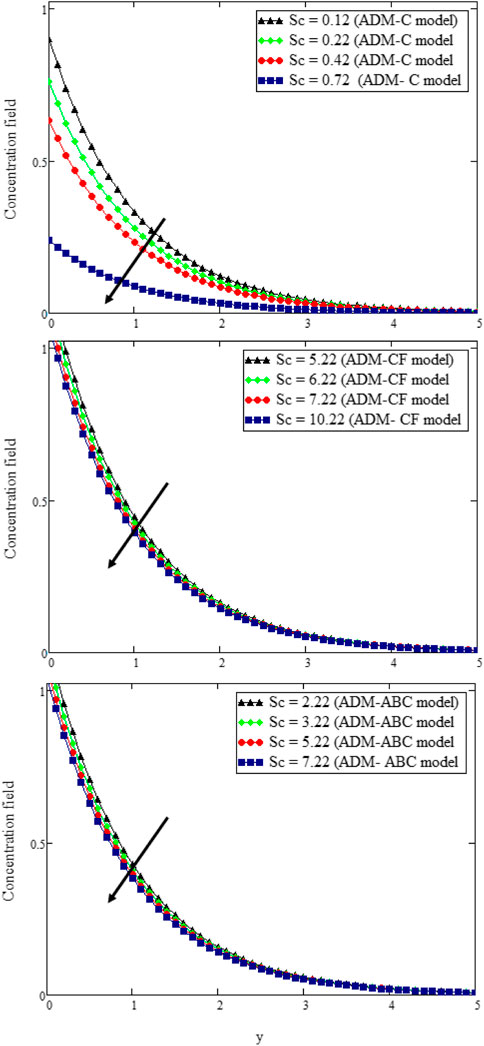
Figure 4 shows the effect of nanoparticle volume fraction ϕ on the temperature domain. Temperature enhances upon increasing the value of nanoparticle volume fraction ϕ; physically, it occurs because of the addition of MWCNT nanoparticles into the Casson fluid, leading to elevated thermic conduction and, therefore, increasing temperature. The plots in Figure 5 help us understand the upshot of Sc on concentration by taking other parameters to be fixed. It is determined, that with an increase of Sc the thickness of the liquid decreases, which is due to a reduction of molecular diffusivity.
The plots in Figure 6 help us envision the impact of SWCNTs and MWCNTs in Casson fluid, which in our case is human blood, on velocity domains obtained by the three fractional approaches. Graphically, it can be envisioned that MWCNTs’ nanoliquid moves faster than SWCNTs’ nanofluid. Physically, this occurs due to the density of carbon nanotube nanoparticles. The density of MWCNTs is (1600Wm−1K−1) whereas the density of SWCNTs is (2600Wm−1K−1), which makes SWCNT-based nanofluid thick, resulting in slower motion of the fluid. Similar behavior can be seen in the work by Imran et al. (2020). Dispersing MWCNT nanoparticles into the Casson liquid decreases its velocity due to increased thickness. Similar patterns can be seen for all three fractional models.
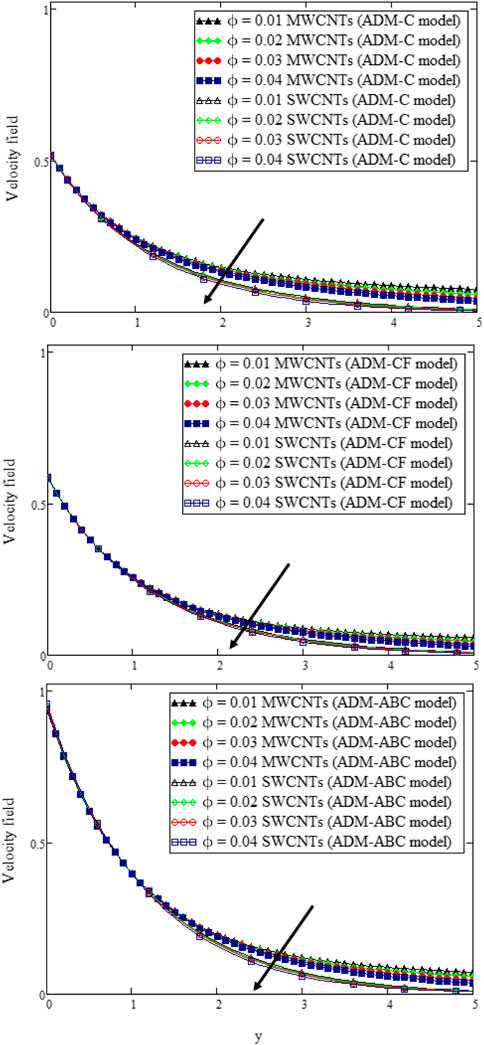
FIGURE 6. u (y, t) with ϕ when t = 0.3, K = 3, Gr = 0.55, Gm = 0.01 η = 0.15, α = β = δ = 0.8, γ = 0.95, Pr = 25, Nr = 18, M = 1.4, and Sc = 1.5.
Figures (7––14) show numerical traits of MWCNTs’ nanospecks and human blood presented in Table 1. Figures 7, 8 determine the outcome of mass and thermal Grashof numbers, i.e., Gm and Gr, respectively. The fluid speed in both cases is enhanced with Gr and Gm. The fluid flow is simply imputable to buoyant pressures. When this force is zero, the fluid will not be no displaced. For Gr > 0, the natural convection is imputable, and heat is channelized to the fluid through the plate; afterward, the plate is tranquilized. When the Grashof number is increased, the buoyant force originates and becomes less glutinous, which institutes liquid flow faster as seen in these graphs for both frameworks. Moreover, Figure 9 is plotted for Preff versus y by keeping other parameters fixed. It is pertinent to mention that by invoking Preff, the fluid speed decreases and the boundary layer thickness is reduced. The reason for this is the increased value of Preff leads to acquiring fluid viscosity, and the reduced caloric boundary layer leads to slower apparent motion. This can be further elaborated from the graphical analysis; the ADMABC model describes the behavior of the function in the best possible way because it holds Mittag–Leffler kernel, which stores the memory factor, and is therefore better in describing the fluid’s flow fields when compared with ADMCF and ADMC. When the fractional parameter approaches 1, ADMABC gives velocity values closer to the classical results.
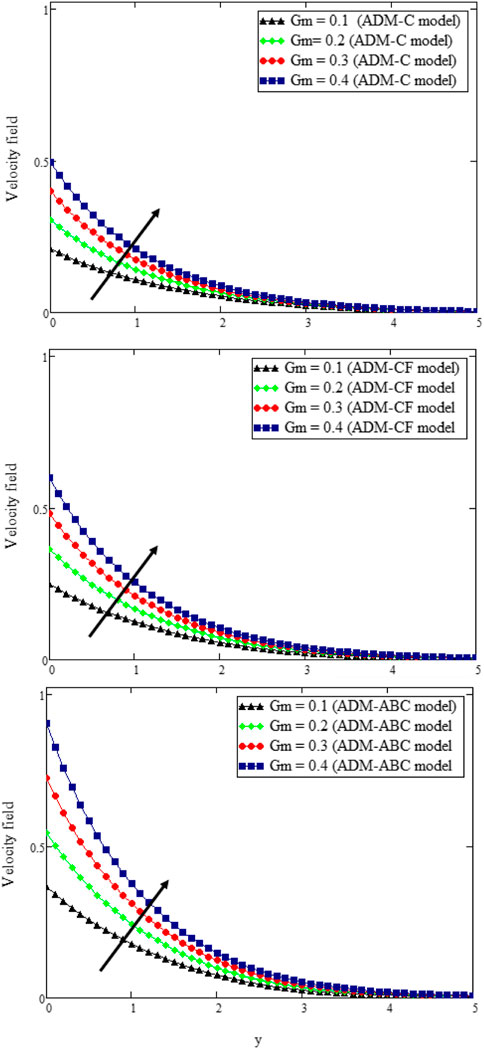
FIGURE 7. u (y, t) with Gm when t = 0.3, K = 2.9, Gr = 0.05, ϕ = 0.02, η = 0.15, α = β = δ = 0.8, γ = 0.95, Pr = 25, Nr = 20, M = 1.4, and Sc = 1.5.
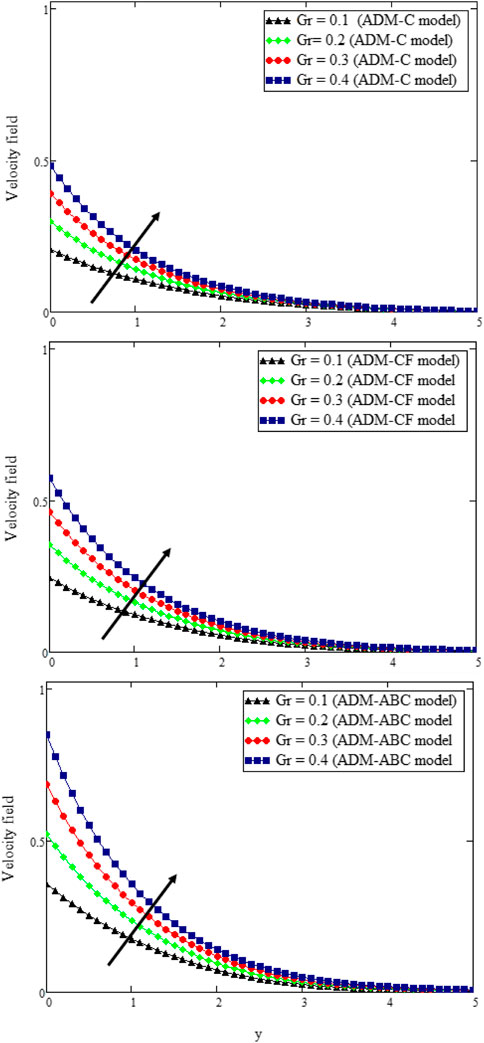
FIGURE 8. u (y, t) with Gr when t = 0.3, K = 2.9, Gm = 0.05, ϕ = 0.02, η = 0.15, α = β = δ = 0.8, γ = 0.95, Pr = 25, Nr = 18, M = 1.4, and Sc = 1.5.
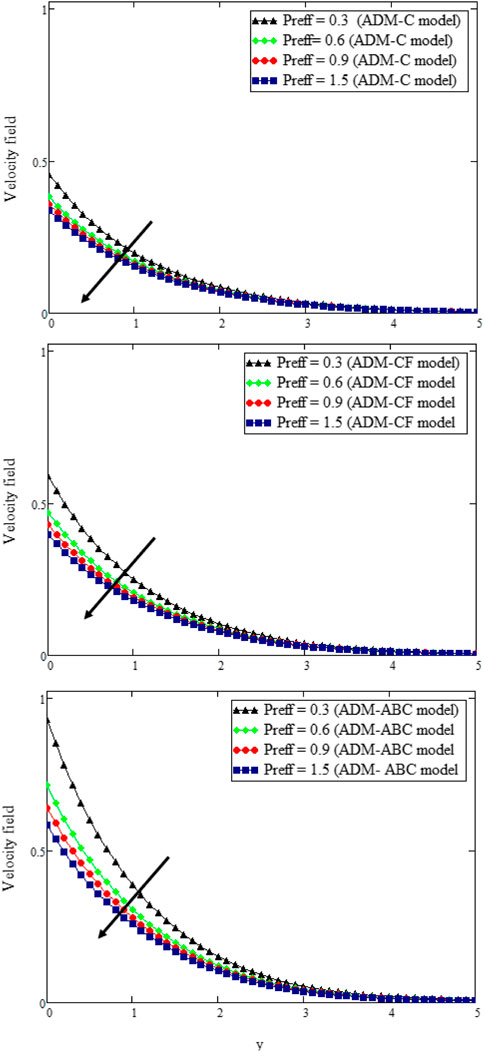
FIGURE 9. u (y, t) with Preff when t = 0.3, K = 2.9, Gm = 0.05, ϕ = 0.02, η = 0.15, α = β = δ = 0.8, γ = 0.95, Gr = 0.25, M = 1.4, and Sc = 1.5.
The plots in Figure 10 probe the invasion of Schmidt number Sc on liquid velocity by confining the parametric quantities constantly. It is observed that an increase in Sc leads to a decrease in the speed. Figure 11 is diagrammed to ascertain the impression of porosity parameter K on velocity. For large values of K, speed and boundary layer thickness are increased. The reason behind this phenomenon is that by increasing the permeability of the porous medium its resistance is decreased, which contributes to increasing the momentum of the flux regime. Figure 12 is diagrammed to project the impression of the Casson parameter γ, which unveils tangible traits of plasticity. When γ decreases, blood plasticity increases, which ultimately deaccelerates the motion of the fluid.
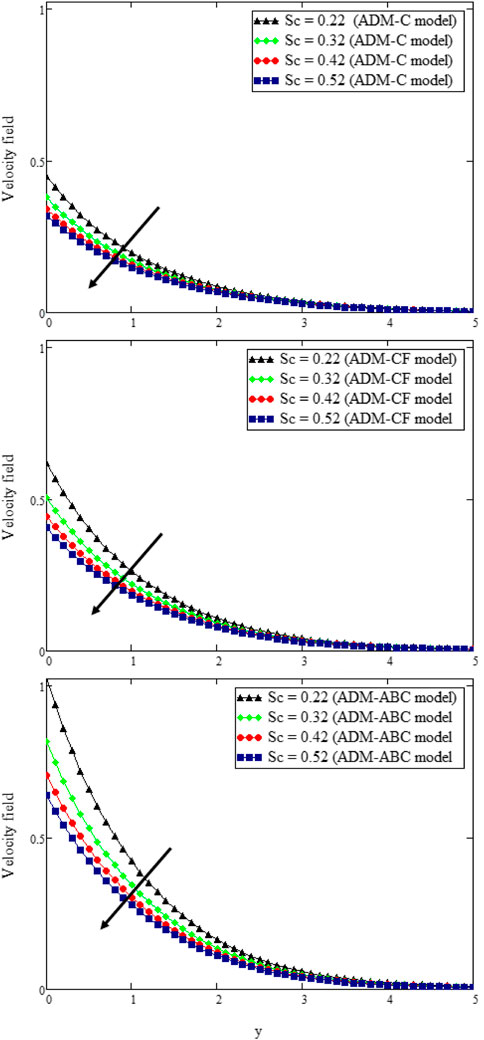
FIGURE 10. u (y, t) with Sc when t = 0.3, K = 2.9, Gm = 0.15, η = 0.15, ϕ = 0.02, α = β = δ = 0.8, γ = 0.95, Pr = 25, Nr = 22, M = 1.4, and Gr = 0.05.
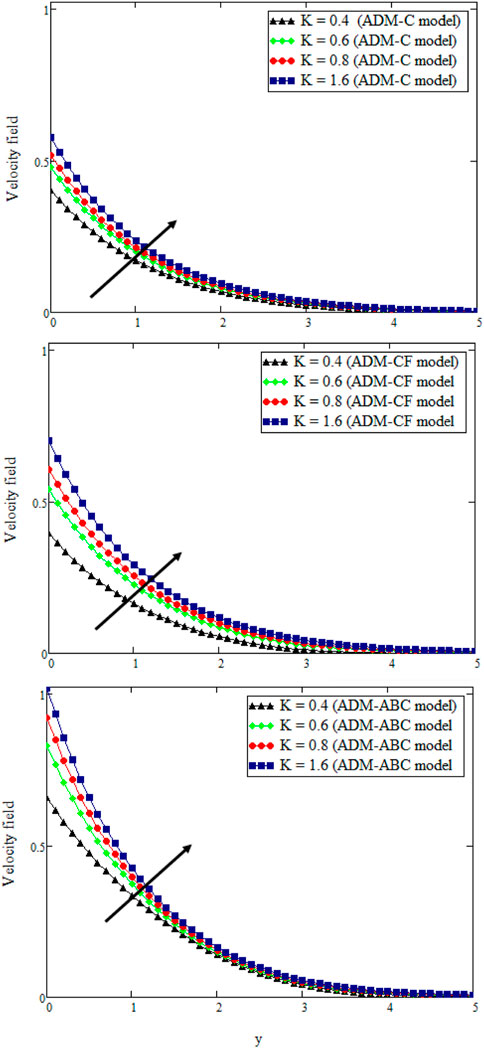
FIGURE 11. u (y, t) with K when t = 0.3, Gm = 0.5, η = 0.15, Sc = 1.2, ϕ = 0.02, α = β = δ = 0.8, γ = 0.95, Pr = 25, Nr = 18, M = 1.5, and Gr = 0.05.
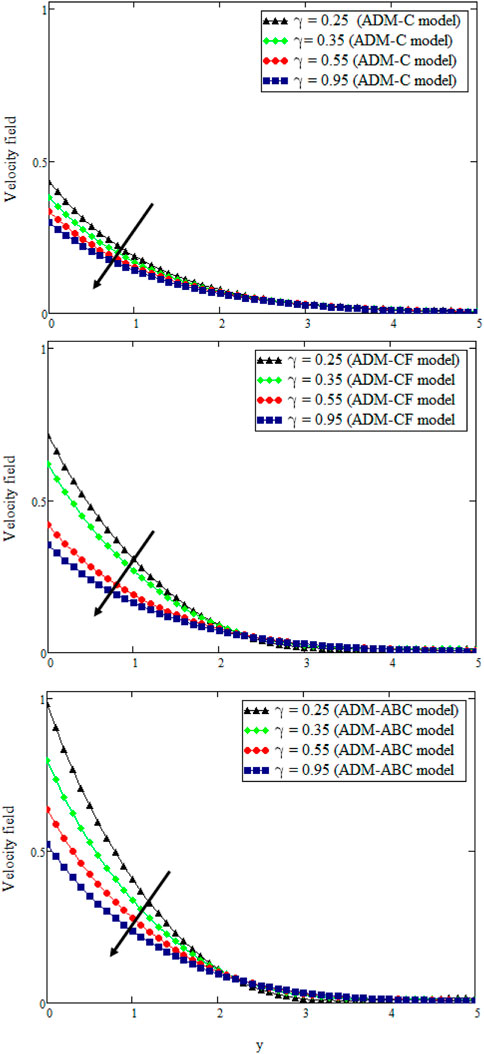
FIGURE 12. u (y, t) with γ when t = 0.3, Gm = 0.05, η = 0.15, Sc = 1.5, ϕ = 0.02, α = β = δ = 0.8, K = 2.95, Pr = 25, Nr = 18, M = 1.4, and Gr = 0.2.
Figure 13 is diagrammed to ascertain the effect of the slip parameter on Casson MWCNTs’ nanofluid. By increasing the value of η, velocity is deaccelerated as displayed in Figure 13 for increasing three fractional models. Figure 14 shows the plots for magnetic field parameter M, which produces a magnetic field during the fluid’s flow. An increase in the magnetic flux parametric quantity decreases the velocity. An increase in the magnetic field parameter engenders the drag force to the stream, termed as Lorentz force. These retarding forces understate the velocity profiles and reduce the thickness of MBL.
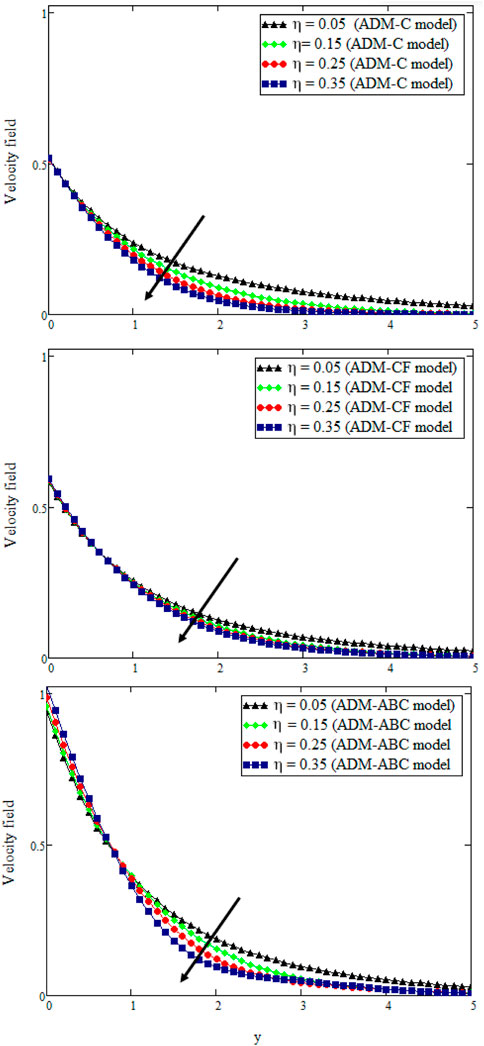
FIGURE 13. u (y, t) with η when t = 0.3, Gm = 0.01, γ = 0.95, Sc = 0.55, ϕ = 0.02, α = β = δ = 0.8, K = 3, Pr = 25, Nr = 18, M = 1.4, and Gr = 0.55.
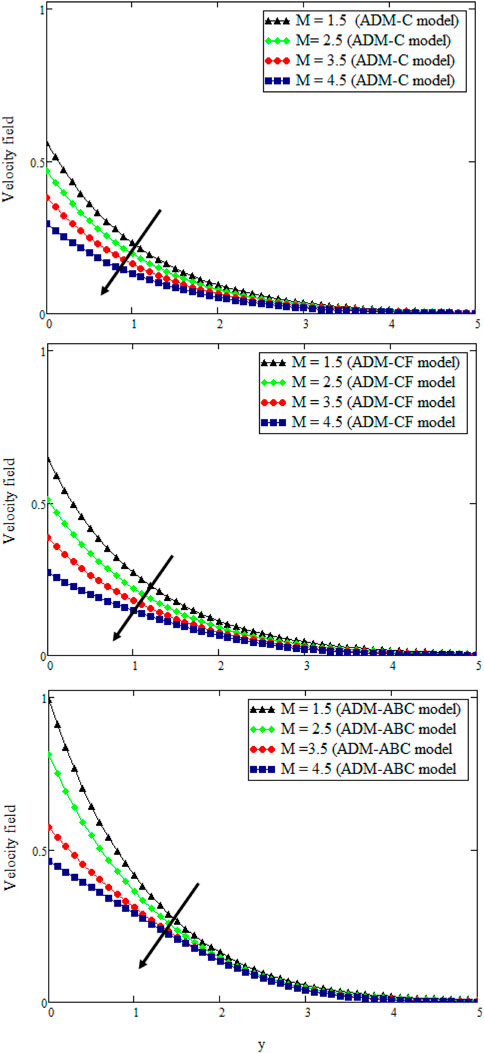
FIGURE 14. u (y, t) with M when t = 0.3, Gm = 0.05, γ = 0.95, Sc = 0.55, ϕ = 0.02, α = β = δ = 0.8, K = 2.9, Pr = 25, Nr = 18, η = 0.15, and Gr = 0.55.
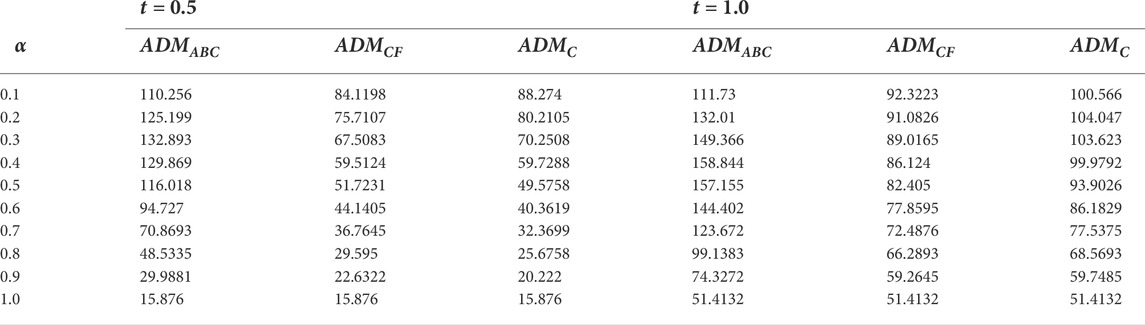
Table 2 presents fractional parameters’ impact on skin friction for small and large durations by keeping other parametric quantities fixed. By increasing the fractional parametric value, skin friction decreases for all models for small and large durations. However, for small duration, results are ADMCF < ADMC < ADMABC, and for large durations, ADMC and ADMABC show reverse behavior. The effect of the fractional variable on Nu, the Nusselt number, and Sherwood number Sh is given in Tables 3 and 4. For large and small durations, Nu and Sh for ADMABC first increase by increasing α and then show a decreasing behavior. For ADMC and ADMCF, Nusselt number and Sherwood number decrease by increasing α. All three models show a similar result for α = 1.
Conclusion
This study was performed to investigate free convective, unsteady, MHD blood flow with single (SWCNTs) and multiwalled carbon nanotubes (MWCNTs) as nanoparticles. The blood flow is considered over an oscillating vertically upright plate engrafted in a porous medium with slip, radiation, and porosity effects. Three fractional approaches Caputo (C), Caputo–Fabrizio (CF), and Atangana–Baleanu (ABC) are used to develop a fractional blood flow model, which is solved by the Adomian decomposition method (ADM). Some key findings are as follows:
1) Fractional parameter controls the rates of heat and mass transfer and maximum rates can be achieved for smaller values of the fractional parameter for small and large durations.
2) Fractional parameters can be used to control the thermal, diffusion, and momentum boundary layers, respectively, and are applicable in some experimental work where needed.
3) Fluid properties can be enhanced by increasing the concentration of nanoparticles and decreasing the velocity.
4) SWCNTs’ nanoparticles are more reliable and efficient in the heating process such as in electronics devices due to the higher value of thermal conductivity.
5) ADMABC model described the behavior of the function in a better way because it holds Mittag–Leffler kernel, which stores memory factors, and therefore is better in describing the fluid’s flow fields when compared with ADMCF and ADMC. When the fractional parameter approaches 1, ADMABC gives velocity values closer to the classical results.
6) Nusselt number and skin frictions are decreasing functions of α. However, for small durations, results are ADMCF < ADMC < ADMABC, and for large durations, ADMC and ADMABC show reverse behavior.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and have approved it for publication.
Acknowledgments
The authors acknowledge the financial support of Taif University Researchers Supporting Project number (TURSP-2020/189), Taif University, Taif, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adomian, G. (1988). A review of the decomposition method in applied mathematics. J. Math. Analysis Appl. 135, 501–544. doi:10.1016/0022-247x(88)90170-9
Adomian, G. (1994). Solving frontier problems of physics: The decomposition method. Boston: Kluwer Academic Publishers.
Ahmad, M., Imran, M. A., Aleem, M., and Khan, I. (2019). A comparative study and analysis of natural convection flow of MHD non-Newtonian fluid in the presence of heat source and first-order chemical reaction. J. Therm. Anal. Calorim. 137, 1783–1796. doi:10.1007/s10973-019-08065-3
Ahmed, N., Mohyud-Din, S. T., and Saleh Hassan, M. (2016). Flow and heat transfer of nanofluid in an asymmetric channel with expanding and contracting walls suspended by carbon nanotubes: A numerical investigation. Aerosp. Sci. Technol. 48, 53–60. doi:10.1016/j.ast.2015.10.022
Aleem, M., Imran, M. A., and Akgul, A. (2021). Heat transfer analysis of magnetohydrodynamic Casson fluid through a porous medium with constant proportional Caputo derivative. Heat. Transf. 50, 6444–6464. doi:10.1002/htj.22179
Ali, F., Ali, F., Sheikh, N. A., Khan, I., and Nisar, K. S. (2020). Caputo–Fabrizio fractional derivatives modeling of transient MHD Brinkman nanoliquid: Applications in food technology. Chaos Solit. Fractals 131. doi:10.1016/j.chaos.2019.109489
Ali, F., Khan, I., and Shafie, S. (2014). Closed form solutions for unsteady free convection flow of a second grade fluid over an oscillating vertical plate. PLoS One 9 (2), e85099. doi:10.1371/journal.pone.0085099
Ali, F., Saqib, M., Khan, I., and Sheikh, N. A. (2016). Application of Caputo–Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 131 (10), 377. doi:10.1140/epjp/i2016-16377-x
Animasaun, I. L., Adebile, E. A., and Fagbade, A. I. (2015). Casson fluid flow with variable thermo physical property along exponentially stretching sheet with suction and exponentially decaying internal heat generation using the homotopy analysis method. J. Niger. Math. Soc. 2 (1), 1–17. doi:10.1016/j.jnnms.2015.02.001
Atangana, A., and Baleanu, D. (2016). New fractional derivatives with non–local and non-singular kernel: Theory and application to heat transfer model. J. Therm. Sci. 20, 763–769. doi:10.2298/tsci160111018a
Bhattacharyya, K. (2013). Boundary layer stagnation-point flow of casson fluid and heat transfer towards a shrinking/stretching sheet. Front. Heat Mass Transf. 4 (2). doi:10.5098/hmt.v4.2.3003
Bhattacharyya, K., Hayat, T., and Alsaedi, A. (2014). Exact solution for boundary layer flow of Casson fluid over a permeable stretching/ shrinking sheet. Z. Angew. Math. Mech. 94 (6), 522–528. doi:10.1002/zamm.201200031
Bourantas, G. C., and Loukopoulos, V. C. (2014). Modeling the natural convective flow of micropolar nanofluids. Int. J. Heat Mass Transf. 68, 35–41. doi:10.1016/j.ijheatmasstransfer.2013.09.006
Caputo, M., and Fabrizio, M. (2015). A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. Int. J. 1 (2), 1–13.
Caputo, M. (1967). Linear models of dissipation whose Q is almost frequency independent. Geophys. J. Int. 13 (5), 529–539. doi:10.1111/j.1365-246x.1967.tb02303.x
Casson, N. (1959). A flow equation for the pigment oil suspensions of the printing ink type, Rheology of Disperse Systems. NewYork, USA: Pergamon, 84–104.
Hassan, M. A., Pathak, M., and Khan, M. K. (2013). Natural convection of viscoplastic fluids in a square enclosure. J. Heat Transf. 135, 122501–122512. doi:10.1115/1.4024896
Hayat, T., Shehzad, S. A., and Alsaedi, A. (2012). Soret and Dufour effects on magnetohydrodynamic (MHD) flow of Casson fluid. Appl. Math. Mech. 33 (10), 1301–1312. doi:10.1007/s10483-012-1623-6
Herrmann, R. (2014). Fractional calculus: An introduction for physicists. 2nd ed. Singapore: World Scientific.
Hussanan, A., Salleh, M. Z., Khan, I., and Tahar, R. M. (2016). Unsteady heat transfer flow of a Casson fluid with Newtonian heating and thermal radiation. J. Teknol. 78, 1–7. doi:10.11113/jt.v78.8264
Imran, M. A., Aleem, M., Ahmadan, A., Salahshour, S., and Ferrara, M. (2020). New trends of fractional modeling and heat and mass transfer investigation of (SWCNTs and MWCNTs)-CMC based nanofluids flow over inclined plate with generalized boundary conditions. Chin. J. Phys. 66, 497–516. doi:10.1016/j.cjph.2020.05.026
Imran, M. A., Aleem, M., and Riaz, M. B. (2018). Exact analysis of MHD Walters’–B fluid flow with non-singular fractional derivatives of Caputo–Fabrizio in the presence of radiation and chemical reaction. J. Polym. Sci. Eng. 1 (2). doi:10.24294/jpse.v1i2.599
Imran, M. A., Sarwar, S., and Imran, M. (2016). Effects of slip on free convection flow of Casson fluid over an oscillating vertical plate. Bound. Value Probl. 30. doi:10.1186/s13661-016-0538-2
Imran, M. A., Shah, N. A., Aleem, M., and Khan, I. (2017). Heat transfer analysis of fractional second-grade fluid subject to Newtonian heating with Caputo and caputo-fabrizio fractional derivatives: A comparison. Eur. Phys. J. Plus 32, 340. doi:10.1140/epjp/i2017-11606-6
Imran, M. A., Shah, N. A., Rafique, K., Sohail, A., and Ejaz, E. (2017). General solutions of convective flows of MHD casson fluid with slip and radiative heat transfer at the boundary. Comput. Therm. Scien. 9 (1), 1–11. doi:10.1615/computthermalscien.2016016971
Kameswaran, P. K., Shaw, S., and Sibanda, P. (2014). Dual solutions of Casson fluid flow over a stretching or shrinking sheet. Sadhana 39 (6), 1573–1583. doi:10.1007/s12046-014-0289-7
Kataria, H. R., and Patel, H. R. (2018). Heat and mass transfer in magnetohydrodynamic (MHD) Casson fluid flow past over an oscillating vertical plate embedded in porous medium with ramped wall temperature. Propuls. Power Res. 7 (3), 257–267. doi:10.1016/j.jppr.2018.07.003
Khalid, A., Khan, I., Khan, A., Shafie, S., and Tlili, I. (2018). Case study of MHD blood flow in a porous medium with CNTS and thermal analysis. Case Stud. Therm. Eng. 12, 374–380. doi:10.1016/j.csite.2018.04.004
Kleppe, J., and Marner, W. J. (1970). Transient free convection in a Bingham plastic on a vertical flat plate. J. Heat Transf. 94, 371–376. doi:10.1115/1.3449954
Kumar, M. S., Sandeep, N., Kumar, B. P., and Saleem, S. (2018). A comparative study of chemically reacting 2D flow of Casson and Maxwell fluids. Alexandria Eng. J. 57 (3), 2027–2034. doi:10.1016/j.aej.2017.05.010
Kumar, M. S., Sandeep, N., Kumar, B. R., and Saleem, S. (2018). Effect of aligned magnetic field on MHD squeezing flow of Casson fluid between parallel plates. Defect Diffusion Forum 384, 1–11. doi:10.4028/www.scientific.net/ddf.384.1
Li, C. P., and Cai, M. (2019). Theory and numerical approximations of fractional integrals and derivatives. Philadelphia: SIAM.
Li, C. P., and Zeng, F. H. (2015). Numerical methods for fractional differential calculus. Boca Raton, USA: Chapman and Hall/CRC.
Loganathan, P., Nirmal, C., and Ganesan, P. (2015). Transient natural convective flow of a nanofluid past a vertical plate in the presence of heat generation. J. Appl. Mech. Tech. Phy. 56 (3), 433–442. doi:10.1134/s002189441503013x
Nadeem, S., Haq, R. U., and Lee, C. (2012). MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 19 (6), 1550–1553. doi:10.1016/j.scient.2012.10.021
Povstenko, Y. (2015). Linear Fractional diffusion–wave equation for scientists and engineers. New York: Birkhäuser.
Pramanik, S. (2014). Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 5 (1), 205–212. doi:10.1016/j.asej.2013.05.003
Rajesh, V., Chamkha, A. J., and Mallesh, M. P., GITAM University Hyderabad Campus, unspecified, GITAM University Hyd. Transient MHD free convection flow and heat transfer of nanofluid past an impulsively started semi-infinite vertical plate, J. Appl. Fluid Mech., 9(5), 2016, 2457–2467. doi:10.18869/acadpub.jafm.68.236.23443
Raju, C. K., Sandeep, N., and Saleem, S. (2016). Effects of induced magnetic field and homogeneous-heterogeneous reactions on stagnation flow of a Casson fluid. Eng. Sci. Technol. Int. J. 19 (2), 875–887. doi:10.1016/j.jestch.2015.12.004
Ramesh, K., and Devakar, M. (2015). Some analytical solutions for flows of Casson fluid with slip boundary conditions. Ain Shams Eng. J. 6 (3), 967–975. doi:10.1016/j.asej.2015.02.007
Rehman, H., Ullah, N., and Imran, M. A. (2019). Highly dispersive optical solitons using Kudryashov’s method. Optik 199, 163349. doi:10.1016/j.ijleo.2019.163349
Sarwar, S. (2020). New rational solutions of fractional–order sharma–tasso–olever equation with atangana–baleanu derivative arising in physical sciences. Results Phys. 19, 103621. doi:10.1016/j.rinp.2020.103621
Shaw, S., Mahanta, G., and Das, M. (2019). Thermal and solutal Marangoni stagnation point Casson fluid flow over a stretching sheet in the presence of radiation, Soret and Dofour effect with chemical reaction. Heat. Trans. Res. 48, 323–342. doi:10.1002/htj.21386
Sheikh, N. A., Ching, D. L. C., Khan, I., Kumar, D., and Nisar, K. S. (2020). A new model of fractional Casson fluid based on generalized Fick’s and Fourier’s laws together with heat and mass transfer. Alexandria Eng. J. 59 (5), 2865–2876. doi:10.1016/j.aej.2019.12.023
Stehfest, H. (1970). Algorithm 368: Numerical inversion of laplace transforms [D5]. Commun. ACM 13, 47–49. doi:10.1145/361953.361969
Tahir, M., Imran, M. A., Raza, N., Abdullah, M., and Aleem, M. (2017). Wall slip and non-integer order derivative effects on the heat transfer flow of Maxwell fluid over an oscillating vertical plate with new definition of fractional Caputo-Fabrizio derivatives. Results Phys. 7, 1887–1898. doi:10.1016/j.rinp.2017.06.001
Tarasov, V. E. (2010). Fractional dynamics: Applications of fractional calculus to dynamics of particles, fields and media. Berlin: Springer.
Tzou, D. Y. (1997). Macro to microscale heat transfer: The lagging behavior. Washington: Taylor & Francis.
Xue, Q. (2005). Model for thermal conductivity of carbon nanotube based composites. Phys. B Condens. Matter 368 (1), 302–307. doi:10.1016/j.physb.2005.07.024
Keywords: heat and mass transfer, radiative heat transfer, Atangana–Baleanu derivative, Caputo–Fabrizio derivative, slip condition
Citation: Aleem M, Inc M, Sarwar S, Asjad MI and Alsubaie ASA (2022) Analysis of fractional MHD convective flow with CTNs’ nanoparticles and radiative heat flux in human blood. Front. Energy Res. 10:962086. doi: 10.3389/fenrg.2022.962086
Received: 05 June 2022; Accepted: 13 July 2022;
Published: 02 September 2022.
Edited by:
Umar Khan, Hazara University, PakistanCopyright © 2022 Aleem, Inc, Sarwar, Asjad and Alsubaie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mustafa Inc, bXVzdGFmYWluYzEwNzFAZ21haWwuY29t
 Maryam Aleem
Maryam Aleem Mustafa Inc
Mustafa Inc Shahzad Sarwar4
Shahzad Sarwar4 Muhammad Imran Asjad
Muhammad Imran Asjad