Research on core power maximization method of natural circulation lead-bismuth cooled fast reactor

To improve the inherent safety and cost-effectiveness of lead-bismuth cooled fast reactors, the SPALLER-100 reactor designed by the University of South China has been selected as the research object to determine the maximum power it can produce. This is a multi-objective, complex, multi-dimensional, nonlinear, and constrained optimization problem. To maintain the transportability, material durability, and long-term operation stability of the reactor core and ensure safety under accident conditions, three steady-state limitations and three accident limitations are proposed. The platform used to calculate the maximum neutronic power produced by the reactor at different core heights has been built using Latin hypercube sampling and the Kriging proxy model. Meanwhile, the cooling power of the reactor at different core heights is calculated by considering its natural circulation capacity. Finally, a design scheme is obtained that meets the requirements of neutronic and thermal-hydraulic assessments, while producing maximum power. Consequently, during the entire life-cycle of SPALLER-100, a safety analysis of three typical accident scenarios (unprotected loss of heat sink, unprotected transient over power, and unprotected coolant inlet temperature undercooling) is performed using a Quasi-Static Reactivity Balance (QSRB) approach. The results show that the platform used to calculate the maximum neutronic power exhibits high accuracy, and that the design scheme with maximum power is safe and economical. Overall, this study can provide reference ideas for designing natural circulation reactors that can maximize power output.

1 Introduction

Although new energy sources are being continuously developed globally, nuclear energy is still one of the important energy sources for humans. Currently, the development and commercialization of small- and medium-sized reactors is increasing since they exhibit a short construction cycle, low investment risk, and flexible layout (Cao et al., 2014). Small natural circulation lead-bismuth reactors are novel nuclear reactors that are safe, compact, cost-effective, and exhibit a long service life; thus, they have good development prospects.

A long-life nuclear reactor requires a sustainable core and fast neutron spectrum for reducing its refueling cost, which allows it to utilize uranium more efficiently than thermal neutron reactors. Moreover, the structural materials of the reactor should be able to withstand irradiation for a long time. The cladding materials of current reactors, such as HT-9 or T-91 steel, can withstand material irradiation of 200 dpa (Cheon et al., 2009). Lead-bismuth eutectic (LBE) exhibits the advantages of stable chemical properties, high thermal conductivity, and favorable natural circulation. However, for a lead-bismuth reactor, LBE has two main disadvantages as a coolant (Zhao, 2017): first, LBE seriously corrodes the structural materials in the reactor; second, LBE leads to the production of radionuclide ²¹⁰Po with a half-life of 138 days. Zrodniko et al. (2006) have developed a method for treating ²¹⁰Po during the refueling and maintenance of the reactor. Meanwhile, Muller (Müller et al., 2002) and Rivai (Rivai and Takahashi, 2008) have developed coating materials for aluminum and silicon that can overcome the corroding effect of LBE. A decreased fuel loading in the core and small core size are essential for meeting the national road transportation regulations. Thus, miniaturization technology enables the transportation of reactors and allows a flexible reactor layout. Furthermore, to ensure natural circulation, a significant difference between the heat levels of the heat exchanger and core is necessary. Owing to the balance between buoyancy and resistance, steady-state natural convection leads to a uniform core temperature distribution, which effectively avoids overheating and even burning accidents of fuel components and core structures, and reduces material damage caused by thermal stress.

To achieve the above-mentioned objectives and improve the safety and cost-effectiveness of reactors, this study uses the Small Passive Long-life LBE-cooled fast Reactor (Liu et al., 2020) (SPALLER) designed by the University of South China (USC) as the research object to achieve maximal output power. First, this study analyzes various design limitations of the LBE reactor under natural circulation. Second, we build a platform that determines the maximum power produced by the reactor, while considering the physical and thermal performance of the reactor. Finally, an accident analysis is performed through the Quasi-static Reactivity Balance (QSRB) approach (Wade and Chang, 1988) proposed by Argonne National Laboratory (ANL). The results show that the proposed reactor scheme exhibits a good thermal safety performance, which can be used to engineer other reactors.

2 Core model and related theory

2.1 SPALLER-100 reactor

The SPALLER-100 reactor has been independently designed by the USC. The thermal power of the reactor core is 100 MW, and the refueling cycle is 20 years. The operating temperature is 320–480°C, and its coolant is LBE. The height of the reactor core active zone is 1.5 m, and the equivalent diameter is 1.7 m. The reactor fuel is PuN-ThN. Furthermore, the reactor exhibits a loading capacity of 5475.88 kg, with fuel assemblies in the inner and outer zones. There are 61 fuel rods in each fuel assembly, with a 4 mm assembly box in the outer layer. The pellet cladding material is made of HT-9 steel. Meanwhile, BeO is used as the moderator, which is filled between the assembly box and the outermost fuel rod.

The SPALLER-100 reactor is shown in Figure 1. The core is composed of 48 fuel assemblies (including inner and outer zones), 66 reflector assemblies, and 126 shielding assemblies. Moreover, the core is also equipped with 3 shutdown assemblies and 10 control assemblies. Among them, the inner zone contains 12 fuel assemblies (Pu mass fraction is 20.5%), and the outer zone contains 36 fuel assemblies (Pu mass fraction is 30.8%).

FIGURE 1

FIGURE 1. Cross-sections of the SPALLER-100 core.

In a reactor, the effective multiplication factor $k_{eff}$ (defined via the neutron equilibrium relationship) is the ratio of the neutron production rate to the total neutron disappearance rate. To quantitatively analyze the effect of changes in the SPALLER core reactivity on reactor operation, the following definitions of reactivity $\rho$ and reactivity swing $\mathrm{\Delta }\rho$ are used:

$\rho =\frac{k_{eff}-1}{k_{eff}}(1)$

$\mathrm{\Delta }\rho =\frac{k_{eff}\left(Max\right)-k_{eff}\left(Min\right)}{k_{eff}\left(Max\right)k_{eff}\left(Min\right)}(2)$

2.2 Latin hypercube sampling

Sampling points are the basis of proxy model construction. In this study, the Latin Hypercube Sampling (LHS) method (Li and Zhang, 2011) is used for data collection. The Monte Carlo (MC) method is often used for reactor physics calculations, which is a traditional sampling method that utilizes the probability distribution of random numbers or pseudorandom numbers. However, low probability results lead to the aggregation of MC sampling data. In contrast to the MC method, LHS can achieve nonoverlapping and space-filling sampling to effectively avoid the problem of sample point aggregation.

The main aim of employing the LHS method is to stratify the input probability distribution (that is, to extract the samples with sample size n from multiple variables) for maximizing the stratification of samples for each single variable. Its general calculation formula is:

$x_{ij}=\frac{\left[x_j\left(i\right)-U_{ij}\right]}{n},1\le i\le n,1\le j\le d(3)$

where $x_j\left(1\right)\dots x_j\left(n\right)$ is a random arrangement of integers 1 to $n$, $U_{ij}\sim U\left[\mathrm{0,1}\right]$ is a uniform random distribution obeying $U\left[\mathrm{0,1}\right]$ , $n$ is the number of samples, and d is the sample dimension.

2.3 Kriging proxy model

Kriging (Kempf et al., 2012) interpolation is implemented using the following steps: for any point in the specified area, $x_0$ is set as the point to be predicted, $x_1,x_2\dots x_n$ are selected as the observation points near $x_0$ the corresponding observation values are $y\left(x_1\right),y\left(x_2\right)\dots y\left(x_n\right)$ , and the prediction value of the point to be predicted is recorded as $\widehat{y}\left(x_0\right)$. Then, the predicted value is obtained by determining the weighted sum of the observed values:

$\widehat{y}\left(x_0\right)={\displaystyle \sum _{i=1}^N{\lambda }_{i}y\left(x_i\right)}(4)$

where ${\lambda }_i$ is the undetermined weighting coefficient. The key to kriging prediction is that the weighting coefficient ${\lambda }_i$ must satisfy the following two conditions:

(1) Assuming that the actual value of the measured point is $y\left(x_0\right)$, the unbiased estimation conditions are as follows:

$E\left[\widehat{y}\left(x_0\right)-y\left(x_0\right)\right]=0, {\displaystyle \sum _{i=1}^N{\lambda }_i=1}(5)$

(2) The variance between the estimated value and true value $y\left(x_0\right)$ is minimal.

The kriging model is mainly composed of a regression model and residual error. Its mathematical expression is as follows:

$y\left(x\right)=F\left(\beta ,x\right)+Z\left(x\right)=f^T\left(x\right)\beta +Z\left(x\right)(6)$

where $\beta$ is the regression coefficient; $f^T\left(x\right)$ is a regression model used to simulate global approximation; and $Z\left(x\right)$ is the residual error, which is used to simulate local error approximation.

3 Design limitations of analysis

To explore the method that maximizes the power produced by the natural circulation LBE reactor, it is necessary to ensure the safety of the reactor during long-term operation. Therefore, this study elucidates the original design limitations (Liu et al., 2020) of SPALLER-100 and puts forward many safety-related guidelines related to accident status and normal operation. Overall, this section mainly includes steady-state limitations and accident limitations.

3.1 Steady state limitations

Steady-state limitations can be divided into three categories based on road transportation, structural materials, and reactor physics: transportation limitations, material limitations, and neutronic limitations (Table 1).

TABLE 1

TABLE 1. Steady-state limitations.

3.1.1 Transportation limitations

According to China’s road transportation restrictions (Geng, 2004), the width of transportation vehicles should not exceed 2.5 m and their height should not be more than 4 m. The initial design goal of SPALLER-100 is to achieve a height of less than 2 m for the active zone of the core, with an equivalent diameter of less than 2 m. To explore the maximum power that can be output from the core, design limitations (an active zone height of less than 2.5 m and an equivalent diameter of less than 2.5 m) have been established by considering the above factors and widely referring to the design scheme of international long-life small natural circulation reactors.

3.1.2 Material limitations

Material limitations are greatly affected by fuels, structural materials, coolants, etc. SPALLER-100 utilizes PuN-ThN as the fuel and its melting point (corresponding to an enrichment of 30% and a burnup of 50 MWd/kgHM) is selected as the maximum temperature limit (2300°C). The cladding material of SPALLER-100 is composed of HT-9. To ensure that cladding materials are damaged and melted under normal and accident conditions, 550°C and 650°C are selected as the maximum cladding temperature limits under normal and accident conditions, respectively, based on an extensive investigation of the temperature limits of lead cooled fast reactors with HT-9 cladding. Each channel design must ensure that the coolant does not boil. Meanwhile, to prevent material corrosion, the speed of the LBE is limited to approximately 2.0 m/s (Hong et al., 2015).

3.1.3 Neutronic limitations

To provide a greater shutdown depth and meet safety requirements, the reactivity swing and maximum excess reactivity should be limited to less than 8 $. The delayed neutron share $\left(\text{β}\right)$ of the core is 0.3% (approximately 300 pcm). Since fast neutrons cause significant radiation damage to cladding and structural materials, the radiation resistance of cladding materials determines the neutron fluence limit during reactor operation. With the operation of the reactor, HT-9 neutron fluence will continue to accumulate. Specific power is proportional to neutron fluence, as shown in Figure 2. Meanwhile, the irradiation limit of HT-9 is 200 dpa and the corresponding neutron fluence is $4\times {10}^{23}c{m}^{-2}$ . When the core is operated for 20 effective full power years (EFPY), the neutron fluence rate in the reactor is limited to $6.34\times {10}^{14}c{m}^{-2}\cdot s^{-1}$ and the specific power does not exceed 19.4 W/gHM.

FIGURE 2

FIGURE 2. Fast neutron fluence for different EFPY.

3.2 Accident limitations

In case of an expected transient accident in a nuclear power plant, an automatic shutdown of the reactor emergency system is needed; however, a subsequent failure of the reactor protection system results in shutdown failure. Such an accident scenario is termed as the Anticipated Transient Without Scram (ATWS). In these scenarios, the reactor does not implement any shutdown protection measures. The ATWS scenarios can be analyzed via the QSRB approach and include five unprotected scenarios: unprotected loss of heat sink (ULOHS) accident, unprotected transient over power (UTOP) accident, unprotected loss of flow (ULOF) accident, unprotected coolant inlet temperature (UCIT) undercooling accident, and unprotected pump over-speed (UPOS) accident. The following equation shows the QSRB equation applicable to natural circulation (Cho et al., 2015):

${\displaystyle \sum \mathit{\Delta }\rho }=\left(P-1\right)A+\left(\frac{P}{F}-1\right)B+\delta T_{in}C=0(7)$

where P is the normalized power, F is the normalized flow, A is the reactive power coefficient (cents), B is the reactive power/flow coefficient (cents), and C is the reactive inlet temperature coefficient (cents/°C). $\delta T_{in}$ is the change in the coolant inlet temperature.

$A=\left({\alpha }_D+{\alpha }_A\right)\mathit{\Delta }{T}_{FC}(8)$

$B=\left({\alpha }_D+{\alpha }_A+{\alpha }_C+2{\alpha }_R\right)\mathit{\Delta }{T}_C/2(9)$

$C={\alpha }_D+{\alpha }_A+{\alpha }_R+{\alpha }_C(10)$

$A^{\prime }={\alpha }_D\mathit{\Delta }{T}_{FC}(11)$

${\alpha }_D$ is the fuel Doppler coefficient, ${\alpha }_A$ is the core axial expansion reactivity coefficient, ${\alpha }_R$ is the core radial expansion reactivity coefficient, ${\alpha }_c$ is the reactivity coefficient of coolant density, $\mathit{\Delta }{T}_{FC}$ is the difference between the average fuel temperature and the average coolant temperature under normal scenarios, and $\mathit{\Delta }{T}_c$ is the temperature rise of core coolant under normal scenarios.

The QSRB approach has an applicable assumption; that is, the reactor can reach its equilibrium state with a total reactivity of 0 through self-regulation after any accident or transient operation for a significant time. The temperature rise at the coolant outlet $\delta T_{out}$ can be expressed using the following formula:

$\delta T_{out}=\delta T_{in}+\left(\frac{P}{F}-1\right)\mathit{\Delta }{T}_{\mathit{C}}(12)$

SPALLER-100 is driven via natural circulation without a coolant pump. It is assumed that the relationship between flow (F) and power (P) under natural circulation is represented as follows: $F\sim P^{1/3}$ (Duffey and Sursock, 1987). Therefore, ULOFS and UPOS accidents will not occur; however, ULOHS, UTOP, and UCIT accidents may still occur. For UTOP and UCIT, it should be noted that coefficient A is applicable to Eq. 11.

3.2.1 Unprotected loss of heat sink

In ULOHS, the heat removal function of the primary coolant system is lost, core heat cannot be exported in time, and average circulation coolant temperature keeps increasing; this leads to a negative reactivity in the core. The decay heat power after the accident depends on the fuel burn-up. It is conservatively assumed that the core power after a long transition is reduced to 7% of the normal full operating power (Todreas Neil and Kazimi Mujid, 1990), which ensures that reactivity stays at 0. If the effect of reactor residual heat is considered, the temperature rise of the coolant at the core exit according to Eqs 7, 12 is:

$\delta T_{\mathrm{out}}=\frac{0.93A+0.83B}{C}-0.83\mathit{\Delta }{T}_C(13)$

3.2.2 Unprotected transient over power

In UTOP, assuming that certain control fuel rods operating at maximum power become out of control and cannot be withdrawn, the reactor core introduces additional positive reactivity, resulting in a rapid increase in core power; the negative reactivity arising from the power rise will eventually smooth out the total core reactivity to 0. In this accident, it is assumed that the core power increases by 10% of the normal operating power due to reactivity insertion. The reactor generates more heat due to the increase in power, and the primary heat trap is unable to effectively absorb the excess heat, causing the average primary coolant temperature to rise; the resulting decrease in reactivity will be compensated for by a reduction in core power, thereby ultimately causing the reactor to shut down. If residual heat is considered, the outlet temperature fluctuation at this point can be expressed as:

$\delta T_{out}=\frac{-\mathit{\Delta }{\rho }_{TOP}-0.1A-0.07B}{C}+0.07\mathit{\Delta }{T}_c(14)$

3.2.3 Unprotected coolant inlet temperature undercooling

In UCIT, the inlet temperature of the primary coolant decreases; the resulting positive reactivity is compensated by boosting the core power, assuming that the relationship between F and P is $F\sim P^{1/3}$. At this point, no external reactivity is introduced and the rise in coolant temperature at the coolant outlet is:

$\delta T_{out}=\delta T_{in}-\frac{\delta T_{in}C\mathit{\Delta }{T}_C}{A+B}(15)$

To ensure the inherent safety of SPALLER-100 and allow the reactor to stop safely under accident conditions, three passive safety design limitations are proposed:

(1) The parameters A, B, and C consist of reactivity coefficients such as ${\alpha }_D,{\alpha }_A,{\alpha }_R,{\alpha }_C$ . Therefore, in addition to ${\alpha }_D,{\alpha }_A,{\alpha }_R,{\alpha }_C$ being negative, A, B, and C need to be less than 0.

(2) The cladding material (HT-9 steel) has a temperature limitation under accident conditions: $T_{ct}$ = 650°C. Assuming that the temperature rise at the core coolant outlet is approximately equal to the rise in the coolant pipe surface temperature, the maximum temperature rise of the coolant at the core outlet is less than $T_{ct}$: $\delta T_{out}<T_{ct}-T_{out};$

(3) The bubbles generated during coolant boiling result in reduced neutron absorption and increased neutron leakage from the moderator; the void coefficient ${\alpha }_V$ needs to be less than 0.

4 Maximum power calculation analysis

For a given reactor, the output power can be theoretically infinite when not considering its fuel consumption and lifecycle. When considering other factors, such as operating life, material life, and the maximum power consumed by the reactor, the reactor output power will be limited to the maximum. Therefore, achieving the maximum output power of a reactor is a multi-objective, complex, multidimensional, nonlinear, and constrained optimization problem. The proxy model is an analytical model with high computational efficiency and computational accuracy, which has been proposed to solve the problems of excessive computation and slow convergence during simulation and simulation experiments.

4.1 Maximum neutronic power

4.1.1 Development of the neutronic power calculation platform

The platform developed in this study to calculate the maximum neutronic power of the reactor is based on Python; this platform utilizes the Monte Carlo code RMC (Liang et al., 2014) to calculate the initial sample points generated using the LHS method, thus generating data that will be used for training a Kriging model to produce a proxy model.

In this study, the SPALLER-100 reactor is taken as the research object. In fact, both the fuel mass fraction and the core height affect the fuel loading, which further influences the neutronic power of the core. Moreover, to ensure the safety of the reactor during operation, the reactivity swing should be as small as possible. Therefore, based on the steady-state limit, the fuel mass fraction, core height, and specific power are selected as the sampling variables, while the reactivity swing, initial excess reactivity, and power are constrained. Figure 3 demonstrates the steps used to design the platform.

FIGURE 3

FIGURE 3. Flow chart of the platform used to calculate the maximum neutronic power.

According to the steady-state limitations, the height of the core ranges from 1 to 2.5 m; the mass fractions in the inner zone and outer zone of the reactor are 20.5% and 30.8%, respectively. To ensure suitable material irradiation (200 dpa), 19.4 W/gHM is selected as the upper limit for specific power. By considering the sampling error caused by significant variations and ensuring a high neutronic power, the lower limit of specific power is assumed to be 12 W/gHM according to experience.

4.1.2 Platform prediction and verification

Figure 4 shows that with an increase in the fuel mass fraction of the Kriging model (also known as the neutronic power calculation platform, which is based on 1200 training sets at different specific powers), the predicted reactivity swing has minimum value (corresponding mass fraction is the optimal mass fraction).

FIGURE 4

FIGURE 4. Plot of reactivity swing, specific power, and mass fraction.

Figure 5 shows that under different specific powers, the predicted reactivity swing of Pu mass fraction (26.5%–28.5%) is relatively small (less than 2500 pcm), which is conducive to the smooth operation of the reactor. Meanwhile, an increase in specific power tends to augment reactivity swing. When the specific power is approximately 19 W/gHM, the optimal mass fraction is 27%.

FIGURE 5

FIGURE 5. Plot of reactivity swing, specific power, and mass fraction (26.5%–28.5%).

Twenty sample points were randomly generated via LHS, and the prediction results obtained using the platform were compared with the RMC calculation results to determine the accuracy of the values predicted by the platform. As shown in Figure 6, the absolute error between the reactivity swing and excess reactivity predicted by the platform and those calculated using the RMC procedure is 367 pcm at maximum. To ensure the safety of the reactor at maximum power, the reactivity swing should be as small as possible.

FIGURE 6

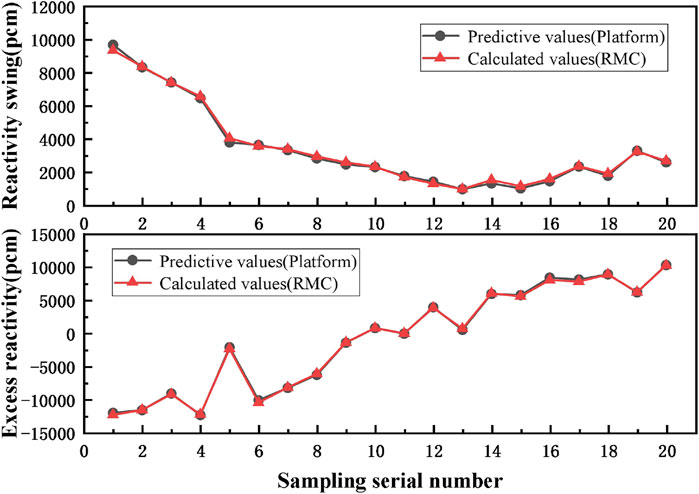
FIGURE 6. Comparison of the reactivity swing and excess reactivity. Predicted using the platform with the corresponding RMC results.

As seen from Figure 7, the maximum absolute error between the power predicted by the platform and the power calculated by the RMC is 5.4 MW for individual sampling points. This error may be due to an insufficient number of training sets for the Kriging model; however, the overall compliance is good, and a solution can be provided by increasing the number of training sets. Therefore, the proposed platform exhibits decent accuracy as well as credibility.

FIGURE 7

FIGURE 7. Comparison of the power predicted by the proposed platform with that predicted using RMC.

4.1.3 Calculate the maximum neutronic power

Finally, based on the kriging proxy model, the maximum power that meets the permitted limits for burnup reactivity swing and excess reactivity at each height is determined. The fuel loading increases with rise in the active zone height of the reactor core, which in turn augments the neutronic power. Figure 8 shows that the maximum neutronic power of the reactor almost exhibits a linear relationship with the active zone height.

FIGURE 8

FIGURE 8. Maximum neutronic power of the SPALLER reactor at different heights.

4.2 Natural circulation power

In the reactor, natural circulation refers to the circulation that occurs without the driving force provided by the pump, which in turn depends on the driving force generated by the differences in density and height that brings out the core power. The pressure drop caused by various resistances has a significant influence on the calculation of cooling power produced via natural circulation because it is the most difficult to predict among many uncertain factors. Since the pressure drop in the primary circuit system is mainly sourced from the core and heat exchanger, this study only considers the friction pressure drop and local pressure drop of the core and heat exchanger for simplification (Figure 9).

FIGURE 9

FIGURE 9. Natural circulation diagram.

4.2.1 Natural circulation capacity principle

In the reactor, the coolant flows into the lower chamber from the inlet connecting pipe, flows through the reactor core from bottom to top, carries the heat generated by nuclear fission in the reactor core, flows out from the outlet connecting pipe of the upper chamber, enters the steam generator through the rising section for heat exchange, and the cooled fluid flows out from the outlet of the steam generator. It then flows from the reactor inlet nozzle through the descending section to complete the natural circulation flow of the primary reactor circulation.

The pressure drop in the core mainly occurs due to the friction loss in the coolant channel and the core inlet and outlet. In addition, the pressure drop in the heat exchanger mainly includes the friction loss in the heat exchanger and the inlet and outlet losses.

The driving force of natural circulation is the buoyancy generated by the differences in density and height. The driving head $P_d$ is given using Eq. 16:

$P_d=\mathit{g}H\left({\rho }_{in}-{\rho }_{out}\right)(16)$

where g is the gravitational acceleration (m/s²), $H$ is the natural circulation height (m), and ${\rho }_{in}$ and ${\rho }_{out}$ are the coolant densities at the inlet and outlet of the core (kg/m³), respectively.

By employing Boussinesq approximation and ignoring the axial heat conduction, heat dissipation of the system, and work done by spatial pressure change, the above formula can be expressed as:

$P_d={\rho }_{c}g{\beta }_{c}H\mathit{\Delta }T(17)$

where ${\rho }_c$ is the coolant density, ${\beta }_c$ is the coefficient of thermal expansion (K⁻¹), and $\mathit{\Delta }T$ is the temperature difference in the coolant between the inlet and outlet (°C).

Therefore, to develop a method that maximizes the power generated by the reactor at a conceptual design level, it is necessary to satisfy the equation associated with a coolant natural circulation design. In steady-state operations, the driving force of natural circulation should be equal to the total pressure drop in the primary system; this ensures that the basic relationship between buoyancy (left) and resistance (right) is maintained:

${\rho }_{c}g\beta H\mathit{\Delta }T={\displaystyle \sum \frac{1}{2}{\rho }_c{V}_i^2\left(k_i+f_i\frac{l_i}{d_i}\right)}(18)$

where $V_i,k_i,f_i,l_i,\text{and} d_i$ represent the coolant flow rate, form resistance coefficient, friction coefficient, flow length, and hydraulic diameter of the $i-th$ area, respectively. The above formula shows that there are two values that have a great impact on the natural circulation power of the primary circulation system. The first is the pressure drop loss caused by the friction coefficient and local resistance coefficient in the primary circulation system; the second is the circulation height: the height difference from the center of the core to the center of the heat exchanger.

The natural circulation power is expressed using Eq. 19 as follows:

$P_{core}=W{C}_P\mathit{\Delta }T={\rho }_c{A}_i{V}_i{C}_P\mathit{\Delta }T(19)$

where $P_{core}$ is the natural circulation power, $W$ is the coolant mass flow, $C_p$ is the specific heat capacity at constant pressure, and $A_i$ represents the coolant flow area of the $i-th$ area.

According to Eqs 18, 19, the functional relationship of $P_{core}$ can be derived via natural circulation:

$2C_p^2{\rho }_c^{2}g\beta \frac{\mathit{\Delta }{T}^3}{P_{core}^2}={\displaystyle \sum \frac{1}{H\cdot A_i^2}\left(f_i\frac{l_i}{d_i}+k_i\right)}(20)$

4.2.2 Calculate the natural circulation power

By solving the above-mentioned theory and Eq. 20, Figure 10 shows the relationship between the natural circulation power and the active zone height in the core.

FIGURE 10

FIGURE 10. Natural circulation power of SPALLER at different heights.

The corrosion and erosion limitations are considered to determine the natural circulation power. Since the pressure drop mainly occurs in the core, the active zone height of the core has a great influence on the total pressure drop. When calculating the natural circulation power, the circulation height must remain unchanged to ensure the advantage of miniaturization. As the active zone height increases, the core pressure drop and pitch-to-diameter ratio also increase. Because an increase in the pitch-to-diameter ratio reduces the total pressure drop in the system, the relationship between natural circulation power and core height is nonlinear. Therefore, based on the maximum neutronic power, these two factors (core height and pitch-to-diameter ratio) are critical for maximizing core power.

5 Power maximization and accident safety analysis

5.1 Maximum power research scheme

The actual maximum power of the reactor core is determined using the natural circulation power. As shown in Figure 11, the neutronic power and natural circulation power tend to be maximum at the same core height. If the reactor core height continues to increase, the rise in natural circulation power becomes negligible and the neutronic power improves significantly; however, this is not conducive to improving the cost-effectiveness of the reactor.

FIGURE 11

FIGURE 11. Maximum power of SPALLER.

To determine neutronic power (red line), the influences of transport limitation, material irradiation limitation, and reactivity limitation are considered; meanwhile, to determine natural circulation (blue curve), the influences of corrosion limitation and temperature limitation are considered. The area below the intersection of the two lines meets the requirements for the natural circulation power and maximum neutronic power. When considering the maximum power constraints and miniaturization constraints of these reactors, increasing the core height implies further increasing the active zone height of the fuel, which leads to increased costs. Therefore, based on a comprehensive consideration of the safety and economical aspects associated with different limitations, the maximum power of SPALLER determined in this study is approximately 120.69 MW, optimal fuel mass fraction is 27%, and corresponding core height is approximately 1.72 m.

According to the above-mentioned research results, Table 2 shows the main design parameters used for maximizing the power of SPALLER. In Section 5.2, accident analysis applicable to the natural circulation QSRB approach has been carried out.

TABLE 2

TABLE 2. Necessary parameters for maximizing the reactor power.

5.2 Accident safety analysis based on quasi-static reactivity balance

Compared with the original design, by implementing RMC modeling while ensuring maximum power, the relevant dynamic parameters at the beginning of life (BOL), middle of life (MOL), and end of life (EOL) are calculated in Table 3, such as $A$, $A^{\prime },B$, $C$, $\beta ,{\alpha }_D,{\alpha }_A,{\alpha }_R, and {\alpha }_C$.

TABLE 3

TABLE 3. Dynamic parameters of SPALLER under different life cycles.

According to the dynamic parameters and QSRB equations, Table 4 lists the relative power and rise in coolant outlet temperature when the reactor core reaches the quasi-static state by relying on its own reactivity feedback after the ULOHS, UTOP, and UCIT accidents. Assuming that the rise in temperature at the outlet of the core coolant is approximately equal to the temperature rise on the surface of the coolant pipe, the maximum temperature of the cladding surface under accident conditions can be estimated.

TABLE 4

TABLE 4. Accident safety analysis of SPALLER under maximum power.

The maximum temperature limit of the cladding under the SPALLER accident condition has been designed to be 650°C, as mentioned in the steady-state limitations. It can be seen from Table 4 that for the original design scheme and the another, the UTOP accident (introducing reactivity of 1 $) at BOL has the most serious consequences among the three accident conditions. The rise in coolant temperature at the outlet are 89.42°C and 81.62°C, respectively; thus, the maximum temperature on the coolant pipeline surface are predicted to be 569.42°C and 561.62°C. This value is slightly higher than the steady-state temperature limit of the cladding (550°C); however, it is far lower than the accidental temperature limit of the cladding (650°C).

Three accident limitations have been considered in the accident limitations analysis, and the calculation results meet the above conditions. First, in addition to the fuel Doppler coefficient ${\alpha }_D$, axial expansion reactivity coefficient of fuel ${\alpha }_A$, core radial expansion reactivity coefficient ${\alpha }_R$, and coolant density reactivity coefficient ${\alpha }_C$ are less than 0; the coefficients $A$, $B$, and $C$ calculated in Table 3 are also less than 0. Second, under ULOHS, UTOP, and UCIT accident conditions, $\delta T_{out}$ does not exceed $T_{ct}-T_{out}$. Third, the void coefficient ${\alpha }_V$ is negative. All the above conditions are within the permitted limits, thereby further revealing the safety characteristics of the SPALLER.

6 Conclusion

To explore the maximum power that the reactor can output, the SPALLER-100 reactor is selected as the research object. The initial samples are generated using the LHS method and many training sets are trained. The Kriging proxy model is constructed and the neutronic power calculation platform is built to reduce the actual amount of calculations while ensuring accuracy. To improve the economy and safety, the maximum neutronic power and natural circulation power at different core heights are calculated by utilizing three steady-state limitations and three accident limitations as constraints. Considering the maximum power that can be achieved via natural circulation, the design scheme that maximizes the power output and meets both the rector thermal-hydraulic and rector physical requirements is finally obtained. The main conclusions of this study are as follows:

(1) The design scheme increases the power of SPALLER-100 from 100 MW thermal power to 120.69 MW maximum power (by more than 20%), which greatly improves the cost-effectiveness of the reactor and provides a reference method for designers.

(2) Three typical reactor accidents (ULOHS, UTOP, and UCIT) are analyzed by using the QSRB approach suitable for natural circulation. The results show that the proposed design scheme exhibits a good safety performance and can be used in future reactor engineering designs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

YX: data curation, writing- original draft preparation. JY: conceptualization, methodology, software. PZ: supervision. TY: visualization, investigation. ZL: reviewing and editing.

Funding

This work is supported by the ‘‘Coupled Response Mechanism of Lead-based Fast Reactor Hot Pool and Cold Pool Thermal stratification under Asymmetric Thermal Load Condition and its Influence on Natural Circulation Performance” project sponsored by the National Natural Science Foundation of China (Grant No. 11905101).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, Y, Wang, S, Xiong, W, et al. (2014). Features and application analysis of small modular reactor (in Chinese). Nucl. Electron. Detect. Technol. 34 (06), 801–806. doi:10.3969/j.issn.0258-0934.2014.06.029

CrossRef Full Text | Google Scholar

Cheon, J. S., Lee, C. B., Lee, B. O., Raison, J., Mizuno, T., Delage, F., et al. (2009). Sodium fast reactor evaluation: Core materials. J. Nucl. Mater. 392 (2), 324–330. doi:10.1016/j.jnucmat.2009.03.021

CrossRef Full Text | Google Scholar

Cho, J., Shin, Y. H., and Hwang, I. S. (2015). Power maximization method for land-transportable fully passive lead–bismuth cooled small modular reactor systems. Nucl. Eng. Des. 289, 240–251. doi:10.1016/j.nucengdes.2015.04.027

CrossRef Full Text | Google Scholar

Duffey, R. B., and Sursock, J. P. (1987). Natural circulation phenomena relevant to small breaks and transients. Nucl. Eng. Des. 102 (2), 115–128. doi:10.1016/0029-5493(87)90244-5

CrossRef Full Text | Google Scholar

Geng, L. (2004). An illustration for standard of P.R.C.《Limits of dimensions, axle load and masses for road vehicles》(in Chinese). Traffic Stand. 0 (8), 10–13. doi:10.3869/j.issn.1002-4786.2004.08.003

CrossRef Full Text | Google Scholar

Hong, S. G., Kim, J. H., and You, W. S. (2015). A neutronic design study of lead-bismuth-cooled small and safe ultra-long-life cores. Ann. Nucl. Energy 85, 58–67. doi:10.1016/j.anucene.2015.04.032

CrossRef Full Text | Google Scholar

Kempf, Stephanie, Forget, Benoit, and Hu, Lin-Wen (2012). Kriging-based algorithm for nuclear reactor neutronic design optimization. Nucl. Eng. Des. 247, 248–253. doi:10.1016/j.nucengdes.2012.03.001

CrossRef Full Text | Google Scholar

Li, J., and Zhang, B. (2011). Probabilistic load flow based on improved Latin hypercube sampling with evolutionary algorithm (in Chinese). Proc. CSEE 31 (25), 90–96. doi:10.13334/j.0258-8013.pcsee.2011.25.012

CrossRef Full Text | Google Scholar

Liang, J., Qiu, Y., Wang, K., and Chai, X. (2014). Research of full core burnup calculations based on tally data decomposition in RMC (in Chinese). Nucl. Power Eng. 35, 231–234. doi:10.13832/j.jnpe.2014.S2.0231

CrossRef Full Text | Google Scholar

Liu, Z., Zhao, P., and Zhang, B. (2020). Research on core concept design of ultra-long life small natural circulation lead-based fast reactor. Atomic Energy Sci. Technol. 54 (7), 1254–1265. doi:10.7538/yzk.2019.youxian.0720

CrossRef Full Text | Google Scholar

Müller, G., Heinzel, A., Konys, J., Schumacher, G., Weisenburger, A., Zimmermann, F., et al. (2002). Results of steel corrosion tests in flowing liquid Pb/Bi at 420–600 °C after 2000 h. J. Nucl. Mater. 301 (1), 40–46. doi:10.1016/s0022-3115(01)00725-5

CrossRef Full Text | Google Scholar

Rivai, A. K., and Takahashi, M. (2008). Compatibility of surface-coated steels, refractory metals and ceramics to high temperature lead–bismuth eutectic. Prog. Nucl. energy 50 (2-6), 560–566. doi:10.1016/j.pnucene.2007.11.081

CrossRef Full Text | Google Scholar

Todreas Neil, E., and Kazimi Mujid, S. Nuclear SystemsI: Thermal hydraulic fundamentals. 1990.

Google Scholar

Wade, D. C., and Chang, Y. I. (1988). The integral fast reactor concept: Physics of operation and safety. Nucl. Sci. Eng. 100 (4), 507–524. doi:10.13182/nse88-2

CrossRef Full Text | Google Scholar

Zhao, pengcheng (2017). Thermal-hydraulic safety analysis of primary cooling system for small modular natural circulation LFR SNCLFR-100 (in Chinese). China: University of Science and Technology of China.

Google Scholar

Zrodnikov, A. V., Toshinsky, G. I., Komlev, O. G., Dragunov, Y., Stepanov, V., Klimov, N., et al. (2006). Nuclear power development in market conditions with use of multi-purpose modular fast reactors SVBR-75/100. Nucl. Eng. Des. 236 (14-16), 1490–1502. doi:10.1016/j.nucengdes.2006.04.005

CrossRef Full Text | Google Scholar