- 1School of Electronic and Electrical Engineering, Shanghai University of Engineering Science, Shanghai, China
- 2Department of Energy Technology, Aalborg University, Aalborg, Denmark
- 3School of Electrical Engineering, Shanghai University of Electric Power, Shanghai, China
Aiming at the problems of promoting new energy consumption, reducing carbon emissions, load fluctuations, and multi-agent conflict of interests in the networked microgrid system, this article proposes a microgrid optimization operation strategy based on demand response and reward-penalty ladder-type carbon trading mechanism. First, in order to determine the electricity sales price of the system, an optimal scheduling model for microgrid operators is established, including gas cost, electricity profit for users, and surplus power supply network profit. Second, a demand response strategy on electricity price and low-carbon compensation incentives is proposed on the user side. The transaction model is embedded between microgrid operators and users into the master–slave game framework, and a multi-slave game collaborative optimization model is established with microgrid operators as leaders and users as followers. The existence and uniqueness of Stackelberg game are proved, and the differential evolution algorithm and CPLEX solver are used to solve the proposed model. Finally, an example of a microgrid system including three community users is provided to show the effectiveness of the proposed model and strategy.
Introduction
With the increasing energy demand of countries around the world today, the contradiction between energy supply and demand and energy problems is also becoming more and more serious. For example, in China, the Chinese government has proposed the “30.60 carbon peak—carbon neutral” strategy (Zhao et al., 2022). Under the influence of this strategy, China’s energy technology development is being fully decarbonized, and efficient, environmentally friendly, and safe new energy utilization technologies are also the mainstream direction of energy development in the world. In the 2021 Opinions of the State Council of the People’s Republic of China on the Implementation of the Key Work Division of the “Government Work Report” (Opinions of the State Council on Implementing the Key Work Division of the "Government Work Report", 2021), in response to the requirements of achieving the two major goals of carbon peaking and carbon neutrality, China is fully promoting the microgrid (MG) system construction work. The emergence of MG combines the advantages and flexibility of traditional grid systems with the flexibility of small-scale distributed renewable energy. With the advancement of science and technology, the rapid development of intelligent digital communication technology has provided technical support for the development of grid-connected microgrid (GCMG), and peer-to-peer energy trading provides a guarantee for the safe operation of the energy trading distribution system (Feng et al., 2022) and has achieved more significant low-carbon and economic benefits.
In addition to vigorously exploiting new technologies such as photovoltaic power generation and wind power generation on the energy supply side, the GCMG system also provides an efficient platform for the consumption of power users. In traditional power grid scheduling, power users are generally regarded as passive consumers, while the microgrid operator (MGO) (Parhizi et al., 2016) formulates the system operation strategy according to the demand response of the user side, and the operation goal is to maximize the economic benefits of the GCMG system (Riou et al., 2021). In recent years, there have been more and more studies on the operation of MG systems, including MG system operation stability analysis (Farrokhabadi et al., 2019), optimization framework (Harmon et al., 2017), control model (Nasser and Fazeli, 2020), and energy management strategy (Shotorbani et al., 2021). The optimization of the MG system must improve operating efficiency and reduce carbon emissions. Generally, energy consumption indicators, operating costs, and carbon emissions are used for evaluation.
With the development of the times, research studies on MG systems such as new energy vehicles (Zhang and Chen, 2014), combined heat and power (CHP) (Sun et al., 2017), and campus microgrid (Muqeet and Ahmad, 2020) are also being carried out gradually. Due to the fact that carbon trading is an effective measure to achieve carbon neutrality, the carbon trading market (Tan and Lin, 2022) has been also gradually emerging in recent years. There are more and more research studies on the introduction of the carbon trading mechanism into the energy system (Wang et al., 2022a) to reduce carbon emissions in the power system, including introducing carbon capture technology into the optimal scheduling of the integrated energy system (Cui et al., 2021a), establishing a low-carbon operation and scheduling model of the energy system based on the carbon comprehensive price (Cheng et al., 2019), and proposing a reward–penalty stepped carbon transaction cost model (Xiaohui et al., 2019; Zhang et al., 2020). The introduction of the reward and punishment ladder carbon trading mechanism into the energy system (Wang et al., 2022b) reduces investment costs, operating costs, and carbon trading costs while improving the low-carbon and economical properties of the system (Cui et al., 2021b). However, these studies did not consider reducing carbon emissions by changing electricity prices to guide users to adjust their electricity loads.
When it comes to smart grid energy management, demand response (DR) (Lin et al., 2022) has been proposed in the field of smart grid as a solution to tap the potential of demand side response on the energy consumption side and effectively improve grid efficiency. By adjusting the price and establishing an incentive response mechanism in the operation of the power grid system, the user side is guided to adjust the energy demand, and the users are transformed from a passive consumer to an active energy manager according to the user’s energy use changes with different electricity prices and incentives, reducing their own operating costs by controlling their own adjustable load and energy storage (Zeng et al., 2016). Adjusting the power load through power demand response DR can also achieve the goals of promoting wind power photovoltaic consumption and reducing grid operating costs (Lu et al., 2017). At the same time, DR can also improve MG’s control of the direct load of the system and promote user economic benefits (Akter et al., 2021). In recent years, some scholars have found that the application of the Stackelberg game (Li et al., 2022) in the demand response model of the power grid can greatly improve the efficiency of the power grid (Maharjan et al., 2013; Alshehri et al., 2015). On this basis, gaming occurs between different stakeholders in the power system, such as sellers and buyers (Belgana et al., 2014; Yu and Hong, 2015; Liu et al., 2017). In general, the seller is the game leader, and the buyer is the follower (Wei, Liu and Mei, 2014; Wei et al., 2017). Sellers use the dynamic electricity price as their own game strategy. Buyers respond according to the electricity price and adjust their own electricity load. In this game framework, each party solves their own optimal strategy, and the final fixed solution of electricity price and load is close to Stackelberg equilibrium. At the same time, in an energy system involving renewable energy, the use of the Stackelberg game strategy can improve the energy efficiency of the system (Li et al., 2021). However, in these studies, the process of grid dispatching only considers the user’s response to the different power prices to adjust the electricity load and does not consider reducing carbon emissions while adjusting the load to promote economic benefits by using the carbon trading mechanism.
Therefore, on the basis of the aforementioned research, this study studies the optimal scheduling strategy of the GCMG system under the framework of the Stackelberg game for the GCMG system and considers the demand response and carbon trading mechanisms at the same time. The contributions are listed as follows:
1) The energy management framework and reward–penalty ladder-type carbon trading model of the GCMG system are introduced.
2) On this basis, an optimal scheduling model is established for multiple subjects of GCMG and constrained.
3) The GCMG Stackelberg game model is introduced, and the existence and uniqueness of the Stackelberg game equilibrium are verified. Then, the differential evolution algorithm (DE) and CPLEX solver are combined to solve the equilibrium solution of the Stackelberg game.
4) In order to verify the advantages of the proposed operation strategy in improving system economic benefits and low-carbon benefits, an optimal scheduling model of GCMG is formulated including multiple constraints, Stackelberg games, and reward–penalty ladder-type carbon trading.
GCMG system and carbon trading mechanism
GCMG energy management framework
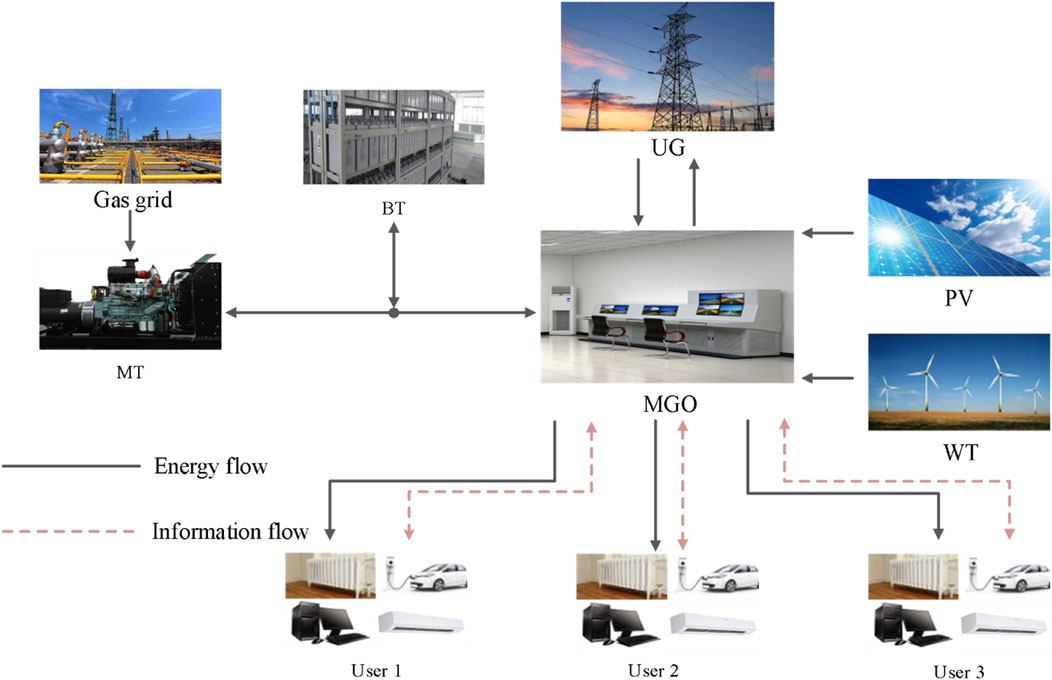
The scheduling framework of the GCMG system is shown in Figure 1. Based on the conventional GCMG system, this article considers the demand response of multiple users simultaneously in the MGO scheduling process. Energy supply equipment of the MG system consists of a micro-gas-turbine (MT), photovoltaic (PV), and wind turbine (WT), and the energy storage device is a battery (BT). MT is driven by natural gas, which is more low-carbon and environmentally friendly than traditional thermal power plants. MT supplies users’ electricity needs together with PV and WT. The excess electricity is stored in BT or sold to the utility grid (UG). When the user’s demand cannot be met, the energy stored in the BT is used to supply the user’s demand. If the power generation of MG still cannot meet the demand or the surplus exceeds the range of energy storage, GCMG will balance the excess or insufficient power by trading with UG. The GCMG system is controlled by MGO, which has the right to decide the operation mode and the transaction price between users.
On the user side of the smart grid, a community energy management system is deployed for each user to collect the user’s electricity demand and load data and receive electricity price information at each time period from the MGO, according to the time-varying electricity price to change the load demand at each time period to control and optimize the user’s energy consumption and reduce carbon emissions.
Reward–penalty ladder-type carbon trading model
With the increasing scale of the carbon trading market in recent years, research on carbon emission trade (CET) mechanisms at home and abroad is also being carried out gradually. The essence of the carbon trading mechanism is to regard carbon emissions as a commodity traded in the market under the carbon emission rules formulated by the governments of various countries. According to the price of carbon emission rights in the market, MGO allocates corresponding emission quotas to stimulate energy conservation and emission reduction of each user to reduce the total carbon emission and reduce the operating cost of the CCMG system.
The free carbon emission allowances for each subject in the GCMG system are determined by the baseline method, and the subjects include the purchase of electricity from the UG and MT.
Here,
On the basis of conventional carbon trading, this article constructs the reward–penalty ladder-type carbon trading cost
Here,
Demand response based on price and carbon trading mechanisms
In the DR of the smart grid, users change their own electricity load according to changes in electricity prices and government economic subsidies, which is an effective solution to improve the efficiency of the grid. The electricity price elasticity matrix method is the most widely used price-based DR modeling method. The electricity load and electricity price change rate are expressed by the electricity price elasticity index (Wang et al., 2020):
where
According to the ratio of the time-of-use electricity price to the fixed electricity price, the elasticity matrix
Here,
The user can adjust the electricity load within a specified time according to the electricity demand. The user-side electric load includes fixed electric load and transferable electric load, which can be expressed as:
Here,
By using DR, a user’s role in the smart grid becomes more proactive, with the goal of maximizing the grid’s comprehensive income, and flexibly controls user’s own electricity loads and battery energy storage. On this basis, the electricity consumption adjusted by users according to price incentives is converted into low-carbon compensation subsidy users according to the carbon trading mechanism, so as to stimulate users’ low-carbon enthusiasm for electricity load and increase the income of MGO. The strategy is as follows:
1) When the electricity demand on the user side is at a peak period, MGO guides users to reduce the electricity load under the condition of satisfying their own satisfaction index by increasing the electricity price and converts the reduced electricity load into carbon emission allowances according to the carbon trading mechanism as a low carbon offset to subsidize users and encourage users to adjust their load demands.
2) When the electricity demand on the user side is at a low point, MGO guides users to increase their own electricity demand by reducing electricity prices while meeting their own satisfaction indicators and uses MG’s own clean energy in the increased electricity load. The electricity is converted into carbon emission quotas according to the carbon trading mechanism as a low-carbon compensation subsidy to users, which motivates users to adjust their own load demands.
GCMG optimal scheduling model
microgrid operator
MGO formulates the electricity sales price strategy based on the time-of-use electricity price of the UG and the electricity demand of users and at the same time optimizes the output value of MT and BT according to the output value of PV and WT. The optimization goal is to maximize the MGO profit while meeting the user’s energy demand, and the objective function is
Here, the superscript t indicates the t period, T is the total number of time periods and takes 24 h of a day in the research,
Here,
User side
Users, based on the MGO electricity price and low-carbon subsidies, also consider their own satisfaction to maximize their own benefits. The optimization objective function is:
where
Here,
Constraints
In the optimization and scheduling process of the GCMG system, in order to ensure the interests of the subject, prevent the problem from degenerating, and avoid direct transactions between UG and users, it should be ensured that the buying (selling) price of UG is slightly higher than the MGO electricity price. The MGO electricity price needs to meet the following constraints:
where
In addition, the electricity sales price must meet:
During the operation of MGO and UG, MGO also needs to meet the interactive power constraints with UG on the basis of electricity price constraints:
Here,
When optimizing the scheduling of the system, for the stable operation of the GCMG, the energy storage state of MG energy supply equipment PV, WT, MT, energy storage equipment BT, and the electricity load on the user side must meet the following requirements at time t:
1) Power balance constraints:
where
2) MT operating constraints:
where
3) BT operating constraints:
where
4) User load constraints:
where
Stackelberg game model
Concept
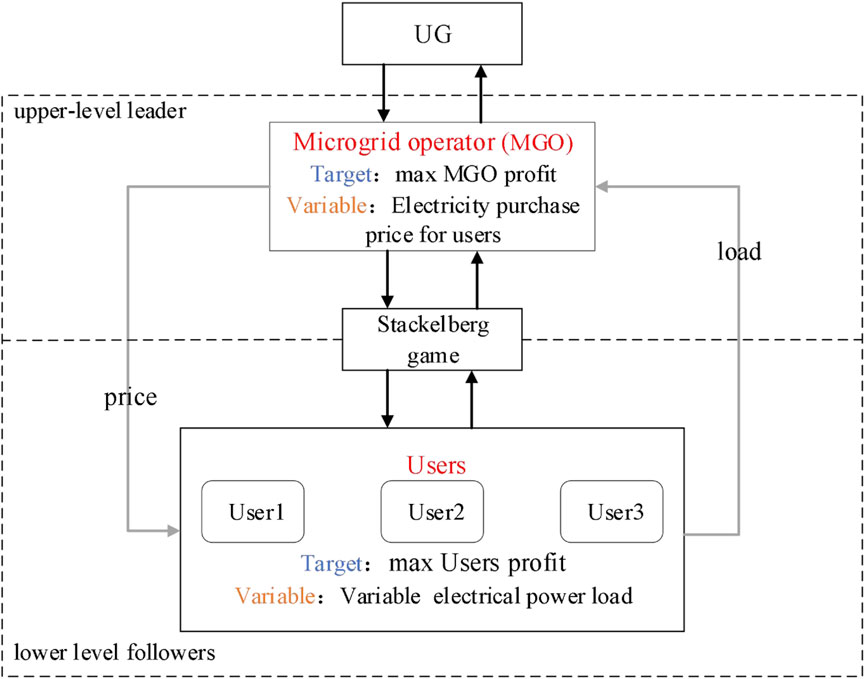
According to the aforementioned description of the GCMG system and its scheduling strategy, the optimization of the MG and the user side is based on the electricity price set by the MGO, and the optimization result reacts to the electricity price of the MGO. This transaction process conforms to the dynamic game situation of the hierarchical structure. Therefore, this articles establishes the Stackelberg game model with one master and multiple slaves and uses MGO as the leader of the game and three power users as the followers of the game. The game model is:
The game model includes three elements: participants, strategies, and benefits. The schematic diagram of the GCMG master–slave game is shown in Figure 2.
Stackelberg game equilibrium
Stackelberg game refers to the decision-making process in which MGO and multiple users pursue their own optimal goals. When all follower users respond optimally according to the leader’s MGO strategy and the leader accepts this response, the game reaches Stackelberg equilibrium.
As mentioned previously, the goals of MGO and users are to maximize their own profits, and the profits are the various objective functions in the previous chapter, which are calculated according to Eqs 10, 18. To this end, MGO will formulate the optimal electricity sales price from MG to the user side, and at the same time, users will also decide the optimal electricity load based on electricity price, carbon trading mechanism, and DR, and the game equilibrium will be reached at this time.
Assuming
In the Stackelberg equilibrium solution, the MGO and the user changing their strategies alone will not improve their own profits. Before solving the Stackelberg equilibrium solution, it is necessary to prove its existence and uniqueness. According to Wei et al. (2017), when the Stackelberg game
1) Both MGO and user strategy sets are non-empty compact convex sets with respect to their Euclidean space.
2)
3)
4)
From Eqs 10–21, the strategy set
In summary, the master–slave game model
Stackelberg game model solution method
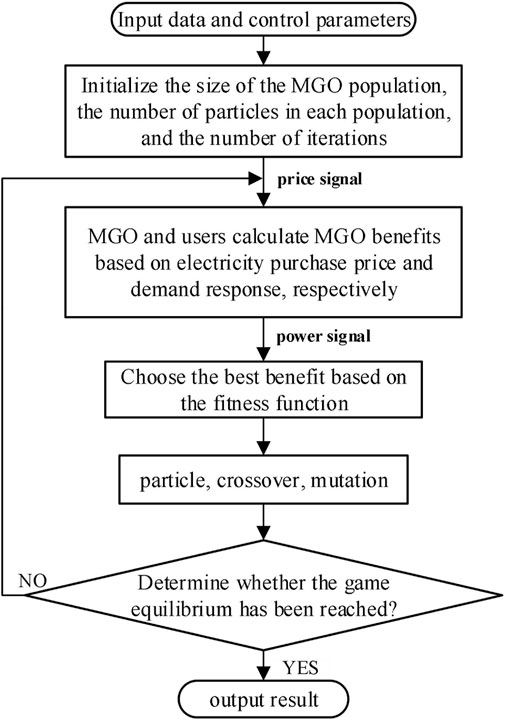
Due to the uncertainty of the upper-layer MGO operating strategy, the formula of the GCMG model is uncertain in different periods. Using a two-layer planning model based on Karush–Kuhn–Tucker (KKT) conditions is relatively difficult to solve, and it cannot protect users’ privacy such as user load data simultaneously. Therefore, this article adopts the DE algorithm combined with the CPLEX solver to solve the established master–slave game model. The algorithm solution flow is shown in Figure 3.
The steps of the upper-level DE algorithm are as follows:
1) Enter initial data and set parameters.
2) Initialize the population size, generate 10 populations, set the number of iterations K = 0, randomly generate the electricity sales price
3) The lower-layer user side uses the CPLEX solver to calculate its own income according to
4) MGO calculates the upper-layer objective function
5) Crossover and mutation are performed on the independent variable
6) Calculate the corresponding upper-level objective function
7) Carry out the selection operation. If
8) Carry out the judgment operation; if the required number of iterations is not reached, go to step (3); otherwise, output the result.
The lower-level user side combines the CPLEX solver to calculate the optimal load power when the user’s profit is the largest according to Eqs 5–9, 19–21, 34, and returns the optimized result to the upper-level leader.
Case study
Basic data
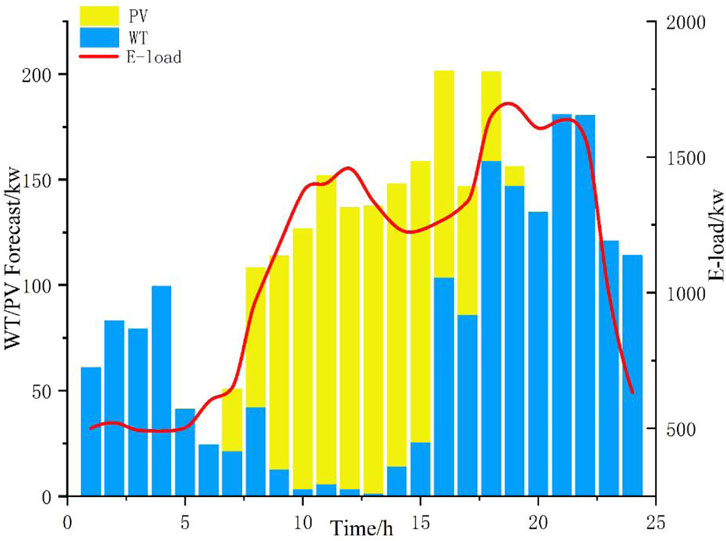
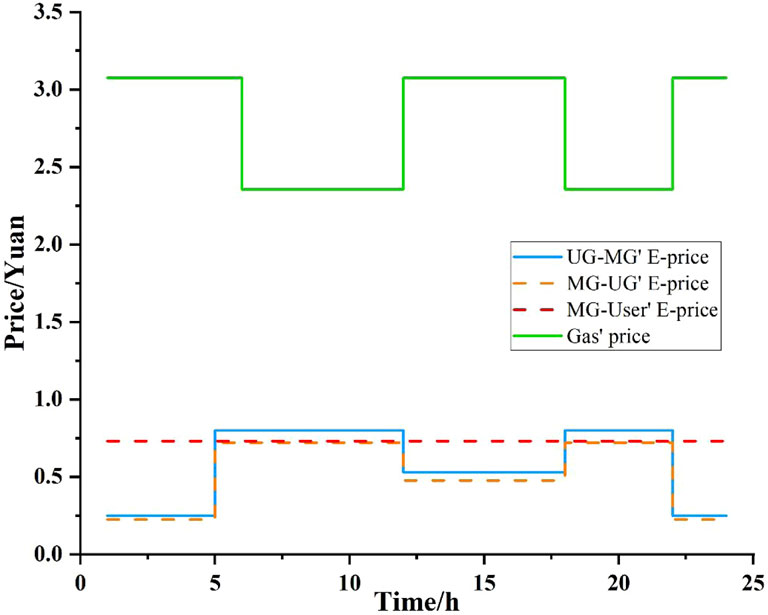
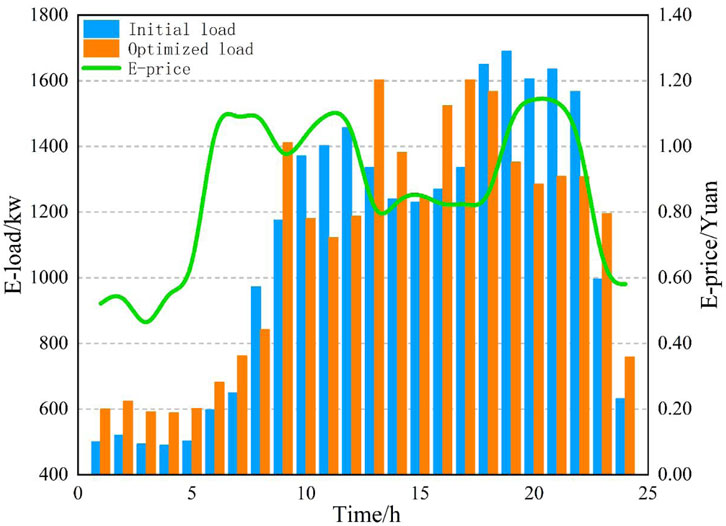
In this article, a community GCMG with three main users is taken as the research object, and the simulation analysis of the GCMG optimal scheduling strategy proposed in this article is carried out. The GCMG system is located in the Xinjiang region of China, and its new energy power generation forecast data and basic electricity load of the GCMG system are shown in Figure 4. The peak electricity load appears at 9:00–12:00 and 18:00–22:00, and the internal initial energy price is shown in Figure 5. It is assumed that the user’s adjustable load accounts for 20% of the total initial load, and the user’s preference coefficients
Comparative analysis of simulation results
In order to illustrate the economic benefits and low-carbon benefits of the GCMG optimal scheduling strategy based on the Stackelberg game and the reward–penalty ladder-type carbon trading mechanism, the following three models are designed for comparative analysis:
Case 1: the GCMG scheduling model without considering the carbon trading mechanism.
Case 2: the GCMG scheduling model that considers the conventional carbon trading mechanism.
Case 3: the GCMG scheduling model that considers the reward–penalty ladder-type carbon trading mechanism.
Advantages of adopting the Stackelberg game
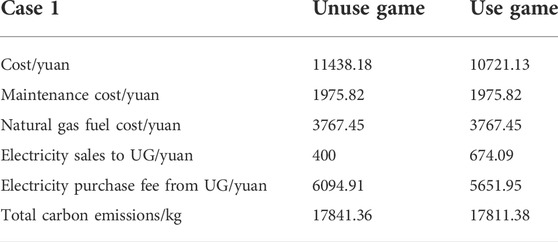
Table 1 shows the comparison between the economic benefits and low-carbon benefits of each GCMG subject when using the Stackelberg game and the non-using game in Case 1. Compared with the scheduling strategy that does not use the game, the total cost of GCMG in Case 1 is significantly lower, which shows that the Stackelberg game can effectively improve the economic benefits of game participants. In terms of reducing system carbon emissions, the Stackelberg game strategy does not show its advantages in promoting low-carbon benefits. Figures 6A, B, respectively, show the output power of each MG subject at each moment in Case 1 without using the Stackelberg game and using the two-layer Stackelberg game optimization strategy. It can be seen from Figure 6 that compared with the strategies that do not consider the game, the electricity load of the Stackelberg game optimization scheduling strategy is significantly reduced, but because the carbon trading mechanism is not considered, the power purchase of UG is gradually increasing, which has little effect on reducing the carbon emissions of the GCMG system. The promotion effect has obvious effectiveness in improving the economic benefits of the system.
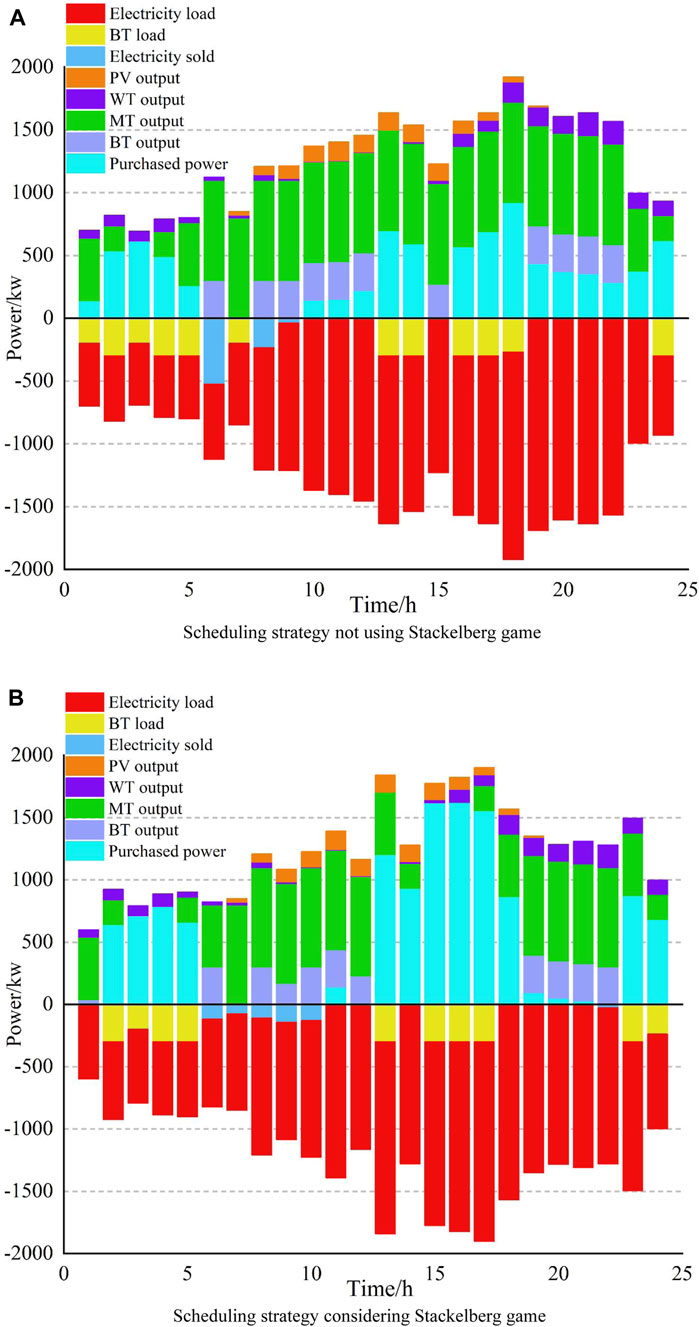
FIGURE 6. Case 1: the power of each subject under different strategies. (A) Scheduling strategy not using Stackelberg game. (B) Scheduling strategy considering Stackelberg game.
Advantages of using the reward–penalty ladder-type carbon trading mechanism
It can be seen from Table 1 that the carbon emission of GCMG has not been significantly reduced compared with that without using the Stackelberg game optimization scheduling strategy. Table 2 shows the total carbon emissions and costs of the system considering different carbon trading mechanisms in the three models. It can be seen from Table 2 that the carbon trading mechanism can further improve the low-carbon benefits of GCMG, while the reward and punishment carbon trading mechanism further reduce the system’s carbon emissions. Compared with the scheduling results without considering the carbon trading mechanism, the total carbon emissions of the system using the reward–penalty ladder-type carbon trading mechanism decreased by 25%, but the economic benefits of the system were not improved significantly. It can be seen that the reward–penalty ladder carbon-type trading mechanism can promote the low-carbon benefit of the GCMG system.
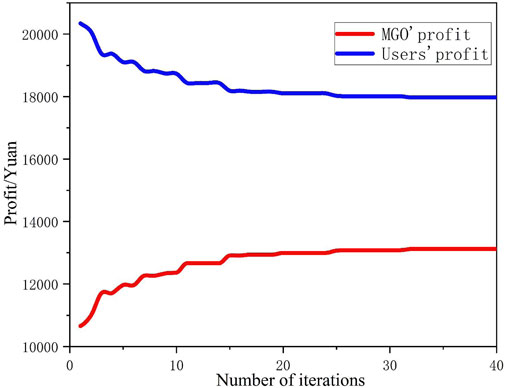
Figure 7 shows the optimization iterative process of MGO profit and user profit using the Stackelberg game strategy based on the DR and reward–penalty ladder carbon trading mechanism for the GCMG system. It can be seen from Figure 7 that before the iteration reaches the equilibrium solution of the Stackelberg game, the MGO profit gradually increases with the number of iterations, and the user revenue gradually decreases. When the iteration reaches about 32 times, both sides of the game converge at the same time, proving the existence and uniqueness of the equilibrium solution of the Stackelberg game. At this time, the MGO profit is stable at 13119.88 yuan, and the user profit is stable at 17970.23 yuan. At this time, the total cost of the GCMG system is 10547.26 yuan, and the carbon emission is 13387.07 kg.
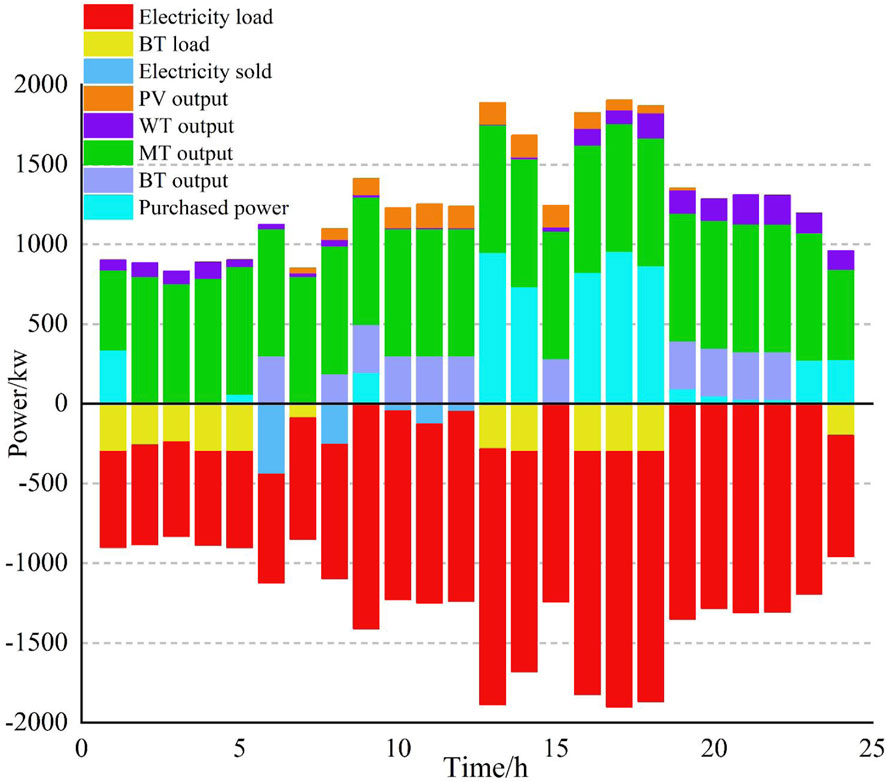
After optimization, the output of each main subject of GCMG is shown in Figure 8. Since photovoltaic generation and wind power generation have their environmental protection significance, the system will give priority to using new energy power generation, MT power generation, and BT energy storage as supplements and finally consider purchasing power from UG to make up for the lack of new energy sources. When comparing the optimized user load with the initial load, when the demand response is at the valley value, in order to obtain higher benefits, the user increases the use of part of the load according to the change in electricity price, and at the same time, the MT output is more. At peak times, users reduce the use of part of their own electricity loads, and most of the missing electricity needs to be purchased from UG. As shown in the optimized load and electricity price diagram in Figure 9, with the change of electricity price, the users adjust the electricity load according to their own demand response and maximize their own profit.
Compared with the GCMG system scheduling result without considering the reward–penalty ladder-type carbon trading mechanism and DR’s Stackelberg game strategy, the total system cost after optimization has decreased by 7.8%, the MGO profit has increased from 7981.59 yuan to 13119.88 yuan, and the total system carbon emission has decreased from 17841.36 kg to 13387.07 kg. It shows that the scheduling strategy proposed in this article reduces the cost of the GCMG system, improves the economic benefits, and also reduces the carbon emissions of the system and improves the low-carbon benefits under the premise of meeting the energy demand of users.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
XF: ideas, development or design of methodology, and writing the initial draft. GZ: data curation and visualization. XZ: visualization and reviewing. JZ: supervision. BH: reviewing and project administration. JL: reviewing and editing.
Funding
This work was supported by the Shanghai Science and Technology Innovation Action Plan (22S31903700 and 21S31904200).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akter, H., Howlader, H. O. R., Saber, A. Y., Mandal, P., Takahashi, H., and Senjyu, T. (2021). Optimal sizing of hybrid microgrid in a remote island considering advanced direct load control for demand response and low carbon emission. Energies 14 (22), 7599. doi:10.3390/en14227599
Alshehri, K., Liu, J., Chen, X., and Başar, T. (2015). “A Stackelberg game for multi-period demand response management in the smart grid,” in 2015 54th IEEE Conference on Decision and Control (CDC) (IEEE), 5889–5894.
Belgana, A., Rimal, B. P., and Maier, M. (2014). Open energy market strategies in microgrids: A stackelberg game approach based on a hybrid multiobjective evolutionary algorithm. IEEE Trans. Smart Grid 6 (3), 1243–1252. doi:10.1109/tsg.2014.2363119
Cheng, Y., Zhang, N., Zhang, B., Kang, C., Xi, W., and Feng, M. (2019). Low-carbon operation of multiple energy systems based on energy-carbon integrated prices. IEEE Trans. Smart Grid 11 (2), 1307–1318. doi:10.1109/tsg.2019.2935736
Cui, Y., Zeng, P., Wang, Z., Wang, M., Zhang, J., and Zhao, Y. (2021a). Low-carbon economic dispatch of electricity-gas-heat integrated energy system with carbon capture equipment considering price-based demand response. Power Syst. Technol. 45 (2), 447–461.
Cui, Y., Zeng, P., Zhong, W., Cui, W., and Zhao, Y. (2021b). Low-carbon economic dispatch of electricity-gas-heat integrated energy system based on ladder-type carbon trading. Electr. Power Autom. Equip. 41, 10–17.
Farrokhabadi, M., Cañizares, C. A., Simpson-Porco, J. W., Nasr, E., Fan, L., Mendoza-Araya, P. A., et al. (2019). Microgrid stability definitions, analysis, and examples. IEEE Trans. Power Syst. 35 (1), 13–29. doi:10.1109/tpwrs.2019.2925703
Feng, C., Liang, B., Li, Z., Liu, W., and Wen, F. (2022). Peer-to-Peer energy trading under network constraints based on generalized fast dual ascent. IEEE Trans. Smart Grid, 1. doi:10.1109/tsg.2022.3162876
Harmon, E., Ozgur, U., Cintuglu, M. H., de Azevedo, R., Akkaya, K., and Mohammed, O. A. (2017). The internet of microgrids: A cloud-based framework for wide area networked microgrids. IEEE Trans. Ind. Inf. 14 (3), 1262–1274. doi:10.1109/tii.2017.2785317
Li, F., Li, X., Fang, Z., and Zhang, L. (2022). A game optimization scheduling strategy of active distribution network with multi-microgrid sharing energy storage. Front. Energy Res. 650. doi:10.3389/fenrg.2022.906406
Li, Y., Wang, C., Li, G., and Chen, C. (2021). Optimal scheduling of integrated demand response-enabled integrated energy systems with uncertain renewable generations: A stackelberg game approach. Energy Convers. Manag. 235, 113996. doi:10.1016/j.enconman.2021.113996
Lin, S., Lin, M., Shen, Y., and Li, D. (2022). An optimal scheduling strategy for integrated energy systems using demand response. Front. Energy Res. 698. doi:10.3389/fenrg.2022.920441
Liu, N., He, L., Yu, X., and Ma, L. (2017). Multiparty energy management for grid-connected microgrids with heat-and electricity-coupled demand response. IEEE Trans. Ind. Inf. 14 (5), 1887–1897. doi:10.1109/tii.2017.2757443
Lu, Z., Guo, K., Yan, G., and He, L. (2017). Optimal dispatch of power system integrated with wind power considering virtual generator units of demand response and carbon trading. Automation Electr. Power Syst. 41 (15), 58–65.
Maharjan, S., Zhu, Q., Zhang, Y., Gjessing, S., and Basar, T. (2013). Dependable demand response management in the smart grid: A stackelberg game approach. IEEE Trans. Smart Grid 4 (1), 120–132. doi:10.1109/tsg.2012.2223766
Muqeet, H. A. U., and Ahmad, A. (2020). Optimal scheduling for campus prosumer microgrid considering price based demand response. IEEE Access 8, 71378–71394. doi:10.1109/access.2020.2987915
Nasser, N., and Fazeli, M. (2020). Buffered-microgrid structure for future power networks; a seamless microgrid control. IEEE Trans. Smart Grid 12 (1), 131–140. doi:10.1109/tsg.2020.3015573
Opinions of the State Council on Implementing the Key Work Division of the "Government Work Report" (2021). Central People's Government of the People's Republic of China. Chinese government website. Available at: http://www.gov.cn/zhengce/content/2021/03/25/content_5595644.htm.
Parhizi, S., Khodaei, A., and Shahidehpour, M. (2016). Market-based versus price-based microgrid optimal scheduling. IEEE Trans. Smart Grid 9 (2), 615–623. doi:10.1109/tsg.2016.2558517
Riou, M., Dupriez-Robin, F., Grondin, D., Le Loup, C., Benne, M., and Tran, Q. T. (2021). Multi-objective optimization of autonomous microgrids with reliability consideration. Energies 14 (15), 4466. doi:10.3390/en14154466
Shotorbani, A. M., Zeinal-Kheiri, S., Chhipi-Shrestha, G., Mohammadi-Ivatloo, B., Sadiq, R., and Hewage, K. (2021). Enhanced real-time scheduling algorithm for energy management in a renewable-integrated microgrid. Appl. Energy 304, 117658. doi:10.1016/j.apenergy.2021.117658
Sun, T., Lu, J., Li, Z., Lubkeman, D. L., and Lu, N. (2017). Modeling combined heat and power systems for microgrid applications. IEEE Trans. Smart Grid 9 (5), 4172–4180. doi:10.1109/tsg.2017.2652723
Tan, R., and Lin, B. (2022). The long term effects of carbon trading markets in China: Evidence from energy intensive industries. Sci. Total Environ. 806, 150311. doi:10.1016/j.scitotenv.2021.150311
Wang, H., Li, K., Zhang, C., Liu, S., Li, S., and Wang, Y. (2020). Distributed coordinative optimal operation of community integrated energy system based on stackelberg game. Proc. CSEE (17), 5435–5445. doi:10.13334/j.0258-8013.pcsee.200141
Wang, R., Cheng, S., Zuo, X., and Liu, Y. (2022a). Optimal management of multi stakeholder integrated energy system considering dual incentive demand response and carbon trading mechanism. Int. J. Energy Res. 46 (5), 6246–6263. doi:10.1002/er.7561
Wang, R., Wen, X., Wang, X., Fu, Y., and Zhang, Y. (2022b). Low carbon optimal operation of integrated energy system based on carbon capture technology, LCA carbon emissions and ladder-type carbon trading. Appl. Energy 311, 118664. doi:10.1016/j.apenergy.2022.118664
Wei, F., Jing, Z. X., Wu, P. Z., and Wu, Q. H. (2017). A Stackelberg game approach for multiple energies trading in integrated energy systems. Appl. energy 200, 315–329. doi:10.1016/j.apenergy.2017.05.001
Wei, W., Liu, F., and Mei, S. (2014). Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty. IEEE Trans. Smart Grid 6 (3), 1364–1374. doi:10.1109/tsg.2014.2376522
Xiaohui, Z., Xiaoyan, L., Jiaqing, Z., and Wenbo, G. (2019). Electricity–gas‐integrated energy planning based on reward and penalty ladder‐type carbon trading cost. IET Gener. Transm. &. Distrib. 13 (23), 5263–5270. doi:10.1049/iet-gtd.2019.0666
Yu, M., and Hong, S. H. (2015). A real-time demand-response algorithm for smart grids: A stackelberg game approach. IEEE Trans. Smart Grid 7 (2), 1–888. doi:10.1109/tsg.2015.2413813
Zeng, M., Wu, G., Li, R., Wang, H., and Sun, C. (2016). Key problems and prospects of integrated demand response in energy internet. Power Syst. Technol. 40 (11), 3391–3398.
Zhang, M., and Chen, J. (2014). The energy management and optimized operation of electric vehicles based on microgrid. IEEE Trans. Power Deliv. 29 (3), 1427–1435. doi:10.1109/tpwrd.2014.2303492
Zhang, T., Guo, Y., Li, Y., and Zhang, J. (2021). Optimization scheduling of regional integrated energy systems based on electric-thermal-gas integrated demand response. Power Syst. Prot. Control (01), 52–61. doi:10.19783/j.cnki.pspc.200167
Zhang, X., Liu, X., and Zhong, J. (2020). Integrated energy system planning considering a reward and punishment ladder-type carbon trading and electric-thermal transfer load uncertainty. Proc. CSEE 40 (19), 6132–6140.
Keywords: demand response, microgrid, ladder-type carbon trading, operation strategy, Stackelberg game
Citation: Fu X, Zeng G, Zhu X, Zhao J, Huang B and Liu J (2022) Optimal scheduling strategy of grid-connected microgrid with ladder-type carbon trading based on Stackelberg game. Front. Energy Res. 10:961341. doi: 10.3389/fenrg.2022.961341
Received: 04 June 2022; Accepted: 03 August 2022;
Published: 06 September 2022.
Edited by:
Jiajia Yang, University of New South Wales, AustraliaReviewed by:
Yumin Zhang, Shandong University of Science and Technology, ChinaZhengmao Li, Nanyang Technological University, Singapore
Copyright © 2022 Fu, Zeng, Zhu, Zhao, Huang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guohui Zeng, emVuZ2doQHN1ZXMuZWR1LmNu
 Xiuwei Fu
Xiuwei Fu Guohui Zeng1*
Guohui Zeng1*