A novel grid-connected microgrid energy management system with optimal sizing using hybrid grey wolf and cuckoo search optimization algorithm

Renewable energy systems, particularly in countries with limited fossil fuel resources, are promising and environmentally sustainable sources of electricity generation. Wind, solar Photovoltaic (PV), and biomass gasifier-based systems have gotten much attention recently for providing electricity to energy-deficient areas. However, due to the intermittent nature of renewable energy, a completely renewable system is unreliable and may cause operation problems. Energy storage systems and volatile generation sources are the best way to combat the problem. This paper proposes a hybrid grid-connected wind-solar PV generation Microgrid (MG) with biomass and energy storage devices to meet the entire value of load demand for the adopted buildings in an intended region and ensure economic dispatch as well as make a trade in the electricity field by supplying/receiving energy to/from the utility grid. The control operation plan uses battery storage units to compensate energy gap if the priority resources (wind turbine and solar PV) are incapable of meeting demand. Additionally, the biomass gasifier is used as a fallback option if the batteries fail to perform their duty. At any time, any excess of energy can be utilized to charge the batteries and sell the rest to the utility. Additionally, if the adopted resources are insufficient to meet the demand, the required energy is acquired from the utility. A Hybrid Grey Wolf with Cuckoo Search Optimization (GWCSO) algorithm is adopted for achieving optimal sizing of the proposed grid-connected MG. To assess the proposed technique’s robustness, the results are compared to those obtained using the Grey Wolf Optimization (GWO) algorithm. The GWCSO method yielded a lower total number of component units, annual cost, total Net Present Cost (NPC), and Levelized Cost Of Energy (LCOE) than the GWO algorithm, whereas the GWCSO algorithm has the lowest deviation, indicating that it is more accurate and robust than the GWO algorithm.

1 Introduction

Renewable-based hybrid energy systems have gained traction recently as environmental concerns, energy demand, fuel prices, and fossil fuel depletion have increased (Alhasnawi et al., 2021a; Alhasnawi et al., 2021b; Alhasnawi et al., 2021c). Increased energy consumption by a specific region’s buildings and households during peak demand necessitates the operation of extra generation units, which consumes a lot of fuel and raises the cost of electricity. Because wind and solar energy have relatively low marginal costs (fuel is not required), increasing the supply of renewable energy tends to decrease the average price per unit of electrical energy. Thus, renewable energy substantially reduces the overall amount of expensive electricity to fulfil the load’s energy and ensure “economic dispatch”. In a renewable energy-based system, it is critical to integrate wind energy with solar PV because solar energy cannot be adopted at night or in cloudy conditions, whereas wind energy can be used even at night. In addition, wind energy is more efficient than solar energy. Wind turbines emit a lower amount of carbon dioxide into the atmosphere. Many studies have been done to determine whether wind-powered systems are viable and how large they should be to maximize their efficiency (Abouzahr and Ramakumar, 1990; Elhadidy and Shaahid, 1999; Elhadidy and Shaahid, 2004).

The major disadvantages of solar energy are its stochastic nature, which raises concerns about the user’s power reliability. As a result, the hybridization of wind and solar energy is a viable option for increasing reliability (the strength of another can compensate for weakness). However, it adds to the complexity of the system (Yang et al., 2008). Due to the unpredictable nature of both wind and solar resources, a standalone solar-wind energy system is limited in its ability to operate without the use of backup power. In the case of an autonomous hybrid system, backup is typically provided by a diesel generator or energy storage devices such as batteries or ultra-capacitors. Using a diesel generator in a hybrid system increases both the cost and the environmental impact. Fortunately, as technology advances, other renewable energy sources such as biogas, biomass, micro-hydro, and fuel cells have been integrated alongside solar and wind energy (Patil et al., 2010). Among the renewable energy sources mentioned previously, biomass appears to be the more viable option, particularly in agriculturally rich countries. Biomass can be converted into a variety of different products, including heat, electricity, and biofuels (Singh et al., 2008). Due to advancements in biomass gasification technology, biomass gasifier-generated electricity is gaining popularity, particularly in rural areas. Biomass power plants have a high load factor and are economically viable (Patil et al., 2011).

According to an earlier discussion, grid-connected and standalone MG adopting wind-PV-biomass for electricity generation, with or without storage devices, is a viable and cost-effective option, especially in developing countries (Bhattacharjee and Dey, 2014; Singh and Kaushik, 2016a). As a result, using renewable energy sources to generate electricity in MG system can allow for grid reconnection in the event of inadequate energy and also provide extra energy to the utility. In the case of hybrid systems, various factors such as the system’s total cost or the size and capacity of renewable energy sources play a significant role. Sizing determines the MG’s resource coordination, proper system configuration, and the component’s capacity to meet the load demand. In the interim, optimization is necessary to ensure that the system operates more efficiently, maximizing economic benefit while minimizing energy consumption, pollutants, and other objectives. Sizing and optimization are interdependent and mutually supportive. This is essential for resolving oversizing and under sizing issues to improve supply reliability. Two critical parameters, the cost of generating energy and the system’s reliability, present significant challenges in hybrid systems. A well-designed system should make the best component selection possible while still ensuring the system’s reliability (Nehrir et al., 2011).

There is little existing literature incorporating wind, PV, and biomass hybrid MG systems with energy storage. The authors in (Akram et al., 2018) proposed two constraint-based iterative search algorithms for optimal sizing of wind turbines, solar PV, and battery energy storage systems in a grid-connected MG. The first algorithm, called source sizing, determines optimal Renewable Energy Resource (RER) sizes, while the second, called battery sizing, determines optimal Battery Energy Storage System (BESS) capacity. Borowy and Salameh (1996) introduced the Loss of Load Probability (LLP) concept for sizing a battery bank and a PV array in a hybrid wind and PV system by building the curve representing the relationship between PV modules and batteries reduces the system cost. Kaabeche et al. (2011) used iterative optimization to follow the Deficiency of Power Supply Probability (DPSP) and the Levelised Cost of Energy (LCE). Belmili et al. (2014) used Loss of Power Supply Probability (LPSP) technique to develop a techno-economic algorithm able to determine the system that would guarantee a reliable energy supply with the least investment. Nacer et al. (2015) described a novel approach for sizing grid-connected hybrid renewable energy systems that include photovoltaic and wind turbines but do not include storage devices or biomass gasifiers. The hybrid system is used to generate environmentally friendly self-consumed energy. Unmet load demand is purchased from the grid, ensuring the system’s reliability at all times. Unlike standalone systems, surplus energy is injected into the grid at a prime rate determined by local policy, reducing the grid-connected system’s cost. Singh and Kaushik (2016b) investigated the sizing problem for grid-connected and off-grid photovoltaic/biomass hybrid systems. The results indicate that grid-connected systems outperform off-grid systems. Wang and Xu Wang et al. (2018) determined the optimal size for a grid-connected photovoltaic/wind/battery hybrid system. The results indicate that grid connectivity is economically advantageous. Abushnaf and Rassau (2018) determined the optimal size of a grid-connected photovoltaic/battery hybrid system and selected a number of photovoltaic panels, batteries, and inverters as decision variables. Cingoz and Sozer Badawy et al. (2016) pinpointed battery storage sizing for a grid-connected photovoltaic/battery hybrid system for various scenarios and the optimal size was derived for each scenario. The optimal size for a PV/wind/battery hybrid system was set in (Nadjemi et al., 2017), and the results indicate that the cost of the system is significantly influenced by the initial cost of the PV and the selling price of renewable electricity. Zhang et al. (2017) explored the sizing and operation of a photovoltaic/battery hybrid system. The results indicate that battery usage is not advantageous with commonly used operation methods. Using the Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) algorithms presented in (Gonzalez et al., 2015), a grid-connected solar PV and wind turbine system has been designed. The results indicated that feeding the load demand could minimize the energy cost. Using the algorithms of GA, firefly algorithm, and GWO, (Biswas and Kumar, 2017), presented a techno-economic analysis of a standalone hybrid system incorporating hybrid pumped and battery energy storage with PV. Considering the case study for feeding a low load, the GWO is capable of minimizing the energy cost of the system. GA has been used to optimize the design of a hybrid energy system for minimizing environmental impacts in an agricultural case study (Kaab et al., 2019) to increase energy-use efficiency. 9ndividual optimization algorithms are used to size and optimize the energy systems to reduce costs (Ahmed et al., 2022). In this article, a PV plant with fuel cell (FC) and battery storage devices has been configured as a standalone MG to supply a nuclear power plant emergency loads. This paper applies and compares the optimization algorithms of bat optimization (BAT), equilibrium optimizer (EQ), and black-hole-based optimization (BHB). The authors of reference (Kyriakarakos et al., 2015) discussed the design and research of decentralized systems for energy management for an autonomous polygeneration MG in a remote area. This was designed to meet the needs of a remote area, such as providing electricity, heating and cooling for buildings, and drinkable water. With the decentralized energy-management system, each component of the MG can be controlled individually. The system design was based on a multi-agent scheme and was implemented using Fuzzy Cognitive Maps. In order to model the strategy exchange between two players/agents as a non-cooperative power management game or a cooperative one, depending on the level of the energy generated by the renewable electricity sources and the energy stored in the battery bank, the energy management problem was formulated through the application of game theory (Karavas et al., 2017). This was done to achieve optimal energy controlling and managing of the MG operation.

Unlike the above studies, the current work proposed a new energy management system with GWCSO algorithm to optimize the size of a grid-connected biomass/photovoltaic/wind/energy storage device hybrid AC/DC MG. To the authors’ knowledge, the optimal sizing of such a hybrid system and algorithm has not been considered in the prior literature. Along with size optimization, this article introduces two new indices for determining power exchange between the hybrid system and the grid: selling and purchasing energy. The contributions of this paper are pointed as:

1. This study proposes a new hybrid gridconnected MG system that includes a photovoltaic, wind, and biomass energy system equipped with a battery bank to provide reliable power to on-grid areas. The mathematical modeling of the proposed system’s various components and operational processes have been discussed in depth.

2. The optimal sizing of a grid-connected hybrid AC/DC MG using wind, photovoltaic, and gasifier energy sources with battery storage has been analyzed and the energy exchange of the proposed MG with the utility grid has been optimally achievedThis study uses the adopted GWCSO. This algorithm has been adopted to determine the size of the optimal components for the proposed system with the lowest annual cost, LCOE and minimizing the system’s NPC. To the best of our knowledge, the sizing of solar PV, wind turbine, storage batteries as well as biomass gasifier units have not been extracted previously by combining GWO and CS in a grid-connected MG.

3. The cost analysis results using the adopted GWCSO algorithm have been compared to those obtained using the GWO algorithm to determine the most cost-effective algorithm.

4. This study provides an illustration of the techno-economic and environmental consequences of grid-connected hybrid systems at various integration levels by optimally reducing the total number of used components and giving priority to renewable energy units to meet power demands, making it easier for investors to select the most appropriate system for their investment objectives.

5. The weather data for Basrah city in Iraq have been adopted in cost analysis and for meeting virtual load demand by weather-based renewable units by adopting both GWCSO and GWO algorithms.

The organization of this paper is divided up into five sections. Section 2 discusses the mathematical modeling of the various components. Section 3 provides a formulation of the problem, an operational strategy, and a brief introduction to the adopted algorithm. In Section 4, the simulation results are illustrated. Section 6 concludes the paper.

2 Proposed system mathematical modeling

This work focuses on developing a hybrid system capable of meeting the demand profile for Residential Loads (RL), Commercial Loads (CL), and Industrial Loads (IL) by supplying reliable power to the grid-connected area. The proposed microgrid’s various components are depicted in Figure 1.

FIGURE 1

FIGURE 1. The proposed grid connected MG.

As illustrated in Figure 1, the AC bus connects the AC loads, wind turbines, and biomass gasifiers. Solar PV panels and batteries are connected to the AC bus via the bidirectional converter. Additionally, a charge controller is used to ensure the smooth flow of power and to regulate the charging and discharging rates of the batteries. The proposed system will aid in reducing reliance on the utility grid through the use of renewable energy sources. The storage devices are used to manage the energy generated by wind, solar, and biomass. The battery banks are adopted here to optimize power distribution, which reduces the intermittency of renewable energy sources. In addition to the energy management strategy, the system under this work focuses on the optimal sizing of each component while maintaining the system’s reliability. The following subsections discuss the mathematical models for various components.

2.1 Solar photovoltaic panel

According to (Ahmad and Enayatzare, 2018; Ramli et al., 2018), the following equation incorporates all important parameters that influence the PV output, such as temperature and solar radiation. The power output of a solar photovoltaic ($P_{sol}\left(t\right)$) panel can be expressed as,

${\mathit{P}}_{\mathit{s}\mathit{o}\mathit{l}}\left(\mathit{t}\right)={\mathit{P}}_{\mathit{P}\mathit{V}}^{\mathit{n}\mathit{o}\mathit{m}}\frac{\mathit{G}}{{\mathit{G}}_{\mathit{r}\mathit{e}\mathit{f}}}\left[\mathbf{1}+\mathit{K}\left({\mathit{T}}_{\mathit{a}\mathit{m}\mathit{b}}+\left(\frac{\mathit{N}\mathit{O}\mathit{C}\mathit{T}-\mathbf{20}}{\mathbf{800}}\mathit{G}\right)-{\mathit{T}}_{\mathit{r}\mathit{e}\mathit{f}}\right)\right](1)$

In this equation, $P_{PV}^{nom}$denotes the nominal power of PV under standard test conditions, $G$ denotes solar radiation (watts per square meter), $G_{ref}$ = 1 kW/m² denotes reference solar radiation, and $K$ is the coefficient of power at different temperatures. $T_{amb}$stands for ambient temperature, $NOCT$ is the nominal operation temperature, while $T_{ref}$ = 25°C is the reference temperature under standard conditions.

2.2 Wind turbine power generation

The amount of energy produced by a wind turbine ($P_{WT}\left(t\right)$) can be calculated as follows:

${\mathit{P}}_{\mathit{W}\mathit{T}}\left(\mathit{t}\right)=\{\begin{array}{c}\mathbf{0}\mathit{V}\left(\mathit{t}\right)\le {\mathit{V}}_{\mathit{c}\mathit{i}\mathit{n}}\mathit{a}\mathit{n}\mathit{d}\mathit{V}\left(\mathit{t}\right)\ge {\mathit{V}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{t}}\\ {\mathit{P}}_{\mathit{r}}^{\mathit{W}}{\mathit{V}}_{\mathit{r}\mathit{a}\mathit{t}}\le \mathit{V}\left(\mathit{t}\right)\le {\mathit{V}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{t}}\\ {\mathit{P}}_{\mathit{r}}^{\mathit{W}}\frac{\mathit{V}\left(\mathit{t}\right)-{\mathit{V}}_{\mathit{c}\mathit{i}\mathit{n}}}{{\mathit{V}}_{\mathit{r}\mathit{a}\mathit{t}}-{\mathit{V}}_{\mathit{c}\mathit{i}\mathit{n}}}{\mathit{V}}_{\mathit{c}\mathit{i}\mathit{n}}\le \mathit{V}\left(\mathit{t}\right)\le {\mathit{V}}_{\mathit{r}\mathit{a}\mathit{t}}\end{array}(2)$

where $P_r^W$denotes the rating of a single wind turbine, $V_{cin}$ represents the cut-in speed, $V_{rat}$ denotes the rated wind speed, $V_{cout}$ acts the cut-out speed, and $V\left(t\right)$ denotes the desired reference height wind speed. Wind speed at hub height varies according to site and geographical location and is not identical to reference height. Additionally, it is expressed as,

$\mathit{V}\left(\mathit{t}\right)={\mathit{V}}_{\mathit{r}}\left(\mathit{t}\right){\left(\frac{{\mathit{H}}_{\mathit{W}\mathit{T}}}{{\mathit{H}}_{\mathit{r}}}\right)}^{\mathit{\lambda }}(3)$

where $V\left(t\right)$ represents the wind speed at height ($H_{WT}$), $V_r\left(t\right)$ represents the wind speed at the reference height $H_r$, and $\lambda$ denotes the friction coefficient. The friction coefficient $\lambda$ is typically 1/7 for smooth surfaces and well-exposed locations (Malheiro et al., 2015; Wu et al., 2015; Singh et al., 2016).

2.3 Biomass gasifier

Biomass gasification technology converts solid bio-residue into a gaseous fuel that is then used to generate electricity. The producer gas is produced during partial combustion and is a combustible gas composed of H₂ (20%), CO (20%), CH₄ (1–2%), and inert gases. The producer gas is used as an input fuel in the case of a biomass gasifier. The annual electricity output ($E_{bmg}$) of a biomass gasifier can be calculated as follows:

${\mathit{E}}_{\mathit{b}\mathit{m}\mathit{g}}={\mathit{P}}_{\mathit{b}\mathit{m}\mathit{g}}\left(\mathbf{8760}*\mathit{C}\mathit{U}\mathit{F}\right)(4)$

where$P_{bmg}$ denotes the system’s rating power and $CUF$ denotes the capacity utilization factor. In the case of a biomass-based energy system, a few parameters such as the calorific value of the biomass, its availability $\left(\frac{Ton}{yr}\right)$, and the hours of operation of the biomass gasifier all play a significant role. The maximum rating for a biomass gasifier installed in a specific area is as follows:

${\mathit{P}}_{\mathit{b}\mathit{m}\mathit{g}}^{\mathit{m}}=\frac{\mathit{T}\mathit{o}\mathit{t}\mathit{a}\mathit{l}\mathit{b}\mathit{i}\mathit{o}\mathit{m}\mathit{a}\mathit{s}\mathit{s}\mathit{a}\mathit{v}\mathit{i}\mathit{a}\mathit{l}\mathit{a}\mathit{b}\mathit{l}\mathit{e}\left(\frac{\mathit{T}\mathit{o}\mathit{n}}{\mathit{y}\mathit{r}}\right)*\mathbf{1000}*\mathit{C}{\mathit{V}}_{\mathit{b}\mathit{m}}*{\mathit{\eta }}_{\mathit{b}\mathit{m}\mathit{g}}}{\mathbf{365}*\mathbf{860}*\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{n}\mathit{g}\mathit{h}\mathit{o}\mathit{u}\mathit{r}\mathit{s}/\mathit{d}\mathit{a}\mathit{y}}(5)$

where ${\eta }_{bmg}$denotes the overall efficiency of biomass to electricity conversion and $C{V}_{bm}$denotes the calorific value of the biomass (Nouni et al., 2007; Gupta et al., 2010; Singh et al., 2016).

2.4 Battery bank

Batteries can be used in hybrid renewable energy systems to store excess energy and to discharge it when renewable energy sources are unavailable or insufficient. Energy measurement is possible with the proper estimation of the state of charge (SOC). The SOC of a battery is a function of time and can be calculated as follows (Singh et al., 2016):

$\frac{\mathit{S}\mathit{O}\mathit{C}\left(\mathit{t}\right)}{\mathit{S}\mathit{O}\mathit{C}\left(\mathit{t}-\mathbf{1}\right)}={\int }_{\mathit{T}-\mathbf{1}}^{\mathit{T}}\frac{{\mathit{P}}_{\mathit{b}}\left(\mathit{t}\right){\mathit{\eta }}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}}{{\mathit{V}}_{\mathit{b}\mathit{u}\mathit{s}}}\mathit{d}\mathit{t}(6)$

where $V_{bus}$is the bus voltage, $P_b\left(t\right)$ is the battery’s input/output power, and ${\eta }_{batt}$is the battery’s round trip efficiency. If $P_b\left(t\right)$is positive, the battery is charging; if it is negative, the battery is discharging. Additionally, a battery’s round-trip efficiency is defined as follows:

${\mathit{\eta }}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}=\sqrt{{\mathit{\eta }}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{c}}{\mathit{\eta }}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{d}}}(7)$

where ${\eta }_{batt}^c$ and ${\eta }_{batt}^d$ denote the battery’s charging and discharging efficiency, respectively (Nouni et al., 2007; National Renewable Energy Laboratory, 2022). The battery bank’s round-trip efficiency is estimated to be 92 percent. Additionally, charging and discharging efficiencies are assumed to differ, at 85 percent and 100 percent, respectively. SOC_max is the maximum state of charge and is equal to the battery bank’s aggregate capacity ($C_n$). It is expressed as follows:

${\mathit{C}}_{\mathit{n}}\left(\mathit{A}\mathit{h}\right)=\frac{{\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}}{{\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{s}}}{\mathit{C}}_{\mathit{b}}\left(\mathit{A}\mathit{h}\right)(8)$

where $C_b$ denotes the capacity of a single battery, $N_{batt}$denotes the total number of batteries, and $N_{batt}^s$ denotes the number of series-connected batteries. The battery bank cannot be discharged below a specified minimum state of charge, referred to as SOC_min. This limit can be used as a system constraint depending on the battery bank’s usage.

Batteries are connected in series to achieve the desired bus voltage. The series connection of batteries can be calculated as,

${\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{s}}=\frac{{\mathit{V}}_{\mathit{b}\mathit{u}\mathit{s}}}{{\mathit{V}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}}(9)$

where $V_{batt}$is the single battery’s voltage.

Another critical factor to consider when modeling batteries is the highest (maximum) charge or discharge power available at any given time. It is proportional to the maximum charge current and is calculated using the following equation:

${\mathit{P}}_{\mathit{b}}^{\mathit{max}}=\frac{{\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}{\mathit{V}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}{\mathit{I}}_{\mathit{max}}}{\mathbf{1000}}(10)$

where $I_{\mathit{max}}$denotes the maximum charging current of the battery in amps.

2.5 Power converter

A power converter must be used if there are both AC and DC elements in the system. Solar PV and batteries produce DC output, whereas the considered load is AC. The size of the converter is determined by the peak power of demand ($P_L^m\left(t\right)$). The inverter rating ($P_{inv}\left(t\right)$) is figured out as shown in Eq. 1 (Singh et al., 2016).

${\mathit{P}}_{\mathit{i}\mathit{n}\mathit{v}}\left(\mathit{t}\right)=\frac{{\mathit{P}}_{\mathit{L}}^{\mathit{m}}\left(\mathit{t}\right)}{{\mathit{\eta }}_{\mathit{i}\mathit{n}\mathit{v}}}(11)$

where ${\eta }_{inv}$stands for the efficiency of the inverter.

3 Problem formulation

This research developed a grid-connected hybrid energy system with both cost-effectiveness and reliability in operation. The rating and sizing of solar PV panels, wind turbines, battery banks, and biomass gasifiers are among the most important decision factors. The operational strategy of the system, the objective function and constraints, and a brief introduction to the algorithm, that has been used, are all discussed in this section.

3.1 Operational strategy

It is necessary to have proper power management in any hybrid energy system in order to achieve system reliability. In this system, the biomass gasifier is kept at the bottom of the priority list, which means that it is only activated when solar, wind, and batteries are unable to meet the load demand. The system’s operating strategy is depicted in the flow chart below (Figure 2). The steps of the proposed operation strategy are illustrated as follows:

1. Input weather and load data.

2. Modeling of solar, wind, inverter, battery and gasifier.

3. Check to see if solar and wind energy are sufficient to meet the electricity demand.

4. If yes, solar and wind energy will be used to meet the load, and any excess energy will be used to charge the batteries.

FIGURE 2

FIGURE 2. The operating strategy flow chart of the proposed system.

3.1.1 Charging function

5. Determine how much extra energy is available for charging.

6. Check to see if all of the energy can really be stored in the battery; if so, store what is available in the battery.

7. Otherwise, sell the excess energy to the grid after charging the batteries.

3.1.2 Discharging function

8. The total amount of energyis required to meet load demand that cannot be met through solar or wind.

9. Determine whether the battery alone can meet the load demand.

10. If the answer is yes, discharge the battery to meet the load demand.

11. Else, determine whether a gasifier operating independently of the grid can meet the load.

12. The gasifier is responsible for meeting the insufficient load.

13. Else take power from the grid to make up for the shortfall.

3.2 Constraints and objective functions

This study minimizes the proposed hybrid system’s total NPC while maintaining an optimal energy flow. For optimal configuration, four major decision factors were chosen: the number of wind turbines, solar photovoltaic panels, batteries, and biomass gasifier rating. Economic analysis is conducted using the system Annualized Cost (ANC), NPC, and LCOE concepts. When all other constraints and parameters are satisfied, the solution with the lowest values of them is evidenced to be the optimal one. The objective function of the total system cost contains of three components: (i) replacement cost, (ii) total capital cost, and (iii) operational and maintenance cost. Installation and civil works costs are included in the component’s capital costs. The following function is taken as the primary objective function that must be minimized within specified constraints (Singh et al., 2016): Minimize ANC

$\mathit{A}\mathit{N}\mathit{C}=\mathit{F}\left({\mathit{N}}_{\mathit{s}\mathit{o}\mathit{l}}{\mathit{C}}_{\mathit{s}\mathit{o}\mathit{l}}+{\mathit{N}}_{\mathit{W}\mathit{T}}{\mathit{C}}_{\mathit{W}\mathit{T}}+{\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}{\mathit{C}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}+{\mathit{P}}_{\mathit{i}\mathit{n}\mathit{v}}{\mathit{C}}_{\mathit{i}\mathit{n}\mathit{v}}+{\mathit{P}}_{\mathit{b}\mathit{m}\mathit{g}}{\mathit{C}}_{\mathit{b}\mathit{m}\mathit{g}}\right)(12)$

Where $C_{WT},C_{sol},C_{inv}and{C}_{batt}$are the cost of wind turbine (per kW), solar PV panel (per kW), inverter (per kW) and battery (per unit) respectively. The cost of the biomass gasifier (per kW) is denoted by$C_{bmg}$, and the rating of the biomass gasifier is denoted by $P_{bmg}$. $P_{inv}$ is the inverter’s rating. $N_{WT},N_{sol}and{N}_{batt}$ are the total units number of wind turbines, solar PV panel and batteries.

The capital and installation costs ($C^{ci}$), replacement costs ($C^r$), annual maintenance costs ($C^m$), operation costs ($C^f$), and salvage costs $\left(C^s\right)$are all included in the ANC of the installed component. Additionally, the total ANC value for each component can be expressed as follows:

${\mathit{C}}_{\mathit{s}\mathit{o}\mathit{l}}={\mathit{C}}_{\mathit{s}\mathit{o}\mathit{l}}^{\mathit{c}\mathit{i}}+{\mathit{C}}_{\mathit{s}\mathit{o}\mathit{l}}^{\mathit{r}}+{\mathit{C}}_{\mathit{s}\mathit{o}\mathit{l}}^{\mathit{m}}-{\mathit{C}}_{\mathit{s}\mathit{o}\mathit{l}}^{\mathit{s}}(13)$

${\mathit{C}}_{\mathit{w}\mathit{i}\mathit{n}\mathit{d}}={\mathit{C}}_{\mathit{W}\mathit{T}}^{\mathit{c}\mathit{i}}+{\mathit{C}}_{\mathit{W}\mathit{T}}^{\mathit{r}}+{\mathit{C}}_{\mathit{W}\mathit{T}}^{\mathit{m}}-{\mathit{C}}_{\mathit{W}\mathit{T}}^{\mathit{s}}(14)$

${\mathit{C}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}={\mathit{C}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{c}\mathit{i}}+{\mathit{C}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{r}}+{\mathit{C}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{m}}-{\mathit{C}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{s}}(15)$

${\mathit{C}}_{\mathit{i}\mathit{n}\mathit{v}}={\mathit{C}}_{\mathit{i}\mathit{n}\mathit{v}}^{\mathit{c}\mathit{i}}+{\mathit{C}}_{\mathit{i}\mathit{n}\mathit{v}}^{\mathit{r}}+{\mathit{C}}_{\mathit{i}\mathit{n}\mathit{v}}^{\mathit{m}}-{\mathit{C}}_{\mathit{i}\mathit{n}\mathit{v}}^{\mathit{s}}(16)$

${\mathit{C}}_{\mathit{b}\mathit{m}\mathit{g}}={\mathit{C}}_{\mathit{b}\mathit{m}\mathit{g}}^{\mathit{c}\mathit{i}}+{\mathit{C}}_{\mathit{b}\mathit{m}\mathit{g}}^{\mathit{r}}+{\mathit{C}}_{\mathit{b}\mathit{m}\mathit{g}}^{\mathit{m}}-{\mathit{C}}_{\mathit{b}\mathit{m}\mathit{g}}^{\mathit{s}}(17)$

With the help of a factor known as the Capacity Recovery Factor (CRF), it is possible to calculate the annualized cost of any component. The CRF (Eq. 18) can be used to compute the present value of money:

$\mathit{C}\mathit{R}\mathit{F}\left(\mathit{N},\mathit{i}\right)=\frac{{\mathit{i}\left(\mathbf{1}+\mathit{i}\right)}^{\mathit{N}}}{{\left(\mathbf{1}+\mathit{i}\right)}^{\mathit{N}}-\mathbf{1}}(18)$

where$N$ is the number of years in the lifetime and $i$ is the yearly interest rate. The objective function is minimized while enforcing a number of constraints, which can be summarized as follows:

$\mathbf{1}\le {\mathit{N}}_{\mathit{s}\mathit{o}\mathit{l}}\le {\mathit{N}}_{\mathit{s}\mathit{o}\mathit{l}}^{\mathit{m}}(19)$

$\mathbf{1}\le {\mathit{N}}_{\mathit{W}\mathit{T}}\le {\mathit{N}}_{\mathit{W}\mathit{T}}^{\mathit{m}}(20)$

$\mathbf{1}\le {\mathit{P}}_{\mathit{b}\mathit{m}\mathit{g}}\le {\mathit{P}}_{\mathit{b}\mathit{m}\mathit{g}}^{\mathit{m}}(21)$

$\mathbf{1}\le {\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}\le {\mathit{N}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{t}}^{\mathit{m}}(22)$

${\mathit{S}\mathit{O}\mathit{C}}_{\mathit{min}}\le \mathit{S}\mathit{O}\mathit{C}\le {\mathit{S}\mathit{O}\mathit{C}}_{\mathit{max}}(23)$

The maximum number of solar PV panels is represented by $N_{sol}^m$, the maximum number of batteries is represented by $N_{batt}^m$, the maximum number of wind turbines is represented by $N_{WT}^m$, and the maximum rating of biomass gasifier is represented by $P_{bmg}^m$.

The most cost-effective and reliable configuration is chosen based on the LCOE and reliability. The LCOE is defined as the average price per kWh of useful energy generated by the system:

$\mathit{L}\mathit{C}\mathit{O}\mathit{E}=\frac{\mathit{A}\mathit{N}\mathit{C}(\frac{\$}{\mathit{Y}\mathit{e}\mathit{a}\mathit{r}})}{\mathit{T}\mathit{o}\mathit{t}\mathit{a}\mathit{l}\mathit{u}\mathit{s}\mathit{e}\mathit{f}\mathit{u}\mathit{l}\mathit{e}\mathit{n}\mathit{e}\mathit{r}\mathit{g}\mathit{y}\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{d}\left(\frac{\mathit{k}\mathit{W}\mathit{h}}{\mathit{Y}\mathit{e}\mathit{a}\mathit{r}}\right)}(24)$

Table 1 shows all the technical and economic parameters associated with the components used in the proposed MG. Several papers were considered during for the purpose of parametrization, while the most proper were selected (Shakti et al., 2016; Karavas et al., 2019).

TABLE 1

TABLE 1. Technical and economic specifications of the proposed system components.

3.3 Hybrid grey wolf optimization and cuckoo search algorithm

3.3.1 Overview

Recently, hybridizing two or more algorithms has gained popularity as a method of identifying superior solutions to optimization problems. The incorporation into hybrid optimized algorithms of many well-known optimization techniques has made them more efficient in dealing with the issues.

The GWO algorithm simulates the hunting mechanism and leadership hierarchy of grey wolves. Grey wolves typically live in groups in the wild. The group consists of four distinct species of wolves. The group’s leader wolf is referred to as alpha (α), and it is located at the top of the pyramid. While the alpha may not be the strongest wolf in the pack, it must be the best leader. It is in charge of making critical group decisions, such as predation behavior and food distribution. Beta (β) is located on the second floor of the pyramid and serves as an alpha assistant, assisting alpha in managing the group. It needs only respect the alpha to be able to command others. The third level wolf is delta (δ), which must follow alpha and beta’s instructions. When alpha and beta reach the end of their useful lives, they are downgraded to delta. The base of the pyramid is referred to as omega (ω). Omega must submit to the rest of the group (Karavas et al., 2019 and Mahmoud et al., 2020).

GWO and cuckoo search (CS) are two popular meta-heuristic algorithms. Nevertheless, their search mechanisms are distinct. GWO is inspired by the hunting behavior of grey wolves and utilizes three types of wolves to search the solution space: the alpha wolf, the beta wolf, and the delta wolf. CS is influenced by the obligatory brood parasitic behavior of cuckoo and utilizes Lévy flight to generate novel solutions. Numerous studies revealed that GWO excels at exploitation (Long et al., 2018; Gupta and Deep, 2019; Saxena et al., 2019), whereas CS is more interested in global exploration (Mlakar et al., 2016). The GWO algorithm has been used in this work to determine the optimal size of the proposed system components, thereby lowering the system’s cost and meeting load demand. When GWO inspects an individual with a high fitness value, a weak global search ability occurs, allowing to fall into the local optimum more easily. A Cuckoo Search Algorithm (CSA) updates the nest’s position with a probability that is independent of the search path and in random directions. As a result, it is much easier to jump from one region to another. Thus, CSA is an extremely beneficial tool and can be adopted to improve GWO. In this paper, CSA has been implicitly employed in the GWO algorithm to update the positions of existing search agents and generate a new set. The new hybrid GWCSO is powerful and can quickly solve optimization problems by extracting the sizing units of solar PV, wind turbine, storage batteries, and biomass gasifier in a grid-connected MG. In this regard, the position updated equation of CSA is used to modify the positions, speeds and convergence accuracies of the grey wolf agent. The flowchart of GWO in conjunction with CSA is depicted in Figure 3.

FIGURE 3

FIGURE 3. The flowchart of GWO with CSA.

3.3.2 Mathematical model of grey wolf optimization

The fitness function determines the level of the grey. According to the fitness value, the alpha wolf, beta wolf, and delta wolf are the best fitness solutions. These three solutions are denoted as the key-group. Omega wolf is responsible for the remaining wolves. Grey wolves’ social hierarchy and hunting technique are mathematically modelled in order to create GWO and optimize it. The following mathematical models are proposed for the social hierarchy, encircling, hunting and attacking prey (Xu et al., 2017; Alhasnawi et al., 2021d):

3.3.2.1 Encircling prey

During the hunt, grey wolves encircle their prey. The following equations are presented to mathematically model encircling behavior:

$\overrightarrow{\mathit{D}}=\left|\overrightarrow{\mathit{C}}.\overrightarrow{{\mathit{X}}_{\mathit{p}}}\left(\mathit{t}\right)-\overrightarrow{\mathit{X}}\left(\mathit{t}\right)\right|(25)$

$\overrightarrow{\mathit{X}}\left(\mathit{t}+\mathbf{1}\right)=\left|\overrightarrow{{\mathit{X}}_{\mathit{p}}}\left(\mathit{t}\right)-\overrightarrow{\mathit{A}}.\overrightarrow{\mathit{D}}\right|(26)$

Where $t+\mathit{1}$denotes the next iteration in these two equations, $\overrightarrow{X}$ denotes the position of a single wolf. $\overrightarrow{X_p}$ denotes the prey’s position, while $\overrightarrow{A}$ and $\overrightarrow{D}$ denote the coefficient vectors. The following equations model the calculation method

$\overrightarrow{\mathit{A}}=\mathbf{2}\overrightarrow{\mathit{a}}.{\overrightarrow{\mathit{r}}}_{\mathbf{1}}-\overrightarrow{\mathit{a}}(27)$

$\overrightarrow{\mathit{C}}=\mathbf{2}.{\overrightarrow{\mathit{r}}}_{\mathbf{2}}(28)$

Where${\overrightarrow{r}}_{\mathit{1}}$ and ${\overrightarrow{r}}_{\mathit{2}}$ are random integers between 0 and 1. Vector $\overrightarrow{a}$ is set to a value between 2 and 0, which causes the number of iterations to decrease linearly during the iterative procedure.

3.3.2.2 Hunting prey

When the wolf group locates prey, the alpha wolf, beta wolf, and delta wolf lead the wolf group in encircling the prey. Assume they are aware of the prey’s location. Thus, creating a key group from the best three solutions obtained thus far and updating the position of each wolf in the group according to the key group. The following equations are used to update the position.

$\overrightarrow{\mathit{X}}\left(\mathit{t}+\mathbf{1}\right)=\frac{{\overrightarrow{\mathit{X}}}_{\mathbf{1}}+{\overrightarrow{\mathit{X}}}_{\mathbf{2}}+{\overrightarrow{\mathit{X}}}_{\mathbf{3}}}{\mathbf{3}}(29)$

${\overrightarrow{\mathit{X}}}_{\mathbf{1}}=\left|{\overrightarrow{\mathit{X}}}_{\mathit{\alpha }}-{\overrightarrow{\mathit{A}}}_{\mathbf{1}}.{\overrightarrow{\mathit{D}}}_{\mathit{\alpha }}\right|(30)$

${\overrightarrow{\mathit{X}}}_{\mathbf{2}}=\left|{\overrightarrow{\mathit{X}}}_{\mathit{\beta }}-{\overrightarrow{\mathit{A}}}_{\mathbf{2}}.{\overrightarrow{\mathit{D}}}_{\mathit{\beta }}\right|(31)$

${\overrightarrow{\mathit{X}}}_{\mathbf{3}}=\left|{\overrightarrow{\mathit{X}}}_{\mathit{\delta }}-{\overrightarrow{\mathit{A}}}_{\mathbf{3}}.{\overrightarrow{\mathit{D}}}_{\mathit{\delta }}\right|(32)$

Where ${\overrightarrow{X}}_{\alpha }$, ${\overrightarrow{X}}_{\beta }$, and ${\overrightarrow{X}}_{\delta }$ denote the top three solutions obtained thus far during the iterative procedure, which constitute the key group. The following equations define additional parameters

${\overrightarrow{\mathit{D}}}_{\mathit{\alpha }}=\left|{\overrightarrow{\mathit{C}}}_{\mathbf{1}}.{\overrightarrow{\mathit{X}}}_{\mathit{\alpha }}-\overrightarrow{\mathit{X}}\right|(33)$

${\overrightarrow{\mathit{D}}}_{\mathit{\beta }}=\left|{\overrightarrow{\mathit{C}}}_{\mathbf{2}}.{\overrightarrow{\mathit{X}}}_{\mathit{\beta }}-\overrightarrow{\mathit{X}}\right|(34)$

${\overrightarrow{\mathit{D}}}_{\mathit{\delta }}=\left|{\overrightarrow{\mathit{C}}}_{\mathbf{3}}{\overrightarrow{.\mathit{X}}}_{\mathit{\delta }}-\overrightarrow{\mathit{X}}\right|(35)$

3.3.2.3 Attacking prey

Grey wolves typically attack their prey when it comes to a halt. Thus, the following equation describes the behavior of grey wolves as they approach their prey.

$\mathit{A}=\mathbf{2}-\mathbf{2}\left(\frac{\mathit{t}}{\mathit{Max}}\right)(36)$

Where $t$ is an integer value between 0 and Max that represents the number of times the present algorithm has run (max number of iteration).

3.3.3 Improving in grey wolf optimization algorithm

As shown in Eq. 29, the GWO algorithm updates the positions of individuals with high fitness values via trend search, which is a key group. Consequently, it will have the poor global-search capability, and it may be easy to slide into the local optimum, particularly when dealing with large data sets. With a random walk and levy-flights, the Cuckoo Search (CS) algorithm updates the positions of the nest, while the search path can be either longer or shorter than the previous one with nearly the same probabilities, and the direction is highly random. As a result, it is much easier to move from one area to another in the future. The CS algorithm must adhere to the three idealized rules listed below.

• To begin, cuckoo birds randomly choose their nests and only lay one egg at a time.

• Second, only the most desirable nests will survive for future generations.

• Thirdly, the number of bird nests and the probability of discovering the eggs are fixed. If the host bird discovers an outsider’s egg, the host bird abandons the nest and builds a new one.

Following these three rules, the nests are updated during iteration by following the next equations.

In the CS operation, a population, from the standpoint of implementation,$E^k\left(X_{\mathit{1}}^k,X_{\mathit{2}}^k,\dots ..,X_N^k\right)$, of $N$ individuals is evolved from a starting point ($k=\mathit{0}$) to a total number of iterations (gen). Each individual $X_i^k$($i\in \left[\mathit{1},\dots .,N\right]$) is an n-dimensional vector with the dimensions ${(X}_{i,\mathit{1}}^k,X_{i,\mathit{2}}^k,\dots ..,X_{i,n}^k)$ each corresponding to a decision variable in the optimization problem to be solved. The quality of each individual, $X_i^k$ (candidate solution), is determined using an objective function, ${f(X}_i^k$), whose final result represents $X_i^k$'s fitness value. Through use of Levy flights to produce new candidate solutions is one of the most advanced features of cuckoo search. A new candidate solution, $X_i^k\left(i\in \left[\mathit{1},\dots .,N\right]\right)$ is generated by perturbing the current $X_i^k$ with a position $c_i$change. To obtain $c_i$, a symmetric Levy distribution generates a random step, $s_i$. Mantegna’s algorithm is used to generate $s_i$(Mantegna, 1994; Cuevas and Reyna-Orta, 2014):

${\mathit{s}}_{\mathit{i}}=\frac{\overrightarrow{\mathit{u}}}{{\left|\overrightarrow{\mathit{v}}\right|}^{\mathbf{1}/\mathit{\beta }}}(37)$

Where $\overrightarrow{u}=\left\{u_{\mathit{1}},u_{\mathit{2}},\dots .u_n\right\}$ and $\overrightarrow{v}=\left\{v_{\mathit{1}},v_{\mathit{2}},\dots .v_n\right\}$ both n-dimensional vectors with a dimension of 3/2. Each component of $\overrightarrow{u}$ and $\overrightarrow{v}$ is calculated using the normal distributions described below (Cuevas and Reyna-Orta, 2014):

$\mathit{u}\sim \mathit{N}\left(\mathbf{0},{\mathit{\sigma }}_{\mathit{u}}^{\mathbf{2}}\right),\mathit{v}\sim \mathit{N}\left(\mathbf{0},{\mathit{\sigma }}_{\mathit{v}}^{\mathbf{2}}\right)(38)$

${\mathit{\sigma }}_{\mathit{u}}=\frac{\mathit{\Gamma }\left(\mathbf{1}+\mathit{\beta }\right).\mathbf{sin}\left(\mathit{\pi }.\frac{\mathit{\beta }}{\mathbf{2}}\right)}{\mathit{\Gamma }\left(\frac{\left(\mathbf{1}+\mathit{\beta }\right)}{\mathbf{2}}\right).\mathit{\beta }.{\mathbf{2}}^{\left(\mathit{\beta }-\mathbf{1}\right)/\mathbf{2}}},{\mathit{\sigma }}_{\mathit{v}}=\mathbf{1}(39)$

where the gamma distribution is denoted by $\Gamma \left(.\right)$. After calculating $s_i$, the required change in position $c_i$ is calculated as follows:

${\mathit{c}}_{\mathit{i}}=\mathbf{0.01}.{\mathit{s}}_{\mathit{i}}\oplus \left({\mathit{X}}_{\mathit{i}}^{\mathit{k}}-{\mathit{X}}^{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}\right)(40)$

where the product $\oplus$ is entry-wise multiplications and $X^{best}$ denotes the best solution that has been observed thus far in terms of fitness value. Finally, the new candidate solution, $X_i^{k+\mathit{1}}$, is determined through the use of Eq. 41

${\mathit{X}}_{\mathit{i}}^{\mathit{k}+\mathbf{1}}={\mathit{X}}_{\mathit{i}}^{\mathit{k}}+{\mathit{c}}_{\mathit{i}}(41)$

As a result, the CS algorithm can efficiently search the solution space because its step changes with small distance detection and occasional long distance walking, and the step length is much longer in the long run (Cai et al., 2003). Figure 4 presents the pseudocodes representation of the GWO and GWCSO algorithm.

FIGURE 4

FIGURE 4. The pseudocode for the GWO and for the GWCSO.

4 Simulation results

The adopted total load profile for (CL, RL, and IL) to determine the optimal size of system components and to conduct energy management analysis is depicted in Figure 5, where (a) shows annual load profile and (b) shows daily load profile. The annual solar irradiance, ambient temperature and wind speed of Basrah city, Iraq are adopted as an annual input weather data as shown in Figures 6A–C respectively.

FIGURE 5

FIGURE 5. The adopted (A) annual load and (B) daily load.

FIGURE 6

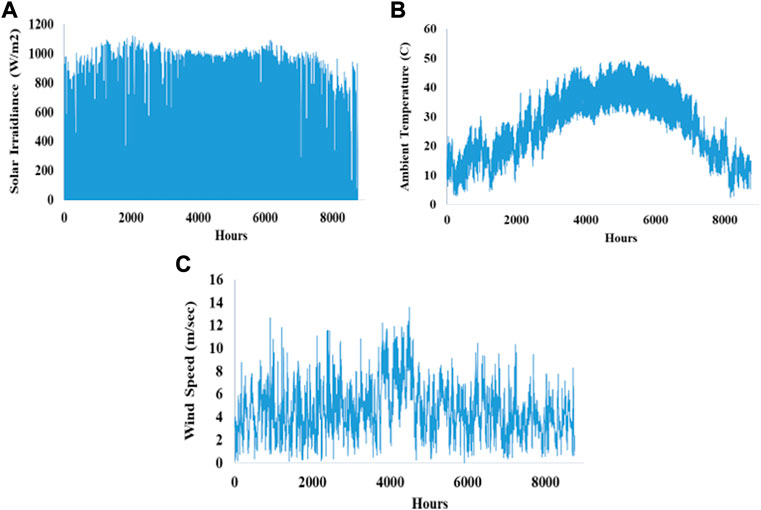
FIGURE 6. The adopted weather data of (A) solar irradiance, (B) ambient temperature and (C) wind speed.

4.1 Optimal sizing results

The optimal findings include the total number of wind turbines, solar PV panels, batteries, and the maximum rating of a gasifier. The most viable and optimal option is ranked according to the ANC and LCOE metrics. Table 2 lists the control parameters for the optimization algorithms used to simulate the proposed technique in MATLAB software. For the case study, GWO and GWCSO algorithms produced comprehensive optimal results, which are presented in Table 3. The results indicate that the GWCSO algorithm predicts the system’s minimum ANC with the lowest LCOE. The GWCSO algorithm predicts 797.38 kW, 2000 kW solar PV wind turbines, 1166.53 batteries, and a 1.47 kW biomass gasifier with 12014467$ total net price cost and an annualized cost of energy of 1084800.5 $, resulting in an LCOE of 0.2052 $/kWh. The GWCSO algorithm forecasts the smallest possible cost of components’ size for the system, as shown in Table 4. This is because the components’ units are the lowest achievable with this optimization algorithm, as shown in Table 3. Additionally, Table 4 demonstrates that energy purchased from the utility grid using GWCSO is less expensive than energy purchased via GWO, and vice versa in the energy sold to the utility grid. The convergence rates of both algorithms are depicted in Figure 7.

TABLE 2

TABLE 2. The control parameters of GWO and GWCSO.

TABLE 3

TABLE 3. The optimal sizing outcome achieved from adopted techniques.

TABLE 4

TABLE 4. The annual cost of the system components and grid purchases and sales ($/year).

FIGURE 7

FIGURE 7. The convergence curve of (A) GWCSO and (B) GWO.

4.2 Energy management analysis

To meet overall energy demand, the proposed system uses solar, wind, batteries, gasifier, and the utility grid for the purchase or sale of needed or extra energy, respectively. Figure 8A depicts the monthly average energy balance over a year. The annual energy produced by wind, solar photovoltaic, battery (input and output), gasifier, and grid (sale and purchase) are depicted for each month. If the total power generated by solar, wind, batteries, and the maximum gasifier power does not meet the load demand, the gasifier power will be zero, and the power purchased from the grid will meet the load demand. On the other hand, if the power generated by solar and wind alone does not meet the demand, a battery is used to compensate for the lack of available power to meet the demand. So, if there is excess solar and wind energy after meeting the load demand, it is necessary to determine whether all of the available energy can be stored in the battery; if so, the remaining energy should be stored in the battery. Alternatively, after battery charging, sell excess energy to the grid. Figure 8B shows the grid sales and energy purchase in the first week of April. The greatest amount of energy sales is in July, because of the high values of solar radiation and temperature in this month, which gives the greatest amount of power from the solar PV units.

FIGURE 8

FIGURE 8. (A) Monthly and (B) Daily average energy balance over a year.

Figure 9 depicts a complete power exchange for the first week in April to illustrate the power exchange between the system’s various components. As shown in the Figure, the battery out (red curve) met the load demand in the interval up to [20 h 24 h] of the first week of April because solar and wind energy alone could not meet the demand. The other intervals in which the battery provides energy are [4 h 6 h], [43 h 49 h], [68 h 76 h], [83 h 86 h], [94 h 102 h], and [116 h 124 h]. As discussed in the operational methodology, the utility grid is used only when solar and wind energy are insufficient to meet load demand, battery capacity is equal to or less than the minimum SOC, and also the biomass gasifier cannot meet the load demand. It is cleared from Figure 9B, the MG purchased energy from utility grid in the intervals [1 h 8 h], [24 h 31 h], [48 h 56 h], [101 h 104 h], and [123 h 126 h]. Except for the time periods when the battery supplies energy and the intervals in which the MG purchases energy, excess energy is often sold to the utility grid, as shown by the blue curve.

FIGURE 9

FIGURE 9. The power exchange between the adopted sources and batteries in (A) and with grid in (B).

Battery State of Charge (SOC) measurement becomes critical in systems that use batteries as storage devices. Throughout the year, Figure 10 depicts the state of charge of the battery bank, as well as the input and output energy. The initial and minimum allowable SOC levels have been set to 100% and 30%, respectively. Additionally, Figure 10 demonstrates that battery SOC is generally good, except for a few instances when natural resources are limited or load demand is greater.

FIGURE 10

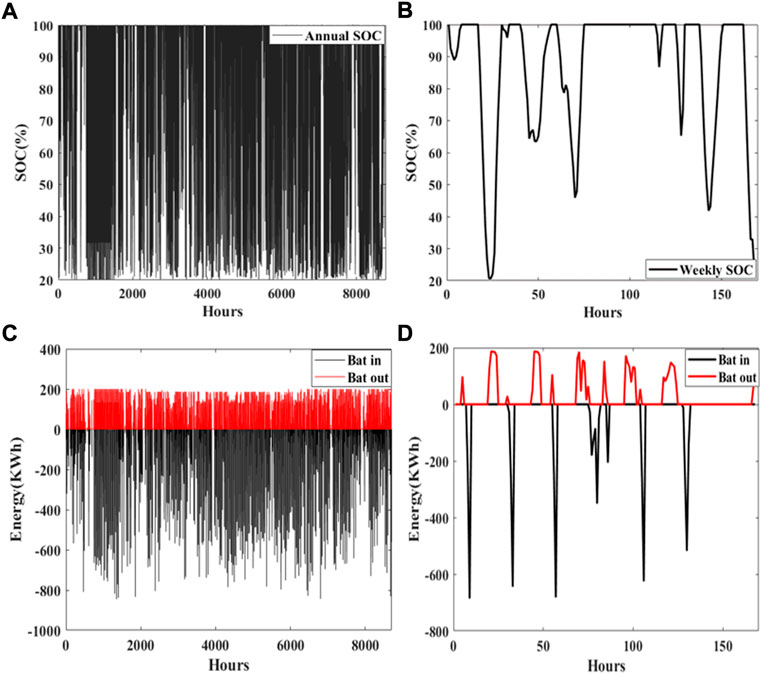
FIGURE 10. Battery SOC and energy (A) annual SOC, (B) SOC of the first week in March, (C) annual input and output energy, and (D) input and output energy of the first week in April.

4.3 Robustness test

To evaluate the robustness of the GWCSO and GWO algorithms, a total of 20 independent runs for each algorithm have been carried out. Figure 11 depicts the mean, maximum, and minimum annual cost values, as well as the standard deviation, for a total of 20 runs. As can be seen in the Figure, the GWCSO algorithm exhibits the smallest amount of deviation, resulting in a low deviation from the mean and thus, making it superior to the GWO algorithm. Additionally, it can be seen in the Figure that the GWCSO algorithms provide the smallest mean, minimum, and maximum values of ANC, TNPC, and LCOE when compared to the values obtained by using GWO.

FIGURE 11

FIGURE 11. The annual values of minimum (A), maximum (B), standard deviation (C), and the mean (D).

5 Conclusion

A reliable, cost-effective, and environmentally friendly hybrid energy management system with solar PV, wind, biomass gasifier and battery storage units for grid connected area has been proposed in this paper. Initially, a brief discussion of the mathematical modeling of the various components adopted in the study is presented; following that, the operational strategy and brief introduction of the GWGSO algorithm are presented. The operating strategy is proposed for energy management by using wind-solar PV renewable sources initially, then energy storage systems, and finally biomass as a last resort, which is the most expensive source. This strategy makes the system capable of trading electrical energy with the utility grid. The GWCSO algorithm has been used to develop a mathematical model for determining the optimal size of components to resolve MG resources coordination, system configuration, and component capacity in order to meet the load demand. Optimization is performed to maximize economic benefit while minimizing energy consumption, pollutants, and other objectives. Finally, the GWCSO algorithm’s results were compared to the GWO algorithm’s results. The results indicate that the GWCSO algorithm can accurately predict the system’s minimum component units, minimum ANC, and lowest LCOE. Also, the proposed algorithm outperformed GWO in terms of robustness due to its lower deviation for multiple runs. The added value of this study is that it illustrates the techno-economic and environmental consequences of grid-connected hybrid systems at various integration levels, making it easier for the investor to choose the optimal system (Mahmoud et al., 2020).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AJ: writing—original draft, methodology, software, and validation; BJ: supervisor, formal analysis, resources, investigation, editing, and writing—review; VB: writing —review, funding, and editing. All authors have read and agreed to the published version of the manuscript.

Funding

The APC was funded by FIM UHK Excellence Project 2022: Decision making processes and models for smart systems. This research has also been partially supported by the Czech Technological Foundation, Project TL03000296.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abouzahr, I., and Ramakumar, R. (1990). Loss of power supply probability of stand alone wind electric conversion system. IEEE Trans. Energy Convers. 5 (3), 445. doi:10.1109/60.105267

CrossRef Full Text | Google Scholar

Abushnaf, J., and Rassau, A. (2018). Impact of energy management system on the sizing of a grid-connected PV/Battery system. Electr. J. 31 (2), 58–66. doi:10.1016/j.tej.2018.02.009

CrossRef Full Text | Google Scholar

Ahmad, G., and Enayatzare, M. (2018). Optimal energy management of a renewable-based isolated microgrid with pumped-storage unit and demand response. Renew. Energy 123, 460–474. doi:10.1016/j.renene.2018.02.072

CrossRef Full Text | Google Scholar

Ahmed, A., El-Rifaie, A. M., Zaky, M. M., and Tolba, M. A. (2022). Optimal sizing of stand-alone microgrids based on recent metaheuristic algorithms. Mathematics 10, 140. doi:10.3390/math10010140

CrossRef Full Text | Google Scholar

Akram, U., Khalid, M., and Shafiq, S. (2018). Optimal sizing of a wind/solar/battery hybrid grid-connected microgrid system. IET Renew. Power Gener. 12 (1), 72–80. doi:10.1049/iet-rpg.2017.0010

CrossRef Full Text | Google Scholar

Alhasnawi, B. N., Jasim, B. H., and Sedhom, B. E. (2021). Distributed secondary consensus fault tolerant control method for voltage and frequency restoration and power sharing control in multi-agent microgrid. Int. J. Electr. Power & Energy Syst. 133, 107251. doi:10.1016/j.ijepes.2021.107251

CrossRef Full Text | Google Scholar

Alhasnawi, B. N., Jasim, B. H., Rahman, Z. A. S. A., Guerrero, J. M., and Esteban, M. D. (2021). A novel internet of energy based optimal multi-agent control scheme for microgrid including renewable energy resources. Int. J. Environ. Res. Public Health 18, 8146. doi:10.3390/ijerph18158146

PubMed Abstract | CrossRef Full Text | Google Scholar

Alhasnawi, B. N., Jasim, B. H., Siano, P., and Guerrero, J. M. (2021). A novel real-time electricity scheduling for home energy management system using the internet of energy. Energies 14, 3191. doi:10.3390/en14113191

CrossRef Full Text | Google Scholar

Alhasnawi, B. A., Jasim, B. H., Rahman, Z. A. S. A., and Siano, P. (2021). A novel robust smart energy management and demand reduction for smart homes based on internet of energy. Sensors 21, 4756. doi:10.3390/s21144756

PubMed Abstract | CrossRef Full Text | Google Scholar

Badawy, M. O., Cingoz, F., and Sozer, Y. (2016). “Battery storage sizing for a grid Tied PV system based on operating cost minimization,” in Proceeding of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, September 2016 (IEEE), 16671891.

CrossRef Full Text | Google Scholar

Belmili, H., Haddadi, M., Bacha, S., Fayçal Almi, M., and Bendib, B. (2014). Sizing standalone photovoltaic–wind hybrid system: Techno-economic analysis and optimization. Renew. Sustain. Energy Rev. 30, 821–832. doi:10.1016/j.rser.2013.11.011

CrossRef Full Text | Google Scholar

Bhattacharjee, S., and Dey, A. (2014). Techno-economic performance evaluation of grid integrated PV-biomass hybrid power generation for rice mill. Sustain. Energy Technol. Assessments 7, 6–16. doi:10.1016/j.seta.2014.02.005

CrossRef Full Text | Google Scholar

Biswas, A., and Kumar, A. (2017). Techno-Economic Optimization of a Stand-alone PV/PHS/Battery systems for very low load situation. Int. J. Renew. Energy Res. 7, 844–856. doi:10.20508/ijrer.v7i2.4900.g7065

CrossRef Full Text | Google Scholar

Cai, W., Yang, C. Y., and He, B. (2003). Preliminary extension logic, science press. Beijing: Simplified Chinese version.

Google Scholar

Cuevas, E., and Reyna-Orta, A. (2014). A cuckoo search algorithm for multimodal optimization. Sci. World J. 2014, 497514. Hindawi Publishing Corporation. doi:10.1155/2014/497514

PubMed Abstract | CrossRef Full Text | Google Scholar

Elhadidy, M. A., and Shaahid, S. (1999). Optimal sizing of battery storage for hybrid (wind+diesel) power systems. Renew. Energy 18, pp77–86. doi:10.1016/s0960-1481(98)00796-4

CrossRef Full Text | Google Scholar

Elhadidy, M. A., and Shaahid, S. M. (2004). Role of hybrid (wind+diesel) power systems in meeting commercial loads. Renew. Energy 29, 109–118. doi:10.1016/s0960-1481(03)00067-3

CrossRef Full Text | Google Scholar

Gonzalez, A., Riba, J. R., Rius, A., and Puig, R. (2015). Optimal sizing of a hybrid grid-connected photovoltaic and wind power system. Appl. Energy 154, 752–762. [CrossRef]. doi:10.1016/j.apenergy.2015.04.105

CrossRef Full Text | Google Scholar

Gupta, A., Saini, R. P., and Sharma, M. P. (2010). Steady-state modelling of hybrid energy system for off grid electrification of cluster of villages. Renew. Energy 35 (2), 520–535. doi:10.1016/j.renene.2009.06.014

CrossRef Full Text | Google Scholar

Gupta, S., and Deep, K. (2019). A novel random walk grey wolf optimizer. Swarm Evol. Comput. 44, 101–112. doi:10.1016/j.swevo.2018.01.001

CrossRef Full Text | Google Scholar

Kaab, A., Sharifi, M., Mobli, H., Nabavi-Pelesaraei, A., and Chau, K. W. (2019). Use of optimization techniques for energy use efficiency and environmental life cycle assessment modification in sugarcane production. Energy 181, 1298–1320. [CrossRef]. doi:10.1016/j.energy.2019.06.002

CrossRef Full Text | Google Scholar

Kaabeche, A., Belhamel, M., and Ibtiouen, R. (2011). Sizing optimization of grid-independent hybrid photovoltaic/wind power generation system. Energy 36, 1214–1222. doi:10.1016/j.energy.2010.11.024

CrossRef Full Text | Google Scholar

Karavas, C-S., Arvanitis, K. G., and Papadakis, G. (2019). Optimal technical and economic configuration of photovoltaic powered reverse osmosis desalination systems operating in autonomous mode. Desalination 466, 97–106. doi:10.1016/j.desal.2019.05.007

CrossRef Full Text | Google Scholar

Karavas, C.-S., Arvanitis, K., and Papadakis, G. (2017). A game theory approach to multi-agent decentralized energy management of autonomous polygeneration microgrids. Energies 10 (11), 1756. doi:10.3390/en10111756

CrossRef Full Text | Google Scholar

Kyriakarakos, G., Arvanitis, K. G., Karavas, C.-S., and Papadakis, G. (2015). A multi-agent decentralized energy management system based on distributed intelligence for the design and control of autonomous polygeneration microgrids. Energy Convers. Manag. 103, 166–179. doi:10.1016/j.enconman.2015.06.021

CrossRef Full Text | Google Scholar

Long, W., Jiao, J., Liang, X., and Tang, M. (2018). An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 68, 63–80. doi:10.1016/j.engappai.2017.10.024

CrossRef Full Text | Google Scholar

Mahmoud, H. Y., Hasanien, H. M., Besheer, A. H., and Abdelaziz, A. Y. (2020). Hybrid cuckoo search algorithm and grey wolf optimiser‐based optimal control strategy for performance enhancement of HVDC‐based offshore wind farms. IET Gener. Transm. &amp. Distrib. 14 (10), 1902–1911. doi:10.1049/iet-gtd.2019.0801

CrossRef Full Text | Google Scholar

Malheiro, A., Castro, P. M., Lima, R. M., and Estanqueiro, A. (2015). Integrated sizing and scheduling of wind/PV/diesel/battery isolated systems. Renew. Energy 83, 646–657. doi:10.1016/j.renene.2015.04.066

CrossRef Full Text | Google Scholar

Mantegna, R. N. (1994). Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes. Phys. Rev. E 49 (4), 4677–4683. doi:10.1103/physreve.49.4677

PubMed Abstract | CrossRef Full Text | Google Scholar

Mlakar, U., Fister, I., and Fister, I. (2016). Hybrid self-adaptive cuckoo search for global optimization. Swarm Evol. Comput. 29, 47–72. doi:10.1016/j.swevo.2016.03.001

CrossRef Full Text | Google Scholar

Nacer, T., Nadjemi, O., and Hamidat, A. (2015). “Optimal sizing method for grid connected renewable energy system under Algerian climate,” in Proceeding of the 6th International Renewable Energy Congress (IREC), Sousse, Tunisia, March 2015 (IEEE).

CrossRef Full Text | Google Scholar

Nadjemi, O., Nacer, T., Hamidat, A., and Salhi, H. (2017). Optimal hybrid PV/wind energy system sizing: Application of cuckoo search algorithm for Algerian dairy farms. Renew. Sustain. Energy Rev. 70, 1352–1365. doi:10.1016/j.rser.2016.12.038

CrossRef Full Text | Google Scholar

National Renewable Energy Laboratory National renewable energy laboratory (USA). [last accessed April, 2022].

Nehrir, M. H., Wang, C., Strunz, K., Aki, H., Ramakumar, R., Bing, J., et al. (2011). A review of hybrid renewable/alternative energy systems for electric power generation: Configurations, control, and applications. IEEE Trans. Sustain. Energy 2 (4), 392–403. doi:10.1109/tste.2011.2157540

CrossRef Full Text | Google Scholar

Nouni, M. R., Mullick, S. C., and Kandpal, T. C. (2007). Biomass gasifier projects for decentralized power supply in India: A financial evaluation. Energy Policy 35 (2), 1373–1385. doi:10.1016/j.enpol.2006.03.016

CrossRef Full Text | Google Scholar

Patil, A. B. K., Saini, R. P., and Sharma, M. P. (2010). Integrated renewable energy systems for off grid rural electrification of remote area. Renew. Energy 35 (6), 1342–1349. doi:10.1016/j.renene.2009.10.005

CrossRef Full Text | Google Scholar

Patil, A. B. K., Saini, R. P., and Sharma, M. P. (2011). Sizing of integrated renewable energy system based on load profiles and reliability index for the state of Uttarakhand in India. Renew. Energy 36 (11), 2809. doi:10.1016/j.renene.2011.04.022

CrossRef Full Text | Google Scholar

Ramli, M. A. M., Bouchekara, H. R. E. H., and Alghamdi, A. S. (2018). Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 121, 400–411. doi:10.1016/j.renene.2018.01.058

CrossRef Full Text | Google Scholar

Borowy, B., and Salameh, Z. (1996). Methodology for optimally sizing the combination of a battery bank and PV array in a wind/PV hybrid system. IEEE Trans. energy Convers. 11, 367–375. doi:10.1109/60.507648

CrossRef Full Text | Google Scholar

Saxena, A., Kumar, R., and Das, S. (2019). β-Chaotic map enabled grey wolf optimizer. Appl. Soft Comput. 75, 84–105. doi:10.1016/j.asoc.2018.10.044

CrossRef Full Text | Google Scholar

Shakti, S., Mukesh, S., and Kaushik, S. (2016). A review on optimization techniques for sizing of solar-wind hybrid energy systems. Int. J. Green Energy 13 (15), 1564–1578. doi:10.1080/15435075.2016.1207079

CrossRef Full Text | Google Scholar

Singh, J., Panesar, B. S., and Sharma, S. K. (2008). Energy potential through agricultural biomass using geographical information system: A case study of Punjab. Biomass Bioenergy 32, 301–307. doi:10.1016/j.biombioe.2007.10.003

CrossRef Full Text | Google Scholar

Singh, S., and Kaushik, S. C. (2016). Optimal sizing of grid integrated hybrid PV‐biomass energy system using artificial bee colony algorithmficial bee colony algorithm. IET Renew. Power Gener. 10 (5), 642–650. doi:10.1049/iet-rpg.2015.0298

CrossRef Full Text | Google Scholar

Singh, S., and Kaushik, S. C. (2016). Optimal sizing of grid integrated hybrid PV-biomass energy system using artificial bee colony algorithm. IET Renew. Power Gener. 10 (5), 642–650. doi:10.1049/iet-rpg.2015.0298

CrossRef Full Text | Google Scholar

Singh, S., Singh, M., and Kaushik, S. C. (2016). Feasibility study of an islanded microgrid in rural area consisting of PV, wind, biomass and battery energy storage system. Energy Convers. Manag. 128, 178–190. doi:10.1016/j.enconman.2016.09.046

CrossRef Full Text | Google Scholar

Wang, P., Wang, W., and Xu, D. (2018). Optimal sizing of distributed generations in DC microgrids with comprehensive consideration of system operation modes and operation targets. IEEE Access 6, 31129–31140. doi:10.1109/access.2018.2842119

CrossRef Full Text | Google Scholar

Wu, K., Zhou, H., An, S., and Huang, T. (2015). Optimal coordinate operation control for windphotovoltaic-battery storage power generation units. Energy Convers. Manag. 90, 466–475. doi:10.1016/j.enconman.2014.11.038

CrossRef Full Text | Google Scholar

Xu, H., Liu, X., and Su, J. (2017). “An improved grey wolf optimizer algorithm integrated with cuckoo search,” in Proceeding of the the 9th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Bucharest, Romania, September 2017 (IEEE).

CrossRef Full Text | Google Scholar

Yang, H., Zhou, W., Lu, L., and Fang, Z. (2008). Optimal sizing method for standalone hybrid solar-wind system with LPSP technology by using genetic algorithm. Sol. Energy 82, 354–367. doi:10.1016/j.solener.2007.08.005

CrossRef Full Text | Google Scholar

Zhang, Y., Lundblad, A., Campana, P. E., Benavente, F., and Yan, J. (2017). Battery sizing and rule-based operation of grid-connected photovoltaic-battery system: A case study in Sweden. Energy Convers. Manag. 133, 249–263. doi:10.1016/j.enconman.2016.11.060

CrossRef Full Text | Google Scholar

Glossary

ANC Annualized Cost

BESS Battery Energy Storage System

CRF Capacity Recovery Factor

CSA Cuckoo Search Algorithm

CS Cuckoo Search

CUF Capacity Utilization Factor

CL Commercial Loads

DPSP Deficiency of Power Supply Probability

GWCSO Hybrid Grey Wolf with Cuckoo Search Optimization

GWO Grey Wolf Optimization

IL Industrial Loads

LCE Levelised Cost of energy

LPSP Loss of Power Supply Probability

LCOE Levelized Cost Of Energy

LLP Loss of Load Probability

MG Microgrid

NPC Net Present Cost

PV Photovoltaic

RER Renewable Energy Resource

RL Residential Loads

SOC State Of Charge

$C{V}_{bm}$ calorific value of the biomass

$C^{ci}$ capital and installation costs

$C^r$ replacement costs

$C_n$ battery bank’s aggregate capacity

$C_b$ capacity of a single battery

$C^m$ annual maintenance costs

$C^f$ operation costs

$C^s$ salvage costs

$C_{WT}$ cost of wind turbine (per kW)

$C_{sol}$ cost of solar PV (per kW)

$C_{inv}$ cost of inverter (per kW)

$C_{batt}$ cost of battery (per kW)

$C_{bmg}$ cost of the biomass gasifier (per kW)

$E_{bmg}$ annual electrical energy output of biomass

$E^k$ population the standpoint of implementation of $N$ individuals ($X_i^k$)

$G$ solar radiation

$G_{ref}$ reference solar radiation

$I_{\mathit{max}}$ maximum charging current of the battery

$i$ yearly interest rate

$K$ coefficient of power at different temperatures

$NOCT$ nominal operation temperature

$N$ number of years in the lifetime

$N_{WT}$ total units number of wind turbines

$N_{sol}$ total units number of solar PV

$N_{batt}$ total units number of batteries total number of batteries

$N_{batt}^s$ number of series-connected batteries

$N_{sol}^m$ maximum number of solar PV panels

$N_{batt}^m$ maximum number of batteries

$N_{batt}$ total units number of batteries total number of batteries

$N_{WT}^m$ maximum number of wind turbines

$P_{WT}\left(t\right)$ wind turbine power

$P_r^W$ rating power of wind turbine

$P_{bmg}$ biomass’s rating power

$P_{bmg}^m$ maximum rating power of biomass maximum rating of biomass gasifier

$P_{sol}\left(t\right)$ power output of solar photovoltaic

$P_{PV}^{nom}$ nominal power of PV

$P_L^m\left(t\right)$ peak power of demand

$P_{inv}\left(t\right)$ inverter rating power

$P_{bmg}^m$ maximum rating power of biomass maximum rating of biomass gasifier

$P_b\left(t\right)$ battery’s input/output power

SOC_min minimum state of charge

$s_i$ random step

$T_{amb}$ ambient temperature

$T_{ref}$ reference temperature under standard conditions

$V_{batt}$ single battery’s voltage

$V_{cin}$ cut-in speed

$V_{bus}$ battery’s bus voltage

$V_{rat}$ rated wind speed

$V_{cout}$ cut-out speed

$V\left(t\right)$ wind speed at height ($H_{WT}$)

$V_r\left(t\right)$ wind speed at the reference height $H_r$

$\overrightarrow{X}$ position of a single wolf

$\overrightarrow{X_p}$ prey’s position

${\overrightarrow{X}}_{\alpha }$, ${\overrightarrow{X}}_{\beta }$, and ${\overrightarrow{X}}_{\delta }$ top three solutions obtained by GWO

$X_i^{k+\mathit{1}}$, new candidate solution

${\eta }_{batt}$ battery’s round trip efficiency

${\eta }_{inv}$ efficiency of the inverter

$\overrightarrow{u}$ and $\overrightarrow{v}$ n-dimensional vectors

$\lambda$ friction coefficient

${\eta }_{batt}^c$ battery’s charging efficiency

${\eta }_{batt}^d$ battery’s discharging efficiency

${\eta }_{bmg}$ overall efficiency of biomass