A Dynamic Evaluation Method for High-Permeability New Energy Distribution Network Planning Considering Multistage Development Trends

With the development of new power systems, high penetration of new energy (HPNE) will become a major feature of power systems in the future. In order to solve the problem that the traditional distribution network planning index makes it difficult to fully consider the impact of new energy access on the distribution network, this paper constructs a distribution network planning evaluation index system considering the characteristics of HPNE, and designs a set of static comprehensive evaluation methods of distribution network planning schemes based on the “over-average penalty” entropy weight method (EWM). At the same time, distribution network planning is a long-term dynamic process, and the static evaluation method makes it difficult to describe the actual situation of the multistage construction process of distribution networks. To this end, a dynamic evaluation method of distribution network planning is proposed, which realizes the comprehensive evaluation of multistage distribution network planning based on dual excitation control lines. Finally, an example of four 10 kV distribution network planning schemes of a power supply bureau are analyzed to prove the effectiveness of the proposed method.

1 Introduction

Vigorously promoting the sustainable development of renewable energy, improving its penetration in the power grid, and achieving the goal of “carbon peaking and carbon neutralization” have become the new trends of building a green and clean power system (NDRC, 2015; Yang et al., 2018). However, high permeability new energy access brings new challenges to the distribution network, such as randomization of the operation state and the complexity of planning objectives (Kang and Yao, 2017; Zhang et al., 2021). Therefore, Zou et al. (2012), Jia et al. (2018), and Wang et al. (2019) used different methods to solve the problem of improving the randomness of distribution network operations after new energy access, and realized the robust planning of new distribution networks. Huang et al. (2016), Su et al. (2016), Sheng and Liu (2017), Wang et al. (2019), and Yao et al. (2019) incorporated economic benefit indicators, energy conservation and emission reduction indicators, power quality indicators, and other objectives into the planning of distributed resources accessing active distribution networks. It can be seen that a large number of distribution network planning studies focus on how to solve the highly stochastic robust planning problem with the penetration of new energy and the collaborative planning problem with different objectives. By contrast, in distribution network planning research, the index quantification and statistical analysis of the impact of HPNE on distribution networks is still in its infancy.

In the evaluation index system of distribution network planning schemes, the traditional distribution network planning indexes can be divided into three categories: economic indexes considering construction cost, reliability indexes considering power supply reliability, and other technical indexes similar to new energy consumption rates. In the context of high permeability new energy access, these traditional indicators make it difficult to fully consider the impact of new energy access on distribution networks. Therefore, some studies have been carried out.

Yan et al. (2018) made a preliminary exploration into the distribution network evaluation indexes of new energy characteristic access, and designed new indexes such as new energy output fluctuation. Zhang et al. (2010) considered various impacts of distributed resource access on distribution networks and put forward corresponding quantitative indexes. Chen et al. (2017) designed a new distribution network evaluation index, considering the voltage and frequency fluctuations of the bus with photovoltaic grid-connection. Considering the penetration of renewable energy, Ma et al. (2019) established a new evaluation index system for economic operation of distribution networks. In addition, many distribution network evaluation systems with different requirements have been established (Cui et al., 2013; Liu et al., 2013; Ou et al., 2014). The above studies have tried to include the impact of new energy on the distribution network evaluation. However, a complete evaluation index system for distribution network planning under the high permeability new energy has not been formed.

As for the comprehensive evaluation method of distribution network planning schemes, many scholars have studied and discussed it. Wang et al. (2018) comprehensively evaluated the intelligent planning schemes of distribution networks by using the analytic hierarchy process. Ding et al. (2015) introduced the utility risk model and fuzzy comprehensive evaluation method into the vulnerability assessment of distribution networks. Gang et al. (2007) attempted to establish a comprehensive Decision-Making System for distribution network planning schemes using the data envelopment method. In Jiang et al. (2021), a comprehensive evaluation system of distribution network indicators was established based on the analytic hierarchy process. These studies depend on the subjective evaluation of the importance of each index. And it is worth noting that every index in distribution network planning is of great significance, especially the reliability index. The disqualification of any index should be reflected in the final evaluation results. However, the current research used the weighted summation method to calculate the final evaluation value, which makes it difficult to reflect the impact of unqualified indicators. In addition, these studies on distribution network planning and evaluation focus more on the static evaluation at the end of distribution network planning, while distribution network planning is actually a multistage dynamic problem.

To sum up, this paper systematically explores the distribution network planning with the characteristics of HPNE, puts forward a distribution network planning index system, and designs a static comprehensive evaluation method for distribution network planning schemes. Furthermore, a dynamic evaluation method considering the characteristics of multistage distribution network planning is introduced to form a complete evaluation system of distribution network planning schemes. The main contributions of the article are as follows:

1) According to the actual impact of HPNE on the distribution network, the evaluation indexes considering the characteristics of HPNE are summarized. Combined with the existing evaluation index system of distribution network planning schemes, a comprehensive evaluation index system more suitable for distribution network planning in the future new power system is proposed in this paper.

2) In order to highlight the impact of unqualified indexes, this paper introduces an “over-average penalty” to improve the entropy weight method (I-EWM), and further puts forward the static comprehensive evaluation method of distribution network planning schemes under the HPNE.

3) Considering that distribution network planning is a multistage dynamic process, a dynamic evaluation method of distribution network planning schemes based on dual excitation control lines is proposed.

2 Evaluation Index System of Distribution Network Planning Schemes Under High Penetration of New Energy

2.1 Characteristics of Grid Integration of New Energy

Grid integration indexes reflect the impact of the energy and distribution characteristics of new energy on the distribution network, including typical output fluctuation index C_F, dispersion index C_D, and line N−1 verification contribution rate index C_N−1.

2.1.1 Typical Output Fluctuation Index C_F

The fluctuation and intermittence of the new energy output will interfere with the operation of the distribution network. Considering that new energy is changeable and highly random, this paper introduces the typical output fluctuation index to quantify the fluctuation of new energy. The typical output of new energy can be extracted by the hierarchical clustering method (Peng et al., 2015).

$C_{\text{F}}=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^{n}P\left(\left(i+1\right)\mathrm{\Delta }T\right)-P\left(i\mathrm{\Delta }T\right)}}{n}}/P_N(1)$

where $n$ refers to the number of time intervals; $\text{Δ}T$ is the time interval; $i$ represents the i-th time intervals; $P\left(i\text{Δ}T\right)$ indicates the output of new energy at i; $P_N$ represents the rated power.

2.1.2 Dispersion Index C_D

In the distribution network, the more dispersed the access of new energy, the more conducive to the local consumption of energy. Therefore, this paper proposes the dispersion index. The calculation formula is:

$C_{\text{D}}=1-\max \left|\frac{P_{N,i}-P_{avg}}{P_{avg}}\right|\times 100\%(2)$

where $P_{avg}$ refers to the average rated power of new energy at all access points connected to the distribution network; $P_{N,i}$ indicates the rated power of the i-th new energy.

2.1.3 Line $\mathit{N}-\mathbf{1}$ Verification Contribution Rate Index ${\mathit{C}}_{\mathit{N}-\mathbf{1}}$

Considering that the new energy can be considered as a standby resource (Pan et al., 2017), it contributes to improving the $N-1$ verification pass rate. So, the index is proposed as:

$C_{N-1}=\frac{N_{\text{DG}}+N}{N_{\text{all}}}\times 100\%(3)$

where $N_{DG}$ indicates the number of lines that have improved the line connection rate after the access of new energy; $N$ refers to the lines in the distribution network that have passed the $N-1$ verification; $N_{\text{all}}$ represents all lines running in the distribution network.

2.2 New Energy Acceptance Capacity

The specific contents of new energy acceptance capacity indexes include effective penetration rate index C_P and peak shaving contribution C_B.

2.2.1 Effective Penetration Rate Index C_P

Considering power flow reverse transmission will pose a threat to security (Chen et al., 2021; Hu et al., 2019), the effective penetration rate index is proposed to investigate the local consumption of new energy.

$C_{\text{P}}=\frac{1}{N}{\displaystyle \sum \frac{\overline{P_{\text{DG}}}}{\overline{P_{\text{load}}}}}\times 100\%(4)$

where $\overline{P_{\text{DG}}}$ represents the average value of typical output of new energy connected to the distribution network; $\overline{P_{\text{load}}}$ refers to the average value of typical load of new energy access points in distribution network planning; N represents the number of new energy access points.

2.2.2 Peak Shaving Contribution Index C_B

In order to consider the contribution of new energy in peak shaving, this paper introduces the peak shaving contribution index as:

$C_{\text{B}}=\min \left(\frac{{\displaystyle \sum _{i=1}^n{P}_{\text{DG}}}}{P_{\text{M,peak}}},\frac{{\displaystyle \sum _{i=1}^n{P}_{\text{DG}}}}{P_{\text{E,peak}}}\right)\times 100\%(5)$

where ${\text{P}}_{\mathrm{M},\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$, ${\text{P}}_{\mathrm{E},\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ represent the load at morning peak and evening peak, respectively.

2.3 Economy of New Energy Access

The economy of new energy access consists of direct and green economic benefits.

2.3.1 Direct Economic Benefits $C_{\text{save}}$

The direct economic benefit is calculated by subtracting the annual cost of new energy installation and operation from its own power generation income.

$\{\begin{array}{l}{C}_{\text{save}}=C_{\text{sal}}-C_{\mathrm{cost}}\\ C_{\text{sal}}=a\times W\\ C_{\text{cost}}={\displaystyle \sum _{i=1}^{n_{\text{e}}}\left(\left(c_{\text{tz}i}+c_{\text{az}i}\right)P_N{f}_{\text{cr}}+c_{\text{wh}i}{P}_N\right)}\\ f_{\text{cr}}=r\frac{{\left(1+r\right)}^{Lf}}{{\left(1+r\right)}^{Lf}-1}\end{array}(6)$

where $C_{\text{sal}}$ represents the income brought by new energy power generation; $a$ is the on-grid electricity price of new energy; $W$ is the total annual power generation under the typical output of new energy; $C_{\text{cost}}$ represents the total annual cost of new energy; $c_{\text{tz}i}$ is the investment cost of new energy at node i; $c_{\text{az}i}$ is the installation cost of new energy at node i; $c_{\text{wh}i}$ is the operation and maintenance cost of new energy at node i; $P_N$ is the rated installation capacity of new energy; $n_{\text{e}}$ is the total installed number of new energy; $f_{\text{cr}}$ is the investment recovery coefficient; $r$ is the discount rate; $Lf$ refers to the service life of new energy.

2.3.2 Green Economic Benefits $C_{\text{e}}$

$C_{\text{e}}$ is the environmental costs that are reduced after new energy replaces traditional energy. It generally includes environmental pollution cost and fines for the discharge of pollutants.

$C_{\text{e}}={\displaystyle \sum _{i=1}^{n_p}\left(V_{ei}{Q}_i+V_i{Q}_i\right)}(7)$

where $V_{ei}$ is the environmental value of the i-th pollutant; $Q_i$ is the discharge amount of the i-th pollutant; the fine amount of the i-th pollutant is denoted as $V_i$; n_p indicates the number of types of pollutants. The i-th pollutant emission is the number of pollutants emitted by coal-fired power generation when the power generation is the same as that of new energy.

2.4 Reliability Indexes

This paper selects the comprehensive power supply availability rate $C_{\text{RS}-3}$ and the average household power outage time $C_{\text{T}}$.

2.4.1 Power Supply Availability Rate $C_{\text{RS}-3}$

The power supply availability rate index is obtained by the power outage time of users.

$C_{\text{RS}-3}=(1-\frac{\mathrm{\sum }{t}_m}{T\times M})\times 100\text{\%}(8)$

where $t_m$ represents the total power outage time of the m-th billing user; $M$ represents the total number of billing users in the distribution network; $T$ represents the statistical time.

2.4.2 Average Household Power Outage Time $C_{\text{T}}$

The $C_{\text{T}}$ is reflected by the user outage duration and the number of user outages.

$C_{\text{T}}=\frac{{\displaystyle \sum t_m}}{{\displaystyle \sum m_j}}(9)$

where $m_j$ represents the number of billed users affected by the j-th power outage.

2.5 Technical Evaluation Indexes

The technical indexes reflect the operation level of the distribution network, which include the voltage qualification rate $C_{\mathrm{U}}$ and the line loss rate $C_{\text{loss}}$.

2.5.1 Voltage Qualification Rate $C_{\mathrm{U}}$

The new energy improves the problem of voltage drop at the end of the distribution network effectively. The larger $C_{\mathrm{U}}$, the higher the overall voltage quality of the distribution network.

$C_{\text{U}}=\left(1-\frac{\mathrm{\sum }{t}_{vm}}{T\times M}\right)\times 100\%(10)$

where $t_{vm}$ represents the total time that the voltage of the m-th billing user in the distribution network exceeds the limit within the statistical time.

2.5.2 Line Loss Rate $C_{\mathrm{loss}}$

Reasonable arrangement of the location and capacity of new energy can effectively reduce the line loss (Bai et al., 2015; Kang and Yao, 2017). Therefore, the line loss rate is introduced to quantify the impact of new energy on the operation of the power grid.

$C_{\text{loss}}=\frac{W_{\text{p}}-W_{\text{s}}}{W_{\text{p}}}\times 100\%(11)$

where $W_p$ and $W_s$ respectively represent the power supply and electricity sales of the distribution network during the statistical period.

So far, the comprehensive evaluation index system for distribution network planning under HPNE has been established.

3 Static Comprehensive Evaluation Method of Distribution Network Planning Schemes Based on the “Over-Average Penalty” Entropy Weight Method

3.1 Standardized Processing Method

There are differences in the dimensions and attributes of each index in the comprehensive evaluation index system for distribution network planning under HPNE. The deviation standardization method is used to normalize the raw data, and all index values are converted into benefit-type values in the [0, 1] interval (that is, the larger the value, the better).

Assuming that m distribution network planning schemes are evaluated at a certain stage $S=\left\{S_1,S_2,\dots ,S_m\right\}$, and the evaluation index set of each scheme is set to $C=\left\{C_1,C_2,\dots ,C_{11}\right\}$ (which represent the indicators in order $\left\{C_{\text{F}},C_{\text{D}},C_{\text{N}-1},C_{\text{B}},C_{\text{save}},C_{\text{e}},C_{\text{RS}-3},C_{\text{T}},C_{\text{U}},C_{\text{loss}}\right\}$), then the value of the j-th evaluation index $C_j$ in the i-th distribution network $S_i$ is recorded as $c_{ij}$, and the set $\left\{x_{ij}\right\}$ is obtained after normalization and dimensionless processing.

If the index $C_j$ is a benefit index, the processing formula is:

$x_{ij}=\frac{c_{ij}-\min \left\{c_{ij}\right\}}{\max \left\{c_{ij}\right\}-\min \left\{c_{ij}\right\}}(12)$

If the index $C_j$ is a cost index, the processing formula is:

$x_{ij}=\frac{\max \left\{c_{ij}\right\}-c_{ij}}{\max \left\{c_{ij}\right\}-\min \left\{c_{ij}\right\}}(13)$

3.2 “Over-Average Penalty” Entropy Weight Method

Considering that the hierarchical order relationship method and the AHP both rely on expert knowledge, their results contain subjective experience. So, this paper adopts the entropy weight method based on the entropy of data information for evaluation.

For the evaluation object $x_{ij}$, its characteristic proportion $p_{ij}$ is calculated as:

$p_{ij}=\frac{x_{ij}}{{\displaystyle {\sum }_{i=1}^m{x}_{ij}}}(14)$

The information entropy of the corresponding index X_j is:

$E_j=-\frac{1}{\ln m}\left({\displaystyle \sum _{i=1}^m{p}_{ij}\ln p_{ij}}\right)(15)$

Considering that each index has rich meanings, and the failure of any indicator should be reflected in the final evaluation result, this paper introduces the “over-average penalty.” When weighting the evaluation value of each scheme, the corresponding weight of the element whose value is lower than the average value of the index is reset to zero.

${\alpha }_{ij}=\{\begin{array}{cc}\frac{1-E_j}{11-{\displaystyle \sum E_j}}& x_{ij}\ge \overline{x_j}\\ 0& x_{ij}<\overline{x_j}\end{array}(16)$

where $\overline{x_j}$ represents the average value of the indicator $C_j$. From this, the final static evaluation result of each object can be calculated as:

$y_i={\displaystyle \sum _{j=1}^{11}{\alpha }_{ij}\left|x_{ij}-\overline{x_j}\right|}(17)$

4 Dynamic Evaluation Method of Distribution Network Planning Schemes Based on Dual Excitation Control Lines

This paper introduces a dynamic evaluation method based on dual excitation control lines, which considers the multistage construction process of the distribution network.

4.1 Information Aggregation Algorithm Based on Dual Excitation Control Lines

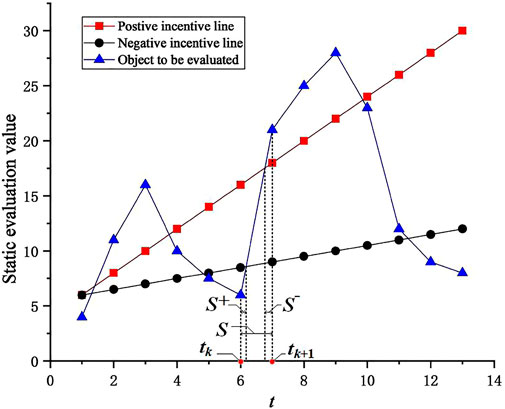
Discrete evaluation points at different stages are transformed into continuous curves within a unit time period and are compared with positive and negative excitation lines. Appropriate rewards and punishments are given to the part above the positive incentive line and the part below the negative incentive line, respectively. The new evaluation value of each time period is obtained after weighted summation based on the positive and negative excitation coefficients. Finally, the new evaluation value is weighted and summed by the time factor to obtain the dynamic comprehensive evaluation value of the evaluation object. Dual excitation lines are usually expressed in linear form:

$y-y_0^{\pm }=k^{\pm }\left(t-t_0\right)(18)$

where$y_0^{\pm }$ represents the ordinate value of the initial point of the positive and negative excitation lines, which is set as the average value of the initial stage evaluation value of each evaluation object for the sake of fairness (Diao et al., 2021; Yi et al., 2007); the slope of the double excitation line is denoted as $k^{\pm }$; $t_0$ is the initial stage of the evaluation; the calculation method of $k^{\pm }$ is as described in Supplementary Appendix A, in which it is necessary to determine the singular value and set the slope offset $V^{+}$ and $V^{-}$ for calculation.

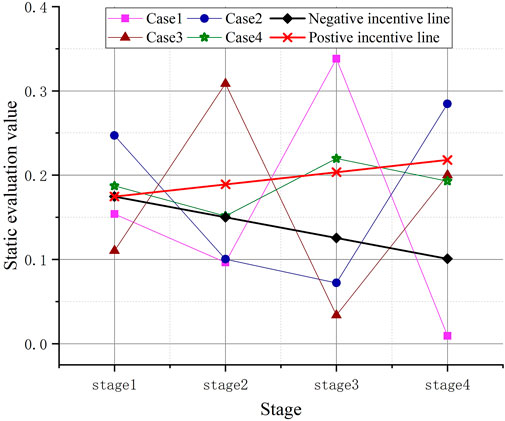
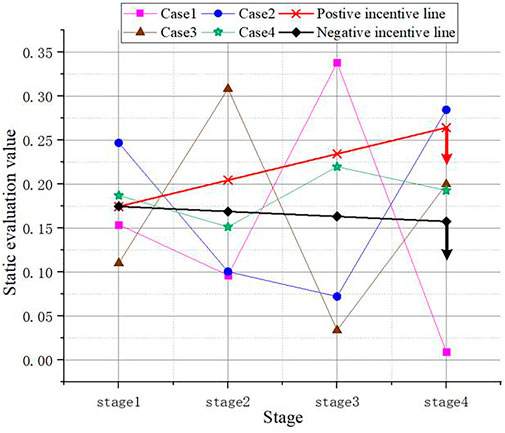
The multistage evaluation value connecting line constitutes the development track of the evaluation object. The area enclosed by it and the horizontal axis reflect the overall condition of the evaluation object in the multi-stage. Therefore, the comprehensive evaluation value can be expressed by an integral. As shown in Figure 1, the area enclosed by the straight line $t_k{y}_{ik}{y}_{i,k+1}{t}_{k+1}$ and the horizontal axis reflects the overall condition of the evaluation object i in $\left[t_k,t_{k+1}\right]$. The underlying dynamic evaluation value is expressed in the form of an integral.

$s_{ik}={\displaystyle {\int }_{t_k}^{t_{k+1}}\left[y_{ik}+\left(t-t_k\right)\frac{\left(y_{i,k+1}-y_{ik}\right)}{\left(t_{k+1}-t_k\right)}\right]dt}(19)$

FIGURE 1

FIGURE 1. Schematic diagram of dual excitation control lines.

Similarly, the comprehensive evaluation value of positive incentive $s_{ik}^{+}$ and the comprehensive evaluation value of negative incentive and $s_{ik}^{-}$ can be obtained, such as the area occupied by the $S^{+}$ and $S^{-}$ parts in Figure 1.

Due to the introduction of positive and negative excitation lines, the dynamic evaluation value includes rewards and punishments for the parts outside the positive and negative excitation lines. Let $s_{ik}^{\pm }$ be the dynamic comprehensive evaluation value of the evaluation object i with excitation in $\left(t_k,t_{k+1}\right)$, then there are:

$s_{ik}^{\pm }={\mu }^{+}{s}_{ik}^{+}+s_{ik}-{\mu }^{-}{s}_{ik}^{-}(20)$

${\mu }^{+}$, ${\mu }^{-}\left({\mu }^{+},{\mu }^{-}>0\right)$ are the positive and negative excitation coefficients, respectively.

Through the weighted synthesis of each time period in the whole process $\left[t_1,t_{T_N}\right]$, the total dynamic comprehensive evaluation value si± of the evaluation object i with excitation is obtained.

$s_i^{\pm }={\displaystyle \sum _{k=1}^{N-1}{h}_k{s}_{ik}^{\pm }}(21)$

where $h_k\left(h_k>0,k=\mathrm{1,2},\dots ,N\right)$ is the time factor, whose setting is adjusted according to the needs of decision makers. For example, to focus on recent developments, $\left\{h_k\right\}$ can be an increasing sequence.

To determine the positive and negative excitation coefficients ${\mu }^{+}$, ${\mu }^{-}$ should follow the following two principles.

1) The principle of conservation of incentives.

For all m evaluation objects, the total number of positive and negative incentives is equal.

${\mu }^{+}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^{N-1}{s}_{ik}^{+}}={\mu }^{-}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^{N-1}{s}_{ik}^{-}}}}(22)$

2) The principle of moderate incentives.

The sum of the positive and negative excitation coefficients is 1.

${\mu }^{+}+{\mu }^{-}=1(23)$

4.2 Multistage Dynamic Comprehensive Evaluation Steps

The basic data of the multistage dynamic comprehensive evaluation should be derived from the static comprehensive evaluation results of the distribution network planning scheme in Section 3. Before the multistage dynamic evaluation of the distribution network planning, the static comprehensive evaluation of each stage needs to be carried out. The evaluation idea of the entire dynamic comprehensive evaluation is shown in the following pseudo code.

Algorithm 1. 1A dynamic evaluation method of distribution network planning schemes based on dual excitation control lines

5 Case Analysis

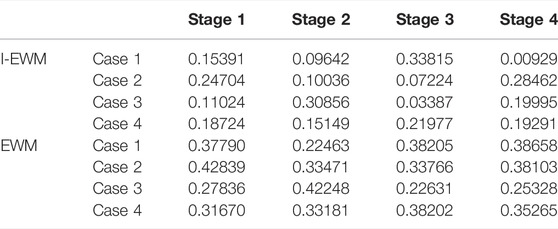
To verify the method proposed in this paper, we conducted an evaluation of four schemes of a 20-year 10 kV distribution network planning bureau in China. Each case is divided into four stages for planning. According to Section 2, the different index values of each case are shown in Supplementary Appendix B. The static evaluation result of I-EWM and EWM is shown in Table 1. The result of I-EWM is smaller than that of EWM, because each case is subject to the over-average penalty.

TABLE 1

TABLE 1. Comprehensive evaluation results by I-EWM and EWM.

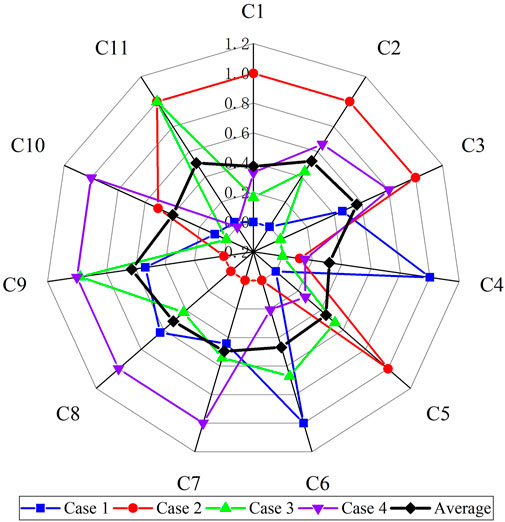
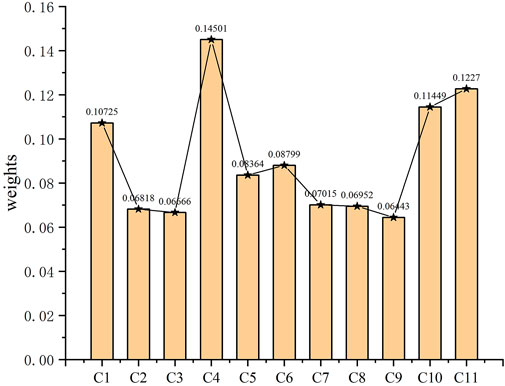
In order to analyze the “over-average penalty”, we took the first stage as an example, and used the radar chart to compare the normalized indicators of each planning scheme with its average value as shown in Figure 2. The weight calculated by the EWM is displayed as shown in Figure 3. From Figure 2, most indicators of case 1 and case 3 are below the average in stage 1. So, they are punished by the average value. In Figure 3, it can be seen that compared to case 4, case 2 has a higher weight for the indicators that are not subject to the mean penalty. Therefore, the final evaluation of case 2 is better than that of case 4.

FIGURE 2

FIGURE 2. Radar chart of indicators compared to the average for each option under planning stage 1.

FIGURE 3

FIGURE 3. Weight value of each index obtained by EWM in planning stage 1.

Further, the multistage dynamic evaluation method is used to realize the comprehensive evaluation of the four cases. $V^{+}$ and $V^{-}$ are set to 0.5. From the result shown in Figure 4, there are no singular cases. The average of static evaluation and the final dynamic evaluation results (DER) are shown in Table 2. Case 4 is suitable for each stage of distribution network development, whose evaluation values are relatively stable in the four stages. So, the result of case 4 is better than other cases as the bold values in Table 2. However, based on the static evaluation results at the end of the planning year, it is easy to conclude that case 2 is superior to other options. This obviously ignores the dynamic evolution of the grid throughout the planning period.

FIGURE 4

FIGURE 4. Dynamic evaluation infographic under $V^{+}=0.5$, $V^{-}=0.5$.

TABLE 2

TABLE 2. Dynamic comprehensive evaluation results of each planning case (${\mathit{V}}^{+}=0.5$, ${\mathit{V}}^{-}=0.5$).

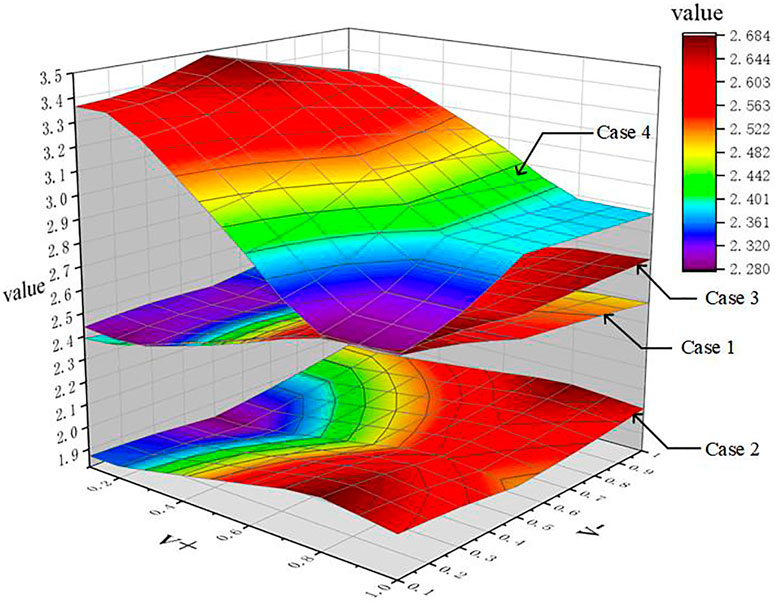
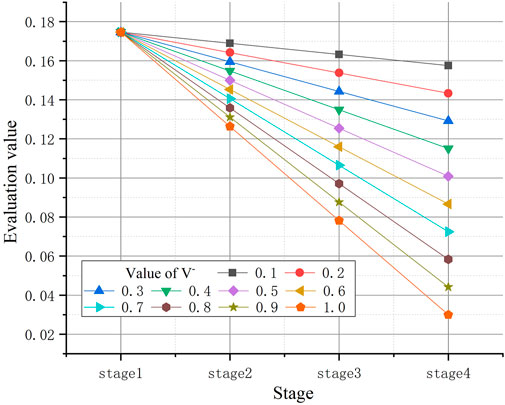
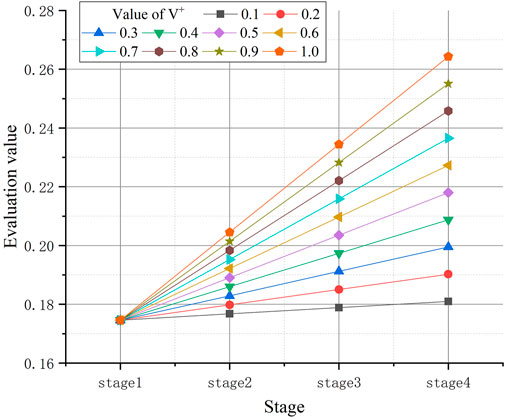
The dynamic evaluation results are closely related to the setting of positive and negative excitation lines. In order to explore the influence of excitation lines, this paper sets the combination of positive and negative slope offsets with an interval of 0.1. The dynamic evaluation surface is shown in Figure 5.

FIGURE 5

FIGURE 5. Dynamic evaluation surfaces of each scheme under different $V^{+},V^{-}$.

From Figure 5, case 4 is always superior to other cases, and case 2 is obviously inferior to other options. Simultaneously, the average value of static evaluation can also reflect the superiority of case 4, but it cannot reflect the disadvantage of case 2 during the overall planning period. In addition, the result of cases 1, 3, and 4 are close when V^+ = 1.0, V^− = 0.1. The positive and negative excitation lines make the evaluation results of the three case reach the same level. So, the results of the change of $V^{-}$ when $V^{+}=1.0$ and the change of $V^{+}$ when $V^{-}=0.1$ are discussed respectively, as shown in Figure 6 and Figure 7.

FIGURE 6

FIGURE 6. The influence of different $V^{-}$ on the dynamic evaluation results of each scheme when $V^{+}=1.0$.

FIGURE 7

FIGURE 7. The influence of different $V^{-}$ on the dynamic evaluation results of each scheme when $V^{+}=1.0$.

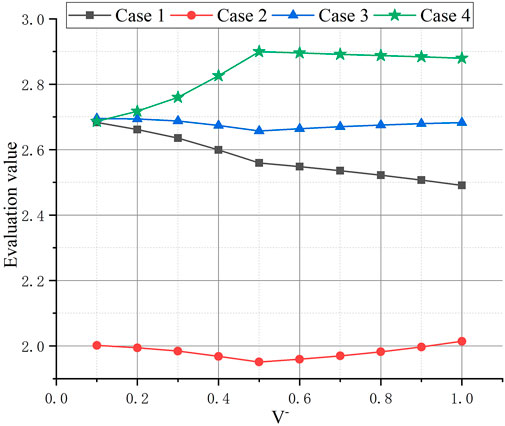
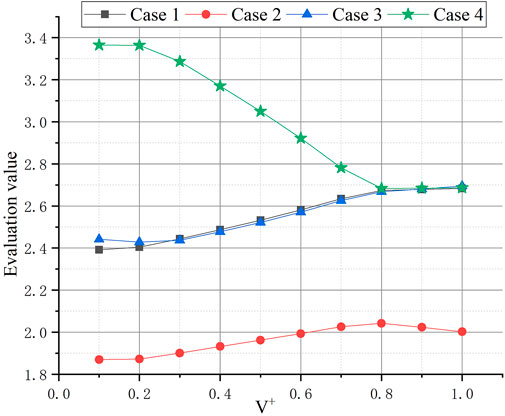
From Figure 6 and Figure 7, the results of each case show different trends with the change of $V^{-}$. According to (19), the basic dynamic evaluation value $s_{ik}$ is fixed. Therefore, the result is related to the positive and negative incentives $s_{ik}^{+}$, $s_{ik}^{+}$ and coefficient ${\mu }^{+}$, ${\mu }^{-}$. When $V^{+}=1.0$, $V^{-}=0.1$, the changes of $V^{-}$ and $V^{+}$ will cause the positive and negative excitation control lines to shift downward, as shown by the red and black arrows in Figure 8. The influence of $V^{-}$ change on the negative excitation control line and the influence of $V^{+}$ change on the positive excitation control line are shown in Figure 9 and Figure 10.

FIGURE 8

FIGURE 8. Dynamic evaluation infographic under $V^{+}=1.0$, $V^{-}=0.1$.

FIGURE 9

FIGURE 9. Influence of different $V^{-}$ on negative excitation line.

FIGURE 10

FIGURE 10. Influence of different $V^{+}$ on negative excitation line.

When $V^{-}$ becomes larger, the negative excitation line will be shifted downward, which will reduce the negative excitation area. Because the negative excitation area decreases while the positive excitation area remains unchanged, the positive excitation coefficient decreases and the negative excitation coefficient increases according to the principle of excitation conservation. For case 4, before $V^{-}$ increases to 0.5, the increase in the evaluation value brought by the reduction of the negative excitation area is greater than the reduction effect brought by the change in the excitation coefficient. However, when $V^{-}$—continues to increase after 0.5, the negative excitation area of case 4 does not change, only the negative influence of the excitation coefficient. Therefore, as shown in Figure 6, with the increase of $V^{-}$, case 4 shows a trend of increasing first and then decreasing. At the same time, since the negative excitation area of case 4 is zero at $V^{-}=0.5$, the rate of reduction of the positive excitation coefficient will slow down with the increase of $V^{-}$. As a result, the change trend of other schemes has also changed after this. Among them, the downward trend of the dynamic evaluation results of case 1 has slowed down, while the downward trend of case 2 and 3 has changed from a downward trend to an upward trend.

From Figure 7, before $V^{+}$ drops to 0.8, case 4 has no positive excitation area, and it is only affected by the increase of the negative excitation coefficient due to the downward movement of the positive excitation line. Therefore, it shows decreasing trend with the decrease of $V^{+}$. After $V^{+}=0.8$, the benefit brought by the positive incentive area is greater than the negative impact brought by the incentive coefficient. The result of case 4 changes to a growth trend. Correspondingly, the decrease of the negative excitation coefficient is more severe at this time, which makes the dynamic evaluation values of other cases decrease more rapidly.

To sum up, the selection of the positive and negative slope offset $V^{+}$, $V^{-}$ will affect the results of the positive and negative excitation control lines, and thus affect the final evaluation results. In general, the smaller the $V^{+}$, the larger the $V^{-}$, the lower the reward threshold, and the higher the penalty threshold. The results at this point are skewed towards incentives. Instead, a punishment mechanism is favored. The selection of this parameter needs to be considered in combination with the needs of the evaluator. When the needs cannot be clearly defined, the more conservative $V^{+}=0.5$ and $V^{-}=0.5$ can be selected for evaluation.

6 Conclusion

In summary, this paper discusses the dynamic comprehensive evaluation of the multistage segment distribution network planning scheme under the characteristics of high permeability new energy. The main contributions are as follows:

1) The evaluation index considering the characteristics of HPNE is summarized and extracted. A comprehensive evaluation index system that is more suitable for the planning of distribution networks under the new power system in the future is proposed.

2) The entropy weight method is improved by introducing the “over-average penalty”. A static comprehensive evaluation method for the distribution network planning scheme under the HPNE is proposed.

3) A dynamic evaluation method based on the multistage development of the dual excitation control line distribution network planning is proposed to realize the dynamic evaluation of the multistage planning scheme of the distribution network.

It needs to be clarified that under the dynamic evaluation method in this paper, the development trend of the static evaluation results and the positive and negative incentives in each stage are fitted to a linear trend, which will make it difficult to accurately describe the distribution network changes in each stage of the planning scheme evaluation. The complex impact of the results and the inability to accurately represent the planner’s reward and punishment need improving, and how to improve them is a direction for further research.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JZ and CG put forward the basic idea of the article and completed the example analysis. TW and YD improved the idea of the article. MX and ZG completed basic data analysis and article polishing.

Funding

The authors declare that this study received funding from the Science and Technology Project of China Southern Power Grid (GDKJXM20212051). The funder had the following involvement with the study: Study design and Interpretation of data.

Conflict of Interestt

Authors ZJ, GC, WT, and DY were employed by the company Guangdong Power Grid Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.958892/full#supplementary-material

References

Bai, J., Xin, S., Liu, J., and Zheng, K. (2015). Roadmap of Realizing the High Penetration Renewable Energy in China. Proc. CSEE 35 (14), 3699–3705. doi:10.13334/j.0258-8013.pcsee.2015.14.026

CrossRef Full Text | Google Scholar

Chen, L., Hu, P., and Wei, J. (2017). A New Evaluation System of Grid-Integrated PV Generation. Power Syst. Prot. Control 45 (2), 105–110. doi:10.7667/PSPC160129

CrossRef Full Text | Google Scholar

Chen, Y., Liu, F., Wei, W., and Mei, S. (2021). Energy Sharing at Demand Side: Concept, Mechanism and Prospect. Automation Electr. Power Syst. 45 (02), 1–11. doi:10.7500/AEPS20200506004

CrossRef Full Text | Google Scholar

Cui, K., Shi, Z., and Zhao, J. (2013). Research on Evaluation System of Power Distribution Network. Electr. Power Constr 34 (02), 18–21. doi:10.3969/j.issn.1000-7229.2013.02.004

CrossRef Full Text | Google Scholar

Diao, P., Hou, F., and Yu, Z. J. (2021). Multi-stage Double Incentive Evaluation Method with Tracking Control Characteristics. J. Syst. Eng. 36 (02), 279–288. in Chinese. doi:10.13383/j.cnki.jse.2021.02.012

CrossRef Full Text | Google Scholar

Ding, M., Guo, Y., and Zhang, J. (2015). Node Yulnerability Assessment for Complex Power Grids Based on Effect Risk Entropy-Weighted Fuzzy Comprehensive Evaluation. Trans. China Electrotech. Soc. 30 (3), 214–223. doi:10.3969/j.issn.1000-6753.2015.03.027

CrossRef Full Text | Google Scholar

Gang, W., Wu, W., and Jia, L. (2007). Comprehensive Judgment for Power System Planning Alternatives Based on SE-DEA Model. Power Syst. Technol. 31 (24), 12–16.

Google Scholar

Hu, J., Wang, K., Xin, A., Han, X., Yang, G., and Xue, Y. (2019). Transactive Energy: an Effective Mechanism for Balancing Electric Energy System. Proc. CSEE 39 (04), 953–966. doi:10.13334/j.0258-8013.pcsee.180537

CrossRef Full Text | Google Scholar

Huang, F., Wang, Q., and Wang, M. (2016). Optimal Allocation of Distributed Generator Based on Carbon Benefits and Time-Sequence Characteristics. Proc. CSUPSA 28 (8), 61–68. doi:10.3969/j.issn.1003-8930.2016.08.011

CrossRef Full Text | Google Scholar

Jia, Q., Zhao, M., and Sun, L. (2018). Planning for Grid-Connection of Distributed PVs Considering the Sequential Feature and Correlation in Active Distribution Network. Proc. CSEE 38 (6), 1719–1728.

Google Scholar

Jiang, S., Yang, W., Deng, J., Zhao, Y., Li, J., Li, P., et al. (2021). “Reliability Index Evaluation System of Distribution Network Based on Maximum Deviation and Application,” in IOP Conference Series: Earth and Environmental Science (IOP Publishing), Bristol, United Kingdom, 645, 012034. doi:10.1088/1755-1315/645/1/012034IOP Conf. Ser. Earth Environ. Sci.1

CrossRef Full Text | Google Scholar

Kang, C., and Yao, L. (2017). Key Scientific Issues and Theoretical Research Framework for Power Systems with High Proportion of Renewable Energy. Automation Electr. Power Syst. 41 (09), 2–11. doi:10.7500/AEPS20170120004

CrossRef Full Text | Google Scholar

Liu, W. X., Zhang, Y. Y., and Li, H. (2013). Reliability-Based Comprehensive Evaluation and Decision-Making for Distribution Network Planning. Appl. Mech. Mater. 336-338, 1103–1108. Trans Tech Publications Ltd. doi:10.4028/www.scientific.net/amm.336-338.1103

CrossRef Full Text | Google Scholar

Ma, L., Wang, Z., Zhu, T., and Lu, Z. (2019). Evaluation Model for Economic Operation of Active Distribution Network Orienting to Energy Internet. J. Electr. Eng. Technol. 14 (3), 1151–1164. doi:10.1007/s42835-019-00164-3

CrossRef Full Text | Google Scholar

NDRC (2015). National Development and Reform Commission, Energy Administration: The 13th Five-Year Plan for Electric Power Development (2016-2020) [EB/OL]. Available at:. https://www.ndrc.gov.cn/xxgk/zcfb/ghwb/201612/P020190905497888172833.pdf. (Accessed April 23, 2022).

Google Scholar

Ou, Y. Q., Cheng, L. F., Wen, J. Z., Qiu, X. Y., and Yu, T. (2014). Research on Reliability Evaluation Methods of Distribution System. Appl. Mech. Mater. 672-674, 1441–1446. Trans Tech Publications Ltd. doi:10.4028/www.scientific.net/amm.672-674.1441

CrossRef Full Text | Google Scholar

Pan, Z., Zhang, X., and Yu, T. (2017). Hierarchical Real-Time Optimized Dispatching for Large-Scale Clusters of Electric Vehicles. Automation Electr. Power Syst. 41 (16), 96–104. in Chinese. doi:10.7500/AEPS20160919012

CrossRef Full Text | Google Scholar

Peng, C., Yu, R., and Sun, H. (2015). Multi-objective DG Planning Based on K-Means Clustering and Multi-Scenario Timing Characteristics Analysis. Electr. Power Autom. Equip. 35 (10), 58–65. in Chinese. doi:10.16081/j.issn.1006-6047.2015.10.009

CrossRef Full Text | Google Scholar

Sheng, S., and Liu, M. (2017). Coordination Planning of Distributed Generation and Energy Storage System in Active Distribution System. Proc. CSUEPSA 29 (2), 71–76. doi:10.3969/j.issn.1003-8930.2017.02.012

CrossRef Full Text | Google Scholar

Su, H., Hu, M., and Liang, Z. (2016). Distributed generation&.Energy Storage Planning Based on Timing Characteristics. Electr. Power Autom. Equip-ment 36 (6), 56–63. doi:10.16081/j.issn.1006-6047.2016.06.009

CrossRef Full Text | Google Scholar

Wang, W., Wu, X., and Zhu, A. (2018). Research and Application of Low-Voltage Intelligent Planning and Comprehensive Treatment Evaluation Technology for Distribution Network Based on Analytic Hierarchy Process. Trans. China Electrotech. Soc. 33 (S2), 569–607. doi:10.19595/j.cnki.1000-6753.tces.180531

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, W., and Li, W. (2019). Optimal Allocation for Distribution Generator Considering Energy Storing and Randomness of Photovoltaic. Electr. Meas. Instrum. 56 (9), 91–96.

Google Scholar

Yan, L., Wang, J., and Wang, S. (2018). Research on Evaluation Indices of New Energy Generation Characteristics and Membership Functions. Power Syst. Prot. Control 46 (8), 43–49. doi:10.7667/PSPC170462

CrossRef Full Text | Google Scholar

Yang, J., Zhang, N., and Wang, Y. (2018). Multi Energy System towards Renewable Energy Accommodation: Review and Prospect. Automation Electr. Power Syst. 42 (4), 11–24.

Google Scholar

Yao, H., Li, Y., and Tan, Y. (2019). Optimal Allocation of Distributed Generations Considering Power Export in Multi-Voltage Level Grid. Power Syst. Prot. Control 47 (19), 54–62. doi:10.19783/j.cnki.pspc.181415

CrossRef Full Text | Google Scholar

Yi, P. T., Guo, Y. J., and Zhang, D. N. (2007). A Multi-phase Information Aggregation Method Based on Double Inspiriting Control Lines. Forecasting 26 (3), 39–43. in Chinese. doi:10.3969/j.issn.1003-5192.2007.03.007

CrossRef Full Text | Google Scholar

Zhang, L., Tang, W., and Zhao, Y. (2010). The Integrated Evaluation of Impact of Distributed Generation on Distribution Network. Power Syst. Prot. Control 38 (21), 132–140. doi:10.7667/j.issn.1674-3415.2010.21.027

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, N., and Du, E. (2021). Review and Countermeasures on Frequency Security Issues of Power Systems with High Shares of Renewables and Power Electronics. Proc. CSEE, 1–23. doi:10.13334/j.0258-8013.pcsee.211425

CrossRef Full Text | Google Scholar

Zou, K., Agalgaonkar, A. P., Muttaqi, K. M., and Perera, S. (2012). Distribution System Planning with Incorporating DG Reactive Capability and System Uncertainties. IEEE Trans. Sustain. Energy 3 (1), 112–123. doi:10.1109/tste.2011.2166281

CrossRef Full Text | Google Scholar