Abstract
In this study, the security secondary control problems are considered for optimal current sharing and voltage restoration of a microgrid distribution network under false data injection (FDI) attacks. To solve these problems, a resilient secondary control method is provided. Specifically, a resilient secondary controller is designed by introducing an adaptive parameter based on the adaptive technique. Then, a theoretical analysis method is provided to show that the designed resilient secondary controller can ensure optimal current sharing and voltage regulation under FDI attacks.
Introduction
In recent years, microgrids (MGs) have received a lot of attention (Wang et al., 2021a; Yao et al., 2022; Wang et al., 2021c; Wang et al., 2020). Specifically, a direct current (DC) MG has been widely investigated owing to it is favorable to the alternating current (AC) MG such as higher reliability and efficiency (Dragicevic et al., 2016; Deng et al., 2022a; Liu et al., 2021). By fully utilizing the inherent DC nature of the distributed generators (DGs) and DC loads, the DC MG avoids multiple conversions between DC/AC and AC/DC to improve the efficiency. According to the current report, the DC MG has been proved to have a 10%–22% improvement in efficiency in comparison to the AC MG. For the DC MG, the control issues mainly include voltage restoration and current sharing. A hierarchical control framework including primary, secondary, and tertiary control is widely adopted to solve such control issues (Ding et al., 2020; Rui et al., 2020; Deng et al., 2021a; Wang et al., 2021b; Lin et al., 2021). The primary control rapidly responds for system disturbance based on the local controller. The secondary control is to eliminate the voltage deviation caused by primary control through certain information exchange. The tertiary control aims to achieve economic dispatch and optimal power flow (Liang et al., 2016). In this study, the secondary control in the islanded DC MG is the main focus.
Recently, distributed secondary control for voltage restoration and current sharing of the DC MG gains more attention due to its flexibility, scalability, and reliability. Compared with centralized control, distributed 26 controls need no central controller and only peer-to-peer information exchange is required (Guo et al., 2020). In recent works, many distributed controllers have been proposed. For example, a distributed finite-time controller is proposed in Guo et al. (2018a) to achieve average voltage regulation and accurate current sharing. Deng et al. (2020) introduced an event-trigger controller to significantly reduce the communication burden. In addition, a fast model predictive control is proposed (Lian et al., 2021a) to regulate the voltage and desired current flows in a DC MG, in which the proposed controller is based on a distributed alternating direction method of the multipliers method.
Although many distributed control methods have been proposed, it should be noted that all the aforementioned distributed secondary control results assume that the communication between networks is reliable. However, network communication between DGs is often sensitive to cyber attacks. Typically, the classical attack modes can be divided into false data injection (FDI) attacks (Yang and Dong, 2019; Yang et al., 2022) and denial-of-service (DoS) attacks (Deng et al., 2021; Ma et al., 2021; Yang et al., 2021; Deng et al., 2022b). FDI attacks are usually launched by attacker injecting some false data, while DoS attacks usually occur by jamming network communication. Recently, some results on FDI attacks for MGs have received considerable attention. The main focuses contain attack detection (Hetel et al., 2017; Sahoo et al., 2020; Habibi et al., 2021a), impact mitigation (Zhang et al., 2021; Habibi et al., 2021b), and resilient controller design (Jiang et al., 2021; Karimi et al., 2021; Cecilia et al., 2022). The detection problem is usually formalized as identifying a change in sets of inferred candidate invariants, which can be solved by the classic analytical method (Hetel et al., 2017; Sahoo et al., 2020) or AI-based algorithm (Habibi et al., 2021a). The attack impact mitigation is another critical concern, which can be achieved by replacing the attacked signal with a reconstructed signal (Zhang et al., 2021) or artificial neural network–based method (Habibi et al., 2021b). In addition, resilient controller design is another effective method to against FDI attacks. The existing methods include observer-based methodology (Cecilia et al., 2022), high-order differentiator–based distributed controller (Jiang et al., 2021), and adaptive controller (Karimi et al., 2021).
Note that in Habibi et al. (2021b), Jiang et al. (2021), Karimi et al. (2021), and Cecilia et al. (2022), current sharing ratios are only set as the inverse of droop gains. However, the optimal current sharing ratios may change online with the change in power generation costs and the updated user demands. Thus, how to develop an optimal current sharing method with the function of resilient the influence of FDI attacks is an interesting and open work. In proposing this method, the following challenges are encountered: 1) the existing secondary control methods for current sharing and voltage regulation are available under the condition that the secondary control information is reliable. However, under the influence of FDI attacks, the accurate information of the secondary control cannot be achieved and thus leading to the voltage deviating from the normal value and the current sharing can be also influenced. Therefore, the first challenge is how to develop a resilient control method to correct the voltage deviation and current sharing derivation caused by FDI attacks. 2) It is difficult to build a linearization model of MG and the closed-loop model of the MG becomes more complex under the influence of FDI attacks. Therefore, another challenge caused by the considered problem is how to propose a stability analysis method for the nonlinear MG under FDI attacks.
To solve this issue, a resilient cooperative control method is proposed to achieve the optimal current sharing and voltage regulation problem for MG based distribution network in the presence of FDI attacks. In this study, the main contributions can be summarized as follows.
1 Based on the designed resilient secondary control method, the DC MG both achieve optimal current sharing and restore the bus voltage simultaneously even under the influence of FDI attacks. In addition, with the help of the designed adaptive parameter, the effects of FDI attacks on MG can be eliminated, which makes the method resilient to FDI attacks. Therefore, both the resilient and the system performance can be improved.
2 Based on the Lyapunov theory, a stability analysis method is established for the overall closed-loop MG system to show that the designed resilient secondary controller can resist the influence of FDI attacks theoretically. In addition, a guideline for the controller design is introduced to facilitate implementation for the designer.
Problem formulation
In this section, the main contents will be elaborated as follows: 1) modeling of the DC MG; 2) introducing the FDI attacks; and 3) presenting the control objectives.
DC MG system
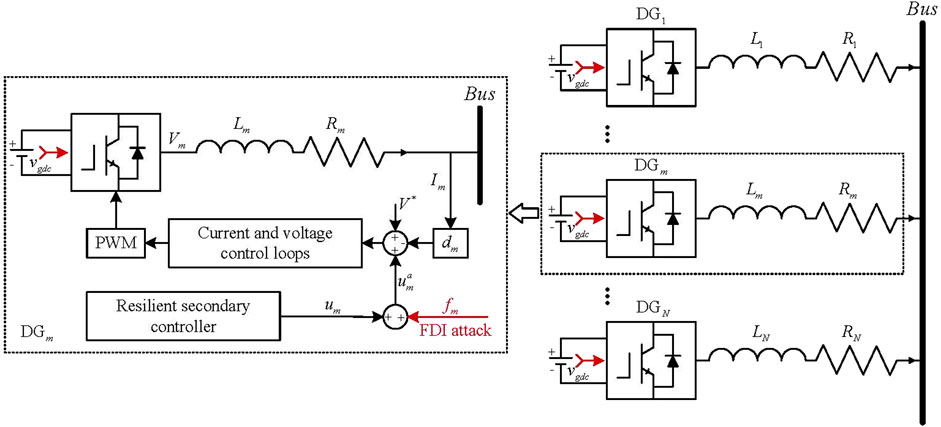
As shown in Figure 1, current and voltage control loops and droop control are the primary control of each DG in the physical layer. As known, the dynamic responses of voltage and current control are much faster than that of the droop control. Therefore, the droop control can decisively indicate the dynamics of the primary control. Based on this analysis, the model of the DG with primary control is given bywhere Vm represents the voltage reference of the mth DG, V∗ is the nominal DC voltage, dm indicates the droop gain, and Im represents the current output. Since the voltage and current control loops have clever designs, the voltage output of the converter can track Vm rapidly. According to the aforementioned statement, Vm can be written as follows:
FIGURE 1
DC MG model under FDI attacks.
According to the relationship between DC bus voltage Vb and can be expressed mathematically as follows:where Rm denotes the resistance of the line between common bus and DG. Based on Wang et al. (2021a) (3), the relationship between current Im and the DC bus voltage Vb immediately is known:
If the values of the line resistance Rmm = 1,2,...,N are much less than dm, that is, Rm ≪ dm, the following equation holds
If the effects of line resistance Rm in (]) is ignored, then the current sharing ratio and the droop gain dm are inversely proportional. Nevertheless, using droop control to solve the current sharing problem also exists.
Some drawbacks, including: 1) line resistance Rmm = 1,2,...,N affect the current sharing accuracy inevitably; 2) larger droop gains dmm = 1,2,...,N may improve the current sharing accuracy, while a larger deviation of DC bus voltage Vb may be generated; 3) with the change in operational condition of DC MG, the optimal current sharing ratio obtained from the tertiary layer will be different, and thus it does not always hold the expected relationship Figure 1.
False data injection attacks in cyber layer
In some situation, the attackers may launch FDI attacks on the control input, which will make the voltage deviates from the normal value and the current sharing can be also influenced. Under FDI attacks, the input um may be regulated to , that is,where fm is an unknown and time-varying attack signal injected by attackers. In this study, the FDI attacks may occur in any control input um, and the constrain of FDI attacks is that the attack signal fm is bounded, that is, the following assumption is satisfied.
Assumption 1It is assumed that is bounded, that is, with being an unknown constant for m = 1,...,N.
Control objectives
From (Eq. 4), it is obvious that, since Im ̸ = 0 when the system tends to stable, there exists error between bus voltage Vb(t) and the nominal value V∗. Then, a secondary controller um will add into the mth DG, which can be summarized as follows,
According to the relationship among
Im,
Ij,
dj,and
dmin (
Eq. 5), it is known that the droop gains
dmfor
m= 1
,2
,...,Nshould be selected large enough to ignore the influence of line resistance
Rm. Unfortunately, larger droop gains
dmwill lead to larger deviation of bus voltage of (
Eq. 4). In addition, optimal current sharing ratios obtained from the tertiary layer will change with the change in the external environment of the MG, which may lead to the failure of the inversely proportional. Thus, the objectives of this study can be summarized as follows;
1 Voltage restoration:
2 Current sharing:
where the piecewise constant function
represents the optimal current sharing ratio obtained from the tertiary layer and
represents the current value at the steady state.
Secondary current sharing and voltage regulation control
In this section, a resilient secondary current sharing and voltage restoration controller will be designed and then provide a stability analysis method based on the Lyapunov stability theory.
Resilient controller design
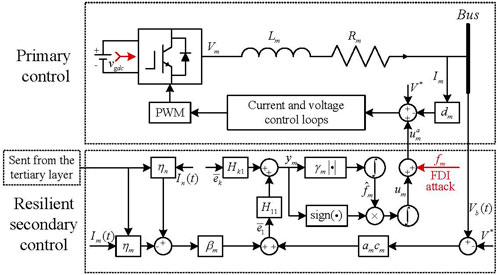
To achieve control objectives (Ding et al., 2020; Rui et al., 2020), the resilient controller is designed as follows:where sign (ym) denotes the sign function of ym, which satisfies
The symbol ym is denoted by with Hkm being the element in row k and column i of the matrix H (the definition of matrix H and variable e¯k will be given later). The term fˆm(t) is an adaptive parameter and is updated by
where the parameter γm is chosen as an arbitrary positive constant. To show the controller more intuitively, the secondary current sharing and voltage restoration controller will be presented in Figure 2.
FIGURE 2
Framework of the resilient secondary controller.
Remark 1Different from the existing results on secondary control (Guo et al., 2018b; Lian et al., 2021b), a resilient secondary control method is proposed in this study. By introducing an adaptive parameter fˆm in the resilient controller um, the advantage of the designed controller is that the FDI attacks can be resisted, that is, the designed controller can ensure that optimal current sharing and voltage regulation can be achieved even under the influence of FDI attacks. The specific effect will be shown in the simulation section.
Stability analysis
Before giving the main result, the model of the DC MG will be firstly derived. Define eV (t) = V∗ − Vb(t). According to Liu et al. (2021), it has
where u(t) = col{um(t)} and I(t) = col{Im(t)} with col{um(t)} representing a column vector composed of elements u1,u2,...,uN. In addition, d = diag{dm} and R = diag{Rm} with diag{dm} representing a diagonal matrix with diagonal elements d1,d2,...,dN.
As discussed in Guo et al. (2020), it assumes that the resistance RL integrates the loads and the resistances between lines. Then, it has
Substituting Guo et al. (2020) into Liang et al. (2016), one getswhere the matrix is invertible, as discussed in Guo et al. (2018a). Based on Liang et al. (2016) and Guo et al. (2018a), it has
Define e¯ = αceV (t)1N − βLηI(t) with α = diag{αm}, c = diag{cm}, β = diag{βm}, and η = diag{ηm}. Then, it haswhere is a Hurwitz matrix (Guo et al., 2020).
Consider the DC MG under FDI attacks satisfying Assumption 1. If the resilient secondary controller um in Deng et al. (2021a) with adaptive parameter fˆm updated by Lin et al. (2021) is used and arbitrary positive constants γm for m = 1,2,...,N are chosen and then the resilient optimal current sharing and voltage regulation problems can be solved, that is, the control objectives Ding et al. (2020) and Rui et al. (2020) can be achieved simultaneously.
Proof: Define . The derivative of V along (Deng et al., 2020) yieldswhere
By using the similar method, it has
Substituting Yang et al. (2022) and Yang and Dong (2019) into Lian et al. (2021a), it has
Define . Then, Deng et al. (2022b) can be rewritten as follows:
According to Assumption 1, it has
Substituting (Eq. 14) into (Eq. 13), one gets
To achieve the main result, the following Lyapunov function is introduced:
The derivative of W(t) is
Substituting Ma et al. (2021) into Sahoo et al. (2020), one gets
Substituting Lin et al. (2021) into Habibi et al. (2021a), one gets
By applying the LaSalle–Yoshizawa theorem, it is easy to show that
According to Deng et al. (2020) and Habibi et al. (2021b), it yields
Thus, it has
By multiplying on each side of Cecilia et al. (2022), one has
If βm (m = 1,2,...,N) such that bm = bn,∀m,n = 1,...,N, then
According to , then it is obtained that
Thus, it has shown that bus voltage regulation and optimal current sharing can be achieved by using the designed resilient secondary controller (Deng et al., 2021a) with adaptive updated law (Lin et al., 2021) even under the influence of FDI attacks.
Remark 2In Theorem 1, a new stability analysis method is provided to show that the resilient secondary controller (Deng et al., 2021a) can resist FDI attacks theoretically. In particular, the term is introduced in the Lyapunov function W(t). Then, the control objectives of voltage regulation and optimal current sharing can be achieved.
Simulation results
To verify the advantage of our designed resilient secondary controller, it is first shown that the developed method is effective to achieve the optimal current sharing and voltage regulation. Then, it is further to prove the effectiveness of our method by comparing with the existing secondary method in Lian et al. (2021b). In the simulation, the detailed DG parameters are given in Table 1 and the Laplacian matrix L is chosen as follows:
TABLE 1
| DGs:1, 2, & 3 | ||||
|---|---|---|---|---|
| DG | VDC | 48 V | fs | 20 kHz |
| Droop gain | d1 = 8, d2 = 4, d3 = 2 | |||
| Proposed controller | α1 = α2 = α3 = 1 | |||
| β1 = β2 = β3 = 0.5 | ||||
| γ1 = γ2 = γ3 = 3 | ||||
| Load | R | |||
| Nominal voltage | V∗ = 48 V | |||
Parameters on controllers and the MG system.
Resilient optimal current sharing and voltage regulation
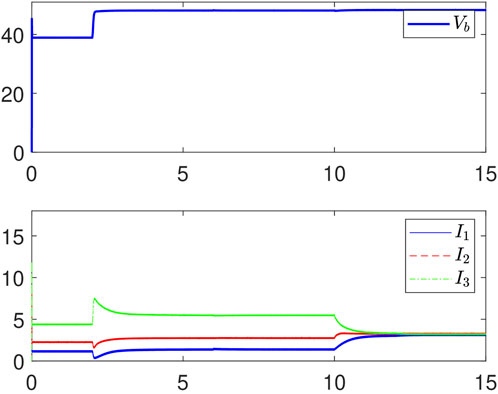
In this subsection, the verification of our resilient secondary controller (
Deng et al., 2021a) against FDI attacks is shown. In this case, there is no attacker to destroy the system, that is,
fm≡ 0 for
m= 1
,2
,...,N.
1) Consider 0–10 s, the experimental results are shown in Figure 3 by using the resilient secondary controller (Deng et al., 2021a). From Figure 3, it is shown that the proposed controller ensures that the bus voltage 156 can be regulated to V∗ after introducing the secondary controller (Deng et al., 2021a). In addition, the ratios of Im for m = 1,2,3 are maintained as I1:I2:I3 ≈ 1:2:4 after introducing the secondary controller (Deng et al., 2021a).
2) Consider 10–15 s, an extra load RL = 5 Ω is added to the MG. According to the solution at the tertiary layer, the optimal sharing ratio is changed to I1:I2:I3 = 1:1:1 when the load is changed. Thus, the parameter ηi (i = 1, 2, 3) of the resilient secondary controller is adjusted to η1:η2:η3 = 1:1:1. Then, the bus voltage will be regulated to V∗ by using the automatic adjustment function of the resilient secondary controller (Deng et al., 2021a). In addition, the current sharing ratio will also alter to I1:I2:I3 ≈ 1:1:1 through our controller.
FIGURE 3
Trajectories of the voltage and the current with load added in.
Comparison studies
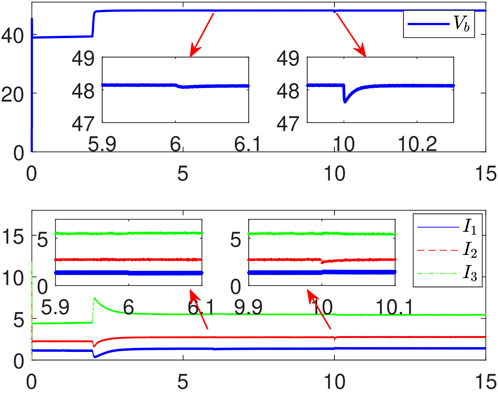
In this case, the designed resilient secondary method and the secondary control method in Lian et al. (2021b) are both applied to solve the optimal current and voltage regulation for DC MG under FDI attacks. Specifically, the secondary controllers are added into the DC MC at t = 2 s. The FDI attack f1 = sin (0.1t) is added into the 1 st DG at t = 6 s and the FDI attacks f2 = 2sin (0.1t) and f3 = 3sin (0.1t) for DGs 2 and 3 are added at t = 10 s. Under our resilient secondary controller and the secondary controller in Lian et al. (2021b), the simulation results are shown in Figures 4,5.
1) Consider 0–6 s, it can be seen that both methods can ensure that the bus voltage be regulated to V∗ and the ratios of Im for m = 1,2,3 are maintained as I1:I2:I3 ≈ 1:2:4 after introducing the secondary controller at t = 2 s.
2) Consider 6–10 s, the FDI attack is added into the 1 st DG at this interval. Our method can ensure that the bus voltage regulates to V∗ by using the resilient secondary controller (Deng et al., 2021a). In addition, the current 176 sharing ratio will also retain to I1:I2:I3 ≈ 1:2 4 through our controller. However, the bus voltage will deviate to V∗ by using the resilient secondary controller (Deng et al., 2021a), and the current sharing ratio will fluctuate with the addition of attacks under the secondary controller (Lian et al., 2021b).
3) Consider 10–15 s, the FDI attacks are added into all DG attacks at this interval. Our method can still ensure that voltage regulates to V∗ and the current sharing ratio will also hold. However, the method in Deng et al. (2021a) does not guarantee these two objectives. Thus, it has shown that the developed method is effective to resist FDI attacks.
FIGURE 4
Trajectories of the voltage and the current under our method.
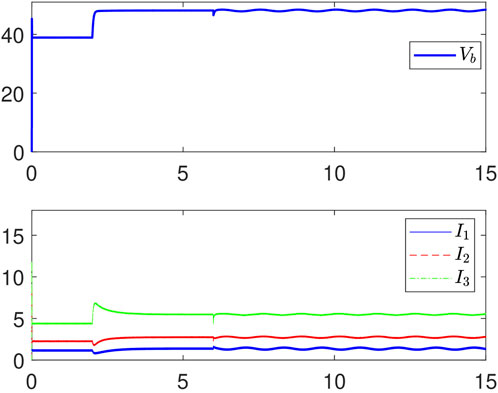
FIGURE 5
Trajectories of the voltage and the current under the method in Lian et al. (2021b).
Conclusion
In this article, it has solved the security secondary control problems for optimal current sharing and voltage restoration of an islanded DC MG under FDI attacks. To solve these problems, a resilient secondary control method has been provided. First, a resilient secondary controller has been designed by introducing an adaptive parameter based on the adaptive technique. Then, a theoretical analysis method has been provided to show that the designed resilient secondary controller can ensure optimal current sharing and voltage regulation under FDI attacks. Finally, a simulation example is given by using the MATLAB testing platform to verify the developed resilient secondary control method. Now, this result cannot be extended to the directed network case due to that the Laplacian matrix is no longer a symmetric matrix under directed network case. Therefore, it is my further work to extend this result to the directed network case.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of interest
Author BW was employed by the company NARI Technology Nanjing Control System Co., Ltd.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Cecilia A. Sahoo S. Dragiceviˇ c T. Costa-Castell´ o R. Blaabjerg F. (2022). On addressing the security and´ stability issues due to false data injection attacks in DC microgrids—an adaptive observer approach. IEEE Trans. Power Electron.37 (3), 2801–2814. 10.1109/tpel.2021.3114990
2
Deng C. Jin X. -Z. Che W. -W. Wang H. (2021). Learning-based distributed resilient fault-tolerant control method for heterogeneous MASs under unknown leader dynamic. IEEE Trans. Neural Netw. Learn. Syst., 1–10. 10.1109/tnnls.2021.3070869
3
Deng C. Wang Y. Wen C. Xu Y. Lin P. (2021). Distributed resilient control for energy storage systems in cyber–physical microgrids. IEEE Trans. Ind. Inf.17 (2), 1331–1341. 10.1109/tii.2020.2981549
4
Deng C. Er M. J. Yang G. Wang N. (2020). Event-triggered consensus of linear multiagent systems with time-varying communication delays. IEEE Trans. Cybern.50 (7), 2916–2925. 10.1109/tcyb.2019.2922740
5
Deng C. Guo F. Wen C. Yue D. Wang Y. (2022). Distributed resilient secondary control for DC microgrids against heterogeneous communication delays and DoS attacks. IEEE Trans. Ind. Electron.69, 11560–11568. to be published. 10.1109/TIE.2021.3120492
6
Deng C. Zhang D. Feng G. (2022). Resilient practical cooperative output regulation for MASs with unknown switching exosystem dynamics under DoS attacks. Automatica, 110172. 10.1016/j.automatica.2022.110172
7
Dragicevic T. Lu X. Vasquez J. C. Guerrero J. M. (2016). DC microgrids—Part I: A review of control´ strategies and stabilization techniques. IEEE Trans. Power Electron.31 (7), 4876–4891. 10.1109/tpel.2015.2478859
8
Ding L. Han Q. Ning B. Yue D. (2020). Distributed resilient finite-time secondary control for heterogeneous battery energy storage systems under denial-of-service attacks. IEEE Trans. Ind. Inf.16 (7), 4909–4919. 10.1109/tii.2019.2955739
9
Guo F. Wang L. Wen C. Zhang D. Xu Q. (2020). Distributed voltage restoration and current sharing control in islanded DC microgrid systems without continuous communication. IEEE Trans. Ind. Electron.67 (4), 3043–3053. 10.1109/tie.2019.2907507
10
Guo F. Xu Q. Wen C. Wang L. Wang P. (2018). Distributed secondary control for power allocation and voltage restoration in islanded DC microgrids. IEEE Trans. Sustain. Energy9 (4), 1857–1869. 10.1109/tste.2018.2816944
11
Guo F. Xu Q. Wen C. Wang L. Wang P. (2018). Distributed secondary control for power allocation and voltage restoration in islanded DC microgrids. IEEE Trans. Sustain. Energy9 (4), 1857–1869. 10.1109/tste.2018.2816944
12
Habibi M. R. Baghaee H. R. Dragiceviˇ c T. Blaabjerg F. (2021). Detection of false data injection´ cyber-attacks in DC microgrids based on recurrent neural networks. IEEE J. Emerg. Sel. Top. Power Electron.9 (5), 5294–5310. 10.1109/jestpe.2020.2968243
13
Habibi M. R. Baghaee H. R. Dragiceviˇ c T. Blaabjerg F. (2021). False data injection cyber-attacks´ mitigation in parallel DC/DC converters based on artificial neural networks. IEEE Trans. Circuits Syst. Ii.68 (2), 717–721. 10.1109/tcsii.2020.3011324
14
Hetel L. Fiter C. Omran H. Seuret A. Fridman E. Richard J. P. et al (2017). Recent developments on the stability of systems with aperiodic sampling: An overview. Automatica76, 309–335. 10.1016/j.automatica.2016.10.023
15
Jiang Y. Yang Y. Tan S. -C. Hui S. Y. R. (2021). A high-order differentiator based distributed secondary control for DC microgrids against false data injection attacks. IEEE Trans. Smart Grid, 1. to be published. 10.1109/TSG.2021.3135904
16
Karimi A. Ahmadi A. Shahbazi Z. Shafiee Q. Bevrani H. (2021). in A resilient control method against false data injection attack in DC microgrids,” 2021 7th International Conference on Control (Tabriz, Iran: Instrumentation and Automation (ICCIA), 1–6.
17
Liu X. K. Wen C. Xu Q. Wang Y. W. (2021). Resilient control and analysis for dc microgrid system under DoS and impulsive FDI attacks. IEEE Trans. Smart Grid12 (5), 3742–3754. 10.1109/tsg.2021.3072218
18
Lian Z. Guo F. Wen C. Deng C. Lin P. (2021). Distributed resilient optimal current sharing control for an islanded DC microgrid under doS attacks. IEEE Trans. Smart Grid12 (5), 4494–4505. 10.1109/tsg.2021.3084348
19
Lin P. Deng C. Yang Y. Lee C. H. T. Tay W. P. (2021). Resilience-oriented control for cyber-physical hybrid energy storage systems using a semi-consensus scheme: Design and practice. IEEE Trans. Ind. Electron., 1. to be published. 10.1109/TIE.2021.3102397
20
Liang G. Weller S. R. Zhao J. Luo F. Dong Z. (2016). The 2015 Ukraine blackout: Implications for false data injection attacks. IEEE Trans. Power Syst.32 (4), 3317–3318, Nov. 10.1109/tpwrs.2016.2631891
21
Lian Z. Deng C. Wen C. Guo F. Lin P. Jiang W. (2021). Distributed event-triggered control for frequency restoration and active power allocation in microgrids with varying communication time delays. IEEE Trans. Ind. Electron.68 (9), 8367–8378. 10.1109/tie.2020.3016272
22
Ma Y. -S. Che W. -W. Deng C. Wu Z. -G. (2021). Distributed model-free adaptive control for learning nonlinear MASs under DoS attacks. IEEE Trans. Neural Netw. Learn. Syst., 1–10. 10.1109/TNNLS.2021.3104978
23
Rui W. Qiuye S. Pinjia Z. Yonghao G. Dehao Q. Peng W. (2020). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Trans. Energy Convers.35 (3), 1585–1595. 10.1109/tec.2020.2980033
24
Sahoo S. Peng J. C. Devakumar A. Mishra S. Dragiceviˇ c T. (2020). On detection of false data in´ cooperative DC microgrids—a discordant element approach. IEEE Trans. Ind. Electron.67 (8), 6562–6571. 10.1109/tie.2019.2938497
25
Wang Y. Mondal S. Satpathi K. Xu Y. Dasgupta S. Gupta A. (2021). Multi-Agent distributed power management of DC shipboard power systems for optimal fuel efficiency. IEEE Trans. Transp. Electrific.7, 3050–3061. 10.1109/TTE.2021.3086303
26
Wang R. Sun Q. Sun C. Zhang H. Gui Y. Wang P. (2021). Vehicle-vehicle energy interaction converter of electric vehicles: A disturbance observer based sliding mode control algorithm. IEEE Trans. Veh. Technol.70 (10), 9910–9921. 10.1109/tvt.2021.3105433
27
Wang R. Sun Q. Han J. Zhou J. Hu W. Zhang H. et al (2021c). Energy-management strategy of battery energy storage systems in DC microgrids: A distributed dynamic event-triggered H∞ consensus control. IEEE Trans. Syst. Man, Cybern. Syst. 10.1109/TSMC.2021.3129184
28
Wang Y. Deng C. Xu Y. Dai J. (2020), Unified real power sharing of generator and storage in islanded microgrid via distributed dynamic event-triggered control. IEEE Trans. Power Syst.36 (3), 1713–1724. 10.1109/TPWRS.2020.3039530
29
Yao W. Wang Y. Xu Y. Deng C. Wu Q. (2022). Distributed weight-average-prediction control and stability analysis for an islanded microgrid with communication time delay. IEEE Trans. Power Syst.37 (1), 330–342. 10.1109/tpwrs.2021.3092717
30
Yang Y. Qian Y. Yue W. (2022). A secure dynamic event-triggered mechanism for resilient control of multi-agent systems under sensor and actuator attacks. IEEE Trans. Circuits Syst. I.69 (3), 1360–1371. 10.1109/tcsi.2021.3132153
31
Yang Y. Dong Y. (2019). Observer-based decentralized adaptive NNs fault-tolerant control of a class of large-scale uncertain nonlinear systems with actuator failures. IEEE Trans. Syst. Man. Cybern. Syst.49 (3), 528–542. 10.1109/tsmc.2017.2744676
32
Yang Yang Li Yanfei Yue Dong Tian Yu-Chu Ding Xiaohua (2021). Distributed secure consensus control with event-triggering for multi-agent systems under DoS attacks. IEEE Trans. Cybern.51 (6), 2916–2928. 10.1109/tcyb.2020.2979342
33
Zhang J. Sahoo S. Peng J. C. -H. Blaabjerg F. (2021). Mitigating concurrent false data injection attacks in cooperative DC microgrids. IEEE Trans. Power Electron.36 (8), 9637–9647. 10.1109/tpel.2021.3055215
Summary
Keywords
resilient control, voltage regulation, current sharing, adaptive control, FDI attacks
Citation
Wang B (2022) Resilient cooperative control for optimal current sharing and voltage regulation of microgrid-based distribution network under FDI attacks. Front. Energy Res. 10:956672. doi: 10.3389/fenrg.2022.956672
Received
30 May 2022
Accepted
07 July 2022
Published
12 August 2022
Volume
10 - 2022
Edited by
Qiuye Sun, Northeastern University, China
Reviewed by
Yao Weitao, Nanyang Technological University, Singapore
Xiaokang Liu, Huazhong University of Science and Technology, China
Yu Wang, Imperial College London, United Kingdom
Updates
Copyright
© 2022 Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Biheng Wang, bihengwang2022@163.com
This article was submitted to Smart Grids, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.