Optimal Coordinated Frequency Regulation of Renewable Energy Systems via an Equilibrium Optimizer

With the urgency of environmental protection, wind power and photovoltaic (PV) projects are continued to be implemented, and the proportion of renewable energy in the power grid will be higher and higher. Therefore, wind power and PV also began to participate in the regional power grid frequency regulation (FR) and have gradually replaced the role of thermal power units in the power grid. To study the characteristics of renewable energy in frequency modulation, an automatic generation control (AGC) model of wind power and photovoltaic participating in the power grid FR is established. At the same time, an equilibrium optimization is proposed to allocate the total power in real-time so as to improve the FR performance by quickly obtaining the optimal power distribution scheme. The simulation results of the proposed model show that the proposed method is feasible. At the same time, the proposed method is compared with the genetic algorithm (GA), which proves the superiority of the proposed method.

Introduction

At present, global energy demand is growing steadily. To achieve environmental protection and sustainable development, a wave of renewable energy has been set off around the world. The grid connection of a large number of renewable energy sources brings great operating pressure to the stable operation of the power grid (Zhang et al., 2021; Zhang et al., 2022; Zhang et al., 2020a; Huo and Xu, 2022; Li et al., 2022). At the same time, the International Energy Agency’s (IEA) electricity market report, released in January, said strong economic growth in 2021 has led to a 6% increase in global electricity demand, resulting in tight supplies of natural gas and coal, and record-high carbon dioxide emissions from the global power sector. The results of the report attracted wide attention from all countries, and at the same time, they further encouraged countries to speed up the construction of renewable energy sources. Moreover, according to recent data from the IEA, renewable energy construction has not been significantly affected by the pandemic, and global renewable energy generation continues to grow rapidly (Electricity Market Report, 2022). Therefore, to adapt to the trend of social development, it is essential to conduct relevant research on the optimization of the frequency regulation (FR) of renewable energy. This will help improve the power supply reliability and high-quality power supply of the power system and, meanwhile, reduce the phenomenon of abandoning light and wind on the generating side, thus reducing the FR pressure of traditional hydro/thermal power plants (Wu et al., 2021).

FR technology is critical to the power grid. Its purpose is to realize the output adjustment of each generator set in the control area through the controller when the power grid is disturbed by load changes so as to ensure that the frequency of the power system is always maintained in a safe range, which is the inevitable premise for the power system to achieve quality and quantity assurance and reliable power supply (Chen et al., 2020; Zhang et al., 2019). The traditional power system FR task is mainly undertaken by thermal power and hydropower units, whose inertia of regulation is too large to quickly respond to the power input command. Meanwhile, the response time of renewable energy is faster. Therefore, from the point of view of the need and necessity of social development, the participation of renewable energy in the FR of a power grid is the general trend and the necessity of social development. Renewable energy can participate in the FR of the power grid by reserving part of the spare capacity, to improve the FR response speed of the power grid.

At present, most of the research on the FR technology of electric systems focuses on the design and improvement of the controller (Li et al., 2020; Zhu et al., 2022; Arya, 2018). To deal with the automatic generation control (AGC) problem of a multi-area power system, a fuzzy integer order PID controller is proposed by Arya (2018a). Liu and Liu (2020) used adaptive proportional integral differential (PID) control to improve the control accuracy and response speed of the AGC system of PV stations. In the study by Hasan et al. (2022), a robust self-tuned AGC controller is proposed to effectively control the load fluctuation and wind fluctuation of wind power. In the study by Arya (2018), a fuzzy PID controller is proposed to deal with the problem of the AGC system. At the same time, sliding mode control (Mohanty, 2015), fuzzy logic control, and other controllers have been studied and applied to FR so as to improve the performance of FR of the power grid (Yousef, 2015). In addition, the booming development of intelligent optimization algorithms has brought more choices to controller parameter settings (Çelik, 2020; Nayak et al., 2022). In the study by Shanmugasundaram (2017), an artificial bee colony algorithm was used to set the controller parameters of the PID controller so as to improve the reliability of the system. In the study by Lal et al. (2016), the gray wolf optimization (GWO) algorithm was used to obtain the optimal gain of the PID controller for the interconnected water-fire power system so as to improve the overall performance of the system. In the study by Gupta and Kumar (2018), the AGC of a multi-source power system with an energy storage system was studied, and the controller parameters were set by the particle swarm optimization (PSO) algorithm. In addition, it also contains the genetic algorithm (GA) (Al-Hamouz et al., 2011; Hakimuddin et al., 2020) and differential evolution (DE) algorithm (Gorripotu et al., 2016; Madasu et al., 2018; Xi et al., 2022). However, most of the aforementioned kinds of literature pay little attention to the synergistic control between renewable energy and conventional FR units. In the study by Cui et al. (2019), the objective function including wind power, photovoltaic, and other resource income is constructed so as to realize the collaborative control between wind power, photovoltaic, and other FR resources. Zhang et al. (2017) studied the coordinated control of wind power, photovoltaic, and traditional FR resources. However, it is difficult to achieve accurate control of the power grid frequency due to simple modeling.

In general, AGC is a complex and difficult problem. In practical engineering applications, power distribution is usually carried out according to the adjustable capacity rather than optimization, which cannot achieve the best control effect. In this study, the equilibrium optimizer (EO) is used to optimize the FR instruction so as to achieve the optimal cooperative control of AGC. Meanwhile, to prove the feasibility and superiority of the EO, we compared EO with the proportion method (PROP) and genetic algorithm (GA), thus proving its superiority.

In the overall structure of this article, in the second section, we introduced the FR model adopted in detail, which has been recognized and adopted by the majority of scholars; in the third section, the EO adopted is introduced in detail, and its optimization process is given. The fourth section gives the initial simulation data and simulation results and analyzes the simulation results in brief. In the end, this article gives the conclusion and expatiates on the main contributions of this study.

Model

Control Framework

In this study, a two-zone load frequency control (LFC) model based on extension is used to verify (Zhang et al., 2020b). The model framework is shown in Figure 1. The framework has two areas; each control area includes the proportional-integral (PI) controller and power optimization distribution two links. The frequency deviation and power deviation of the link line are converted into regional control deviation by the PI controller, which is taken as the input. In addition, the total real-time regulated power (△P) of the whole area is used as the output. Then, △P is allocated to each AGC FR unit using a power allocation algorithm. Compared with the AGC FR system dominated by hydropower units and thermal power units, this study will make full use of the regulation potential of renewable energy with a fast response speed. Meanwhile, wind and light abandonment and other phenomena are reduced so as to improve the FR effect of the AGC FR system.

FIGURE 1

FIGURE 1. AGC multi-source coordinated control model.

AGC Unit Dynamic Response Model

An appropriate dynamic model is very important to accurately describe the power response process of the unit after receiving the power regulation instruction. According to different types, the dynamic response model includes not only the common links such as capacity adjustment, climbing rate, and FR delay but also the transfer links with energy conversion (Yu et al., 2011; Datta and Senjyu, 2013). In this study, the frequency-domain model is shown in Figure 2. T_d is FR delay. Its general form is shown in Table 1. The power output in the time domain can be obtained by calculating the input power, as shown as follows:

$\mathrm{\Delta }{P}_i^{\text{out}}\left(t\right)=L^{-1}\left[\frac{G_i\left(s\right)}{s(1+T_{\text{d}}^{i}s)}\cdot {\displaystyle \sum _{k=1}^N\left[e^{-\mathrm{\Delta }T\cdot (k-1)s}\cdot D_i^{\mathrm{in}}\left(k\right)\right]}\right],(1)$

$D_i^{\text{in}}\left(k\right)=\mathit{\Delta }{P}_i^{\text{in}}\left(k\right)-\mathit{\Delta }{P}_i^{\text{in}}\left(k-1\right),(2)$

$\mathit{\Delta }{P}_i^{\text{out}}\left(k\right)=\mathit{\Delta }{P}_i^{\text{out}}\left(t=k\cdot \mathit{\Delta }T\right),(3)$

where i is the ith unit; k is the kth discrete control cycle; $\mathit{\Delta }T$ is the AGC control period, which is generally 1–16 s.

FIGURE 2

FIGURE 2. Response models. GRC: generation ramp constraint.

TABLE 1

TABLE 1. Transfer function.

Optimized Mathematical Model

In the AGC optimal cooperative control model established in this study, its optimization objective is to improve performance. In order to achieve the aforementioned objectives, the control objective is to minimize the power response deviation, as shown in the following figure.

$minf={\displaystyle \sum _{j=k}^N{\displaystyle \sum _{i=1}^n\left|\mathit{\Delta }{P}_i^{\text{in}}\left(j\right)-\mathit{\Delta }{P}_i^{\text{out}}\left(j\right)\right|}}.(4)$

For the aforementioned considerations, various constraints are required, as shown as follows.

$\mathit{\Delta }{P}^{\mathrm{in}}\left(k\right)={\displaystyle \sum _{i=1}^n\mathit{\Delta }{P}_i^{\text{in}}\left(k\right)},(5)$

$\mathit{\Delta }{P}^{\text{in}}\left(k\right)\cdot \mathit{\Delta }{P}_i^{\text{in}}\left(k\right)\ge 0, i=\mathrm{1,2},\text{L},n,(6)$

$\mathit{\Delta }{P}_i^{\text{min}}\le \mathit{\Delta }{P}_i^{\text{in}}\left(k\right)\le \mathit{\Delta }{P}_i^{\text{max}}, ,i=\mathrm{1,2},\text{L},n,(7)$

$\left|\mathit{\Delta }{P}_i^{\text{in}}\left(k\right)-\mathit{\Delta }{P}_i^{\text{in}}\left(k-1\right)\right|\le \mathit{\Delta }{P}_i^{\text{rate}}, ,i=\mathrm{1,2},\text{L},n,(8)$

where $\mathit{\Delta }{P}^{\text{in}}$ is the power regulation instruction, and $\mathit{\Delta }{P}_i^{\text{rate}}$ is the maximum climbing rate of AGC units.

Equilibrium Optimization

The EO used in the study is a heuristic algorithm (Faramarzi et al., 2020). The algorithm is mainly inspired by the control volume mass balance model. Compared with other heuristic optimization algorithms, the EO algorithm effectively balances the relationship between exploration and exploitation and has attracted extensive attention since its appearance (Ahmadipour et al., 2022; Wang et al., 2021; Soliman et al., 2021; Alham et al., 2022). The optimization principle of the EO algorithm is similar to the PSO algorithm. The mathematical representation of the optimization process of the EO algorithm is as follows:

Step 1. Initialization

The first step in the optimization process of EO is initialization as shown as follows:

$C_i^{\text{initial}}=C_{\text{min}}+{\text{rand}}_i\left(C_{\text{max}}-C_{\text{min}}\right), i=\mathrm{1,2}, ,n,(9)$

where n is the number of total particles.

Step 2. Equilibrium pool

In general, the equilibrium state is considered to be globally optimal. The algorithm determines equilibrium candidate solutions when searching in the search space. These candidate particles are the four currently best-performing particles with the arithmetic mean of the four particles. The four equilibrium candidate solutions are helpful to improve the exploration ability, and the arithmetic mean is helpful in improving the mining ability. The five equilibrium candidates form the equilibrium pool:

${\overrightarrow{C}}_{\text{eq},\text{pool}}=\left\{{\overrightarrow{C}}_{\text{eq}\left(1\right)},{\overrightarrow{C}}_{\text{eq}\left(2\right),},{\overrightarrow{C}}_{\text{eq}\left(3\right)},{\overrightarrow{C}}_{\text{eq}\left(4\right)},{\overrightarrow{C}}_{\text{eq}\left(\text{ave}\right)}\right\}.(10)$

Step 2. Exponential term(F)

$\overrightarrow{F}=e^{-\overrightarrow{\lambda }(t-t_0)},(11)$

$t={\left(1-\frac{Iter}{Max\_iter}\right)}^{\left(a_2\frac{Iter}{Max\_iter}\right)},(12)$

where $a_2$ is a constant value. In addition, to ensure convergence, the algorithm is also considered:

${\overrightarrow{t}}_0=\frac{1}{\overrightarrow{\lambda }}ln\left(-a_{1}sign(\overrightarrow{r}-0.5)[1-e^{-\overrightarrow{\lambda }t}]\right)+t,(13)$

where $a_1=2$ and $a_2=1$. According to Eqs 11, 12, Eq. 10 can be expressed as follows:

$\overrightarrow{F}=a_{1}sign(\overrightarrow{r}-0.5)[e^{-\overrightarrow{\lambda }t}-1].(14)$

Step 4. Generation rate (G)

In the EO algorithm, G is the most important one. Its update rules are as follows:

$\overrightarrow{C}={\overrightarrow{C}}_{eq}+(\overrightarrow{C}-{\overrightarrow{C}}_{eq}).\overrightarrow{F}+\frac{\overrightarrow{G}}{\overrightarrow{\lambda }V}(1-\overrightarrow{F}).(15)$

The collaboration of all equilibrium candidate particles on sample particles in the optimization process of the EO algorithm and how they affect concentration update are shown in Figure 3 as a conceptual sketch.

FIGURE 3

FIGURE 3. Optimization schematic diagram of the EO algorithm.

Case Studies

Simulation Model

In this study, simulation verification is carried out in the two-region load frequency control model under IEEE standards, and a single equivalent unit in control area A is replaced with five FR units of different types, as shown in Figure 1. Meanwhile, Tables 2, 3 give the main parameters. The AGC control period is set to 4 s. To verify the superiority of the EO algorithm, PROP and GA are introduced to compare. To ensure a fair comparison of control effects between algorithms, the population size of GA and EO algorithms was set to 10, respectively.

TABLE 2

TABLE 2. Parameters of transfer functions.

TABLE 3

TABLE 3. Main parameters.

Step Power Disturbance of −80 MW

To test the optimization performance of EO, the step power disturbance of △P_L = 80 MW is applied to region A in this example. The comparison of online optimization results between the EO algorithm and PROP method is shown in Figure 4. As can be seen from Figure 4, after power instruction allocation is optimized by the EO algorithm, the variation range of regional control deviation decreases due to changes in the regulating output of the unit, resulting in changes in the tracking curve of regional total power regulation, making the actual total output curve closer to the command output curve. At the same time, compared with the PROP method, the EO algorithm can obtain a smaller power deviation and avoid an overshoot of total power instruction. Meanwhile, wind power and PV with fast response speed can quickly balance power disturbance by assuming more power disturbance.

FIGURE 4

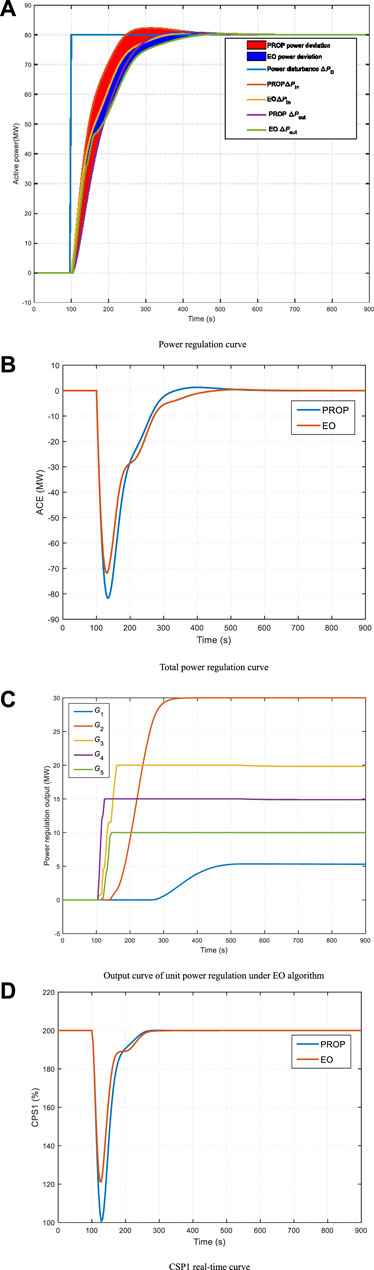
FIGURE 4. Result of optimization when △PL = 80 MW. ACE: area control error; CPS: control performance standard.

In this study, in order to verify that EO is better than other methods, EO is presented in Table 4; the optimized result with the other two methods, including $\left|\text{ACE}\right|$, $\left|\Delta f\right|$, and CPS1, said the average in the process of simulation, respectively. As shown in Table 4, the intelligent optimization algorithm can greatly reduce the power bias, thus significantly improving the response performance. At the same time, compared with the GA algorithm, the optimization results of the EO algorithm are more excellent, which proves that the EO algorithm is more suitable for solving the optimal cooperative control problem of renewable energy participation in the FR process.

TABLE 4

TABLE 4. Result of optimization.

Step Power Disturbance of −50 MW

The step power disturbance of △P_L = −50 MW is applied to region A in this example. The comparison of online optimization results between the EO algorithm and PROP method is shown in Figure 5. As can be seen from Figure 5, after power instruction allocation is optimized by the EO algorithm, the variation range of regional control deviation decreases due to changes in the regulating output of the unit, resulting in changes in the tracking curve of regional total power regulation, making the actual total output curve closer to the command output curve. At the same time, compared with the PROP method, the EO algorithm can obtain a smaller power deviation and avoid overshoot. In addition, wind power and PV with fast response speed can quickly balance power disturbance by assuming more power disturbance.

FIGURE 5

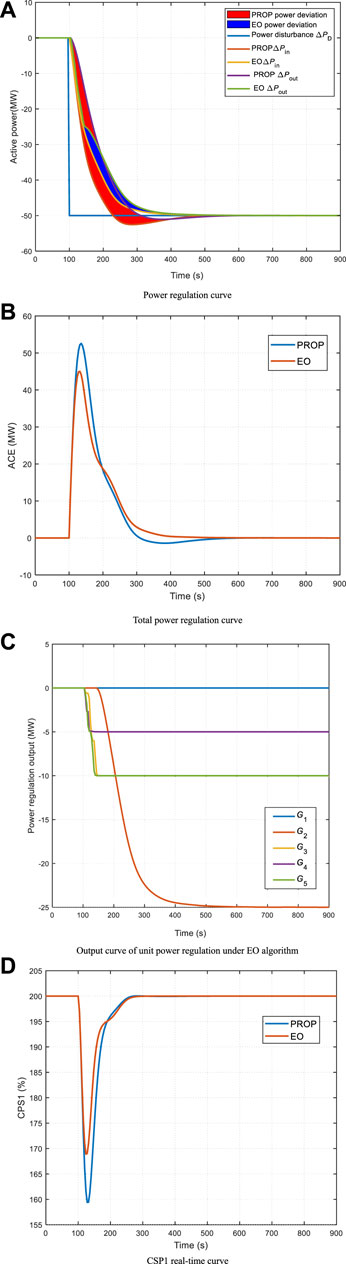
FIGURE 5. Result of optimization when △PL = −50 MW. ACE: area control error; CPS: control performance standard.

In this study, in order to verify the EO is better than other methods, EO is presented in Table 5; the optimized result with the other two methods, including $\left|\text{ACE}\right|$, $\left|\Delta f\right|$ and CPS1, said the average in the process of simulation, respectively. As shown in Table 5, the intelligent optimization algorithm can greatly reduce the power bias, thus improving the response performance index of the system. Moreover, compared with the GA algorithm, the optimization results of the EO algorithm are more excellent, which proves that the EO algorithm is more suitable for solving the optimal cooperative control problem of renewable energy participation in the FR process.

TABLE 5

TABLE 5. Result comparison.

Conclusion

To deal with the control problem of renewable energy participation in FR of the regional power grid, an optimal cooperative FR method based on the EO algorithm is proposed in the study.

1) The multi-source cooperative FR control model of the regional power grid is constructed, which provides a reference model for renewable energy to participate in the regional power grid FR. In order to improve the dynamic response performance, renewable energy is preferentially involved in the secondary FR of the regional power grid at the initial stage of FR.

2) An optimization method of regional power grid multi-source optimal cooperative control based on an EO algorithm is designed. This method can not only meet the real-time control requirements of AGC but also obtain a high-quality frequency control scheme stably and quickly, thus effectively improving the dynamic response performance of computers in the whole area.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Research on New Energy Consumption Evaluation under Carbon Emission Target 031000QQ00210015.

Conflict of Interest

MZ, JH, and XH were employed by Jiangsu Kanion Pharmaceutical Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadipour, M., Murtadha Othman, M., Alrifaey, M., Bo, R., and Kit Ang, C. (2022). Classification of Faults in Grid-Connected Photovoltaic System Based on Wavelet Packet Transform and an Equilibrium Optimization Algorithm-Extreme Learning Machine. Measurement 197, 111338. doi:10.1016/j.measurement.2022.111338

CrossRef Full Text | Google Scholar

Al-Hamouz, Z., Al-Duwaish, H., and Al-Musabi, N. (2011). Optimal Design of a Sliding Mode AGC Controller: Application to a Nonlinear Interconnected Model. Electr. Power Syst. Res. 81, 1403–1409. doi:10.1016/j.epsr.2011.02.004

CrossRef Full Text | Google Scholar

Alham, M. H., Fathy Gad, M., and Khalil Ibrahim, D. (2022). Potential of Wind Energy and Economic Assessment in Egypt Considering Optimal Hub Height by Equilibrium Optimizer. Ain Shams Eng. J. 30, 101816. doi:10.1016/j.asej.2022.101816

CrossRef Full Text | Google Scholar

Arya, Y. (2018). AGC of Two-Area Electric Power Systems Using Optimized Fuzzy PID with Filter Plus Double Integral Controller. J. Frankl. Inst. 355, 4583–4617. doi:10.1016/j.jfranklin.2018.05.001

CrossRef Full Text | Google Scholar

Arya, Y. (2018). Improvement in Automatic Generation Control of Two-Area Electric Power Systems via a New Fuzzy Aided Optimal PIDN-FOI Controller. ISA Trans. 80, 475–490. doi:10.1016/j.isatra.2018.07.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Çelik, E. (2020). Improved Stochastic Fractal Search Algorithm and Modified Cost Function for Automatic Generation Control of Interconnected Electric Power Systems. Eng. Appl. Artif. Intell. 88, 103407. doi:10.1016/j.engappai.2019.103407

CrossRef Full Text | Google Scholar

Chen, G., Fan, C. W., Zhu, T., Teng, Y. F., Shi, H. B., and Xiao, X. (2020). Study on AGC Strategy Involving the Frequency Control of HVDC Power Regulation. The International Conference on Powe Engineering (ICPE 2020), Dec. 19-21, 2020, Guangzhou, China 8, 498–505.

Google Scholar

Cui, Y., Li, P., Ji, D. S., and Du, Z. J. (2019). Joint Operation Strategy of Wind Power-Photovoltaic-Pumped Storage Hydro Energy Based on Multilateral Income. Electr. Power Autom. Equip. 39 (4), 161–166.

Google Scholar

Datta, M., and Senjyu, T. (2013). Fuzzy Control of Distributed PV Inverters/energy Storage Systems/electric Vehicles for Frequency Regulation in a Large Power System. IEEE Trans. Smart Grid 4 (1), 479–488. doi:10.1109/tsg.2012.2237044

CrossRef Full Text | Google Scholar

Electricity Market Report. Paris: International Energy Agency. 2022,Available at: https://www.iea.org/reports/electricity-market-report-january-2022.

Google Scholar

Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020). Equilibrium Optimizer: A Novel Optimization Algorithm. Knowledge-Based Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190

CrossRef Full Text | Google Scholar

Gorripotu, T. S., Sahu, R. K., and Panda, S. D. E. (2016). Optimized PID Controller with Derivative Filter for AGC of Interconnected Restructured Power System. Springer India.

Google Scholar

Gupta, N., and Kumar, N. (2018). Particle Swarm Optimization Based Automatic Generation Control of Interconnected Power System Incorporating Battery Energy Storage System. Procedia Comput. Sci. 132, 1562–1569. doi:10.1016/j.procs.2018.05.120

CrossRef Full Text | Google Scholar

Hakimuddin, N., Khosla, A., and Garg, J. K. (2020). Centralized and Decentralized AGC Schemes in 2-area Interconnected Power System Considering Multi Source Power Plants in Each Area. J. King Saud Univ. - Eng. Sci. 32, 123–132. doi:10.1016/j.jksues.2018.07.003

CrossRef Full Text | Google Scholar

Hasan, N., Alsaidan, I., Sajid, M., Khatoon, S., and Farooq, S. (2022). Robust Self Tuned AGC Controller for Wind Energy Penetrated Power System. Ain Shams Eng. J. 13, 101663. doi:10.1016/j.asej.2021.101663

CrossRef Full Text | Google Scholar

Huo, Z., and Xu, C. (2022). Distributed Cooperative Automatic Generation Control and Multi-Event Triggered Mechanisms Co-design for Networked Wind-Integrated Power Systems. Renew. Energy 193, 41–56. doi:10.1016/j.renene.2022.05.011

CrossRef Full Text | Google Scholar

Lal, D. K., Barisal, A. K., and Tripathy, M. (2016). Grey Wolf Optimizer Algorithm Based Fuzzy PID Controller for AGC of Multi-Area Power System with TCPS. Procedia Comput. Sci. 92, 99–105. doi:10.1016/j.procs.2016.07.329

CrossRef Full Text | Google Scholar

Li, J., Yu, T., Zhu, H., Li, F., Lin, D., and Li, Z. (2020). Multi-Agent Deep Reinforcement Learning for Sectional AGC Dispatch. IEEE Access 8, 158067–158081. doi:10.1109/access.2020.3019929

CrossRef Full Text | Google Scholar

Li, Z., Luan, R., and Lin, B. (2022). The Trend and Factors Affecting Renewable Energy Distribution and Disparity across Countries. Energy 254, 124265. doi:10.1016/j.energy.2022.124265

CrossRef Full Text | Google Scholar

Liu, Q., and Liu, Q. (2020).Research on Automatic Generation Control System of Photovoltaic Power Station Based on Adaptive PID Control Algorithm, 2020 IEEE 3rd International Conference on Information Systems and Computer Aided Education (ICISCAE), 27-29 Sept. 2020, Dalian, China. IEEE. doi:10.1109/ICISCAE51034.2020.9236877

CrossRef Full Text | Google Scholar

Madasu, S. D., Sai Kumar, M. L. S., and Singh, A. K. (2018). A Flower Pollination Algorithm Based Automatic Generation Control of Interconnected Power System. Ain Shams Eng. J. 9 (4), 1215–1224. doi:10.1016/j.asej.2016.06.003

CrossRef Full Text | Google Scholar

Mohanty, B. (2015). TLBO Optimized Sliding Mode Controller for Multi-Area Multi-Source Nonlinear Interconnected AGC System. Int. J. Electr. Power & Energy Syst. 73, 872–881. doi:10.1016/j.ijepes.2015.06.013

CrossRef Full Text | Google Scholar

Nayak, J. R., Shaw, B., Sahu, B. K., and Naidu, K. A. (2022). Application of Optimized Adaptive Crow Search Algorithm Based Two Degree of Freedom Optimal Fuzzy PID Controller for AGC System. Eng. Sci. Technol. Int. J. 32, 101061. doi:10.1016/j.jestch.2021.09.007

CrossRef Full Text | Google Scholar

Shanmugasundaram, V. (2017).Artificial Bee Colony Algorithm Based Automatic Generation Control in Two-Area Non-reheat Thermal Power System Using SMES, IEEE International Conference on Power, Control, Signals and Instrumentation Engineering, 21-22 Sept. 2017, Chennai, India. IEEE. doi:10.1109/ICPCSI.2017.8392092

CrossRef Full Text | Google Scholar

Soliman, M. A., Al-Durra, A., and Hasanien, H. M. (2021). Electrical Parameters Identification of Three-Diode Photovoltaic Model Based on Equilibrium Optimizer Algorithm. IEEE Access 9, 41891–41901. doi:10.1109/access.2021.3065386

CrossRef Full Text | Google Scholar

Wang, J., Yang, B., Li, D., Zeng, C., Chen, Y., Guo, Z., et al. (2021). Photovoltaic Cell Parameter Estimation Based on Improved Equilibrium Optimizer Algorithm. Energy Convers. Manag. 236, 114051. doi:10.1016/j.enconman.2021.114051

CrossRef Full Text | Google Scholar

Wu, J., Liu, M., Lu, W., and Xie, K. (2021). Real-time Optimization of Active Distribution Networks with Distributed Energy Resources Participating in Frequency Regulation. J. Clean. Prod. 328, 129597. doi:10.1016/j.jclepro.2021.129597

CrossRef Full Text | Google Scholar

Xi, Lei., Zhang, L., Xu, Y. C., Wang, S. X., and Yang, C. (2022). Automatic Generation Control Based on Multiple-step Greedy Attribute and Multiple-Level Allocation Strategy. CSEE J. Power Energy Syst. 8 (1), 281–292. doi:10.17775/CSEEJPES.2020.02650

CrossRef Full Text | Google Scholar

Yousef, H. (2015). Adaptive Fuzzy Logic Load Frequency Control of Multi-Area Power System. Int. J. Electr. Power & Energy Syst. 68, 384–395. doi:10.1016/j.ijepes.2014.12.074

CrossRef Full Text | Google Scholar

Yu, T., Wang, Y. M., Ye, W. J., Zhou, B., and Chan, K. W. (2011). Stochastic Optimal Generation Command Dispatch Based on Improved Hierarchical Reinforcement Learning Approach. IET Gener. Transm. Distrib. 5 (8), 789–797. doi:10.1049/iet-gtd.2010.0600

CrossRef Full Text | Google Scholar

Zhang, D., Zhang, H., Zhang, X., Li, X., Ren, K., Zhang, Y., et al. (2020). Research on AGC Performance during Wind Power Ramping Based on Deep Reinforcement Learning. IEEE Access 8, 107409–107418. doi:10.1109/access.2020.3000784

CrossRef Full Text | Google Scholar

Zhang, F., Fu, A., Ding, L., Wu, Q., Zhao, B., and Zi, P. (2019). Optimal Sizing of ESS for Reducing AGC Payment in a Power System with High PV Penetration. Int. J. Electr. Power & Energy Syst. 110, 809–818. doi:10.1016/j.ijepes.2019.03.029

CrossRef Full Text | Google Scholar

Zhang, Q., Tang, H., Wang, Z., Wu, X., and Lv, K. (2022). Flexible Selection Framework for Secondary Frequency Regulation Units Based on Learning Optimisation Method. Int. J. Electr. Power & Energy Syst. 142, 108175. doi:10.1016/j.ijepes.2022.108175

CrossRef Full Text | Google Scholar

Zhang, X. S., Tan, T., Yu, T., Yang, B., and Huang, X. M. (2020). Bi-objective Optimization of Real-Time AGC Dispatch in a Performance-Based Frequency Regulation Market. CESS J. Power Energy Syst. (Early Access), 1–9. doi:10.17775/CSEEJPES.2020.01860

CrossRef Full Text | Google Scholar

Zhang, X. S., Yu, T., Pan, Z. N., Yang, B., and Bao, T. (2017). Lifelong Learning for Complementary Generation Control of Interconnected Power Grids with High-Penetration Renewables and EVs. IEEE Trans. Power Syst. 33 (4), 4097–4110. doi:10.1109/TPWRS.2017.2767318

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power & Energy Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhu, X., Han, X., Xu, Y., and Li, J. (2022). Distributed Optimal-Tracking Control to Coordinate the Optimization of Active Distribution Networks with Automatic Generation Control. Int. J. Electr. Power & Energy Syst. 136, 107566. doi:10.1016/j.ijepes.2021.107566

CrossRef Full Text | Google Scholar

Nomenclature

AGC automatic generation control

EO equilibrium optimization

FR frequency regulation

GWO grey wolf optimizer

IEA international energy agency

LFC load frequency control

PROP proportion method

PV photovoltaic