Research on Efficient Channel Decoding Algorithm for Memory Channel and Short Packet Transmission in Smart Grid

Many smart factories use the smart grid for power system automation, and its wireless control technology requires low-time-delay and high-reliability communication. Guessing random additive noise decoding algorithm has outstanding short packet error correction performance. In the decoding process, the order of noise parameter combination affects the decoding delay. Aiming at the communication problem of the smart grid in the process of factory power supply and distribution, this study analyzes the characteristics of the original noise parameter ranking algorithm. When the steady-state flip probability is large, more search times are required to obtain the correct combination of noise parameters, which means that greater delay is required for decoding in the time-varying channel. To solve the aforementioned problems, this study optimizes the noise parameter ranking before the noise error mode arrangement and proposes a noise parameter ranking algorithm for predicting the symbol string. First, the channel perception is completed by edge computing. Then, the algorithm uses the obtained soft information to rank the channel noise parameters. Simulation results show that the proposed algorithm has better search performance than the original sorting algorithm, especially when the channel parameter b is greater than 0.5. Finally, by comparing the BM Decoding Algorithm of BCH with different noise parameter ranking algorithms of decoding, the results show that the noise parameter ranking algorithm proposed in this study has better decoding performance in the environmental channel of the smart factory, so as to improve the reliability of the smart grid in the process of factory power supply and distribution.

Introduction

With the advent of the industry 4.0 era, wireless control technology has become a solution for intelligent factories to improve the real time and stability of control instructions (Pang et al., 2017). For the power system automation technology in the smart grid, its communication control technology mostly adopts wireless control technology. Compared with wired control technology, its main advantages are as follows: wireless control technology can reduce the deployment cost and maintenance cost of transmission media; in wired transmission, the cable may be aged or damaged, while in wireless transmission, there will be no such disadvantage; wireless networks can be arranged in harsh environments where the cables commonly used cannot be used, such as high-temperature scenes, high-voltage scenes, and mobile scenes.

A basic feature of the smart grid is the information flow on a high-speed, reliable and safe data communication network, so as to effectively and intelligently manage complex power systems (Abrahamsen et al., 2021). In order to meet the requirements of high reliability and low delay communication of smart grid wireless control, while traditional wireless systems achieve high reliability through packet retransmissions, this would impair the latency as an approach based on channel coding is preferable in industrial applications (Zhan et al., 2018a; Zhan et al., 2019). This technology trades for high reliability of communication at the expense of certain computational complexity and bandwidth resources.

In the general channel coding and decoding algorithm, because the number of bits of error detection and error correction of error correction code has an upper limit, if there are multiple bits of errors in a code word, the error correction code needs more complex coding for error correction, which takes up more bandwidth resources (Zhan et al., 2018b). Therefore, in the traditional channel coding and decoding algorithm, it is generally considered that the channel is memoryless and the correlation of channel noise is not considered (Gilbert, 1960). This contradiction is particularly prominent in the factory production environment. The production process of the factory is periodic, and the pulse introduced from the ground wire will interfere with the RF transmission signal of the control equipment (Platschek et al., 2015a). The arc discharge is caused by various welding and frequent start and stop of electrical equipment [(2013), 1613]. These highly correlated channel noises will directly affect the quality of control signal reception and then lead to misoperation in the process of industrial production (Platschek et al., 2015b). A simple Gilbert-Elliotts model can describe these highly correlated impulse disturbances in a bursty channel with a Markov chain (Platschek et al., 2015b).

In the classical decoding algorithm, an interleaver is introduced to solve the problem of channel noise correlation (Barbulescu and Pietrobon, 1994). The interleaver scrambles the sequence order through interleaving and then converts the burst error in the transmission process into random error, which is the error type “preferred” by the classical decoding algorithm and has a high error correction probability for this type of error. However, in the production process of an intelligent factory, the control instruction is short packet transmission (Ho et al., 2021). For the interleaving of short packets, the interleaved sequence may experience the same channel condition (Barac et al., 2013; Zhan et al., 2021). At the same time, the introduction of interleaver will introduce a large time delay, which cannot meet the requirements of high reliability and low time delay communication.

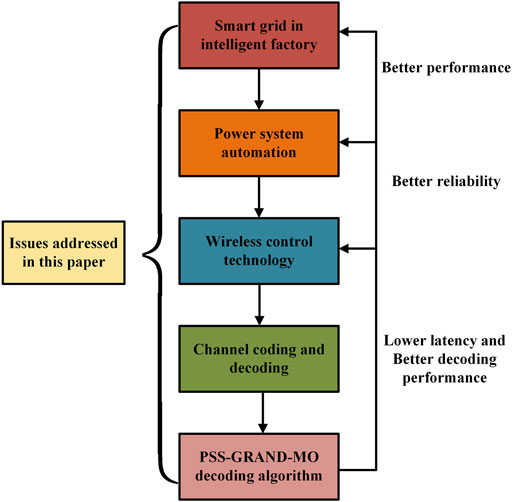
Guessing Random Additive Noise Decoding (GRAND) is a noise-centered algorithm, which may meet the requirements of high reliability and low delay at the same time. As a general decoding algorithm to achieve channel capacity, many variants have been developed (refer to chapter 2) in order to resist the challenge of the strong correlation of channel noise under short packet conditions. GRAND-MO has the potential to become an effective decoding scheme. The GRAND-MO algorithm regards burst errors as common in discrete channels by querying the noise error patterns assumed in the Markov order (MO) (An et al., 2022). Compared with the classical channel coding and decoding algorithm, this algorithm considers the correlation of channel noise in principle, and the goal is to solve the channel noise rather than pay attention to the coding itself. The motivation of this study is shown in Figure 1.

FIGURE 1

FIGURE 1. Research motivation of this study.

The chapters of this study are arranged as follows: the first chapter mainly introduces the shortcomings of the traditional channel coding technology in the power supply and distribution process of intelligent factories and introduces the grand algorithm. The second chapter mainly introduces the related work on the GRAND algorithm in recent years. The third chapter introduces the basic strategy of the grand algorithm and the channel modeling of the GRAND-MO algorithm and introduces the mechanism of the original noise parameter ranking algorithm. In Chapter 4, the original noise parameter ranking algorithm is simulated. The results show that when the channel changes, there will be more times to search the noise parameters. The fifth chapter introduces the algorithm proposed in this study, the PSS-GRAND-MO algorithm, and describes, analyzes, and simulates it in detail. The sixth chapter summarizes the work of this study.

Related Works

The GRAND algorithm is a novel algorithm. Many decoding processes need to be designed. (Zhan et al., 2022) proposed an efficient noise pattern generation algorithm based on successive addition and subtraction. (An et al., 2022) queried the putative noise error patterns in the Markov order (MO). The GRAND-MO algorithm regards burst errors as a universal existence in discrete channels. It proposed the method to arrange the noise parameters in the noise parameter ranking process. (Abbas et al., 2021) gives and implements the VLSI hardware architecture of the GRAND algorithm, including each decoding process. The classical GRAND algorithm is decoded by hard demodulation information, while literature (Duffy and Médard, 2019) provides an extension of the GRAND algorithm. The algorithm name is SGRAND (Soft GRAND) algorithm, which contains soft detection symbol reliability information and is decoded by maximum likelihood decoding; (Solomon et al., 2020) evaluated the performance of SGRAND on CA polar code and compared its accuracy with CRC-assisted continuous cancellation list decoding (CA-CSL). (Duffy, 2021) makes further use of the advantages of SGRAND and retains the ideal parallelism of SGRAND in high-throughput hardware implementation, so as to form an ordered reliable bit GRAND (ORBGRAND) variant with better performance gain. (Condo, 2022) proposed an improved ORBGRAND mode scheduling. When used for 5G radio cyclic redundancy check auxiliary polarity code, the decoding complexity of the ORBGRAND algorithm is lower than that of the CRC auxiliary continuous cancellation list (CA-SCL) algorithm. By connecting with input distributed sensing (IDA) decoding (Condo and Nicolescu, 2021), ORBGRAND is extended to an optimized IDA-ORBGRAND algorithm, and its decoding complexity is reduced by 33%. At present, algorithms derived from GRAND have entered different application fields (Duffy et al., 2020; An et al., 2021; Solomon et al., 2021).

The GRAND algorithm opens up a new possibility for the URLLC requirements of any short code and high-speed code, and its performance varies with the order of noise error modes. From the perspective of feasibility, the most serious challenge at present is to generate noise error patterns more effectively (Condo et al., 2021). (Abbas et al., 2020; Abbas et al., 2022) have enhanced their error correction ability by reordering the ORBGRAND algorithm, where the noise error mode is output by the logic weight. Another noise error pattern generation algorithm is described in (Condo et al., 2021), and the noise error pattern can be calculated by the previous error pattern.

At the same time, the optimization goal of the aforementioned literature is to optimize the noise error mode, and the original noise parameter ranking algorithm is still used. The literature (Yiqian et al., 2019) pointed out that the channel of the industrial scene has time variability. Manipulators, forklifts, cranes, robots, and other equipment will cause channel time-varying, resulting in Doppler frequency offset; second, component to component mobility exists in industrial scenes, which will lead to occlusion effect; finally, in the case of moving objects or antennas, rapid conversion between LOS and NLOS channel conditions may occur. This study focuses on the arrangement of noise parameters in the GRAND-MO algorithm, and proposes a noise parameter ranking algorithm for predicting symbol strings, we call it PSS-GRAND-MO. When compared with the previous noise parameter ranking algorithms, when encountering time-varying channels, it can more efficiently match the noise error mode and improve the coding performance. Table 1 shows the channel type applications of different algorithms based on GRAND. Different from other studies, this study takes into account the time-varying channel. At the same time, in order to maintain the excellent performance of the decoding algorithm in a non-time-varying channel, the PSS-GRAND-MO algorithm is proposed.

TABLE 1

TABLE 1. Contributions of this study.

Basic Strategy of the GRAND-MO Algorithm

In principle, the impulse noise in the channel is considered in the GRAND-MO decoding algorithm. Its essence is to remove the noise in the channel to obtain a pure codebook, and then carry out the subsequent codebook decoding operation.

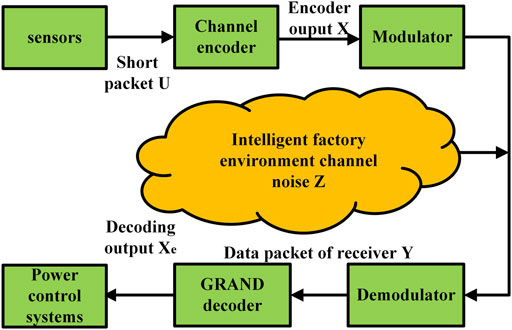
The communication architecture based on the GRAND-MO decoder for power system automation is shown in Figure 2. Consider a short packet input sequence as

$U=\{u_{1,}{u}_{2,}\dots u_N\}.(1)$

FIGURE 2

FIGURE 2. Communication architecture of the GRAND decoder for power system automation.

In Eq. 1, N is the package length. After being encoded by the channel encoder, the output is

$X=\{x_1,x_2,\dots ,x_N\}.(2)$

It enters the wireless channel after modulation by the modulator. At this time, the noise added to the channel of the intelligent factory is mainly the additive Gaussian white noise with serial pulse interference, which is defined as

$Z=\{z_1,z_2,\dots ,z_N\}.(3)$

The data generated by the demodulator through hard demodulation is

$Y=\{y_1,y_2,\dots ,y_N\}.(4)$

The relationship between Eq. 2—Eq. 4 is shown as

$Y=X\mathrm{\oplus }Z.(5)$

Defining $\oplus$ as XOR

The GRAND-MO decoder generates the noise error mode through the noise parameters and defines the noise error mode as

$S=\{s_1,s_2,\dots ,s_N\}.(6)$

The noise error mode is calculated with the demodulated data to obtain the coded estimation sequence, as shown in the following equation:

$X_e=\{x_{e1},x_{e2},\dots ,x_{eN}\}.(7)$

The coding estimation sequence can be solved by

$X_e=S\oplus Y .(8)$

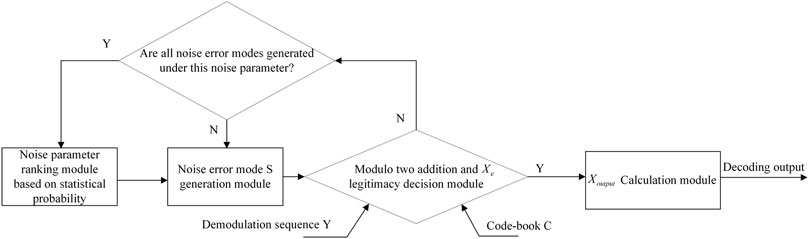
The coding estimation sequence obtained by the GRAND-MO decoder is compared with the codebook C. If it meets the codebook sequence C, it is judged that the decoding is successful and the sequence is output.

$X_{output}=\{x_{output1},x_{output2},\dots ,x_{outputN}\}.(9)$

The calculation process is shown in Eq. 10. The structure of the GRAND-MO decoder is shown in Figure 3.

$\{\begin{array}{c}{X}_{output}=X_e,X_e\in C\\ continue to generate the next noise error mode S and execute \left(8\right) \left(10\right),X_e\notin C\end{array}.(10)$

FIGURE 3

FIGURE 3. Structure of the GRAND-MO decoder.

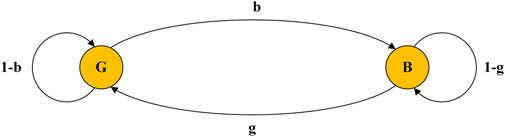
In GRAND-MO, because the channel has memory, a two-state Markov chain can be used to describe the intelligent factory environment channel, as shown in Figure 4. Among them, the small noise interference leads to a hard decision. The good state of accurate decision is G, corresponding to the symbol ″0″ in Z. Large noise interference leads to hard decision error. The bad state of decision is B, corresponding to the symbol ″1″ in Z. The probability of the channel changing from a good state to a bad state is b; in a good state, the probability of maintaining a good state is 1-b; the probability of changing from bad state to good state is g; in a bad state, the probability of maintaining a bad state is 1-g.

FIGURE 4

FIGURE 4. Channel state transition diagram.

Because the Markov chain has time homogeneity, its k-step transition probability matrix is shown as

${\xi }^{\left(k\right)}={\xi }^k=\left[\begin{array}{cc}1-g& g\\ b& 1-b\end{array}\right].(11)$

When $k\to \infty$, Eq. 12 can be derived from Eq. 11.

$\underset{k\to \infty }{\lim }{\xi }^{(k{)}^{\prime }}=\underset{k\to \infty }{\lim }({\xi }^k{)}^{\prime }=\frac{1}{b+g}\left[\begin{array}{cc}b& b\\ g& g\end{array}\right].(12)$

Let the initial probability values of states g and b be 1-p and P. Then, the steady-state probability matrix is as shown in the following equation:

$P=\frac{1}{b+g}\left[\begin{array}{cc}b& b\\ g& g\end{array}\right]\left[\begin{array}{c}p\\ 1-p\end{array}\right]=\left[\begin{array}{c}\frac{b}{b+g}\\ \frac{g}{b+g}\end{array}\right].(13)$

From Eq. 13, the steady-state turnover probabilities are derived as

$P_G=\frac{g}{b+g},(14)$

$P_B=\frac{b}{b+g},(15)$

wherein Eq. 14 is the steady-state probability that the channel is in a good state, and Eq. 15 is the steady-state probability that the channel is in a bad state.

According to the knowledge of probability and statistics, the length of a ″1″ string in an interference sequence obeys geometric distribution. The correlation coefficient is 1-b-g. Both b and g can be measured through channel perception and edge computing. Set the noise parameter combination as $\{\widehat{m},\widehat{l_m}\}$, where m is the number of ″1″ symbol strings in the Z-interference sequence (one ″1″ symbol is also a special ″1″ symbol string) and $l_m$ is the total number of ″1″ symbols in the z-interference sequence. Considering that in the sequence with a total number of digits of N, the number of ″1″ symbol strings is m and the number of ″1″ symbols is $l_m$. There are three scenarios, and their statistical probabilities are as follows:

Scenario 1: if the beginning and end of the interference sequence are ″0″ strings, the probability of this scenario is

$p_1=\frac{g^{m+1}{(1-b)}^{N-l_m-(m+1)}{b}^m}{(b+g){(1-g)}^{m-l_m}}.(16)$

Assuming that the length of the noise sequence is N, the number of ″1″ symbol strings is m, the number of ″1″ symbol is l_m, and both ends of the sequence are 0, then the number of ″0″ symbol strings of the sequence must be 1 more than the number of ″1″ symbol strings. Therefore, the number of ″0″ symbol strings is $(m+1)$. g is the probability of state transition, that is, the probability of changing from a ″1″ symbol string to a ″0″ symbol string. After removing the initial ″0″ element, there are m ″0″ symbol strings. Then its probability is $g^m$. Since the steady-state transition probability has been obtained from the previous text, it is $g/ (b+g)$, $(1-g)$ and $(1-b)$ are the bad state persistence probability and the good state persistence probability, respectively, which can be understood as the same symbol probability as the first bit except for the first bit of the ″1″ or ″0″ symbol string. Similarly, since the number of ″1″ symbol strings is m, the probability of m ″1″ symbol strings is $b^m$. Multiply the aforementioned parameters to obtain Eq. 16, which is the same as the following.

Scenario 2: if the start or end symbol string in the interference sequence is a ″0″ string and the other place is a ″1″ string, the probability of this scenario is

$p_2=\frac{1-b}{g}{p}_1.(17)$

Scenario 3: if the start and end symbol strings in the interference sequence are ″1″ strings, the probability of this scenario is

$p_3={\left(\frac{1-b}{g}\right)}^2{p}_1.(18)$

In reality, when the channel condition is good, the steady-state flip probability $\frac{b}{b+g}<1/2$, i.e., $b<g$. When the channel has memory, i.e., positive correlation, the correlation coefficient is greater than 0, so that $\frac{1-b}{g}>1$. Therefore, under the same combination of noise parameters, the statistical probability ranking of the three scenarios is

$p_1<p_2<p_3.(19)$

From Eqs. 16–18, in the ranking of noise parameter combination, the ″1″ symbol string is the same, and the more the number of ″1″ symbols, the lower the statistical probability. The number of ″1″ symbols is the same, and the more the number of ″1″ symbol strings, the lower the statistical probability. When there is a combination of two parameters, each party has more parameters than the other party and fewer parameters than the other party, specific analysis is required. The literature (Barac et al., 2013) proposed taking $p_1=p_3$ as the standard, calculate how many symbols should be compensated for if the symbol string is different by 1, so as to make the probability of the combination of the two parameters equal. Mark the difference between the number of ″1″ symbols as $\mathrm{\Delta }l$, the expression is shown in Eq. 20. Because the channel has memory, so $\mathrm{\Delta }l>0$, for the convenience of sorting, it is generally rounded down.

$\mathrm{\Delta }l=l_m-l_{m+1}=\frac{\log \left(\frac{b}{g}\right)}{\log \left\{\frac{1-g}{1-b}\right\}}-1.(20)$

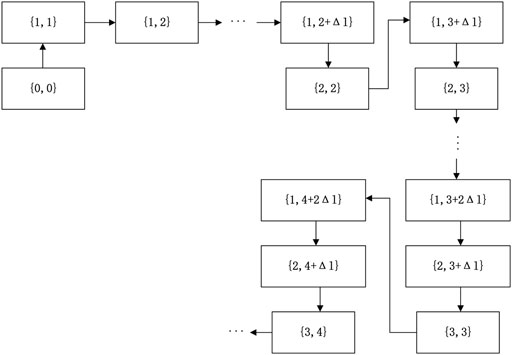
The sequence diagram of noise parameter combination is shown in Figure 5. The parameter combinations are sorted with the arrows. The combinations before the arrows are in the front, and the combinations after the arrows are in the back.

FIGURE 5

FIGURE 5. Schematic diagram of the noise parameter sorting algorithm.

The ranking of noise parameters is to put the greater statistical probability in front so that the decoder can find the corresponding combination of noise parameters faster, so as to complete the decoding operation faster and achieve the low delay communication index. Therefore, the noise parameter ranking algorithm is very important. It is defined that the search times for the decoder to find the noise parameter combination is the number of steps, the English variable is $STEP$, the total number of noise parameters is M, and the noise parameter combination in the real interference sequence is $\left\{m,l_m\right\}$。The noise ranking matrix is

$Noise=[\left\{m_1,l_{m1}\right\}\left\{m_2,l_{m2}\right\},\dots ,\left\{m_M,l_{mM}\right\}].(21)$

The larger the $STEP$, the fewer times the decoder needs to search for the correct combination of noise parameters, and the greater the delay. The smaller the $STEP$, the fewer times the decoder needs to search for the correct combination of noise parameters, and the smaller the delay. The following mainly measures the performance of searching noise parameters based on this index.

$STEP=ar{g}_q(Noise\left(q\right)=\left\{m,l_m\right\}).(22)$

After the noise parameters are determined, the ″1″ symbol string and the number of ″1″ symbols can be obtained, and the noise error pattern can be generated through arrangement and combination. e.g., If $\left\{m,l_m\right\}$ = $\left\{\mathrm{4,8}\right\}$, which means the number of ″1″ symbol strings is 4, and the number of ″1″ symbols is 8. Now we can “guess” how the “1” symbols are distributed in a finite sequence. Our “guess” method is to list all possible noise combinations under the condition of the noise parameter in a permutation and combination way so that the ″1″ symbol string and the ″0″ symbol string are alternately embedded, and then the noise error pattern is generated.

Noise Parameter Ranking Algorithm Based on Statistical Probability

In the GRAND-MO decoding algorithm, because there are multiple code words in the codebook space and there is a minimum distance between code words, there will also be a decoder that decodes and outputs the wrong codebook. Therefore, it is necessary to sort the noise error modes, so that the decoder can decode and output with the correct code word as much as possible. In order to achieve this goal, the noise parameters need to be sorted.

Eqs. 17, 18 evolved from Eq. 16, so Eq. 16 is analyzed. There are two main situations of channel:

1) If the channel parameters b and g differ greatly, i.e., $b\ll g$, then the in steady-state turnover probability $b/(b+g)$ and $g/(b+g)$ exists obvious preference, i.e., the initial value has a high probability of appearing in a good state. At this time, the sorting algorithm in the literature (Platschek et al., 2015b) has a good effect;

2) If the channel parameters start to change, the channel parameters b and g have little difference, and $b<g$. Then the steady-state turnover probability $b/(b+g)$ and $g/(b+g)$ is relatively close, the probability of the initial value of the sequence appearing in the good state and the bad state is close. If it appears in the bad state, there is a probability of $1-g$ to continue the bad state at this time, as a result, there are more ″1″ symbols. At this time, if the original sorting algorithm is still used, there will be a larger number of search steps.

The distribution of ″1″ symbol number and symbol string number in cases 1) and 2) are shown in Figure 6 (a); the comparative relationship between the distribution of search times ($STEP$) in the two cases is shown in Figure 6 (b). It can be seen that in case (1), most sequences only need to be searched once, and the delay at this stage is low. However, in case (2), the search times are widely distributed within 90 times. If the original algorithm is still used to sort and search at this time, it needs to spend a large number of search times to search the corresponding noise parameters, resulting in a waste of computing resources, and it is easy to find the wrong codebook and decode the output. Therefore, it is necessary to find a more efficient algorithm to sort the noise parameters more effectively, so that in all cases in time-varying channels, the search can be completed with lower delay and computing resources, and the correct code word can be output.

FIGURE 6

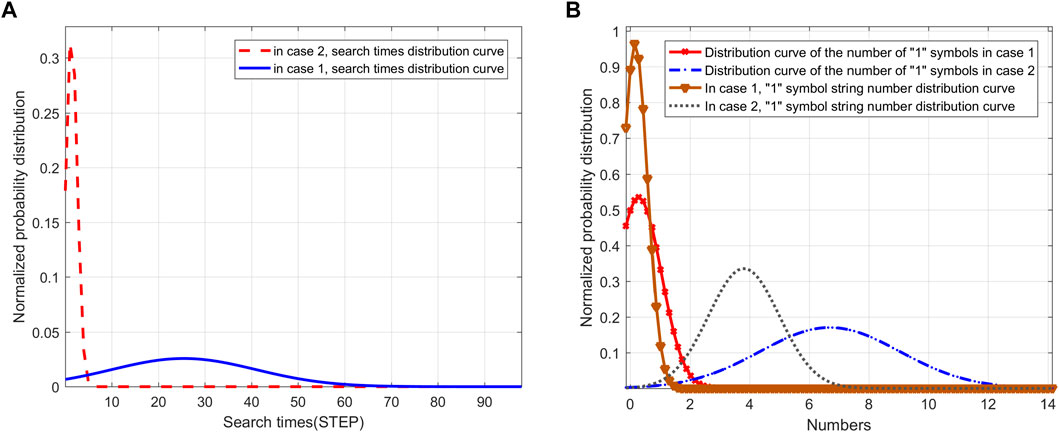
FIGURE 6. List of “1” symbol string distribution and search times. (A) Distribution of “1” symbol number and symbol string number. (B) Distribution of search times.

Noise Parameter Ranking Algorithm of the Prediction Symbol String Algorithm

In order to reduce the number of searches and increase the accuracy of code word output, a noise parameter ranking algorithm for predicting symbol strings is proposed in this study. First, the noise parameters are predicted as the best noise parameters, then the original ranking matrix is reordered based on the best noise parameters, and finally, a new noise parameter ranking method is obtained.

Prediction of the Noise Parameter

It is known that the length of serial error ″1″ in interference sequence Z follows the geometric distribution with a mean value of $1/g$ and variance of $(1-g)/g^2$, and the ″0″ symbol string follows the geometric distribution with a mean value of $1/b$ and variance of $(1-b)/b^2$. The ″1″ symbol string in interference sequence Z is always alternately chimed with the ″0″ symbol string, which mainly includes the following three scenarios:

Scenario 1: the start and end bits of the arrangement is "0"; scenario 2: the start or end bit of the arrangement is "0"; scenario 3: the start and end bits of the arrangement is "1".

The three cases correspond to different numbers of "0" symbol strings. In order to simplify the algorithm, it is assumed that the number of "0" symbol strings and "1" symbol strings are equal in noise mode S. $\widehat{m}$ is the predicted value of the "1" symbol string, which can be obtained by the following equation:

$\widehat{m}=\lfloor N/(\frac{1}{b}+\frac{1}{g})\rfloor .(23)$

Eq. 23 describes a symbol string composed of one "1" symbol string and one "0" symbol string and the number of such symbol strings in a short packet. According to the aforementioned assumptions, there are as many "1" symbol strings as there are combined symbol strings in the short packet.

After the predicted value of the "1" symbol string is obtained, the predicted value of the number of "1" symbols can be obtained, as shown in the following equation:

$\widehat{l_m}=\lfloor \widehat{m}/g\rfloor .(24)$

Design of the Reordering Mechanism

After the predicted noise parameter combination $\{\widehat{m},\widehat{l_m}\}$ is obtained, take it as the initial value, and then sort the noise combination.

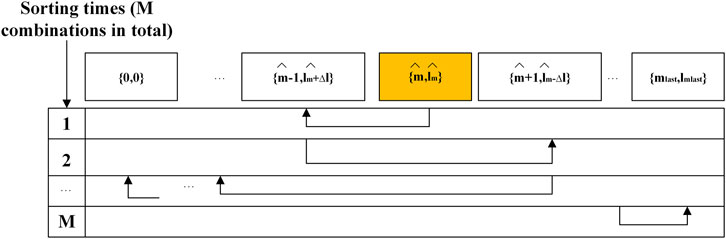
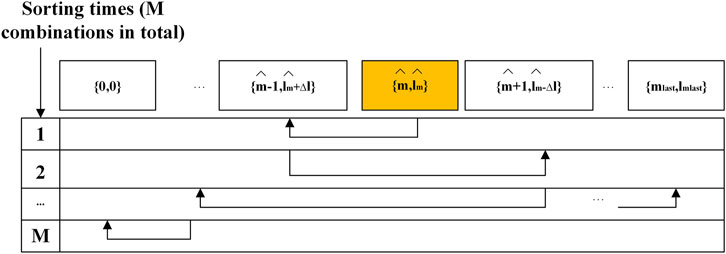
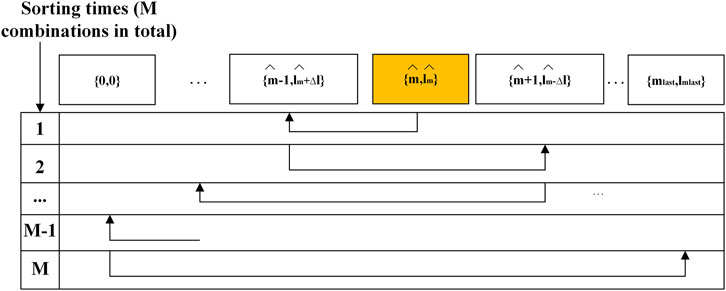
The reordering mechanism should consider the ergodicity of noise parameters and the robustness of the sorting algorithm, that is, it also has a performance similar to the original algorithm under a small steady-state turnover probability. Taking the packet length of 20 as an example, the mechanism has three scenarios, representing different search approaches:

1) Before the sorting is completed, the noise combination $\left\{\mathrm{0,0}\right\}$ is sorted first. At this time, the remaining noise combinations are ranked in the order of near to far from the predicted noise parameter combination. The sorting order is shown in Figure 7.

2) Before the sorting is completed, the rightest noise combination is sorted first. At this time, the remaining noise combinations are ranked in the order of near to far from the predicted noise parameter combination. The sorting order is shown in Figure 8.

3) The predicted noise combination is in the middle, ranking to {0, 0} in the (M-1)-th time and rightest combination in the M-th time. The sorting order is shown in Figure 9.

FIGURE 7

FIGURE 7. Scenario 1 noise parameter ranking diagram.

FIGURE 8

FIGURE 8. Scenario 2 noise parameter ranking diagram.

FIGURE 9

FIGURE 9. Scenario 3 noise parameter ranking diagram.

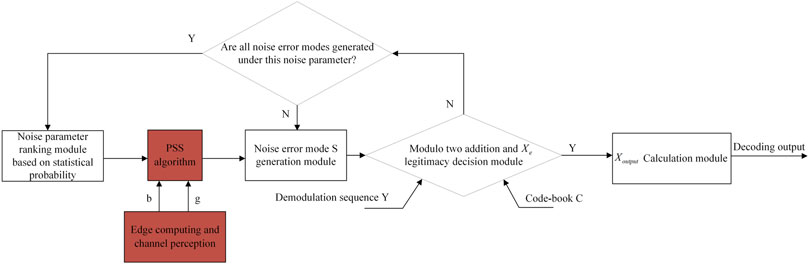
Steps of the PSS algorithm

The steps of the PSS noise parameter sorting algorithm are shown in the following, and its structure is shown in Figure 10. The contribution of this study is to add the red module in Figure 10.

FIGURE 10

FIGURE 10. Structure of the GRAND-MO decoder using the PSS algorithm.

Algorithm 1. PSS Algorithm.

Performance Comparison of the Noise Parameter Ranking Algorithm

The noise parameter ranking algorithm based on the prediction symbol string proposed in this study is compared with the original algorithm under the conditions of case 1 and case 2, as shown in Figure 11. It can be seen that the search frequency distribution of the algorithm proposed in this study is close to that of the original algorithm in case 1. Under the condition of case 2, the search number distribution of the proposed algorithm is smaller than that of the original algorithm, that is, it can spend fewer times to search to obtain the corresponding combination of noise parameters and reduce the decoding delay.

FIGURE 11

FIGURE 11. The distribution curves are compared.

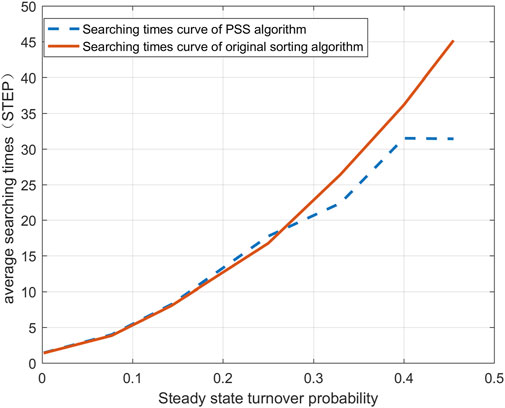
Taking multiple values for b and g, and judge the effectiveness of the algorithm by simulating the influence of the average search times under the condition of multiple steady-state flip probabilities, as shown in Figure 12 When the steady-state flip probability is low, the search performance of the original algorithm is equivalent to that of the algorithm proposed in this study. As the steady-state flip probability gradually increases, when the steady-state flip probability exceeds 0.25, the search times of the original algorithm rise rapidly. The algorithm proposed in this study leads 1–14 times in the average search times, and the leading situation gradually increases with the increase of the steady-state flip probability. Therefore, this algorithm has better search performance than the original algorithm.

FIGURE 12

FIGURE 12. Comparison of average search times.

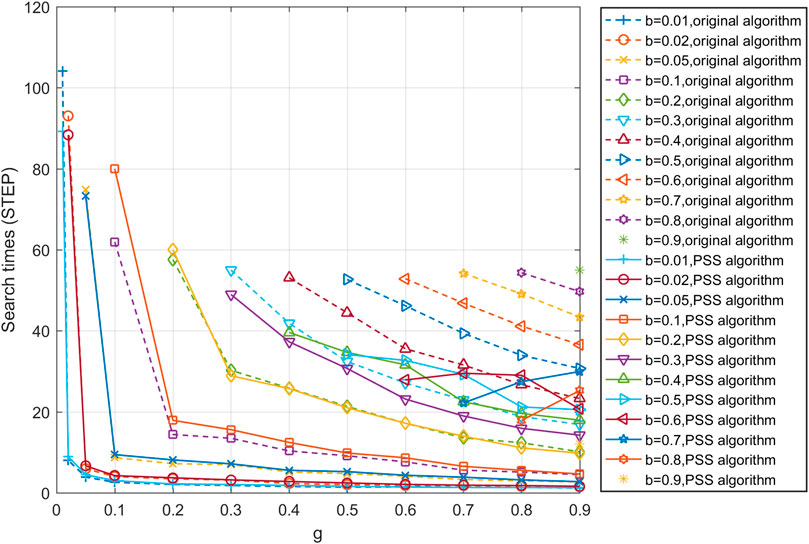
Without losing generality, assuming that g is greater than b in the channel, the search times of the two algorithms corresponding to different combinations of channel parameters are simulated and compared. The results show that when the channel parameter b is less than 0.5, the average search times of the PSS algorithm are equivalent to that of the original sorting algorithm with the change of the channel parameter g. When b is greater than 0.5, the PSS algorithm is 5∼40 times ahead of the original algorithm with the change of the channel parameter g, as shown in Figure 13.

FIGURE 13

FIGURE 13. Comparison of average search times under different channel parameters.

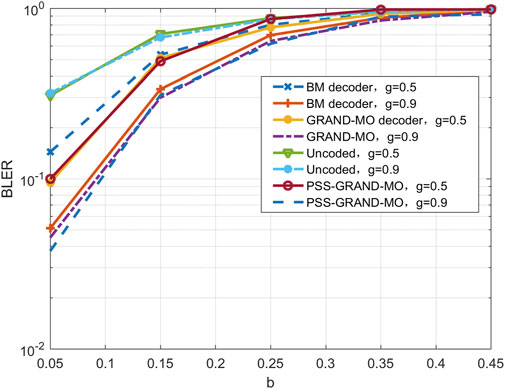
At the same time, too many searches may find the wrong code word, which will lead to decoding errors. Combined with the algorithm in this study, the decoding performance of the BCH code (15,7) in guess decoder and the BM decoder under different channel parameters b and g is simulated. The smaller the channel parameter B, the greater the length of the string ″0″ in the error sequence; the larger g, the smaller the length of the string ″1″ in the error sequence, which represents the better channel condition. The results in Figure 14 show that the noise parameter ranking algorithm proposed in this study has better decoding performance under the same parameters.

FIGURE 14

FIGURE 14. Comparison of decoding performance of noise parameter ranking algorithm.

Conclusion

As a new decoding algorithm, the grand algorithm can effectively solve the short packet transmission problem of burst error channel, and then improve the reliability of the smart grid in the process of factory power supply and distribution. This study first analyzes the channel characteristics under serial impulse interference, constructs a Markov channel, and analyzes its steady-state flip probability. It points out that the original noise parameter ranking algorithm has the problem of more search times when the steady-state flip probability is large. The original algorithm is improved, and a noise parameter ranking algorithm for predicting symbol strings is proposed. Compared with the original algorithm, this algorithm has great advantages when the steady-state flip probability is large. When the channel parameter b is greater than 0.5, it can effectively reduce the number of noise parameter combination searches in time-varying channels. At the same time, when the channel parameter b is less than 0.5, it has the same performance as the original noise parameter ranking algorithm. Finally, simulation results show that the proposed algorithm can improve decoding performance. The research in this study provides a more effective noise error mode sorting strategy for the future GRAND-MO algorithm to reduce decoding delay and provides a basis for further optimizing noise error modes in the future. In the future, it will be jointly optimized with the noise bit error mode of the GRAND-MO decoder to comprehensively evaluate the decoding performance and continuously improve the decoding strategy.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

MQ completed the writing of the article, YG proposed the idea and completed the experimental design, BH, HW, YY, and WZ completed the review of the article.

Funding

This work was supported by the Sichuan Provincial Science and Technology Department “Research on Key Technologies of Adaptive Communication in Complex Environment,” project number 2019YJ0309.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publishers, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank professor YY, lecturer HW, lecturer QZ and TL, FK, ZZ, YL, ZC, HW, WZ, CG for the completion of this article. The correspondance author YG especially thanks FW for her support to him. We thank the project “Research on Key Technologies of Adaptive Communication in Complex Environment” (Project No. 2019YJ0309) of the Sichuan Provincial Science and Technology Department for its support of this work.

References

(2013) (1613). IEEE.1-2013 - IEEE Standard Environmental and Testing Requirements for Communications Networking Devices Installed in Transmission and Distribution Facilities

Google Scholar

Abbas, S. M., Tonnellier, T., Ercan, F., and Gross, W. J. (2020). High-throughput VLSI Architecture for GRAND. 2020 IEEE Workshop on Signal Processing Systems (SiPS). IEEE, 1–6. doi:10.1109/sips50750.2020.9195254

CrossRef Full Text | Google Scholar

Abbas, S. M., Tonnellier, T., Ercan, F., Jalaleddine, M., and Gross, W. J. (2022). High-throughput and Energy-Efficient VLSI Architecture for Ordered Reliability Bits GRAND. IEEE Transactions on Very Large Scale Integration (VLSI) Systems.doi:10.1109/tvlsi.2022.3153605

CrossRef Full Text | Google Scholar

Abbas, S. M., Tonnellier, T., Ercan, F., Jalaleddine, M., and Gross, W. J. (2021). High-throughput VLSI Architecture for Soft-Decision Decoding with ORBGRAND. ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 8288–8292. doi:10.1109/icassp39728.2021.9414908

CrossRef Full Text | Google Scholar

Abrahamsen, F. E., Ai, Y., and Cheffena, M. (2021). Communication Technologies for Smart Grid: A Comprehensive Survey. Sensors 21 (23), 8087. doi:10.3390/s21238087

PubMed Abstract | CrossRef Full Text | Google Scholar

An, W., Médard, M., and Duffy, K. R. (2021). CRC Codes as Error Correction Codes. ICC 2021-IEEE International Conference on Communications. IEEE, 1–6. doi:10.1109/icc42927.2021.9500279

CrossRef Full Text | Google Scholar

An, W., Médard, M., and Duffy, K. R. (2022). Keep the Bursts and Ditch the Interleavers. IEEE Trans. Commun. doi:10.1109/tcomm.2022.3171798

CrossRef Full Text | Google Scholar

Barac, F., Gidlund, M., and Zhang, T. (2013). Channel Coding and Interleaving in Industrial WSN: Abiding to Timing Constraints and Bit Error Nature. IEEE International Workshop on Measurements & Networking (M&N). IEEE, 46–51. doi:10.1109/iwmn.2013.6663775

CrossRef Full Text | Google Scholar

Barbulescu, A. S., and Pietrobon, S. S. (1994). Interleaver Design for Turbo Codes. Electron. Lett. 30 (25), 2107–2108. doi:10.1049/el:19941434

CrossRef Full Text | Google Scholar

Condo, C. (2022). A Fixed Latency ORBGRAND Decoder Architecture with LUT-Aided Error-Pattern Scheduling. IEEE Transactions on Circuits and Systems I: Regular Papers.doi:10.1109/tcsi.2022.3150583

CrossRef Full Text | Google Scholar

Condo, C., Bioglio, V., and Land, I. (2021). High-performance Low-Complexity Error Pattern Generation for ORBGRAND Decoding. 2021 IEEE Globecom Workshops (GC Wkshps). IEEE, 1–6. doi:10.1109/gcwkshps52748.2021.9682165

CrossRef Full Text | Google Scholar

Condo, C., and Nicolescu, A. (2021). Input-distribution-aware Parallel Decoding of Block Codes. 2021 11th International Symposium on Topics in Coding (ISTC). IEEE, 1–5. doi:10.1109/istc49272.2021.9594071

CrossRef Full Text | Google Scholar

Duffy, K. R., and Médard, M. (2019). Guessing Random Additive Noise Decoding with Soft Detection Symbol Reliability Information-SGRAND. IEEE International Symposium on Information Theory (ISIT). IEEE, 480–484. doi:10.1109/isit.2019.8849297

CrossRef Full Text | Google Scholar

Duffy, K. R. (2021). Ordered Reliability Bits Guessing Random Additive Noise Decoding. ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 8268–8272. doi:10.1109/icassp39728.2021.9414615

CrossRef Full Text | Google Scholar

Duffy, K. R., Solomon, A., Konwar, K. M., and Médard, M. (2020). 5G NR CA-Polar Maximum Likelihood Decoding by GRAND. 2020 54th Annual Conference on Information Sciences and Systems (CISS). IEEE, 1–5. doi:10.1109/ciss48834.2020.1570617412

CrossRef Full Text | Google Scholar

Gilbert, E. N. (1960). Capacity of a Burst-Noise Channel. Bell Syst. Tech. J. 39 (5), 1253–1265. doi:10.1002/j.1538-7305.1960.tb03959.x

CrossRef Full Text | Google Scholar

Ho, C. D., Nguyen, T.-V., Huynh-The, T., Nguyen, T.-T., da Costa, D. B., and An, B. (2021). Short-packet Communications in Wireless-Powered Cognitive IoT Networks: Performance Analysis and Deep Learning Evaluation. IEEE Trans. Veh. Technol. 70 (3), 2894–2899. doi:10.1109/tvt.2021.3061157

CrossRef Full Text | Google Scholar

Pang, Z., Luvisotto, M., and Dzung, D. (2017). Wireless High-Performance Communications: The Challenges and Opportunities of a New Target. EEE Ind. Electron. Mag. 11 (3), 20–25. doi:10.1109/mie.2017.2703603

CrossRef Full Text | Google Scholar

Platschek, A., Thiemann, B., and Zeilinger, H. (2015). Modelling Burst Errors in Industrial Networks. IEEE World Conference on Factory Communication Systems (WFCS). IEEE, 1–4. doi:10.1109/wfcs.2015.7160587

CrossRef Full Text | Google Scholar

Platschek, A., Thiemann, B., Zeilinger, H., and Sauter, T. (2015). An Error Model for Safe Industrial Communication. IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society. IEEE, 004672–004677. doi:10.1109/iecon.2015.7392829

CrossRef Full Text | Google Scholar

Solomon, A., Duffy, K. R., and Médard, M. (2021). Managing Noise and Interference Separately-Multiple Access Channel Decoding Using Soft GRAND2021 IEEE International Symposium on Information Theory (ISIT). IEEE, 2602–2607. doi:10.1109/isit45174.2021.9517890

CrossRef Full Text | Google Scholar

Solomon, A., Duffy, K. R., and Médard, M. (2020).Soft Maximum Likelihood Decoding Using GRAND. ICC 2020-2020 IEEE International Conference on Communications (ICC). IEEE, 1–6. doi:10.1109/icc40277.2020.9149208

CrossRef Full Text | Google Scholar

Yiqian, L. I., Liu, L. I. U., Huiting, L. I., and Kun Zhang, Z. Y. (2019). Research on Characteristics of Industrial IoT Wireless Channel. Chin. J. Internet Things 3 (4), 34.

Google Scholar

Zhan, M., Pang, Z., Dzung, D., Luvisotto, M., Yu, K., and Xiao, M. (2019). Towards High-Performance Wireless Control: Packet Error Rate in Real Factory Environments. IEEE Trans. Industrial Inf. (99), 1.

Google Scholar

Zhan, M., Pang, Z., Dzung, D., and Xiao, M. (2018). Channel Coding for High Performance Wireless Control in Critical Applications: Survey and Analysis. IEEE Access 6, 29648–29664. doi:10.1109/access.2018.2842231

CrossRef Full Text | Google Scholar

Zhan, M., Pang, Z., Xiao, M., Luvisotto, M., and Dzung, D. (2018). Wireless High-Performance Communications: Improving Effectiveness and Creating Ultrahigh Reliability with Channel Coding. EEE Ind. Electron. Mag. 12 (3), 32–37. doi:10.1109/mie.2018.2850661

CrossRef Full Text | Google Scholar

Zhan, M., Pang, Z., Yu, K., and Dzung, D. (2021). Interleaver in Coded Short Packets Transmission: A Preliminary Result. 2021 17th IEEE International Conference on Factory Communication Systems (WFCS). IEEE, 111–114. doi:10.1109/wfcs46889.2021.9483603

CrossRef Full Text | Google Scholar

Zhan, M., Pang, Z., Yu, K., Xu, J., Wu, F., and Xiao, M. (2022). Noise Error Pattern Generation Based on Successive Addition-Subtraction for GRAND-MO. IEEE Commun. Lett. 26 (4), 743–747. doi:10.1109/lcomm.2022.3148302

CrossRef Full Text | Google Scholar