Short-term frequency regulation of power systems based on DFIG wind generation

Short-term frequency regulation is important for the safety and efficiency of power systems based on wind generation units. However, unmodeled dynamics and stochastic disturbances in wind speed and load present a challenge for frequency regulation. This paper offers a frequency regulation scheme that caters for doubly fed induction generator-based wind power units requiring short-term frequency regulation. To this end, a data-driven additive controller is cast into a stochastic framework. Since the survival information potential (SIP) of a random variable has some advantages over information potential, the SIP of frequency deviation is presented in order to simultaneously evaluate droop control and inertial control. Thereafter, the optimal additive control coefficient can be obtained using a particle swarm optimization technique and an arithmetic mean filter. Finally, simulation results demonstrate the effectiveness of the proposed approach over traditional additive control strategies.

Introduction

In recent years, doubly fed induction generator (DFIG) based-wind turbines have been widely connected to power systems. With the increasing penetration of wind energy, power system frequency performance tends to deteriorate when there are severe disturbances, due to lack of inertia and primary frequency response. In this context, wind power generation units are expected to provide inertial response and primary frequency regulation. Moreover, analysis has been made of the system frequency response of power systems with high penetration wind power (Ela et al., 2014; Ghosh et al., 2016; Wu et al., 2018).

Frequency regulation plays an important role in maintaining the balance between generation and load. The frequency response is usually classified into four kinds: inertia response, primary frequency response (PFR), secondary frequency response, and tertiary frequency response. Because wind turbine generation units can play an important role in mitigating the steady-state frequency deviation before any secondary frequency regulation, this paper focuses on investigating a control method for DFIG-based wind turbines for short-term frequency regulation support in power systems.

Some attempts have been made to investigate short-term frequency regulation by DFIG-based wind turbines. These works can be roughly classified under three categories: deloading strategies, inertial control, and primary frequency regulation.

DFIG-based wind turbines participating in frequency regulation need to operate in a suboptimal mode through deloading. This is so a certain margin of spinning reserve or headroom is always available to supply additional active power in case of frequency contingency. A primary reserve can be obtained by “balance” control, “delta” control, or “fixed reserve” control (Wu et al., 2018). Zertek et al. (2012) employed a control strategy to reduce the deloading margin, while providing the same amount of power reserve for PFR. The governor droop and the mechanical power reserve can be resolved to ensure that the combined inertia and mechanical power reserves are equal to the desired value.

With the increasing penetration of wind power in power systems, system inertia will decrease. For this reason, it is necessary to study inertial control methods. Ekanayake and Jenkins (2004) present an inertial control strategy and compare the responses of fixed-speed induction generators and DFIGs. Morren et al. (2006) investigate an inertial controller and droop controller for a DFIG-based variable speed wind turbine. Kim and Muljadi (2019a) explore the dynamic possibilities of boosting the inertial response of an energy storage embedded DFIG to enhance the frequency nadir in the system. A capability-coordinated frequency control scheme is presented for a virtual power plant in Kim et al. (2019b).

To emulate the PFR of conventional synchronous generators, droop control is also used in DFIG-based wind turbines, where additional active power is provided based on the grid frequency deviation. In Ackermann et al. (2012), the droop controller with a fixed slope and a pre-defined dead band prevent system frequency decline and minimize the steady-state frequency deviation. In addition, the slope and dead band of a droop curve can be adjusted in real-time according to the variable wind speed, deloaded level, or rate of change of frequency (ROCOF) value. Vidyanandan and Senroy (2013) improve primary frequency response by continuously adjusting the droop value of the wind turbine in response to wind velocity. The droop parameter is varied by assigning decreasing values of droop against increasing values of power reserve margin. The root mean square (RMS) value of frequency deviations then dramatically diminishes. In order to prevent large frequency excursions and facilitate smooth recovery of the kinetic energy of wind turbine generators, Garmroodi et al. (2018)propose a time-variable droop characteristic for frequency support from wind turbine generators. The frequency nadir following a contingency can be largely improved. At the same time, the wind turbine generators can smoothly regain kinetic energy and continue operating at the maximum power point. In Datta et al. (2019), based on P-f sensitivity, a novel dynamic sectional droop control is designed for DFIG-based wind turbines. The droop control is divided into a highly sensitive region for low-frequency deviation and a less sensitive region for higher frequency deviation. Indeed, it is greatly beneficial to adjust the droop coefficient in real time. Wang et al. (2020) propose an advanced adaptive droop control method for DFIG operating under cyber uncertainty, in order to improve the response speed of wind turbines for frequency support. Yang et al. (2022) present an adaptive droop control scheme with smooth rotor speed recovery capability in order to improve the frequency nadir and minimize the second drop in the frequency. A variable droop gain-based control strategy is presented to maximize frequency support in Li et al. (2018), in which the droop gains are adjusted based on different rotor speeds. Nevertheless, the abovementioned time-variable droop controllers do not take stochastic disturbance into account. In practice, stochastic disturbances, mainly induced by wind speed, are non-Gaussian rather than Gaussian distribution. Topp-Leone Lindley distribution was thus introduced to model wind speed in Jia et al. (2020).

In addition, some coordinated control strategies are introduced that integrate deloading strategies, inertial control, droop control, and so on. Thus, Ma et al. (2010)combine inertial control, rotor speed control, and pitch angle control approaches to a DFIG-based wind turbine participating in frequency regulation. Zhang et al. (2012)propose a frequency regulation strategy for DFIG-based wind turbines by coordinating inertial control, rotor speed control, and pitch angle control. The coordinated strategies between rotor speed and pitch angle controls can be divided into low, medium, or high wind speed modes. Margaris et al. (2012) present a frequency controller for DFIG-based wind turbines by incorporating both inertial control and droop control. Wu et al. (2019)present a coordinated control strategy for frequency regulation at a wind farm. The inertial gain and the droop gain are described by a parabolic function and a linear function, respectively. The time-varying gains of the inertial and droop control loops are determined based on the desired frequency response time. Lee et al. (2016a), Lee et al. (2016b) adjusts the gains of the inertial controller and droop controller depending on rotor speed, so that a DFIG operating at a higher rotor speed releases more kinetic energy. Compared with a constant gain control scheme, the gains are proportional to the kinetic energy stored in a DFIG-based wind turbine. Accordingly, the frequency nadir can be improved, while ensuring stable operation of all DFIG-based wind turbines. In Zhang et al. (2012), a novel frequency regulation by DFIG-based wind turbines is presented to coordinate inertial control, rotor speed control, and pitch angle control. The gain in inertia control is calculated through analysis of the worst-case scenario, rather than on twice the total inertia constant of the DFIG-based wind turbine. Some scholars put forward power reference-based short-term frequency regulation methods. Bao et al. (2021) propose a hierarchical control scheme, which includes a wind farm level coordination, plus a wind turbines/battery energy storage system level coordination in active power outputs. Yang et al. (2018) presents a dynamic frequency support scheme, which supplies constant power during the deceleration period, and smoothly decreases the output of a DFIG during the acceleration period. Kang et al. (2016) present a stable adaptive inertial control scheme for a doubly fed induction generator, in which the power reference is defined in deceleration and acceleration periods respectively.

Short term frequency regulation is a challenge, due to inevitable uncertainties, such as hypothesis simplification, model linearization, time-varying parameters, and stochastic disturbances. The traditional model-based controller, based on the nominal linear model, cannot obtain satisfactory control performance when the operating condition changes, stimulating the data-driven control method to deal with the uncertainties with acceptable online computation.

The motivations for using the data-driven stochastic controller for short-term frequency regulation, rather than the traditional model-based controller, are as follows:

• It is difficult to build an accurate model for studying model-based PFR methods due to non-linearities, random disturbances, time-varying, and coupling in power systems. In addition, it could be expensive and time-consuming to obtain an accurate model to represent the system frequency response of a power system with DFIG-based wind generation units.

• Fluctuation of wind power affected by wind speed is introduced into power systems. In particular, the wind speed is not necessarily Gaussian. Hence, it is necessary to investigate short-term frequency regulation under a stochastic framework. The information-theoretic quantities estimated directly from the data can be used to design the frequency controller.

• A data-driven controller is more appealing, due to the advantages of a lighter computation burden and ease of coding.

The main contributions of this paper are as follows: 1) Following the abovementioned coordinated short-term frequency regulation strategy, this work proposes a new frequency regulation strategy to deal with non-Gaussian disturbances. It incorporates an improved dynamic additive control method, where the droop control coefficient can be tuned adaptively according to a real-time state. 2) The adaptive additive controller is designed from a data-driven method, rather than a model-based method, and the proposed optimal control strategy is iteratively solved with high solution efficiency. 3) The survival information potential (SIP) of the frequency deviation can characterize its uncertainty well. Hence, the SIP of frequency deviation is employed to construct the performance index for a power system with wind power generation units. 4) A particle swarm optimization (PSO) technique and arithmetic mean filter are utilized to obtain the optimal additive control law.

The paper is organized as follows: A section on coordinated frequency regulation presents an overall short-term frequency controller architecture and illustrates DFIG-based wind turbine model development. The section on additive control proposes a performance index to evaluate PFR and inertial control simultaneously, and then a data-driven additive control methodology is presented. Afterward, the implementation results of the proposed controller on a DFIG-based wind turbine participating in short-term frequency regulation are discussed under a section titled “Simulations.”

Coordinated frequency regulation

When a wind turbine is running in MPPT mode, although it can capture maximal wind energy, it cannot continuously increase the active power when system frequency changes suddenly. It is thus necessary to use a deloading strategy to store part of the active reserve capacity and hence continuously provide active power for regulating frequency.

Vector control technology is used to realize the decoupling control of the active and reactive components of the wind turbine. In this way, controlling the variable speed operation of the wind turbine and providing reactive voltage support are possible. However, because its speed is decoupled from the grid frequency, the speed of the wind turbine itself does not change significantly when the grid frequency changes. Therefore, the supplementary frequency controller should be employed in order to enable the wind turbine to provide additional system frequency response.

The coordinated frequency regulation system shown in Figure 1 integrates the deloading strategy, inertial control, and droop control (Zhang et al., 2020). The deloading strategy maintains a certain power reserve for frequency regulation. The additional frequency controller, including the inertial controller and the droop controller, can provide additional power for the generator power reference. In this work, the additive controller is designed under the framework of stochastic control. A PSO method is employed to solve the optimal additive control solution by minimizing the survival information potential (SIP) of the frequency deviation. Consequently, the coordinated control outperforms inertial or droop control.

FIGURE 1

FIGURE 1. Coordinated frequency regulation system.

Wind turbine generator system

DFIG-based wind turbines are widely used on large-scale wind farms and are connected to the grid as shown in Figure 2. The wind turbine and the generator are connected by a centralized mass mechanical transmission system. The generator stator is directly connected to the network, while the rotor side is connected to the grid through back-to-back dual PWM converters (Lara et al., 2009). Both the stator and the rotor can feed the grid. In this section, the DFIG-based wind turbine is modelled.

FIGURE 2

FIGURE 2. DFIG-based wind turbine connected to grid.

Wind speed model

The wind speed on a wind farm usually depends on certain factors, such as the climate, topography and landform of the local area. The Weibull distribution is generally used to describe the probability density function (PDF) of the wind speed. This is often used to reflect seasonal or annual wind speed changes over a long time scale. Moreover, a large amount of actual wind farm data is needed to represent Weibull distribution during simulation analysis. Therefore, a relatively simple combined wind speed model (Anderson et al., 1983) will be used in this work to describe the random and intermittent characteristics of wind speed in the short term.

1) Base wind

The base wind reflects the change in the average wind speed. During the operation of the wind turbine, the base wind always exists. In considering the simulation analysis of the second-level time period, the average wind speed can be taken as a constant.

$v_b=k(1)$

where $k$ is a constant.

2) Gust wind

Wind speed by nature is not always stable. A gust wind model with cosine characteristics over a period of time can be used to simulate this characteristic of wind.

$v_g=\{\begin{array}{cc}\begin{array}{c}0\\ \frac{v_{gmax}}{2}\left[1-\text{cos}2\pi \left(\frac{t-t_{g1}}{T_g}\right)\right]\\ 0\end{array}& \begin{array}{c}t<t_{g1}\\ t_{g1}\le t\le t_{g1}+T_g\\ t>t_{g1}+T_g\end{array}\end{array}(2)$

where $v_g$ is the gust wind, $v_{gmax}$, $t_{g1}$, and $T_g$ stand for the start time of the gust wind, the amplitude of the gust wind, and the period of the gust wind, respectively.

3) Ramp wind

The following ramp wind model is used to describe the gradual change characteristics of wind speed:

$v_r=\{\begin{array}{cc}\begin{array}{c}0\\ v_{rmax}\frac{t-t_{r1}}{t_{r2}-t_{r1}}\\ 0\end{array}& \begin{array}{c}t<t_{r1}\\ t_{r1}\le t\le t_{r2}\\ t>t_{r2}\end{array}\end{array}(3)$

where $v_r$ is the ramp wind, $v_{rmax}$ the amplitude of the ramp wind, $t_{r1}$ the start time of the ramp wind, and $t_{r2}$ the start time of the ramp wind.

4) Noise wind

Even if the wind speed in the actual wind farm is maintained near a certain average value, the wind speed value at each moment is irregular, so a random component can be superimposed on the average wind speed to reflect the random fluctuation in wind speed.

$v_n=v_{nmax}\cdot Rand\left(-\mathrm{1,1}\right)\text{cos}\left({\omega }_{n}t+\phi \right)(4)$

where $v_n$ is the noise wind, and $v_{nmax}$ represents the amplitude of noise wind. $Rand\left(-1, 1\right)$ stands for a random number evenly distributed between −1 to 1, ${\omega }_n$ is the average distance of wind speed fluctuation between $0.5\pi \text{ to} 2\pi \left(ras/s\right)$, and $\phi$ represents a random number evenly distributed between 0 to $2\pi$.

By superimposing the above four wind speed models, the following combined wind speed model is obtained to describe the wind speed changes in the short term.

$v=v_b+v_g+v_r+v_n(5)$

Wind turbine model

The relationship between the mechanical power captured by wind turbines from wind energy and wind speed (Kundur, 1994; Lara et al., 2009) is:

$P_m=T_m{\omega }_t=\frac{1}{2}\rho \pi R^2{\upsilon }^3{C}_p(6)$

where $T_m$ is the mechanical torque applied to the rotor, ${\omega }_t$ and $v$ are the angular speed of the wind turbine and the wind speed, respectively, while $\rho$ and $R$ represent the density of air and the length of blade, respectively. $C_p$ is known as the coefficient of the performance of the wind turbine, which can be calculated by

$C_p=\left(0.44-0.0167\beta \right)\sin \left[\frac{\pi \left(\lambda -3\right)}{15-0.3\beta }\right]-0.00184\left(\lambda -3\right)\beta (7)$

where $\beta$ and $\lambda$ are the pitch angle and the ratio of the turbine blade tip speed, respectively

$\lambda =\frac{R{\omega }_t}{\nu }(8)$

Drive train model

The drive train of the DFIG wind turbine can be represented by the following two-mass model (Ela et al., 2014; Ghosh et al., 2016)

$\frac{d{\omega }_r}{dt}=\frac{1}{J_{eq}}\left(T_m-T_e-B{\omega }_t\right)(9)$

where $T_e$ and $B$ are the electromagnetic torque applied to the rotor by the generator and the total friction factor of the DFIG system, respectively, and $J_{eq}$ stands for the combined rotor and wind turbine inertia constant.

Converter model

In this work, the investigated DFIG uses two back-to-back PWM voltage-sourced converters to connect to the grid: the rotor-side converter $\left(C_{rotor}\right)$ and the grid-side converter $\left(C_{grid}\right)$. Both $C_{rotor}$ and $C_{grid}$ have an independent vector control system. $C_{rotor}$ uses vector control technology to decompose the DFIG rotor current into decoupled active and reactive components, and the control goal of the $C_{grid}$ is to keep the intermediate DC link voltage stable.

The simplified model of the main circuit of the PWM converter is shown in Figure 3.

FIGURE 3

FIGURE 3. PWM converter main circuit simplified model.

Assuming that $S_i$ is the switching function of phase i (i = a, b or c), then $S_i$ can be expressed as follows:

$S_i=\{\begin{array}{cc}1& i-\text{phase upper arm is on}\\ 0& i-\text{phase lower arm is on}\end{array}(10)$

The mathematical model of the voltage source PWM converter in the three-phase static coordinate system is

$\{\begin{array}{c}\begin{array}{c}{L}_c\frac{d{i}_a}{dt}=e_a-R_c{i}_a-\left(S_a-\frac{S_a+S_b+S_c}{3}\right)U_{dc}\\ L_c\frac{d{i}_b}{dt}=e_b-R_c{i}_b-\left(S_b-\frac{S_a+S_b+S_c}{3}\right)U_{dc}\\ L_c\frac{d{i}_c}{dt}=e_c-R_c{i}_c-\left(S_c-\frac{S_a+S_b+S_c}{3}\right)U_{dc}\end{array}\\ C\frac{d{U}_{dc}}{dt}=i_r-\left(S_a{i}_a+S_b{i}_b+S_c{i}_c\right)\end{array}(11)$

where $R_c$ and $R_L$ are the AC side resistance and inductance of the converter, respectively, $e_a,e_b$, and $e_c$ represent the grid voltage, and $i_a,i_b$, and $i_c$ stand for the AC side current of the converter. $U_{dc}$ is the DC side voltage.

In order to achieve decoupling control of active and reactive power, the mathematical model of the converter in the three-phase stationary coordinate system can be simplified in the dq two-phase synchronous coordinate system through Park’s Transformation.

$\left[\begin{array}{c}{F}_d\\ F_q\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}\mathit{cos}\theta & \mathit{cos}\left(\theta -\frac{2}{3}\pi \right)& \mathit{cos}\left(\theta +\frac{2}{3}\pi \right)\\ -\mathit{sin}\theta & -\mathit{sin}\left(\theta -\frac{2}{3}\pi \right)& -\mathit{sin}\left(\theta +\frac{2}{3}\pi \right)\end{array}\right]\left[\begin{array}{c}{F}_A\\ F_B\\ F_C\end{array}\right](12)$

where $F_A$, $F_B$, and $F_C$ are coefficients in the abc three-phase stationary coordinate system, and $F_d$ and $F_q$ represent the transformed coefficients in the dq two-phase synchronous coordinate system.

According to Eq. 12, the mathematical model of the voltage source PWM converter in the dq two-phase static coordinate system is

$\{\begin{array}{c}{L}_c\frac{d{i}_d}{dt}=u_{sd}-R_c{i}_d+{\omega }_e{L}_c{i}_q-u_d\\ L_c\frac{d{i}_q}{dt}=u_{sq}-R_c{i}_q+{\omega }_e{L}_c{i}_d-u_q\\ C\frac{d{U}_{dc}}{dt}=i_r-\left(\frac{u_d}{U_{dc}}{i}_{dg}+\frac{u_q}{U_{dc}}{i}_{qg}\right) \end{array}(13)$

where $i_d$ and $i_q$ are the d-axis and q-axis components of the AC two-phase current of the converter, respectively. $U_{dc}$ and $R_c$ represent the DC voltage and the AC side resistance of the inverter, $L_c$ is the AC side inductance of the inverter, $u_d$ and $u_q$ are the d-axis and q-axis components of the AC side voltage of the converter, respectively, and $i_{dg}$ and $i_{qg}$ stand for the d-axis and q-axis components of $i_g$, respectively.

Generator model

In this section, the model of the DFIG is investigated under the same basic assumptions as Kundur (1994). The induction machine is controlled in a synchronously rotating dq-axis framer. There is no magnetic coupling between the two-phase windings. As shown in Figure 4, the stator and rotor voltage equations are

$\{\begin{array}{c}{u}_{sd}=R_s{i}_{sd}-{\omega }_e{\psi }_{sq}+\frac{d{\psi }_{sd}}{dt}\\ u_{sq}=R_s{i}_{sq}+{\omega }_e{\psi }_{sd}+\frac{d{\psi }_{sq}}{dt}\end{array}(14)$

$\{\begin{array}{c}{u}_{rd}=R_r{i}_{rd}-\left({\omega }_e-{\omega }_r\right){\psi }_{rq}+\frac{d{\psi }_{rd}}{dt}\\ u_{rq}=R_r{i}_{rq}+\left({\omega }_e-{\omega }_r\right){\psi }_{rd}+\frac{d{\psi }_{rq}}{dt}\end{array}(15)$

where $u_{sd}$ and $u_{sq}$ are the voltage components of the stator d-axis and q-axis, respectively, $u_{rd}$ and $u_{rq}$ represent the voltage components of the rotor d-axis and q-axis, respectively, $i_{sd}$ and $i_{sq}$ stand for the stator d-axis and q-axis current components, and $i_{rd}$ and $i_{rq}$ are the rotor d-axis and q-axis current components, respectively. $R_s$ and $R_r$ represent the equivalent resistance of the stator and rotor, ${\omega }_e$ and ${\omega }_r$ are the synchronous angular velocity and the rotor angular speed, respectively, ${\psi }_{sd}$ and ${\psi }_{sq}$ stand for the flux linkage components of the stator d-axis and q-axis, respectively, and ${\psi }_{rd}$ and ${\psi }_{rq}$ are the flux linkage components of the rotor d-axis and q-axis, respectively.

FIGURE 4

FIGURE 4. Diagram of the DFIG equivalent model in the dq coordinate system.

The stator and rotor flux linkage equations are

$\{\begin{array}{c}{\psi }_{sd}=L_s{i}_{sd}+L_m{i}_{rd}\\ {\psi }_{sq}=L_s{i}_{sq}+L_m{i}_{rq}\end{array}(16)$

$\{\begin{array}{c}{\psi }_{rd}=L_m{i}_{sd}+L_r{i}_{rq}\\ {\psi }_{rq}=L_m{i}_{sq}+L_r{i}_{rq}\end{array}(17)$

where $L_m$ is the mutual inductance between the stator winding and rotor winding in the dq coordinate system, $L_s$ stands for the self-inductance between the stator windings in the dq coordinate system, and $L_r$ is the self-inductance between the rotor windings in the dq coordinate system.

The active and reactive power on the stator side are

$\{\begin{array}{c}{p}_s=-\frac{3}{2}\left(u_{sd}{i}_{sd}+u_{sq}{i}_{sq}\right)\\ q_s=-\frac{3}{2}\left(u_{sq}{i}_{sd}-u_{sd}{i}_{sq}\right)\end{array}(18)$

and the active and reactive power on the rotor side are

$\{\begin{array}{c}{p}_r=-\frac{3}{2}\left(u_{rd}{i}_{rd}+u_{rq}{i}_{rq}\right)\\ q_r=-\frac{3}{2}\left(u_{rq}{i}_{rd}-u_{rd}{i}_{rq}\right)\end{array}(19)$

The electromagnetic torque equation is

$T_e=\frac{3}{2}{p}_n\left({\psi }_{sq}{i}_{sd}-{\psi }_{sd}{i}_{sq}\right)(20)$

where $p_n$ is the pairs of poles of the generator.

The voltages behind the transient reactance of the stator d-axis and q-axis (Kundur, 1994) are as follows:

$\{\begin{array}{c}{E}_d=-{\omega }_e\frac{L_m}{L_r}{\psi }_{rq}\\ E_q={\omega }_e\frac{L_m}{L_r}{\psi }_{rd} \end{array}(21)$

Aggregated model

A large-scale wind farm usually consists of several hundred units. When studying the frequency regulation strategy of the power system with wind power, the equivalent wind farm model is usually needed. First, all the units in a wind farm can be divided into several sections, according to the wind speed. Then the units in the same section can be equitably aggregated. As shown in Figure 5, the whole wind farm is divided into M sections, and each section is composed of dozens of wind turbines with the same capacity and specifications.

FIGURE 5

FIGURE 5. Units in a section.

n units in the same section are aggregated, the equivalent unit capacity is the sum of all wind turbine capacities of the same group:

$S_{eq}={\displaystyle \sum _{i=1}^n{S}_i}(22)$

where $S_{eq}$ and $S_i$ are the equivalent unit capacity and the capacity of the ith unit, respectively. The ratio of the capacity of the aggregated unit to the total capacity of the units in the section is defined as the weight coefficient

$W_i=\frac{S_i}{S_{eq}}(23)$

The equivalent unit still maintains the same power output characteristics as a single unit. The equivalent principles of rotor impedance, excitation reactance, stator impedance, inertia time constant, damping coefficient and other parameters are as follows:

$X_{eq}={\displaystyle \sum _{i=1}^n{W}_i{X}_i}(24)$

where X is the parameter that needs to be aggregated, such as the rotor resistance, the leakage inductance, and the viscous friction factor.

According to the principle of equivalence above, the aggregate model of a wind farm can be obtained, which then lays a foundation for the study of a primary frequency regulation strategy for wind farms.

A simplified model of a DFIG-based wind turbine can be used to describe the generator’s mechanical torque according to the incoming wind speed. Besides the rotor model, the drive train model, and the induction generator model, the simplified wind turbine model still includes the rotor speed controller represented by the power-speed control curve and the blade pitch angle controller.

It is difficult to build an accurate physical model on principles. However, it should be noted that a simplified model can be used to investigate the dynamic characteristics of the wind turbine generator system, or to perform small-signal stability analysis (Margaris et al., 2012; Wang et al., 2018).

Deloading strategy

The frequency of the power system depends on the balance between the power generation on the power generation side, and the load on the power consumption side. As shown in Figure 1, the coordinated control system is designed for the DFIG based-wind turbine to implement short-term frequency regulation.

A deloading strategy is needed to curtail the power output earlier, in order that the droop control can respond to an under-frequency disturbance. As shown in Figure 6, the unit will deviate from the original MPPT mode in red to the sub-optimal mode in green.

FIGURE 6

FIGURE 6. Relation of output power and speed.

Deloading at low wind speeds

It can be observed from Figure 6 that when the wind speed is greater than the cut-in wind speed $\left(v_{in}\right)$ and less than the minimum wind speed for starting the pitch angle $\left(v_1\right)$ control, the unit runs along the AB segment in MPPT mode. To reduce the output power of the unit, the operating point can be shifted to the left or right by reducing or increasing the speed (de Almeida and Pecas Lopes, 2007). The right shift operating point is usually selected, because the left shift curve can cause system instability (Lara et al., 2009). The unit runs along $A^{\prime }{B}^{\prime }$, the pitch angle is zero, and the load reduction can then be achieved only by increasing the speed. The deloaded active power curve $P_{deloaded}$ can be expressed as in Pourbeik et al. (2013):

$P_{deloaded}=\left(1-d\%\right)P_m(25)$

where $d\%$ is the deload margin.

Deloading at middle wind speeds

It is evident from Figure 6 that the unit operates at point C when the wind speed reaches the maximum value $v_2$. In order to ensure the safe operation of the generator, the speed cannot be increased further. However, it cannot achieve the ideal deloading requirement only by overspeed. Therefore, when the wind speed is greater than $v_1$ and less than $v_2$, the unit runs along $B^{\prime }{C}^{\prime }$. It is necessary to start the pitch angle control to further reduce the power and to store a sufficient active power reserve for frequency regulation. The pitch angle reference ${\beta }_{ref}$ is expressed by Kundur (1994), as follows:

${\beta }_{ref}=\left({\omega }_t-{\omega }_{ref}\right)\left(k_p+\frac{k_i}{s}\right)\left(\frac{1}{1+s{T}_{\beta }}\right)(26)$

where ${\omega }_{ref}$ is the synchronous speed reference, $k_p$ and $k_i$ are the proportional and integral gains, respectively, and $T_{\beta }$ is the pitch time constant.

Deloading at high wind speeds

When the wind speed is $v_{out}$, it is no longer possible to limit the power by increasing the speed. Therefore, when the wind speed is greater than $v_2$ and less than $v_{out}$, the power is reduced only by pitch angle control to perform load shedding control.

Based on the above analysis, a complete wind power PFR strategy can be obtained. As shown in Figure 6, the deloading strategy stores a certain power reserve for frequency regulation.

Additive control

Additive control plays an important role in mitigating the steady state frequency deviation before the secondary frequency response. The variable additive gain can effect a compromise between improved frequency response and reduced impacts on the structural loading (Wu Z et al., 2018). It can be observed from Figure 1 that the additive gain can be tuned online according to the ROCOF value, deloaded level, or variable wind speed conditions.

Conventional additive control

A variable speed wind turbine, controlled by a power electronic converter, can adjust the active power flexibly and controllably. As shown in Figure 1, the additional frequency regulation incorporates the inertial control and droop control. Although the droop control contributes less at the beginning of a sudden frequency drop, the rotational kinetic energy of the DFIG-based wind turbine is released and converted to electrical energy. Consequently, the power output can be increased, and the additional frequency regulation can decrease the initial ROCOF and the frequency nadir. The generator power reference $\mathrm{\Delta }{P}_f$ is provided by the inertial control and droop control loop.

$\mathrm{\Delta }{P}_f=\mathrm{\Delta }{P}_{f1}+\mathrm{\Delta }{P}_{f2}(27)$

where $\mathrm{\Delta }{P}_{f1}$ and $\mathrm{\Delta }{P}_{f2}$ are the output of the inertial and droop control loop, respectively.

In order to realize the inertial response of the wind turbine, the active power reference signal $\mathrm{\Delta }{P}_{f1}$ related to ROCOF is

$\mathrm{\Delta }{P}_{f1}=-K_f\frac{df}{dt}(28)$

where $K_f$ is the inertial control constant. After a sudden change in the load, the inertial control can quickly generate a response and suppress the rapid change in the frequency. The adjustment time is generally several seconds.

In addition, the wind turbine can emulate the traditional governor response for PFR. Droop control is introduced to adjust the active power output of the wind turbine according to the frequency deviation. The power reference signal related to the frequency deviation $\mathrm{\Delta }{P}_{f2}$ is

$\mathrm{\Delta }{P}_{f2}=-\frac{1}{R}\mathrm{\Delta }f(29)$

where the droop gain $1/R$ is the inverse of the droop slope $R$, and $\mathrm{\Delta }f$ stands for the system frequency deviation. A high droop gain provides a large output from the droop control loop. The existing droop control gain is usually fixed. Although the variable droop control methods are presented in Vidyanandan and Senroy (2013); Garmroodi et al. (2018); Li et al. (2018); Datta et al. (2019); and Wang et al. (2020), these variable droop controllers are a little conservative and do not consider stochastic disturbances at all. In this work, the optimal additive control gain can be obtained online, based on a novel performance index discussed in the next section.

Survival information potential

The distribution of wind speed is usually non-Gaussian (Ma et al., 2010). Furthermore, there are non-linearities in DFIG-based wind turbines, and hence, it is necessary for an adaptive additive controller to decrease the randomness of the output of the additive control loop. The minimum error entropy (MEE) criterion has been applied to the design controller and filter (Yin et al., 2009; Guo et al., 2019; Li et al., 2020), which outperforms conventional criteria when dealing with non-linearities and non-Gaussian disturbances. The goal of the MEE-based control is to find a control signal to ensure the PDF of the closed-loop tracking error approach to a narrowly shaped normal distribution. In practice, the entropy is replaced by information potential (IP), because the IP can be calculated by a double summation over all samples directly. Recently, SIP was employed to design filters instead of IP (Chen et al., 2012; Zhang et al., 2016). SIP has some advantages over IP, such as shift-variant properties, easy estimation from sample data, robust measurement of uncertainty, and consistent definitions in both continuous and discrete domains.

For a random vector $X$ in ${\mathrm{ℝ}}^m$, the SIP of order $\alpha$ is defined as follows:

${\mathit{S}}_{\mathit{\alpha }}\left(X\right)={\displaystyle {\int }_{{\mathrm{ℝ}}_{+}^m}{\overline{F}}_{\left|X\right|}^{\alpha }\left(x\right)dx}(30)$

where ${\overline{F}}_{\left|X\right|}\left(x\right)=P\left(\left|X\right|>x\right)=E\left[\mathbb{I}\left(\left|X\right|>x\right)\right]$ is the survival function of the random vector $\left|X\right|$, and ${\mathrm{ℝ}}_{+}^m=\left\{x\in {\mathrm{ℝ}}^m:x=\left(x_1,\dots ,x_m\right), x_i\ge 0, i=1,\dots ,m \right\}$. $\left|X\right|>x$ means that $\left|X_i\right|>x_i$ and $\mathbb{I}(.)$ stand for the indication function (Chen et al., 2012).

Adaptive additive control

In this section, an adaptive additive control method is proposed for power systems with DFIG-based wind generation units. As indicated in Figure 7, the control horizon at instant $k$ is divided into $\overline{R}$ batches with $L$ frequency deviation data within each batch. For the $j^{th}$ batch, the frequency deviation data $e_j\left(i\right)|i=1,\dots ,L-1,L$ can be used to calculate the SIP of the frequency deviation ${\widehat{S}}_{\alpha j}$, then the optimal additive gain in the $j^{th}$ batch, $-1/R_j$, can be solved by minimizing ${\widehat{S}}_{\alpha j}$.

FIGURE 7

FIGURE 7. Additive control horizon.

From instant $k-1$ to instant $k$, there are $\overline{R}$ batches in which $L$ frequency deviation samples are collected. For each instant $k$, the optimal additive gain $\frac{1}{R^{\ast }\left(k\right)}$ can then be smoothed by the following arithmetic mean filter

$\frac{1}{R^{\ast }\left(k\right)}=\frac{1}{\overline{R}}{\displaystyle \sum _{j=1}^{\overline{R}}\frac{1}{R_j}}(31)$

where the optimal additive gain $\frac{1}{R_j}$ can be solved by minimizing the SIP of order $\alpha$ of the frequency deviation obtained by the collected frequency deviation samples in the $j^{th}$ batch.

In this work, the frequency deviation is scalar data case, i.e., $m=1$. As shown in Figure 7, based on the collected frequency deviation samples in the $j^{th}$ batch during $\left[k-1,k\right]$, the SIP of order $\alpha$ of the frequency deviation can then be calculated by

${\widehat{S}}_{\alpha }\left(e\left(k\right)\right)={\displaystyle \sum _{j=1}^L{\left(\frac{L-j+1}{L}\right)}^{\alpha }\left(\left|e{\left(k\right)}_j\right|-\left|e{\left(k\right)}_{j-1}\right|\right)}(32)$

where $e{\left(k\right)}_0=0$, (32) can be reformulated by

${\widehat{\mathit{S}}}_{\alpha }\left(e\left(k\right)\right)={\displaystyle \sum _{j=1}^L{\lambda }_j\left(\left|e{\left(k\right)}_j\right|\right)}(33)$

where ${\lambda }_j={\left(\frac{L-j+1}{L}\right)}^{\alpha }-{\left(\frac{L-j}{L}\right)}^{\alpha }$.

Since the ${\widehat{\mathit{S}}}_{\alpha }\left(e\left(k\right)\right)$ at $e{\left(k\right)}_j=0$ is unsmooth, the $\alpha$ order SIP of the frequency deviation is selected as the performance index to design the additive controller. Moreover, let the order $\alpha =2$ in this work.

The frequency deviation has played a vital role in the assessment of short-term frequency regulation performance, and so has the derivative of the frequency deviation. Hence, the frequency deviation $e\left(k\right)$ in Eq. 33 is replaced by

$\overline{e}\left(k\right)=k_1\left(\mathrm{\Delta }f\right)+k_2\left(\frac{d\mathrm{\Delta }f}{dt}\right)(34)$

where $k_1$ and $k_2$ are the weights of the frequency deviation and the derivatives of the frequency deviation. Consequently, the optimal additive coefficient in the $j^{th}$ batch can be solved by minimizing the following SIP of the hybrid term $\overline{e}\left(k\right)$ in ${\widehat{\mathit{S}}}_{\mathit{\alpha }}\left(\overline{e}\left(k\right)\right)$.

Thus, the additive gain in the $j^{th}$ batch can be solved by minimizing ${\widehat{\mathit{S}}}_{\mathit{\alpha }}\left(\overline{e}\left(k\right)\right)$, using a particle swarm optimization (PSO) technique (Dziwinski and Bartczuk, 2020). It can be observed from Figure 1 that the frequency deviation time series reflects influences from the ROCOF value, deloading level, and variable wind speed conditions.

The PSO algorithm originated from the study of bird predation behavior in nature. Each particle represents a potential solution to the problem to be solved. Each particle corresponds to an objective function value. The current speed of the particle determines the direction and distance of the particle movement. The speed varies with the particle itself and other particles. The experience is dynamically adjusted to achieve the individual’s optimization in the solvable space.

In a D-dimensional search space, population $X=\left(X_1,X_2,\dots ,X_n\right)$ consists of n particles. The D-dimensional vector $x_i={\left(x_{i1},x_{i2},\dots ,x_{iD}\right)}^T$ is the position of the ith particle in the D-dimensional search space, and also represents a potential solution to the problem of calculating the value of the objective function corresponding to each particle position $X_1$. The velocity of the ith particle is $V_i={\left(V_{i1},V_{i2},\dots ,V_{iD}\right)}^T$, the individual extreme value $P_i={\left(P_{i1},P_{i2},\dots ,P_{iD}\right)}^T$, and the population extreme value $P_g={\left(P_{g1},P_{g2},\dots ,P_{gD}\right)}^T$.

For the ith particle, the position at the time is determined by the position and velocity at the previous time:

$x_i^{k+1}=x_i^k+V_i^k(35)$

where the velocity of the particle at time k, $V_i^k$, is calculated by

$V_i^k=w{V}_i^{k-1}+c_1{r}_1\left(P_{best,i}-x_i^k\right)+c_2{r}_2\left(G_{best}-x_i^k\right)(36)$

where $w$ is the inertia weight, $c_1$ and $c_2$ are individual learning factors and social learning factors, respectively, and $r_1$ and $r_2$ represent random numbers distributed in 0∼1. $P_{best,i}$ stands for the optimal position of the individual with the ith particle, and $G_{best}$ is the best position for all particles. The flow chart of solving optimal additive gain using the particle swarm algorithm is shown in Figure 8.

FIGURE 8

FIGURE 8. Flowchart of PSO.

According to the above presentation, the additive control gain at instant $k$ can be computed, and the steps for implementing the data-driven control are summarized as follows:

Step 1: Acquire the frequency deviation data within $\overline{R}$ batches respectively at instant $k$.

Step 2: Compute the SIP of the hybrid term $\overline{e}\left(k\right)$ for the $j^{th}$ batch using Eq. 35.

Step 3: Calculate additive control gain $R^{\ast }$ in the $j^{th}$ batch by minimizing ${\widehat{\mathit{S}}}_{\mathit{\alpha }}\left(\overline{e}\left(k\right)\right)$ using PSO technique.

Step 4: Repeat the procedure from steps 2 and 3 for the next batch, $j=j+1$.

Step 5: Solve the optimal additive gain at the instant $k$ using the arithmetic mean filter in Eq. 31 to smooth the additive gains obtained in $\overline{R}$ batches.

Step 6: Implement the additive control gain $R^{\ast }$ on the power system and collect the frequency deviation data. Then repeat the procedure from Step 2 to Step 5 for the next instant, $k=k+1$.

Simulations

In this section, some simulations are conducted to verify the feasibility of the proposed coordinated frequency regulation method. The simulation system is shown in Figure 9. The system consists of a 600 MW thermal power plant $G_1$ and a 150 MW wind farm $G_2$ (100 units × 1.5 MW equivalent DFIG wind turbines). The DFIG parameters are described in Table 1, and the transmission line parameters are described in Table 2. All variables use per unit values, the frequency of the grid-side PWM carrier is set to 2700 Hz and the frequency of the rotor-side PWM carrier is set to 1620 Hz. Load stands for the active power of the load matching the capacity of the generating side.

FIGURE 9

FIGURE 9. Simulation system.

TABLE 1

TABLE 1. Parameters of DFIG.

TABLE 2

TABLE 2. Parameters of transmission line.

The collected frequency data is divided into 10 batches during two adjacent instants, i.e., $L=10$. $c_1$ and $c_2$ in Eq. 36 are set to 1.49445 and 1.49445 by trial and error. The deload margin $d\text{\% is set to }10\text{\%}$. To compare the conventional droop controller with the proposed adaptive additive controller, the conventional constant droop down and droop up coefficients are set to 0.05 and 0.02, respectively, according to the grid code in the Northeast Regulatory Bureau of National Energy Administration (2019). The frequency-power characteristics of the conventional droop control are shown in Figure 10.

FIGURE 10

FIGURE 10. Droop curve of wind turbine.

Scenario 1: Comparison between conventional and the proposed additive control strategies.

The wind speed in the farm is simulated as shown in Figure 11. The conventional additive control utilizes fixed inertial and droop coefficients. In this work, the inertial control constant in Eq. 28 is set to $K_f=10$ by trial and error, while the constant droop down and droop up coefficients are tuned, as shown in Figure 10. Figure 12 illustrates the results of the simulation of scenario 1. The system frequency dynamics demonstrated in Figure 12A are compared in terms of three cases: 1) DFIG-based wind power units do not participate in short-term frequency regulation (0, 20 s). 2) DFIG-based wind power units participate in short-term frequency regulation under the conventional additive control (red lines in Figure 12). 3) DFIG-based wind power units participate in short-term frequency regulation using the proposed adaptive additive control after 20 s (blue lines in Figure 12).

FIGURE 11

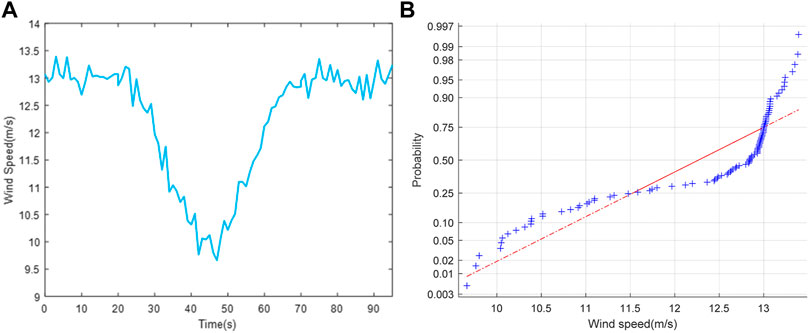
FIGURE 11. Wind speed and its probability distribution. (A) Wind speed. (B) Normal probability distribution test of wind speed.

FIGURE 12

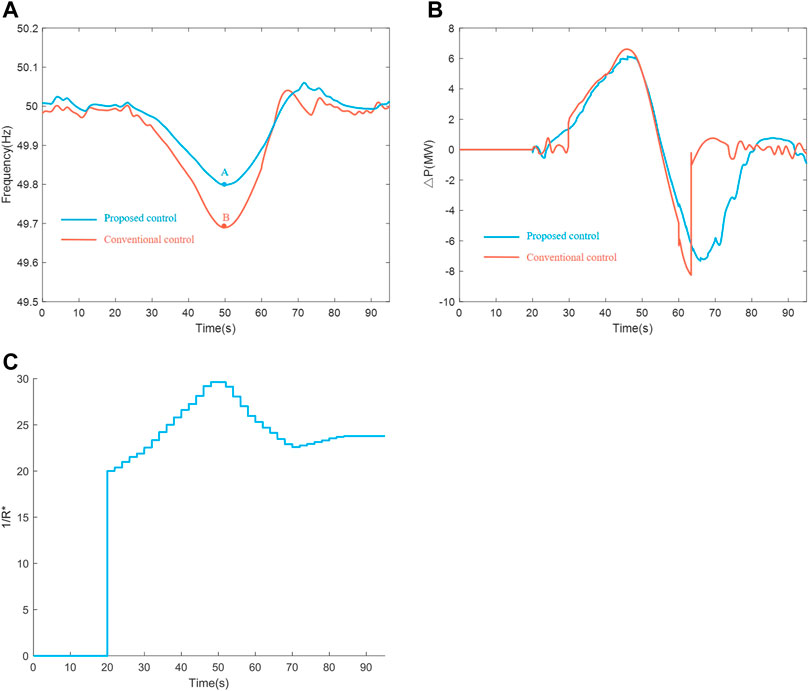
FIGURE 12. Comparison of system dynamic response. (A) Frequency response. (B) Power variations of wind power plant. (C) Optimal additive gain.

Case 1: DFIG-based wind power units do not participate in short-term frequency regulation.

It can be observed from Figure 11A that the wind speed varied slightly (0, 20 s), and DFIG-based wind power units did not participate in frequency regulation during this period. It can be seen from Figure 11B that the probability density function of wind speed was non-Gaussian.

Case 2: DFIG-based wind power units participate in short-term frequency regulation under conventional additive control.

The inertial control constant is $K_f=10$ by trial and error, while the constant droop down and droop up coefficients are set to 0.05 and 0.02, respectively. The gusty wind shown in Figure 11A was imposed from 20 to 70 s, and then the wind speed randomly fluctuated around 13 m/s after 70 s. The frequency response is illustrated by the red-dash line in Figure 12A. The minimum and maximum values of the frequency are 49.69 Hz (point B) and 50.04 Hz, respectively.

Case 3: DFIG-based wind power units participate in short-term frequency regulation under the proposed adaptive additive control.

When DFIG based wind power units participated in short term frequency regulation under the proposed adaptive additive control method, the frequency response is illustrated by the solid blue line in Figure 12A. Figure 12B shows the power variations of the wind power plant. The additive control gain 1/ $R^{\ast }$ obtained by PSO technique is demonstrated in Figure 12C. It is clear that 1/ $R^{\ast }$ gradually increased with decreasing gusty wind speed; thus the wind turbine began to increase the power for frequency regulation. Later on the gusty wind speed started to increase from 50 s. Meanwhile, 1/ $R^{\text{*}}$ declined gradually. Due to the additive control of the wind turbine, the frequency increased gradually from 50s. The minimum and maximum values of the frequency are 49.79 Hz (point A) and 50.05 Hz, respectively. The randomly fluctuating wind speed varied slightly after 70 s. The system frequency also fluctuated around 50Hz, and the rate of change was small, so the additive control coefficient fluctuated within a narrow range.

Comparing the red-dash line with the solid blue line in Figure 12A, the proposed adaptive additive control outperforms the conventional additive control.

In order to better evaluate the proposed frequency regulation method, five performance metrics are utilized to evaluate the control quality, which include root mean square error (RMSE), mean absolute error (MAE), mean squared error (MSE), mean absolute percent error (MAPE), and standard deviation (SD).

Table 3 shows that the proposed frequency control method outperforms the traditional control method based on five performance metrics.

TABLE 3

TABLE 3. Performance metrics in scenario 1.

Scenario 2: DFIG-based wind power units participate in short-term frequency regulation under the proposed additive control with different wind penetrations.

In this simulation, the investigated wind farm is composed of some DFIG-based wind power units participating in short-term frequency regulation. The number of units depends on wind penetration. The wind power capacity penetration (WPCP) is defined as

$\text{WPCP}=\frac{Wind turbine assembly capacity\left(MW\right)}{Maximum system load\left(\mathrm{M}\mathrm{W}\right)}(37)$

where WPCP describes the proportion of the installed wind power capacity in the area to the maximum load of the system (Wang et al., 2015). In this work, the three kinds of WPCPs investigated are 37.6, 25.0, and 18.8%, respectively. For simplicity, these DFIG-based wind power units are equitably aggregated based on the aggregated model described above.

The wind speed of the wind farm is also shown in Figure 11A. The frequency response is shown in Figure 13A; the frequency nadirs obtained by the proposed adaptive controls are 49.68 Hz (point C), 49.80 Hz (point B), and 49.86 Hz (point A), with 37.6, 25.0, and 18.8% WPCPs respectively. The frequency nadir decreases with increasing WPCPs. The power variations of the wind power plant are shown in Figure 13B. The proposed adaptive additive controller is suitable for different WPCPs. Figure 13C demonstrates variations in the proposed adaptive additive coefficients during the transient period. The time-variable additive control coefficients with three WPCPs are shown as Figure 13C.

FIGURE 13

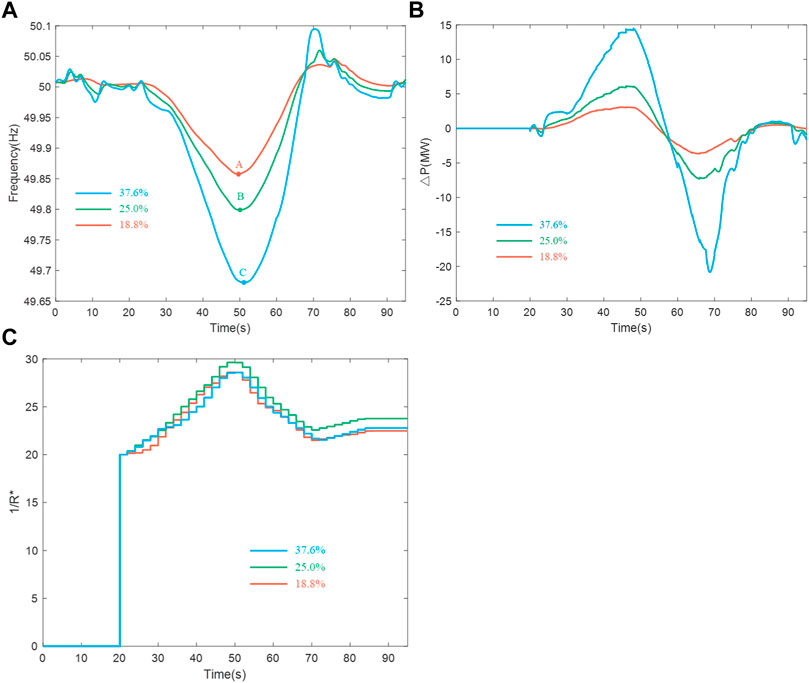
FIGURE 13. SFR in scenario 2. (A) Frequency response. (B) Power variations of wind power plant. (C) Additive control coefficients.

It can be observed from Table 4 that the performance metrics increase with increasing WPCP. The proposed method can deal with frequency regulation of a power system with high wind power capacity penetration.

TABLE 4

TABLE 4. Performance metrics in scenario 2.

Conclusion

This paper presents an overall frequency regulation scheme for DFIG-based wind power units participating in short-term frequency regulation. A data-driven additive controller is cast into a stochastic framework. Since there are non-Gaussian disturbances in wind power systems, the SIP performance index is employed to update the additive control law. Some batches are divided during adjacent instants, in which the optimal additive control coefficient can be adaptively updated in each batch by using PSO technique. The optimal additive control signal between adjacent instants can then be obtained by inputting all the additive control coefficients to an arithmetic mean filter. The effectiveness of the proposed approach, in comparison with traditional additive control strategies, is confirmed by simulation results.

Due to the randomness of wind speed on actual wind farms, and the communication delay between dispatch centers and wind farms, it will be a challenge to extend this scheme to coordinate control of multiple wind farms. The coordinate control of multiple wind farms will thus be considered in the future to improve frequency support capability. In addition, the proposed data-driven method can be extended to any processes with non-linearities and non-Gaussian noise distributions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary materials, and further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, RS and JZ; methodology, RS and QM; resources, GZ, LW, and BL; software, RS and QM; writing—original draft, RS; writing—review and editing, QM and JZ. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key R&D Program of China, No. 2019YFB1505400.

Acknowledgments

The authors would like to thank the reviewers for their valuable comments.

Conflict of interest

RS was employed by Chn Energy United Power Technology Company Ltd. GZ, LW, and BL were employed by State Grid Liaoning Electric Power Supply Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ackermann, T. (2012). Wind power in power systems. Hoboken John: Wiley & Sons.

Google Scholar

Anderson, P., and Bose, A. (1983). Stability simulation of wind turbine systems. IEEE Trans. Power Apparatus Syst. 102, 3791–3795. doi:10.1109/tpas.1983.317873

CrossRef Full Text | Google Scholar

Bao, W., Wu, Q., Ding, L., Huang, S., and Terzija, V. (2021). A Hierarchical inertial control scheme for multiple wind farms with besss based on ADMM. IEEE Trans. Sustain. Energy 12, 751–760. doi:10.1109/tste.2020.2995101

CrossRef Full Text | Google Scholar

Chen, B., Zhu, P., and Principe, J. C. (2012). Survival information potential: A new criterion for adaptive system training. IEEE Trans. Signal Process. 60, 1184–1194. doi:10.1109/tsp.2011.2178406

CrossRef Full Text | Google Scholar

Datta, U., Shi, J., and Kalam, A. (2019). Primary frequency control of a microgrid with integrated dynamic sectional droop and fuzzy based pitch angle control. Int. J. Electr. Power & Energy Syst. 111, 248–259. doi:10.1016/j.ijepes.2019.04.001

CrossRef Full Text | Google Scholar

de Almeida, R. G., and Pecas Lopes, J. A. (2007). Participation of doubly fed induction wind generators in system frequency regulation. IEEE Trans. Power Syst. 22, 944–950. doi:10.1109/tpwrs.2007.901096

CrossRef Full Text | Google Scholar

Dziwinski, P., and Bartczuk, L. (2020). A new hybrid particle swarm optimization and genetic algorithm method controlled by fuzzy logic. IEEE Trans. Fuzzy Syst. 28, 1140–1154. doi:10.1109/tfuzz.2019.2957263

CrossRef Full Text | Google Scholar

Ekanayake, J., and Jenkins, N. (2004). Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency. IEEE Trans. Energy Convers. 19, 800–802. doi:10.1109/tec.2004.827712

CrossRef Full Text | Google Scholar

Ela, E., Gevorgian, V., Fleming, P., Zhang, Y. C., Singh, M., Muljadi, E., et al. (2014). Active power controls from wind power: Bridging the gaps. Golden, CO, USA: National Renewable Energy Laboratory. NREL/TP-5D00-60574.

Google Scholar

Garmroodi, M., Verbic, G., and Hill, D. J. (2018). Frequency support from wind turbine generators with a time-variable droop characteristic. IEEE Trans. Sustain. Energy 9, 676–684. doi:10.1109/tste.2017.2754522

CrossRef Full Text | Google Scholar

Ghosh, S., Kamalasadan, S., Senroy, N., and Enslin, J. (2016). Doubly fed induction generator (DFIG)-based wind farm control framework for primary frequency and inertial response application. IEEE Trans. Power Syst. 31, 1861–1871. doi:10.1109/tpwrs.2015.2438861

CrossRef Full Text | Google Scholar

Guo, L., Yi, Y., Yin, L., and Wang, H. (2019). Modeling analysis and control theory of non-Gaussian random distribution system. Beijing: Science Press.

Google Scholar

Jia, J., Yan, Z., Peng, X., and An, X. (2020). A new distribution for modeling the wind speed data in inner Mongolia of China. Renew. Energy 162, 1979–1991. doi:10.1016/j.renene.2020.10.019

CrossRef Full Text | Google Scholar

Kang, M., Muljadi, E., Hur, K., and Kang, Y. C. (2016). Stable adaptive inertial control of a doubly-fed induction generator. IEEE Trans. Smart Grid 7, 2971–2979. doi:10.1109/tsg.2016.2559506

CrossRef Full Text | Google Scholar

Kim, J., Muljadi, E., Gevorgian, V., and Hoke, A. F. (2019a). Dynamic capabilities of an energy storage-embedded DFIG system. IEEE Trans. Ind. Appl. 55, 4124–4134. doi:10.1109/tia.2019.2904932

CrossRef Full Text | Google Scholar

Kim, J., Muljadi, E., Gevorgian, V., Mohanpurkar, M., Luo, Y., Hovsapian, R., et al. (2019b). Capability-coordinated frequency control scheme of a virtual power plant with renewable energy sources. IET Gener. Transm. Distrib. 13, 3642–3648. doi:10.1049/iet-gtd.2018.5828

CrossRef Full Text | Google Scholar

Kundur, P. (1994). Power system stability and control. New York: McGraw-Hill.

Google Scholar

Lara, O., Jenkins, N., Ekanayake, J., Cartwright, P., and Hughes, M. (2009). Wind energy generation: Modelling and control. Hoboken John: Wiley & Sons.

Google Scholar

Lee, J., Jang, G., Muljadi, E., Blaabjerg, F., Chen, Z., and Cheol Kang, Y. (2016a). Stable short-term frequency support using adaptive gains for a DFIG-Based wind power plant. IEEE Trans. Energy Convers. 31, 1068–1079. doi:10.1109/tec.2016.2532366

CrossRef Full Text | Google Scholar

Lee, J., Muljadi, E., Sorensen, P., and Kang, Y. C. (2016b). Releasable kinetic energy-based inertial control of a DFIG wind power plant. IEEE Trans. Sustain. Energy 7, 279–288. doi:10.1109/tste.2015.2493165

CrossRef Full Text | Google Scholar

Li, Y., Xu, Z., Zhang, J., and Wong, K. P. (2018). Variable gain control scheme of DFIG-based wind farm for over-frequency support. Renew. Energy 120, 379–391. doi:10.1016/j.renene.2017.11.055

CrossRef Full Text | Google Scholar

Li, Z., Xing, L., and Chen, B. (2020). Adaptive filtering with quantized minimum error entropy criterion. Signal Process. 172, 107534. doi:10.1016/j.sigpro.2020.107534

CrossRef Full Text | Google Scholar

Ma, H. T., and Chowdhury, B. H. (2010). Working towards frequency regulation with wind plants: Combined control approaches. IET Renew. Power Gener. 4, 308. doi:10.1049/iet-rpg.2009.0100

CrossRef Full Text | Google Scholar

Margaris, I. D., Papathanassiou, S. A., Hatziargyriou, N. D., Hansen, A. D., and Sorensen, P. (2012). Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Sustain. Energy 3, 189–199. doi:10.1109/tste.2011.2174660

CrossRef Full Text | Google Scholar

Morren, J., Pierik, J., and de Haan, S. W. H. (2006). Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 76, 980–987. doi:10.1016/j.epsr.2005.12.002

CrossRef Full Text | Google Scholar

Northeast Regulatory Bureau of National Energy Administration (2019). Grid code for auxiliary service management of grid connected power plants in Northeast China.

Google Scholar

Pourbeik, P. (2013). Proposed changes to the WECC WT4 generic model for type 4 wind turbine generators. Salt Lake: The Electric Power Research Institute.

Google Scholar

Vidyanandan, K. V., and Senroy, N. (2013). Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 28, 837–846. doi:10.1109/tpwrs.2012.2208233

CrossRef Full Text | Google Scholar

Wang, H., Liu, Y., Zhou, B., Voropai, N., Cao, G., Jia, Y., et al. (2020). Advanced adaptive frequency support scheme for DFIG under cyber uncertainty. Renew. Energy 161, 98–109. doi:10.1016/j.renene.2020.06.085

CrossRef Full Text | Google Scholar

Wang, P., Zhang, Z., Huang, Q., Wang, N., Zhang, X., and Lee, W.-J. (2018). Improved wind farm aggregated modeling method for large-scale power system stability studies. IEEE Trans. Power Syst. 33, 6332–6342. doi:10.1109/tpwrs.2018.2828411

CrossRef Full Text | Google Scholar

Wang, Y., Zhu, X., and Zhao, S. (2015). Modeling and simulation of wind power system. Beijing: China Water Conservancy and Hydropower Press.

Google Scholar

Wu, Y.-K., Yang, W.-H., Hu, Y.-L., and Dzung, P. Q. (2019). Frequency regulation at a wind farm using time-varying inertia and droop controls. IEEE Trans. Ind. Appl. 55, 213–224. doi:10.1109/tia.2018.2868644

CrossRef Full Text | Google Scholar

Wu, Z., Gao, W., Gao, T., Yan, W., Zhang, H., Yan, S., et al. (2018). State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean. Energy 6, 1–16. doi:10.1007/s40565-017-0315-y

CrossRef Full Text | Google Scholar

Yang, D., Jin, Z., Zheng, T., and Jin, E. (2022). An adaptive droop control strategy with smooth rotor speed recovery capability for type III wind turbine generators. Int. J. Electr. Power & Energy Syst. 135, 107532. doi:10.1016/j.ijepes.2021.107532

CrossRef Full Text | Google Scholar

Yang, D., Kim, J., Kang, Y. C., Muljadi, E., Zhang, N., Hong, J., et al. (2018). Temporary frequency support of a dfig for high wind power penetration. IEEE Trans. Power Syst. 33, 3428–3437. doi:10.1109/tpwrs.2018.2810841

CrossRef Full Text | Google Scholar

Yin, L., and Guo, L. (2009). Fault isolation for multivariate nonlinear non-Gaussian systems using generalized entropy optimization principle. Automatica 45, 2612–2619. doi:10.1016/j.automatica.2009.07.023

CrossRef Full Text | Google Scholar

Zertek, A., Verbic, G., and Pantos, M. (2012). A novel strategy for variable-speed wind turbines’ participation in primary frequency control. IEEE Trans. Sustain. Energy 3, 791–799. doi:10.1109/tste.2012.2199773

CrossRef Full Text | Google Scholar

Zhang, J., Kuai, Y., Ren, M., Luo, Z., and Lin, M. (2016). Event-triggered distributed filtering for non-Gaussian systems over wireless sensor networks using survival information potential criterion. IET Control Theory &amp. Appl. 10, 1524–1530. doi:10.1049/iet-cta.2015.1014

CrossRef Full Text | Google Scholar

Zhang, J., Shan, R., Xu, F., Hu, B., Zhou, G., Hou, G., et al. (2020). “Coordinated dispatching and frequency control strategy of power systems with large scale wind power penetration,” in 2020 Chinese Automation Congress (CAC) (Shanghai, China: IEEE), 6956–6961. doi:10.1109/CAC51589.2020.9327417

CrossRef Full Text | Google Scholar

Zhang, Z.-S., Sun, Y.-Z., Lin, J., and Li, G.-J. (2012). Coordinated frequency regulation by doubly fed induction generator-based wind power plants. IET Renew. Power Gener. 6, 38. doi:10.1049/iet-rpg.2010.0208

CrossRef Full Text | Google Scholar