- 1Department of EEE, SRMIST, Chennai, India
- 2Electrical Engineering Department, College of Engineering, Jazan University, Jizan, Saudi Arabia
- 3Electrical Engineering Department, College of Engineering, Prince Sattam bin Abdulaziz University, Wadi Al Dawasir, Saudi Arabia
- 4Electrical Engineering Department, Aswan Faculty of Engineering, Aswan University, Aswan, Egypt
- 5Department of Electrical Engineering, Valley High Institute of Engineering and Technology, Science Valley Academy, Qalyubia, Egypt
The microgrid (MG) ensures a reliable power supply as it can work in a grid-independent mode. This mode requires a coordinated control strategy among distributed generators (DGs). One major challenge in a grid-independent MG is the reactive power-sharing issue. The reactive power sharing is affected by the mismatch of feeder impedance and private loads. This study thus proposed a proportionate reactive power-sharing scheme in a grid-independent mode by mathematically computing the equivalent impedance without the need for communication lines. A mathematical formula is derived to compute the equivalent impedance as a function of the total power output of DG and the power fed to the feeder. Based on the computed equivalent impedance, the virtual impedance is added to each feeder. The inclusion of virtual impedance in each line compensates the mismatch in feeder impedance and private loads providing accurate reactive power sharing among DGs. MATLAB Simulink was used to verify the effectiveness of the proposed control strategy. Furthermore, the real-time OPAL-RT simulator was used to verify the results.
1 Introduction
Microgrids (MGs) are micro-power systems with several distributed generators (DGs) that can work along with the grid or independently. The fact that the MG works independently of the grid implies continuous power supply even if there is a grid outage. The absence of grid calls for a proper coordinated control scheme to provide electricity per grid standards. Of the various issues in a grid-independent MG, the issue of proportionate power sharing among DGs needs to be critically addressed because it leads to the overloading of few DGs while leaving the other DGs unloaded. This issue is more challenging to handle in a grid-independent mode rather than in a grid-connected mode because of the low inertia of the DG, its intermittent nature, its limited capacity, and changing loads (Parvizimosaed and Zhuang, 2020). The conventional droop control provides power sharing in grid-independent MG, which is decentralized and devoid of any communication lines (Han et al., 2017; Gupta et al., 2020). Because frequency is a global variable, the conventional droop control provides precise real-power sharing, whereas the reactive power sharing is unsatisfactory because the DG terminal voltage depends on various factors (Han et al., 2017; Zandi et al., 2018; Zhu et al., 2018). At present, the research on accurate reactive power sharing in grid-independent MG may be broadly categorized into a communication-based and communicationless strategy (Rosini et al., 2021).
Reactive power-sharing schemes with communication between DGs are widely employed MG control. (Huang et al., 2022). Presents a dynamically reconfigurable master–slave control architecture where a dynamically chosen master sends the reference command to the other DGs to modify their respective DG outputs to obtain precise reactive power sharing. Lu et al., 2022 proposed a methodology to regulate the virtual impedance, which involves communication between the DGs at event triggered instants. (Mahmood et al., 2015; Tuan, 2018; Pham and Lee, 2021; Anitha and Suchitra, 2022) Introduces a central and local controller to provide precise reactive power sharing. The reactive power contribution from each DG is communicated to the central controller, which in turn provides each DG with the reactive power reference. Integral controllers at the DGs track the reference power giving accurate reactive power sharing. Afshar et al. (2019) incorporates a neural network (NN)-based communication strategy using the load power to provide the inverter reference voltages for the sources in the MG. The NN needs to be retrained whenever the MG configuration changes. Wang et al. (2019) aimed to provide precise reactive power sharing by introducing separate energy server units with capacitor banks to provide reactive power. These methods require information on reactive power at the load end, meaning the effectiveness of control depends on the communication network. Macana et al. (2020) proposed reactive power sharing by distributed consensus scheme with fast transient response. They also analyzed the effect of communication failures and communication lags. (Xuan Hoa Thi Pham, 2020; Kumar Jha et al., 2021; Shreeram and Gaonkar, 2021). Presents improved droop control schemes for virtual impedance estimation (Deng et al., 2022). Introduces adaptive virtual impedance based on inverter output currents (ElmetwalyElmetwaly et al., 2022). Provides power sharing by designing energy management system using optimization techniques. In addition, MGs help advancing the incorporation of electric vehicle (Al- Gabalawy et al., 2020; Al- Gabalawy et al., Forthcoming 2022). Overall, communication-based reactive-power-sharing schemes claim accuracy in power-sharing independent of network topology and without the knowledge of system parameters. However, the effectiveness of control depends on the communication network; furthermore, the inclusion of communication increases the complexity and decreases the system reliability.
Thereby, communicationless strategies have also been explored for correcting reactive power-sharing errors Fan et al. (2021) proposed a communicationless scheme that estimates a virtual impedance based on the local parameters, namely, the reactive power output and the terminal voltage of the DG. This scheme does not require the line impedance value. However, this scheme has been validated on a basic MG configuration with only common load.An et al. (2021) introduced tuning of virtual impedance by successive approximation method to achieve accurate reactive power sharing using local parameters. Yet, this method requires communication links for synchronization. Sellamna et al. (2020) introduced a tuned adaptive virtual impedance with local parameters to adjust the virtual impedance continuously until no change in reactive power sharing was achieved. Gupta et al. (2020) proposed an improved reactive power-sharing scheme by calculation an adaptive Q − V droop coefficient after each load change. However, this method requires a special algorithm for the identification of load change and a gradually applied slope to avoid transients. Zhu et al. (2018) presented an optimization technique to optimize the parameters of the virtual impedance controller. These optimization techniques require complex algorithms with challenges in implementation. Anitha and Suchitra (2021) introduced a fuzzy controller to estimate the value of virtual impedance with local signals as inputs. This method is a communicationless strategy. The communicationless strategies for reactive power sharing are summarized in Table 1.
Thus, most communicationless strategies are investigated on simple MG configurations or when incorporated in practical MG configurations involves iterative, complex algorithms for power sharing. This paper aims to develop a simple controller that computes the virtual impedance when the value of feeder impedance is given. The major contributions of this work are
(i) The proposed controller addresses the effect of mismatch in line impedances and the offset in private loads, which are the primary causes of improper reactive power sharing. Both of the above causes are parameterized by a mathematically computed equivalent impedance.
(ii) Precise reactive power sharing is achieved by the inclusion of the estimated virtual impedance from the equivalent impedance. The proposed scheme calculates the virtual impedance mathematically providing an excellent dynamic response.
(iii) Power sharing among the DGs is ensured for changing loads without the need for communication lines since only local parameters are used in the computation of virtual impedance.
The paper is organized in the following manner: Section 2 deals with the study on key factors impacting reactive power sharing. Section 3 elaborates on the proposed concept of equivalent impedance in a MG. Section 4 briefs the overall control scheme incorporating the proposed equivalent impedance and virtual impedance calculation for proportionate power sharing. Section 5 validates the proposed strategy for changing loads with the MATLAB simulation and OPAL RT simulator. In conclusion, Section 6 concludes the research work.
2 Study on Power Sharing Issues
A generalized MG configuration with private and common loads has been considered in studies on power sharing. The MG configuration considered for this study is depicted in Figure 1. To study the core factors influencing reactive power sharing, only two DGs were considered with equal ratings. The DG terminal voltages
where
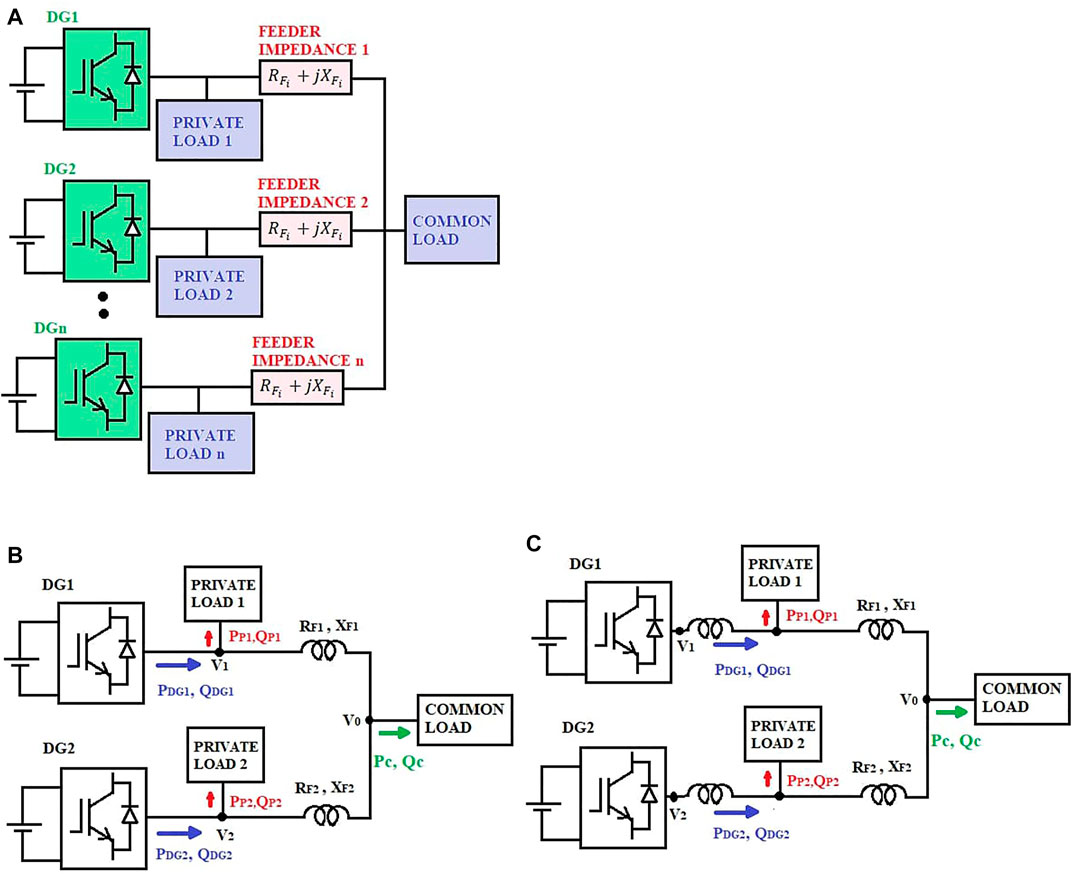
FIGURE 1. Microgrid (MG) for the investigation of reactive power sharing: (A) configuration of the MG considered, (B) power flow without virtual impedance, and (C) power flow with virtual impedance.
The voltage drop
where
For the MG configuration without virtual impedance shown in Figure 1 (b)
where
The total reactive and real power components of load in the MG is given as
In addition,
where
Manipulating Eq. 18, the error in reactive power sharing is obtained as
When an inductive line is considered,
From Eq. 10, it is explicit that the mismatch in feeder impedance and the offset in private loads are the key causes for reactive power-sharing error. The above-said factors make the terminal DG voltages to be different causing the reactive power–voltage (Q/V) droop to set different values of reference Q for the DGs. Thus, the reactive power sharing is not equal even when the ratings of DGs are equal. However, when the DG terminal voltages are made equal by some means, the reference Q of every DGs becomes the same (provided the capacity of the DGs are the same), thus ensuring proportionate reactive power sharing. To make the terminal voltages at the DGs equal, an appropriate virtual impedance is added along with every DG as shown in Figure 1C. With virtual impedance added to the circuit, Eqs. 4 and 5 get modified as
where
When an inductive line is considered,
The value of virtual impedance varies depending on the private loads and feeder impedance. The methodology used to compute the virtual impedance is briefed in the next section.
3 Concept of Equivalent Impedance
As seen in Section 2, the inequalities in the line impedances of the DGs and the offset in private loads are the primary issues affecting reactive power sharing. The influence of these factors is mathematically formulated by combining the private and common loads into a single load and replacing the feeder impedance with an equivalent impedance. Figure 2A shows the MG with combined private and common loads, which is equivalent to the MG considered in Figure 1.
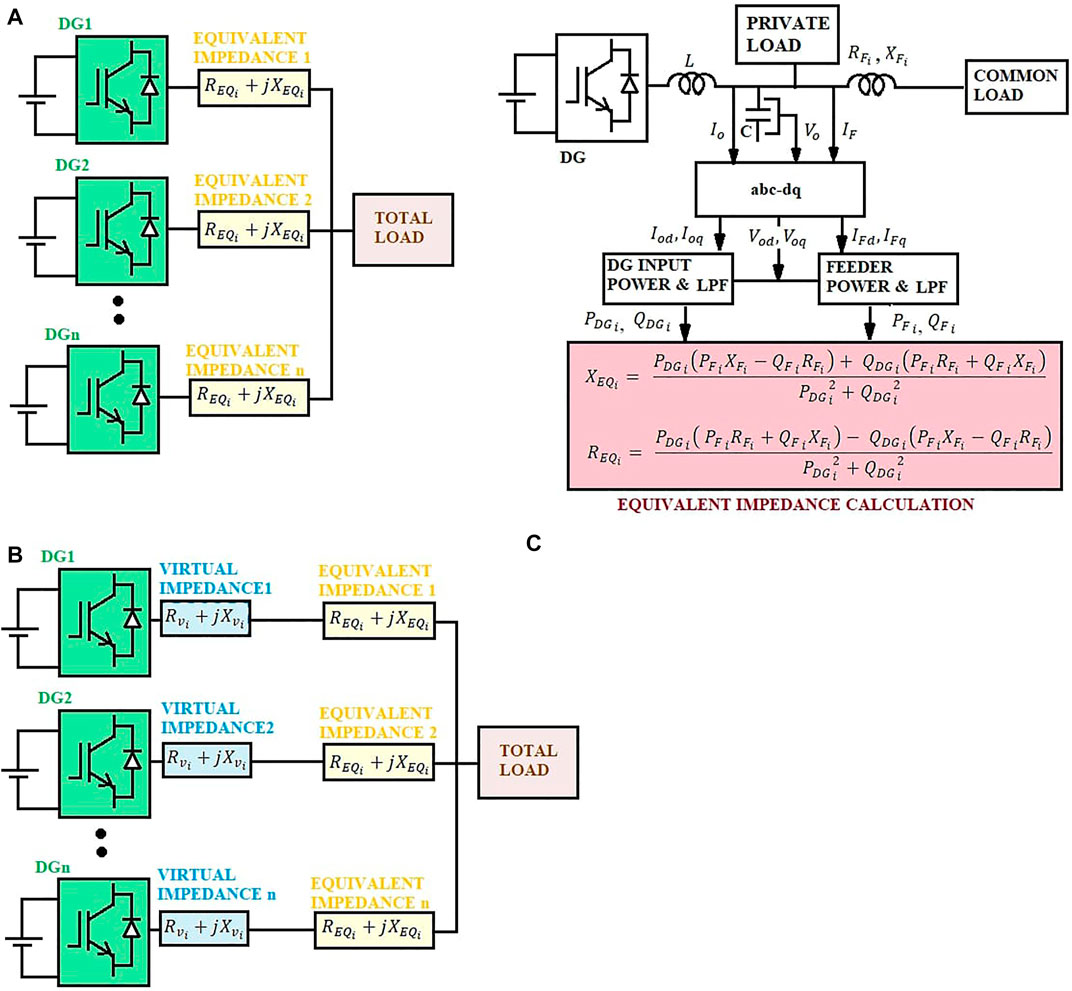
FIGURE 2. (A) equivalent of the MG with combined loads and equivalent impedance; (B) block diagram for equivalent impedance computation; and (C) equivalent of the MG with series virtual impedance.
The power generation of a DG at any given instant is the sum of power drawn by private load and power injected to the feeder.
With the combined loads and equivalent impedance, the power output of the ith DG is given as
where
The power fed to the feeder is given by
where
where
Eqs. 23 and 24 give the equivalent impedance when the private and common loads are combined. The equivalent impedance can be mathematically computed with known values of DG power output, power fed to the feeder, and feeder impedance. The block diagram for equivalent impedance computation is shown in Figure 2B.
With this information, the virtual impedance
The virtual impedance is given by
where
This mathematical formulation eliminates the need for communication links making the control robust and fast. However, these equations are specific to the given MG configuration and require foreknowledge of the feeder impedance in the system. The MG after the addition of virtual impedance is shown in Figure 2C.
4 Overall Control Strategy for Islanded Microgrid
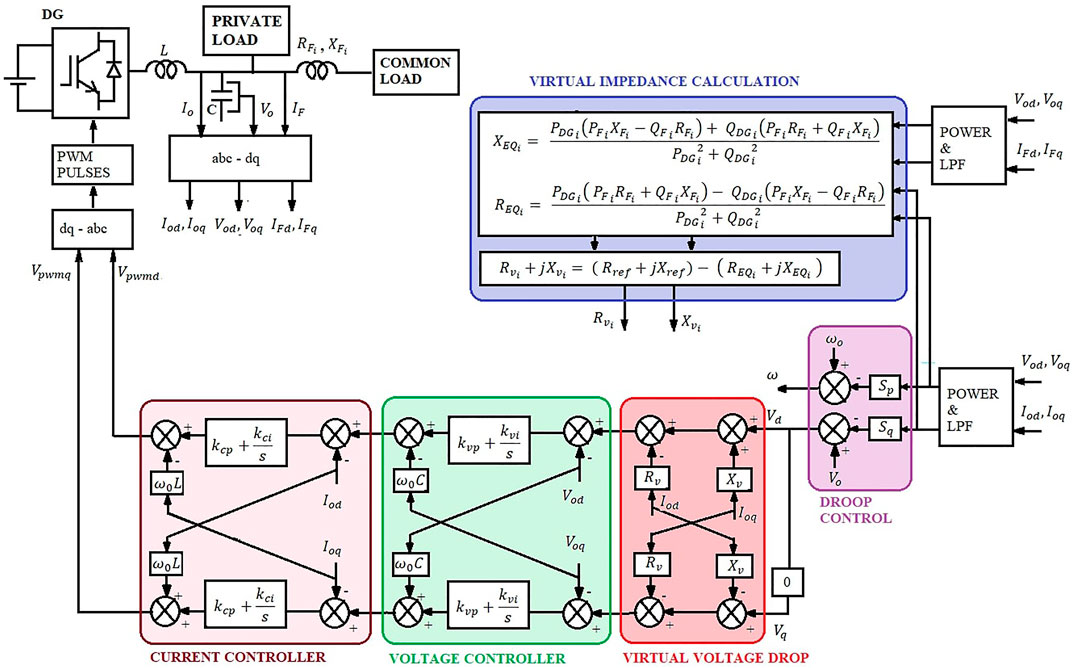
The overall control structure for power sharing in an islanded MG has the following control loops: droop controller, equivalent impedance and virtual impedance estimation, inner voltage, and current controller. The complete block diagram of the control system is presented in Figure 3.
4.1 Droop Control
In a grid-independent mode, the parallelly operated DGs use a conventional droop controller for power sharing. For a given line, the real power is proportional to the frequency and the reactive power to voltage magnitude. The droop equations are given by
where
4.2 Equivalent Impedance and Virtual Impedance Estimation
The private load and the feeder impedance are combined to obtain the equivalent impedance. Furthermore, the virtual impedance compensates for the mismatch reflected by the equivalent impedance. The mathematical computation of equivalent impedance and virtual impedance are shown in Eqs. 23, 24, and 25. The voltage drop across the computed virtual impedance is given by
where
4.3 Inner Voltage and Current Loop
The inner double-loop control is used to track the reference voltage and generate the PWM pulses for the inverter switches. The voltage and the current loops have PI controllers, and they are mathematically expressed as
where
5 Simulation Results and Discussion
To validate the efficacy of the proposed communicationless reactive power-sharing strategy for a grid-independent MG, two parallel DGs of equal and unequal ratings are simulated and tested in MATLAB/Simulink. For the system with equal DG rating, the power capacity of both the DGs are taken as 50 kW, 30 kVAR. For the system with unequal DG ratings, the power capacity of DG1 is taken as 50 kW, 30 kVAR, while that of DG2 is 25kW, 15 kVAR. The system configuration is presented in Figure 1 (b), and its parameters are listed in Table 2. The controller parameters are successfully tuned by trial-and-error method for the proper operation of the system, and these parameters are listed in Table 3.
5.1 Grid-Independent Microgrids With Equally Rated Distributed Generators
The effectiveness of the proposed controller is analyzed for the grid-independent MG with equally rated DGs with changing private and common loads. The load in the MG at different instants for varying private and common loads are listed in Table 4. Figure 4A shows the power-sharing among DGs with the changing private and common loads. With the changing loads, the power contribution by both DGs is equal at every instant of time. This figure shows the effectiveness of the proposed control strategy in terms of power sharing. Figures 4B and 4C show the equivalent and virtual impedance for both line impedances. It is observed that the equivalent impedance changes as a function of private load and line impedance. It is understood that without virtual impedance, more reactive power would have been drawn from the DG connected to the feeder with lower impedance, but the addition of virtual impedance equalized the net impedance on both feeders so that the drawn reactive power is equal. From Figures 4B,C, it is observed that whenever the equivalent impedance becomes greater than the fixed reference impedance, the virtual impedance is negative, and vice versa. Thus, the virtual impedance value may be positive or negative. The added virtual impedance equalizes the impedance to the reference value at both the lines. Grid-independent MG with unequally rated DGs.
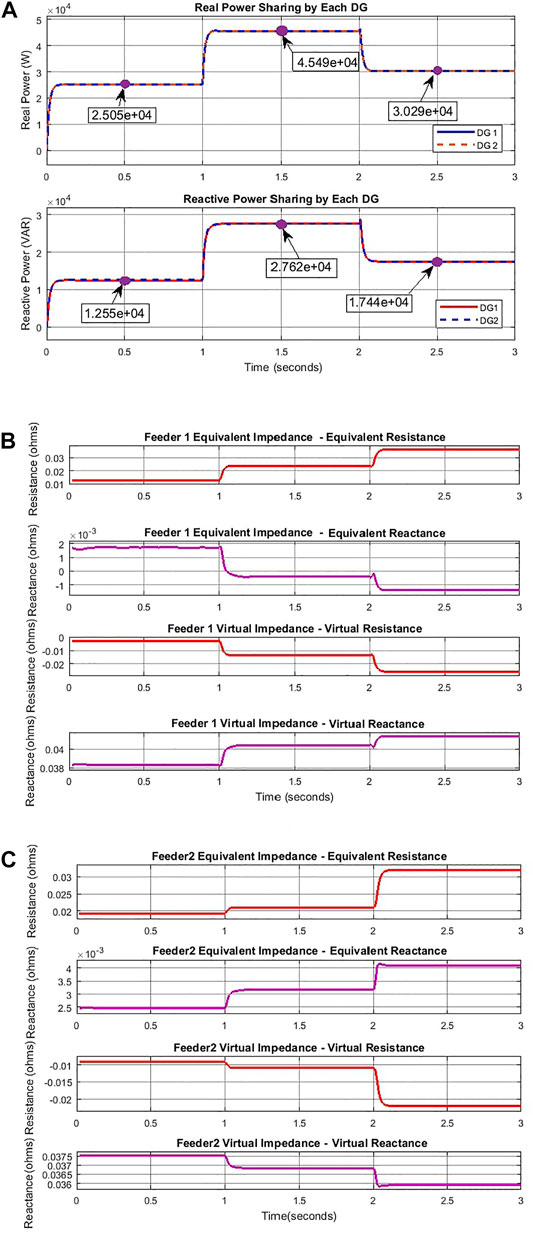
FIGURE 4. Simulation results for EQUAL DG RATING: (A) power sharing by DGs, (B) equivalent impedance and virtual impedance of line 1, and (C) equivalent impedance and virtual impedance of line 2.
The proposed controller is also implemented and analyzed in a grid-independent MG with unequally rated DGs. First, the applied common load is 35 kW, 5kVAR and the private loads are 10kW, 15kVAR and 15kW, 15kVAR. At t = 0.3, the common load is changed to 20kW, 8kVAR, and the private loads to 10kW, 5kVAR and 6kW, 5kVAR. Figure 5A shows that DG1 shares twice as much power as DG2, which is proportional to the individual DG rating. Figures 5B and 5C show the equivalent and the virtual impedance computed for the given loads. It can be seen that the equivalent impedance changes as a function of private load and the line impedance. The MATLAB simulation results show the effectiveness of the communicationless scheme with changing loads applied to MG with equally rated DGs.
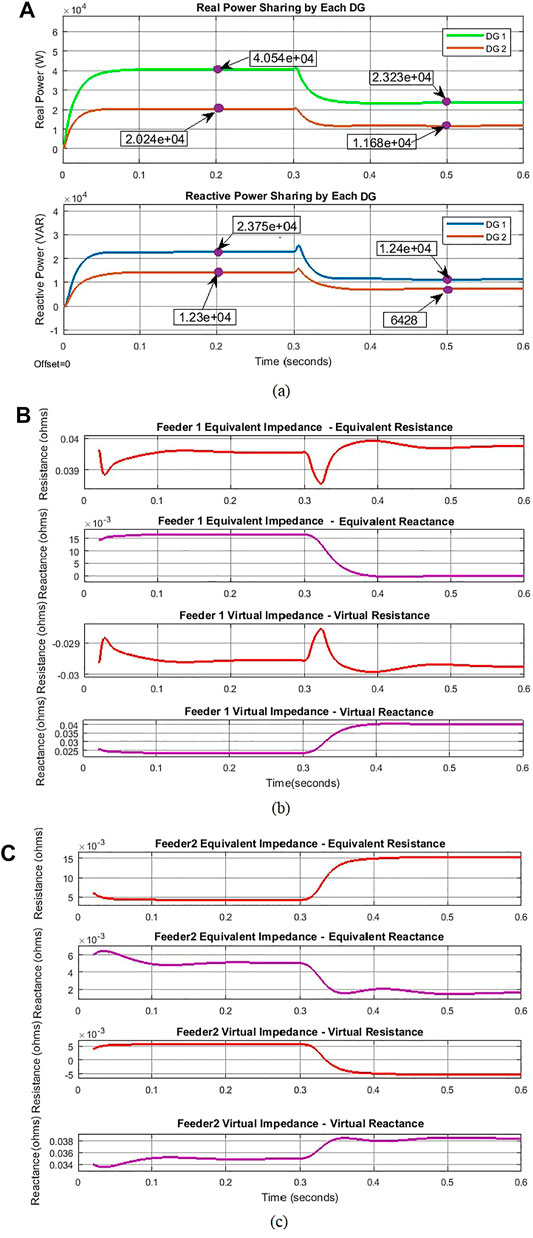
FIGURE 5. Simulation results for UNEQUAL DG RATING: (A) power sharing by DGs, (B) equivalent impedance and virtual impedance of line 1, and (C) equivalent impedance and virtual impedance of line 2.
The control of equally rated parallel DGs with changing private and common loads utilizing the proposed communicationless technique was also tested using the OPAL-RT platform in a real-time simulator. The results for changing common loads and private loads are shown in Figure 6A–C. Figure 6A shows the real and reactive power output from DG1 and DG2. First, the applied common load and the private loads were 20kW 10kVAR, 20kW 10kVAR, and 10kW 5kVAR, respectively. Between 0.5 and 0.8 s, the common load is changed to 40kW 25kVAR and the private loads to 30kW 15kVAR and 5kW 5kVAR, respectively. In conclusion, after 0.8s, the common load is 45kW 30kVAR, private load at DG1 is 15kW 5kVAR and the private load at DG2 is zero. The computed equivalent impedance and the virtual impedance of line one and line 2 are depicted in Figure 6B and Figure 6C. It is observed that the equivalent impedance changes depending on changing private load and the value of line impedance. The efficiency of the proposed communication-based strategy for changing private and common loads has been validated in a real-time environment using the OPAL-RT simulator. The simulation and real-time studies shows precise real and reactive power sharing for changing loads.
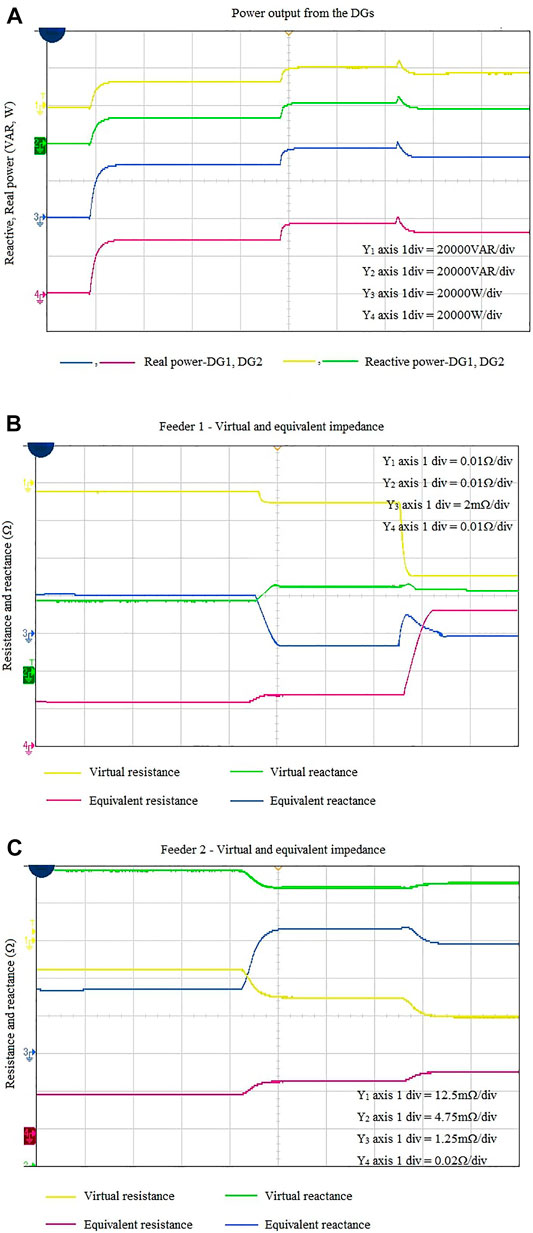
FIGURE 6. OPAL-RT results for EQUAL DG RATING: (A) power sharing by DGs; (B) equivalent impedance and virtual impedance of line 1; and (C) equivalent impedance and virtual impedance of line 2.
6 Conclusion
This research work deals with a practical MG with common and private loads working in a grid-independent mode. The issues in reactive power sharing have been analyzed, and the key factors responsible for errors in reactive power sharing have been identified. The significance and role of virtual impedance in nullifying these errors have also been validated mathematically. This paper proposes an indirect method for computation of equivalent impedance and virtual impedance that quantifies the effect of private loads and mismatched line impedances. The controller is proved to be efficient in handling DGs with both equal and unequal ratings. The real-time simulation of parallel DGs with communicationless controller was implemented using the OPAL RT platform. The mathematical computation of virtual impedance also improves the dynamic response of the system. This method suits well a MG with known line impedance because it is devoid of any communication and its associated drawbacks. Further work may be carried out to mathematically formulate equivalent impedance for other MG configurations like the networked and meshed MGs. Moreover, these configurations may be analyzed using the communicationless secondary control.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Afshar, Z., Mollayousefi, M., Bathaee, S. M. T., Bina, M. T., and Gharehpetian, G. B. (2019). A Novel Accurate Power Sharing Method versus Droop Control in Autonomous Microgrids with Critical Loads. IEEE Access 7, 89466–89474. doi:10.1109/access.2019.2927265
Al-Gabalawy, M., Hosny, N. S., Dawson, J. A., and Omar, A. I. (2020). State of Charge Estimation of a Li-Ion Battery Based on Extended Kalman Filtering and Sensor Bias. Int. J. Energy Res. 45 (5), 6708. doi:10.1002/er.6265
Al-Gabalawy1, M., Ahmed, H., Adel Younis, R., and Ahmed, I. (Forthcoming 2022). Omar Temperature Prediction for Electric Vehicles of Permanent Magnet Synchronous Motor Using Robust Machine Learning Tools. J. Ambient Intell. Humaniz. Comput.. doi:10.1007/s12652-022-03888-9
An, R., Liu, Z., and Liu, J. (2021). Successive-Approximation-Based Virtual Impedance Tuning Method for Accurate Reactive Power Sharing in Islanded Microgrids. IEEE Trans. Power Electron. 36 (1), 87–102. doi:10.1109/tpel.2020.3001037
Anitha, D., and Suchitra, D. (2022). Effective Communication-Based Reactive Power Sharing Scheme for Meshed Microgrid in an Islanded Mode. J. Circuits, Syst. Comput. 31 (07), 2250124. doi:10.1142/S0218126622501249
Anitha, D., and Suchitra, D. (2021). Adaptive Virtual Impedance Estimation by Fuzzy Logic Controller for Wireless Reactive Power Sharing in Islanded Microgrid. Int. J. Fuzzy Syst. 23, 947–966. doi:10.1007/s40815-021-01054-5
Deng, F., Petucco, A., Mattavelli, P., and Zhang, X. (2022). An Enhanced Current Sharing Strategy for Islanded Ac Microgrids Based on Adaptive Virtual Impedance Regulation. Int. J. Electr. Power. Energy Syst. 134, 107402. doi:10.1016/j.ijepes.2021.107402
ElmetwalyElmetwaly, A. H., ElDesouky, A. A., Omar, A. I., and Attya Saad, M. (2022). Operation Control, Energy Management, and Power Quality Enhancement for a Cluster of Isolated Microgrids. Ain Shams Eng. J. 13 (5), 101737. doi:10.1016/j.asej.2022.101737
Fan, B., Li, Q., Wang, W., Yao, G., Ma, H., Zeng, X.-j., et al. (2021). A Novel Droop Control Strategy of Reactive Power Sharing Based on Adaptive Virtual Impedance in Microgrids. IEEE Trans. Ind. Electron. 69, 1. doi:10.1109/TIE.2021.3123660
Gupta, Y., Chatterjee, K., and Doolla, S. (2020). A Simple Control Scheme for Improving Reactive Power Sharing in Islanded Microgrid. IEEE Trans. Power Syst. 35 (4), 3158–3169. doi:10.1109/tpwrs.2020.2970476
Han, Y., Li, H., Shen, P., Coelho, E. A. A., and Guerrero, J. M. (2017). Review of Active and Reactive Power Sharing Strategies in Hierarchical Controlled Microgrids. IEEE Trans. Power Electron. 32 (3), 2427–2451. doi:10.1109/tpel.2016.2569597
Huang, W., Shuai, Z., Shen, X., Li, Y., and Shen, Z. J. (2022). Dynamical Reconfigurable Master-Slave Control Architecture (DRMSCA) for Voltage Regulation in Islanded Microgrids. IEEE Trans. Power Electron. 37 (1), 249–263. doi:10.1109/tpel.2021.3099482
Kumar Jha, S., Kumar, D., and Lehtonen, M. (2021). Modified V-I Droop Based Adaptive Vector Control Scheme for Demand Side Management in a Stand-Alone Microgrid. Int. J. Electr. Power Energy Syst. 130, 130. doi:10.1016/j.ijepes.2021.106950
Lu, J., Zhao, M., Golestan, S., Dragicevic, T., Pan, X., and Guerrero, J. M. (2022). Distributed Event-Triggered Control for Reactive, Unbalanced, and Harmonic Power Sharing in Islanded AC Microgrids. IEEE Trans. Ind. Electron. 69 (2), 1548–1560. doi:10.1109/tie.2021.3057018
Macana, C. A., Mojica-Nava, E., Pota, H. R., Guerrero, J., and Vasquez, J. C. (2020). Accurate Proportional Power Sharing with Minimum Communication Requirements for Inverter-Based Islanded Microgrids. Int. J. Electr. Power Energy Syst. 121, 121. doi:10.1016/j.ijepes.2020.106036
Mahmood, H., Michaelson, D., and Jiang, J. (2015). Accurate Reactive Power Sharing in an Islanded Microgrid Using Adaptive Virtual Impedances. IEEE Trans. Power Electron. 30 (3), 1605–1617. doi:10.1109/tpel.2014.2314721
Parvizimosaed, M., and Zhuang, W. (2020). Enhanced Active and Reactive Power Sharing in Islanded Microgrids. IEEE Syst. J. 14 (4), 5037–5048. doi:10.1109/jsyst.2020.2967374
Pham, M.-D., and Lee, H.-H. (2021). Effective Coordinated Virtual Impedance Control for Accurate Power Sharing in Islanded Microgrid. IEEE Trans. Ind. Electron. 68 (3), 2279–2288. doi:10.1109/tie.2020.2972441
Rosini, A., Labella, A., Bonfiglio, A., Procopio, R., and Guerrero, J. M. (2021). A Review of Reactive Power Sharing Control Techniques for Islanded Microgrids. Renew. Sustain. Energy Rev. 141, 141. doi:10.1016/j.rser.2021.110745
Sabzevari, K., Karimi, S., Khosravi, F., and Abdi, H. (2019). A Novel Partial Transient Active-Reactive Power Coupling Method for Reactive Power Sharing. Int. J. Electr. Power. Energy Syst. 113, 758–771. doi:10.1016/j.ijepes.2019.06.028
Sellamna, H., Pavan, A. M., Mellit, A., and Guerrero, J. M. (2020). An Iterative Adaptive Virtual Impedance Loop for Reactive Power Sharing in Islanded Meshed Microgrids. Sustain. Energy, Grids Netw. 24, 100395. doi:10.1016/j.segan.2020.100395
Shreeram, V., and Gaonkar, D. N. (2021). Improved Droop Control Strategy for Parallel Connected Power Electronic Converter Based Distributed Generation Sources in an Islanded Microgrid. Surathkal, India: Electric Power Systems Research, 201.
Tuan, V. (2018). Hoang and Hong-Hee Lee, an Adaptive Virtual Impedance Control Scheme to Eliminate the Reactive-Power-Sharing Errors in an Islanding Meshed Microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 6 (2), 966. doi:10.1109/JESTPE.2017.2760631
Wang, K., Yuan, X., Geng, Y., and Wu, X. (2019). A Practical Structure and Control for Reactive Power Sharing in Microgrid. IEEE Trans. Smart Grid 10 (2), 1880–1888. doi:10.1109/tsg.2017.2779846
Xuan Hoa Thi Pham (2020). Power Sharing Strategy in Islanded Microgrids Using Improved Droop Control. Electr. Power Syst. Res., 180.
Zandi, F., Fani, B., Sadeghkhani, I., and Orakzadeh, A. (2018). Adaptive Complex Virtual Impedance Control Scheme for Accurate Reactive Power Sharing of Inverter Interfaced Autonomous Microgrids. IET Gener. Transm. Distrib. 12 (22), 6021–6032. doi:10.1049/iet-gtd.2018.5123
Keywords: reactive power sharing, communicationless control, grid-independent microgrid, equivalent impedance, virtual impedance
Citation: D S, D A, S GF, Alaas ZM, Ali ZM and Abdel Aleem SHE (2022) Communicationless Adaptive Control Strategy for Effective Reactive Power Sharing in a Grid-Independent AC Microgrid. Front. Energy Res. 10:946872. doi: 10.3389/fenrg.2022.946872
Received: 18 May 2022; Accepted: 03 June 2022;
Published: 15 July 2022.
Edited by:
Jagabar Sathik, Prince Sultan University, Saudi ArabiaReviewed by:
Anantha Raman Lakshmipathi, Madanapalle Institute of Technology and Science, IndiaAhmed Omar, El Shorouk Academy, Egypt
Maheswaran Gunasekaran, Dr. M.G.R. Educational and Research Institute, India
Copyright © 2022 D, D, S, Alaas, Ali and Abdel Aleem. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anitha D, YW5pdGhhZGEyOUBnbWFpbC5jb20=
 Suchitra D1
Suchitra D1 Anitha D
Anitha D George Fernandez S
George Fernandez S Ziad M. Ali
Ziad M. Ali Shady H. E. Abdel Aleem
Shady H. E. Abdel Aleem