Research on the Rotor Fault Diagnosis Method Based on QPSO-VMD-PCA-SVM

The rotor system is a core part of rotating machinery equipment. Its safe and reliable operation directly affects the economic benefit of using the equipment and the personal safety of users. To fully explore the complex feature mapping relationship between rotor vibration signals and fault types, rotor vibration signals were studied under different working conditions from the perspective of feature parameter construction and feature information mining. First, a variational mode decomposition algorithm was used to decompose the vibration signals, and quantum behavior particle swarm optimization was used to minimize the mean envelope entropy of intrinsic mode function components to determine the optimal combination of modal number and penalty coefficient. Second, the principal component analysis was used to reduce the dimensionality of IMF components of vibration signals. Finally, a support vector machine was used to mine the feature mapping relationship between vibration data after dimensionality reduction and rotor operation state to accurately identify rotor fault types. The proposed method was used to analyze the measured vibration signals of the rotor system. The experimental results showed that the proposed method effectively extracted characteristic information of the rotor running state from the vibration data, and the accuracies of four types of fault diagnoses were 100%, 88.89%, 100%, and 100%, respectively. In addition, the accuracies of the four fault diagnoses in this study were better than those of the previously reported models.

Introduction

With the development of large mechanical equipment, motor-driven rotor systems have an important role in the fields of power and industrial control. Their safe and reliable operation state determines the safety and economic benefits of using mechanical equipment. Among all types of faults related to rotating machinery, the most obvious is the abnormal vibration of a rotor system (Liu and Tan, 2022; Miao et al., 2022; Song et al., 2022; Zhang et al., 2022). Therefore, it is important to improve the safe and efficient operation of mechanical equipment to fully explore the relationship between the rotor vibration signal and rotor system operation state. To date, there have been many in-depth global studies in the field of rotor system fault diagnosis. Shi et al. (2021) analyzed rotor vibration signals from the perspective of time domain, frequency domain, and time-frequency domain, and used a local-global balanced orthogonal discriminant projection algorithm to reduce the high-dimensional features obtained. Luong and Wang (2020) proposed a fault detection method for induction motors based on current harmonic and vibration signals. Experimental results showed that the cooperative use of mechanical vibration and current harmonics effectively improved the accuracy of induction motor fault diagnosis. Hong et al. (2021) proposed a rotor system fault diagnosis model based on a residual neural network for multi-source heterogeneous data fusion. By fully mining the state relationship between multi-sensor heterogeneous monitoring data and the rotor system, the fault diagnosis accuracy was effectively improved.

The vibration signal of a rotor system is nonlinear and non-stationary. It is a key step to improving the accuracy of fault diagnosis by analyzing the characteristic information of signals in time-frequency domains and constructing characteristic parameters that fully represent the rotor operating conditions (Dhiman and Kumar, 2017; Dhiman and Kumar, 2018; Dhiman and Kaur, 2019). In recent years, the rapid development of signal processing technologies such as time domain and frequency domain analysis using the Hilbert transform technique, empirical mode decomposition (EMD), intrinsic time-scale decomposition (ITD), time-frequency analysis methods such as ITD and variational mode decomposition have become research hotspots in the field of fault diagnosis (Vekteris et al., 2020; Chen et al., 2021a; Chen et al., 2021b; Espinoza-Sepulveda and Sinha, 2021). Vekteris et al. (2020) combined EMD with the improved wavelet threshold decomposition method to fully explore the feature mapping relationship between the vibration signals of an aeroengine rotor and the operation status of mechanical equipment. Hu et al. (2021) proposed a fault diagnosis method for planetary gearboxes based on ITD and permutation entropy, and evaluated the fault degree by solving the PE of vibration signals. Dragomiretskiy and Zosso (2014) proposed the variational mode decomposition (VMD) analysis method to better solve the problems of modal aliasing and adaptive failure in time-frequency domain analysis methods such as EMD and wavelet analysis. Wang et al. (2015) proposed a VMD-based multi-friction vibration signal analysis method, which effectively improved the diagnostic accuracy of rotor and stator friction faults in rotating equipment. Experimental results showed that the VMD signal decomposition method better characterized the characteristic information of vibration signals compared with other time-frequency domain signal analysis methods. However, the above vibration signal analysis method ignored the influence of signal noise on fault characteristic information, and modal aliasing was common during signal decomposition, which led to a poor generalization performance of subsequent fault diagnosis models.

Therefore, to further improve the rotor fault diagnosis accuracy in rotating systems, rotor vibration signals were studied from the perspective of feature parameter construction and feature information mining and a rotor fault diagnosis model based on quantum behavior particle swarm optimization (QPSO)-VMD-PCA-support vector machine (SVM) was proposed. Considering that the rotor vibration signal was unstable and susceptible to noise, VMD was used to decompose the vibration signal, and the QPSO algorithm was used to optimize the number of modes and penalty coefficient of VMD to minimize the mean value of the intrinsic mode envelope entropy. Then, PCA was used to solve the variance contribution rate of the high-dimensional vibration signal features composed of each IMF-i component, and the feature compression of the vibration signal was realized based on this. Then, an SVM-based rotor fault diagnosis model was constructed based on the preprocessed vibration signal data set. Finally, the proposed rotor fault diagnosis method was compared with back propagation neural network (BPNN), extreme learning machine (ELM), and SVM under different frequency domain analysis methods and feature pretreatment methods to demonstrate its effectiveness.

Mathematical Theory

Variational Mode Decomposition

Dragomiretskiy and Zosso (2014) proposed a completely non-recursive signal decomposition method, the VMD algorithm. Compared with signal time-frequency domain analysis methods such as EMD, ensemble empirical mode decomposition (EEMD), and wavelet decomposition, VMD breaks away from the common thinking pattern of progressive recursive decomposition and transforms it into solving constrained variational problems, which can better analyze unbalanced signals and solve modal aliasing and adaptive problems (Liu and Tan, 2022; Miao et al., 2022; Song et al., 2022; Zhang et al., 2022).

Suppose that the original signal a(t) is decomposed into $u_i\left(t\right),i=\mathrm{1,2},\dots ,K$ by VMD, where $u_i\left(t\right)$ represents the ith IMF component. The algorithm implementation steps are as follows:

1) According to the Hilbert change formula, the unilateral spectrum of the Hilbert transformation of modal components is expressed as follows:

$H_i=(\delta \left(t\right)+\frac{j}{\text{π}t})\ast u_i\left(t\right)(1)$

In the formula, $\delta \left(t\right)$ represents the impulse function, $H_i$ represents the Hilbert transformation expression of $u_i\left(t\right)$, j represents an imaginary unit, and “*” represents the convolution operation.

2) The frequency spectrum of each mode is moved to the corresponding base band:

$H_{f_i,i}=[(\delta \left(t\right)+\frac{j}{\text{π}t})\ast u_i\left(t\right)]e^{-j{\omega }_{i}t}=H_i{e}^{-j{\omega }_{i}t}(2)$

In the formula, ${\omega }_i$ represents the center angular frequency of the ith mode, and $H_{f_i,i}$ represents the Hilbert transformation expression of shifting the center frequency of $H_i$ to f_i.

3) Demodulation signal $H_{f_i,i}$ has Gaussian smoothness, so the square norm of the gradient can be used to solve the bandwidth of each modal component. The specific calculation method is as follows:

$\{\begin{array}{l}\underset{u_i\left(t\right),{\omega }_i}{\min }{{\displaystyle \sum _{i=1}^K\Vert {\partial }_t[(\delta \left(t\right)+\frac{j}{\text{π}t})\ast u_i\left(t\right)]e^{-j{\omega }_{i}t}\Vert }}_2^2\\ s.t.{\displaystyle \sum _{i=1}^K{u}_i\left(t\right)}=a\left(t\right)\end{array}(3)$

where ${\partial }_t$ is the partial derivative with respect to t.

According to the convex optimization theory, to form the above highly nonlinear and non-convex variational problem, the augmented Lagrange function can be obtained:

$\begin{array}{l}L(\left\{u_i\left(t\right)\right\},\left\{{\omega }_i\right\},\lambda \left(t\right))=\alpha {{\displaystyle \sum _{i=1}^K\Vert {\partial }_t[(\delta \left(t\right)+\frac{j}{\text{π}t})\ast u_i\left(t\right)]e^{-j{\omega }_{i}t}\Vert }}_2^2+\\ {\Vert a\left(t\right)-{\displaystyle \sum _{i=1}^K{u}_i\left(t\right)}\Vert }^2+<\lambda \left(t\right),a\left(t\right)-{\displaystyle \sum _{i=1}^K{u}_i\left(t\right)}>\end{array}(4)$

where $\alpha$ is the penalty factor and $\lambda \left(t\right)$ is the Lagrange factor. The alternating direction method of multipliers was used to solve the variational constraint problem of Eq. 4 to determine the optimal solution $\left\{u_i\left(t\right)\right\},\left\{{\omega }_i\right\},\lambda \left(t\right)$ of the Lagrange function.

Quantum Behavior Particle Swarm Optimization-Variational Mode Decomposition

Particle swarm optimization (PSO) is a classical meta-heuristic optimization algorithm. In recent years, many studies have shown that the performance of the algorithm is greatly affected by the particle update speed, and even falls into local optimization and fails to converge globally (Luo et al., 2021; Yu et al., 2021). Therefore, van den Bergh and Engelbrecht (2002) integrated the concept of quantum mechanics into the updating process of individual position and proposed a QPSO algorithm. Compared with the PSO algorithm, the QPSO algorithm eliminates the concept of speed and uses Eq. 5 to update its position, which improves the global search ability and efficiency and accuracy of algorithm optimization to a certain extent.

$\{\begin{array}{l}{p}_{ij}^t={\phi }_{ij}^t{p}_{ij}^t+(1+{\phi }_{ij}^t)G_j^t\\ x_{ij}^{t+1}=p_{ij}^t\pm \beta \left|x_{ij}^t-C_j^t\right|\ln \left(\frac{1}{Q}\right)\end{array}(5)$

where $p_{ij}^t$ and β are the individual historical optimum and control coefficient, respectively. Q∈ (0,1) represents a random number; $C_j^t$ represents the mean value of individual optimal particles; $x_{ij}^t$ and $x_{ij}^{t+1}$ represent individual positions of particles before and after iteration, respectively; ${\phi }_{ij}^t$ ∈ (0,1) represents a random number; and $G_j^t$ represents the globally optimal individual position iterated to round t.

The decomposition effect of the VMD algorithm is significantly different from that of the number of modes K and the parameter configuration of the penalty coefficient α (Kaur et al., 2020; Dhiman et al., 2021a; Dhiman et al., 2021b). To obtain the best decomposition effect, this paper used the QPSO algorithm to optimize the VMD algorithm parameters. Entropy value is an effective method to measure the randomness and complexity of signals (Liu et al., 2020). The more obvious the periodic law of vibration signals, the lower the complexity, and the smaller the entropy value. Therefore, if the IMF component obtained by the VMD algorithm contains more periodic fault characteristic information, the envelope entropy value will be smaller, and the noise interference of the IMF component will be lower. At this point, the IMF component decomposed by the VMD algorithm better represents the characteristic information of the vibration signal, with better robustness.

$\{\begin{array}{l}{E}_i=-{\displaystyle \sum _{i=1}^N{p}_{i,j}\lg p_{i,j}}\\ p_{i,j}=b_i\left(j\right)/{\displaystyle \sum _{j=1}^N{b}_i\left(j\right)}\end{array}(6)$

Eq. 6 shows the formula used to solve the envelope entropy of the IMF component after Hilbert demodulation, where E_i represents the envelope entropy value; $b_i\left(j\right)$ represents the envelope function of IMF-i; and $p_{i,j}$ represents the normalized value of $b_i\left(j\right)$. As shown in Eq. 7, we used the mean of the k IMF component envelope entropy as the fitness function of the QPSO algorithm, and optimized the VMD algorithm parameters by minimizing the IMF component envelope entropy.

$f=\frac{1}{k}{\displaystyle \sum _{i=1}^k{E}_i}(7)$

Support Vector Machines

SVM is a machine learning algorithm with strong classification performance in small sample learning. The essential idea is to use a kernel function to map problems that are not linearly separable to a high-dimensional space and establish a hyperplane in the high-dimensional space to classify the samples (Huang et al., 2020).

SVM can be used for binary classification problems, for example, the sample set $D=\left\{\left(x_i,y_i\right)\right\}$, $x_i\in {ℝ}^d$, $y_i\in \{-\mathrm{1,1}\}$, $i=1,2,\dots n$, where y_i represents the label of the sample, D represents the dimension of the sample, and n represents the number of samples. The mathematical model expression of SVM is shown in Eq. 8:

$\begin{array}{l}\underset{\omega ,b}{\min }\frac{\text{||}\omega {\text{||}}^2}{2}+C{\displaystyle \sum _{i=1}^m{\epsilon }_i}\\ \text{s}\text{.t}\text{. }{y}_i({\omega }^{\text{T}}{x}_i+b)\ge 1-{\epsilon }_i\text{, }i=1\text{, }2\text{, }\dots n.\\ {\epsilon }_i\ge 0,i=1\text{, }2\text{, }\cdots n.\end{array}(8)$

To improve the generalization performance of the SVM algorithm, Eq. 8 was converted into a dual problem based on convex optimization theory and the kernel method was introduced to obtain Eq. 9:

$\begin{array}{l}\underset{\alpha }{\max }{\displaystyle \sum _{i=1}^m{\alpha }_i-\frac{1}{2}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)}}}\\ \text{s}\text{.t}\text{. }{\displaystyle \sum _{i=1}^m{\alpha }_i{y}_i=0,}\\ 0\le {\alpha }_i\le C,i=1\text{, }2,\cdots ,m.\end{array}(9)$

where ${\alpha }_i$ is the Lagrange multiplier and $K(x_i,x_j)$ is the kernel function.

Principal Component Analysis

PCA is a common dimensionality reduction method for the pre-processing of high-dimension feature data. It achieves the compression of feature data by calculating a covariance matrix and correlation coefficient for orthogonal change and finally obtains mutually independent principal components (Fattoh and Safwat, 2022; Jamal et al., 2022). The characteristic compression mathematical expression of PCA for original data D is shown as follows:

$Y_i=a_{i1}{\mathbf{d}}_1+a_{i2}{\mathbf{d}}_2+\dots +a_{ip}{\mathbf{d}}_p={\mathbf{A}}_i^T\mathbf{D}(10)$

where ${\mathbf{A}}_i={[a_{i1},a_{i1},\dots ,a_{ip}]}^{\text{T}}$ is the characteristic vector corresponding to the covariance matrix, and $Y_i$ is the principal component after orthogonal change. Each principal component compressed by the PCA algorithm corresponds to variance in the original data. The sum of the total variances is equal to the sum of the original variables. The ratio of variance to total variance represents the principal component contribution rate.

Rotor Fault Diagnosis Model Based on the Quantum Behavior Particle Swarm Optimization-Variational Mode Decomposition-Principal Component Analysis-Support Vector Machine Method

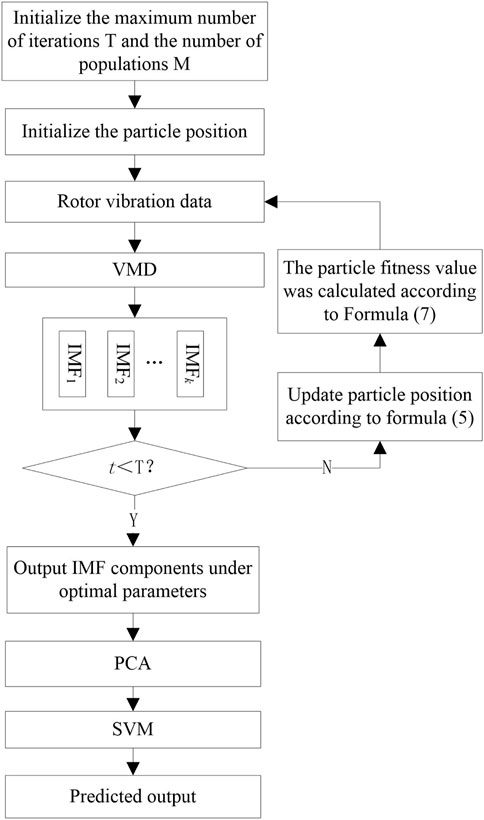
Considering the influence of the number of modes K and penalty coefficient α on the decomposition effect of the VMD algorithm, the QPSO algorithm was used to optimize the parameters of the VMD algorithm to minimize the envelope entropy. Then, the PCA algorithm was used to compress the IMF components obtained by VMD decomposition under optimal parameters. Finally, the vibration data preprocessed were input into the SVM model to predict the rotor system state. Figure 1 shows the flow chart of the rotor fault diagnosis model based on the QPSO-VMD-PCA-SVM method in this study. The specific realization steps were as follows:

1) Initialize the maximum iteration time T and population number M of the QPSO algorithm. The maximum number of iterations T in this study was 50. The number of populations was set to 100;

2) Initialize the particle position: the search range of the modal number was (5, 20), and the corresponding dimension data adopted an integer type; the penalty weight search range was (5000, 10000);

3) Configure the VMD algorithm parameters according to individual positions and decompose the rotor vibration data;

4) If the number of iterations t ≤ T, the particle position and particle fitness values were updated according to Eq. 5 and Eq. 7 successively; otherwise, the IMF component of the vibration signal under optimal parameter was output;

5) The PCA algorithm was used to perform feature compression for high-dimensional features with IMF components;

6) Trained the SVM model to predict the rotor fault type.

FIGURE 1

FIGURE 1. Flow chart of the rotor fault diagnosis model based on the QPSO-VMD-PCA-SVM method.

Results and Discussion

Introduction of Experimental

The sample data used in this paper were from the open data set of rotor vibration from the state Key Laboratory of Hydraulic Machinery, Ministry of Education of China (Liu et al., 2019; Li et al., 2021a; Li et al., 2021b; Le et al., 2021; Toyoda and Wu, 2021). The sample size of the rotor vibration data set is shown in Table 1. There were 180 samples in four rotor system operating states. The original data set was divided into training and test sets at a ratio of 8:2. The experimental platform of the data set simulated the rotor unbalance, dislocation, and friction by controlling the mass block distribution at the edge of the rotor mass disc, the relative position of the two shafts on the coupling, and the contact between the friction screw shell and the rotating bearing. During signal collection, the rotor speed was set to 1200 r/min, the sampling frequency was set to 2048 Hz, and the sampling time length was 1 s.

TABLE 1

TABLE 1. Statistics of the sample number of rotor vibration data.

Analysis of Simulation Results

According to the rotor system fault diagnosis flow chart shown in Figure 1, the rotor vibration signal was decomposed by VMD, and then the number of modes K and penalty coefficient α were optimized by the QPSO algorithm. After 50 iterations of the optimization algorithm, the optimal values of the modal number K and penalty coefficient α were 8 and 5016.8, respectively. The VMD algorithm was re-initialized according to the optimal value, and the original vibration signals were decomposed. Figure 2 shows the original signals and curves of each modal component of the vibration signals of the rotor system under different working conditions. The yellow curve in Figure 2 represents the envelope entropy curve of each IMF component after Hilbert demodulation. The curve in Figure 2 shows that the optimized IMF components had a relatively obvious cyclical fluctuation trend in the time domain, and the corresponding envelope entropy curves of each component had good stationarity and uniformity. In addition, the IMF components of the vibration signals of the rotor system under different operating conditions were markedly different. Therefore, the QPSO-VMD algorithm proposed in this paper is feasible for the decomposition of the vibration signals of a rotating subsystem. The IMF component obtained could be used to extract the periodic rules of the vibration signals, and was markedly different under different working conditions, providing greater distinguishing feature information for the subsequent fault diagnosis model.

FIGURE 2

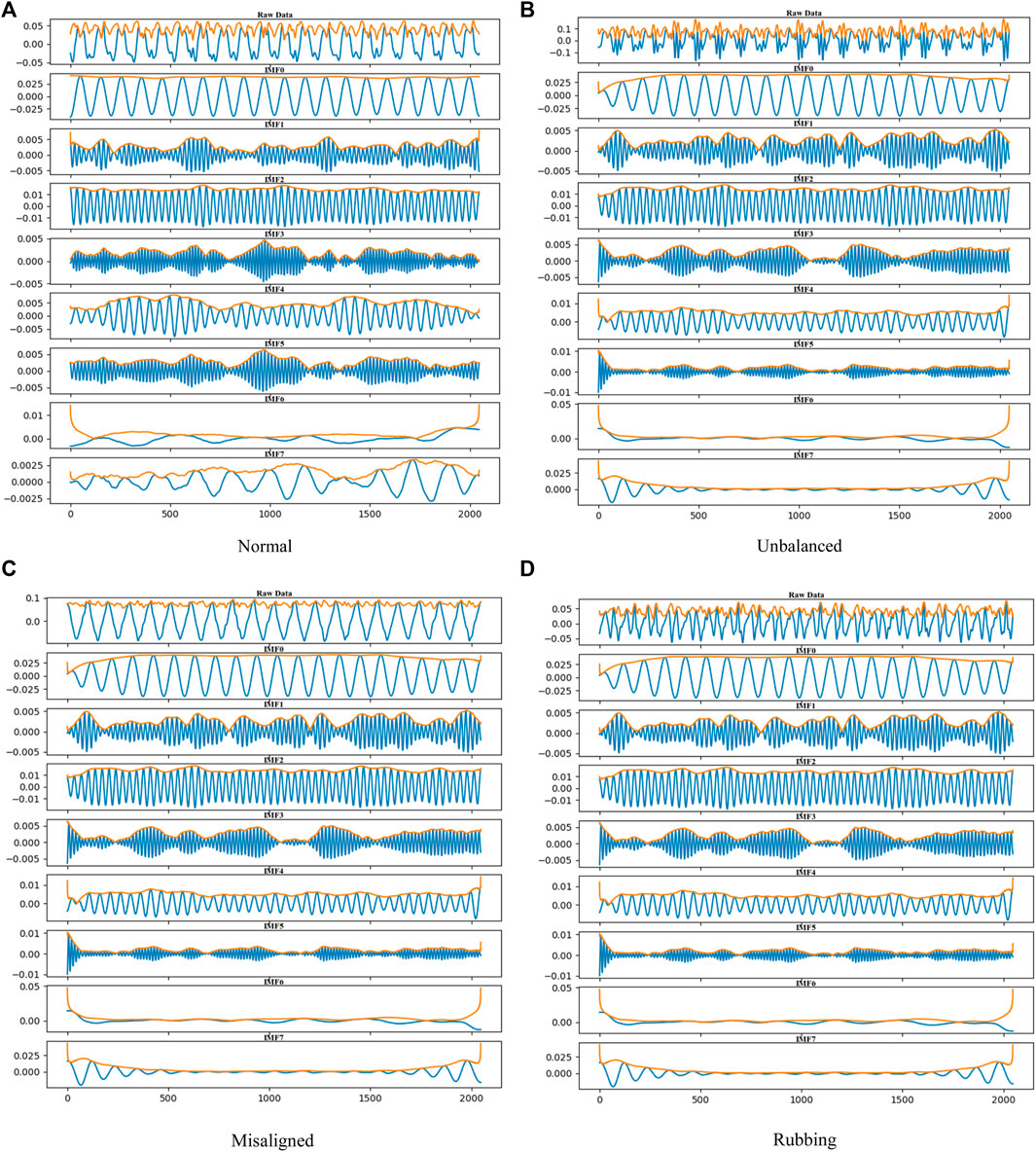
FIGURE 2. VMD decomposition of various vibration signals. (A) Normal. (B) Unbalanced. (C) Misaligned. (D) Rubbing.

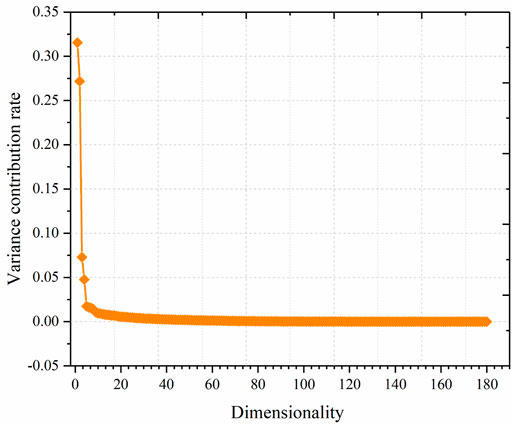
After the original vibration signal was decomposed by the VMD algorithm, the data dimension of the IMF component obtained was 8 times that of the original signal. To improve the robustness of the fault diagnosis model and reduce the sparsity of data in the high-dimensional space, the PCA algorithm was used to perform feature compression on the decomposed vibration signal. Figure 3 shows the characteristic contribution rates of each dimension under different characteristic compression scales. The curve in Figure 3 shows the feature contribution rate was mainly concentrated in feature dimensions 1 to 5, and when the feature dimension exceeded 5, the feature contribution rate tended to be 0. Therefore, this study used the PCA algorithm to compress high-dimensional vibration signals into 5-dimensional data.

FIGURE 3

FIGURE 3. Curve of the characteristic contribution rate.

To verify the effectiveness of the proposed method, we compared it with ELM, BPNN, and SVM based on different vibration signal decomposition methods, including the QPSO-VMD algorithm and EMD-PCA. Table 2 shows the fault diagnosis accuracy rate of rotor systems under different fault diagnosis methods. In this study, the accuracy rate of each optimal type is marked in bold. Data in the table show that the proposed method had the highest fault diagnosis accuracy in the normal, dislocation, and friction classes, with accuracy reaching 100%. The overall accuracy of the proposed method was also optimal. Compared with other fault diagnosis methods, the overall accuracy was increased by 5.55%. Compared with various fault diagnosis methods based on the QPSO-VMD algorithm, the proposed method achieved the optimal fault diagnosis performance, which indicates that the proposed PCA algorithm effectively improved the robustness of the fault diagnosis model using high-dimensional IMF component compression. Compared with various fault diagnosis methods based on the EMD-PCA algorithm, the proposed method still achieved optimal results, which indicates that the QPSO-VMD decomposition method had a better performance for the analysis of vibration signals in a rotor system.

TABLE 2

TABLE 2. Accuracy statistics of different fault diagnosis methods.

Vibration signal feature processing methods directly affect the accuracy of rotor fault diagnosis models, as shown in Figure 4, which is an SVM fault diagnosis confusion matrix based on different signal processing methods. By comparing the confusion matrices under different signal processing methods in Figure 4, we found that the fault diagnosis effect of the QPSO-VMD-PCA processing method was the best with an accuracy rate of 97.22%.

FIGURE 4

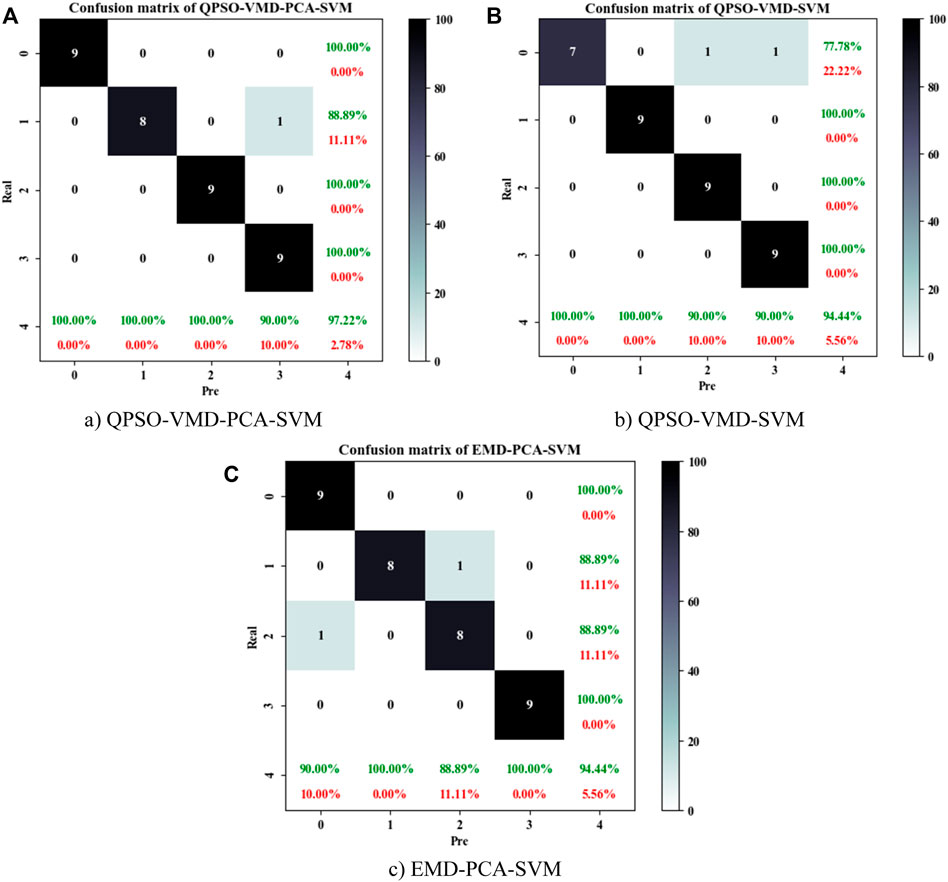
FIGURE 4. Confusion matrix of the rotor fault diagnosis model under different signal processing methods. (A) QPSO-VMD-PCA-SVM. (B) QPSO-VMD-SVM. (C) EMD-PCA-SVM.

Conclusion

To improve the accuracy of rotor system fault diagnosis, relevant studies were performed from the perspective of characteristic parameter analysis and characteristic information mining of vibration signals. A rotor fault diagnosis method based on QPSO-VMD-PCA-SVM was proposed, and the main conclusions were as follows:

1) The IMF components obtained by the vibration signal analysis method in this study contained more characteristic information about the periodic laws and showed marked differences in vibration signal components under different working conditions. Compared with the SVM fault diagnosis model based on the QPSO-VMD and EMD-PCA signal analysis methods, the proposed method achieved an optimal effect and its accuracy was improved by 2.78%.

2) The PCA algorithm ith was used in this study to compress the high-dimensional features of IMF components, which can reduce the sparsity of small-sample data in the high-dimensional feature space and improve the accuracy of the fault diagnosis model. Compared with the ELM, BPNN, and SVM models based on the QPSO-VMD method, the accuracy of the proposed method was improved by 2.78%, 5.55%, and 2.78%, respectively.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Author Contributions

LW was responsible for model design and program writing; HL was responsible for data analysis, paper writing and revision; JL and LZ were responsible for the proofreading of the mathematical formula. QJ and JW were responsible for English editing.

Funding

This research was supported by the Key Research and Development Program of the Cangzhou Science and Technology Plan (204204003, 213101007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, J., Feng, Y., Lu, C., and Fei, C. (2021). Fusion Fault Diagnosis Approach to Rolling Bearing with Vibrational and Acoustic Emission Signals. Cmes-Computer Model. Eng. Sci. 129 (2), 1013–1027. doi:10.32604/cmes.2021.016980

CrossRef Full Text | Google Scholar

Chen, W., Yu, M., and Fang, M. (2021). Research on Identification and Localization of Rotor-Stator Rubbing Faults Based on AF-VMD-KNN. J. Vib. Eng. Technol. 9 (8), 2213–2228. doi:10.1007/s42417-021-00357-z

CrossRef Full Text | Google Scholar

Dhiman, G., Garg, M., Nagar, A., Kumar, V., and Dehghani, M. (2021). A Novel Algorithm for Global Optimization: Rat Swarm Optimizer. J. Ambient. Intell. Hum. Comput. 12 (8), 8457–8482. doi:10.1007/s12652-020-02580-0

CrossRef Full Text | Google Scholar

Dhiman, G., and Kaur, A. (2019). STOA: A Bio-Inspired Based Optimization Algorithm for Industrial Engineering Problems. Eng. Appl. Artif. Intell. 82, 148–174. doi:10.1016/j.engappai.2019.03.021

CrossRef Full Text | Google Scholar

Dhiman, G., and Kumar, V. (2018). Emperor Penguin Optimizer: A Bio-Inspired Algorithm for Engineering Problems. Knowledge-Based Syst. 159, 20–50. doi:10.1016/j.knosys.2018.06.001

CrossRef Full Text | Google Scholar

Dhiman, G., and Kumar, V. (2017). Spotted Hyena Optimizer: A Novel Bio-Inspired Based Metaheuristic Technique for Engineering Applications. Adv. Eng. Softw. 114, 48–70. doi:10.1016/j.advengsoft.2017.05.014

CrossRef Full Text | Google Scholar

Dhiman, G., Oliva, D., Kaur, A., Singh, K. K., Vimal, S., Sharma, A., et al. (2021). BEPO: A Novel Binary Emperor Penguin Optimizer for Automatic Feature Selection. Knowledge-Based Syst. 211, 106560. doi:10.1016/j.knosys.2020.106560

CrossRef Full Text | Google Scholar

Dragomiretskiy, K., and Zosso, D. (2014). Variational Mode Decomposition. IEEE Trans. Signal Process. 62 (3), 531–544. doi:10.1109/TSP.2013.2288675

CrossRef Full Text | Google Scholar

Espinoza-Sepulveda, N., and Sinha, J. (2021). Mathematical Validation of Experimentally Optimised Parameters Used in a Vibration-Based Machine-Learning Model for Fault Diagnosis in Rotating Machines. Machines 9 (8), 155. doi:10.3390/machines9080155

CrossRef Full Text | Google Scholar

Fattoh, I. E., and Safwat, S. (2022). Prediction of Diabetic Obese Patients Using Fuzzy KNN Classifier Based on Expectation Maximization, PCA and SMOTE Algorithms. Ijacsa 13 (1), 233–238. doi:10.14569/IJACSA.2022.0130128

CrossRef Full Text | Google Scholar

Hong, X., Duan, L., and Zhang, L. (2021). Multi-sensor Heterogeneous Data Fusion Method for Rotor System Diagnosis Based on Multi-Mode Residual Network and Discriminant Correlation Analysis. Meas. Sci. Technol. 32 (no. 10), 105114. doi:10.1088/1361-6501/ac05f6

CrossRef Full Text | Google Scholar

Hu, A., Zhu, L., and Xiang, L. (2021). Fault Diagnosis Method of Planetary Gearbox Based on ITD and Permutation Entropy. China Eng. J. 19 (06), 542–548. doi:10.15999/j.carolcarrollnki311926.2021.06.010

CrossRef Full Text | Google Scholar

Huang, X., Huang, X., Wang, B., and Xie, Z. (2020). Fault Diagnosis of Transformer Based on Modified Grey Wolf Optimization Algorithm and Support Vector Machine. IEEJ Trans. Elec Electron Eng. 15 (3), 409–417. doi:10.1002/tee.23069

CrossRef Full Text | Google Scholar

Jamal, M. Z., Lee, D.-H., and Hyun, D. J. (2022). Making a Case for Application of the Unsupervised PCA Algorithm for Simultaneous and Proportional Myoelectric Intention Estimation of Individual Fingers. IEEE Trans. Instrum. Meas. 71, 1–12. doi:10.1109/TIM.2022.3152234

CrossRef Full Text | Google Scholar

Kaur, S., Awasthi, L. K., Sangal, A. L., and Dhiman, G. (2020). Tunicate Swarm Algorithm: A New Bio-Inspired Based Metaheuristic Paradigm for Global Optimization. Eng. Appl. Artif. Intell. 90, 103541. doi:10.1016/j.engappai.2020.103541

CrossRef Full Text | Google Scholar

Le, S., Wu, Y., Guo, Y., and Vecchio, C. D. (2021). Game Theoretic Approach for a Service Function Chain Routing in NFV with Coupled Constraints. IEEE Trans. Circuits Syst. II 68, 3557–3561. Published online. doi:10.1109/TCSII.2021.3070025

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. K. (2021). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Liu, C., and Tan, J. (2022). An Enhanced Variational Mode Decomposition Based on Correntropy and a Periodicity-Assisted Log-Cycligram for Bearing Fault Diagnosis. Meas. Sci. Technol. 33 (6), 065108. doi:10.1088/1361-6501/ac50e5

CrossRef Full Text | Google Scholar

Liu, D., Xiao, Z., Hu, X., Zhang, C., and Malik, O. P. (2019). Feature Extraction of Rotor Fault Based on EEMD and Curve Code. Measurement 135, 712–724. doi:10.1016/j.measurement.2018.12.009

CrossRef Full Text | Google Scholar

Liu, Y., Chen, C., and Yang, R. (2020). Grounding Fault Location Method of DC System in Substation Based on Wavelet Relative Entropy. High. Volt. Electr. Equip. 56 (01), 169–174. doi:10.13296/j.1001-1609.hva.2020.01.025

CrossRef Full Text | Google Scholar

Luo, J., Shao, Y., Liao, X., Liu, J., and Zhang, J. (2021). Complex Permittivity Estimation for Cloths Based on QPSO Method over (40 to 50) GHz. IEEE Trans. Antennas Propagat. 69 (1), 600–605. doi:10.1109/TAP.2020.3005032

CrossRef Full Text | Google Scholar

Luong, P., and Wang, W. (2020). Smart Sensor-Based Synergistic Analysis for Rotor Bar Fault Detection of Induction Motors. IEEE/ASME Trans. Mechatron. 25 (2), 1067–1075. doi:10.1109/TMECH.2020.2970274

CrossRef Full Text | Google Scholar

Miao, Q., Shu, Q., Wu, B., Sun, X., and Song, K. (2022). A Modified Complex Variational Mode Decomposition Method for Analyzing Nonstationary Signals with the Low-Frequency Trend. Sensors 22 (5), 1801. doi:10.3390/s22051801

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, M., Zhao, R., Wu, Y., and He, T. (2021). Fault Diagnosis of Rotor Based on Local-Global Balanced Orthogonal Discriminant Projection. MEASUREMENT 168, 108320. doi:10.1016/j.measurement.2020.108320

CrossRef Full Text | Google Scholar

Song, Q., Jiang, X., Wang, S., Guo, J., Huang, W., and Zhu, Z. (2022). Self-Adaptive Multivariate Variational Mode Decomposition and its Application for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 71, 1–13. doi:10.1109/TIM.2021.3139660

CrossRef Full Text | Google Scholar

Toyoda, M., and Wu, Y. (2021). Mayer-type Optimal Control of Probabilistic Boolean Control Network with Uncertain Selection Probabilities. IEEE Trans. Cybern. 51, 3079–3092. (Regular Paper). doi:10.1109/tcyb.2019.2954849

PubMed Abstract | CrossRef Full Text | Google Scholar

van den Bergh, F., and Engelbrecht, A. P. (2002). A New Locally Convergent Particle Swarm Optimiser. IEEE Int. Conf. Syst. Man Cybern. 3, 6. doi:10.1109/ICSMC.2002.1176018

CrossRef Full Text | Google Scholar

Vekteris, V., Trumpa, A., Turla, V., Mokšin, V., Viselga, G., and Jurkonis, E. (2020). Diagnosing Faults in Rolling-Element Bearings of Rotor Systems Equipped with Vibration Dampers. Adv. Mech. Eng. 12 (no. 4), 168781402091541. doi:10.1177/1687814020915417

CrossRef Full Text | Google Scholar

Wang, Y., Markert, R., Xiang, J., and Zheng, W. (2015). Research on Variational Mode Decomposition and its Application in Detecting Rub-Impact Fault of the Rotor System. Mech. Syst. Signal Process. 60-61, 243–251. doi:10.1016/j.ymssp.2015.02.020

CrossRef Full Text | Google Scholar

Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy Iteration Approach to the Infinite Horizon Average Optimal Control of Probabilistic Boolean Networks. IEEE Trans. Neural Netw. Learn Syst. 32 (6), 2910–2924. (Regular Paper). doi:10.1109/TNNLS.2020.3008960

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, S., Tan, W., Zhang, C., Fang, Y., Tang, C., and Hu, D. (2021). Research on Hybrid Feature Selection Method of Power Transformer Based on Fuzzy Information Entropy. Adv. Eng. Inf. 50, 101433. doi:10.1016/j.aei.2021.101433

CrossRef Full Text | Google Scholar

Zhang, X., Li, D., Li, J., and Li, Y. (2022). Grey Wolf Optimization-Based Variational Mode Decomposition for Magnetotelluric Data Combined with Detrended Fluctuation Analysis. Acta Geophys. 70 (1), 111–120. doi:10.1007/s11600-021-00714-2

CrossRef Full Text | Google Scholar