A Review of Wind Energy Output Simulation for New Power System Planning

The uncertain and volatile nature of wind energy have brought huge challenges to power system planning and operation. Therefore, it is necessary to model the wind power output. In this paper simulation models of wind energy output for new power system planning are reviewed. We begin by discussing the characteristics of wind power output, and then introduce the wind power output simulation model based on different application scenarios that are based on probability and time series. Finally, the directions for further research in the future are anticipated.

1 Introduction

The energy business is experiencing unprecedented profound changes as a result of the economic development of society and the advancement of science and technology. The operations and planning of power systems are becoming increasingly complicated as new types of energy sources become available (Shortt et al., 2013). In response to the global energy and environmental crisis, governments all over the world have stated that they want to establish a system that uses a large amount of renewable energy (Kroposki et al., 2017). As a result of the revolution in power systems, power system planning studies face new challenges. Increased penetration of renewable energy in power systems, in particular, has resulted in significant uncertainty and fluctuation in power systems (Conejo et al., 2017).

Electricity generated by wind energy differs significantly from that generated by traditional sources. The main distinction is that wind power is uncertain and intermittent (Han et al., 2021). The operation of the power system is made more uncertain by intermittent renewable energy sources. New energy production’s growing effect in the power system puts new demands on planning and operation.

Wind energy and other new energy products now play a significant role in the modern power system. Despite the fact that the new energy power generation sector is rapidly expanding, it is difficult to address the issue of new energy power generation planning in the short term due to lack of planning, unstable development, and inadequate associated legislation. Therefore, it is critical to accurately evaluate new energy production efficiency, account for the rational allocation of new energy and conventional energy, increase unified planning and operation scheduling, and promote the industry’s overall harmonious growth.

The output of wind farms is an uncontrollable source of energy, and its contribution to the capacity of the power system when it is connected to the grid differs significantly from that of conventional units. As a result, objective evaluation of the wind farm capacity credit is critical for long-term planning, optimal system operation, reliability assessment and other associated concerns.

Because of the scarcity of primary energy, wind power have significant seasonal, random, and fluctuating characteristics, necessitating greater use of flexible resources over a variety of time scales, such as cross-seasonal distribution, cross-day adjustment, intraday adjustment, and real-time power and electricity balance. Renewable energy power is increasingly converting the power system into a multi-energy complementary power system (Zhou et al., 2018).

The modeling and processing of stochastic power supply is a key problem in the simulation of renewable energy-led power system production. Wind power output simulation is widely used in power system planning, operation, and reliability assessment. Effective wind energy simulation can boost wind power’s grid-connected potential while lowering wind farm operating costs (Zhang et al., 2022).

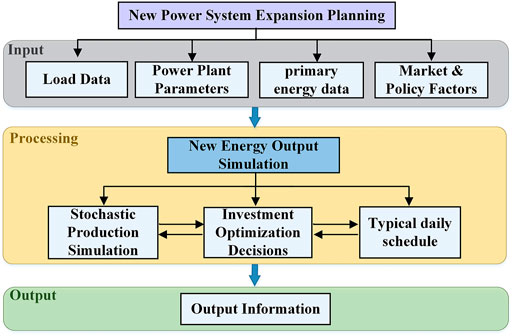
Figure 1 shows the role of wind power simulation in the expansion planning of the new power system. There are three levels as a whole. The first is to input the basic data required to build the power optimization model, mainly including load data (electricity demand, typical load curve, etc.), power plant data (power plant type, fuel price, average coal consumption, etc.), primary energy data (hydrological information, incoming wind conditions, etc.) and market and policy factors (discount rates, fuel prices, new energy subsidies, etc.). The second layer is the core processing layer of the program, which is responsible for the calculation of power optimization planning. The last layer is the input and output information layer, which includes global information of power supply planning results such as power installation progress, annual investment, annual operating costs, power and electricity balance, and new energy simulation and modeling, stochastic production simulation, typical daily operation simulation, etc. Important results of the module during the iterative computation process.

FIGURE 1

FIGURE 1. Structure of the new power system planning.

However, many previous studies on wind power output have focused solely on wind speed forecasting, with little attention paid to wind power simulation.

To focus on addressing the long-term variability and uncertainties of renewables, we particularly limit our discussions to the following areas: 1) Modeling of wind power output without considering time series, primarily based on the long-term characteristics of wind power to carry out modeling based on probability statistics, which is used for power balance, reliability assessment, etc.; 2) Time series modeling of wind power output, mainly used to arrange the operation mode of units under sequential production simulation; 3) Time series and probability modeling, which overcomes the shortcomings of the previous two categories and incorporates both uncertainty and volatility into the model.

The contributions of the paper are listed as follows. First, the characteristics of wind power output are summarized including the uncertainties, peak shaving and correlation. Second, various wind power models based on probability distributions and stochastic scenarios are introduced. Third, wind power output time series modeling, primarily used to arrange the operation mode of units under sequential production simulation, is discussed in this paper.

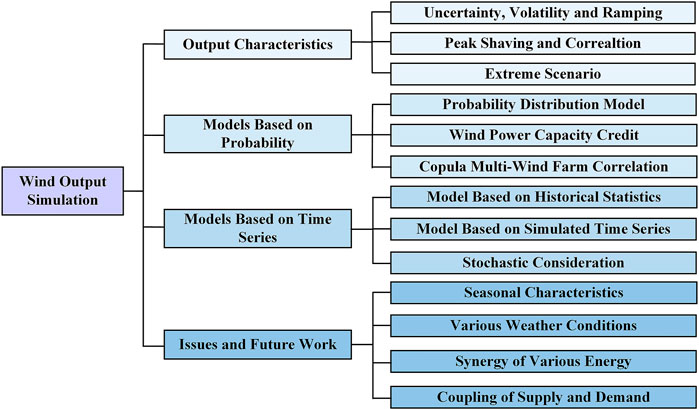
The remainder of this paper is organized as follows. In Section 2 the output characteristics of wind power are summarized, including uncertainty, volatility, correlation, peak shaving characteristics. In Section 3, the probability-based wind power modeling is summarized, including probability distribution model, capacity confidence, and Copula multi-wind farm correlation. In Section 4, time series-based wind power modeling is explained. Section 5 is about the current concerns and challenges of renewable energy production modeling. Finally, Section 6 adds a brief summary of the content of the article and a brief outlook. And the structure of this paper is shown in Figure 2.

FIGURE 2

FIGURE 2. Structure of this paper.

2 Wind Power Output Characteristics

In this section, the output characteristics of wind power are discussed.

2.1 Uncertainty, Volatility and Ramping Characteristics

The power generation capacity and power generation of wind farms have a strong dependence on wind energy. Unlike fuel and water storage, wind energy cannot be stored on a large scale. The features of wind energy largely impact the output characteristics of wind power. The random and fluctuating characteristics of wind energy result in high unpredictability and volatility in the output and power generation of wind farms. Daily wind power production variations, monthly average power changes, and variances in output characteristics in different seasons all represent the unpredictability and volatility of wind power output.

Uncertainty and volatility are the essential characteristics of new energy power generation such as wind power. Uncertainty makes short-term production arrangements and long-term system planning a certain risk, while volatility has a significant impact on the short-term operation of the power system, requiring the system to be equipped with more many flexible resources.

Ramps events are a significant source of uncertainty in wind power generation. Wind power ramps are defined as large variations in wind power production that must adhere to a set of rules, such as a minimum power swing or duration (Sevlian and Rajagopal, 2012; Sevlian and Rajagopal, 2013; Ganger et al., 2014). Extreme wind ramp events need to be closely examined since such a ramp can cause power system security concerns.

2.2 Peak Shaving Characteristics

Wind power’s peak shaving characteristics refer to the relationship between wind power and load over the course of a day. Whether wind power can be connected to the grid for power generation mainly depends on whether the system has sufficient peak shaving capacity.

The impact of wind power output power on system peak regulation can be divided into three situations based on the different effects of wind power on the peak-to-valley difference of the system equivalent load: negative peak regulation, positive peak regulation, and over peak regulation. Wind power has obvious anti-peak characteristics, according to statistical analysis (Yang et al., 2014).

2.3 Correlation

2.3.1 Autocorrelation

Autocorrelation is the correlation of a series with itself after applying a given lag (Feijoo and Villanueva, 2016). Autocorrelation can be induced in a series of data by means of autoregressive models, i.e., AR, MA, ARMA, ARIMA (Kashyap, 1982; Zhang, 2003).

2.3.2 Cross-Correlation

Wind resources differ greatly for wind turbines that are far apart in a wind farm or wind farms that are farther apart in different regions, according to studies. Wind resources in different parts of the region show obvious differences due to spatial dispersion. The decoupling or offsetting of each other’s fluctuations through the synergistic decoupling effect of each part in the region, thus alleviating the adverse effects on the whole. Grid operation has intermittent fluctuation characteristics. The correlation between multiple output series is used to mathematically express the smoothing effect of wind farm group output.

The following formula can be used to calculate the correlation coefficient between two wind farms:

${\rho }_{ij}=\frac{{\displaystyle \sum _{t=1}^T\left(p_{it}-{\overline{p}}_i\right)\left(p_{jt}-{\overline{p}}_j\right)}}{\sqrt{{\displaystyle \sum _{t=1}^T\left(p_{it}-{\overline{p}}_i\right)}}\sqrt{{\displaystyle \sum _{t=1}^T\left(p_{jt}-{\overline{p}}_j\right)}}}(1)$

Among them, $p_{i,t}$ , $p_{j,t}$ are the sampling values of output in wind farm $i$, $j$ , and ${\overline{p}}_i$ , ${\overline{p}}_j$ are the sampling mean output of wind farm $i$, $j$.

If the two output series have a positive correlation, the effect of the volatility superposition will cause the overall output curve to show a trend of large fluctuations, exacerbating the fluctuation of the wind farm group’s output. The smoothing effect is influenced by the negative correlation between outputs. The output fluctuations cancel and complement each other, “cutting peaks and filling valleys,” as it were. A smooth effect can be seen in the overall output curve and output volatility.

2.4 Extreme Output Scenario

The wind power extreme scenario relates to the situation in which the average net load (load minus renewable energy power) varies the greatest over time. When the downhill event of wind power and the load rise occur at the same time, for example, wind desertion and load shedding may occur, compromising the power system’s safety and stability.

In extreme circumstances of wind power production, robust optimization may be employed to discover the best dispatching system. The uncertainty set is primarily utilized to represent the variation range of wind power fluctuations, and even in the worst-case circumstances, a solution with high performance may be found.

3 Wind Power Modeling Based on Probability

In this section, the probability-based wind power modeling is summarized, including probability distribution model, capacity confidence, and Copula multi-wind farm correlation.

3.1 Probability Distribution Model

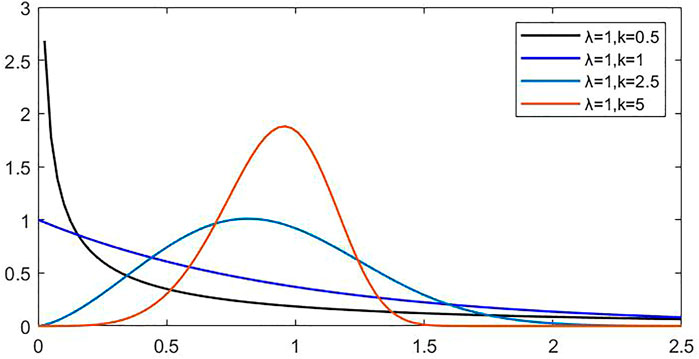
Wind power has a range of outputs from 0 to its installed capacity. Therefore, typical two-state models of conventional units cannot be used to establish wind power output models. The long-term characteristics of wind power obey the Weibull distribution, according to research and analysis dating back to the 1980s, and a multi-state unit model was developed as a result (Wang et al., 1984).

From the perspective of probability theory and statistics, Weibull Distribution is a continuous probability distribution, as shown in Figure 3, and its probability density is:

$f\left(x;\lambda ,k\right)=\{\begin{array}{ll}\frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{-{\left(x/\lambda \right)}^k}\hfill & x\ge 0\hfill \\ 0\hfill & x<0\hfill \end{array}(2)$

FIGURE 3

FIGURE 3. PDF of the Weibull distribution.

The PDF of the Weibull distribution, f, has been widely described in the literature, and can be expressed as a function of three parameters, i.e. random variable (x), scale (λ) and shape (k).

The multi-state unit model works by dividing the range of wind power production (output) into numerous periods and calculating the probability that the wind power output falls within each interval (Kim et al., 2012). Wind power is regarded as a multi-state unit whose output may take values at these discrete points, with each interval corresponding to a discrete output value (typically the middle of the period).

$\{\begin{array}{l}p\left(x_i=c_{i,j}\right)=p_{i,j}\hfill \\ {\displaystyle \sum _j{p}_{i,j}}=1\hfill \end{array}(3)$

where the available capacity and probability of the unit in state $j$ are denoted by $c_{i,j}$ and $p_{i,j}$ respectively.

As can be seen, the continuous output curve of wind power is the basis for the multi-state unit model. The form of the model is consistent with the two-state model of conventional units. On a longer time scale, it can properly capture the randomness of wind power output and reflect the characteristics of wind power replacing traditional power generation. The system reliability of wind farms is directly calculated and considered in the case of reliability calculation models and methods, which is widely used in the research of wind power credit capacity. Also, it is convenient to combine with the stochastic production simulation calculation method based on equivalent continuous load curve and electricity function.

Although the multi-state unit model is introduced in this section on wind farm output modeling, the methods connected with it may be applied to other units as well. Conventional units may have local failures or individual auxiliary equipment failures, but they are not always out of service. Instead, the generator output may not achieve its rated output. The multi-state unit model may also be used to model in this circumstance.

The probability distribution model can depict the long-term power characteristics and power distribution range of renewable energy, but short-term output fluctuation characteristics are difficult to describe (Shao et al., 2021; Feng et al., 2022). The demand for peak shaving and ramping of wind power has also been neglected.

3.2 Wind Power Capacity Credit

Due to the intermittency of wind power output, wind power units of the same capacity have different load-carrying capabilities from conventional thermal power or hydro-power units. Therefore, in the power system sufficiency analysis, wind power capacity cannot be treated the same as conventional units, which is not conducive to the power planning.

The concept of power generation capacity credit was first proposed by Garver (Garver, 1966) in 1966, to measure the load carrying capability of units with different random outage rates in the sense of reliability. And then in the late 1970s, Edward Kahn (Kahn, 1979) and Haslett John (Haslett and Diesendorf, 1981) first applied the concept of capacity credibility to the analysis of wind power, making it possible for uncontrollable, fluctuating and random wind power to participate in traditional power planning analysis and calculation.

The credible capacity of wind power assesses how many conventional units the wind farm can replace in the power balance, or how much creditable capacity the wind farm can produce with a reasonable or acceptable probability of confidence (Voorspools and D'Haeseleer, 2006). Wind power capacity credit is defined as the ratio of capacity that is equivalent to conventional generation to supply the load with the same level of reliability (Zhang et al., 2015).

The concept of wind power capacity credit is usually separated into the following four categories in present research (Amelin, 2009; Graham and Cooper, 2013; Zhang et al., 2015): 1) Equivalent Firm Capacity, EFC; 2) Equivalent Conventional Generation Capacity, ECGC; 3) Equivalent Load-carrying Capability, ELCC; 4) Guaranteed Capacity, GC. From the standpoint of uncertainty analysis, these four categories all specify the fraction of wind power that should be examined under the dimension of conventional unit capacity.

The above four definitions can be grouped into two categories, from the power supply side and the load side, respectively, under the premise of maintaining the reliability unchanged, the conventional unit capacity or additional payload that renewable energy can replace.

These two types of understanding each have their own practical significance: on the power side, how much wind power should be installed to replace conventional units that are about to be retired in order to achieve energy savings and emission reduction targets; on the load side, how much wind power should be planned to meet future load demand increases.

3.3 Copula Multi-Wind Farm Correlation

Multiple wind farms with identical geographical locations in the same wind region are common in places with abundant and concentrated wind energy resources. The output of each wind farm will be highly correlated due to the continuity of wind speed. The impact of integrating wind power into the electricity system will not be correctly evaluated if the correlation between the production of multiple wind farms in the same wind region is overlooked, which would raise the insecurity of system functioning.

Copula function, as a linking function between multiple random variables, is based on Sklar’s theorem (Kole et al., 2007). According to Sklar’s theorem, when the marginal distribution of multivariate random variables and the appropriate Copula function are determined, the joint probability distribution of these random variables can be obtained, which is the advantage of the Copula function in practical applications.

Copula function connects the marginal distributions of numerous random variables to a joint probability distribution. This function can capture nonlinearity, asymmetry, and tail correlation between variables and theoretically and does not limit the choice of marginal distribution. In (Hong et al., 2010), researchers assess the influence of wind farm connection system reliability when wind speeds are entirely related vs. completely independent. The Copula theory was added into the output modeling of several wind farms in (Li et al., 2013), which described the correlation characteristics across wind farms. In (Cai et al., 2013), Copula function is introduced to systematically model the dependent structure between wind speed and output power of wind farms, and a joint distribution function of wind speed and power of multiple wind farms is established. Scientists utilized the Copula function to model the dependent wind speed and wind power production of several wind farms in (Zhang et al., 2013). Researchers employed the Copula function to characterize the output correlation between neighboring wind farms in space and built a combined probability distribution model for the output of many wind farms in (Wu et al., 2015). On this foundation, a method for assessing multi-wind farm capacity reliability based on output is proposed.

The use of the Copula function can more correctly depict the nonlinear correlation of wind power output (Li et al., 2013; Wang et al., 2013; Ji et al., 2014; Xie et al., 2016), according to (Li et al., 2019). But the modeling approach is difficult, and adaptability is poor when there are a large number of wind farms (Xu et al., 2016). Furthermore (Yang et al., 2018), describes the correlation of the output of several wind farms using an adaptive multivariable nonparametric kernel density function, which can effectively improve the local adaptability problem of the Copula function method.

In (Xu et al., 2021), Wind farms in adjacent locations are affected by similar meteorological factors, and their output shows strong spatial and temporal correlation. Copula function can describe the dependencies between non-normal random variables in detail, and it has become a common method for modeling the joint probability distribution of random variables.

4 Wind Power Output Simulation Based on Time Series

In this section, the time series-based wind power output simulation is summarized, including model based on historical statistics, model based on simulated time series, and model considering both stochastics and variability.

4.1 Model Based on Historical Statistics

In addition to multi-state modeling, the load correction approach, in which the new energy curve is subtracted from the system sequential load curve, is also a widely used method for modeling wind power production. In this way, the system could be spared the effects of random fluctuations in new energy output.

From historical meteorological statistical data, the output curve can be calculated (Hasche et al., 2011). The historical statistics can well reflect the seasonal, diurnal, and autocorrelation characteristics of wind speed, but it is difficult to depict the stochastic characteristics. Especially when the measurement conditions are limited or the wind speed data is scarce, the data may not reflect the annual variation characteristics of wind speed.

In some previous studies, historical meteorological data reanalysis and downscaling techniques have been used to calculate the historical output curve of wind power by restoring the historical wind speed (Hawkins et al., 2011), which solves the data quality problem.

4.2 Simulation Model Based on Time Series

Previous studies have proposed a variety of statistical methods to simulate the sequential output of wind power to compensate for the difficulty of obtaining actual wind power output, with the goal of restoring the stochastic characteristics of wind power output through stochastic simulation.

Auto-Regressive and Moving Average (ARMA) model is the most widely used model in wind power output simulation. First, the autoregressive and moving average model parameters of each order are identified from the historical wind speed data. Then the identified ARMA model is sampled to obtain the time series of wind speed. Finally the wind speed time series is converted into wind power output through the wind output characteristic curve (Billinton et al., 2009; Gao and Billinton, 2009; Chen et al., 2010; Kloeckl and Papaefthymiou, 2010; Qu et al., 2013). ARMA model can accurately describe the volatility of wind speed. However, the wind speed simulated by the ARMA model is frequently normal rather than Weibull distributed, and dealing with the spatial correlation of the output of multiple wind farms is more difficult with the ARMA model. To reflect the spatiotemporal correlation (Lucheroni et al., 2019), employs a multi-dimensional ARMA model. In addition, the ST-ARMA model is used in (Zou et al., 2019) to statistically model the spatiotemporal coupling correlation of multidimensional sequences in a relatively concise form. The ST-ARMA model can generate a large amount of simulated data with the same statistical properties as actual wind output.

The Markov chain model is based on the wind power multi-state unit model, assuming that the state transition of wind power output is only related to the position of the previous state. The state transition matrix of wind power output is established based on historical data, and it is sequentially sampled to obtain the wind power output time series (Leite et al., 2006; Dobakhshari and Fotuhi-Firuzabad, 2009; Salehi-Dobakhshari and Fotuhi-Firuzabad, 2011; Luo et al., 2014). The probability distribution curve of wind power output has no shape constraints. The actual sampling frequency of each state, however, is difficult to stably converge to the expected probability due to the strong autocorrelation of wind power output (Billinton and Huang, 2011).

Furthermore, In (Li et al., 2019) a new method on modeling correlated power time series of multiple wind farms was proposed based on hidden Markov model (HMM). A Markov chain was adopted to model the state of time-varying correlations between wind farms, and wind power outputs at two adjacent moments were set as observations of HMM, which established the mathematical mapping model between wind power correlations and power outputs at two adjacent moments.

(Ning et al., 2010; Olsson et al., 2010) have used the stochastic differential equation model to simulate the wind power output considering the wind speed fluctuation characteristics and the spatial correlation of the output of multiple wind farms.

In general, the time series model of wind power can take into account the time series characteristics of wind power output, but it requires more information on these time series characteristics. In the time series simulation of wind power, it is technically difficult to consider the fluctuation of wind power output, daily characteristics, seasonality, and output correlation of multiple wind farms at the same time.

4.3 Stochastic Consideration

For stochastic factors in power systems, there are two main optimization methods: stochastic optimization and robust optimization. Stochastic optimization requires the use of a random variable probability distribution model, which is incapable of adequately describing the complex variations in real-world uncertainty variables. While robust optimization uses an uncertainty set to determine the changes in an uncertain factor. It is not necessary to assume a probability distribution model in advance, but when considering the optimal solution in the worst-case scenario, the optimal scheduling results may be conservative.

Therefore, stochastic multi-scenario models are described first in this section, followed by robust uncertainty sets. A time series multi-state model based on the Markov chain is further created, and the randomness, volatility, and ramping features are extensively addressed.

4.3.1 Multi-Scenario Model

Researchers suggest a stochastic multi-scenario model for optimal scheduling (Wang et al., 2008). The basic idea of the multi-scenario method is to select and determine multiple typical daily output curves of new energy sources, and then describe the randomness of new energy output using different typical daily curves and their corresponding probabilities.

The data of multiple scenes is generated by sampling based on the input typical new energy data and the normal distribution probability model. The researchers used Monte Carlo sampling (Wang X. et al., 2016) to form the basic scene, and used Latin hypercube sampling to generate the wind power scenario (Li and Zhu, 2016). They may also start with the probability density function of output at a single moment and discretize it using the Wasserstein distance (Wang Q. et al., 2015), with the time series connection generating the basic scene set. The precise probability distribution of wind power production can be established by sampling typical scenarios to represent a large number of complex scenes.

This model is a useful attempt to simultaneously describe the randomness and volatility of energy output. However, it should be noted that the process of creating this type of model is relatively difficult, and the complexity of related calculations will skyrocket as the number of scenes grows. This makes deciding on the number of scenes difficult. If the number of selected scenes is small, it will be difficult to fully describe the randomness of the output distribution. But if the number of scenes is large, analysis and calculation will be difficult.

4.3.2 Robust Uncertainty Set

Researchers built a robust model (Bertsimas et al., 2013) using an uncertainty set (Dvorkin et al., 2016) to characterize the power prediction error of renewable energy.

Robust optimization (RO) (Zeng and Zhao, 2013) is an common optimization approach to deal with data uncertainty. It is derived to hedge against any perturbation in the input data. Due to the improved modeling capability, two-stage RO has become a popular decision making tool.

Robust optimization is able to cope with any changes in random variables. Traditional robust optimization replaces the probability distribution information of stochastic variables with uncertain sets and determines the best solution that meets all of the requirements. Its solution speed is fast, and its decision-making outcomes are still viable even when numerous unknown parameters are perturbed at the same time.

The budget of the uncertain set was introduced to balance the conservatism and economy of robust optimization. At the same time, the method of reducing the cost of robustness was explored, and a robust optimization model with adjustable conservatism was proposed. Flexible uncertainty sets were first proposed (Zhao et al., 2015), whose upper and lower bounds are optimization variables rather than given values. Flexible uncertainty sets can be applied to economic scheduling, reserve optimization, and unit combination problems (Wang C. et al., 2016; Doostizadeh et al., 2016; Shao et al., 2017).

In (Xu et al., 2020), The suggested method uses kernel density estimation to create an ambiguous set of continuous multivariate probability distributions, and the integrated dispatch optimization model is composed of stochastic and resilient optimization problems.

Furthermore, in (Xu et al., 2022), the researchers propose a data-driven distributed robust optimization method for power system scheduling to deal with the power system operation problem considering wind power uncertainty. The distributed robust optimization method constructed is a combination of stochastic optimization and robust optimization, which can ensure the reliability of the optimization results while making full use of the statistical information of random variables.

4.3.3 Temporal Multi-State Model

Several output curves can retain the fluctuation characteristics of renewable energy output, but cannot fully describe its randomness. Multiple different output states and corresponding probabilities can describe the random characteristics of renewable energy output, but it is difficult to describe its volatility. Simultaneously, the ramping rate and the ramping features of the probability distribution of the ramping rate, as an essential part of the output characteristics of renewable energy, have not been adequately addressed or explained in the aforementioned two kinds of modeling methodologies.

Researchers have proposed a temporal multi-state unit model (Zhaohong et al., 2009), which involves using different multi-state unit models to describe the output characteristics of renewable energy over time in order to account for its randomness and volatility.

In addition, a sequential multi-state unit formation method based on Markov process (王锡凡 et al., 2015) has been proposed to describe the relationship between renewable energy output in adjacent periods while taking into account its ramping characteristics. The multi-state unit model reflects the randomness renewable energy output. The multi-state model of time series further contains the time series fluctuation characteristics of the output of renewable energy. And the Markov state transition matrix intuitively reflects the transition of renewable energy output from a certain state to another state. Compared with the existing methods, the method can more comprehensively describe the output characteristics of renewable energy.

5 Issues, Challenges and Future Work

Issues and challenges in wind power output modeling research are as follows:

1) Simulation model of wind power output in different seasons: Existing wind power output simulation models frequently use wind power and load data for a whole year, with the calculation results representing wind power’s contribution to system reliability throughout the year. However, wind power in some areas has distinct seasonal and daily characteristics. At the same time, in power planning, the calculation of power balance is carried out on a monthly basis, and the peak load on a typical day of each month is used for calculation.

2) Changes in wind power with various weather conditions: Part of the cause for the 2021 Texas blackout was that wind turbines were unable to produce energy owing to equipment freezing, resulting in an inadequate power supply on the power supply side. Under a variety of meteorological conditions, the output power of wind power is unstable and intermittent. Only a scientific power dispatch mode can ensure the stable output of wind power.

3) Synergy of various forms of energy: Compared to traditional power systems, which are primarily based on a single form of energy source and utilization, new power systems realize the transition from one energy source to multiple energy forms on the energy source side. The output modeling of a new energy system must take into account not just a single energy form as the modeling object, but also the coupling and complimentary interactions between the various energy forms. Further research is required in order to realize the complementary coordination of multiple energy sources at various time and space scales.

4) Coupling of the energy supply side and the energy demand side: The new energy power system realizes not only the transformation from a single energy source to a variety of energy forms on the energy supply side, but also the change from traditional electrical loads to multi-type loads on the energy demand side (such as energy storage, electric vehicles, etc.). As a result, the output modeling of the new energy power system must take into account the information interaction between supply and demand. And a new energy power system output modeling that complements supply and demand must be established.

So for these issues, future work for new power system planning considering variable wind power output will be as follows:

1) It is necessary to research on the simulation model of wind power output in different seasons to better support the power balance.

2) It is an important measure to improve the security of the power system to study the relationship between wind power and meteorological conditions, correctly simulate the wind power output, and improve the emergency support capability.

3) To increase the power system’s ability to absorb new energy, it is necessary to investigate the coordinated and complementary properties of numerous energy sources at various time and space scales.

4) To support the overall coordinated control and performance optimization of the system, it is vital to consider the information interaction between the supply side and the demand side as a whole, and to develop a new energy power system model with coupling linkage and complementary supply and demand.

6 Conclusion

Simulation models of wind energy output for new power system planning have been reviewed. This paper focuses on addressing the long-term variability and uncertainties of renewables, thus discussing the following parts: 1) Modeling of wind power output without considering time series, primarily based on the long-term characteristics of wind power to carry out modeling based on probability statistics, which is used for power balance, reliability assessment, etc.; 2) Time series modeling of wind power output, mainly used to arrange the operation mode of units under sequential production simulation; 3) Time series and probability modeling, which overcomes the shortcomings of the previous two categories and incorporates both uncertainty and volatility into the model. Finally, this paper highlights issues and challenges in wind power output modeling research, such as considering wind power output in different seasons, wind power output change under various meteorological conditions, coordinating multiple energy sources, and coupling energy supply and demand. And some future work for new power system planning considering variable wind power output is proposed.

Author Contributions

XiL: Conceptualization, Writing- Original draft. YY: Methodology, Writing- Original draft. XH: Analysis, Writing- Original draft preparation. WX: Supervision, Writing- Original draft preparation. XuL: Supervision, Writing- Reviewing and Editing.

Funding

This research is supported by the Science and Technology Project of China Southern Power Grid Co., Ltd. grant number 030000KK52210022 (GDKJXM20212056).

Conflict of Interest

XiL, WX, and XuL Were employed by the company Guangdong Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amelin, M. (2009). Comparison of Capacity Credit Calculation Methods for Conventional Power Plants and Wind Power. IEEE Trans. Power Syst. 24 (2), 685–691. doi:10.1109/tpwrs.2009.2016493

CrossRef Full Text | Google Scholar

Bertsimas, D., Litvinov, E., Sun, X. A., Zhao, J., and Zheng, T. (2013). Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem. IEEE Trans. Power Syst. 28 (1), 52–63. doi:10.1109/tpwrs.2012.2205021

CrossRef Full Text | Google Scholar

Billinton, R., and Dange Huang, D. (2011). Incorporating Wind Power in Generating Capacity Reliability Evaluation Using Different Models. IEEE Trans. Power Syst. 26 (4), 2509–2517. doi:10.1109/tpwrs.2011.2120633

CrossRef Full Text | Google Scholar

Billinton, R., Yi Gao, Y., and Karki, R. (2009). Composite System Adequacy Assessment Incorporating Large-Scale Wind Energy Conversion Systems Considering Wind Speed Correlation. IEEE Trans. Power Syst. 24 (3), 1375–1382. doi:10.1109/tpwrs.2009.2023263

CrossRef Full Text | Google Scholar

Cai, F., Yan, Z., Zhao, J., Feng, D., Guo, J., and Hu, D. (2013). Dependence Structure Models for Wind Speed and Wind Power Among Different Wind Farms Based on Copula Theory. Automation Electr. Power Syst. 37 (17), 9–16. doi:10.7500/AEPS201207293

CrossRef Full Text | Google Scholar

Chen, P., Pedersen, T., Bak-Jensen, B., and Chen, Z. (2010). ARIMA-based Time Series Model of Stochastic Wind Power Generation. IEEE Trans. Power Syst. 25 (2), 667–676. doi:10.1109/tpwrs.2009.2033277

CrossRef Full Text | Google Scholar

Conejo, A. J., Cheng, Y., Cheng, Y., Zhang, N., and Kang, C. (2017). Long-term Coordination of Transmission and Storage to Integrate Wind Power. Csee Jpes 3 (1), 36–43. doi:10.17775/cseejpes.2017.0006

CrossRef Full Text | Google Scholar

Dobakhshari, A. S., and Fotuhi-Firuzabad, M. (2009). A Reliability Model of Large Wind Farms for Power System Adequacy Studies. IEEE Trans. Energy Convers. 24 (3), 792–801. doi:10.1109/tec.2009.2025332

CrossRef Full Text | Google Scholar

Doostizadeh, M., Aminifar, F., Ghasemi, H., and Lesani, H. (2016). Energy and Reserve Scheduling under Wind Power Uncertainty: An Adjustable Interval Approach. IEEE Trans. Smart Grid 7 (6), 2943–2952. doi:10.1109/tsg.2016.2572639

CrossRef Full Text | Google Scholar

Dvorkin, Y., Lubin, M., Backhaus, S., and Chertkov, M. (2016). Uncertainty Sets for Wind Power Generation. IEEE Trans. Power Syst. 31 (4), 3326–3327. doi:10.1109/tpwrs.2015.2476664

CrossRef Full Text | Google Scholar

Feijóo, A., and Villanueva, D. (2016). Assessing Wind Speed Simulation Methods. Renew. Sustain. Energy Rev. 56, 473–483. doi:10.1016/j.rser.2015.11.094

CrossRef Full Text | Google Scholar

Feng, C., Liang, B., Li, Z., Liu, W., and Wen, F. (2022). Peer-to-Peer Energy Trading under Network Constraints Based on Generalized Fast Dual Ascent. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2022.3162876

CrossRef Full Text | Google Scholar

Ganger, D., Zhang, J., and Vittal, V. (2014). Statistical Characterization of Wind Power Ramps via Extreme Value Analysis. IEEE Trans. Power Syst. 29 (6), 3118–3119. doi:10.1109/tpwrs.2014.2315491

CrossRef Full Text | Google Scholar

Gao, Y., and Billinton, R. (2009). Adequacy Assessment of Generating Systems Containing Wind Power Considering Wind Speed Correlation. IET Renew. Power Gener. 3 (2), 217–226. doi:10.1049/iet-rpg:20080036

CrossRef Full Text | Google Scholar

Garver, L. (1966). EFFECTIVE LOAD CARRYING CAPABILITY OF GENERATING UNITS. IEEE Trans. Power Apparatus Syst. PAS-85 (8), 910–919. doi:10.1109/tpas.1966.291652

CrossRef Full Text | Google Scholar

Graham, W. J., and Cooper, W. H. (2013). Taking Credit. J. Bus. Ethics 115 (2), 403–425. doi:10.1007/s10551-012-1406-3

CrossRef Full Text | Google Scholar

Han, X., Li, T., Zhang, D., and Zhou, X. (2021). New Issues and Key Technologies of New Power System Planning under Double Carbon Goals. High. Volt. Eng. 47 (9), 3036–3046. doi:10.13336/j.1003-6520.hve.20210809

CrossRef Full Text | Google Scholar

Hasche, B., Keane, A., and O'Malley, M. (2011). Capacity Value of Wind Power, Calculation, and Data Requirements: the Irish Power System Case. IEEE Trans. Power Syst. 26 (1), 420–430. doi:10.1109/tpwrs.2010.2051341

CrossRef Full Text | Google Scholar

Haslett, J., and Diesendorf, M. (1981). The Capacity Credit of Wind Power: A Theoretical Analysis. Sol. Energy 26 (5), 391–401. doi:10.1016/0038-092x(81)90218-8

CrossRef Full Text | Google Scholar

Hawkins, S., Eager, D., and Harrison, G. P. (2011). “Characterising the Reliability of Production from Future British Offshore Wind Fleets,” in IET Conference on Renewable Power Generation (RPG 2011), 1–6. doi:10.1049/cp.2011.0183

CrossRef Full Text | Google Scholar

Hong, L., Shi, L., Yao, L., Masoud, B., and Ni, Y. (2010). Fuzzy Modelling and Solution of Load Flow Incorporating Uncertainties of Wind Farm Generation. Trans. China Electrotech. Soc. 25 (8), 116–122. 130. doi:10.19595/j.cnki.1000-6753.tces.2010.08.019

CrossRef Full Text | Google Scholar

Ji, F., Cai, X., and Wang, J. (2014). Wind Power Correlation Analysis Based on Hybrid Copula. Automation Electr. Power Syst. 38 (2), 1–5. 32. doi:10.7500/AEPS201208067

CrossRef Full Text | Google Scholar

Kahn, E. (1979). The Reliability of Distributed Wind Generators. Electr. Power Syst. Res. 2 (1), 1–14. doi:10.1016/0378-7796(79)90021-x

CrossRef Full Text | Google Scholar

Kashyap, R. L. (1982). OPTIMAL CHOICE OF AR AND MA PARTS IN AUTOREGRESSIVE MOVING AVERAGE MODELS. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-4 (2), 99–104. doi:10.1109/tpami.1982.4767213

CrossRef Full Text | Google Scholar

Kim, H., Singh, C., and Sprintson, A. (2012). Simulation and Estimation of Reliability in a Wind Farm Considering the Wake Effect. IEEE Trans. Sustain. Energy 3 (2), 274–282. doi:10.1109/tste.2011.2174260

CrossRef Full Text | Google Scholar

Klöckl, B., and Papaefthymiou, G. (2010). Multivariate Time Series Models for Studies on Stochastic Generators in Power Systems. Electr. Power Syst. Res. 80 (3), 265–276. doi:10.1016/j.epsr.2009.09.009

CrossRef Full Text | Google Scholar

Kole, E., Koedijk, K., and Verbeek, M. (2007). Selecting Copulas for Risk Management. J. Bank. Finance 31 (8), 2405–2423. doi:10.1016/j.jbankfin.2006.09.010

CrossRef Full Text | Google Scholar

Kroposki, B., Johnson, B., Zhang, Y., Gevorgian, V., Denholm, P., Hodge, B.-M., et al. (2017). Achieving a 100% Renewable Grid. Ieee Power & Energy Mag. 15 (2), 61–73. doi:10.1109/mpe.2016.2637122

CrossRef Full Text | Google Scholar

Leite, A. P., Borges, C. L. T., and Falcao, D. M. (2006). Probabilistic Wind Farms Generation Model for Reliability Studies Applied to Brazilian Sites. IEEE Trans. Power Syst. 21 (4), 1493–1501. doi:10.1109/tpwrs.2006.881160

CrossRef Full Text | Google Scholar

Li, J., Wen, J., Cheng, S., and Wei, H. (2013). A Scene Generation Method Considering Copula Correlation Relationship of Multi-Wind Farms Power. Proc. CSEE 33 (16), 30–36. doi:10.13334/j.0258-8013.pcsee.2013.16.012

CrossRef Full Text | Google Scholar

Li, J., and Zhu, D. (2016). Combination of Moment‐matching, Cholesky and Clustering Methods to Approximate Discrete Probability Distribution of Multiple Wind Farms. Iet Renew. Power Gener. 10 (9), 1450–1458. doi:10.1049/iet-rpg.2015.0568

CrossRef Full Text | Google Scholar

Li, P., Liu, C., Huang, Y., Wang, W., and Li, Y. (2019). Modeling Correlated Power Time Series of Multiple Wind Farms Based on Hidden Markov Model. Proc. Chin. Soc. Electr. Eng. 39 (19), 5683–5691. doi:10.13334/j.0258-8013.pcsee.182412

CrossRef Full Text | Google Scholar

Lucheroni, C., Boland, J., and Ragno, C. (2019). Scenario Generation and Probabilistic Forecasting Analysis of Spatio-Temporal Wind Speed Series with Multivariate Autoregressive Volatility Models. Appl. Energy 239, 1226–1241. doi:10.1016/j.apenergy.2019.02.015

CrossRef Full Text | Google Scholar

Luo, G., Shi, D., Chen, J., and Wu, X. (2014). A Markov Chain Monte Carlo Method for Simulation of Wind and Solar Power Time Series. Power Syst. Technol. 38 (2), 321–327. doi:10.13335/j.1000-3673.pst.2014.02.008

CrossRef Full Text | Google Scholar

Olsson, M., Perninge, M., and Söder, L. (2010). Modeling Real-Time Balancing Power Demands in Wind Power Systems Using Stochastic Differential Equations. Electr. Power Syst. Res. 80 (8), 966–974. doi:10.1016/j.epsr.2010.01.004

CrossRef Full Text | Google Scholar

Qu, C., Wang, X., Xie, S., and Wu, X. (2013). Impacts of Different Wind Speed Models and Reliability Indices on Capacity Credit Evaluation of Wind Power. Power Syst. Technol. 37 (10), 2896–2903. doi:10.13335/j.1000-3673.pst.2013.10.020

CrossRef Full Text | Google Scholar

Salehi-Dobakhshari, A., and Fotuhi-Firuzabad, M. (2011). Integration of Large-Scale Wind Farm Projects Including System Reliability Analysis. IET Renew. Power Gener. 5 (1), 89–98. doi:10.1049/iet-rpg.2008.0110

CrossRef Full Text | Google Scholar

Sevlian, R., and Rajagopal, R. (2013). Detection and Statistics of Wind Power Ramps. IEEE Trans. Power Syst. 28 (4), 3610–3620. doi:10.1109/tpwrs.2013.2266378

CrossRef Full Text | Google Scholar

Sevlian, R., and Rajagopal, R. (2012). “Wind Power Ramps: Detection and Statistics,” in Proceeding of the 2012 IEEE Power and Energy Society General Meeting. doi:10.1109/PESGM.2012.6344969

CrossRef Full Text | Google Scholar

Shao, C., Feng, C., Fu, X., Yang, P., Wang, X., and Wang, X. (2021). Multi Energy Power System Production Simulation:State of Arts and Challenges. Proc. Chin. Soc. Electr. Eng. 41 (6), 2029–2039. doi:10.13334/j.0258-8013.pcsee.200801

CrossRef Full Text | Google Scholar

Shao, C., Wang, X., Shahidehpour, M., Wang, X., and Wang, B. (2017). Security-Constrained Unit Commitment with Flexible Uncertainty Set for Variable Wind Power. IEEE Trans. Sustain. Energy 8 (3), 1237–1246. doi:10.1109/tste.2017.2673120

CrossRef Full Text | Google Scholar

Shortt, A., Kiviluoma, J., and O'Malley, M. (2013). Accommodating Variability in Generation Planning. IEEE Trans. Power Syst. 28 (1), 158–169. doi:10.1109/tpwrs.2012.2202925

CrossRef Full Text | Google Scholar

Voorspools, K. R., and D'Haeseleer, W. D. (2006). An Analytical Formula for the Capacity Credit of Wind Power. Renew. Energy 31 (1), 45–54. doi:10.1016/j.renene.2005.03.017

CrossRef Full Text | Google Scholar

Wang, C., Liu, F., Wang, J., Wei, W., and Mei, S. (2016a). Risk-Based Admissibility Assessment of Wind Generation Integrated into a Bulk Power System. IEEE Trans. Sustain. Energy 7 (1), 325–336. doi:10.1109/tste.2015.2495299

CrossRef Full Text | Google Scholar

Wang, J., Cai, X., and Ji, F. (2013). Simulation Method of Correlated Random Variables Based on Copula. Proc. CSEE 33 (22), 75–82.

Google Scholar

Wang, J., Shahidehpour, M., and Li, Z. (2008). Security-constrained Unit Commitment with Volatile Wind Power Generation. IEEE Trans. Power Syst. 23 (3), 1319–1327. doi:10.1109/tpwrs.2008.926719

CrossRef Full Text | Google Scholar

Wang, Q., Dong, W., and Yang, L. (2015a). A Wind Power/Photovoltaic Typical Scenario Set Generation Algorithm Based on Wasserstein Distance Metric and Revised K-Medoids Cluster. Proc. Chin. Soc. Electr. Eng. 35 (11), 2654–2661. doi:10.13334/j.0258-8013.pcsee.2015.11.003

CrossRef Full Text | Google Scholar

Wang, X., Shao, C., Wang, X., Jin, X., and Lu, S. (2015b). A Renewable Energy Power Modeling Method Based on Markov Process.

Google Scholar

Wang, X., Dai, H.-z., and Thomas, R. (1984). Reliability Modeling of Large Wind Farms and Associateed Electric Utility Interface Systems. IEEE Trans. Power Apparatus Syst. PAS-103 (3), 569–575. doi:10.1109/tpas.1984.318746

CrossRef Full Text | Google Scholar

Wang, X., Hu, Z., Zhang, M., and Hu, M. (2016b). “Two-stage Stochastic Optimization for Unit Commitment Considering Wind Power Based on Scenario Analysis,” in Proceeding of the 2016 China International Conference on Electricity Distribution (CICED) (IEEE).

CrossRef Full Text | Google Scholar

Wu, Y., Zhang, L., Li, H., Lou, S., and Yang, Y. (2015). Wind-power Capacity Credibility Assessment Considering Power Output Correlation of Multiple Wind Farms. Electr. Power Autom. Equip. 35 (11), 8–12. doi:10.16081/j.issn.1006-6047.2015.11.002

CrossRef Full Text | Google Scholar

Xie, M., Xiong, J., Liu, M., and Zhou, S. (2016). Modeling of Multi Wind Farm Output Correlation Based on Copula and its Application in Power System Economic Dispatch. Power Syst. Technol. 40 (4), 1100–1106. doi:10.13335/j.1000-3673.pst.2016.04.018

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., Yan, Z., and Li, H. (2022). Distributionally Robust Optimal Dispatch Method Considering Mining of Wind Power Statistical Characteristics. Automation Electr. Power Syst. 46 (2), 33–42. doi:10.7500/AEPS20210413003

CrossRef Full Text | Google Scholar

Xu, X., Wang, H., Yan, Z., Lu, Z., Kang, C., and Xie, K. (2021). Overview of Power System Uncertainty and its Solutions under Energy Transition. Automation Electr. Power Syst. 45 (16), 2–13. doi:10.7500/AEPS20210301003

CrossRef Full Text | Google Scholar

Xu, X., Yan, Z., Shahidehpour, M., Li, Z., Yan, M., and Kong, X. (2020). Data-Driven Risk-Averse Two-Stage Optimal Stochastic Scheduling of Energy and Reserve with Correlated Wind Power. IEEE Trans. Sustain. Energy 11 (1), 436–447. doi:10.1109/tste.2019.2894693

CrossRef Full Text | Google Scholar

Xu, Y., Chen, K., Li, J., and Nie, Y. (2016). A New Method Analyzing Output Correlation of Multi-Wind Farms Based on Combination of Copula Function and Kernel Estimation Theory. Trans. China Electrotech. Soc. 31 (13), 92–100. doi:10.19595/j.cnki.1000-6753.tces.2016.13.011

CrossRef Full Text | Google Scholar

Yang, D., Zhou, S., and Bao, F. (2014). Analysis on Peak Load Regulation Capability of Power Grid Integrated with Wind Farms in Valley Load Period. Power Syst. Technol. 38 (6), 1446–1451. doi:10.13335/j.1000-3673.pst.2014.06.004

CrossRef Full Text | Google Scholar

Yang, N., Huang, Y., Ye, D., Wang, X., Li, H., Li, S., et al. (2018). Modeling of Output Correlation of Multiple Wind Farms Based on Adaptive Multivariable Nonparametric Kernel Density Estimation. Proc. Chin. Soc. Electr. Eng. 38 (13), 3805–3812. doi:10.13334/j.0258-8013.pcsee.171751

CrossRef Full Text | Google Scholar

Zeng, B., and Zhao, L. (2013). Solving Two-Stage Robust Optimization Problems Using a Column-And-Constraint Generation Method. Operations Res. Lett. 41 (5), 457–461. doi:10.1016/j.orl.2013.05.003

CrossRef Full Text | Google Scholar

Zhang, G. P. (2003). Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing 50, 159–175. doi:10.1016/s0925-2312(01)00702-0

CrossRef Full Text | Google Scholar

Zhang, N., Kang, C., Duan, C., Tang, X., Huang, J., Lu, Z., et al. (2010). Simulation Methodology of Multiple Wind Farms Operation Considering Wind Speed Correlation. Int. J. Power Energy Syst. 30 (4), 264–273. doi:10.2316/Journal.203.2010.4.203-4843

CrossRef Full Text | Google Scholar

Zhang, N., Kang, C., Xiao, J., Li, H., Wang, Z., Shi, R., et al. (2015). Review and Prospect of Wind Power Capacity Credit. Proc. Chin. Soc. Electr. Eng. 35 (1), 82–94. doi:10.13334/j.0258-8013.pcsee.2015.01.011

CrossRef Full Text | Google Scholar

Zhang, N., Kang, C., Xu, Q., Jiang, C., Chen, Z., and Liu, J. (2013). Modelling and Simulating the Spatio-Temporal Correlations of Clustered Wind Power Using Copula. J. Electr. Eng. Technol. 8 (6), 1615–1625. doi:10.5370/jeet.2013.8.6.1615

CrossRef Full Text | Google Scholar

Zhang, S., Wang, C., Liao, P., Xiao, L., and Fu, T. (2022). Wind Speed Forecasting Based on Model Selection, Fuzzy Cluster, and Multi-Objective Algorithm and Wind Energy Simulation by Betz's Theory. Expert Syst. Appl. 193, 116509. doi:10.1016/j.eswa.2022.116509

CrossRef Full Text | Google Scholar

Zhao, J., Zheng, T., and Litvinov, E. (2015). Variable Resource Dispatch through Do-Not-Exceed Limit. IEEE Trans. Power Syst. 30 (2), 820–828. doi:10.1109/tpwrs.2014.23333f67

CrossRef Full Text | Google Scholar

Zhaohong, B., Xin, Z., Zijing, W., and Xifan, W. (2009). “Studies on Models and Algorithms of the Power System Probabilistic Production Simulation Integrated with Wind Farm,” in Proceeding of the 2009 IEEE Power & Energy Society General Meeting.

Google Scholar

Zhou, X., Chen, S., Lu, Z., Huang, Y., Ma, S., and Zhao, Q. (2018). Technology Features of the New Generation Power System in China. Proc. Chin. Soc. Electr. Eng. 38 (7), 1893–1904. doi:10.13334/j.0258-8013.pcsee.180067

CrossRef Full Text | Google Scholar

Zou, J., Zhu, J., Lai, X., Xie, P., and Xuan, P. (2019). Simulation of Wind Power Output Series Based on Space-Time Auto-Regressive Moving Average Model. Automation Electr. Power Syst. 43 (3), 101–107. doi:10.7500/AEPS20180328002

CrossRef Full Text | Google Scholar