- 1Laboratory of Study and Research for Applied Mathematics, Mohammadia School of Engineers, Mohammed V University, Rabat, Morocco
- 2Engineering for Smart and Sustainable Systems Research Center, Mohammadia School of Engineers, Mohammed V University, Rabat, Morocco
- 3Electrical Engineering Department, Faculty of Engineering, Aswan University, Aswan, Egypt
- 4Department of Electrical Engineering, College of Engineering, Prince Sattam Bin Abdulaziz University, Al-Kharj, Saudi Arabia
- 5Department of Electrical Power and Machines Engineering, Faculty of Engineering, Helwan University, Helwan, Egypt
This study presents an improved chaotic flower pollination algorithm (CFPA) with a view to handle the optimal power flow (OPF) problem integrating a hybrid wind and solar power and generate the optimal settings of generator power, bus voltages, shunt reactive power, and tap setting transformers. In spite of the benefits of FPA, it encounters two problems like other evolutionary algorithms: entrapment in local optima and slow convergence speed. Thus, to deal with these drawbacks and enhance the FPA searching accuracy, a hybrid optimization approach CFPA which combines the stochastic algorithm FPA that simulates the flowering plants process with the chaos methodology is applied in this manuscript. Therefore, owing to the various nonlinear constraints in OPF issue, a constraint handling technique named superiority of feasible solutions (SF) is embedded into CFPA. To confirm the performance of the chaotic FPA, a set of different well-known benchmark functions were employed for ten diverse chaotic maps, and then the best map is tested on IEEE 30-bus and IEEE 57-bus test systems incorporating the renewable energy sources (RESs). The obtained results are analyzed statistically using non-parametric Wilcoxon rank-sum test in view of evaluating their significance compared to the outcomes of the state-of-the-art meta-heuristic algorithms such as ant bee colony (ABC), grasshopper optimization algorithm (GOA), and dragonfly algorithm (DA). From this study, it may be established that the suggested CFPA algorithm outperforms its meta-heuristic competitors in most benchmark test cases. Additionally, the experimental results regarding the OPF problem demonstrate that the integration of RESs decreases the total cost by 12.77% and 33.11% for the two systems, respectively. Thus, combining FPA with chaotic sequences is able to accelerate the convergence and provide better accuracy to find optimal solutions. Furthermore, CFPA (especially with the Sinusoidal map) is challenging in solving complex real-world problems.
1 Introduction
Nature-inspired computation algorithms have been evolved during the last few decades, supplying a varied source of approaches that address diverse fields, such as industrial designs, economics, business activities, engineering, etc. Generally, there are two categories of optimization techniques: stochastic and deterministic algorithms (Vasant, 2012). The deterministic kind of approaches proceed rigorously; they produce an accurate outcome for a given design variable. However, in spite of their fast convergence, they fail to reach the global solution; hence, they get stuck in local optima and fail to deal with derivative-free issues. In contrast, the stochastic algorithms are among the best and effective strategies in finding optimal solutions, conflicting with the classical optimization approaches. This kind of algorithm has been widely utilized due to its capability to obtain global optimum solutions escaping from local optima and its ease of implementation. Some of the well-regarded meta-heuristic algorithms are as follows: Genetic Algorithm (GA), which is the first stochastic algorithm inspired by John Holland in 1960 (Holland, 1975), followed by Simulated Annealing (SA) in 1983 (Kirkpatrick et al., 1983), Particle Swarm Optimization (PSO) in 1995 by Kennedy (Kennedy and Eberhart, 1995), and more approaches that were developed later, such as Ant Bee Colony (ABC) (Basturk and Karaboga, 2006), Arithmetic Optimization Algorithm (AOA) (Abualigah et al., 2021a), Harris Hawks Optimization (HHO) (Heidari et al., 2019), Sin Cosine Algorithm (SCA) (Mirjalili, 2016), Black Widow Optimization (BWO) (Hayyolalam and Pourhaji, 2020), Dynamic differential annealed optimization (DDAO) (Ghafil and Jármai, 2020), Levy Flight Distribution (LFD) (Essam et al., 2020), Salp Swarm Algorithm (SSA) (Mirjalili et al., 2017), Henry Gas Solubility Optimization (HGSO) (Hashim et al., 2019), Manta Ray Foraging Optimization (MRFO) (Zhao et al., 2020), starling murmuration optimizer (SMO) (Zamani et al., 2022), Honey Badger Algorithm (HBA) (Hashim et al., 2022), Reptile Search Algorithm (RSA) (Abualigah et al., 2022), Aquila Optimizer (AO) (Abualigah et al., 2021b), and so on. All these algorithms divide the search process into two important characteristics: exploration and exploitation with a specific probability; these two phases are also called diversification and intensification. The first phase is considered as the essential step in which the algorithm can examine the search space more effectively and generate a new diverse solution as possible with jumping out from any local optima. Meanwhile, the exploitation or intensification phase attempts to use the information of the obtained current best solutions from the exploration or diversification phase (Yang, 2010). In numerous instances, exploitation and exploration are not balanced, and due to the random nature of meta-heuristic algorithms, there is no explicit frontier between these two mechanisms (Mirjalili et al., 2014). Therefore, these issues leave the stochastic approaches stuck in the local optimum without balancing properly between the exploitation and exploration. Moreover, in spite of the benefits of the intelligence algorithms, they require some improvement to satisfy the diverse characteristics of complex real-world applications, which means that no approach is qualified in resolving the diverse kind of optimization problems. In that regard, the No-Free Lunch (NFL) theorem (Wolpert and Macready, 1997) validates this and opens the way for developers to create new approaches and enhance the quality of the existing ones.
Recently, a third group of nature algorithms can be considered, and it is a hybrid between stochastic and deterministic algorithms. The combination of meta-heuristics with conventional methods is a practical remedy to enhance both exploitation and exploration and then to raise the performance of stochastic algorithms, by overcoming the slow convergence drawback, local optima entrapment, and the meta-heuristics random constructions. One of the most known mathematical techniques is combining chaotic sequences with stochastic algorithms. Additionally, the chaos is a random state which can appear in the nonlinear dynamical systems and bounded properties, non-convergent and non-periodic (Alatas, 2010). This chaos can be integrated in the stochastic algorithms with the intention of optimizing their performances. Accordingly, the chaos has been extensively embedded in several evolutionary approaches. In this regard, here are some computation algorithms that have been improved: chaotic firefly algorithm (CFA) (Gandomi et al., 2013), chaotic ant swarm optimization (CASO) (Cai et al., 2007), chaotic genetic algorithm (CGA) (Abdullah et al., 2012), chaotic particle swarm optimization (CPSO) (He et al., 2009), hybridizing chaotic sequences with memetic differential evolution algorithm (Jia et al., 2011), chaotic krill herd algorithm (CKHA) (Wanga et al., 2014), chaotic bio-geography based optimization (CBBO) (Saremi et al., 2014), chaotic artificial immune system algorithm (CAIS) (Jordehi, 2015), chaotic water cycle algorithm (CWCA) (Heidari et al., 2017), chaotic based big bang-big crunch algorithm (BBBC) (Jordehi, 2014), chaotic manta ray foraging optimization (CMRFO) (Daqaq et al., 2022), chaotic bat algorithm (CBA) (Mugemanyi et al., 2020), chaotic atom search optimization (CAS) (Too and Abdullah, 2020), Coyote Optimization Algorithm (COA) (Tong et al., 2022), etc.
In this current work, the authors focus on the hybridization of chaos maps with a stochastic approach named flower pollination algorithm (FPA), in view of switching between local and global pollination. Instead of random numbers of diverse parameters of FPA, chaotic maps are replaced to not follow the uniform distribution. With regard to the FPA, it has been pointed out in diverse academic fields and real-world applications, especially in science and engineering, that it performs better than other well-known algorithms. From this perspective, the powerful advantages of FPA and its borrowed approaches motivate us to develop a novel version of FPA based on chaos maps in view of solving the OPF incorporating RESs. In that aspect, among these studies that have been published on FPA and its variants, the study by (Singh and Kaur, 2019) selects the optimal features for anomaly detection in networks using the standard flower pollination algorithm. According to the study by (Samy et al., 2019), the authors applied FPA to develop a techno-economic feasibility analysis for an off-grid hybrid renewable energy system. In the study by (Priya and Rajasekar, 2019), PEMFC modeling has been successfully tackled by using FPA. A recent study (Wang et al., 2019a) presented FPA with the wireless sensor networks to deploy heterogeneous node radiation. In another research work (Wang et al., 2019b), a discrete flower pollination algorithm–based multi-objective optimization is investigated to solve the stochastic two-sided partial disassembly line. A hybridization of FPA with wind-driven optimization is adopted in the study by (Niu et al., 2019) in order to develop the global and local pollination processes. (Rodrigues et al., 2020) suggested an adaptive flower pollination algorithm that can dynamically modify its parameter. (Shambour et al., 2019) employed the direct search method in the global pollination process to improve the convergence and accuracy of the original FPA. For more information concerning the FPA and its variants, refer to the recent review (Abdel-Basset and Shawky, 2019). In relation to the previously published work and in an attempt to prove the FPA superiority, the proposed approach is validated and tested on thirteen benchmark test problems. In addition to these test suites, a real-world problem under the name of optimal power flow (OPF) is applied to affirm the capability and effectiveness of this novel algorithm in solving real complex functions.
The OPF has played an important task in the planning and operation of power systems over recent decades (Bonab et al., 2016). Furthermore, the optimal power flow problem is characterized as a non-convex, nonlinear, large-scale, and highly constrained optimization problem (Vaccaro and Cañizares, 2018), and the main key of the OPF issue is to diminish some objectives such as fuel cost, emission, voltage deviation, and power loss by decreasing the control variable values with respect to the different constraints such as equal and inequal limitations. Moreover, the optimal power flow issue, including renewable energy, has taken up increasing attention in many research studies owing to the environmental benefits and low operation cost. Besides, the renewable resources used most in the world are solar and wind power. On this basis, this current work formulates and solves the OPF problem with and without merging a hybrid wind-photovoltaic energy into 30-bus and 57-bus systems. In that aspect, the renewable sources are installed instead of some conventional generators. Accordingly, an extensive number of meta-heuristic algorithms have been undertaken to deal with the OPF problem. Some recently introduced approaches that have been efficiently applied in this field can be found in these references (Abaci and Yamacli, 2016; Bouchekara et al., 2016a; Bouchekara et al., 2016b; Bouchekara et al., 2016c; Chaib et al., 2016; Trivedi et al., 2016; Bentouati et al., 2017; Duman, 2017; Mohamed et al., 2017; Yuan et al., 2017; Biswas et al., 2018a; Biswas et al., 2018b; El-Fergany and Hasanien, 2018; Morshed et al., 2018; Taher et al., 2019a; Taher et al., 2019b; El-Sattar et al., 2019; Elattar, 2019; Nguyen, 2019; Shilaja and Arunprasath, 2019; Alhejji et al., 2020; Warid, 2020; Alasali et al., 2021; Daqaq et al., 2021; Meng et al., 2021; Sulaiman et al., 2021; Yessef et al., 2022a; Yessef et al., 2022b; Houssein et al., 2022).
Experimental results display that the proposed chaotic FPA outstrips the basic FPA and some re-implemented algorithms such as ant bee colony (ABC), grasshopper optimization algorithm (GOA), dragonfly algorithm (DA), and even the existing well-known algorithms reported in the literature.
The major features of this research study can be listed as follows:
• A novel hybridization method based on FPA and chaos sequences is proposed.
• Ten chaotic maps widely used in the literature are integrated.
• A constraint handling method has been merged in CFPA, named superiority of feasible solutions (SF).
• Thirteen benchmark problems are implemented to show the performance of CFPA.
• The best chaotic map is applied to OPF with thermal, wind, and solar power.
• Some evaluation measures are utilized, such as mean, max, min fitness, standard deviation, and statistical Wilcoxon test.
• The proposed algorithm is compared with basic FPA and other stochastic methods.
The rest of the manuscript is arranged as follows: Section 2 gives a brief introduction of the standard FPA, its chaotic variant CFPA-based SF strategy, and a description of the ten chaos maps’ functions. Section 3 introduces the wind, solar, and OPF models. The findings and discussions are investigated in Section 4. Finally, in Section 5, the article ends with a conclusion.
2 Problem methodology
2.1 Renewable energy model
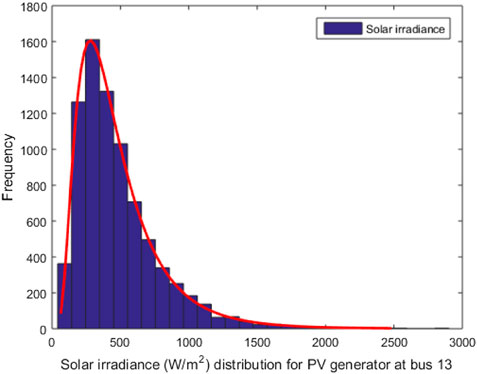
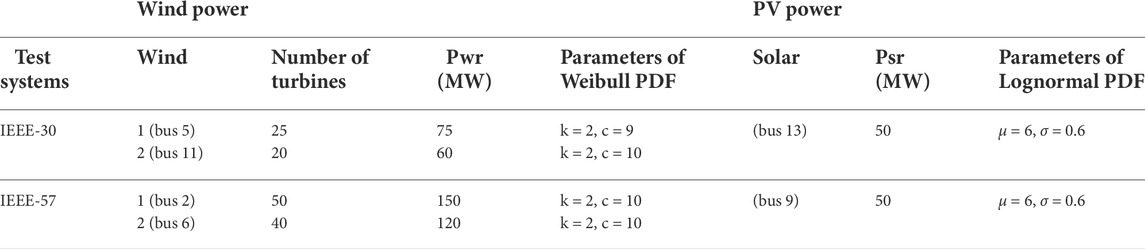
Nowadays, the treatment of renewable energy resources (RESs) in power systems is developing rapidly, especially wind and PV power. The RESs contribute in decreasing CO2 emissions and enhancing the quality and reliability of the power system. Solar irradiance and wind distribution are modeled using the Lognormal and Weibull probability density function, respectively (Biswas et al., 2017). Lognormal fitting of solar irradiance, Weibull fitting of wind speed, and frequency distribution are generated after 8,000 runs of Monte Carlo simulation, as depicted in Figures 1, 2 (Xie et al., 2018). The associated cost of each of these resources consists of three terms: the direct cost, penalty cost, and reserve cost (Biswas et al., 2017). Table 1 tabulates the parameters of the considered systems. Table 2 provides the cost and emission coefficients for the thermal generators of IEEE 30-bus and 57-bus test systems. All parameters of the solar and the wind are described in detail in Table 3.
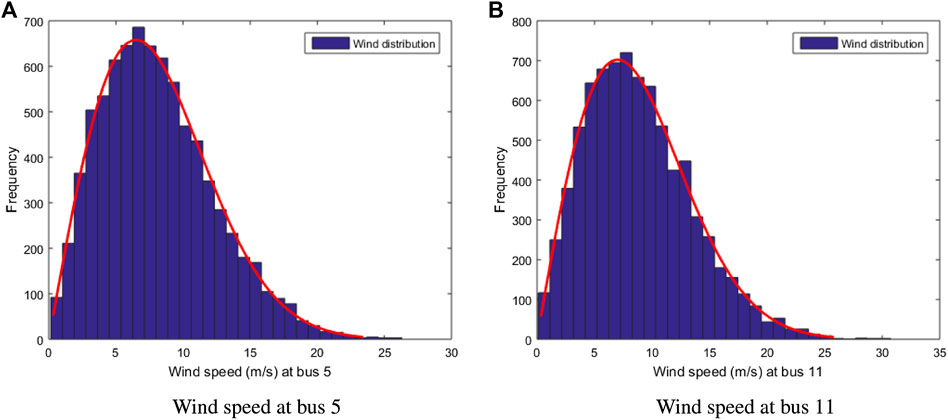
FIGURE 1. Distribution of wind speed for wind generators. (A) Wind speed at bus 5 and (B) wind speed at bus 11.
2.1.1 Wind power
For modeling the variability of wind flow, a Weibull probability distribution function is applied (Chang, 2010):
where k and c represent the shape and scale factors of Weibull distribution, respectively.
The wind generator’s output power can be defined using the stochastic wind speed as follows (Chang, 2010):
where vout, vin, vr, v, and pwr are cut-out wind speed, cut-in wind speed, rated wind speed, actual wind speed, and rated output power, respectively.
The total cost of wind energy consists of direct cost associated with scheduled power, penalty cost of underestimation, and reserve cost for overestimation (Biswas et al., 2017), as represented below:
with
where dw,i is the coefficient of direct cost of the ith wind generator. Koew,i and Kuew,i are the over- and under-estimation cost coefficients pertaining to the ith wind power plant. pws,i is the scheduled power.
2.1.2 Solar power
The probability distribution function used to calculate the PV output power is lognormal distribution, as shown below (Chang, 2010):
The available power Ps(G) of solar irradiation G is determined as follows (Chang, 2010):
where Psr, Gstd, G, and Rc are the rated output power of solar PV, solar irradiation in standard environment, forecasted solar irradiation, and certain irradiance point, respectively.The PV’s total cost is formulated as follows (Biswas et al., 2017):
with
where ds,i is the coefficient of direct cost of the ith wind generator. Pss,i is the scheduled power. Koes,i and Kues,i are the over- and under-estimation cost coefficients of the solar power plant.
2.2 Optimal power flow model
As mentioned before, the OPF is one of the most significant power system issues. Its major task is recognizing the optimal steady-state operation of power system network components to satisfy the power flow equations and constraints. It is worth noting that the employment of a stochastic technique within power systems has seen important progress over the last few years. The objective functions to be optimized in this work are fuel cost, emission, voltage deviation, and power loss. To this end, the formulation of all variables, objectives, and constraints can be mathematically formulated as follows:
where F(s, c) is the fitness function to be minimized, g(s, c) is the equality constraints, h(s, c) is the inequality constraints, s and c are the vectors of state and control variables.
2.2.1 Variables
The state variables s can be defined as follows (Biswas et al., 2017):
where Pg1 is the active power output at the slack bus. VL is the voltage magnitude at PQ buses. Qg is the reactive power output of all generator units. Sl is the transmission line loading (line flow). Npq, Ng, and Nl denote the number of load buses, number of generating units, and number of transmission lines, respectively.
The control variables c can be expressed as follows (Biswas et al., 2017):
where Pg is the active power generation at the PV buses, except at the slack bus. Vg is the generation bus voltage magnitude at PV buses. T is the transformer tap settings. Qc is the shunt VAR compensation. Ng, Nc, and NT are the number of generators, number of regulating transformers, and number of VAR (shunt) compensators, respectively.
2.2.2 Objective functions
In this division, five fitness functions are considered as objectives:
2.2.2.1 Fuel cost only
The conventional generator total fuel cost of the network is modeled as a quadratic function, and its formulation can be expressed as follows (Biswas et al., 2017):
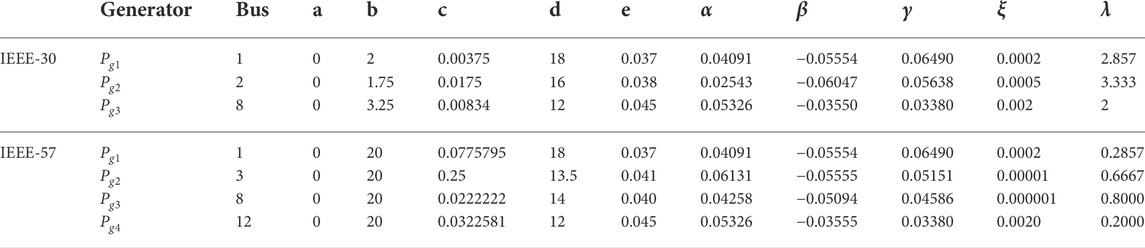
where ai, bi, ci, di, and ei are the conventional generator cost coefficients.
2.2.2.2 Emission
The emission function is formulated using an exponential function and the previous quadratic function as shown below (Biswas et al., 2017):
where αi, βi, γi, ξi, and λi are the emission coefficients of the power plant.
2.2.2.3 Fuel cost with renewable energy cost
The network total cost including the wind-solar-thermal powers is expressed as follows (Biswas et al., 2017):
The voltage deviation and power loss are also important in the power system. These two functions are calculated as shown below.
2.2.2.4 Voltage deviation
The load bus voltages are picked from 1.0 per unit in order to grab the problem of an unattractive voltage profile. The voltage deviation can be defined as follows (Elattar and ElSayed, 2019):
2.2.2.5 Power loss
The transmission system power losses are necessary due to the inherent resistance of lines. Its mathematical modeling is formulated by the following expression (Elattar and ElSayed, 2019):
where Gl(i,j) represents the conductance of line l. δij = δi − δj represents the voltage angle difference between bus i and bus j.
2.2.3 Constraints
The equality and inequality constraints play an important role in optimal power flow studies; they stand for the limitations of physical equipment. These constraints have been modeled as shown below.
2.2.3.1 Equality constraints
The power flow equations are assumed as equality constraints that are represented by the following (Elattar and ElSayed, 2019):
where Nb is the number of buses. Qgi and Pgi are generated reactive and active power, respectively. Qdi and Pdi are reactive and active power demand, respectively. Gij and Bij represent the admittance matrix components Yij = Gij + jBij named conductance and susceptance.
2.2.3.2 Inequality constraints
The inequality constraints are given as shown below (Elattar and ElSayed, 2019):
– Generator constraints:
where
– Transformer constraints:
where NT is the number of tap changer transformers.
– Shunt VAR compensator constraints:
where Nc is the number of capacitor components.
– Security constraints:
where Nl is the number of transmission lines. Sli and
3 Optimization methodology
3.1 Flower pollination algorithm
Flower pollination algorithm (FPA) is a stochastic approach in the field of swarm intelligence algorithms. It was proposed for solving nonlinear single-objective optimization problems by Xin-She Yang in 2012 (Yang, 2012). As its name signifies, FPA is inspired by the flower pollination process. Besides, the transfer of pollen generally leads to flower pollination, and this transfer is often associated with some pollinators such as butterflies, bats, birds, etc. As a matter of fact, certain insects and flowers have developed a very specialized flower–pollinator partnership (Yang, 2014). Generally speaking, the pollination process can be categorized into two sorts of pollination: cross-pollination and self-pollination. The self-pollination or abiotic pollination transfers the pollen itself without requiring any pollinators; thus, this process is used for local pollination. Meanwhile, cross or biotic pollination requires pollinators to transfer the pollen from one plant to another, and these pollinators carrying pollen move in a way that obeys the distribution of the Lévy flights (Pavlyukevich, 2007). This type of pollination can be recognized as global pollination. Moreover, the global and local pollination are controlled using a random parameter p called switch probability in which its value is in the range [0, −,1]. The mathematical representation of these two processes is given below:
• The global pollination is governed by the following (Yang, 2012):
where
where Γ(λ) is the gamma function distribution (Yang, 2014) that is valid for 0 ≪ s. The s0 expression with the Gaussian distributions U and V are as shown below:
where N (0, σ2) and N (0, 1) signify a zero mean for both U and V and a variance of σ2 for U and 1 for V. The variance can be calculated by the following (Yang, 2014):
• The local pollination process is represented by the following (Yang, 2012):
where
Selecting FPA is due to its tendency to search both global and local search space, its easiness of implementation, and its small number of parameters. This method is efficient in dealing with the problems which have lower dimensions; in contrast, it faces some difficulties in handling the higher-dimensional constrained optimization issues. Therefore, to tackle these complications, a chaotic method is suggested in the next section.
3.2 Chaos theory
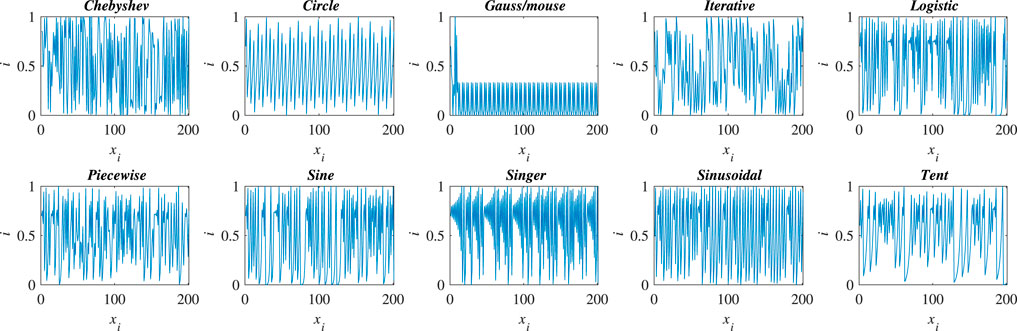
Generally, chaos theory is a deterministic technique observed in the dynamical and nonlinear systems, which are bounded, non-convergent, and non-periodic. The chaos utilizes chaotic variables instead of random variables (Arora and Singh, 2017), which means a small change in its initial conditions may change its future behavior. Besides, owing to the ergodicity properties of chaos and its non-repetition, its use can be more advantageous. Furthermore, in recent years, chaotic sequences have been widely employed in several optimization subject areas due to the fact that they possess the ability to enhance global convergence and avoid the local minimum (Letellier, 2019). For that reason, ten well-known chaos sequences are chosen in this research work, as depicted in Figure 3 (Sayed et al., 2017). Their names, mathematical expressions, and ranges are listed in Table 4.
3.3 Constraint handling superiority of feasible solutions
SF is a constrained handling strategy based on the dominant relationship. This concept is used by Deb (Deb, 2000) in order to handle the superiority of feasible solutions on infeasible ones. The feasible candidate can always dominate the infeasible one, while the candidate with the smaller violation degree always dominates the one with the higher violation value. The SF technique uses a tournament selection operator, where two solutions are compared at a time. Solution Xi is considered superior to Xj if
• An infeasible solution Xj is dominated by a feasible one Xi
• if both Xi, Xj are feasible, but Xj is worse than Xi
• if both Xi, Xj are infeasible, and Xj has the greatest constraint violation.
Referring to Eq. 13, the equality constraints are converted to inequality constraints, and thus, total constraint is introduced as follows (Deb, 2000):
where δ is a tolerance parameter for the equality constraints, and Hi(X) is the inequality constraint.
The overall expression of the constraint violation for an infeasible solution can be summarized as follows (Deb, 2000):
where wi is a weight parameter, and Hmax ,i is the maximum value for violation of constraint.
3.4 Chaotic flower pollination algorithm based SF
All the previous studies prove that FPA gets trapped in local optima and converges slowly toward the minimal solutions. Therefore, in order to make FPA an efficient algorithm, it should properly balance between the diversification and intensification to approximate the global optima. As was pointed out earlier, p is the main parameter of FPA, which balances these two components of the pollination, and it influences the algorithm convergence speed. In this present study, chaotic maps are suggested to deal with these shortcomings and enrich the search behavior due to the fact that chaos sequences can help swarm algorithms to get rid of the local optimum. The proposed chaotic flower pollination algorithm is a hybrid method that tunes the parameter of FPA by replacing random values with chaotic variables. In addition, the chaos is applied to manipulate the local pollination and the switch probability p. This parameter is considered as a single parameter in standard FPA, but in this study, p is proportionally decreased by increasing the iteration numbers; it is modified as follows:
where T characterizes the maximum value of iterations, and t signifies the actual iteration value. pmin = 0.6 and pmax = 0.8 indicate the minimum and maximum value of p, respectively.
The proposed approach based on FPA, chaos, and SF is described in Algorithm 1. The rand values in the basic FPA are substituted in CFPA-SF by the chaotic sequence values to supply chaos behaviors as shown in steps 9 and 13 in the pseudo-code, where C(t) is the chaotic sequence value of the tth iteration.
Algorithm 1. Chaos Flower Pollination Algorithm based SF (CFPA-SF)
1: Initialize the chaotic FPA parameters (Iterations(MaxIter), population size(nPop), bounds(Ub, Lb), dimension(d), switch probability(pmin, pmax), chaotic maps(C))
2: Generate the random initial population of flowers x respect to Ub and Lb: x = Lb + rand*(Ub − Lb)
3: Compute the optimal value, constraint violations in the initial population using Eqs 38, 39
4: Generate random numbers using chaotic maps(C)
5: Determine the switch probability Eq. 40, p ∈ [pmin, pmax] :
6: while t < MaxIter (stopping criteria) do
7: Update parameter values for SF constraint handling technique
8: for i = 1 : nPop do
9: if C(t) < p then
10: Draw the step size parameter L which obeys lévy distribution
11: proceed global pollination through Eq. 33,
12: else
13: Draw ∈ from chaotic maps through ∈ = C(t)
14: proceed local pollination through Eq. 37,
15: end if
16: Compute the new optimal fitness value, total constraint violations using Eqs 38, 39
17: If new solution is better, update it in the population
18: end for
19: Update the current global best solution
20: end while
21: Extract the optimal solution reached
4 Experimental results
4.1 Simulation results of benchmark functions
In this subsection, all the outcomes are averaged over 30 independent runs, for 13 test suites that have 30 dimensions. The population size considered for all functions is nPop = 30, the maximum iteration number is fixed at T = 500, and the switch probability value is set at p = 0.8 for the traditional FPA. All the approaches are executed on a personal computer core i5 with a 4 GB-RAM Processor @1.8 GHz using MATLAB R2016b.
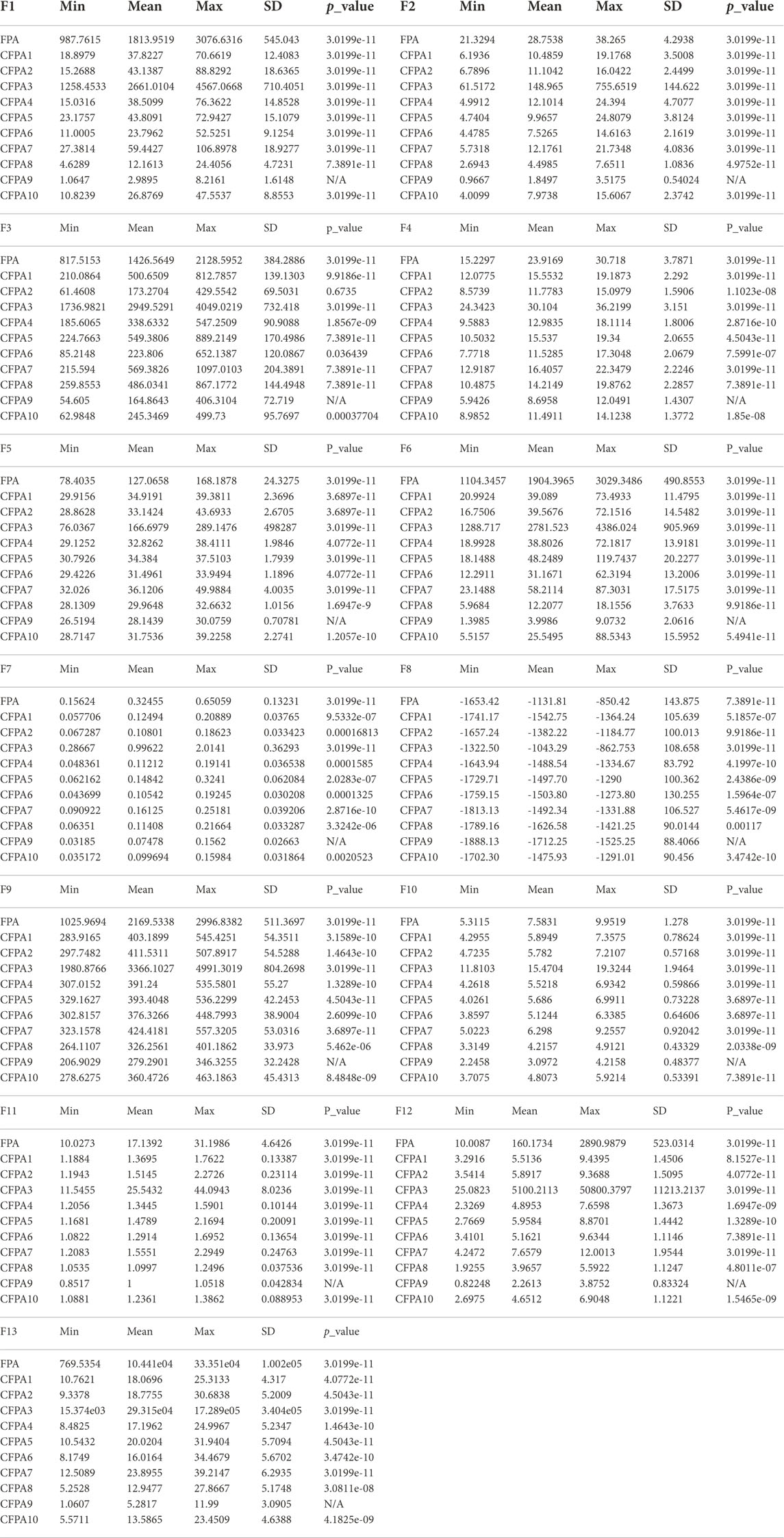
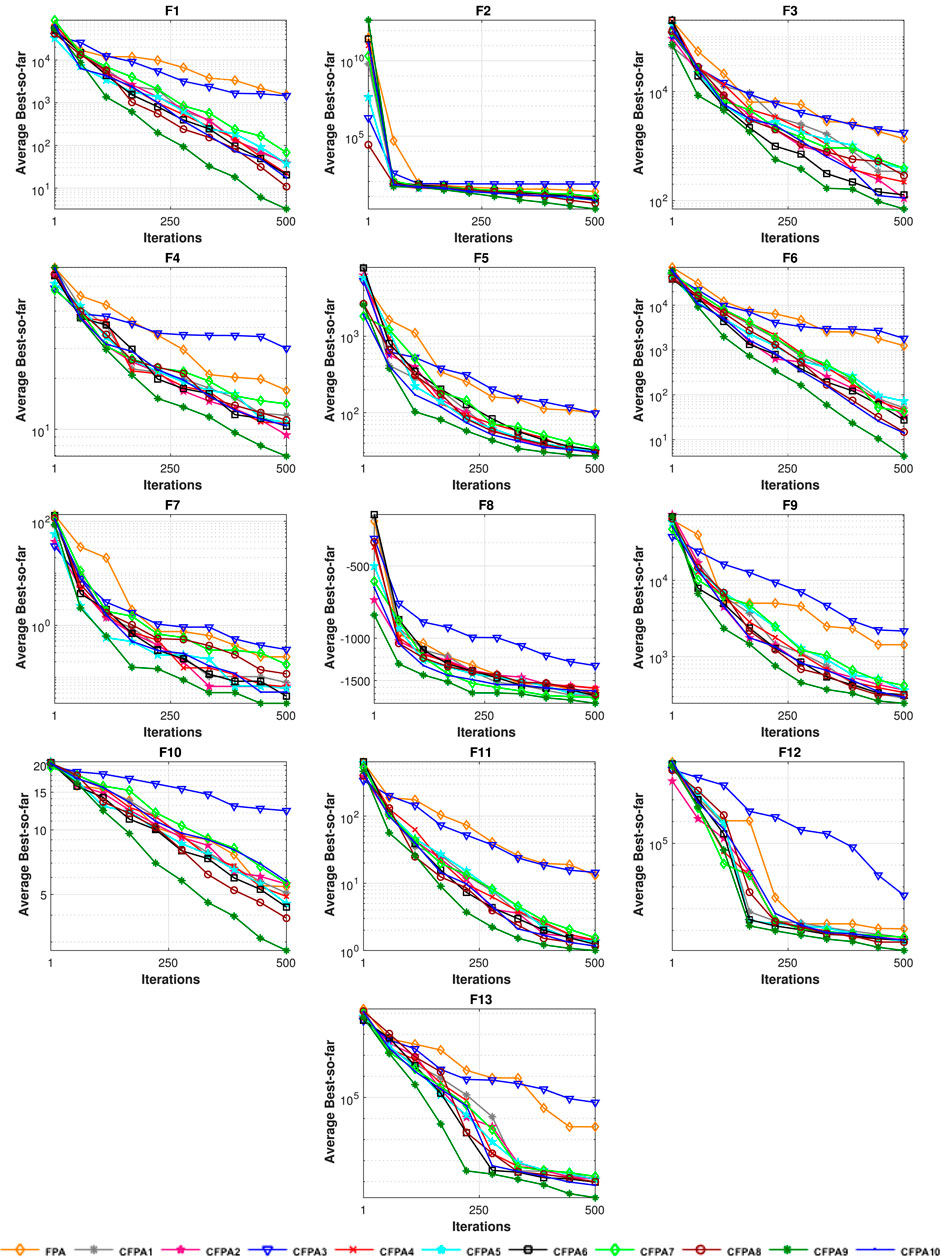
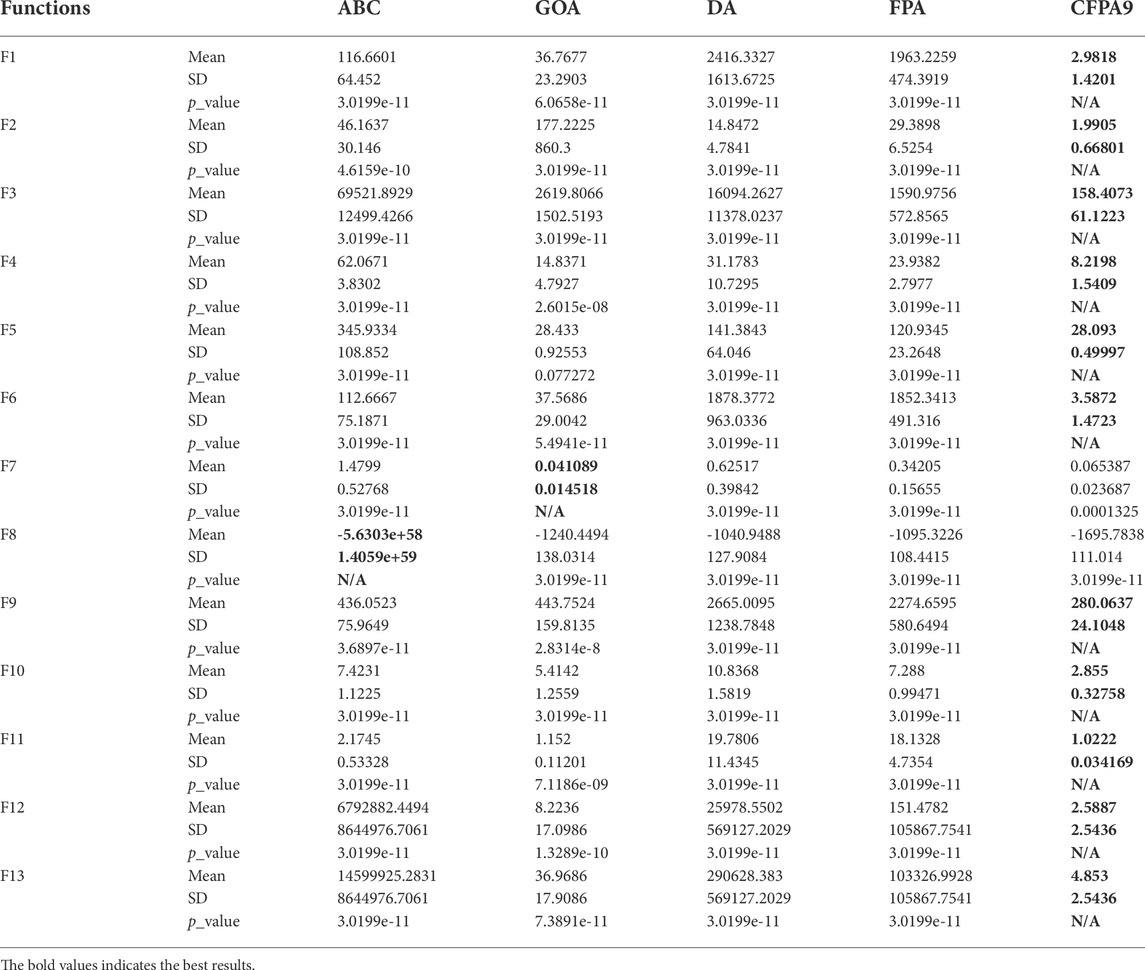
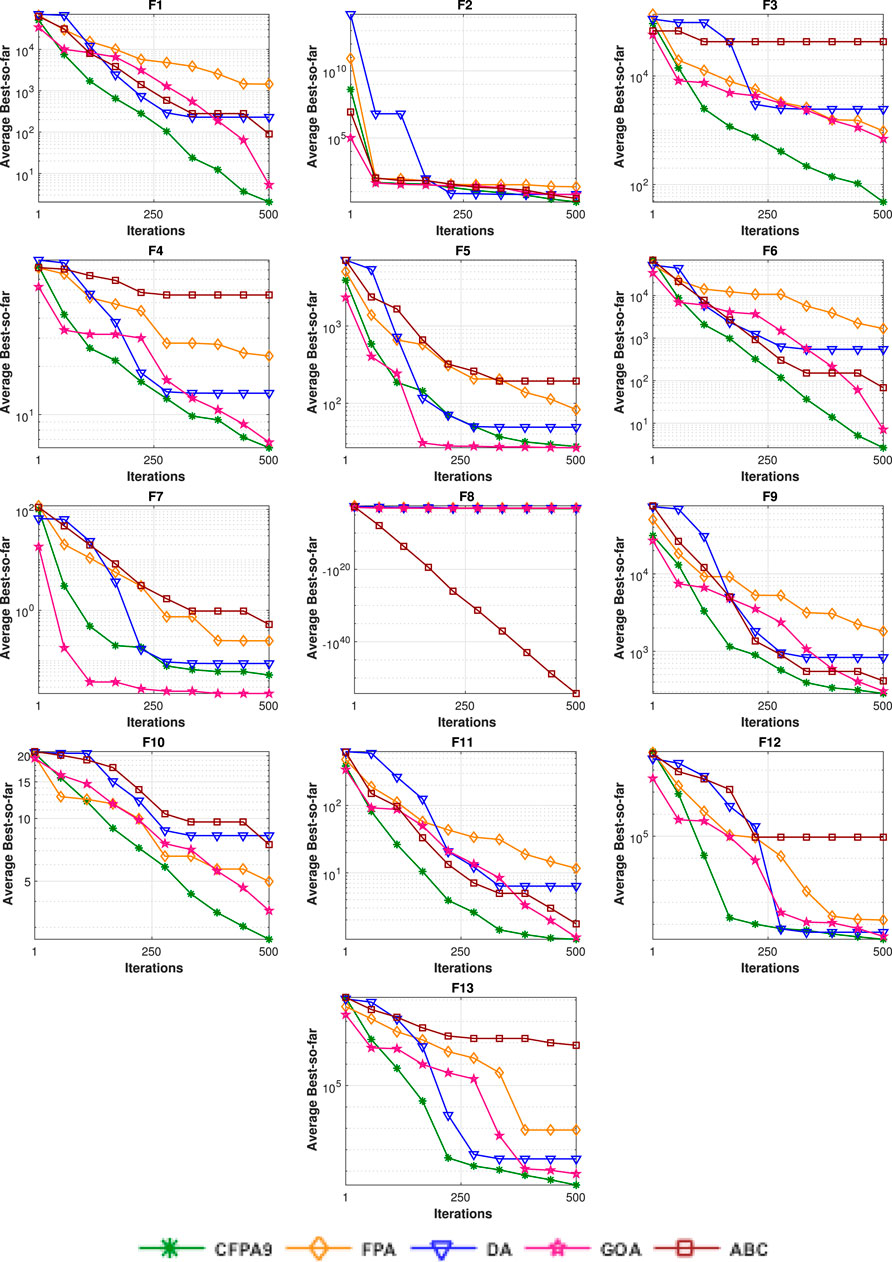
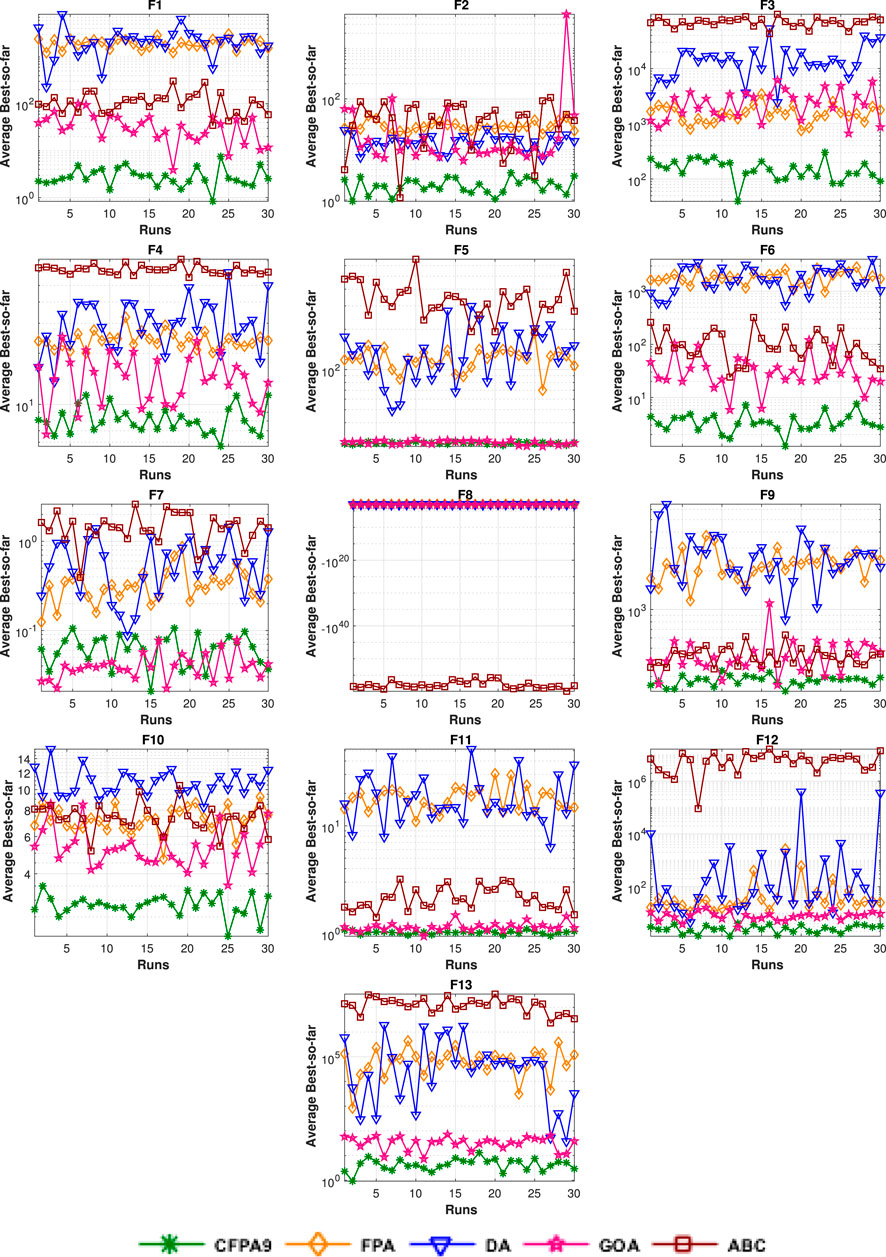
The 13 test functions are utilized in order to prove the performance of the suggested approach CFPA. Their details are tabulated in Table 5, where D and Bound represent the dimension (number of variables) and limits of variables, respectively. Additionally, these test suites are classified into four types: multimodal, unimodal, separable, and non-separable. Thus, the multimodal functions are more suitable for assessing the potential performances of algorithms’ exploration, although the exploitation capability can generally be checked using the unimodal functions. Therefore, to demonstrate which of the ten CFPAs is significantly improved compared to the standard FPA, five different testing parameters were investigated including the Min, Max, and Mean fitness values, p_value of Wilcoxon’s rank sum test, and standard deviation (SD ) (Wilcoxon, 1945), (Derrac et al., 2011). The p_value less than 5% implies the significant improvement of the algorithm and determines which chaotic sequence is the best. As shown in Table 6, the optimal findings are shown in bold text, while the N/A indicates “not applicable,” meaning that the best chaotic map could not statistically be compared with itself.The experimental results provide that all CFPA algorithms are much superior to the classical FPA except CFPA3 (Gausse/mouse map). Moreover, it can be observed that the outcomes of CFPA9 (Sinusoidal map) occupied the first rank on all types of test functions compared to the original FPA and its other chaotic variants. Besides, as it is apparent, most of the obtained Wilcoxon rank-sum test (p-values) are less than the assumed significant level of 5% compared to other approaches, which means that the combination of the sinusoidal map with FPA enhances the performance of the FPA approach. The fastest convergence rates toward the global optimum shown in Figure 4 guarantee its improvement. Also, this figure indicates that the FPA and CFPA3 algorithms supply the worst solution. Furthermore, to better validate the efficiency of our proposed hybrid method, the performance of the Sinusoidal map based on the statistical mean is compared with the fitness values of three state-of-the-art algorithms, such as DA, GOA, and ABC, as illustrated in Table 7. It bears mentioning that the optimal statistical results of each testing parameter are the lowest values. The bold values designate the optimum solutions. These numerical findings obviously show that the CFPA9 ranks first for the various types of the benchmark suite by supplying 11 significant solutions out of 13 test functions. Meanwhile, ABC and GOA each rank first for one function, F8 and F7, respectively. Despite the fact that CFPA9 fails to reach the optimum results for some functions, it holds second place. By contrast, the DA approach achieves the worst outcomes in most cases. Consequently, as it can be seen from the evolution curve’s fitness value shown in Figure 5, CFPA9 converges faster than the stochastic algorithms mentioned above for all benchmark functions except F7 and F8, where the GOA and ABC outperform CFPA9. The best fitness values of all competitive algorithms have been plotted according to the best run. Moreover, the comparisons of the optimal fitness value done over 30 runs are demonstrated in Figure 6, and it is clear that our approach has a consistent global searching stability and ability.
4.2 Simulation results of optimal power flow
To ensure the quality of the CFPA-based SF with the Sinusoidal map, the optimal power flow issue integrating wind-PV power is investigated. Precisely, the CFPA9 is applied on the two standard benchmark systems, IEEE 30-bus and IEEE 57-bus power systems. All the simulation findings have been implemented for 30 populations, their convergences are examined from the plots obtained of the various objective functions over 200 iterations, and they have been independently run 30 times for each function to perform the statistical analysis. Besides, the CFPA9 performance is compared with that of the original FPA and those algorithms found in the literature.The considered power systems are examined via four case studies defined as follows:
• Case 1 & 3: Fuel cost minimization
These cases are calculated according to Equation 16. They reflect the main case, which aims to decrease the cost of fuel only considering power loss, voltage deviation, and emission.
• Case 2 & 4: Fuel cost with RES minimization
Equation 18 stands for these test cases; the OPF issue is described with wind-PV power, taking into account the power loss, voltage deviation, and emission.
4.2.1 IEEE 30-bus test system
This power test system possesses 30 buses in which the 1st bus is taken as the slack bus, and there are 6 generators, 4 transformers, 41 lines, and 9 shunt VAR compensators. The generators’ voltage magnitude bounds are assumed to vary between 0.95p.u. and 1.1p.u. Moreover, the tap ratio transformers are presumed to be in the range of 0.9p.u. to 1.1p.u. The bounds of compensators are taken to be between 0 and 5p.u. The detailed data (line and bus data) for the considered IEEE system are given in (IEEE 30-bus test system data, 1961). Reactive and active powers are given as 126.2MVAR and 283.4MW, respectively. Figure 7 depicts the considered IEEE 30-bus test system.
Two different cases were considered for this system. As depicted before, case 1 minimizes the total fuel cost only, while the second case reduces the total fuel cost, inserting RESs. The wind power generators have replaced the traditional generators at buses 5 and 11; these wind turbines are the sum of 25 and 20 turbines, respectively. Meanwhile, the generator of bus 13 is changed by a PV generator. The allocation of these RESs into the grid is selected according to the study by (Biswas et al., 2017).
• Case 1: Minimization of IEEE 30-bus fuel cost only
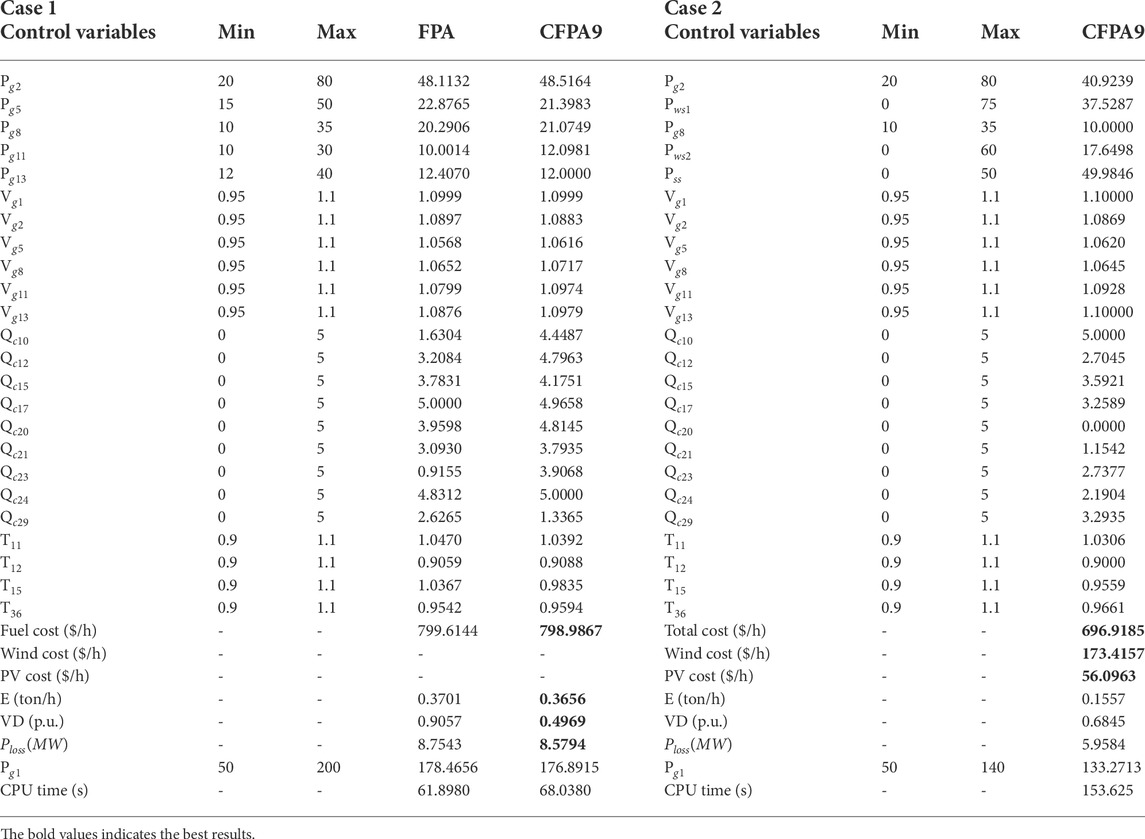
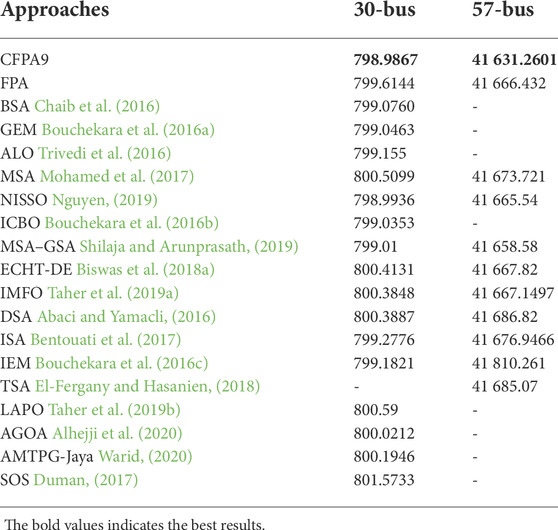
All obtained simulation results including control variables of the CFPA9 and FPA algorithms are tabulated in Table 8. Thus, according to the best run, Figure 8 illustrates the convergence curves and distribution runs of the fitness value for case 1. It is clear from this figure that the suggested CFPA9 is superior and converges faster to the optimum than its original algorithm. The fuel cost findings attained in this case for both algorithms, FPA and CFPA9, are 799.6144 ($/h) and 798.9867($/h), respectively. In minimizing the cost, the simulation results of power loss, voltage deviation, and emission are 8.5794(MW), 0.4969(p.u.), and 0.33656(ton/h), respectively. Furthermore, the comparison analysis of the outcomes found from all optimization approaches is illustrated in Table 9. From that, it is clearly seen that the fuel cost minimum is better than those reported in the literature. According to Figure 9A, all load bus voltage profiles obtained from both FPA and CFPA9 are within their specified limits, which means that the feasibility is checked.
• Case 2: Minimization of IEEE 30-bus fuel cost with wind and PV

FIGURE 8. Fuel cost convergence and run for FPA vs. CFPA9 for case 1. (A) Convergence curves of CFPA9 versus FPA and (B) runs of CFPA9 versus FPA.
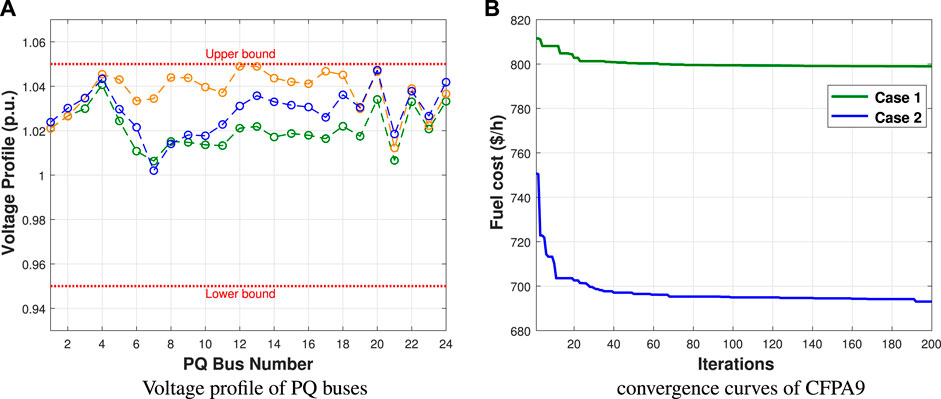
FIGURE 9. Voltage profile and convergence curves of CFPA9 for cases 1 and 2. (A) Voltage profile of PQ buses and (B) convergence curves of CFPA9.
This case aims to optimize the power flow issue by minimizing the total fuel cost that includes the wind-PV cost. Figure 9B illustrates the convergence curves of CFPA9 with and without including RESs. The optimal values of control variables are given in Table 8. The obtained total fuel cost, emission, voltage deviation, and power loss values are 696.9185($/h), 0.1557(ton/h), 0.6845(p.u.), and 5.9584(MW). The cost functions of wind and solar power achieved 173.4157($/h) and 56.0963($/h), respectively. Based on these findings, the value of the fuel cost is reduced by 12.77% in comparison with the previous case study.
4.2.2 IEEE 57-bus test system
The proposed approach is implemented on the 57-bus test system in this section. The reactive and active power demands of the studied system are 336.4 (MVAR) and 1250.8 (MW), respectively. The line and bus data are taken from (IEEE 57-bus test system data, 1960). This system has seven generating units in which bus 1 is chosen as the slack bus and 80 lines, 50 load buses, three shunt reactive power injections, and 15 transformers. The tap setting for transformers is assumed to vary between 0.9 p. u. and 1.1 p. u. The bounds of voltage magnitude are assumed to be within the range of 0.94–1.06 p. u. The limits of compensators are taken to be between 0 and 20 p. u. Like the first system, the 57-bus test system has been changed by replacing some generators with RESs; two of them are changed by wind generators at buses 2 and 6, and these wind turbines are the sum of 50 and 40 turbines, respectively. Then, bus 9 is considered as the PV generator.
• Case 3: Minimization of IEEE 57-bus fuel cost only
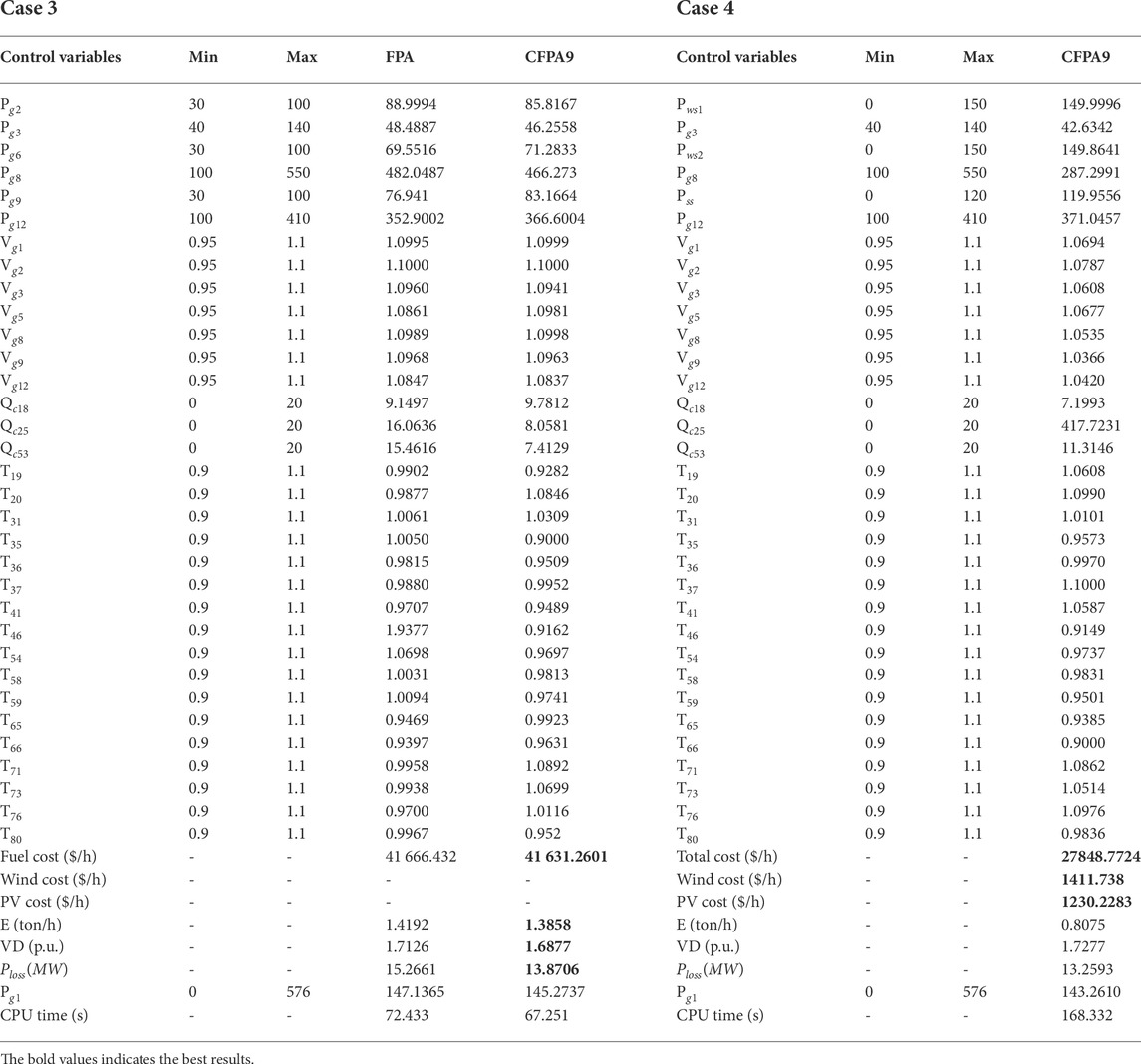
For this case study, the attained outcomes are recorded in Table 10. Figure 10 shows a comparison graph of original FPA and the best chaotic FPA on the basis of the best run which consists of the convergence curves and distribution runs. The fuel cost of both algorithms are 41666.432 ($/h) and 41631.2601($/h). In addition, the achieved emission, voltage deviation, and power loss values are 1.3858(ton/h), 1.6877(p.u.), and 13.8706(MW), respectively. Furthermore, compared to the outcomes obtained from the newest research studies as illustrated in Table 9, the CFPA9 has a lower fitness value. Hence, it should be noted that the simulation findings yielded in this case disclose that the CFPA9 provides better fitness values than other approaches without any violation of any constraint as presented in Figure 11A.
• Case 4: Minimization of IEEE 57-bus fuel cost with wind-solar
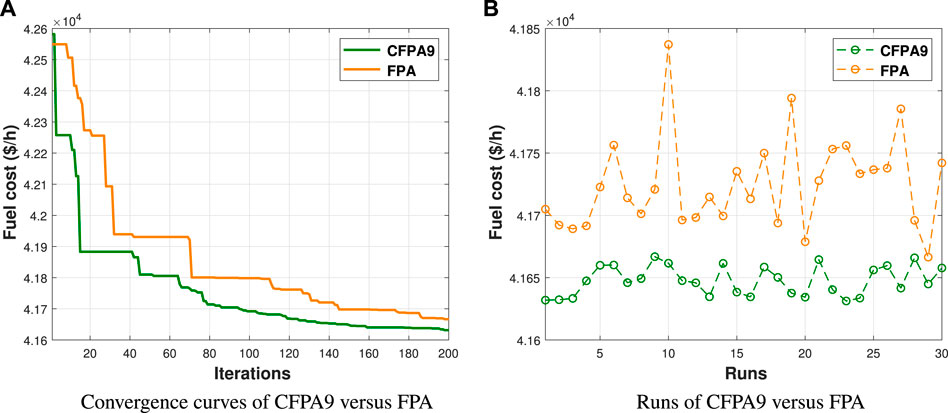
FIGURE 10. Fuel cost convergence and runs for FPA vs. CFPA9 for case 3. (A) Convergence curves of CFPA9 versus FPA and (B) runs of CFPA9 versus FPA.
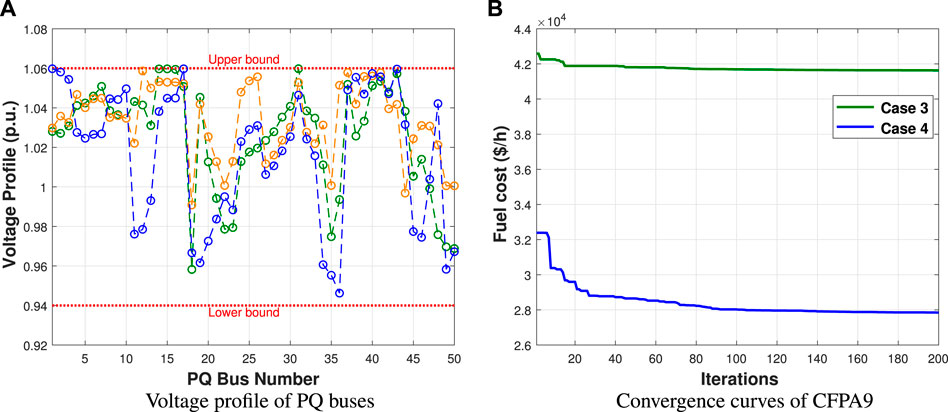
FIGURE 11. Voltage profile and convergence curves of CFPA9 for cases 3 and 4. (A) Voltage profile of PQ buses and (B) convergence curves of CFPA9.
Similar to case 2, CFPA9 has been employed to optimize the optimal power flow issue by minimizing the total fuel cost with the wind and PV generators. Regarding the convergence curves shown in Figure 11B, the CFPA9 converges faster to the optimum solution than FPA. According to the best solutions of CFPA9 presented in Table 9 (case 4), the fuel cost value is 27848.7724(ton/h). This fuel cost was reduced by 33.11% compared to case 3 (without RESs). Moreover, the wind and PV costs are 1411.738(ton/h) and 1230.2283(ton/h), respectively.
To evaluate the performance of the CFPA9, a statistical result was used. Minimum, maximum, mean, standard deviation, and p_value of 30 runs’ values were calculated as shown in Table 11 and demonstrated the improvement of CFPA9. To this end, it is observed that the attained statistical findings of CFPA9 are close, which means that the outcomes are statistically significant.
5 Conclusion
In this current study, an efficient constrained flower pollination algorithm based on chaos has been suggested and successfully employed to deal with the optimal power flow issue integrating hybrid wind-solar power for case studies involving 30-bus and 57-bus power systems. First, ten different chaotic sequences were employed to enhance the FPA performance. Thus, in view of validating the proposed chaotic algorithms, thirteen benchmark tests are utilized, some of which are multimodal. Accordingly, the obtained results confirm the efficiency and capability of the chaotic FPAs in getting the best solutions, as it outstripped the standard version of the FPA and the well-known approaches ABC, GOA, and DA. Along these lines, these proposed novel chaotic flower pollination algorithms have the ability to handle the various drawbacks of the basic algorithm, in terms of balancing between the exploration and exploitation processes as well as improving the convergence speed. In addition, the overall statistical results proved that the Sinusoidal chaotic map CFPA9 significantly enhances the features of accuracy, reliability, and efficiency in finding the global optimal solution. Second, the best-performing chaotic map, CFPA9, out of the ten chaotic sequences has been recommended to deal with the real-world problem of OPF incorporating wind-PV energy. Furthermore, the outcomes show that CFPA9 with the appropriate constraint handling technique superiority of feasible solution can efficiently improve all objective functions of OPF, which implies that the suggested method is slightly potential and powerful in solving constrained nonlinear complex real-world problems. In accordance with these remarkable outcomes, the authors recommend CFPA with Sinusoidal sequence and SF strategy to handle the OPF issue for a realistic and higher dimension as considered in this present research.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abaci, K., and Yamacli, V. (2016). Differential search algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power and Energy Syst. 79, 1–10. doi:10.1016/j.ijepes.2015.12.021
Abdel-Basset, M., and Shawky, L. A. (2019). Flower pollination algorithm: A comprehensive review. Artif. Intell. Rev. 52 (4), 2533–2557. doi:10.1007/s10462-018-9624-4
Abdullah, A., Enayatifa, R., and Lee, M. (2012). A hybrid genetic algorithm and chaotic function model for image encryption. AEU - Int. J. Electron. Commun. 66, 806–816. doi:10.1016/j.aeue.2012.01.015
Abualigah, L., Diabat, A., Mirjalili, S., Abd-Elaziz, M., and Gandomi, A. H. (2021a). The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 376 (2), 113609. doi:10.1016/j.cma.2020.113609
Abualigah, L., Yousri, D., Elaziz, M. A., Ewees, A. A., Al-qaness, A., and Gandomi, A. H. (2021b). Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Industrial Eng. 157, 107250. doi:10.1016/j.cie.2021.107250
Abualigah, L., Abd Elaziz, M., Sumari, P., Geem, Z., and Amir, H. (2022). Reptile search algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 191, 116158. doi:10.1016/j.eswa.2021.116158
Alasali, F., Nusair, K., Obeidat, A. M., Foudeh, H., and Holderbaum, W. (2021). An analysis of optimal power flow strategies for a power network incorporating stochastic renewable energy resources. Int. Trans. Electr. Energy Syst. 31, e13060. doi:10.1002/2050-7038.13060
Alatas, B. (2010). Chaotic bee colony algorithms for global numerical optimization. Expert Syst. Appl. 37, 5682–5687. doi:10.1016/j.eswa.2010.02.042
Alhejji, A., Ebeed, M., Kamel, S., and Alyami, S. (2020). Optimal power flow solution with an embedded center-node unified power flow controller using an adaptive grasshopper optimization algorithm. IEEE Access 99, 119020–119037. doi:10.1109/ACCESS.2020.2993762
Arora, S., and Singh, S. (2017). An improved butterfly optimization algorithm with chaos. J. Intell. Fuzzy Syst. 32, 1079–1088. doi:10.3233/JIFS-16798
Basturk, B., and Karaboga, D. (2006). “An artificial bee colony (ABC) algorithm for numeric function optimization,” in Proceedings of the IEEE Swarm Intelligence Symposium (Indianapolis: USA), 4–12.
Bentouati, B., Chettih, S., and Chaib, L. (2017). Interior search algorithm for optimal power flow with non-smooth cost functions. Cogent Eng. 4, 1292598–1292617. doi:10.1080/23311916.2017.1292598
Biswas, P., Suganthan, P., and Amaratunga, G. (2017). Optimal power flow solutions incorporating stochastic wind and solar power. Energy Convers. Manag. 148, 1194–1207. doi:10.1016/j.enconman.2017.06.071
Biswas, P. P., Suganthan, P., Mallipeddi, R., and Amaratunga, G. A. (2018a). Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 68, 81–100. doi:10.1016/j.engappai.2017.10.019
Biswas, P. P., Suganthan, P. N., Qu, B. Y., and Amaratunga, G. A. (2018b). Multiobjective economic-environmental power dispatch with stochastic wind-solar-small hydro power. Energy 150 (5), 1039–1057. doi:10.1016/j.energy.2018.03.002
Bonab, S. M. M., Rabiee, A., and Ivatloo, B. (2016). Voltage stability constrained multi-objective optimal reactive power dispatch under load and wind power uncertainties: A stochastic approach. Renew. Energy 85, 598–609. doi:10.1016/j.renene.2015.07.021
Bouchekara, H. R. E. H., Chaib, A. E., and Abido, M. A. (2016a). Multi-objective optimal power flow using a fuzzy based grenade explosion method. Energy Syst. 7, 699–721. doi:10.1007/s12667-016-0206-8
Bouchekara, H. R. E. H., Chaib, A. E., Abido, M. A., and El-Sehiemy, R. A. (2016b). Optimal power flow using an improved colliding bodies optimization algorithm. Appl. Soft Comput. 42, 119–131. doi:10.1016/j.asoc.2016.01.041
Bouchekara, H. R. E. H., Abido, M. A., and Chaib, A. E. (2016c). Optimal power flow using an improved electromagnetism-like mechanism method. Electr. Power Components Syst. 44 (4), 434–449. doi:10.1080/15325008.2015.1115919
Cai, J. J., Ma, X. Q., Li, X., Yang, Y., Peng, H., and Wang, X. (2007). Chaotic ant swarm optimization to economic dispatch. Electr. Power Syst. Res. 77, 1373–1380. doi:10.1016/j.epsr.2006.10.006
Chaib, A. E., Bouchekara, H. R. E. H., Mehasni, R., and Abido, M. A. (2016). Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm. Int. J. Electr. Power & Energy Syst. 81, 64–77. doi:10.1016/j.ijepes.2016.02.004
Chang, T. (2010). Investigation on frequency distribution of global radiation using different probability density functions. Intern. J. Appl. Sci. Eng. 8 (2), 99–107. doi:10.6703/IJASE.2010.8(2).99
Daqaq, F., Ouassaid, M., and Ellaia, R. (2021). A new meta-heuristic programming for multi-objective optimal power flow. Electr. Eng. 103, 1217–1237. doi:10.1007/s00202-020-01173-6
Daqaq, F., Ellaia, R., Ouassaid, M., Zawbaa, M. H., and Kamel, S. (2022). Enhanced chaotic manta ray foraging algorithm for function optimization and optimal wind farm layout problem. IEEE Access 10, 78345–78369. doi:10.1109/ACCESS.2022.3193233
Deb, K. (2000). An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 186 (2), 311–338. doi:10.1016/s0045-7825(99)00389-8
Derrac, J., Garcia, S., Molina, D., and Herrera, F. (2011). A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 1, 3–18. doi:10.1016/j.swevo.2011.02.002
Duman, S. (2017). Symbiotic organisms search algorithm for optimal power flow problem based on valve-point effect and prohibited zones. Neural comput. Appl. 28, 3571–3585. doi:10.1007/s00521-016-2265-0
Elattar, E., and ElSayed, S. K. (2019). Modified JAYA algorithm for optimal power flow incorporating renewable energy sources considering the cost, emission, power loss and voltage profile improvement. Energy 178, 598–609. doi:10.1016/j.energy.2019.04.159
Elattar, E. E. (2019). Optimal power flow of a power system incorporating stochastic wind power based on modified moth swarm algorithm. IEEE Access 7, 89581–89593. doi:10.1109/access.2019.2927193
El-Fergany, A. A., and Hasanien, H. M. (2018). Tree-seed algorithm for solving optimal power flow problem in large-scale power systems incorporating validations and comparisons. Appl. Soft Comput. 64, 307–316. doi:10.1016/j.asoc.2017.12.026
El-Sattar, S. A., Kamel, S., el Sehiemy, R. A., Jurado, F., and Yu, J. (2019). Single and multi-objective optimal power flow frameworks using Jaya optimization technique. Neural comput. Appl 31, 8787–8806. doi:10.1007/s00521-019-04194-w
Essam, H. H., Mohammed, R. S., Fatma, A. H., Hassan, S., and Hassaballah, M. (2020). Lévy flight distribution: A new metaheuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 94, 103731. doi:10.1016/j.engappai.2020.103731
Gandomi, A., Yang, X. S., Talatahari, S., and Alavi, A. (2013). Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 18, 89–98. doi:10.1016/j.cnsns.2012.06.009
Ghafil, H. N., and Jármai, K. (2020). Dynamic differential annealed optimization: New metaheuristic optimization algorithm for engineering applications. Appl. Soft Comput. 93, 106392. doi:10.1016/j.asoc.2020.106392
Hashim, F. A., Houssein, E. H., Mabrouk, M. S., Al-Atabany, W., and Mirjalili, S. (2019). Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 101, 646–667. doi:10.1016/j.future.2019.07.015
Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., and Al-Atabany, W. (2022). Honey badger algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 192, 84–110. doi:10.1016/j.matcom.2021.08.013
Hayyolalam, V., and Pourhaji, K. A. A. (2020). Black Widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 87, 103249. doi:10.1016/j.engappai.2019.103249
He, Y. Y., Zhou, J. Z., Zhou, X. Q., Chen, H., and Qin, H. (2009). Comparison of different chaotic maps in particle swarm optimization algorithm for long term cascaded hydroelectric system scheduling. Chaos Solit. Fractals 42, 3169–3176. doi:10.1016/j.chaos.2009.04.019
Heidari, A. A., Abbaspour, R. A., and Jordehi, A. R. (2017). An efficient chaotic water cycle algorithm for optimization tasks. Neural comput. Appl. 28, 57–85. doi:10.1007/s00521-015-2037-2
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M. M., and Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028
Holland, J. (1975). Adaptation in natural and artificial systems. Ann Arbor, MI, USA: University of Michigan Press.
Houssein, E. H., Hassan, M. H., Mahdy, M. A., and Kamel, S. (2022). Development and application of equilibrium optimizer for optimal power flow calculation of power system. Appl. Intell. 1–22. doi:10.1007/s10489-022-03796-7
IEEE 57-bus test system data (1960). Power systems test case archive. Available from: http://labs.ece.uw.edu/pstca/pf57/pg_tca57bus.htm.
IEEE 30-bus test system data (1961). Power systems test case archive. Available from: http://labs.ece.uw.edu/pstca/pf30/pg_tca30bus.htm.
Jia, D., Zheng, G., and Khan, M. K. (2011). An effective memetic differential evolution algorithm based on chaotic local search. Inf. Sci. (N. Y). 181, 3175–3187. doi:10.1016/j.ins.2011.03.018
Jordehi, A. R. (2014). A chaotic-based big bang-big crunch algorithm for solving global optimization problems. Neural comput. Appl. 25, 1329–1335. doi:10.1007/s00521-014-1613-1
Jordehi, A. R. (2015). A chaotic artificial immune system optimisation algorithm for solving global continuous optimisation problems. Neural comput. Appl. 26, 827–833. doi:10.1007/s00521-014-1751-5
Kennedy, J., and Eberhart, R. C. (1995). “Particle swarm optimization,” in Proceedings of the IEEE international conference on neural networks (Piscataway, NJ, USA, 1942–1948.
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220 (4598), 671–680. doi:10.1126/science.220.4598.671
Meng, A., Zeng, C., Wang, P., Zhou, T., and Zheng, X. (2021). A high-performance crisscross search based grey wolf optimizer for solving optimal power flow problem. Energy 225, 120211. doi:10.1016/j.energy.2021.120211
Mirjalili, S., Lewis, A., and Mirjalili, S. M. (2014). Adaptive gbest-guided gravitational search algorithm. Neural comput. Appl. 25, 1569–1584. doi:10.1007/s00521-014-1640-y
Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., and Mirjalili, S. M. (2017). Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi:10.1016/j.advengsoft.2017.07.002
Mirjalili, S. S. C. A. (2016). Sca: A sine cosine algorithm for solving optimization problems. Knowl. Based. Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022
Mohamed, A. A. A., Mohamed, Y. S., El-Gaafary, A. A., and Hemeida, A. M. (2017). Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 142, 190–206. doi:10.1016/j.epsr.2016.09.025
Morshed, M. J., Hmida, J. B., and Fekih, A. (2018). A probabilistic multi-objective approach for power flow optimization in hybrid wind-PV-PEV systems. Appl. Energy 211, 1136–1149. doi:10.1016/j.apenergy.2017.11.101
Mugemanyi, S., Qu, Z., Rugema, F. X., Dong, Y., Bananeza, C., and Wang, L. (2020). Optimal reactive power dispatch using chaotic bat algorithm. IEEE Access 8, 65830–65867. doi:10.1109/ACCESS.2020.2982988
Nguyen, T. T. (2019). A high performance social spider optimization algorithm for optimal power flow solution with single objective optimization. Energy 171, 218–240. doi:10.1016/j.energy.2019.01.021
Niu, P., Li, J., Chang, L., Zhang, X., Wang, R., and Li, G. (2019). A novel flower pollination algorithm for modeling the boiler thermal efficiency. Neural process. Lett. 49, 737–759. doi:10.1007/s11063-018-9854-0
Pavlyukevich, I. (2007). Lévy flights, non-local search and simulated annealing. J. Comput. Phys. 226, 1830–1844. doi:10.1016/j.jcp.2007.06.008
Priya, K., and Rajasekar, N. (2019). Application of flower pollination algorithm for enhanced proton exchange membrane fuel cell modelling. Int. J. Hydrogen Energy 44 (33), 18438–18449. doi:10.1016/j.ijhydene.2019.05.022
Rodrigues, D., De Rosa, G. H., Passos, L. A., and Papa, J. P. (2020). “Adaptive improved flower pollination algorithm for global optimization,” in Nature-inspired computation in data mining and machine learning (Springer), 1–21.
Samy, M., Barakat, S., and Ramadan, H. (2019). A flower pollination optimization algorithm for an off-grid pv-fuel cell hybrid renewable system. Int. J. hydrogen energy 44, 2141–2152. doi:10.1016/j.ijhydene.2018.05.127
Saremi, S., Mirjalili, S., and Lewis, A. (2014). Biogeography-based optimisation with chaos. Neural comput. Appl. 25, 1077–1097. doi:10.1007/s00521-014-1597-x
Sayed, G. I., Hassanien, A. E., and Azar, A. T. (2017). Feature selection via a novel chaotic crow search algorithm. Neural comput. Appl. 31, 171–188. doi:10.1007/s00521-017-2988-6
Shambour, M. K. Y., Abusnaina, A. A., and Alsalibi, A. I. (2019). Modified global flower pollination algorithm and its application for optimization problems. Interdiscip. Sci. Comput. Life Sci. 11, 496–507. doi:10.1007/s12539-018-0295-2
Shilaja, C., and Arunprasath, T. (2019). Optimal power flow using moth swarm algorithm with gravitational search algorithm considering wind power. Future Gener. Comput. Syst. 98, 708–715. doi:10.1016/j.future.2018.12.046
Singh, A. P., and Kaur, A. (2019). Flower pollination algorithm for feature analysis of kyoto 2006+ data set. J. Inf. Optim. Sci. 40 (2), 467–478. doi:10.1080/02522667.2019.1580886
Sulaiman, M. H., Mustaffa, Z., Mohamad, A. J., Saari, M. M., and Mohamed, M. R. (2021). Optimal power flow with stochastic solar power using barnacles mating optimizer. Int. Trans. Electr. Energy Syst. 31, e12858. doi:10.1002/2050-7038.12858
Taher, M. A., Kamel, S., Jurado, F., and Ebeed, M. (2019a). An improved moth-flame optimization algorithm for solving optimal power flow problem. Int. Trans. Electr. Energy Syst. 29, e2743. doi:10.1002/etep.2743
Taher, M. A., Kamel, S., Jurado, F., and Ebeed, M. (2019b). Optimal power flow solution incorporating a simplified UPFC model using lightning attachment procedure optimization. Int. Trans. Electr. Energy Syst. 30, e12170. doi:10.1002/2050-7038.12170
Tong, H., Zhu, Y., Pierezan, J., Xu, Y., and Coelho, L. d. S. (2022). Chaotic Coyote optimization algorithm. J. Ambient. Intell. Humaniz. Comput. 13 (1), 2807–2827. doi:10.1007/s12652-021-03234-5
Too, J., and Abdullah, A. R. (2020). Chaotic atom search optimization for feature selection. Arab. J. Sci. Eng. 45 (8), 6063–6079. doi:10.1007/s13369-020-04486-7
Trivedi, I. N., Jangir, P., and Parmar, S. A. (2016). Optimal power flow with enhancement of voltage stability and reduction of power loss using ant-lion optimizer. Cogent Eng. 3, 1208942. doi:10.1080/23311916.2016.1208942
Vaccaro, A., and Cañizares, C. A. (2018). A knowledge-based framework for power flow and optimal power flow analyses. IEEE Trans. Smart Grid 9, 230–239. doi:10.1109/PESGM.2017.8273989
Vasant, P. M. (2012). Meta-heuristics optimization algorithms in engineering business, economics, and finance. IGI Glob. doi:10.4018/978-1-4666-2086-5
Wang, Z., Xie, H., He, D., and Chan, S. (2019a). Wireless sensor network deployment optimization based on two flower pollination algorithms. IEEE Access 7, 180590–180608. doi:10.1109/access.2019.2959949
Wang, K., Li, X., and Gao, L. (2019b). A multi-objective discrete flower pollination algorithm for stochastic two-sided partial disassembly line balancing problem. Comput. Industrial Eng. 130, 634–649. doi:10.1016/j.cie.2019.03.017
Wanga, G., Guo, L., Gandomi, A., Hao, G., and Wangb, H. (2014). Chaotic krill herd algorithm. Inf. Sci. (N. Y). 274, 17–34. doi:10.1016/j.ins.2014.02.123
Warid, W. (2020). Optimal power flow using the AMTPG-jaya algorithm. Appl. Soft Comput. 91, 106252. doi:10.1016/j.asoc.2020.106252
Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biom. Bull. 1, 80–83. doi:10.2307/3001968
Wolpert, D. H., and Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1, 67–82. doi:10.1109/4235.585893
Xie, Z. Q., Ji, T. Y., Li, M. S., and Wu, Q. H. (2018). Quasi-Monte Carlo based probabilistic optimal power flow considering the correlation of wind speeds using copula function. IEEE Trans. Power Syst. 33, 2239–2247. doi:10.1109/tpwrs.2017.2737580
Yang, X. S. (2010). Engineering optimization: An introduction with metaheuristic applications. New Jersey: John Wiley & Sons. doi:10.1002/9780470640425
Yang, X. S. (2012). Flower pollination algorithm for global optimization. Int. Conf. Unconv. Comput. Nat. Comput., 240–249. doi:10.1007/978-3-642-32894-7_27
Yessef, M., Bossoufi, B., Taoussi, M., and Lagrioui, A. (2022a). Enhancement of the direct power control by using backstepping approach for a doubly fed induction generator. Wind Eng. 46 (5), 1511–1525. doi:10.1177/0309524X221085670
Yessef, M., Bossoufi, B., Taoussi, M., Lagrioui, A., and Chojaa, H. (2022b). Overview of control strategies for wind turbines: ANNC, FLC, SMC, BSC, and PI controllers. Wind Eng. [Epub ahead of print 28 June 2022]. doi:10.1177/0309524X221109512
Yuan, X., Zhang, B., Wang, P., Liang, J., Yuan, Y., Huang, Y., et al. (2017). Multi-objective optimal power flow based on improved strength Pareto evolutionary algorithm. Energy 122, 70–82. doi:10.1016/j.energy.2017.01.071
Zamani, H., Mohammad, H., and Gandomi, A. H. (2022). Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 392, 114616. doi:10.1016/j.cma.2022.114616
Keywords: constraint handling technique, flower pollination algorithm, chaotic map, wind-solar system, optimal power flow
Citation: Daqaq F, Ouassaid M, Kamel S, Ellaia R and El-Naggar MF (2022) A novel chaotic flower pollination algorithm for function optimization and constrained optimal power flow considering renewable energy sources. Front. Energy Res. 10:941705. doi: 10.3389/fenrg.2022.941705
Received: 11 May 2022; Accepted: 28 July 2022;
Published: 29 September 2022.
Edited by:
Pallavi Choudekar, Amity University, IndiaReviewed by:
Essam Halim Houssein, Minia University, EgyptMourad Yessef, Sidi Mohamed Ben Abdellah University, Morocco
Copyright © 2022 Daqaq, Ouassaid, Kamel, Ellaia and El-Naggar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fatima Daqaq, ZmF0aS5kYXFhcUBnbWFpbC5jb20=; Salah Kamel, c2thbWVsQGFzd3UuZWR1LmVn
 Fatima Daqaq
Fatima Daqaq Mohammed Ouassaid
Mohammed Ouassaid Salah Kamel
Salah Kamel Rachid Ellaia1,2
Rachid Ellaia1,2 Mohamed F. El-Naggar
Mohamed F. El-Naggar