Optimal Allocation of BESS in Distribution Network Based on Improved Equilibrium Optimizer

The battery energy storage system (BESS) can accommodate the uncertainties of renewable energy sources (RESs) and load demand. Proper allocation of the BESS in the distribution network (DN) can bring cost-effectiveness and enhance system stability. To realize the reliable and economic operation of BESS in the DN, a multi-objective optimization model for optimal BESS allocation is established, which aims at minimizing the annual overall cost of the whole system, including life cycle cost (LCC), power loss cost, peak-shaving cost, tie-line fluctuation penalty, and voltage deviation penalty. Then, a novel implementation of the improved equilibrium optimizer (IEO) algorithm is proposed to solve the optimal BESS allocation scheme. In order to verify the effectiveness of the proposed method, the simulation experiment based on the IEEE 33-bus test system is performed. Simulation results prove that the IEO algorithm is capable of rapid stable convergence and efficient searching for optimum in the multidimensional space. By the end of the iteration, the annual overall cost of the whole system records a minimum value of $1.8692e+06 every year. A meticulous techno-economic analysis demonstrates that the obtained BESS allocation scheme not only effectively ensures cost-effectiveness of BESS but also significantly reduces power loss, load peak-valley difference, tie-line power fluctuation, and voltage deviation.

1 Introduction

With rapid expansion of global economy, excessive exploitation and utilization of various traditional fossil fuels has aggravated ecological environment degradation in the past few decades, which significantly hinders the world’s sustainable and stable development (Yang et al., 2018; Zhang et al., 2019a). To solve this thorny issue, a variety of renewable energy sources (RESs) such as wind, solar, and wave energy have obtained widespread concerns (Yang et al., 2021). However, due to the intermittent and randomness of RESs, the integration of a significant amount of RESs into power grids will pose crucial challenges to the safe, stable, and economical operation of the system such as load peak-valley difference, tie-line power fluctuation, voltage violation, RESs curtailment, and line congestion (Das et al., 2018; Guchhait and Banerjee, 2020).

The battery energy storage system (BESS) is not only regarded as one of the most promising candidates for adjusting energy structure and building an environmentally friendly world due to its prominent advantages, for example, high energy conversion efficiency, reliable operation stability, and emission-free (Luburić et al., 2018) but also BESS has been a viable solution which can provide diverse economic benefits and technical support to different power system stakeholders, especially distribution network (DN), including power loss reduction, stability enhancement, and congestion alleviation (Luo et al., 2015). In addition, the BESS can provide an effective supplement for RESs in smoothing output fluctuations.

However, optimal placement and sizing of the BESS are two crucial factors to ensure satisfactory performance of BESS application. Given this, considerable research studies have been carried out either in BESS allocation models or solution algorithms (Yang et al., 2020). Nazaripouya et al. (2015) performed voltage sensitivity analysis to optimize the best placement and sizing of the BESS, where voltage regulation in the presence of RESs is achieved. In the study by Zakeri and Syri (2015), the dynamic programming method is used to plan the BESS in a low-voltage grid so as to minimize power loss. However, such traditional methods as analytical methods and mathematical optimizations consume a long time to converge due to computational complexity and easily trap at local optimum and so has low solution efficiency and accuracy. BESS planning is a complex nonlinear optimization problem with discrete optimization variables, and it is difficult to solve the problem effectively with the abovementioned numerical methods. Meta-heuristic algorithms are popular for various optimization problems by means of their merits of model-free, minimal storage requirement, high convergence rate, and strong search ability (Iba, 1994; Jayasekara et al., 2016). In the study by Kerdphol et al. (2016), particle swarm optimization (PSO) is implemented to obtain optimum sizing of the BESS with high economic profitability. In the study by Wong et al. (2019), a whale optimization algorithm is introduced to optimize placement and sizing of the BESS for power loss reduction, while the performances of these algorithms do not achieve huge breakthroughs. Also, most of the literature only has a single technical benefit or economic benefit.

Therefore, this study establishes a multiobjective mathematical model for BESS optimal allocation, in which life cycle cost (LCC) of the BESS, power loss, peak-shaving effect, tie-line fluctuation, and voltage deviation of the DN are comprehensively considered. In order to solve this model, a novel metaheuristic algorithm, improved equilibrium optimizer (IEO), is proposed to search an optimal solution for the BESS allocation strategy. The proposed algorithm owns advanced updating mechanisms of searching agents, which can effectively avoid falling into local optimum and reach significant improvement on search ability. To verify the effectiveness, the proposed model and algorithm are implemented in the extended IEEE-33 bus test system.

The remaining of this article is organized as follows: Section 2 is system description of the BESS connected to the power grid; Section 3 develops the optimal allocation model of the BESS; the IEO algorithm for the model solution is introduced in Section 4; Case studies are undertaken in Section 5; Section 6 summarizes the main contributions of this study.

2 System Description

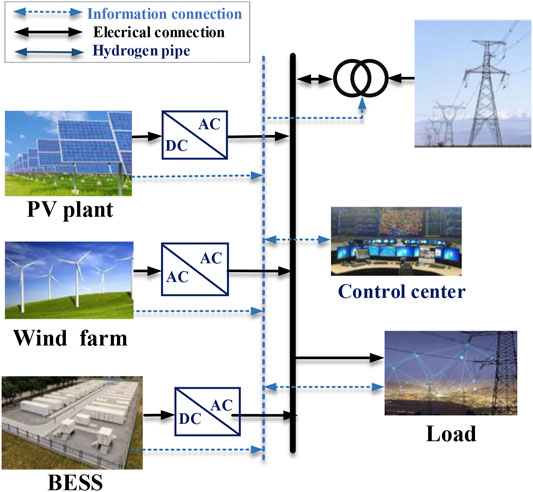
The schematic diagram for BESS access to the power grid is shown in Figure 1. The energy storage controller controls the fast charging/discharging operation of the BESS via real-time monitoring operation condition of the system so as to realize energy exchange between the BESS and the power grid. The remaining charge of the BESS at any moment, namely, the state of charge (SOC) is an important parameter to characterize the charging/discharging operation of the BESS. This relationship needs to be taken into account in the optimal configuration model of the BESS, and rated capacity and charging/discharging power of the BESS are regarded as control variables. SOC of the ith BESS at time t is calculated as follows (Farrokhifar, 2016):

$\{\begin{array}{c}\mathrm{SO}{\mathrm{C}}_i\left(t\right)=(1-\delta \cdot \mathrm{\Delta }t)\cdot \mathrm{SO}{\mathrm{C}}_i(t-1)+(P_{\mathrm{cha},i}\left(t\right)\cdot {\eta }_{\mathrm{cha},i})\cdot \mathrm{\Delta }t,\mathrm{s}.\mathrm{t}.P_{\mathrm{cha},i}\left(t\right)>0,\\ \mathrm{SO}{\mathrm{C}}_i\left(t\right)=(1-\delta \cdot \mathrm{\Delta }t)\cdot \mathrm{SO}{\mathrm{C}}_i(t-1)-(P_{\mathrm{dis},i}\left(t\right)/{\eta }_{\mathrm{dis},i})\cdot \mathrm{\Delta }t,\mathrm{s}.\mathrm{t}.P_{\mathrm{dis},i}\left(t\right)<0.\end{array}(1)$

FIGURE 1

FIGURE 1. Typical configuration of the BESS directly connected to the power grid.

The power exchanged between the BESS and power grid can be expressed as

$P_{\mathrm{grid},i}\left(t\right)=P_{\mathrm{cha},i}\left(t\right)-P_{\mathrm{dis},i}\left(t\right).(2)$

It should be noted that charging power and discharging power at the same time are mutually exclusive, so the power exchange between the BESS and the power grid must be satisfied as follows:

$P_{\mathrm{cha},i}\left(t\right)\cdot P_{\mathrm{dis},i}\left(t\right)=0.(3)$

3 Optimal Allocation Model of the Battery Energy Storage System

In this study, the allocation of the BESS of the DN is expected to minimize investment and operation costs of the BESS, power loss, peak-valley difference of load and tie-line power fluctuation, and voltage deviation. Therefore, a high-dimensional multi-objective optimization model is established. Here, it is considered that all goals are of equal importance, and thus a simple weighting method is adopted to simplify this multi-objective model. Therefore, the optimal allocation model of the BESS that takes annual overall cost including the previously mentioned expenses as the optimization objective is as follows:

$\{\begin{array}{c}\min \mathit{F}\left(\mathit{x}\right)=\min (F_1\left(\mathit{x}\right)+F_2\left(\mathit{x}\right)+F_3\left(\mathit{x}\right)+F_4\left(\mathit{x}\right)+F_5\left(\mathit{x}\right))\\ \mathrm{s}.\mathrm{t}.\mathit{H}\left(x\right)\le 0 \end{array},(4)$

where $\mathit{F}\left(\mathit{x}\right)$ denotes target space that consisted by five objective functions, that is, $F_1$, $F_2$, $F_3$, $F_4$, and $F_5$ are, respectively, life cycle costs (LCC) of the BESS, power loss cost, peak-shaving cost, tie-line power fluctuation penalty fee, and voltage deviation penalty fee; $\mathit{x}$ means the decision space that constituted by all optimization variables, that is, optimal placement and sizing of BESS; $\mathit{H}\left(\mathit{x}\right)$ represents all equality and inequality constraints that need to be satisfied in the optimal allocation model of BESS.

3.1 Objective Functions

3.1.1 Life Cycle Cost

Life cycle cost (LCC) is an important indicator to evaluate the economy of the BESS, which accommodates all the expenses expected to occur during the lifetime of the BESS, such as total capital cost (TCC), maintenance cost (MC), operation cost (OC), replacement cost (RC), and disposal and recycling cost (DRC) (Zakeri and Syri, 2015). From an ownership perspective, it is crucial to perform a comparative LCC analysis of the BESS. Here, LCC is mathematically formulated as annualized cost, as follows:

$F_1=LC{C}_{BESS}=TCC+MC+OC+RC-DRC.(5)$

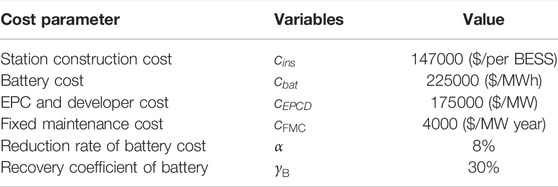
It should be noted that the main cost parameters of the BESS were taken from both the National Renewable Energy Laboratory (Ran et al., 2018), which are tabulated in Table 1.

TABLE 1

TABLE 1. Main cost parameters of the BESS.

3.1.1.1 Total Capital Cost of the Battery Energy Storage System

$TCC={\mu }_{\mathrm{CRF}}\cdot {\sum }_{i=1}^{N_{\mathrm{BESS}}}(c_{\mathrm{ins}}+c_{\mathrm{bat}}\cdot E_{\mathrm{BESS},i}+c_{\mathrm{EPCD}}\cdot P_{\mathrm{BESS},i}),(6)$

where $N_{\mathrm{BESS}}$ means the number of BESSs deployed in DN; $c_{\mathrm{ins}}$ is the initial construction cost of energy storage power station; $C_{\mathrm{bat}}$ represents battery cost per unit capacity; $c_{\mathrm{EPCD}}$ represents the engineering, procurement, and construction (EPC) costs and developer cost of the BESS; $E_{\mathrm{BESS},i}$ is energy capacity of the ith BESS; $P_{\mathrm{BESS},i}$ is power capacity of the ith BESS; ${\mu }_{\mathrm{CRF}}$ denotes capital recovery factor (CRF), which signifies the costs throughout the lifetime of the BESS to the initial moment of investment, as follows:

${\mu }_{\mathrm{CRF}}=\frac{r\cdot {(1+r)}^y}{{(1+r)}^y-1},(7)$

where $y$ is BESS lifetime and is assumed to be 15 years; $r$ means discount rate calculated by the weighted average cost of capital (Harvey, 2020) in Eq. 8 and is calculated as 6%.

$r=f_{\text{d}}\cdot i_{\text{d}}+(1-f_{\text{d}})\cdot i_{\text{e}}.(8)$

3.1.1.2 Maintenance Cost of the Battery Energy Storage System

MC of the BESS refers to the maintenance cost to ensure BESS operation, which is proportional to the rated power of the BESS, as follows:

$MC={\sum }_{i=1}^{N_{\mathrm{BESS}}}{c}_{\text{FMC}}\cdot P_{\mathrm{BESS},i},(9)$

where $C_{\text{FMC}}$ denotes annual fixed maintenance cost.

3.1.1.3 Operation Cost of the Battery Energy Storage System

In terms of energy arbitrage of the BESS in the electricity market, the BESS is cost-effective if the algebraic sum of purchasing electricity cost and selling electricity income is a negative number. Annual $OC$ is computed as follows:

$OC=365\cdot {\sum }_{i=1}^{N_{\mathrm{BESS}}}{\sum }_{t=1}^T(c_{\mathrm{pur}}\left(t\right)\cdot P_{\mathrm{cha},i}\left(t\right)-{\rho }_{\mathrm{sell}}\left(t\right)\cdot P_{\mathrm{dis},i}\left(t\right)),(10)$

where T means 24 h in a day; $c_{\mathrm{pur}}$ and ${\rho }_{\mathrm{sell}}$, respectively, represent the time-of-use (TOU) price to purchase and sell electricity (Zhang et al., 2019b); $P_{\mathrm{cha},i}$ and $P_{\mathrm{dis},i}$, respectively, are denote charging and discharging power of the ith BESS.

3.1.1.4 Replacement Cost of the Battery Energy Storage System

RC of the BESS is mainly from replaceable batteries, as follows:

$RC={\mu }_{\mathrm{CRF}}\cdot {\sum }_{i=1}^{N_{\mathrm{BESS}}}{\sum }_{k=1}^{n_{\mathrm{B}}}(\frac{{(1-\alpha )}^{k{t}_{\mathrm{r}}}}{{(1+r)}^{k{t}_{\text{r}}}}\cdot c_{\mathrm{bat}}\cdot E_{\mathrm{BESS},i}),(11)$

where $n_{\text{B}}$ and t_r mean replacement times of the battery during the lifetime of the BESS and replacement period and are, respectively, 3 and 5; $\alpha$ denotes annual reduction rate of battery cost, set to 8%; $r$ is the discount rate.

3.1.1.5 Disposal and Recycling Cost of the Battery Energy Storage System

$DRC={\mu }_{CRF}\cdot {\sum }_{i=1}^{N_{BESS}}{\sum }_{k=1}^{n_{\text{B}}}\frac{r}{{\left(1+r\right)}^{kt}-1}\cdot ({\gamma }_{\text{B}}\cdot c_{\text{bat}}\cdot E_{BESS,i}),(12)$

where ${\gamma }_{\text{B}}$ is recovery coefficient of the battery, set to 30%.

3.1.2 Power Loss Cost

The grid-connected BESS will change the power flow of DN (Injeti and Thunuguntla, 2020). Furthermore, different placement and sizing of the BESS will have different influences on power loss. For the sake of minimizing the total active power loss, the power loss index in the form of expenses is established in the optimization model, as follows:

$F_2={\sum }_{t=1}^T\left(P_{\mathrm{loss}}\left(t\right)\cdot {\rho }_{\mathrm{sell}}\left(t\right)\right) ,(13)$

$P_{\mathrm{loss}}\left(t\right)={\sum }_{j=1}^L{R}_j{I}_j^2\left(t\right),(14)$

where $F_2$ denotes the power loss expense quantified by a dollar value; $P_{\mathrm{loss}}\left(t\right)$ represents power loss at time $t$; $L$ is the total number of lines in the DN; $R_j$ means the resistance on the jth line; $I_j\left(t\right)$ denotes the current on the jth line at time $t$. The lower $F_2$ is that the greater positive effect of BESS deployment in reducing power loss.

3.1.3 Peak-Shaving Cost

$F_3={\sum }_{t=1}^T(a{P}_{\text{G}}^2\left(t\right)+b{P}_G+c)+(P_{\mathrm{load}}^{\max }\cdot c_{\text{pun},\text{ FL}}),(15)$

where $F_3$ represents the peak-shaving cost, including operation cost of the thermal power unit and additional peak shaving cost of maximum load; $P_G$ represents the active output of thermal power units at time t; a, b, and c are generation cost coefficients of conventional generators; $P_{\mathrm{load}}^{\max }$ represents maximum equivalent load for the year; $c_{\text{pun},\text{ FL}}$ is additional peak shaving cost for maximum load, set to 200000 ($/MW) (Jayasekara et al., 2016).

3.1.4 Tie-Line Fluctuation Penalty Fee

Owing to the intermittency of RESs in their nature, the integration into the power grid poses significant power fluctuation in the grid connection point. However, the BESS can smooth power fluctuation brought from RESs to improve power stability (Sun et al., 2019). Tie-line power fluctuation in the form of expenses can be expressed as

$F_4=365\cdot \sqrt{{\sum }_{t=1}^T{\left(P_{\mathrm{grid}}\left(t\right)-{\overline{P}}_{\mathrm{grid}}\right)}^2}\cdot c_{\text{pun},\text{g}},(16)$

where $F_4$ is total penalty fee brought from tie-line power fluctuation in the grid connection point through the year; $P_{\mathrm{grid}}\left(t\right)$ represents tie-line power fluctuation at time $t$; ${\overline{P}}_{\mathrm{grid}}$ means the mean value of tie-line power over a day; $c_{\text{pun},\text{g}}$ means penalty coefficient for tie-line power fluctuation, set to 50 ($/MW).

3.1.5 Voltage Deviation Penalty Fee

To ensure the power quality of DN, node voltages should be stabilized at a certain level. Here, the penalty fee of voltage deviation encourages node voltages to the nominal voltage (Jayasekara et al., 2016), which is calculated as

$F_5=365\cdot {\sum }_{j=1}^{N_{\mathrm{nodes}}}{\sum }_{t=1}^T\left|V_j\left(t\right)-{\overline{V}}_j\right|\cdot c_{\text{pun},\text{v}},(17)$

where $F_5$ is voltage deviation penalty fee through the year; $N_{\mathrm{nodes}}$ is node number of DN; $V_j\left(t\right)$ represents the voltage per-unit value in the node j at time $t$; ${\overline{V}}_j$ means the average voltage in the node j over a day; $c_{\text{pun},\text{v}}$ is penalty fee for voltage deviation, is set to 50 ($/p.u.).

3.2 Constraints

3.2.1 Power Balance

$\{\begin{array}{c}{P}_i\left(t\right)=V_i\left(t\right){\sum }_{j=1}^N{V}_j\left(t\right)\left(G_{ij}\text{cos}{\theta }_{ij}\left(t\right)+B_{ij}\text{sin}{\theta }_{ij}\left(t\right)\right),\\ Q_i\left(t\right)=V_i\left(t\right){\sum }_{j=1}^N{V}_j\left(t\right)\left(G_{ij}\text{sin}{\theta }_{ij}\left(t\right)-B_{ij}\text{cos}{\theta }_{ij}\left(t\right)\right),\end{array}(18)$

where $P_i\left(t\right)$ and $Q_i\left(t\right)$ represent the injected active power and reactive power at ith node in the DN at time $t$, respectively; $G_{ij}$ and $B_{ij}$ represent admittance and susceptance between the ith node and the jth node, respectively; ${\theta }_{ij}\left(t\right)$ is power angle between the ith node and the jth node at time $t$.

3.2.2 Range of Node Voltages

$V_i^{\text{min}}<V_i<V_i^{\text{max}},(19)$

where $V_i^{\text{min}}$ and $V_i^{\text{max}}$ represent the upper and lower limits of voltage of the ith node, respectively. The voltage limits are now a priority.

3.2.3 Power Limits of Grid Connection Point

$\{\begin{array}{l}{P}_{\text{grid}}^{\min }\le P\text{grid}\left(t\right)\le P_{\text{grid}}^{\max }\\ Q_{\text{grid}}^{\min }\le Q\text{grid}\left(t\right)\le Q_{\text{grid}}^{\max }\end{array},(20)$

where $P_{\text{grid}}^{\max }$, $P_{\text{grid}}^{\min }$, $Q_{\text{grid}}^{\max }$, and $Q_{\text{grid}}^{\min }$ are the upper and lower limits of active and reactive power of the connection point, respectively.

3.2.4 Range of Battery Energy Storage System Capacity

$\{\begin{array}{c}{E}_{\mathrm{BESS},i}\le E_{\mathrm{BESS}}^{\text{max}} \\ P_{\mathrm{BESS},i}\le P_{\mathrm{BESS}}^{\text{max}}\end{array} ,(21)$

where $E_{\mathrm{BESS}}^{\text{max}}$ and $P_{\mathrm{BESS}}^{\text{max}}$ denote the upper limits of energy capacity and power capacity of the BESS, respectively.

3.2.5 Charging and Discharging Power Limits of the Battery Energy Storage System

$\{\begin{array}{c}0\le P_{\mathrm{cha},i}\left(t\right)\le P_{\mathrm{BESS},i}\cdot {\eta }_{\mathrm{cha}}\\ -P_{\mathrm{BESS},i}\cdot {\eta }_{\mathrm{dis}}\le P_{\mathrm{dis},i}\left(t\right)\le 0\end{array} .(22)$

3.2.6 State of Charge Limits of the Battery Energy Storage System

${\text{SOC}}^{\text{min}}<\text{SOC}\left(\text{t}\right)<{\text{SOC}}^{\text{max}},(23)$

where ${\text{SOC}}^{\text{min}}$ and ${\text{SOC}}^{\text{max}}$, respectively, mean the upper and lower limits of SOC, which are 20% and 90%.

3.2.7 Charging Rate Limits of the Battery Energy Storage System

$\{\begin{array}{l}C\text{rate}\le 4\text{C,}\\ C\text{rate}=k\text{C, }k=0.5,\mathrm{1,2,4},\end{array}(24)$

where C represents the current intensity of the BESS when it is fully discharged within 1 hour. The charging rate of the BESS is generally 0.5 C, 1 C, and 2 C, and the maximum is 4 C.

4 Model Solution Based on Improved Equilibrium Optimizer

The optimal allocation of the BESS is a highly non-convex optimization problem with high dimensions, multi objectives, and complicated constraints (Li et al., 2018). To solve this problem, an IEO algorithm is designed in this study. The search mechanisms of the proposed IEO and the overall optimization procedure for BESS allocation are elaborated in this section.

4.1 Equilibrium Optimizer

4.1.1 Principle of EO

EO is a physics-based meta-heuristic algorithm, which was first presented by Faramarzi, Heidarinejad, et al. (2019) (Faramarzi et al., 2020). It is based on control volume mass balance models, and each particle with its concentration represents a searching agent. All searching agents randomly update their concentration based on an equilibrium candidate to reach an equilibrium state. The equilibrium candidate is regarded as the best solution.

In the EO algorithm, a generic mass balance formula in the first-order ordinary differential equation form is utilized to describe the physical process of mass entering, leaving, and generated in the control volume, as follows:

$V\frac{dC}{dt}=Q{C}_{\text{eq}}-QC+G,(25)$

where $V\frac{dC}{dt}$ denotes the change rate of mass, while C is concentration in control volume; Q represents flow rate in and out of control volume; C_eq means concentration under equilibrium state that is desired to be global optimum; G represents mass generation rate in the control volume.

Then, Eq. 26 can be obtained by solving differential Eq. 25, as follows:

$C=C_{\text{eq}}+\left(C_0-C_{\text{eq}}\right)F+\frac{G}{\lambda V}\left(1-F\right),(26)$

where λ is defined as turnover rate; C₀ is the initial concentration at time t₀; factor F is the exponential coefficient as Eq. 27.

$F=\exp \left[-\lambda \left(t-t_0\right)\right].(27)$

4.1.2 Optimization Mechanism of EO

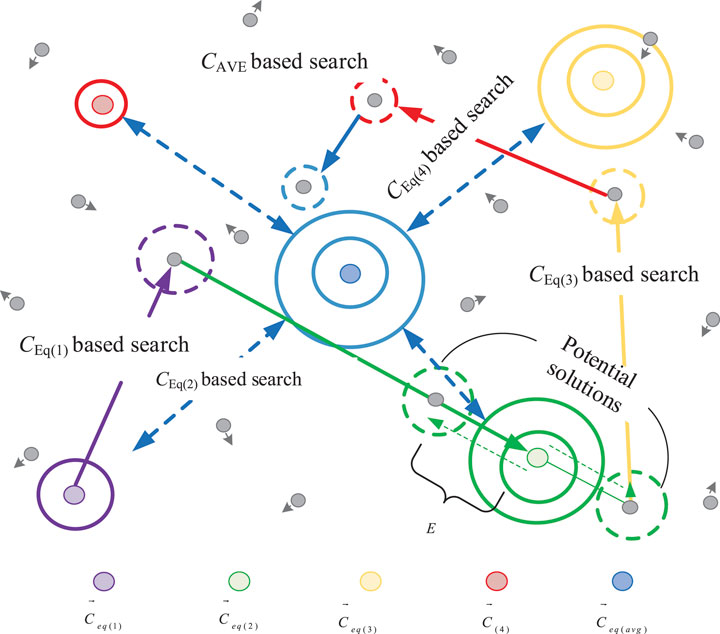
The optimization process of EO is performed based on Eq. 25. As for an optimization problem, concentration C on the left-hand side of the equation represents the current solution; C_eq denotes the best solution ever found. Similar to the speed updating mechanism of the PSO algorithm, concentration is regarded as the individual solution. The collaboration between different individuals for solutions updating in 2D dimensions is shown in Figure 2. The optimization mechanisms are designed as follows (Faramarzi et al., 2020):

FIGURE 2

FIGURE 2. Illustration of solutions updating principle of IEO.

4.1.2.1 Initialization

During the initialization stage, concentrations are generated by performing random initialization within the upper and lower bounds of each optimization variable, as follows:

$\stackrel{\mathrm{r}}{C_i^0}={\stackrel{\mathrm{r}}{C}}_{\min }+{\stackrel{\mathrm{r}}{r}}_i\left({\stackrel{\mathrm{r}}{C}}_{\max }-{\stackrel{\mathrm{r}}{C}}_{\min }\right),i=\mathrm{1,2},\mathrm{...},n,(28)$

where $\stackrel{\mathrm{r}}{C_i^0}$ means the ith particle’s initial concentration; ${\stackrel{\mathrm{r}}{C}}_{\max }$ and ${\stackrel{\mathrm{r}}{C}}_{\min }$ represent maximum value and minimum value for dimensions, respectively; ${\overrightarrow{r}}_i$ is a random vector between 0 and 1; n denotes the number of particles.

4.1.2.2 Equilibrium Pool and Candidates

In order to improve the global search ability of EO and effectively avoid local optimum stagnation, the ultimately convergent equilibrium state contains four best-so-far particles, which are defined as equilibrium candidates, all of which constitute an equilibrium pool:

${\stackrel{\mathrm{r}}{C}}_{\text{eq,pool}}=\left\{{\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(1\right)},{\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(2\right)},{\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(3\right)},{\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(4\right)},{\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(\text{ave}\right)}\right\},(29)$

where ${\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(1\right)}$, ${\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(2\right)}$, ${\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(3\right)}$, and ${\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(4\right)}$ are four best-so-far particles; ${\stackrel{\mathrm{r}}{C}}_{\text{eq,}\left(\text{ave}\right)}$ denotes the equilibrium state of four solutions.

4.1.2.3 Exponential Term F

Exponential term F is crucial to properly balance global exploration and local exploitation during concentration updating, which is expressed as

$\overrightarrow{F}=e^{-\overrightarrow{\lambda }(t-t_0)},(30)$

where $\overrightarrow{\lambda }$ denotes a random vector between 0 and 1, while time $t$ represents a function of iteration, as follows:

$t={(1-\frac{iter}{ite{r}_{\text{max}}})}^{\left(a_2\frac{iter}{ite{r}_{\text{max}}}\right)},(31)$

where $iter$ and $ite{r}_{\text{max}}$ represent current and maximum number of iterations, respectively; and $a_2$ denotes a constant value adopted for local exploitation adjustment.

To effectively avoid premature convergence, the following is also considered, as follows:

${\overrightarrow{t}}_0=\frac{1}{\overrightarrow{\lambda }}\ln \left[-a_1\text{sign}\left(\overrightarrow{r}-0.5\right)\right]\left(1-e^{-\overrightarrow{\lambda }t}\right)+t,(32)$

where a₁ denotes a constant value adopted for an adjustment between global search and local exploitation; sign is symbolic function; $\stackrel{\mathrm{r}}{r}$ and $\stackrel{\mathrm{r}}{\lambda }$ are random vector between 0 and 1.

Substituting Eq. 32 into Eq. 30, yields

$\stackrel{\mathrm{r}}{F}=a_{1}sign\left(\stackrel{\mathrm{r}}{r}-0.5\right)\left[e^{-\stackrel{\mathrm{r}}{\lambda }t}-1\right].(33)$

It is noted that the higher the a1, the better the exploration ability and consequently the lower exploitation performance. Similarly, the higher the a2, the better the exploitation ability, and the lower the exploration ability. In addition, sign (r−0.5) affects the direction of exploration and exploitation.

4.1.2.4 Generation Rate G

Generation rate G is critical to improve the local exploitation stage, and G is devised as follows:

$\stackrel{\mathrm{r}}{G}={\stackrel{\mathrm{r}}{G}}_{\text{CP}}\left({\stackrel{\mathrm{r}}{C}}_{\text{eq}}-\stackrel{\mathrm{r}}{\lambda }\stackrel{\mathrm{r}}{C}\right),(34)$

${\stackrel{\mathrm{r}}{G}}_{\text{CP}}=\{\begin{array}{l}0.5{\stackrel{\mathrm{r}}{r}}_1,\text{ if }{r}_2\ge 0.5\\ 0\text{, otherwise}\end{array},(35)$

where ${\stackrel{\mathrm{r}}{G}}_{\text{CP}}$ is defined as the control parameter of generation rate; ${\stackrel{\mathrm{r}}{r}}_1$ and r₂ are two random variables between 0 and 1.

4.1.2.5 Solutions Update

Therefore, the overall updating rule of EO can be described by

$\stackrel{\mathrm{r}}{C}={\stackrel{\mathrm{r}}{C}}_{\text{eq}}+\left(\stackrel{\mathrm{r}}{C}-{\stackrel{\mathrm{r}}{C}}_{\text{eq}}\right)\cdot \stackrel{\mathrm{r}}{F}+\frac{\stackrel{\mathrm{r}}{G}}{\stackrel{\mathrm{r}}{\lambda }V}\left(1-\stackrel{\mathrm{r}}{F}\right).(36)$

4.2 Improved Equilibrium Optimizer

Compared with the original EO algorithm, different equilibrium candidates of the IEO algorithm are allocated by different selection probabilities to all equilibrium candidates according to their fitness values instead of randomly selecting an equilibrium candidate from the equilibrium pool. That is to say, an equilibrium candidate with a smaller fitness value will receive a higher selection probability, which can achieve a deeper exploitation modified equilibrium candidate assignment mechanism.

It should be noted that the fitness values of all equilibrium candidates are normalized to range from 0 to 1, and then the selection probabilities can be obtained by

$p_j=p_{\text{min}}+\left(p_{\text{max}}-p_{\text{min}}\right)\times \frac{\underset{i\in E_{\text{p}}}{\max }{F}_i-F_j}{\underset{i\in E_{\text{p}}}{\max }{F}_i-\underset{i\in E_{\text{p}}}{\min }{F}_i}, j\in E_{\text{p}}(37)$

where $p_{\text{min}}$ and $p_{\text{max}}$ are the minimum and maximum selection probabilities, respectively; $p_j$ denotes probability of selecting the jth equilibrium candidate; $F_j$ denotes fitness value of the jth equilibrium candidate; $E_{\text{p}}$ is the set of equilibrium candidates.

Due to IEO dynamically adjusting equilibrium candidate selection probabilities based on their fitness value during iterations, it can implement deeper exploitation and improve overall optimization efficiency to search for a higher quality optimum.

4.3 Design of Improved Equilibrium Optimizer for Battery Energy Storage System Allocation Application

4.3.1 Optimization Variable Processing

The IEO individuals are characterized by the optimization variables, including installation placement, power capacity, and energy capacity of two BESSs, all of which need to be constricted in a reasonable range; otherwise, some negative effects on the power flow, relay protection, voltage, and waveform of the original power grid will be observed. In this study, nodes in the range of [2, 33] are selected as the installation node, in which environmental and geographical nodes need to be considered in engineering practice. In addition, the limits of power and energy capacities are determined to consider the topology of DN, the power limit of the interconnection point, and especially the total load power. Therefore, the power capacities allowed to access the power grid of two BESSs are determined so as to satisfy the total active power load of the power grid. In order to give full play to the charging and discharging capacity of the BESS, the ratio of energy capacity limit to power capacity limit is 4 to 1, as follows:

$\{\begin{array}{c}{P}_{\mathrm{BESS},i}\le P_{\mathrm{BESS}}^{\text{max}}\\ E_{\mathrm{BESS},i}\le E_{\mathrm{BESS}}^{\text{max}}\end{array} ,(38)$

where $P_{\mathrm{BESS}}^{\text{max}}$ and $E_{\mathrm{BESS}}^{\text{max}}$ denote the upper limits of the energy capacity and power capacity of the BESS, which are, respectively, 2 MW and 8 MWh.

It should be noted that these four variables, that is, power and energy capacities of two BESSs are continuous, while these two variables, that is, installation placement are discrete. In this study, continuous variables can converge to the optimal value in the iteration process, while the optimal value of discrete variables is needed to be rounded in the continuous space (Zhang et al., 2017).

4.3.2 Fitness Function Processing

The fitness function should be combined with the objective function and constraint conditions of the BESS optimal allocation model. First, the updated solutions will perform power flow calculation, where constraints need to be satisfied, that is, Eqs. 18–24. Then, objective functions of all solutions are evaluated based on the results of the power flow calculation. Once the constraint condition is not satisfied, a large penalty factor will be added to the objective function. Therefore, the fitness function can be designed as follows:

$Fit\left(\stackrel{\mathrm{r}}{C}\right)=\mathit{F}\left(\stackrel{\mathrm{r}}{C}\right)+\eta q,(39)$

where η is the penalty factor for violating constraints, generally set to a larger normal number, and q means the number of unsatisfied constraints.

4.3.3 Solving Procedure of the Model

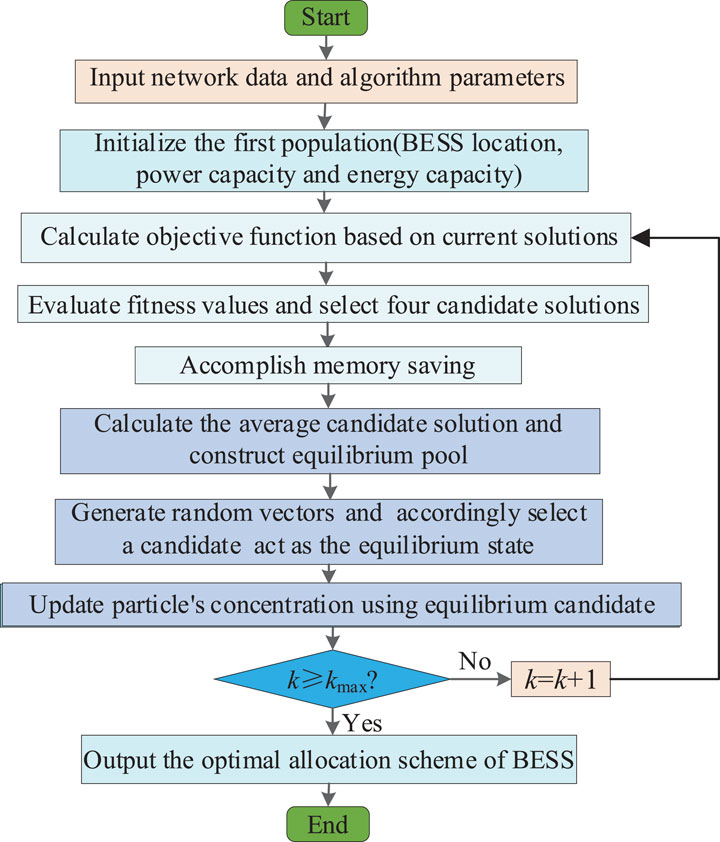
To sum up, the execution procedure of IEO for BESS optimal allocation is given in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of IEO for optimal allocation of the BESS.

5 Simulation Model and Case Study

5.1 The IEEE-33 Test System

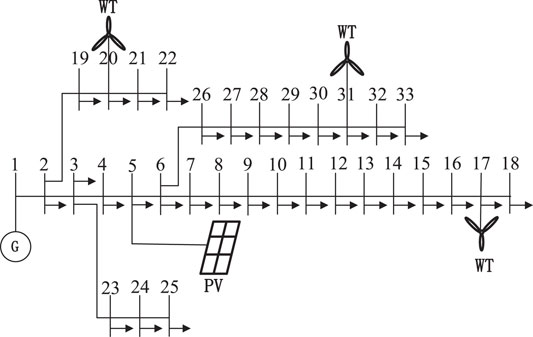
In this section, BESS optimal allocation is implemented in the extended IEEE-33 bus system for verifying the effectiveness of the proposed method. The topology structure of the test system with the total load of 3.715+j2.3 MVA is depicted in Figure 4 (Goswami and Basu, 1992). In addition, the population size of IEO is set to be 100, and the maximum iterations are set to be 100. Some specific parameters are set to the default values. Tables 1, 2, respectively, provide the main cost parameters of BESS and TOU electricity prices.

FIGURE 4

FIGURE 4. Extended IEEE-33 bus test system.

TABLE 2

TABLE 2. TOU electricity price.

5.2 Case Data of Source and Load Sides

It is assumed that one PV plant and three wind power plants are in the DN, where the maximum generation limits of wind and PV are 3 MW and 2.5 MW, respectively. In view of the uncertainty of load, wind, and PV output powers, this study adopts load, wind, and PV power curves under different typical daily scenarios to represent the actual operation of DN in the whole year.

First, annual historical data of load, wind, and PV powers in one area are generated based on wind and PV output models. Furthermore, a C-means clustering algorithm (Askari, 2021) is used to obtain typical daily curves of load, wind, and PV power, where the temporal correlation of source and load sides is considered, and four typical scenarios are obtained via scene fitting, as demonstrated in Figure 5, which can accurately simulate the uncertainty of DN.

FIGURE 5

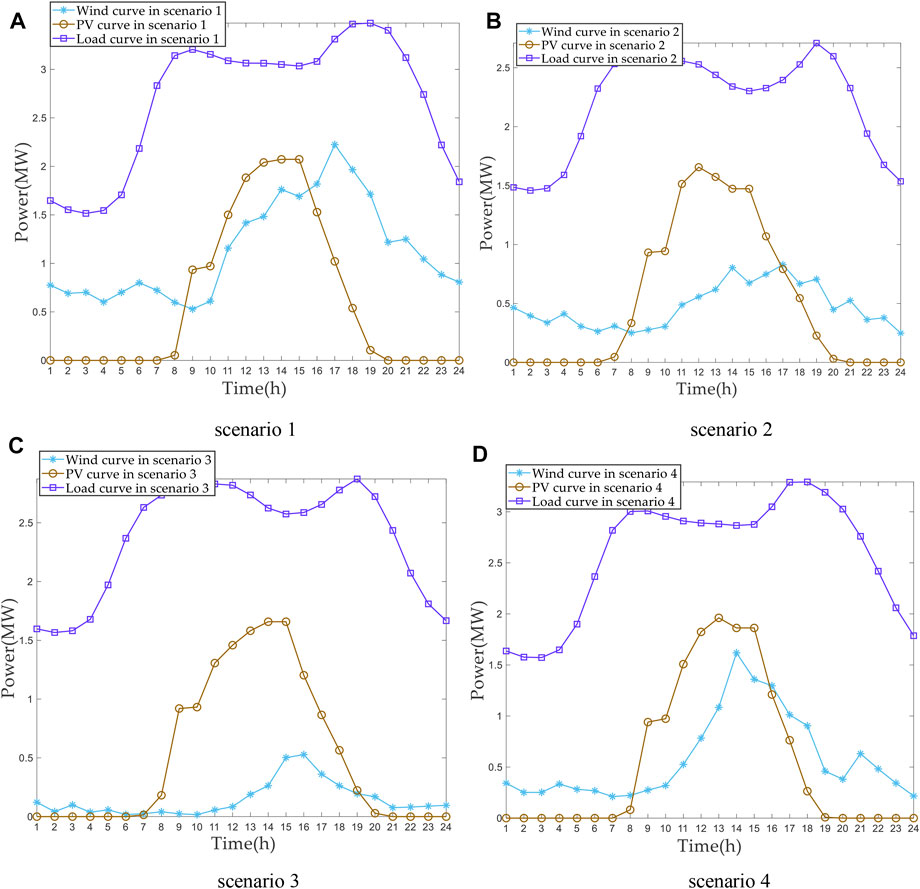
FIGURE 5. Clustered four typical operating scenarios. (A) Scenario 1. (B) Scenario 2. (C) Scenario 3. (D) Scenario 4

5.3 Simulation Results and Analysis

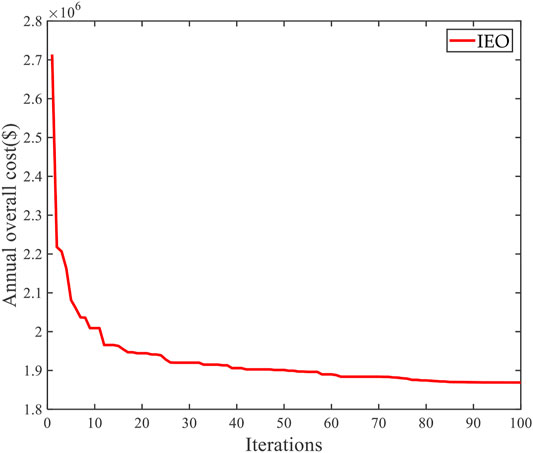
In order to prove the convergence performance of the proposed algorithm, taking annual overall cost as optimization objective, the optimization history (convergence curve) of optimal individual fitness of the IEO algorithm is presented in Figure 6. This metric is the fitness of the best-so-far particle C_eq (1) from the first to the last iteration. It can be seen that the proposed algorithm can converge to the minimum value with fewer iterations to avoid falling into the local optimum, which is a benefit by the design of the exponential term.

FIGURE 6

FIGURE 6. Clustering for typical diurnal curves.

BESS optimal allocation scheme and optimization results of DN obtained by IEO algorithms are given in Table 3. The results show that the allocation scheme is the most cost-effective when the BESSs with the capacities of 0.2504 MW/1.0015 MWh and 0.8535 MW/1.7069 MWh, respectively, are installed in bus 32 and bus 7. The annual overall cost including power loss cost, peak-shaving cost, tie-line fluctuation penalty fee, and voltage deviation penalty fee, is only $1.8692e+06 in the case of the BESS for 15 years in the DN with a high proportion of RESs, of which LCC of the BESS is $-7.4236e+04. It is obvious that two BESSs are expected to achieve a total profit of $1.1135+06 in the lifecycle, even where the ancillary services of the BESS in the electricity market are not considered.

TABLE 3

TABLE 3. Allocation results of IEO algorithms.

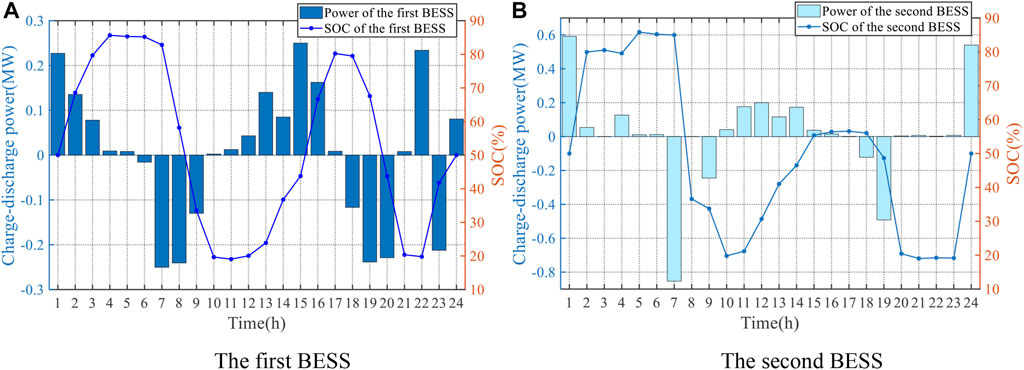
In addition, the obtained allocation scheme of the BESS by means of the IEO algorithm can help guarantee two BESSs operate at the optimum conditions with optimal placement and sizing in terms of economic and reliability requirements of DN. Figure 7 shows the charge–discharge power and SOC of two BESSs. It can be seen from Figure 7 that SOC gradually increased with the charge of the BESS and decreased with the discharge of the BESS, all of which are kept at 50% at the start and end of the day to ensure continuous and stable operation.

FIGURE 7

FIGURE 7. Real-time operation conditions of two BESSs. (A) First BESS and (B) second BESS

FIGURE 8

FIGURE 8

In order to verify the technical and economic benefits of the BESS, Table 4. provides several criteria of DN in two cases and the corresponding improvement rate. In particular, the annual total power loss of DN reduces by 538.5 MW when two BESSs are properly allocated in DN based on the proposed method, the maximum peak-valley difference decreases to 2.9097 MW from 8.6214 MW, and the improvement rates of average tie-line power fluctuation and average voltage deviation reach 47%.

TABLE 4

TABLE 4. Optimization results of DN via the BESS.

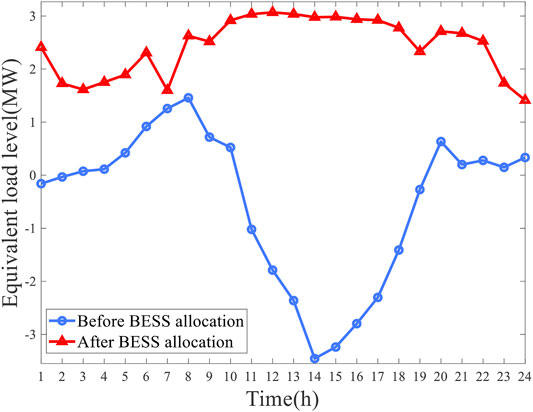
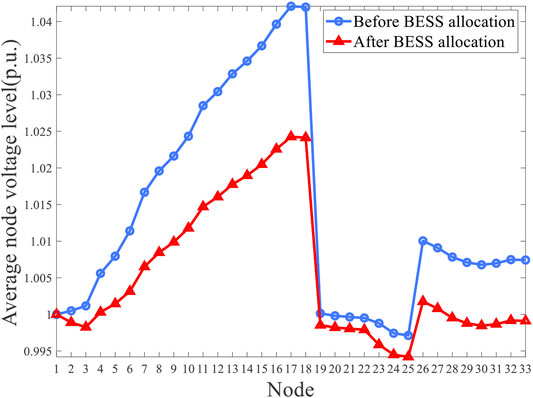
In addition, equivalent load curves and average node voltage curves of DN under two cases are shown in Figures 9, 10. It is obvious that reasonable BESS planning can significantly reduce peak-valley difference and load fluctuation and improve voltage level.

FIGURE 9

FIGURE 9. Average node voltage curves under two cases.

6 Conclusion

In this study, a new method for determining the placement and sizing of the BESS, with the purpose of economy and reliability improvements in the DN, has been proposed. The contributions of the proposed method are drawn as follows:

● A multi-objective BESS allocation model takes economic criteria that incorporate time value into costs and technical criteria that relate to system reliability into consideration is established, which aims at achieving excellent cost-effectiveness and reliable operation of DN with RESs and BESS. Economic criteria accommodate all the expenses expected to occur during the lifetime of the BESS. For the sake of a common dimension of objective function, technical criteria are quantified by a dollar value, that is, power loss cost, peak-shaving cost, and the penalty fees of tie-line fluctuation and voltage deviation.

● A solution algorithm based on IEO is proposed to solve the BESS allocation model, whose specific application and design process are given. Compared with EO, the proposed IEO improves global search ability due to the fact that it dynamically adjusts equilibrium candidate selection probabilities rather than random selection of equilibrium candidate from equilibrium pool, which owns strong global search ability and good convergence effect, and thus can quickly search high-quality optimum solution.

● The multi-scenario clustering using a C-means clustering algorithm is conducted to capture the time-variable natures and uncertainties related to RESs and load demand. Ultimately, four typical scenarios are obtained via scene fitting according to the probability distribution of different scenarios. Compared to the direct average for seasonal data of source and load sides, the scenario clustering and fitting adopted in this study can more accurately simulate the actual operation condition of the DN, meanwhile balancing the simulation accuracy.

● To achieve practical study and verify the effectiveness of the proposed model and IEO algorithm, a procedure has been demonstrated on the extended IEEE-33 bus test system, which effectively verifies the optimality of the solution found. The optimal BESS allocation strategy obtained by the IEO algorithm converges to the lowest overall cost, which substantially reduces power loss, peak-valley difference, tie-line fluctuation, and voltage deviation. Hence, it is concluded that the proposed method is capable of finding the appropriate placement and sizing of the BESS and is beneficial for DN to increase economic efficiency and improve system reliability.

The future research work is devoted to investigating smart charging/discharging operations and suitable grid-connected control strategy of the BESS to be applied in real-time networks so as to facilitate BESS planning.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

WZ: writing—reviewing and editing; SL: supervision and fundings.

Funding

The work is funded by the National Natural Science Fund of China (62076027).

Conflict of Interest

Author WZ was employed by Yunnan Provincial Energy Investment Group Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Reference

Askari, S. (2021). Fuzzy C-Means Clustering Algorithm for Data with Unequal Cluster Sizes and Contaminated with Noise and Outliers: Review and Development. Expert Syst. Appl. 165, 113856. doi:10.1016/j.eswa.2020.113856

CrossRef Full Text | Google Scholar

Das, C. K., Bass, O., Kothapalli, G., Mahmoud, T. S., and Habibi, D. (2018). Overview of Energy Storage Systems in Distribution Networks: Placement, Sizing, Operation, and Power Quality. Renew. Sustain. Energy Rev. 91, 1205–1230. doi:10.1016/j.rser.2018.03.068

CrossRef Full Text | Google Scholar

Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020). Equilibrium Optimizer: A Novel Optimization Algorithm. Knowledge-Based Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190

CrossRef Full Text | Google Scholar

Farrokhifar, M. (2016). Optimal Operation of Energy Storage Devices with RESs to Improve Efficiency of Distribution Grids; Technical and Economical Assessment. Int. J. Electr. Power & Energy Syst. 74, 153–161. doi:10.1016/j.ijepes.2015.07.029

CrossRef Full Text | Google Scholar

Goswami, S. K., and Basu, S. K. (1992). A New Algorithm for the Reconfiguration of Distribution Feeders for Loss Minimization. IEEE Trans. Power Deliv. 7 (3), 1484–1491. doi:10.1109/61.141868

CrossRef Full Text | Google Scholar

Guchhait, P. K., and Banerjee, A. (2020). Stability Enhancement of Wind Energy Integrated Hybrid System with the Help of Static Synchronous Compensator and Symbiosis Organisms Search Algorithm. Prot. Control Mod. Power Syst. 5 (2), 138–150. doi:10.1186/s41601-020-00158-8

CrossRef Full Text | Google Scholar

Harvey, H. L. D. (2020). Clarifications of and Improvements to the Equations Used to Calculate the Levelized Cost of Electricity (LCOE), and Comments on the Weighted Average Cost of Capital (WACC). Energy 207, 118340. doi:10.1016/j.energy.2020.118340

CrossRef Full Text | Google Scholar

Iba, K. (1994). Reactive Power Optimization by Genetic Algorithm. IEEE Trans. Power Syst. 9 (2), 685–692. doi:10.1109/59.317674

CrossRef Full Text | Google Scholar

Injeti, S. K., and Thunuguntla, V. K. (2020). Optimal Integration of DGs into Radial Distribution Network in the Presence of Plug-In Electric Vehicles to Minimize Daily Active Power Losses and to Improve the Voltage Profile of the System Using Bioinspired Optimization Algorithms. Prot. Control Mod. Power Syst. 5 (1), 21–35. doi:10.1186/s41601-019-0149-x

CrossRef Full Text | Google Scholar

Jayasekara, N., Masoum, M. A. S., and Wolfs, P. J. (2016). Optimal Operation of Distributed Energy Storage Systems to Improve Distribution Network Load and Generation Hosting Capability. IEEE Trans. Sustain. Energy 7 (1), 250–261. doi:10.1109/tste.2015.2487360

CrossRef Full Text | Google Scholar

Kerdphol, T., Fuji, K., Mitani, Y., Watanabe, M., and Qudaih, Y. (2016). Optimization of a Battery Energy Storage System Using Particle Swarm Optimization for Stand-Alone Microgrids. Int. J. Electr. Power & Energy Syst. 81, 32–39. doi:10.1016/j.ijepes.2016.02.006

CrossRef Full Text | Google Scholar

Li, R., Wang, W., Chen, Z., and Wu, X. (2018). Optimal Planning of Energy Storage System in Active Distribution System Based on Fuzzy Multi-Objective Bi-level Optimization. J. Mod. Power Syst. Clean. Energy 6 (2), 342–355. doi:10.1007/s40565-017-0332-x

CrossRef Full Text | Google Scholar

Luburić, Z., Pandžić, H., Plavšić, T., Teklić, L., and Valentić, V. (2018). Role of Energy Storage in Ensuring Transmission System Adequacy and Security. Energy 156, 229–239. doi:10.1016/j.energy.2018.05.098

CrossRef Full Text | Google Scholar

Luo, X., Wang, J., Dooner, M., and Clarke, J. (2015). Overview of Current Development in Electrical Energy Storage Technologies and the Application Potential in Power System Operation. Appl. Energy 137, 511–536. doi:10.1016/j.apenergy.2014.09.081

CrossRef Full Text | Google Scholar

Nazaripouya, H., Wang, Y., Chu, P., Pota, H. R., and Gadh, R. (2015). Optimal Sizing and Placement of Battery Energy Storage in Distribution System Based on Solar Size for Voltage Regulation. IEEE Power & Energy Society General Meeting, 1–5. doi:10.1109/pesgm.2015.7286059

CrossRef Full Text | Google Scholar

Ran, F., Timothy, R., and Robert, M. (2018). Utility-scale Photovoltaics-Plus-Energy Storage System Costs Benchmark. Natl. Renew. Energy Lab. 10, 2172.

Google Scholar

Sun, Y., Tang, X., Sun, X., Jia, D., and Zhang, G. (2019). Microgrid Tie‐line Power Fluctuation Mitigation with Virtual Energy Storage. J. Eng. 2019 (16), 1001–1004. doi:10.1049/joe.2018.8553

CrossRef Full Text | Google Scholar

Wong, L. A., Ramachandaramurthy, V. K., Walker, S. L., Taylor, P., and Sanjari, M. J. (2019). Optimal Placement and Sizing of Battery Energy Storage System for Losses Reduction Using Whale Optimization Algorithm. J. Energy Storage 26, 100892. doi:10.1016/j.est.2019.100892

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Chen, Y., Li, D., Zeng, C., Chen, Y., et al. (2020). Optimal Sizing and Placement of Energy Storage System in Power Grids: A State-Of-The-Art One-Stop Handbook. J. Energy Storage 32, 101814. doi:10.1016/j.est.2020.101814

CrossRef Full Text | Google Scholar

Yang, B., Yu, L., Chen, Y., Ye, H., Shao, R., Shu, H., et al. (2021). Modelling, Applications, and Evaluations of Optimal Sizing and Placement of Distributed Generations: A Critical State‐of‐the‐art Survey. Int. J. Energy Res. 45 (3), 3615–3642. doi:10.1002/er.6104

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energy 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Zakeri, B., and Syri, S. (2015). Electrical Energy Storage Systems: A Comparative Life Cycle Cost Analysis. Renew. Sustain. Energy Rev. 42, 569–596. doi:10.1016/j.rser.2014.10.011

CrossRef Full Text | Google Scholar

Zhang, H., Lu, Z., Hu, W., Wang, Y., Dong, L., and Zhang, J. (2019). Coordinated Optimal Operation of Hydro-Wind-Solar Integrated Systems. Appl. Energy 242, 883–896. doi:10.1016/j.apenergy.2019.03.064

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., and Cheng, L. (2017). Accelerating Bio-Inspired Optimizer with Transfer Reinforcement Learning for Reactive Power Optimization. Knowledge-Based Syst. 116, 26–38. doi:10.1016/j.knosys.2016.10.024

CrossRef Full Text | Google Scholar

Zhang, Z., Yu, T., Wang, D. Z., Zhenning, P., and Xiaoshun, Z. (2019). Optimal Solution of Time-Of-Use Price Based on Ensemble Learning for Electricity-Gas-Heat Commercial Building. Proc. CSEE 39 (1), 112–125. doi:10.13334/j.0258-8013.pcsee.181584

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

BESS Battery energy storage system

CRF Capital recovery factor

DN Distribution network

DRC Disposal and recycling cost

EPC Engineering, procurement, and construction

IEO Improved equilibrium optimizer

LCC Life cycle cost

MC Maintenance cost

RC Replacement cost

RESs Renewable energy sources

OC Operation cost

SOC State of charge

TOU Time-of-use

Variables

$P_{BESS,i}$ Power capacity of the ith BESS

$E_{BESS,i}$ Energy capacity of the ith BESS

$P_{cha,i}$ Charging power of the ith BESS

$P_{dis,i}$ Discharging power of the ith BESS

$c_{pur}$ TOU price to purchase electricity

${\rho }_{sell}$ TOU price to sell electricity

$c_{\text{pun},\text{ FL}}$ Additional peak clipping cost for maximum load

$c_{\text{pun},\text{g}}$ Penalty fee for tie-line power fluctuation

$c_{\text{pun},\text{v}}$ Penalty fee for voltage deviation

C Concentration in control volume that denotes current solutions of all particles

C_eq Concentration under an equilibrium state that denotes the best solution ever found

C_{eq (avg)} Mean concentration of four solutions

C_{eq, pool} Equilibrium pool contains four candidates and an equilibrium state