- Department of Physics, College of Science, King Faisal University, Al-Ahsa, Saudi Arabia
The current research letter is materialized to examine the combined effect of thermophoretic dust particle diffusion and magnetic dipole flow toward a stretchable sheet. The slip effect is used in the development of the momentum equation. Water is considered as a base fluid, and single-walled carbon nanotubes and multiwalled carbon nanotubes are nanoparticles. The aforementioned rheological model is formulated in the way of nonlinear partial differential equations (PDEs). The structure of nonlinear biformed ordinary differential equations (ODEs) is obtained from the modeled nonlinear PDEs by incorporating valid sameness transformations. The system of ODEs is then figured out by employing the tool of MATLAB function bvp4c. The significant nature of the contributing parameter for both the single-wall and multiwall cases is presented via graphs. From the results, we conclude that an impact of the melting effect, mounting of
Introduction
Nanofluids may be used to improve the performance of different electronic and mechanical devices regarding heat transfer due to their high thermal conductivity. Therefore, researchers have suggested many proposals to upgrade the capability of transfer of heat in the fluids. Nanofluids are an advanced way to enhance the heat-transfer rate in liquids. They contain nanoparticles homogeneously dissolved in simple fluids, for example, oil, water, and glycerin. There are many kinds of nanoparticles, such as aluminum, silver, gold, titanium, copper, the oxides of these metals, and carbon nanotubes. These fluids have several applications in industries, like vehicle cooling, heat exchangers, electronic cooling, nuclear reactors, cooling thermal insulation, cancer therapy, energy production, and so on.
Moreover, nanofluids have several applications, like micromachines in microreactors, cars, computer chips, microelectronics, and cooling agents in aeroplanes. Nanofluid properties may depend on different parameters such as particle dimension, particle distribution, shapes, size, and so on. Choi, 1995 was the first to observe that adding nanoparticles to a host fluid boosts its thermic strength. Later, Choi et al., 2001 showed through experiments that the enhancement in fluid thermic strength could also be achieved by taking oil as the base fluid. After the pioneering work of Choi, several scientists start working on nanofluids. Sheikholeslami et al., 2018 examined the nanofluid flow over a permeable channel in addition to Lorentz forces. Chen et al., 2015 inspected the nanofluid flow over a vertical symmetrical heated parallel plate with magnetic effects. Hayat and Nadeem, 2017 collectively worked on silver and copper oxide-based hybrid nanofluids to boost the heat-transfer rate. Dogonchi and Ganji (Dogonchi and Ganji, 2016) discussed the thermal radiation effect and flow of magnetohydrodynamic nanofluids between the contracting walls. Bilal et al. (Bilal et al., 2018) investigated the nanofluid flow across the contracting cylinder. Hayat et al., 2016 hypothesized the stagnation point flow with mass flux and variable heat conductivity, where a linear stretched surface subordinates the flow. Recent studies regarding the slip motion can be found in Rizwan Ul Haq et al., 2017; Ul Haq et al., 2018; Rizwan et al., 2020; and Ul Haq et al., 2020.
In the presence of an electrically conducting fluid, the phenomenon is called magnetohydrodynamics (MHD) when the magnetic field is applied across the moving fluid. MHD plays an essential role in many technological and industrial sectors such as nuclear fuels, cancer tumor treatment, blood pump machines, MHD generators, flow meters, and accelerator pumps. In the existence of the magnetic field, convection problems of the electrically conducting fluid have significant results because of its broad uses in astrophysics, missile technology, geophysics, and plasma physics. It is also frequently used in biomedicine industries. It is noticed that the combined impact of thermal radiation and MHD is an essential factor in the study of fluid dynamics owing to their extensive applications in furnace design, nuclear reactor safety, fire spreads, glass production, modern energy transformation devices, turbid water bodies, natural gas-fired and open cycle coal, photochemical reactors, natural convection in cavities, and many others. Metallurgy industries, petroleum, and chemical engineering are some specific processes where the importance of MHD along with thermal radiation can be observed. Qayyum et al. (Fakour et al., 2015) examined the nonlinear chemical reactions in MHD flow above the stretched sheet having a variable thickness. They also examined heat absorption/generation and nonlinear convection. Pourmehran et al. (Qayyum et al., 2017) considered the bouncy effects bygone a vertical sheet for investigating the MHD convective nanofluid. Shiekholeslami (Mahanthesh et al., 2017) used the Lattice Boltzmann technique as a mesoscopic methodology to inspect the convective flow of MHD nanofluids in a porous cubic container. Zhao et al. (Pourmehran et al., 2016) focused on the thermally generated flow of a nanofluid (water) through porous nanotubes and discussed heat-transfer features. Hayat et al., 2018 designed the magnetic-micropolar flow transverse to a curved stretching surface with homogeneous/heterogeneous interactions through an analytical technique. Khan et al. (Sheikholeslami, 2017) explained the flow of an unsteady MHD Newtonian fluid with coupled mass and heat transfer where wall shear stress is applied to the fluid. Using the vertical microchannel having conducting and non-conducting walls, Jha and Aina (Zhao et al., 2019) focused on studying applied and induced magnetic fields and natural convective flow. Hayat et al. (Hayat et al., 2017a) investigated the fluid flow rate in the existence of thermal surface boundary conditions. Hashemi et al. (Reddy et al., 2018) discussed the dynamics of a micropolar nanofluid in a radiative porous medium coupled with MHD natural convection and incorporation of an elliptical heat source. Alkanhal et al. (Alkanhal et al., 2019) studied the thermal management of MHD nanofluids within a porous medium enclosed in a wavy shaped cavity with a square obstacle in the presence of a radiation heat source. M.G. Reddy et al. (Reddy et al., 2022) discussed the effect of thermal conductivity on Blasius–Rayleigh–Stokes flow and heat transfer over a moving plate by considering the magnetic dipole moment.
The no-slip condition is also an essential part of Navier Stoke’s equations. For most of the non-Newtonian fluids, the no-slip condition is inadequate as few polymers melt frequently, showing the microscopic wall slip, which has a modulating impact and has a nonlinear relationship between traction and slip velocity. Partial velocity slip occurs when the liquid flows over the polish surface or through different processes such as suspension, emulsions, polymer solutions, and foams. The Navier velocity slip condition has typical importance while observing the slip phenomena. Solutal slip and thermal slip conditions may also appear in different industrial procedures. The boundary layer slip flow problem occurs in internal cavities and the polishing of heart valves. Many researchers and scientists have investigated the behavior of flow under no-slip conditions. However, in real-life applications, it is not mandatory in every case because there are different circumstances in which velocities of body and fluid particles are distinct. The behavior of flow in microstructures/nanostructures such as hard drives, microvalves, micropumps, and micronozzles is indicated by the slip boundary conditions. Recent studies regarding the slip motion can be found in Hayat et al., 2013; Mukhopadhyay, 2013; Shen et al., 2015; Hayat et al., 2017b; Ul Haq et al., 2017; Hashemi et al., 2018; and Hayat et al., 2019.
This article examines the magnetic dipole flow and melting heat transfer over suspended dust particles with carbon nanotubes and the slip effect. To compose a nanofluid, the water base fluid is mixed up with two types of carbon nanotubes [single-walled carbon nanotubes (SWCNTs) and multiwalled carbon nanotubes (MWCNTs)]. By applying significant similarity transformation, nonlinear partial differential equations (PDEs) are being modified into a system of ordinary differential equations (ODEs); employing the MATLAB function bvp4c, we were able to get numerical solutions to these nonlinear ordinary differential equations. Tables and graphs are used to demonstrate the impact of different physical characteristics.
Mathematical formulation
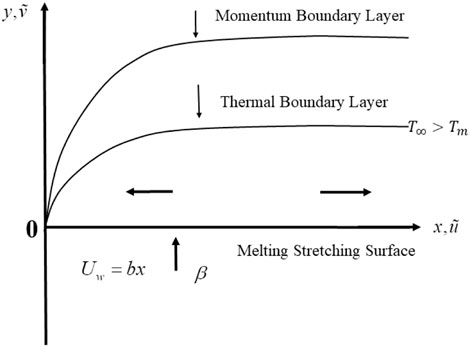
Presumptions of the flow:
• Assume the 2D flow of dusty carbon nanotubes in an elaborated sheet where the flow is time-reliant as considered.
•
• The stretching surface as measured with the
• The fluid utilized here is a dusty base fluid with the composition of water and carbon nanotubes (SWCNT/MWCNT).
• Equilibrium is assumed to be established between carbon nanotubes and the dust base fluid and the slip amid them.
• The magnetic dipole field induced is ignored as the Reynolds number assumed is the least.
After using boundary layer approximation Bernoulli’s equation in the free stream, the system of governing equations in the form of PDEs is as follows (Ramesh et al., 2012; Kumar et al., 2019):
Fluid phase
Dust phase
The corresponding boundary conditions are given by
The expressions for viscosity, density, specific heat, and thermal conductivity of the carbon nanotube are as follows:
Due to the magnetic dipole, the assumed liquid flow is affected by the magnetic field, whose magnetic scalar potential is given by (Everts et al., 2020; Reddy et al., 2022)
where
From Eq. 9, one can get
We assume that the applied field
where
On employing the above, Eqs 1, 4 are satisfied identically, and Eqs 2, 3, 5, 6 reduce as
Fluid phase:
Dust phase:
Reduced boundary conditions:
The skin friction coefficient and Nusselt number are defined as
The transformed form of the above one is
The following are the dimensionless parameters that exist in the problem:
Numerical procedure
The reformed system of coupled nonlinear ODEs (Eqs 12–15) in conjunction with boundary conditions (Eq. 16) is worked out for various parameters by employing the tool of MATLAB function bvp4c. It is an efficient method used by several authors to tackle such problems. A fair amount of computations are executed by using the tool mentioned above, so to deal with it, we considered
Fluid phase
Dust phase
Reduced boundary conditions:
Results and discussion
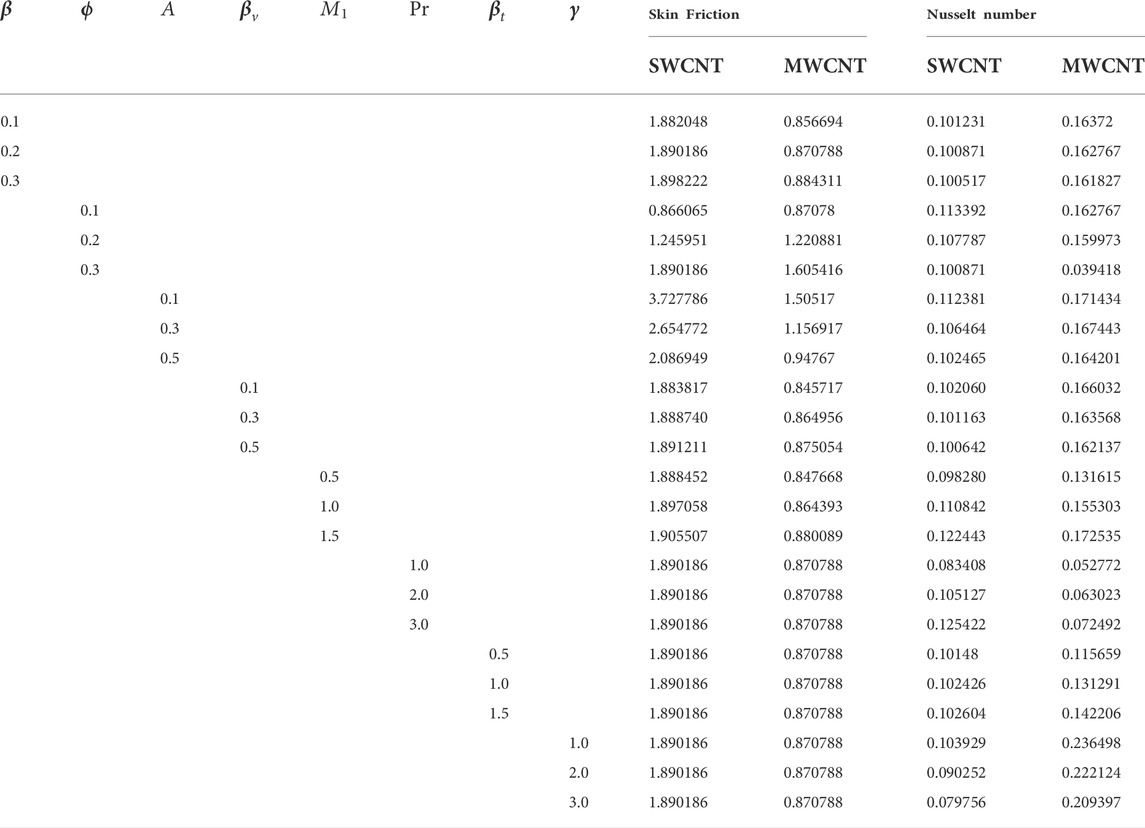
In the present article, the investigation is carried out on the significance of magnetic dipole flow and melting heat transfer over suspended dust particles and carbon nanotubes. Table 2 represents the mathematical form of transport characteristics of the nanofluid. The computation for the various profiles is deliberated via graphs, whereas the rate quantities’ numerical results are displayed in a tabular form (Table 3).
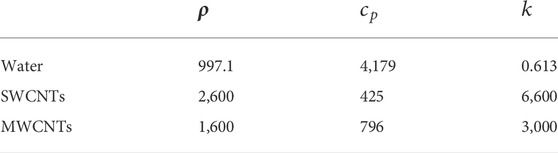
TABLE 2. Thermophysical properties of water and nanotubes (Reddy and Kumar, 2021).
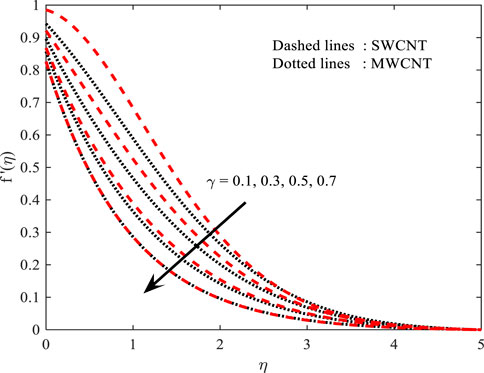
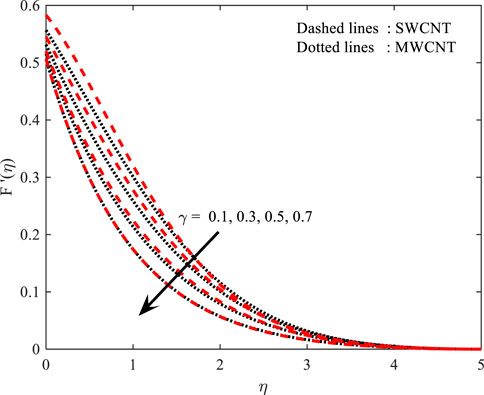
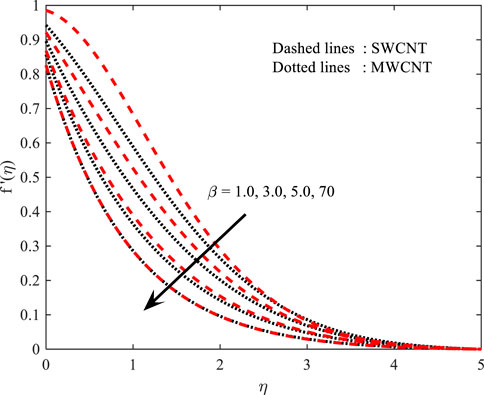
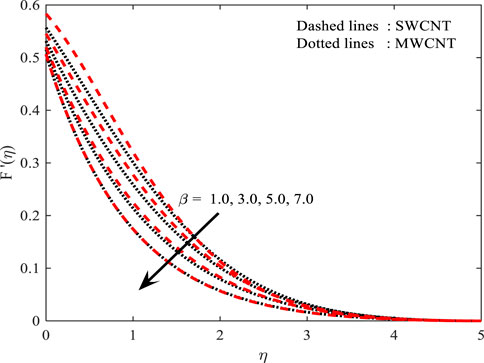
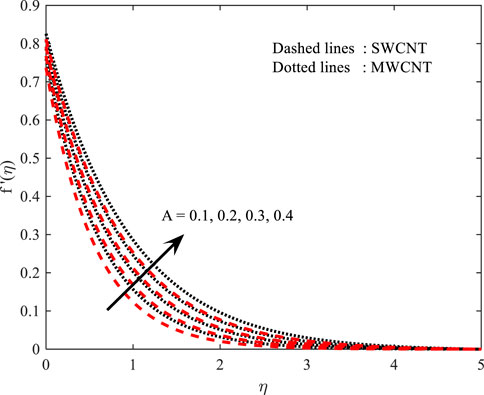
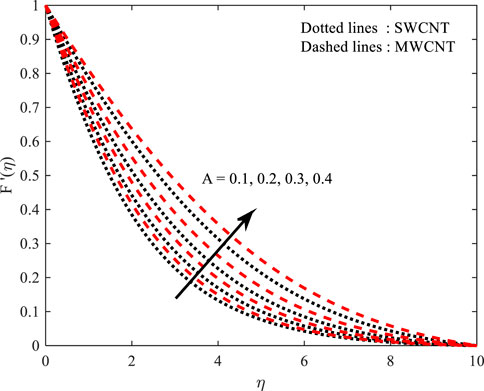
Velocity profile (
The magnetic field strength (
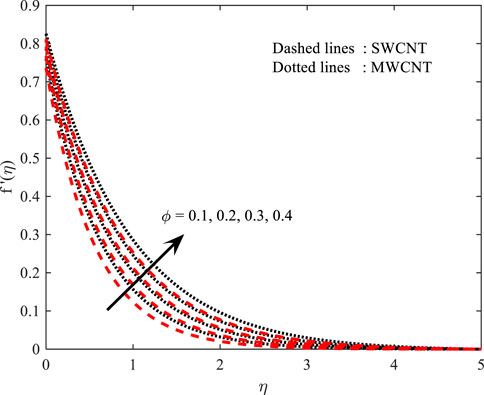
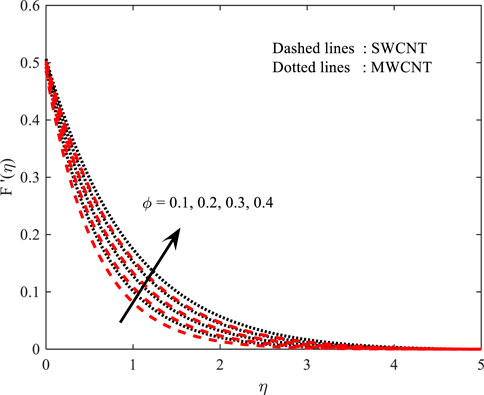
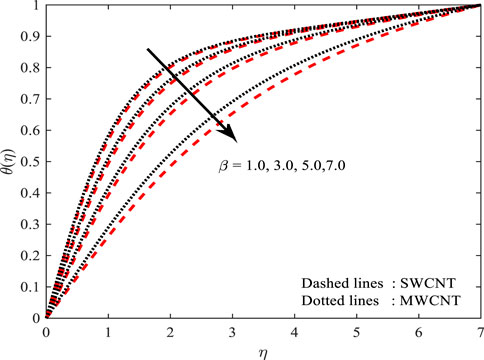
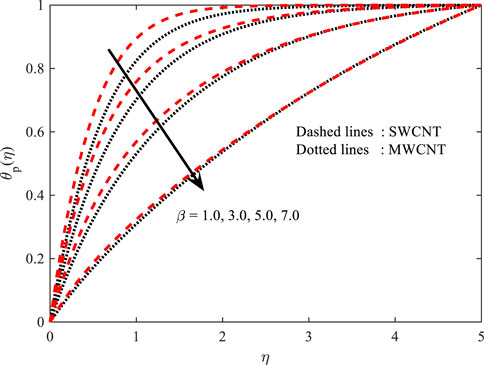
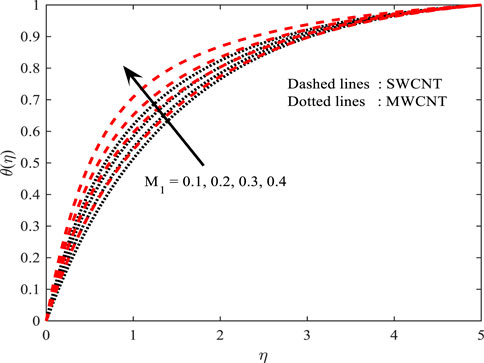
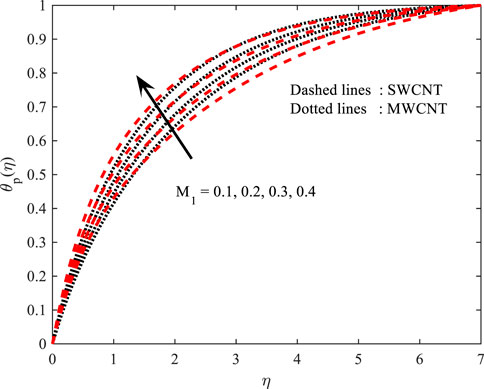
In Figures 4, 5, the behavior of
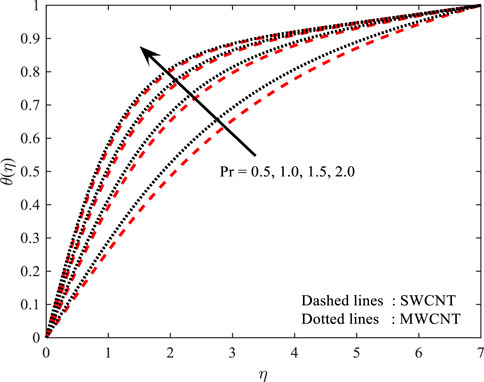
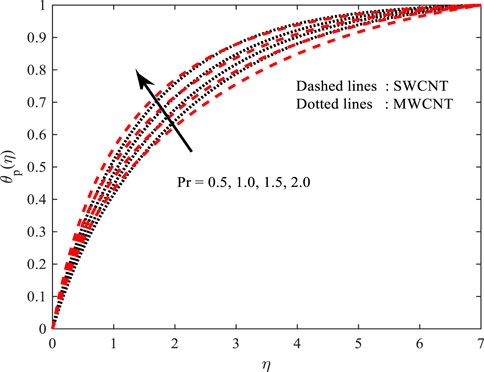
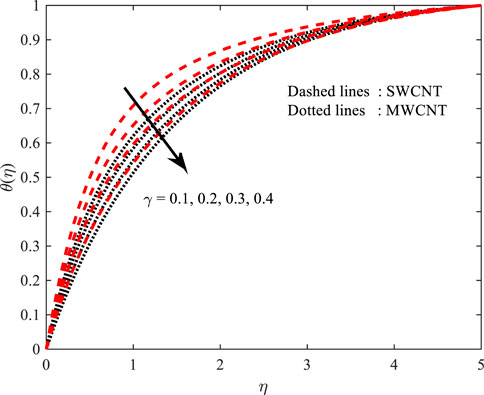
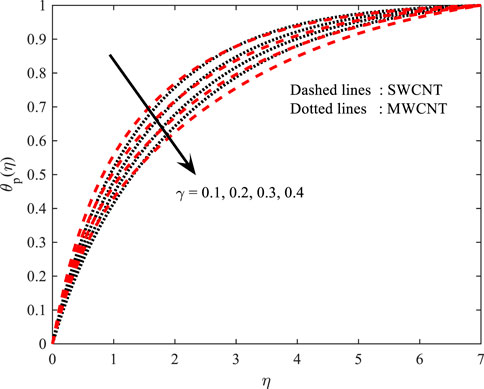
Temperature profile
Figures 10, 11 portray the performance of the Prandtl number on the thermal gradient for both
Numerical outcomes of
Conclusion
This research work inspected the significance of magnetic dipole flow and melting heat transfer over suspended dust particles. The impact of melting is also discussed in the energy equation. Fluid flow and the heat-transfer rate are discussed through a mathematical model of second-order, nonlinear ODEs, which is analyzed numerically. The effectiveness of appropriate parameters is elaborated graphically. The impacts of essential parameters are reported.
• The velocity field declined against the impact of
• The velocity of the fluid increases with higher estimations of
• The fluid temperature decays with a bulkier assessment of
• Because of melting, the thermal field is more for the rising assessment of
• On enlarging the values of parameters
•
• The velocity field is dramatically shortened with higher
• The slip parameter plays a significant role in enhancing the velocity profile.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
HA: conceptualization, methodology, validation, investigation, resources, data curation, writing—original draft, writing—review and editing, visualization, and supervision.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Project No. GRANT639).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
References
Alkanhal, T. A., Sheikholeslami, M., Usman, M., Rizwan, ul Haq, Shafeeg, Ahmad, Abdullah, S-A., et al. (2019). Thermal management of MHD nanofluid within the porous medium enclosed in a wavy shaped cavity with square obstacle in the presence of radiation heat source. Int. J. Heat Mass Transf. 139, 87. doi:10.1016/j.ijheatmasstransfer.2019.05.006
Bilal, M., Sagheer, M., and Hussain, S. (2018). Numerical study of magnetohydrodynamics and thermal radiation on Williamson nanofluid flow over a stretching cylinder with variable thermal conductivity. Alexandria Eng. J. 57, 3281–3289. doi:10.1016/j.aej.2017.12.006
Chen, C. K., Chen, B. S., and Liu, C. C. (2015). Entropy generation in mixed convection magnetohydrodynamic nanofluid flow in vertical channel. Int. J. Heat Mass Transf. 91, 1026–1033. doi:10.1016/j.ijheatmasstransfer.2015.08.042
Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows, 231. New York: ASME, 99–105.
Choi, S. U. S., Zhang, Z. G., Yu, W., Lockwood, F. E., and Grulke, E. A. (2001). Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 79, 2252–2254. doi:10.1063/1.1408272
Dogonchi, A. S., and Ganji, D. D. (2016). Investigation of MHD nanofluid flow and heat transfer in a stretching/shrinking convergent/divergent channel considering thermal radiation. J. Mol. Liq. 220, 592–603. doi:10.1016/j.molliq.2016.05.022
Everts, M., Bhattacharyya, S., Bashir, A. I., and Meyer, J. P. (2020). Heat transfer characteristics of assisting and opposing laminar flow through a vertical circular tube at low Reynolds numbers. Appl. Therm. Eng. 179, 115696. doi:10.1016/j.applthermaleng.2020.115696
Fakour, M., Vahabzadeh, A., and Ganji, D. D. (2015). Study of heat transfer and flow of nanofluid in permeable channel in the presence of magnetic field. Propuls. Power Res. 4, 50–62. doi:10.1016/j.jppr.2015.02.005
Hashemi, H., Namazian, Z., Zadeh, S. M. H., and Mehryan, S. A. M. (2018). MHD natural convection of a micropolar nanofluid flowing inside a radiative porous medium under LTNE condition with an elliptical heat source. J. Mol. Liq. 271, 914–925. doi:10.1016/j.molliq.2018.09.010
Hayat, T., Aslam, N., Khan, M. I., Khan, M. I., and Alsaedi, A. (2019). Physical significance of heat generation/absorption and Soret effects on peristalsis flow of pseudoplastic fluid in an inclined channel. J. Mol. Liq. 275, 599–615. doi:10.1016/j.molliq.2018.11.055
Hayat, T., Khan, M. I., Farooq, M., Yasmeen, T., and Alsaedi, A. (2016). Water-carbon nanofluid flow with variable heat flux by a thin needle. J. Mol. Liq. 224, 786–791. doi:10.1016/j.molliq.2016.10.069
Hayat, T., Muhammad, T., Shehzad, S. A., and Alsaedi, A. (2017). An analytical solution for magnetohydrodynamic Oldroyd-B nanofluid flow induced by a stretching sheet with heat generation/absorption. Int. J. Therm. Sci. 111, 274–288. doi:10.1016/j.ijthermalsci.2016.08.009
Hayat, T., and Nadeem, S. (2017). Heat transfer enhancement with AgCuO/water hybrid nanofluid. Results Phys. 7, 2317–2324. doi:10.1016/j.rinp.2017.06.034
Hayat, T., Rashid, M., Khan, M. I., and Alsaedi, A. (2018). Melting heat transfer and induced magnetic field effects on flow of water based nanofluid over a rotating disk with variable thickness. Results Phys. 9, 1618–1630. doi:10.1016/j.rinp.2018.04.054
Hayat, T., Sajjad, R., Ellahi, R., Alsaedi, A., and Muhammad, T. (2017). Homogeneous-heterogeneous reactions in MHD flow of micropolar fluid by a curved stretching surface. J. Mol. Liq. 240, 209–220. doi:10.1016/j.molliq.2017.05.054
Hayat, T., Shehzad, S. A., and Qasim, M. (2013). Slip effects on the unsteady stagnation point flow with variable free stream. Walaialk J. 10, 385–394.
Kumar, K. G., Gireesha, B. J., Rudraswamy, N. G., and Krishnamurthy, M. R. (2019). An unsteady flow and melting heat transfer of a nanofluid over a stretching sheet embedded in a porous mediumAn Unsteady Flow and Melting Heat Transfer of a Nanofluid over a Stretching Sheet Embedded in a Porous Medium. Int. J. Appl. Mech. Eng. 24 (2), 245–258. doi:10.2478/ijame-2019-0016
Mahanthesh, B., Gireesha, B. J., and Gorla, R. S. R. (2017). Unsteady three-dimensional MHD flow of a nano Eyring-Powell fluid past a convectively heated stretching sheet in the presence of thermal radiation, viscous dissipation and Joule heating. J. Assoc. Arab Univ. Basic Appl. Sci. 23, 75–84. –84. doi:10.1016/j.jaubas.2016.05.004
Mukhopadhyay, S. (2013). MHD boundary layer slip flow along a stretching cylinder. Ain Shams Eng. J. 4, 317–324. doi:10.1016/j.asej.2012.07.003
Pourmehran, O., Gorji, M. R., and Ganji, D. D. (2016). Heat transfer and flow analysis of nanofluid flow induced by a stretching sheet in the presence of an external magnetic field. J. Taiwan Inst. Chem. Eng. 65, 162–171. doi:10.1016/j.jtice.2016.04.035
Qayyum, S., Hayat, T., and Alsaedi, A. (2017). Chemical reaction and heat generation/absorption aspects in MHD nonlinear convective flow of third grade nanofluid over a nonlinear stretching sheet with variable thickness. Results Phys. 7, 2752–2761. doi:10.1016/j.rinp.2017.07.043
Ramesh, G., Gireesha, B., Bagewadi, C., Ramesh, G. K., Gireesha, B. J., and Bagewadi, C. S. (2012). MHD flow of a dusty fluid near the stagnation point over a permeable stretching sheet with non-uniform source/sink. Int. J. Heat Mass Transf. 55 (17–18), 4900–4907. doi:10.1016/j.ijheatmasstransfer.2012.05.003
Reddy, G. J., Kethireddy, B., Kumar, M., and Hoque, M. M. (2018). A molecular dynamics study on transient non-Newtonian MHD Casson fluid flow dispersion over a radiative vertical cylinder with entropy heat generation. Journal of Molecular Liquids 252, 245–262. doi:10.1016/j.molliq.2017.12.077
Reddy, M. G., Sudharani, M., Praveena, M. M., and Kumar, K. G. (2022). Effect of thermal conductivity on Blasius–Rayleigh–Stokes flow and heat transfer over a moving plate by considering magnetic dipole moment. Eur. Phys. J. Plus 137 (1), 1–13. doi:10.1140/epjp/s13360-021-02259-1
Reddy, M. G., and Kumar, K. G. (2021). Cattaneo-christov heat flux feature on carbon nanotubes filled with micropolar liquid over a melting surface: A stream line studyCattaneo-christov heat flux feature on carbon nanotubes filled with micropolar liquid over a melting surface: A stream line study. Int. Commun. Heat Mass Transf. 122, 105142. doi:10.1016/j.icheatmasstransfer.2021.105142
Rizwan, U. H., Raza, A., Ebrahem, A. A., and Iskander, T. (2020). Heat transfer analysis of water based SWCNTs through parallel fins enclosed by square cavity. Int. Commun. Heat Mass Transf. 119, 104797. doi:10.1016/j.icheatmasstransfer.2020.104797
Rizwan Ul Haq, S., Naveed, K., and Toufik, M. (2017). Thermal management of water-based SWCNTs enclosed in a partially heated trapezoidal cavity via FEM. Int. J. Heat Mass Transf. 112, 972. doi:10.1016/j.ijheatmasstransfer.2017.05.041
Sheikholeslami, M. (2017). Lattice Boltzmann method simulation for MHD non-Darcy nanofluid free convection. Phys. B Condens. Matter 516, 55–71. doi:10.1016/j.physb.2017.04.029
Sheikholeslami, M., Shehzad, S. A., and Li, Z. (2018). Nanofluid heat transfer intensification in a permeable channel due to magnetic field using Lattice Boltzmann method. Phys. B Condens. Matter 542, 51–58. doi:10.1016/j.physb.2018.03.036
Shen, M., Wang, F., and Chen, H. (2015). MHD mixed convection slip flow near a stagnation-point on a nonlinearly vertical stretching sheet. Bound. Value Probl. 78, 2015. doi:10.1186/s13661-015-0340-6
Ul Haq, R., Rashid, I., Khan, Z., Rashid, I., and Khan, Z. H. (2017). Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J. Mol. Liq. 243, 682–688. doi:10.1016/j.molliq.2017.08.084
Ul Haq, R., Raza, A., Algehynec, E. A., and Iskander, T. (2020). Dual nature study of convective heat transfer of nanofluid flow over a shrinking surface in a porous medium. Int. Commun. Heat Mass Transf. 114, 104583. doi:10.1016/j.icheatmasstransfer.2020.104583
Ul Haq, R., Soomro, F. A., Hammouch, Z., and Ur Rehman, S. (2018). Heat exchange within the partially heated C-shape cavity filled with the water based SWCNTs. Int. J. Heat Mass Transf. 127, 506–514. doi:10.1016/j.ijheatmasstransfer.2018.07.101
Zhao, G., Wang, Z., and Jian, Y. (2019). Heat transfer of the MHD nanofluid in porous microtubes under the electrokinetic effects. Int. J. Heat Mass Transf. 130, 821–830. doi:10.1016/j.ijheatmasstransfer.2018.11.007
Nomenclature
MWCNT multiwall carbon nanotube
SWCNT single-wall carbon nanotube
Keywords: melting surface, magnetic dipole, carbon nanotubes, slip flow, numerical analysis
Citation: Alfannakh H (2022) Significances of magnetic dipole flow and melting heat transfer over suspended dust particles along with carbon nanotubes. Front. Energy Res. 10:935108. doi: 10.3389/fenrg.2022.935108
Received: 03 May 2022; Accepted: 11 July 2022;
Published: 09 August 2022.
Edited by:
Iskander Tlili, TunisiaCopyright © 2022 Alfannakh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huda Alfannakh, aGFsZmFubmFraEBrZnUuZWR1LnNh
 Huda Alfannakh
Huda Alfannakh