Model Predictive Control–Based Load-Frequency Regulation of Grid-Forming Inverter–Based Power Systems

The high-penetrated renewables enable flexible and versatile dispatchable resources in power systems. As the digitalization process improves with the help of information and communication technology (ICT), a real-time online control framework is essential to regulate such a low-inertia power system dominated by renewables. To enable control practices, a control-oriented model is developed linking load increments to frequency dynamics. Based on such a control-oriented model, a model predictive control (MPC)–based online feedback algorithm is well designed by the virtue of rapid data transmission enabled by digitalization. The MPC optimization is a convex quadratic programming, where an objective function that balances frequency deviations and load increments is formulated and operational constraints are integrated into a matrix-type inequality. In the end, the proposed MPC-based load-frequency control framework is illustrated by several case studies, where validations and analyses of constraints inside the model are also included.

Introduction

Driven by the global climate change, renewables such as solar and wind are increasingly developed and connected to the current power system (Creutzig et al., 2014; Ge et al., 2022) using a concept of grid-forming (GFM) converter. Such renewables bring more dispatchable resources but also challenge the existing power system control framework due to the fact that most renewables have limited inertia support to the power system operation (Milano et al., 2018; Ratnam et al., 2020). To regulate such a low-inertia power system effectively and efficiently, a digitalization process has been conducted supported by information and communication technology (ICT) to enable rapid regulations in response to fast dynamics induced by low inertia (Ratnam et al., 2020; Di Silvestre et al., 2018). Such digitalization allows for high amounts of data, fast data transmission, and high-efficiency computation to further achieve a fully intelligent feedback control scheme in future power systems (Di Silvestre et al., 2018; Wu et al., 2021).

By the virtue of such a digitalization process, various control algorithms (Obaid et al., 2019; Fernández-Guillamón et al., 2019) have been investigated to maintain frequency stability (a priority in power system control). For example, Lyapunov-based stability analysis methods (Jin et al., 2019; Luo et al., 2020; Shang-Guan et al., 2020) are developed to guarantee frequency stability; the H₂/H_∞ controller (Zou et al., 2021) is designed to optimize the frequency dynamics performance; and a fuzzy event-triggered scheme (Shangguan et al., 2021) is employed to improve frequency control stability with limited communication expense. Moreover, different kinds of control properties can be satisfied in frequency control, that is, asymptotic (Guerrero et al., 2010; Xu et al., 2018; Singhal et al., 2022), finite-time (Zuo et al., 2016; Ge et al., 2020), and fixed-time (Ni et al., 2016), if we can model the system dynamics appropriately. However, many of these methods require full or partial models available at dispatchable points, which may not be feasible under the case where the load-frequency dynamics are aggregated by massive and small-capacity dispatchable loads such as residential PVs and electric vehicles.

On the other hand, owing to the fast response of feedback control methods (Zou et al., 2021; Shangguan et al., 2021; Zuo et al., 2016), control input saturations are considered in the actuation, which would not lead to optimized input sequences. Hence, practical operation constraints, for example, frequency nadir and RoCoF (rate of change of frequency), are essential to be considered in frequency regulation. If we cannot appropriately consider such constraints, the optimal operation would be degraded, or the system would face security issues. Such constraints have also been considered in the existing research work (Markovic et al., 2018; Stanojev et al., 2020). However, constrained load-frequency control regulation has not been fully investigated in terms of comprehensive constraints.

Therefore, to move forward even one step to cope with the aforementioned challenges, a real-time online control framework is proposed to regulate such a low-inertia power system frequency utilizing dispatchable load resources. The main contributions can be concluded as follows. To narrow down the gap between power-electronic dynamics and power flow models, we model the whole system dynamics by combining power-electronic–dominated dynamics and steady-state power flow–based Jacobian matrix. More specifically, GFM-inverter–based generator dynamics is unified in either a droop type or a VSG type. Based on such a control-oriented model concerning load increment and frequency dynamics, to fully consider the operational rules in practice, inspired by Stanojev et al. (2020) and Ge et al. (2021), we design a model predictive control (MPC)–based online feedback algorithm utilizing rapid sensing, computation, and actuation enabled by the power system digitalization trend. The constraints of frequency deviations, RoCoF, dispatchable load capacity, and load change ramping rate are integrated into a matrix-type inequality, which can be easily optimized subjected to an objective function that balances frequency deviations and load increments.

The rest of this article is organized as follows. Section 2 gives the model of GFM-inverter–involved power systems. In Section 3, an MPC-based control design is provided. Section 4 demonstrates the control performance, and Section 5 concludes this article.

Modeling for GFM-Based System

In this section, we will present the detailed modeling of an inverter-based power system. First, we start from a unified model of GFM inverters, where droop-based control and virtual synchronized generator–based control are included. Then, a control-oriented model of the whole system that considers the line impedance effect is proposed, which will bring the benefits in the grid-level control and operation.

System Description

A GFM inverter normally consists of three control loops, that is, power control loop, voltage control loop, and current control loop, as depicted in Figure 1. The power controller provides the reference for the voltage controller and the reference angular frequency for the whole inverter control system, while the voltage controller and current controller guarantee the non-steady-error–tracking performance of output voltage. Two mainstream power control loops of GFM inverters are VSG-based control and droop-based control, the dynamics of which can be, respectively, expressed as

$\begin{array}{c}\text{VSG: }M\dot{\omega }=-D\left(\omega -{\omega }_{ref}\right)+\frac{P_{ref}-P_G}{{\omega }_n},\\ \text{Droop: }\omega ={\omega }_{ref}+m_P\frac{{\omega }_c}{{\omega }_c+s}\left(P_{ref}-P_G\right),\end{array}(1)$

where $\omega ,{\omega }_{ref},and{\omega }_n$ denote the real-time value, set point, and nominal value of the inverter’s angular frequency, respectively, and $P_{ref},P_G$ are the set point and real-time measurement of the inverter’s active power output. For the VSG-based model, $M,D$ are inertia and damping coefficients, while for the droop-based model, $m_P,{\omega }_c$ represent the f/p droop coefficient and cut-off frequency of active power measurement. It should be noted that such two dominated GFM models are equivalent by $M={\left({\omega }_c{m}_P\right)}^{-1},D={\left(m_P\right)}^{-1}$ (Markovic et al., 2021). Therefore, we use the VSG model (1) hereafter for further discussion.

FIGURE 1

FIGURE 1. Diagram of a GFM inverter.

A unified small-signal model that describes one inverter’s frequency dynamics can be expressed by

$\left[\begin{array}{c}\mathrm{\Delta }\dot{\delta }\\ \mathrm{\Delta }\dot{\omega }\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& -\frac{D}{M}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }\delta \\ \mathrm{\Delta }\omega \end{array}\right]+\left[\begin{array}{c}0\\ -\frac{1}{M{\omega }_n}\end{array}\right]\mathrm{\Delta }{P}_G(2)$

2.2 Control-Oriented Model of a Multi-GFM-Inverter–Penetrated Power System

Eq. 2 builds a relationship between the generator’s power output and system frequency dynamics, and it can be expanded to a multi-GFM system with appropriate stacking. However, in current power systems, massive load resources can also provide huge capability participating in frequency response. Compared to inverter-based generators, loads are owned by local aggregators who can use flexible loads to offer frequency regulation capability. Hence, it is of great importance to directly link the load change to the system’s frequency dynamics, further guiding the participation of load aggregators. The challenge is that the dynamics from flexible and massive loads are difficult to depict because aggregated and equivalent inertia and damping are not available directly. Hence, we hereafter build a control-oriented model, which utilizes the inverter’s dynamics and network topology, describing load-frequency dynamics.

For the sake of modeling multi-inverter systems, we generalize the model (2) with the subscript $i$ for the inverter-based DG i, that is,

${\dot{x}}_i=\left[\begin{array}{c}\mathrm{\Delta }{\dot{\delta }}_i\\ \mathrm{\Delta }{\dot{\omega }}_i\end{array}\right]={\mathit{A}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{B}}_{\mathit{i}}{\mathit{u}}_{\mathit{i}}=\left[\begin{array}{cc}0& 1\\ 0& -\frac{D_i}{M_i}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\delta }_i\\ \mathrm{\Delta }{\omega }_i\end{array}\right]+\left[\begin{array}{c}0\\ -\frac{1}{M_i{\omega }_n}\end{array}\right]\mathrm{\Delta }{P}_{Gi}(3)$

For a multi-inverter system, the dynamics can be easily extended. Define a power system with m inverters:

$\dot{\mathit{x}}={\mathit{A}}_{\mathbf{0}}\mathit{x}+{\mathit{B}}_{\mathbf{0}}{\mathit{u}}_{\mathbf{0}}(4)$

with $\begin{array}{l}\mathit{x}={\left[{\mathit{x}}_1^T,{\mathit{x}}_2^T,\dots ,{\mathit{x}}_m^T\right]}^T,{\mathit{u}}_0={\left[{\mathit{u}}_1^T,{\mathit{u}}_2^T,\dots ,{\mathit{u}}_m^T\right]}^T,\\ {\mathit{A}}_0=diag\left(\left[{\mathit{A}}_1,{\mathit{A}}_2,\dots ,{\mathit{A}}_m\right]\right),{\mathit{B}}_0=diag\left(\left[{\mathit{B}}_1,{\mathit{B}}_2,\dots ,{\mathit{B}}_m\right]\right).\end{array}$

The model (4) is developed from a generator perspective. However, a power grid also includes lines and loads. To involve such line impedance and load demand, we recall the power flow equation that has been widely investigated (Shen et al., 2020; Zimmerman et al., 2010), that is, $\mathrm{\Delta }\mathit{P}=\mathit{J}\mathrm{\Delta }\mathit{\delta }$, where $\mathrm{\Delta }\mathit{P}\in {ℝ}^n,\mathrm{\Delta }\mathit{\delta }\in {ℝ}^n$ denote the incremental values of active power and node phase and $J\in {ℝ}^{n\times n}$ denotes the Jacobian matrix of power flow calculation.

To form a control-oriented model of the whole power system, we split the power flow equation into generator nodes and load nodes, that is,

$\left[\begin{array}{c}\mathrm{\Delta }{\mathit{P}}_G\\ \mathrm{\Delta }{\mathit{P}}_L\end{array}\right]=\left[\begin{array}{cc}{\mathit{J}}_{GG}& {\mathit{J}}_{GL}\\ {\mathit{J}}_{LG}& {\mathit{J}}_{LL}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{\delta }}_G\\ \mathrm{\Delta }{\mathit{\delta }}_L\end{array}\right](5)$

where the subscript G means the generator node, while the subscript L means the load node. From the second row of (5), we can obtain $\mathrm{\Delta }{\mathit{\delta }}_L={\mathit{J}}_{LL}^{-1}(\mathrm{\Delta }{\mathit{P}}_L-{\mathit{J}}_{LG}\mathrm{\Delta }{\mathit{\delta }}_G)$, which can be substituted into the first row to obtain $\mathrm{\Delta }{\mathit{P}}_G=({\mathit{J}}_{GG}-{\mathit{J}}_{GL}{\mathit{J}}_{LL}^{-1}{\mathit{J}}_{LG})\mathrm{\Delta }{\mathit{\delta }}_G+{\mathit{J}}_{GL}{\mathit{J}}_{LL}^{-1}\mathrm{\Delta }{\mathit{P}}_L$. Then, the whole power system with multi-inverter penetration is formed as

$\dot{\mathit{x}}=\mathit{A}\mathit{x}+\mathit{B}\mathit{u}(6)$

where $\mathit{A}={\mathit{A}}_0+\left({\mathit{B}}_0\left({\mathit{J}}_{GG}-{\mathit{J}}_{GL}{\mathit{J}}_{LL}^{-1}{\mathit{J}}_{LG}\right)\right)\otimes \left[\begin{array}{cc}1& 0\end{array}\right],\mathit{B}={\mathit{B}}_0{\mathit{J}}_{GL}{\mathit{J}}_{LL}^{-1}$, and $\mathit{u}=\mathrm{\Delta }{\mathit{P}}_L\in {ℝ}^{n_u}$ ($\otimes$ is the Kronecker product). The model (6) describes the system frequency dynamics by linking the load increment to the generator’s output frequency dynamics. This is meaningful in the demand frequency response scenario considering grid-following inverter–based renewable integrations and dispatchable loads. Thus, such model is a control-oriented model, by which the control applications will be discussed in Section 3.

3 Modeling Application: Model Predictive Control Design

In this section, based on the previous model, we proposed a secondary frequency control method based on the MPC algorithm.

Currently, the digitalization in the power system leads to a digital control mode; hence, we need to form the system in a discrete-time way that is more practical in the real world. Based on the continuous model (6), the discrete-time state-space model using the sampling time $\mathrm{\Delta }T$ can be expressed as:

$\begin{array}{l}\mathit{x}\left(k+1\right)=\mathit{G}\mathit{x}\left(k\right)+\mathit{H}\mathit{u}\left(k\right),\\ \mathit{y}\left(k\right)=\mathit{C}\mathit{x}\left(k\right),\end{array}(7)$

where $\mathit{G}=e^{A\mathrm{\Delta }T},\mathit{H}={\displaystyle {\int }_0^{\mathrm{\Delta }T}{e}^{A\tau }\mathit{B}d\tau ,\mathit{C}={\mathit{I}}_m\otimes \mathrm{diag}\left(\left[\begin{array}{cc}0& 1\end{array}\right]\right)}$, where ${\mathit{I}}_m$ denotes the mth identity matrix. $y\left(k\right)$ is the output (i.e., the angular frequency deviations) that is concerned in load-frequency control.

MPC is an optimal control that can fully consider state, output, and input constraints. Such constraints are useful in frequency control because the load increment and output frequency have intrinsic limits. The first thing to form predictive control is to form a model-based prediction system based on (7), that is,

$\begin{array}{l}{\mathit{y}}_k=\mathit{F}\mathit{x}\left(k\right)+\mathit{L}{\mathit{u}}_k,\\ \mathit{F}=\left[\begin{array}{c}\mathit{C}\\ \mathit{C}\mathit{G}\\ \mathit{C}{\mathit{G}}^2\\ \mathit{M}\\ \mathit{C}{\mathit{G}}^N\end{array}\right],L=\left[\begin{array}{cccc}0& 0& L& 0\\ \mathit{C}\mathit{H}& & & \\ \mathit{C}\mathit{G}\mathit{H}& \mathit{C}\mathit{H}& & \\ \mathit{M}& \mathit{M}& \mathit{O}& \\ \mathit{C}{\mathit{G}}^{N-1}\mathit{H}& \mathit{C}{\mathit{G}}^{N-2}\mathit{H}& \mathit{L}& \mathit{C}\mathit{H}\end{array}\right],\end{array}(8)$

where N denotes the prediction horizon and “$\left(k\right)$” denotes the discrete model at the time instant k, while the subscript k is utilized in the prediction model. Due to the small-signal property of the proposed model (6) and (7), $y_k$ is the deviation variable induced by the input; thus, we have angular frequency predicted errors by ${\tilde{y}}_k=\left(1_{N+1,N+1}^{\nabla }\otimes I_m\right)y_k+\left(1_{N+1}\otimes I_m\right)\mathrm{\Delta }\omega$, where $1_{N+1,N+1}^{\nabla },1_{N+1}$ are, respectively, the lower triangular matrix and vector with all elements being one and $\mathrm{\Delta }\omega =\omega -{\omega }_{ref}$ is the real-time angular frequency error vector between measurements of m generators and reference. Owing to the fact that $x\left(k\right)$ and $\mathrm{\Delta }\omega$ are both seen as measured variables from the system, we can integrate them to a combined form by defining $T_1=1_{N+1,N+1}^{\nabla }\otimes I_m,T_2=1_{N+1}\otimes I_m$,

${\tilde{\mathit{y}}}_{\mathit{k}}={\mathit{T}}_1\left(\mathit{F}\mathit{x}\left(\mathit{k}\right)+\mathit{L}{\mathit{u}}_k\right)+{\mathit{T}}_2\mathrm{\Delta }\mathit{\omega }=\left[\begin{array}{cc}{\mathit{T}}_1\mathit{F}& {\mathit{T}}_2\end{array}\right]\left[\begin{array}{c}\mathit{x}\left(k\right)\\ \mathrm{\Delta }\mathit{\omega }\end{array}\right]+{\mathit{T}}_1\mathit{L}{\mathit{u}}_{\mathit{k}}={\mathit{T}}_{\mathit{x}}{\mathit{x}}_{in}+{\mathit{T}}_{\mathit{u}}{\mathit{u}}_{\mathit{k}}(9)$

with ${\mathit{T}}_{\mathit{x}}=\left[\begin{array}{cc}{\mathit{T}}_1\mathit{F}& {\mathit{T}}_2\end{array}\right],{\mathit{x}}_{in}=\left[\begin{array}{c}\mathit{x}\left(k\right)\\ \mathrm{\Delta }\mathit{\omega }\end{array}\right],{\mathit{T}}_u={\mathit{T}}_1\mathit{L}$.

Then, we can use the prediction model (8) to form the objective as follows:

$\mathit{S}={\tilde{y}}_k^T\tilde{\mathit{Q}}{\tilde{\mathit{y}}}_k+{\mathit{u}}_k^T\tilde{\mathit{R}}{\mathit{u}}_k(10)$

with $\tilde{Q}=diag\left(\left[\begin{array}{ccc}Q& \cdots & Q\end{array}\right]\right),\tilde{R}=diag\left(\left[\begin{array}{ccc}R& \cdots & R\end{array}\right]\right)$ being the weight matrices. The synchronization of the frequency represents the main target addressed in this article. For this reason, the weighting factors Q, R are selected to emphasize the former term. The objective function is to utilize the minimal control input to minimize the frequency deviations. Substituting (8) into (10), after some algebra collection in terms of $u_k$ and $x\left(k\right)$, the objective function can be formed in a standard way as

$\begin{array}{l}\mathit{S}={\mathit{u}}_k^T\mathit{U}{u}_k+\mathbf{2}{x}_{in}^T{\mathit{V}}^T{u}_k+{\mathit{x}}_{in}^T\mathit{W}{x}_{in}\\ \mathit{U}={\mathit{T}}_u^T\mathit{Q}{\mathit{T}}_u+\tilde{\mathit{R}},\mathit{V}={\mathit{T}}_u^T\tilde{\mathit{Q}}{\mathit{T}}_x,\mathit{W}={\mathit{T}}_x^T\tilde{\mathit{Q}}\mathit{T}\end{array}(11)$

It should be noted that the matrices $\mathit{U},\mathit{V},\mathit{W}$ can be computed offline, which gives a huge efficiency in optimizing the input vector $u_k$, except that it can be easily known before implementing the MPC optimization algorithm.

Throughout the load-frequency control of demand response, there are four classes of constraints, that is, frequency security limits, RoCoF (rate of change of frequency) limits, dispatchable load capacity limits, and load change ramping limits. For the frequency security limits, we should guarantee the generator frequency inside the valid operation limits, that os, $1_{(N+1)m}\mathrm{\Delta }\underset{¯}{\omega }\le {\tilde{y}}_k\le 1_{(N+1)m}\mathrm{\Delta }\overline{\omega }$, which can be re-expressed by extending ${\tilde{y}}_k$ using (9):

$\left[\begin{array}{c}{\mathit{I}}_{(N+1)m}\\ -{\mathit{I}}_{(N+1)m}\end{array}\right]{\tilde{y}}_k\le \left[\begin{array}{c}{\mathbf{1}}_{(N+1)m}\mathit{\Delta }\overline{\omega }\\ -{\mathbf{1}}_{(N+1)m}\mathit{\Delta }\underset{¯}{\omega }\end{array}\right]\Rightarrow A_{y1}{\mathit{u}}_k\le {\mathit{b}}_{y1}+{\mathit{B}}_{y1}{\mathit{x}}_{in}(12)$

where ${\mathit{A}}_{y1}=\left[\begin{array}{c}{\mathit{I}}_{(N+1)m}\\ -{\mathit{I}}_{(N+1)m}\end{array}\right]{\mathit{T}}_u,{\mathit{b}}_{y1}=\left[\begin{array}{c}{\mathbf{1}}_{(N+1)m}\mathrm{\Delta }\overline{\omega }\\ -{\mathbf{1}}_{(N+1)m}\mathrm{\Delta }\underset{¯}{\omega }\end{array}\right],{\mathit{B}}_{y1}=-\left[\begin{array}{c}{\mathit{I}}_{(N+1)m}\\ -{\mathit{I}}_{(N+1)m}\end{array}\right]{\mathit{T}}_x$, and $\mathrm{\Delta }\overline{\omega },\mathrm{\Delta }\underset{¯}{\omega }$ are upper and lower bounds of frequency deviations. The RoCoF limits can be similarly expressed by $1_{(N+1)m}\mathrm{\Delta }\underset{¯}{\dot{\omega }}\le \frac{y_k}{\mathrm{\Delta }T}\le 1_{(N+1)m}\mathrm{\Delta }\overline{\dot{\omega }}$, which also can be extended using (8):

$\left[\begin{array}{c}{\mathit{I}}_{\left(N+1\right)m}\\ -{\mathit{I}}_{\left(N+1\right)m}\end{array}\right]y_k\le \left[\begin{array}{c}{\mathbf{1}}_{\left(N+1\right)m}\mathrm{\Delta }\overline{\dot{\omega }}\mathrm{\Delta }\mathit{T}\\ -{\mathbf{1}}_{\left(N+1\right)m}\mathrm{\Delta }\underset{¯}{\dot{\omega }}\mathrm{\Delta }\mathit{T}\end{array}\right]\Rightarrow {\mathit{A}}_{y2}{\mathit{u}}_k\le {\mathit{b}}_{y2}+{\mathit{B}}_{y2}{\mathit{x}}_{in}(13)$

where ${\mathit{A}}_{y2}=\left[\begin{array}{c}{\mathit{I}}_{\left(N+1\right)m}\\ -{\mathit{I}}_{\left(N+1\right)m}\end{array}\right]\mathit{L},{\mathit{b}}_{y2}=\left[\begin{array}{c}{\mathbf{1}}_{\left(N+1\right)m}\mathrm{\Delta }\overline{\dot{\omega }}\mathrm{\Delta }\mathit{T}\\ -{\mathbf{1}}_{\left(N+1\right)m}\mathrm{\Delta }\underset{¯}{\dot{\omega }}\mathrm{\Delta }\mathit{T}\end{array}\right],{\mathit{B}}_{y2}=\left[\begin{array}{cc}-\left[\begin{array}{c}{\mathit{I}}_{(N+1)m}\\ -{\mathit{I}}_{(N+1)m}\end{array}\right]\mathit{F}& {\mathbf{0}}_{2\left(N+1\right)m,m}\end{array}\right]$, and $\mathrm{\Delta }\overline{\dot{\omega }},\mathrm{\Delta }\underset{¯}{\dot{\omega }}$ are upper and lower bounds of the RoCoF. Then, we move to the constraints of dispatchable load capacity limits $1_{N{n}_u}\underset{¯}{u}\le \left(1_{N,N}^{\nabla }\otimes I_{n_u}\right)u_k+\left(1_N\otimes I_{n_u}\right)u_{in}\le 1_{N{n}_u}\overline{u}$ with $u_{in}$ being the measured dispatchable load amount, that is,

$\left[\begin{array}{c}{\mathbf{1}}_{N,N}^{\nabla }\otimes {\mathit{I}}_{n_u}\\ -{\mathbf{1}}_{N,N}^{\nabla }\otimes {\mathit{I}}_{n_u}\end{array}\right]u_k\le \left[\begin{array}{c}{\mathbf{1}}_{N{n}_u}\overline{u}-\left({\mathbf{1}}_N\otimes {\mathit{I}}_{n_u}\right){\mathit{u}}_{in}\\ -{\mathbf{1}}_{N{n}_u}\underset{¯}{u}+\left({\mathbf{1}}_N\otimes {\mathit{I}}_{n_u}\right){\mathit{u}}_{in}\end{array}\right]\Rightarrow {\mathit{A}}_{u1}{\mathit{u}}_k\le {\mathit{b}}_{u1}+{\mathit{B}}_{u1}{\mathit{u}}_{in}(14)$

where ${\mathit{A}}_{u1}=\left[\begin{array}{c}{\mathbf{1}}_{N,N}^{\nabla }\otimes {\mathit{I}}_{n_u}\\ -{\mathbf{1}}_{N,N}^{\nabla }\otimes {\mathit{I}}_{n_u}\end{array}\right],{\mathit{b}}_{u1}=\left[\begin{array}{c}{\mathbf{1}}_{N{n}_u}\overline{u}\\ -{\mathbf{1}}_{N{n}_u}\underset{¯}{u}\end{array}\right],{\mathit{B}}_{u1}=\left[\begin{array}{c}-{\mathbf{1}}_N\otimes {\mathit{I}}_{n_u}\\ {\mathbf{1}}_N\otimes {\mathit{I}}_{n_u}\end{array}\right]$, and $\overline{u},\underset{¯}{u}$ are upper and lower bounds of dispatchable loads. For the load change ramping limits, we have $1_{N{n}_u}\mathrm{\Delta }\underset{¯}{u}\le u_k\le 1_{N{n}_u}\mathrm{\Delta }\overline{u}$ with $\mathrm{\Delta }\overline{u},\mathrm{\Delta }\underset{¯}{u}$ being upper and lower load change ramping bounds, that is,

$\left[\begin{array}{c}{\mathit{I}}_{N{n}_u}\\ -{\mathit{I}}_{N{n}_u}\end{array}\right]{\mathit{u}}_k\le \left[\begin{array}{c}{\mathbf{1}}_{N{n}_u}\mathrm{\Delta }\overline{u}\\ -{\mathbf{1}}_{N{n}_u}\mathrm{\Delta }\underset{¯}{u}\end{array}\right]\Rightarrow {\mathit{A}}_{\mathit{u}2}{\mathit{u}}_k\le {\mathit{b}}_{u2}(15)$

As a result, combining all objective function and constraints from (10) to (15), we can obtain the MPC optimization problem in a compact matrix form:

$\begin{array}{l}\underset{u_k}{\min }{\mathit{u}}_k^T\mathit{U}{\mathit{u}}_k+\mathbf{2}{\mathit{x}}_{in}^T{\mathit{V}}^T{\mathit{u}}_k\\ \mathrm{s.t.}{\mathit{A}}_c{\mathit{u}}_k\le {\mathit{b}}_c+{\mathit{B}}_c{\mathit{x}}_c,\end{array}(16)$

where ${\mathit{A}}_c=\left[\begin{array}{c}{\mathit{A}}_{y1}\\ {\mathit{A}}_{y2}\\ {\mathit{A}}_{u1}\\ {\mathit{A}}_{u2}\end{array}\right],b_c=\left[\begin{array}{c}{\mathit{b}}_{y1}\\ {\mathit{b}}_{y2}\\ {\mathit{b}}_{u1}\\ {\mathit{b}}_{u2}\end{array}\right],B_c=\left[\begin{array}{cc}{\mathit{B}}_{y1}& \mathbf{0}\\ {\mathit{B}}_{y2}& \mathbf{0}\\ \mathbf{0}& {\mathit{B}}_{u1}\\ \mathbf{0}& \mathbf{0}\end{array}\right],{\mathit{x}}_c=\left[\begin{array}{c}{\mathit{x}}_{in}\\ {\mathit{u}}_{in}\end{array}\right].$

It should be noted that the objective function is simplified from (11) by reducing the constant term $x_{in}^{T}W{x}_{in}$ that does not affect the optimization solving results. After optimizing the system operation using (16), only the first sequence of the input vector $u_k$ as a command is sent to each GFM controller. In addition to that, only $x_c$ (i.e., real-time measurement of angular frequency variables and dispatchable load variables) is required from each GFM; hence, the proposed MPC-based frequency control does not impose more communication burden. On the other hand, due to the prediction horizon N, the optimization dimension becomes higher. However, thanks to the quadratic objective function and the convex constraints, the problem can be easily solved by many current well-developed optimization tools (e.g., Gurobi, Cplex, and Mosek), either commercial or academic. Based on such convex optimization and commercialized optimization solver, it is not difficult to handle the frequency problem of power system networks. The proposed MPC problem can be further converted into an explicit form, where the solving only requires direct numerical calculations (see Tøndel et al. (2003) for more details). In the optimization (16), frequency security limits and RoCoF limits can be obtained from the system operation rules in a case-by-case way, while dispatchable load capacity limits and load change ramping limits are determined by the load characteristics.

The proposed MPC-based secondary frequency control has two main advantages compared to conventional methods such as PI controllers. More specifically, the PI controller is a non-constrained control method, while the proposed MPC method can handle frequency constraints, which will be investigated comprehensively in. On the other side, the MPC method can even give sequential control commands in the presence of random packet loss due to its prediction horizon mechanism, although the tolerant packet loss length is limited by the prediction horizon. The fault tolerance capability is obvious because the system operator can use the sequential control commands of $u_k$ once the communication failure occurs.

Due to the modeling of the whole power system based on the small-signal model (6), we need to update the Jacobian matrix $J$ periodically. Thanks to the operator who optimizes the power flow in a periodic way (e.g., every 15 min or every 5 min), we can obtain the latest Jacobian matrix that improves the accuracy of the proposed control-oriented model. In summary, the whole control procedure is given in Table 1.

TABLE 1

TABLE 1. Implementation of the proposed MPC frequency regulation algorithm.

provides a solution to regulate system frequency dynamics using dispatchable loads. However, the MPC algorithm itself would not be feasible if system constraints such as the load change ramping rate and load change capability have strict limits. To handle this problem, we should evaluate and then relax the constraints firstly. Then, if the constraints cannot make the MPC optimization feasible, we should combine the generator’s capability and load-shedding operation to guarantee frequency stability. This topic is out of this article’s scope and will be considered in our future work.

Simulation Results

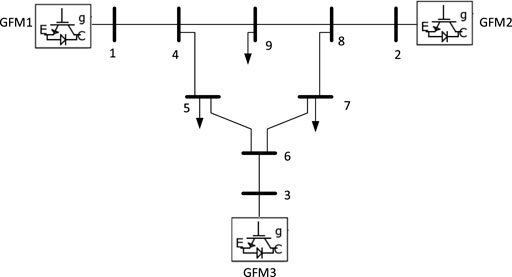
In this section, we will establish a modified IEEE 9 bus system (Zimmerman et al., 2010) with three GFM inverters to illustrate the effectiveness of the propose MPC optimization–based secondary load-frequency control using a control-oriented model. The topology and the parameter of the system are detailed in Figure 2 and Table 2, respectively.

FIGURE 2

FIGURE 2. Topology of a modified IEEE 9 bus test system with three GFM inverters.

TABLE 2

TABLE 2. Parameters of the IEEE 9 bus test system with three GFM inverters.

General Frequency Control Performance

In the first case study, we evaluate the control performance of the proposed MPC-based frequency regulation algorithm. The system is operating under the situation where there exist small frequency deviations initially. At t = 4 s, the proposed MPC optimization is activated, and a load increase of 0.02 p.u. and a load decrease of 0.025 p.u. occur at node 7, t = 7 s and node 9, t = 10 s, respectively. As shown in Figure 3, the frequency deviations can be restored to the reference value with appropriate load change, and all constraints are fully satisfied.

FIGURE 3

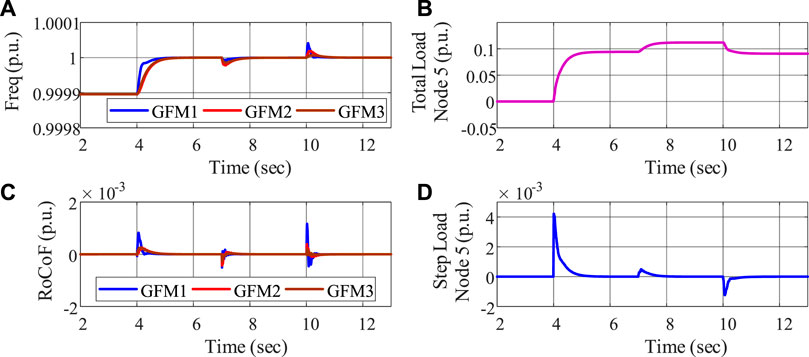
FIGURE 3. Load-frequency response: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.

Validation and Analysis of Constraints

To validate the constraint implementation, the case in is seen as the baseline case. We first set the dispatchable load capacity $-0.1\le u\le 0.1$ based on the case in Table 2. As shown in Figure 4where Figures 4A–D show the frequency, total load, RoCoF, and load ramping respectively, due to limited dispatchable loads (see Figure 4B), the frequency cannot be fully restored to the reference value after the load increase at node 7, t = 7 s. However, after the load decrease at node 9, t = 10 s, the frequency can be regulated without synchronized deviations within the limited dispatchable load resources. Then, we set the load ramping constraints to $-0.003\le \mathrm{\Delta }u\le 0.003$ similarly. Figure 5 witnesses the corresponding slower frequency response compared to the baseline case due to the limited load ramping rate (see Figure 5D). Especially, the detailed effect is reflected on the comparisons between (A1) and (A2), i.e., zoomed-in figure of Figure 5A and Figure 3A, respectively. Hence, both dispatchable load capacity constraints and load ramping constraints, which have been designed in the proposed MPC-based algorithm, affect the frequency regulation performance.

FIGURE 4

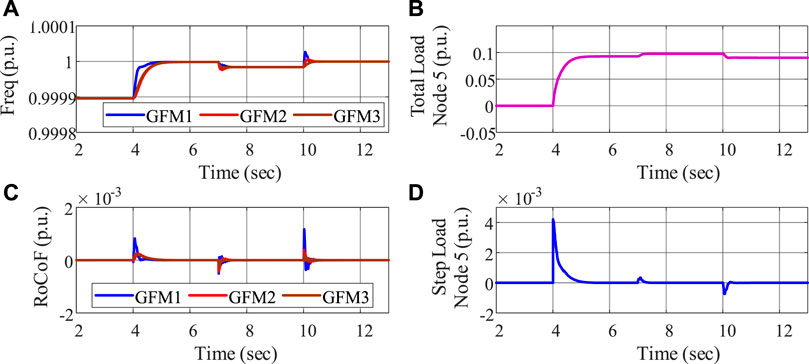
FIGURE 4. Dispatchable load capacity constraint evaluation: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.

FIGURE 5

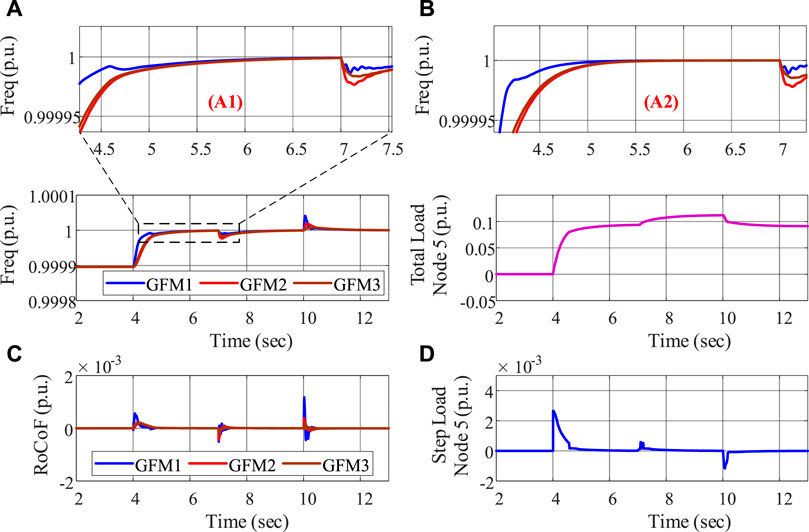
FIGURE 5. Load ramping rate constraint evaluation: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.

Then, we turn to frequency constraints, for which we first double the loads on all nodes to enlarge the frequency deviations and set $-0.5\le u\le 0.5$ based on the baseline case. As seen in Figure 6, both the dispatchable load capacity and the load ramping rate are utilized immediately after activating the frequency regulation at t = 4 s. Under this case, if we force the frequency to be regulated into $-0.003\le \mathrm{\Delta }f\le 0.003$ in one control step, the MPC optimization problem will become infeasible, which means the current load constraints cannot satisfy the frequency constraint requirement. After setting $-0.5\le u\le 1.8$ and canceling the ramping rate requirement, the corresponding regulation performance will become Figure 7, showing the similarly immediate load change, which demonstrates the effectiveness of frequency constraints. Furthermore, the RoCoF prediction performance is shown in Figure 8 under the baseline case. We found that the predicted RoCoF is larger than the real-time one, but they are in the same order of magnitudes. This guides us to set RoCoF constraints in practice (i.e., tightening RoCoF constraints). Moreover, in practice, to accurately predict RoCoF values, we can apply data-driven methods such as machine learning to find the relationship between real-time values and predicted ones using operational databases. This work is out of this article’s scope and will be investigated in our future work. The reason for such phenomenon is the linearization process using the Jacobian matrix leading to prediction errors. Considering the proposed model is based on the small-signal modeling method, and the update of such control-oriented model is of great significance. As for the effectiveness of RoCoF constraints, they are relatively similar to the other constraints as analyzed before and hence omitted here.

FIGURE 6

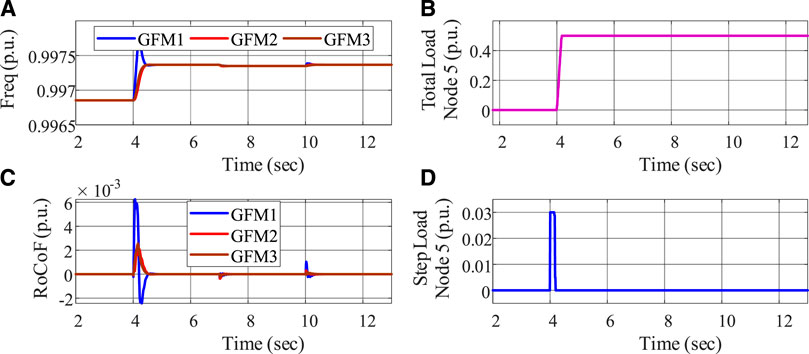
FIGURE 6. Frequency constraint evaluation with tight input constraints: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.

FIGURE 7

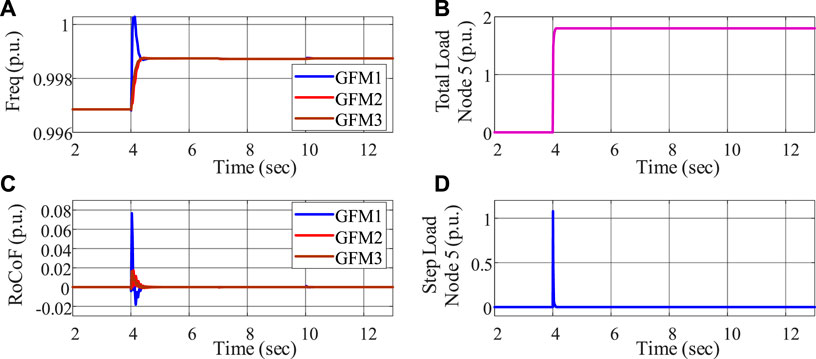
FIGURE 7. Frequency constraint evaluation with relaxed input constraints: (A) frequency, (B) total load decrease, (C) RoCoF, and (D) load ramping.

FIGURE 8

FIGURE 8. Analysis of the RoCoF prediction model: (A) RoCoF and (B) one-step RoCoF prediction.

Conclusion

This article proposed a control-oriented model to link the load increment to the frequency dynamics of the GFM-based generator. This model combines the well-developed power flow analysis to obtain the steady-state Jacobian matrix and state-space dynamic models of GFM generators, to formulate the simplified and linearized power system model. Based on this model, though there exists some modeling uncertainty due to the linearization process, we can design the control algorithm to enable rapid load-frequency regulations. To fully consider constraints in frequency regulation, the MPC optimization algorithm is utilized to form an online feedback control that satisfies frequency security limits, RoCoF limits, dispatchable load capacity limits, and load change ramping limits. The constraints normally come from the practical operational rules, which can be easily integrated into convex quadratic programming and solved using well-developed tools. The effectiveness of the proposed frequency regulation algorithm is finally validated by comprehensive simulations and analyses based on a modified IEEE 9 bus system using MATLAB/Simulink.

However, the proposed method is based on the small-signal analysis, which limits the model applicability near the equilibrium point of the power system. In the future, to fully depict the system operation dynamics, large-signal methods should be further involved, and we will consider this in our following research.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

XQ: establishing the model, running the simulation, and writing the paper. JZ: advising and revising the paper. FM: advising and revising the paper.

Funding

This work was funded by the Key R&D Plan of Jiangsu Province (BE2020027) and Jiangsu International Science and Technology Cooperation Project (BZ2021012).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Creutzig, F., Goldschmidt, J. C., Lehmann, P., Schmid, E., von Blücher, F., Breyer, C., Fernandez, B., Jakob, M., Knopf, B., Lohrey, S., Susca, T., and Wiegandt, K. (2014). Catching Two European Birds with One Renewable Stone: Mitigating Climate Change and Eurozone Crisis by an Energy Transition. Renew. Sustain. Energy Rev. 38, 1015–1028. doi:10.1016/j.rser.2014.07.028

CrossRef Full Text | Google Scholar

Di Silvestre, M. L., Favuzza, S., Riva Sanseverino, E., and Zizzo, G. (2018). How Decarbonization, Digitalization and Decentralization Are Changing Key Power Infrastructures. Renew. Sustain. Energy Rev. 93, 483–498. doi:10.1016/j.rser.2018.05.068

CrossRef Full Text | Google Scholar

Fernández-Guillamón, A., Gómez-Lázaro, E., Muljadi, E., and Molina-García, Á. (2019). Power Systems with High Renewable Energy Sources: A Review of Inertia and Frequency Control Strategies over Time. Renew. Sustain. Energy Rev. 115, 109369. doi:10.1016/j.rser.2019.109369

CrossRef Full Text | Google Scholar

Ge, P., Chen, B., and Teng, F. (2021). Event‐triggered Distributed Model Predictive Control for Resilient Voltage Control of an Islanded Microgrid. Int. J. Robust Nonlinear Control 31 (6), 1979–2000. doi:10.1002/rnc.5238

CrossRef Full Text | Google Scholar

Ge, P., Dou, X., Quan, X., Hu, Q., Sheng, W., Wu, Z., et al. (2020). Extended-state-observer-based Distributed Robust Secondary Voltage and Frequency Control for an Autonomous Microgrid. IEEE Trans. Sustain. Energy 11 (1), 195–205. doi:10.1109/tste.2018.2888562

CrossRef Full Text | Google Scholar

Ge, P., Teng, F., Konstantinou, C., and Hu, S. (2022). A Resilience-Oriented Centralised-To-Decentralised Framework for Networked Microgrids Management. Appl. Energy 308, 118234. doi:10.1016/j.apenergy.2021.118234

CrossRef Full Text | Google Scholar

Guerrero, J. M., Vasquez, J. C., Matas, J., De Vicuña, L. G., and Castilla, M. (2010). Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach toward Standardization. IEEE Trans. industrial Electron. 58 (1), 158–172. doi:10.1109/TIE.2010.2066534

CrossRef Full Text | Google Scholar

Jin, L., Zhang, C.-K., He, Y., Jiang, L., and Wu, M. (2019). Delay-dependent Stability Analysis of Multi-Area Load Frequency Control with Enhanced Accuracy and Computation Efficiency. IEEE Trans. Power Syst. 34 (5), 3687–3696. doi:10.1109/tpwrs.2019.2902373

CrossRef Full Text | Google Scholar

Luo, H., Hiskens, I. A., and Hu, Z. (2020). Stability Analysis of Load Frequency Control Systems with Sampling and Transmission Delay. IEEE Trans. Power Syst. 35 (5), 3603–3615. doi:10.1109/tpwrs.2020.2980883

CrossRef Full Text | Google Scholar

Markovic, U., Chu, Z., Aristidou, P., and Hug, G. (2018). LQR-Based Adaptive Virtual Synchronous Machine for Power Systems with High Inverter Penetration. IEEE Trans. Sustain. Energy 10 (3), 1501–1512. doi:10.1109/TSTE.2018.2887147

CrossRef Full Text | Google Scholar

Markovic, U., Stanojev, O., Aristidou, P., Vrettos, E., Callaway, D., and Hug, G. (2021). Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 36 (5), 3997–4017. doi:10.1109/tpwrs.2021.3061434

CrossRef Full Text | Google Scholar

Milano, F., Dörfler, F., Hug, G., Hill, D. J., and Verbič, G. (2018). “Foundations and Challenges of Low-Inertia Systems,” in 2018 Power Systems Computation Conference (PSCC) (New York: IEEE), 1–25.

Google Scholar

Ni, J., Liu, L., Liu, C., Hu, X., and Li, S. (2016). Fast Fixed-Time Nonsingular Terminal Sliding Mode Control and its Application to Chaos Suppression in Power System. IEEE Trans. Circuits Syst. II Express Briefs 64 (2), 151–155. doi:10.1109/TCSII.2016.2551539

CrossRef Full Text | Google Scholar

Obaid, Z. A., Cipcigan, L. M., Abrahim, L., and Muhssin, M. T. (2019). Frequency Control of Future Power Systems: Reviewing and Evaluating Challenges and New Control Methods. J. Mod. Power Syst. Clean. Energy 7 (1), 9–25. doi:10.1007/s40565-018-0441-1

CrossRef Full Text | Google Scholar

Ratnam, K. S., Palanisamy, K., and Yang, G. (2020). Future Low-Inertia Power Systems: Requirements, Issues, and Solutions - A Review. Renew. Sustain. Energy Rev. 124, 109773. doi:10.1016/j.rser.2020.109773

CrossRef Full Text | Google Scholar

Shang-Guan, X., He, Y., Zhang, C., Jiang, L., Spencer, J. W., and Wu, M. (2020). Sampled-data Based Discrete and Fast Load Frequency Control for Power Systems with Wind Power. Appl. Energy 259, 114202. doi:10.1016/j.apenergy.2019.114202

CrossRef Full Text | Google Scholar

Shangguan, X. C., He, Y., Zhang, C. K., Jiang, L., and Wu, M. (2021). Adjustable Event-Triggered Load Frequency Control of Power Systems Using Control Performance Standard-Based Fuzzy Logic. IEEE Trans. Fuzzy Syst. 30 (8), 3297–3311. doi:10.1109/tfuzz.2021.3112232

CrossRef Full Text | Google Scholar

Shen, J., Li, W., Liu, L., Jin, C., Wen, K., and Wang, X. (2020). Frequency Response Model and its Closed-form Solution of Two-Machine Equivalent Power System. IEEE Trans. Power Syst. 36 (3), 2162–2173. doi:10.1109/TPWRS.2020.3037695

CrossRef Full Text | Google Scholar

Singhal, A., Vu, T. L., and Du, W. (2022). Consensus Control for Coordinating Grid-Forming and Grid-Following Inverters in Microgrids. IEEE Trans. Smart Grid, 1. doi:10.1109/tsg.2022.3158254

CrossRef Full Text | Google Scholar

Stanojev, O., Markovic, U., Aristidou, P., Hug, G., Callaway, D. S., and Vrettos, E. (2020). MPC-Based Fast Frequency Control of Voltage Source Converters in Low-Inertia Power Systems. IEEE Trans. Power Syst. 37, 3209–3220. doi:10.1109/TPWRS.2020.2999652

CrossRef Full Text | Google Scholar

Tøndel, P., Johansen, T. A., and Bemporad, A. (2003). An Algorithm for Multi-Parametric Quadratic Programming and Explicit MPC Solutions[J]. Automatica 39 (3), 489–497. doi:10.1016/S0005-1098(02)00250-9

CrossRef Full Text | Google Scholar

Wu, Y., Wu, Y., Guerrero, J. M., and Vasquez, J. C. (2021). Digitalization and Decentralization Driving Transactive Energy Internet: Key Technologies and Infrastructures. Int. J. Electr. Power & Energy Syst. 126, 106593. doi:10.1016/j.ijepes.2020.106593

CrossRef Full Text | Google Scholar

Xu, Y., Sun, H., Gu, W., Xu, Y., and Li, Z. (2018). Optimal Distributed Control for Secondary Frequency and Voltage Regulation in an Islanded Microgrid. IEEE Trans. Industrial Inf. 15 (1), 225–235.

Google Scholar

Zimmerman, R. D., Murillo-Sánchez, C. E., and Thomas, R. J. (2010). MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. power Syst. 26 (1), 12–19. doi:10.1109/TPWRS.2010.2051168

CrossRef Full Text | Google Scholar

Zou, Y., Qian, J., Zeng, Y., Ismail, S., Dao, F., Feng, Z., Nie, C., and Mei, H. (2021). Optimized Robust Controller Design Based on CPSOGSA Optimization Algorithm and H 2/H ∞ Weights Distribution Method for Load Frequency Control of Micro-grid. IEEE Access 9, 162093–162107. doi:10.1109/access.2021.3132729

CrossRef Full Text | Google Scholar

Zuo, S., Davoudi, A., Song, Y., and Lewis, F. L. (2016). Distributed Finite-Time Voltage and Frequency Restoration in Islanded AC Microgrids. IEEE Trans. Ind. Electron. 63 (10), 5988–5997. doi:10.1109/tie.2016.2577542

CrossRef Full Text | Google Scholar