Synchrotron-based techniques for characterizing STCH water-splitting materials

Understanding the role of oxygen vacancy–induced atomic and electronic structural changes to complex metal oxides during water-splitting processes is paramount to advancing the field of solar thermochemical hydrogen production (STCH). The formulation and confirmation of a mechanism for these types of chemical reactions necessitate a multifaceted experimental approach, featuring advanced structural characterization methods. Synchrotron X-ray techniques are essential to the rapidly advancing field of STCH in part due to properties such as high brilliance, high coherence, and variable energy that provide sensitivity, resolution, and rapid data acquisition times required for the characterization of complex metal oxides during water-splitting cycles. X-ray diffraction (XRD) is commonly used for determining the structures and phase purity of new materials synthesized by solid-state techniques and monitoring the structural integrity of oxides during water-splitting processes (e.g., oxygen vacancy–induced lattice expansion). X-ray absorption spectroscopy (XAS) is an element-specific technique and is sensitive to local atomic and electronic changes encountered around metal coordination centers during redox. While in operando measurements are desirable, the experimental conditions required for such measurements (high temperatures, controlled oxygen partial pressures, and H₂O) practically necessitate in situ measurements that do not meet all operating conditions or ex situ measurements. Here, we highlight the application of synchrotron X-ray scattering and spectroscopic techniques using both in situ and ex situ measurements, emphasizing the advantages and limitations of each method as they relate to water-splitting processes. The best practices are discussed for preparing quenched states of reduction and performing synchrotron measurements, which focus on XRD and XAS at soft (e.g., oxygen K-edge, transition metal L-edges, and lanthanide M-edges) and hard (e.g., transition metal K-edges and lanthanide L-edges) X-ray energies. The X-ray absorption spectra of these complex oxides are a convolution of multiple contributions with accurate interpretation being contingent on computational methods. The state-of-the-art methods are discussed that enable peak positions and intensities to be related to material electronic and structural properties. Through careful experimental design, these studies can elucidate complex structure–property relationships as they pertain to nonstoichiometric water splitting. A survey of modern approaches for the evaluation of water-splitting materials at synchrotron sources under various experimental conditions is provided, and available software for data analysis is discussed.

1 Introduction

Solar thermochemical hydrogen production, termed STCH, is an emerging process for thermochemical water-splitting technologies with little or no greenhouse gas emissions (Steinfeld, 2005; Rao and Dey, 2017; Lu et al., 2019). Out of the numerous STCH cycles described in the literature (Steinfeld, 2005; Perret, 2011; Muhich et al., 2015; Rao and Dey, 2017; Lu et al., 2019), the two-step redox-active metal oxide cycle is one of the more promising candidate approaches. The fundamental basis for the oxide cycle is simple—a metal oxide is reduced at a high temperature to create oxygen vacancies that are subsequently filled when the defected material is exposed to steam, splitting the H₂O molecule, generating H₂, and completing the cycle (Figure 1). Efficacious STCH water splitting necessitates a metal oxide that can undergo reduction via non-stoichiometry at sufficiently low temperatures, demonstrate fast reoxidation kinetics with H₂ present in the steam feed, and exhibit structural stability over the course of up to hundreds of thousands of redox cycles. Identifying an oxide material with the necessary chemical properties for robust water splitting has thus far eluded researchers and is a key challenge that must be overcome for STCH to be considered a viable technology for large-scale hydrogen production. The development of novel STCH materials is contingent on unraveling the relationship between a material’s structural and electronic response to the enthalpy and entropy of vacancy formation, requiring empirical and modeling efforts working in tandem (Zinkevich et al., 2006; Lany, 2008; Deml et al., 2014; Hao et al., 2014; Bork et al., 2015; Deml et al., 2015; Muhich et al., 2015; Zhang et al., 2015; Emery et al., 2016; Tsvetkov et al., 2016; Naghavi et al., 2017; Sai Gautam et al., 2020).

FIGURE 1

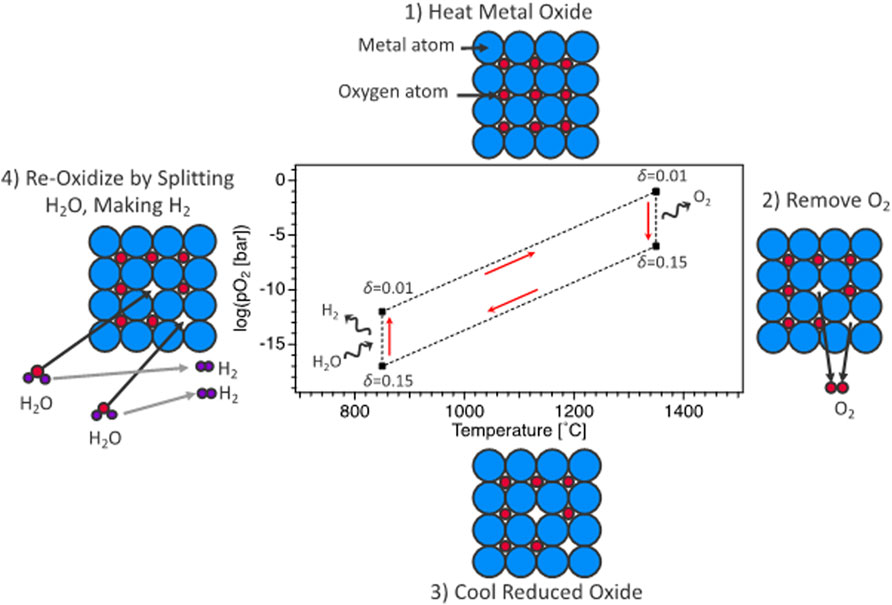
FIGURE 1. Representation of oxygen-vacancy STCH cycle divided into four thermochemical steps: 1) heating of metal oxide at constant (low) vacancy concentration, 2) high-temperature reduction resulting in oxygen vacancy creation, 3) cooling of metal oxide at constant (high) vacancy concentration, and 4) steam reaction where STCH material vacancy concentration decreases (reoxidization) and H₂O is reduced to H₂.

Currently, ceria is the benchmark material for two-step metal-oxide–based STCH (Hao et al., 2014; Rothensteiner et al., 2015; Tanwar et al., 2016; Lu et al., 2019). Ceria demonstrates phase stability in the reduced state (Zinkevich et al., 2006; Chueh et al., 2012; Hao et al., 2014; Rothensteiner et al., 2015; Naghavi et al., 2017; Lu et al., 2019), fast reoxidation kinetics (McDaniel et al., 2013; Hao et al., 2014; Ackermann et al., 2015), and importantly, a high tolerance to hydrogen in the steam stream during reoxidation (Chueh et al., 2012; Hao et al., 2014; Barcellos et al., 2018). Unfortunately, temperatures in excess of 1,500°C are required to reduce ceria appreciably, limiting practical viability (Barcellos et al., 2018; Cheng et al., 2021). Increasingly, researchers are turning their attention away from simple oxide materials to more complex material systems, which include redox-active nonstoichiometric oxides such as Sr_xLa_1−xMn_yAl_1−yO_3−δ (SLMA) (McDaniel et al., 2013; Suntivich et al., 2014) and BaCe_0.25Mn_0.75O_3−δ (BCM) (Barcellos et al., 2018). Here, δ is used to indicate the deviation in oxygen stoichiometry from the fully oxidized state. However, there are multiple ways to define or discuss δ such as normalizations by formula units of oxygen, cations, or volume (e.g., concentration and vacancies·cm⁻³). The perovskite-based oxides have demonstrated significant promise through an increased per-cycle yield at lower temperatures, governed by changes in oxygen vacancy concentration between the reduced and reoxidized states (Δδ), at given H₂ to H₂O ratios. Continued progress in STCH materials’ development requires a more complete understanding of the water-splitting mechanism. The impact of oxygen vacancies on the structural response of materials can be subtle and is often difficult to observe with conventional laboratory instruments, thus requiring synchrotron radiation–enabled techniques such as X-ray diffraction (XRD) for precise determination of complex structures and element-specific localized electronic responses to redox through X-ray absorption spectroscopy (XAS).

Typical changes in oxygen vacancy concentration, Δδ, during redox cycling between reduced and reoxidized states are in the order of Δδ ≥ 0.1 mol O mol⁻¹ cation. The high brilliance of photons and broad range of energies accessible at a synchrotron X-ray source furnish exceptional signal-to-noise ratio for probing structural and electronic changes arising from the small concentration of oxygen defects and enable measurements under in situ or in operando experimental conditions that align with realistic STCH operating parameters. Herein, in operando refers to an experiment carried out under conditions that fully align with all conditions of a representative redox water-splitting cycle (i.e., an experiment to study reoxidation behavior at realistically high temperatures and representative steam:H₂ ratio), while in situ refers to an experiment in which a single condition, or subset of conditions, is being probed (i.e., an experiment at elevated temperature but under ultrahigh vacuum). However, although possible, the full range of operating conditions of STCH materials are for the most part prohibitively difficult to reach for fully in operando experiments and challenging at best with typical in situ experimental apparatuses, with temperatures ranging from 700°C to 1,600°C, and oxygen partial pressures ranging from (pO₂) = 1 bar to ≤1 × 10⁻²⁰ bar. While certain ambitious in situ experiments can capture subranges of the full operating range of STCH materials and are sometimes necessary for unraveling structural behavior at high temperatures, careful sample preparation and experimental design allow ex situ experiments to reveal a wealth of structural and electronic responses of materials to reduction.

Developing next-generation STCH materials will be dependent on understanding the structural and electronic changes that enable reversible oxygen defect formation in complex metal oxides. The high brilliance and variable energy of synchrotron sources provide the resolution and sensitivity necessary for probing the impact of a relatively small percentage of oxygen defects in a bulk material, unobtainable with conventional laboratory-scale techniques. This informs an increasingly useful computational model of these high defect oxides. Despite this, the use of synchrotron characterization has been limited in the STCH field. Herein, we strive to inform researchers of the mechanistic insight that synchrotron experiments can provide into STCH material behavior and provide the best practices for carrying out experiments and interpreting the resultant data. First, we demonstrate a methodology of quenching complex metal oxides in known reduced states such that oxygen vacancies are preserved upon cooling to room temperature. Quenching of samples into a range of known reduced states is achieved using a combination of variable oxygen partial pressures and determination of mass loss during quenching using thermogravimetric analysis (TGA) to determine, and ultimately control, the extent of reduction. The ability to quench oxygen deficient states enables the ex situ probing of a material’s structural and electronic response to reduction. We therefore describe the applicability of XAS and XRD techniques for characterizing STCH materials which includes the information that each technique provides, best practices for carrying out the experiments, and advanced data analysis methods for interpreting complex data. Finally, recently developed tools for in situ characterization of water-splitting materials under STCH operating parameters are summarized.

2 Preparation of controllably reduced samples for ex situ experiments

Although in operando or in situ experiments are ideal, the conditions required for STCH cycling are typically prohibitive and well-designed ex situ experiments can provide valuable insights. In this section, we detail the best practices for quenching in defects for ex situ characterization.

Generating fully oxidized materials for ex situ studies is relatively straightforward. Fully oxidized samples may be prepared by heating and cooling in atmosphere or at 1 bar O₂. Even under 1 bar of O₂, most samples develop small levels of oxygen vacancy concentration at or near the surface during cooling, with the depth-dependent concentration depending on bulk diffusivity, surface reaction kinetics, and morphology of samples. However, for fully oxidized samples, the difference in oxygen vacancy concentration between the near surface and bulk should be small when compared with the oxygen vacancy concentration between operational reduced and reoxidized states. In other words, care should be taken to not overanalyze small differences between fully oxidized samples, but when comparing fully oxidized and reduced samples, the results should be relatively insensitive to the exact mechanism of creating the fully oxidized samples.

By contrast, making representative reduced STCH samples for ex situ testing requires careful preparation. Essentially, almost all reduced STCH samples are metastable at room temperature in atmosphere. Only the slow kinetics of surface reoxidation and bulk oxygen diffusion prevent reduced samples from reoxidizing in air. At low temperatures, bulk oxygen diffusion in oxide ceramics is anticipated to be much slower than surface reactions, that is, some surface reoxidation is possible in the top couple of nanometers while the bulk is expected to remain in a reduced state (Li et al., 2021). Therefore, the samples are reduced under controlled reducing conditions and are then “quenched” to room temperature where slow kinetics traps the desired reduced states.

One method for determining the amount of reduction quenched into the ex situ sample is to use thermogravimetric analysis (thermogravimetric analysis) either to quench reduced samples or replicate as precisely as possible the cooling rates, temperatures, and pO₂ values used for sample reduction. In Figure 2, we give an example plot of thermogravimetric analysis data taken during isobaric (fixed pO₂) cooling from high temperature for preparation of reduced samples of BaCe_0.25Mn_0.75O₃ (BCM) for ex situ studies. In thermogravimetric analysis, the change in oxygen vacancy concentration can be seen as (and calculated from) the loss of sample mass during the experiment, with reduction appearing as mass loss and reoxidation as mass gain. Using the thermogravimetric analysis data, the reduction state trapped at room temperature can be quantified. Similarly, if bulk samples are prepared in a furnace, the pO₂ and cooling rate can be duplicated using thermogravimetric analysis to approximate the ex situ sample reduction.

FIGURE 2

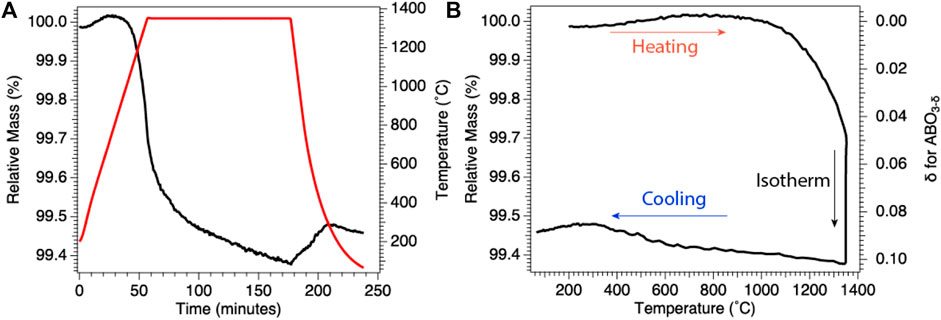
FIGURE 2. Results of representative BCM thermogravimetric analysis under reducing conditions. (A) Change in relative mass (black), instantaneous mass/initial mass, with temperature (red), demonstrating mass loss during 1,350°C isothermal reduction. (B) Relative mass from (A) plotted as a function of temperature (left axis) and with relative mass transformed into oxygen off-stoichiometry, δ (inverted right axis), for BCM. Results demonstrate quenching of a known reduced state for subsequent ex situ investigations.

Achieving the desired degree of reduction in quenched samples requires controlling the temperature and pO₂. Ideally, pO₂ and temperature are chosen to align with a condition of interest. However, if the equipment used for reducing samples cannot meet the conditions of interest, alternate temperatures and pO₂ can be used to reduce samples to equivalent extents. Environments with the same pO₂ are more reducing at high temperatures than at low temperatures, and similarly, environments with the same temperature are more reducing at lower pO₂ than higher pO₂. The pO₂ range of interest can span over 20 orders of magnitude, and pO₂ is often very difficult to control precisely over this full range due to the presence of trace leaks and virtual sources of O₂ in many vacuum systems. Options for controlling pO₂ include using blends of gas with known fractions of pO₂.

Samples must also equilibrate at the reducing conditions, and equilibration times differ dramatically between bulk, nanoparticle, and thin film samples. One ideal way to measure equilibration times is to examine bulk samples using thermogravimetric analysis (TGA) under reducing environments and determine the length of time necessary for the mass loss to reach an asymptote that aligns with the in operando condition that the ex situ experiment is attempting to mimic (for example, if 1% of the oxygen is removed during reduction in a water-splitting cycle of interest, then the sample being prepared for ex situ analysis should also be monitored such that 1% of the oxygen is removed). Monitoring for asymptotic mass loss is important to prevent samples from developing steep reduction gradients that can be unrepresentative when later probed with surface-sensitive measurements.

Controlling the cooling rate is an equally important consideration when preparing ex situ reduced oxides. Under isobaric pO₂ conditions, the samples tend to reoxidize during cooling. The maximum rate of reoxidation that will occur during cooling depends on a sample’s reoxidation kinetics (at a given temperature) and the difference between the current and equilibrium oxygen vacancy concentrations and availability of oxygen. In general, the faster the sample is cooled, the more closely the extent of reduction will be preserved from high temperature into the quenched sample.

A number of precautions should be taken when performing measurements on and analyzing the data from ex situ reduced samples. The formation of surface layers of carbonate, hydroxyl, or other non-oxide coatings is possible and potentially more likely in reduced samples due to the reactivity of oxygen vacancies. Special care should be taken when using structural characterization techniques that are selective to only the sample surface. Another important consideration is that the effects of oxygen vacancy concentration on atomic and electronic structures can exhibit temperature dependence. For example, the concentration of oxygen vacancies causes concentration-dependent structural distortions, often referred to as chemical expansion, where crystal lattices tend to expand when oxygen vacancies are present. This chemical expansion is temperature dependent, so the difference in lattice parameters between reduced and reoxidized samples will depend on the temperature (Marrocchelli et al., 2012). Likewise, the location of oxygen vacancies in the crystal lattice may differ between high and low temperatures, with an increased probability of vacancies occurring at higher energy sites at high temperatures due to contributions from configurational entropy and k_BT terms. While the examination of samples ex situ can be representative of materials under operating conditions, the aforementioned warnings stress the importance of not assuming an identical behavior between the quenched oxides and samples maintained under operating conditions. The following two sections focus specifically on XAS and XRD techniques for characterizing quenched samples.

3 X-ray absorption spectroscopy for solar thermochemical hydrogen production material characterization

X-ray absorption spectroscopy (XAS) is a powerful technique for characterizing STCH materials. XAS provides invaluable insights into the oxygen binding environment and quantification of cation oxidation states, enabling the redox-active elements to be identified and unraveling more complex phenomena, such as those where the cations reduce further in multi-cation systems with more than one redox-active element. Comparing the oxidation binding environments and cation oxidation states of STCH materials before and after, or during, reduction can provide significant insights into water-splitting mechanisms. Here, we provide a brief introduction to the fundamentals underlying XAS (Section 3.1) and how XAS is applicable for characterizing STCH materials specifically (Section 3.2), and finally, introducing advanced data analysis methods for interpreting the complex spectra (Section 3.3).

3.1 Brief introduction to X-ray absorption spectroscopy

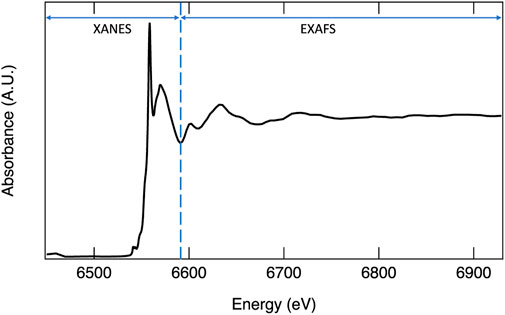
X-ray absorption spectroscopy probes the excitation of electrons from core orbitals to unoccupied or partially occupied orbitals, or to the continuum. Incident photons generated by a synchrotron source over a range of well-defined energies interact with a material, and X-ray absorption (I/I_o) at each energy step is measured. Sharp increases in absorption occur at edges where the incident X-ray energy corresponds to the energy necessary for ejecting a core electron to a partially filled or unoccupied orbital. The term XANES, or X-ray absorption near edge structure, refers to the portion of the spectrum containing the edge step, a loosely defined region just before the edge termed the pre-edge, and the region up to approximately 50 eV after the edge (Figure 3). The XANES region can provide quantitative information on the oxidation state, extent of hybridization, and insights into coordination geometry. At higher energies, the core electron is ejected to the continuum with kinetic energy dependent on the energy of the incident photon. To understand the higher energy region, referred to as the extended X-ray absorption fine structure (EXAFS), the wave nature of an electron must be considered. The ejected electron can interact with electrons from neighboring atoms causing it to backscatter. The outgoing wave can interfere with the backscattered wave either constructively or destructively. At incident photon energies resulting in constructive interference, the probability of absorption increases, while destructive interference results in a decreased probability of adsorption (Calvin, 2013). Thus, the EXAFS region often exhibits periodic oscillations (Figure 3). The Fourier transform of this region can be modeled to provide the identity of neighboring atoms and quantitative information such as coordination number and bond distances. One significant advantage of XAS is that the technique is suitable for both crystalline and amorphous materials. For more detailed information on XANES and EXAFS analyses, interested readers are referred to the following sources: Stöhr (1992), Bunker (2010), Calvin (2013), and Frati et al. (2020).

FIGURE 3

FIGURE 3. X-ray absorption spectrum of Mn K-edge with XANES and EXAFS regions identified.

Most XAS data are collected using transmission mode, total electron yield (TEY), or fluorescence yield (FY), as represented in Figure 4. All three of these techniques measure the absorption of X-ray photons as a function of energy. More specifically, they are a measure of the absorption coefficient as a function of energy, as defined in Eq. 1.

$I=I_o{e}^{-\mu \left(E\right)t},(1)$

where I_o is the intensity of the incident photons, I is the intensity of the photons after the beam passes through the sample (unabsorbed photons), μ is the absorption coefficient (linear attenuation coefficient), and t is the thickness of the material. In the transmission mode, the linear attenuation of X-rays [μ(E)t = ln(I_o/I)] is measured directly by monitoring the intensity of photons before (I_o) and after (I) the sample is positioned, often using ionization chambers. Due to the strong attenuation of soft X-rays by many materials, transmission experiments are typically carried out only with hard energy X-rays capable of penetrating the sample. FY detection is an alternative technique for measuring X-ray absorption, whereby a fluorescent photon is emitted during the relaxation of an electron from a higher energy state to the core hole formed by the initial X-ray absorption event. The intensity of fluorescent photons is proportional to the fraction of the incident photons absorbed $\mu \left(E\right)\propto I_f/I_o$, where I_f is the intensity of fluoresced electrons. Electron yield methods for XAS detection rely on the measurement of electrical current generated from electrons excited from core levels during absorption, where the current is proportional to the fraction of incident X-rays absorbed. These techniques are particularly advantageous at soft X-ray energies where methods based on photon emission struggle due to low escape depths. Additional measurement techniques include partial fluorescent and photoemission-based methods. For additional information on all of the aforementioned techniques and the best practices for collecting high-quality data with each method, readers are directed to the books ‘XAFS for Everyone’ by Scott Calvin (Calvin, 2013) and ‘Introduction to XAFS: A Practical Guide to X-ray Absorption Fine Structure Spectroscopy’ by Grant Bunker (Bunker, 2010).

FIGURE 4

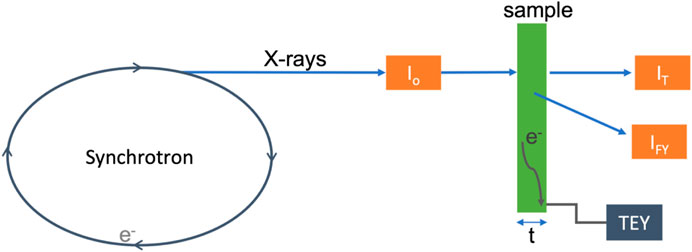
FIGURE 4. Simplified schematic of an XAS experiment, with the sample in green. The orange boxes represent detectors, where I_o measures the incident photons, I_T measures the transmitted photons, and I_F measures the fluoresced photons. The arrow with e⁻ indicates electrons at the sample surface from excitation measured via electron yield experiments, indicated by the gray box labeled TEY.

3.2 Application of X-ray absorption spectroscopy to solar thermochemical hydrogen production materials

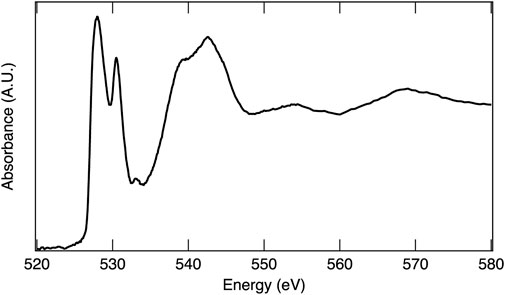
In an XAS experiment, the energy of the absorption event is dependent on both the element and the specific electronic transition probed. The ability to observe an electronic transition is governed by the electric dipole selection rules (e.g., single electron, Δℓ ± 1)³¹, thus transitions from 1s to 2p orbitals and 2p to 3d orbitals result in high absorption intensity. The full range of X-ray energies available at a synchrotron X-ray source enables absorption measurements on most of the elements across the periodic table, which include low Z elements such as oxygen, making XAS a powerful tool for investigating material structures, chemical properties, and electronic behaviors of STCH materials. The oxygen 1s electron binding energy is 543.1 eV, relative to the vacuum level (Thompson et al., 2009). XAS at the oxygen K-edge excites 1s electrons to 2p orbitals and is essentially a measure of empty 2p states, providing a wealth of information on oxygen–metal hybridization. As an example, the oxygen K-edge spectrum of MnO₂ is provided in Figure 5 and is representative of the oxygen in 3d transition metal oxides where hybridization occurs between the oxygen 2p and transition metal 3d orbitals. The lower energy peaks between approximately 525 eV and 535 eV are within the pre-edge region and correspond to O 2p states hybridized with Mn 3d, with the doublet arising from crystal field splitting. The first peak with maximum intensity at 528 eV arises from the spin down t_2g and spin up e_g, which are too close in energy to separately resolve, while the second peak, 2.4 eV higher in energy, is related to the spin down e_g. The broader peaks at higher energy are O 2p with Mn 4s and 4p character. The area under the curve related to O 2p with transition metal 3d character is quantitatively correlated to the extent of oxygen–transition metal hybridization (Suntivich et al., 2014). Figure 6 overlays the oxygen K-edge spectrum of MnO₂ with the BCM water-splitting material. Significant differences in the pre-edge region are readily observable arising from the different oxygen binding environments, which include covalency and electronic configuration. Transition metal oxides play a prominent role in materials being pursued for STCH applications. XAS provides a means to compare the oxygen binding environments between materials, and more importantly, between a single material in reduced and reoxidized states necessary for providing insights into water-splitting mechanisms.

FIGURE 5

FIGURE 5. X-ray absorption spectrum of MnO₂ at the O K-edge.

FIGURE 6

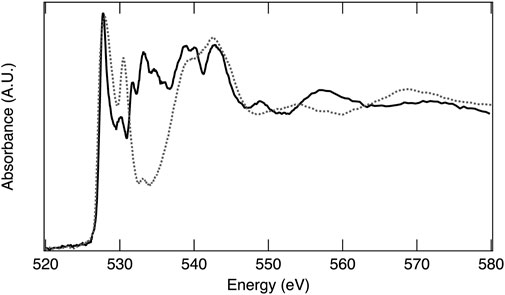
FIGURE 6. X-ray absorption spectra of reoxidized BCM (solid line) and MnO₂ (dashed line) at the O K-edge.

Reduction of a redox-active cation is integral to the two-step metal-oxide STCH cycle. Lower energy X-rays (termed soft X-rays when <1 keV and tender X-rays when between 1 and 5 keV) probe lower energy electron transitions in metals and transition metals, while higher energy X-rays (>5 keV termed hard X-rays) probe higher energy transitions. For example, at the Mn L-edge, 2p electrons are excited to unoccupied or partially occupied 3d states with soft X-rays, whereas at the higher energy K-edge, 1s electrons are excited to 2p states with hard X-rays. The L-edge is split into two states due to spin orbital coupling, resulting in two separate peaks in the L-edge spectrum. The lower energy L₃ edge involves transitions from the 2p_3/2, while the higher energy L₂ edge involves transitions from the 2p_1/2 with 3/2 and 1/2, referencing the total angular momentum quantum number, J = l + s (Figure 7). The L- and K-edges shift to lower energies with reduction as a consequence of greater nuclear shielding by the surrounding electron cloud. Thus, XAS at both the L- and K-edges provide a means to determine which cations are redox active and the extent of reduction in the mixed cation systems, enabling elucidation of the redox behavior in STCH materials (Figure 7). It should be noted that despite probing transitions to the 3d orbitals (which are hybridized with the oxygen 2p orbital), the L-edge does not necessarily provide information on oxygen–metal hybridization. For example, with 3d transition metals, the local effects such as the 2p spin orbital coupling and 2p–3d electron interaction contribute strongly to the L-edge spectrum shape such that, unlike the oxygen 1s, it is not a measure of unoccupied states (Frati et al., 2020). In addition to oxidation state information from the XANES region of metals and transition metals, detailed analysis of the EXAFS region can provide structural information such as identification of neighboring atoms and bond distances. This method is particularly useful for weakly crystalline or amorphous materials where XRD provides little assistance.

FIGURE 7

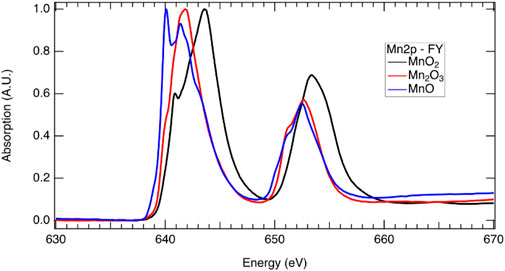
FIGURE 7. X-ray absorption spectra at the Mn 2p edge demonstrating the shift in energy associated with oxidation state which includes a sample that is predominately Mn²⁺ from MnO (blue), Mn³⁺ from Mn₂O₃, and Mn⁴⁺ from MnO₂ (black). The L₃ edge is at approximately 640 eV, while the L₂ edge is at approximately 652 eV (see above for discussion on the L₂ and L₃ edges). Multiple peaks are present for all three samples in the L₃ and L₂ edges, indicating that the samples are not pure and have some contribution from other Mn oxidation states.

When choosing an XAS measurement technique, it is imperative that the experimentalist be cognizant of limitations and potential pitfalls. TEY probes only the first few nanometers of the sample (de Groot and Kotani, 2008) and is therefore a surface-sensitive technique, the results from which may not be representative of the bulk material. FY probes the bulk of the sample material from the first hundreds of nanometers to several micrometers depending on the incident energy and sample composition, making it an effective method for studying bulk changes in STCH materials. However, FY is not without its limitations. In thick samples where the element of interest is concentrated, as is the case with metal oxide powders, self-absorption is a prevalent issue. In fluorescence yield, at an absorption edge, the penetration depth of the incident photons decreases such that they interact with fewer atoms and the relationship between the florescence signal and absorption is no longer linear resulting in artifacts being introduced into the spectral intensity and shape (Bunker, 2010). At energies above the edge, when the element being probed is concentrated, it becomes more likely that the incident photons will be absorbed regardless of the energy suppressing the EXAFS oscillations (Calvin, 2013). There are experimental techniques to reduce or eliminate self-adsorption, such as working with thinner samples and changing the angle of the incident energy or detector angle, as well as data analysis methods that correct for self-absorption, details of which can be found elsewhere (Bunker, 2010; Calvin, 2013). Often, it is possible to collect TEY and FY data simultaneously. Although small differences between the two methods may be expected, significant differences in relative peak intensities is a strong indication that self-absorption is an issue, an example of which is provided in Figure 8. It is recommended that both TEY and FY be collected, when possible, for STCH materials.

FIGURE 8

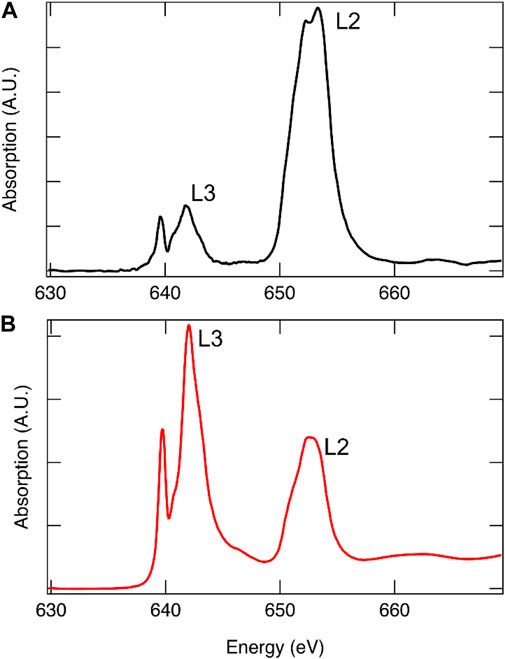
FIGURE 8. Mn L-edge of 12R-Ba₄Ce₁Mn₃O₁₂ collected using FY[(A), black] and TEY [(B), red]. Due to spin–orbit coupling, the L-edge is comprised of two edges, with the lower energy edge arising from J = (1 + s) = 3/2 transitions termed L₃ and the higher energy from J = (1 − s) = 1/2 transitions termed L₂. From degeneracy of the states, it is expected that the L3:L2 intensity ratio is approximately 2:1. Self-absorption is readily apparent in the FY spectrum where the relative intensities are not correct.

3.3 Data analysis

The oscillations of the EXAFS region are a well-understood phenomenon that can be accurately modeled as a function of wavenumber with the EXAFS equation (Eq. 2)²⁷.

$\chi \left(k\right)=S_o^2{\displaystyle \sum }_i{N}_i\frac{f_i\left(k\right)}{k{D}_i^2}{e^{-\frac{2D_i}{\lambda \left(k\right)}}e}^{-2k^2{\sigma }_i^2}\sin \left(2k{D}_i+\delta \left(k\right)\right).(2)$

The EXAFS equation is a sum of all paths between the absorbing atom and the scattering atoms, termed scattering paths, or i in the equation. For examples, when Ce is the absorbing element in CeO₂, the predominant path contributing to the first peak in the Fourier transform would be the path between Ce and its nearest oxygen neighbors. S_o is an amplitude reduction factor that accounts for the experimental Fourier transform amplitude being less than that predicted with the EXAFS equation, N is the degeneracy of the scattering path, D is the half path length or distance between the absorbing and scattering atom, σ² is a measure in the variance of the half path length, k is wavenumber, f is related to the probability of scattering, and δ is a phase shift that acts as a correction for assuming the electron maintains a constant wavenumber throughout the round trip (the wavenumber varies due to its interaction with the absorbing and scattering atoms’ potential wells). After some data processing (such as normalization to the incident energy, removing the background contribution, and converting from energy to wavenumber), the Fourier transform of the EXAFS region can be fit using the EXAFS equation, where N, D, and σ² are the fit parameters. $\delta$(k) and f(k) are atomic number dependent and are typically calculated within the fitting software. S_o is chemically transferable and often determined via running a standard with known structure, therefore with known D and N, making S_o readily determined from running a fit on a standard where the coordination number is known for each path. Figure 9 provides an example of an X-ray absorption spectrum at the Mn K-edge of an STCH material and its corresponding Fourier transform of the EXAFS region. From fitting the EXAFS, neighboring species can be identified with bond distances and coordination number quantitatively determined (Alia et al., 2017). For example, in Figure 9, the first peak in the Fourier transform corresponds to the Mn-O paths, thus fitting the first peak would provide the average number of oxygen atoms neighboring each manganese and the average bond distance. Depending on the quality and extent of the EXAFS data collected, the fit can incorporate atoms beyond the nearest neighbors to the absorbing element. There are excellent software packages available free to the research community for data processing and fitting that include detailed tutorials and other resources with extensive information on the best practices for data analysis that target both the novice and experienced experimentalists (Ravel et al., 2005; Webb, 2005).

FIGURE 9

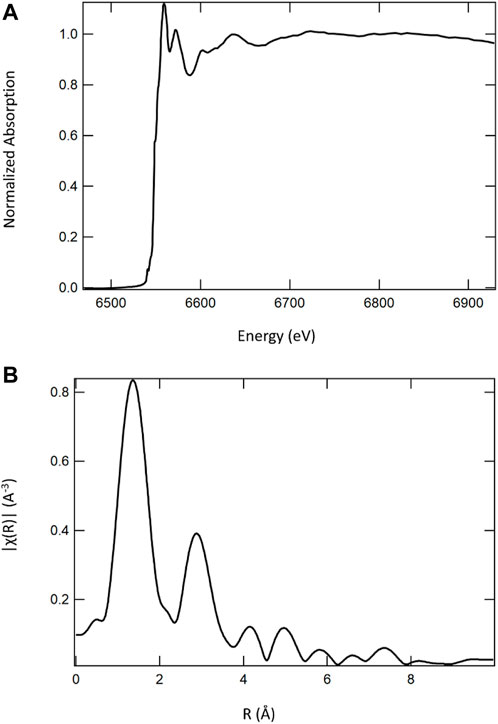
FIGURE 9. Mn K-edge X-ray absorption spectrum (A) of a calcium cerium–manganese oxide STCH material and its corresponding Fourier transform (B). It is the Fourier transform that would be fit with the EXAFS equation to determine nearest neighbors, bond distances, and coordination numbers.

The EXAFS equation is not applicable to the XANES region of the spectra. Analysis of the XANES region is typically more qualitative, although some quantitative information is retrievable. If multiple molecular species are present in a sample, the observed spectrum becomes a linear combination of contributions from the different species. As such, a linear combination fit to the experimental XANES spectrum can often provide the relative weight fractions of the constituents. Particularly applicable to studying STCH materials, oxidation states can also be quantitatively determined. At higher oxidation states, there is less electron shielding of the positively charged atomic nucleus and a greater energy is required to eject a core electron, moving the edge position to higher energy. When using the edge shift to determine the oxidation state, it is important to ensure that the shift is not an artifact of a change in the experimental configuration, such as a shift in the monochromator angle. It is usually possible to collect XAS data on a known reference material simultaneously with data collected on the sample. The spectrum from the reference material provides a reference spectrum for each sample measured. Each sample spectrum is then essentially tied to its corresponding reference spectrum so that by aligning the reference spectra and shifting the sample spectra equivalently, robust alignment is possible and shifts in edge energy can be associated with differences in the oxidation state.

As described above, pre-edge features in the XANES region are often attributable to more complex material properties and behavior, such as transition metal–oxygen hybridization and electronic configuration, both important for relating the STCH material structure to performance. However, the extraction of physical meaning from the pre-edge region requires correlating the peaks in a XANES spectrum to the specific molecular orbitals into which an excited core electron transitions, often necessitating a computational approach. The density functional theory (DFT) is a valuable tool for unraveling complex contributions to X-ray absorption spectra. Like the Schrodinger wave equation that other quantum chemical methods rely on, the DFT is rooted in an electronic structure (Hohenberg and Kohn, 1964). However, instead of attempting to solve the wave equation, DFT uses exchange–correlation energy functional to define a system’s electronic density. These functionals are a mathematical description of how electrons interact with each other. This key element of DFT is how one can approach an interacting problem (solving the wave equation) by mapping it exactly to an easier-to-solve noninteracting problem (electron density) (Burke, 2007). From the electron density, it is then possible to determine the ground state electronic structure of the system from which materials’ physical properties arise. Calculated vibrational force constants provide insights into chemical bonding or behavior with other species (i.e., electrical polarizability and relative energies in chemical reactions). In relation to spectroscopic properties one can also find excitation energies to the nth excited state and the probabilities of their occurrence, also known as the density of states (DOS) (Kohn et al., 1996). As XAS is essentially a measure of partially occupied or unoccupied states available for an electron transition, DFT is a useful tool for associating X-ray absorption spectra peaks to specific core level electron transitions to unoccupied molecular orbitals. In other words, calculating the DOS identifies the unoccupied orbitals to which the core electrons can transition. However, the substantial difference in resolution between theory and experiment can readily lead to erroneous assignments; for example, from the DFT, it is known that the two lowest unoccupied states in MnO₂ are the t_2g spin-down and e_g spin-up, but these do not correspond to the first two peaks in the X-ray absorption spectrum (Figure 5) as the energy states are only separated by a few tenths of an electron volt and cannot be resolved using XAS. The first peak represents a combination of these two electronic transitions. Although computationally more intensive, simulating the X-ray absorption spectrum, as detailed below, can be critical to resolving multiple contributions to complex spectra for robust peak identifications, such as those resulting from hybridized states. In addition, when a simulated spectrum matches the experimental spectrum, it can be assumed that the DFT structural model that was used to simulate the XANES spectrum is accurate and the subsequent computational analyses are more likely to be reliable. The following two subsections provide further details on the DFT, and calculations are used to simulate XANES spectra.

3.3.1 Density functional theory

The density functional theory (DFT), which has consistently been the leading workhorse in electronic structure calculations with applications across a wide variety of systems and phenomena (Becke, 2014; Tozer and Peach, 2014; Jones, 2015; Besley, 2021), can be extremely useful in prediction, verification, and analysis of the experimental results in STCH research. The DFT is rooted in the two Hohenberg–Kohn theorems (Hohenberg and Kohn, 1964) which state that for any system of interacting electrons: 1) the external potential is uniquely determined by the ground state electron density, and 2) this density and the associated energy can be found variationally by minimizing the total energy as a function of the density. In practice, the DFT is used mostly within the Kohn–Sham (KS) (Kohn and Sham, 1965) framework, which seeks a fictitious noninteracting system of electrons whose densities equal that of the interacting system. Such a system is under the influence of the multiplicative KS potential: v_KS = v_ext + v_H + v_XC, where v_ext is the external potential on the interacting system, v_H is the classical Hartree potential corresponding to the electron density, and v_XC is the exchange–correlation (XC) potential, which accounts for the quantum mechanical exchange interaction and the effects of correlation that arise from the interaction between individual electron pairs beyond a mean-field treatment. The exact form of v_XC is as yet unknown and depending on the problem at hand, various approximations (Kohn and Sham, 1965; Becke, 1988; Lee et al., 1988; Perdew et al., 1996a; Rappoport et al., 2011) are used for this term. Additionally, for the sake of computational efficiency, many DFT calculations (especially those that use plane waves as the basis function) replace the collective effect of the core electrons with a pseudopotential (Hellmann, 1935; Schwerdtfeger, 2011) term dependent on the atomic species.

Even though KS-DFT does not guarantee an equivalence (Kohn et al., 1996) [the highest occupied level is an exception (Janak, 1978; Perdew et al., 1982; Perdew and Levy, 1997)] between the single-particle wave functions/energies of the KS system and those associated with the addition or removal of electrons in the real system, such an equivalence is often observed in many systems to an appreciable extent, although this can be subject to the use of exchange–correlation functionals pertaining to the generalized KS framework (Seidl et al., 1996; Kümmel and Kronik, 2008; Perdew et al., 2017). Therefore, the KS energies and wave functions are routinely used as approximate quasiparticle (Onida et al., 2002) counterparts in several contexts (e.g., band structure plots). However, it must be noted that commonly used (semi-)local XC potentials, within the local density approximation (LDA) (Kohn and Sham, 1965) or the generalized gradient approximation (GGA) (Perdew et al., 1996a; Perdew et al., 1996b), tend to delocalize the electron density unphysically (Mori-Sánchez et al., 2008) due to inherent self-interaction errors (Perdew, 1985), whereby each electron interacts spuriously with itself via the mean-field of all electrons. For STCH materials, the description of the electrons in the localized d and f orbitals of the transition metal/rare earth atoms can be heavily affected by such an error. Therefore, v_KS is usually supplemented with an additional orbital-dependent, nonlocal Hubbard correction (Himmetoglu et al., 2014) term that with a user-specified Hubbard parameter U [often obtained empirically (Wang et al., 2006)] enforces electron localization by penalizing fractional occupation in some predefined atomic d and/or f orbitals. Inclusion of a fraction of nonlocal exact exchange in v_KS (analogous to the Hartree–Fock calculations) can also counteract the self-interaction error, although typically at a much higher computational expense.

Regarding STCH research, the DFT can play a crucial role in complementing XRD experiments for structural analysis and XAS experiments for the analysis of electronic structure. The former is typically accomplished with the help of a calculation of geometry relaxation, which entails computing the net force on each ion as the gradient of the total energy and optimizing the structure until the force drops below a certain threshold. Additionally, the thermal motion of the ions can be simulated with the help of molecular dynamics (MD) (Car and Parrinello, 1985; Iftimie et al., 2005) or calculation of phonon (Giannozzi et al., 1991; Parlinski et al., 2005) modes. DFT-based computational tools are also routinely used in prediction and analysis of various spectroscopic experiments. KS-DFT is found to be particularly adept at simulating the K-edge absorption spectra (such as the oxygen K-edge) since multiplet effects typically play a minor role in such excitations and consequently, the corresponding many-body state can be approximated as a single-reference system (de Groot and Kotani, 2008), consistent with the existing common approximations to the exchange–correlation functional within the DFT.

3.3.2 Simulation of X-ray absorption spectra

Within the framework of KS-DFT, one tries to simulate the X-ray absorption spectrum by using Fermi’s golden rule #2 to compute the absorption probability:

$W\left(\omega \right)\propto \omega {\sum }_f{\left|\langle {\mathrm{\Psi }}_f\left|\widehat{T}\right|{\mathrm{\Psi }}_i\rangle \right|}^2\delta \left(E_f-E_i-\hslash \omega \right),(3)$

where $\omega$ is the angular frequency of the absorbed photon, $\widehat{T}$ is the transition operator, $|{\mathrm{\Psi }}_i\rangle \left(|{\mathrm{\Psi }}_f\rangle \right)$ is the initial (final) state associated with the X-ray absorption process, and $E_i\left(E_f\right)$ is the energy thereof. In the large-wavelength limit, $\widehat{T}$ can be expressed as the dipole operator $\mathit{e}·\widehat{\mathit{R}}$, where $\mathit{e}$ is a unit vector along the polarization direction and $\widehat{\mathit{R}}$ is the many-body position operator.

In practice, the absorption cross-section probability is found with the help of two separate KS self-consistent field (SCF) calculations: 1) a ground state SCF calculation for simulating the initial state and 2) another DFT calculation run on a positively charged system in which the core of the excited atom is represented by a modified pseudopotential mimicking a full core-hole (FCH) [alternatively, this calculation can be run with a neutral cell producing the excited-electron core-hole (XCH) state]. The latter calculation, referred to as the FCH state calculation hereafter, is used for extracting information on the final core-excited states. In the so-called single-particle treatment, the dipole matrix element is approximated as

$\langle {\mathrm{\Psi }}_{\mathrm{f}}\left|\mathit{e}.\widehat{\mathit{R}}\right|{\mathrm{\Psi }}_{\mathrm{i}}\rangle \approx \mathrm{S}\langle {\stackrel{\sim }{\varphi }}_c\left|\mathit{e}.\widehat{\mathit{r}}\right|{\mathrm{\varphi }}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}\rangle ,(4)$

where $\widehat{\mathit{r}}$ is the one-body position operator, ${\mathrm{\varphi }}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ denotes a core orbital, and ${\stackrel{\sim }{\varphi }}_c$, which is the orbital of the excited electron after the absorption, is an unoccupied (conduction) KS orbital of the FCH state. The recently developed many-body X-ray absorption spectroscopy (MBXAS) method (Liang et al., 2017; Liang and Prendergast, 2018; Liang and Prendergast, 2019) seeks to improve upon the single-particle treatment by approximating the many-body state $|{\mathrm{\Psi }}_f\rangle \left(|{\mathrm{\Psi }}_i\rangle \right)$ by a Slater determinant (SD) constructed by populating the relevant KS orbitals obtained from the FCH (ground) state calculation. Note that each possible final state will have a different set of occupied orbitals, and then, with some algebra, the transition matrix element reduces to

$\langle {\mathrm{\Psi }}_{\mathrm{f}}\left|\mathit{e}.\widehat{\mathit{R}}\right|{\mathrm{\Psi }}_{\mathrm{i}}\rangle =\sum _c^{empty}\langle {\mathrm{\Psi }}_{\mathrm{f}}|{\mathrm{\Psi }}_i^c\rangle \langle {\varphi }_c\left|\mathit{e}.\widehat{\mathit{r}}\right|{\mathrm{\varphi }}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}\rangle ,(5)$

where the sum is over all the unoccupied orbitals ${\varphi }_c$ of the ground state system and $|{\mathrm{\Psi }}_i^c\rangle$, which is a neutral core-excited state with an excited electron in the orbital ${\varphi }_c$, is represented (non–self-consistently) by an SD composed of the ground state–occupied valence KS orbitals in combination with ${\varphi }_c$. The term $\langle {\mathrm{\Psi }}_{\mathrm{f}}|{\mathrm{\Psi }}_i^c\rangle$, which is an inner product between two Slater determinants built from orbitals of two different SCF calculations (i.e., FCH and ground state calculation), can be reexpressed as the complex conjugate of a determinant composed of the overlap matrix elements between the FCH and ground state orbitals. Thus, in a nutshell, MBXAS expresses each transition matrix element as a weighted sum of single-particle transitions $\langle {\varphi }_c\left|\mathit{e}.\widehat{\mathit{r}}\right|{\mathrm{\varphi }}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}\rangle$ with the weighing factor given by the projection of the corresponding SD expressed in terms of the ground state orbitals onto an SD representing the actual final state of interest. It is important to note here that the abovementioned simulation methods, which use the KS eigenvalues/eigenfunctions in their pristine form, present a computationally cheaper and faster alternative to the techniques (Vinson et al., 2011; Gilmore et al., 2015; Vorwerk et al., 2019) rooted in many-body perturbation theory (Shirley, 1998; Rohlfing and Louie, 2000). They are particularly useful and efficient for systems with large unit cells (such as materials with defects) or for systems where the effect of finite-temperature lattice dynamics needs to be incorporated via molecular dynamics (Prendergast and Galli, 2006; Pascal et al., 2014; Roychoudhury et al., 2021a).

Using pseudopotentials (i.e., instead of including the core electrons explicitly) necessitates the use of an overall empirical shift to align to experimental energy scales. In addition, we must also account for the so-called chemical shifts associated with different chemical or coordination environments of the same excited element, for example, at symmetry inequivalent atomic sites in a given crystal or in entirely different materials. The use of two different sets of pseudopotentials for the ground and excited state calculations prevents us from relying on the raw total energy differences to align spectral contributions of inequivalent atoms. The relative excitation energies for distinct atomic sites are determined with respect to a common theoretical reference, the isolated atom (England et al., 2011; Jiang et al., 2013; Roychoudhury et al., 2021b). To this end, for excitation of atom X, the term $\left(E_f-E_i\right)$ in Eq. 3 is replaced by an effective formation energy difference,

$∆E_F=\left[E_f-e_X^{\prime }\right]-\left[E_{GS}-e_X\right],(6)$

where $e_X\left(e_X^{\prime }\right)$ denotes the total energy of the isolated, neutral atom X using the pseudopotential employed in the ground state (FCH) calculation. The total energy $E_f$ of any final state can now be estimated as

$E_f=E_{XCH}+\left({\displaystyle \sum }_i{\stackrel{\sim }{\epsilon }}_i-{\displaystyle \sum }_j{\stackrel{\sim }{\epsilon }}_j\right),(7)$

where $\stackrel{\sim }{\epsilon }$ denotes a Kohn–Sham orbital eigenenergy of the core hole–excited self-consistent field. The index i runs over all orbitals that are occupied in the final state of interest (f) but unoccupied in the so-called excited-electron core-hole (XCH) state (Prendergast and Galli, 2006), which is the core-excited state with the lowest energy. Conversely, the index j runs over all orbitals that are unoccupied in the final state f but occupied in the XCH state. The total energy $E_{XCH}$ of the XCH state can be found from a separate DFT SCF calculation on the neutral system employing the pseudopotentials used in the FCH calculation. In the simplest case involving the creation of only a single electron–hole pair upon X-ray absorption [denoted as $f^{\left(1\right)}$ in Liang and Prendergast (2018)], the realignment of the final state energies is accomplished with a simpler expression (since there is only one term in each sum above) for a system with $N$ valence electrons and a final excited state with a hole in the core orbital and an electron in orbital $f>N$:

$E_f=E_{XCH}+\left({\stackrel{\sim }{\epsilon }}_f-{\stackrel{\sim }{\epsilon }}_{N+1}\right).(8)$

This alignment scheme is crucial not only for comparing the onset energy of the spectra of different materials but also for simulating the accurate line shape of the resultant spectrum for a material in which the excited atomic species occupy multiple inequivalent sites. In particular, the aforementioned formalism has proven to be highly effective in simulating the O K-edge spectra, both in terms of line shape and onset energy, of transition metal oxides (Roychoudhury et al., 2021b).

Figure 10 shows the simulated O K-edge X-ray absorption spectra of CeO₂ (ceria) using the single-particle treatment (Eq. 4) and the MBXAS method (Eq. 5), with the latter being calculated separately using three different values of Hubbard U. It must be noted that even though Ce⁴⁺ is in a 4f₀ configuration in ceria, it is still important to use a Hubbard correction for the f electrons due to the hybridized nature of the electronic orbitals. Hubbard parameters ranging from U = 4.5 eV to U = 6 eV have been suggested (Fabris et al., 2005; Da Silva et al., 2007; Loschen et al., 2007; Ismail et al., 2011; Grieshammer et al., 2014; Grieshammer, 2018) in the existing literature. Comparison of the top three spectra in Figure 10 can attest to the importance of Hubbard U in XAS simulation of STCH materials. The two plots at the bottom of Figure 10, both of which are obtained using the same Hubbard parameter (U = 5.4 eV), show a severe underestimation of the pre-peak height in the single-particle FCH treatment when compared to the MBXAS spectrum, which is in good agreement with the experimental results (Aguiar et al., 2010). This underestimation is reported for oxides of a large number of transition metals and can be explained with the help of a simple tight-binding model (Liang and Prendergast, 2018). Thus, MBXAS, which can be seen to rectify the relative peak heights, is a particularly useful tool for research on STCH materials, which are typically transition metal/rare-earth oxides. Finally, we note that DFT-based simulations provide valuable information regarding the nature and constitution of the single-particle orbitals of the excited electrons. As representative examples, in Figure 11, we show the isovalue plots of three KS orbitals, transitions to which contribute appreciably to the first three peaks in the MBXAS spectrum shown with the green curve in Figure 10.

FIGURE 10

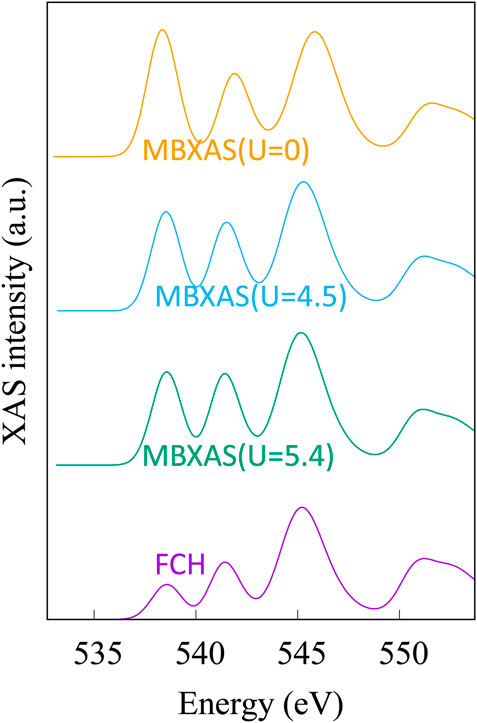
FIGURE 10. Simulated XAS plots for oxygen K-edge of CeO₂. In the “FCH” plot, the dipole matrix element is obtained with the single-particle treatment presented in Eq. 4. This plot is obtained from KS-DFT calculations using a Hubbard parameter of U = 5.4 eV. The three MBXAS plots, which correspond to different values of Hubbard U (namely, 5.4, 4.5, and 0 eV), use the many-body expression of Eq. 5 to calculate the dipole term.

FIGURE 11

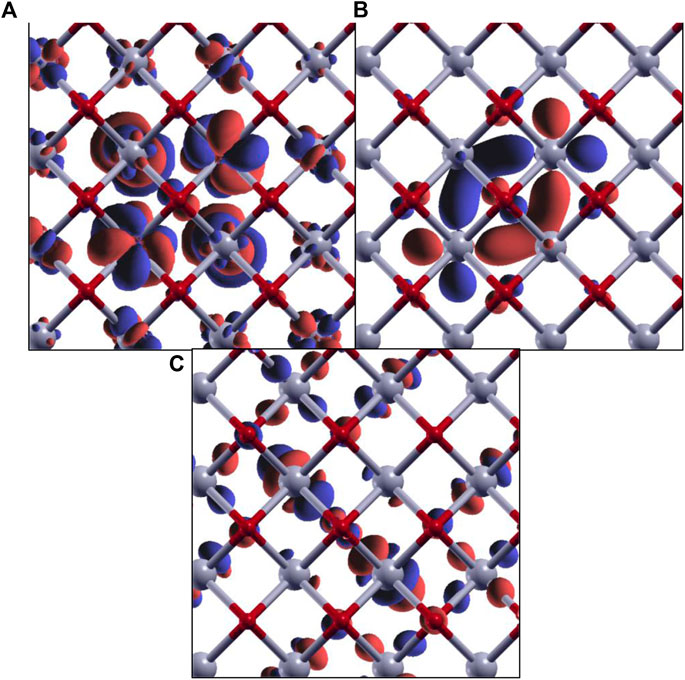
FIGURE 11. Isovalue plots of KS orbitals of the core-excited state with significant contribution in the first (A), second (B), and third (C) peaks in the O K-edge MBXAS plot, as shown in Figure 10 (green line). The red and gray spheres represent oxygen and cerium atoms, respectively. Note that these are all hybrid orbitals containing O p and Ce d/f characters, with different degrees of hybridization.

4 X-ray diffraction for solar thermochemical hydrogen production material characterization

XRD with a synchrotron X-ray source provides sensitivity and resolution unachievable with conventional laboratory-source diffractometers. Synchrotron XRD enables complex crystal structures to be solved (and resolved), subtle changes in the structure (such as strain or changes in bond distances) to be detected, and low-concentration impurity phases to be identified and quantified, features critical to unraveling STCH material behavior. The following provides a brief description of the fundamentals underlying XRD (Section 4.1) and its applicability for characterizing STCH materials (Section 4.2).

4.1 Brief introduction to X-ray diffraction

X-ray diffraction (XRD) is a scattering-based technique suitable for investigating the identity and arrangement of atoms within a given lattice. Here, an elementary background on the theory behind X-ray diffraction will be presented such that the reader is made familiar with how a diffraction experiment can aid the structural characterization and development of STCH materials.

Photon scattering is encountered when the wavelength of radiation is comparable to interatomic spacing. For incident photons having wave vector, k, scattering from two positions separated by r into scattered photons with wave vector, k’, the difference in the path length between the scattered wave vectors must be equal to (k—k’) · r = Q r, i.e., the normal projection of r onto Q. For elastic scattering, the phase difference between the incident and scattered waves must be equal to 2π/λ times the path difference in order for the photon to constructively interfere with the wave scattered from the adjacent atom. The Laue equations are formed when this one-dimensional example is further expanded into three dimensions. The intensity of scattering from a lattice of ordered atoms is defined by the crystal structure factor:

$F\left(\mathit{Q}\right)={\displaystyle \sum }_{{\mathit{r}}_j}{f}_j\left(\mathit{Q}\right)e^{i\mathit{Q}\bullet {\mathit{r}}_j}{\displaystyle \sum }_{{\mathit{R}}_n}{e}^{i\mathit{Q}\bullet {\mathit{R}}_n}.(9)$

The value of F(Q) is nonzero when Q coincides with a reciprocal lattice vector. f_j(Q) in the first summation of the expression above defines the atomic form factor, which is a measure of the X-ray “scattering efficiency” for a given atom. Since photons scatter via interactions with electrons, the form factor naturally increases monotonically as a function of atomic number, Z. The first summation in Eq. 9 describes scattering from atomic sites within a given unit cell, where j is the number of distinct atoms within the unit cell. The second summation extends the scattering contribution to the lattice sum and together these summations make up the crystal structure factor (Als-Nielsen and McMorrow, 2011).

4.2 Application of X-ray diffraction to solar thermochemical hydrogen production materials

As it pertains to STCH processes, ex situ XRD measurements provide the ability to solve the crystal structures of new candidate STCH compounds, demonstrate phase purities of as-synthesized and redox-cycled materials, and determine/differentiate lattice changes associated with thermal expansion and oxygen non-stoichiometry in the reduced state (Metcalfe et al., 2019). These properties are critical for evaluating the performance of a new candidate STCH material by identifying/separating contributions from the known impurity compounds/phases. In situ XRD measurements (e.g., high temperature and controlled gaseous environments) provide a valuable route for deriving relationships between atmospheric redox conditions and material structure (i.e., structure–property relationships) (Metcalfe et al., 2019; Mastronardo et al., 2020). The advantage of XRD with a synchrotron source is exemplified by Bell et al. (2022), where impurity phases at less than 0.4 weight percent were identified within the high-purity STCH material BCM, as well as by Strange et al. (2022), where a novel BCM polytype was identified and found to form under high-temperature reducing conditions. The results described in both studies would have not been observed with conventional laboratory-source XRD. The high brilliance offered by a synchrotron X-ray source also enables kinetic studies where structural changes can be monitored as fast as 1 kHz with hybrid photon counting detectors.

Using the most basic definition of a structural refinement, the atomic identities and positions are determined from experimental diffraction patterns in order to describe the crystal structure. Since the atomic form factor exhibits a dependence on atomic number, X-rays are relatively insensitive to oxygen atoms, especially when present in a lattice of elements with high Z (e.g., period 6 and 7 elements), which is the case for the top contending STCH materials. This limitation can be overcome with neutron diffraction, where the coherent scattering cross sections are independent of Z, and scattering from oxygen is appreciably relative to the cations. Additionally, in XRD, atoms with similar atomic numbers are not readily distinguished in a structural refinement since differences in form factor contributions are relatively low. To overcome this limitation, resonant X-ray diffraction is more suitable, whereby the diffraction intensities are recorded as the energy scanned over an atom’s absorption edge. The relative changes in diffraction intensities then allow for differentiation of site occupancies.

The two most common XRD measurement geometries are Debye–Scherrer (transmission) and Bragg–Brentano (reflection), both exhibiting advantages and disadvantages. Transmission measurements require small sample volumes and are often performed in capillaries that offer a uniform cylindrical geometry with respect to the scattering angle. Sample absorption is of particular concern in transmission geometry, but a correction to the observed diffraction intensities as a function of the scattering angle can be made with a priori knowledge of μ t (where μ is the linear attenuation coefficient and t is the sample thickness) and an estimated particle packing fraction. The primary advantage of transmission geometry is the ability to perform measurements in extreme environments (e.g., high/low temperatures and pressures and controlled atmospheres) with low attenuation from the sample cell (typically thin-walled borosilicate glass, quartz, or sapphire). Reflection geometries overcome the absorption problem but present additional complications. When performing in situ measurements with a heating stage, the poor thermal conductivity of STCH materials (e.g., thermally insulating ceramics) results in a severe temperature gradient between the heating element and radiated sample volume, particularly when the sample is in the form of a pressed puck. Powders measured in reflection geometry must be uniformly deposited using a suitable nonreactive solvent in order to prevent movement of the sample during gas flow. Using this approach, there are also potential complications with sample roughness, i.e., the change in apparent density as a function of powder depth. Alternatively, a thin film may be used, but there are uncertainties regarding the structure and STCH performance of thin films when compared to their bulk counterparts. In reflection geometries, since the heating element and sample are likely to expand as a function of increasing temperature, an external calibration should be performed such that the degree of expansion is known (and reproducible) and a manual correction of offset sample position can be applied to the data. Knowledge of the temperature-dependent sample displacement is especially important when differentiating the relative contributions of thermal vs chemical expansion of an oxide during STCH.

5 Survey of solar thermochemical hydrogen production applicable in situ tools

While laboratory in situ measurements of STCH materials are widely performed (such as thermogravimetric analysis mass spectrometry of the effluent gas to correlate mass loss or gain to the species lost), in situ measurements via X-ray methods at a synchrotron are much less common. For redox-active materials used in water-splitting processes, the temperatures required for reduction typically exceed 1,000°C and require fine control over pO₂. Some of the primary challenges associated with in situ measurements are access of photons at necessary energies to the sample (typically achieved through the choice of the window/capillary material), and a well-controlled sample environment exhibiting uniform temperature under simultaneous gas flow with a known composition. Heating samples to over 1,000°C is particularly challenging due to instrumental and material-based limitations. Conduction heating is highly inefficient for X-ray cells, which cannot be completely enclosed by heating elements and insulation. On the materials side, the number of mechanically stable and inert compounds, which are still permeable to X-rays, is very limited (Rothensteiner et al., 2015). Furthermore, the interpretation of structural data can be especially difficult at high temperatures where lattice motions distort the time-averaged depiction of the crystal structure. However, there are notable successes in the literature where synchrotron experiments have been carried out under realistic operating conditions, or a subset thereof, which are summarized below.

Among the studies that have used in situ synchrotron X-ray measurements for thermochemical cycling conditions, the most common techniques used are XPS, XAS, and XRD. Thermochemical energy storage materials have been investigated at temperatures under 1,000°C for materials systems such as Mg-H-F (Tortoza et al., 2018) for using H₂ as a hydrogen storage material, SrFeCuO₃ (Vieten et al., 2019) for oxygen storage and air separation, and reactive carbon composites such as BaCO₃ (Møller et al., 2020) and CaMg(CO₃)₂ (Humphries et al., 2019). These studies often use a quartz capillary tube with thin walls to hold the sample, allowing a controlled gas flow across the sample during transmission XRD, X-ray photoemission spectroscopy (XPS), and/or XAS measurements.

For ceria-based materials, which in some cases contain other elements such as Hf or Zr, the cerium K-edge has been measured under realistic thermochemical conditions, with the reduction occurring at 1,500°C and reoxidation at 800°C in the presence of steam or CO₂ (Rothensteiner et al., 2015; Rothensteiner et al., 2016; Rothensteiner et al., 2017). These studies use synchrotron X-rays to ultimately perform XAS, XRD, and simultaneous mass spectrometry (MS) in transmission geometry to measure full thermochemical cycles, ramping up to 1,500°C in Ar for reduction of the ceria, and cooling to 800°C before introducing CO₂ or steam for reoxidation. The heating source used was an infrared focusing furnace to heat an alumina inner tube while maintaining a cooler environment for the outer quartz tube leading to the gas outlet and MS (Rothensteiner et al., 2017). Additional studies have also been done using XANES under conditions up to 1,100°C with exposure to ambient air, vacuum, and hydrogen to examine surface concentration of Ce³⁺ in ceria–zirconia catalyst materials (Yuan et al., 2020).

6 Conclusion

Developing a robust redox-active metal oxide that performs well under reasonable operating conditions is key for realizing STCH as a commercially viable process for clean hydrogen generation. Progress in material development is contingent on developing structure–property relationships, which requires a mechanistic understanding of reactions, material stability, and failure routes. Synchrotron radiation is a powerful tool for characterizing STCH materials. X-ray absorption spectroscopy identifies those cations that are redox active and the extent to which they are reduced under quenched conditions. By probing the oxygen K-edge, XAS provides quantitative information on the extent of metal–oxygen hybridization and qualitative information on how the oxygen electronic environment responds to defects and reoxidation. X-ray diffraction provides the ability to solve the crystal structure of new materials and quantify purity, as well as identify secondary phases and determine how the crystal structure responds to oxygen defects during a redox cycle. The high-energy X-rays generated by a synchrotron source opens up opportunities for in situ experiments unobtainable with laboratory-scale techniques. While it would be impossible to cover all the information and details necessary to design and carry out the various synchrotron experiments, the goal herein has been to make interested readers aware of what can be learned from the various techniques relevant to STCH materials and provide a wealth of resources that can be further consulted.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Funding was provided by the HydroGEN Advanced Water Splitting Materials Consortium, established as part of the Energy Materials Network under the United States Department of Energy, Office of Energy Efficiency and Renewable Energy, Hydrogen and Fuel Cell Technologies Office, under Award Number DE-EE0008087. Computational work (SR and DP) was carried out using supercomputing resources of the National Energy Research Scientific Computing Center (NERSC). The work by SR and DP at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the United States Department of Energy under Contract No. DEAC02-05CH11231. The use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the United States Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. SS acknowledges funding from theWalter Ahlstróm Foundation. SS has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 841621.

Licenses and permissions

This work was authored in part by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the United States Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. The United States Government retains the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, and worldwide license to publish or reproduce the published form of this work, or allow others to do so, for United States Government purposes.

Conflict of interest

SS, RB, LM, KH and DG are employees of Alliance for Sustainable Energy, LLC. AM is employee of Sandia National Laboratories.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

The views expressed in the article do not necessarily represent the views of the DOE or the United States Government.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.931364/full#supplementary-material.

References

Ackermann, S., Sauvin, L., Castiglioni, R., Rupp, J. L., Scheffe, J. R., and Steinfeld, A. (2015). Kinetics of CO2 reduction over nonstoichiometric ceria. J. Phys. Chem. C 119 (29), 16452–16461. doi:10.1021/acs.jpcc.5b03464

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguiar, J., Grönbech-Jensen, N., Perlov, A., Milman, V., Gao, S., Pickard, C., et al. (2010). Electronic structure of oxide fuels from experiment and first principles calculations. J. Phys. Conf. Ser. 241, 012062. doi:10.1088/1742-6596/241/1/012062

CrossRef Full Text | Google Scholar

Alia, S., Ngo, C., Shulda, S., Dameron, A., Weker, J., Neyerlin, K., et al. (2017). Exceptional oxygen reduction reaction activity and durability of platinum–nickel nanowires through synthesis and post-treatment optimization. ACS Omega 2, 1408–1418. doi:10.1021/acsomega.7b00054

PubMed Abstract | CrossRef Full Text | Google Scholar

Als-Nielsen, J., and McMorrow, D. (2011). Elements of modern X-ray physics. Second Edition. Chichester, West Sussex, PO19 8SQ, United Kingdom: John Wiley & Sons, Ltd: The Atrium, Southern Gate.

Google Scholar

Barcellos, R. D., Sanders, M. D., Tong, J., McDaniel, A. H., and O'Hayre, R. P. (2018). BaCe0.25Mn0.75O3−δ—A promising perovskite-type oxide for solar thermochemical hydrogen production. Energy Environ. Sci. 11 (11), 3256–3265. doi:10.1039/c8ee01989d

CrossRef Full Text | Google Scholar

Becke, A. D. (1988). Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A . Coll. Park. 38 (6), 3098–3100. doi:10.1103/physreva.38.3098

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (2014). Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 140 (18), 18A301. doi:10.1063/1.4869598

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, R., Strange, N., Plattenberger, D., Shulda, S., Park, J., Ambrosini, A., et al. (2022). Synthesis of high-purity BaCe0.25Mn0.75O3; an improved material for thermochemical water splitting. Acta Crystallographica Section B. doi:10.1107/S2052520622010393

CrossRef Full Text | Google Scholar

Besley, N. A. (2021). Modeling of the spectroscopy of core electrons with density functional theory. WIREs Comput. Mol. Sci. 11 (6), e1527. doi:10.1002/wcms.1527

CrossRef Full Text | Google Scholar

Bork, A. H., Kubicek, M., Struzik, M., and Rupp, J. L. M. (2015). Perovskite La0.6Sr0.4Cr1−xCoxO3−δ solid solutions for solar-thermochemical fuel production: Strategies to lower the operation temperature. J. Mat. Chem. A Mat. 3 (30), 15546–15557. doi:10.1039/c5ta02519b

CrossRef Full Text | Google Scholar

Bunker, G. (2010). Introduction to XAFS: A practical guide to X-ray absorption fine structure spectroscopy. Cambridge: Cambridge University Press.

Google Scholar

Burke, K. (2007). The ABC of DFT. Irvine, CA: Department of Chemistry, University of CA.

Google Scholar

Calvin, S. (2013). XAFS for Everyone. 1 ed. Boca Raton: CRC Press, 457.

Google Scholar

Car, R., and Parrinello, M. (1985). Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55 (22), 2471–2474. doi:10.1103/physrevlett.55.2471

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, W.-H., de la Calle, A., Atwater, H. A., Stechel, E. B., and Xiang, C. (2021). Hydrogen from sunlight and water: A side-by-side comparison between photoelectrochemical and solar thermochemical water-splitting. ACS Energy Lett. 6 (9), 3096–3113. doi:10.1021/acsenergylett.1c00758

CrossRef Full Text | Google Scholar

Chueh, W. C., McDaniel, A. H., Grass, M. E., Hao, Y., Jabeen, N., Liu, Z., et al. (2012). Highly enhanced concentration and stability of reactive Ce3+ on doped CeO2 surface revealed in operando. Chem. Mat. 24 (10), 1876–1882. doi:10.1021/cm300574v

CrossRef Full Text | Google Scholar

Da Silva, J. L. F., Ganduglia-Pirovano, M. V., Sauer, J., Bayer, V., and Kresse, G. (2007). Hybrid functionals applied to rare-Earth oxides: The example of ceria. Phys. Rev. B 75 (4), 045121. doi:10.1103/physrevb.75.045121

CrossRef Full Text | Google Scholar

de Groot, F., and Kotani, A. (2008). Core level spectroscopy of solids. 1 ed. Boca Raton: CRC Press.

Google Scholar

Deml, A. M., Holder, A. M., O'Hayre, R. P., Musgrave, C. B., and Stevanovic, V. (2015). Intrinsic material properties dictating oxygen vacancy formation energetics in metal oxides. J. Phys. Chem. Lett. 6 (10), 1948–1953. doi:10.1021/acs.jpclett.5b00710

PubMed Abstract | CrossRef Full Text | Google Scholar

Deml, A. M., Stevanović, V., Muhich, C. L., Musgrave, C. B., and O'Hayre, R. (2014). Oxide enthalpy of formation and band gap energy as accurate descriptors of oxygen vacancy formation energetics. Energy Environ. Sci. 7 (6), 1996. doi:10.1039/c3ee43874k

CrossRef Full Text | Google Scholar

Emery, A. A., Saal, J. E., Kirklin, S., Hegde, V. I., and Wolverton, C. (2016). High-throughput computational screening of perovskites for thermochemical water splitting applications. Chem. Mat. 28 (16), 5621–5634. doi:10.1021/acs.chemmater.6b01182

CrossRef Full Text | Google Scholar

England, A. H., Duffin, A. M., Schwartz, C. P., Uejio, J. S., Prendergast, D., and Saykally, R. J. (2011). On the hydration and hydrolysis of carbon dioxide. Chem. Phys. Lett. 514 (4), 187–195. doi:10.1016/j.cplett.2011.08.063

CrossRef Full Text | Google Scholar

Fabris, S., de Gironcoli, S., Baroni, S., Vicario, G., and Balducci, G. (2005). Taming multiple valency with density functionals: A case study of defective ceria. Phys. Rev. B 71 (4), 041102. doi:10.1103/physrevb.71.041102

CrossRef Full Text | Google Scholar

Frati, F., Hunault, M. O. J. Y., and Groot, F. M. F. d. (2020). Oxygen K-edge X-ray absorption spectra. Chem. Rev. 120 (9), 4056–4110. doi:10.1021/acs.chemrev.9b00439

PubMed Abstract | CrossRef Full Text | Google Scholar

Giannozzi, P., de Gironcoli, S., Pavone, P., and Baroni, S. (1991). Ab initio calculation of phonon dispersions in semiconductors. Phys. Rev. B 43 (9), 7231–7242. doi:10.1103/physrevb.43.7231

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilmore, K., Vinson, J., Shirley, E. L., Prendergast, D., Pemmaraju, C. D., Kas, J. J., et al. (2015). Efficient implementation of core-excitation Bethe–Salpeter equation calculations. Comput. Phys. Commun. 197, 109–117. doi:10.1016/j.cpc.2015.08.014

CrossRef Full Text | Google Scholar

Grieshammer, S., Grope, B. O. H., Koettgen, J., and Martin, M. (2014). A combined DFT + U and Monte Carlo study on rare Earth doped ceria. Phys. Chem. Chem. Phys. 16 (21), 9974–9986. doi:10.1039/c3cp54811b

PubMed Abstract | CrossRef Full Text | Google Scholar

Grieshammer, S. (2018). Influence of the lattice constant on defects in cerium oxide. Phys. Chem. Chem. Phys. 20 (30), 19792–19799. doi:10.1039/c8cp03677b

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, Y., Yang, C.-K., and Haile, S. M. (2014). Ceria–zirconia solid solutions (Ce_1–<i>x</i>Zr_<i>x</i>O_2−δ, x ≤ 0.2) for solar thermochemical water splitting: A thermodynamic study. Chem. Mat. 26 (20), 6073–6082. doi:10.1021/cm503131p

CrossRef Full Text | Google Scholar

Hellmann, H. (1935). A new approximation method in the problem of many electrons. J. Chem. Phys. 3 (1), 61. doi:10.1063/1.1749559

CrossRef Full Text | Google Scholar

Himmetoglu, B., Floris, A., de Gironcoli, S., and Cococcioni, M. (2014). Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems. Int. J. Quantum Chem. 114 (1), 14–49. doi:10.1002/qua.24521

CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136 (3B), B864–B871. doi:10.1103/physrev.136.b864

CrossRef Full Text | Google Scholar

Humphries, T. D., Møller, K. T., Rickard, W. D. A., Sofianos, M. V., Liu, S., Buckley, C. E., et al. (2019). Dolomite: A low cost thermochemical energy storage material. J. Mat. Chem. A Mat. 7 (3), 1206–1215. doi:10.1039/c8ta07254j

CrossRef Full Text | Google Scholar

Iftimie, R., Minary, P., and Tuckerman, M. E. (2005). Ab initio molecular dynamics: Concepts, recent developments, and future trends. Proc. Natl. Acad. Sci. U. S. A. 102 (19), 6654–6659. doi:10.1073/pnas.0500193102

PubMed Abstract | CrossRef Full Text | Google Scholar

Ismail, A., Hooper, J., Giorgi, J. B., and Woo, T. K. (2011). A DFT+U study of defect association and oxygen migration in samarium-doped ceria. Phys. Chem. Chem. Phys. 13 (13), 6116–6124. doi:10.1039/c0cp02062a

PubMed Abstract | CrossRef Full Text | Google Scholar

Janak, J. F. (1978). Proof that∂E∂ni=εin density-functional theory. Phys. Rev. B 18 (12), 7165–7168. doi:10.1103/physrevb.18.7165

CrossRef Full Text | Google Scholar

Jiang, P., Prendergast, D., Borondics, F., Porsgaard, S., Giovanetti, L., Pach, E., et al. (2013). Experimental and theoretical investigation of the electronic structure of Cu2O and CuO thin films on Cu(110) using x-ray photoelectron and absorption spectroscopy. J. Chem. Phys. 138 (2), 024704. doi:10.1063/1.4773583

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, R. O. (2015). Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 87 (3), 897–923. doi:10.1103/revmodphys.87.897

CrossRef Full Text | Google Scholar

Kohn, W., Becke, A. D., and Parr, R. G. (1996). Density functional theory of electronic structure. J. Phys. Chem. 100 (31), 12974–12980. doi:10.1021/jp960669l

CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140 (4A), A1133–A1138. doi:10.1103/physrev.140.a1133

CrossRef Full Text | Google Scholar

Kümmel, S., and Kronik, L. (2008). Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 80 (1), 3–60. doi:10.1103/revmodphys.80.3

CrossRef Full Text | Google Scholar

Lany, S. (2008). Semiconductor thermochemistry in density functional calculations. Phys. Rev. B 78 (24), 245207. doi:10.1103/physrevb.78.245207

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37 (2), 785–789. doi:10.1103/physrevb.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Kuang, X., and Sun, J. (2021). Rare Earth elements based oxide ion conductors. Inorg. Chem. Front. 8 (5), 1374–1398. doi:10.1039/d0qi00848f

CrossRef Full Text | Google Scholar

Liang, Y., and Prendergast, D. (2018). Quantum many-body effects in x-ray spectra efficiently computed using a basic graph algorithm. Phys. Rev. B 97 (20), 205127. doi:10.1103/physrevb.97.205127

CrossRef Full Text | Google Scholar

Liang, Y., and Prendergast, D. (2019). Taming convergence in the determinant approach for x-ray excitation spectra. Phys. Rev. B 100 (7), 075121. doi:10.1103/physrevb.100.075121

CrossRef Full Text | Google Scholar

Liang, Y., Vinson, J., Pemmaraju, S., Drisdell, W. S., Shirley, E. L., and Prendergast, D. (2017). Accurate X-ray spectral predictions: An advanced self-consistent-field approach inspired by many-body perturbation theory. Phys. Rev. Lett. 118 (9), 096402. doi:10.1103/physrevlett.118.096402

PubMed Abstract | CrossRef Full Text | Google Scholar

Loschen, C., Carrasco, J., Neyman, K. M., and Illas, F. (2007). Erratum: First-principles LDA+U and GGA+U study of cerium oxides: Dependence on the effective U parameter [Phys. Rev. B75, 035115 (2007)]. Phys. Rev. B 75 (3), 199906. doi:10.1103/physrevb.84.199906

CrossRef Full Text | Google Scholar

Lu, Y., Zhu, L., Agrafiotis, C., Vieten, J., Roeb, M., and Sattler, C. (2019). Solar fuels production: Two-step thermochemical cycles with cerium-based oxides. Prog. Energy Combust. Sci. 75, 100785. doi:10.1016/j.pecs.2019.100785

CrossRef Full Text | Google Scholar

Marrocchelli, D., Bishop, S. R., Tuller, H. L., and Yildiz, B. (2012). Understanding chemical expansion in non-stoichiometric oxides: Ceria and zirconia case studies. Adv. Funct. Mat. 22 (9), 1958–1965. doi:10.1002/adfm.201102648

CrossRef Full Text | Google Scholar

Mastronardo, E., Qian, X., Coronado, J. M., and Haile, S. M. (2020). The favourable thermodynamic properties of Fe-doped CaMnO3 for thermochemical heat storage. J. Mat. Chem. A Mat. 8 (17), 8503–8517. doi:10.1039/d0ta02031a

CrossRef Full Text | Google Scholar

McDaniel, A. H., Miller, E. C., Arifin, D., Ambrosini, A., Coker, E. N., O'Hayre, R., et al. (2013). Sr- and Mn-doped LaAlO3−δ for solar thermochemical H2 and CO production. Energy Environ. Sci. 6 (8), 2424. doi:10.1039/c3ee41372a

CrossRef Full Text | Google Scholar

Metcalfe, I. S., Ray, B., Dejoie, C., Hu, W., de Leeuwe, C., Dueso, C., et al. (2019). Overcoming chemical equilibrium limitations using a thermodynamically reversible chemical reactor. Nat. Chem. 11 (7), 638–643. doi:10.1038/s41557-019-0273-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Møller, K. T., Williamson, K., Buckley, C. E., and Paskevicius, M. (2020). Thermochemical energy storage properties of a barium based reactive carbonate composite. J. Mat. Chem. A Mat. 8 (21), 10935–10942. doi:10.1039/d0ta03671d

CrossRef Full Text | Google Scholar

Mori-Sánchez, P., Cohen, A. J., and Yang, W. (2008). Localization and delocalization errors in density functional theory and implications for band-gap prediction. Phys. Rev. Lett. 100 (14), 146401. doi:10.1103/physrevlett.100.146401

PubMed Abstract | CrossRef Full Text | Google Scholar

Muhich, C. L., Ehrhart, B. D., Witte, V. A., Miller, S. L., Coker, E. N., Musgrave, C. B., et al. (2015). Predicting the solar thermochemical water splitting ability and reaction mechanism of metal oxides: A case study of the hercynite family of water splitting cycles. Energy Environ. Sci. 8 (12), 3687–3699. doi:10.1039/c5ee01979f

CrossRef Full Text | Google Scholar

Naghavi, S. S., Emery, A. A., Hansen, H. A., Zhou, F., Ozolins, V., and Wolverton, C. (2017). Giant onsite electronic entropy enhances the performance of ceria for water splitting. Nat. Commun. 8 (1), 285. doi:10.1038/s41467-017-00381-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Onida, G., Reining, L., and Rubio, A. (2002). Electronic excitations: Density-functional versus many-body green's-function approaches. Rev. Mod. Phys. 74 (2), 601–659. doi:10.1103/revmodphys.74.601

CrossRef Full Text | Google Scholar

Parlinski, K. (2005). “Lattice dynamics: Vibrational modes,” in Encyclopedia of condensed matter physics. Editors F. Bassani, G. L. Liedl, and P. Wyder (Oxford: Elsevier), 98–102.

CrossRef Full Text | Google Scholar

Pascal, T. A., Boesenberg, U., Kostecki, R., Richardson, T. J., Weng, T.-C., Sokaras, D., et al. (2014). Finite temperature effects on the X-ray absorption spectra of lithium compounds: First-principles interpretation of X-ray Raman measurements. J. Chem. Phys. 140 (3), 034107. doi:10.1063/1.4856835

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Wang, Y. (1996). Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 54 (23), 16533–16539. doi:10.1103/physrevb.54.16533

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P. (1985). Density functional theory and the band gap problem. Int. J. Quantum Chem. 28 (S19), 497–523. doi:10.1002/qua.560280846

CrossRef Full Text | Google Scholar

Perdew, J. P., and Levy, M. (1997). Comment on “Significance of the highest occupied Kohn-Sham eigenvalue”. Phys. Rev. B 56 (24), 16021–16028. doi:10.1103/physrevb.56.16021

CrossRef Full Text | Google Scholar

Perdew, J. P., Parr, R. G., Levy, M., and Balduz, J. L. (1982). Density-functional theory for fractional particle number: Derivative discontinuities of the energy. Phys. Rev. Lett. 49 (23), 1691–1694. doi:10.1103/physrevlett.49.1691

CrossRef Full Text | Google Scholar

Perdew, J. P., Yang, W., Burke, K., Yang, Z., Gross, E. K. U., Scheffler, M., et al. (2017). Understanding band gaps of solids in generalized Kohn–Sham theory. Proc. Natl. Acad. Sci. U. S. A. 114 (11), 2801–2806. doi:10.1073/pnas.1621352114

PubMed Abstract | CrossRef Full Text | Google Scholar

Perret, R. (2011). Solar thermochemical hydrogen production research (STCH): Thermochemical cycles selection and investment priority. New Mexico, United States: Sandia National Laboratories.

Google Scholar

Prendergast, D., and Galli, G. (2006). X-ray absorption spectra of water from first principles calculations. Phys. Rev. Lett. 96 (21), 215502. doi:10.1103/physrevlett.96.215502

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, C. N. R., and Dey, S. (2017). Solar thermochemical splitting of water to generate hydrogen. Proc. Natl. Acad. Sci. U. S. A. 114 (51), 13385–13393. doi:10.1073/pnas.1700104114

PubMed Abstract | CrossRef Full Text | Google Scholar

Rappoport, D., Crawford, N. R. M., Furche, F., and Burke, K. (2011). “Approximate density functionals: Which should I choose?,” in Encyclopedia of inorganic and bioinorganic Chemistry (New Jersey, United States: Wiley Online Library).

Google Scholar

Ravel, B., Newville, M., and Athena, A. R. T. E. M. I. S. (2005). ATHENA, artemis, hephaestus: Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 12 (4), 537–541. doi:10.1107/s0909049505012719

PubMed Abstract | CrossRef Full Text | Google Scholar

Rohlfing, M., and Louie, S. G. (2000). Electron-hole excitations and optical spectra from first principles. Phys. Rev. B 62 (8), 4927–4944. doi:10.1103/physrevb.62.4927

CrossRef Full Text | Google Scholar

Rothensteiner, M., Bonk, A., Vogt, U. F., Emerich, H., and van Bokhoven, J. A. (2016). Structural changes in Ce0.5Zr0.5O2−δ under temperature-swing and isothermal solar thermochemical looping conditions determined by in situ Ce K and Zr K edge X-ray absorption spectroscopy. J. Phys. Chem. C 120 (26), 13931–13941. doi:10.1021/acs.jpcc.6b03367

CrossRef Full Text | Google Scholar

Rothensteiner, M., Jenni, J., Emerich, H., Bonk, A., Vogt, U. F., and van Bokhoven, J. A. (2017). In situ flow cell for combined X-ray absorption spectroscopy, X-ray diffraction, and mass spectrometry at high photon energies under solar thermochemical looping conditions. Rev. Sci. Instrum. 88 (8), 083116. doi:10.1063/1.4994890

PubMed Abstract | CrossRef Full Text | Google Scholar

Rothensteiner, M., Sala, S., Bonk, A., Vogt, U., Emerich, H., and van Bokhoven, J. A. (2015). Ce K edge XAS of ceria-based redox materials under realistic conditions for the two-step solar thermochemical dissociation of water and/or CO2. Phys. Chem. Chem. Phys. 17 (40), 26988–26996. doi:10.1039/c5cp03179f

PubMed Abstract | CrossRef Full Text | Google Scholar

Roychoudhury, S., Qiao, R., Zhuo, Z., Li, Q., Lyu, Y., Kim, J.-H., et al. (2021). Deciphering the oxygen absorption pre-edge: A caveat on its application for probing oxygen redox reactions in batteries. Energy Environ. Mat. 4 (2), 246–254. doi:10.1002/eem2.12119

CrossRef Full Text | Google Scholar

Roychoudhury, S., Zhuo, Z., Qiao, R., Wan, L., Liang, Y., Pan, F., et al. (2021). Controlled experiments and optimized theory of absorption spectra of Li metal and salts. ACS Appl. Mat. Interfaces 13 (38), 45488–45495. doi:10.1021/acsami.1c11970

PubMed Abstract | CrossRef Full Text | Google Scholar

Sai Gautam, G., Stechel, E. B., and Carter, E. A. (2020). Exploring Ca–Ce–M–O (M = 3d transition metal) oxide perovskites for solar thermochemical applications. Chem. Mat. 32, 9964–9982. doi:10.1021/acs.chemmater.0c02912

CrossRef Full Text | Google Scholar

Schwerdtfeger, P. (2011). The pseudopotential approximation in electronic structure theory. ChemPhysChem 12 (17), 3143–3155. doi:10.1002/cphc.201100387

PubMed Abstract | CrossRef Full Text | Google Scholar

Seidl, A., Görling, A., Vogl, P., Majewski, J. A., and Levy, M. (1996). Generalized Kohn-Sham schemes and the band-gap problem. Phys. Rev. B 53 (7), 3764–3774. doi:10.1103/physrevb.53.3764

PubMed Abstract | CrossRef Full Text | Google Scholar

Shirley, E. L. (1998). Ab initio inclusion of electron-hole attraction: Application to X-ray absorption and resonant inelastic X-ray scattering. Phys. Rev. Lett. 80 (4), 794–797. doi:10.1103/physrevlett.80.794

CrossRef Full Text | Google Scholar

Steinfeld, A. (2005). Solar thermochemical production of hydrogen––a review. Sol. Energy 78 (5), 603–615. doi:10.1016/j.solener.2003.12.012

CrossRef Full Text | Google Scholar

Stöhr, J. (1992). NEXAFS spectroscopy. 1 ed. Germany: Springer-Verlag Berlin Heidelberg, 404.

Google Scholar

Strange, N. A., Park, J. E., Goyal, A., Bell, R. T., Trindell, J. A., Sugar, J. D., et al. (2022). formation of 6H-Ba3Ce0.75Mn2.25O9 during thermochemical reduction of 12R-Ba4CeMn3O12: Identification of a polytype in the Ba(Ce, Mn)O3 family. Inorg. Chem. 61 (16), 6128–6137. doi:10.1021/acs.inorgchem.2c00282

PubMed Abstract | CrossRef Full Text | Google Scholar

Suntivich, J., Hong, W. T., Lee, Y.-L., Rondinelli, J. M., Yang, W., Goodenough, J. B., et al. (2014). Estimating hybridization of transition metal and oxygen states in perovskites from O K-edge X-ray absorption spectroscopy. J. Phys. Chem. C 118, 1856–1863. doi:10.1021/jp410644j

CrossRef Full Text | Google Scholar

Tanwar, K., Jaiswal, N., Kumar, D., and Parkash, O. (2016). Synthesis & characterization of Dy and Ca Co-doped ceria based solid electrolytes for IT-SOFCs. J. Alloys Compd. 684, 683–690. doi:10.1016/j.jallcom.2016.05.223

CrossRef Full Text | Google Scholar

Thompson, A., Attwood, D., Gullikson, E., Howells, M., Kim, K.-J., Kirz, J., et al. (2009). X-ray data booklet. 3 ed. Berkeley, CA: Lawernce Berkeley National Laboratory.

Google Scholar

Tortoza, M. S., Humphries, T. D., Sheppard, D. A., Paskevicius, M., Rowles, M. R., Sofianos, M. V., et al. (2018). Thermodynamics and performance of the Mg–H–F system for thermochemical energy storage applications. Phys. Chem. Chem. Phys. 20 (4), 2274–2283. doi:10.1039/c7cp07433f

PubMed Abstract | CrossRef Full Text | Google Scholar

Tozer, D. J., and Peach, M. J. G. (2014). Density functional theory and its applications. Phys. Chem. Chem. Phys. 16 (28), 14333. doi:10.1039/c4cp90074j

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsvetkov, N., Lu, Q., Sun, L., Crumlin, E. J., and Yildiz, B. (2016). Improved chemical and electrochemical stability of perovskite oxides with less reducible cations at the surface. Nat. Mat. 15 (9), 1010–1016. doi:10.1038/nmat4659

PubMed Abstract | CrossRef Full Text | Google Scholar

Vieten, J., Bulfin, B., Starr, D. E., Hariki, A., de Groot, F. M. F., Azarpira, A., et al. (2019). Redox behavior of solid solutions in the SrFe1-xCuxO3-δ system for application in thermochemical oxygen storage and air separation. Energy Technol. 7 (1), 131–139. doi:10.1002/ente.201800554

CrossRef Full Text | Google Scholar

Vinson, J., Rehr, J. J., Kas, J. J., and Shirley, E. L. (2011). Bethe-Salpeter equation calculations of core excitation spectra. Phys. Rev. B 83 (11), 115106. doi:10.1103/physrevb.83.115106

PubMed Abstract | CrossRef Full Text | Google Scholar

Vorwerk, C., Aurich, B., Cocchi, C., and Draxl, C. (2019). Bethe–salpeter equation for absorption and scattering spectroscopy: Implementation in the exciting code. Electron. Struct. 1 (3), 037001. doi:10.1088/2516-1075/ab3123

CrossRef Full Text | Google Scholar

Wang, L., Maxisch, T., and Ceder, G. (2006). Oxidation energies of transition metal oxides within theGGA+Uframework. Phys. Rev. B 73 (19), 195107. doi:10.1103/physrevb.73.195107

CrossRef Full Text | Google Scholar

Webb, S. M. (2005). Sixpack: A graphical user interface for XAS analysis using ifeffit. Phys. Scr., 1011. doi:10.1238/physica.topical.115a01011

CrossRef Full Text | Google Scholar

Yuan, W., Ma, Q., Liang, Y., Sun, C., Narayanachari, K. V. L. V., Bedzyk, M. J., et al. (2020). Unexpected trends in the enhanced Ce3+ surface concentration in ceria–zirconia catalyst materials. J. Mat. Chem. A Mat. 8 (19), 9850–9858. doi:10.1039/d0ta02762f

CrossRef Full Text | Google Scholar

Zhang, S., Han, N., and Tan, X. (2015). Density functional theory calculations of atomic, electronic and thermodynamic properties of cubic LaCoO3 and La1−xSrxCoO3surfaces. RSC Adv. 5 (1), 760–769. doi:10.1039/c4ra12563k

CrossRef Full Text | Google Scholar

Zinkevich, M., Djurovic, D., and Aldinger, F., Thermodynamic modelling of the cerium–oxygen system☆. Solid State Ionics 2006, 177 (11-12), 989–1001. doi:10.1016/j.ssi.2006.02.044

CrossRef Full Text | Google Scholar