Analysis of Digital Operation of Rural Sewage Treatment System in Big Data Environment by Discrete Dynamic Modeling Technology

Sewage treatment is a process with high energy consumption and pollution. In the current situation of energy shortage and fierce competition in the paper industry market, how to reduce the energy cost is related to the survival and development of every sewage treatment plant. With the rise of big data environment in the internet, discrete dynamic modeling technology has developed very rapidly. Discrete dynamic modeling technology is a dynamic model system that can connect the information of different things, so as to form a dynamic model system that can control all devices or data. The object attributes processed by the model system also determine the nature of the dynamic model system. As we all know, the big data environment is a large database with complex data types, so the dynamic model system in the big data environment is nonlinear. This paper mainly studies the historical development trend of big data environment and discrete dynamic modeling technology, as well as the stability method of five level H-bridge when discrete dynamic modeling technology controls rural sewage treatment system. Finally, the control of chaotic bifurcation in discrete dynamic model system under digital background is studied. It includes the rectifier modeling of the current data required by large devices in the sewage treatment system and the result analysis of the generated values.

Introduction

With increasing strictness in emission limits of pollutants, the cost of water pollution control is increasing with every year. The energy consumption of the sewage treatment plant accounts for about 40% of the operating cost. High energy consumption seriously hinders the construction and operation of sewage treatment plants, so many sewage treatment plants are unable to sustain development, so it is the trend of the industry to reduce energy consumption and achieve sustainable development of sewage treatment.

Discrete dynamic modeling technology has been fully integrated into human beings. This technology has very high practical value in society. Because, the essence of this technology belongs to the modeling knowledge in mathematics, it is difficult to fully master the discrete dynamic modeling technology (matekenya Dunstan et al., 2021) (Dunstan et al., 2021). With the historical development of discrete dynamic modeling technology, researchers around the world have invested a lot of human and material resources in the exploration and innovation of this technology, breakthrough in application fields and system R and D. Discrete dynamic modeling technology is also evolving with the development trend of computer science, and is gradually applied in various fields (Alain djazet et al., 2020) (Djazet et al., 2020). Although the development of discrete dynamic modeling technology has not reached the final form, data errors often occur in the application process. However, the future development prospect of this technology is very broad, and its development has also become a hot spot of social concern (Zhongxin Ni et al., 2020) (Ni et al., 2021). With the innovation of material industry, the material of manufacturing discrete dynamic model system has achieved the goal of reducing manufacturing cost. Due to the characteristics of low manufacturing cost, discrete dynamic modeling technology is gradually applied to various industries.

Discrete dynamic modeling technology began to be developed abroad earlier, and relevant foreign researchers are more mature in terms of cognition and reference methods of this technology. Discrete dynamic modeling technology originated from mathematical model, and then applied to data statistics, discrimination, and calculation and so on. Discrete dynamic modeling technology mainly depends on the data information generated by things. By classifying, calculating and assimilating the data, the overall data trend is finally obtained, which also provides convenience for users applying discrete dynamic modeling technology (A. I. sukhinov et al., 2020) (Sukhinov et al., 2020). In the process of realizing discrete dynamic modeling technology, the principle of data transportation should be followed. The data information of things is processed and analyzed through a special data transmission device. Discrete dynamic model system can be regarded as an integrator of data. It not only includes big data environment, but also includes data processing system and anti loss system (D. a. Komarov et al., 2020) (Komarov et al., 2020). We can regard the discrete dynamic model system as an internal memory of the computer. It is a model environment for interacting with data. People can clearly understand all kinds of information between data through the computer.

This paper is mainly composed of three parts.

1) Firstly: introduces the application of discrete dynamic modeling technology in rural sewage treatment system, and the development status of discrete dynamic modeling technology.

2) Secondly: Research the stability of rural sewage treatment system under discrete dynamic modeling technology and the control of rural sewage treatment system under discrete dynamic modeling technology.

3) Thirdly: result analysis of rural sewage treatment system under discrete dynamic modeling technology, and the control result analysis of rural sewage treatment system under discrete dynamic modeling technology.

Related Work

The related concepts of discrete dynamic modeling technology have been put forward a long time ago, and its emergence indirectly reflects the positive development of big data in the Internet. It also promotes the innovation and application of discrete dynamic modeling technology (Nauman Raza et al., 2020) (Raza et al., 2020). The embryonic stage of discrete dynamic modeling technology first appeared in the 1950s. Subsequently, it appeared in the paper jointly issued by French mathematician David Ruelle and Dutch mathematician Floris Takens, and proposed the formation mechanism of using chaotic data to describe the results for the first time in the field of mathematics. Later, mathematicians from various countries put forward more kinds of related concepts and began to carry out experimental application in the 1970s (Antonio gon ç Alves et al., 2020) (Gonçalves et al., 2020). However, due to the immature development of computers at that time, the progress of experimental application was very slow. Many error messages also appeared in the application process, so that the technology was affected by conditions and did not get very big response at that time (lorella Fatone et al., 2020) (Fatone and Mariani, 2020). Then, due to the development of computers in the 1990s, discrete dynamic modeling technology gradually broke through the difficulties. Relevant researchers have applied discrete dynamic modeling technology to the processing of stock data and achieved great success. This is also the first time that discrete dynamic modeling technology has been applied to human life (Wen Ling Tian et al., 2020) (Tian et al., 2020).

The development speed of discrete dynamic modeling technology in the United States is faster than that in other countries. The first successful application of discrete dynamic systems to practice was in the United States (Mengjie Zhang et al., 2019) (Zhang et al., 2019). Discrete dynamic modeling technology is combined with stock information to systematically analyze the rise and fall data of various stocks. The stock information data processed with discrete dynamic modeling technology can better reflect the fluctuation trend of stock data over a period of time compared with all kinds of disorderly data (babita K. Verma et al., 2019) (Verma et al., 2019). With the application of discrete dynamic modeling technology to integrate stock data, it is gradually applied to other directions in the financial field. The introduction of this technology has also taken a big step forward for the American economy.

Japan’s discrete dynamic modeling technology has made a breakthrough in medicine (Wei Chao Li et al., 2019) (Li et al., 2019). They use discrete dynamic modeling technology to integrate the patient’s vital signs data, and then transmit the processed vital signs data to the screen, so as to observe the patient’s vital signs in real time. Japanese researchers have used the discrete dynamic model system to create a data collection database for data, which can not only collect the vital signs data of patients, but also classify and calculate the data (Truong thi Nguyen et al., 2019) (Nguyen et al., 2019). However, at that time, the technology was not widely used in major hospitals. Later, with the development of society, people gradually realized the importance of medical treatment and began to apply it on a large scale. Today, medical institutions all over the country have fully covered the technology.

France applies discrete dynamic modeling technology to military field. They mainly apply discrete dynamic modeling technology to detect vehicle faults. In order to improve the work quality of inspectors, discrete dynamic modeling technology needs to be combined with the original data information of normal vehicle components. Then compare the real-time information transmitted by the tested vehicle with the data. Once the data deviation is large, the tester can accurately find the fault and repair the vehicle in time (Joseph F. hair et al., 2019) (Hair et al., 2019). The introduction of this technology can greatly save the capital cost of the army. In the actual combat drill, the quality of vehicles is also directly related to the training effect, which also provides a guarantee for the safety of soldiers.

China has moved discrete dynamic modeling technology to the transportation industry. As we all know, Chinese people generally like to shop online, and the transportation volume of goods is also very huge. Because discrete dynamic modeling technology can classify and process the data of things, it can accurately store and output the package information. Classify the package data information to the greatest extent, so as to improve the delivery speed of products (Daniel Ioan et al., 2019) (Ioan et al., 2019). The combination of discrete dynamic modeling technology and transportation industry has directly affected the domestic economy and made China the largest transportation country in the world (Li et al., 2021a; Li et al., 2021b; Le et al., 2021; Toyoda and Wu, 2021; Wu et al., 2021; Zhang et al., 2022).

What is mentioned above is the historical development trend and status of discrete dynamics modeling technology in each country, both of which reflect the remarkable characteristics of discrete dynamics modeling technology for social development.

Methodology

Study on Stability of Rural Sewage Treatment System Based on Discrete Dynamic Modeling Technology

The rural sewage treatment system contains five level H bridge. Usually, in order to observe the stability of the bridge in the sewage treatment equipment, the discrete dynamic modeling technology is combined to observe the data. At present, the phenomenon of bifurcation and chaos in the bridge is of practical significance to the correlation design of data parameter information and stability analysis. When analyzing and processing the stability of data parameters, it is mainly to build a discrete dynamic model based on the state of bridge inverter, and then analyze the data information. The discrete dynamic model constructed cannot be an ordinary discrete model, but must be a discrete dynamic model for accurate analysis of data. Because the composition of the bridge is a very complex form of current pulse, the number of levels obtained during data sampling in the sewage treatment system are different. In order to solve this problem, this paper introduces the virtual ergodic modeling method into the refined discrete dynamic model. With the addition of this method, the influence of data complexity on system stability is easily solved.

As shown in Figure 1A, the power consumption per ton of sewage in traditional sewage treatment is between 0.305 and 0.5 kW h, and the fluctuation is large, with a fluctuation range of up to 57%. The energy consumption after using discrete dynamic modeling technology is between 0.167 and 0.221, and the fluctuation range is reduced to about 32%. The most important thing is that the overall power consumption shows a downward trend, up to 64.7%, that is, the same ton of wastewater is treated. the power consumption is reduced by 64.7%

FIGURE 1

FIGURE 1. Five level data modulation diagram.

The virtual traversal method mainly samples the data at different times, and obtains the model mapped within the system from the obtained data and the state variables in a period of time. For the five level H-bridge, the virtual ergodic method combined with carrier modulation is used to determine the dynamic model of the system. The modulation schematic diagram of five level SPWM is shown in Figure 1B.

It can be seen from Figure 1B that the level generated in different time periods is different, so it is difficult to establish the discrete dynamic system within the sampling time. Combined with the modulation principle of the above five-level SPWM, this paper extends the level state in the sewage treatment system, and then constructs the discrete dynamic model. The level expansion phase equation in the system is as follows:

$\frac{\mathrm{di}}{dt}=-\frac{R}{L}i+\frac{\delta E}{L},\delta \in \left\{\mathrm{2,1}\right\}\cup \left\{\mathrm{1,0}\right\}\cup \left\{0,-1\right\}\cup \left\{-1,-2\right\}(1)$

Among them, the generated level coefficient can be taken within a period of time, and the value can be eight values. In the ordinary sampling time period, only two values can be taken, so the method studied in this paper is called virtual traversal method. In order to solve the above formula, a standard differential equation is given as follows:

$\frac{\mathrm{dy}}{dt}=ay+b,y=-\frac{a}{b}+C_e^{at}(2)$

After the numerical solution is brought in, the solution of the equation is obtained, and then the current state is transmitted. After the final current goes through the eighth state, the relevant formula about the value is as follows:

$i_{n+1}=\frac{{\delta }_{8}E}{R}+\left(i_n-\frac{{\delta }_{1}E}{R}\right)e^{-\frac{R}{L}{T}^2}+\left\{{\displaystyle \sum _{k=1}^7\left[\frac{\left({\delta }_k-{\delta }_{k+1}\right)E}{R}{e}^{\frac{R}{L}{\displaystyle \sum _{j=1}^k{d}_j{T}_{\text{s}}}}\right]}\right\}{e}^{-\frac{R}{L}{T}_S}(3)$

The above contents are also the final discrete dynamic model of sewage treatment system and discrete dynamic modeling technology. In the above formula, it is mainly obtained by comparing the device modulation wave with the carrier wave. In this experiment, the duty cycle inside the model needs to be determined. Since the current has eight states, it can be seen that there are eight duty cycles. Since the duty cycle can be expressed by matrix function, the symbolic function is used to unify the duty cycle. The relevant formula is as follows:

$\mathrm{sgn}\left(x\right)=\left\{\begin{array}{c}1,x\ge 0\\ -1,x<0\end{array}\right\}(4)$

$\frac{d\mathrm{sgn}\left(x\right)}{dx}=2\delta \left(x\right)(5)$

It should be noted that in the function formula, the function is meaningful only when it is zero. Finally, the duty cycle is finally expressed with the above symbols, and the form formula is as follows:

${\left[d1\dots d7\right]}^T=T\left(V^{\ast }\right)=T_{\mathrm{s}}.\left[\frac{\mathrm{sgn}\left(x\right)+\mathrm{sgn}\left(x\prime \right)}{2}\left(V^{\ast }\right)\right](6)$

According to the above formula, the key content of the virtual traversal method is to obtain all the data information of the internal state of the system. The combination of discrete dynamic modeling technology and rural sewage treatment system focuses on the composition between data duty cycle and modulation. Only when the data between them are expressed in a functional way can the stability of the whole system be analyzed later. In this paper, the method of transforming data relationship into symbolic function is also very suitable for solving the modeling problem of device data in the system.

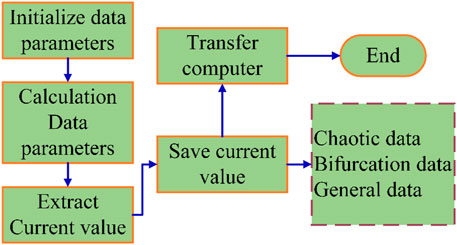
After the discrete dynamic model system is established, the stability of the inverter bridge can be analyzed. The process of determining whether the system is stable is shown in Figure 2.

FIGURE 2

FIGURE 2. Flow chart for judging system stability.

As can be seen from Figure 2, the flow chart is mainly divided into three layers. The innermost layer is mainly used to calculate the current data, and the other two layers are mainly used to convert the data. In the process of calculation, the relevant formulas for the definition of variables and the characteristic equation of the matrix are as follows:

$X={\gamma }_{R_{n-2}},y_n={\gamma }_{R_{n-1}},z_n=i_{n-1},q_n=i_n(7)$

$p\left(z\right)=a_0{z}^4+a_1{z}^3+a_2{z}^2+a_{3}z+a_4(8)$

According to the above formula, in the rural sewage treatment system in this paper, the data generated by four devices are mainly studied, so four new variable sets are defined. Then calculate and convert the data of the four variables, and finally transmit them to the visual end.

Because the system combines the virtual traversal method, the data calculation error caused by environmental factors can be avoided in the process of converting the current data generated by the internal devices of the sewage treatment system. Then the converted data parameters are transmitted to the computer to form a three-dimensional stable area of the sewage treatment system. The angle and area inside the three-dimensional stability region can analyze and judge the stability of the whole system, so as to improve the work efficiency and accuracy of the system.

Research on Control of Rural Sewage Treatment System Based on Discrete Dynamic Modeling Technology

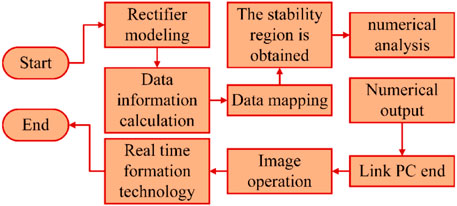
In the process of control in the rural sewage treatment system using discrete dynamic modeling technology, in order to avoid the bifurcation chaos such as noise, irregular data oscillation and system instability during the operation of SPWM. In this paper, a nonlinear method is used to stroboscopic map the data to the whole system. This mapping method is also the main means to deal with chaos and bifurcation. The single-phase SPWM rectifier in the system mainly presents two states during operation. When performing stroboscopic mapping, it needs to be solved twice continuously, which is also very difficult. In this paper, the stroboscopic mapping in the single-phase SPWM rectifier in the system is modeled by simplifying the calculation process. Then the chaos and bifurcation phenomena are analyzed by using discrete dynamic modeling technology. Finally, the control parameters that can control the whole system are obtained, and the control module in the whole rural sewage treatment system can be seen more intuitively. The specific design flow of the whole control system is shown in Figure 3.

FIGURE 3

FIGURE 3. Control flow chart of the system.

As can be seen from Figure 3, firstly, the working principle of single-phase SPWM rectifier is modeled. Then the bifurcation phenomenon of the constructed model is analyzed, and finally the stability region is solved and the numerical value is analyzed. The control circuit in single-phase SPWM rectifier is mainly composed of two closed loops, and the corresponding formula is as follows:

$\{\begin{array}{c}L\frac{di}{dt}=-Ri+E\sin \left(\omega t\right)-U_{dc}\\ C\frac{d{U}_{dc}}{dt}=-\frac{1}{R_L}{U}_{dc}\pm i\end{array}(9)$

After calculating the working time of the data, the stroboscopic mapping of single-phase SPWM rectifier can be obtained. However, when dealing with more complex data information, the solution process becomes difficult. In this paper, Adomian polynomials are added to the original system model. With the addition of Adomian, the solution of nonlinear differential equations becomes easy. Adomian can automatically transform the solution into form, and the more data, the more accurate it is. Adomian’s relevant formula is as follows:

$Lu+Ru+Nu=g(10)$

$A_n\left(u_0,u_1,\dots ,u_n\right)=\frac{1}{n!}{\left[\frac{d^n}{d{\lambda }^n}N\left({\displaystyle \sum _{i=0}^{\mathrm{\infty }}{\lambda }^i{u}_i}\right)\right]}_{\lambda =0}(11)$

The core content of Adomian polynomial is to solve the high-order derivative, and the polynomial is mainly composed of variables, so it is more suitable for the discrete dynamic system studied in this paper.

When analyzing the bifurcation phenomenon in the whole system, we must first understand the information of the relevant data generated by the bifurcation chaos phenomenon. The source of data is mainly generated by the peak current, and the peak current can be collected directly. The current peak segmentation number generated by the internal components of the sewage treatment system studied in this paper is 70, that is, when it is greater than 70, the data appear chaotic bifurcation phenomenon. By analyzing the bifurcation chaotic data of nonlinear attributes, it is convenient to judge the chaotic bifurcation characteristics of the whole system in a fixed time. As long as the trend of the image presented on the computer side is symmetrical, we can know that the whole system is running stably.

After taking some chaotic bifurcation data, the stroboscopic mapping method is added to the model system. In the process of adding, the transfer function formula of the controller is:

$F\left(s\right)=K_p+\frac{K_r.s}{s^2+{\omega }_1^2}(12)$

Before the controller transmits data, because there is still sinusoidal quantity in the rectifier, the sinusoidal quantity needs to be replaced by variables before data transmission. The formula related to variable substitution is as follows:

$\{\begin{array}{c}\frac{dz}{dt}=\omega E\cos \left(\omega t\right)\\ \frac{d^{2}z}{d{t}^2}=-{\omega }^{2}E\sin \left(\omega t\right)=-{\omega }^{2}z\end{array}(13)$

After replacing the data form, the controller maps the data transmitted to the computer to the SPWM rectifier in the discrete dynamic system. The related formulas of discrete mapping are as follows:

$X_{n+1}=F\left(X\right)=\left\{\begin{array}{c}f1\left(x_n,y_n,m_n,z_n\right)\\ f2\left(x_n,y_n,m_n,z_n\right)\\ f3\left(x_n,y_n,m_n,z_n\right)\\ f4\left(x_n,y_n,m_n,z_n\right)\end{array}\right\}(14)$

Through the above content, the whole discrete dynamic system is updated. Next, we need to solve the stable region in the system. In this paper, the Jacobian matrix method is mainly used for solving, and the relevant formulas are as follows:

$J_m=\left[\begin{array}{c}\frac{d}{d{x}_n}{f}_m\cdot \cdots \cdot \frac{d}{d{s}_n}{f}_m\\ \cdot \cdots \cdot \\ \frac{d}{d{x}_n}{f}_m\cdot \cdots \cdot \frac{d}{d{s}_n}{f}_m\end{array}\right](15)$

Through the introduction of data, the eigenvalues of Jacobian matrix are obtained. By comparing and calculating with all data node values in the internal parameter area of the system, all characteristic values that meet the internal area of the system can be obtained. The higher the switching frequency of sewage treatment system components, the larger the stability range of the system. We can also operate the system by controlling the internal eigenvalues. Although the addition of control methods can systematically collect and track data, it also reduces the stability of the whole system to a certain extent.

Finally, the numerical value generated by the system in processing data is analyzed. Because the stroboscopic mapping can continuously iterate the data within the system, the waveform variables generated by the data in different states can be obtained. After collecting the internal current waveform, the system stores the filtered wave peak separately, and obtains the chaotic bifurcation of the data in the system. If sampling is selected at only one point, all output data results are limited to a single state; If data sampling is selected at two points, all output data results have only two states; If the data is sampled at many nodes, the data obtained is polymorphic and contains bifurcation chaos. According to the above content, only continuous sampling of multiple nodes can be helpful to the research content of this paper and improve the accuracy of the results.

Result Analysis and Discussion

Stability Analysis of Rural Sewage Treatment System Based on Discrete Dynamic Modeling Technology

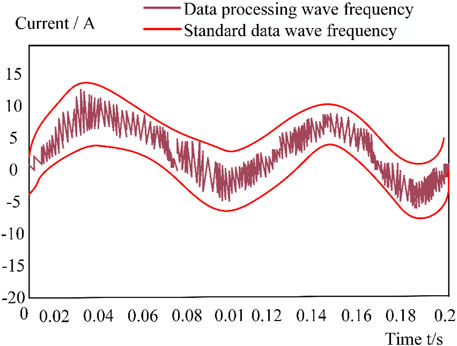
By combining the discrete modeling technology with the rural sewage treatment system, the data information of the current required in the components is obtained. In the initial stage of data processing, it is only data acquisition and transmission, in which the virtual traversal method of control data and system stability is added. After real-time collection, analysis and processing of the attributes and status of machine component data, the whole discrete dynamic system can be clearly monitored by the computer. The real-time waveform data generated in the process of system operation can indirectly analyze the stability of the whole discrete dynamic system. In order to further verify the overall stability of the combination of discrete modeling technology and rural sewage treatment system. In this paper, the internal current data of machine components are sampled, and a period of time during the operation of the system is intercepted. Finally, the stability of the whole system is verified by the sample data wave frequency generated by the system when processing data. The operating wave frequency of the obtained discrete dynamic system is shown in Figure 4.

FIGURE 4

FIGURE 4. Wave frequency diagram of discrete dynamic system when processing data.

It can be seen from Figure 4 that the combined discrete dynamic model system processes the sample data generated by the machine over a period of time. From the electromagnetic wave frequency generated by the data in the figure, the operation process of the system processing data is very stable. Although the data frequency values in different periods still fluctuate significantly, they are all within the standard value. When the system is in a relatively stable operation state, it can play its original role with maximum efficiency. Therefore, according to the wave frequency generated by the above discrete dynamic system when processing data, it can be concluded that the discrete dynamic model system studied in this paper has good stability and good performance.

Analysis of Control Results of Rural Sewage Treatment System Based on Discrete Dynamic Modeling Technology

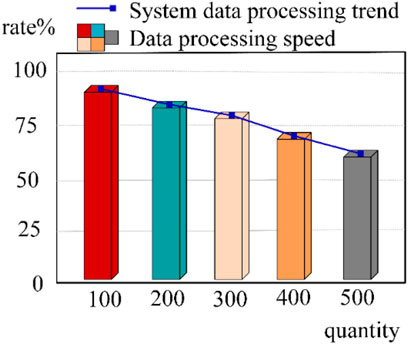
It is far from enough to design and study the stability of a system. Based on the enhanced discrete dynamic modeling technology, combined with the rural sewage treatment system, the control function is also added. The traditional discrete dynamic model can not directly control the model in the modeling process, and the algorithm can only control the data and system manually. For example, repeatedly adding data and switching the system. The discrete dynamic model studied in this paper combines the method of stroboscopic mapping. After being added into the system modeling, this method directly replaces the original status of artificial data and system control. In order to further verify the control performance of rural sewage treatment system under discrete dynamic modeling technology, five groups of sample data with different quantity and category are selected for processing. Finally, through the optimized discrete dynamic system, the data processing rate and the authenticity of the results are analyzed in detail. The data processing efficiency trend of the optimized discrete dynamic system in the experiment is shown in Figure 5.

FIGURE 5

FIGURE 5. Data processing efficiency diagram of optimized discrete dynamic system.

It can be seen from Figure 5 that the optimized discrete dynamic system has very high data processing efficiency. The smaller the amount of data processed, the higher the processing rate of the corresponding system. Although the rate is reduced when processing huge data, the rate is still as high as 60%. It can be seen that the control performance of the whole system is very good. In the previous research data, the data processing rate of ordinary discrete model is no more than 40%, and system failures often occur. In contrast, the discrete dynamic model system studied in this paper can maintain the stability of the system and data, and can automatically control it. It also indirectly proves that the technology has strong social application value.

Conclusion

In the big data environment, discrete dynamic technology can be combined with many fields. This paper combines this technology with rural sewage treatment system. Firstly, the virtual traversal method is added to the system to construct the model, which strengthens the stability of the whole data and the system. Inside the virtual traversal method, all possible conditions are considered. In this way, the final model is established to improve the overall accuracy to the greatest extent. After ensuring the stability of the system, the model of SPWM rectifier in the system is transformed. By controlling the data type, the overall performance of the system is improved. It mainly uses the occupied space value to achieve the mapping between data, and also provides a new idea for stroboscopic mapping modeling. The final system has stable and controllable excellent properties, and can also analyze and process the data in the rural sewage treatment system. The sewage treatment method in this paper can not only reduce the expenditure of energy costs but also bring more economic benefits. Hence, the water consumption and drug consumption of the whole process will be optimized simultaneously.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WL independently completed all the contents of the article.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Djazet, A., Fewo, S. I., Nkouankam, E. B. N., and Kofané, T. C. (2020). Stability Analysis for Moving Dissipative Solitons in Two-Dimensional Dynamical Model. Eur. Phys. J. D 74 (4), 67. doi:10.1140/epjd/e2020-100467-7

CrossRef Full Text | Google Scholar

Dunstan, M., Xavier, E. A., Fatima, A., and Marta, G. (2021). Using Mobile Data to Understand Urban Mobility Patterns in Freetown. Sierra Leone: The World Bank.

Google Scholar

Fatone, L., and Mariani, F. (2020). Systemic Risk Governance in a Dynamical Model of a Banking System with Stochastic Assets and Liabilities. J. Econ. Interact. Coord. 15 (12), 183–219. doi:10.1007/s11403-019-00277-y

CrossRef Full Text | Google Scholar

Gonçalves, A., Mentré, F., Lemenuel-Diot, A., and Guedj, J. (2020). Model Averaging in Viral Dynamic Models. AAPS J. 22 (12), 48. doi:10.1208/s12248-020-0426-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hair, J. F., Ringle, C. M., Gudergan, S. P., Fischer, A., Nitzl, C., and Menictas, C. (2019). Partial Least Squares Structural Equation Modeling-Based Discrete Choice Modeling: an Illustration in Modeling Retailer Choice. Bus. Res. 12 (1), 115–142. doi:10.1007/s40685-018-0072-4

CrossRef Full Text | Google Scholar

Ioan, D., Bărbulescu, R., Silveira, L. M., and Ciuprina, G. (2019). Reduced Order Models of Myelinated Axonal Compartments. J. Comput. Neurosci. 47 (2-3), 141–166. doi:10.1007/s10827-019-00726-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Komarov, D. A., Maslennikov, S. P., Yakushkin, E. P., and Paramonov, Yu. N. (2020). Influence of External Electric Circuits on the Static and Dynamic Mode of Operation of Multipath Collectors of Powerful Klystrons. J. Commun. Technol. Electron. 65 (3), 306–310. doi:10.1134/s1064226920030080

CrossRef Full Text | Google Scholar

Le, S., Wu, Y., Guo, Y., and Vecchio, C. D. (2021). Game Theoretic Approach for a Service Function Chain Routing in NFV with Coupled Constraints. IEEE Trans. Circuits Syst. II 68, 3557–3561. doi:10.1109/TCSII.2021.3070025

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. K. (2021). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, W. C., Deng, G., Cao, W., Xu, C., Chen, J., and Lee, M. L. (2019). Discrete Element Modeling of the Hongshiyan Landslide Triggered by the 2014 Ms 6.5 Ludian Earthquake in Yunnan, China. Environ. Earth Sci. 78 (16), 520. doi:10.1007/s12665-019-8438-2

CrossRef Full Text | Google Scholar

Nguyen, T-T., André, D., and Huger, M. (2019). Analytic Laws for Direct Calibration of Discrete Element Modeling of Brittle Elastic Media Using Cohesive Beam Model. Comput. Part. Mech. 6 (3), 393–409. doi:10.1007/s40571-018-00221-0

CrossRef Full Text | Google Scholar

Ni, Z., Lu, X., and Xue, W. (2021). Does the Belt and Road Initiative Resolve the Steel Overcapacity in China? Evidence from a Dynamic Model Averaging Approach. Empir. Econ. 61. doi:10.1007/s00181-020-01861-z

CrossRef Full Text | Google Scholar

Raza, N., Afzal, J., Bekir, A., and Rezazadeh, H. (2020). Improved TanΦ(ξ)2$\tan \left (\frac {\Phi (\xi )}Brazilian Journal of Physics\right )$ -Expansion Approach for Burgers Equation in Nonlinear Dynamical Model of Ion Acoustic Waves. Braz. J. Phys. (prepublish).

Google Scholar

Sukhinov, A. I., Ougolnitsky, G. A., and Usov, A. B. (2020). Methods of Solving the Theoretic Game Models for Coordinating Interests in Regulating the Fishery Industry. Math. Models Comput. Simulations 12 (2), 176–184. doi:10.1134/s2070048220020143

CrossRef Full Text | Google Scholar

Tian, W-L., Yang, S-Q., and Huang, Y-H. (2020). Discrete Element Modeling on Crack Evolution Behavior of Sandstone Containing Two Oval Flaws under Uniaxial Compression. Arabian J. Geosciences 13 (1), 418. doi:10.1007/s12517-020-05348-0

CrossRef Full Text | Google Scholar

Toyoda, M., and Wu, Y. (2021). Mayer-type Optimal Control of Probabilistic Boolean Control Network with Uncertain Selection Probabilities. IEEE Trans. Cybern. 51, 3079–3092. doi:10.1109/tcyb.2019.2954849

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, B. K., Subramaniam, P., and Vadigepalli, R. (2019). Model-based Virtual Patient Analysis of Human Liver Regeneration Predicts Critical Perioperative Factors Controlling the Dynamic Mode of Response to Resection. BMC Syst. Biol. 13 (1), 9. doi:10.1186/s12918-019-0678-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy Iteration Approach to the Infinite Horizon Average Optimal Control of Probabilistic Boolean Networks. IEEE Trans. Neural Netw. Learn Syst. 32 (6), 2910–2924. doi:10.1109/TNNLS.2020.3008960

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., Yuan, X., Guan, D., Liu, H., Zhang, G., Wang, K., et al. (2019). Eco-exergy Evaluation of New Wetlands in the Yanzhou Coalfield Subsidence Areas Using Structural-Dynamic Modelling. Mine Water Environ. 38 (4), 746–756. doi:10.1007/s10230-019-00628-y

CrossRef Full Text | Google Scholar

Zhang, Y., Qian, T., and Tang, W. (2022). Buildings-to-distribution-network Integration Considering Power Transformer Loading Capability and Distribution Network Reconfiguration. Energy 244, 3104. doi:10.1016/j.energy.2022.123104

CrossRef Full Text | Google Scholar