Load Reduction of Semi-Submersible Floating Wind Turbines by Integrating Heaving-Type Wave Energy Converters with Bang-Bang Control

Floating offshore wind turbines (FOWTs) are subject to intensive structural loads due to the extra degrees of freedom (DOF) of the floating platform, which may shorten the fatigue lifetime of critical wind turbine structures. Integrating wave energy converters (WECs) into FOWTs could potentially help improve both overall energy capture and platform dynamic responses and, thus, is expected to reduce the levelized cost of energy (LCOE). In this work, a novel hybrid wind-wave energy platform consisting of a semi-submersible FOWT and three heaving-type WECs is proposed, and the feasibility of reducing FOWT dynamic responses and fatigue loads by integrating heaving-type WECs with different PTO control schemes is investigated. More specifically, the aero-hydro-servo-elastic-mooring coupled numerical model is established, and a preliminary study is performed to evaluate the dynamic responses and power production of the hybrid platform under various environmental conditions. Particularly, the two kinds of PTO control strategies have been comparatively studied, which have shown that the active bang-bang control could effectively suppress the platform heave and pitch motion by up to 34.6 % and 17.1%, respectively. Moreover, the tower-base fatigue damage equivalent load (DEL) has been reduced by up to 11.21%, and the system power production could be increased by almost 6%. Therefore, it is shown that integrating heaving-type wave energy converters with bang-bang control is able to effectively reduce the dynamic responses and fatigue loads of semi-submersible FOWT while absorbing additional wave energy at the same time.

1 Introduction

Offshore wind energy is expected to be an effective solution to meet the enormous demand for electricity in coastal areas (Schallenberg -Rodríguez and Montesdeoca, 2018). In recent years, due to the limitation of wind farm sites in shallow waters, researchers have been focusing on developing offshore wind energy in deep waters with abundant and less turbulent wind resources (Wang et al., 2018). Offshore floating wind turbines (FOWT) are considered to be more economical than bottom-fixed ones when the installation water depth exceeds 60 m (Pérez- Collazo et al., 2015). However, the FOWT suffers from more severe dynamic responses and structural loads due to the extra degrees of freedom (DOF), which has a detrimental effect on the fatigue life of critical components and may increase the failure risk (Jonkman and Matha, 2011). To overcome these challenges, various methods have been proposed for FOWT load mitigation and power optimization, including blade pitch control (Sarkar et al., 2020), generator torque control (Lin et al., 2018), and structural control (Si et al., 2014). However, there is a trade-off between power production and structural loads for multi-object control strategies, and the power increase is limited (Njiri et al., 2019). Alternatively, integrating wave energy converters (WECs) into FOWTs seems to be another potential way to reduce the cost of energy (CoE) of FOWTs, since they can capture considerable wave energy and share infrastructures such as floating platforms and mooring lines (Perez- Collazo et al., 2019). The WECs with reasonable configuration might also suppress the dynamic responses of FOWTs by rationalizing the synergistic coupling mechanism between WECs and FOWTs (Perez- Collazo et al., 2018).

Research on hybrid wind-wave energy concepts has been driven and conducted by several EU funded projects aiming at the combined utilization of wind and wave energy, such as MARINA (Armentia and Auer, 2014), MERMAID (Koundouri et al., 2017), H2OCEAN (Brennan and Kolios, 2014), etc. A number of wind-wave combined concepts have been proposed and primarily studied. For instance, three wind-wave combined concepts have been proposed based on the WindFloat FOWT with point-absorber-type (Peiffer et al., 2011), flap-type (Peiffer and Roddier, 2012), and oscillation water column (OWC) type WECs (Aubault et al., 2011), respectively. Muliawan et al. proposed the STC concept consisting of a spar-type wind turbine and a point-absorber WEC (Muliawan et al., 2012), and both numerical and experimental studies have been carried out to investigate the fundamental performance of the hybrid system (Ren et al., 2015) (Gao et al., 2016). Similarly, the SFC concept, including a 5 MW semi-submersible wind turbine and three flap-type WECs, has been designed and comprehensively studied (Michailides et al., 2016a) (Michailides et al., 2016b). Besides, there are some other combined concepts, including tension-leg type (Ren et al., 2020) or semi-submersible type (Wang et al., 2022a) FOWT with a torus-type WEC, semi-submersible type FOWT with multiple point-absorber type WECs (Hu et al., 2020) (Kamarlouei et al., 2020), etc. In these works, the mechanical coupling process between FOWTs and WECs has been simplified, and the power take-off (PTO) system of WECs has been represented by a passive linear damping coefficient, which may be far from optimal for loads mitigation and power increase in the hybrid systems. As stated in (Si et al., 2021), the results revealed the significant influence of WEC PTO control on both power production and platform dynamics of the DeepCwind-Wavestar combined concept. Therefore, the effect of active WEC PTO control on the hybrid wind-wave energy concepts needs further investigation.

In this work, we aim to investigate how much platform motions and structural loads of FOWT may be reduced by introducing WECs and active PTO control. For this purpose, we proposed a novel wind-wave combined concept consisting of a DeepCwind FOWT developed by NREL and three heaving-type WECs (Robertson et al., 2014). An aero-hydro-servo-elastic-mooring coupled numerical model has been established based on the F2A framework (Yang et al., 2020a) and then verified against OpenFAST (Wang et al., 2022b). Numerical simulations involving free decay, regular wave, and irregular wave tests have been conducted to investigate the influence of the additional WECs and applied active PTO control on the dynamic responses of the combined concept. Platform motions, structural loads, and wave power production behaviors have been comparatively analyzed. The results have demonstrated the beneficial effect of proper WEC PTO control on this hybrid wind-wave energy platform.

The remainder of the article is organized as follows. Section 2 presents the detailed design of the hybrid platform and the PTO system. Section 3 describes the established aero-hydro-servo-elastic-mooring coupled numerical model and its verification. Section 4 shows the PTO control scheme of the WECs and the main parameters of the controller. Section 5 presents the numerical results and comparatively analyses the influence of the additional WECs and the PTO control on the platform motions, structural loads, and power production. The conclusions are drawn in Section 6.

2 Concept Description

2.1 Hybrid Wind-Wave Energy Platform

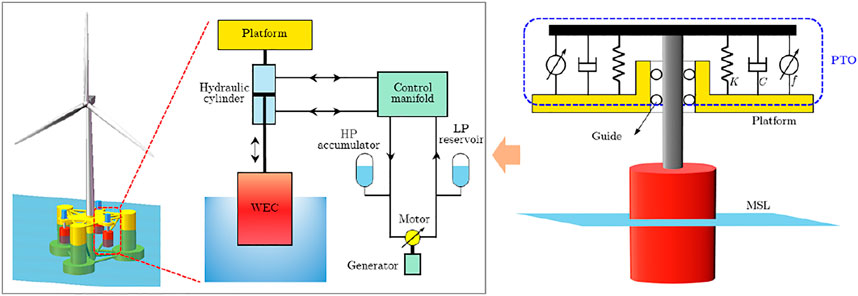
The hybrid wind-wave energy platform consists of a 5-MW DeepCwind FOWT (Robertson et al., 2014) and three heaving-type WECs, as shown in Figure 1. The main design parameters of the hybrid platform are listed in Table 1. In the hybrid platform, three cylindrical WECs are installed symmetrically around the center column of the platform, and the relative movement between WEC and platform is constrained to the heave direction by the guide structure, as shown in Figure 2. Note that it is possible to integrate more than three WECs with different shapes in the hybrid platform, while a simplified design is applied in this work for preliminary study.

FIGURE 1

FIGURE 1. Concept design of the hybrid wind-wave energy platform.

TABLE 1

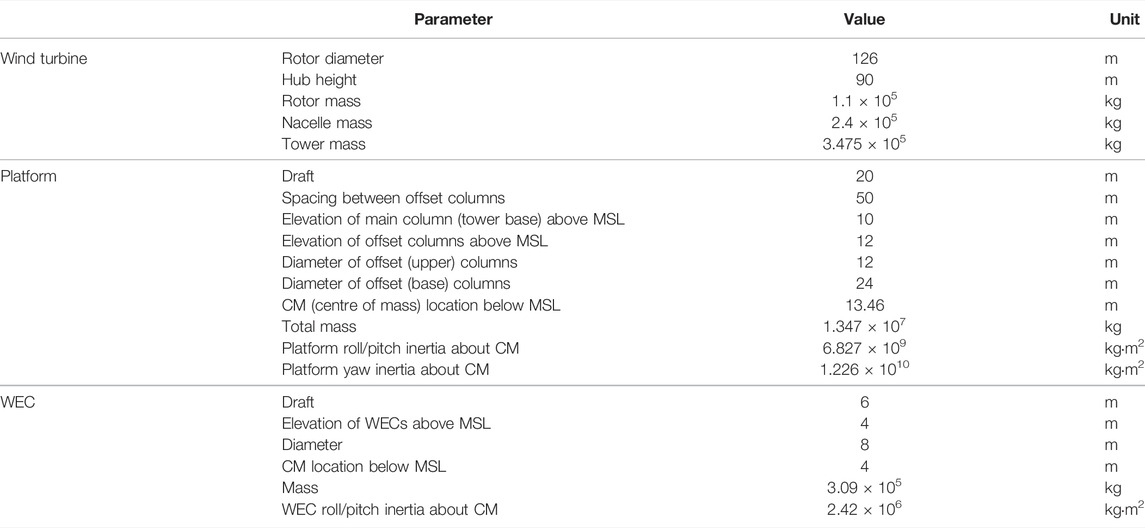
TABLE 1. Main parameters of the hybrid system (Robertson et al., 2014) (Jonkman et al., 2009).

FIGURE 2

FIGURE 2. Schematic of the WEC PTO system.

2.2 Power Take-Off System

As shown in Figure 2, the WEC is constrained to move in only one DOF by the guide structure, and the PTO system is installed in the direction of relative motion between the WEC and platform. More specifically, the hydraulic PTO system is used to convert wave energy into electrical energy, and then the PTO system has been simplified as a linear spring-damper system with a controlled input for control design. As a result, the wave energy can be captured through the relative motion caused by the wind and wave loads (Ren et al., 2018). Meanwhile, the dynamic interaction between the WEC and platform has a direct impact on the dynamic responses on the hybrid platform, which may be utilized for motion suppression and load mitigation.

3 Numerical Modeling

In this section, the aero-hydro-servo-elastic-mooring coupled numerical model of the proposed hybrid platform is described. The numerical model has been established based on the F2A framework (Yang et al., 2020a) (Yang et al., 2020b), which implements the coupling simulation of ANSYS-AQWA (Ansys, 2013) and FAST (Jonkman and Buhl, 2005) through user-defined dynamic-link libraries (DLLs). FAST modules, including aerodynamics module AeroDyn, control module ServoDyn, and structural dynamic module ElastoDyn, are completely compiled into the DLL, which can be called by AQWA solver during time-domain simulations. The platform displacement, velocity, and acceleration data at each time step in AQWA are transferred to FAST for calculating the dynamic responses of the wind turbine. At the same time, the tower-base loads obtained from FAST will be transferred to AQWA as external loads, which are imposed on the tower-base position of the platform. More details of the F2A can be found in (Yang et al., 2020a). Besides, the PTO control system of the WECs is also formulated and compiled into the DLL so that the dynamic performances of the hybrid platform can be improved by this mechanical interaction.

3.1 Aerodynamic and Structural Loads

FAST code has been used for predicting aerodynamic and structural loads of the wind turbine in this work since FAST is an aero-hydro-servo-elastic-mooring coupled simulation code for wind turbine analysis, including AeroDyn, ServoDyn, ElastoDyn and HydroDyn modules (Jonkman and Buhl, 2005). However, the HydroDyn module is not involved in F2A as the hydrodynamics are calculated in AQWA. The aerodynamics are calculated based on the blade element momentum theory by the AeroDyn module (Moriarty and Hansen, 2005), where the blade is divided into a series of sectional airfoils with specific lift coefficients C_L and drag coefficients C_D. The aerodynamic thrust and torque of the sectional airfoils can be represented by

$dT=\frac{1}{2}{\rho }_a{V}_a^{2}c(C_L\cos \phi +C_D\sin \phi ),(1)$

$dM=\frac{1}{2}{\rho }_a{V}_a^{2}c(C_L\sin \phi -C_D\cos \phi ),(2)$

where ρ_a is the air density, V_a is the absolute velocity, c is the aerofoil chord length, and φ is the inflow angle. The ServoDyn (Jonkman and Jonkman, 2016) module deals with the wind turbine control issues, including blade pitch control, generator torque control, and yaw control. Meanwhile, aerodynamic loads obtained from the AeroDyn module are transferred to ElastoDyn for structural load calculation based on Kane’s equation:

$F_r\ast +F_r=0,(3)$

where F_r^* is the generalized inertia force vector and F_r is the generalized active force vector.

3.2 Hydrodynamic and Mooring Loads

The hydrodynamic loads of the hybrid platform are calculated by AQWA based on the linear potential flow theory, which assumes that the flow is inviscid, incompressible, and irrotational (Ansys, 2013). The hydrodynamic radiation and diffraction coefficients are solved through the panel method and inviscid potential flow theory in the frequency domain, and the hydrodynamic interaction between multi bodies is included. The wave-structure interaction behavior is described as the Laplace equation:

$\nabla \varphi =0,(4)$

where $\varnothing$ is the three-dimensional velocity potential. Since the viscous effect is not included in the linear potential flow theory, an extra Morison drag matrix has to be added to the numerical model in AQWA (Robertson et al., 2014). The Morison drag force accounted for neglected viscosity can be expressed by

$F_{\text{drag}}=\frac{1}{2}\rho C_{d}Du\left|u\right|,(5)$

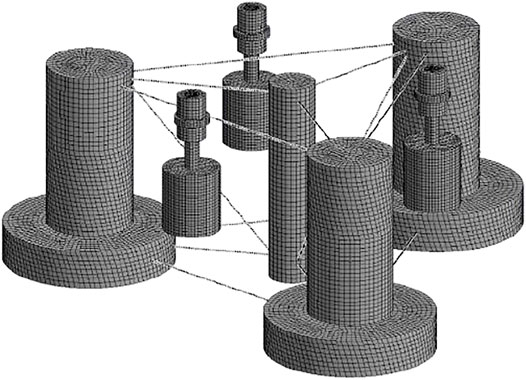
where ρ is the fluid density, C_d is the drag coefficient, D is the structure diameter, and u is the flow velocity. In this work, C_d = 1.0 is adopted for the WECs according to their shape and size (Shi et al., 2012). The quadratic drag coefficients for the platform are obtained from (Robertson et al., 2014), as listed in Table 2. The generated mesh for the hybrid platform is shown in Figure 3, and the mesh quality has been analyzed to meet the requirements of mesh independence.

TABLE 2

TABLE 2. Quadratic drag coefficients C_ii for the semi-submersible platform and WECs (Robertson et al., 2014).

FIGURE 3

FIGURE 3. Generated mesh of the hybrid platform and WECs.

3.3 Power Take-Off System Modeling

As shown in Figure 2, The PTO system has been modeled as a linear spring-damper system with a controlled input force (Ma et al., 2019), where the spring-damper system includes a linear spring K_PTO and a linear damper B_PTO with a controlled force f. Then the PTO control force and power production of each PTO system can be expressed as

$F_{\text{PTO}}=K_{\text{PTO}}\cdot \mathrm{\Delta }x+B_{\text{PTO}}\cdot \mathrm{\Delta }\dot{x}+f,(6)$

$P_{\text{PTO}}=F_{\text{PTO}}\cdot \mathrm{\Delta }\dot{x},(7)$

where K_PTO is the linear spring stiffness coefficient, B_PTO is the linear damping coefficient, and Δx is the relative displacement between the WEC and platform. Here, f can be determined by a designed force controller.

3.4 Motion Equation

In this work, the proposed hybrid wind-wave platform consists of a semi-submersible floating wind turbine and three heaving-type WECs. The floating platform and WECs are treated as rigid bodies, and the WECs can only move along the guide on the platform. Therefore, except for the wind turbine (including rotor-nacelle-assembly and the tower), there are 9 DOFs with six motion DOFs for the platform and three relative DOFs for the WECs. Then, the motion equation for multi-body coupling can be established as follows based on Cummins theory (Taghipour et al., 2008)

$\left[\begin{array}{cccc}{M}^P+A^P& A^{P{W}_1}& A^{P{W}_2}& A^{P{W}_3}\\ A^{W_{1}P}& M^{W_1}+A^{W_1}& 0& 0\\ A^{W_{2}P}& 0& M^{W_2}+A^{W_2}& 0\\ A^{W_{3}P}& 0& 0& M^{W_3}+A^{W_3}\end{array}\right]\left[\begin{array}{c}{\ddot{X}}^P\\ {\ddot{X}}^{W_1}\\ {\ddot{X}}^{W_2}\\ {\ddot{X}}^{W_3}\end{array}\right]=\left[\begin{array}{c}{F}_{aero}^P+F_{hydro}^P+F_{grav}^P+F_{moor}^P-F_{PT{O}_1}^P-F_{PT{O}_2}^P-F_{PT{O}_3}^P+F_{W_1}^P+F_{W_2}^P+F_{W_3}^P\\ F_{hydro}^{W_1}+F_{grav}^{W_1}+F_{PT{O}_1}^{W_1}+F_P^{W_1}\\ F_{hydro}^{W_2}+F_{grav}^{W_2}+F_{PT{O}_2}^{W_2}+F_P^{W_2}\\ F_{hydro}^{W_3}+F_{grav}^{W_3}+F_{PT{O}_3}^{W_3}+F_P^{W_3}\end{array}\right],(8)$

where superscripts P and W represent the platform and WECs, respectively. PW_i and W_iP denote the coupling terms between the platform and WECs. M is the mass matrix, A is the added mass matrix at infinite high frequencies, and X is the displacement vector. F_aero is the aerodynamic load, F_hydro is the hydrodynamic load (including wave force and buoyancy), F_grav is the gravity force, F_moor is the mooring load, F_PTO is the PTO force, $F_W^P$ and $F_P^W$ are the connection interactions of the guide structure.

3.5 Model Verification

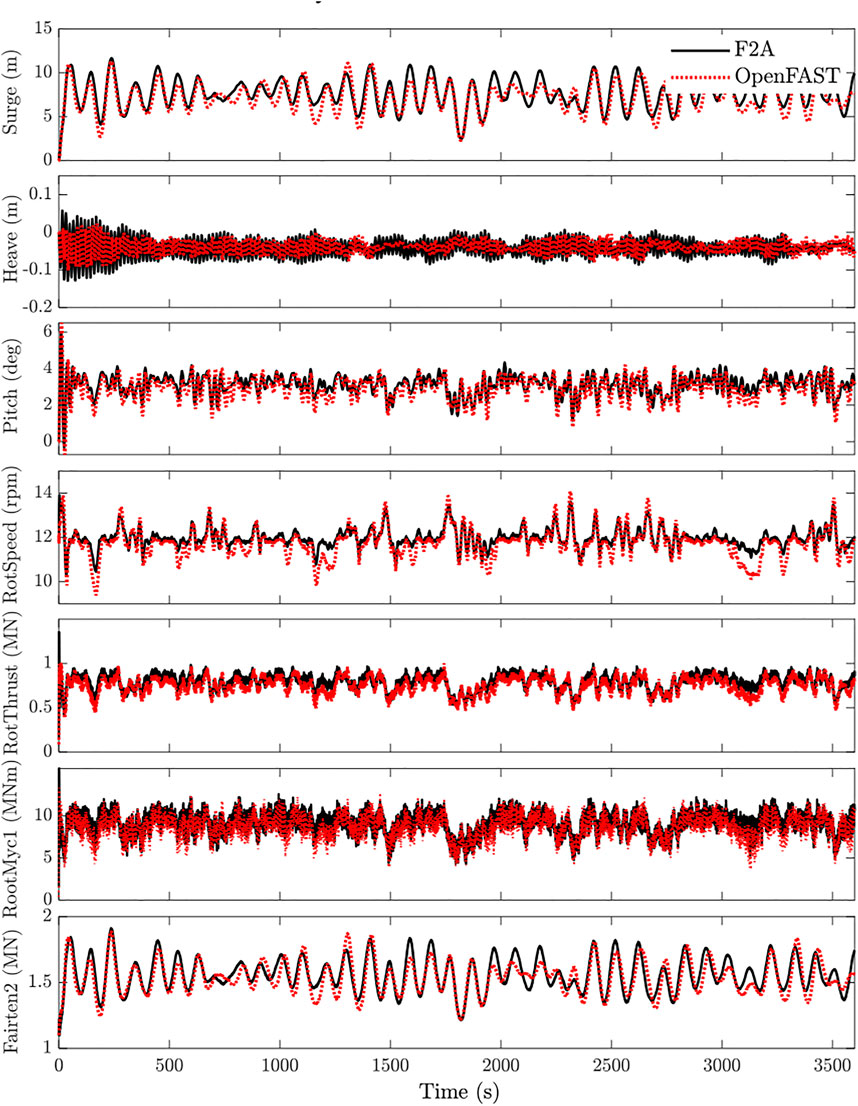
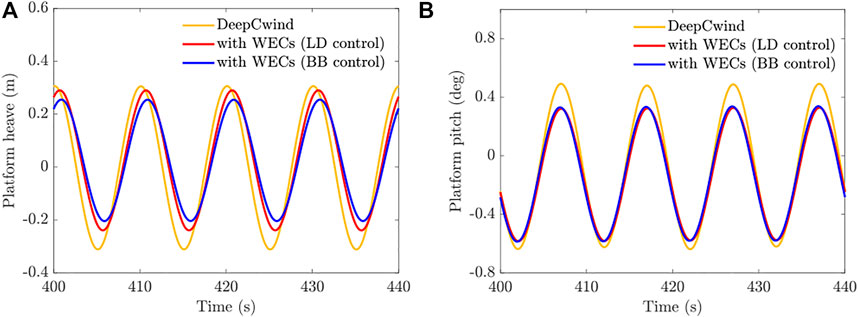
In order to ensure the correctness of the numerical model, particularly for the dynamic behaviors of the DeepCwind FOWT, numerical results of the established model in F2A have been compared with that of OpenFAST for verification. Then the WECs were mounted to the DeepCwind platform for integrated simulation. A typical operational condition has been chosen for simulation with significant wave height H_s = 3 m, peak wave period T_p = 10 s, mean wind velocity v = 11.3 m/s and turbulence intensity I = 15%. As shown in Figure 4, the comparison results of dynamic responses are in good agreement, which indicates the reliability of the established numerical model.

FIGURE 4

FIGURE 4. Comparison of dynamic responses between F2A and OpenFAST.

4 Power Take-Off Control Design

In this article, two different WEC PTO control strategies are proposed, which are designed to both reduce platform motions and mitigate structural loads. They have been used to comparatively analyze the effects of active PTO control on improving the dynamic responses of the hybrid platform.

4.1 Linear Damping Control

The first kind of control strategy is linear damping (LD) control, which has been widely used as a primary method in the field of WEC control (Drew et al., 2009). As shown in Figure 5, the resonant period of the WECs is around 6.3 s, and the optimal PTO damping for wave energy extraction can be represented by (Hansen, 2013)

$B_{\text{PTO}}=B_{\text{hydro}},(9)$

where B_hydro is the frequency-dependent hydrodynamic damping coefficient due to the power dissipation of radiate waves. Hence, the formula of the linear damping control can be expressed as

$F_{\text{PTO}-\text{LD}}=B_{\text{PTO}}\cdot \mathrm{\Delta }\dot{x},$

where Δx is the relative displacement between the WEC and platform.

FIGURE 5

FIGURE 5. Heave response amplitude operator (RAO) of the WECs.

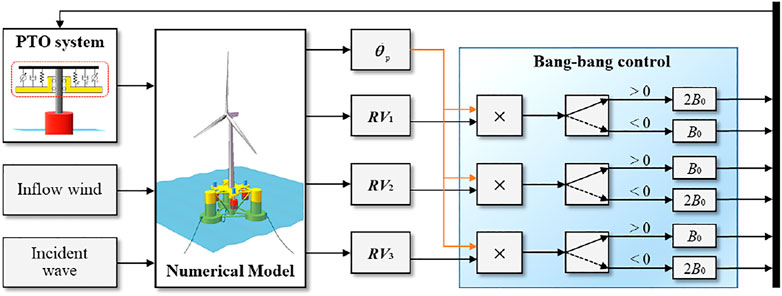
4.2 Bang-Bang Control

According to (Kusnick et al., 2015), the nacelle acceleration of a wind turbine is supposed to be less than 0.3 g to avoid power electronics damage and mitigate structural loads, which is partly determined by platform pitch. Therefore, a specific bang-bang (BB) control has been proposed to improve the fatigue life of the wind turbine by suppressing the platform pitch (Babarit and Clément, 2006). In general, a bang-bang controller (two-step or on-off controller) is a type of feedback controller that switches abruptly between two states, which is often used in optimal control design for wave energy extraction maximization (Zou et al., 2017). In this work, the two states are set to be two linear damping coefficients based on the linear damping control mentioned above. As shown in Figure 6, one of the damping coefficients is equal to the optimal PTO damping B₀ = B_hydro, while the other one is designed to be twice the value of B₀ to provide over damping for pitch motion. Note that the proposed control only requires the knowledge of the motion responses of the hybrid platform without the need for wave prediction. With the assumption that the wind and wave directions are along the X-axis, then the control law for WEC 1 can be written as

$F_{\text{PTO}-\text{BB}}=\{\begin{array}{c}{B}_0,{\dot{\theta }}_P\cdot R{V}_1<0\\ 2B_0,{\dot{\theta }}_P\cdot R{V}_1\ge 0\end{array},(10)$

where ${\dot{\theta }}_P$ is the platform pitch velocity, and RV₁ is the relative velocity between the WEC and platform.

FIGURE 6

FIGURE 6. Flow diagram of the bang-bang control for the WEC PTO system.

5 Results and Discussion

This section presents the simulation results of the hybrid platform under different environmental conditions, including free decay, regular wave, and typical wind-wave combined tests. The free decay tests are firstly carried out to investigate the natural behaviors of the hybrid platform with the additional WECs and PTO damping. Then, the regular wave tests and several typical wind-wave combined tests are performed to comparatively study the influence of the proposed PTO control strategies on suppressing the platform motions, mitigating the structural loads, and increasing power production. Here, the label of results of the proposed hybrid platform with PTO control is denoted by “with WECs”.

5.1 Free Decay Test

Free decay tests have been done in the numerical simulation to identify the natural periods and decay rates of the hybrid platform with different WEC PTO damping coefficients. The initial conditions were set as surge 5 m, heave 2 m, and pitch 5°, respectively. Here, the decay rate δ is defined to characterize the rate of decay motions, which is calculated by

$\delta =P_1\text{/}{P}_{\text{0}},(11)$

where P₀ is the initial displacement of the decay motion, and P₁ is the second peak value. Figure 7 shows the time series of free decay tests with different PTO dampings for the hybrid platform and DeepCwind. Figure 8 shows the comparisons of natural periods and free decay rates with different PTO dampings. It can be seen that the integrated WECs with PTO control have changed the natural periods of the platform to a certain extent, in which the natural period of the surge is slightly increased while the natural periods of heave and pitch are reduced. More specifically, the natural periods of heave and pitch will decrease with increasing PTO damping, as shown in Figure 8A. Simultaneously, the free decay rates of the platform are all reduced with additional WECs, indicating a larger percentage of attenuation in every period. As seen in Figure 8B, the heave and pitch decay rates are decreased, especially when the PTO damping is around 1 MN/(m/s).

FIGURE 7

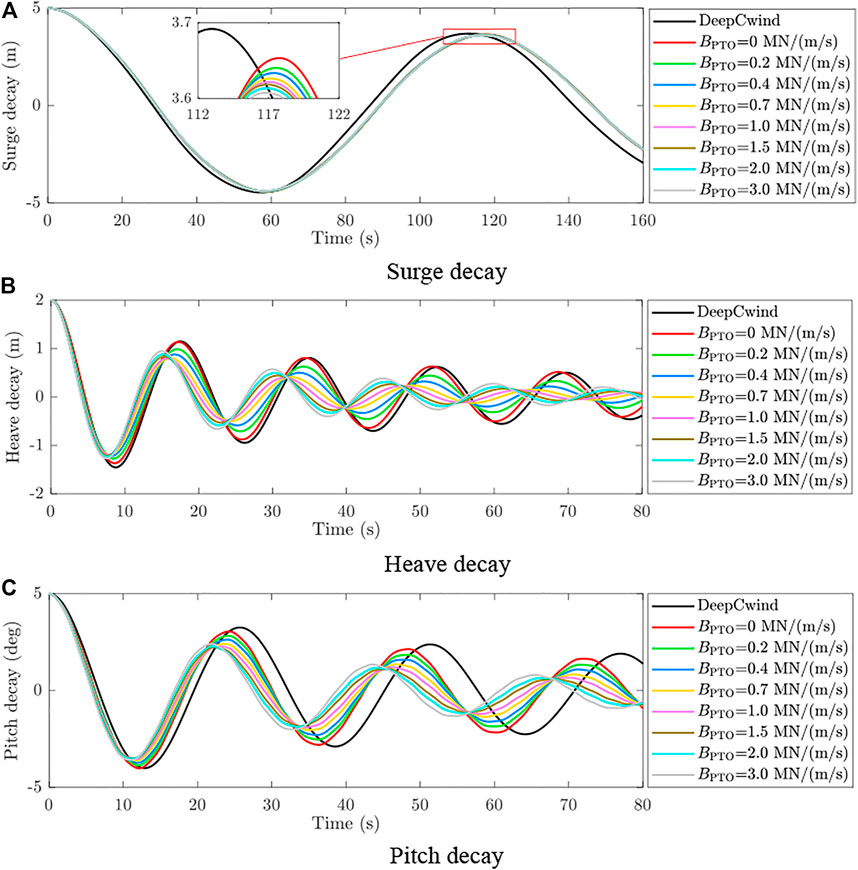
FIGURE 7. Time series of free decay tests with different PTO dampings. (A) Surge decay. (B) Heave decay. (C) Pitch decay.

FIGURE 8

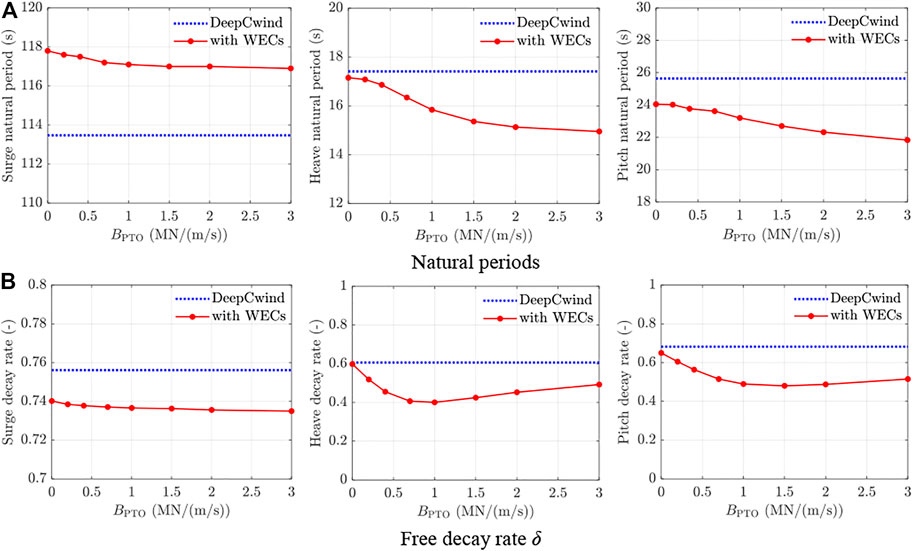
FIGURE 8. Comparisons of natural period and free decay rate with different PTO dampings. (A) Natural periods. (B) Free decay rate δ.

5.2 Regular Wave Test

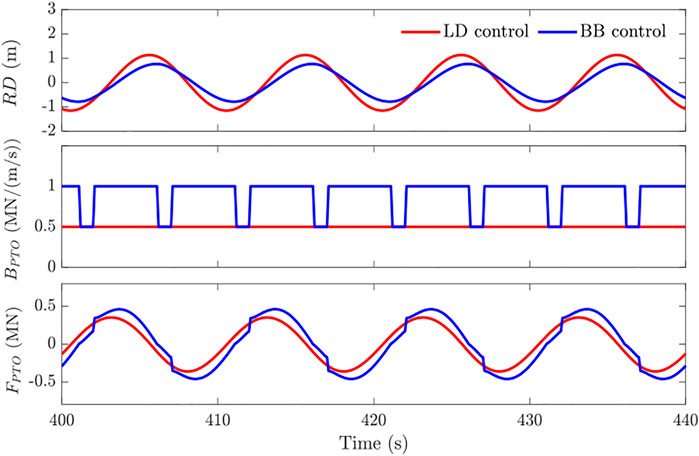
To primarily study the effect of additional WECs and PTO control on FOWT dynamic behaviors, a regular wave test has been performed in the simulation with wave height H = 3 m and wave period T = 10 s. The platform motion responses with different PTO control strategies are shown in Figure 9, and the PTO system dynamic responses are shown in Figure 10. It can be found that the heave and pitch motion amplitudes of the platform are reduced when the WECs and PTO control strategies are introduced. Regarding heave motion, the amplitude is reduced by 13.1% and 24.6% for the LD control and BB control relative to that of the DeepCwind, respectively. As for pitch motion, the amplitude reduction is 19.1% and 18.1% for the two control strategies. As shown in Figure 10, the BB control results in a smaller relative displacement (RD) between the WEC and platform due to the over-damped state, and it can be seen that the PTO system is mostly in the over-damped state, which is consistent with the motion reduction (in Figure 9).

FIGURE 9

FIGURE 9. Comparisons of platform motions with different PTO control strategies.

FIGURE 10

FIGURE 10. Comparisons of PTO system dynamics with different PTO control strategies for WEC 1.

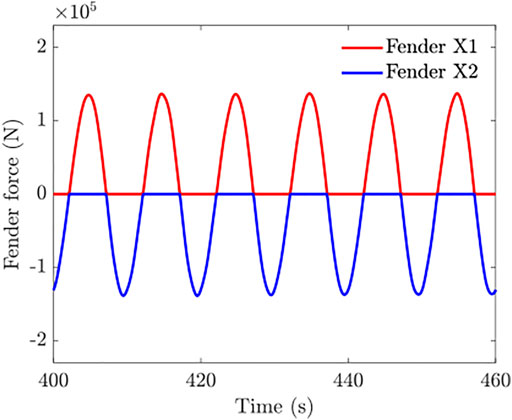
Figure 11 shows the fender force of the coupling between the platform and WEC. X1 and X2 denote the connection point along the X-axis direction, with X1 in front of the WEC and X2 behind the WEC. The fender feature behaves well in the dynamic coupling of the hybrid platform.

FIGURE 11

FIGURE 11. Fender force between the platform and WEC 1 in the horizontal direction.

The wave power production can be calculated by

$P_{\text{WEC}}={\displaystyle \sum _{i=1}^3{F}_{\text{PTO, }i}\cdot }R{V}_i.(12)$

Then, the total wave power production with different PTO control strategies can be obtained, as shown in Figure 12. The mean wave power of the LD and BB control is 331.8 and 368.6 kW, respectively, indicating the higher wave energy capture efficiency of the BB control.

FIGURE 12

FIGURE 12. Comparisons of total wave power production with different PTO control strategies.

5.3 Typical Operational Environmental Condition Test

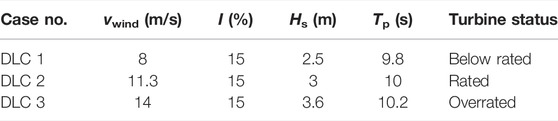
Typical operational environmental condition tests have been performed to investigate the added WEC and PTO system influence on performances of the FOWT under real sea conditions, where the dynamic responses of platform motions, structural loads, and wave power production are comprehensively analyzed. Several typical operational and environmental conditions have been applied in the numerical simulation, as listed in Table 3 (TC88 -MT, 2005) (Hasselmann et al., 1973). The JONSWAP spectrum (λ = 3.3) has been used to describe the irregular waves, and the turbulent wind of the IEC Kaimal model has been generated by TurbSim (Jonkman, 2009).

TABLE 3

TABLE 3. Design load cases (DLCs) for typical operational environmental condition tests.

5.3.1 Platform Motion Analysis

Comparison of time series and statistical results of the platform motions with different PTO control strategies are shown in Figure 13 and Figure 14, respectively. The mean, standard deviation (STD), maximum (Max), and minimum (Min) values of the simulation results are calculated by eliminating the startup transient effects. It can be seen that the platform heave and pitch have been effectively suppressed with additional WECs and PTO control strategies, while the surge almost has not been affected. Especially for the heave, the STD value is reduced by up to 27.3% and 36.4% for the LD and BB control, respectively, compared to DeepCwind. Similarly, the pitch STD is reduced by up to 10.0% and 17.1% in the selected DLCs. This has demonstrated the effectiveness of the additional WECs and active PTO control in suppressing the heave and pitch motion oscillation of the FOWT platform.

FIGURE 13

FIGURE 13. Time series of platform motions with different PTO control strategies. (A) DLC 1. (B) DLC 2. (C) DLC 3.

FIGURE 14

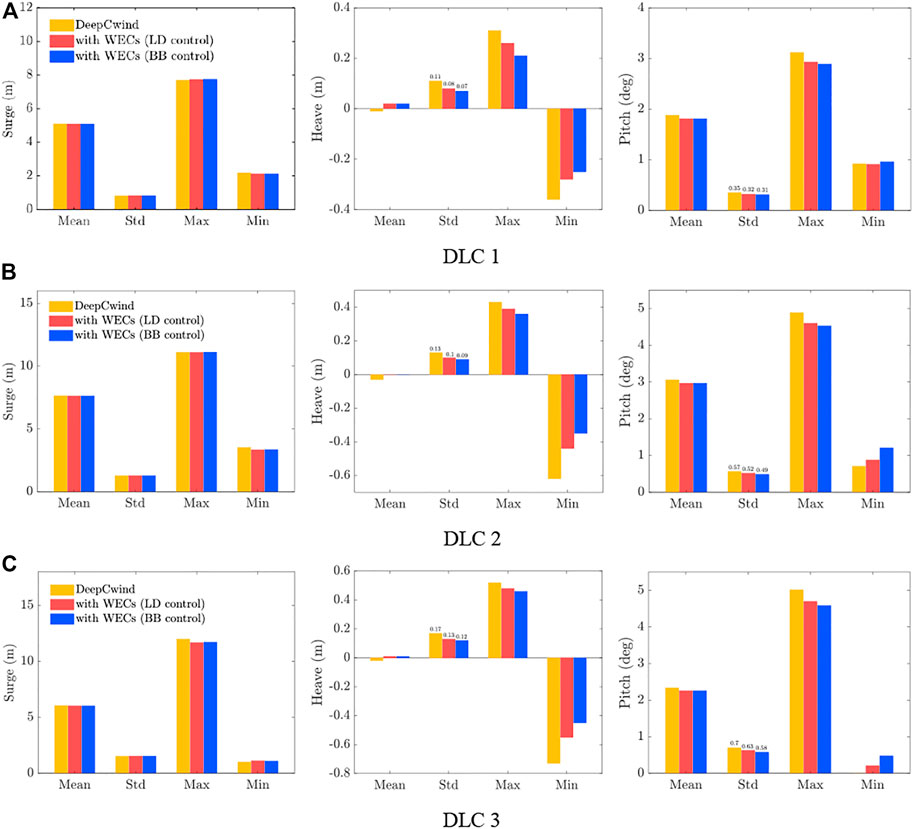
FIGURE 14. Statistical results of platform motions with different PTO control strategies. (A) DLC 1. (B) DLC 2. (C) DLC 3.

Figure 15 shows the smoothed power spectra of the platform motions with different PTO control strategies. It can be found that the platform heave is reduced by suppressing the wave frequency response, and the BB control leads to a more impressive improvement. Regarding pitch motion, the oscillation reduction is dominated by suppressing the wave frequency response in the below-rated case, while it tends to be dominated by suppressing the pitch resonant response in the rated and overrated cases as the increasing wind velocity.

FIGURE 15

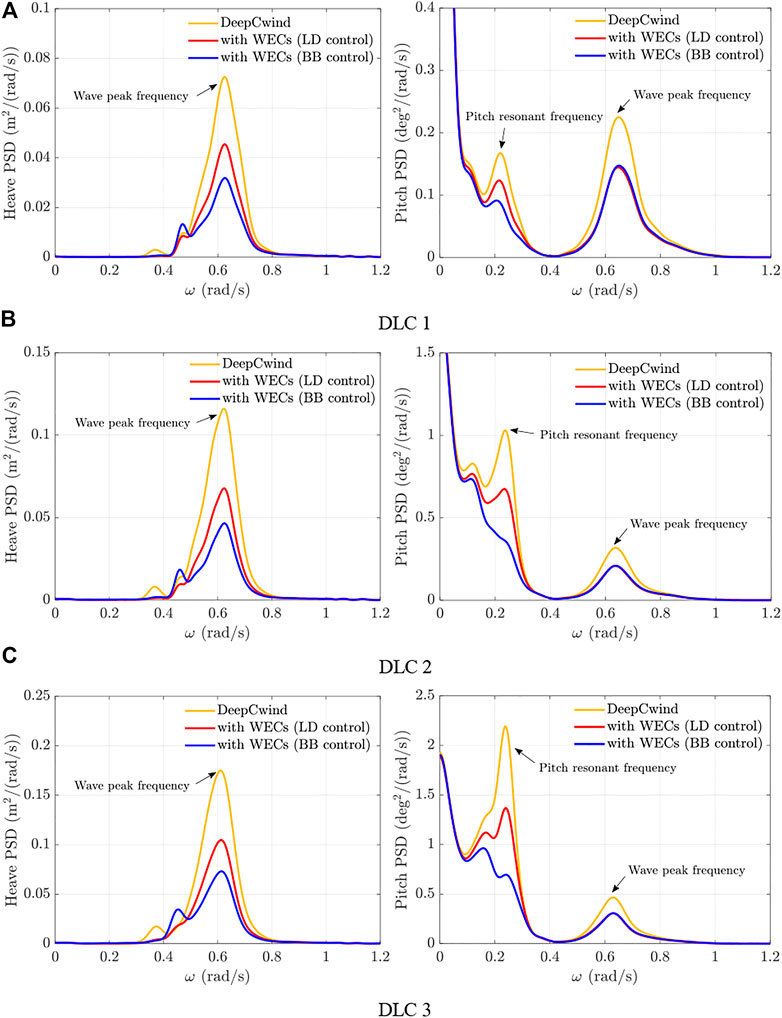
FIGURE 15. Smoothed power spectra of the platform motions with different PTO control strategies. (A) DLC 1. (B) DLC 2. (C) DLC 3.

5.3.2 PTO Dynamic Analysis

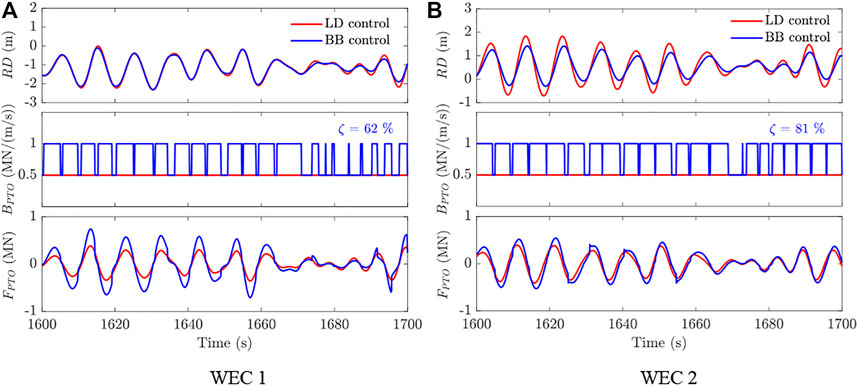
The PTO system dynamics are investigated to reveal the mechanism of the interaction between the WEC and platform, and the time series of control system dynamic responses in DLC 2 is shown in Figure 16. It is seen that the relative response RD deviation between two control strategies of WEC 2 is more evident than that of WEC 1, in which the over-damped state accounts for a higher proportion of the control process in simulation. Here, the percentage of the over-damped state can be expressed as

$\zeta =\frac{T_{\text{over}-\text{damped}}}{T_{\text{total}}}\cdot 100\left(\text{\%}\right)\text{,}(13)$

where T_over-damped is the time in the over-damped state, and T_total is the total simulation duration. It can be inferred that WEC 2 has more contributions to motion suppression by providing additional damping since the larger percentage of the over-damped state ζ = 81% of WEC 2.

FIGURE 16

FIGURE 16. Time series of PTO system dynamic responses in DLC 2. (A) WEC 1. (B) WEC 2.

5.3.3 Power Production Analysis

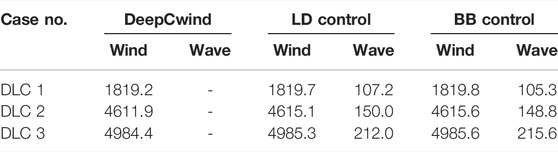
Wave power production of the hybrid platform under the selected typical operational environmental conditions is shown in Figure 17. It can be observed from Figure 17B that the mean value of wave power production for BB control is almost the same as the LD control, and the STD for BB control is slightly increased compared to LD control. Therefore, the wave power production is not much affected when the PTO control is altered from LD control to BB control. The statistical results of the power production for the wind turbine and WECs are summarized in Table 4. It can be noticed that considerable wave energy is captured by the additional WECs, and the total power production of the floating system is enhanced, which can be increased by nearly 6%, especially for the below-rated condition.

FIGURE 17

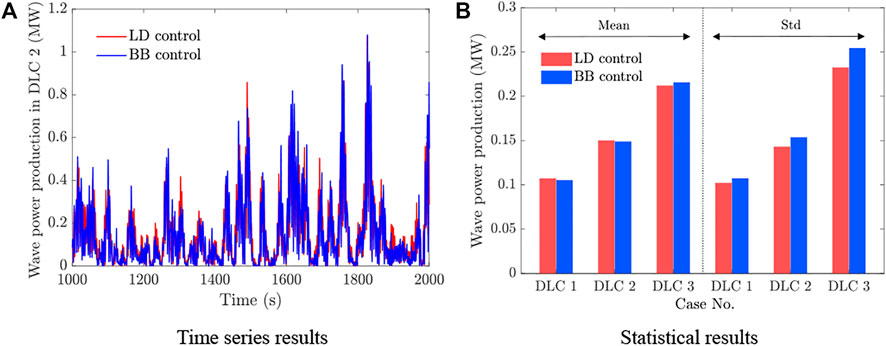
FIGURE 17. Wave power production under typical operational environmental conditions. (A) Time series results. (B) Statistical results.

TABLE 4

TABLE 4. Statistical results of mean power production for the wind turbine and WECs (kW).

5.3.4 Structural Load Analysis

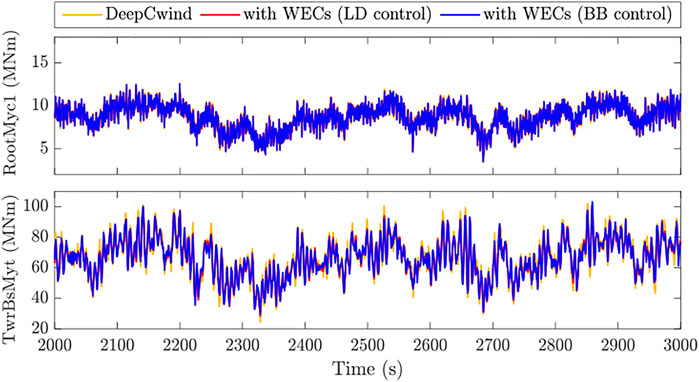
To better study the influence of added WECs with PTO control on structural loads, the fatigue damage equivalent loads (DEL), and ultimate loads of blade-root flapwise moment (RootMyc) and tower-base fore-aft moment (TwrBSMy) have been calculated and analyzed. Figure 18 shows the time series of blade-root and tower-base loads in DLC 2, and the statistical results of structural loads for different PTO control strategies are summarized in Table 5. Note that the statistical results denote the relative reduction of the WEC introduced results compared to DeepCwind only results. It is shown that the tower-base loads are effectively mitigated when the WECs are introduced, and the DEL of the tower base is reduced by up to 11.21%. Particularly, the BB control shows a potential advantage of reducing fatigue loads in more severe conditions (DLC 2 and 3), while the LD control behaves better in moderate conditions (DLC 1). Similar conclusions can be drawn for the ultimate load reduction for the PTO control strategies.

FIGURE 18

FIGURE 18. Time series of blade-root and tower-base loads in DLC 2.

TABLE 5

TABLE 5. Statistical results of structural loads for different PTO control strategies (%).

6 Conclusion

In this article, the potential to reduce the dynamic responses and fatigue loads of FOWT by integrating WECs with different PTO control strategies is investigated. More specifically, a novel hybrid wind-wave energy platform consisting of a DeepCwind floating wind turbine and three heaving-type WECs been proposed. The aero-hydro-servo-elastic-mooring coupled numerical model of the hybrid platform with a PTO system has been established based on the F2A framework. Two different PTO control schemes are comparatively studied, including the passive linear damping control and the active bang-bang control. Various environmental condition tests have been conducted to evaluate the WEC performances in improving the FOWT dynamics in terms of platform motion, structural load, and power production. The following conclusions can be drawn based on the above numerical simulation result analysis:

1. The integrated WECs with PTO control have changed the natural periods of the platform, where the natural periods of heave and pitch have been decreased with increasing PTO damping. The additional WECs lead to a larger rate of attenuation for heave and pitch decay, especially when the PTO damping is around 1 MN/(m/s).

2. The PTO control strategies are shown to have significant impacts on platform motion responses. The surge has almost not been influenced while the heave and pitch have been effectively suppressed. The bang-bang control has shown better performance on motion suppression due to the introduced extra damping effect in both heave and pitch mode, where the motion oscillation can be reduced by up to 34.6% and 17.1%, respectively.

3. The bang-bang control strategies have an effective impact on mitigating the structural loads, especially on the tower base. The bang-bang control performs better in DLC 2 and DLC 3, where the DEL and ultimate load have been reduced by up to 11.21% and 6.96%, respectively. In contrast, the linear damping control shows a larger advantage in the moderate condition DLC 1 with the reduction of DEL and ultimate load by up to 10.32% and 7.05%.

4. The wave power production seems to have no significant difference between the simulation with the two kinds of control strategies. Besides, the integrated WECs can increase the system power production by up to 6% under the below-rated condition.

In summary, the integrated WECs with reasonable PTO control strategies could effectively improve the dynamic responses of the FOWT. Note that the PTO control strategies proposed in this work are only designed for motion suppression. Therefore, multi-objective optimal PTO control design in regards to both power increment and load reduction needs to be further investigated in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

ZC: numerical simulation, validation, writing—original draft. JY: validation and data processing. JS: validation and writing—review and editing. MT: methodology and writing—review and editing. SY: methodology and data processing. YY: data processing and writing—review and editing. PQ: data curation and writing—review and editing. DZ: methodology and writing—review and editing. YS: correspondence, data processing, and writing—review and editing.

Funding

The study is supported by the National Natural Science Foundation of China (Grant Nos. 51879233 and 51705453), Key Research and Development Program of Zhejiang Province (Grant Nos. 2021C01150 and 2021C03182), the Natural Science Foundation of Zhejiang Province (Grant No. LHY20E090001), the Bureau of Science and Technology of Zhoushan (Grant No. 2021C81001), and the Fundamental Research Funds for the Central Universities (Grant No. 226-2022-00096). The authors are grateful for the provision of financial support.

Conflict of Interest

Author YY was employed by the company Zhejiang Windey Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ansys, A. (2013). Theory manual[J]. Canonsburg, PA, USA: ANSYS Inc.

Google Scholar

Armentia, M. S., and Auer, G. (2014). MARINA Platform Final Summary Report[R]. Tech. Rep.. Available at: https://cordis.europa.eu/docs/results/241/241402/final1-publishable-summary-d1-12-marina-final-summary-report-final.pdf.

Google Scholar

Aubault, A., Alves, M., and Sarmento, A. (2011). “Modeling of an Oscillating Water Column on the Floating Foundation WindFloat[C],” in International Conference on Offshore Mechanics and Arctic Engineering, 235–246.

Google Scholar

Babarit, A., and Clément, A. H. (2006). Optimal Latching Control of a Wave Energy Device in Regular and Irregular Waves. Appl. Ocean Res. 28 (2), 77–91. doi:10.1016/j.apor.2006.05.002

CrossRef Full Text | Google Scholar

Brennan, F., and Kolios, A. (2014). “Structural Integrity Considerations for the H2Ocean Multi Modal Wind-Wave Platform[C],” in European Wind Energy Association Conference and Exhibition 2014 (Barcelona: EWEA).

Google Scholar

Drew, B., Plummer, A. R., and Sahinkaya, M. N. (2009). A Review of Wave Energy Converter technology[J].

Google Scholar

Gao, Z., Moan, T., Wan, L., and Michailides, C. (2016). Comparative Numerical and Experimental Study of Two Combined Wind and Wave Energy Concepts. J. Ocean Eng. Sci. 1 (1), 36–51. doi:10.1016/j.joes.2015.12.006

CrossRef Full Text | Google Scholar

Hansen, R. H. (2013). Design and Control of the Power Take-Off System for a Wave Energy Converter with Multiple absorbers[M]. Aalborg: Department of Energy Technology, Aalborg University.

Google Scholar

Hasselmann, K., Barnett, T. P., and Bouws, E. (1973). Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP)[J]. Hamburg: Ergaenzungsheft zur Deutschen Hydrographischen ZeitschriftReihe A.

Google Scholar

Hu, J., Zhou, B., Vogel, C., Liu, P., Willden, R., Sun, K., et al. (2020). Optimal Design and Performance Analysis of a Hybrid System Combing a Floating Wind Platform and Wave Energy Converters. Appl. energy 269, 114998. doi:10.1016/j.apenergy.2020.114998

CrossRef Full Text | Google Scholar

Jonkman, B. J. (2009). TurbSim User's Guide: Version 1.50[R]. Golden, CO (United States): National Renewable Energy Lab.NREL.

Google Scholar

Jonkman, B., and Jonkman, J. (2016). FAST V8. 16.00 a-bjj[J]. Golden: National Renewable Energy Laboratory.

Google Scholar

Jonkman, J., Butterfield, S., and Musial, W. (2009). Definition of a 5-MW Reference Wind Turbine for Offshore System development[R]. Golden, CO (United States): National Renewable Energy Lab.NREL.

Google Scholar

Jonkman, J. M., and Buhl, M. L. (2005). FAST User's guide[M]. Golden, CO, USA: National Renewable Energy Laboratory.

Google Scholar

Jonkman, J. M., and Matha, D. (2011). Dynamics of Offshore Floating Wind Turbines-Analysis of Three Concepts. Wind Energy 14 (4), 557–569. doi:10.1002/we.442

CrossRef Full Text | Google Scholar

Kamarlouei, M., Gaspar, J. F., Calvario, M., Hallak, T. S., Mendes, M. J. G. C., Thiebaut, F., et al. (2020). Experimental Analysis of Wave Energy Converters Concentrically Attached on a Floating Offshore Platform. Renew. Energy 152, 1171–1185. doi:10.1016/j.renene.2020.01.078

CrossRef Full Text | Google Scholar

Koundouri, P., Airoldi, L., Boon, A., Giannouli, A., Levantis, E., Moussoulides, A., et al. (2017). “Introduction to the MERMAID Project[M],” in The Ocean of Tomorrow. Cham: Springer, 1–8. doi:10.1007/978-3-319-55772-4_1

CrossRef Full Text | Google Scholar

Kusnick, J., Adams, D. E., and Griffith, D. T. (2015). Wind Turbine Rotor Imbalance Detection Using Nacelle and Blade Measurements. Wind Energy 18 (2), 267–276. doi:10.1002/we.1696

CrossRef Full Text | Google Scholar

Lin, Z., Chen, Z., Wu, Q., Yang, S., and Meng, H. (2018). Coordinated Pitch & Torque Control of Large-Scale Wind Turbine Based on Pareto Efficiency Analysis. Energy 147, 812–825. doi:10.1016/j.energy.2018.01.055

CrossRef Full Text | Google Scholar

Ma, Z., Wang, S., Wang, Y., Ren, N., and Zhai, G. (2019). Experimental and Numerical Study on the Multi-Body Coupling Dynamic Response of a Novel Serbuoys-TLP Wind Turbine. Ocean. Eng. 192, 106570. doi:10.1016/j.oceaneng.2019.106570

CrossRef Full Text | Google Scholar

Michailides, C., Gao, Z., and Moan, T. (2016). Experimental and Numerical Study of the Response of the Offshore Combined Wind/wave Energy Concept SFC in Extreme Environmental Conditions. Mar. Struct. 50, 35–54. doi:10.1016/j.marstruc.2016.06.005

CrossRef Full Text | Google Scholar

Michailides, C., Gao, Z., and Moan, T. (2016). Experimental Study of the Functionality of a Semisubmersible Wind Turbine Combined with Flap-type Wave Energy Converters. Renew. Energy 93, 675–690. doi:10.1016/j.renene.2016.03.024

CrossRef Full Text | Google Scholar

Moriarty, P. J., and Hansen, A. C. (2005). AeroDyn Theory manual[R]. Golden, CO (US): National Renewable Energy Lab.

Google Scholar

Muliawan, M. J., Karimirad, M., and Moan, T. (2012). “STC (Spar-Torus Combination): a Combined Spar-type Floating Wind Turbine and Large Point Absorber Floating Wave Energy Converter—Promising and Challenging[C],” in International Conference on Offshore Mechanics and Arctic Engineering (American Society of Mechanical Engineers ASME), 667–676.

Google Scholar

Njiri, J. G., Beganovic, N., Do, M. H., and Söffker, D. (2019). Consideration of Lifetime and Fatigue Load in Wind Turbine Control. Renew. energy 131, 818–828. doi:10.1016/j.renene.2018.07.109

CrossRef Full Text | Google Scholar

Peiffer, A., Roddier, D., and Aubault, A. (2011). “Design of a Point Absorber inside the WindFloat Structure[C],” in International Conference on Offshore Mechanics and Arctic Engineering, 247–255.

Google Scholar

Peiffer, A., and Roddier, D. (2012). “Design of an Oscillating Wave Surge Converter on the Windfloat Structure[C],” in Proceedings of the 2012 4th International Conference on Ocean Energy (Dublin, Ireland: ICOE), 17–19.

Google Scholar

Pérez-Collazo, C., Greaves, D., and Iglesias, G. (2015). A Review of Combined Wave and Offshore Wind Energy[J]. Renew. Sustain. energy Rev. 42, 141–153.

Google Scholar

Perez-Collazo, C., Greaves, D., and Iglesias, G. (2018). Hydrodynamic Response of the WEC Sub-system of a Novel Hybrid Wind-Wave Energy Converter. Energy Convers. Manag. 171, 307–325. doi:10.1016/j.enconman.2018.05.090

CrossRef Full Text | Google Scholar

Perez-Collazo, C., Pemberton, R., Greaves, D., and Iglesias, G. (2019). Monopile-mounted Wave Energy Converter for a Hybrid Wind-Wave System. Energy Convers. Manag. 199, 111971. doi:10.1016/j.enconman.2019.111971

CrossRef Full Text | Google Scholar

Ren, N., Gao, Z., Moan, T., and Wan, L. (2015). Long-term Performance Estimation of the Spar-Torus-Combination (STC) System with Different Survival Modes. Ocean. Eng. 108, 716–728. doi:10.1016/j.oceaneng.2015.08.013

CrossRef Full Text | Google Scholar

Ren, N., Ma, Z., Fan, T., Zhai, G., and Ou, J. (2018). Experimental and Numerical Study of Hydrodynamic Responses of a New Combined Monopile Wind Turbine and a Heave-type Wave Energy Converter under Typical Operational Conditions. Ocean. Eng. 159, 1–8. doi:10.1016/j.oceaneng.2018.03.090

CrossRef Full Text | Google Scholar

Ren, N., Ma, Z., Shan, B., Ning, D., and Ou, J. (2020). Experimental and Numerical Study of Dynamic Responses of a New Combined TLP Type Floating Wind Turbine and a Wave Energy Converter under Operational Conditions. Renew. Energy 151, 966–974. doi:10.1016/j.renene.2019.11.095

CrossRef Full Text | Google Scholar

Robertson, A., Jonkman, J., and Masciola, M. (2014). Definition of the Semisubmersible Floating System for Phase II of OC4[R]. Golden, CO (United States): National Renewable Energy Lab.NREL.

Google Scholar

Sarkar, S., Fitzgerald, B., and Basu, B. (2020). Individual Blade Pitch Control of Floating Offshore Wind Turbines for Load Mitigation and Power Regulation[J]. IEEE Trans. Control Syst. Technol. 29 (1), 305–315.

Google Scholar

Schallenberg-Rodríguez, J., and Montesdeoca, N. G. (2018). Spatial Planning to Estimate the Offshore Wind Energy Potential in Coastal Regions and Islands. Practical Case: The Canary Islands[J]. Energy 143, 91–103. doi:10.1016/j.energy.2017.10.084

CrossRef Full Text | Google Scholar

Shi, W., Park, H.-C., Baek, J.-H., Kim, C.-W., Kim, Y.-C., and Shin, H.-K. (2012). Study on the Marine Growth Effect on the Dynamic Response of Offshore Wind Turbines. Int. J. Precis. Eng. Manuf. 13 (7), 1167–1176. doi:10.1007/s12541-012-0155-7

CrossRef Full Text | Google Scholar

Si, Y., Chen, Z., Zeng, W., Sun, J., Zhang, D., Ma, X., et al. (2021). The Influence of Power-Take-Off Control on the Dynamic Response and Power Output of Combined Semi-submersible Floating Wind Turbine and Point-Absorber Wave Energy Converters. Ocean. Eng. 227, 108835. doi:10.1016/j.oceaneng.2021.108835

CrossRef Full Text | Google Scholar

Si, Y., Karimi, H. R., and Gao, H. (2014). Modelling and Optimization of a Passive Structural Control Design for a Spar-type Floating Wind Turbine. Eng. Struct. 69, 168–182. doi:10.1016/j.engstruct.2014.03.011

CrossRef Full Text | Google Scholar

Taghipour, R., Perez, T., and Moan, T. (2008). Hybrid Frequency-Time Domain Models for Dynamic Response Analysis of Marine Structures. Ocean. Eng. 35 (7), 685–705. doi:10.1016/j.oceaneng.2007.11.002

CrossRef Full Text | Google Scholar

Tc88-Mt, I. E. C. (2005). Iec 61400-3: Wind Turbines–Part 1: Design requirements[J]. Geneva: International Electrotechnical Commission, 64.

Google Scholar

Wang, L., Robertson, A., and Jonkman, J. (2022). OC6 Phase I: Improvements to the OpenFAST Predictions of Nonlinear, Low-Frequency Responses of a Floating Offshore Wind Turbine Platform[J]. Renew. Energy 187, 282–301. doi:10.1016/j.renene.2022.01.053

CrossRef Full Text | Google Scholar

Wang, X., Zeng, X., Li, J., Yang, X., and Wang, H. (2018). A Review on Recent Advancements of Substructures for Offshore Wind Turbines. Energy Convers. Manag. 158, 103–119. doi:10.1016/j.enconman.2017.12.061

CrossRef Full Text | Google Scholar

Wang, Y., Shi, W., Michailides, C., Wan, L., Kim, H., and Li, X. (2022). WEC Shape Effect on the Motion Response and Power Performance of a Combined Wind-Wave Energy Converter. Ocean. Eng. 250, 111038. doi:10.1016/j.oceaneng.2022.111038

CrossRef Full Text | Google Scholar

Yang, Y., Bashir, M., Michailides, C., Li, C., and Wang, J. (2020). Development and Application of an Aero-Hydro-Servo-Elastic Coupling Framework for Analysis of Floating Offshore Wind Turbines. Renew. Energy 161, 606–625. doi:10.1016/j.renene.2020.07.134

CrossRef Full Text | Google Scholar

Yang, Y., Bashir, M., Wang, J., Michailides, C., Loughney, S., Armin, M., et al. (2020). Wind-wave Coupling Effects on the Fatigue Damage of Tendons for a 10 MW Multi-Body Floating Wind Turbine. Ocean. Eng. 217, 107909. doi:10.1016/j.oceaneng.2020.107909

CrossRef Full Text | Google Scholar

Zou, S., Abdelkhalik, O., Robinett, R., Bacelli, G., and Wilson, D. (2017). Optimal Control of Wave Energy Converters. Renew. energy 103, 217–225. doi:10.1016/j.renene.2016.11.036

CrossRef Full Text | Google Scholar