Power Coordinated Control and Parameter Analysis for Spiral Spring Energy Storage Systems Based on Backstepping Control Under Current Vector Orientation

1 Introduction

The exploitation of new energy sources is an effective means for environmental protection and sustainable development, while natural features of intermittence and fluctuation restrict the large scale of the new energy sources connected to the grid (Kumar et al., 2020). Research and investigation of energy storage technologies are increasingly available as an important approach to suppress the adverse effects of new energy sources (Ghaemi and Mirsalim, 2017; Zhang and Zhu, 2018; Gonzalez ‐ Gonzalez et al., 2020). The spiral spring energy storage (SSES) system shown in Figure 1, which has been devised and improved in recent years, is paid special attention due to its various merits such as low cost, long lifetime, high safety, high efficiency, environmental friendliness, high power density, and easy adjustment of energy storage capacity (Yu et al., 2016; Yu et al., 2020). The permanent magnet synchronous machine (PMSM) with full power converters is selected as its energy conversion equipment, owing to a high ratio of torque to inertia and simple structure (Ye et al., 2021).

FIGURE 1

FIGURE 1. Structural diagram of the mechanical spiral spring energy storage system.

Basic characteristics of the variable torque and inertia for the spiral spring in operation (Caballero et al., 2018) make the SSES system output decrease in power, and it is difficult for the SSES system to store or release electrical energy, according to the stable power signal from/to the grid with previous control methods. The reversal torque property of the spiral spring (Yu et al., 2018a) also requires the control algorithm to respond quickly and run fast.

For the participation in power regulation of the SSES system with a proper control approach of the full power converters, the control technique for both the grid-side converter (GSC) and the machine-side converter (MSC) should be considered. For the GSC, its power control mainly includes indirect current control, direct current control, and direct power control (DPC) (Gui et al., 2019). In contrast to the indirect current control with a relatively poor dynamic performance, direct current control has the advantages of high precision and good dynamic performance. Active and reactive power could be controlled by changing the d-axis and q-axis currents, respectively. But the proportional–integral (PI)-based double closed-loop control has a relatively slow response and is hard to set the parameters (Mallik et al., 2017). DPC with its fast response can control instantaneous active power and reactive power directly (Kim, 2018). However, the switching frequency in a traditional switching table-based DPC is not fixed. DPC with constant switching frequency is discussed in Gui et al. (2018), and DPC based on model predictive control is proposed in Zhang et al. (2015), but they are both affected by a big computational burden. In view of its simple structure, flexible control, and strong parameter robustness of backstepping control (BC), backstepping control-based DPC is proposed in Wai et al. (2018), which improves the stability of the control system. At present, the GSC is primarily used to stabilize the voltage of the direct current (DC) bus, and few studies have revealed its power control scenario directly responding to the external power signal such as from the grid, which is realized by coordinating with the MSC or the load power. The power control of PMSM is still dominated by DPC. In Zhang and Qu (2015), a switching table-based DPC is investigated through the instantaneous power principle. A fast response DPC with fixed switching frequency under stator current vector orientation is presented by combining SVPWM with the instantaneous reactive power principle in Ali et al. (2017). The references of active power and reactive power obtained by direct calculation are used to replace the PI-based double closed-loop controller in Kwak et al. (2019), and its MSC merely uses the uncontrollable rectification mode. The output power of PMSM under DPC is supplied to the load. If the power signal looked at from the grid side is responded to in this way, the actual power involved in regulation will become inaccurate due to the losses of the machine and converters. Currently, most of the studies focus on bilateral converters from the perspective of isolation and decoupling. To reduce the power imbalance caused by the load fluctuation, it is suitable to increase the coupling capacitor, which leads to a higher cost and lower reliability. Therefore, the coordinated control of the GSC and MSC has been concerned (Yu et al., 2018b).

To achieve good integration and improve the dynamic response speed of the overall system, it is essential to optimize the independent control on both sides of GSC and MSC and target them as a whole to design the coordinated control. A coordinated control scheme based on active power and DC voltage to reduce the oscillation of DC voltage is proposed in Tian et al. (2014), but the PI control is used, and it cannot track the alternating current signal without steady-state error. Coordinated passive control of PMSM based on the dual PWM converter is realized in Li et al. (2018), and it can restrain the fluctuation of the DC bus voltage effectively. In contrast, the passive control is relatively complicated and increases the implementation difficulty in practice. Aiming at the energy relationship of each part in the coordinated control, a mathematical model from the energy viewpoint is established in Bo et al. (2017) to improve the ability of the motor to manage the external energy fluctuation. However, the system still faces the problem of regulating the load power and does not participate in power regulation directly.

BC starts with the control objectives and selects virtual state variables and virtual stability functions to construct the actual controller step-by-step. BC can achieve an accurate and fast tracking of the control targets, and its stability is strictly guaranteed by the Lyapunov stability theory. The application of BC in related fields (Xiong and Sun, 2016; Yang et al., 2020) shows that it is superior to the traditional PI control in control accuracy, control speed, and other performance indexes. In allusion to the variable torque and inertia of the spiral spring, the spring driven by PMSM is realized by BC in Yu et al. (2018b). The results show that BC has a rapid response and small tracking error, so it is also adopted as the control scheme in this research. The choice of the control parameters in BC is an important task and will affect its control performance. The current rule of selecting control parameters is basically based on the theory of Lyapunov stability, which requires that the control parameters satisfy the positive definite condition (Delavari and Naderian, 2019; Achlerkar and Panigrahi, 2020; Li et al., 2020). In Liu et al. (2019), it is pointed out that one of the reasons for the poor dynamic performance of BC is that its control parameters only satisfy the stability condition without considering the convergence rate of the steady-state error and other factors. It can be seen that it is of great significance to select the appropriate backstepping control parameters, but few studies have been involved in the optimization of control parameters. The ability of BC to cope with the change in structural parameters is enhanced in Lu et al. (2015) by adjusting the control parameters. In Jeon et al. (2020), it is further pointed out that the selection of the control parameters in BC should consider the range of the uncertain parameters. The control parameters of BC are optimized and determined in Yu et al. (2016) by the differential evolution algorithm. The control parameters of BC do affect the control performance. But current research optimizes the control parameters mainly through intelligent algorithms and does not directly study the method of parameter selection from the perspective of the control performance.

In summary, a coordinated power control scheme of GSC and MSC for the SSES system based on BC under current vector orientation will be proposed in the research study. Under the current vector orientation, for GSC, the control of the grid current amplitude and power factor angle can ensure the rapid and accurate response to the external power signal; and for PMSM, the coordinated control, including the stability of the DC side voltage, is achieved by regulating the stator current and torque angle. Active coordinated control can greatly simplify the control structure. Meanwhile, for the SSES system with a strong nonlinearity, the control parameters in the designed controller are analyzed and selected in terms of the control performance of the system. Ultimately, through the capacitor in the DC side, the GSC can actively track the power signal from the grid, with the MSC coordinating with it to ensure that the SSES system can participate in power regulation accurately and quickly.

The contribution of this research is reflected in two aspects: First, with the DC-link capacitor to help realize the power coordinated control of the SSES, the coordinated controllers of GSC and MSC are proposed based on BC in the grid current-oriented coordinate system for GSC and in the stator current-oriented coordinate system for MSC, respectively. Second, for multiple control parameters in the proposed control scheme, the determination approach of the control parameters is devised based on the perspective of the control performance. The structure of this context is as follows: Section 2 introduces the modeling of the SSES system. The formulation and design of the controllers in GSC and PMSM are carried out in Section 3. In Section 4, the determination of the control parameters is completed. Section 5 gives the simulation and experimental results. The last section draws the conclusions.

2 Modeling of the SSES System

The schematic diagram of the SSES system shown in Figure 1 indicates that the system can be divided into four subsystems: spiral spring, PMSM, AC-DC-AC bidirectional converter, and the controller.

2.1 Modeling of the Spiral Spring

The spiral spring is the energy storage device of the SSES system. According to the knowledge of material mechanics (Yu et al., 2018b), the mathematical model of the spiral spring can be described by the torque characteristic:

$T_{\mathrm{L}}=\frac{Eb{h}^3}{12L}\delta =\frac{Eb{h}^3}{12L}{\omega }_{\text{r}}t,(1)$

where T_L is the output torque, E is the elasticity modulus, b, h, and L are the width, thickness, and length of the spring, respectively, δ is the rotation angle of the motor, ω_r is the mechanical angular velocity of the motor, and t is the time.

2.2 Modeling of the Grid-Side Converter Under Grid Current Vector Orientation

Based on the original dqo synchronous rotating coordinate system oriented on the grid voltage vector u_g, a new rotating coordinate system TMo plotted in Figure 2 is introduced and oriented on the grid current vector i_g, where the T-axis is the real axis, and the M-axis is the imaginary axis. The grid current i_g overlaps with the T-axis. θ_c is the included angle between T and d axes. ω_g is the angular speed of the grid voltage.

FIGURE 2

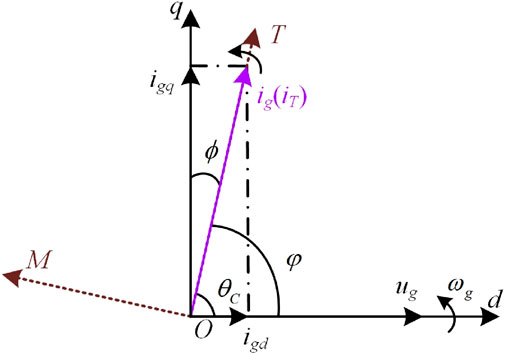
FIGURE 2. Space vector model of the grid-side converter under the current vector orientation coordinate system.

In TMo, the state equation of GSC with i_g and θ_C selected as the state variables can be expressed as follows:

$\{\begin{array}{l}{u}_{\text{g}T}=R_{\text{g}}{i}_{\text{g}}+L_{\text{g}}\frac{d{i}_{\text{g}}}{dt}+u_T,\\ u_{\text{g}M}={\omega }_{\text{g}}{L}_{\text{g}}{i}_{\text{g}}+L_{\text{g}}{i}_{\text{g}}\frac{d{\theta }_{\text{C}}}{dt}+u_M,\end{array}(2)$

where u_gT and u_gM are the voltages in T and M axes, u_T and u_M are the output voltages of GSC in T and M axes, and R_g and L_g are the resistance and inductor.

According to Figure 2, θ_C just represents the power factor angle φ in the TMo coordinate system. The response to external power signals can be realized quickly by controlling the amplitude of the grid current i_g, and the angle φ. Eq. 2 also shows that the differential items of i_g and θ_C only exist in u_gT and u_gM, respectively. It means that the control of i_g and θ_C can be achieved by u_gT and u_gM individually.

2.3 Modeling of PMSM

Another synchronous rotating coordinate system DQo shown in Figure 3 is established to control PMSM, where DQ axes are the real and imaginary axes individually. The stator current i_s overlapped with the D-axis. θ_L is the included angle between D and d axes. u_s is the stator voltage, and ψ_r is the permanent magnet flux linkage of PMSM.

FIGURE 3

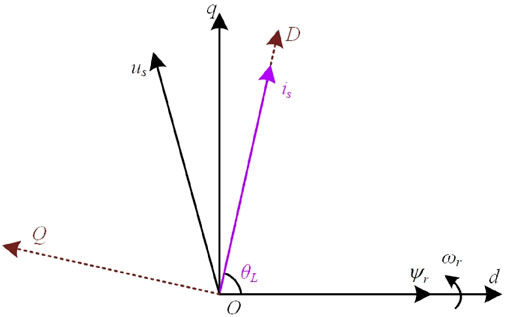
FIGURE 3. Space vector model of the machine-side converter under the current vector orientation coordinate system.

Based on the DQo coordinate system, the electromagnetic torque of PMSM is rewritten as follows:

$T_{\text{e}}=\frac{3}{2}{n}_{\text{p}}{i}_{\text{s}}\sin {\theta }_{\text{L}}{\psi }_{\text{r}},(3)$

where T_e is the electromagnetic torque, n_p is the number of pole pairs, i_s is the amplitude of the stator current, and θ_L is the torque angle.

The rotation equation of PMSM can be written as follows:

$J\frac{d{\omega }_{\text{r}}}{dt}=T_{\text{e}}-T_{\text{L}},(4)$

where J is the moment of inertia.

In DQo, the control framework of surface-mounted PMSM with i_s and θ_L as the state variables can be expressed as follows (Yu et al., 2018a):

$\{\begin{array}{l}{u}_{\text{s}D}=R_{\text{s}}{i}_{\text{s}}+L_{\text{s}}\frac{d{i}_{\text{s}}}{dt}+n_{\text{p}}{\psi }_{\text{r}}{\omega }_{\text{r}}\sin {\theta }_{\text{L}},\\ u_{\text{s}Q}=L_{\text{s}}{i}_{\text{s}}\frac{d{\theta }_{\text{L}}}{dt}+n_{\text{p}}{\psi }_{\text{r}}{\omega }_{\text{r}}\cos {\theta }_{\text{L}}+n_{\text{p}}{\omega }_{\text{r}}{L}_{\text{s}}{i}_{\text{s}},\end{array}(5)$

where u_sD and u_sQ are the stator voltages in the D and Q axes, and R_s and L_s are the resistance and inductor.

Eq. 5 shows that the differential items of i_s and θ_L only exist in u_sD and u_sQ, respectively. Similarly, with the modeling of GSC, the control of i_s and θ_L can be achieved by u_sD and u_sQ, respectively. The control framework established in this research can realize the control effect similar to the direct torque control that rapidly improves the response speed.

According to the motor convention, the dynamic equation of the DC-link capacitor is written as follows:

$C\frac{d{u}_{\text{dc}}}{dt}=\frac{P_{\text{s}}}{u_{\text{dc}}}-\frac{P_{\text{g}}}{u_{\text{dc}}},(6)$

where P_g and P_s are the current flowing in and out of the DC-link capacitor respectively, and u_dc is the DC-side voltage.

3 Coordinated Control Scheme Based on Backstepping Control

The control targets are determined as the following: 1) for GSC, it should regulate the grid current i_g and the angle θ_C to track active and reactive powers from the grid. An indirect current control method employed in the research means that the tracked power signals need to be converted into the expression of i_g and θ_C. 2) For MSC, it should coordinate with the output of GSC and accomplish two jobs. First, the capacitor voltage u_dc on the DC side could be stabilized by adjusting the stator current i_s to keep the power of MSC equal to the power of GSC. This objective differs obviously from the power control under the usual voltage vector orientation that stabilizes the DC-link voltage by GSC. Second, based on the determined stator current amplitude, the energy from the grid side can be stored as much as possible when the control torque angle θ_L is π/2, so the angle reference θ_Lref is selected as π/2.

3.1 Design of the Grid-Side Converter Controller

It is assumed that active power and reactive power outputted by GSC are P and Q, respectively. They can be expressed as follows:

$\{\begin{array}{l}P=u_{\text{g}M}\cdot i_{\text{g}M}+u_{\text{g}T}\cdot i_{\text{g}T}=u_{\text{g}T}\cdot i_{\text{g}T}\\ =u_{\text{g}T}\cdot i_{\text{g}}=u_{\text{g}}\cos \phi \cdot i_{\text{g}},\\ Q=u_{\text{g}T}\cdot i_{\text{g}M}-u_{\text{g}M}\cdot i_{\text{g}T}=-u_{\text{g}M}\cdot i_{\text{g}T}\\ =-u_{\text{g}M}\cdot i_{\text{g}}=-u_{\text{g}}\sin \phi \cdot i_{\text{g}}.\end{array}(7)$

If the references of active power and reactive power are P_ref and Q_ref, the references of the grid current i_gref and power factor angle θ_Cref can be calculated as follows:

$\{\begin{array}{l}{i}_{\text{gref}}=\sqrt{P_{\text{ref}}^2+Q_{\text{ref}}^2}/u_{\text{g}},\\ {\theta }_{\text{Cref}}=\arctan \left(-Q_{\text{ref}}/P_{\text{ref}}\right).\end{array}(8)$

e_ig is defined as the tracking error of i_g, which means $e_{\text{ig}}=i_{\text{gref}}-i_{\text{g}}$. Based on BC, the derivative of e_ig is calculated as follows:

$\begin{array}{c}{\dot{e}}_{\text{ig}}={\dot{i}}_{\text{gref}}-{\dot{i}}_{\text{g}}\\ ={\dot{i}}_{\text{gref}}-\frac{1}{L_{\text{g}}}\left(u_{\text{g}}\cos {\theta }_{\text{C}}-R_{\text{g}}{i}_{\text{g}}-u_T\right).\end{array}(9)$

The first actual control variable u_T is designed as follows:

$u_T=u_{\text{g}}\cos {\theta }_{\text{C}}-R_{\text{g}}{i}_{\text{g}}-L_{\text{g}}{k}_{\text{ig}}{e}_{\text{ig}}-L_{\text{g}}{\dot{i}}_{\text{gref}},(10)$

where k_ig is a positive control gain and will be determined in the following section.

Substituting Eq. 10 into Eq. 9, we obtain the following:

${\dot{e}}_{\text{ig}}=-k_{\text{ig}}{e}_{\text{ig}}.(11)$

e_θc is defined as the tracking error of θ_C, which means $e_{\text{θc}}={\theta }_{\text{Cref}}-{\theta }_{\text{C}}$. The derivative of e_θc is calculated as follows:

$\begin{array}{c}{\dot{e}}_{\text{θc}}={\dot{\theta }}_{\text{Cref}}-{\dot{\theta }}_{\text{C}}\\ ={\dot{\theta }}_{\text{Cref}}-\frac{1}{L_{\text{g}}{i}_{\text{g}}}\left(-u_{\text{g}}\sin {\theta }_{\text{C}}-{\omega }_{\text{g}}{L}_{\text{g}}{i}_{\text{g}}-u_M\right).\end{array}(12)$

The second actual control variable u_M is designed as follows:

$u_M=-u_{\text{g}}\sin {\theta }_{\text{C}}-{\omega }_{\text{g}}{L}_{\text{g}}{i}_{\text{g}}-L_{\text{g}}{i}_{\text{g}}{k}_{\text{θc}}{e}_{\text{θc}}-L_{\text{g}}{i}_{\text{g}}{\dot{\theta }}_{\text{Cref}},(13)$

where k_θc is a positive control gain of the power factor angle and will also be determined in the following section.

Substituting Eq. 13 into Eq. 12, we obtain the following:

${\dot{e}}_{\text{θc}}=-k_{\text{θc}}{e}_{\text{θc}}.(14)$

For e_ig and e_θc, a Lyapunov function V₁ is selected as

$V_1=\frac{1}{2}{e}_{\text{ig}}^2+\frac{1}{2}{e}_{\text{θc}}^2.(15)$

The derivative of V₁ is calculated as follows:

${\dot{V}}_1=e_{\text{ig}}{\dot{e}}_{\text{ig}}+e_{\text{θc}}{\dot{e}}_{\text{θc}}=-k_{\text{ig}}{e}_{\text{ig}}^2-k_{\text{θc}}{e}_{\text{θc}}^2\le 0.(16)$

Due to V₁ being bounded and k_ig and k_θc being larger than zero, according to the Barbalat theorem, $\underset{t\to \infty }{\lim }{V}_1\left(t\right)=0$ can be obtained. Therefore, the closed-loop system is asymptotically stable.

Eqs 10, 13 give the controllers of the grid current and the power factor angle in GSC. The control block diagram of GSC can be drawn in Figure 4, where u_dc can be regarded as an equivalent DC voltage source, and the power factor angle can be obtained through active power and reactive power.

FIGURE 4

FIGURE 4. Control diagram block of the grid-side converter.

3.2 Design of the PMSM-Side Converter Controller

According to Eq. 6, the square of DC voltage is chosen as the control variable in order to make the expression simplified, which can be referred as u₂.

$\frac{d{u}_2}{dt}=\frac{2}{C}\left(i_g{u}_T-i_s{u}_{sD}\right).(17)$

e_u is defined as the tracking error of u₂, which means that $e_u=u_{2ref}-u_2$; the derivative of e_u is calculated as follows:

$\begin{array}{c}{\dot{e}}_{\text{u}}={\dot{u}}_{2\text{ref}}-{\dot{u}}_2\\ ={\dot{u}}_{2\text{ref}}-\frac{2}{C}\left(i_{\text{g}}{u}_T-i_{\text{s}}{u}_{\text{s}D}\right).\end{array}(18)$

In accordance with Eq. 18, the first actual control variable u_sD is designed as follows:

$u_{\text{s}D}=-\frac{C}{2i_{\text{s}}}{k}_{\text{u}}{e}_{\text{u}}-\frac{C}{2i_{\text{s}}}{\dot{u}}_{2\text{ref}}+\frac{i_{\text{g}}{u}_T}{i_{\text{s}}},(19)$

where k_u is a positive control gain and will be chosen in the following section.

Substituting Eq. 19 into Eq. 18, we obtain the following:

${\dot{e}}_{\text{u}}=-k_{\text{u}}{e}_{\text{u}}.(20)$

e_θl is defined as the tracking error of θ_L, which means that $e_{\text{θl}}={\theta }_{\text{Lref}}-{\theta }_{\text{L}}$; the derivative of e_θl is calculated as follows:

$\begin{array}{c}{\dot{e}}_{\text{θl}}={\dot{\theta }}_{\text{Lref}}-{\dot{\theta }}_{\text{L}}\\ ={\dot{\theta }}_{\text{Lref}}+\frac{1}{L_{\text{s}}{i}_{\text{s}}}\left(u_{\text{s}Q}+n_{\text{p}}{\psi }_{\text{r}}{\omega }_{\text{r}}\cos {\theta }_L+n_{\text{p}}{\omega }_{\text{r}}{L}_{\text{s}}{i}_{\text{s}}\right).\end{array}(21)$

In accordance with Eq. 21, the second actual control variable u_sD is designed as follows:

$u_{\text{s}Q}=-n_{\text{p}}{\psi }_{\text{r}}{\omega }_{\text{r}}\cos {\theta }_{\text{L}}-L_{\text{s}}{i}_{\text{s}}\left(n_{\text{p}}{\omega }_{\text{r}}+{\dot{\theta }}_{\text{Lref}}+k_{\text{θl}}{e}_{\text{θl}}\right),(22)$

where k_θl is a positive control gain and will be chosen in the following section.

Substituting Eq. 22 into Eq. 21, we obtain the following:

${\dot{e}}_{\text{θl}}=-k_{\text{θl}}{e}_{\text{θl}}.(23)$

For e_u and e_θl, the selection of a Lyapunov function V₂ could be written as follows:

$V_2=\frac{1}{2}{e}_{\text{u}}^2+\frac{1}{2}{e}_{\text{θl}}^2.(24)$

The derivative of V₂ is calculated as follows:

$\begin{array}{c}{\dot{V}}_2=e_{\text{u}}{\dot{e}}_u+e_{\text{θl}}{\dot{e}}_{\text{θl}}\\ =-k_{\text{u}}{e}_{\text{u}}^2-k_{\text{θl}}{e}_{\text{θl}}^2\le 0.\end{array}(25)$

Because V₂ is bounded and e_u and e_θl values are larger than zero, according to the Barbalat theorem, $\underset{t\to \infty }{\lim }{V}_2\left(t\right)=0$ can be obtained. Hence, the closed-loop system is asymptotically stable.

The DC-side voltage controller shown in Eq. 19 and the torque angle controller shown in Eq. 22 are completed based on BC. Thus, the control block diagram of MSC proposed in the research can be drawn in Figure 5.

FIGURE 5

FIGURE 5. Control diagram block of the machine-side converter.

4 Control Parameter Analysis

4.1 Analysis of System Performance

By substituting the controller designed by BC into the original differential equation of the system, the following error functions can be obtained:

${\dot{\mathit{e}}}_X=-\mathit{K}{\mathit{e}}_X,(26)$

where e_X is the error matrix, and K is the gain matrix, ${\mathit{e}}_X={\left[\begin{array}{cccc}{e}_{\text{ig}}& e_{\text{θc}}& e_{\text{u}}& e_{\text{θl}}\end{array}\right]}^T$, and $\mathit{K}=diag\left[k_{\text{ig}}{k}_{\text{θc}}{k}_{\text{u}}{k}_{\text{θl}}\right]$.

In terms of Eq. 26, the following equation can be obtained:

$\left[\begin{array}{c}{\dot{i}}_{\text{g}}\\ {\dot{\theta }}_{\text{C}}\\ {\dot{u}}_2\\ {\dot{\theta }}_{\text{L}}\end{array}\right]=-\left[\begin{array}{c}{k}_{\text{ig}}{i}_{\text{g}}\\ k_{\text{θc}}{\theta }_{\mathrm{C}}\\ k_{\text{u}}{u}_2\\ k_{\text{θl}}{\theta }_{\text{L}}\end{array}\right]+\left[\begin{array}{c}{k}_{\text{ig}}{i}_{\text{gref}}\\ k_{\text{θc}}{\theta }_{\text{Cref}}\\ k_{\text{u}}{u}_{2\text{ref}}\\ k_{\text{θl}}{\theta }_{\text{Lref}}\end{array}\right]+\left[\begin{array}{c}{\dot{i}}_{\text{gref}}\\ {\dot{\theta }}_{\text{Cref}}\\ {\dot{u}}_{2\text{ref}}\\ {\dot{\theta }}_{\text{Lref}}\end{array}\right].(27)$

If θ_Lref could be controlled in π/2 and i_gref and θ_Cref will not change when power signals remain the same, then, ${\dot{\theta }}_{\text{Lref}}$, ${\dot{i}}_{\text{gref}}$, and ${\dot{\theta }}_{\text{Cref}}$ are all zero. Eq. 27 can be rewritten as follows:

$\left[\begin{array}{c}{\dot{i}}_g\\ {\dot{\theta }}_C\\ {\dot{u}}_{dc}\\ {\dot{\theta }}_L\end{array}\right]=-\left[\begin{array}{cccc}{k}_{ig}& & & \\ & k_{\theta c}& & \\ & & k_u& \\ & & & k_{\theta l}\end{array}\right]\left[\begin{array}{c}{i}_g\\ {\theta }_C\\ u_2\\ {\theta }_L\end{array}\right]+\left[\begin{array}{cccc}{k}_{ig}& & & \\ & k_{\theta c}& & \\ & & k_u& \\ & & & k_{\theta l}\end{array}\right]\left[\begin{array}{c}{i}_{gref}\\ {\theta }_{Cref}\\ u_{2ref}\\ {\theta }_{Lref}\end{array}\right].(28)$

Eq. 28 can be expressed as $\dot{\mathit{X}}=\mathit{AX}+\mathit{BU}$, then

$\mathit{X}\left(\mathit{s}\right)={\left(s\mathit{I}-\mathit{A}\right)}^{-1}\mathit{BU}\left(\mathit{s}\right).(29)$

Supposing $\mathit{G}\left(\mathit{s}\right)={\left(s\mathit{I}-\mathit{A}\right)}^{-1}\mathit{B}$, (29) can be simplified as follows:

$\mathit{X}\left(\mathit{s}\right)=\mathit{G}\left(\mathit{s}\right)\mathit{U}\left(\mathit{s}\right).(30)$

G(s) is the system transfer function matrix, which can be calculated in Eq. 31. It indicates that the step responses of the grid current, power factor angle, and torque angle are all first-order, and the step response of the DC-link voltage is second-order. Meanwhile, the output of the stator current is relevant to the grid current and DC-link voltage. Then, the various control gains will be analyzed.

$\begin{array}{c}\mathit{G}\left(s\right)={\left(s\mathit{I}-\mathit{A}\right)}^{-1}\mathit{B}\\ ={\left[\begin{array}{cccc}s+k_{\text{ig}}& & & \\ & s+k_{\text{θc}}& & \\ & & s+k_{\text{u}}& \\ & & & s+k_{\text{θl}}\end{array}\right]}^{-1}\left[\begin{array}{cccc}{k}_{\text{ig}}& & & \\ & k_{\text{θc}}& & \\ & & k_{\text{u}}& \\ & & & k_{\text{θl}}\end{array}\right]\\ =\left[\begin{array}{cccc}\frac{k_{\text{ig}}}{s+k_{\text{ig}}}& & & \\ & \frac{k_{\text{θc}}}{s+k_{\text{θc}}}& & \\ & & \frac{k_{\text{u}}}{s+k_{\text{u}}}& \\ & & & \frac{k_{\text{θl}}}{s+k_{\text{θl}}}\end{array}\right].\end{array}(31)$

4.2 Selection of Control Parameters

First, the grid current, power factor angle, and torque angle are all classical first-order systems. The control gain of the grid current is determined and taken as an instance.

Based on Eqs 9, 11, the signal flow diagram of the grid current controller can be shown in Figure 6.

FIGURE 6

FIGURE 6. Signal flow diagram of the grid current controller.

According to the signal flow diagram, the transfer function of the grid current can be calculated as follows:

${\mathit{G}}_{\text{ig}}\left(s\right)=\frac{1}{\frac{s}{k_{\text{ig}}}+1}.(32)$

For a first-order inertia system, its time constant is $T_{\text{ig}}=1/k_{\text{ig}}$. If the response curve reaches 95% of the steady-state value, the adjustment process could be considered completed, and the time required to reach the response value will be 3T_ig. If the adjustment time of the active power is set to 0.06 s, we can determine $T_{\text{ig}}=\text{0}\text{.}02\text{s}$. It means that the control gain k_ig can be chosen as 50. The selection of the control parameters in reactive power control is similar to this and will not be described repeatedly.

5 Simulation and Experimental Analysis

5.1 Simulation Analysis

To verify the effectiveness of the proposed power coordinated control scheme for the SSES system, three groups of simulations are carried out on MATLAB software. The solver used in simulation is the Runge–Kutta algorithm, and the time step is 0.1 ms. The controller performance is observed through the tracking effects of active power and reactive power, and the stability of the system is investigated by the grid current amplitude, stator current amplitude, power factor angle, torque angle, and DC-link voltage. The simulation parameters are given in Table 1, and the control gains determined by the method described in Section 4 are k_ig = 50, k_θc = 50, k_u = 50, and k_θl = 50.

TABLE 1

TABLE 1. Simulation parameters.

5.1.1 Simulation for Steady Operation

The simulation for an entire cycle of energy storage lasts for 10 s. The active power signal is 4.5 kW, while the reactive power signal is 0.3 kVar.

The simulation results of the steady operation are shown in Figure 7 and indicate that the SSES system can accurately track the power signals in a short time. The grid current amplitude, power factor angle, torque angle, and DC-link voltage can all reach their stable states within the given time. Figure 7H shows that the speed of PMSM increases first with the sudden increase in the electromagnetic torque T_e. When the load torque T_L increases similarly to the electromagnetic torque T_e, the speed of PMSM will begin to decrease. If the speed reduces to zero, the energy stored in the spiral spring will be terminated.

FIGURE 7

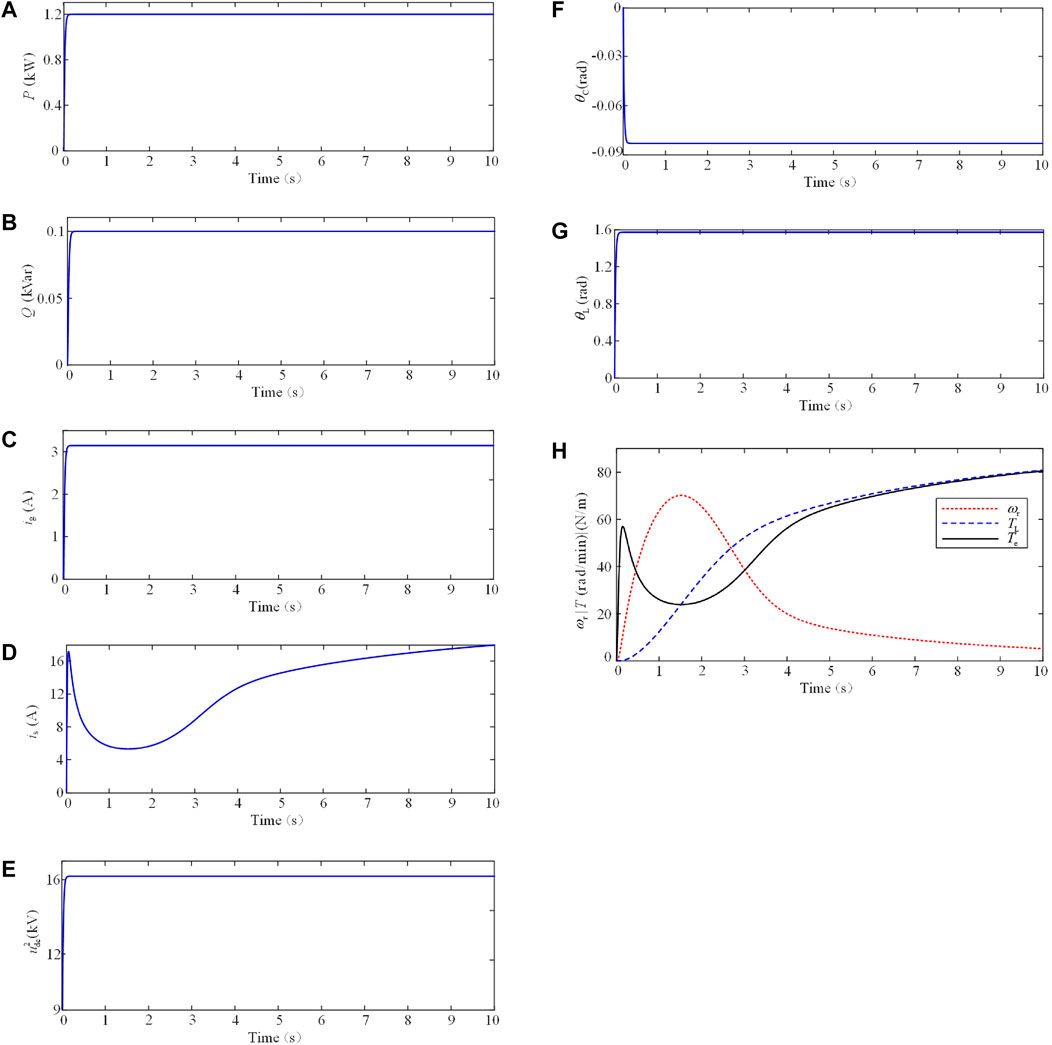
FIGURE 7. Demonstration of steady control performance. (A) Active power. (B) Reactive power. (C) Grid current. (D) Stator current. (E) Square of the DC-side voltage. (F) Power factor angle. (G) Torque angle. (H) Rotating speed and torque of PMSM.

5.1.2 Simulation for Dynamic Operation

To test the dynamic tracking performance of the controller, the proposed backstepping control is compared with the PI control, and it is assumed that the active power and reactive power signal changes start at 4.5 kW and 0.3 kVar, respectively. Then, after 3 s, the active power signal and reactive power signals change to 2 kW and 0.15 kVar, respectively. Finally, at 7 s, the active power signal becomes 5 kW, and the reactive power signal turns into 0.4 kVar. The simulation results are displayed in Figure 8. Figures 8A,B demonstrate that the active and reactive power with the proposed controller can track their power references faster than the PI control and without oscillation. Even when the power signals change, active power and reactive power regulated by the proposed controller experience almost no power oscillation. The amplitude of the grid current shown in Figure 8C also adjusts and enters the steady-state quickly. It indicates that the coordinated control has a good tracking performance. Additionally, by observing the grid current, it can be found that the current can reach stability within the given time of 0.06s, which verifies the correctness of the control parameter’s determination approach in Section 4.

FIGURE 8

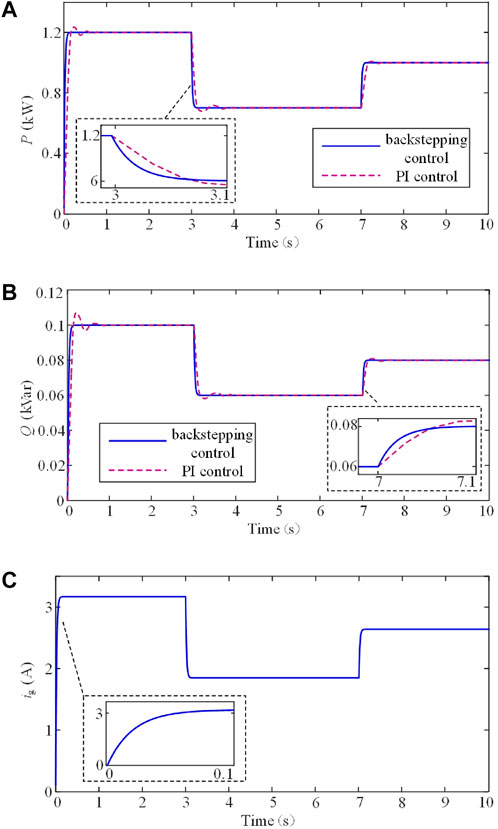
FIGURE 8. Demonstration of dynamic control performance. (A) Active power. (B) Reactive power. (C) Grid current.

5.1.3 Comparison of the Control Parameters

To further check the correctness and superiority of the control parameters determined by the control performance, three groups of simulations are conducted for each control parameter. Figure 9 demonstrates that the time for the system to enter into the steady-state reduces along with the increase in the control parameter in the first-order system.

FIGURE 9

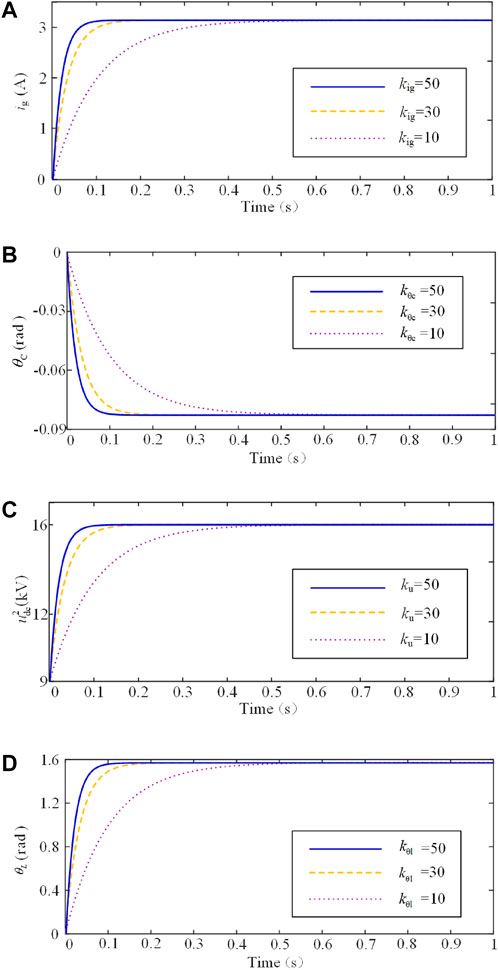
FIGURE 9. Control gain comparison in a first-order system. (A) Grid current. (B) Power factor angle. (C) Square of the DC-side voltage. (D) Torque angle.

5.2 Hardware experiment

To further verify the control algorithm proposed in the research, the experimental platform shown in Figure 10 is set up, and the hardware experiment is carried out. The system parameters are consistent with the simulation.

FIGURE 10

FIGURE 10. Hardware setup.

The control signals for active power and reactive power are 4.5 kW and 0.3 kVar, respectively. The experimental results are displayed in Figure 11. It can be seen that both active power and reactive power can reach the steady-state within the designated time of 0.06 s and are well consistent with the simulation results.

FIGURE 11

FIGURE 11. Experimental result.

In summary, both the simulation and experimental results show that the proposed power coordinated control scenario and control parameter’s determination approach for the SSES system based on BC is feasible and effective, which can ensure that the SSES system responds to the power signal of the grid accurately and quickly. Ultimately, the conversion between mechanical energy and electrical energy can be realized well.

6 Conclusion

The power coordinated control scheme and corresponding control parameter’s determination method are devised for the spiral spring energy storage system based on backstepping control under current vector orientation. Both the simulation and hardware experiments verify the correctness and effectiveness of the proposed control scheme. The conclusions are drawn as follows:

1) The proposed power control scheme can coordinate the grid-side converter with the machine-side converter of the spiral spring energy storage system to regulate the power signal accurately and rapidly.

2) The designed backstepping control under current vector orientation improves static-state and dynamic control performance and simplifies the control difficulty.

3) The determined control parameters improve the control performance effectively.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

YY: Methodology, conception, writing—review and editing, and project administration. MW: software, writing, and formal analysis. RZ: software and data analysis. ZM: conduction and supervision. XZ: validation.

Funding

This work was supported in part by the National Natural Science Foundation of China under the Grant No. 52077078 and in part by the Natural Science Foundation of Hebei Province in China under Grant E2019502163.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Achlerkar, P. D., and Panigrahi, B. K. (2020). Robust Backstepping Output Voltage Controller for Standalone Voltage‐sourced Converters. IET Renew. Power Gener. 14 (12), 2211–2220. doi:10.1049/iet-rpg.2020.0023

CrossRef Full Text | Google Scholar

Ali, Z. H., Zhao, J., Manla, E., Ma, J., and Song, W. (2017). “Novel Direct Power Control of Single-phase Three-Level SVPWM Inverter for Photovoltaic Generation,” in 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), 1–5. doi:10.1109/ISGT.2017.8085959

CrossRef Full Text | Google Scholar

Bo, F., Bowen, D., Ning, G., and Weiwei, Z. (2017). Double PWM Coordinated Control Based on Energy Mathematic Model. Chin. Autom. Congr. (CAC) 2017, 4301–4306. doi:10.1109/CAC.2017.8243536

CrossRef Full Text | Google Scholar

Caballero, D. F., Guijosa, J. M. M., and de la Cruz, V. R. (2018). Generalized Spiral Torsion Spring Energetic Model. Arch. Appl. Mech. 88 (6), 999–1008. doi:10.1007/s00419-018-1354-1

CrossRef Full Text | Google Scholar

Delavari, H., and Naderian, S. (2019). Backstepping Fractional Sliding Mode Voltage Control of an Islanded Microgrid. IET Gener. Transm. & Distrib. 13 (12), 2464–2473. doi:10.1049/iet-gtd.2018.5909

CrossRef Full Text | Google Scholar

Ghaemi, E., and Mirsalim, M. (2017). Design and Prototyping of a New Flywheel Energy Storage System. IET Electr. Power Appl. 11 (9), 1517–1526. doi:10.1049/iet-epa.2017.0074

CrossRef Full Text | Google Scholar

Gonzalez‐Gonzalez, J. M., Martin, S., Lopez, P., and Aguado, J. A. (2020). Hybrid Battery‐ultracapacitor Storage System Sizing for Renewable Energy Network Integration. IET Renew. Power Gener. 14 (13), 2367–2375. doi:10.1049/iet-rpg.2019.1310

CrossRef Full Text | Google Scholar

Gui, Y., Kim, C., Chung, C. C., Guerrero, J. M., Guan, Y., and Vasquez, J. C. (2018). Improved Direct Power Control for Grid-Connected Voltage Source Converters. IEEE Trans. Ind. Electron. 65 (10), 8041–8051. doi:10.1109/TIE.2018.2801835

CrossRef Full Text | Google Scholar

Gui, Y., Wang, X., and Blaabjerg, F. (2019). Vector Current Control Derived from Direct Power Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 34 (9), 9224–9235. doi:10.1109/TPEL.2018.2883507

CrossRef Full Text | Google Scholar

Jeon, B.-J., Seo, M.-G., Shin, H.-S., and Tsourdos, A. (2020). Understandings of Classical and Incremental Backstepping Controllers with Model Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 56 (4), 2628–2641. doi:10.1109/TAES.2019.2952631

CrossRef Full Text | Google Scholar

Kim, S. K. (2018). Robust Output Voltage Tracking Algorithm for Three‐phase Rectifier with Variable Sliding Surface. IET Power Electron. 11 (6), 1119–1127. doi:10.1049/iet-pel.2017.0866

CrossRef Full Text | Google Scholar

Kumar, S., Saket, R. K., Dheer, D. K., Holm‐Nielsen, J. B., and Sanjeevikumar, P. (2020). Reliability Enhancement of Electrical Power System Including Impacts of Renewable Energy Sources: a Comprehensive Review. IET Gener. Transm. & Distrib. 14 (10), 1799–1815. doi:10.1049/iet-gtd.2019.1402

CrossRef Full Text | Google Scholar

Kwak, B., Um, J.-H., and Seok, J.-K. (2019). Direct Active and Reactive Power Control of Three-phase Inverter for AC Motor Drives with Small Dc-Link Capacitors Fed by Single-phase Diode Rectifier. IEEE Trans. Ind. Appl. 55 (4), 3842–3850. doi:10.1109/TIA.2019.2915061

CrossRef Full Text | Google Scholar

Li, J., Guo, Y.-N., Zhang, L.-H., and Shi, W.-T. (2018). “Coordinated Passivity Control of Permanent Magnet Synchronous Generator Based on Dual PWM Converter,” in 2018 IEEE International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), 94–99. doi:10.1109/IESES.2018.8349856

CrossRef Full Text | Google Scholar

Li, L., Xiao, J., Zhao, Y., Liu, K., Peng, X., Luan, H., et al. (2020). Robust Position Anti-interference Control for PMSM Servo System with Uncertain Disturbance. Trans. Electr. Mach. Syst. 4 (2), 151–160. doi:10.30941/CESTEMS.2020.00020

CrossRef Full Text | Google Scholar

Liu, Y., Cheng, S., Ning, B., and Li, Y. (2019). Performance Enhancement Using Durational Model Predictive Control Combined with Backstepping Control and Disturbance Observer for Electrical Drives. J. Vib. Control 25 (4), 946–959. doi:10.1177/1077546318807018

CrossRef Full Text | Google Scholar

Lu, P., van Kampen, E.-J., and Chu, Q. P. (2015). “Robustness and Tuning of Incremental Backstepping Approach,” in AIAA Guidance, Navigation, and Control Conference, Kissimmee, USA (Kissimmee, FL: AIAA), 2780–2794. doi:10.2514/6.2015-1762

CrossRef Full Text | Google Scholar

Mallik, A., Ding, W., Shi, C., and Khaligh, A. (2017). Input Voltage Sensorless Duty Compensation Control for a Three-phase Boost PFC Converter. IEEE Trans. Ind. Appl. 53 (2), 1527–1537. doi:10.1109/TIA.2016.2626247

CrossRef Full Text | Google Scholar

Tian, Y., Chen, Z., Deng, F., Sun, X., and Hu, Y. (2014). “Coodinative Control of Active Power and DC-link Voltage for Cascaded Dual-Active-Bridge and Inverter in Bidirectional Applications,” in 2014 IEEE Energy Conversion Congress and Exposition (ECCE), 2249–2256. doi:10.1109/ECCE.2014.6953703

CrossRef Full Text | Google Scholar

Wai, R.-J., Yang, Y., and Wang, Y.-Q. (2018). “Design of Backstepping Control for Direct Power Control of Three-phase PWM Rectifier,” in 2018 3rd International Conference on Intelligent Green Building and Smart Grid (IGBSG), 1–4. doi:10.1109/IGBSG.2018.8393555

CrossRef Full Text | Google Scholar

Xiong, P., and Sun, D. (2016). Backstepping-based DPC Strategy of a Wind Turbine-Driven DFIG under Normal and Harmonic Grid Voltage. IEEE Trans. Power Electron. 31 (6), 4216–4225. doi:10.1109/TPEL.2015.2477442

CrossRef Full Text | Google Scholar

Yang, T., Cai, Z., and Xun, Q. (2020). Adaptive Backstepping-Based H${_{\infty}}$ Robust Controller for Photovoltaic Grid- Connected Inverter. IEEE Access 8, 17263–17272. doi:10.1109/ACCESS.2019.2962280

CrossRef Full Text | Google Scholar

Ye, S., Zhou, D., Yao, X., and Blaabjerg, F. (2021). Component-level Reliability Assessment of a Direct-Drive PMSG Wind Power Converter Considering Two Terms of Thermal Cycles and the Parameter Sensitivity Analysis. IEEE Trans. Power Electron. 36 (9), 10037–10050. doi:10.1109/TPEL.2021.3064363

CrossRef Full Text | Google Scholar

Yu, Y., Chang, D., Zheng, X., Mi, Z., Li, X., and Sun, C. (2018). A Stator Current Oriented Closed-Loop $I\text{--} F$ Control of Sensorless SPMSM with Fully Unknown Parameters for Reverse Rotation Prevention. IEEE Trans. Power Electron. 33 (10), 8607–8622. doi:10.1109/TPEL.2017.2780191

CrossRef Full Text | Google Scholar

Yu, Y., Cong, L., Tian, X., Mi, Z., Li, Y., Fan, Z., et al. (2020). A Stator Current Vector Orientation Based Multi-Objective Integrative Suppressions of Flexible Load Vibration and Torque Ripple for PMSM Considering Electrical Loss. Trans. Electr. Mach. Syst. 4 (3), 161–171. doi:10.30941/CESTEMS.2020.00021

CrossRef Full Text | Google Scholar

Yu, Y., Mi, Z., Guo, X., Xu, Y., and Zhao, T. (2016). Low Speed Control and Implementation of Permanent Magnet Synchronous Motor for Mechanical Elastic Energy Storage Device with Simultaneous Variations of Inertia and Torque. IET Electr. Power Appl. 10 (3), 172–180. doi:10.1049/iet-epa.2015.0159

CrossRef Full Text | Google Scholar

Yu, Y., Mi, Z., Mi, Z., Guo, X., Zheng, X. X., and Sun, C. (2018). Control Design and Implementation of a Spiral Spring Energy Storage System Connected to a Grid via PMSG. Csee Jpes 4 (3), 339–351. doi:10.17775/CSEEJPES.2016.00860

CrossRef Full Text | Google Scholar

Zhang, S. Q., and Zhu, Y. Q. (2018). Pumped‐storage Power Generation System Based on Wave Energy. J. Eng. 2017 (13), 2334–2338. doi:10.1049/joe.2017.0748

CrossRef Full Text | Google Scholar

Zhang, Y., Peng, Y., and Qu, C. (2015). “Comparative Study of Model Predictive Control and Direct Power Control for PWM Rectifiers with Active Power Ripple Minimization,” in 2015 IEEE Energy Conversion Congress and Exposition (ECCE), 3823–3830. doi:10.1109/ECCE.2015.7310200

CrossRef Full Text | Google Scholar

Zhang, Y., and Qu, C. (2015). Table-Based Direct Power Control for Three-phase AC/DC Converters under Unbalanced Grid Voltages. IEEE Trans. Power Electron. 30 (12), 7090–7099. doi:10.1109/TPEL.2014.2387694

CrossRef Full Text | Google Scholar