- Key Laboratory of Exploration Technologies for Oil and Gas Resources (Yangtze University), Ministry of Education, Wuhan, China
Introduction
Hydraulic fracturing monitoring is an essential technical means for unconventional oil and gas (e.g., tight oil, tight gas, shale oil, shale gas, hot dry rock) development. Hydraulic fracturing monitoring can be applied to evaluate the degree of development and scale of fractures in target reservoirs and to diagnose the extent of fracturing fluid. It can then be used to estimate the stimulated reservoir volume (SRV). Therefore, it is critical to forecast reservoir yields and unconventional oil and gas resource utilisation. Conventional hydraulic fracturing monitoring is predominantly based on microseismic monitoring, which can effectively delineate the range and main direction of the fracturing fractures. However, microseismic fractures have limitations (Warpinski, 2014). It is difficult to guarantee that the volume of fracturing in the seismically active fractures is equal to that in the fracturing reservoirs. Recently, as an emerging technology in the field of fracturing monitoring, the electromagnetic (EM) exploration method is based on the substantial conductivity difference between the fracturing fluid and the surrounding rock, which uses the change in the EM signals collected during multiple stages of fracturing. It can then be used to evaluate the degree of fracturing development quantitatively. In addition, EM exploration has the significant advantages of low cost and high efficiency, and has become highly valued by many scholars. Magnetotelluric and frequency-domain control-source EM (CSEM) methods have been applied for fracturing monitoring. Considerable research has been conducted using these methods for hydraulic fracturing monitoring (He et al., 2015; Tietze et al., 2015; Ahmadian et al., 2018; Li et al., 2019). Hickey et al. (2015) conducted 3D CSEM forward modelling for the injection of hydraulic fracturing, studied the EM response characterization and demonstrated the ability of a CSEM system to detect changes in the subsurface due to hydraulic fluid injection. Jones et al. (2019) presented an CSEM method application for the three-well monitoring hydraulic fracture in Permian Basin, they captured the EM response changes within the fractured reservoir. However, unconventional oil and gas resources are primarily distributed in areas with complex topographies and geological conditions. In these areas, the target reservoirs for fracturing stimulation are buried at great depth and small in dimensions. However, the resolution of the frequency-domain EM method also has limitations. In 2017, the Advanced Energy Consortium (AEC), together with other organisations, implemented a test for hydraulic fracturing monitoring using the transient electromagnetic (TEM) method with a long wire source, in which the casing wells in fracturing construction sites were used as a long wire source, and anomalous signals from induced fractures at a depth of 2 km were detected (Hibbs and Wilt, 2016; Li and Yang, 2019). The high-power TEM method with a long wire source has the distinct advantages of high signal-to-noise ratio, considerable depth of exploration, and low cost, and it has gradually become the focus of research for deep mineral and unconventional oil and gas exploration (Di et al., 2019). Yan et al. (2018) successfully applied the long-wire source TEM method to the dynamic monitoring of hydraulic fracturing in shale gas development in southern China. They captured electromagnetic signals from a depth of 3 km caused by the fracturing of a target reservoir. Notably, the target reservoirs for hydraulic fracturing are primarily composed of fracturing media and have the characteristics of a large burial depth, small dimensions, and apparent anisotropy. Conventional one- or two-dimensional TEM data inversion is insufficient to satisfy the interpretation of complex hydraulic fracturing regions. Using three-dimensional (3D) inversion to reconstruct the complex properties of fracturing formations is necessary. In contrast, forward modelling is the core of 3D inversion. Therefore, the data interpretation of hydraulic fracturing monitoring presents a new challenge for TEM 3D forward modelling. In the following section, we briefly introduce the developments in TEM 3D forward modelling and its application status in hydraulic fracturing monitoring. In addition, we propose some suggestions on TEM forward modelling for applications for hydraulic fracturing monitoring.
A Short Review of 3D Forward TEM Modelling Developments and Its Applications for Hydraulic Fracturing Monitoring
The accuracy and efficiency of 3D forward modelling directly restrict 3D inversion. 3D forward modelling can be divided into direct and indirect methods. The indirect method is based on the time-frequency transformation technique (Newman et al., 1986), which transforms the frequency-domain response to the time domain. The integral equation (Cox et al., 2010), finite difference (Liu and Yin, 2014; Hoversten et al., 2015; Sun et al., 2021), finite-element (Li et al., 2016; Cai et al., 2017; Li et al., 2018; Qi et al., 2019), finite-volume (Jahandari and Farquharson, 2014; Ren et al., 2017; Liu et al., 2018; Zhou et al., 2018), and other numerical methods are applied to calculate the frequency-domain EM response. Widely used frequency-time transformation techniques include the sine (cosine) transform method, the GS inverse Laplace transform method, and the Hankel numerical filtering method (Knight and Raiche, 1982; Guptasarma, 1982; Chen Xiangbin et al., 2008; Sasaki and Cho, 2011; Yin et al., 2013; Li et al., 2016; Li et al., 2018). However, when using the frequency-time transformation method to calculate the TEM response, it is necessary to cover as wide a frequency range as possible. Furthermore, this leads to a large number of calculations and directly affects the calculation efficiency. In addition, precision differences in the calculations exist among these transformation methods, especially with complex geoelectric models, and the transformation methods will become unstable. A full-time TEM response with an arbitrary waveform has an inherent singularity at t = 0. To avoid this singularity, Yin et al. (2013) proposed a convolution operation using the step current and the derivative of the current. However, this requires a high sampling rate of time, further leading to a loss of calculation accuracy.
In terms of direct methods, some breakthroughs have been achieved with the development of the explicit time-domain finite-difference (FDTD) (Sun et al., 2013; Lu et al., 2021), implicit time-domain finite-element (FETD) (Yin et al., 2016; Li et al., 2020b), and other numerical methods. Wang and Hohmann (1993) used a combination of Yee’s staggered grid and a relatively stable and improved Du Fort-Frankel difference method to discretise the Maxwell equation in the time domain directly and alternately determined the electric and magnetic fields. Commer and Newman (2004) applied parallel computing to a TEM response solution based on Wang and Hohmann (1993). Owing to the strong versatility of the FDTD method, it does not need to solve large linear equations, and is easy to implement in parallel. Many scholars have applied this method to study 3D electromagnetic forward modelling (Sun et al., 2013; Commer et al., 2015; Lu et al., 2016). However, Wang and Hohmann (1993) and Commer and Newman (2004) demonstrated that the explicit method requires a strict selection of the time step to obtain a stable and accurate solution. Thus, the forward modelling efficiency is limited. In addition, because FDTD is based on a regular hexahedral mesh for discretisation, this type of mesh restricts the simulation of the TEM response with complex geoelectric models. Compared with the explicit method, the implicit method has a stable solution and is less limited by the time step, but it needs to solve a large linear equation system to obtain the TEM response of each time channel, so it requires high computer memory.
With improvements in computer performance and the development of solving techniques, the application of implicit methods has gradually increased (Movahhedi et al., 2007; Um et al., 2011;Lu et al., 2018; Zhou et al., 2018). Research on implicit methods is represented by the EM inversion team headed by Oldenburg and Haber. Oldenburg et al. (2013) combined a parallel direct solver with an implicit finite-difference space discretisation method to solve a multi-source TEM response. (Haber et al., 2007) developed codes for modelling the TEM response by combining the backward Euler scheme with the finite-volume method. Haber et al. (2007) applied the parallel method to improve the computational efficiency and realised 3D TEM forward modelling and inversion. Yin et al. (2016), Li et al. (2020) referred to Haber et al. (2007) developed the TEM forward modelling based on the unstructured finite-element method and backward Euler scheme, which is flexible to modelling complex earth model TEM response. Recently, another direct algorithm, the direct solution method based on the time-domain Krylov subspace (Druskin et al., 1999), which is different from explicit and implicit methods, has been applied to 3D TEM forward modelling. This method starts with the governing equations in the time domain and independently solves the electromagnetic response at any time in the Krylov subspace. Liu et al. (2018) implemented the Krylov subspace finite-volume method to solve the semi-airborne TEM response and verified its effectiveness.
The integral equation and finite-difference methods are generally based on a regular hexahedral mesh, which is difficult to adapt to complex models. The finite-element method and finite-volume method can fit complex models through deformed hexahedral or tetrahedral meshes, but it is usually assumed that the EM field in each element changes linearly or constantly, so it is necessary to perform fine meshing to improve the accuracy. The detailed mesh subdivision directly affects the forward and inversion efficiencies.
To date, research on simulating dynamic changes in hydraulic fracturing monitoring based on conventional 3D TEM forward modelling is particularly limited. Generally, conventional modelling techniques (detailed mesh subdivision) and forward modelling methods (e.g., finite-element method, finite-volume method) have been used. Hoversten et al. (2015) implemented FDTD to conduct a 3D TEM forward modelling test for fracturing monitoring. For the isotropic thin layer model, a grid with a minimum size of 12.22 mm was used for discretisation in the fracture area, and the number of calculations was substantial. Curcio (2021) studied the TEM signals of a 2D anisotropic earth model based on the finite-element method applied to fracturing electromagnetic monitoring. Hoversten and Schwarzbach (2020) applied a 3D OcTree finite-volume code for modelling borehole-to-surface TEM responses with especially fine meshing around the wells and fractures. Liu et al. (2020) conducted 3D forward modelling for a controlled source electromagnetic method based on a mixed numerical method combining the integral equation method and finite-element method, assuming that the conductivity change caused by fracturing was uniform and did not match the actual situation.
Challenges of 3D Forward Modelling for Hydraulic Fracturing Monitoring Application
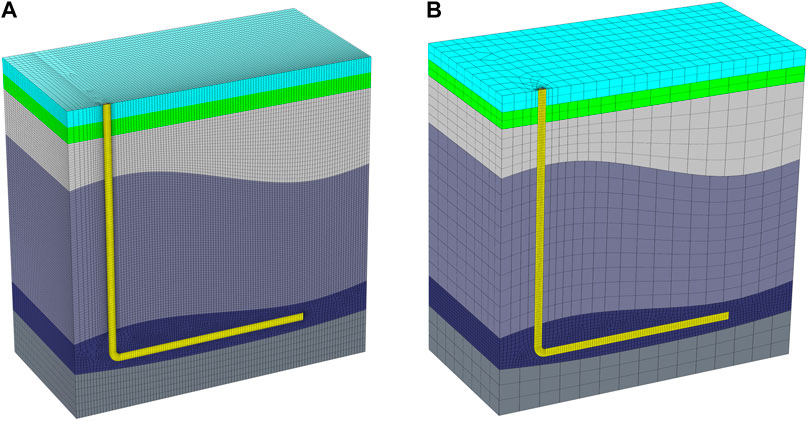
The physical properties of the hydraulic fracturing region, including the fracturing media, considerable burial depth, small dimensions, and apparent anisotropy, cannot be ignored. The burial depth of the hydraulic fracturing target layer is generally greater than 2 km, and the width of each fracturing layer is several metres. The thickness of the SRV is within several centimetres. Additionally, there are high-conductivity casings with a diameter of only several centimetres in the fracturing formation. The multiscale and complex characteristics of the fractured formations cannot be ignored. Therefore, a detailed mesh subdivision containing a large depth scale and small fracture scale should be clearly described, or a 3D multi-scale TEM forward modelling applicable to fracturing monitoring should be adopted. Figure 1 show the mesh subdivision for the traditional earth modelling and multi-scale modelling, we can clearly see that the multi-scale mesh subdivision just uses small dimensional mesh for the small fracture scale, and applies large dimensional mesh for other modelling area.
For the calculation of multiscale physical problems, the solution of the coefficient matrix often consumes huge computing resources via a conventional algorithm (e.g., finite-difference, finite-element), and it is difficult to achieve optimal results, even with traditional iterative solutions. In recent years, the discontinuous Galerkin method has been studied (Angulo et al., 2015; Marras et al., 2016; Xu et al., 2018; Zhan et al., 2018) to solve the problem of multiscale physical model simulations, with increasing applications in fluid mechanics, elastic mechanics, computational electromagnetics, and other fields. In contrast to the traditional Galerkin method, this method adopts a similar approach to the finite-volume method to define continuous numerical fluxes of tangential field components at each interface and allows the solution space of discrete elements to be completely discontinuous at the boundary surfaces between adjacent elements. Furthermore, it can increase the flexibility of the conventional finite-element method. Therefore, the discontinuous Galerkin method effectively partitions and decomposes the overall computational domain and allows the solution of multiscale physical problems with large-scale degrees of freedom. Thus, the discontinuous Galerkin method provides a new technique for the multiscale TEM forward modelling problem for applications in fracturing monitoring.
It is generally assumed that the fracturing formation is isotropic in the analysis of TEM signals for fracturing monitoring. However, anisotropy is widespread (Liu et al., 2018). Different levels of stress on fractures in each direction cause differences in the extension of microscopic fractures. When the scale of the fracturing layer is sufficiently large, the cumulative effect of multiple fracturing causes prominent anisotropic characteristics in the macroscopic formation. This has been confirmed in microseismic monitoring and experimental studies of petrophysical electrical properties (Thiel and Stephan, 2017). It is vital to study the TEM anisotropic response characteristics and effectively identify these characteristics during the fracturing monitoring process. Therefore, electrical anisotropy is also a key factor in TEM forward modelling of hydraulic fracturing monitoring applications.
Additionally, the fracture system is an essential channel for oil and gas storage and transportation. Hydraulic fracturing opens and reforms oil and gas migration channels by constructing artificial fractures. It can then achieve efficient development of unconventional oil and gas. Li et al. (2020a) studied the electrical properties of fractured sandstone with a slightly increased equivalent dielectric conductivity model, indicating that small-scale fractures have a significant impact on the dielectric properties of sandstone. Shen et al. (2009) demonstrated that electrical anisotropy increases with increasing fracture density; in particular, when the formation pressure changes, the anisotropy characteristics of the fracturing formation change significantly. Yan et al. (2020) established an equivalent dielectric conductivity model for sloping anisotropic fracturing rocks, building a theoretical bridge between microfracturing anisotropic media and fracturing anisotropic formations. The scale of microscopic fractures in the fracturing layer is at the millimetre level, and the comprehensive action of different types of fluids and their concentration parameters in the fracturing rock determine the electrical characteristics of the hydraulic fracturing formation (Ahmadian et al., 2018). The influence of rock composition and microstructures on the electromagnetic response is typically ignored in conventional EM forward modelling (Hu et al., 2019). However, considering these physical properties is essential for evaluating the degree of fracture development and determining the fracturing fluid direction. Therefore, forward modelling using a macroscopic equivalent medium model that considers the physical properties of the microscopic fracturing medium is the premise and guarantee for obtaining a highly accurate TEM response of the fracturing zone.
Notably, the signals measured by the TEM-based fracturing monitoring contain feedback information of the entire subsurface medium (high-conductivity casing, non-fracturing formations, and fracturing formations), and the effect of the high-conductivity casing on the measurement signal cannot be ignored. In the process of multiple fracturing, the electrical characteristics of the fracturing stratum are often time shifted. In contrast, the physical properties of the casing and non-fracturing strata remained unchanged. Therefore, considering the non-fracturing formation and high-conductivity casing as the background conductivity and using the EM signal difference value between two adjacent multi-stage fracturing processes, the EM signal variations of the fracturing formation are extracted. Hu et al. (2022) proposed an efficient numerical approach to manage the discretion of well casings by assigning lumped conductive properties to the mesh edges.
Conclusion
Based on the equivalent conductivity of fracturing rocks combined with a numerical algorithm that considers accuracy and efficiency, a multi-scale forward modelling technology for TEM anisotropy suitable for fracturing monitoring areas should be developed. Differences in EM signals, excluding the contribution of high-conductivity well casings and non-fracturing formations to the measurement signals, effectively extract information on the stimulation of oil and gas reservoirs due to dynamic fracturing in fracturing formations and establish TEM parameters of hydraulic fracturing target layers. The identification method of the anisotropic response is a critical and urgent problem that needs to be solved in TEM 3D forward modelling. Solving these technical difficulties will undoubtedly promote hydraulic fracturing monitoring technology for unconventional oil and gas exploration.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
We declare all sources of funding received for the research being submitted. This study was supported by the Natural Science Foundation of China (NSFC) (Grant Nos 42104070, 42030805, 42004053) and Open Fund of Key Laboratory of Exploration Technologies for Oil and Gas Resources (Yangtze University), Ministry of Education (K2021-03 and K2021-07).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmadian, M., LaBrecque, D., Liu, Q. H., Slack, W., Brighan, R., Yuan, F., et al. (2018). “Demonstration of Proof of Concept of Electromagnetic Geophysical Methods for High Resolution Illumination of Induced Fracture Networks,” in SPE Hydraulic Fracturing Technology Conference and Exhibition, The WoodlandsTexasUSA:Society of Petroleum Engineersdoi:10.2118/189858-MS
Angulo, L. D., Alvarez, J., Bretones, A. R., Garcia, S. G., and Pantoja, M. F. (2015). Discontinuous Galerkin Time Domain Methods in Computational Electrodynamics: State of the Art, Forum Electromagnetic. Res. Methods Appl. Technol. 10, 1
Cai, H., Hu, X., Xiong, B., and Zhdanov, M. S. (2017). Finite-element Time-Domain Modeling of Electromagnetic Data in General Dispersive Medium Using Adaptive Padé Series. Comput. Geosciences 109, 194–205. doi:10.1016/j.cageo.2017.08.017
Commer, M., Hoversten, G. M., and Um, E. S. (2015). Transient-electromagnetic Finite-Difference Time-Domain Earth Modeling over Steel Infrastructure. Geophysics 80 (2), E147–E162. doi:10.1190/geo2014-0324.1
Commer, M., and Newman, G. (2004). A Parallel Finite‐difference Approach for 3D Transient Electromagnetic Modeling with Galvanic Sources. Geophysics 69 (5), 1192–1202. doi:10.1190/1.1801936
Cox, L. H., Wilson, G. A., and Zhdanov, M. S. (2010). 3D Inversion of Airborne Electromagnetic Data Using a Moving Footprint. Explor. Geophys. 41, 250–259. doi:10.1071/eg0636310.1071/eg10003
Curcio, A. (2021). Symmetries and Configurations of Hydraulic Fracturing Electromagnetic Monitoring: A 2D Anisotropic Approach. Geomechanics Geophys. Geo-Energy Geo-Resources 7 (1), 213. doi:10.1007/s40948-020-00213-6
Di, Q., Zhu, R., and Xue, G. (2019). New Development of the Electromagnetic (EM)methods for Deep Exploration. Chin. J. Geophys. (in Chinese) 62 (6), 2128–2138. doi:10.6038/cjg2019M0633
Druskin, V. L., Knizhnerman, L. A., and Lee, P. (1999). New Spectral Lanczos Decomposition Method for Induction Modeling in Arbitrary 3-D Geometry. Geophysics 64 (3), 701–706. doi:10.1190/1.1444579
Guptasarma, D. (1982). Computation of the Time‐domain Response of a Polarizable Ground. Geophysics 47 (11), 1574–1576. doi:10.1190/1.1441307
Haber, E., Oldenburg, D. W., and Shekhtman, R. (2007). Inversion of Time Domain Three-Dimensional Electromagnetic Data. Geophysi. J. Int. 171 (2), 550–564. doi:10.1111/j.1365-246X.2007.03365.x
He, Z., Hu, Z., Gao, Y., He, L., Meng, C., and Yang, L. (2015). Field Test of Monitoring Gas Reservoir Development Using Time-Lapse Continuous Electromagnetic Profile Method. Geophysics 80 (2), WA127–WA134. doi:10.1190/geo2014-0195.1
Hibbs, A., and Wilt, M. (2016). Evaluation of Deep Subsurface Resistivity Imaging for Hydrofracture Monitoring. San Diego, CA (United States): GroundMetrics, Inc. doi:10.2172/1333115
Hickey, M. S., Treviño, S., and Everett, M. E. (2015). Detection and Characterization of the Injection of Hydraulic Fracturing Fluid Using Ground-Based Controlled-Source Electromagnetics. SEG Tech. Program Expanded Abstracts. doi:10.1190/segam2015-5916792.1
Hoversten, G. M., Commer, M., Haber, E., and Schwarzbach, C. (2015). Hydro-frac Monitoring Using Ground Time-Domain Electromagnetics. Geophysical Prospecting 63 (6), 1508–1526. doi:10.1111/1365-2478.12300
Hoversten, G. M., and Schwarzbach, C. (2021). Monitoring Hydraulic Fracture Volume Using Borehole to Surface Electromagnetic and Conductive Proppant. Geophysics 86 (1), E93–E109. doi:10.1190/GEO2020-0410.1
Hu, X., Li, J., and Peng, R. (2019). Forward Modeling Approaches for Geophysical Time-Domain Electromagnetic Methods(in Chinese). Beijing: Science Press.
Hu, Y., Yang, D. K., Li, Y. C., Wang, Z., and Lu, Y. (2022). 3-D Numerical Study on Controlled Source Electromagnetic Monitoring of Hydraulic Fracturing Fluid with the Effect of Steel-Cased Wells. IEEE Trans. on Geosci. Remote. Sensin. 60, 4504210. doi:10.1109/tgrs.2021.3100774
Jahandari, H., and Farquharson, C. G. (2014). A Finite-Volume Solution to the Geophysical Electromagnetic Forward Problem Using Unstructured Grids. Geophysics 79 (6), E287–E302. doi:10.1190/geo2013-0312.1
Jones, D., Pieprzica, C., Vasquez, O., Oberle, J., Morton, P., Treviño III, S., et al. (2019). Monitoring Hydraulic Fracture Flowback in the Permian Basin Using Surface-Based, Controlled-Source Electromagnetics. Unconvention. Res. Tech. Conf. doi:10.15530/urtec-2019-230
Li, B., Han, T., and Fu, Li. (2020a). Dielectric Properties of Fractured Reservoir Sandstones Based on Digital Rock Physics Technique. Chin. J. Geophys. 63 (12), 4578–4591. doi:10.6038/cjg2020O0026
Li, J., Farquharson, C. G., and Hu, X. (2016). Three Effective Inverse Laplace Transform Algorithms for Computing Time-Domain Electromagnetic Responses. Geophysics 81 (2), E113–E128. doi:10.1190/geo2015-0174.1
Li, J., Hu, X., Cai, H., and Liu, Y. (2020b). A Finite‐element Time‐domain Forward‐modelling Algorithm for Transient Electromagnetics Excited by Grounded‐wire Sources. Geophysical Prospecting 68 (4), 1379–1398. doi:10.1111/1365-2478.12917
Li, J., Lu, X., Farquharson, C. G., and Hu, X. (2018). A Finite-Element Time-Domain Forward Solver for Electromagnetic Methods with Complex-Shaped Loop Sources. Geophysics 83 (3), E117–E132. doi:10.1190/geo2017-0216.1
Li, Y., Liu, D., and Zhai, Y. (2019). 3-D FEM Azimuth Forward Modeling of Hydraulic Fractures Based on Electromagnetic Theory. Ieee Geosci. Remote Sensing Let. 18 (2), 246–250. doi:10.1109/LGRS.2020.2970441
Li, Y., and Yang, D. (2019). Fast Electrical Imaging of Injected Fluid in Hydraulic Fracturing Using a Practical Interactive Parameter Estimation Method SEG Technical Program Expanded Abstracts 2019, San Antonio, Texas, USA:Society of Exploration Geophysicistsdoi:10.1190/segam2019-3215758.1
Liu, R., Liu, J., Wang, J., Liu, Z., and Guo, R. (2020). A Time-Lapse CSEM Monitoring Study for Hydraulic Fracturing in Shale Gas Reservoir. Marine and Petroleum Geology 120, 104545. doi:10.1016/j.marpetgeo.2020.104545
Liu, W., Zhou, J., Li, X., and Farquharson, C. G. (2018). 3D Modeling of Grounded Electric-Source Airborne Time-Domain Electromagnetic Data Using Rational Krylov Subspace Method. SEG Technical Program Expanded Abstracts, 919–923. doi:10.1190/segam2018-2997941.1
Liu, Y., and Yin, C. (2014). 3D Anisotropic Modeling for Airborne EM Systems Using Finite-Difference Method. J. Appl. Geophys. 109, 186–194. doi:10.1016/j.jappgeo.2014.07.003
Liu, Y., Yin, C., and Cai, J. (2018). Review on Research of Electrical Anisotropy in Electromagnetic Prospecting. Chin. J. Geophys.(in Chinese) 61 (8), 3468–3487. doi:10.6038/cjg2018L0004
Lu, X., Farquharson, C., Miehé, J.-M., and Harrison, G. (2021). 3D Electromagnetic Modeling of Graphitic Faults in the Athabasca Basin Using a Finite-Volume Time-Domain Approach with Unstructured Grids. Geophysics 86 (6), B349–B367. doi:10.1190/geo2020-0657.1
Marras, S., Kelly, J. F., Moragues, M., Müller, A., Kopera, M. A., Vázquez, M., et al. (2016). A Review of Element-Based Galerkin Methods for Numerical Weather Prediction: Finite Elements, Spectral Elements, and Discontinuous Galerkin. Arch Computat Methods Eng 23 (4), 673–722. doi:10.1007/s11831-015-9152-1
Movahhedi, M., Abdipour, A., Nentchev, A., Dehghan, M., and Selberherr, S. (2007). Alternating-direction Implicit Formulation of the Finite-Element Time-Domain Method. IEEE Trans. Microwave Theory Techn. 55 (6), 1322–1331. doi:10.1109/TMTT.2007.897777
Newman, G. A., Hohmann, G. W., and Anderson, W. L. (1986). Transient Electromagnetic Response of a Three‐dimensional Body in a Layered Earth. Geophysics 51 (8), 1608–1627. doi:10.1190/1.1442212
Oldenburg, D. W., Haber, E., and Shekhtman, R. (2013). Three Dimensional Inversion of Multisource Time Domain Electromagnetic Data. Geophysics 78 (1), E47–E57. doi:10.1190/geo2012-0131.1
Qi, Y., Li, X., Yin, C., Qi, Z., Zhou, J., Liu, Y., et al. (2019). Weighted Goal-Oriented Adaptive Finite-Element for 3D Transient EM Modeling. Jeeg 24 (2), 249–264. doi:10.2113/JEEG24.2.249
Ren, X., Yin, C., Liu, Y., Cai, J., Wang, C., and Ben, F. (2017). Efficient Modeling of Time-Domain AEM Using Finite-Volume Method. J Environ Eng Geophys 22 (3), 267–278. doi:10.2113/JEEG22.3.267
Shen, J., Su, B., and Guo, N. (2009). Study on the Anisotropic Characteristics of the Electric Response to Fractured Reservoir. Chin. J. Geophys.(in Chinese) 52 (11), 2903–2912. doi:10.3969/j.issn.0001-5733.2009.11.026
Sun, H., Li, X., Li, S., Peng, Q. Z., Peng, W. Y., Xin, S. M., et al. (2013). Three-dimensional FDTD Modeling of TEM Excited by a Loop Source Considering Ramp Time. Chin. J. Geophys.(in Chinese) 56 (3), 1049–1064. doi:10.6038/cjg20130333
Sun, H., Liu, S., and Yang, Y. (2021). Crank-Nicolson FDTD 3D Forward Modeling for the Transient Electromagnetic Field. Chinese Journal of Geophysics (in Chinese) 64 (1), 343–354. doi:10.6038/cjg2021O0229
Thiel, S., and Stephan, T. (2017). Electromagnetic Monitoring of Hydraulic Fracturing: Relationship to Permeability, Seismicity, and Stress. Surv Geophys 38 (1), 1133–1169. doi:10.1007/s10712-017-9426-2
Tietze, K., Ritter, O., and Veeken, P. (2015). Controlled-source Electromagnetic Monitoring of Reservoir Oil Saturation Using a Novel Borehole-To-Surface Configuration. Geophysical Prospecting 63 (6), 1468–1490. doi:10.1111/1365-2478.12322
Um, E. S., Harris, J. M., and Alumbaugh, D. L. (2010). 3D Time-Domain Simulation of Electromagnetic Diffusion Phenomena: A Finite-Element Electric-Field Approach. Geophysics 75 (4), F115–F126. doi:10.1190/1.3473694
Wang, T., and Hohmann, G. W. (1993). A Finite‐difference, Time‐domain Solution for Three‐dimensional Electromagnetic Modeling. Geophysics 58 (6), 797–809. doi:10.1190/1.1443465
Warpinski, N. R. (2014). A Review of Hydraulic-Fracture Induced Microseismicity, 48th US Rock Mechanics/Geomechanics Symposium. AMERICA: American Rock Mechanics Association.
Xu, H., Cantwell, C. D., Monteserin, C., Eskilsson, C., Engsig-Karup, A. P., and Sherwin, S. J. (2018). Spectral/hp Element Methods: Recent Developments, Applications, and Perspectives. J Hydrodyn 30 (1), 1–22. doi:10.1007/s42241-018-0001-1
Yan, H., Han, T., and Fu, L. Y. (2020). Theoretical Models for the Effective Electrical Conductivity of Transversely Isotropic Rocks with Inclined Penny‐Shaped Cracks. J. Geophys. Res. Solid Earth 125 (10), 1–28. doi:10.1029/2020JB020371
Yan, L.-J., Chen, X.-X., Tang, H., Xie, X.-B., Zhou, L., Hu, W.-B., et al. (2018). Continuous TDEM for Monitoring Shale Hydraulic Fracturing. Appl. Geophys. 15 (1), 26–34. doi:10.1007/s11770-018-0661-1
Yin, C., Huang, W., and Beng, F. (2013). The Full-Time Electromagnetic Modeling for Time Domain Airborne Electromagnetic Systems. Chin. J. Geophys.(in Chinese) 56 (9), 3153–3162. doi:10.6038/cjg20130928
Yin, C., Qi, Y., Liu, Y., and Cai, J. (2016). 3D Time-Domain Airborne EM Forward Modeling with Topography. J. Appl. Geophys. 134, 11–22. doi:10.1016/j.jappgeo.2016.08.002
Zhan, Q., Ren, Q., Zhuang, M., Sun, Q., and Liu, Q. H. (2018). An Exact Riemann Solver for Wave Propagation in Arbitrary Anisotropic Elastic Media with Fluid Coupling. J. Chin. Med. Assoc. 329, 24–39. doi:10.1016/j.cma.2017.09.007
Keywords: TEM, hydraulic fracturing monitoring, 3D, forward modelling, fracturing medium
Citation: Huang X, Yan L, Cao X, Zhou L and Xie X (2022) Development and Consideration of 3D Transient Electromagnetic Forward Modelling for the Hydraulic Fracturing Monitoring. Front. Energy Res. 10:922445. doi: 10.3389/fenrg.2022.922445
Received: 18 April 2022; Accepted: 09 May 2022;
Published: 06 June 2022.
Edited by:
Hui Pu, University of North Dakota, United StatesReviewed by:
Shangyu Du, China Coal Technology and Engineering Group Corp, ChinaWentao Liu, Changʼan University, China
Copyright © 2022 Huang, Yan, Cao, Zhou and Xie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaoyue Cao, Y2FveHlfZW1AMTYzLmNvbQ==
 Xin Huang
Xin Huang Liangjun Yan
Liangjun Yan Xiaoyue Cao
Xiaoyue Cao