Hierarchical Optimization and Grid Scheduling Model for Energy Internet: A Genetic Algorithm-Based Layered Approach

The old economic and social growth model, characterized by centralized fossil energy consumption, is progressively shifting, and the third industrial revolution, represented by new energy and Internet technology, is gaining traction. Energy Internet, as a core technology of the third industrial revolution, aims to combine renewable energy and Internet technology to promote the large-scale use and sharing of distributed renewable energy as well as the integration of multiple complex network systems, such as electricity, transportation, and natural gas. This novel technology enables power networks to save energy. However, multienergy synchronization optimization poses a significant problem. As a solution, this study proposed an optimized approach based on the concept of layered control–collaborate optimization. The proposed method allows the distributed device to plan the heat, cold, gas, and electricity in the regional system in the most efficient way possible. Moreover, the proposed optimization model is simulated using a real-number genetic algorithm. It improved the optimal scheduling between different regions and the independence of distributed equipment with minimal cost. Furthermore, the inverse system and energy and cost saving rate of the proposed method are better than those of existing methods, which prove its effectiveness.

1 Introduction

The photovoltaic power generation industry has developed tremendously since the introduction of a new energy production policy, and photovoltaic grid-connected systems are increasingly undergoing large-scale development (Fakhri et al., 2021). The conventional economic and social development model, which is based on the concentrated use of fossil fuels, is increasingly evolving, and the third industrial revolution, which is based on new energy and Internet technology, is gaining traction. As a central technology of the third industrial revolution, energy Internet aims to merge renewable energy and Internet technology to facilitate the large-scale use and sharing of distributed renewable energy as well as the convergence of multiple complex networks, such as power, transportation, and natural gas (Khan and Singh, 2018; Alsafasfeh et al., 2019a; Alsafasfeh et al., 2019b; Alsafasfeh et al., 2019c; Hussain et al., 2019; Alsafasfeh et al., 2020; Ma et al., 2020). By examining the literature, we can see that scholars have obtained comparatively more research results on energy Internet as a result of its growth. Internet technology and energy integration are research hotspots. The top-level design and concrete demonstration projects have been assessed, and there are multiple research findings in the fields of policy practice and theory. However, some works lack in terms of formal theory and realistic experience. At this point, the research community and industry still need to study the energy Internet’s growth and related policy formulation considering the successful experiences of developing countries (Lee et al., 2018; Saraereh et al., 2018; Mohammad et al., 2020; Mostafa et al., 2020; Motiagh et al., 2020; Shahjehan et al., 2020).

The current global energy system is hastening the change, with large-scale distributed energy access, the rapid growth of emerging entities, such as virtual power plants, and the transition to renewable and low-carbon energy posing new demands for energy consumption and utilization. Many experts and academics have turned their attention to improving energy efficiency, encouraging the consumption of distributed energy, and understanding the organized use of multiple energy sources (Cakmak et al., 2020). As a result, the energy Internet was created to investigate the ways in which the emerging entities, such as distributed energy, energy storage, flexible load, and electric vehicles would participate in the market and use the information and communication technologies facilitating the multienergy collaborative transactions and broad access to multiple marketers and new solutions for high-quality energy production (Fang et al., 2012; Kantarci and Mouftah, 2015; Heymann et al., 2018).

Several megawatt-scale grid-connected photovoltaic power stations have been constructed and exist in various regions at this time. To increase the capability of large-scale photovoltaic power plants, the inverter parallel structure is frequently used. The greater the potential of a photovoltaic power station, the more inverters are connected in parallel, and the greater the grid impedance equal to a single inverter. This will result in a major decrease in grid link point voltage, likely oscillation, and grid connection loss (Hua et al., 2019).

Rapid economic growth has resulted in significant energy and environmental crises, and developing sustainable and renewable energy, improving energy structure, and increasing energy consumption efficiency are important ways to solve the energy crisis (Fan et al., 2013; Kumar et al., 2019; Attarha et al., 2020; Cepeda et al., 2020). Renewable energy technology is becoming more mature, and its penetration rate in the power grid is increasing; however, when connected to a large power grid, it will have an effect on the power system’s safe and stable operation as well as power quality control (Manoharan et al., 2020). The energy Internet, which was spawned by the third industrial revolution, offers practical strategies for deploying distributed renewable energy on a wide scale. However, the processing of large-scale decision variables is a problem for the energy management system, as is the joint scheduling and optimization of multiple energy flows of electricity, gas, cooling, and heating, as well as the enhancement of overall energy efficiency. The energy Internet has different aspects, such as economic dispatch analysis via cyber attacks (Huang et al., 2022), router-based analysis (Guo et al., 2019), communication delay analysis (Huang et al., 2019), security planning (Lv et al., 2020), and distributed control schemes in a multisite scenario (Wang et al., 2020a).

Studies have (Masood and Ali, 2013; Zhang L. et al., 2020) established an optimal configuration model of the multienergy system with energy storage with the goal of configuration economy, and it achieved the optimal configuration effect. Some studies have (Li D. et al., 2020; Chen et al., 2021; Li and Zhao, 2021) focused on the operational economy, with environmental protection as their goal, and the optimal dispatch model of a combined cooling, heating, and power system was established. Other studies (Eshraghi et al., 2019; Yang et al., 2021) aimed at the operation economy of the integrated energy system and established an optimal dispatch model of the multienergy system, which achieves the optimal operation effect. Furthermore, (Wang et al., 2017) comprehensively considered the consumption rate of renewable energy and the operating cost of the microgrid, and they established a microgrid-optimized operation model containing renewable energy and multiple energy forms of cold, heat, and electricity. In the abovementioned studies, optimal scheduling and operation were separated and optimized, and only the multienergy complementary optimization on the energy supply side was considered, whereas the demand side flexible factors were not introduced in the optimized operation.

Focused on the energy core, (Zhao et al., 2018) developed an electricity–gas–heat hybrid energy system model. Based on the adjustable heat-to-power ratio model of the energy center, (Zhang et al., 2019) developed a two-layer optimization model of the microenergy grid. A joint dispatch model for wind, water, fire, and multienergy bases was developed in (Long et al., 2017). These studies emphasized the energy Internet’s multienergy complementary comprehensive applications, device coordination, and optimization power. The system architecture design and related operation control strategies of energy Internet’s multienergy coordination and optimization were discussed in (Zhang et al., 2017; Wang et al., 2019). The authors of (Godina et al., 2018) created a decentralized hierarchical scheduling model and solved optimization problems using the adaptive evolutionary algorithms. The authors of (Zhang Y. et al., 2020) proposed a method based on stochastic model predictive control energy local area network optimization dispatch, which optimizes and coordinates the device model using mixed-integer quadratic programming. In (Degefa et al., 2016), the authors proposed a two-layer control model based on multi-agent consistency to realize multienergy complementation and device-coordinated optimization control in the energy Internet. As a result, designing an energy Internet optimization model and choosing teamwork techniques have become common research topics.

To overcome these shortcomings, this study focused on the multilevel coordination and optimization approach of the energy Internet with renewable energy and developed a hierarchical optimization scheduling model called the “system layer–regional layer.”

The main contributions of the proposed study are the following:

• This study begins with the basic concept of the energy Internet and divides it into a system layer, regional layer, and device layer on a spatial scale.

• It then sets different optimization goals according to different scheduling subjects to achieve a “hierarchical control-global optimization” multilevel control mode, which is combined with the current research status of the energy Internet.

• A genetic algorithm-based approach is proposed to achieve the proposed optimal scheduling model.

• The hierarchical optimization scheduling approach can effectively solve the problems in the system management and control of distributed equipment according to the MATLAB simulation.

The rest of this article is organized as follows. In Section 2, the hierarchical design of the energy Internet is discussed and the layered architecture is highlighted. In Section 3, the multisource and multilayer optimization model is proposed. In Section 4, the genetic-algorithm-based optimization scheduling is explained. In Section 5, the case study and simulation results analysis is provided, while Section 6 gives the conclusion.

2 Hierarchical Design of energy Internet Dispatching

2.1 Layered Optimization Architecture

The number of distributed devices has significantly increased due to the distributed existence of the energy Internet. Optimizing scheduling decisions necessitates analyzing and manipulating large volumes of data as well as presenting new criteria for the conventional centralized unified scheduling system. For nonlinear high-dimensional problems and large data-processing problems, hierarchical optimization is a solution. The basic concept is to divide the device into many levels based on certain standards (such as voltage levels) and then divide it into various areas based on the system’s physical characteristics. A region appoints a representative to oversee the regulation of distributed equipment. Wind and solar energies, as well as cooling and heating, have geographically concentrated load demand. The regional energy Internet is set up to achieve energy autonomy, which is organized and optimized by superior scheduling. This hierarchical control is analogous to the division of the device functional level at the spatial or physical level, which helps with scheduling architecture design and integration.

2.2 Overall Design of Dispatching Level

The energy Internet connected to the distribution network is divided into three layers on the spatial scale, according to the abovementioned hierarchical optimization architecture: system, regional, and device layers (Degefa et al., 2016). Figure 1 depicts the layered structure.

FIGURE 1

FIGURE 1. Proposed architecture.

The device layer’s primary duty is to maintain shared cooperation between the regional energy Internet and interaction between the regional energy Internet and the upper-level distribution network to ensure the secure and cost-effective operation of the entire energy interconnection. The regional layer is composed of many interconnected regional energy networks whose primary objective is to organize the performance of controllable distributed power sources within a region, reduce regional operating costs, and achieve regional energy autonomy.

Wind turbines, photovoltaics, distributed generators, batteries (batteries), and combined cooling, heating, and power (CCHP) systems are included in the equipment sheet. The system layer is primarily in charge of starting and stopping the system (power grid) as well as regulating its operating status and reporting its parameters and responding to orders from the upper layer.

3 Multisource and Multilevel Optimal Scheduling Model

3.1 System-level Optimization Scheduling Model

A system-level optimal scheduling model was developed for the energy Internet framework shown in Figure 1. The goal of optimum scheduling is to reduce the system’s overall operating costs. The objective function’s mathematical expression is

$\min F={\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{n=1}^{N}f\left(P_n\left(t\right)\right)+f\left(P_{\text{grid},n}\left(t\right)\right)(1)$

where $T$ is the dispatch period; $N$ is the number of regional energy Internet; $P_n\left(t\right)$ is the total power generation in area $n$; and $P_{\text{grid},n}\left(t\right)$ is the exchange power between area $n$ and the distribution network. The positive means that area $n$ sells electricity to the distribution network, and negative means it purchases electricity from the distribution network.

$f\left(P_n\left(t\right)\right)=a_n{P}_n{\left(t\right)}^2+b_n{P}_n\left(t\right)+c_n(2)$

$f\left(P_{\text{grid},n}\left(t\right)\right)={\alpha }_n{P}_{\text{grid},n}{\left(t\right)}^2+p\left(t\right)P_{\text{grid},n}\left(t\right)(3)$

where $f\left(P_n\left(t\right)\right)$ is the power-generation cost of the regional energy Internet $n$. Each region is equivalent to a power-generation unit, and its power-generation cost is a quadratic function relationship with the total power generation of the region (Eshraghi et al., 2019). $a_n$, $b_n$, and $c_n$ are the regional power-generation cost coefficients. $f\left(P_{\text{grid},n}\left(t\right)\right)$ is the exchange power cost, where the transmission cost and the exchange power have a quadratic function relationship, and ${\alpha }_n$ is the transmission cost coefficient. The term $p\left(t\right)$ is the electricity price.

At the device level, the total sum of the regional power generation and the exchange power between the region and the distribution network are the optimization variables. As a result, the upper and lower limits of the regional energy Internet’s total output, power balance, and tie-line constraints must be considered (Gao et al., 2017).

3.2 Regional Optimization Scheduling Model

The aim of regional optimal scheduling is to reduce regional operating costs by rationally controlling the performance of each controllable unit. Each region’s primary role is as follows:

$\min C_{\text{area},n}={\displaystyle \sum }_{t=1}^T\left[C_{\text{WT}}\left(t\right)+C_{\text{PV}}\left(t\right)+C_{\text{DG}}\left(t\right)+C_{\text{CCHP}}\left(t\right)\right](4)$

where $C_{\text{area},n}$ is the total operating cost of the regional energy Internet $n$. The four variables on the right side of the equation are the cost of wind and solar power generation, the cost of controllable distributed power generation, and the sum of the cost of heating and power supply of the CCHP system.

The regional-level optimal scheduling model for each regional energy Internet must satisfy the regional power balance, which involves the balance of electric and thermal power.

(1) The cost of wind and solar power generation. We only consider the daily operation and maintenance costs of wind and solar equipment:

$C_{\text{WT}}\left(t\right)={\alpha }_{\text{WT}}{P}_{\text{WT}}\left(t\right)(5)$

$C_{\text{PV}}\left(t\right)={\alpha }_{\text{PV}}{P}_{\text{PV}}\left(t\right)(6)$

where ${\alpha }_{\text{WT}}$ and ${\alpha }_{\text{PV}}$ are the operation and maintenance cost coefficients per unit of wind and solar power generation.

(2) Controllable generating unit cost and constraints. Controllable units usually use a quadratic function model to express the cost:

$C_{\text{DG}}\left(t\right)={\displaystyle \sum }_{i=1}^I\left[a_{\text{DG},i}{P}_{\text{DG},i}{\left(t\right)}^2+b_{\text{DG},i}{P}_{\text{DG},i}\left(t\right)+c_{\text{DG},i}\right](7)$

where $P_{\text{DG},i}\left(t\right)$ is the output power of the ith unit and $a_{\text{DG},i}$, $b_{\text{DG},i}$, and $c_{\text{DG},i}$ are the cost coefficients of the controllable unit.

During operation, the controllable generator set is limited by its technical parameters; thus, the upper and lower limits of its performance, as well as the constraints of its climbing power, must be considered.

(3) The cost of battery energy storage and its constraints. During the operation of the battery, only its operation and maintenance costs are considered:

$C_{\text{BESS}}\left(t\right)=C_{\text{inv}}\frac{P_{\text{ch}}\left(t\right)+P_{\text{dis}}\left(t\right)}{L\left(t\right)}(8)$

where $C_{\text{inv}}$ is the initial investment and construction cost, and $P_{\text{ch}}\left(t\right)$ and $P_{\text{dis}}\left(t\right)$ are charge and discharge power, respectively. $L\left(t\right)$ is the service life of the battery. During the operation of the battery, the state of charge and the constraints of charge and discharge power are primarily considered.

(4) CCHP. The structure of the CCHP system is presented in Figure 2.

FIGURE 2

FIGURE 2. Combined cooling, heating, and power model.

The cost is mainly the cost of natural gas fuel $C_{\text{fuel}}$ (Pasetti et al., 2018) includes the fuel costs of microturbines (MT) and gas boilers (GB):

$C_{\text{fuel}}=C_{\text{MT}}+C_{\text{GB}}(9)$

$C_{\text{MT}}=c_{\text{g}}{F}_{\text{MT}}(10)$

$F_{\text{MT}}=\frac{E_{\text{MT}}}{Q_{\text{LHV}}{\eta }_{\text{MT}}}=\frac{P_{\text{MT}}\left(t\right)\mathrm{\Delta }t}{Q_{\text{LHV}}{\eta }_{\text{MT},t}}(11)$

where $C_{\text{MT}}$ is the fuel cost of MT, $C_{\text{GB}}$ is the fuel cost of the GB, $c_{\text{g}}$ is the price of natural gas, $F_{\text{MT}}$ is the natural gas consumption of MT, $E_{\text{MT}}$ is the energy provided by MT in $\mathrm{\Delta }t$ time, which is the product of the power $P_{\text{MT}}\left(t\right)$ by the MT in $\mathrm{\Delta }t$, $Q_{\text{LHV}}$ is the calorific value of natural gas, and ${\eta }_{\text{MT},t}$ is the power-generation efficiency of MT at time $t$, which is related to the model of MT, usually a third-order efficiency model (Kumar et al., 2020).

There is heat leakage loss $H_{\text{MT}}\left(t\right)$ in the process of electrothermal conversion, which is expressed by the conversion coefficient ${\eta }_{\text{CCHP}}$ as follows (Zhu et al., 2018):

$P_{\text{MT}}\left(t\right)=\frac{H_{\text{MT}}\left(t\right)}{{\eta }_{\text{CCHP}}}(12)$

Heat output is linked to efficiency in gas-fired boilers, and both factors influence fuel costs (Li Z. et al., 2020):

$C_{\text{GB}}=c_{\text{g}}{F}_{\text{GB}}(13)$

$F_{\text{GB}}=\frac{Q_{\text{GB}}}{Q_{\text{LHV}}{\eta }_{\text{GB}}}=\frac{H_{\text{GB}}\left(t\right)\mathrm{\Delta }t}{Q_{\text{LHV}}{\eta }_{\text{GB}}}(14)$

where $F_{\text{GB}}$ is the natural gas consumption of GB, $c_{\text{g}}$ is the cost of natural gas, $Q_{\text{GB}}$ is the heat production within $\mathrm{\Delta }t$, $H_{\text{GB}}\left(t\right)$ is the heat/cold power output at time $t$, and ${\eta }_{\text{GB}}$ is the heat production efficiency.

During the MT power-generation process, high-temperature gas is generated, and the heat recovery system recovers the heat from the flue gas and outputs it as cooling and heating power. When the amount of heat provided by MT exceeds the amount needed for heating and cooling, the excess heat is dissipated as heat in the air. When the heat generated by MT is inadequate, GB (Liu et al., 2020) fills the gap in the cooling and heating capacity.

3.3 Interaction Between the System Layer and Regional Layer

Both the system and the regional layer have objective functions, optimization decision variables, and constraints in the energy Internet multisource and multilevel optimal dispatch model defined above, and the two are related by the total regional power generation, $P_n\left(t\right)$. To jointly complete the optimum scheduling of the entire system, the system layer and the regional layer must conduct required information exchanges. Figure 3 depicts the interaction mechanism. The device layer uses a genetic algorithm to calculate the energy Internet’s energy efficiency and total production. Then, the total power generation of each area is delivered to the regional level. Each region configures the performance of each distributed device using a centralized optimization process, calculates the power-generation cost coefficient of each region based on the total regional power generation issued by the system layer, and decides if the coefficient needs to be fed back to the system layer for the update.

FIGURE 3

FIGURE 3. Proposed interaction framework.

It is worth noting that at the regional stage, the electric output of the MT and the heat output of the GB are used as optimization decision variables to achieve joint optimal dispatch under the condition of multienergy coupling of cold, heat, and electricity. There is a drawback that large-scale and long-distance transmission cannot be carried out due to the substantial loss of energy transmission in the form of cold and heat. The two energy systems are connected to organize and optimize the realization of long-distance cross-regional energy coupling while saving money through lower-loss transmission.

(1) The regional power-generation cost coefficient update rule (Yin et al., 2020). The cumulative power-generation cost coefficient of the regional energy Internet, according to Eq. 2, is $a_n$, $b_n$, and $c_n$. It is worth noting that the current generator composition cost coefficients in the region with the lowest marginal cost coefficient are $a_{\text{DG},i}^{\text{min}}$ and$b_{\text{DG},i}^{\text{min}}$.

As the regional energy Internet’s total power generation $P_n\left(t\right)$ increases, the controllable unit with the lowest marginal cost within the area reacts. As a result, the whole region’s marginal cost can be made equal to the unit’s marginal cost. This ensures that the interaction between the device layer and the regional layer remains cost consistent. The following are the rules for updating the regional energy Internet’s power-generation cost coefficient:

$a_n=a_{\text{DG},i}^{\text{min}}(15)$

$b_n=2a_{\text{DG},i}^{\text{min}}{P}_n\left(t\right)+b_{\text{DG},i}^{\text{min}}-2a_{\text{DG},i}^{\text{min}}{P}_{\text{DG},i}\left(t\right)(16)$

$c_n=2a_{\text{DG},i}^{\text{min}}{P}_n\left(t\right)+2b_{\text{DG},i}^{\text{min}}{P}_{\text{DG},i}\left(t\right)-a_{\text{DG},i}^{\text{min}}{P}_{\text{DG},i}\left(t\right)(17)$

(2) Between the device layer and the regional layer, there is an interactive iteration stop criterion. The iteration ends when the regional energy Internet’s total power-generation transition satisfies Eq. 18 or when the maximum number of iterations is reached.

$\mathrm{\Delta }{P}_n\le \epsilon (18)$

4 Optimization Scheduling Based on Genetic Algorithm

4.1 Description

The genetic algorithm is based on natural and simple optimization ideas embodied in the evolution of organisms (Mao et al., 2020). Each individual in the population is coded and corresponds to a candidate solution in the feasible region of the optimization problem. As a consequence, the population is a solution set made up of several viable alternatives (Zhong et al., 2005; Bevrani et al., 2016; Hua et al., 2018; Javaid et al., 2018; Hua et al., 2021; Perera et al., 2021). The fitness feature is a yardstick for measuring the advantages and disadvantages of individuals in the evolutionary phase (Li and Wang, 2019; Luo et al., 2019; Elmouatamid et al., 2020; Hussain et al., 2020; Wang et al., 2020b; Zand et al., 2020).

Assuming that the energy Internet regional layer is divided into $N$ regions, the optimal scheduling period is $T$. Then, we establish a population with a population size of $M$ and use a real-number coding strategy to code the population:

$X_m=\{\begin{array}{c}{X}_{11}{X}_{12}{X}_{13}\dots X_{1T}\\ X_{21}{X}_{22}{X}_{23}\dots X_{2T}\\ X_{N1}{X}_{N2}{X}_{N3}\dots X_{NT}\end{array}m=\mathrm{1,2},\dots , M(19)$

Each chromosome has $T$ alleles, and a human $X_m$ in the population has $N$ chromosomes. The basic concept is that these $N$ chromosomes belong to $N$ regions. The total power generation of region $n$ at time $t$ is defined by the gene $X_{nt}$ on the chromosome, which is a real number. Once an individual has been coded, the individual now contains all the information about each area’s effort at any given time.

The fitness function of the system-level genetic algorithm is mapped to the optimization goal Eq. 1 in the proposed work. The regional layer’s fitness function is mapped to the Eq. 4 optimization objective function, which are minimum optimization problems. The inverse of the minimum problem is converted into the maximum problem because the objective function’s value is positive in the feasible field.

4.2 Optimization Process

It is applied to the solution of the proposed multisource and multilevel optimal scheduling strategy of the energy Internet, which is based on the basic theory of genetic algorithms. Figure 4 depicts the solution process.

(1) Start the data and set them up. Regional power-generation cost coefficient, regional production upper and lower limits, wind and solar output forecast, regional power load and thermal load demand, regional equipment cost coefficients, technology, and capacity constraints are among the parameters that must be initialized.

(2) Begin optimizing the device layer. The system-level optimization scheduling model is solved using the genetic algorithm technique. The total power generation $P_n\left(t\right)$ of each region is shared with the power distribution network $P_{\text{grid},n}\left(t\right)$ after the evolutionary algorithm is completed, and $P_n\left(t\right)$ is distributed to each area.

(3) Begin by optimizing the area. The performance of each piece of equipment in the region is organized on the basis of the total regional generation power issued by the system layer, with the goal of the lowest regional operating cost, and the result of distributed equipment coordination at the regional level is obtained.

(4) Termination decision optimization. We calculate the marginal cost of generating units based on the effects of regional optimization and use Eqs. 15 and 16 to obtain cost coefficients that can be used in the next iteration. According to Eq. 17, check whether it is necessary to update the coefficient. If the iterative stop condition is not met, go back to step (2). If the iterative stop condition is met, the optimization process ends and go to step (5).

(5) Optimization results output. The machine layer and regional layer optimization results are obtained after iterative optimization. According to the results, the regional layer sends scheduling instructions to the system, and it responds to the instructions to complete the optimal scheduling.

FIGURE 4

FIGURE 4. Flowchart of the proposed optimization process.

5 Case Analysis

5.1 Proposed System Configuration

A framework containing four regional energy Internets is defined according to the hierarchical structure, as shown in Figure 1. The maximum exchange power between each area and the distribution network tie line is 100 kW, as shown in Figure 5. The status parameters are presented in Table 1.

FIGURE 5

FIGURE 5. Proposed system configuration.

TABLE 1

TABLE 1. Status parameters.

5.2 Simulation Results

5.2.1 System-level Optimization Scheduling Results

Figure 6 depicts each regional energy Internet’s total power output, while Figure 7 depicts the power shared between each region and the primary distribution network. The area purchases electricity from the distribution network when the regional marginal cost is higher than the electricity price. The region sells electricity to the distribution network when the regional marginal cost is lower than the electricity price.

FIGURE 6

FIGURE 6. Comparison of total generated power of each region.

FIGURE 7

FIGURE 7. Comparison of exchange power between each region.

Since the power generation cost of Region 3 is low, the time when its exchange power with the primary distribution network is >0 is longer, according to the optimization results in Figure 7. Region 3 makes money by selling electricity to the distribution network, while Regions 2 and 4 have higher power generation costs due to excessive resource consumption and primarily buy electricity from the distribution network. Through a popular bus, each region can communicate using electricity. The power flow path of the tie line is not the same as the theoretical flow direction due to the randomness of the genetic algorithm in the optimization process, but the pattern of regional power purchase and selling activity is consistent with the theoretical analysis result in the dispatch period. Owing to the comparatively high cost of generators in Region 1, a portion of the energy purchased from the distribution network is mostly supplied to the consumers to minimize the economic costs.

5.2.2 Analysis of Regional Optimization Scheduling Results

The optimal scheduling outcome of a standard winter energy Internet system is defined by regional energy Internet 1. The heat load is high in the winter, when the day and night temperatures are low, and the heat load during the day is small; thus, the cooling load fluctuates a little. Figures 8 and 9 show the simulation effects of the regional optimization scheduling. Figure 8 mainly shows the supply and demand relationship of electric energy in the system, whereas Figure 9 mainly shows the supply and demand relationship of thermal energy. The results indicate that the MT has been operating at full power except from 10:00 to 17:00. This is because the MT has the cheapest power generation rate. The MT produces as much power as possible to satisfy its power demand in the power network, but its output is also limited by the thermal network, and the thermal demand decreases abruptly between 10:00 and 17:00. As a result, the MT must reduce its performance to maintain a balance between heat production and demand. Even though the cost of power generation is lower for the MT than for other units, the excess heat produced during the power-generation process is ultimately dissipated in the air, thereby resulting in energy waste.

FIGURE 8

FIGURE 8. Comparison of power optimization of the first region.

FIGURE 9

FIGURE 9. Comparison of thermal optimization of the first region.

In the power network, the inadequate power in the case of maximum MT is made up by the lower-cost Unit 1 and battery discharge, and the higher-cost Unit 2 does not produce energy due to the limited electric load at 0:00–5:00. Units 1 and 2 distribute their output according to the concept of fair consumption at a small increase rate as the load increases steadily. When the load is thin, the accumulator is charged early in the morning and late at night, and when the load is high, it is discharged between 8:00 and 14:00 to cut peaks and fill valleys. Owing to the comparatively high cost of generators in Region 1, a portion of the energy purchased from the distribution network is mostly supplied to the consumers to minimize the economic costs.

The heating load is high in the heating network from 0:00 to 8:00 and 17:00 to 24:00, and the MT cannot satisfy the cooling and heating load demands when the MT is running at full capacity. As a result, the GB contributes to compensate for the difference in the heating load. The heat load declines significantly from 11:00 to 18:00. To maintain energy balance in the heating network, the MT reduces performance, and the GB shuts down. The MT tracks the cooling load shift.

A typical summer energy Internet system’s optimal dispatch result is reflected by the regional energy Internet 2. The cooling load is heavy in the summer, when the temperature is high at noon, and the day and night cooling loads are minimal. Figures 10 and 11 show the regional optimization scheduling simulation results. It can be seen that the cooling load in the heating network is poor during the hours of 0:00–8:00 and 21:00–24:00. The MT primarily arranges output according to the cooling and heating load demands, and its output power varies as the cooling and heating load varies. From 8:00, the cooling load increases dramatically. The complete MT is still unable to satisfy the cooling load demand at this time. As a result, the GB began to compensate for the heat shortage, and the GB is largely responsible for cooling and heating loads. The power load is relatively flat in comparison to Region 1, but it varies greatly. The production of Units 1 and 2 is distributed according to the concept of equal consumption with a slight increase rate. The battery, which serves as a power source for discharge at the height of the load and as a load for charging at the valley, is primarily responsible for regulating load fluctuation. Since Region 2’s power-generation cost coefficient is relatively high, it purchases energy from the distribution network during peak load periods to maintain the region’s lowest overall operating cost.

FIGURE 10

FIGURE 10. Comparison of power optimization of the second region.

FIGURE 11

FIGURE 11. Comparison of thermal optimization of the second region.

Figures 12 and 13 show the simulation results for Regions 3 and 4. The load in Region 3 is relatively low at 00:00–6:0 and 21:00–24:00. At this time, the higher-cost Unit 6 is turned off, and Unit 5 supplies power to the load on its own. The hourly load is relatively high between 6:00 and 21:00; thus, the output of the two units is distributed according to the concept of equal consumption at a slow rate. The battery is charged at a low load and discharged at a high load, thereby effectively following the load shift and performing peak-shaving and valley-filling functions. Region 4 outcome interpretation is close to Region 3, and it is not repeated here.

FIGURE 12

FIGURE 12. Comparison of power optimization of the third region.

FIGURE 13

FIGURE 13. Comparison of power optimization of the fourth region.

To verify the performance of the algorithm proposed in this article, (Li and Zhao, 2021) and (Wang et al., 2017)’s algorithms and the proposed algorithms were compared, and the optimization solution of a typical summer day was taken as an example. Figure 14 shows the algorithm optimization vs. the number of iterations. It can be seen that the number of iterations of (Li and Zhao, 2021) algorithm is 29, which is better than the 37 iterations of (Wang et al., 2017) algorithm; however, the optimal solution corresponding to the proposed algorithm is better than the (Li and Zhao, 2021) algorithm.

FIGURE 14

FIGURE 14. Comparison of the proposed and existing algorithms vs. number of iterations.

Although the convergence speed of the proposed algorithm is lower than that of the (Li and Zhao, 2021) algorithm, it jumps out of the local optimum, and the optimization result is better than the (Wang et al., 2017) algorithm. The proposed algorithm exerts its powerful optimization performance in the application of energy interconnection microgrid system operation strategy.

To further validate the effectiveness of the proposed method, Figure 15 compares the proposed algorithm with (Eshraghi et al., 2019) and (Liu et al., 2020) algorithms under a different number of iterations. It can be seen that the system cost of the proposed algorithm is lower than that of references (Eshraghi et al., 2019) and (Liu et al., 2020) algorithms. In addition, the inverse system energy saving and emission rates of the proposed algorithm are better than for those algorithms, which makes it suitable for deploying in distributed energy management system of the energy Internet.

FIGURE 15

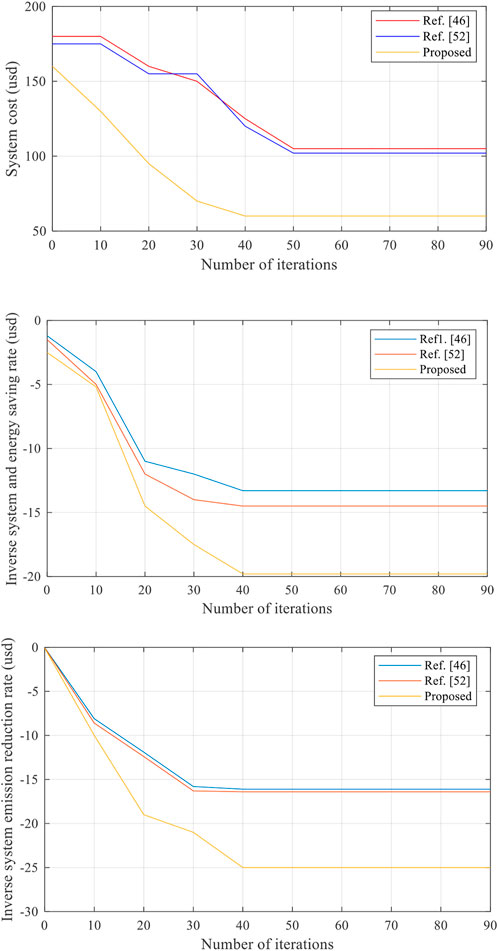
FIGURE 15. Comparison of the proposed algorithm with references (Eshraghi et al., 2019; Liu et al., 2020) algorithms for a different number of iterations.

6 Conclusion

This study focused on the multilevel coordination and optimization approach of the energy Internet with renewable energy, and it developed a hierarchical optimization scheduling model called “system layer–regional layer.” The device layer is in charge of network optimization, while the regional layer introduces regional energy autonomy based on optimized performance. Through simulation research, the following conclusions can be drawn:

(1) Distributed renewable clean energy, such as wind turbines and photovoltaic equipment, runs in the highest power monitoring point mode in the regional energy Internet and should be prioritized for use as much as possible.

(2) Controlled equipment fills the void left after photovoltaic and fan consumption. The evolutionary optimization concept is used by the genetic algorithm based on real-number coding to determine the best collaboration technique that minimizes the regional costs.

(3) Through a spatial design of the physical structure, the multilevel coordination optimization model offers an efficient approach for the processing of large-scale decision variables and realizes the management and control of distributed equipment in the energy Internet.

(4) The energy Internet’s multisource, multilevel integrated dispatch encourages the localized use of high-penetration renewable energy and increases overall energy utilization.

In summary, the simulation results indicate that the proposed algorithm provides better performance in terms of cost effectiveness compared with existing algorithms.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author Contributions

LL: conceptualization, methodology. AA: supervision, investigation, and writing—original draft. AA: software, validation, and visualization. ZA: visualization, supervision, investigation, writing—original draft, and writing—review and editing. IK: conceptualization, methodology, supervision, writing—original draft, and writing—review and editing. KR: supervision, investigation, writing—original draft, and writing—review and editing. IB: visualization, supervision, and investigation. XL: methodology, software, validation, investigation, writing—original draft, and writing—review and editing. K-IK: software, validation, visualization, supervision, investigation, writing—original draft, and writing—review and editing.

Funding

This work was supported by Institute for Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2022-0-01200, Training Key Talents in Industrial Convergence Security). This study is supported by State Grid XZ Electric Power Co., Ltd. science and Technology project: “Impact of Energy Storage Technology Application on Power Grid” (SGXZJY00JHJS2000007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Alsafasfeh, Q., Saraereh, O. A., Khan, I., and Choi, B. J. (2019). A Robust Decentralized Power Flow Optimization for Dynamic Pv System. IEEE Access 7, 63789–63800. doi:10.1109/access.2019.2916974

CrossRef Full Text | Google Scholar

Alsafasfeh, Q., Saraereh, O. A., Khan, I., and Kim, S. (2019). Ls-solar-pv System Impact on Line Protection. Electronics 8 (2), 1–13. doi:10.3390/electronics8020226

CrossRef Full Text | Google Scholar

Alsafasfeh, Q., Saraereh, O. A., Khan, I., and Kim, S. (2019). Solar Pv Grid Power Flow Analysis. Sustainability 11 (6), 1–17. doi:10.3390/su11061744

CrossRef Full Text | Google Scholar

Alsafasfeh, Q., Saraereh, O. A., Alsafasfeh, M., Maqableh, A., Khan, I., and Choi, B. J. (2020). An Efficient Algorithm for Power Flow Optimization in Pv Inverters Systems. Electr. Power Components Syst. 48 (12), 1362–1377. doi:10.1080/15325008.2020.1854373

CrossRef Full Text | Google Scholar

Attarha, S., Narayan, A., Hassan, B. H., Kruger, C., Castro, F., Babazadeh, D., et al. (2020). Virtualization Management Concept for Flexible and Fault-Tolerant Smart Grid Service Provision. Energies 13 (9), 2196. doi:10.3390/en13092196

CrossRef Full Text | Google Scholar

Bevrani, H., Feizi, M. R., and Ataee, S. (2016). Robust Frequency Control in an Island Microgrid: and -Synthesis Approaches. IEEE Trans. Smart Grid 7 (2), 706–717. doi:10.1109/TSG.2015.2446984

CrossRef Full Text | Google Scholar

Cakmak, N. K., Said, Z., Sundar, L. S., Ali, Z. M., and Tiwari, A. K. (2020). Preparation, Characterization, Stability, and Thermal Conductivity of rGO-Fe₃O₄-TiO₂ Hybrid Nanofluid: An Experimental Study. Powder Technol. 372 (24), 235–245. doi:10.1016/j.powtec.2020.06.012

CrossRef Full Text | Google Scholar

Cepeda, C., Henao, C. O., Percybrooks, W., Rivera, J. D., Montoya, O. D., and Walter, G. G. (2020). Intelligent Fault Detection System for Microgrids. Energies 13, 1–21. doi:10.3390/en13051223

CrossRef Full Text | Google Scholar

Chen, S., Arabkoohsar, A., Yang, Y., Zhu, T., and Nielsen, M. P. (2021). Multi-Objective Optimization of a Combined Cooling, Heating, and Power System with Subcooled Compressed Air Energy Storage Considering Off-Design Characteristics. Appl. Therm. Eng. 187, 929–937. doi:10.1016/j.applthermaleng.2021.116562

CrossRef Full Text | Google Scholar

Degefa, M. Z., Alahaivala, A., Kilkki, O., Humayun, M., Seilonen, I., Vyatkin, V., et al. (2016). MAS-Based Modeling of Active Distribution Network: The Simulation of Emerging Behaviors. IEEE Trans. Smart Grid 7 (6), 2615–2623. doi:10.1109/tsg.2015.2510547

CrossRef Full Text | Google Scholar

Elmouatamid, A., Ouladsine, R., Bakhouya, M., Kamoun, N. E., Khaidar, M., and Zine-Dine, K. (2020). Review of Control and Energy Management Approaches in Micro-Grid Systems. Energies 14 (1), 168. doi:10.3390/en14010168

CrossRef Full Text | Google Scholar

Eshraghi, A., Salehi, G., Heibati, S., and Lari, K. (2019). Developing Operation of Combined Cooling, Heat, and Power System Based on Energy Hub in a Micro-Energy Grid: The Application of Energy Storages. Energy Environ. 30 (8), 1356–1379. doi:10.1177/0958305x19846577

CrossRef Full Text | Google Scholar

Fakhri, A. B., Mohammed, S. L., Khan, I., Sadiq, A. S., Alkazemi, B., Pillai, P., et al. (2021). Industry 4.0: Architecture and Equipment Revolution. Comput. Mater. Continua 66 (2), 1175–1194. doi:10.32604/cmc.2020.012587

CrossRef Full Text | Google Scholar

Fan, Z., Kulkarni, P., Gormus, S., Efthymiou, C., Kalogridis, G., Sooriyabandara, M., et al. (2013). Smart Grid Communications: Overview of Research Challenges, Solutions, and Standardization Activities. IEEE Commun. Surv. Tutorials 15 (1), 21–38. doi:10.1109/surv.2011.122211.00021

CrossRef Full Text | Google Scholar

Fang, X., Misra, S., Xue, G., and Yang, D. (2012). Smart Grid - The New and Improved Power Grid: A Survey. IEEE Commun. Surv. Tutorials 14 (4), 944–980. doi:10.1109/surv.2011.101911.00087

CrossRef Full Text | Google Scholar

Gao, H., Liu, J., Wang, L., and Wei, Z. (2017). Decentralized Energy Management for Networked Microgrid in Future Distribution Systems. IEEE Trans. Power Syst. 33 (4), 3599–3610. doi:10.1109/TPWRS.2017.2773070

CrossRef Full Text | Google Scholar

Godina, R., Rodrigues, E. M., Pouresmaeil, E., Matias, J., and Catalao, J. S. (2018). Model Predictive Control Home Energy Management and Optimization Strategy with Demand Response. Appl. Sci. 8 (3), 1–14. doi:10.3390/app8030408

CrossRef Full Text | Google Scholar

Guo, H., Wang, F., Zhang, L., and Luo, J. (2019). A Hierarchical Optimization Strategy of the Energy Router-Based Energy Internet. IEEE Trans. Power Syst. 34 (6), 4177–4185. doi:10.1109/tpwrs.2019.2907323

CrossRef Full Text | Google Scholar

Heymann, B., Bonnans, J. F., Martinon, P., Silva, F. J., Lanas, F., and Jiménez-Estévez, G. (2018). Continuous Optimal Control Approaches to Microgrid Energy Management. Energy Syst. 9, 59–77. doi:10.1007/s12667-016-0228-2

CrossRef Full Text | Google Scholar

Hua, H., Hao, C., Qin, Y., and Cao, J. (2018). A Class of Control Strategies for Energy Internet Considering System Robustness and Operation Cost Optimization. Energies 11 (6), 1–20. doi:10.3390/en11061593

CrossRef Full Text | Google Scholar

Hua, H., Qin, Y., Hao, C., and Cao, J. (2019). Optimal Energy Management Strategies for Energy Internet via Deep Reinforcement Learning Approach. Appl. Energy 239, 598–609. doi:10.1016/j.apenergy.2019.01.145

CrossRef Full Text | Google Scholar

Hua, H., Wei, Z., Qin, Y., Wang, T., Li, L., and Cao, J. (2021). Review of Distributed Control and Optimization in Energy Internet: From Traditional Methods to Artificial Intelligence‐Based Methods. IET Cyber-Phys. Syst. 6 (2), 63–79. doi:10.1049/cps2.12007

CrossRef Full Text | Google Scholar

Huang, B., Liu, L., Zhang, H., Li, Y., and Sun, Q. (2019). Distributed Optimal Economic Dispatch for Microgrids Considering Communication Delays. IEEE Trans. Syst. Man. Cybern. Syst. 49 (8), 1634–1642. doi:10.1109/tsmc.2019.2900722

CrossRef Full Text | Google Scholar

Huang, B., Li, Y., Zhan, F., Sun, Q., and Zhang, H. (2022). A Distributed Robust Economic Dispatch Strategy for Integrated Energy System Considering Cyber-Attacks. IEEE Trans. Ind. Inf. 18, 880–890. doi:10.1109/TII.2021.3077509

CrossRef Full Text | Google Scholar

Hussain, S. M., Nadeem, F., Aftab, M. A., Ali, I., and Ustun, T. S. (2019). The Emerging Energy Internet: Architecture, Benefits, Challenges, and Future Prospects. Electronics 8 (9), 1–25. doi:10.3390/electronics8091037

CrossRef Full Text | Google Scholar

Hussain, H. M., Narayanan, A., Nardelli, P. H. J., and Yang, Y. (2020). What is Energy Internet? Concepts, Technologies, and Future Directions. IEEE Access 8, 183127–183145. doi:10.1109/access.2020.3029251

CrossRef Full Text | Google Scholar

Javaid, N., Hafeez, G., Iqbal, S., Alrajeh, N., Alabed, M. S., and Guizani, M. (2018). Energy Efficient Integration of Renewable Energy Sources in the Smart Grid for Demand Side Management. IEEE Access 6, 77077–77096. doi:10.1109/access.2018.2866461

CrossRef Full Text | Google Scholar

Kantarci, M. E., and Mouftah, H. T. (2015). Energy-Efficient Information and Communication Infrastructures in the Smart Grid: A Survey on Interactions and Open Issues. IEEE Commun. Surv. Tutorials 17 (1), 179–197. doi:10.1109/comst.2014.2341600

CrossRef Full Text | Google Scholar

Khan, I., and Singh, D. (2018). Energy-Balance Node-Selection Algorithm for Heterogeneous Wireless Sensor Networks. ETRI J. 40 (5), 604–612. doi:10.4218/etrij.2017-0349

CrossRef Full Text | Google Scholar

Kumar, P., Lin, Y., Bai, G., Paverd, A., Dong, J. S., and Martin, A. (2019). Smart Grid Metering Networks: A Survey on Security, Privacy and Open Research Issues. IEEE Commun. Surv. Tutorials 21 (3), 2886–2927. doi:10.1109/comst.2019.2899354

CrossRef Full Text | Google Scholar

Kumar, N. M., Chand, A. A., Malvoni, M., Prasad, K. A., Mamun, K. A., Islam, F. R., et al. (2020). Distributed Energy Resources and the Application of Ai, Iot, and Blockchain in Smart Grids. Energies 13 (21), 5739. doi:10.3390/en13215739

CrossRef Full Text | Google Scholar

Lee, B. M., Patil, M., Hunt, P., and Khan, I. (2018). An Easy Network Onboarding Scheme for Internet of Things Networks. IEEE Access 7, 8763–8772. doi:10.1109/ACCESS.2018.2890072

CrossRef Full Text | Google Scholar

Li, X., and Wang, S. (2019). A Review on Energy Management, Operation Control and Application Methods for Grid Battery Energy Storage Systems. CSEE J. Power Energy Syst. 7, 1026–1040. doi:10.17775/CSEEJPES.2019.00160

CrossRef Full Text | Google Scholar

Li, J., and Zhao, H. (2021). Multi-Objective Optimization and Performance Assessments of an Integrated Energy System Based on Fuel, Wind and Solar Energies. Entropy 23 (4), 431. doi:10.3390/e23040431

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, D., Zhang, S., and Xiao, Y. (2020). Interval Optimization-Based Optimal Design of Distributed Energy Resource Systems under Uncertainties. Energies 13 (13), 1–18. doi:10.3390/en13133465

CrossRef Full Text | Google Scholar

Li, Z., Zhang, W., Zhang, R., and Sun, H. (2020). Development of Renewable Energy Multi-Energy Complementary Hydrogen Energy System (A Case Study in china): A Review. Energy Explor. Exploit. 38 (6), 2099–2127. doi:10.1177/0144598720953512

CrossRef Full Text | Google Scholar

Liu, B., Li, J., Zhang, S., Gao, M., Ma, H., Li, G., et al. (2020). Economic Dispatch of Combined Heat and Power Energy Systems Using Electric Boiler to Accommodate Wind Power. IEEE Access 8, 41288–41297. doi:10.1109/access.2020.2968583

CrossRef Full Text | Google Scholar

Long, R., Liu, J., Lu, C., Shi, J., and Zhang, J. (2017). Coordinated Optimal Operation Method of the Regional Energy Internet. Sustainability 9 (5), 848. doi:10.3390/su9050848

CrossRef Full Text | Google Scholar

Luo, Y. H., Zhang, X. W., Yang, D. S., Sun, Q. Y., and Zhang, H. G. (2019). Optimal Operation and Cost-Benefit Allocation for Multi‐Participant Cooperation of Integrated Energy System. IET Gener. Transm. Distrib. 13 (22), 5239–5247. doi:10.1049/iet-gtd.2019.0894

CrossRef Full Text | Google Scholar

Lv, Z., Kong, W., Zhang, X., Jiang, D., Lv, H., and Lu, X. (2020). Intelligent Security Planning for Regional Distributed Energy Internet. IEEE Trans. Ind. Inf. 16 (5), 3540–3547. doi:10.1109/tii.2019.2914339

CrossRef Full Text | Google Scholar

Ma, D., Lan, G., Hassan, M., Hu, W., and Das, S. K. (2020). Sensing, Computing, and Communications for Energy Harvesting Iots: A Survey. IEEE Commun. Surv. Tutorials 22 (2), 1222–1250. doi:10.1109/comst.2019.2962526

CrossRef Full Text | Google Scholar

Manoharan, H., Teekaraman, Y., Kirpichnikova, I., Kuppusamy, R., Nikolovski, S., and Baghaee, H. R. (2020). Smart Grid Monitoring by Wireless Sensors Using Binary Logistic Regression. Energies 13 (15), 3974. doi:10.3390/en13153974

CrossRef Full Text | Google Scholar

Mao, Y., Wu, J., and Zhang, W. (2020). An Effective Operation Strategy for CCHP System Integrated with Photovoltaic/Thermal Panels and Thermal Energy Storage. Energies 13 (23), 1–21. doi:10.3390/en13236418

CrossRef Full Text | Google Scholar

Masood, E., and Ali, K. (2013). Sizing the Prime Mover of a Residential Micro-Combined Cooling Heating and Power (CCHP) System by Multi-Criteria Sizing Method for Different Climates. Energy 54, 291–301. doi:10.1016/j.energy.2013.01.061

CrossRef Full Text | Google Scholar

Mohammad, M. A., Awwad, E. M., El-Sherbeeny, A., Nasr, E. A., and Ali, Z. M. (2020). Optimal Scheduling of Reconfigurable Grids Considering Dynamic Line Rating Constraint. IET Gener. Transm. Distrib. 14 (10), 1862–1871. doi:10.1049/iet-gtd.2019.1570

CrossRef Full Text | Google Scholar

Mostafa, M. H., Aleem, S. H. E. A., Ali, S. G., Abdelaziz, A. Y., Ribeiro, P. F., and Ali, Z. M. (2020). Robust Energy Management and Economic Analysis of Microgrids Considering Different Battery Characteristics. IEEE Access 8, 54751–54775. doi:10.1109/access.2020.2981697

CrossRef Full Text | Google Scholar

Motiagh, N. H., Mohammdrezaei, M., Hunt, J., and Zakeri, B. (2020). Internet of Things (IoT) and the Energy Sector. Energies 13 (2), 494. doi:10.3390/en13020494

CrossRef Full Text | Google Scholar

Pasetti, M., Rinaldi, S., and Manerba, D. (2018). A Virtual Plant Architecture for the Demand-Side Management of Smart Prosumers. Appl. Sci. 8 (3), 1–14. doi:10.3390/app8030432

CrossRef Full Text | Google Scholar

Perera, A. T. D., Wang, Z., Nik, V. H., and Scartezzini, J. L. (2021). Towards Realization of an Energy Internet: Designing Distributed Energy Systems Using Game-Theoretic Approach. Appl. Energy 283, 929–937. doi:10.1016/j.apenergy.2020.116349

CrossRef Full Text | Google Scholar

Saraereh, O. A., Khan, I., and Lee, B. M. (2018). An Efficient Neighbor Discovery Scheme for Mobile wsn. IEEE Access 7, 4843–4855. doi:10.1109/ACCESS.2018.2886779

CrossRef Full Text | Google Scholar

Shahjehan, W., Bashir, S., Mohammed, S. L., Fakhri, A. B., Isaiah, A. A., Khan, I., et al. (2020). Efficient Modulation Scheme for Intermediate Relay-Aided Iot Networks. Appl. Sci. 10 (6), 2126. doi:10.3390/app10062126

CrossRef Full Text | Google Scholar

Wang, J., Zhong, H., Xia, Q., Kang, C., and Du, E. (2017). Optimal Joint‐Dispatch of Energy and Reserve for CCHP‐Based Microgrids. IET Gener. Transm. Distrib. 11 (3), 785–794. doi:10.1049/iet-gtd.2016.0656

CrossRef Full Text | Google Scholar

Wang, L., Wang, X., Jiang, C., Yin, S., and Yang, M. (2019). Dynamic Coordinated Active-Reactive Power Optimization for Active Distribution Network with Energy Storage Systems. Appl. Sci. 9 (6), 1129. doi:10.3390/app9061129

CrossRef Full Text | Google Scholar

Wang, Y., Nguyen, T. L., Syed, M. H., Xu, Y., Sansano, E. G., Nguyen, V-H., et al. (2020). A Distributed Control Scheme of Microgrids in Energy Internet Paradigm and its Multisite Implementation. IEEE Trans. Industr. Inf. 17 (2), 1141–1153. doi:10.1109/TII.2020.2976830

CrossRef Full Text | Google Scholar

Wang, Y., Wu, X., Li, Y., Yan, R., Tan, Y., Qiao, X., et al. (2020). Autonomous Energy Community Based on Energy Contract. IET Gener. Transm. Distrib. 14 (4), 682–689. doi:10.1049/iet-gtd.2019.1223

CrossRef Full Text | Google Scholar

Yang, L., Tianyu, L., and Shusen, H. (2021). Coordination and Optimization of CCHP Microgrid Group Game Based on the Interaction of Electric and Thermal Energy Considering Conditional Value at Risk. IEEE Access 9, 88664–88673. doi:10.1109/access.2021.3089591

CrossRef Full Text | Google Scholar

Yin, S., Xia, J., and Jiang, Y. (2020). Characteristics Analysis of the Heat-To-Power Ratio from the Supply and Demand Sides of Cities in Northern china. Energies 13 (1), 1–21. doi:10.3390/en13010242

CrossRef Full Text | Google Scholar

Zand, M., Nasab, M. A., Sanjeevikumar, P., Maroti, P. K., and Holm‐Nielsen, J. B. (2020). Energy Management Strategy for Solid‐state Transformer‐Based Solar Charging Station for Electric Vehicles in Smart Grids. IET Renew. Power Gener. 14 (18), 3843–3852. doi:10.1049/iet-rpg.2020.0399

CrossRef Full Text | Google Scholar

Zhang, F. X., Zhang, T., and Wang, R. (2017). Optimizing Hierarchical Power Distribution of Multiple Local Energy Network Systems in Grid-Connected Mode. Pol. J. Environ. Stud. 26 (5), 1981–2000. doi:10.15244/pjoes/69440

CrossRef Full Text | Google Scholar

Zhang, D., Du, T., Yin, H., Xia, S., and Zhang, H. (2019). Multi-Time-Scale Coordinated Operation of a Combined System with Wind-Solar-Thermal-Hydro Power and Battery Units. Appl. Sci. 9 (17), 3574. doi:10.3390/app9173574

CrossRef Full Text | Google Scholar

Zhang, L., Lizhi, Z., Sun, B., Zhang, C., and Li, F. (2020). Nested Optimization Design for Combined Cooling, Heating, and Power System Coupled with Solar and Biomass Energy. Int. J. Electr. Power Energy Syst. 123, 1–15. doi:10.1016/j.ijepes.2020.106236

CrossRef Full Text | Google Scholar

Zhang, Y., Song, X., Li, Y., Zeng, Z., Yong, C., Sidorov, D., et al. (2020). Two-Stage Active and Reactive Power Coordinated Optimal Dispatch for Active Distribution Network Considering Load Flexibility. Energies 13 (12), 5922. doi:10.3390/en13225922

CrossRef Full Text | Google Scholar

Zhao, Y., Peng, K., Xu, B., Li, H., Liu, Y., and Zhang, X. (2018). Bilevel Optimal Dispatch Strategy for a Multi-Energy System of Industrial Parks by Considering Integrated Demand Response. Energies 11 (8), 1942. doi:10.3390/en11081942

CrossRef Full Text | Google Scholar

Zhong, J., Hu, X., Zhang, J., and Gu, M. (2005). “Comparison of Performance between Different Selection Strategies on Simple Genetic Algorithms,” in IEEE International Conference on Computational Intelligence for Modelling, Control and Automation, Vienna, Austria, 28-30 November 2005, 1115–1121.

Google Scholar

Zhu, L., Zhou, X., Zhang, X.-P., Yan, Z., Guo, S., and Tang, L. (2018). Integrated Resources Planning in Microgrids Considering Interruptible Loads and Shiftable Loads. J. Mod. Power Syst. Clean. Energy 6, 802–815. doi:10.1007/s40565-017-0357-1

CrossRef Full Text | Google Scholar