Performance Assessment of Open-Loop and Closed-Loop Generation Rate Constraint Models for Optimal LFC of the Three-Area Reheat Thermal System

In this article, a novel investigation is performed to showcase the best suitable structure of the generation rate constraint (GRC) for the three-area reheat thermal power system (RTPS) to obtain load frequency control (LFC) optimally. For investigation purposes, two GRC models which are widely implemented in the literature without providing any discussion of their selection and suitability are confiscated in this article. The two GRC structures deliberated in the present article are termed as open-loop and closed-loop models. The performance of the three-area reheat thermal unit is examined with these two GRC structures for a perturbation of 10% step load (10% SLP) on area-1. An investigation is performed under the governance of a three-degree-of-freedom PID (3DOFPID) controller, fine-tuned using a water cycle algorithm (WCA) subjected to index integral square error (ISE) minimization. However, the efficacy of the proposed WCA-tuned 3DOFPID controller is revealed with other control approaches available in the literature upon implementation of a widely accepted model of a two-area hydrothermal system. Finally, the simulation results and sensitivity analysis showed the suitable GRC structure for a three-area reheat thermal unit to obtain LFC optimally with high performance.

Introduction

In modern power systems, LFC is an indispensable peculiar function when it comes to the regulation of the parameter frequency. However, to get the exact, precise divination of the issue LFC, it is necessary to consider the inherent requirements and main practical constraints like GRC with the power generation utilities. The physical constraint GRC compels the rate of change of opening the steam valve, which significantly influences the dynamical behavior of the power system. Thus, the GRC nonlinearity property affects the power system performance practically. In realistic nature, the rate at which the deviation in real power generated by the units in the thermal plant is cramped by the GRC maximum limits. Thus, LFC design for thermal units without considering the physical constraints like GRC may not be realistic (Kalyan and Rao, 2020a). The intention of considering thermal units with GRC is that the rapid rise in load demand brings out an excessive steam from the boiler and causes condensation because of adiabatic expansion. In general expectation, the steam condensation in thermal units is not more than 20% of the required temperature and pressure. Thus, it is only facilitated to alter power generation of about 1.2Pu of nominal power generation throughout the first few 10 s (Morsali et al., 2014). Once the generation unit reaches its maximum capacity, then the GRC restricts incremental variation in turbine power. Because of the significant impact of GRC on the performance of LFC, proper encompassment of realistic GRC constraints within the system will enhance the control mechanism. Otherwise, the power system will suffer from momentarily significant disturbances in a controller design.

The demand on the power system will never be constant and will fluctuate continuously. With these, the control signals will also deviate. The frequency deviations will be compensated by altering the actual power generation provided through ramping limits in GRC. Moreover, the effect of GRC under significant disturbances is even more noticeable, and the system tries to raise the generation to sustain the stability in a faster time horizon. However, the negative impact of GRC on the thermal units maybe even worse with the consideration of another nonlinearity such as the governor dead band (GDB). The plant may not attain a stable condition and falls into an unstable state, and then, the protective relay will operate to isolate the generation utilities. The literature survey presents that with the consideration of both GDB and GRC, the system responses will face more significant deviations in peak overshoots/undershoots and more considerable settling time for the situation of not conceiving GDB and GRC (Kalyan and Rao, 2021). Hence, the aforementioned limitations need to be considered to avoid the instability of an interconnected system. With the incorporation of GDB and GRC, the system becomes highly nonlinear, which degrades the secondary controller performance. Thus, intense care must be taken while designing regulators, especially for the thermal units with GDB and GRC.

Over the past few years, researchers have considered mainly two structures of GRC for the frequency analysis, termed as openvloop and closed loop. In Lal et al. (2016), a dual area hydrothermal (DAHT) system is considered with an open-loop GRC structure, but the effect of GDB is not incorporated. Nanda et al. (2015) regarded a dual area thermal-hydro-gas (THG) system for the investigation and employed the open-loop GRC for the thermal unit, but the ramp rate limits are not considered. Researchers in Rahman et al. (2017) evaluated GDB and GRC of open-loop for the two-area thermal system. Later, renewable sources like solar thermal and wind turbines are taken in both areas. Raju et al. (2016) and Çelik (2020) considered a three-area reheat thermal system with the GRC structure of an open loop, but the impact of GDB on the system performance is not taken into account. The impact of GDB and GRC in a three-area thermal system is investigated by the researchers in Padhy and Panda (2017), but the analysis is restricted to the deployment of an open-loop GRC structure without briefing its selection. Furthermore, the LFC of the reheat thermal system is extended to five areas by the researchers in Shiva and Mukherjee (2016) by considering the open-loop structure of GRC and not considering the effect of GDB. In Rajesh et al. (2019), the five-area THG system is investigated by considering a thermal unit with an open-loop GRC.

Pan and Das (2015) investigated the dual area thermal system with a closed-loop GRC model, and the effect of GDB is also taken into analysis. Morsali et al. (2017) and Ahmed et al. (2022) performed the LFC of the dual area THG system and employed the closed-loop GRC for the thermal units in both the areas and considered the GDB effect on system performance. After that, the authors in Sahu et al. (2016a) considered a closed-loop GRC structure for the three areas of RTPS, and the coordination of GDB with GRC was not analyzed. Kalyan and Suresh (2021a) considered GDB and GRC of a closed-loop for the LFC analysis of the DAHT system and, the coordination of GDB and GRC impact on the performance of the system is not demonstrated.

After a careful literature survey, it is concluded that the researchers had widely utilized the GRC open loop and closed loop with and without considering the effect of GDB on the multi-area thermal units. But the proper reason for selecting the GRC structure for thermal units has not been demonstrated so far to the best. This motivates the authors in this work to analyze the performances of these two GRC structures in the LFC of the multi-area thermal units by considering the coordination of GRC and GDB. A similar kind of investigation is performed in Morsali et al. (2014), but the analysis is strictly restricted to the dual-area systems and that too under the governing of particle swarm optimization (PSO)-based traditional PID controller.

Furthermore, the literature survey discloses the wide implementation of traditional PI/PID and fractional order (FO) controllers for LFC study with different soft computing algorithms such as the seagull optimization algorithm (SOA) (Harideep et al., 2021), artificial field algorithm (AEFA) (Kalyan and Rao, 2020b), flower pollination algorithm (FPA) (Madasu et al., 2018), moth flame algorithm (MFA) (Lal and Barisal, 2019), ant–lion optimizer (ALO) (Pradhan et al., 2020), differential evolution (DE) (Kalyan and Suresh, 2021b), chemical reaction optimizer (CRO), mine blast optimizer (MBO), gravitational search algorithm (GSA) (Sahu et al., 2015), Harris Hawks optimizer (HHO) (Yousri et al., 2020), grasshopper optimizer (GHO) (Nosratabadi et al., 2019), volley ball algorithm (VBA) (Prakash et al., 2019), sine-cosine algorithm (SCA) (Tasnin and Saikia, 2018), water cycle algorithm (WCA) (Goud et al., 2021), teaching–learning-based (TLBO) optimizer (Sahu et al., 2016b), multi-verse optimizer (MVO) (Kumar and Hote, 2018), symbiotic asymptotic search (SAS) (Nayak et al., 2018) algorithm, slap swarm optimizer (SSO) (Sariki and Shankar, 2021), gray wolf optimizer (GWO) (Kalyan, 2021a), and hybrid (H) algorithms like DE-AEFA (Kalyan and Rao, 2020c), HAEFA (Sai Kalyan et al., 2020), whale optimization (WOA) algorithm (Elsisi, 2020), lightening search algorithm (LSA) (Elsisi and Abdelfattah, 2020), and arithmetic optimization algorithm (AOA) (Elsisi et al., 2021). are extensively reported. Furthermore, the aforementioned soft computing-based regulators are not only applied to thermal-based energy systems but also extended to the energy systems with renewable generation sources the researchers.

However, the FO and conventional controllers are not robust enough for the power system models perceived with practical constraints of GRC and GDB. In contrast to the abovementioned intelligent fuzzy systems, the controllers are widely applied to the LFC of power systems with GRC and GDB. However, membership function selections and framing of the rule-based system involve more approximations which may degrade the power system performance. Thus, researchers are more likely to tend toward higher-order DOF controllers in the LFC studies with the benefit of individual control loops. But the implementation of 3DOFPID for the LFC study is not seen much, and WCA tuned 3DOFPID is a maiden attempt.

Considering the limitations in the aforementioned literature, the contributions in this work are as follows:

(a) The three-area reheat thermal system is designed and developed in the MATLAB/SIMULINK (R2016a) platform.

(b) LFC analysis is performed by injecting 10% SLP disturbance in area-1.

(c) The performances of GRC open-loop and closed-loop models in LFC are investigated and demonstrated.

(d) The WCA-based 3DOFPID controller is implemented as a regulator in all the three areas.

(e) Efficacy of 3DOFPID tuned with WCA is showcased with other recently presented regulators such as HAEFA/TLBO-tuned PID and WCA tuned 2DOFPID by implementing on the DAHT system.

(f) Sensitivity analysis is conducted to showcase the robustness of the presented control scheme.

Power System Modeling

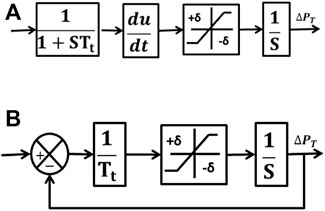
The power system model that has been initially deliberated in this work is the DAHT system with the unique generation capacities. DAHT depicted in Figure 1 has been widely implemented by the researchers in recent years to analyze the behavior of the system with the proposed control schemes. The necessary data to design the DAHT system in MATLAB/SIMULINK are perceived from Goud et al. (2021). On the other side, the second power system model is a three-area RTPS having generation capacities in the ratio of 1:2:4 for area-1: area-2: area-3, respectively, conceived for investigation purposes. The model of the three-area system is displayed in Figure 2, the conceived GRC structures are depicted in Figure 3 (Morsali et al., 2014), and the various subsystems in the reheat thermal unit are modeled as follows:

FIGURE 1

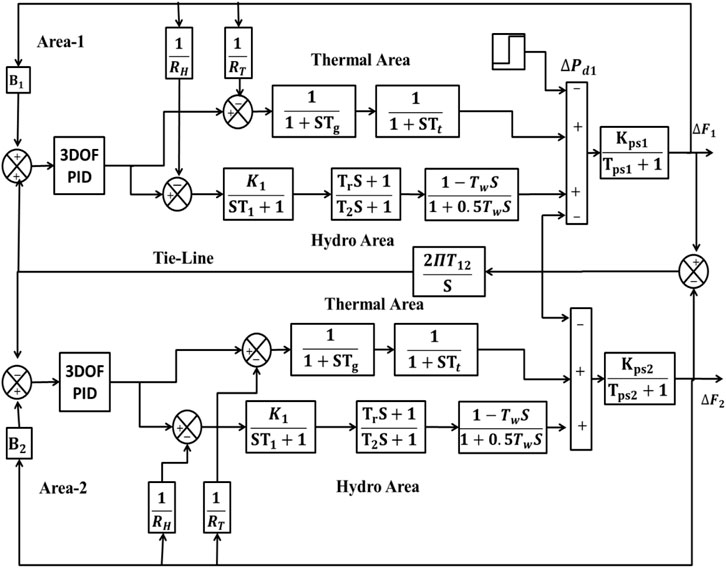
FIGURE 1. Model of the DAHT power system (Goud et al., 2021).

FIGURE 2

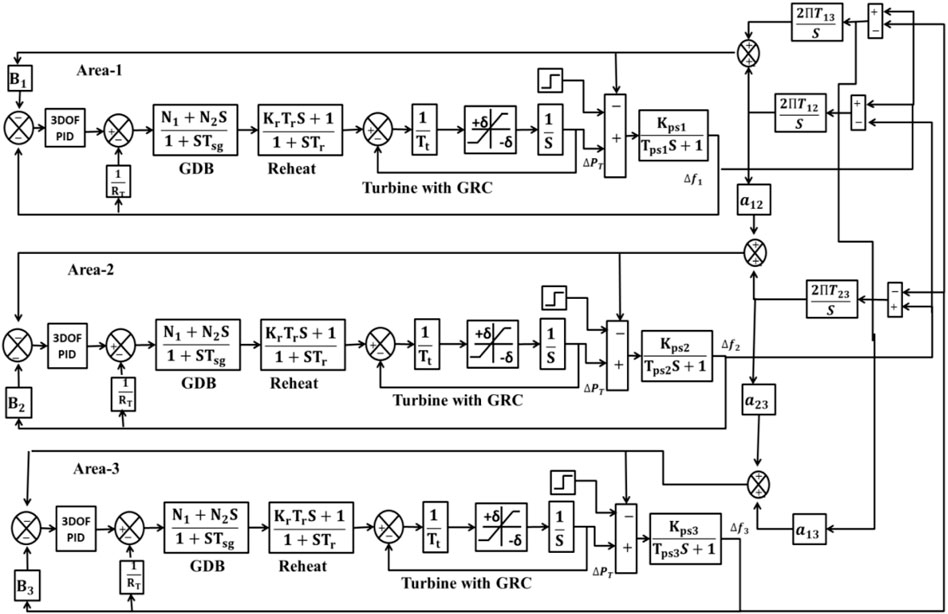
FIGURE 2. Model of the three-area RTPS system (Morsali et al., 2014).

FIGURE 3

FIGURE 3. GRC structure. (A) Open-loop and (B) closed-loop.

The governor dead band is expressed as follows:

$\frac{{\text{N}}_1+{\text{N}}_2\text{S}}{1+{\text{ST}}_{\text{sg}}}.(1)$

The reheat turbine can be expressed as follows:

$\frac{{\mathrm{K}}_{\mathrm{r}}{\mathrm{T}}_{\mathrm{r}}\mathrm{S}+1}{1+\mathrm{S}{\mathrm{T}}_{\mathrm{r}}}.(2)$

The power plant can be expressed as follows:

$\frac{{\mathrm{K}}_{\mathrm{p}\mathrm{s}}}{{\mathrm{T}}_{\mathrm{p}\mathrm{s}}\mathrm{S}+1}.(3)$

The GRC value for both the closed- and open-loop structures is considered as 10%/min and is modeled as

$\left|\mathrm{\Delta }{P}_T\right|=0.1\left(pu/\min \right)=0.0017\left(pu/\sec \right).(4)$

Thus, for the thermal units, the value of GRC for the closed-loop and open-loop structures can be taken into account by limiters as ±0.0017 in the reheat turbine. In general, the definition of GDB is related to a change in the speed magnitude within which there may not be any alteration in the turbine valve position. After reviewing the literature, in this article, Fourier coefficients of N1 and N2 are modeled in GDB.

The incremental change in power flow between the ith and jth areas is modeled as

${\text{ΔP}}_{\text{ij}}\left(\text{s}\right)=\frac{{2\text{π T}}_{\text{ij}}}{\text{s}}\left(\text{Δ}{\text{f}}_{\text{i}}\left(\text{s}\right)-{\text{Δf}}_{\text{j}}\left(\text{s}\right)\right).(5)$

During the operation of the thermal plant with incremental change in the load demand, deviation in the ith area frequency is modeled as

${\text{Δf}}_{\text{i}}\left(\text{s}\right)=\frac{{\text{K}}_{\text{ps}}}{1+{\text{sT}}_{\text{ps}}}\left[{\text{ΔP}}_{\text{T}}\left(\text{s}\right)-{\text{ΔP}}_{\text{d}}\left(\text{s}\right)-{\text{ΔP}}_{\text{ij}}\left(\text{s}\right)\right].(6)$

These deviations in area frequency will be fully damped out using a secondary regulator by changing the alternator set point valve operation by taking the area control error (ACE) as the input. The ACE signal to the regulator in the ith area will be modeled as

${\text{ACE}}_{\text{i}}={\text{B}}_{\text{i}}{\text{Δf}}_{\text{i}}+{\text{ΔP}}_{\text{ij}}.(7)$

3DOF-PID Controller

DOF controllers are technically elucidated as the number of closed loops that can be independently adjusted. Thus, the 3DOF-PID controller consists of three closed-loop independent transfer functions that are responsible for closed-loop stability, closed-loop response shaping, and rejection of disturbance. The three inputs to the individual control loops are R(s), which indicates the reference input signal, Y(s), which indicates the feedback taken from the output of the test system, and D(s), which represents a disturbance in the load. For the 3DOF-PID controller, the closed-loop expression is indicated in Eq. 8 and is shown in Figure 4 (Rahman et al., 2016).

$\text{Y}\left(\text{s}\right)=\left[\frac{\text{C}\left(\text{s}\right)\text{P}\left(\text{s}\right)}{1+\text{C}\left(\text{s}\right)\text{P}\left(\text{s}\right)}{\text{R}}_{\text{c}}\left(\text{s}\right)\right]\text{R}\left(\text{s}\right)+\left[\frac{\text{P}\left(\text{s}\right)-\text{C}\left(\text{s}\right)\text{P}\left(\text{s}\right){\text{FF}}_{\text{c}}\left(\text{s}\right)}{1+\text{C}\left(\text{s}\right)\text{P}\left(\text{s}\right)}\right]\text{D}\left(\text{s}\right).(8)$

FIGURE 4

FIGURE 4. 3DOF-PID controller closed loop expression (Elsisi, 2020).

The structure of 3DOF-PID employed as the frequency regulator in this work is depicted in Figure 5 (Rahman et al., 2016). Out of this, the closed-loop stability is attained with component C(s), and the quality of the output response in both the static and dynamic nature is maintained by the components C(s) and R_C(s). The disturbance D(s) in the interconnected system is eliminated by the component feed-forward controller FFC(s) if Eq. 9 is satisfied.

$\text{P}\left(\text{s}\right)-\text{C}\left(\text{s}\right)\text{P}\left(\text{s}\right){\text{FF}}_{\text{C}}\left(\text{s}\right)=\text{0}\text{.}(9)$

FIGURE 5

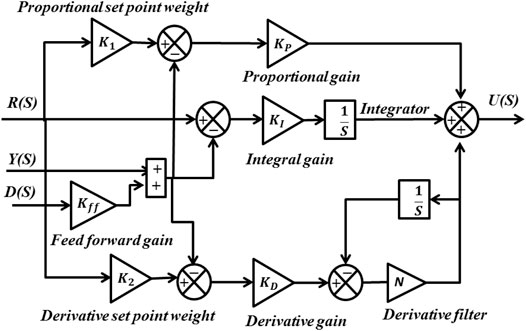
FIGURE 5. Structure of the 3DOF-PID controller (Elsisi, 2020).

The proportional-integral-derivative parameter is indicated with K_P, K_I, and K_D, and N represents the filter coefficient. K₁ and K₂ are the proportional and derivative weight signals for the component R_C(s).

However, the gains of 3DOF-PID are to be rendered optimally with a heuristic optimization algorithm subjected to the minimization of the time-domain index. Owing to the benefits of maintaining the equilibrium between dampening the peak undershoot/overshoot deviations and bringing the responses to stable conditions in quick time, the ISE objective function (Naga Sai Kalyan and Sambasiva Rao, 2020) is employed in this article, as mentioned in Eq. 10.

${\text{J}}_{\text{ISE}}={\displaystyle \underset{\text{0}}{\overset{{\text{T}}_{\text{sim}}}{\int }}\left(\text{Δ}{\text{f}}_1^2+{\text{Δf}}_2^2+{\text{Δf}}_3^2+{\text{ΔP}}_{\text{tie}12}^2+{\text{ΔP}}_{\text{tie}13}^2+{\text{ΔP}}_{\text{tie}23}^2\right)}\text{dt}\text{.}(10)$

WCA Algorithm

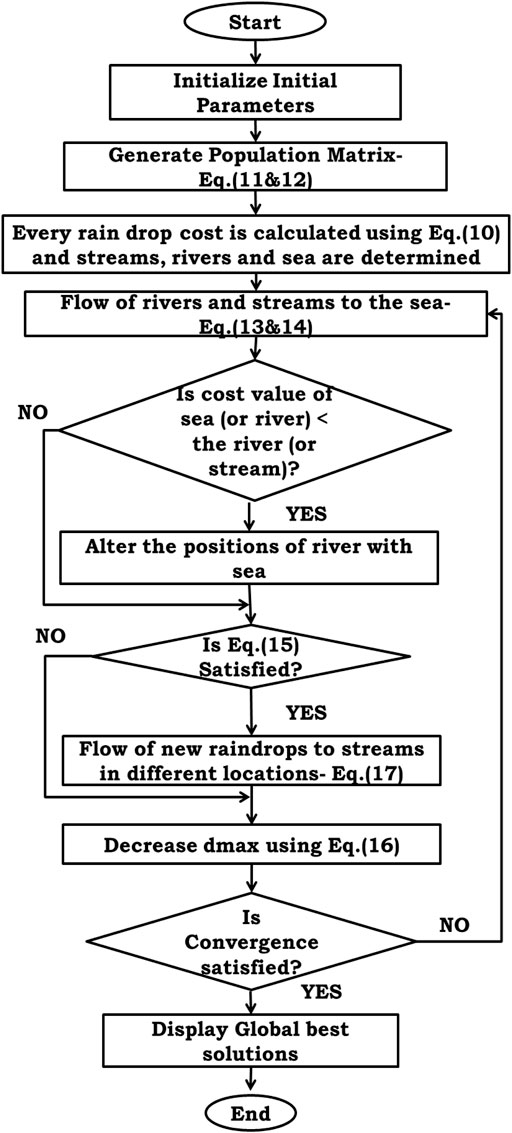
In the LFC study, the selection of an optimization search algorithm is equally important to the design of a secondary controller. In this work, 3DOF-PID is taken as a secondary controller in every area. However, the optimal operation of the controller strongly depends on the optimization algorithm that has been considered. For this, a new and efficient searching methodology was proposed by Eskandar et al. (2012), named as the water cycle algorithm (WCA), which mimics the continuous water movement. Until now, the WCA mechanism is chosen by researchers all over the world as a solution to complex nonconstrained and constrained optimization problems. But implementation of the WCA approach for the optimization of modern interconnected power systems is not seen much. This motivates the authors to adopt the WCA algorithm in this article.

Moreover, WCA can locate an optimal solution for both maximization and minimization of an objective function with a high convergence rate and accuracy. In this article, WCA is utilized to optimize 3DOF-PID controller gains subjected to ISE minimization provided in Eq. 10 so that the oscillations in system responses will be damped out completely in a short time. The strategy of WCA starts with a minute particle in the water cycle which is a raindrop or snowdrop. The raindrops or snow droplets on the mountains flow down to form streams or rivers. The rivers or streams continue their flow until they adjoin the sea at last. In search space, initially, the populations are the raindrops created randomly to solve the problem, and the sea is selected as the best, which is treated as the global best solution.

Evaporation and raining loop are added to impart the equilibrium of exploration and exploitation phenomena to the WCA mechanism. During evaporation, water evaporates and accumulates at the top of the atmosphere and forms a cloud, when it condenses and again returns to earth in the form of rain (Kalyan, 2021b; Kalyan, 2021c).

Initialization

The raindrops (RD) initialized for Nvar variables in this work are as follows:

${\text{RD}}_{\text{i}}={\text{Y}}_{\text{i}}=\left[{\text{y}}_1{\text{,y}}_2\mathrm{.........}{\text{y}}_{\text{Nvar}}\right],(11)$

$\text{RD}\text{Population}=\left[\begin{array}{c}{\text{RD}}_1\\ \begin{array}{c}\begin{array}{ccc}-& -& -\end{array}\\ {\text{RD}}_{\text{i}}\end{array}\\ \begin{array}{ccc}-& -& -\end{array}\\ {\text{RD}}_{{\text{N}}_{\text{POP}}}\end{array}\right].(12)$

The matrix “RD Population” indicates a randomly generated population, and NPOP represents the number of populations. Thereafter, the cost of every raindrop will be evaluated using Eq. 10.

Stream Flows Into the River (or) River Flow Into the Sea

Initially, the positions of rivers and streams are initialized subjected to the assumption that these will flow into the sea finally.

${\text{P}}_{\text{stream}}^{\text{new}}={\text{P}}_{\text{stream}}+\text{rand}\mathrm{()}\text{∗}\text{C}\text{∗}\left({\text{P}}_{\text{river}}-{\text{P}}_{\text{stream}}\right),(13)$

${\text{P}}_{\text{river}}^{\text{new}}={\text{P}}_{\text{river}}+\text{rand}\mathrm{()}\ast \text{C}\ast \left({\text{P}}_{\text{sea}}-{\text{P}}_{\text{river}}\right),(14)$

where “C” is a constant taken from Morsali et al., (2014) and Kalyan and Rao, (2020a) and rand () generated between [0–1]. Suppose, if the stream generates a solution much more compromising than its connecting river, then in this situation, the locations of the river and stream get interchanged. The aforementioned methodology will be implemented in the rivers and seas.

Evaporation and Raining

To overcome the solution getting into the trap of local minima and to impart the nature of exploration and exploitation into the searching strategy, the evaporation and raining loop was incorporated.

The process of evaporation terminates if it satisfies the following condition.

$\left|{\text{P}}_{\text{sea}}-{\text{P}}_{\text{river}}\right|<{\text{d}}_{\text{max}}.(15)$

The d_max value will be decreased automatically using Eq. 16, and usually, it is nearer to zero.

${\text{d}}_{\text{max}}^{\text{new}}={\text{d}}_{\text{max}}-\left({\text{d}}_{\text{max/}}/\text{max}\text{.iteration}\right).(16)$

The raining process will begin immediately at the end of evaporation. During rain, the new raindrops will create different new streams, which will be located as

${\text{P}}_{\text{stream}}^{\text{new}}={\text{P}}_{\text{sea}}+\sqrt{\text{U}}\text{X}\text{rand}\left(1\text{,}{\text{N}}_{\text{var}}\right).(17)$

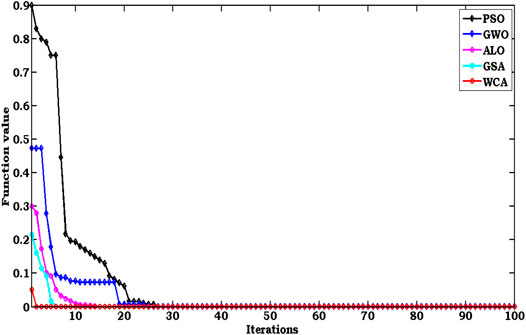
The parameter ‘U’ indicates the rate of exploration nearer to the sea. The WCA exhibits the global solution right after the completion of the maximum iteration or reaching the stopping criteria. The parameters utilized in algorithm WCA are displayed in Table 1, and the flowchart is depicted in Figure 6 (Goud et al., 2021). Moreover, the WCA is applied to the Booth function given in Eq. 18 before being discharged to the study of LFC. Along with the WCA approach, different optimizations like PSO/GWO/ALO/GSA are also implemented to optimize the Booth function one at a time for a maximum of 100 iterations with 50 populations. The characteristics of various algorithms in the criteria of convergence in an appliance to Booth function are compared in Figure 7. It is noticed from Figure 7 that compared to other optimizations, the WCA converges quickly in less iteration. Furthermore, the functional value with the mechanism WCA initializes with a very low value compared to the other soft computing approaches of ALO/GWO/PSO. This shows the inherent feature of WCA in balancing the phases of exploration and exploitation. Moreover, the benefit of the optimization process that the algorithm initiates with a low function value is that there will be less chance to get the solution diversified. Hence, considering all the aspects of the WCA mechanism urges to accomplish in the study of LFC.

$\text{f}\left(\text{x,y}\right)={\left(\text{x}+2\text{y}-7\right)}^2+{\left(2\text{x}+\text{y}-5\right)}^2.(18)$

TABLE 1

TABLE 1. WCA parameters.

FIGURE 6

FIGURE 6. WCA flowchart.

FIGURE 7

FIGURE 7. Convergence of different optimizations tested on Booth function.

Results and Discussion

Case-1: Analysis of the DAHT System With Different Control Strategies

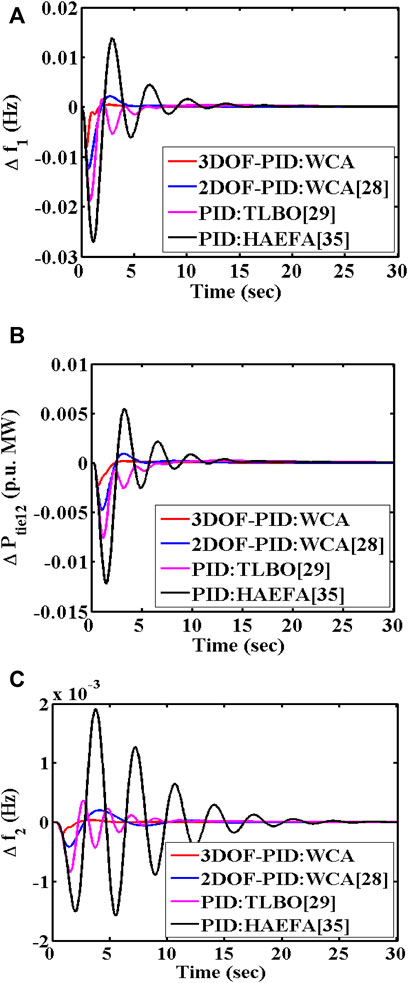
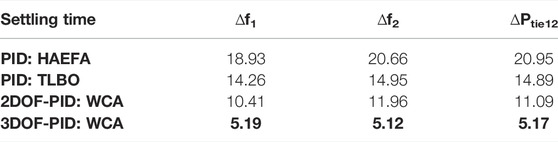
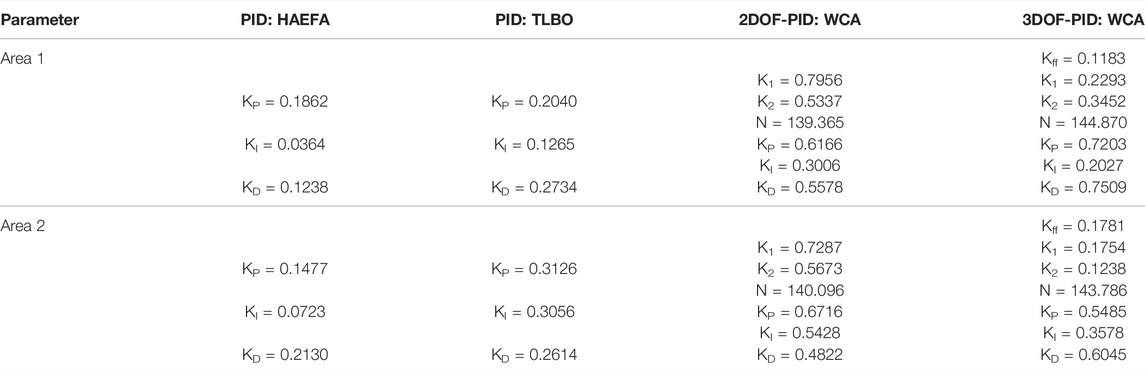
The operational efficacy of the 3DOF-PID fine-tuned WCA approach is visualized upon implementing this regulator on an extensively utilized test system DAHT model with 10% SLP on area 1. Different control mechanisms like PID tuned with HAEFA (Sai Kalyan et al., 2020), TLBO (Sahu et al., 2016b), 2DOF-PID fine-tuned with WCA (Goud et al., 2021), and 3DOF-PID tuned with WCA are chosen as regulators in every area of the DAHT system one by one. The system responses with different soft computing-based secondary regulators under the same load disturbances are compared in Figure 8, to reveal the best one. Dynamic behaviors of DAHT are transliterated in settling time and noted in Table 2, and the respective optimum gains are provided in Table 3. From Figure 8 and Table 2, it is concluded that the presented 3DOF-PID tuned with the WCA algorithm outperforms the recently proposed control strategies of HAEFA and TLBO-based PID and WCA-tuned 2DOF-PID. Compared to other control approaches, the proposed regulator is effective in dampening the oscillations by altering the generator’s set-point valve according to the load fluctuations and is more sovereign in bringing the deviations to a steady position in a short time.

FIGURE 8

FIGURE 8. Case 1 responses. (A) ∆f₁, (B) ∆P_tie12, and (C) ∆f₂.

TABLE 2

TABLE 2. Response settling time (in s) with various controllers for the DAHT system.

TABLE 3

TABLE 3. Controller optimal gains employed for the DAHT system.

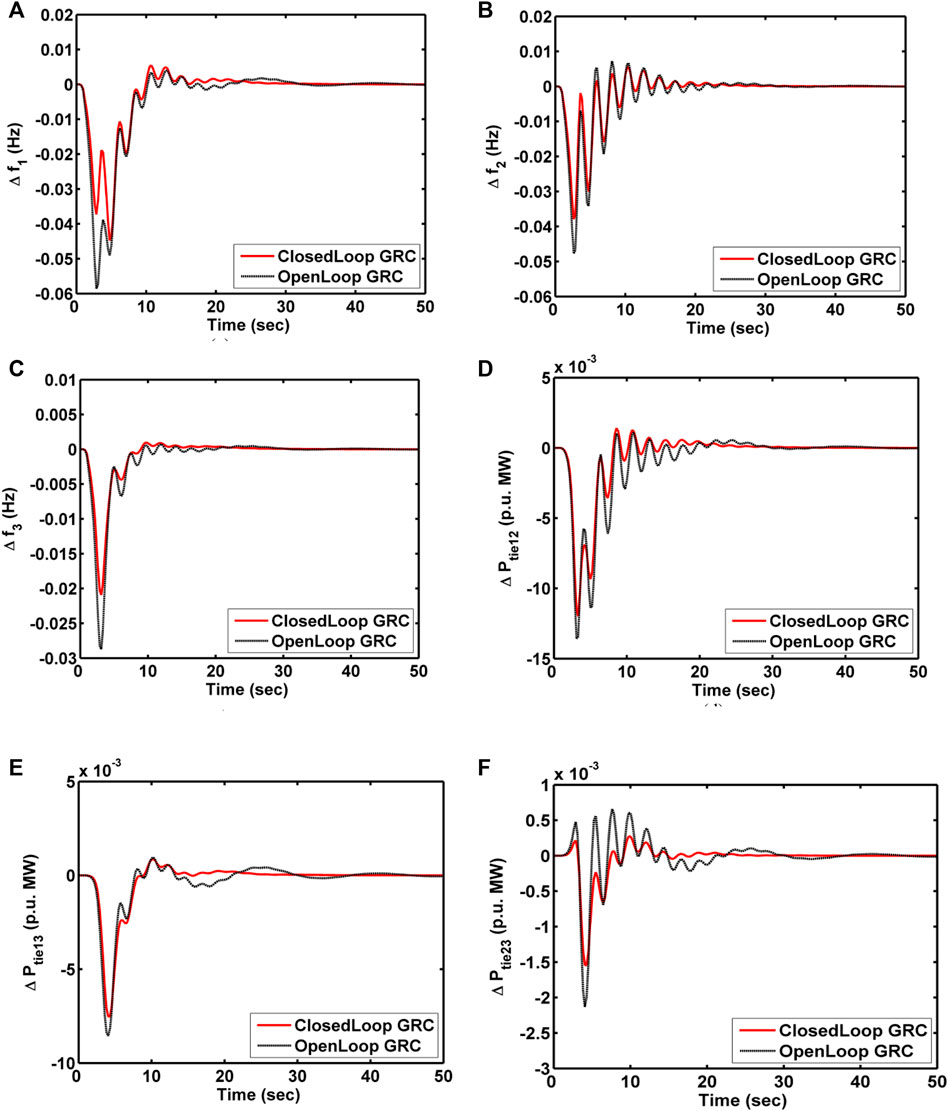
Case-2: Analysis of Three-Area RTPS With Open- and Closed-Loop GRC Structures

In this subsection, the considered three-area RTPS model of the test system is analyzed in a time-domain simulation platform upon laying a disturbance of 10% SLP on area-1. The test system model is investigated with the open- and closed-loop structures of GRC individually, under the governance of the 3DOFPID regulator, which is rendered optimally with the WCA mechanism. Dynamical responses of three-area RTPS with GRC structures of the open- and closed-loop are compared in Figure 9, to reveal the best. System responses that are retrieved under perturbed conditions are area frequency and power deviations in the transmission line. Numerically, these responses are analyzed in settling time and provided in Table 4. The gains of the 3DOF-PID regulator that are founded optimally using the WCA approach employed with the system having different GRC structures are placed in Table 5. Noticing the responses compared in Figure 9, we came to infer that the system responses are greatly diversified with the employing of the open-loop GRC model and hardly reaches stable condition. On the other hand, responses of the thermal systems with a closed-loop GRC model are less deviated in connection with peak undershoot/overshoot, and also, within less time, the responses attained a steady-state position. Moreover, the ISE index value is also improvised with a closed-loop GRC structure by 53.28% with an open-loop GRC structure. Furthermore, the time taken to find the optimal parameters of the 3DOFPID regulator using the WCA approach is more with an open loop compared to that of employing a closed loop. Thus, it is concluded that for the LFC studies the thermal units with the open-loop GRC structure are struggling a lot to regain stability during load disturbances even under the regulation of secondary controllers. Hence, this work strongly suggests employing the GRC structure of closed loop, especially for the thermal generating units in LFC studies.

FIGURE 9

FIGURE 9. Case 2 responses. (A) ∆f₁, (B) ∆f₂, (C) ∆f₃, (D) ∆P_tie12, (E) ∆P_tie13, and (F) ∆P_tie23.

TABLE 4

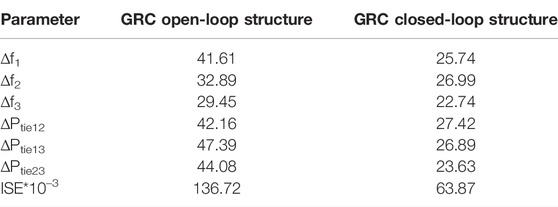
TABLE 4. Response settling time (in s) with the WCA-tuned 3DOF-PID controller for the three-area RTPS model.

TABLE 5

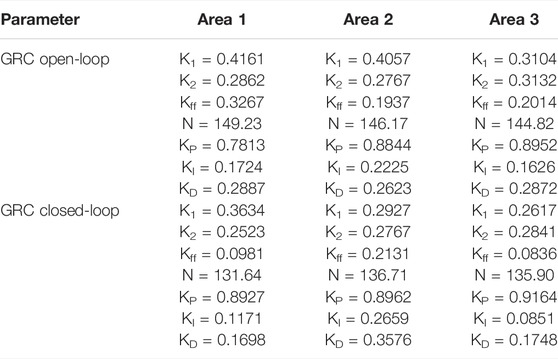
TABLE 5. Optimal gains of the 3DOF-PID controller found using the WCA algorithm for the three-area thermal system.

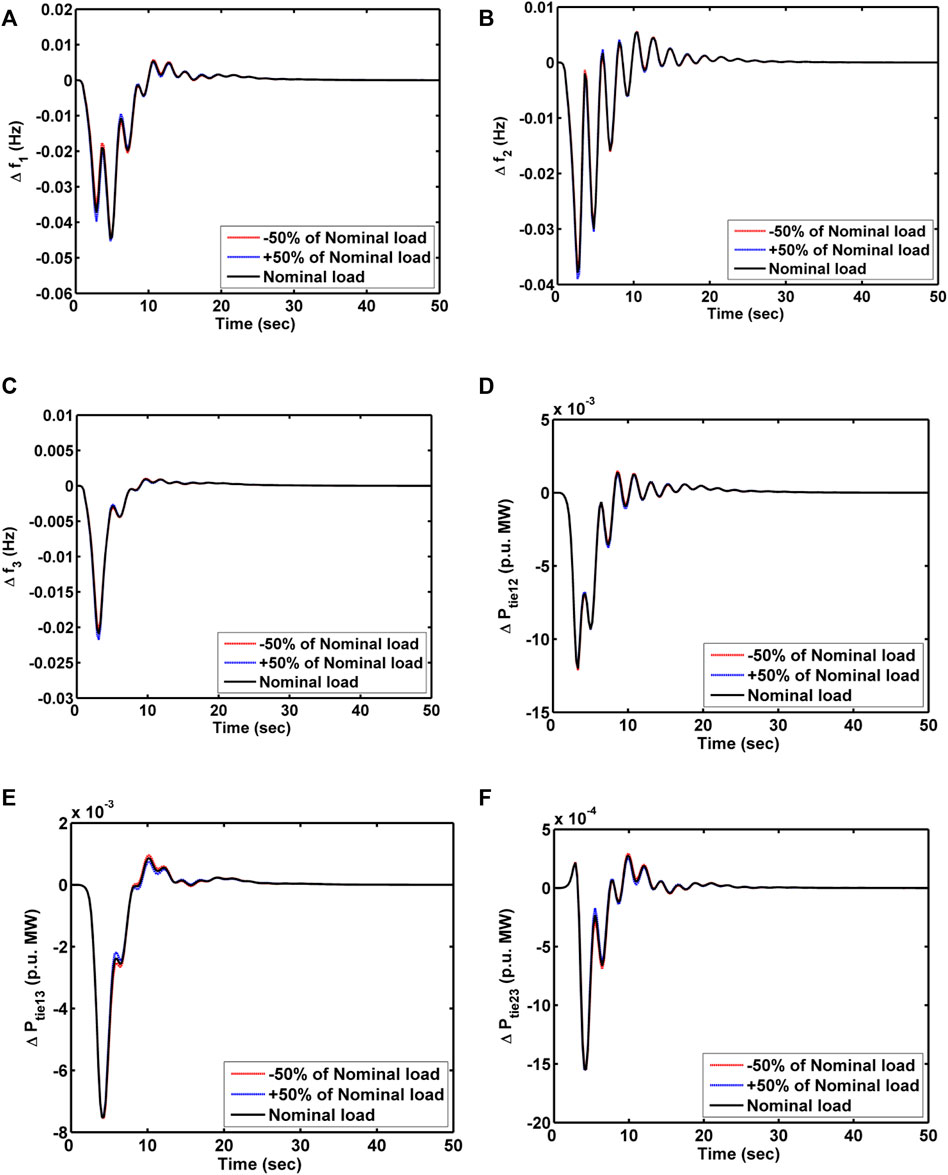
Case-3: Sensitivity Test Against Wide Load Variations and Uncertainties in System Parameters

Closed-loop GRC structure performance efficacy for the thermal units in fully dampening the oscillations to zero in a short time is revealed in the aforementioned case. Therefore, a sensitivity analysis is needed to be conducted to demonstrate the robustness of the closed-loop GRC structure in coordination with the proposed WCA-based 3DOF-PID regulator. The system loading has been varied to the wide range of ±50% from nominal load, and the parameters of the thermal system like the time constant of the steam turbine (T_t) and tie-line are varied by ±50% from the normal parameter. The sensitivity analysis subjected to wide variations of loading is presented in Figure 10, and it has also numerically analyzed about settling time provided in Table 4. Perceiving from Figure 10, the responses are not disturbed much, even though the system is targeted with a wide variation of load from the nominal load. Moreover, almost all the responses attained stable conditions at the same time, regardless of load variations. The settling time of the system responses against uncertainty in parameters is noted in Table 4. From the sensitivity analysis, it is concluded that three-area RTPS possessing the closed-loop GRC structure in coordination with the WCA-based 3DOFPID regulator does not encounter any difficulty in regaining the steady-state condition despite parametric uncertainties. Thus, the obtained optimal parameters of the 3DOF-PID controller using WCA optimization are robust and not necessary to alter the 3DOF-PID parameters, even under situations of uncertainty.

FIGURE 10

FIGURE 10. Case 3 responses. (A) ∆f₁, (B) ∆f₂, (C) ∆f₃, (D) ∆P_tie12, (E) ∆P_tie13, and (F) ∆P_tie23.

Conclusion

The performance of three-area RTPS considering the realistic constraints of GDB and GRC is examined with the open-loop GRC structure and the closed-loop GRC structure independently. The analysis is performed under the governance of the WCA-based 3DOFPID controller for a 10%SLP disturbance on area 1. Moreover, the efficacy of the proposed regulatory mechanism is deliberated with different soft computing-based control structures that are available in the recently reported literature on the widely utilized model of DAHT. Dynamical responses of the three-area thermal system in the time-domain reveal the efficacy of the GRC closed-loop structure in dampening the frequency deviations and transmission line power flow. Furthermore, the investigation is stretched to the implementation of a sensitivity test to examine the rigidness of the proposed control scheme. The sensitivity test is administered for considering system loading and parameters with uncertainties. The simulation results reveal the efficacy and robustness of the WCA-based 3DOFPID regulator in performing satisfactorily even under the conditions of parametric and loading uncertainties with a closed-loop GRC structure. Fabrication of intelligent fuzzy aided regulator for the optimal LFC of the multi-area RTPS may be undertaken in future. Moreover, a similar study would be extended to the multi-area RTPS with the integration of renewable energy sources. Thus, this article recommended adopting the GRC structure of closed loop for the RTPS models in LFC studies.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

CK, BG, and CR contributed to the conception and design of the study. MK organized the database. MB performed the statistical analysis. ME-N and SK wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, M., Magdy, G., Khamies, M., and Kamel, S. (2022). Modified TID Controller for Load Frequency Control of a Two-Area Interconnected Diverse-Unit Power System. Int. J. Electr. Power & Energy Syst. 135, 107528. doi:10.1016/j.ijepes.2021.107528

CrossRef Full Text | Google Scholar

Çelik, E. (2020). Improved Stochastic Fractal Search Algorithm and Modified Cost Function for Automatic Generation Control of Interconnected Electric Power Systems. Eng. Appl. Artif. Intell. 88, 103407. doi:10.1016/j.engappai.2019.103407

CrossRef Full Text | Google Scholar

Elsisi, M., and Abdelfattah, H. (2020). New Design of Variable Structure Control Based on Lightening Search Algorithm for Nuclear Reactor Power System Considering Load-Following Operation. Nucl. Eng. Technol. 52 (3), 544–551. doi:10.1016/j.net.2019.08.003

CrossRef Full Text | Google Scholar

Elsisi, M., Tran, M.-Q., Hasanien, H. M., Turky, R. A., Albalawi, F., and Ghoneim, S. S. M. (2021). Robust Model Predictive Control Paradigm for Automatic Voltage Regulators against Uncertainty Based on Optimization Algorithms. Mathematics 9 (22), 2885. doi:10.3390/math9222885

CrossRef Full Text | Google Scholar

Elsisi, M. (2020). New Design of Robust PID Controller Based on Meta-Heuristic Algorithms for Wind Energy Conversion System. Wind Energy 23 (2), 391–403. doi:10.1002/we.2439

CrossRef Full Text | Google Scholar

Eskandar, H., Sadollah, A., Bahreininejad, A., and Hamdi, M. (2012). Water Cycle Algorithm - A Novel Metaheuristic Optimization Method for Solving Constrained Engineering Optimization Problems. Comput. Struct. 110-111, 151–166. doi:10.1016/j.compstruc.2012.07.010

CrossRef Full Text | Google Scholar

Goud, B. S., Kalyan, C. N. S., Keerthi, N., Reddy, C. R., Bajaj, M., and Reddy, B. N. (2021). “AGC of Multi Area Multi Fuel System with Water Cycle Algorithm Based 3DOF-PID Controller and Integration of PEVs,” in 2021 International Conference on Data Analytics for Business and Industry (ICDABI). 464–469. doi:10.1109/ICDABI53623.2021.9655899

CrossRef Full Text | Google Scholar

Harideep, P., Pavan Sai Reddy, V., Ganesh, G., Bhanu Prakash, O., Naga Sai Kalyan, C., and Suresh, C. V. (2021). Seagull Optimization Tuned Traditional PID Controller with Set Point Filter for LFC of Hydro Thermal System Based on Performance Indices, 2021 4th International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), October2021, 85–89. Noida, India. doi:10.1109/RDCAPE52977.2021.9633523

CrossRef Full Text | Google Scholar

Kalyan, C. N. S., and Rao, G. S. (2020). Impact of Communication Time Delays on Combined LFC and AVR of a Multi-Area Hybrid System with IPFC-RFBs Coordinated Control Strategy. Prot. Control Mod. Power Syst. 6. 1. doi:10.1186/s41601-021-00185-z

CrossRef Full Text | Google Scholar

Kalyan, C. N. S., and Rao, G. S. (2020). Performance Comparison of Various Energy Storage Devices in Combined LFC and AVR of Multi Area System with Renewable Energy Integration. Int. J. Renew. Energy Res. 10, 933–944.

Google Scholar

Kalyan, C. N. S., and Rao, G. S. (2020). Combined Frequency and Voltage Stabilization of Multi-Area Multisource System by DE-AEFA Optimized PID Controller with Coordinated Performance of IPFC and RFBs. Int. J. Ambient Energy. 1. 1. doi:10.1080/01430750.2020.1860130

CrossRef Full Text | Google Scholar

Kalyan, C. N. S., and Rao, G. S. (2021). Coordinated Control Strategy for Simultaneous Frequency and Voltage Stabilization of the Multi-Area Interconnected System Considering Communication Time Delays. Int. J. Ambient Energy. 1. 1. doi:10.1080/01430750.2021.1967192

CrossRef Full Text | Google Scholar

Kalyan, C. N. S., and Suresh, C. V. (2021a). PIDD Controller for AGC of Nonlinear System with PEV Integration and AC-DC Links, January 2021 Proceedings of the International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 1–6. doi:10.1109/SeFet48154.2021.9375756

CrossRef Full Text | Google Scholar

Kalyan, C. N. S., and Suresh, C. V. (2021b). Differential Evolution Based Intelligent Control Approach for LFC of Multiarea Power System with Communication Time Delays, February2021 Proceedings of the International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), , 868–873. Greater Noida, India. doi:10.1109/ICCCIS51004.2021.9397112

CrossRef Full Text | Google Scholar

Kalyan, C. N. S. (2021a). UPFC and SMES Based Coordinated Control Strategy for Simultaneous Frequency and Voltage Stability of an Interconnected Power System, Proceedings of the 2021 1st International Conference on Power electronics and Energy (ICPEE), January 2021, 1–6. Bhubaneswar, India. doi:10.1109/ICPEE50452.2021.9358576

CrossRef Full Text | Google Scholar

Kalyan, C. N. S. (2021b). Determination of Appropriate GRC Modelling for Optimal LFC of Multi Area Thermal System, Proceedings of the 2021 IEEE International Power and Renewable energy Conference (IPRECON), September 2021, 1–6. Kollam, India. doi:10.1109/IPRECON52453.2021.9640892

CrossRef Full Text | Google Scholar

Kalyan, C. N. S. (2021c). Water Cycle Algorithm Based Intelligent Controller for Frequency Regulation of Dual Area Hybrid System with Time Delays. Proceedings of the 2021 IEEE International Power and Renewable energy Conference (IPRECON), September 2021, 1–5. Kollam, India. doi:10.1109/IPRECON52453.2021.9640646

CrossRef Full Text | Google Scholar

Kumar, M., and Hote, Y. V. (2018). Robust CDA-PIDA Control Scheme for Load Frequency Control of Interconnected Power Systems. IFAC-PapersOnLine 51, 616–621. doi:10.1016/j.ifacol.2018.06.164

CrossRef Full Text | Google Scholar

Lal, D. K., and Barisal, A. K. (2019). Combined Load Frequency and Terminal Voltage Control of Power Systems Using Moth Flame Optimization Algorithm. J. Electr. Syst. Inf Technol 6, 8. doi:10.1186/s43067-019-0010-3

CrossRef Full Text | Google Scholar

Lal, D. K., Barisal, A. K., and Tripathy, M. (2016). Grey Wolf Optimizer Algorithm Based Fuzzy PID Controller for AGC of Multi-Area Power System with TCPS. Procedia Comput. Sci. 92, 99–105. doi:10.1016/j.procs.2016.07.329

CrossRef Full Text | Google Scholar

Madasu, S. D., Sai Kumar, M. L. S., and Singh, A. K. (2018). A Flower Pollination Algorithm Based Automatic Generation Control of Interconnected Power System. Ain Shams Eng. J. 9, 1215–1224. doi:10.1016/j.asej.2016.06.003

CrossRef Full Text | Google Scholar

Morsali, J., Zare, K., and Tarafdar Hagh, M., (2014). Appropriate Generation Rate Constraint (GRC) Modeling Method for Reheat Thermal Units to Obtain Optimal Load Frequency Controller (LFC), 2014 5th Conference on Thermal Power Plants (CTPP), 10–11. Iran, Tehran. June 2014, . doi:10.1109/CTPP.2014.7040611

CrossRef Full Text | Google Scholar

Morsali, J., Zare, K., and Tarafdar Hagh, M. (2017). Applying Fractional Order PID to Design TCSC-Based Damping Controller in Coordination with Automatic Generation Control of Interconnected Multi-Source Power System. Eng. Sci. Technol. Int. J. 20, 1–17. doi:10.1016/j.jestch.2016.06.002

CrossRef Full Text | Google Scholar

Naga Sai Kalyan, C., and Sambasiva Rao, G. (2020). Frequency and Voltage Stabilisation in Combined Load Frequency Control and Automatic Voltage Regulation of Multiarea System with Hybrid Generation Utilities by AC/DC Links. Int. J. Sustain. Energy 39, 1009–1029. doi:10.1080/14786451.2020.1797740

CrossRef Full Text | Google Scholar

Nanda, J., Sreedhar, M., and Dasgupta, A. (2015). A New Technique in Hydro Thermal Interconnected Automatic Generation Control System by Using Minority Charge Carrier Inspired Algorithm. Int. J. Electr. Power & Energy Syst. 68, 259–268. doi:10.1016/j.ijepes.2014.12.025

CrossRef Full Text | Google Scholar

Nayak, J. R., Shaw, B., and Sahu, B. K. (2018). Application of Adaptive-SOS (ASOS) Algorithm Based Interval Type-2 Fuzzy-PID Controller with Derivative Filter for Automatic Generation Control of an Interconnected Power System. Eng. Sci. Technol. Int. J. 21, 465–485. doi:10.1016/j.jestch.2018.03.010

CrossRef Full Text | Google Scholar

Nosratabadi, S. M., Bornapour, M., and Gharaei, M. A. (2019). Grasshopper Optimization Algorithm for Optimal Load Frequency Control Considering Predictive Functional Modified PID Controller in Restructured Multi-Resource Multi-Area Power System with Redox Flow Battery Units. Control Eng. Pract. 89, 204–227. doi:10.1016/j.conengprac.2019.06.002

CrossRef Full Text | Google Scholar

Padhy, S., and Panda, S. (2017). A Hybrid Stochastic Fractal Search and Pattern Search Technique Based Cascade PI-PD Controller for Automatic Generation Control of Multi-Source Power Systems in Presence of Plug in Electric Vehicles. CAAI Trans. Intell. Technol. 2, 12–25. doi:10.1016/j.trit.2017.01.002

CrossRef Full Text | Google Scholar

Pan, I., and Das, S. (2015). Fractional-order Load-Frequency Control of Interconnected Power Systems Using Chaotic Multi-Objective Optimization. Appl. Soft Comput. 29, 328–344. doi:10.1016/j.asoc.2014.12.032

CrossRef Full Text | Google Scholar

Pradhan, R., Majhi, S. K., Pradhan, J. K., and Pati, B. B. (2020). Optimal Fractional Order PID Controller Design Using Ant Lion Optimizer. Ain Shams Eng. J. 11, 281–291. doi:10.1016/j.asej.2019.10.005

CrossRef Full Text | Google Scholar

Prakash, A., Murali, S., Shankar, R., and Bhushan, R. (2019). HVDC Tie-Link Modeling for Restructured AGC Using a Novel Fractional Order Cascade Controller. Electr. Power Syst. Res. 170, 244–258. doi:10.1016/j.epsr.2019.01.021

CrossRef Full Text | Google Scholar

Rahman, A., Saikia, L. C., and Sinha, N. (2016). Automatic Generation Control of an Unequal Four‐area Thermal System Using Biogeography‐based Optimised 3DOF‐PID Controller. IET Gener. Transm. &amp; Distrib. 10, 4118–4129. doi:10.1049/iet-gtd.2016.0528

CrossRef Full Text | Google Scholar

Rahman, A., Saikia, L. C., and Sinha, N. (2017). Automatic Generation Control of an Interconnected Two-Area Hybrid Thermal System Considering Dish-Stirling Solar Thermal and Wind Turbine System. Renew. Energy 105, 41–54. doi:10.1016/j.renene.2016.12.048

CrossRef Full Text | Google Scholar

Rajesh, K. S., Dash, S. S., and Rajagopal, R. (2019). Hybrid Improved Firefly-Pattern Search Optimized Fuzzy Aided PID Controller for Automatic Generation Control of Power Systems with Multi-type Generations. Swarm Evol. Comput. 44, 200–211. doi:10.1016/j.swevo.2018.03.005

CrossRef Full Text | Google Scholar

Raju, M., Saikia, L. C., and Sinha, N. (2016). Automatic Generation Control of a Multi-Area System Using Ant Lion Optimizer Algorithm Based PID Plus Second Order Derivative Controller. Int. J. Electr. Power & Energy Syst. 80, 52–63. doi:10.1016/j.ijepes.2016.01.037

CrossRef Full Text | Google Scholar

Sahu, R. K., Panda, S., and Padhan, S. (2015). A Novel Hybrid Gravitational Search and Pattern Search Algorithm for Load Frequency Control of Nonlinear Power System. Appl. Soft Comput. 29, 310–327. doi:10.1016/j.asoc.2015.01.020

CrossRef Full Text | Google Scholar

Sahu, R. K., Gorripotu, T. S., and Panda, S. (2016). Automatic Generation Control of Multi-Area Power Systems with Diverse Energy Sources Using Teaching Learning Based Optimization Algorithm. Eng. Sci. Technol. Int. J. 19, 113–134. doi:10.1016/j.jestch.2015.07.011

CrossRef Full Text | Google Scholar

Sahu, R. K., Panda, S., Rout, U. K., and Sahoo, D. K. (2016). Teaching Learning Based Optimization Algorithm for Automatic Generation Control of Power System Using 2-DOF PID Controller. Int. J. Electr. Power & Energy Syst. 77, 287–301. doi:10.1016/j.ijepes.2015.11.082

CrossRef Full Text | Google Scholar

Sai Kalyan, C. N., Rao, G. S., and Rao, G. S. (2020). Coordinated SMES and TCSC Damping Controller for Load Frequency Control of Multi Area Power System with Diverse Sources. ijeei 12, 747–769. doi:10.15676/ijeei.2020.12.4.4

CrossRef Full Text | Google Scholar

Sariki, M., and Shankar, R. (2021). Optimal CC-2DOF(PI)-PDF Controller for LFC of Restructured Multi-Area Power System with IES-Based Modified HVDC Tie-Line and Electric Vehicles, Engineering Science and Technology. Int. J. 1. 1. doi:10.1016/j.jestch.2021.09.004

CrossRef Full Text | Google Scholar

Shiva, C. K., and Mukherjee, V. (2016). Design and Analysis of Multi-Source Multi-Area Deregulated Power System for Automatic Generation Control Using Quasi-Oppositional Harmony Search Algorithm. Int. J. Electr. Power & Energy Syst. 80, 382–395. doi:10.1016/j.ijepes.2015.11.051

CrossRef Full Text | Google Scholar

Tasnin, W., and Saikia, L. C. (2018). Comparative Performance of Different Energy Storage Devices in AGC of Multi-Source System Including Geothermal Power Plant. J. Renew. Sustain. energy 10, 024101. doi:10.1063/1.5016596

CrossRef Full Text | Google Scholar

Yousri, D., Babu, T. S., and Fathy, A. (2020). Recent Methodology Based Harris Hawks Optimizer for Designing Load Frequency Control Incorporated in Multi-Interconnected Renewable Energy Plants. Sustain. Energy, Grids Netw. 22, 100352. doi:10.1016/j.segan.2020.100352

CrossRef Full Text | Google Scholar

Nomenclature

f system frequency (60Hz)

∆f frequency deviation

i The subscript indicating the area number (i = 1, 2, 3)

∆P_d change in the load demand (10%SLP)

∆P_T change in thermal power generation

∆P_tie change in the tie-line power flow

R_T speed regulation

B₁,B₂,B₃ area bias parameter (0.4312Pu.MW/Hz)

T_ij synchronizing coefficient of the tie-line between areas i and j (i $\ne$ j) (0.0433 pu.MW/rad)

T_sg steam time governor time constant (0.06s)

T_sim simulation time

K_r reheat steam turbine constant (0.3)

K_ps1, K_ps2, and K_ps3 power plant model constant (80)

T_r reheat steam turbine time constant (10.2s)

T_ps1,T_ps2, and T_ps3 power plant model time constant (12s)

T_t The time constant of the steam turbine (0.3s)

N₁ and N₂ GDB Fourier coefficients (0.8, -0.6366)

±δ GRC ramp rate limits (±0.0005)