Operation state assessment of wind power system based on PSO + AHP—FCE

Aiming at the shortcomings of the analytic hierarchy process in the comprehensive evaluation of wind power system operation status with strong subjectivity in determining weights, this thesis proposes an analytic hierarchy process (AHP) based on particle swarm optimization (PSO) and constructs an analytic hierarchy process combined with a particle swarm optimization algorithm (PSO + AHP) model to optimize the weights. It overcomes the disadvantage that once given the judgment matrix in the AHP method, the weight values and consistency cannot be improved. In this article, the comparison chart of the consistency indexes calculated according to this method shows that the one-time indexes of $C_a$ as well as $C_1-C_7$ are reduced to different degrees, so a weight value with a relatively high degree of consistency can be obtained by this method. Second, for the situation that there are several judgment indexes in the sub-project layer that deviate seriously at the same time, introduce the degradation index, and apply the fuzzy comprehensive judgment method to establish the model of wind power system operation status assessment. Finally, based on the actual monitoring data of a wind farm over a period of time, its operational status was evaluated using the proposed PSO-AHP model based on FCE, and a score that can indicate the operational status can be obtained by calculation. In this article, the evaluation score of a wind farm is 0.556, indicating that the staff needs to carry out maintenance at this time. The comparative analysis shows that compared to the traditional AHP-FCE evaluation method, the assessment results proposed in this article are relatively good and have practical value and significance for improving the real-time reliability of grid-connected operation of wind turbines, optimizing the maintenance strategy of wind turbines, and reducing the cost of wind power generation.

1 Introduction

To solve the problem of energy shortage, the exploration and use of renewable energy have become extremely important. The main renewable energy sources that are expected to achieve large-scale use are wind, solar, nuclear energy, etc. Among them, wind energy resources have many advantages; they are clean, pollution-free, inexhaustible, and renewable. Wind energy resources are abundant all over the world. It can be seen that the market prospect of wind power generation is extremely promising; wind power generation technology is also constantly improving. With the large-scale development of the wind power industry and the progress of wind power technology, wind energy has gradually become an energy type that mankind can rely on in the future. Therefore, timely, comprehensive, and accurate monitoring and evaluation of the operational status of wind power systems, and effective avoidance of faults and chain failures, are of great practical significance for optimizing the maintenance strategy of wind farms and achieving safe and efficient grid connection of large-scale wind power generation (Zhang et al., 2019).

At present, wind farms still take the traditional way of after-the-fact maintenance and planned preventive maintenance, often failing to understand the operating status and reliability of the system in a comprehensive and timely manner. At present, there is a lack of data and experience on unit operation in China, and there is no excessive accumulation and analysis of reliability test data for the time being. Although the remote monitoring system of wind farms can collect operational data on wind turbines, it lacks effective evaluation algorithms and cannot assess the comprehensive status of the turbines in a timely manner (Yang et al, 2020). Therefore, it is of great academic value and application prospect to find a method to evaluate the operating condition of wind turbines based on online monitoring information without relying too much on the test data of the turbines. At present, knowledge-based expert systems, intelligent methods based on neural networks, probabilistic statistical methods, and fuzzy comprehensive evaluation have been gradually applied to the condition assessment of thermal power units and large power transformers (Bo et al., 2016). Xiong et al. (2007) evaluated the operating condition of power transformers using the grey hierarchy method, and Zhu et al. (2019) evaluated the typical faults of coupled torsional vibration in thermal power units by calculating. In recent years, these algorithms have also been gradually applied to the assessment of wind power; Li et al. (2010) used the object element method to evaluate the operating condition of wind turbines, and many scholars have evaluated the individual components of the units by using various intelligent algorithms. However, all these evaluation methods need a large amount of data support to be implemented, so it becomes extremely necessary to seek an evaluation method that does not rely too much on data. Since AHP-FCE does not need to rely too much on the analysis of experimental data, it is widely used in evaluation work in other fields, and the literature (Zhou, 2020; Li et al., 2021; Wenyan et al., 2021) applied the AHP-FCE method to the evaluation of commercial concrete production process, agricultural product supply chain, and Pimpernel germplasm resources, respectively. So, we can apply this method to the operation state evaluation and fault diagnosis of wind systems in complex operating environments and complex working conditions. However, the weights determined using a single hierarchical analysis method can be subject to a certain degree of chance; therefore, there is a need to find a method to optimize the weights determined by the hierarchical analysis method. In Hu et al. (2012), the AHP ranking weights were optimally calculated by a simulated annealing algorithm, and the literature (Xiao et al., 2022; Liu et al., 2013) optimizes the AHP by means of a particle swarm optimization algorithm and applies this method to the evaluation of LNG tankers as well as distributed power networks, respectively. Zhang et al. (2018) optimize the weights by combining the particle swarm algorithm with rough set theory and apply this method to the evaluation of irrigation water use. Therefore, to address the shortcomings in weight determination, this article proposes an improved AHP-FCE method to evaluate wind power systems (Shi and Zheng, 2012; Zhou, 2020; Li et al., 2021; Wenyan et al., 2021).

According to the online monitoring information of wind turbines, by analyzing the physical quantities of wind turbines and external environment control system, this article applies AHP to construct a framework of project layers and sub-project layers with important characteristics reflecting the operating status of the unit and uses traditional AHP to calculate the weights. At the same time, aiming at the disadvantage of determining the weight in the comprehensive evaluation of AHP, based on the PSO, this article constructs the PSO + AHP model (Liu et al., 2013; Zhang et al., 2018) and uses this model to solve the optimized weight (Xiao et al., 2022); by comparison, we found that the optimized model calculates a relatively high weighted one-time indicator. Second, aiming at the serious deviation of multiple evaluation indexes in the sub-project level at the same time, the introduction of the deterioration index to establish an evaluation and improvement method and model of the online operation state of the wind power system. Then, through the actual monitoring information of a wind farm for a while, apply the operation state evaluation model proposed in this article to calculate and evaluate. Finally, a summary of the work done and the shortcomings of this article is given.

2 Evaluation model of wind power system operation state

2.1 Selection of operation status evaluation indicators

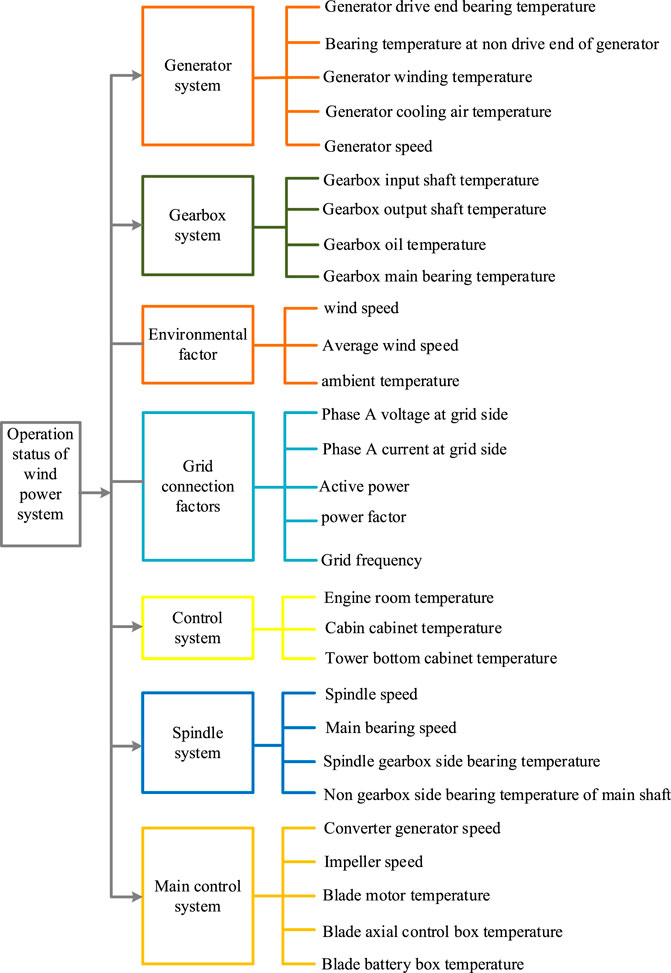
Because the online monitoring data of wind power systems can reflect the operation state of the system in real-time, this article, therefore, looks at both the performance of the unit and the external factors that affect the operating condition of the system, established a hierarchical wind power system operating condition assessment index system (Xiong et al., 2007; Li et al., 2010). In order to make a fair and objective evaluation of the operation status of wind power systems, it is particularly urgent to establish a set of scientific and reasonable evaluation index systems that can fully reflect the characteristics of the operation status of wind power systems. Therefore, the selection of evaluation indicators should follow the principles of comprehensiveness, operability, systematicness, and objectivity. Therefore, considering the characteristics of the wind power system, seven first-class indexes, including generator system, gearbox system, environmental factors, grid connection factors, control system, spindle system, and main control system, with a total of 29 second-class indexes, are selected to build the operation state evaluation index system of the wind power system (Xiao et al., 2014; Huang et al., 2015; Min, 2017; Li, 2019; Zhang, 2019; Bianhui, 2020; Wang and Shi, 2021).

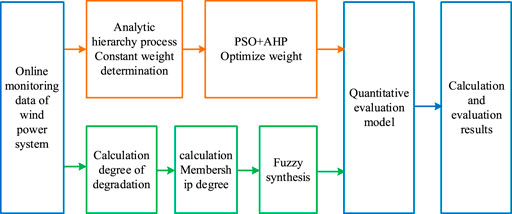
2.2 Fuzzy comprehensive evaluation (FCE) model with improved hierarchical analysis (PSO + AHP)

The fuzzy evaluation model based on the improved analytic hierarchy process is an effective combination of the improved analytic hierarchy process and the fuzzy comprehensive evaluation method. It is a multi-criteria and multi-level decision analysis method combining qualitative and quantitative analysis.

According to the principle, the construction steps of the fuzzy comprehensive evaluation method model based on the improved analytic hierarchy process are shown in Figure 1:

FIGURE 1

FIGURE 1. Operation status evaluation process of wind power system based on PSO + AHP and FCE.

2.2.1 Construction of hierarchical evaluation index system

American operational research scientist SATTY in the 1970s introduced the analytic hierarchy process. To establish the hierarchical structure model, first, through in-depth analysis of practical problems, decomposing the individual factors in question into levels according to different attributes, the factors in the same layer belong to the upper layer or have an impact on the upper layer, and the middle layer can have one or more layers. Then, using an appropriate scale, we compare quantitatively the importance of each factor, construct the evaluation index, and use the judgment matrix to calculate the weight of each index, so as to obtain the weight vector and sort the evaluation criteria.

In this article, we take the operation state evaluation of the wind power system as the target layer of the index system, take the main reasons affecting the operation state (generator system, gearbox system, environmental factors, grid connection factors, control system, spindle system, and main control system) as the criterion layer, and take the single influencing factors contained in the criterion layer as the index layer. Therefore, the target layer is represented as:

$A=\left\{B_1,B_2,B_3,B_4,B_5,B_6,B_7\right\}.$(2.1)

Eq. 2.1 represents each factor of the criterion layer.

Taking $B_1$ as an example, express the factors of the criterion layer as follows through the index layer:

$B_1=\left\{C_1,C_2,C_3,C_4,C_5\right\}.$(2.2)

In Eq. 2.2, $C_1-C_5$ are the factors of the index layer.

2.2.2 Applying analytic hierarchy process to determine index weight

According to the scaling theory of the “9-division” method shown in Table 1, constructing the judgment matrix J (Hu et al., 2012) for the indicator and criterion layers:

$J={\left(a_{ij}\right)}_{n\times n}.$(2.3)

TABLE 1

TABLE 1. ″9-division” table.

In Eq. 2.3, $a_{ij}$ is the importance scale of factor i compared with factor j, $a_{ij}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$a_{ji}$}\right.$, and $a_{ii}=1$. Among the formulas, $i=\mathrm{1,2},\mathrm{...},n$; $j=\mathrm{1,2},\mathrm{...},n$.

The specific steps are:

(1) Normalize the column vector of the judgment matrix:

${\overline{\omega }}_i=\frac{a_{ij}}{{\displaystyle \sum _{j=1}^n{a}_{ij}}}.$(2.4)

(2) Calculate the arithmetic mean of the row vector of ${\overline{\omega }}_i$:

${\omega }_i=\frac{{\displaystyle \sum _{i=1}^n{a}_{ij}}}{n}.$(2.5)

Get $\omega ={({\omega }_1,{\omega }_2,\mathrm{...}{\omega }_n)}^T$, which is the relative weight of each factor.

(3) Calculate the maximum eigenvalue ${\lambda }_{\max }$ of the judgment matrix:

${\lambda }_{\max }={\displaystyle \sum _{i=1}^n\frac{{\left(J\omega \right)}_i}{n{\omega }_i}}.$(2.6)

(4) Calculate the consistency index of the judgment matrix:

$CI=\frac{{\lambda }_{\max }-n}{n-1},$(2.7)

$CR=\frac{CI}{RI}.$(2.8)

In the formula, ${\lambda }_{\max }$ is the maximum characteristic root; $n$ is the order of the judgment matrix; RI is the average random consistency index, which can be found in Table 2.

TABLE 2

TABLE 2. Random consistency index of 12 order judgment matrix.

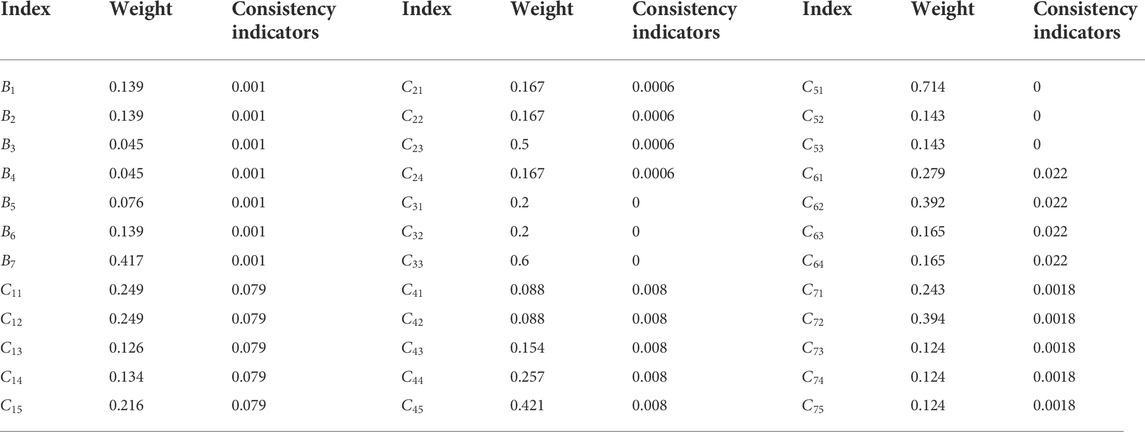
This article selects the SCADA monitoring data of a wind farm in Inner Mongolia and uses the aforementioned method to obtain the weight distribution of each index shown in Figure 2, as shown in Table 3.

FIGURE 2

FIGURE 2. Operation status evaluation index system of the wind power system.

TABLE 3

TABLE 3. Calculation results of index weight and consistency index at all levels of the AHP model.

It can be seen from Table 3 that the one-time index of the single analytic hierarchy process is less than 0.1, meeting the consistency requirements. However, the single use of the analytic hierarchy process to determine the weight has strong subjectivity. Therefore, this article proposes to use a particle swarm optimization algorithm to optimize the weight determined by the analytic hierarchy process.

2.3 Optimization of AHP weight based on PSO

The analytic hierarchy process has strong subjectivity in determining the weight, but due to the limited understanding level of people and the inconsistency of opinions among evaluation experts, the judgment matrix usually does not have satisfactory consistency. Moreover, when the weight is determined by the analytic hierarchy process, once the judgment matrix is determined, the consistency of the judgment matrix and the weight value are also determined, the two cannot be improved. Therefore, to improve these problems, this article applies particle swarm optimization (PSO) (Jin et al., 2019) to the analytic hierarchy process, constructs a PSO + AHP (Liu et al., 2013; Zhang et al., 2018) model, and optimizes the weight calculated by the analytic hierarchy process to make the result of a comprehensive evaluation more scientific and reliable.

According to the relative importance of each index, we can construct the judgment matrix $J={\left\{a_{ij}\right\}}_{n\times n}$, in which the formula, $i,j=\mathrm{1,2},\dots ,n,$where $a_{ij}$ indicates the importance of the indicator $u_i$ relative to the indicator $u_j$. Let ${\omega }_k$ be the weight of each index. According to the definition of the judgment matrix, there is ${\omega }_i/{\omega }_j=a_{ij}$ in theory, and at this time, the judgment matrix $J$ has complete consistency. Then, there:

${\displaystyle \sum _{k=1}^n({\omega }_i/{\omega }_k){\omega }_k=n{\omega }_i}.$(2.9)

Namely:

${\displaystyle \sum _{i=1}^n\left|{\displaystyle \sum _{k=1}^n\left({\mathrm{a}}_{ik}{\omega }_k\right)-\mathrm{n}{\omega }_i}\right|=0}.$(2.10)

As can be seen from Eq. 2.10, the smaller the value at the left end of the formula, the higher the consistency of the judgment matrix. If Eq. 2.10 is established, the judgment matrix has complete consistency. Therefore, the weight value determination and consistency test of each index can be reduced to the following optimization problems:

$\min CIF\left(n\right)={\displaystyle \sum _{i=1}^n\left|{\displaystyle \sum _{k=1}^n\left(a_{ik}{\omega }_k\right)-n{\omega }_i}\right|/n}.$(2.11)

In the formula, $CIF\left(n\right)$ is the consistency index function; ${\omega }_k$ is the optimization variable.

Among them, the constraints are

${\displaystyle \sum _{i=1}^n{\omega }_k=1}.$(2.12)

When the function $CIF\left(n\right)$ reaches the optimal value in the global range and the optimal value is less than 0.1, it is considered that the constructed judgment matrix $J$ has satisfactory consistency, and the corresponding optimal solution is the subjective weight to be obtained. When the global minimum value is 0, the judgment matrix $J$ has complete consistency. According to the constraint condition ${\displaystyle \sum _{i=1}^n{\omega }_k=1}$, the global minimum is unique.

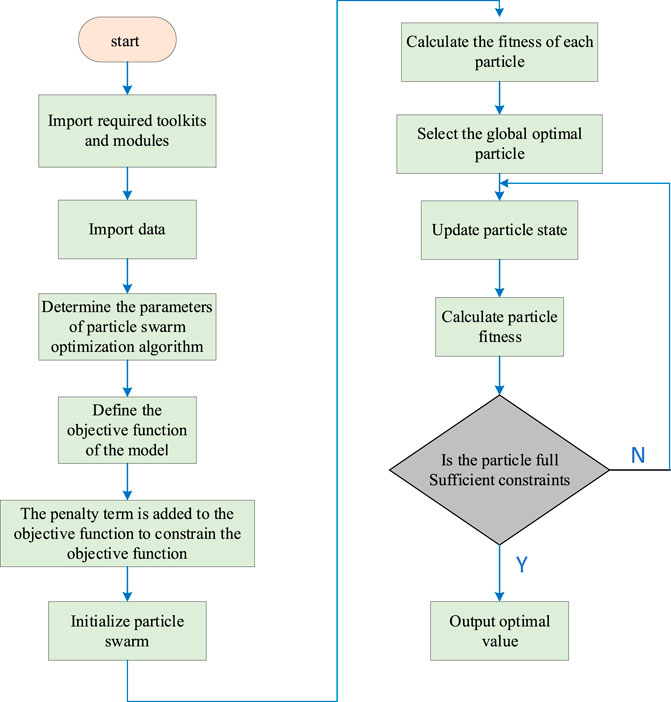
For the aforementioned PSO + AHP model, in this article, we use the Python tool to solve and optimize the weights by constructing the fitness function, using the particle swarm optimization algorithm. The specific process is shown in Figure 3.

FIGURE 3

FIGURE 3. Python flow chart of PSO + AHP calculation optimization weight.

Bring the judgment matrix constructed by the hierarchical analysis into the model as an input layer, so as to optimize the deficiency of calculating weight by a single analytic hierarchy process. In the model, the population size is 40, the number of iterations is 200, and the penalty degree of the penalty item is 10,000. The calculation results are shown in Table 4.

TABLE 4

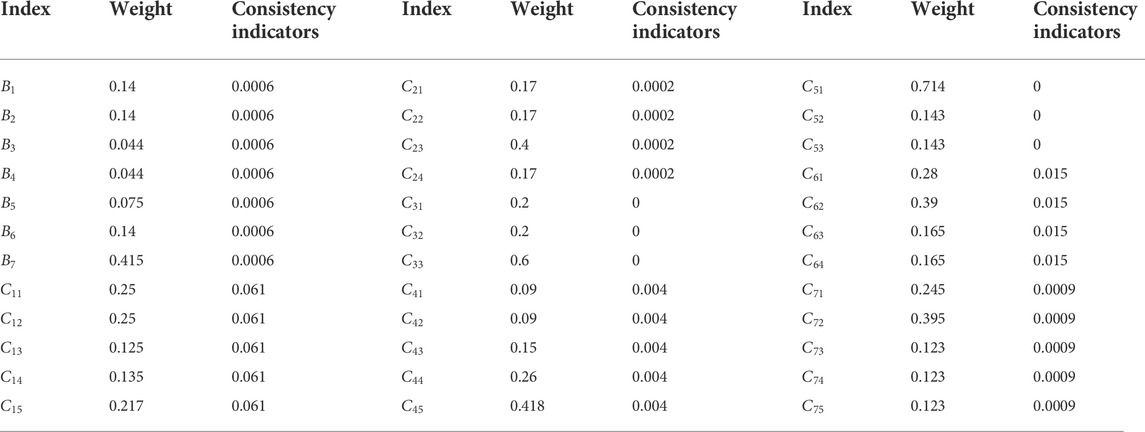
TABLE 4. Calculation results of index weight and consistency index at all levels of the PSO + AHP model.

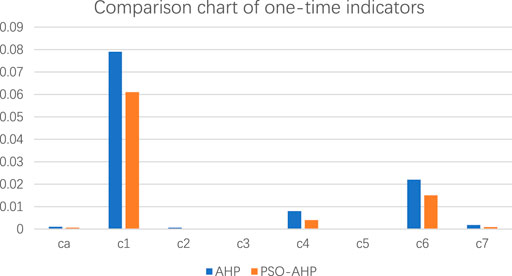
By comparing the calculation results in Tables 3 and 4, the comparison diagram of consistency indicators shown in Figure 4 can be obtained.

FIGURE 4

FIGURE 4. Comparison of consistency indexes of AHP and PSO + AHP.

It can be seen from the figure that the consistency index function values of these judgment matrices are less than 0.1. Among them, $C_3$ and $C_5$ have full consistency, but compared with the single AHP method, the results show that the PSO algorithm directly solves the judgment matrix by multiple particle iteration, which significantly reduces the consistency index of the PSO + AHP method, and the calculation effect is better than the single AHP method, which greatly improves the accuracy of calculation results.

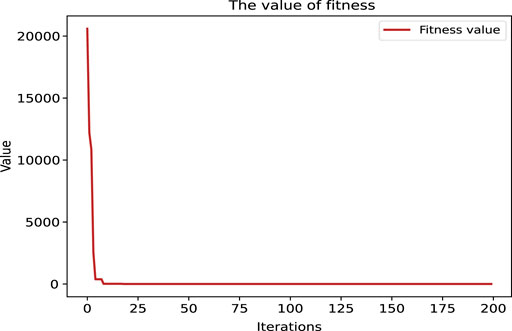
The change curve of characteristic particle guidance ability in the iteration process of the PSO + AHP algorithm is shown in Figure 5.

FIGURE 5

FIGURE 5. Variation of characteristic particle guidance ability during algorithm iteration.

As can be seen from Figure 5, the particle swarm algorithm can obtain better consistent results with fewer iterations, indicating that the PSO + AHP model performs a fast adaptive globalized optimal search in the interval of ranking weights (0,1) with stable computational results and can optimize the weights well.

2.4 Fuzzy evaluation and score

Chinese scholar Wang Peizhuang first proposed the fuzzy comprehensive evaluation method (Liao et al., 2008). A fuzzy comprehensive evaluation method can collect and quantify people’s uncertain thinking in the process of looking at things and make a correct evaluation of the qualitative concept of things through mathematical calculation. The mathematical modeling process of the fuzzy comprehensive evaluation method is simple. In the process of practical application, it shows its good evaluation performance for the multi-factor complex system. It is a method that cannot be replaced by other mathematical models. The modeling process usually includes the following specific steps:

(1) Set up the evaluation set of the index set in AHP:

$V=\left\{\mathrm{1,0.67},0.33,0\right\}.$(2.13)

(2) Determine the membership of each index.

Calculation of deterioration degree:

The characteristic state parameters in each subsystem have their own physical significance and normal range and need to be normalized in order to allow for comprehensive comparative analysis. For this reason, the analysis method of relative deterioration is used, i.e., the actual operating condition is good or bad according to the values of each parameter. The value is converted to a specific value between the interval [0, 1], where 0 represents the best and 1 the worst, and the size of the value taken corresponds to the degree of deterioration of the assessed index.

Biased small assessment metrics:

For the evaluation indexes of temperature type such as gearbox oil temperature and gearbox main bearing temperature, the smaller the parameter, the better the system operation status of the system, and this type of evaluation index belongs to the smaller the better type, and its deterioration degree is calculated as follows:

$g\left(x\right)=\{\begin{array}{l}0x\text{<}{x}_{\min },\\ \frac{x-x_{\min }}{x_{\max }-x_{\min }}\text{, }{x}_{\min }<x<x_{\max },\\ 1x\text{>}{x}_{\max }.\end{array}$(2.14)

$x$ is the parameter value of the evaluation index; $x_{\min }$ and $x_{\max }$ are the threshold of the critical interval of the evaluation index parameters.

Intermediate assessment metrics:

For the evaluation indexes such as speed, frequency, active power, etc., the parameters are too small or too large to characterize the poor system operation of the system, and the formula for calculating the degradation degree of such evaluation indexes is as follows:

$g\left(x\right)=\{\begin{array}{l}1x\text{<}{x}_{\min },\\ \frac{x-x_{\min }}{x_a-x_{\min }}\text{, }{x}_{\min }<x<x_a,\\ 0x_a<x<x_b,\\ \frac{x-x_b}{x_{\max }-x_b}\text{, }{x}_b<x<x_{\max },\\ 1x\text{>}{x}_{\max }.\end{array}$(2.15)

$x_a$ and $x_b$ is the boundary value of the reasonable interval of the evaluation index parameters.

Biased large assessment metrics:

For other types of evaluation metrics, the larger the parameter, the better the system operation status of the system, and the formula for calculating large evaluation metrics is as follows:

$g\left(x\right)=\{\begin{array}{l}1x\text{<}{x}_{\min },\\ \frac{x_{\max }-x}{x_{\max }-x_{\min }}\text{, }{x}_{\min }<x<x_{\max },\\ 0x\text{>}{x}_{\max }.\end{array}$(2.16)

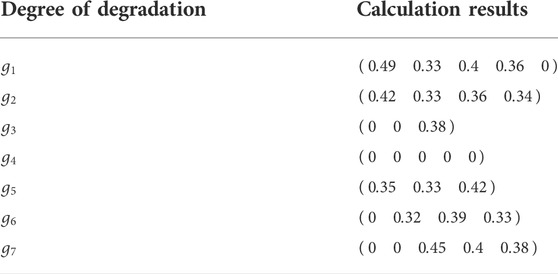
According to the above formula, the degree of degradation is calculation in the Table 5:

TABLE 5

TABLE 5. Calculation results of deterioration degree.

Obtain the membership matrix according to the degree of degradation.

According to the degradation degree of each factor, the degree of affiliation corresponding to each evaluation level can be obtained. The selection of the affiliation function should reasonably cover the whole degradation degree taking value interval; this article takes the trapezoidal distribution affiliation function as an example to describe the fuzzy relationship of each state space, and the affiliation function of each evaluation level is shown below.

The membership function of each evaluation grade is as follows:

$r_g=\{\begin{array}{l}1\text{ g<0}\text{.}2\text{,}\\ \frac{0.3-g}{0.1}\text{, 0}\text{.}2\le \text{g}\le 0.3,\\ 0\text{ g>0}\text{.}3\text{,}\end{array}$(2.17)

$r_g=\{\begin{array}{l}0\text{ g<0}\text{.}2\text{,}\\ \frac{g-0.2}{0.1}\text{, 0}\text{.}2\text{<g}\le \text{0}\text{.}3\text{,}\\ \frac{0.4-g}{0.1}\text{, 0}\text{.}3\text{<g<0}\text{.}4\text{,}\\ 0\text{ g}\ge \text{0}\text{.}4\text{,}\end{array}$(2.18)

$r_g=\{\begin{array}{l}0\text{ g<0}\text{.}3\text{,}\\ \frac{g-0.3}{0.1}\text{, 0}\text{.}3\text{<g}\le \text{0}\text{.}4\text{,}\\ \frac{0.5-g}{0.1}\text{, 0}\text{.}4\text{<g<0}\text{.}5\text{,}\\ 0\text{ g}\ge \text{0}\text{.}5\text{,}\end{array}$(2.19)

$r_g=\{\begin{array}{l}0\text{ g}\le \text{0}\text{.}4\text{,}\\ \frac{g-0.4}{0.1}\text{, 0}\text{.}4\text{<g<0}\text{.}5\text{,}\\ 1\text{ g}\ge \text{0}\text{.}5\text{.}\end{array}$(2.20)

According to the degree of degradation obtained above, the evaluation membership matrix of the detection items of the wind power system can be obtained by bringing the membership degree calculation formula in Eqs 2.17–2.20, which are, respectively:

$R_{B1}=\left[\begin{array}{cccc}0& 0& 0.1& 0.9\\ 0& 0.7& 0.3& 0\\ 0& 0& 1& 0\\ 0& 0.4& 0.6& 0\\ 1& 0& 0& 0\end{array}\right],$(2.21)

$R_{B2}=\left[\begin{array}{cccc}0& 0& 0.8& 0.2\\ 0& 0.7& 0.3& 0\\ 0& 0.4& 0.6& 0\\ 0& 0.4& 0.6& 0\end{array}\right],$(2.22)

$R_{B3}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 0.2& 0.8& 0\end{array}\right],$(2.23)

$R_{B4}=\left[\begin{array}{cccc}0& 0.5& 0.5& 0\\ 0& 0.7& 0.3& 0\\ 0& 0& 0.8& 0.2\end{array}\right],$(2.24)

$R_{B5}=\left[\begin{array}{cccc}0& 0.5& 0.5& 0\\ 0& 0.7& 0.3& 0\\ 0& 0& 0.8& 0.2\end{array}\right],$(2.25)

$R_{B6}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0.8& 0.2& 0\\ 0& 0.1& 0.9& 0\\ 0& 0.7& 0.3& 0\end{array}\right],$(2.26)

$R_{B7}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 0& 0.5& 0.5\\ 0& 0& 1& 0\\ 0& 0.2& 0.8& 0\end{array}\right].$(2.27)

(3) Fuzzy synthesis

Considering that the final quantitative score should be achieved, we can obtain the single score of each element index by integrating the fuzzy evaluation matrix $R$ and the evaluation set matrix $V$:

$Q=R\cdot V^T.$(2.28)

Using the weight $\omega$ of each factor index obtained by PSO + AHP to weight the single score $Q$ of each element index, we can obtain the quantitative evaluation model of the wind power system operation state as follows:

$C=\omega \cdot Q=\omega \cdot R\cdot V^T.$(2.29)

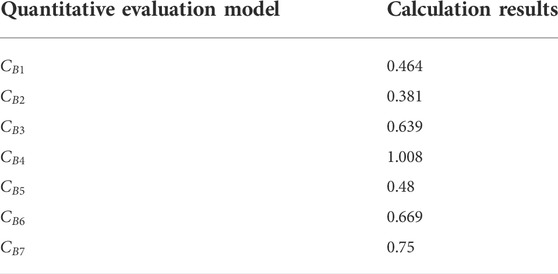
According to the formula of the quantitative evaluation model in (Eq 2.29),we can obtain Table 6:

TABLE 6

TABLE 6. Results of the quantitative evaluation model.

The operation status of the wind power system is evaluated as follows:

$C_A={\omega }_A\cdot {\left[C_{B1},C_{B2},C_{B3},C_{B4},C_{B5},C_{B6},C_{B7}\right]}^{-1}\cdot V^T=\mathrm{0.556.}$(2.30)

It can be seen from the previous formula that the evaluation score of the operation state of the wind power system is 0.556. If the values {Excellent, Good, OK, Bad} are used, the overall operational status of the wind power system is assessed as OK, indicating that the operation state of the system has reached a critical state. If it is not repaired in time, the system will fail. At this time, the monitoring personnel shall take corresponding measures to prevent further deterioration of the system state.

3 Conclusion

In order to evaluate the operation status of the wind power system scientifically and reasonably, this article adopts an evaluation method based on particle swarm optimization hierarchical analysis and fuzzy comprehensive evaluation, the main idea is to decompose the wind power system into multiple subsystems, and then the SCADA monitoring index data associated with the subsystems are simulated by Python tools to achieve comprehensive evaluation. The main research work of this article is summarized as follows:

1. The wind power system operation status assessment system is constructed by hierarchical analysis, which divides the wind power system into seven parts: gearbox system, generator system, environmental factors, grid connection factors, control system, spindle system, and main control system, and links each subsystem with the monitoring items of SCADA. Then, obtain the judgment matrix for each subsystem by counting the distribution of faults and consulting experts to obtain the influence weight of each detection index on the operational status of the wind power system and subsystems.

2. In order to improve the shortcomings of the single hierarchical analysis method to determine the weights subjectively and improve the accuracy of the calculation results, in this article, we introduce the particle swarm optimization algorithm to optimize the hierarchical analysis method and establish the PSO + AHP model to calculate the influence weight of each detection index on the operation status of the wind power system and subsystems.

3. For the data obtained from monitoring items of different magnitudes, the method of calculating the degradation degree is used so that they are all in the range of (0,1) and achieve the alignment of the data.

4. Using actual system failure data, evaluation of system operation status through simulation with Python tools, and through verification, the calculation results obtained from the evaluation model established in this article match with the actual operation state, indicating that this model can better reflect the real operation state of the system. Therefore, the evaluation model established in this article can be applied in remote monitoring of wind power systems to provide a technical reference for further realization of wind power system condition maintenance.

Due to the limited experimental conditions, the research work in this thesis has shortcomings, which are mainly manifested in the following aspects:

1. Online assessment. The method is used for real-time online evaluation, thus allowing the owner to visualize the operational status of the wind power system and its subsystems.

2. Fault prediction. Use the operating status trend from the evaluation as a reference for wind power system fault prediction to effectively reduce system operation and maintenance costs.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: System operation data of Baotou Power Supply Company.

Author contributions

JZ: methodology, software, formal analysis, and writing—original draft. JB: conceptualization, validation, writing—review and editing, supervision, and funding acquisition. WF: visualization. ZZ: data curation.

Acknowledgments

JB, WF, and ZZ are thanked for their valuable contributions. The authors thank the Jilin Provincial Department of Science and Technology for funding the projects “AI-based Intelligent Artificial Ventilator Research and Development” (Project No. 20210204116YY) and “Cloud-based Energy and Equipment Monitoring and Early Warning and Energy Efficiency Assessment System” (Project No. 20200403133SF).

Conflict of interest

Author ZZ was employed by Baotou Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bianhui, (2020). The construction and simulation of the operating state evaluation model of wind turbine variable blade system monitored [J]. Automation&Instrumentation (07), 81–84. doi:10.14016/j.cnki.1001-9227.2020.07.081

CrossRef Full Text | Google Scholar

Bo, J., Ye, Y., and Lu, H. (2016). A clustering algorithm based on empowered joint probability model[J]. J. Data Acquis. Process. 31 (01), 130–138. doi:10.16337/j.1004-9037.2016.01.013

CrossRef Full Text | Google Scholar

Hu, J. Y., Yan, H., and Liu, N. N. (2012). Calculation of AHP ranking weights based on simulated annealing particle swarm algorithm[J]. Comput. Technol. Dev. 22 (06), 14–21. doi:10.3969/j.issn.1673-629X.2012.06.004

CrossRef Full Text | Google Scholar

Huang, B., He, Y., and Wang, T. Y. (2015). Fuzzy synthetic evaluation of the operational status of offshore direct-drive wind turbines[J]. J. Tsinghua Univ. Nat. Sci. Ed. 55 (05), 543–549. doi:10.16511/j.cnki.qhdxxb.2015.05.011

CrossRef Full Text | Google Scholar

Jin, T., Dong, P., Li, Y., Ren, L., and Fan, P. (2019). Optimization of fractional PID controller parameters based on improved PSO algorithm [J]. J. Comput. Appl. 39 (03), 796–801. doi:10.11772/j.issn.1001-9081.2018081698

CrossRef Full Text | Google Scholar

Li, F., Hu, Y., Tang, X., and Liu, Z. (2010). Method for on-line operating conditions assessment for a grid-connected wind turbine generator system [J]. Proc. CSEE 30 (33), 2010. doi:10.13334/j.0258-8013.pcsee.2010.33.004

CrossRef Full Text | Google Scholar

Li, Q. (2019). The state evaluation method of wind turbine rased on big data modeling and analysis[D]. Beijing: North China Electric Power University.

Google Scholar

Li, S., Bai, Y. H., Li, X. B., and Wang, Z. L. (2021). Quality evaluation of commercial concrete production process based on AHP-FCE method[J]. Sci. Technol. Innovation (15), 30–31+38. doi:10.15913/j.cnki.kjycx.2021.15.014

CrossRef Full Text | Google Scholar

Liao, R., Wang, Q., Luo, S., Liao, Y., and Sun, C. (2008). A fuzzy integrated evaluation model for power transformer operating condition based on fuzzy evaluation[J]. Automation Electr. Power Syst. (03), 70–75. doi:10.3321/j.issn:1000-1026.2008.03.017

CrossRef Full Text | Google Scholar

Liu, W., Zhang, H. Y., Shi, J., Sun, Y. G., and Qu, P. (2013). Optimum allocation of distributed power network based on improved PSO and AHP algorithm[J]. J. Syst. Simul. 25 (12), 3057–3063. doi:10.16182/j.cnki.joss.2013.12.022

CrossRef Full Text | Google Scholar

Min, Q. (2017). Research on wind turbine drive train condition monitoring system based on cloud platform[D]. Chongqing: Chongqing University.

Google Scholar

Shi, Z. G., and Zheng, B. (2012). Construction and application of PSO-AHP model in comprehensive evaluation. J]. Statistics Decis. Mak. (01), 30–33. doi:10.13546/j.cnki.tjyjc.2012.01.005

CrossRef Full Text | Google Scholar

Wang, Y., and Shi, J. (2021). Condition monitoring method of wind turbine transmission system based on DNN model[J]. Electr. Power Sci. Eng. 37 (09), 26–34. doi:10.3969/j.ISSN.1672-0792.2021.09.004

CrossRef Full Text | Google Scholar

Wenyan, L., Zhou, J., Zhang, X., Zhou, C., Huang, L., Lu, M., et al. (2021). Comprehensive evaluation of appleberry germplasm resources based on AHP-FCE mathematical model and DTOPSIS method[J]. South. J. Agric. 52 (06), 1557–1567. doi:10.3969/j.issn.2095-1191.2021.06.015

CrossRef Full Text | Google Scholar

Xiao, L., Zhang, Y., Wang, T., and Li, C. (2022). Risk evaluation of tankers by means of PSO-AHP[J]. Saf. Environ. Eng. 29 (02), 91671–151556. doi:10.13578/j.cnki.issn.1671-1556.20210426

CrossRef Full Text | Google Scholar

Xiao, Y., Wang, K., He, G., Sun, Y., and Yang, X. (2014). Fuzzy comprehensive evaluation for operating condition of large-scale wind turbines based on trend predication [J]. Proc. CSEE 34 (13), 2132–2139. doi:10.13334/j.0258-8013.pcsee.2014.13.015

CrossRef Full Text | Google Scholar

Xiong, H., Sun, C., Zhang, Y., Tan, Z., and Yao, D. (2007). Gray level evaluation model of power transformer operation status[J]. Automation Electr. Power Syst. (07), 55–60. doi:10.3321/j.issn:1000-1026.2007.07.012

CrossRef Full Text | Google Scholar

Xu, G., and Xu, B. (2019). Time series generation and complex correlation assessment for multiple wind farms. IOP Conf. Ser. Earth Environ. Sci. 295 (4), 012068. doi:10.1088/1755-1315/295/2/012068

CrossRef Full Text | Google Scholar

Yang, X., Yang, Y., Liu, Y., and Deng, Z. (2020). A reliability assessment approach for electric power systems considering wind power uncertainty[J]. IEEE Access 8. doi:10.1109/access.2020.2966275

CrossRef Full Text | Google Scholar

Zhang, J., Jiang, N., Li, H., and Li, L. (2019). Online health assessment of wind turbine based on operational condition recognition. Trans. Inst. Meas. Control 41 (10), 2970–2981. doi:10.1177/0142331218810070

CrossRef Full Text | Google Scholar

Zhang, L. (2019). Operational status assessment of wind power systems based on data driven [D], 2019. Shijiazhuang: Hebei University of Technology.000857.

Google Scholar

Zhang, Z., Liu, D., Zhang, H., and Li, G. X. (2018). Irrigation water use efficiency evaluation based on combination weighting of PSO-AHP and rough set theory [J]. Water Conserv. Irrig. (10), 59–63+67. doi:10.3969/j.issn.1007-4929.2018.10.014

CrossRef Full Text | Google Scholar

Zhou, Y (2020). Evaluation of agricultural supply chain performance based on AHP-FCE model [J]. .Statistics Decis. Mak. 36 (23), 178–180. doi:10.13546/j.cnki.tjyjc.2020.23.039

CrossRef Full Text | Google Scholar

Zhu, Y., Zhu, C., Song, C., Li, L., Chen, X., and Yong, B. (2019). Improvement of reliability and wind power generation based on wind turbine real-time condition assessment. Int. J. Electr. Power & Energy Syst. 113 (C), 344–354. doi:10.1016/j.ijepes.2019.05.027

CrossRef Full Text | Google Scholar